Computational and Experimental Insights into the Mechanism of Substrate Recognition and Feedback Inhibition of Protoporphyrinogen Oxidase

Abstract

Protoporphyrinogen IX oxidase (PPO; EC 1.3.3.4) is an essential enzyme catalyzing the last common step in the pathway leading to heme and chlorophyll biosynthesis. Great interest in PPO inhibitors arises from both its significance to agriculture and medicine. However, the discovery of PPO inhibitors with ultrahigh potency and selectivity is hampered due to lack of structural and mechanistic understanding about the substrate recognition, which remains a longstanding question central in porphyrin biology. To understand the mechanism, a novel binding model of protogen (protoporphyrinogen IX, the substrate) was developed through extensive computational simulations. Subsequently, amino acid residues that are critical for protogen binding identified by computational simulations were substituted by mutagenesis. Kinetic analyses of these mutants indicated that these residues were critical for protogen binding. In addition, the calculated free energies of protogen binding with these mutants correlated well with the experimental data, indicating the reasonability of the binding model. On the basis of this novel model, the fundamental mechanism of substrate recognition was investigated by performing potential of mean force (PMF) calculations, which provided an atomic level description of conformational changes and pathway intermediates. The free energy profile revealed a feedback inhibition mechanism of proto (protoporphyrin IX, the product), which was also in agreement with experimental evidence. The novel mechanistic insights obtained from this study present a new starting point for future rational design of more efficient PPO inhibitors based on the product-bound PPO structure.

Introduction

To understand the function of an enzyme, the binding of the substrate (S) and the structure of the enzyme–substrate (ES) complex are central issues in determining the catalytic mechanism. The structural information obtained from the ES complex at the atomic level is required for understanding the substrate recognition mechanism of the enzyme. However, due to the enzyme’s catalytic transformation of substrate into product, it is often difficult to grow an intact crystal and to determine the crystal structure of the ES complex. New approaches to examine the binding model of the substrate and the enzymatic mechanism are topics of intense investigation in current enzymology.

Tetrapyrroles, such as chlorophyll, heme, bilins, and porphyrins, play pivotal roles in electron transfer-dependent energy generating processes including photosynthesis and respiration of all biological systems [1]. One of the steps of tetrapyrrole biosynthesis rely on protoporphyrinogen IX oxidase (PPO; EC 1.3.3.4), which catalyzes the six-electron oxidation of protogen (protoporphyrinogen IX, the substrate) to proto (protoporphyrin IX, the product) in both eukaryotic and prokaryotic organisms ( Figure 1 ) [2], [3]. PPO plays a significant and pivotal role in the life cycle by the oxidation of protogen which is a prerequisite step for the synthesis of heme and chlorophylls and thus the molecular mechanism associated with the substrate recognition by PPO has attracted great interest in recent decades [4], [5], [6], [7], [8].

Figure 1. Protoporphyrinogen oxidase (PPO) catalyzes the oxidation reaction of protoporphyrinogen IX (protogen) (left) with molecular oxygen to produce protoporphyrin IX (proto) (right).

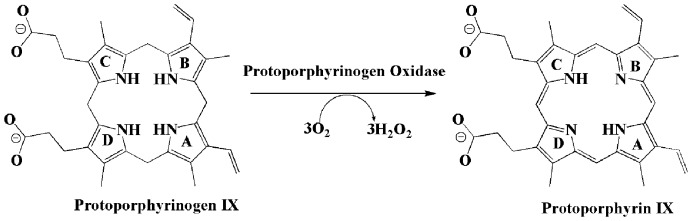
In this reaction, the molecular oxygen is reduced to hydrogen peroxide, and six hydrogen atoms are eliminated.

The inhibition or functional loss of PPO results in the accumulation of protogen, which can be spontaneously oxidized to proto by oxygen. As a photosensitizer, in the presence of light, proto can further induce the production of singlet oxygen, causing lipid peroxidation and cell death [9]. Thus, PPO is considered an important target for herbicide discovery [10], [11] and may be a focus for bactericide and fungicide design [5], [12]. Inhibitors of PPO may also find application in cancer treatment through photodynamic therapy (PDT) [13], [14], [15]. The discovery of PPO inhibitors with high potency and selectivity has been hampered by the lack of structural and mechanistic understanding of substrate recognition. Due to its spontaneous oxidation and the instability of protogen, determination of the crystal structure of the substrate-bound PPO has not been achieved.

Due to the extremely high time resolution and atomic level representation, computational simulation has been increasingly used in understanding the detailed mechanism of substrate recognition in proteins [16], [17]. Hence, in the present study, extensive computational simulations and experimental techniques were integrated to discover the binding model and detailed recognition mechanism of the substrate by PPO. We used conformational analysis based molecular docking, molecular dynamics (MD) simulation, molecular mechanic/Poisson-Boltzmann surface area (MM/PBSA) calculations, umbrella sampling MD simulations, and potential of mean force (PMF) calculations. We also introduced mutations into PPO by site-directed mutagenesis and then conducted enzyme kinetics studies. A proposed novel mechanism for substrate recognition and product feedback inhibition by PPO based on computational simulation was in agreement with site-directed mutagenesis and enzyme kinetic study. This is the first report of the substrate recognition and feedback inhibition mechanism of PPO that combines theoretical and experimental methods. The demonstrated structural and energetic profiles provide a new starting point for future structure- and product-based design of highly potent PPO inhibitors for the development of agrochemicals or PDT cancer therapy.

Results and Discussion

Identification of the Substrate Binding Model

Molecular docking studies were performed to simulate the binding of protogen to PPO. However, conventional docking methods do not take into account the flexibility of macrocyclic compounds. So, an extensive conformational analysis of protogen was performed to obtain a total of 18 conformers (M1–M18, see details in Figure S1), all of which were used as starting structures for docking.

According to the binding affinities determined by Autodock4, conformers M2 (−11.03 kcal/mol), M14 (−10.99 kcal/mol), M15 (−11.88 kcal/mol), M16 (−12.48 kcal/mol), M17 (−11.20 kcal/mol), and M18 (−11.18 kcal/mol) should be the most feasible structures. To avoid the limitations of the Autodock score, MM/PBSA calculations were performed, identifying conformers M6 (−26.32 kcal/mol), M7 (−35.62 kcal/mol), M9 (−29.98 kcal/mol), M10 (−42.73 kcal/mol), M14 (−44.47 kcal/mol), and M15 (−35.66 kcal/mol) as the more favorable ligand conformations. The ligand must always undergo deformation from the solution conformation to the binding conformation. Additionally, the conformational energy penalty for the bioactive conformations should be less than 6 kcal/mol [18]. We therefore calculated the conformational energy penalty of each conformer by using Gaussian 03 at 6-31+G* basis set with the B3LYP method plus PCM solvation model. In addition, at the active site, the methylene bridge atom in the meso position of protogen and the N₅ atom of the FAD (Table S2) should be close enough to each other to produce the correct reaction orientation. The potential binding models were ultimately identified through the overall evaluation of the docking score of Autodock, MM/PBSA calculations, reaction orientations, and conformational energy penalties (See details in Table S1 and Table S2). Additionally, to avoid the shortcomings of the Autodock program and the conformational analysis method, we tested other docking programs (i.e., Gold) with different starting structures and obtained very similar results (see details in Figure S2). Ultimately, conformers M14 and M15 were selected as potential binding models for further analysis. Particularly, M14 was similar with the binding model proposed by Koch et al. [19].

Since the docking algorithm did not fully account for the structural flexibility of the protein, we performed MD simulations for M14 and M15, using PPO from Nicotiana tabacum mitochondria (mtPPO). According to the analysis of RMSD and some key distances of the MD trajectories (Figure S3), the simulations reached equilibrium states. Further, the MD simulations of M14 and M15 were also repeated with different sets of parameters and force-fields to validate the convergence of the simulations (see details in Figure S4). The binding model associated with stronger hydrogen bonding networks was the most reasonable. Hence, the strengths of the hydrogen bonding networks of M14 and M15 were evaluated by performing HBE (hydrogen bond energy) calculation and hydrogen bond distance analysis (summarized in Table 1 ). For M14, the carbonyl oxygen atoms of the propionate group formed up to two hydrogen bonds with R98 (N–H…O) and one hydrogen bond with S235 (O–H…O) in tobacco mtPPO. The total HBE is −12.0 kcal/mol. For M15, however, the carbonyl oxygen atoms of the protogen propionate group formed up to three hydrogen bonds with R98 (N–H…O) and the pyrrole cycle formed two hydrogen bonds with G175 (N–H…O) in tobacco mtPPO. The total HBE is −17.4 kcal/mol. Further, the binding free energy of M15 was much lower than that of M14 based on a large amount of MD sampling (Table S2). Although the conformational energy penalty of M15 was slightly higher than M14, the reaction orientation of M15 was more advantageous than that of M14 (Table S2). These computational results suggest that M15 should be a significantly more favorable binding conformation than M14 ( Table 1 ).

Table 1. Hydrogen bond networks of the M14 and M15 conformations in complex with tobacco mtPPO.

Bind Model	Acceptor	Donor	Mark	%a	Maxb	Min	Ave	HBEc	THBEd
M14	TEMe	S235	D1	99.8	3.1	1.5	1.8 (0.16)	−1.9 (0.24)	−12.0
	TEM	R98	D2	98.3	3.1	1.6	1.9 (0.19)	−6.2 (0.50)
	TEM	R98	D3	92.5	3.4	1.7	2.2 (0.22)	−3.9 (0.46)
M15	G175	TEM	D1	93.3	2.9	1.7	2.4 (0.16)	−2.0 (0.24)	−17.4
	G175	TEM	D2	82.8	3.4	1.9	2.5 (0.23)	−1.6 (0.23)
	TEM	R98	D3	99.7	2.8	1.6	1.9 (0.13)	−6.8 (0.40)
	TEM	R98	D3	91.1	3.2	1.7	2.3 (0.29)	−2.9 (0.46)
	TEM	R98	D3	84.7	3.7	1.6	2.2 (0.39)	−4.0 (0.58)

[a] Occupancy of hydrogen bonds (The occupancy >70% were listed).

[b] Hydrogen bond distance (Å).

[c] Hydrogen bond energy (kcal/mol), calculated according to equation: 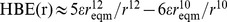, the parameters: r_eqm = 1.8 Å, ε = 8.4 kcal/mol. We calculated the HBE of every snapshot of the MD simulation and then took the average value, as in our previous studies [36], [46], [47], [48]. The values in the parentheses are the standard deviations.

[d] Total hydrogen bond energy (kcal/mol). The total HBE value is the average of the HBE values calculated by using the instantaneous distances in all of the snapshots.

[e] The substrate name in pdb file.

Based on the identified binding model (M15) of protogen in tobacco mtPPO, the surrounding amino acid residues that interacted with rings A, B, C, and D of protogen were further analyzed. Ring A of protogen interacted with A174 and was kept in position by π-π stacking interaction with F392 ( Figure 2A ). Ring B of protogen was inserted into a slot of T176 and made π-π stacking interaction with cofactor FAD. Ring C of protogen interacted with F172 and G175, while ring D interacted with residues F353 and L356. In addition, the propionate groups of both rings C and D could form hydrogen bonds with R98 in tobacco mtPPO.

Figure 2. The binding models of protogen in tobacco mtPPO and hPPO.

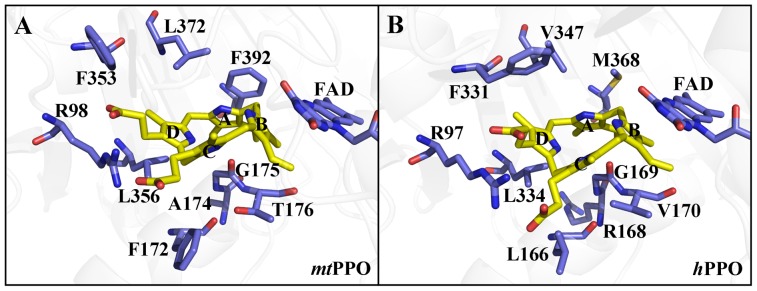
(A) Side view of protogen surrounded by R98, F172, A174, G175, T176, F353, L356, F392, and FAD in tobacco mtPPO. (B) Side view of protogen surrounded by R97, L166, R168, G169, V170, F331, L334, M368, and FAD in hPPO.

The computationally identified novel binding model was consistent with available experimental data obtained from site-directed mutagenesis studies on tobacco mtPPO [20]. According to the simulated binding model, conserved residues F392, L356, L372, and R98 are essential for protogen binding. The apparent K _m value of purified wild-type tobacco mtPPO for protogen was 1.17 µM. The site-directed mutagenesis studies on tobacco mtPPO revealed a range of decreased binding affinities of the mutants for protogen: F392H (inactive), F392E (K _m = 11.2 µM), L356N (K _m = 11.0 µM), L356V (K _m = 7.3 µM), L372N (K _m = 16.4 µM), L372V (K _m = 103 µM), R98K (K _m = 2.6 µM), R98E (K _m = 12.5 µM), and R98A (K _m = 8.3 µM). The binding free energy shifts of protogen with mutants was also estimated ( Table 2 ). Plots of the experimental vs. the calculated values showed a good linear relationship with a correlation coefficient of r ² = 0.95 further confirming the reliability of the substrate binding model in tobacco mtPPO (The binding models of each mutant are shown in Figure S5).

Table 2. Calculated Binding Free Energy Shifts (kcal/mol) in Comparison with Those Derived from Experimental Data.

mtPPOa	ΔΔHb	−TΔΔS	ΔΔG		hPPO	ΔΔHb	−TΔΔS	ΔΔG
			calc.	expt.				calc.c	expt.d
F392E	5.82	−1.34	4.48	1.34	M368Q	3.62	0.49	4.11	1.13
L356N	3.40	0.65	4.05	1.33	M368K	1.98	1.04	3.02	0.59
L356V	4.32	−0.48	3.84	1.09	R168S	3.66	0.01	3.67	1.01
L372N	5.97	−1.38	4.59	1.57	G169A	1.00	−0.80	0.20	0.02
L372V	6.64	0.62	7.26	2.66	V170T	−0.61	1.09	0.48	0.21
R98K	3.76	−2.45	1.31	0.47	L166N	1.15	1.04	2.19	0.54
R98E	5.26	−0.89	4.37	1.41	R97G	4.96	−0.22	4.74	1.33
R98A	6.83	−3.56	3.28	1.16	F331T	0.13	0.41	0.54	0.22
					F331A	1.57	1.06	2.63	0.69
					L334V	1.87	1.25	3.12	0.73

The data were determined using both tobacco mtPPO and hPPO wild type proteins and the indicated mutants.

[a] The kinetic data of tobacco PPO mutants were reported in ref. 20.

[b] ΔΔ = Δ (MT) -Δ (WT).

[c] ΔΔG_calt. were calculated by Computational Mutation Scanning (CMS) protocol based on the WT binding model (see ref. 42).

[d] ΔΔG_expt. (kcal/mol) = −RT ln(K_mMut/K_mWT), where R is the ideal gas constant, and T is the temperature in K.

Theoretically, PPO from different species with similar folding and substrate binding envelopes should have similar substrate binding models. Previously, we have determined the crystal structure of human PPO (hPPO) at a resolution of 1.9 Å and found that it has very similar three dimensional structure and conserved substrate binding envelope as compared to that of tobacco mtPPO [21], [22]. Hence, we constructed the three dimensional structure of protogen-bound hPPO by superimposing it with the tobacco mtPPO-substrate complex and we performed subsequent energy minimization ( Figure 2B ). According to the sequence alignment and structure superimposition between tobacco mtPPO and hPPO, residues R97, L166, R168, G169, V170, F331, L334, and M368 of hPPO correspond to the respective residues R98, F172, A174, G175, T176, F353, L356, and F392 of tobacco mtPPO. The binding model revealed that for hPPO, ring A of protogen interacted with R168 and was kept in position by hydrophobic interaction with M368. Ring B of protogen is sandwiched between hPPO residue V170 and FAD. Residues involved in the interaction with ring C of protogen were L166 and G169 and ring D was sandwiched between hPPO residues F331 and L334. The propionate groups of rings C and D could form hydrogen bonds with R97.

In order to further validate the substrate binding model of PPO, site-directed mutagenesis and enzyme kinetic studies were performed on hPPO. We constructed an appropriate set of mutant hPPO genes, isolated the respective mutant proteins and determined their kinetic parameters via continuous fluorometric method and compared the results with wild-type hPPO. We introduced both conservative and non-conservative amino acid exchanges for residues of interest in order to evaluate their chemical contribution to the binding of substrate and catalysis. The apparent K _m value of purified wild-type hPPO for protogen was 2.08 µM with a k _cat value of 2.97 min⁻¹ ( Table 3 ). The protogen binding model was evaluated by a series of mutagenesis on hPPO ( Table 3 ). Substitution of Ser for R168 resulted in a 5.4-fold loss of binding for protogen. When M368 was mutated to glutamine, the K _m for protogen declined by 6.7-fold, while introduction of lysine at the same site decreased protogen binding by 2.7-fold, compared to wild type hPPO. To mimic the corresponding residue in tobacco mtPPO, V170 was mutated to threonine. V170T was reasonably active, with an acceptable catalytic efficiency and only a slight decrease of protogen binding activity. For the mutants L166N and G169A, protogen binding was reduced by a modest 2.5-fold or was virtually unaffected. However, for these two mutants the reduced catalytic efficiency (K _m/k _cat = 0.35 µΜ⁻¹ • min⁻¹ and K _m/k _cat = 0.17 µΜ⁻¹ • min⁻¹ respectively), demonstrating their important roles for hPPO catalysis. Consistently, the mutants R97G, F331T, F331A, and L334V showed decreased binding capacity (K _m = 19.64 µM, 3.02 µM, 6.60 µM, and 7.08 µM respectively) compared with the wild-type. The binding free energy shifts of protogen with mutants were also estimated ( Table 2 ). Plots of the experimental values vs. the calculated values were linear, with a correlation coefficient of r ² = 0.95 further quantitatively confirming the reliability of the substrate binding model in hPPO (The binding models of each mutant are shown in Figure S6).

Table 3. Kinetic parameters of wild-type and mutant hPPO.

Protein mutants	K m (µΜ)	k cat (min−1)	k cat/K m(µΜ−1 • min−1)
Wild-type (WT)	2.08±0.11	2.97±0.15	1.43
Substrate ring A
R168S	11.33±0.93	3.32±0.22	0.29
M368Q	13.89±1.29	9.29±0.75	0.67
M368K	5.63±0.26	14.17±1.10	2.52
Substrate ring B
V170T	2.97±0.31	7.70±0.66	2.59
Substrate ring C
L166N	5.13±0.71	1.82±0.13	0.35
G169A	2.16±0.17	0.37±0.04	0.17
Substrate ring D
R97G	19.64±2.14	76.37±9.15	3.89
F331T	3.02±0.28	9.08±0.76	3.01
F331A	6.60±0.72	4.36±0.39	0.66
L334V	7.08±0.54	51.19±6.21	7.23

The determination of kinetic constants was performed as described in the Experimental section. The Michaelis–Menten constant K _m, the k _cat and the k _cat/K _m values for hPPO were determined from substrate velocity plots by measuring the constant velocity formation of proto from protogen.

By comprehensively integrating HBE, binding free energy, conformational energy penalty, reaction orientation and coordinates, and with the aid of mutagenesis studies, the model for the binding of protogen to PPO was identified ( Figure 2 ). Consequently, the binding model of the product of the reaction, proto, can also be identified (Figure S7).

Binding Pathway and Free Energy Profile

Conventional MD does not clearly simulate the processes of binding and dissociation of substrate and product at the atomic level and therefore is not useful for investigating the protogen/proto recognition by PPO. Therefore, we undertook potential of mean force (PMF) simulations based on the states of protogen- and proto-bound PPOs. During the PMF simulations, the reaction coordinate (RC) is defined as the distance from the mass center of the non-hydrogen atoms of protogen/proto to the mass center of the non-hydrogen atoms of PPO, which was determined based on the structural features. To better understand the energy barriers of the transition, a free energy profile of the entire process was needed. So, based on the data collected from PMF simulations, the corresponding free energy profiles of the egress processes of protogen and proto were determined ( Figure 3 ).

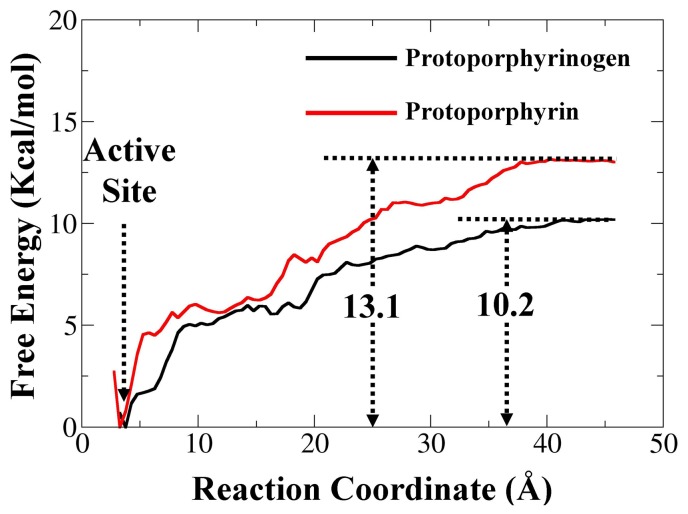
Figure 3. Free energy profiles determined for PPO binding with protogen (black curve) and proto (red curve).

The reaction coordinate was defined as the distance between the methylene bridge atom in the meso position of protogen and the N5 atom of the FAD. The binding free energy corresponding to protogen and proto of the transformation process are also labeled (units of kcal/mol).

Along the chosen RC, no energy barrier was identified from the free energy profile of the two egress processes. For the substrate protogen, the minimum of the free energy curve was stabilized with RC = ∼3.2 Å, corresponding to the event when the carboxyl oxygen atoms of protogen formed three hydrogen bonds with R98 in tobacco mtPPO, and when the nitrogen atoms of the pyrrole formed two hydrogen bonds with G175 ( Figure 4A ). With the increase of the free energy profile, the protogen began to detach from the binding site with the breakup of the initial interactions. Two plateaus in the free energy profile were observed from ∼5.0 Å to 6.5 Å and ∼9.0 to 11.0 Å of the RC, reflecting the counterbalance of interactions that switched with a counterclockwise rotation around the binding pocket. For example, the carboxyl oxygen atoms of the side chain formed new contacts with S474, while the nitrogen atoms of the pyrrole formed new contacts with S235, when RC = ∼9.0 Å ( Figure 4B ). After slowly increasing from ∼11.0 to 14.5 Å of RC, a fluctuation of the free energy profile was observed from ∼14.5 to 20.0 Å of RC and several energy wells occurred, corresponding to the local binding event on the entrance of the pocket. For example, the carboxyl oxygen atoms of protogen formed new contacts with T70, S72, and R233 with RC = ∼19.0 Å ( Figure 4C ). Finally, a slow increase in the curve occurred from ∼20.0 to 40.0 Å of RC as the protogen pulled away ( Figure 4D ) and converged at 10.2 kcal/mol ( Figure 3 ).

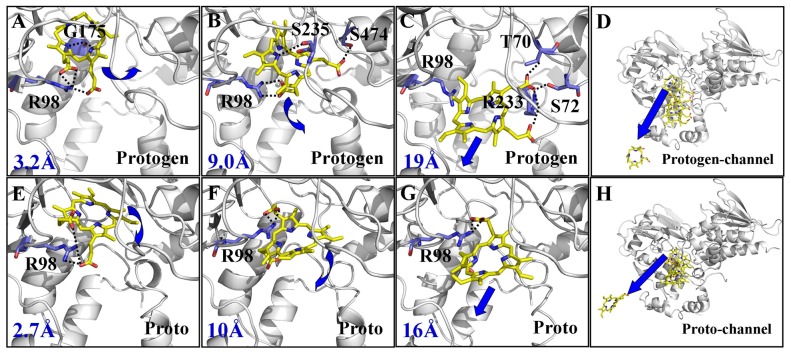
Figure 4. The intermediate states of protogen/proto in the egress process derived from PMF simulations.

A, Binding structure of protogen in the active site derived from the snapshot at the beginning of PMF trajectory. The carboxyl oxygen atoms of protogen can form three hydrogen bonds with the amino NH hydrogen atoms of R98 and the nitrogen atoms of the pyrrole can form two hydrogen bonds with G175. Tobacco mtPPO is displayed as white ribbon. Protogen and its recognition residues are displayed in stick style. Residues of tobacco mtPPO are colored by blue and protogen is colored in yellow. Dashed lines represent the hydrogen bond distances. B, View of the counterclockwise rotation of protogen in the egress process with RC = ∼9.0 Å. With the counterbalance of interactions switched, one of the carboxyl oxygen atoms of protogen can form new contacts with S474 and one of the nitrogen atoms of the pyrrole can hydrogen bond with S235. C, The complex structure of the transition state with RC = ∼19.0 Å. Protogen passes through the opening with the carboxyl oxygen atoms interacting with T70, S72, and R233. D, Side view of protogen passing through the new channel. E, Binding structure of proto in the active site derived from the snapshot at the beginning of PMF trajectory. The carboxyl oxygen atoms of proto can form three hydrogen bonds with the amino NH hydrogen atoms of R98. F, View of the clockwise rotation of proto in the egress process, when RC = ∼10.0 Å with maintenance of the hydrogen bonding between the carboxyl oxygen atoms of proto and the amino NH hydrogen atoms of R98, which was favorable for proto passing through the channel. G, The complex structure of the transition state with RC = ∼16.0 Å. Proto passing through the opening with the carboxyl oxygen atoms maintaining interaction with R98. H. Side view of proto passing through the new channel.

In contrast, the outcome for the simulated structure of the product proto was remarkably different. No plateau in the free energy profile was observed from the active site to the outside and a clockwise rotation of proto was observed. The minimum of the free energy curve stabilized at RC = ∼2.7 Å, corresponding to the event when the carboxyl oxygen atoms of proto formed three hydrogen bonds with the amino nitrogen atoms of R98 ( Figure 4E ). The curve increased steeply from ∼3.0 to 5.0 Å followed by a fluctuating rise from ∼5.0 to 10.0 Å of RC with a small energy barrier appearing at RC = ∼10.0 Å, which corresponded to the event of the breaking of the initial interactions. One of the hydrogen bonds between the carbonyl oxygen atom of the propionate group and the amino nitrogen atom of R98 was destroyed with the clockwise rotation of proto around the entrance of the binding pocket ( Figure 4F ). Then the free energy profile was slowly increased from ∼10.0 to 16.0 Å of the RC, which could also be reflected by maintaining one of the hydrogen bonds between the carbonyl oxygen atom of the propionate group and the amino nitrogen atom of R98 ( Figure 4G ). After that, the curve slowly increased as the proto left the active site ( Figure 4H ) and finally converged at 13.1 kcal/mol ( Figure 3 ). According to the PMF simulated transient intermediates of protogen and proto, the same residue, R98, formed hydrogen bond interactions throughout the recognition process. The participation of R98 was more important for proto than for protogen in the recognition process. From the PMF calculation, we deduced that the protogen binding process should be very fast, but the proto dissociation process should be slower. To explore the possible role of R98 during the recognition mechanism, the structures of WT and R98A PPO were compared (Figure S8). R98 was located in the pocket between the active site and the pathway. Hence, the replacement of R98 with the non-polar amino acid alanine could enlarge the mouth of the pocket and improve the turnover of protogen/proto in the absence of the hydrogen bond, which was especially more favorable to establish an orientation for the proto egress and thus improve the enzyme activity. A previous study established that the R98A mutant had an ∼8-fold larger Michaelis-Menten constant (K _m = 1.17 µM in WT and = 8.30 µM in R98A) and a ∼60-fold (k _cat = 6 s⁻¹ in WT and = 365 s⁻¹ in R98A) improved enzyme activity [20]. This result further supported the recognition mechanism discovered here and suggested that R98 was more important for proto than protogen in the recognition process.

To further examine the accuracy of the values of binding free energies (ΔG_bind) as calculated by PMF, the corresponding experimental values of ΔG_bind for protogen were also estimated from the available experimental data (i.e., the experimental values of K _m) using the well-known rapid equilibration assumption, i.e., K _m ≈ K _d (dissociation constant) [23]. Tobacco mtPPO exhibited a value of K _m = 1.17 µM for protogen [20]. Based on this assumption, we may calculate that ΔG _bind,expt. = −RTlnK _d ≈ -RTlnK _m = −8.1 kcal/mol for PPO binding with protogen. The finally estimated ΔG_bind,calt. = −10.2 kcal/mol of protogen compares well with ΔG _bind,expt. = −8.1 kcal/mol, although the PMF calculation overestimated the binding affinity by ∼2 kcal/mol, which was likely due to the finite size of the simulation box and the inherent limits of the empirical force field.

Enzyme Kinetics

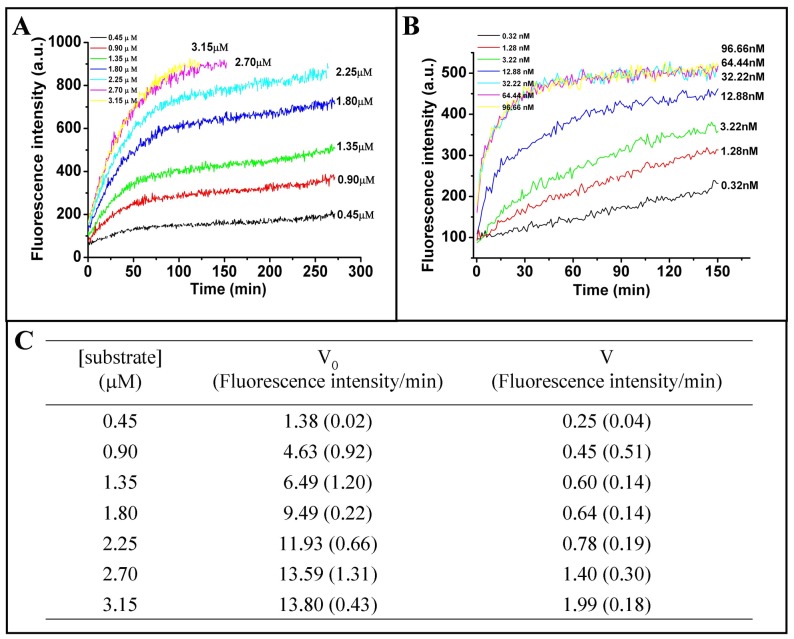
From PMF-derived values for ΔG_bind (PPO-protogen) and ΔG_bind (PPO-proto) and the MM/PBSA results of protogen and proto (Table S2), proto should have a stronger binding affinity than protogen and should regulate PPO by feedback-inhibition. Kinetic studies of the enzyme-catalytic oxidation activity were determined via a continuous fluorescence method and were examined in conjunction with the data from the auto-oxidation of protogen in order to examine the occurrence of feedback inhibition. The initial phase of product formation curves was linear, but decreased with time, approaching straight lines (steady states) ( Figure 5A ). However, the product formation was not complete (see the velocities in Figure 5C ). This kind of kinetic time-course demonstrated that the enzymatic activity decreased gradually along with the product formation and finally the enzyme became inhibited. The curvilinear functions displayed by the curves were consistent with the presence of a slow, tight-binding inhibitor [24]. This type of kinetic behavior is usually due to a process characterized by the rapid formation of reactant-enzyme complex, followed by a slower dissociation of the product-enzyme complex [25]. The steady states of the product formation curves exhibited a trend of slow rise after the inflection point ( Figure 5A ), which showed that the enzyme was slowly becoming inhibited by the accumulation of product.

Figure 5. A comparison of the conversion of protoporphyrinogen IX to protoporphyrin IX as monitored by fluorescence assay as catalyzed by PPO.

A, The enzyme kinetic time-courses with increasing protogen concentrations. The auto-oxidation time-course was excluded from the curve. Reactions were initiated by the addition of enzyme. Data were obtained in the presence of the indicated concentrations of protogen. B, Kinetics of the enzymatic catalysis of a fixed amount of protogen (0.34 µM) with different concentrations of hPPO. Data were obtained in the presence of the indicated concentrations of hPPO enzyme. C. The initial velocity (V₀) and velocity after inflexion (V) (steady state) of each curve in Figure 5A . The values in the parentheses are the standard deviations.

To further verify feedback inhibition, different concentrations of PPO enzyme were assayed to catalyze a fixed amount of protogen. The product inhibition phenomenon was obvious at low concentrations of PPO ( Figure 5B ), but as the concentration of PPO increased, the reaction finished within ∼30 min and no product inhibition was observed. Therefore, product inhibition of PPO only existed at limited concentration of enzyme and a certain amount of product accumulation, which is a hallmark of feedback inhibition mechanism [26], [27]. In addition, the occurrence of feedback inhibition in agreement with, in turn, that the computation-derived relative order, i.e., ΔG _bind (PPO-protogen)>ΔG _bind (PPO-proto), is reliable.

Conclusion

In summary, a novel binding model for protogen with PPO has been identified by combining extensive computational simulations and mutagenesis studies. Based on this newly identified binding model, the enzyme-substrate (ES), enzyme-product (EP) recognition pathway, the corresponding free energy profiles, and the feedback inhibition mechanism have been identified. The simulated PMF free energy profile was barrierless for protogen binding, which indicates that the protogen binding process should be very fast. But the free energy profiles showed that the dissociation process for proto should be slower than protogen, indicating that PPO activity is modulated by a feedback inhibition with respect to proto. The kinetic time courses also displayed a burst of product formation followed by a linear steady-state rate when reactions were initiated by the addition of enzyme, which is a hallmark of feedback inhibition. We believed that the established structural and energetic insights into the entire ES binding and EP dissociation process provide a valuable basis for future structure- and product-based design of highly potent PPO inhibitors for application in the development of agrochemicals or PDT cancer therapy.

Methods

System Setup and Molecular Docking

The X-ray crystal structure of Nicotiana tabacum PPO (mtPPO) used for the study was downloaded from RCSB [19]. The initial structure was revised first by means of adding lost residues and hydrogen atoms, checking bonds and bumps, then energy minimized for 2,000 steps of steepest descent calculations and 2,000 steps of conjugated gradient calculations by using SYBYL 7.0 (Tripos Inc., USA). Four kinds of the macrocycle conformations of protogen were constructed by using SYBYL 7.0 (Figure S1). The molecular geometries of the four conformations were optimized by performing ab initio electronic structure calculation with Gaussian03 program at the HF/6-31+G* level [28]. The optimized geometries were used to construct the entire structures of protogen and the final structures of different conformations were optimized with the macrocycle fixed by using conjugated gradient in SYBYL 7.0. The different conformations were used as the starting structures for docking studies.

Docking calculations were performed on these conformations with AutoDock4.0 [29]. The protein and ligand structures were prepared with AutoDock Tools [30]. The atomic Gasteiger-Huckel charges were assigned to the ligand and receptor. A total of 256 runs were launched. Most of the parameters for the docking calculation were set to the default values recommended by the software. Each docked structure was scored by the built-in scoring function and was clustered by 0.8 Å of RMSD criterions. For each binding model, molecular mechanics/Poisson-Boltzmann surface area (MM/PBSA) was performed (see details in Table S1). Before the MM/PBSA calculation, the complex structure was further refined with the steepest descent algorithm first and then the conjugated gradient algorithm by using the AMBER9 package [31]. During the energy minimization process, the receptor was first fixed and only the ligand was kept free; then the ligand and residue sidechains were kept free; finally all atoms of the system were kept free and refined to a convergence of 0.01 kcal/(mol·Å). To avoid the drawbacks of the Autodock program and the conformational analysis method, we also tested other docking programs and methods. See Supporting Information (Figure S2) for detailed results.

Molecular Dynamics Simulation and Free Energy Calculation

Based on the analysis of docking results, two binding models were selected for MD simulation. Prior to that, with the Gaussian-optimized geometries, the electrostatic potential and partial atomic charges were determined by performing the electrostatic potential (ESP) fitting according to the Merz–Singh–Kollman scheme [32], [33]. The RESP charges of the ligand was produced by using the standard RESP protocol [34], [35] implemented in the Antechamber module of the AMBER9 program [31]. The system was solvated in an octahedral box of TIP3P water with the crystallographic water molecules kept. The edge of the box was at least 10 Å from the solute. Appropriate sodium counterions were added to the system to preserve neutrality. The solvated system had a total of about 58,496 atoms, with about 7,381 of them belonging to the solute. Before the MD simulation, some energy minimization steps were applied to the system. First, the solute was kept fixed with a constraint of 500 kcal mol⁻¹ Å⁻², waters and counterions were minimized; the backbone atoms of the protein were then fixed with the ligand, sidechains, and other atoms free to move; finally, the entire system was fully minimized without any constraint. In each step, energy minimization was first performed by using the steepest descent algorithm for 2,000 steps and then the conjugated gradient algorithm for another 3,000 steps.

The MD simulation was performed under periodic boundary conditions by using the Sander module of the AMBER9 program, as we have done for the same protein before [36]. First, the system was fixed to make the heating only for waters and counterions for 10 ps to make sure the solute was fully solvated; then, the whole system was gradually heated from 10 to 298 K by weak-coupling method [37] and equilibrated for 100 ps with the protein backbone fixed; lastly, the system was switched to a constant pressure equilibration to 3 ns. During the MD simulation, the particle mesh Ewald (PME) algorithm [38], [39] was used to deal with long-range electrostatic interactions with a cutoff distance of 10 Å, which was also used for the van der Waals (vdW) energy terms. All of the angles and bonds involving hydrogen atoms were constrained by using the SHAKE algorithm [40]. The time step used for the MD simulations was 2.0 fs and the coordinates were collected every 1 ps.

Because the flexibility of the side chain and the ligand-protein interaction was of concern, a shorter simulation time (3 ns) was adopted. The MD simulations were performed with all the hydrogen bond distances constrained at the beginning, which were then slowly relaxed. As shown by the small fluctuations of the key distances along the simulation time in Figure S3, the MD simulations reached equilibrium after ∼1 ns of simulations. The stable MD trajectory was used to perform the binding free energy (ΔG _bind) calculation by using MM/PBSA method [41]. A total of 1,000 snapshots were taken from the last 1 ns trajectory with an interval of 1 ps to analyze the binding energy and at the same time, the counterions and water molecules (waters related to the crucial hydrogen bond were not included) were stripped. Our MM/PBSA calculation was performed in the same way as we reported elsewhere [42]. In order to evaluate the convergence of the MD simulation, the MM/PBSA calculation with snapshots from different intervals of the last 1 ns trajectory were compared (see details in Table S2). Further, the MD simulations of M14 and M15 were also repeated with different sets of parameters and force-field (see details in Figure S4). The final binding free energy was determined as the average of all the snapshots and the standard errors were also calculated with the same method reported before [42]. Finally, hydrogen bond energies (HBE) were also calculated by using a previously published method [43].

Potential of Mean Force (PMF) Calculations

In order to explore the free energy profile of the PPO-protogen/proto binding and dissociation process, PMF calculations were performed by using umbrella-sampling MD simulations [44]. In this calculation the reaction coordinate was divided into 120 windows separated by 0.1, 0.2, and 0.5 Å, each of which is sampled separately. The initial complex structure was adopted directly from our previous MD simulations. The biasing force constant applied in different windows of umbrella-sampling ranged from 4.0 to 60.0 kcal/mol•Å². The selected structure for each window was first equilibrated for 50 ps and then kept running for 1,000 ps. In order to examine the convergence of the PMF results, additional PMF calculations with different intervals were performed (provided as Figure S9). The three curves (associated with the MD simulations during 0.2∼0.6, 0.2∼0.8, and 0.2∼1.0 ns) depicted in Figure S9 are indistinguishable or identical, which suggests 1.0 ns is sufficient for each window of the PMF simulations. Finally, the data collected from separate simulation windows were combined along the reaction coordinate and a 120 ns trajectory was obtained for each system, which were then used to calculate the PMF along the whole recognition pathway with the weighed histogram analysis method (WHAM) [45].

Kinetic Assays for PPO and its Mutants

The recombinant plasmid (pHPPO-X) was a generous gift from Dr. Harry A. Dailey (University of Georgia, Athens, GA, USA). hPPO mutations were generated from the recombinant plasmid (pHPPO-X) using the DpnI-mediated site-directed mutagenesis kit (Biocrest Manufacturing LP, Cedar Creek, TX, USA), and mutations were confirmed by sequence analysis. Expression and purification methods of hPPO were the same as used with our previous publication [21].

hPPO activity was assayed by measuring the velocity of the formation of proto from protogen on a 96-well plate using the continuous fluorometric method [21]. The product had a maximum excitation wavelength of 410 nm and a maximum emission wavelength of 630 nm. The total volume of the reaction mixture was 200 µL and consisted of 0.1 M potassium phosphate buffer (pH 7.4), 5 mM DTT, 1 mM EDTA, 0.2 M imidazole, and 0.03% Tween 80 (v/v). The reaction was initiated by the addition of substrate, and the autoxidation rate was subtracted. The kinetic parameters, including the Michaelis-Menten constant (K _m), the maximal velocity (V_max), and the catalytic constant (k _cat), were determined by a Lineweaver-Burk plot.

Kinetic Assays for Feedback Inhibition

Two experiments were performed to verify the occurrence of feedback inhibition. Experiment 1: The concentration of hPPO enzyme was 3.22 nM. The reaction was initiated by the addition of various concentrations of the substrate (0.45, 0.90, 1.35, 1.80, 2.25, 2.70, and 3.15 µM). The auto-oxidation rate of protogen was measured in the absence of enzyme and this rate was excluded from the final enzyme kinetic time-course. Experiment 2: Different concentrations of hPPO enzyme (0.32, 1.28, 3.22, 12.88, 32.22, 64.44, and 96.66 nM) were assayed to catalyze a fixed amount of protogen (0.34 µM).

Supporting Information

Figure S1

The scheme of the spacial conformation of the macrocycle of the substrate.

(TIF)

Figure S2

A. Comparison between the obtained binding modes through Autodock (M15) and Gold program (NO. 785). B. Comparison between the obtained binding modes through Autodock (M14) and Gold program (NO. 644). C. Conformational distribution ratio of the 1000 conformers.

(TIF)

Figure S3

View of the binding modes of the substrate in the PPO active site, plots of key distance changes versus simulation time, and substrate-residues interaction spectrums of M14 and M15.

(TIF)

Figure S4

Plots of RMSD and key distance changes versus simulation time in the repeated MD simulations of M14 and M15.

(TIF)

Figure S5

The models of protogen binding with different mtPPO mutants.

(TIF)

Figure S6

The models of protogen binding with different hPPO mutants.

(TIF)

Figure S7

View of the binding modes of proto in the PPO active site.

(TIF)

Figure S8

The structural comparison between WT and R98A.

(TIF)

Figure S9

PMF-simulated free energy profiles for PPO binding with protogen (A) and proto (B).

(TIF)

Table S1

Docking Study Results of Different Conformers.

(DOC)

Table S2

Energetic results of MM-PBSA calculation based on MD sampling and the corresponding convergence analysis.

(DOC)

Funding Statement

This work was supported in part by the National Basic Research Program of China (No. 2010CB126103), the NSFC (No. 20902034, and 20925206), and the National Key Technologies R&D Program (2011BAE06B05). The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.