A direct thin-film path towards low-cost large-area III-V photovoltaics

Abstract

III-V photovoltaics (PVs) have demonstrated the highest power conversion efficiencies for both single- and multi-junction cells. However, expensive epitaxial growth substrates, low precursor utilization rates, long growth times, and large equipment investments restrict applications to concentrated and space photovoltaics (PVs). Here, we demonstrate the first vapor-liquid-solid (VLS) growth of high-quality III-V thin-films on metal foils as a promising platform for large-area terrestrial PVs overcoming the above obstacles. We demonstrate 1–3 μm thick InP thin-films on Mo foils with ultra-large grain size up to 100 μm, which is ~100 times larger than those obtained by conventional growth processes. The films exhibit electron mobilities as high as 500 cm²/V-s and minority carrier lifetimes as long as 2.5 ns. Furthermore, under 1-sun equivalent illumination, photoluminescence efficiency measurements indicate that an open circuit voltage of up to 930 mV can be achieved, only 40 mV lower than measured on a single crystal reference wafer.

The growth of semiconductor nanowires (NWs)¹,²,³,⁴,⁵ via the VLS growth mode and the epitaxial layer transfer⁶,⁷ of semiconductors has proven to be very versatile, yielding a wide variety of materials on a multitude of substrates with excellent optoelectronic properties⁴,⁵,⁸. VLS-grown NWs exhibit circular or faceted cross-sections⁹, depending on the surface energy constraints of the nucleation seed on the substrate. Shape- and geometry-controlled¹⁰ nanowire growth using tubular templates has also been reported. Here, by utilizing a planar reaction template that (i) prevents dewetting of the growth seed from the substrate, and (ii) is permeable to the vapor phase, the VLS growth technique is extended to thin film geometries for the first time. InP is chosen as a prototypical model system to demonstrate the TF-VLS growth process as it not only has a near-optimal band gap for a single junction PV device¹¹, but is reported to have a low unpassivated surface recombination velocity⁸,¹²,¹³,¹⁴, making it a promising material system for polycrystalline films-based optoelectronics. We show that large grain (up to 100 μm), continuous, polycrystalline InP thin films are readily grown on Mo foils within a large growth parameter window, with optical and electronic properties approaching those of similarly-doped, single-crystalline InP.

Results

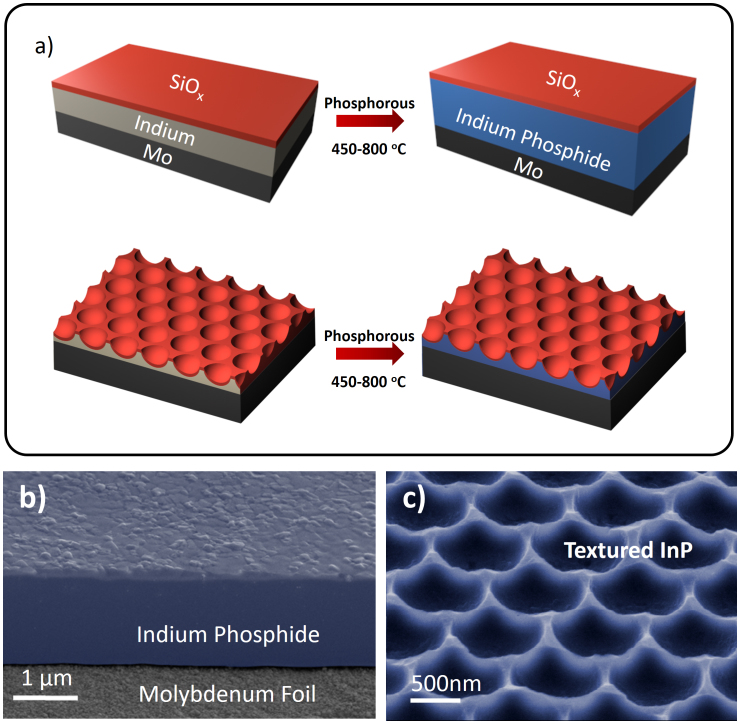
The TF-VLS process is schematically illustrated in Fig. 1a. Indium films (tunable thickness of 0.2–2 μm) are deposited on electropolished molybdenum foils (thickness of ~25 μm) by either electron-beam (e-beam) evaporation or electroplating, followed by e-beam evaporation of a 50 nm silicon oxide (SiO_x) cap. The Mo/In/SiO_x stack is then heated in hydrogen to a growth temperature of 450–800°C, which is above the melting point of indium (~157°C). The thin SiO_x capping layer enables the liquid indium to maintain a planar geometry by preventing it from dewetting. After temperature stabilization, phosphorous vapor is introduced into the chamber, either by PH₃ gas or a heated red phosphorous solid source. The diffusion of phosphorous vapor through the capping layer and dissolution in the liquid indium results in the precipitation of solid InP crystals as predicted by the indium-phosphorus phase diagram. This process closely resembles the self-catalyzed VLS growth of nanowires², but instead produces continuous polycrystalline thin films. Figure 1b shows a tilt-view cross-sectional scanning electron microscope (SEM) image of a TF-VLS InP film on Mo foil. This image is representative of the film across the growth substrate. The as-grown InP film thickness is roughly double the original indium thickness (Fig. S1), matching the expected volume expansion from In to InP and implying near unit utilization of the indium film.

Figure 1. Growth technique and resulting InP films.

(a), Schematic view of the thin-film VLS growth technique for planar and textured InP films. (b), 30° tilt view false-color SEM of planar InP film on Mo foil, showing the InP surface, cross-section, and the Mo foil surface. (c), Tilt view false-color SEM image of contoured InP grown via pre-texturing the Indium film.

Interestingly, the morphology of the grown InP films can be tuned by the morphology of the starting In film and its corresponding template. As an example, an evaporated indium thin film was coated with closely packed silica beads (~1 μm in diameter) through a Langmuir-Blodgett (LB) process (see Methods) followed by a mechanical press to embed the beads into the indium film. After subsequent capping by SiO_x and phosphorization, a nanotextured InP thin film with a hermispherical morphology was obtained (Fig. 1c). The ability to readily control the shape and morphology of the semiconductor film presents a unique feature of the TF-VLS process with important implications for light management¹⁵,¹⁶ and carrier collection¹⁷ in future devices.

The structural characteristics of the TF-VLS InP were probed by x-ray diffraction (XRD), electron backscatter diffraction (EBSD) and SEM. Both as-grown InP films on Mo and free standing InP films, which were obtained by peeling off the InP layer from the substrate, were examined. XRD analysis (Fig. 2a) establishes three points. First, the films are zinc blende InP. Second, the lack of indium peaks indicates that the film has turned into InP within the detection limit of the XRD (InP:In ratio >10⁴ based on the peak ratio method). Third, the films are polycrystalline and slightly textured as evident by the larger 111 peak intensity as compared to that of 200. EBSD mapping of the InP films was used to determine the grain size. The maps (Fig. 2b) show that the grain sizes vary between 10 μm to greater than 100 μm, despite a film thickness of ~3 μm. These grains are 10–100 times larger than those previously reported for vapor phase growth of InP thin films on metal foils using metal organic chemical vapor deposition (MOCVD)¹² and close spaced sublimation¹³. The large crystal grain size obtained with TF-VLS leads to excellent optoelectronic properties as discussed in detail below. A plan view SEM image is shown in Fig. 2c; faceted edges of the grains are visible, providing further evidence of the large grain size.

Figure 2. Structural characterization.

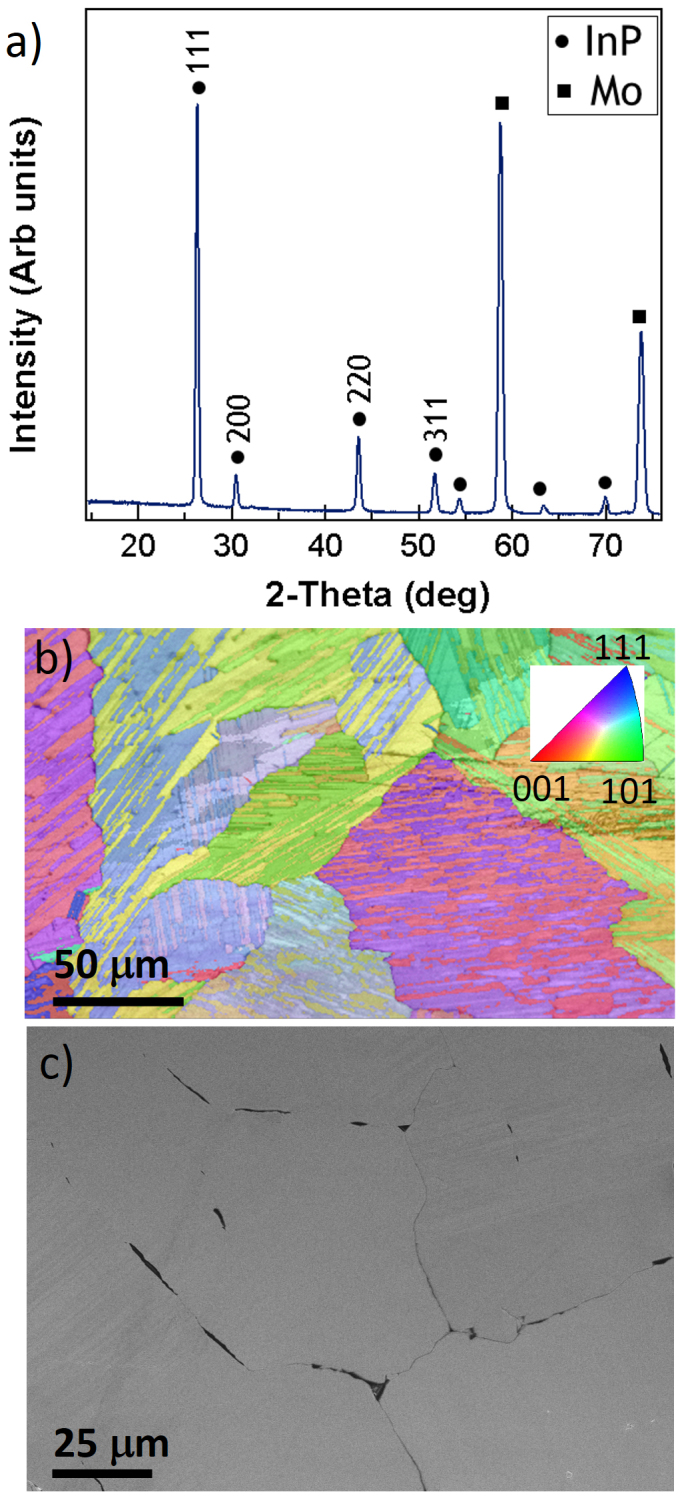
(a), XRD spectrum of an InP film grown at 750°C. (b), EBSD image of the backside of a peeled off TF-VLS InP film, indicating large grain sizes of ~10–100 μm. (c), Top-view SEM image of InP peeled off from Mo foil, partially etched in 1% HCl to highlight grain boundaries.

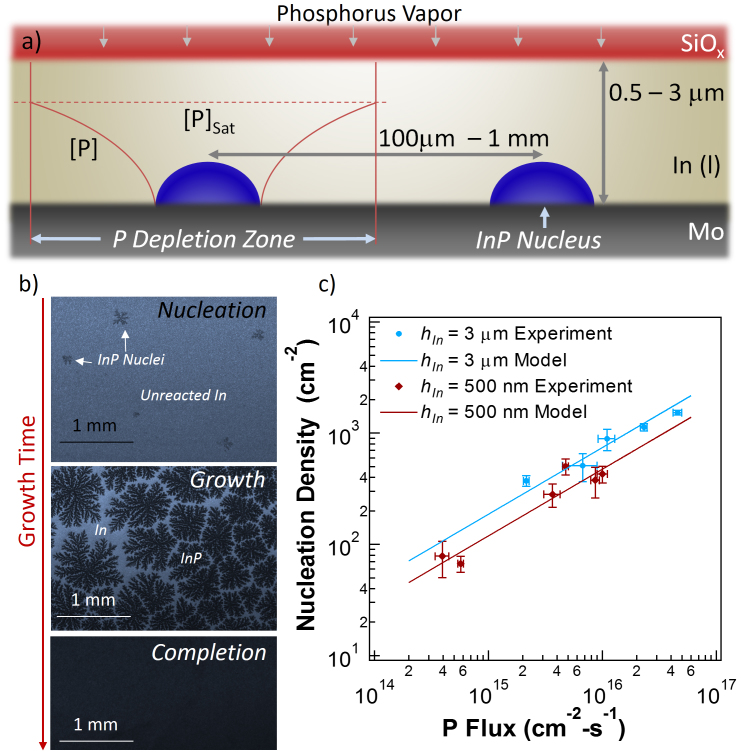
Important features of the TF-VLS growth process are highlighted through a qualitative model (Fig. 3a). The process involves P diffusion through the SiO_x cap into the liquid indium film, increasing the P concentration, [P], until the concentration slightly exceeds saturation, [P]_Sat, enabling nucleation of the solid InP phase on the Mo substrate. It should be noted that InP does not nucleate on the SiO_x surface (Fig. S2) due to the high surface energy¹⁸. Once InP nuclei are formed, they grow via diffusion of nearby P to the In/InP interface, and subsequent incorporation into the solid phase. This diffusion/incorporation process creates a depletion zone near each nucleus, limiting subsequent nucleation events allowing large grain sizes. Figure 3b shows optical microscope images at various stages of the film growth (i.e. different growth times). Starting with separate InP nuclei formation, spaced ~100 μm–1 mm apart, the separate islands begin to converge, followed by the completion of film growth. The dendritic morphology is indicative of the rapid diffusion of phosphorous towards the nuclei relative to the rate at which the solid phase relaxes towards its equilibrium shape¹⁹.

Figure 3. Growth schematic.

(a), Qualitative diagram of the TF-VLS growth process, showing the phosphorous vapor diffusing through the cap layer, initial InP nucleus, and phosphorus concentration [P] as a function of distance from the nucleus. The depletion zone is defined as the area where [P] < [P]_Sat. (b), Optical microscopy images of the growth of the InP films. Initially, separate InP nuclei/islands form, followed by growth outwards in a dendritic fashion. Finally, separate InP islands converge together and growth completes as the In film turns into InP. (c), Nucleation density as a function of incident P flux for two different starting In film heights.

A simple model helps to identify the factors that determine the density of nuclei (see Supplementary Information for details). The model suggests that the density of nuclei scales as 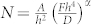, where F is the flux of P into the liquid indium, D is the diffusivity of P within the liquid phase, h is the initial thickness of the indium film, α is a positive constant less than one related to the critical nucleus size, and A is a unitless constant related to the capture cross section of P atoms by other atoms and existing islands. Based on this simple scaling law, the key to producing a small number of nuclei and thus large grains is to insure that the flux of the incoming P is slow in comparison to the rate at which P diffuses within the liquid phase. To examine this simple model, InP thin films were partially grown (i.e., the growth was stopped prior to the full convergence of the islands) with varied PH₃ partial pressure and thereby P flux, F. The nucleation density for each sample was then obtained by optical microscopy. Two different indium film thicknesses of h ~ 500 nm and 3 μm were used. Details of the growths are reported in the supplementary information. The results of this study (Fig. 3c) depict the strong dependence of the nucleation density on the incident flux. Specifically, the nucleation density is tuned by approximately two orders of magnitude for the explored flux range. The lowest obtained nuclei density is ~50 cm⁻² for F ~ 4 × 10¹⁴ cm⁻²s⁻¹, corresponding to a grain size on the order of ~1 mm. A good fit between the experimental data and the model described above is obtained (Fig. 3c) when using α ~ 0.6 and A ~ 9.25 × 10⁻⁹ as the fitting parameters for both initial indium film thicknesses (see SI for details).

Next, we focus on the detailed electrical and optical characterization of InP thin films (~3 μm in thickness) as a function of growth temperature (T_Growth = 450–800°C). After growth, the SiO_x cap was etched away in HF. Surface cleaning and passivation was then carried out by a 30 second treatment of 1% HCl followed by a 30 second treatment of 1% HNO₃ The HCl treatment removes the native oxide, while the HNO₃ treatment results in a dense surface oxide layer which was previously shown to improve the surface properties²⁰. The resulting films were characterized via Hall measurements, steady state photoluminescence (SSPL), time resolved PL (TRPL), and external luminescence efficiency measurements (η_ext).

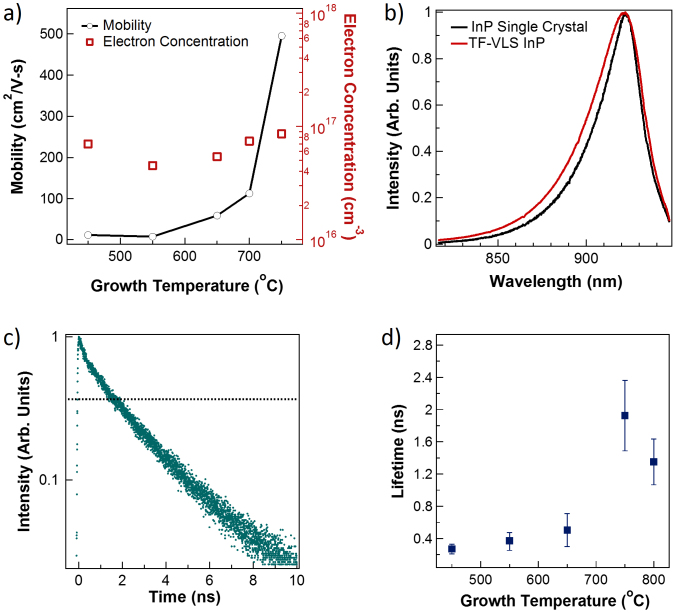
Hall measurements (Fig. 4a) were carried out on InP films peeled off from the Mo substrate to extract carrier concentration and mobility. InP films were found to be n-type with an unintentional doping concentrations between 4 to 8 × 10¹⁶ cm⁻³, regardless of growth temperature. Notably, this relatively low carrier concentration is obtained without the use of ultrahigh purity Mo foil and indium source. Electron mobility across multiple-grains (over an area of ~1 cm²), however, exhibits a strong dependence on the growth temperature, increasing from ~12 cm²/V-s for T_Growth = 450°C, to ~500 cm²/V-s for T_Growth = 750°C. The electron mobility value for the sample grown at 750°C is respectable compared that of single crystal InP, which range from ~1500–4000 cm²/V-s depending on doping and compensation ratio²¹.

Figure 4. Optoelectronic characterization.

(a), Mobility and carrier concentrations as a function of growth temperature obtained from Hall measurements carried out on peeled off InP films. (b), Steady state photoluminescence characterization of a TF-VLS InP film grown at 750°C (red line) and a similarly doped single-crystal wafer as a reference (black line). (c), Representative TRPL curve for a TF-VLS InP sample grown at 750°C. The dashed line represents 1/e of the initial peak intensity. (d), Average time-resolved photoluminescence lifetimes as a function of InP growth temperature. All measurements were performed at room temperature.

Micro-SSPL was used to determine (i) the wavelength of the peak photoluminescence intensity, and (ii) the quantum yield of the emission, used to measure the external luminescence efficiency (η_ext) and calculate the quasi Fermi level splitting (ΔE_F). A representative polycrystalline InP (T_growth = 750°C) SSPL curve is shown in Fig. 4b. As a reference, a single crystal n-type InP wafer with a comparable doping concentration (~3 × 10¹⁶ cm⁻³) is also plotted. A HeNe laser at λ = 632.8 nm was used as the excitation source and measurements were performed at ambient temperature. The polycrystalline InP exhibits a SSPL peak position of ~921.7 nm (1.345 eV) and full width half maximum (FWHM) of ~37 nm. These measured values are similar to the single crystal reference, which exhibits a peak position of 922.2 nm and a FWHM of 29 nm. TRPL measurements were carried out at room temperature on the polycrystalline InP films to determine the effective minority carrier lifetimes (Fig. 4c). The samples were illuminated with a 800 nm pulsed laser, and the time dependent photoluminescence intensity was recorded at the peak wavelength, as measured by SSPL. Figure 4d shows the 1/e lifetime as a function of InP growth temperature. The measured effective lifetimes show a clear dependence on the growth temperature, with the InP grown at 450°C exhibiting the lowest average effective lifetime of ~0.25 ns, while the films grown at 750°C exhibit the highest average effective lifetime of ~2 ns. We hypothesize that at higher temperatures, the InP is more thoroughly annealed during growth, reducing the excess number of point defects and thereby improving the electronic and optoelectronic properties.

Discussion

While minority carrier lifetimes offer some insight into the material quality, the key metric for solar cell performance is the open-circuit voltage, V_OC²²,²³. In a semiconductor under illumination, the upper limit for V_OC is the difference in the chemical potential between the electron and hole population, defined as the quasi-Fermi level splitting, ΔE_F. Thus, extraction of ΔE_F allows for a quantitative prediction of the photovoltaic performance limits of a material. ΔE_F may be extracted²² by direct measurement of the external luminescence efficiency, η_ext = (number of photons emitted)/(number of photons absorbed), as described in the methods section²⁴. The dependence can be qualitatively understood by considering that for a solar cell to reach the Shockley-Quessier (SQ) limit, the only loss mechanism should be radiative recombination¹¹. Thus, at the SQ limit under open circuit conditions, one photon must be emitted for each photon absorbed (η_ext = 100%)²²,²³. The η_ext is determined by two factors, the internal luminescence efficiency, η_int = (radiative recombination rate)/(total recombination rate), and the parasitic optical absorption. From the data obtained by varying incident laser intensity and monitoring the output photoluminescence intensity, we extract the external luminescence efficiency, internal luminescence efficiency, and quasi-Fermi level splitting (Fig. 5 and Fig. S4). Details of the measurement and analyses are provided in the methods section.

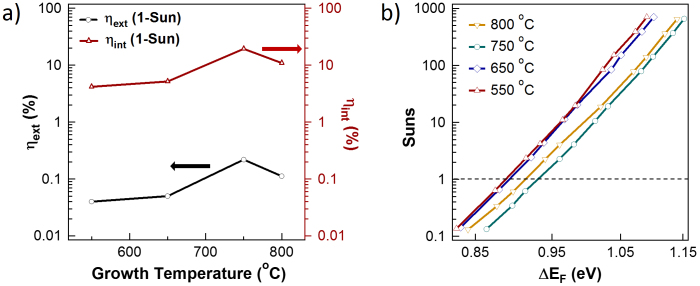
Figure 5. Luminescence yield.

(a), Measured external luminescence efficiency and extracted internal luminescence efficiency as a function of growth temperature. (b), Optically measured “I–V” curves obtained from external luminescence efficiency measurements. Here, Suns represents the intensity of the absorbed laser light (1-sun = 100 mW/cm²), and corresponds to the photogenerated current level. The quasi-Fermi level splitting (ΔE_F) represents the resulting V_OC that would occur to balance the photogenerated current.

Figure 5a shows η_ext and η_int at 1-sun equivalent power as a function of InP growth temperature. As expected, the trend follows that of the measured minority carrier lifetimes in Fig. 4d, with the luminescence efficiency increasing with the growth temperature up to 750°C. Peak η_ext is ~0.2% for T_growth = 750°C (Fig. 5a). This value compares favorably to other polycrystalline materials used in the state-of-the-art thin film cells, including copper indium gallium selenide (CIGS) and CdTe with η_ext between 0.0001–0.19%²³. The extracted η_int is ~20% for T_growth = 750°C (Fig. 5a), which is high given that our thin film InP is in direct contact with the Mo substrate. In comparison, a similarly doped single crystal InP wafer was measured to have η_int ~ 50% with the same setup. It should be possible to further increase the luminesce yields for TF-VLS InP by replacing the Mo foil with a more reflective back contact, while exploring various surface and grain boundary passivation techniques. Nevertheless, the obtained values confirm that TF-VLS growth results in optoelectronic quality InP; quite remarkable considering that the material was grown non-epitaxially on a metal substrate without the use of ultra-high purity materials.

Figure 5b shows the optically measured “I–V” curves for TF-VLS InP films. Specifically, the incident excitation intensity is plotted versus the extracted quasi-Fermi level splitting (ΔE_F) for various growth temperatures (see methods for analyses details). Here, the incident light intensity correlates to the photogenerated current level while ΔE_F/q represents the corresponding V_OC that would occur to balance the photogenerated current. This technique presents a simple approach for projecting the device performance limit of a given material. The data illustrates that InP samples grown at 750°C exhibit a high ΔE_F of ~0.93 eV under 1-sun illumination. This extracted ΔE_F value is only ~40 meV lower than that of a single-crystalline InP wafer with a similar unintentional doping concentration (N_d ~ 10¹⁶ cm⁻³) measured using the same experimental set-up. Additionally, ΔE_F for the TF-VLS InP is higher than those previously reported for CIGS thin films (ΔE_F = 0.75–0.87 eV)²⁵. This is an important observation given that the highest efficiency polycrystalline PVs reported to date have been based on CIGS; suggesting favorable performance projection for the TF-VLS InP. Additionally, the inverse slope of the incident light intensity versus ΔE_F curves is given as ηln(10)kT, where η is the ideality factor (analogous to that of a diode), k is the Boltzmann's constant and T is the temperature. From the inverse slopes, we obtain η ~ 1.2 which is close to the ideal limit (where η = 1), further suggesting the high optoelectronic quality of our material.

In conclusion, the ability to grow InP thin films on metal foils with large crystallites and material properties approaching those of single crystals presents a route towards low-cost, large-area III-V photovoltaics. Specifically, it should be noted that the TF-VLS process has important advantages in terms of processing costs, especially given the high material utilization yield for indium (which can be electrodeposited) as compared to conventional epitaxial growth processes, such as MOCVD/MOVPE. While in this work, we focused on the use of non-epitaxial metal foil substrates, the TF-VLS process also enables single crystalline film growth with epitaxial substrates. As a proof of concept, TF-VLS of homoepitaxial single-crystalline thin films of InP is demonstrated in the Supplementary Information (Fig. S5). These results demonstrate the versatility of this process for growth on both epitaxial and non-epitaxial substrates. In the future, in-situ doping techniques can be explored by introducing dopant species in the vapor phase. Finally, although InP was utilized as a model system here, this growth technique should be general within the constraints summarized here: (i) the diffusivity of the rate limiting component (here, P) in the liquid (In) should be fast as compared to the incident flux, (ii) a single stable phase should precipitate out of the melt (InP), (iii) the capping layer (SiO_x) must facilitate structural confinement of the liquid on the substrate without inducing nucleation, and (iv) the substrate should be both inert with respect to the reaction components (In, P) and promote nucleation of the desired phase (InP).

Methods

InP growth

InP was grown from starting Mo/In/SiO_x stacks utilizing a 1-zone furnace with a phosphorus source of 10% PH₃ (99.9995%) in H₂ (99.9999%), or utilizing a 2-zone furnace with a red phosphorus (99.999%) source and H₂ carrier gas. Samples were first heated in a hydrogen environment, followed by exposure to the phosphorus source once the furnace stabilized at the growth temperature. Samples were held at the growth temperature and exposed to the phosphorous source for 20 minutes, followed by cooling (~20 seconds) to room temperature.

InP transfer

For certain characterization work, including Hall measurements, InP was peeled from the Mo foil substrate. First, polyimide (PI) was spin coated onto the InP films, followed by thermal curing at 200°C for 6 hours. Once the PI film was cured, the InP was removed from the Mo foil by mechanical peeling at room temperature using tweezers.

Indium texturing via Langmuir-Blodgett

In order to grow patterned InP, a planar Mo/In stack was uniformly coated with a monolayer of 1 μm silica beads via a Langmuir-Blodgett process. First, the silica beads were dispersed in DI water; next, the Mo/In substrate was dipped into suspension and slowly removed. These beads were then mechanically pressed into the underlying indium.

Time resolved photoluminescence measurements

Minority carrier lifetimes for these samples were measured utilizing a time correlated single photon counting measurement system with a λ = 800 nm 200 fs duration pulsed laser. The laser intensity was set such that the initial carrier density at the InP surface was ~5 × 10¹⁷ cm⁻³.

Luminescence yield

To simulate the response of these materials under varying solar illumination, samples were excited with a HeNe laser (λ = 632.8 nm) of varying intensity from ~15 mW/cm² (.15 suns) to ~7 × 10⁴ mW/cm² (700 suns). This intensity represents the absorbed photon flux, calculated by multiplying the incident photon flux by the normal transmission coefficient, separately measured at the laser wavelength. The resulting external luminescence efficiency was calculated by: η_ext = (ϕ_InP/ η_sys)/(ϕ_inc × T) where ϕ_inc and ϕ_InP are the incident HeNe photon flux and the measured InP photon flux, respectively, T is the transmission coefficient at the air/InP boundary as measured via absorption measurements, and η_sys is the collection efficiency of the system for a Lambertian reference. Here, the Lambertian reference used was a thick (>3 mm) Spectralon® layer was used as the Lambertian reference.

The internal luminescence efficiency, η_int is extracted via²⁶:

where L is the InP thickness, n is the band-edge refractive index, and α is the band-edge absorption coefficient. It should be noted that Eqn. 1 assumes an ideal back surface mirror. In the experimental work, the back surface (i.e., Mo substrate) is a non-ideal mirror which provides a loss mechanism for the emitted photons. Thereby, the extracted η_int values reported here are lower bounds.

The quasi-Fermi level splitting (ΔE_F) is calculated by²⁷,²²:

where R_abs is the absorbed photon flux per unit area in the InP, a(E,θ) is the absorbance of the semiconductor, and b(E) is the blackbody spectrum at temperature T. The absorbance of the InP was taken to be: a(E,θ) = a(E) × T(θ), where a(E) = 1 for E > 1.344 eV, and a(E) = 0 for E < 1.344 eV. This simplifying assumption was made due to the relatively long optical path of the InP films here (3 μm). The angular dependence T(θ) is the transmission coefficient as determined by the Fresnel equations. The black body spectrum was given by: 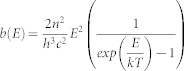. Here, n is the refractive index of air, h is Planck's constant, c is the speed of light, k is the Boltzmann constant, and T = 300 K is temperature. It should be noted that since the surface is not truly random, nor flat, the assumption of Fresnel transmission at the top surface adds a small error of ~5 meV, which is a relative error of ~0.5%.

Author Contributions

R.K., Z.Y. and A.J. designed the experiments. R.K., Z.Y., H.-H.H.W., M.Z., C.B., M.H., D.K., K.T., P.L. and J.W.B. carried out the experiments. R.K. and D.C.C. developed the growth model. R.K., Z.Y., M.Z., C.B., P.L., J.W.A., R.M., D.C.C. and A.J. contributed to the data analysis. R.K. Z.Y. and A.J. wrote the paper while all authors provided feedback.

Supplementary Material

Supplementary Information

A direct thin-film path towards low-cost large-area III-V photovoltaics