Machine learning for predicting the response of breast cancer to neoadjuvant chemotherapy

Abstract

Objective

To employ machine learning methods to predict the eventual therapeutic response of breast cancer patients after a single cycle of neoadjuvant chemotherapy (NAC).

Materials and methods

Quantitative dynamic contrast-enhanced MRI and diffusion-weighted MRI data were acquired on 28 patients before and after one cycle of NAC. A total of 118 semiquantitative and quantitative parameters were derived from these data and combined with 11 clinical variables. We used Bayesian logistic regression in combination with feature selection using a machine learning framework for predictive model building.

Results

The best predictive models using feature selection obtained an area under the curve of 0.86 and an accuracy of 0.86, with a sensitivity of 0.88 and a specificity of 0.82.

Discussion

With the numerous options for NAC available, development of a method to predict response early in the course of therapy is needed. Unfortunately, by the time most patients are found not to be responding, their disease may no longer be surgically resectable, and this situation could be avoided by the development of techniques to assess response earlier in the treatment regimen. The method outlined here is one possible solution to this important clinical problem.

Conclusions

Predictive modeling approaches based on machine learning using readily available clinical and quantitative MRI data show promise in distinguishing breast cancer responders from non-responders after the first cycle of NAC.

Background and significance

Chemotherapy for early stage breast cancer is most often administered after surgery, in the adjuvant setting. However, for patients with larger tumors, tumors fixed to the chest wall, or those with clinically matted lymph nodes or skin involvement, neoadjuvant chemotherapy (NAC) is often used. In the neoadjuvant setting, patients receive chemotherapy before surgery to decrease the size of the tumor to make it more amenable to surgery, that is, to allow for a lumpectomy rather than a mastectomy. NAC also provides an excellent opportunity to observe whether a particular regimen is actually beneficial. When chemotherapy is given in the adjuvant setting, no ‘marker’ is available to determine whether a treatment is eradicating micrometastatic disease; neoadjuvant administration allows the primary breast mass to function as this marker. If the primary breast tumor responds to NAC, any systemic micrometastases may also be responding. If the primary tumor continues to grow, the treatment can be changed to a regimen that could be more effective for both primary and metastatic disease. With the numerous options for neoadjuvant treatment that have become available, development of a method to predict response early in the course of therapy is especially needed. Furthermore, given the cumulative effect of chemotherapy toxicity, early identification of patients who are not responding to a particular treatment would allow for switching to a potentially more effective regimen thereby avoiding unnecessary side effects. Patients whose disease is chemorefractory could be referred directly for surgery. Unfortunately, by the time most patients are found not to be responding—often after 3–5 months of treatment—their disease may no longer be surgically resectable.

The current standard of care radiological assessment of tumor response to treatment is based on the response evaluation criteria in solid tumors (RECIST).¹ RECIST offers a practical method for assessing the overall tumor burden at baseline and comparing that measurement to subsequent measurements obtained during the course of therapy. The data for a RECIST analysis are based on high-resolution images (typically MRI or CT) acquired at baseline before treatment has commenced. In these image sets, ‘target lesions’ are determined and the sum of their longest dimensions is recorded. Additional scans are then acquired during or after therapy and similarly analyzed. The change in the sum of the longest diameters from baseline to the follow-up studies are then calculated and then used to divide treatment response into one of four categories: complete response (disappearance of all target lesions); partial response (>30% decrease in the sum of the longest diameters of the target lesions); progressive disease (>20% increase in the sum of the longest diameters of the target lesions); and stable disease (none of the above). It is well recognized that this approach needs to be significantly improved because, for example, the metric for positive response is based on one dimensional changes that can be grossly misleading. Furthermore, this metric is based on anatomical changes that are (temporally) downstream manifestations of underlying physiological, cellular, or molecular changes. In particular, RECIST-based evaluations generally do not indicate whether a tumor is responding until several treatment cycles of a therapy have been given; a particularly important problem in the era of targeted therapies. We need newer methods to characterize quantitatively the underlying changes as they are highly likely to offer earlier and more specific responses to treatment indices than changes in longest dimensions. One approach is to begin to incorporate some of the more quantitative and specific non-invasive imaging methods into clinical trials and practice; two such examples are dynamic contrast enhanced MRI (DCE-MRI) and diffusion weighted MRI (DW-MRI).

Going forward, early response assessment is especially relevant as targeted therapies have found increasing use in the neoadjuvant setting.^2–4 In this contribution we seek to combine two emerging, quantitative MRI methods (DCE-MRI and DW-MRI) with routine clinical data to provide input to the machine learning framework with the overall goal of developing an algorithm to predict accurately the eventual therapeutic response after a single cycle of NAC.

Machine learning approaches have the capability to generate models for prediction by extensively searching through the model and parameter space. Traditional statistical approaches typically consider a limited finite set of hypotheses and evaluate them, while machine learning methods generate a large number of models and search through them. Machine learning methods have been embraced by the biomedical informatics community for predictive modeling and decision making in biomedicine. For example, machine learning methods have been employed for breast cancer screening,⁵ to discriminate malignant and benign microcalcifications,⁶ for predicting breast cancer survival,⁷ and to model prognosis of breast cancer relapse.⁸ Machine learning methods have been shown to substantially improve the accuracy of determining cancer susceptibility (risk), as well as outcome (prognosis).⁹ As machine learning methods can build models from large and complex datasets by identifying the most relevant subset of features and combining them to maximise predictive accuracy they are appropriate for model building using a combination of clinical and imaging data.

Researchers have begun investigating the application of machine learning techniques to imaging data for predicting response to NAC in breast cancer.¹⁰ For example, using data from 96 patients with tumor sizes assessed by positron emission tomography at various stages of their chemotherapy treatment Gyftodimos et al¹⁰ demonstrated the efficacy of machine learning methods for differentiating low responders to treatment from high responders at an early stage of treatment. The positron emission tomography imaging data were manually processed by a domain expert in their study while we use automated feature extraction methods from magnetic resonance images in our work. Two recent studies have used MRI for predicting therapeutic response following NAC.^{11 12} The second study¹² also considered gene expression profiles in addition to MRI. However, both these studies used traditional statistical methods for predictive model building.

In this study, we use Bayesian logistic regression (BLR) with feature selection within a machine learning framework and integrate clinical and imaging data obtained before and after one cycle of NAC to predict the eventual response in breast cancer patients undergoing NAC.

Materials and methods

Patient population

Patients who were undergoing NAC as a component of their clinical care were eligible for the study. No previous systemic therapies for breast cancer were allowed. All patients had histologically documented invasive carcinoma of the breast with a sufficient risk of recurrence to warrant the use of NAC at the discretion of their treating medical oncologist. Participating patients provided written informed consent to our institutional review board-approved study.

Treatment regimens

The selection of NAC protocol was at the discretion of the treating oncologist. Patients with HER2+ tumors had one of the following regimens: adriamycin/cytoxan followed by taxol/trastuzumab; docetaxel, carboplatin, and trastuzumab; or lapatinib and trastuzumab. Patients with HER2 disease were treated with one of the following regimens: adriamycin/cytoxan followed by taxol, or cisplatin/paclitaxel ± RAD001. Patients who had ER/PR + tumor all received endocrine therapy at the completion of chemotherapy.

Study design

Twenty-eight patients with stage II/III breast cancer were enrolled in the study and completed at least two of the three scans to provide usable data for the analysis. Quantitative MRI data were acquired at baseline before initiating NAC (t₁), after one cycle of NAC (t₂), and at the conclusion of NAC but just before surgery (t₃). The median age of the patients was 45 years (range 28–67 years). The median time between t₁ and t₂ was 14 days (range 5–28 days) and the median time between t₂ and t₃ was 109 days (range 57–209 days). The post-therapy tumor size was determined from the surgical specimen, and the patients were classified according to the residual tumor size found at the primary tumor sites; 11 patients were defined as responders as there was no residual tumor in the breast or lymph nodes (ie, they achieved pathological complete response), while 17 patients were defined as non-responders as there was the presence of cancer in the breast and/or lymph nodes.

MRI methods

There are two emerging, quantitative MRI methods that are employed in this study, DCE-MRI and DW-MRI. A brief introduction to the two methods including how MRI data were acquired and processed for this study is provided in supplementary appendix I (available online only). A total of 118 imaging variables was derived from the DCE-MRI and DW-MRI data. A listing of all the imaging variables with a short description is provided in supplementary table A (available online only).

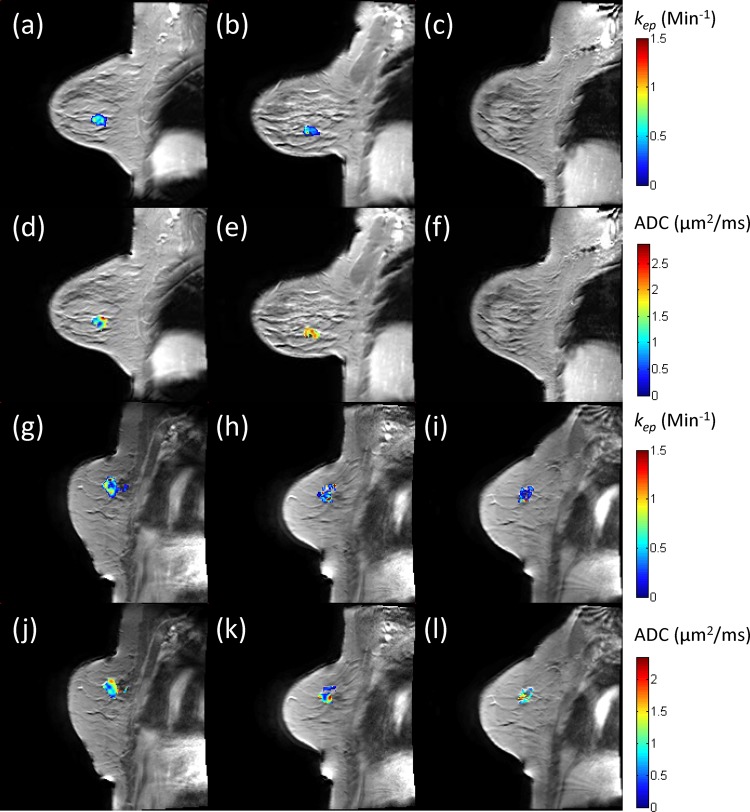
Figure 1 presents illustrative DCE-MRI and DW-MRI data at the three time points for a patient who achieved complete pathological response (panels a–f) and a patient who was a non-responder (panels g–l). Panels a–c display the k_ep map from the Tofts–Kety (TK) model, while panels d–f display the apparent diffusion coefficient (ADC) map. Similar data are presented for the non-responder in panels g–l. Observe how, in the responding patient, there is a substantial decrease in k_ep from t₁ to t₂ as well as an increase in ADC between these two time points. Conversely, in the non-responding patient there is an increase in k_ep and a decrease in the ADC between these two time points.

Figure 1.

Illustrative dynamic contrast enhanced MRI (DCE-MRI) and diffusion weighted MRI (DW-MRI) data at the three time points for a patient who achieved complete pathological response (a–f) and a patient who was a non-responder (g–l). Panels a–c display the k_ep map from the Tofts–Kety model, while panels d–f display the apparent diffusion coefficient (ADC) map. Similar data are presented for the non-responder in panels g–l. Observe how, in the responding patient, there is a 21% decrease in k_ep from t₁ to t₂ as well as a 38% increase in ADC between these two time points. Conversely, in the non-responding patient there is a 27% increase in k_ep and a 25% decrease in the ADC between these two time points.

Clinical variables

Eleven clinical variables available before initiation of the first cycle of NAC were used for generating the predictive models. A list of the variables with a short description for each is provided in table 1. Clinical and pathological variables have been successfully combined to predict outcomes for patients with early stage breast cancer. These rely primarily on pathological data obtained at the time of surgery. For patients with locally advanced disease who will be receiving NAC, this information (tumor size and nodal status) is no longer available. Therefore, prediction models in the setting of NAC are not as robust. Nomograms have been developed to estimate the probability of pathological complete response following preoperative chemotherapy. Clinical variables are based on these previously published nomograms^{13 14} and data that would be available to the clinician at the time of diagnosis.

Table 1.

List of pretreatment clinical variables with a short description

Clinical variable	Description
Age	Age at the time of diagnosis
ER+	Estrogen receptor
PR+	Progesterone receptor
HER2+	Human epidermal growth factor receptor
Clinical grade	Pretreatment clinical grade
Proliferative rate	No of cells in mitosis per 10 high power fields
Nodal status	Pathologically confirmed by fine needle aspiration or sentinel node evaluation
Clinical-T	Pretreatment clinical size based on clinical imaging (ie, physical examination, ultrasound, mammogram, conventional MRI) judged to be most accurate for each case. In patients in whom these measurements were discordant, the most reliable measurement (as deemed by the treating physician) was utilized to determine tumor size before chemotherapy
Clinical-N	Pretreatment nodal stage based on pathologically confirmed by fine needle aspiration of node or sentinel evaluation
Clinical stage	Staging of the breast cancer before initiation of NAC. Clinical staging includes physical examination as well as standard imaging including ultrasound, mammogram and clinical MRI
Physical examination	Longest diameter by physical examination (cm)

NAC, neoadjuvant chemotherapy.

Machine learning methods

We generated three datasets: (1) imaging with 118 variables plus the outcome variable (ie, response as measured by surgical pathology); (2) clinical with 11 variables plus the outcome variable; and (3) imaging plus clinical consisting of 129 variables plus the outcome variable. All the three datasets were used for predictive modeling.

We defined the predictive modeling task using machine learning methods as follows: can we predict if the patient will achieve complete pathological response by the conclusion of NAC given imaging and clinical measurements of this patient obtained no later than t₂? In our previous pilot study we used a representative set of machine learning algorithms for our predictive modeling task and the best performer was BLR.¹⁵ To increase predictive performance, feature (attribute) selection algorithms are often used to select a subset of the features that are highly predictive of the class. By selecting a small number of the most relevant features one is able to reduce the risk of overfitting the training data, thereby generating a more parsimonious model. Three state-of-the-art feature selection methods were used in our experiments: HITON-MB,¹⁶ Gram–Schmidt orthogonalization (GS) with a maximum number of 10 features output (GS-10),^{17 18} and BLCD-MB.^{16 19} HITON-MB and BLCD-MB are guaranteed to find the Markov blanket (MB) of the class (outcome) variable in the large sample limit. The MB of a node X is the set of nodes in a Bayesian network, which when conditioned on makes all the other nodes (V\(MB(X) U X)) independent of X where V denotes the set of variables in a Bayesian network. The GS feature selection algorithm is particularly useful in practice. It adds a greedy forward search to the ranking of variables obtained by the Pearson correlation coefficient by conditioning on the variables already selected (hence orthogonal to the set of variables already in the selected feature set).²⁰

We applied the GS algorithm by using the CLOP package.²¹ The only parameter of GS is the maximum number of features. We used 10 so that GS would output a maximum of 10 top ranking features over the entire feature set. We used the implementations of HITON-MB and BLCD-MB in the causal explorer package.²² For HITON-MB, we used Fisher's z-test for continuous variables and the G² test for discrete variables (all variables in both clinical and imaging datasets were treated as continuous). For BLCD-MB, we set the maximum size of MB at 12.

We used a modified version of the BLR described in Saria et al.²³ BLR is similar to the basic logistic regression in the regression step, but uses a Bayesian modeling framework to capture the non-linear relationships between variables and the outcome. We assumed that all continuous variables have a Gaussian distribution, and the variables were evaluated based on the parametric distribution conditional on the outcome variable. For binary variables, the class conditional probability was considered along with non-informative priors. The log OR for each independent variable was incorporated into the BLR model. We tested the Gaussian assumption for the variables using the Lilliefors test. However, 75 variables out of the 118 imaging variables and nine out of 11 clinical variables did not conform to a normal distribution at the 0.05 significance level. The details of the BLR logistic function are provided in supplementary appendix II (available online only).

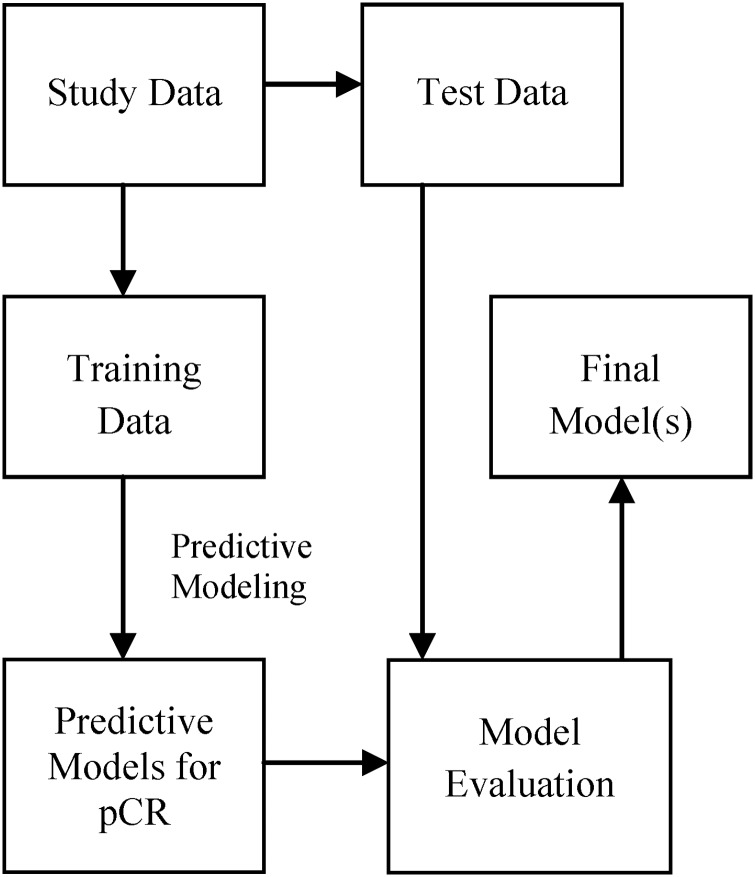
Because of the modest sample size (n=28) we implemented the leave one out (n-fold) cross-validation method, which uses one sample in the test set and all the others for training. This was repeated 28 times using a different test sample for each run. Predictive models were built using the training samples and evaluated on the test sample. The general schema for predictive model building is shown in figure 2. For each test sample we output the probability of the positive class and use a threshold (>0.5) to classify the sample as positive class (otherwise, it is labeled negative). Note that this threshold may not be optimal to obtain the best binary prediction. However, it is typically used in machine learning and has the advantage of not overfitting the data. To evaluate the probability output, we used the area under the curve (AUC) score (ie, area under receiver operator characteristic curve). To evaluate the binary output, we used accuracy, precision (positive predictive value), recall (sensitivity) and specificity; 95% CI for all the outcome measures were estimated using bootstrapping.

Figure 2.

A general schema for predictive model building and evaluation showing that model evaluation is performed using test data that are not used for model building. pCR, pathological complete response.

We also compared the BLR method with a non-BLR. The comparison results reported are based on the use of HITON-MB for feature selection as it performed the best among the feature selection algorithms used in the study.

Results

Three datasets were used for prediction (with and without feature selection) and the results for clinical, imaging, and clinical plus imaging datasets are shown in tables 2–4. The two MB-based feature selection algorithms HITON-MB and BLCD-MB were parsimonious in selecting only two (ER+, PR+) from clinical, only two (mean ADC post one cycle of treatment, mean of the change of the top 15% of k_ep as estimated by the TK model) from imaging, and four (listed earlier for clinical and imaging) when clinical and imaging variables were combined. On the other hand, GS-10 selected all the 11 clinical variables (range 15–28 folds), 58 imaging variables (range 1–24 folds) and 60 (range 1–27 folds) when clinical and imaging variables were combined. The range denotes the number of times a feature was selected over the 28 cross-validation runs for each dataset.

Table 2.

Results using only clinical parameters (11 variables)

FS method	Accuracy (95% CI)	Precision (95% CI)	Recall (95% CI)	Specificity (95% CI)	AUC (95% CI)
No-FS	0.750 (0.571 to 0.893)	0.813 (0.619 to 1.0)	0.765 (0.550 to 0.947)	0.727 (0.444 to 1.0)	0.759 (0.678 to 0.841)
GS-10	0.750 (0.571 to 0.893)	0.813 (0.600 to 1.0)	0.765 (0.533 to 0.944)	0.727 (0.455 to 1.0)	0.759 (0.678 to 0.841)
HITON-MB	0.786 (0.643 to 0.929)	1.000 (1.000 to 1.0)	0.647 (0.417 to 0.857)	1.000 (1.000 to 1.0)	0.647 (0.581 to 0.713)
BLCD-MB	0.786 (0.643 to 0.929)	1.000 (1.000 to 1.0)	0.647 (0.421 to 0.875)	1.000 (1.000 to 1.0)	0.647 (0.581 to 0.713)

FS, feature selection.

Each row represents the result by each feature selection method (no-FS means no feature selection or using all features).

Using only clinical parameters HITON-MB and BLCD-MB selected ER+ variable as the best and only predictor for 27 out of the 28 cross-validations runs.

Table 3.

Results using only imaging parameters (118 variables)

FS method	Accuracy (95% CI)	Precision (95% CI)	Recall (95% CI)	Specificity (95% CI)	AUC (95% CI)
No-FS	0.643 (0.464 to 0.821)	0.706 (0.471 to 0.923)	0.706 (0.471 to 0.905)	0.545 (0.231 to 0.857)	0.578 (0.484 to 0.672)
GS-10	0.464 (0.286 to 0.643)	0.583 (0.286 to 0.857)	0.412 (0.188 to 0.650)	0.545 (0.250 to 0.833)	0.545 (0.458 to 0.633)
HITON-MB	0.821 (0.679 to 0.964)	0.875 (0.688 to 1.000)	0.824 (0.615 to 1.000)	0.818 (0.556 to 1.000)	0.856 (0.785 to 0.926)
BLCD-MB	0.821 (0.679 to 0.964)	0.875 (0.688 to 1.000)	0.824 (0.625 to 1.000)	0.818 (0.556 to 1.000)	0.845 (0.775 to 0.915)

AUC, area under the curve; FS, feature selection.

Table 4.

Results using both clinical and imaging data (129 variables)

FS method	Accuracy (95% CI)	Precision (95% CI)	Recall (95% CI)	Specificity (95% CI)	AUC (95% CI)
No-FS	0.607 (0.429 to 0.786)	0.667 (0.438 to 0.882)	0.706 (0.474 to 0.923)	0.455 (0.143 to 0.750)	0.588 (0.496 to 0.680)
GS-10	0.643 (0.464 to 0.821)	0.733 (0.500 to 0.938)	0.647 (0.412 to 0.875)	0.636 (0.286 to 0.909)	0.674 (0.583 to 0.765)
HITON-MB	0.857 (0.714 to 0.964)	0.882 (0.692 to 1.000)	0.882 (0.700 to 1.000)	0.818 (0.556 to 1.000)	0.856 (0.781 to 0.930)
BLCD-MB	0.857 (0.714 to 0.964)	0.882 (0.706 to 1.000)	0.882 (0.706 to 1.000)	0.818 (0.556 to 1.000)	0.856 (0.781 to 0.930)

AUC, area under the curve; FS, feature selection.

Table 3 shows that feature selection played a key role and two of the feature selection algorithms (HITON-MB and BLCD-MB) selected only two (mean ADC post one cycle of treatment, mean of the change of the top 15% of k_ep as estimated by the TK model) of 118 features for all the cross-validation runs. HITON-MB and BLCD-MB generated an accuracy of 0.82 (23/28).

When both clinical and imaging features were combined the accuracy increased to 0.86 (24/28) as shown in table 4. The top two predictors were ER+ and the mean of the change of the top 15% of k_ep as estimated by the TK model.

The comparison results of BLR with logistic regression are presented in table 5. BLR outperformed logistic regression in all the evaluation parameters for all the three datasets except the AUC for the clinical variables only dataset.

Table 5.

BLR results compared with non-BLR

Data method	Accuracy (95% CI)	Precision (95% CI)	Recall (95% CI)	Specificity (95% CI)	AUC (95% CI)
Clinical-LR	0.714 (0.536 to 0.857)	0.846 (0.632 to 1.000)	0.647 (0.412 to 0.867)	0.818 (0.556 to 1.000)	0.674 (0.596 to 0.752)
Clinical-BLR	0.786 (0.643 to 0.929)	1.000 (1.000 to 1.000)	0.647 (0.417 to 0.857)	1.000 (1.000 to 1.000)	0.647 (0.581 to 0.713)
Image-LR	0.571 (0.393 to 0.750)	0.647 (0.409 to 0.875)	0.647 (0.412 to 0.875)	0.455 (0.143 to 0.769)	0.620 (0.541 to 0.699)
Image-BLR	0.821 (0.679 to 0.964)	0.875 (0.688 to 1.000)	0.824 (0.615 to 1.000)	0.818 (0.556 to 1.000)	0.856 (0.785 to 0.926)
Clin-Img-LR	0.786 (0.607 to 0.929)	0.824 (0.625 to 1.000)	0.824 (0.619 to 1.000)	0.727 (0.429 to 1.000)	0.840 (0.764 to 0.915)
Clin-Img-BLR	0.857 (0.714 to 0.964)	0.882 (0.692 to 1.000)	0.882 (0.700 to 1.000)	0.818 (0.556 to 1.000)	0.856 (0.781 to 0.930)

AUC, area under the curve; BLR, Bayesian logistic regression; LR, logistic regression.

HITON-MB was used for feature selection. Larger values are in bold. Clin-Img denotes clinical and imaging features.

We used bootstrapping to generate CI to compare the results presented in tables 2 and 4, as well as for tables 3 and 4. If the 95% CI of the performance difference includes 0, then the difference is not significant, otherwise the difference is significant. Our significance testing results (see tables 6 and 7) show that 95% CI of accuracy and AUC include 0, therefore these differences are not significant. The details are provided in tables 6 and 7.

Table 6.

95% CI of performance difference for the different methods between the clinical only dataset and clinical plus imaging dataset (table 2 vs table 4)

FS	Accuracy 95% CI	Precision 95% CI	Recall 95%CI	Specificity 95% C	AUC 95% CI
No FS	−0.321 to 0.036	−0.350 to 0.034	−0.267 to 0.143	−0.636 to 0.100	−0.451 to 0.103
GS-10	−0.250 to 0.036	−0.275 to 0.100	−0.294 to 0.000	−0.429 to 0.222	−0.272 to 0.077
HITON-MB	−0.107 to 0.250	−0.294 to 0.000	0.056 to 0.462	−0.429 to 0.000	−0.057 to 0.475
BLCD-MB	−0.107 to 0.250	−0.294 to 0.000	0.056 to 0.462	−0.429 to 0.000	−0.057 to 0.475

Bold entries are significant (recall using HITON-MB and BLCD-MB).

AUC, area under the curve; FS, feature selection.

Table 7.

95% CI of performance difference for the different methods between the imaging only dataset and clinical plus imaging dataset (table 3 vs table 4)

FS	Accuracy 95%CI	Precision 95% CI	Recall 95% CI	Specificity 95% CI	AUC 95% CI
No-FS	−0.179 to 0.107	−0.191 to 0.099	−0.167 to 0.167	−0.400 to 0.222	−0.206 to 0.211
GS-10	−0.071 to 0.429	−0.152 to 0.462	0.000 to 0.500	−0.400 to 0.571	−0.200 to 0.442
HITON-MB	−0.071 to 0.143	−0.021 to 0.049	−0.133 to 0.263	0.000 to 0.000	−0.059 to 0.059
BLCD-MB	−0.071 to 0.143	−0.021 to 0.049	−0.133 to 0.263	0.000 to 0.000	−0.056 to 0.086

AUC, area under the curve; FS, feature selection.

We assessed the calibration of BLR output by calculating the Hosmer–Lemeshow (H-L) goodness-of-fit statistic. The H-L statistic tests the hypothesis that the observed data are significantly different from the predicted values of the model. A lower H-L statistic and a higher p value (p > 0.05) indicate better calibration (degrees of freedom equal to 2 for χ² distribution). Note that the direction of the p value to indicate significance is different than many standard statistical tests. BLR models with no feature selection and GS-10 using clinical data were well calibrated. Likewise, BLR models with HITON-MB and BLCD-MB using imaging data and imaging plus clinical datasets were also well calibrated. The detailed results are shown in table 8.

Table 8.

BLR output calibrated by the H-L method

FS	Clinical data		Imaging data		Imaging data+clinical data
	H-L statistic	p Value	H-L statistic	p Value	H-L statistic	p Value
No-FS	3.9102	0.1416	9.4337	0.0089	6.4345	0.0401
GS-10	4.0066	0.1349	12.1981	0.0022	185.1241	0.0000
HITON-MB	8.9063	0.0116	3.3800	0.1845	1.2964	0.5230
BLCD-MB	8.9067	0.0116	3.3926	0.1834	1.2964	0.5230

FS, feature selection; H-L, Hosmer–Lemeshow.

Significant (well calibrated) results are shown in bold. A lower H-L statistic and a higher p value (p>0.05) indicate better calibration.

We also evaluated the response to the first cycle of chemotherapy using the current state-of-the-art RECIST criteria as follows. We calculated the percentage change of the longest dimension as measured by MRI from t₁ to t₂ and then performed the receiver operator characteristic analysis. The AUC was 0.67, and the sensitivity, specificity, accuracy, and precision were 81.8%, 64.7%, 71.4%, and 60.0%, respectively. We used the Youden index to calculate these measures.

Discussion

With the numerous options for neoadjuvant treatment that have become available, development of a method to predict response early in the course of therapy is especially needed. Given the large number of patients being treated for breast cancer, and the fact that most of the adverse effects of chemotherapy are cumulative, identifying patients who are not responding to a particular treatment would allow for switching to a potentially more effective regimen and avoiding unnecessary side effects. Unfortunately, by the time most patients are found not to be responding, their disease may no longer be surgically resectable, and this situation could be avoided by the development of techniques to assess response earlier in the treatment regimen. If we could identify non-responders after the first cycle of chemotherapy, we could use alternative agents instead of subjecting the patient to the side effects of therapies that are destined to fail.

Response to the first cycle of chemotherapy is currently measured using physical examination. Only patients who show clear progression by clinical criteria are taken off therapy and often then go directly to mastectomy. The development of imaging parameters that could detect early response to treatment would allow clinicians to change therapy early in the course of disease. Such image-guided treatment strategies have been successfully used in other diseases such as lymphomas.

The ability to identify—early in the course of therapy—patients who are not going to achieve pathological complete response with a given therapeutic regimen is highly significant. In addition to limiting patients’ exposure to the toxicities associated with unsuccessful therapies, it would allow patients the opportunity to switch to a potentially more efficacious treatment. As there are many therapeutic regimens available, and many more being developed, switching treatment early in the course of therapy is a very real option—but only if a reliable method to determine early response were available. Unfortunately, existing methods of determining response are inadequate as they require long (ie, months) clinical observation times and are often unreliable.

Although there are many studies that have used either serial MRI scans or clinical parameters to assess tumor response to NAC, this study is one of the few that has combined both clinical and quantitative MRI parameters to predict response to chemotherapy. This cohort of 28 patients has served as our predictive model learning set. In our study, predictive modeling approaches using quantitative MRI parameters show promise in distinguishing responders from non-responders after the first cycle of NAC for breast cancer. Although imaging had better overall performance than clinical parameters separately, using imaging and clinical variables together boosted the performance of BLR, resulting in an accuracy of 0.86 and an AUC also of 0.86. The gain in performance was not statistically significant. However, the models generated using a combination of clinical and imaging parameters were much better calibrated (see table 8). In general, models generated using HITON-MB and BLCD-MB feature selection methods performed better than GS-10 and no feature selection. This implies that the 118 imaging and possibly the 11 clinical variables used in our study had many irrelevant attributes. The novel MB induction methods such as HITON-MB^{16 24} and BLCD-MB^{19 25} performed better because under the broad distributional assumption of faithfulness, they find a unique and smallest set of predictors that gives the largest predictive performance.²⁶ Typically, researchers have applied feature selection methods based on greedy search that are not optimal and the GS-10 feature selection method is also based on greedy search. The Gaussian assumption made by BLR was violated by many of the variables. It is likely that feature selection mitigated performance degradation due to violation of this assumption.

Predicting pathological complete response with a high degree of certainty following the first cycle of neoadjuvant therapy will enable providers to stratify patients based on response and channel early non-responders to alternative therapeutic protocols. In our study we found that BLR with HITON-MB/BLCD-MB feature selection algorithms using both clinical and imaging parameters generated the best predictive model. This approach was able to yield an AUC of 0.86 and an accuracy of 0.86, with a sensitivity of 0.88 and a specificity of 0.82. In comparison, the current state-of-the-art RECIST approach yielded an AUC of 0.67 and an accuracy of 0.71, with a sensitivity of 0.82 and a specificity of 0.65, which is much lower than our BLR with HITON-MB/BLCD-MB performance.

If the proposed method is validated in a greatly expanded (and potentially multisite) patient set, then there exists the possibility that the approach could be directly incorporated into the current clinical workflow. More specifically, a second quantitative MRI examination (including both DCE-MRI and DW-MRI) would need to be acquired after the first cycle of therapy. Then the data from the pretreatment and post one cycle imaging data could be combined with the clinical data and provided as input to the algorithm/model as described above. The model will then make a prediction as to whether the patient under investigation is likely to achieve pathological complete response. At that point, the decision to stay on the current therapy, switch to a new one, or go straight to surgery would be made by the patient's oncology team. Again, this can only be accomplished if the preliminary results obtained in this study are validated in a larger investigation.

Because of our modest sample size we were not able to test response based on the specific chemotherapeutic agent(s). Likewise, we did not attempt to build patient-specific predictive models using a subset of patients to tailor treatment more effectively. We plan to test the predictive ability of this model in a separate test set of patients from another institution before putting it to clinical use.

Conclusion

We conclude that predictive modeling approaches based on machine learning using readily available clinical and quantitative MRI data show promise in distinguishing breast cancer responders from non-responders after the first cycle of NAC.