Breast cancer survivability prediction using labeled, unlabeled, and pseudo-labeled patient data

Abstract

Background

Prognostic studies of breast cancer survivability have been aided by machine learning algorithms, which can predict the survival of a particular patient based on historical patient data. However, it is not easy to collect labeled patient records. It takes at least 5 years to label a patient record as ‘survived’ or ‘not survived’. Unguided trials of numerous types of oncology therapies are also very expensive. Confidentiality agreements with doctors and patients are also required to obtain labeled patient records.

Proposed method

These difficulties in the collection of labeled patient data have led researchers to consider semi-supervised learning (SSL), a recent machine learning algorithm, because it is also capable of utilizing unlabeled patient data, which is relatively easier to collect. Therefore, it is regarded as an algorithm that could circumvent the known difficulties. However, the fact is yet valid even on SSL that more labeled data lead to better prediction. To compensate for the lack of labeled patient data, we may consider the concept of tagging virtual labels to unlabeled patient data, that is, ‘pseudo-labels,’ and treating them as if they were labeled.

Results

Our proposed algorithm, ‘SSL Co-training’, implements this concept based on SSL. SSL Co-training was tested using the surveillance, epidemiology, and end results database for breast cancer and it delivered a mean accuracy of 76% and a mean area under the curve of 0.81.

Introduction

Breast cancer is the most common type of cancer and the second leading cause of cancer deaths in women.^{1 2} The major clinical problem associated with breast cancer is predicting its outcome (survival or death) after the onset of therapeutically resistant disseminated disease. In many cases, clinically evident metastases have already occurred by the time the primary tumor is diagnosed. In general, treatments such as chemotherapy, hormone therapy, or a combination are considered to reduce the spread of breast cancer because they decrease distant metastases by one-third. Therefore, the ability to predict disease outcomes more accurately would allow physicians to make informed decisions about the potential necessity of adjuvant treatment. This could also lead to the development of individually tailored treatments to maximize the treatment efficiency.^{3 4} Three predictive foci are related to cancer prognosis: the prediction of cancer susceptibility (risk assessment); the prediction of cancer recurrence (redevelopment of cancer after resolution); and the prediction of cancer survivability. In the third case, research is focused on predicting the outcome in terms of life expectancy, survivability, progression, or tumor-drug sensitivity after the diagnosis of the disease. In this study, we focused on survivability prediction, which involves the use of methods and techniques for predicting the survival of a particular patient based on historical data.⁵ In general, ‘survival’ can be defined as the patient remaining alive for a specified period after the diagnosis of the disease. If the patient is still living 1825 days (5 years) after the date of diagnosis, the patient is considered to have survived.⁶ Note that the prediction of survivability is mainly used for analyses in which the interest is observing the time to death of a patient, whereas we addressed it as a classification problem, that is, predicting whether the patient belonged to the group who survived after a specified period.

Research into breast cancer using data mining or machine learning methods has improved treatments, particularly less invasive predictive medicine. In Cruz and Wishart,⁷ the authors conducted a wide-ranging investigation of different machine learning methods, discussing issues related to the types of data incorporated and the performance of these techniques in breast cancer prediction and prognosis. That review provides detailed explanations leading to first-rate research guidelines for the application of machine learning methods during cancer prognosis. Delen et al⁵ used two popular data mining algorithms, artificial neural networks (ANN) and decision trees, together with a common statistical method, logistic regression, to develop prediction models for breast cancer survivability. The decision tree was shown to be the best predictor. An improvement in the results of decision trees for the prognosis of breast cancer survivability is described in Khan et al.⁴ The authors propose a hybrid prognostic scheme based on weighted fuzzy decision trees. This hybrid scheme is an effective alternative to crisp classifiers that are applied independently. This approach analyzes the hybridization of accuracy and interpretability by using fuzzy logic and decision trees. In Thongkam et al,⁸ the authors conducted data preprocessing with RELIEF attribute selection and used the Modest AdaBoost algorithm to predict breast cancer survivability. The study used the Srinagarind Hospital database. The results showed that Modest AdaBoost performed better than Real and Gentle AdaBoost. The authors⁹ then proposed a hybrid scheme to generate a high quality dataset to develop improved breast cancer survival models.

A large volume of breast cancer patient data is required to build predictive models. In the machine learning or data mining domain, the types of data are categorized as ‘labeled’ (feature/label pairs) or ‘unlabeled’ (features without labels). For patient data related to breast cancer survivability, the label tags a patient as ‘survived’ if they survived for a specified period or ‘not survived’ if they did not. Accumulating a large quantity of labeled data is time consuming, costly, and it requires confidentiality agreements. In general, the collection of labeled survival data requires at least 5 years.^{5 6} Moreover, oncologist consultation fees must be paid to confirm survivability. Furthermore, doctors and patients seldom reveal their information. Therefore, is it worth waiting for 5 years to acquire the survival data, while also paying a significant fee, expending considerable effort, and persuading patients to disclose their personal medical data? By contrast, unlabeled data can be collected with much less effort. Censored data are abundant in survival analysis because in many cases the patient data have not been updated recently, so they remain unlabeled. Therefore, an economical solution may be to utilize a large quantity of unlabeled data when building a predictive model. This is achievable using semi-supervised learning (SSL) algorithms, which have recently emerged in the machine learning domain. SSL is an appealing method in areas where labeled data are hard to collect. It has been used in areas such as text classification,¹⁰ text chunking,¹¹ document clustering,¹² time-series classification,¹³ gene expression data classification,^{14 15} visual classification,¹⁶ question-answering tasks for ranking candidate sentences,¹⁷ and webpage classification.¹⁸ As with these examples in other domains, SSL may be a good solution because it can use censored data to modify or reprioritize survivability predictions obtained using labeled patient data alone. A good example of the application of SSL to the prognosis of breast cancer survivability can be found in Shin et al,¹⁹ in which the successful implementation of SSL predicted survival outcomes with reasonable accuracy and stability, thereby relieving oncologists of the burden of collecting labeled patient data.

SSL is capable of utilizing unlabeled patient data, but the prediction accuracy of SSL increases with the amount of labeled patient data, like most algorithms in machine learning. To overcome the aforementioned difficulties in the collection of labeled patient data, it may be possible to obtain more labeled data by generating labels for unlabeled data and treating them as if they were labeled. These may be referred to as ‘pseudo-labeled’ data. Note that labeled and unlabeled patient data are obtained directly from a given dataset, whereas pseudo-labeled data are generated artificially by the proposed model in this paper. This is the motivation of our study. The proposed model is named as SSL Co-training. The model is based on SSL and more than two member models are used to generate pseudo-labels. Unlabeled data become pseudo-labeled when agreement on labeling is reached by the member models. This process is repeated until no more agreement can be obtained. An increased prediction accuracy for breast cancer survivability using labeled, unlabeled, and pseudo-labeled patient data will allow medical oncologists to select the most appropriate treatments for cancer patients.

The remainder of the paper is organized as follows. The next section introduces SSL, which is the base algorithm for our proposed co-training algorithm. The section entitled ‘Proposed method: semi-supervised co-training’ explains our proposed SSL Co-training algorithm in detail. The section on experiments provides the experimental results for a comparison of our proposed algorithm and the latest machine learning models such as support vector machines (SVM), ANN, and graph-based SSL. We used the surveillance, epidemiology, and end results (SEER) cancer incidence database, which is the most comprehensive source of information on cancer incidence and survival in the USA.²⁰ The final section presents our conclusions.

Semi-supervised learning

In many real-world classification problems, the number of class-labeled data points is small because they are often difficult, expensive, or time consuming to acquire and they may require qualified human annotators, as described in Choi and Shin²¹ and Shin and colleagues.^{22 23} By contrast, unlabeled data can be gathered easily and it can provide valuable information for learning, as discussed in He et al.²⁴ However, traditional classification algorithms such as supervised learning algorithms only use labeled data so they encounter difficulties when only a few labeled data are available. SSL uses labeled and unlabeled data to improve the performance of supervised learning, as shown in He et al²⁴  and Chapelle et al.²⁵ In SSL, the classification function is trained using a small set of labeled data 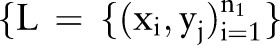and a large set of unlabeled data 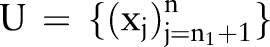, where y=±1 indicates the labels. The total number of data points is n=n₁=n_u.²⁶ There are several types of SSL algorithms, but graph-based SSL was used in our study. In graph-based SSL, a weighted graph is constructed in whiche the nodes represent the labeled and unlabeled data points while the edges reflect the similarity between data points. According to Zhu,²⁷ graph-based SSL methods are non-parametric, discriminative, and transductive in nature. They assume label smoothness over the graph. According to this assumption, if two data points are coupled by a path of high density (eg, it is more likely that both belong to the same group or cluster), their outputs are likely to be close, whereas their outputs need not be close if they are separated by a low-density region.²⁵ There are many graph-based SSL algorithms, for example, mincut, Gaussian random fields and harmonic functions, local and global consistency, Tikhonov regularization, manifold regularization, graph kernels from the Laplacian spectrum, and tree-based Bayes.^{17 27} There are many technical differences, but all of these methods use labeled nodes to set the labels 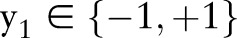, while the unlabeled nodes are set to zero (y_u=0), and the pairwise relationships between nodes are represented using a similarity matrix.²² Figure 1 depicts a graph with eight data points, which are linked by the similarity between them.

1

Figure 1.

Graph-based semi-supervised learning: labeled nodes are represented by ‘+1’ (survived) and ‘−1’ (not survived), whereas unlabeled nodes are represented by ‘?’ (to be predicted).

The similarity between the two nodes x_i and x_j is represented by w_ij in a weight matrix W. A label can propagate from (labeled) node  to (unlabeled) node x_j only when the value of w_ij is large. The value of w_ij can be measured using the Gaussian function:²⁵

In Eq. (1), i∼j indicates that an edge (link) can be constructed between nodes x_i and x_j using the k nearest-neighbors algorithm, where k is a user-defined hyperparameter. The algorithm will output an n-dimensional real-valued vector 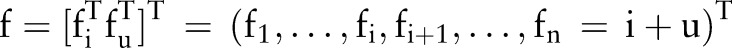, which can generate a threshold value to perform the label predictions on (f₁,…,f_n) as a result of the learning. There are two assumptions: a loss function (f_i should be close to the given label of y_i in labeled nodes) and label smoothness (overall, f_i should not be too different from f_i for the neighboring nodes). These assumptions are reflected in the value of f by minimizing the following quadratic function:^{21 22 28 29}

2

where 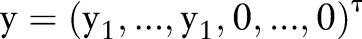and the matrix L, which is known as the graph Laplacian matrix, is defined as L=D − W where . The parameter μ trades off loss and smoothness. Therefore, the solution of this problem becomes

3

Proposed method: semi-supervised co-training

SSL may be a good candidate to use as a predictive model for cancer survivability, particularly when the available dataset for model learning has an abundance of unlabeled patient cases but a lack of labeled ones. Like many other machine learning algorithms, however, the availability of more labeled data leads to better performance. A solution for obtaining more labeled data is to assign labels to unlabeled data, that is, ‘pseudo-labels,’ and use them for model learning as if they were labeled. The proposed model generates pseudo-labels and it increases the performance of SSL. The model involves multiple member models in which pseudo-labels are determined based on agreements among the members. Therefore, it is named SSL Co-training. SSL Co-training is described in this section, in which we limit the number of members to two for the sake of simplicity.

The proposed algorithm is presented in figure 2. Let L and U denote the sets of labeled and unlabeled datasets, respectively. We assume that two member models, F₁ and F₂, are provided (more concretely, two SSL classifiers) and that they are independent. At the start of the algorithm, each of the two classifiers is trained on L and U following the objective function in Eq. (2) as an ordinary SSL classifier. After training, both classifiers produce two sets of prediction scores for U according to Eq. (3). Let us denote them as f₁ and f₂, respectively. The values of f₁ are continuous, so discretization is required to make binary labels for U. A simple rule of setting the midpoint of f₁ as the cutoff value m₁ provides labels for all of the unlabeled data: y¹_u=1 if f₁ is larger than m₁, whereas y¹_u=−1otherwise. For the classifier F₂, y²_u is similarly obtained from the prediction score f₂ and its midpoint of m₂. The labels of F₁ may be concordant or conflict with those of F₂. For unlabeled data points in U, the algorithm assigns pseudo-labels y_u only when all of the members agree on labeling because it gives higher confidence about the newly made labels. An unlabeled data point takes the value of its pseudo-label y_u either from F₁ or from F₂ when y¹_u=y²_u, or it remains unlabeled. The unlabeled data points that failed to obtain pseudo-labels are denoted as ‘boosted samples’. During the next iteration, the unlabeled data points with pseudo-labels are added to the labeled dataset L, whereas the boosted samples remain in the unlabeled dataset U. As the iteration proceeds, the size of L increases whereas that of U decreases. The iteration stops if the size of U (the number of boosted samples) stops decreasing. Figure 3A shows the decreasing pattern for the number of boosted samples during the iterations. Figure 3B shows the increasing pattern of the model performance due to the increasing size of the labeled data points (note that the performances of the two member classifiers also increase). The toy example shown in figure 4 is helpful for understanding the proposed algorithm.

Figure 2.

The semi-supervised learning (SSL) Co-training algorithm.

Figure 3.

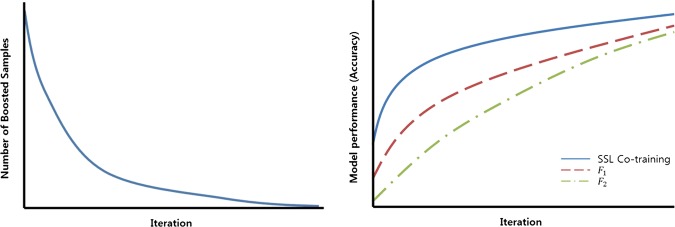
Patterns of (a) the number of boosted samples and (b) model performance during the iterations of semi-supervised learning (SSL) Co-training.

Figure 4.

Schematic description of semi-supervised learning Co-training. In the beginning (iteration 0), the two data points x1 and x5 belong to the labeled set L={(x₁ 1), (x₂, −1)} and the labels are given as y₁=+1 and y₅=−1, respectively. x₂, x₃ and x₄ belong to the unlabeled dataset U={x₂, x₂, x₃}. After training (iteration 1), the predicted labels for the three data points are given by F₁ and F₂. For x₂, the two classifiers agree on labeling y¹₂=y²₂=+1, so its pseudo-label becomes x₂=1. Likewise, x₄ obtains the pseudo-label y₄=−1. However, the two classifiers disagree on the labeling of x₃:y¹₃=+1 but y²₃=−1. Therefore, x₃ is a boosted sample, according to the definition of the proposed algorithm, and it remains unlabeled. In the next iteration (iteration 2), the labeled dataset is increased by the two pseudo-labeled data points L={(x₁,+1),(x₂,+1),(x₄,−1)}, and the unlabeled dataset is decreased to U={x₃}. Similar to the previous iteration, F₁ and F₂ provide x₃ with the predicted labels y¹₃=+1 and y²₃=−1 1, respectively. However, they still fail to agree on the labeling of x₃. The number of boosted samples is the same as the previous iteration, so the algorithm stops.

The member composition used for SSL Co-training can be diverse. First, the number of members is not limited, so they can be multiple. Second, different member models can be built from different data sources or different model parameters. In the current study, the two member models, F₁ and F₂, were built by splitting a dataset into two sub-datasets. The split is conducted so the two sub-sets are maximally uncorrelated, that is, the attributes in one set are not correlated with those in the other set.

Experiments

Data, performance measurement, and experimental setting

The breast cancer survivability dataset (1973–2003) from SEER was used for the experiment, which is an initiative of the National Cancer Institute and the premier source for cancer statistics in the USA (http://www.seer.cancer.gov).²⁰ SEER claims to have one of the most comprehensive collections of cancer statistics. It includes incidence, mortality, prevalence, survival, lifetime risk, and statistics by race/ethnicity. The data consists of 162 500 records with 16 predictor features and one target class variable. There are 16 features: tumor size, number of nodes, number of primaries, age at diagnosis, number of positive nodes, marital status, race, behavior code, grade, extension of tumor, node involvement, histological type according to the international classification of diseases (ICD), primary site, site-specific surgery, radiation, and stage. The target variable ‘survivability’ in the SEER dataset is a binary categorical feature with values ‘–1’ (not survived) or +1 (survived). Table 1 summarizes the features and their descriptions. The breast cancer survival dataset contains 128 469 positive cases and 34 031 negative cases. To avoid the difficulties in model learning caused by the large-sized and class-imbalanced dataset, 40 000 data points were used for the training set and 10 000 for the test set, which were drawn randomly without replacement. The equipoise dataset of 50 000 data points was eventually divided into 10 groups and fivefold cross validation was applied to each.

Table 1.

Prognostic elements related to breast cancer survivability

No.	Features	Description	No.	Features	Description
1	Stage	Defined by size of cancer tumor and its spread	9	Site-specific surgery	Information on surgery during first course of therapy, whether cancer-directed or not
2	Grade	Appearance of tumor and its similarity to more or less aggressive tumors	10	Radiation	None, beam radiation, radioisotopes, refused, recommended, etc.
3	Lymph node involvement	None, (1–3) minimal, (4–9) significant, etc	11	Histological type	Form and structure of tumor
4	Race	Ethnicity: white, black, Chinese, etc	12	Behavior code	Normal or aggressive tumor behavior is defined using codes.
5	Age at diagnosis	Actual age of patient in years	13	No of positive nodes examined	When lymph nodes are involved in cancer, they are known as positive.
6	Marital status	Married, single, divorced, widowed, separated	14	No of nodes examined	Total nodes (positive/negative) examined
7	Primary site	Presence of tumor at particular location in body. Topographical classification of cancer.	15	No of primaries	No of primary tumors (1–6)
8	Tumor size	2–5 cm; at 5 cm, the prognosis worsens	16	Clinical extension of tumor	Defines the spread of the tumor relative to the breast
17	Survivability	Target binary variable defines class of survival of patient.

We used the accuracy and the area under the receiver operating characteristic curve (AUC) as performance measures.^{10 30} Accuracy is a measure of the total number of correct predictions when the value of the classification threshold is set to 0. By contrast, the AUC assesses the overall value of a classifier, which is a threshold-independent measure of model performance based on the receiver operating characteristic curve that plots the trade-offs between sensitivity and 1−specificity for all possible values of threshold.

Four representative models, that is, ANN, SVM, SSL, and SSL-Co training, were used to perform classification for breast cancer survivability. The model parameters were searched over the following ranges for the respective models. For ANN, the number of ‘hidden nodes’ and the ‘random seed’ for the initial weights were searched over hidden-node={3, 6, 9, 12, 15} and random-seed={1, 3, 5, 7, 10}.³¹ For SVM, the values for the RBF kernel width ‘gamma’ and the loss penalty term ‘C’ were selected by searching the ranges of C={0.2, 0.4, 0.6, 0.8, 1} and gamma={0.0001, 0.001, 0.01, 0.1, 1}.³² For the SSL and SSL-Co training models, the values for the number of neighbors ‘k’ and the trade-off parameter ‘mu’ between the smoothness condition and loss condition in (1) were searched over k={3, 7, 15, 20, 30} and mu={0.0001, 0.01, 1, 100, 1000}, respectively.

Results

SSL Co-training using each of the 10 datasets proceeded with iterations between 3 and 5. Figure 5 shows the typical changes in the number of boosted samples and AUC as the iterations proceeded. The number of boosted samples decreased as the iterations proceeded, as shown in figure 5A, while the AUC performance in figure 5B increased due to the enhancement of the labeled dataset with pseudo-labeled data points. Note that the increasing patterns in the AUC for the two member models F₁ and F₂ demonstrate the success of co-training between them, that is, F₁ helps to raise the performance of F₂ and vice versa.

Figure 5.

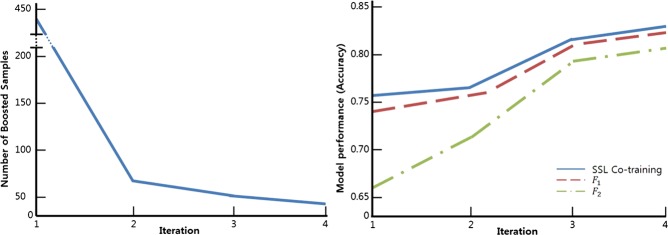
Changes during semi-supervised learning (SSL) Co-training iterations: (A) the number of boosted samples and (B) area under the curve.

Table 2 shows a comparison of the results with ANN, SVM, SSL, and SSL Co-training in terms of the accuracy and AUC. For each of the four models, the best performance was selected by searching over the respective model-parameter space. For the 10 datasets, the best performance among the four models is marked in bold face. In terms of accuracy, SSL Co-training delivered outstanding performance with an average accuracy of 0.76 while SSL was ranked the second best. In terms of the AUC, SSL Co-training produced an average AUC of 0.81, which was the best of the three models, although comparable performance was delivered by SVM. Figure 6 summarizes the performance of the four models using two radar graphs.

Table 2.

Performance comparison using ANN, SVM, SSL, and SSL Co-training with the 10 datasets

Dataset	Accuracy				AUC
	ANN	SVM	SSL	SSL Co-training	ANN	SVM	SSL	SSL Co-training
1	0.66	0.52	0.72	0.77	0.68	0.79	0.77	0.84
2	0.67	0.52	0.72	0.79	0.72	0.79	0.79	0.82
3	0.62	0.50	0.70	0.76	0.68	0.80	0.78	0.78
4	0.67	0.51	0.68	0.75	0.72	0.79	0.76	0.81
5	0.64	0.52	0.71	0.77	0.66	0.82	0.78	0.82
6	0.62	0.52	0.71	0.76	0.68	0.78	0.77	0.83
7	0.63	0.51	0.69	0.77	0.67	0.79	0.77	0.83
8	0.69	0.51	0.73	0.76	0.73	0.82	0.80	0.82
9	0.66	0.52	0.70	0.74	0.71	0.81	0.78	0.78
10	0.64	0.51	0.73	0.77	0.73	0.81	0.80	0.81
Average	0.65	0.51	0.70	0.76	0.70	0.80	0.78	0.81

ANN, artificial neural network; AUC, area under the curve; SSL, semi-supervised learning; SVM, support vector machine.

Bold numbers represent best performance among the four models.

Figure 6.

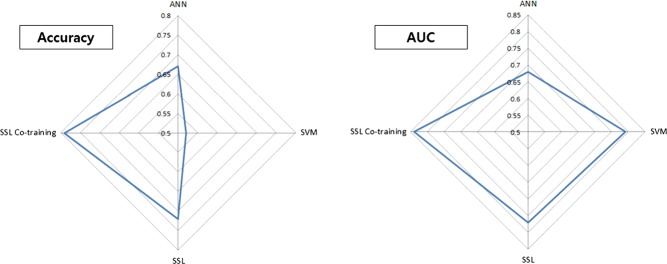
Performance comparison using artificial neural networks (ANN), support vector machines (SVM), semi-supervised learning (SSL), and SSL Co-training: (A) accuracy and (B) area under the curve (AUC).

Conclusion

To predict cancer survivability, the acquisition of more patient data with labels of either ‘survived’ or ‘not survived’ is an important issue because better predictive models can be produced based on them. In practice, however, there are many obstacles when collecting patient labels because of the limitations of time, cost, and confidentiality conflicts. Therefore, researchers have been attracted to predictive models that can also utilize unlabeled patient data, which are relatively more abundant. SSL has thus been highlighted as a promising candidate. However, the tenet that ‘the more labeled data, the better prediction’ still applies to SSL because it is a learning algorithm guided by information contained in the labeled data, like other machine learning algorithms. To compensate for the lack of labeled data, therefore, SSL Co-training was proposed in this paper. Our proposed algorithm generates pseudo-labels by co-training multiple SSL member models, which assign them to unlabeled data before treating them as if they were labeled. As the process iterates, the labeled data increase and the predictive performance of SSL also increases. An empirical validation of SSL Co-training using the SEER breast cancer database demonstrated its superior performance compared with the most representative machine learning algorithms such as ANN, SVM, and ordinary SSL. Using pseudo-labeled patient data, as well as labeled and unlabeled patient data, will improve the technical quality of the prognosis of cancer survivability, which is expected to lead to better treatment for cancer patients.

Our proposed SSL Co-training approach remains in a nascent stage. Therefore, further studies should be carried out in the near future. The composition of the member models for co-training will be addressed in future research, that is, we need to determine the optimum member size and how to make them sufficiently diverse. More sophisticated methods are also required in the pseudo-labeling process, that is, we need to set the cutoff value to improve the confidence of labeling.