Role of genetic heterogeneity and epistasis in bladder cancer susceptibility and outcome: a learning classifier system approach

Abstract

Background and objective

Detecting complex patterns of association between genetic or environmental risk factors and disease risk has become an important target for epidemiological research. In particular, strategies that provide multifactor interactions or heterogeneous patterns of association can offer new insights into association studies for which traditional analytic tools have had limited success.

Materials and methods

To concurrently examine these phenomena, previous work has successfully considered the application of learning classifier systems (LCSs), a flexible class of evolutionary algorithms that distributes learned associations over a population of rules. Subsequent work dealt with the inherent problems of knowledge discovery and interpretation within these algorithms, allowing for the characterization of heterogeneous patterns of association. Whereas these previous advancements were evaluated using complex simulation studies, this study applied these collective works to a ‘real-world’ genetic epidemiology study of bladder cancer susceptibility.

Results and discussion

We replicated the identification of previously characterized factors that modify bladder cancer risk—namely, single nucleotide polymorphisms from a DNA repair gene, and smoking. Furthermore, we identified potentially heterogeneous groups of subjects characterized by distinct patterns of association. Cox proportional hazard models comparing clinical outcome variables between the cases of the two largest groups yielded a significant, meaningful difference in survival time in years (survivorship). A marginally significant difference in recurrence time was also noted. These results support the hypothesis that an LCS approach can offer greater insight into complex patterns of association.

Conclusions

This methodology appears to be well suited to the dissection of disease heterogeneity, a key component in the advancement of personalized medicine.

Background and significance

A major goal for epidemiologists is the identification of genetic and environmental factors that predict common complex diseases (eg, cancer). Traditional Mendelian (single-gene) approaches, such as those typically adopted in genome-wide association studies, have yielded limited success when applied to most common diseases, at best identifying common variants that contribute only modestly to a given phenotype.^{1 2} Perceived problems, common to these analyses, such as the lack of reproducibility,^{3 4} the observation of ‘missing heritability’,^{2 5 6} and the sheer number of candidate factors identified as potentially related to disease, are all suggestive of a complex pattern of association. Complexity references the number of factors involved, the influence of interaction (eg, additive or epistatic), and the inconsistency of heterogeneity. From an evolutionary perspective, these types of complex disease associations would be expected as the logical byproduct of canalization and the accumulation of cryptic genetic variation.⁷

The term epistasis was coined to describe a genetic ‘masking’ effect viewed as a multi-locus extension of the dominance phenomenon, where a variant at one locus prevents the variant at another locus from manifesting its effect.⁸ This type of interaction might plausibly occur between sets of genetic or environmental factors. To date, the detection and modeling of epistasis and general interaction effects, has received a great deal of attention. Random forests,⁹ multifactor dimensionality reduction (MDR),¹⁰ detection of informative combined effects (DICE),¹¹ combinatorial partitioning method,¹² logistic regression,¹³ patterning and recursive partitioning,¹⁴ and Bayesian pathway modeling¹⁵ represent just a handful of the available strategies. By comparison, strategies that accommodate heterogeneity are in the minority. The meaning of the term heterogeneity depends on the context. In the context of admixture, heterogeneity simply refers to genetic differences in population structure.¹⁶

In genetic modeling, a heterogeneous model describes the independent effect of a number of factors.¹⁷ Similarly, in association studies, heterogeneity refers to an independence effect seen in three different phenomena: allelic heterogeneity, locus heterogeneity, and phenocopy.¹⁸ Allelic heterogeneity occurs when two or more alleles of a single locus are independently associated with the same trait, while locus heterogeneity occurs when two or more DNA sequence variations at distinct loci are independently associated with the same trait. Heterogeneity, typically classified as either genetic (locus and allelic) or environmental (ie, phenocopy), occurs when an individual, or set, of factors is independently predictive of the same phenotype. Additionally, trait heterogeneity occurs when a trait or disease has been defined with insufficient specificity such that it is actually two or more distinct underlying traits.¹⁸ In the context of mining genetic and environmental patterns within an association study, there is no practical distinction between genetic heterogeneity, trait heterogeneity, and phenocopy, since these phenomena manifest the same type of independent associations. From a computer science prospective, the problem of heterogeneity is similar to a latent or ‘hidden’ class problem. While the disease status (case or control) of each patient is already known, the individuals making up either class would be more accurately subgrouped into two or more ‘hidden’ classes, each characterized by an independent predictive model of disease.

As mentioned, there are far fewer successful strategies for dealing with the heterogeneity problem. Most strategies that examine epistasis, neglect to consider the impact of heterogeneity. An exception to this is seen in an evaluation of MDR that demonstrated that simulated heterogeneity dramatically hinders MDR's power to detect all underlying modeled factors.¹⁹ Statistical approaches such as the admixture test,²⁰ M test,²¹ and β test²² are specific to family-based data and can only identify the existence of heterogeneity rather than characterize it. The most common approach to heterogeneity is to try to remove its confounding effect by data stratification. This has been done using strategies such as ordered subset analysis,²³ latent class analysis,^{24 25} tree-based recursive partitioning,²⁶ and clustering.^{27 28} These methods preprocess the dataset based on genetic risk factors, demographic data, phenotypic data, or endophenotypes in order to form more homogeneous subsets of subjects. This is in line with the standard epidemiological paradigm that seeks to find a single best disease model within a given homogeneous sample. The obvious drawback of these methods is that their success completely relies on the availability, quality, and relevance of these covariates. Additionally, stratification represents a relative reduction in sample size, leading to an inevitable loss in power to detect associations within these homogeneous subsets.

Only a few strategies have been considered that concurrently examine the problems of epistasis and heterogeneity without resorting to some form of stratification. These include MDR,^{19 29} random forests,³⁰ association rule discovery,³¹ and clique-finding for heterogeneity and multidimensionality in biomedical and epidemiological research (CHAMBER).³² While some algorithms have been successful in accommodating the problem of heterogeneity, explicit characterization has remained a major challenge. CHAMBER, an algorithm that uses graph building was the first to consider the joint characterization of interaction and heterogeneity. Specifically, heterogeneity was characterized through the identification of groups of individuals, within which, different predictive attributes were correlated with disease risk. In the context of data mining and machine learning, the word attribute refers to a variable such as a single nucleotide polymorphism (SNP) or a demographic variable such as gender that is used to make a prediction. While CHAMBER represents a unique step in the direction of data-driven approaches to heterogeneity and epistasis, its exhaustive search strategy limits its application to much smaller datasets. Also, the CHAMBER algorithm has yet to be externally applied, and is not accessible for download.

Given the apparent complexity of common disease, and the likelihood that multi-locus interactions and heterogeneity are present and likely to be ubiquitous components of disease risk,^{33 34} it is critical to develop powerful new strategies that concurrently deal with these phenomena. Strategies that make assumptions about the nature, number, or source of underlying factors will inevitably be susceptible to complicating phenomena. Learning classifier systems (LCSs)³⁵ are a rule-based class of algorithms that combine machine learning with evolutionary computing and other heuristics to produce an adaptive system. They represent solutions as sets of rules, affording them the ability to learn iteratively, form niches, and adapt. This class of algorithm breaks from the traditional single model paradigm by evolving a solution comprising multiple rules, consequently avoiding the need for data stratification. These characteristics make the application of LCSs to the problem of heterogeneity, in particular, intrinsically appealing.

Previously, we explored the application of different LCS algorithms to the detection and modeling of simulated epistatic and heterogeneous genetic disease associations and demonstrated their ability to successfully detect predictive factors in the presence of heterogeneity, and an extreme, precisely defined form of epistasis referred to as pure epistasis.^{36 37} A purely epistatic interaction occurs between n loci that do not display any main effects.^{38 39} These proof-of-principle analyses identified Michigan-style LCSs (M-LCSs) as the most promising implementation for our particularly complex, noisy problem domain. However, knowledge discovery in M-LCSs remained problematic. In another study⁴⁰ we developed an analysis pipeline with visualization-guided knowledge discovery to overcome this obstacle. In addition to significance testing, the pipeline presented subjective visualization strategies for inferring patterns of attribute interaction and heterogeneity from the rule-set. Still lacking, was a strategy for explicitly identifying heterogeneity and linking instances in the dataset to respective heterogeneous subgroups. With AF-UCS (attribute feedback-sUpervised Classifier System)⁴¹ we introduced attribute tracking and feedback as mechanisms to deal with this problem, and improve learning and generalization in the M-LCS algorithm. While the aforementioned efforts to apply LCSs to the characterization of both epistatic and heterogeneous patterns of association were evaluated over a diverse spectrum of simulated datasets, we have yet to apply them to a real-world investigation of common complex disease. In this study we applied our extended M-LCS approach to the investigation of bladder cancer susceptibility.

Like other common complex diseases, cancer is recognized as a multifactorial disease that results from complex interactions between many genetic and environmental factors. In an effort to validate the utility of our M-LCS approach we investigated the relationship between DNA repair gene SNPs, smoking, and bladder cancer susceptibility in 355 cases and 559 controls enrolled in a population-based study of bladder cancer. This dataset was previously analyzed by Andrew et al⁴² using a multifaceted statistical approach that included the application of logistic regression, MDR, and information theory. These previous findings identified XPD codon 751 and 312 SNPs together with smoking as the best predictors of bladder cancer.

In this study, we applied AF-UCS,⁴¹ to the same dataset in an attempt to replicate these previous findings and characterize any patterns of interaction or heterogeneity that might be associated with bladder cancer risk. We have demonstrated how the clustering of attribute tracking scores within instances of the dataset may be used to identify sample subsets, after training. These subsets aim to capture heterogeneous patterns of disease associations. Additionally, we have attempted to validate these subgroups with statistical comparisons examining clinical outcome variables. Specifically, we examined age of diagnosis, survivorship, age of recurrence, and tumor stage/grade between reliable patient clusters.

Materials and methods

In this section we describe (1) the bladder cancer data examined in this study, (2) the AF-UCS algorithm and associated run parameters, and (3) the analytical pipeline and statistical analysis used in this study.

Dataset

The bladder cancer dataset considered in this study was previously collected and examined by Andrew et al.⁴² After removal of subjects with missing SNP values, the dataset included 355 cases and 559 controls each with seven SNPs, age, gender, and cigarette smoking history. DNA repair gene SNPs were examined that had been previously related to bladder cancer (XRCC1, XRCC3, XPD, XPC) and other pathway members that physically interact with these genes (APE1). A full description of this dataset is given by Andrews et al.⁴² Along with the variables considered in that publication,⁴² additional clinical outcome variables were recorded for the cases in this study group that are used in this study. These included (1) tumor stage and grade, (2) age at diagnosis (years), (3) survival time in years (ie, survivorship), and (4) time to first recurrence in years. Censoring occurs when we do not know the time of death or recurrence for all subjects. Censoring indicators were included in the dataset corresponding to both survivorship and recurrence. Tumor stage and grade was included as a categorical variable with the following categories: (1) non-invasive low grade, (2) non-invasive missing grade, (3) non-invasive high grade, (4) in situ tumor, (5) stage II, (6) stage III, and (7) stage IV. Non-invasive, low-grade tumors are the least aggressive and have the best prognosis. Stage II and higher-stage tumors are tumors that are ‘invading’ through the bladder wall, which can then metastasize to other organs. In this study, analysis of the described dataset was completed without access to unique patient identifiers in accordance with institutional review board human subject protection. Any identifiers added to track patients during learning, clustering, and comparison of clinical variables, were arbitrarily assigned for the purposes of this study.

Summary of previous findings

The results of previous analyses performed by Andrew et al⁴² are summarized here. Overall, no significant associations were identified between any single DNA repair gene SNP and bladder cancer risk. A marginally significantly increased risk was seen in the XPD codon 751 homozygote variant among subjects who never smoked. The XRCC1 191 variant allele was associated with reduced bladder cancer risk among heavy smokers. MDR analysis identified pack-years smoking as the strongest single factor for predicting bladder cancer risk (average testing accuracy=0.63). The best two-factor model included XPD 751 and XPD 312 (average testing accuracy=0.65). The best three-factor model (also the best overall model) added pack-years smoking to XPD 751 and XPD 312 (average testing accuracy=0.66). The application of information theory suggested that the relationship between the two XPD SNPs and bladder cancer is mostly non-additive (ie, epistatic), while the effect of smoking is mostly additive. It was noted that the two XPD SNPs were in significant linkage disequilibrium. Further analysis indicated that the combination of these SNPs into a haplotype indicated that a variant XPD haplotype was more susceptible to bladder cancer, an effect that was magnified with the inclusion of smoking. XPD stands for xeroderma pigmentosum group D, the gene encoding an enzyme in the nucleotide excision repair pathway. This enzyme is known to remove certain DNA crosslinks, ultraviolet photolesions, and bulky chemical adducts.⁴³ Interactions between XPD 312 and XPD 751 have also been seen in relation to lung cancer risk, and several studies found that the risk of lung cancer associated with the variant allele was higher among non-smokers than among smokers.^{44 45}

AF-UCS

The most unique feature of M-LCS is that it evolves a population of rules which collectively constitute the learned prediction model. Learning proceeds iteratively, with the rule population training on one instance from the dataset at a time. Rule discovery is largely achieved with a genetic algorithm operating at the level of individual rules within the population. For a complete LCS introduction and review, see Urbanowicz and Moore.³⁵ UCS⁴⁶ is an M-LCS based largely on the popular XCS (eXtended Classifier System) algorithm⁴⁷ but replaces reinforcement learning with supervised learning. UCS was designed specifically to deal with single-step problems such as classification and data mining, where delayed reward is irrelevant, and showed particular promise when applied to epistasis and heterogeneity as we showed in a previous study.³⁶ Previously, we developed the AF-UCS algorithm,⁴¹ an expansion of UCS which incorporated attribute tracking and feedback into the basic supervised learning algorithm. The AF-UCS algorithm is outlined in figure 1. Each rule includes a condition and class (ie, if certain instance attributes have a specific state, then the rule predicts the specified class). Rules are built using a quaternary representation, where each attribute of the condition will either specify an SNP genotype encoding (ie, 0, 1, 2) or that attribute will be generalized (ie, ‘#’, wild/don't care). The right-hand yellow box in figure 1 gives an example (C) including three hypothetical rules represented in this manner. Notice that their conditions all match the example training instance, and they all specify the correct class of the instance.

Figure 1.

Outline of the AF-UCS (attribute feedback-sUpervised Classifier System) algorithm. (1) Learning occurs iteratively, focusing on a single training instance from the dataset at a time. (2) Training instance passed to the population of rules (P). (3) Match set (M) is formed, including any rule in (P) that that has a condition matching the attribute states of the instance. (4) Correct set (C) is formed, including any rule in (M) which specifies the correct class of the instance. (5) If no rules are found for (C), randomly generate such a rule using the covering mechanism. (6) Update rule parameters in (M) and (C) (eg, rule fitness). (7) Use rules in (C) to update attribute tracking scores for current instance. (8) The genetic algorithm (GA) selects parent rules from (C) based on fitness and generates offspring rules which are added to (P). If attribute feedback is being used, the attribute tracking scores for the current instance are applied as weights to guide the GA. (9) Deletion mechanism removes rules from (P) based on fitness whenever the size of (P) is greater than the user-specified maximum population size.

While the majority of AF-UCS is equivalent to UCS, the dark blue box in figure 1 highlights the mechanism unique to our algorithm. Attribute tracking is a collective form of memory designed to be applied to single-step supervised learning problems. Essentially this mechanism learns which attributes are most important to the accurate classification of each individual instance, storing and accumulating this knowledge independently of the rule population. Attribute feedback is a heuristic that draws upon the knowledge learned in attribute tracking to promote efficient generalization and improve learning in the presence of noisy, complex, and heterogeneous data. Attribute feedback probabilistically directs generalization pressures in the GA based on relative attribute tracking scores. Specifically, attribute feedback has been applied to the mutation and crossover mechanisms.

Previously, AF-UCS was evaluated using only simulated datasets. In order to accommodate the nature of real-world datasets, one minor modification was made to the algorithm. To address the calculation of training and testing accuracy when the algorithm is applied to unbalanced datasets we replaced the traditional accuracy calculation with balanced accuracy as described by Velez et al.⁴⁸

We had previously implemented attribute tracking and feedback into AF-UCS, a python encoding of the UCS algorithm.^{36 41} We adopted mostly default M-LCS run parameters. Parameters unique to this study include 200 000 learning iterations, a rule population size of 1000, tournament selection, uniform crossover, subsumption, attribute mutation probability=0.04, crossover probability=0.8, and a ν of 1. ν has been described as a ‘constant set by the user that determines the strength (of) pressure toward accurate classifiers’⁴⁹ and is typically set to 10 by default. A low ν was used to place less emphasis on high accuracy in this type of noisy problem domain, where 100% accuracy is only indicative of over-fitting. Also, as in our previous study,³⁶ we employed a quaternary rule representation, where for each SNP attribute, a rule can specify genotype or covariates as (0, 1, or 2), or instead generalize with ‘#’, a character that implies that the rule does not care about the state of that particular attribute. Generally speaking, the use of larger population sizes and a greater number of learning iterations can improve the resulting performance of the evolved M-LCS rule population. This study adopted modest values for these parameters. It is likely that optimization of these and other run parameters would further improve the performance of the AF-UCS algorithm.

Statistical analysis

We adopted the analysis pipeline⁴⁰ for the identification of significant predictive attributes identified by the AF-UCS algorithm. We extended this pipeline for the analysis of real data. In summary, our analysis includes the following steps: (1) run the AF-UCS algorithm on the dataset using 10-fold cross-validation (CV), (2) run a permutation test with 1000 permutations, (3) confirm significance of testing accuracy, (4) identify significant attributes and significantly co-occurring pairs of attributes, (5) train the AF-UCS algorithm on the whole dataset (no CV), (6) generate visualization for pattern characterization, (7) repeat steps 1–3 as a second pass on the dataset that only includes attributes identified as significant from the first pass, (8) identify significant, stable clusters of subjects using attribute tracking scores, and (9) compare clinical variables between identified subject clusters. Although we do not claim that this analysis pipeline is necessarily optimal, we have attempted to assemble a logical series of analytical steps that rely primarily on statistically significant empirical observations. Indeed it is likely that there are other reasonable ways to approach knowledge discovery and hypothesis generation in this context.

Our first-pass analysis of the bladder cancer data (summarized by steps 1–6) began by running AF-UCS on the dataset using 10-fold CV strategy in order to determine average testing accuracy and account for over-fitting. The dataset was randomly partitioned into 10 equal parts and AF-UCS was run 10 separate times during which 9/10 of the data was used to train the algorithm, and the other 1/10 was set aside for testing. We averaged training and testing accuracies over these 10 runs. Next we set up our permutation test. We generated 1000 permuted versions of the original dataset by randomly permuting the affection status (class) of all samples, while preserving the number of cases and controls. For each permuted dataset we ran UCS using 10-fold CV. In total, permutation testing required 10 000 runs of AF-UCS. We performed this analysis using ‘Discovery’, a 1576 processor Linux cluster.

Next, we confirmed that the average testing accuracy was significantly higher than expected by random chance. If average testing accuracy had not been significantly high, this would have suggested that AF-UCS was unable to learn any useful generalizations from the data, excluding a need for further analysis. We used a typical one-tailed permutation test with a significance threshold of p<0.05. Once a significant testing accuracy was confirmed, we used the permutation test to identify attributes in the dataset that showed significant importance in making accurate classifications. As detailed elsewhere,⁴⁰ we used the following statistics for making such an inference from the rule population: (1) specificity sum (SpS) and (2) accuracy-weighted specificity sum (AWSpS). Additionally, we used the permutation test to evaluate attribute interactions and to help to discriminate between interaction and heterogeneity. This was achieved by evaluating a co-occurrence statistic (CoS) that examined all pairwise attribute co-occurrence within rules of the population.⁴⁰ We calculated CoS for every non-redundant pairwise combination of attributes in the dataset. In this 10-attribute dataset we calculated 45 CoSs. These CoSs were also used to generate the co-occurrence network given in the results. To generate the co-occurrence network we used Gephi (http://gephi.org/)—open-source graph visualization software. With the 45 CoSs calculated above, we generated an adjacency matrix in a format consistent with Gephi requirements. Using Gephi, we generated a fully connected, undirected network, where nodes represent individual attributes, the diameter of a node is the SpS for that attribute, edges represent co-occurrence, and the thickness of an edge is the respective CoS. Gephi offers a built-in function to filter edges from the network based on edge weight. We used this feature to focus on significant co-occurrence attribute pairs.

Next we trained AF-UCS on the entire dataset with no CV. This was for rule population visualization purposes (ie, the generation of a rule population heat-map). In another study⁴⁰ we detailed the re-encoding of the rule-population in preparation for visualization. We employed agglomerative hierarchical clustering using hamming distance as the distance metric http://gephi.org/. Clustering was performed on both axes (ie, across rules and attributes). Both clustering and 2D heat-map visualization were performed in R using the hclust and gplots packages, respectively.

We extended this analysis to a second pass over the data that focused exclusively on those attributes identified as significant in the first pass. We repeated steps 1–3 including CV, permutation testing, and statistical evaluation of average testing accuracy. Also, we ran AF-UCS without CV on a subset of the dataset that included only these significant attributes in order to obtain a matrix of attribute tracking scores for further investigation.

Attribute tracking keeps a record of which attributes are most important for accurate classification for each subject in the dataset. Therefore, by clustering subjects in the dataset by these attribute tracking scores we aimed to identify homogeneous groups of subjects defined by similar patterns of attributes determined to be important for accurate classification. As we discussed elsewhere,⁴¹ before clustering we normalized attribute tracking scores within each instance such that they lay between 0 and 1. Normalization was achieved by dividing each tracking score by the sum of all tracking scores for that instance. This allowed us to compare relative attribute patterns between instances in the dataset.

Our strategy for the selection of significant stable subject clusters involved hierarchical clustering with an assessment of uncertainty. We applied pvclust, an R package that calculated p values for hierarchical clustering via multiscale bootstrap resampling.⁵⁰ Significant clusters were identified using approximately unbiased (AU) p values, where AU values >95% were deemed significant. We applied the default ‘average’ method of agglomerative clustering, and the default distance measure of ‘correlation’. One thousand bootstrap replications were performed in determining AU values. Once calculation of p values was complete we assigned alphabetical group IDs to unique, significant clusters. Note that clusters included both patients with bladder cancer and healthy control subjects. Finally, we compared the clinical variables between cases found in respective significant subject clusters. The clinical variable data was only applicable to the bladder cancer cases in our study group. Thus, control subjects were not used for this portion of the analysis. All the following statistical evaluations were also performed in R.

Next, we discuss our evaluation of the continuous clinical variables (ie, age at diagnosis, survivorship, and time to recurrence). The non-parametric Kruskal–Wallis one-way analysis of variance was used to determine whether these clinical variables differ by cluster. Pairwise comparisons between subject clusters were performed using the non-parametric Mann–Whitney test. In addition, we performed ‘time-to-failure’ analyses (ie, survival analysis) for age at diagnosis, survivorship, and time to recurrence including failure curves (ie, Kaplan–Meier curves) for each. Since both survivorship and time to recurrence data include censored values, we adopted a Cox proportional hazard regression model (coxph), most widely used in medical studies. Since age at diagnosis could logically affect survivorship or time to recurrence we included it as a covariate in the covariance analysis model. We began with a Cox proportional hazard model including the interaction between cluster ID and age at diagnosis. Next we used the step function to choose the best factors to keep in the model by Akaike's information criterion (AIC). AIC takes into account the balance between goodness of fit, and the number of parameters included in a model. Follow-up analysis of variance between the best model identified by AIC, and a similar model excluding group specification, indicates whether there is a significant difference in our clinical outcome variable based on group designation. Comparisons were considered to be significant at p≤0.05. Since tumor stage and grade was a categorical variable, we adopted a χ² test of homogeneity in order to look for differences between the cases of different clusters. Noting that certain cells of the table had very few counts, we followed up with a Fisher's exact test.

Results and discussion

After a first-pass analysis of the bladder cancer dataset with AF-UCS we observed an average training accuracy of 0.6995 and a significant average testing accuracy of 0.6042 averaged over 10-fold CV (p=0.001). Table 1 summarizes the SpS and AWSpS statistics for each factor in the dataset. Note that significantly larger SpS and AWSpS statistics were seen for XPD 751, XPD 312, and pack-years than would be expected by chance. This indicates that these attributes were predictive of disease risk. This finding corresponds with the results obtained using MDR in the study by Andrew et al.⁴² Although not statistically significant, the next largest SpS or AWSpS was seen for XRCC1 194. Recall that the study by Andrew et al,⁴² a smoking-conditional decreased risk was found for this SNP.

Table 1.

SpS, AWSpS, and significant CoS results

Attribute	SpS	p Value	AWSpS	p Value	Attribute Pairs	CoS	p Value
XPD.751	5686	0.001*	4001.86	0.001*	XPD.751 & XPD.312	3367	0.001*
XPD.312	5077	0.007*	3550.64	0.001*	XPD.751 & pack.yr	2757	0.001*
pack.yr	4827	0.037*	3383.68	0.006*	XPD.751 & XRCC1.194	2530	0.001*
XRCC1.194	4206	0.461	2818.81	0.179	XPD.312 & pack.yr	2375	0.006*
age.50	4151	0.721	2800.63	0.308	XPD.751 & age.50	2345	0.016*
male	4048	0.745	2752.61	0.358	XRCC1.194 & pack.yr	2120	0.04*
XRCC1.399	3797	0.729	2595.78	0.427	XPD.312 & XRCC1.194	2105	0.046*
APE1	3524	0.891	2418.03	0.667
XRCC3	3172	0.989	2166.09	0.91
XPC.PAT	2975	1.0	1994.75	0.98

AWSpS, accuracy-weighted specificity sum; CoS, co-occurrence statistic; SpS, specificity sum.

*p Value <0.05.

Table 1 also summarizes significant results for the CoS statistic. Seven of the possible 45 attribute combinations were found to occur more frequently than would be expected by chance. In particular, notice that the largest CoS value was found for the attribute combination (XPD 751 & XPD 312). This is in line with the best two-attribute model identified by MDR in Andrew et al.⁴² We also noted that the (XPD 751 & pack-year) CoS value was the second most strongly observed pair. This seems to correspond with the observation in Andrew et al⁴² that the XPD 751 homozygote variant indicated a marginally significant increase in risk among subjects who never smoked. In fact, all pairwise combinations including XPD 751, XPD 312, and pack-year were found to be significantly over-represented here, including (XPD 312 & pack-year). However, the CoS value for (XPD 751 & XPD 312) was about 1.5 times larger than that for (XPD 312 & pack-year). The relative dissimilarity of the CoSs for these pairwise combinations does not support a clear three-way interaction to explain the dataset as a whole.⁴⁰ If it did, we would expect more similar CoS scores for all three combinations.

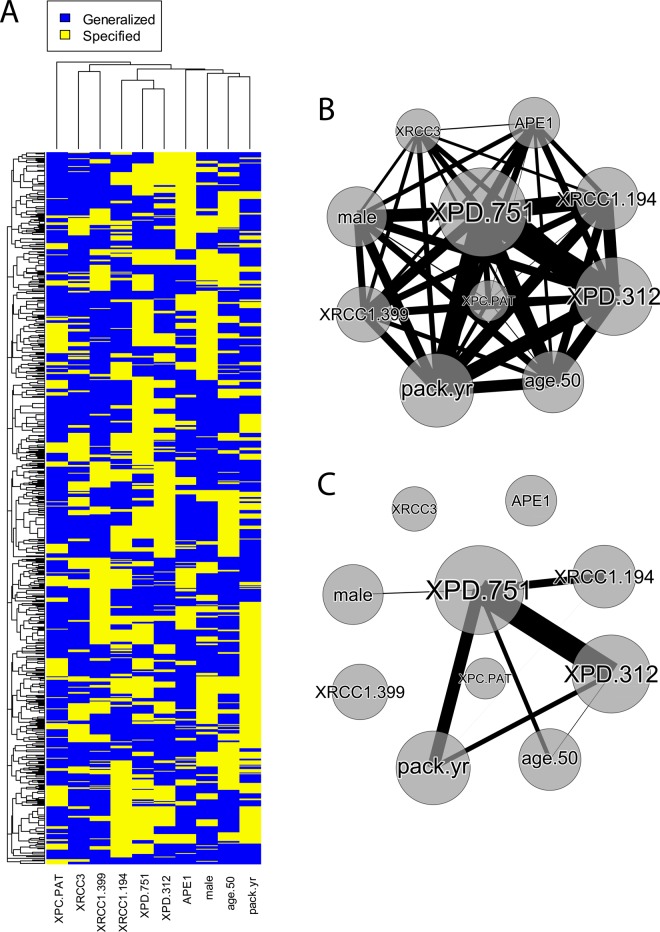
Figure 2A presents a visualization of the rule population evolved by AF-UCS when trained on the entire bladder cancer dataset. Although somewhat noisy, couple trends can be seen within the rule population. First, XPD 751 and XPD 312 clustered together as columns indicating a tendency for both SNPs to be specified in rules concurrently. Second, specification of pack-years did not cluster together with XPD 751 and XPD 312, suggesting an independent, and potentially heterogeneous relationship. Figure 2B,C give the co-occurrence network constructed using the CoS values from this analysis. It represents a direct visualization of the results presented in table 1. Again we observed evidence of interaction between XPD 751 and XPD 312, and somewhat less evidence for other attribute pairs.

Figure 2.

Rule population visualizations. (A) Heat-map visualization of the evolved AF-UCS (attribute feedback-sUpervised Classifier System) rule population. Each row in the heat-map is 1 of 1000 rules comprising the population. Each column is one of the 10 attributes. Yellow indicates specification of a respective attribute within a rule, while blue indicates generalization (ie, ‘#’/‘don't care’. The attribute ‘male’ refers to gender. (B) Illustrates the co-occurrence network, appearing as a fully connected network before any filtering is applied. The diameter of a node is the SpS for that attribute, edges represent co-occurrence, and the thickness of an edge is the respective CoS. (C) The network after filtering out all CoSs that did not meet the significance cut-off point. CoS, co-occurrence statistic; SpS, specificity sum.

Clustering of normalized attribute tracking scores with pvclust, for the set of 10 attributes in the data yielded a total of 82 significant stable clusters. The largest cluster included only 106 subjects, with subject counts in subsequent clusters dropping off quickly. The large number of clusters is the result of including attribute patterns that are not necessarily useful in characterizing the significant underlying associations with disease risk.

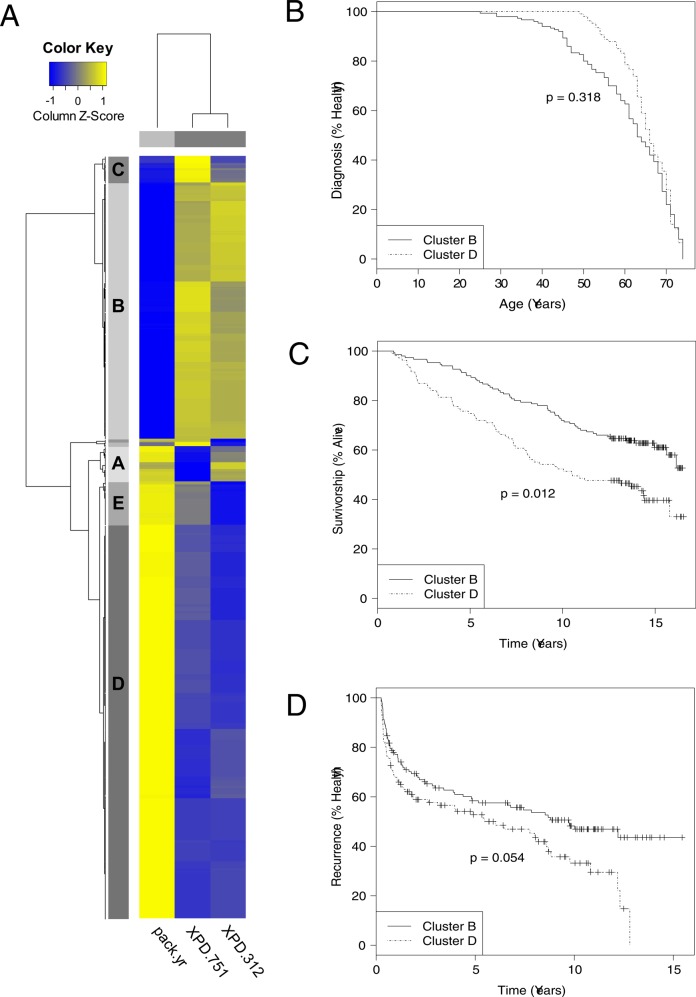
In the interest of exploring an analysis pathway that focuses only on significant attributes, we performed a second-pass analysis of the data that included only attributes XPD 751, XPD 312, and pack-years. We expected that this would yield larger clusters of subjects for comparison. After this secondary analysis of the bladder cancer dataset, including only attributes (XPD 751, XPD 312, and pack-years), we observed an average training accuracy of 0.6989 and a significant average testing accuracy of 0.6968 averaged over 10-fold CV (p=0.001). Recall that the MDR model that included these attributes reported a testing accuracy of 0.66, and an accuracy of 0.5 would be expected by random chance. We trained AF-UCS on the entire three-attribute dataset and used pvclust to identify significant, stable clusters of samples as previously described. A visualization of these clustered and normalized attribute tracking scores is given in figure 3A. By far, the largest two clusters were B and D. Cluster B indicated a strong pattern of high attribute tracking scores in XPD 751 and XPD 312, while cluster D indicated a strong pattern of high attribute tracking scores for pack-years.

Figure 3.

Subgroup identification and analysis. (A) Heat-map of normalized AF-UCS (attribute feedback-sUpervised Classifier System) attribute tracking scores for entire bladder cancer dataset (three significant attributes). Each row in the heat-map is one of 914 instances comprising the dataset. Each column is one of three attributes. Yellow indicates higher normalized tracking scores, while blue indicates lower ones. Significant subject clusters are delineated by the blocks on the y axis labeled alphabetically. Owing to their small size, clusters F and G are not labeled, but can be seen between clusters A and B. Cluster G is adjacent to B, while cluster F is adjacent to A. In order to better highlight the attribute patterns underlying these clusters, the normalized attribute tracking scores are further scaled by instance using the scale feature in pvclust. (B–D) Kaplan–Meier plots comparing different clinical variables for clusters B and D. Plus signs in the curve indicate censoring.

Once clusters were identified we looked for differences in clinical outcome variables for the cases in these groups. Cluster G included no cases, and therefore was not included in our subsequent analysis of clinical variables. Kruskal–Wallis analysis between the cases of clusters A–F yielded a marginally significant difference for age at diagnosis (p=0.076), a significant difference for survival time (p<0.05), and a marginally significant difference for time to first recurrence (p=0.094). For the remainder of this analysis we focused on clusters B and D, as they were by far the largest of the subject clusters. Mann–Whitney tests comparing clusters B and D yielded a significant difference for age at diagnosis, survival time, and recurrence (p<0.05).

Figure 3B–D give Kaplan–Meier plots illustrating ‘time to failure’ differences between clusters B and D. We supplemented these curves by performing failure analysis for each, as previously described. Examination of age of diagnosis yielded no significant difference between curves B and D as illustrated in figure 3B. Our examination of survivorship included age of diagnosis as a covariate. Stepwise regression analysis indicated no significant interaction effect between diagnosis and cluster ID. However, AIC suggested that the best model included both factors as main effects. The final survival model indicated that both age at diagnosis (HR=0.07, 95% CI 1.05 to 1.10) and cluster ID (HR=0.63, 95% CI 0.44 to 0.91) were significant (p<0.05). Follow-up analysis of variance comparing the model with and without cluster ID indicated that there was indeed a significant survivorship difference between clusters B and D (p<0.05) even after correcting for age at diagnosis as a covariant.

A similar analysis of recurrence indicated no significant interaction effect between recurrence and cluster ID. AIC again suggested that the best model included both factors as main effects. However, subsequent analysis of the final model indicated that while age of diagnosis (HR=1.03, 95% CI 1.01 to 1.05) was significant (p<0.05), cluster ID (HR=0.71, 95% CI 0.50 to 1.00) was only marginally significant (p=0.054). Follow-up analysis of variance comparing the model with and without cluster ID confirmed that the difference in recurrence between clusters B and D was only marginally significant after taking age of diagnosis into account (p=0.052).

Lastly, we found that the data were too sparse to successfully complete either a χ² test or a Fisher's exact test between all clusters and all stage/grade categories. Examination of stage/grade counts showed that the vast majority of cases included in the study were characterized as non-invasive low grade (the least severe of the categories). Comparisons of stage/grade between clusters B and D alone yielded no significant findings.

Conclusion

This study explored the application of an M-LCS analysis pathway to the investigation of bladder cancer susceptibility and clinical outcome. Our approach employed an adaptive stochastic search algorithm that makes no assumptions about the underlying patterns of association. We extended a previously described analysis pipeline for knowledge discovery and an attribute tracking strategy for the characterization of heterogeneity. This extension affords us the potential to identify etiologically heterogeneous patient subsets. This investigation successfully replicated previous findings that implicate XPD 751, XPD 312, and pack-years of smoking as significant predictors of bladder cancer susceptibility.⁴²

Additionally, we extended the characterization of these predictive factors, identifying evidence of interaction between XPD 751 and XPD 312, and evidence of heterogeneity between smoking and these genetic factors. We identified two large subgroups of subjects, with unique underlying patterns of attributes important for accurate classification. Statistical analyses comparing clinical phenotypes between these groups yielded a significant and dramatic difference in patient survival time, together with a marginally significant difference in time to first bladder tumor recurrence (each after correcting for age of diagnosis). Closer inspection showed that patients within cluster B (within which the two XPD SNPs were the most important factors for accurate classification) tended to be diagnosed earlier, displayed a significantly increased survivorship, and a marginally significant increase in time to recurrence. Alternatively, patients in cluster D (within which pack-years smoking was the most important factor for accurate classification) tended to be diagnosed later with a significantly shorter survivorship and a marginally significant decrease in time to recurrence.

Although it is certainly no revelation that smoking can negatively influence patient health, we have uncovered evidence of a potentially heterogeneous smoking effect (ie, phenocopy) not previously characterized. These findings support our claim that this proposed M-LCS analytic pathway can accommodate underlying heterogeneity and can also be used to characterize it. This methodology was designed to guide the dissection of disease heterogeneity, supporting the identification of patient subgroups which may be indicative of disease subtypes. Additionally, the ability to characterize a patient-specific pattern of association is advantageous for the development of personalized medicine. Specifically, this strategy could be applied to enable targeting personalized screening and treatment regimens to appropriate subsets of patients.

While the results presented in this study illustrate the promise of our proposed methodology, we do not claim that it has been optimized. However, this algorithm has the advantage of making no assumptions about the underlying patterns of association. It can uniquely identify predictive attributes in the context of higher-order interactions while simultaneously identifying subject subsets with respect to heterogeneous patterns, something no other established methodology can boast. Alternative strategies for determining patient subsets from attribute tracking scores will be considered in future work.

Additionally, the hypotheses generated by this work must be followed up with laboratory validation. Perceived heterogeneous patterns might alternatively be indicative of higher-order interaction, or the absence of other critically predictive factors. Alternative algorithms that specialize in modeling epistatic interactions (such as MDR) may subsequently be run independently on subject subsets to better characterize the predictive attributes involved in these ideally more homogeneous groups. This proposed strategy should benefit the generation of a more targeted hypothesis and help to identify patient subgroups based directly on patterns of association as opposed to potentially inappropriate or incomplete covariate-based data stratification.