Abstract
Objective
To explore the feasibility of a novel approach using an augmented one-class learning algorithm to model in-laboratory complications of percutaneous coronary intervention (PCI).
Materials and methods
Data from the Blue Cross Blue Shield of Michigan Cardiovascular Consortium (BMC2) multicenter registry for the years 2007 and 2008 (n=41 016) were used to train models to predict 13 different in-laboratory PCI complications using a novel one-plus-class support vector machine (OP-SVM) algorithm. The performance of these models in terms of discrimination and calibration was compared to the performance of models trained using the following classification algorithms on BMC2 data from 2009 (n=20 289): logistic regression (LR), one-class support vector machine classification (OC-SVM), and two-class support vector machine classification (TC-SVM). For the OP-SVM and TC-SVM approaches, variants of the algorithms with cost-sensitive weighting were also considered.
Results
The OP-SVM algorithm and its cost-sensitive variant achieved the highest area under the receiver operating characteristic curve for the majority of the PCI complications studied (eight cases). Similar improvements were observed for the Hosmer–Lemeshow χ2 value (seven cases) and the mean cross-entropy error (eight cases).
Conclusions
The OP-SVM algorithm based on an augmented one-class learning problem improved discrimination and calibration across different PCI complications relative to LR and traditional support vector machine classification. Such an approach may have value in a broader range of clinical domains.
Keywords: Statistical Model, Support Vector Machines, Computing Methodologies, Percutaneous Coronary Intervention, Decision Support Systems
Article I. Introduction
Despite a decline in the rate of complications during percutaneous coronary intervention (PCI) in the current stent era, the mortality and morbidity associated with these complications remains constant and high. Risk scores or decision-support algorithms that can accurately discriminate between high and low-risk PCI cases are important in reducing this burden, by providing valuable clinical tools to evaluate patients by the bedside, as well as to assess quality and outcomes for PCI procedures more broadly. Such tools also fit particularly well within a hub-and-spoke model of PCI hospitals. However, predicting PCI complications has traditionally represented a challenging proposition, with no satisfactory predictors for these outcomes.1
The challenges of developing clinical models for PCI usually stem, in part, from existing datasets available for model derivation being small (thousands or tens of thousands of patients) and suffering from class imbalance. Traditionally, clinical models have been developed within a supervised learning framework. However, supervised learning approaches focus on characterizing the differences between patients who do or do not experience clinical events, and suffer from the lack of sufficient positive (ie, event) examples for model training.2 Collecting additional data to address this issue is often infeasible because of delays, expenses, and burden to both patients and caregivers. It is further complicated by the multifactorial nature of clinical events, which requires the availability of many positive examples to reflect the varied aspects of the physiological processes underlying these clinical events. The costs and complexity of collecting extensive data annotated by experts have impeded the spread of even well validated and effective healthcare quality interventions.3
There is a growing body of recent work focusing on these issues in the context of unsupervised learning.4–10 In the presence of small datasets with few positive examples, these efforts evaluate patients by learning the support of the available data and by comparing the clinical characteristics of new patients to the distribution of existing patient records. In studies on different clinical applications, these approaches have successfully discriminated patients at increased or decreased risk of clinical events. While these results are promising, however, in general the unsupervised learning approaches do not consistently improve performance relative to models developed through supervised learning.
In this paper, we address this situation by introducing a novel support vector machine (SVM) classifier that solves a one-class learning problem augmented with information from a two-class learning problem. At a high level, our approach can be interpreted as developing a model similar to the one-class support vector machine (OC-SVM) with constraints that handle errors on positive and negative training examples differently, in a manner resembling the two-class support vector machine (TC-SVM). We focus on using this approach to develop models for PCI procedures. We evaluate our work on data from the Blue Cross Blue Shield of Michigan Cardiovascular Consortium (BMC2) multicenter cardiology registry data, and demonstrate the ability of our SVM method to achieve moderate to high levels of discrimination for many PCI endpoints, while providing improved performance for multiple PCI endpoints relative to both the standard OC-SVM and TC-SVM algorithms.
Article II. Background
We start with a brief review of TC-SVM and OC-SVM to establish notation and basic concepts. SVM are among the most widely used methods in machine learning, and are increasingly popular in clinical research.11 12 A more thorough review of SVM is available in Schölkopf and Smola.13
In the presentation that follows, we denote data from patients 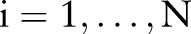 as training pairs of the form
as training pairs of the form 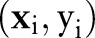 , where
, where 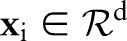 is a feature vector corresponding to clinical measurements from the ith patient and
is a feature vector corresponding to clinical measurements from the ith patient and 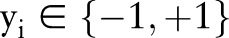 is its binary label indicating clinical outcome of the patient. By convention, adverse clinical events are positively labeled
is its binary label indicating clinical outcome of the patient. By convention, adverse clinical events are positively labeled 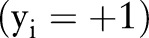 , and non-events are negatively labeled
, and non-events are negatively labeled 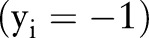 .
.
Two-class support vector machine
The TC-SVM14 maps each data point 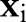 via a non-linear function
via a non-linear function 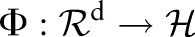 to a high (possibly infinite) dimensional Hilbert space
to a high (possibly infinite) dimensional Hilbert space 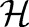 generated by a positive-definite kernel
generated by a positive-definite kernel 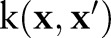 . The kernel function corresponds to an inner product in
. The kernel function corresponds to an inner product in 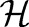 through
through 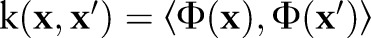 .
.
The TC-SVM finds a separating hyperplane by maximizing the margin between the positive and negative classes.14 When no such hyperplane exists, it allows some data points to be inside the margin or on the wrong side of the hyperplane. More formally, the TC-SVM solves the following optimization problem:
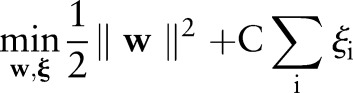 |
| 1 |
where 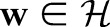 is the normal vector of the hyperplane and
is the normal vector of the hyperplane and  is a parameter that controls the trade-off between maximizing the margin and minimizing the margin errors.
is a parameter that controls the trade-off between maximizing the margin and minimizing the margin errors.
In practice, this primal optimization problem is solved via its dual:
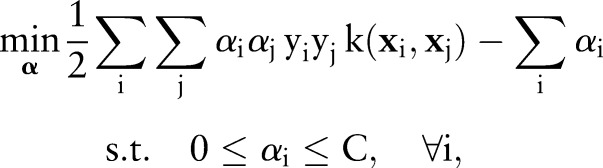 |
2 |
which is optimized over the Lagrange multipliers 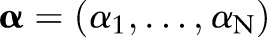 . The primal and the dual parameters are related through
. The primal and the dual parameters are related through 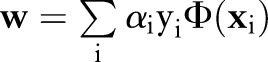 .
.
Once an optimal solution 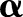 is found, the sign of the decision function:
is found, the sign of the decision function:
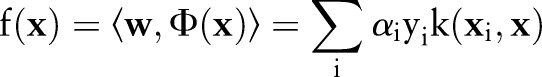 |
3 |
assigns 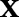 to one of the classes.
to one of the classes.
One-class support vector machine
The OC-SVM15
16 was proposed to estimate the support of a distribution from observations 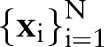 . Contrary to the TC-SVM, the OC-SVM searches for a hyperplane in
. Contrary to the TC-SVM, the OC-SVM searches for a hyperplane in  that separates the data from the origin by maximizing the distance between the hyperplane and the origin (margin). To maximize the margin, some data points are allowed to fall inside the margin by introducing non-negative penalties. In contrast to the TC-SVM, the OC-SVM does not require labeled data in the training set.
that separates the data from the origin by maximizing the distance between the hyperplane and the origin (margin). To maximize the margin, some data points are allowed to fall inside the margin by introducing non-negative penalties. In contrast to the TC-SVM, the OC-SVM does not require labeled data in the training set.
The primal of the OC-SVM is formulated by:
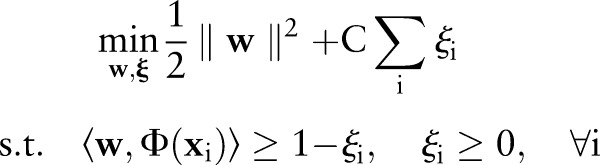 |
4 |
where  is a cost parameter that controls the margin violations. This quadratic program is also solved via its dual:
is a cost parameter that controls the margin violations. This quadratic program is also solved via its dual:
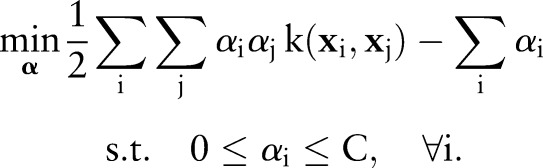 |
5 |
The decision function can be written as:
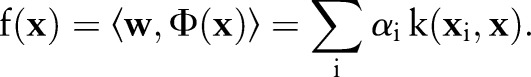 |
6 |
the OC-SVM output is expected to be higher for a non-event (negative) data point and lower for an event (positive) data point.
Methods
A growing body of recent work4–10 has focused on the use of the OC-SVM as a way to address issues of small datasets and class imbalance. One of the challenges faced by these efforts, however, is that the OC-SVM does not use the data labels in the training set. Even when data labels are available from historical data, the OC-SVM model is typically trained only on the negative examples to characterize the non-event patient population. However, this simple approach wastes the information in any available positive (event) examples.
We introduce a novel SVM formulation that addresses this inefficiency and uses all available training data labels to improve and augment the OC-SVM further. Our proposed formulation, which we term the one-plus-class support vector machine (OP-SVM), shares some similarities with both the standard OC-SVM and TC-SVM formulations described above, but differs in important ways from either approach.
One-plus-class support vector machine
The OP-SVM aims to find a hyperplane in 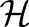 that separates negative examples from the origin with maximum margin, while allowing a small number of negative examples to be between the hyperplane and the origin in exchange for non-negative penalties. On the other hand, positive data points are free to be inside the margin without incurring any costs. However, a positive example is penalized when the data point and the origin are on the opposite side of the hyperplane.
that separates negative examples from the origin with maximum margin, while allowing a small number of negative examples to be between the hyperplane and the origin in exchange for non-negative penalties. On the other hand, positive data points are free to be inside the margin without incurring any costs. However, a positive example is penalized when the data point and the origin are on the opposite side of the hyperplane.
The primal for our OP-SVM formulation is:
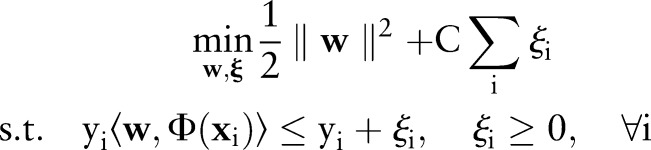 |
where  controls the trade-off between margin maximization and margin error minimization. Figure 1 presents a geometric illustration of this formulation, focusing on how the learned hyperplane separates data points for the OP-SVM while considering their labels.
controls the trade-off between margin maximization and margin error minimization. Figure 1 presents a geometric illustration of this formulation, focusing on how the learned hyperplane separates data points for the OP-SVM while considering their labels.
Figure 1.
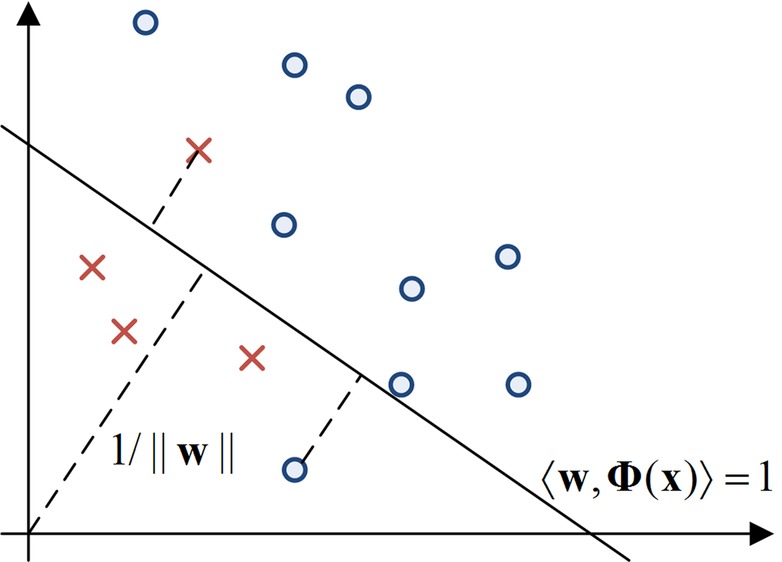
The diagram depicts the one-plus-class support vector machine (OP-SVM) in a two-dimensional toy example. Small circles and crosses represent negative and positive data points, respectively. The hyperplane is chosen to separate the circles from the origin with maximal margin. The circle between the hyperplane and the origin and the cross on the other side of the hyperplane are penalized in the objective function.
Similar to the OC-SVM and TC-SVM, instead of directly solving the primal, it is more convenient to solve its dual. To derive the dual, we first construct the Lagrangian:
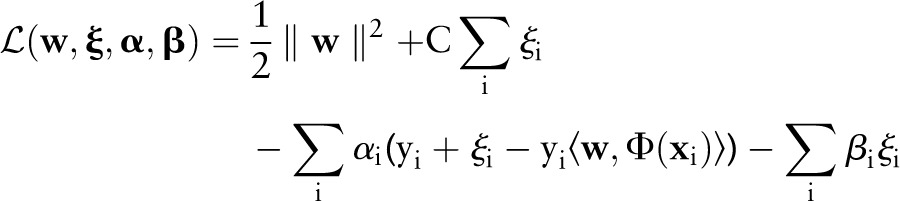 |
where 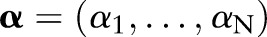 and
and 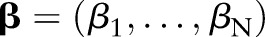 are the vectors of non-negative Lagrange multipliers corresponding to the inequality constraints in Equation (7). Taking the derivatives of
are the vectors of non-negative Lagrange multipliers corresponding to the inequality constraints in Equation (7). Taking the derivatives of 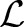 with respect to
with respect to 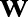 and
and 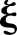 and setting to zero, we have:
and setting to zero, we have:
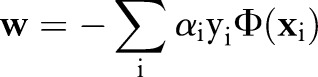 |
8 |
| 9 |
Substituting Equations (8) and (9) into the Lagrangian 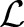 eliminates the primal variables and leads to the following dual optimization problem:
eliminates the primal variables and leads to the following dual optimization problem:
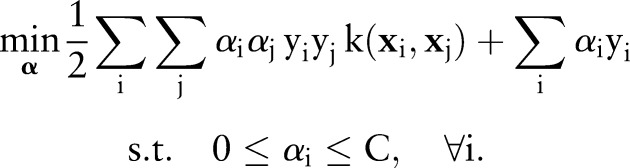 |
10 |
It is easy to see that the primal (7) and the dual (10) of the OP-SVM reduce to the primal (4) and the dual (5) of the OC-SVM when 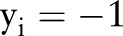 for
for  . The resulting decision function is then expressed by:
. The resulting decision function is then expressed by:
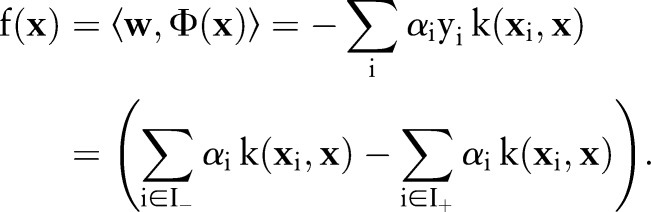 |
The expanded form of 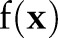 clearly shows that the decision function value lowers near the positive examples in training data when the kernel function
clearly shows that the decision function value lowers near the positive examples in training data when the kernel function 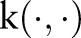 is positive valued (eg, Gaussian kernels or polynomial kernels of even orders).
is positive valued (eg, Gaussian kernels or polynomial kernels of even orders).
The primal and dual formulations of the TC-SVM, OC-SVM and OP-SVM are compared in table 1. While these equations look similar, they show differences in handling margin errors of positive examples and negative examples. We will show how these differences affect their behavior and performance in subsequent sections.
Table 1.
The primal and dual formulations of the TC-SVM, the OC-SVM and the proposed OP-SVM
| TC-SVM | OC-SVM | OP-SVM | |
|---|---|---|---|
| (P) | 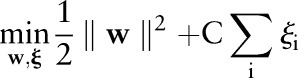 |
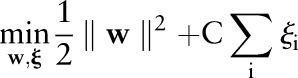 |
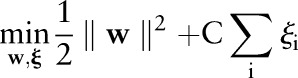 |
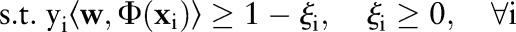 |
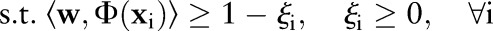 |
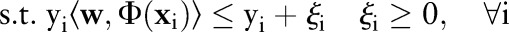 |
|
| (D) | 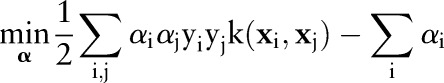 |
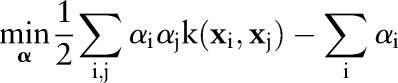 |
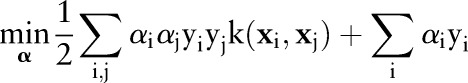 |
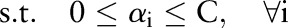 |
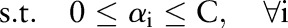 |
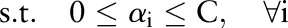 |
D, dual; P, primal; OC-SVM, one-class support vector machine; OP-SVM one-plus-class support vector machine; TC-SVM, two-class support vector machine.
Decomposition algorithm
The above dual optimization problem in Equation (10) can be solved using a standard quadratic programming algorithm. However, it will be infeasible for even small to medium-sized problems because the dual involves 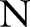 parameters and a matrix with
parameters and a matrix with 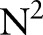 elements. We describe a computationally efficient algorithm that sequentially minimizes the dual objective function.17
18 The algorithm decomposes the large optimization problem into a series of smaller problems and solves them iteratively. It turns out that the sub-problem has an analytic solution and can be solved easily.
elements. We describe a computationally efficient algorithm that sequentially minimizes the dual objective function.17
18 The algorithm decomposes the large optimization problem into a series of smaller problems and solves them iteratively. It turns out that the sub-problem has an analytic solution and can be solved easily.
At every iteration, the decomposition algorithm chooses a data point 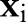 and updates the value of the corresponding dual variable
and updates the value of the corresponding dual variable 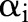 while leaving other variables fixed. The algorithm repeats the selection and update processes until the optimality condition error falls below a predetermined tolerance.
while leaving other variables fixed. The algorithm repeats the selection and update processes until the optimality condition error falls below a predetermined tolerance.
Without loss of generality, suppose that 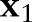 is chosen and
is chosen and 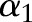 will be updated while the other
will be updated while the other 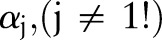 remain unchanged. Rewriting the dual objective function in Equation (10) with respect to
remain unchanged. Rewriting the dual objective function in Equation (10) with respect to 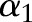 yields:
yields:
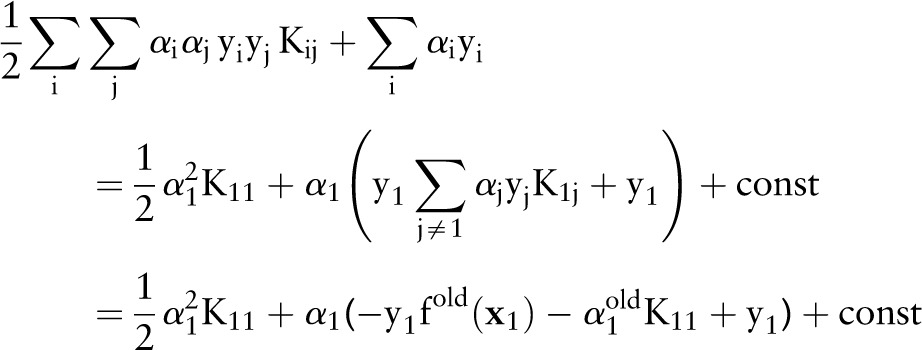 |
where 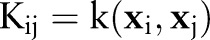 . During the derivation, all the terms that are not relevant to
. During the derivation, all the terms that are not relevant to 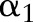 are collapsed in
are collapsed in 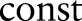 . In the last line,
. In the last line, 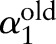 and
and 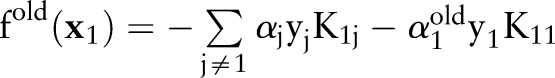 denote the variable and the output before the current update. These values can be easily obtained from the previous iteration step. The algorithm minimizes the reduced optimization problem with respect to
denote the variable and the output before the current update. These values can be easily obtained from the previous iteration step. The algorithm minimizes the reduced optimization problem with respect to 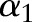 , leading to the following analytic solution:
, leading to the following analytic solution:
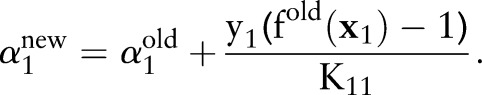 |
If this solution is feasible, 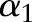 is updated with
is updated with 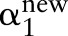 . Otherwise, it is clipped to the interval
. Otherwise, it is clipped to the interval 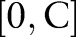 so that the updated
so that the updated 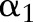 accords the inequality constraints in Equation (10). The update rule increases the value of
accords the inequality constraints in Equation (10). The update rule increases the value of 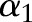 when
when 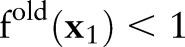 if
if 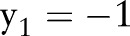 and
and 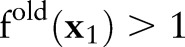 if
if 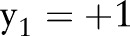 ; that is,
; that is, 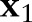 violates the margin constraint. For a negative example, this means that
violates the margin constraint. For a negative example, this means that 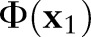 lies between the origin and the hyperplane. Likewise, for a positive example, this means that
lies between the origin and the hyperplane. Likewise, for a positive example, this means that 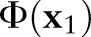 and the origin are on the opposite sides of the hyperplane.
and the origin are on the opposite sides of the hyperplane.
To determine the termination of the iteration, we check the Karush–Kuhn–Tucker (KKT) optimality condition19 of the current solution. The KKT conditions require the solution to satisfy
Therefore, the optimal 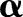 should obey the following conditions
should obey the following conditions
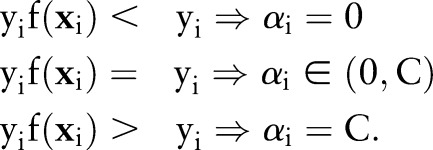 |
If any 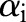 violates these conditions, the decomposition algorithm continues to update
violates these conditions, the decomposition algorithm continues to update 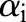 until the KKT conditions are fulfilled. Furthermore, during the variable selection step, the algorithm can assess the extent to which each
until the KKT conditions are fulfilled. Furthermore, during the variable selection step, the algorithm can assess the extent to which each 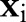 violates the KKT conditions, and choose the data point that maximally fails to meet these conditions. The pseudo code of the decomposition algorithm is given in Algorithm 1.
violates the KKT conditions, and choose the data point that maximally fails to meet these conditions. The pseudo code of the decomposition algorithm is given in Algorithm 1.
Results
To evaluate the proposed support vector method, we performed two sets of experiments. The first experiment was performed on a synthetic benchmark dataset to evaluate better the behavior of the proposed approach under varying conditions. The second experiment was performed on data drawn from the BMC2 registry to evaluate the clinical utility of our research on a representative PCI population.
Synthetic benchmark data
We studied the OP-SVM approach on the two-dimensional banana dataset publically available online.20
21 The banana dataset was randomly permuted 100 times, and partitioned into training and test sets each with 4900 and 400 data points, respectively. To simulate the scenario where events occur infrequently, we removed all but a few positive examples from the training set at random. The number of retained positive examples 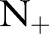 was varied from 5 (0.18%) to 50 (1.85%).
was varied from 5 (0.18%) to 50 (1.85%).
On each of the datasets, we applied the methods described in the Background section and the Methods section, and compared the following modeling approaches:
LR: a logistic regression model trained on the entire training set;
OC-SVM: a standard OC_SVM trained on the entire training set;
OC-SVM(Neg): another OC-SVM trained only on the negative (non-event) examples in the training set;
TC-SVM: a standard two-class SVM trained on the entire training set; and
OP-SVM: the proposed one-plus-class SVM trained on the entire training set.
In addition to the models above, we also studied cost-sensitive variants of TC-SVM and OP-SVM:
TC-SVM(CS): a two-class SVM with cost-sensitive weights for the positive and negative examples in Equation (1); and
OP-SVM(CS): a one-plus-class SVM with cost-sensitive weights.
The cost-sensitive SVM assigns different penalties or costs for false negatives and false positives. It is often shown to be effective when dealing with imbalanced numbers of positive and negative examples.22 More formally, cost-sensitive weighting is achieved by replacing the cost-insensitive loss 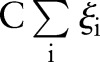 in Equations (1) and (7) with a cost-sensitive loss
in Equations (1) and (7) with a cost-sensitive loss 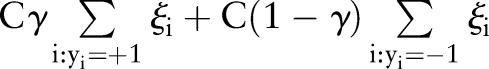 , where the cost asymmetry between false positives and false negatives was regulated by
, where the cost asymmetry between false positives and false negatives was regulated by 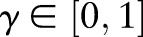 . In our study, we set the cost asymmetry parameter
. In our study, we set the cost asymmetry parameter 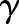 to the proportion of the negative examples in the training set.23 As the OC-SVM formulation (Equation (4)) does not involve the data labels, no cost-sensitive variant of the OC-SVM was compared.
to the proportion of the negative examples in the training set.23 As the OC-SVM formulation (Equation (4)) does not involve the data labels, no cost-sensitive variant of the OC-SVM was compared.
We used a Gaussian kernel 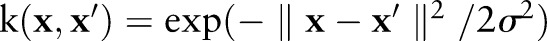 for a consistent comparison between the SVM methods, because a Gaussian kernel makes data separable from the origin and satisfies the OC-SVM assumption.16 For each model, we fixed the cost parameter
for a consistent comparison between the SVM methods, because a Gaussian kernel makes data separable from the origin and satisfies the OC-SVM assumption.16 For each model, we fixed the cost parameter 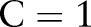 , and searched for the kernel bandwidth
, and searched for the kernel bandwidth  over 10 logarithmically spaced grid from
over 10 logarithmically spaced grid from 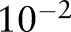 to
to 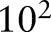 . The kernel bandwidth
. The kernel bandwidth  was chosen via threefold cross-validation.
was chosen via threefold cross-validation.
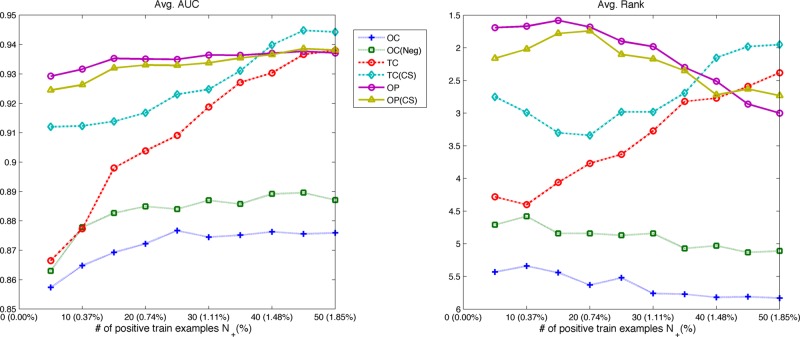
We computed the area under the receiver operating characteristic curve (AUROC) to assess the discriminative ability of the approaches above on the banana dataset. The results in table 2 show the average AUROC and its SE over the 100 permutations. The AUROC of the best performing method is in boldface, and the second best in italics. For each permutation and each positive example size 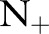 , we additionally ranked the algorithms from 1 (best) to 6 (worst) based on their AUROC values. Figure 2 shows the average AUROC and the average rank of each algorithm over the number of positive examples in the training set.
, we additionally ranked the algorithms from 1 (best) to 6 (worst) based on their AUROC values. Figure 2 shows the average AUROC and the average rank of each algorithm over the number of positive examples in the training set.
Table 2.
The average AUROC for each of the methods on banana data
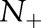 |
LR | OC-SVM | OC-SVM (Neg) | TC-SVM | TC-SVM (CS) | OP-SVM | OP-SVM (CS) |
|---|---|---|---|---|---|---|---|
| 5 (0.18%) | 0.513 (±0.004) | 0.857 (±0.005) | 0.863 (±0.006) | 0.867 (±0.007) | 0.912 (±0.003) | 0.929 (±0.002) | 0.925 (±0.003) |
| 10 (0.37%) | 0.520 (±0.004) | 0.865 (±0.004) | 0.878 (±0.003) | 0.877 (±0.004) | 0.912 (±0.002) | 0.932 (±0.002) | 0.926 (±0.003) |
| 15 (0.55%) | 0.517 (±0.004) | 0.869 (±0.004) | 0.883 (±0.003) | 0.898 (±0.003) | 0.914 (±0.002) | 0.935 (±0.001) | 0.932 (±0.002) |
| 20 (0.74%) | 0.517 (±0.004) | 0.872 (±0.004) | 0.885 (±0.002) | 0.904 (±0.003) | 0.917 (±0.002) | 0.935 (±0.001) | 0.933 (±0.001) |
| 25 (0.92%) | 0.521 (±0.004) | 0.877 (±0.003) | 0.884 (±0.002) | 0.909 (±0.003) | 0.923 (±0.002) | 0.935 (±0.001) | 0.933 (±0.002) |
| 30 (1.11%) | 0.525 (±0.004) | 0.875 (±0.003) | 0.887 (±0.002) | 0.919 (±0.003) | 0.925 (±0.002) | 0.936 (±0.001) | 0.934 (±0.002) |
| 35 (1.29%) | 0.523 (±0.005) | 0.875 (±0.003) | 0.886 (±0.002) | 0.927 (±0.002) | 0.931 (±0.002) | 0.936 (±0.001) | 0.935 (±0.001) |
| 40 (1.48%) | 0.527 (±0.004) | 0.876 (±0.003) | 0.889 (±0.002) | 0.930 (±0.002) | 0.940 (±0.002) | 0.937 (±0.001) | 0.937 (±0.001) |
| 45 (1.66%) | 0.530 (±0.004) | 0.876 (±0.003) | 0.890 (±0.002) | 0.937 (±0.002) | 0.945 (±0.002) | 0.938 (±0.001) | 0.939 (±0.001) |
| 50 (1.85%) | 0.528 (±0.004) | 0.876 (±0.003) | 0.887 (±0.002) | 0.938 (±0.002) | 0.944 (±0.002) | 0.937 (±0.001) | 0.938 (±0.002) |
The proportion of positive examples in training sets was varied from 0.18% to 1.85%. The best AUROC values are shown in boldface, with the second best shown in italics.
AUROC, area under the receiver operating characteristic curve; LR, logistic regression; OC-SVM, one-class support vector machine classification; OP-SVM, one-plus-class support vector machine; TC-SVM, two-class support vector machine classification.
Figure 2.
The average AUROC and the average rank of each method on the banana data as the number of positive train examples increases. The OP-SVM and OP-SVM (CS) showed generally high and fairly steady AUROC over the range of positive example numbers. Their performance degraded very little even with very small numbers of positive examples. The TC-SVM and TC-SVM (CS) improved, as more positive examples were available for model training. With more than 40 positive training examples, the TC-SVM eventually achieved the highest AUROC and outperformed the other approaches. AUROC, area under the receiver operating characteristic curve; OP-SVM, one-plus-class support vector machine; TC-SVM, two-class support vector machine classification.
There are several trends to note in the results. The proposed OP-SVM and OP-SVM (CS) performed best for the most values of 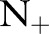 . Their performance was less affected by
. Their performance was less affected by 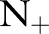 , and degraded very little even in the presence of very small numbers of positive examples. As more positive examples were retained for model training, the AUROC of all the approaches generally increased. The improvement was particularly pronounced for the TC-SVM and TC-SVM (CS) approaches. The performance of these approaches showed a sharp increase and eventually outperformed the other approaches when more than 40 positive examples were available in the training set. The cost-sensitive weighting was also beneficial for the TC-SVM. In particular, for the smaller values of
, and degraded very little even in the presence of very small numbers of positive examples. As more positive examples were retained for model training, the AUROC of all the approaches generally increased. The improvement was particularly pronounced for the TC-SVM and TC-SVM (CS) approaches. The performance of these approaches showed a sharp increase and eventually outperformed the other approaches when more than 40 positive examples were available in the training set. The cost-sensitive weighting was also beneficial for the TC-SVM. In particular, for the smaller values of 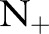 , the discrepancy between the TC-SVM and the TC-SVM (CS) was clear. Due to the lack of sufficient numbers of positive examples, the TC-SVM performed as poorly as the OC-SVM for
, the discrepancy between the TC-SVM and the TC-SVM (CS) was clear. Due to the lack of sufficient numbers of positive examples, the TC-SVM performed as poorly as the OC-SVM for 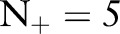 and 10. However, the gap between TC-SVM and TC-SVM (CS) narrowed for larger
and 10. However, the gap between TC-SVM and TC-SVM (CS) narrowed for larger 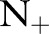 . The OC-SVM and the OC-SVM (Neg) were the worst for all the values of
. The OC-SVM and the OC-SVM (Neg) were the worst for all the values of 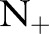 . As the OC-SVM (Neg) excluded the outlying positive examples from the training set and trained exclusively on the negative training examples, the OC-SVM (Neg) performed slightly better than the OC-SVM. The LR is a linear classifier and performed very poorly on this linearly inseparable data.
. As the OC-SVM (Neg) excluded the outlying positive examples from the training set and trained exclusively on the negative training examples, the OC-SVM (Neg) performed slightly better than the OC-SVM. The LR is a linear classifier and performed very poorly on this linearly inseparable data.
For better illustration of the proposed OP-SVM, we compared the decision boundaries of OC-SVM, TC-SVM and OP-SVM on banana data. Figure 3 shows the decision boundaries of the three algorithms on the same dataset. Their differences are most clearly visible near positive examples (red crosses). The decision boundary of the OC-SVM includes the entire positive examples because it treats all the training examples as labeled the same. The TC-SVM approach, on the other hand, uses the labels for model training, but the resulting decision boundary looks overly complex in separating the positive examples from the negative examples (green dots). On the other hand, the OP-SVM seems to be somewhere between the OC-SVM and the TC-SVM. The figure shows a smoother decision boundary compared to the OC-SVM and the TC-SVM.
Figure 3.
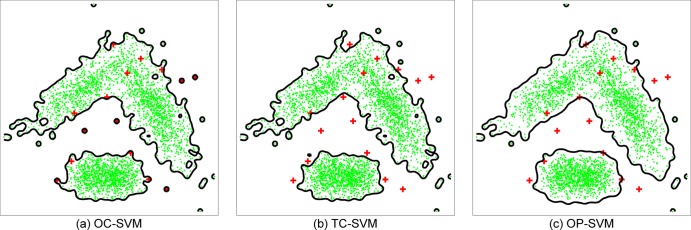
The comparison of OC-SVM, TC-SVM and OP-SVM on banana data. The green dots are negative examples and the red crosses are positive examples. The black contours represent the decision boundaries. The differences of algorithms are most clearly visible near positive examples. The OC-SVM ignores the training data labels and its decision boundary includes all the positive examples. The TC-SVM generates a complex decision boundary to separate the positive examples from the negative examples. The decision boundary of the OP-SVM is smoother than the others, and does not include or exclude all the positive examples. OC-SVM, one-class support vector machine classification; OP-SVM, one-plus-class support vector machine; TC-SVM, two-class support vector machine classification.
BMC2 data
To assess the clinical utility, we further evaluated our proposed OP-SVM on data from patients who underwent PCI in the BMC2 registry. This dataset was collected to assess the outcomes of PCI across different hospitals in Michigan and to determine the impact of quality improvement programs on the practice of interventional cardiology.
Details of the BMC2 registry and its data collection and auditing process have been described previously.24 25 All non-federal hospitals that perform PCI in the state of Michigan currently participate in this registry. The BMC2 is a physician-run quality improvement collaborative that is supported by, but independent of, the funding agency, Blue Cross Blue Shield of Michigan. A physician advisory committee is responsible for setting the quality goals and developing quality improvement efforts without any input from or sharing of data with the study sponsor. Procedural data on all consecutive patients undergoing PCI at participating hospitals are collected by dedicated data abstractors using standardized data collection forms. All data elements have been prospectively defined, and the protocol is approved by the local institutional review board at each hospital. The data definitions in the BMC2 regsitry are broadly similar to those used by the ACC-NCDR CathPCI registry.26 In addition to a random audit of 2% of all cases, medical records of all patients undergoing multiple procedures or coronary artery bypass grafting and of patients who died in the hospital are reviewed routinely to ensure data accuracy.
The medical records of 22 023 patients who underwent PCI in 2008 were used for model training in our study, with model parameters selection performed on 18 993 patients who underwent the procedure in 2007. The data collected from 20 289 patients treated with PCI in 2009 was used for model testing.
The data records included 13 in-laboratory binary outcomes: death during coronary angioplasty (IL-DTH), emergency coronary artery bypass graft (IL-ECABG), stroke (IL-STRK), cardiac tamponade (IL-TAMPONADE), perforation coronary artery (IL-PERF), acute closure (IL-AC-CL), pulmonary edema (IL-P-ED), untreated dissection (IL-UNTRTD-DISSECTION), side branch occlusion (IL-SBO), no reflow (IL-N-RFL), VT/VF requiring cardioversion (IL-VTVFC), cardiogenic shock (IL-CS), and angina for 30 min or longer (IL-ANG). The number of clinical events in the training, parameter selection, and testing sets are summarized in table 3. The datasets are highly imbalanced with the rate of in-laboratory clinical events during PCI being well below 1%. Our experiments were performed on each of these clinical endpoints separately.
Table 3.
The number of patients and the number of clinical events in patients undergoing PCI in the BMC2 registry
| Year | 2007 Validation | 2008 Training | 2009 Test | |
|---|---|---|---|---|
| Total patients | 18993 | 22023 | 20289 | |
| Death | IL-DEATH | 12 (0.06%) | 24 (0.11%) | 19 (0.09%) |
| Emergency coronary artery bypass graft | IL-ECABG | 48 (0.25%) | 39 (0.18%) | 48 (0.24%) |
| Stroke | IL-STRK | 1 (0.01%) | 4 (0.02%) | 6 (0.03%) |
| Cardiac tamponade | IL-TAMPONADE | 17 (0.09%) | 24 (0.11%) | 8 (0.04%) |
| Perforation coronary artery | IL-PERF | 72 (0.38%) | 61 (0.28%) | 49 (0.24%) |
| Acute closure | IL-AC-CL | 87 (0.46%) | 82 (0.37%) | 75 (0.37%) |
| Pulmonary edema | IL-P-ED | 38 (0.20%) | 42 (0.19%) | 31 (0.15%) |
| Untreated dissection | IL-UNTRTD-DISSECTION | 123 (0.65%) | 126 (0.57%) | 108 (0.53%) |
| Side branch occlusion | IL-SBO | 143 (0.75%) | 138 (0.63%) | 130 (0.64%) |
| No reflow | IL-N-RFL | 184 (0.97%) | 171 (0.78%) | 146 (0.72%) |
| VT/VF requiring cardioversion | IL-VTVFC | 132 (0.69%) | 161 (0.73%) | 152 (0.75%) |
| Cardiogenic shock | IL-CS | 163 (0.86%) | 199 (0.90%) | 220 (1.08%) |
| Angina ≥30 min | IL-ANG | 578 (3.04%) | 398 (1.81%) | 391 (1.93%) |
The BMC2 2008 was used for model training, and the BMC2 2007 was used as a validation set for model parameter selection. The models were tested on the BMC2 2009. The event rates for the most clinical endpoints were below 1%.
BMC2, Blue Cross Blue Shield of Michigan Cardiovascular Consortium; PCI, percutaneous coronary intervention.
For each patient, 69 clinical variables related to patient characteristics, cardiac status, PCI in the setting of myocardial infarction, comorbidities, pre-procedure laboratory results, contraindications, pre-procedure therapies, and cardiac anatomy and function were used as features for model training and testing. Table 4 shows these clinical variables in detail.
Table 4.
Clinical variables recorded in the BMC2 data
| Features | |
|---|---|
| Patient characteristics | Gender, body mass index, age |
| Cardiac status | Priority, staged PCI, salvage, ad hoc PCI, stable angina, cardiac arrest, unstable angina, high-risk non-cardiac surgery, atypical angina, patient turned down for coronary artery bypass graft by surgeon |
| PCI in the setting of myocardial infarction | Primary PCI, symptom to PCI time: 0–6 h, 6–12 h, 12–24 h and >24 h of symptoms, PCI of infarct related vessel, cardiogenic shock, recurrent ventricular tachycardia or ventricular fibrillation, post infarct angina, lytic therapy |
| Comorbidities | Current smoker, hypertension, insulin dependent diabetes, non-insulin-dependent diabetes, congestive heart failure, peripheral vascular disease, renal failure requiring dialysis, significant valve disease, current or recent gastrointestinal bleed, chronic obstructive pulmonary disorder, cerebrovascular disease, atrial fibrillation, history of cardiac arrest, previous myocardial infarction, previous PCI |
| Pre-procedure laboratory results | Creatinine, hemoglobin |
| Contraindications | Aspirin, angiotensin-converting enzyme inhibitors, β-blockers, cholesterol-lowering agents, clopidogrel |
| Pre-procedure therapy | Aspirin, intravenous heparin, low molecular weight heparin, bivalirudin, angiotensin-converting enzyme inhibitors, β-blockers, calcium antagonists, diuretics, coumadin, clopidogrel, thienopyridine, intra-aortic balloon pump, intubation |
| Cardiac anatomy and function | Left main artery stenosis, ejection fraction, no of diseased vessels, left ventricular end-diastolic pressure, graft lesion, grafts with >70% stenosis, ostial lesion, moderate to heavy calcification, thrombus, and chronic total occlusion |
BMC2, Blue Cross Blue Shield of Michigan Cardiovascular Consortium; PCI, percutaneous coronary intervention.
The BMC2 data experiments were performed in an analogous manner to the synthetic data experiments described earlier. The Gaussian kernel bandwidth  was selected through the validation set (BMC2 2007) over a grid of 10 points spaced logarithmically from
was selected through the validation set (BMC2 2007) over a grid of 10 points spaced logarithmically from 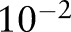 to
to 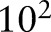 . The cost parameter was fixed to
. The cost parameter was fixed to 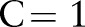 , and the cost-sensitive weight
, and the cost-sensitive weight 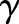 was set to the ratio of the negative examples in the training set. We note that the test set (BMC2 2009) was never used during the model training.
was set to the ratio of the negative examples in the training set. We note that the test set (BMC2 2009) was never used during the model training.
To measure the performance of each algorithm, the AUROC was computed. The results are reported in table 5. The AUROC is generally accepted as a standard and is widely used in biomedicine for model evaluation.27 In practice, it is generally considered that the AUROC of 0.7 to 0.8 has moderate clinical utility, and greater than 0.8 has high clinical utility.28 We also ranked the algorithms in the order of their AUROC values. The best performing algorithm is shown in boldface and the second best in italics. The last two rows show the average AUROC and the average rank of each algorithm over the 13 PCI endpoints.
Table 5.
The AUROC values for each clinical endpoint among patients undergoing PCI
| LR | OC | OC (Neg) | TC | TC (CS) | OP | OP (CS) | |
|---|---|---|---|---|---|---|---|
| IL-DEATH | 0.662 | 0.895 | 0.896 | 0.896 | 0.909 | 0.918 | 0.916 |
| IL-ECABG | 0.654 | 0.729 | 0.729 | 0.691 | 0.802 | 0.765 | 0.817 |
| IL-STRK | 0.498 | 0.735 | 0.735 | 0.740 | 0.560 | 0.655 | 0.634 |
| IL-TAMPONADE | 0.665 | 0.732 | 0.732 | 0.672 | 0.662 | 0.702 | 0.646 |
| IL-PERF | 0.604 | 0.630 | 0.630 | 0.640 | 0.709 | 0.644 | 0.709 |
| IL-AC-CL | 0.597 | 0.643 | 0.643 | 0.642 | 0.652 | 0.643 | 0.661 |
| IL-P-ED | 0.710 | 0.850 | 0.853 | 0.856 | 0.883 | 0.835 | 0.892 |
| IL-UNTRTD-DISSECTION | 0.597 | 0.643 | 0.643 | 0.646 | 0.661 | 0.643 | 0.660 |
| IL-SBO | 0.582 | 0.541 | 0.541 | 0.594 | 0.633 | 0.531 | 0.643 |
| IL-N-RFL | 0.735 | 0.643 | 0.653 | 0.652 | 0.770 | 0.673 | 0.750 |
| IL-VTVFC | 0.810 | 0.750 | 0.750 | 0.782 | 0.822 | 0.780 | 0.828 |
| IL-CS | 0.863 | 0.767 | 0.769 | 0.830 | 0.889 | 0.820 | 0.889 |
| IL-ANG | 0.719 | 0.536 | 0.550 | 0.599 | 0.712 | 0.583 | 0.701 |
| Average AUROC | 0.669 | 0.700 | 0.702 | 0.711 | 0.743 | 0.707 | 0.750 |
| Average rank | 5.23 | 4.92 | 4.92 | 4.00 | 2.54 | 4.23 | 2.15 |
The best values are indicated in boldface and the second best in italics. The OP-SVM (CS) performed best on seven PCI endpoints and second best on three PCI endpoints. The last rows show the average AUROC and the average ranks of the algorithms.
AUROC, area under the receiver operating characteristic curve; LR, logistic regression; OP-SVM, one-plus-class support vector machine; PCI, percutaneous coronary intervention.
Among the seven models compared in table 5, the OP-SVM (CS) achieved the highest AUROC for seven PCI outcomes (the OP-SVM additionally achieved the highest AUROC for another endpoint). The OP-SVM performed the best for more PCI outcomes than any other approach did. The next best approach TC-SVM (CS) achieved the highest AUROC only for two PCI outcomes. Furthermore, the OP-SVM (CS) ranked the second for three PCI outcomes. On average, the OP-SVM (CS) showed the best AUROC and rank. It is noteworthy that not only did the OP-SVM (CS) outperform all of the other approaches for these endpoints, but in addition, it led to AUROC values corresponding to moderate to high clinical utility (>0.7) in eight cases.28
We note that the TC-SVM did not clearly outperform the OC-SVM and OC-SVM (Neg) despite its focus on using both positive and negative data labels for model training. We believe this result can be explained by the diminished prevalence of the PCI complications, which leads to an insufficient number of positive examples to characterize the patients experiencing clinical events adequately.
The table also compares a logistic regression model (LR) to the six support vector models for each PCI endpoint as a point of reference. LR models are commonly studied in clinical model development.29 30 However, the performance of the LR was the worst for many PCI endpoints. It was comparable to other approaches only for the cases with more clinical events (the last four endpoints in table 5). While there are excellent LR models for in-hospital mortality (patient died after the procedure and before the discharge from the hospital),29 the class imbalance of in-laboratory mortality (patient died in the catheterization laboratory) is much more severe and therefore challenging to predict accurately.
Our results also show that the discriminative ability of OC-SVM (Neg) was almost identical to that of OC-SVM for the different PCI endpoints. This result was noted even though OC-SVM (Neg) attempted to use data labels to separate the non-event patients from the event patients. Our experiments suggest that OC-SVM (Neg) was inefficient in its use of the labeled training data (ie, focusing exclusively on negative labels). Instead, our results prove that even the small number of positive examples available for model training can be leveraged by the OP-SVM and OP-SVM (CS) approaches to improve discrimination of patient risk.
In addition to the AUROC, we computed the Hosmer–Lemeshow goodness-of-fit statistic (HL χ2)31 and the mean cross-entropy error (CEE)32 to measure calibration of the models. As the HL test and CEE are developed on a probabilistic metric, we first transformed the SVM outputs into probabilities using the Platt scaling.33–35 Tables 6 and 7 show the evaluated values of the HL test and CEE. Smaller HL χ2 and CEE indicate better model calibration. The tables show the best results in boldface and the second best in italics. The OP-SVM (CS) achieved the best results more often than any of the other algorithms as can be seen in the tables.
Table 6.
The Hosmer–Lemeshow goodness-of-fit test (HL χ2) of each algorithm
| LR | OC | OC (Neg) | TC | TC (CS) | OP | OP (CS) | |
|---|---|---|---|---|---|---|---|
| IL-DEATH | 2.3E+06 | 9.7E+03 | 1.1E+04 | 2.8E+02 | 8.3E+00 | 5.6E+00 | 7.4E+00 |
| IL-ECABG | 3.4E+04 | 2.2E+01 | 2.2E+01 | 2.6E+02 | 9.9E+00 | 2.9E+01 | 6.3E+01 |
| IL-STRK | 2.0E+01 | 2.6E+01 | 2.6E+01 | 1.6E+01 | 1.7E+02 | 1.9E+01 | 2.2E+01 |
| IL-TAMPONADE | 4.5E+01 | 1.1E+01 | 1.1E+01 | 3.4E+01 | 1.7E+01 | 1.2E+01 | 1.4E+01 |
| IL-PERF | 3.1E+02 | 6.4E+00 | 6.4E+00 | 9.0E+02 | 1.1E+01 | 5.3E+01 | 6.7E+00 |
| IL-AC-CL | 5.9E+02 | 2.0E+04 | 2.0E+04 | 2.8E+09 | 1.4E+01 | 2.0E+04 | 2.9E+00 |
| IL-P-ED | 7.7E+03 | 1.3E+04 | 1.1E+04 | 3.7E+02 | 3.9E+01 | 1.9E+04 | 1.1E+01 |
| IL-UNTRTD-DISSECTION | 2.5E+02 | 3.4E+01 | 1.3E+04 | 1.5E+04 | 1.5E+01 | 2.0E+01 | 8.8E+00 |
| IL-SBO | 2.3E+02 | 2.5E+01 | 2.5E+01 | 2.6E+01 | 3.1E+01 | 2.0E+04 | 1.4E+01 |
| IL-N-RFL | 6.9E+01 | 8.4E+00 | 1.1E+01 | 2.1E+04 | 1.3E+01 | 7.7E+00 | 1.8E+01 |
| IL-VTVFC | 6.5E+01 | 8.0E+00 | 1.2E+01 | 4.2E+06 | 1.3E+01 | 1.1E+01 | 1.0E+01 |
| IL-CS | 1.2E+02 | 4.5E+03 | 1.7E+04 | 1.8E+08 | 2.3E+01 | 2.0E+01 | 3.0E+01 |
| IL-ANG | 3.1E+01 | 1.9E+01 | 8.6E+00 | 1.9E+13 | 2.0E+01 | 2.7E+01 | 2.2E+01 |
The best values are indicated in boldface and the second best in italics.
Table 7.
The cross entropy error of each algorithm for each of the PCI endpoint
| LR | OC | OC (Neg) | TC | TC (CS) | OP | OP (CS) | |
|---|---|---|---|---|---|---|---|
| IL-DEATH | 0.0161 | 1.0678 | 1.6277 | 0.0192 | 0.0059 | 0.0061 | 0.0058 |
| IL-ECABG | 0.0283 | 0.0162 | 0.0162 | 0.0184 | 0.0150 | 0.0161 | 0.0157 |
| IL-STRK | 0.0533 | 0.0027 | 0.0027 | 0.0033 | 0.0031 | 0.0027 | 0.0027 |
| IL-TAMPONADE | 0.0043 | 0.0037 | 0.0037 | 0.0053 | 0.0037 | 0.0038 | 0.0037 |
| IL-PERF | 0.0244 | 0.0168 | 0.0168 | 0.0574 | 0.0163 | 0.0175 | 0.0162 |
| IL-AC-CL | 0.0362 | 14.5079 | 4.7685 | 0.8055 | 0.0239 | 4.6065 | 0.0237 |
| IL-P-ED | 0.0186 | 3.0288 | 2.0682 | 0.0264 | 0.0101 | 3.6230 | 0.0101 |
| IL-UNTRTD-DISSECTION | 0.0510 | 0.0334 | 2.9816 | 2.8834 | 0.0324 | 0.0329 | 0.0323 |
| IL-SBO | 0.0484 | 0.0389 | 0.0389 | 0.0392 | 0.0387 | 4.9099 | 0.0382 |
| IL-N-RFL | 0.0509 | 0.0422 | 0.0421 | 1.9923 | 0.0388 | 0.0414 | 0.0403 |
| IL-VTVFC | 0.0400 | 0.0409 | 0.0408 | 0.8040 | 0.0367 | 0.0400 | 0.0362 |
| IL-CS | 0.0532 | 0.3149 | 3.8002 | 0.8545 | 0.0459 | 0.0524 | 0.0469 |
| IL-ANG | 0.0889 | 0.0952 | 0.0951 | 1.3053 | 0.0887 | 0.0950 | 0.0894 |
The best values are indicated in boldface and the second best in italics.
PCI, percutaneous coronary intervention.
Conclusion
In this paper, we focused on developing clinical tools to evaluate patients undergoing PCI. Our goal was to model PCI complications that occur with diminished prevalence but that are associated with substantial mortality and morbidity. We believe that models for PCI complications have clinical value both for patient care by the bedside and for the quality and outcomes assessment. Our proposed OP-SVM realizes these opportunities to improve care for PCI patients, exploring in particular the idea of simultaneously leveraging the principles of the two-class SVM and the OC-SVM to develop a clinical model from imbalanced data.
We demonstrated the effectiveness of the proposed approach on a synthetic dataset and on data from patients undergoing PCI in the BMC2 registry. For many clinically important endpoints, the OP-SVM and its cost-sensitive variant showed improved discrimination and calibration compared to both the TC-SVM and OC-SVM methods. We note that in many biomedical data analysis problems besides the immediate PCI application considered in this paper, progress is limited by difficulties associated with data collection and clinical events that have diminished prevalence. Our study presents a way to address these challenges in the setting of modeling PCI complications. While we believe that our ideas may also have value in other clinical domains, a broader evaluation is needed to validate this hypothesis.
| Algorithm 1. The decomposition algorithm of the OP-SVM |
|---|
Input: training data 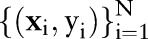 , cost parameter , cost parameter 
|
| Initialize: |
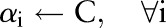 |
| Repeat |
| Compute: |
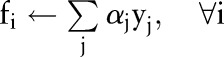 |
| Choose a data point xi such that |
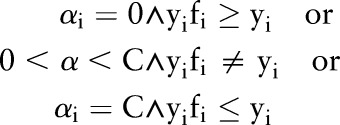 |
| Update: |
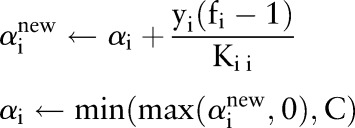 |
| Until Accuracy conditions are satisfied |
Output: dual parameters 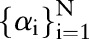
|
Footnotes
Contributors: GL, HSG and ZS participated in the study design, analysis and manuscript drafting. All authors read and approved the manuscript.
Competing interests: None.
Ethics approval: The data are de-identified. The University of Michigan institutional review board has approved use of these data for research without any subsequent approvals.
Provenance and peer review: Not commissioned; externally peer reviewed.
References
- 1.Shubrooks SJ, Jr, Nesto RW, Leeman D, et al. Urgent coronary bypass surgery for failed percutaneous coronary intervention in the stent era: Is backup still necessary? Am Heart J 2001;142:190–6 [DOI] [PubMed] [Google Scholar]
- 2.Jiang X, El-Kareh R, Ohno-Machado L. Improving predictions in imbalanced data using Pairwise Expanded Logistic Regression. AMIA Annu Symp Proc 2011;2011:625–34 [PMC free article] [PubMed] [Google Scholar]
- 3.Schilling PL, Dimick JB, Birkmeyer JD. Prioritizing quality improvement in general surgery. J Am Coll Surg 2007;207:698–704 [DOI] [PubMed] [Google Scholar]
- 4.Syed Z, Rubinfeld I. Unsupervised risk stratification in clinical datasets: identifying patients at risk of rare outcomes. Proceedings of the 27th International Conference on Machine Learning, Haifa, Israel; 2010;1023–30 [Google Scholar]
- 5.Hauskrecht M, Valko M, Kveton B, et al. Evidence-based anomaly detection in clinical domains. AMIA Annu Symp Proc 2007;11:319–23 [PMC free article] [PubMed] [Google Scholar]
- 6.Tarassenko L, Hayton P, Cerneaz N, et al. Novelty detection for the identification of masses in mammograms. Fourth International Conference on Artificial Neural Networks, University of Cambridge, UK; 1995;442–7 [Google Scholar]
- 7.Campbell C, Bennett KP. A linear programming approach to novelty detection. Adv Neural Inf Process Syst 2001;13:395–401 [Google Scholar]
- 8.Roberts S, Tarassenko L. A probabilistic resource allocating network for novelty detection. Neural Comput 1994;6:270–84 [Google Scholar]
- 9.Chia C, Rubinfeld I, Scirica B, et al. Looking beyond historical patient outcomes to improve clinical models. Sci Transl Med 2012;4:131ra49. [DOI] [PubMed] [Google Scholar]
- 10.Chia C, Karam Z, Lee G, et al. Improving surgical models through one/two class learning. IEEE Eng Med Biol Conf Proc; 2012;2012:5098–101 [DOI] [PubMed] [Google Scholar]
- 11.Verplancke T, Van Looy S, Benoit D, et al. Support vector machine versus logistic regression modeling for prediction of hospital mortality in critically ill patients with haematological malignancies. BMC Med Inform Decis Mak 2008;8:56. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Matheny ME, Resnic FS, Arora N, et al. Effects of SVM parameter optimization on discrimination and calibration for post-procedural PCI mortality. J Biomed Inform 2007;40:688–97 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Schölkopf B, Smola AJ. Learning with Kernels. Cambridge, MA: MIT Press, 2002 [Google Scholar]
- 14.Vapnik V. Statistical learning theory. New York: Wiley, 1998 [Google Scholar]
- 15.Tax DMJ, Duin RPW. Support vector domain description. Pattern Recognit Lett 1999;20:1191–9 [Google Scholar]
- 16.Schölkopf B, Platt JC, Shawe-Taylor J, et al. Estimating the support of a high-dimensional distribution. Neural Comput 2001;13:1443–72 [DOI] [PubMed] [Google Scholar]
- 17.Platt J. Sequential Minimal Optimization: A Fast Algorithm for Training Support Vector Machines. Microsoft Research; 1998. MSR-TR-98–14
- 18.Lee G, Scott C. Nested support vector machines. IEEE Trans Signal Process 2010;58:1648–60 [Google Scholar]
- 19.Bazaraa MS, Sherali HD, Shetty CM. Nonliear programming: theory and algorithms. 3rd edn. Hoboken, NJ, USA: John Wiley & Sons, 2006 [Google Scholar]
- 20.Mika S, Ratsch G, Weston J, et al. Fisher discriminant analysis with kernels. Neural Networks for Signal Processing IX, 1999 Proceedings of the 1999 IEEE Signal Processing Society Workshop; 1999;41–8 [Google Scholar]
- 21.Mldata.org. http://mldata.org/repository/tags/data/IDA_Benchmark_Repository / (accessed 14 Sept 2011) [Google Scholar]
- 22.Osuna E, Freund R, Girosi F. Support vector machines: Training and applications. MIT Artificial Intelligence Laboratory; 1997. AIM-1602
- 23.Morik K, Brockhausen P, Joachims T. Combining statistical learning with a knowledge-based approach—A case study in intensive care monitoring. Proc Int Conf Mach Learn; 1999;268–77 [Google Scholar]
- 24.Kline-Rogers E, Share D, Bondie D, et al. Blue Cross Blue Shield of Michigan Cardiovascular Consortium (BMC2). Development of a multicenter interventional cardiology database: the Blue Cross Blue Shield of Michigan Cardiovascular Consortium (BMC2) experience. J Interv Cardiol 2002;15:387–92 [DOI] [PubMed] [Google Scholar]
- 25.Moscucci M, Rogers EK, Montoye C, et al. Association of a continuous quality improvement initiative with practice and outcome variations of contemporary percutaneous coronary interventions. Circulation 2006;113:814–22 [DOI] [PubMed] [Google Scholar]
- 26.Cannon CP, Battler A, Brindis RG, et al. American College of Cardiology key data elements and definitions for measuring the clinical management and outcomes of patients with acute coronary syndromes. J Am Coll Cardiol 2001;38:2114–30 [DOI] [PubMed] [Google Scholar]
- 27.Altman DG. Practical statistics for medical research. London: Chapman and Hall, 1991 [Google Scholar]
- 28.Ohman EM, Granger CB, Harrington RA, et al. Risk stratification and therapeutic decision making in acute coronary syndromes. JAMA 2000;284:876–8 [DOI] [PubMed] [Google Scholar]
- 29.Moscucci M, Kline-Rogers E, Share D, et al. Simple bedside additive tool for prediction of in-hospital mortality after percutaneous coronary interventions. Circulation 2001;104:263–8 [DOI] [PubMed] [Google Scholar]
- 30.Singh M, Rihal CS, Lennon RJ, et al. Bedside estimation of risk from percutaneous coronary intervention: the new Mayo Clinic risk scores. Mayo Clin Proc 2007;82:701–8 [DOI] [PubMed] [Google Scholar]
- 31.Lemeshow S, Hosmer DW., Jr A review of goodness of fit statistics for use in the development of logistic regression models. Am J Epidemiol 1982;115:92–106 [DOI] [PubMed] [Google Scholar]
- 32.Kullback S, Leibler RA. On information and sufficiency. Ann Math Stat 1951;22:79–86 [Google Scholar]
- 33.Platt J. Probabilistic outputs for support vector machines and comparison to regularized likelihood methods. In: Smola AJ, Bartlett P, Schoelkopf B, et al., eds. Advances in large margin classifiers. Cambridge, MA: MIT Press, 1999: 61–74 [Google Scholar]
- 34.Zadrozny B, Elkan C. Transforming classifier scores into accurate multiclass probability estimates. The Eighth International Conference on Knowledge Discovery and Data Mining, Edmonton, Alberta, Canada; 2002:694–9 [Google Scholar]
- 35.Jiang X, Osl M, Kim J, et al. Calibrating predictive model estimates to support personalized medicine. J Am Med Inform Assoc 2011;19:273–4 [DOI] [PMC free article] [PubMed] [Google Scholar]