Abstract
New free-electron laser and high-harmonic generation X-ray light sources are capable of supplying pulses short and intense enough to perform resonant nonlinear time-resolved experiments in molecules. Valence-electron motions can be triggered impulsively by core excitations and monitored with high temporal and spatial resolution. We discuss possible experiments that employ attosecond X-ray pulses to probe the quantum coherence and correlations of valence electrons and holes, rather than the charge density alone, building on the analogy with existing studies of vibrational motions using femtosecond techniques in the visible regime.
Keywords: ultrafast, core hole, electron correlation, coherence, stimulated Raman
1. INTRODUCTION
1.1. Time-Domain X-Ray Sources and Spectroscopy
Nonlinear spectroscopy with visible light became feasible soon after the laser was invented in the 1960s. When the applied electric fields are weak compared with those inside an atom or a molecule (5.14 × 1011 V m−1 for an electron and a proton at a distance of 1 Bohr radius, which corresponds to a power intensity of 3.5 × 1016 W cm−2), the response and optical signals are linear in the incoming intensities and reveal some valuable information about excited states and their transition dipoles through a two-point correlation function of the dipole operator. At higher field intensities, a nonlinear response is observed, and the resulting signals encode much more information than the linear response, related to higher-order multiple-point correlation functions (12). The development of nonlinear spectroscopy was enabled by progress in laser technology. As pulse durations shortened from picoseconds in the 1970s to femtoseconds in the 1980s, they were employed in increasingly sophisticated time-resolved probes of molecular excited states (2). This review describes possible extensions of these techniques facilitated by recent developments of attosecond X-ray pulses.
X-ray linear absorption (3-5) probes the unoccupied density of states around the resonant core; the jump in signal intensity as the frequency reaches the first available unoccupied state is called the core edge. The low-energy region of the spectrum, the X-ray absorption near-edge structure (XANES), is a direct probe of these virtual orbitals weighted by their atomic core dipole matrix elements. Higher-energy spectral features, the extended X-ray absorption fine structure (EXAFS), are created by backscattering of the photoionized core electron. A Fourier transform of these spectra yields the structure factor of the nuclei surrounding the resonant core (6-8), as the tightly bound core electrons on neighboring atoms have the largest cross section for reflecting this photoelectron. X-ray diffraction (off-resonant elastic scattering) of a few kiloelectron volt photons solely probes the charge density and can be treated classically. Various forms of X-ray spectroscopy techniques (4) are summarized in Figure 1.
Figure 1.
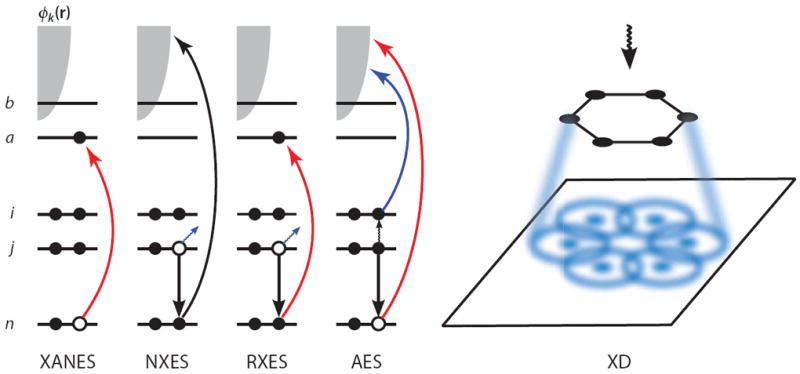
A schematic showing the electronic transitions involved in traditional, linear X-ray spectroscopy techniques. n denotes the core orbital, i and j are occupied valence orbitals, a and b are unoccupied valence orbitals, and the continuum of photoelectron states is represented by the gray shaded area. In the X-ray absorption near-edge structure (XANES), an electron is promoted from the core orbital to an unoccupied valence orbital. In nonresonant X-ray emission spectroscopy (NXES), a core electron is ejected owing to interaction with an applied field, and a valence electron falls into the core hole, emitting a red-shifted X-ray photon. In resonant X-ray emission spectroscopy (RXES), the core electron is promoted to an unoccupied valence orbital rather than being ejected, and another electron then fills the core hole while emitting a photon. In Auger electron spectroscopy (AES), the applied field ejects a core electron and a valence electron fills the hole, and the energy released by this transition is then transferred to another valence electron, which is subsequently ejected. In X-ray diffraction (XD), the elastically scattered field is spatially resolved, resulting in a diffraction pattern that can be used to elucidate structure.
These traditional X-ray measurements reveal single-particle characteristics of the many-body ground-state wave function. Quantum coherence (i.e., the phase in a superposition of states), which is revealed by nonlinear spectroscopy, does not play a role in these techniques. Coherent X-ray sources pave the way to look into these quantum effects. Two recent reviews of the X-ray free-electron laser (XFEL) (9) and tabletop attosecond X-ray sources (10) summarize the state of the art in experimental attosecond and X-ray technologies. These are only briefly surveyed here. The current review examines possible attosecond time-resolved X-ray spectroscopies by drawing on the analogy with their visible and infrared (IR) counterparts.
The first sources of X-rays were anode targets for cathode rays in vacuum (11). The high cross section for X-ray photon capture in matter, and the short lifetime of the core hole, meant that modifying traditional laser cavities to create a population inversion and lasing at X-ray frequencies would be difficult (12). Fortunately, synchrotron radiation, considered an undesired loss in high-energy particle experiments, was found incredibly useful for performing experiments in chemistry, biology, and condensed matter physics (13). These large facilities convert electron-bunch kinetic energy into short, broadband bursts of bright X-ray radiation (14). The intensity and high frequencies of the photons available at the highly intense XFEL sources built at DESY and LCLS, e.g., 1012 photons in 85 as at a frequency of 8 keV (15), can generate sequences of pulses suitable for coherent spectroscopy applications (16). Methods for generating intense ~1-fs pulses with UV and VUV frequencies have been proposed (17).
In a parallel development, tabletop attosecond higher-harmonic generation (HHG) (18-22) sources provide an alternative to the XFEL. These generate pulses of high-frequency light through a process in which a weakly bound electron in the molecule is ionized and then accelerated back toward the molecule as the driving field changes phase. The photoelectron has two chances to recombine with the hole it leaves behind for each cycle of the field, leading to a highly nonlinear frequency-doubling process capable of generating very-high-frequency components, which can be recombined to form attosecond pulses. Ultrafast pulses with central frequency ~800-eV and ~700-eV bandwidths were recently reported, potentially yielding a 2.5-as Fourier transform–limited pulse after compression (23, 24). HHG pulse intensities (~107 photons per pulse) are considerably lower than those from the XFEL (~1012–13 photons per pulse). XUV pulses with widths as short as 80 as (at 80-eV central frequencies) were generated (25).
Coherent spectroscopic techniques have historically built on earlier technological advances in lower-frequency regimes. Optical techniques benefited from the vast experience in nuclear magnetic resonance (NMR) spectroscopy, which uses radio waves to study spins, where the pulse technology had existed since the 1940s. Similarly, emerging X-ray studies could draw on the analogy with advances made in the 1980s in the visible and IR regimes. The current status of ultrafast X-ray studies is reminiscent of the early days of nonlinear optical spectroscopy (26). Coherent attosecond pulses (27) offer a new set of tools to the experimenter, allowing the direct real-time study of core and valence excitations (28). The detailed information gained regarding electron correlations and their response to impulsive perturbations may serve as experimental tests of many-body theory. In principle, time-domain techniques provide the same information as their frequency-domain counterparts; the two are connected by multidimensional Fourier transforms (29). However, ultrafast signals may be interpreted intuitively in terms of wave-packet evolution, and pulsed experiments can be designed to reveal desired information, which in many cases is highly averaged and hard to extract in frequency-domain techniques (2). Multidimensional time-domain signals, obtained in response to sequences of impulsive temporally well-separated pulses, probe the correlation between dynamical events occurring during different controlled interpulse delays by observing spins (NMR), vibrations (optical and IR), or valence and core electrons (X-rays) (30). This review focuses on possible applications of multidimensional all-X-ray time-domain techniques toward the study of valence excitations in molecules with high spatial and temporal resolution.
1.2. Nonlinear X-Ray Spectroscopy
Nonlinear effects in the X-ray regime have long been observed in the frequency domain (28), including parametric downconversion (31-33), hard X-ray frequency doubling (34), and two-photon X-ray fluorescence (35). X-ray parametric downconversion has been used to visualize valence charge motion in optically excited diamond crystals (36). Parametric downconversion (37) and two-photon emission from inner-core states (38) were among the first nonlinear X-ray processes to be treated theoretically. The X-ray/optical stimulated Raman process was studied (39-41).
Time-dependent X-ray diffraction (TDXD) can measure the nonequilibrium change in the charge density triggered by interaction with a visible pump pulse (42-44). Synchrotron radiation sources have vastly increased the quality of protein crystallography measurements using X-ray diffraction (45). The high intensity of the XFEL sources allows the collection of X-ray diffraction from a single molecule in response to a single pulse. This has been proposed as a method for structure determination without making crystals (46). The two-decade gap between the early theoretical papers on TDXD (47-50) and the experimental measurement of phonon (42, 51) and polariton (52) dynamics in solids gives some indication of the experimental difficulties associated with this technique. TDXD has been used to measure the ultrafast melting of a metal after excitation with a laser pulse (53). In the past decade, picosecond time-resolved EXAFS has been used to measure vibrational and valence electronic dynamics in photoactive inorganic complexes (8). In contrast to diffraction, resonant attosecond X-ray pulses can prepare coherent superpositions of core and valence states, revealing a qualitatively higher level of information about orbitals and spatial coherence that goes beyond the charge density. A detailed theoretical description of valence particle and hole propagation in atoms and molecules showed that ultrafast charge motion driven by electronic interactions accompanies a sudden perturbation of the ground-state charge density (54).
Intense X-ray pulses trigger a complex cascade of core excitations and Auger decays in atomic targets (55, 56). XFEL pulses are intense enough to create double core-hole (DCH) states in molecular nitrogen (57) and to ionize the tightly bound core orbitals leading to a rate-limiting step of Auger decay in the photoionization (58). DCH Auger electron spectroscopy in N2 has been reported (59). Investigators have also carried out time-domain pump-probe measurements (60). Experiments on the M-edge of krypton atoms were used to quantify the core lifetime with subfemtosecond precision (61) and to measure real-time valence-electron motion by an extreme ultraviolet (UV) probe of a molecule photoionized by a near-IR pulse (62).
HHG sources have been used to study vibrational motions in N2O2 (63, 64) and dynamic bond breaking in (65). The photoelectron generated in the course of an HHG process can also be used to investigate the molecular ion through an interferometric process, a kind of stimulated electron spectroscopy (66). The high intensity of the XFEL sources and the precision of the HHG sources are complementary. Electromagnetically induced transparency studies (67) at X-ray frequencies have recently led to experiments (68) that offer the possibility of augmenting the precision of the weaker HHG pulses with the stronger XFEL radiation, allowing the generation of strong and coherent pulses.
X-ray signals involve single-particle, field-driven transitions between core and valence electronic orbitals and the many-body valence response to a transiently created core hole (60, 69, 70). Pump-probe and stimulated Raman spectroscopy were among the very first nonlinear techniques employed with visible light (71-73) to study the vibrational states of aggregates (74) and molecules (75). These signals are robust as they do not require any phase control, and the detection is relatively simple. We first focus on all-X-ray stimulated Raman experiments in which the pump and probe pulses have X-ray frequencies. We then discuss more elaborate four-wave mixing techniques.
2. OPTICAL RAMAN SPECTROSCOPY OF VIBRATIONS VERSUS X-RAY RAMAN SPECTROSCOPY OF ELECTRONS
To set the stage for time-domain Raman spectroscopy, we first briefly survey some key features of the frequency-domain optical and X-ray Raman techniques. In both regimes, the relevant molecular states form two bands, denoted g and e. The energy gap between the bands is much larger than the intraband splittings. In vibrational spectroscopy, the states g and g′ (e and e′) represent vibrational states in the ground (excited) electronic state. In the case of core spectroscopy, g and g′ are valence excitations whereas e and e′ are core-excited states.
The absorption of light by a molecule can be described by Fermi’s golden rule
| (1) |
where P(g) is the population of state g, 〈ψg′ ∣μ∣ ψg〉 ≡ μg′ g is the dipole moment, and ωg′ g is the transition frequency between states g and g′. Raman scattering is an inelastic two-photon process in which an ω1 photon is absorbed, and an ω2 photon is generated. It can be described by the Kramers-Heisenberg expression, whereby the dipole operator coupling the material to the field in Equation 1 is replaced by a transition polarizability α,
| (2) |
α is given by a sum over the states of the molecule,
| (3) |
where Γeg is a dephasing rate. Both IR absorption and Raman signals access states in a similar spectral region (ω, ω1 – ω2 ~ 100 – 3,000 cm−1) but observe it through a different window. The former depends on the vibrational transition dipole moments between the initial and final states, whereas the latter depends on the electronic dipole moment between the ground and much higher excited states ∣ψe〉. These intermediate scattering states are responsible for the difference in selection rules between the two techniques. ∣ψg〉 and ∣ψg′〉 are ground and vibrationally excited states in the lowest-energy electronic state. Thus optical frequency light transiently excites a fast, high-frequency system (the valence electronic excitations) to gain information about a slow, low-frequency system (the vibrations). Plotting the signal versus ω1 – ω2 provides a one-dimensional (1D) projection of the vibrations.
In summary, in the optical regime we have high-frequency electronic excitations and low-frequency vibrational excitations, which can be studied by visible and IR absorption, respectively. The Raman technique examines the low-frequency vibrations through a polarizability that derives from the high-frequency excitation (see Figure 2, left column).
Figure 2.
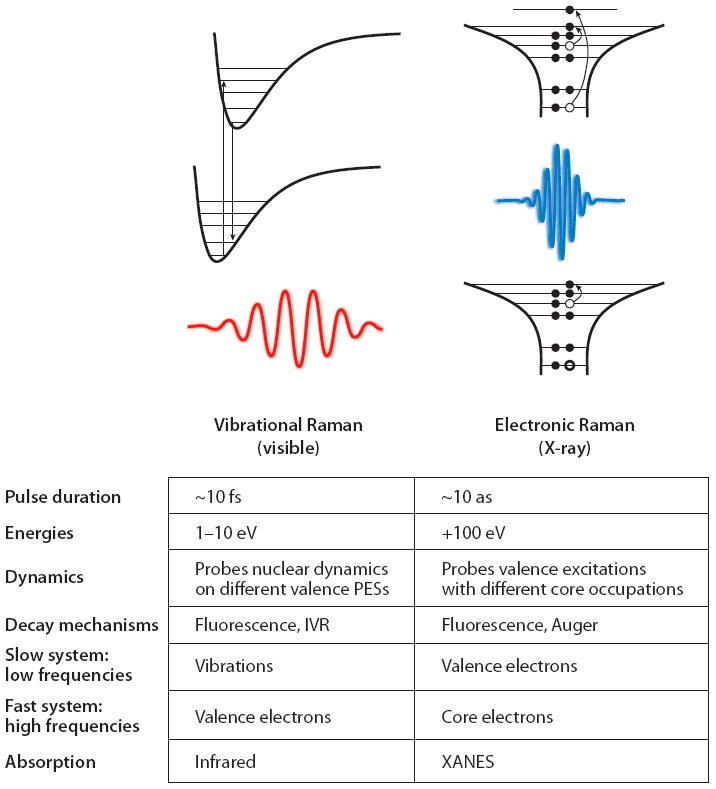
A comparison between vibrational and electronic Raman spectroscopy. Abbreviation: XANES, X-ray absorption near-edge structure.
An analogous description applies to X-ray Raman scattering. Resonant inelastic X-ray scattering (RIXS) is a well-established spontaneous frequency-domain technique that probes the occupied and unoccupied single-particle density of states around the resonant core by measuring the spontaneously emitted, energy-resolved X-ray radiation from a core-excited state (76, 77). Here the high frequencies are core excitations (≥100 eV), which can be studied by direct absorption through the XANES (Figure 2, right column). The low-frequency (few electron volts) valence excitations can be studied by visible or UV absorption. With RIXS one can study the valence excitations by a polarizability created by the core transitions.
Photons with energies of hundreds or thousands of electron volts are scattered off a system, and the frequency and momentum of the scattered light are resolved (78). The absorption of an X-ray photon promotes an electron from a closed-shell core orbital into the valence band. At this point, either the molecule can relax nonradiatively, through an Auger decay mechanism, or an electron can fall into the core hole, spontaneously emitting a photon. In the latter case, the electron that falls into the core hole need not be from the same orbital into which the original core electron was promoted, and the emitted radiation will be red-shifted with respect to the incident photon. The final state in this process is either the ground state (elastic, Rayleigh scattering) or a state with valence excitations (inelastic Raman scattering). Thus the analogy with optical Raman is established, with the core and valence electrons playing the role of the fast and the slow degrees of freedom, respectively. Note that elastic Rayleigh scattering is not a special case of Raman scattering, but it has a different mechanism; the scattered radiation is coherent and has a well-defined phase, whereas in the Raman case, the phase is random and the average signal field vanishes (79). Using contemporary terminology, the matter and scattered photon are entangled in a Rayleigh process, but not entangled in the Raman technique.
Vibrational Raman spectroscopy may be described by expanding the polarizability perturbatively in the normal modes Qi of the molecule,
| (4) |
where
| (5) |
and are boson creation (annihilation) operators. Similarly, in X-ray Raman scattering, we can expand the polarizability in the space of valence excitations as
| (6) |
where and ci are the Fermi creation and annihilation operators for an electron in the i-th valence orbital. Electron-hole pairs represented by thus play the same role in X-ray Raman scattering as the vibrational oscillators Qi in optical Raman scattering.
The dipole matrix elements that enter into Equation 3 in vibrational Raman spectroscopy can be calculated using the Condon approximation as
| (7) |
The ground-state and excited-state molecular wave functions are products of vibrational (∣Φ〉) and electronic (∣Ψ〉) wave functions, and is the electronic transition dipole connecting the two electronic states. In general, the vibrational normal modes in the excited state (Q1, …, QN) are not the same as those in the ground electronic state (q1, …, qN). The two sets of modes are connected by a linear transformation , where S is the Duschinsky rotation matrix, and d represents the displacement of the potential minimum upon excitation. The overlaps 〈ψe∣ψg〉, known as Franck-Condon factors, are multidimensional integrals that may not be generally factorized into single-mode contributions. That the nuclei evolve transiently under a different potential before the system returns to the ground electronic state is responsible for the inelastic Raman scattering (g ≠ g′ in Equation 13).
Similarly, in X-ray Raman spectroscopy, core-excited eigenstates are represented by Slater determinants in which the orbitals are calculated in the presence of the core hole. Core-excited states are represented compactly from a reference that includes the strong effect of the hole self-consistently. These orbitals are generally different from ground-state orbitals. The core-excited and ground-state electronic wave functions are written as linear combinations of Slater determinants,
| (8) |
q = {q̃i} are the occupied orbitals in the core-excited basis, and p = {pi} are the occupied orbitals in the ground state. The sum is over all possible permutations κ = {κj} of these orbitals, and Pκ is the parity of each of these permutations. In the many-body eigenstate description of the core-excited molecule, the X-ray dipole matrix element can be written as a weighted sum of determinant overlaps.
The matrix element of the dipole operator can be calculated by tracing the single-electron operator over the transition density matrix
| (9) |
For core-edge excitations, typically only the resonant transitions , where n is the resonant core orbital, are considered. The transition density is between Slater determinants written using nonorthogonal basis functions and can be calculated using Løwdin’s rules:
| (10) |
Equation 9 contains multidimensional electronic Franck-Condon factors between Slater determinants made of different orbitals. The overlap of two Slater determinants written in different bases is given in Equation 10 by the determinant of a subset of the overlap matrix between the two basis sets, including only the rows occupied in the bra and the columns occupied in the ket (80).
There are two possible causes for inelastic Raman transitions of vibrations. First, the dipole operator can change the vibrational state instantaneously upon electronic excitation through its dependence on the vibrational coordinate. However, even if the vibrational state does not change upon excitation, when the vibrational eigenstates in the ground and excited electronic states are different (owing to a change in the potential surface), then the excitation prepares a superposition of electronically excited vibrational states whose subsequent time evolution then changes the vibrational state. In the Condon approximation, the dependence of the electronic dipole operator on the nuclear coordinates is neglected, and only the second mechanism applies. Similarly, in the X-ray regime, the difference of orbitals with and without the core hole gives rise to electronic wave-packet evolution in the core excited state. Because the electronic dipole operator does depend on the valence state, this electronic Franck-Condon effect occurs in addition to direct dipole-coupled transitions between states with different core occupations.
Valence excitations can be represented by many-electron wave functions, which may be calculated by a broad arsenal of computational tools and approximations. It is hard to compute and visualize these wave functions that live in a high-dimensional space. An alternative approach that treats the valence excitations as a collection of quasiparticle boson oscillators provides a more intuitive picture (81). Boson techniques have a long history in X-ray spectroscopy; they were first employed to explain the X-ray edge singularity in metals (82-86). The Mahan-Nozieres De-Dominicis Hamiltonian developed to explain this phenomenon treated the core hole as an instantly created coulomb potential for the valence electrons (87, 88). The many-electron dynamics can be formally mapped into composite bosons (89, 90). This approach offers new approximations that could reduce computational costs and offer useful physical insights into the nature of electronic excitations.
We next turn to time-domain Raman techniques. The two-pulse time-domain impulsive Raman technique became feasible in the 1990s (91). This technique is 1D as it depends on a single variable delay period (see Figure 3). Multiple-pulse 2D extensions were proposed (92) and realized experimentally in molecular liquids (93-95). Resonant excitation with visible light can be described using different contributions, “pathways,” in which the system can be prepared either in the ground state or in the excited state. Ground-state vibrational dynamics can be studied by tuning the fields off-resonance and monitoring stimulated Raman processes. In the X-ray regime, we would like to use resonant excitation that exploits the localized nature of core transitions to prepare localized electronic wave packets. The lifetime of core-excited states is ~7.1 fs for nitrogen, ~5.0 fs for oxygen (96), ~1.1 fs for sulfur (97), and 0.4 fs for zinc (96). By limiting the observation window to longer delay times, we can solely probe the valence excitations. Soft or hard X-ray pulses with ≃ 10-eV bandwidths can create superpositions of electronic excited states. We can thus combine the resonant selectivity of excitations at a desired atom with the ability to focus solely on valence excitations. Any core-excited population created by the pulses has decayed before the arrival of the next pulse. Researchers examined the feasibility of stimulated and coherent Raman experiments using the XFEL (98), and schemes for tailoring the electron bunches to generate pairs of attosecond pulses suited for stimulated X-ray Raman experiments have been suggested (99, 100).
Figure 3.
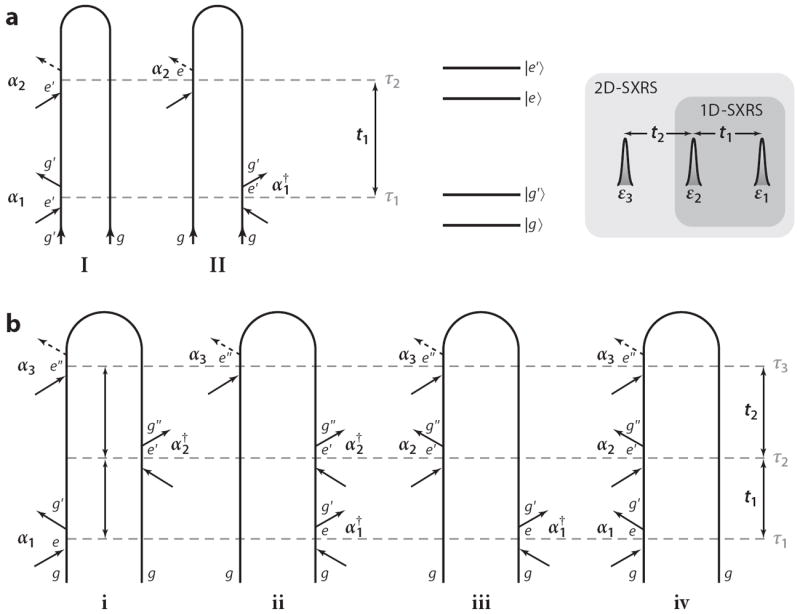
(a) Loop diagrams for 1D stimulated X-ray Raman spectroscopy (1D-SXRS). Pulse arrival times τj and interpulse delays tj are given on the right. Expressions for the signal (Equation 14) can be read directly off the diagrams. (b) Loop diagrams for 2D-SXRS. The four terms in Equation 18 correspond to the four diagrams, respectively. For example, contribution iv to 2D-SXRS can be written in the Schrödinger picture as 〈α3 G(t2)α2 G(t1)α1〉 or the Heisenberg picture as 〈α3(t2 + t1)α2(t1)α1(0)〉.
Below we survey X-ray Raman techniques in increasing order of complexity. We start with RIXS, which is a spontaneous frequency-domain linear technique. We then discuss the simplest time-domain technique, 1D stimulated X-ray Raman spectroscopy (1D-SXRS), which involves two impulsive pulses that result in a nonlinear signal scaling as ~I2 with the pulse intensities. Under certain conditions, 1D-SXRS is simply the Fourier transform of RIXS; however, it can also provide additional information. Finally, we describe 2D stimulated X-ray Raman spectroscopy (2D-SXRS), which uses three pulses, scales as ~I3, and provides higher-order correlation information.
3. SPONTANEOUS VERSUS STIMULATED X-RAY RAMAN TECHNIQUES
3.1. Frequency-Domain Spontaneous Raman Scattering: Resonant Inelastic X-Ray Scattering
The optical resonant Raman technique probes those vibrational modes of a molecule that are perturbed by the selected electronic excitation; only modes whose potential is different in the ground and excited electronic states show Franck-Condon activity. In RIXS a core electron is excited into a vacant (virtual) orbital, and the core hole is then filled by another electron. Inelastic losses representing valence excitations can be created directly, when an electron other than the excited core electron drops into the core hole (a two-electron transition), or indirectly, when the Coulomb potential of the transiently created core hole creates valence excitations (78, 101, 102). The energy satellite spectra for the indirect process represent valence shakeup states and depend on the excitation frequency. Momentum-resolved RIXS (103) has been used to measure a spatial exciton density in LiF (104) and density disturbances in the electronic structure of disordered liquid water (105). 1s2p RIXS in transition metals has been reviewed by Glatzel & Bergmann (106). We note that inelastic loss and satellite lines result from two-electron transitions.
Figure 4 displays the calculated RIXS spectrum for trans-N-methylacetamide [trans-NMA (CH3CONHCH3)], which is a model for the peptide bond, with the incident light tuned to the nitrogen K-edge. The RIXS intensity falls off as the laser frequency is detuned from the strong core-edge transition. The spectrum varies with ω1, as the intensity also depends on the transition dipole between the valence-excited state in question and the core-excited state in resonance with the laser frequency. When ω1 = 401.7 eV (the transition frequency for the lowest-energy N1s core-excited state), the valence-excited states S2 and S5 dominate the signal (Si are the excited singlet states in order of energy). When ω1 is tuned to the second core-excited state, these are replaced by a strong S3 peak. When the excitation frequency changes to 406.5 eV (the ninth core-excited state), the dominant peak now corresponds to the S19 state.
Figure 4.
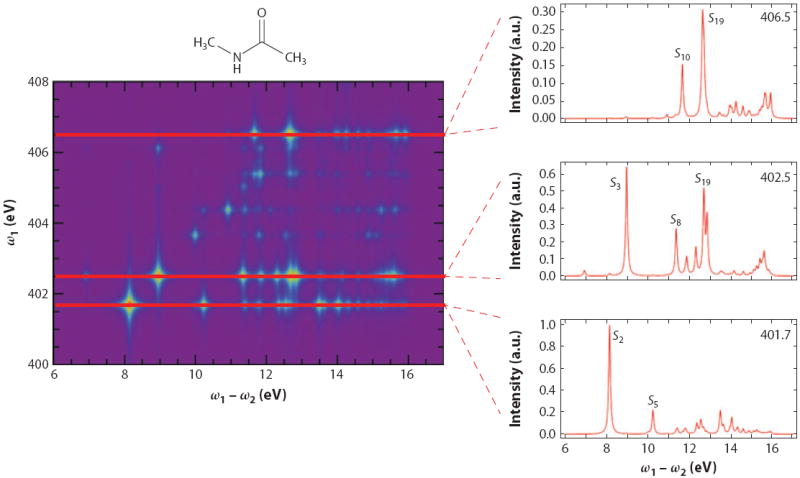
Calculated resonant inelastic X-ray scattering signal from trans-NMA at the nitrogen K-edge. Figure reprinted with permission from Reference 107. Copyright 2012.
3.2. 1D Impulsive Stimulated Raman Spectroscopy: 1D-SXRS
The 1D-SXRS signal is a time-domain extension of RIXS generated by two short pulses with a variable delay (Figure 3). An X-ray photon is absorbed from the first pulse, exciting a core electron to an empty spin orbital, and an electron drops into the core hole, emitting a photon. The process is repeated with a second pulse, and the signal, defined as the change in transmission of the second pulse due to the first, is recorded versus a variable delay t1. The signal is displayed as the Fourier transform with respect to this delay,
| (11) |
Peaks in S1D(Ω) represent valence excitations generated through electronic Franck-Condon factors with core-excited intermediates.
Investigators have proposed the use of SXRS to investigate the electronic properties of molecules (108), and it has been simulated in conjugated π-bonded organic molecules (109) and excitonic systems (110) using a tight-binding model Hamiltonian. Several extensions and refinements of 1D-SXRS were considered, including the use of attosecond pulses to prepare entangled particle-hole states (111), frequency-domain coherent anti-Stokes Raman spectroscopy with wide-and narrowband pulses (112), and a many-body Green’s function–based method suitable for calculating the SXRS of larger systems (113). X-ray spectra of molecules with cores separated from each other at some distance were also discussed (114).
The 1D-SXRS signal can be described and interpreted using the loop diagrams shown in Figure 3, which represent the evolution of the many-electron wave function when subjected to two impulsive perturbations. The description of the process using these diagrams involves both forward and backward time evolution.1 The 1D-SXRS signal is given by the two diagrams shown (111) in Figure 3a, which yield the following two contributions, respectively:
| (12) |
where the operators are written in the Heisenberg picture. In Equation 12 and below, angular brackets 〈A〉 denote expectation values with respect to the ground state 〈go ∣A∣go〉. The signal is given by the difference between two time correlation functions of the effective polarizability, which generalizes Equation 3 to include the broad pulse envelopes
| (13) |
where ej, εj, and ωj are the polarization vector, spectral envelope function (centered at zero), and carrier frequency of the j-th pulse, respectively. αj selectively excites valence transitions g′ ← g″, whose frequencies lie within its bandwidth. Owing to the denominator of Equation 13, the Raman amplitude is enhanced when the carrier frequency is resonant with a core transition.
Equation 12 may alternatively be recast in the Schrödinger picture as
| (14) |
where we have set the ground-state energy to zero. The physical picture of the process is as follows. In the first term, interaction with the first pulse through α1 creates a valence wave packet. The retarded Green’s function G describes the forward time evolution of the free molecule during the delay t1:
| (15) |
This is finally projected onto the state 〈go ∣α2 by the second pulse. The valence-excited states composing the wave packet in Equation 15 can be represented as linear combinations of electron-hole excitations,
| (16) |
where is the creation (annihilation) operator for the virtual (occupied) orbital a (i). In the second term of Equation 14, a valence wave packet α2∣go〉 is created by the second pulse; the advanced Green’s function G† then propagates it backward during t1 until it is finally projected onto by interaction with pulse 1. A compact visualization of these particle-hole wave packets may be obtained by using natural transition orbitals that represent the reduced single electron particle and hole density matrix (116, 117).
1D-SXRS generalizes RIXS in two ways. First, a two-color setup is possible in which pulses 1 and 2 are tuned to be resonant with different core transitions. This allows one to prepare a wave packet in the vicinity of one atom and probe it around a second atom; RIXS is limited to one color. Second, in RIXS the polarizations of the field exciting the molecule and the emission may be varied independently. In SXRS, both excitation and emission are stimulated by the same pulse and must have the same polarization, but the relative polarizations of the two pulses can be varied. From Equation 13, we see that α contains scalar products between the field polarization vector and the molecular dipole moments for the upward and downward transitions, making α a second-rank tensor. For an isotropic ensemble of molecules, the signal must be averaged over all lab-frame orientations of the molecules. There are three independent tensor signal contributions for third-order signals, such as RIXS, 1D-SXRS, and the photon-echo technique discussed below (118). In RIXS, it is possible to send the incident and scattered radiation through independent polarization filters so that the two stimulated upward transitions interact with the same lab-frame polarization. Similarly, the two spontaneous downward transitions interact with the same polarization (76). In 1D-SXRS, however, the first (second) up-and-down transitions interact with the lab-frame polarization of the first (second) pulse. In a system of randomly oriented molecules, by setting the polarization vectors of the first and second pulses at the magic angle relative to each other (where 3 cos2 θ − 1 = 0), one can isolate the signal contribution that depends only on the isotropic polarizability,
| (17) |
which is a scalar. It is not possible to have an RIXS signal that depends only on ᾱ.
Unlike RIXS, S1D(Ω) results from the interference of the two pathways shown in Figure 3a and may not be written in the Kramers-Heisenberg form. The signal is collected in the time domain and is Fourier transformed. The interpulse delay t1 should be kept longer than the core-hole lifetime (>10 fs). Core-excited populations will then decay to an ionized state through an Auger process and will not contribute to the signal (114). For shorter delays, additional non-Raman core-excitation contributions must be taken into account, which complicates the analysis.
Figure 5 displays the calculated modulus of the 1D-SXRS spectra for trans-NMA. An intense elastic scattering (g′ = g) at Ω = 0 is not shown. The peaks are labeled by the corresponding excited state Sj. The single-color NN signal (where both pulses are tuned to the nitrogen K-edge transition) is dominated by S2, which is absent from the OO signal. The different intensities for the one-color signals reflect the degree to which a given valence-excited state is perturbed by the transient presence of a core hole on either an oxygen or a nitrogen atom. The two-color ON (oxygen first, then nitrogen) and NO (nitrogen first) signals contain peaks from valence states that are perturbed by both core holes and show up in both the NN and OO signals. Far off-resonance, the effective polarizability is purely real, the two terms in Equation 14 are complex conjugates of each other, and the ON and NO signals are identical (time-reversal symmetry). On resonance, αg′ g″ is a complex number and α ≠ α†. The difference of the two signals provides information on the complex phase of the effective polarizability.
Figure 5.
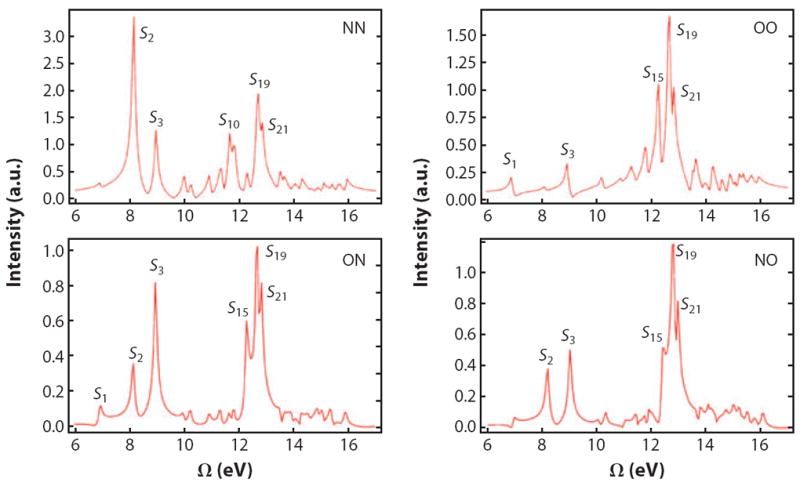
Calculated stimulated X-ray Raman spectra of trans-NMA; both pulses are polarized parallel to the lab-frame V axis. We use Gaussian pulses, 128-as full width at half-maximum in intensity, with the center frequency set to either 401.7 eV (N1s) or 532.0 (O1s). Pulse sequences for the two-color signals (bottom row) are given from left to right in chronological order; i.e., in ON the O pulse come first and the N pulse comes second. Figure reprinted with permission from Reference 107. Copyright 2012.
3.3. 2D Impulsive Stimulated Raman Scattering: 2D-SXRS
2D-SXRS extends 1D-SXRS by adding one more pulse (Figure 3). 2D correlation plots are generated by varying the two interpulse delays t1 and t2. During these delays, the system is in a coherence either between a valence-excited state and the ground state or between different valence-excited states.
The 2D-SXRS signal is described by the four loop diagrams shown in Figure 3, which result in the following expression:
| (18) |
Equation 18 contains interfering contributions of various forward and backward evolution periods. In diagram iii in Figure 3b, for example, we first excite with α2 (with “first” being along the loop, not in real time!), creating the state α2∣go〉; propagate forward for t2 [G(t2)]; then act with α3; propagate backward for t1 + t2 [G†(t1 + t2)]; and finally project the valence wave packet into . The other terms can be described similarly.
The 2D signals are displayed as frequency-frequency correlation plots
| (19) |
Figure 6 depicts the OOO 2D-SXRS spectrum of trans-NMA, together with several 1D horizontal and diagonal traces. For comparison, we also show the corresponding traces from the OON pulse sequence. These two signals differ only in the frequency of the third pulse. In both, the first and the second pulses are resonant with the oxygen K-edge, whereas the third is resonant with nitrogen (OON) or oxygen (OOO). A trace along the diagonal line Ω1 = Ω2, shown in Figure 6a, is similar to the OO 1D-SXRS signal, with narrower line widths.
Figure 6.
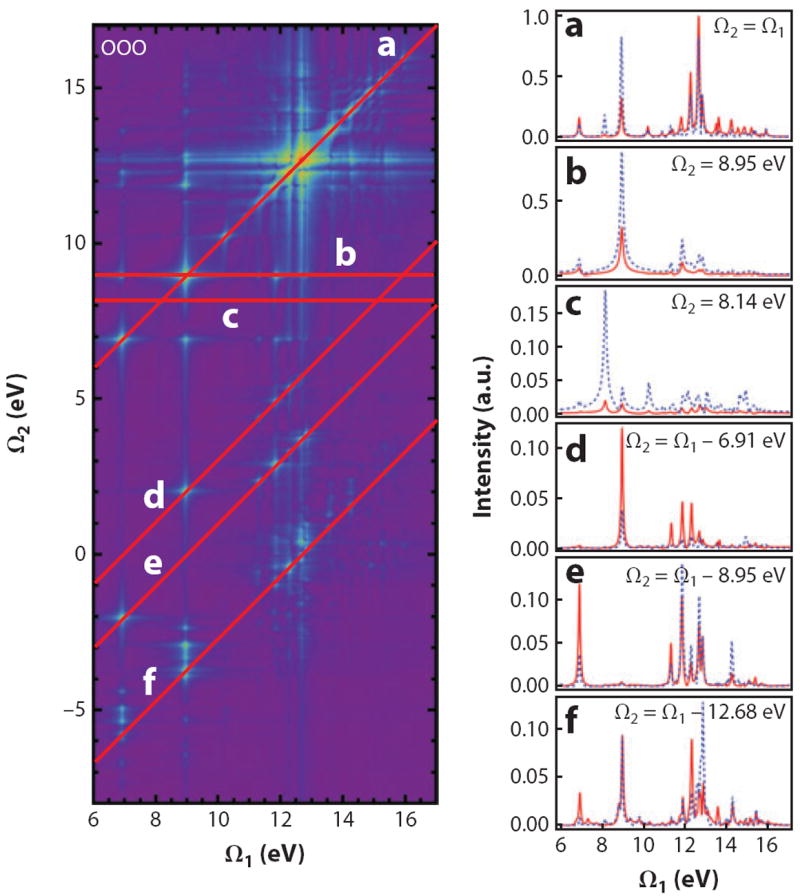
(Left column) The OOO 2D stimulated X-ray Raman spectrum of trans-NMA, plotted using a nonlinear scale. (Right column) Horizontal and diagonal slices, plotted using a linear scale, of the 2D spectrum on the left (red). The corresponding traces from the OON (dashed, blue) technique demonstrate the effect of changing the probe pulse in the three-pulse sequence. Figure reprinted with permission from Reference 107. Copyright 2012.
The off-diagonal Ω1 ≠ Ω2 peaks seen in Figure 6b,c result from interference between diagrams ii and iv in Figure 3. Only off-diagonal peaks carry information about the polarizability matrix elements between valence-excited states. The diagonal peak at (Ω1, Ω2) = (8.95 eV, 8.95 eV) in Figure 6b, for example, depends on products such as αO;S0S3 αO;S3S3 αO;S3S0, where the polarizability between the ground and valence-excited states, which determine the 1D SXRS signal, is multiplied by a diagonal element of the polarizability. Figure 6d–f shows diagonal traces for which Ω2 is equal to the difference between two valence-excitation frequencies. The peaks in Figure 6d result from interference between diagrams i and iii in Figure 3. 2D signals probe molecular valence excitations in greater detail than the 1D techniques.
Another control knob is provided by the polarizations of different pulses that may be varied independently to yield the various components of the nonlinear response tensor (119). The signal is given by a linear combination of three-point correlation functions of the tensor components of the dipole operator, weighted according to the polarizations of the applied fields. It is possible to design 2D-SXRS signals in an ensemble of randomly oriented molecules that are given by a linear combination of correlation functions of the isotropic polarizability (Equation 17) (118), greatly simplifying interpretation and analysis. This is accomplished by the super-magic-angle configuration (120).
3.4. Direct Observation of Core Excitations by X-Ray Four-Wave Mixing
Raman techniques require no phase control of the pulses and may be performed in a simple collinear geometry. Because we use the core transitions as a trigger and observe only valence excitations, the time window is determined by the lifetimes and dephasing times of valence states, which can be hundreds of femtoseconds. The direct observation of core excitations is more tricky because of the shorter time window (few femtoseconds) limited by Auger processes and the stringent requirements for phase control.
Schweigert & Mukamel (121) proposed the use of X-ray photon-echo signals and simulated them for the para, meta, and ortho isomers of aminophenol. This is a four-photon stimulated process in which the molecule interacts with four short pulses with wave vectors k1, k2, k3, and kI (in chronological order), where kI = –k1 + k2 + k3 (see Figure 7a). The signal is given by the change in transmission of the kI pulse induced by the other pulses. In the semiclassical theory of radiation-matter coupling, this four-wave mixing process is described in a different language: The interaction of the molecule with the first three pulses creates a polarization. This generates a signal field that is heterodyne detected by interfering it with the fourth pulse. In a quantum description of the fields, all four fields are treated on the same footing. The dominant contributions to the induced polarization come from specific third-order interactions with the fields (29). These are known as excited-state stimulated emission, ground-state bleach, and excited-state absorption (Figure 7b). In the excited-state stimulated emission and excited-state absorption, pathways in both branches of the loop are in a core-excited state during the second delay period (usually called the population or waiting time in optical and IR photon-echo studies). The third pulse then either stimulates emission down (stimulated emission) or gets absorbed to a higher state (excited-state absorption).
Figure 7.
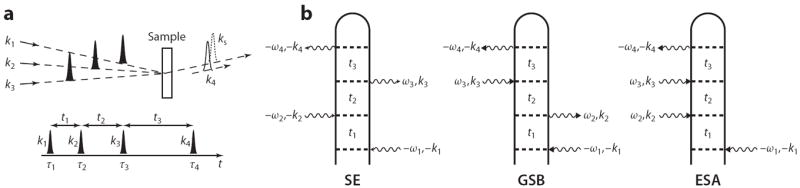
(a) Pulse sequence in a four-wave mixing experiment. Three pulses k1, k2, and k3 induce a polarization in the molecule, which is probed by the heterodyne field kI at kI = −k1 +k2 +k3. t1–t3 denote time intervals between consecutive pulses. (b) Loop diagrams representing the stimulated-emission (SE), ground-state-bleaching (GSB), and excited-state-absorption (ESA) contributions to the signal.
X-ray photon-echo signals were also simulated in Watson-Crick base pairs in DNA at the nitrogen K-edge (122). Unlike the aminophenol isomers discussed above, the base pairs have multiple nitrogen atoms with different chemical environments, which produce a chemical shift of a few electron volts. Therefore, excitation with a broadband X-ray pulse will create a superposition of core-excited states with the core hole on amine or imine nitrogen atoms. The effect of different geometries may then be investigated. This study suggests that cross-peak widths and intensities in the nitrogen K-edge 2D X-ray correlation spectroscopy signal can be used to assign the relative geometry of two nucleobases. Four-wave mixing in systems with multiple resonant cores is analogous to homonuclear NMR, whereas multicolor experiments resemble heteronuclear NMR (123).
The kI signal may be used to trace the origin of the Raman resonances that contribute to the 1D- and 2D-SXRS signals. We take t2 to be long compared with the core-excited lifetimes, allowing us to focus only on the ground-state-bleaching contribution, in the same way as discussed above with 1D-SXRS. This contribution to the kI signal is similar to the 1D-SXRS spectrum when t1 and t3 are set to zero (note the similarity between the middle diagram of Figure 7b to the top right diagram in Figure 3a). The signal is recorded versus the three delay times t1, t2, and t3 and is subsequently Fourier transformed to give the 3D signal (by direct extension of Equation 18):
| (20) |
This expression reveals how the pulse bandwidths select the various relevant core transitions.
Figure 8 depicts the kI signal for the amino acid cysteine, with all four Gaussian pulses tuned to the nitrogen core edge (full width at half-maximum of 128 as, 14.2 eV) (124). We focus on the 5 eV ≤ Ω2 ≤ 13 eV region corresponding to the valence-excited states that contribute to the 1D-SXRS spectrum. We also show horizontal 2D slices of the 3D plot for constant Ω2 values corresponding to the three most prominent peaks in the 1D-SXRS spectrum. In this way, we are able to determine which core-excited state is coupled to which valence-excited state. Some of the valence states (e.g., peak a) are associated with a single core-excited state. This indicates a single-particle transition in which the core electron is promoted to an unoccupied valence orbital, following which an electron from an occupied valence orbital then falls in to fill the core hole, leaving a single electron-hole pair in the valence band. Two core-excited states contribute to peak b, indicating that this valence excitation may not be described in a single-particle picture. Multiple, nearly degenerate core-excited states contribute to peak c. Thus the 3D photon echo can unravel the various pathways that contribute to a given SXRS peak.
Figure 8.
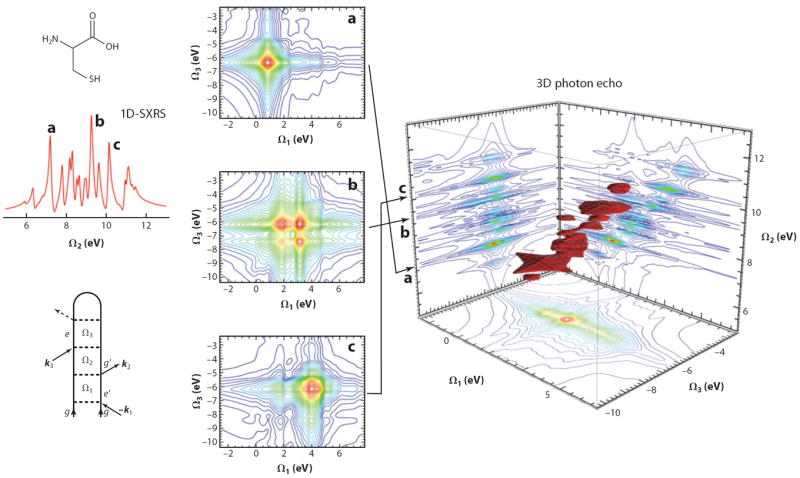
(Right panel) A 3D plot of calculated for the amino acid cysteine. All four Gaussian pulses are tuned to the nitrogen core edge (128-as full width at half-maximum, 14.2 eV), along with the 2D projections. We show only the Ω2 > 0 region to focus on the relation to the stimulated Raman signal (far left panel). (Middle panel) 2D slices of the 3D signal for constant Ω2 corresponding to a given valence excitation.
3.5. Detecting Multiple Core Holes by Double-Quantum-Coherence Four-Wave Mixing
DCH states, created through the absorption of two X-ray photons, exist in two varieties: single site and two site. Recent experiments (125) demonstrated the sensitivity of the DCH energy to the chemical environment (i.e., the chemical shifts are nonadditive). Using intense pulses with energies far above the K-edge, investigators measured the single and double ionization potentials of several di- and triatomic molecules by kinetic-energy-resolved photoelectron spectroscopy. Chemical shifts, the difference between the double ionization potential and twice the single ionization potential, were observed for both single-site and two-site states. The former states exhibit a rather large chemical shift, between 70 and 90 eV for carbon, oxygen, and nitrogen. The latter chemical shifts are between 10 and 16 eV and strongly depend on the bonding environment of the atoms in question. For example, the shift for the O−1C−1 two-site state is 11.2 eV in carbon dioxide and 16.3 eV in carbon monoxide, in excellent agreement with theoretical predictions (126).
2D X-ray correlation spectroscopy can provide a unique insight into the dynamics of two-site DCH states. 120-as X-ray pulses have a bandwidth of ~21.5 eV (full width at half-maximum in intensity), covering ground to single core-hole transitions as well as single (e) to DCH (f) transitions. The signal in the kIII = k1 + k2 − k3 direction provides a unique window into the DCH state (127, 128). This technique, the X-ray analog of double-quantum coherence in NMR (123), has been demonstrated to show high sensitivity to exciton coupling in the IR (129, 130) and the visible spectra (131, 132). Only two excited-state absorption pathways contribute to this signal, both involving DCH states, and the signal is proportional to
| (21) |
where ωeg is the energy difference between the ground and singly core-excited state, and ωfe is the energy difference between doubly and singly core-excited states. The two pathways interfere destructively if the two core transitions are uncoupled (i.e., when ωeg = ωfe). This entire signal is thus induced by the coupling between core transitions, giving it extra sensitivity to many-body effects (133).
The new era of attosecond core spectroscopy poses important theoretical and computational challenges to many-body theory. Resonant X-ray spectroscopy signals require core-excited states that lie high above many valence-excited states. Conventional protocols for valence-excited state simulations, which calculate the eigenstates from the bottom up, become tedious. In addition, core electrons are close to the nucleus and carry high kinetic energies. Relativistic effects should be considered for systems with heavy atoms, and self-interaction correction is necessary. For density functional theory methods, nonadiabatic dynamics for superpositions of many-electron states is a challenge as core electrons are localized (134). Time-dependent density functional theory within the adiabatic approximation, the most popular quantum chemistry method for excited states, can deal with single core-excited states; however, it cannot handle double or multiple core-excited states. All these issues make calculations for core-excited state more challenging than those for valence-excited states.
If the photon energy is above the ionization threshold of the system studied, metastable states (resonances) might be created. Resonances are eigenvectors of non-Hermitian Hamiltonians (135) on which the numerical algorithms for Hermitian quantum mechanics may not apply. This poses a great computational challenge. The most popular method for resonance calculations is the R-matrix method (136), which could be computationally demanding for molecular systems. Density functional resonance theory (137) is under development for a balance of computational cost and accuracy.
4. CONTROL PARAMETERS IN X-RAY NONLINEAR SPECTROSCOPIES
4.1. Wave Vectors and Phases of the Applied Pulses
Many types of control knobs are commonly used to refine the information in optical spectroscopy. Here we briefly describe their potential use in the X-ray regime. The wave vectors and phases of the applied pulses may be used to separate and resolve different contributions (pathways) to nonlinear optical signals. The electric field may be represented as
| (22) |
The phases ϕj and wave vectors kj enter in a similar way and offer equivalent methods for pathway selectivity. Each possible combination of wave vectors ±k1 ± k2 ± k3 generates a signal that appears in a distinct direction and probes a certain group of pathways (as can be seen from the diagrams). By looking at a particular direction, we get some pathway selectivity. Alternatively, one can perform the experiment in a collinear geometry in which all the signals appear on top of each other. Nevertheless, it is possible to recover the same pathway selectivity by repeating the measurement with different phases and selecting the desired component with the desired phase ±ϕ1 ± ϕ2 ± ϕ3. Eight independent choices of phase are needed to separate the eight contributions. This protocol, known as phase cycling (138, 139), allows one to use fluorescence detection in high-Z atoms and even carry out the experiment on a single molecule (140). NMR measurements must use phase cycling because the radio wavelength is larger than the sample size and the signals are isotropic.
4.2. Spectroscopy with Quantum or Stochastic Fields
XFEL pulses are intense [1012 photons at 8 keV (15)] but noisy. Harmonic sources are coherent but much weaker (e.g., ~105 photons in 1% of the bandwidth at 1 keV) (23). Although most nonlinear X-ray techniques require both bright and coherent sources, some techniques can make use of the noise. In the 1980s, investigators used noisy nanosecond sources to perform femtosecond measurements, utilizing the short correlation time (29, 141, 142). The noisier the source is, the shorter the field correlation time and the better the time resolution! Theoretical studies have shown that the noise in XFEL pulses may increase the efficiency of DCH ionization (70).
The nonlinear response can be written as a product of two multipoint correlation functions: one corresponding to the material and one to the field, i.e.,
| (23) |
The signals thus depend on multipoint correlation functions of the field rather than the field amplitudes themselves. Raman and four-wave mixing signals depend on four-point correlation functions of the field. The same approach may also be used to describe fields of a quantum nature, such as entangled photons (143-146), that are characterized by different types of correlation functions. New types of multidimensional signals are then possible by varying the parameters of the photon wave function.
4.3. Means of Detection: Photons Versus Photoelectrons
X-ray fields can ionize the molecule, and the ejected electrons’ energies and angular properties can be resolved (147, 148). Pairing the X-ray pulse with an actinic optical pump that prepares the molecule in a nonequilibrium state can result in other types of multidimensional signals. The molecule can be excited by multiple pulses. The last pulse is ionizing, and the photoelectron is detected. The phase cycling protocol can be used to select pathways as is done in the case of photon detection. Photoelectron detection is typically more sensitive than photon detection.
The dependence of the angle-resolved photoelectron current on the electronic state of the molecule was examined theoretically (149). The time-resolved photoelectron current can be written in terms of dipole transitions between a time-dependent effective single-particle field, called the Dyson orbital (149), and the measured photoelectron. The Dyson amplitude for destroying an electron in the orbital i if the molecule in the core-excited state ∣f〉 is
| (24) |
The Dyson orbital is a linear combination of orbitals weighted by these amplitudes,
| (25) |
The dipole operator that couples the many-body excited states can be written as a single-particle dipole operator:
| (26) |
All information on the time evolution of the many-body wave packet is encoded in the time dependence of this single-particle Dyson orbital. These orbitals have been used to investigate the time-resolved photoelectron spectra of optically excited pulses (149) and to trace the nuclear motion of molecules on valence-excited-state potential energy surfaces (150).
4.4. Pulse Shaping: Intrapulse Phase Control
Pulse shaping (27, 138, 151) controls the amplitude and phase of various modes of the field, written as ε(ω)eiϕ(ω), and may be used to optimize the nonlinear optical and Raman signals and highlight desired features. The experimental difficulties for X-ray pulse shaping are daunting, but technological progress in this area is proceeding rapidly. The expression for the effective polarizability given in Equation 13 can be easily extended to cover the possibility that the upward and downward transitions are facilitated by different coincident pulses. In the optical domain, there has been much success in using a narrowband pulse to electronically excite the system, which is then de-excited by a broadband pulse (152, 153). Another possibility is to split the Raman pulse into a train of pulses, whose interpulse delays are set to match the inverse of the Raman transition frequency (91). We can thus selectively excite a single Raman active mode at the expense of other allowed transitions. Another dimension can be added by dispersing the frequency of the signal (156).
By gaining the degree of control over spectral phase and amplitude for attosecond X-ray pulses that is currently available for femtosecond pulses in the optical regime, it may become possible to sculpt valence-electron wave packets. When paired with recursive optimal control algorithms, it should be possible to control, for example, charge migration or energy-transfer processes (154, 155).
SUMMARY POINTS.
New X-ray light sources will enable nonlinear spectroscopy of core excitations in molecules.
Stimulated X-ray Raman spectroscopies launch and probe valence-electron wave packets though core-excited-state intermediates.
X-ray four-wave mixing can reveal coupling between core-excited states.
Pulse wave vectors, phases, polarizations, and delays can be used to control the nonlinear signals.
FUTURE ISSUES.
More elaborate pulse sequences can be designed to apply the rapidly developing X-ray light source technology to the exploration of fundamental questions regarding many-body interactions in molecular systems.
By adapting existing coherent, classical, nonlinear techniques to experiments using quantum and noisy sources, investigators can design new classes of signals, and additional opportunities to measure them with existing XFEL sources will be made possible.
Complete control over the phase and amplitude of an intense X-ray pulse would allow sophisticated shaping techniques used in optical and IR spectroscopy to be applied to the X-ray regime.
Simulations and experimental studies will be required to apply these techniques to study charge and energy transfer in systems such as photosynthetic complexes, donor-acceptor complexes, and semiconductor excitonic systems.
Acknowledgments
The support of the Chemical Sciences, Geosciences and Biosciences Division, Office of Basic Energy Sciences, Office of Science, US Department of Energy, the National Science Foundation (grant CHE-1058791), and the National Institutes of Health (grant GM059230) is gratefully acknowledged.
Glossary
- XANES
X-ray absorption near-edge structure
- EXAFS
extended X-ray absorption fine structure
- XFEL
X-ray free-electron laser
- HHG
higher-harmonic generation
- Double core hole (DCH)
the two holes can be on a single site or on two sites
- RIXS
resonant inelastic X-ray scattering
- SXRS
stimulated X-ray Raman spectroscopy
Footnotes
An alternative ladder diagram approach is based on the many-body density matrix (rather than the wave function) and only requires forward evolution, which is more intuitive. However, for many-body problems the wave-function approach is much more practical, at the price of having to deal with backward evolution.
DISCLOSURE STATEMENT
The authors are not aware of any affiliations, memberships, funding, or financial holdings that might be perceived as affecting the objectivity of this review.
LITERATURE CITED
- 1.Bloembergen N. Nonlinear optics and spectroscopy. Rev Mod Phys. 1982;54:685–95. doi: 10.1126/science.216.4550.1057. [DOI] [PubMed] [Google Scholar]
- 2.Zewail AH. Femtochemistry: atomic-scale dynamics of the chemical bond. J Phys Chem A. 2000;104:5660–94. doi: 10.1002/1521-3773(20000804)39:15<2586::aid-anie2586>3.0.co;2-o. [DOI] [PubMed] [Google Scholar]
- 3.Stöhr J. NEXAFS Spectroscopy. New York: Springer; 1996. [Google Scholar]
- 4.de Groot F, Kotani A. Core Level Spectroscopy of Solids. Boca Raton, FL: CRC; 2008. [Google Scholar]
- 5.Santra R. Concepts in X-ray physics. J Phys B. 2009;42:023001. [Google Scholar]
- 6.Chen LX, Jäger WJH, Jennings G, Gosztola DJ, Munkholm A, Hessler JP. Capturing a photoexcited molecular structure through time-domain X-ray absorption fine structure. Science. 2001;292:262–64. doi: 10.1126/science.1057063. [DOI] [PubMed] [Google Scholar]
- 7.Rehr JJ, Albers RC. Theoretical approaches to X-ray absorption fine structure. Rev Mod Phys. 2000;72:621–54. [Google Scholar]
- 8.Bressler C, Chergui M. Ultrafast X-ray absorption spectroscopy. Chem Rev. 2004;104:1781–812. doi: 10.1021/cr0206667. [DOI] [PubMed] [Google Scholar]
- 9.Ullrich J, Rudenko A, Moshammer R. Free-electron lasers: new avenues in molecular physics and photochemistry. Annu Rev Phys Chem. 2012;63:635–60. doi: 10.1146/annurev-physchem-032511-143720. [DOI] [PubMed] [Google Scholar]
- 10.Gallmann L, Cirelli C, Keller U. Attosecond science: recent highlights and future trends. Annu Rev Phys Chem. 2012;63:447–69. doi: 10.1146/annurev-physchem-032511-143702. [DOI] [PubMed] [Google Scholar]
- 11.Röntgen WC. On a new kind of rays. In: Stanton A, translator. Nature. Vol. 53. 1895. pp. 274–76. [Google Scholar]
- 12.Duguay MA, Rentzepis PM. Some approaches to vacuum UV and X-ray lasers. Appl Phys Lett. 1967;10:350–52. [Google Scholar]
- 13.Perlman ML, Watson RE, Rowe EM. Synchrotron radiation: light fantastic. Phys Today. 1974;27:30–37. [Google Scholar]
- 14.Duke P. Synchrotron Radiation: Production and Properties. New York: Oxford Univ. Press; 2009. [Google Scholar]
- 15.Emma P, Akre R, Arthur J, Bionta R, Bostedt C, et al. First lasing and operation of an angstrom-wavelength free-electron laser. Nat Photonics. 2010;4:641–47. Demonstrates that the Linac Coherent Light Source is capable of producing ultrafast pulses in the 0.5–10-keV range. [Google Scholar]
- 16.Nugent KA. Coherent methods in the X-ray sciences. Adv Phys. 2010;59:1–99. [Google Scholar]
- 17.Reiter F, Graf U, Serebryannikov EE, Schweinberger W, Fiess M, et al. Route to attosecond nonlinear spectroscopy. Phys Rev Lett. 2010;105:243902. doi: 10.1103/PhysRevLett.105.243902. [DOI] [PubMed] [Google Scholar]
- 18.Kapteyn H, Cohen O, Christov I, Murnane M. Harnessing attosecond science in the quest for coherent X-rays. Science. 2007;317:775–78. doi: 10.1126/science.1143679. [DOI] [PubMed] [Google Scholar]
- 19.Krausz F, Ivanov M. Attosecond physics. Rev Mod Phys. 2009;81:163–234. [Google Scholar]
- 20.Wörner HJ, Corkum PB. Attosecond spectroscopy. In: Quack M, Merkt F, editors. Handbook of High-Resolution Spectroscopy. New York: Wiley; 2011. pp. 1781–803. [Google Scholar]
- 21.Hentschel M, Kienberger R, Spielmann C, Reider GA, Milosevic N, et al. Attosecond metrology. Nature. 2001;414:509–13. doi: 10.1038/35107000. [DOI] [PubMed] [Google Scholar]
- 22.Popmintchev T, Chen M, Arpin P, Murnane MM, Kapteyn HC. The attosecond nonlinear optics of bright coherent X-ray generation. Nat Photonics. 2010;4:822–32. [Google Scholar]
- 23.Popmintchev T, Chen M, Popmintchev D, Arpin P, Brown S, et al. Bright coherent ultrahigh harmonics in the keV X-ray regime from mid-infrared femtosecond lasers. Science. 2012;336:1287–91. doi: 10.1126/science.1218497. Used high harmonic generation to create ultra broadband (2.5 as) with energies up to 1.6 keV. [DOI] [PubMed] [Google Scholar]
- 24.Bourzac K. Tabletop X-rays light up. Nature. 2012;486:172. doi: 10.1038/486172a. [DOI] [PubMed] [Google Scholar]
- 25.Goulielmakis E, Schultze M, Hofstetter M, Yakovlev VS, Gagnon J, et al. Single-cycle nonlinear optics. Science. 2008;320:1614–17. doi: 10.1126/science.1157846. [DOI] [PubMed] [Google Scholar]
- 26.Bucksbaum PH, Coffee R, Berrah N. The first atomic and molecular experiments at the Linac Coherent Light Source X-ray free electron laser. In: Arimondo E, Berman PR, Lin CC, editors. Advances in Atomic, Molecular, and Optical Physics. Vol. 60. New York: Elsevier; 2011. pp. 239–89. [Google Scholar]
- 27.Walmsley IA, Dorrer C. Characterization of ultrashort electromagnetic pulses. Adv Opt Photonics. 2009;1:308–437. [Google Scholar]
- 28.Adams B. Nonlinear Optics, Quantum Optics, and Ultrafast Phenomena with X-Rays. New York: Springer; 2003. [Google Scholar]
- 29.Mukamel S. Principles of Nonlinear Optical Spectroscopy. New York: Oxford Univ. Press; 1995. [Google Scholar]
- 30.Mukamel S, Tanimura Y, Hamm P, editors. Special issue on coherent multidimensional optical spectroscopy. Acc Chem Res. 2009;42:1207–469. doi: 10.1021/ar900227m. [DOI] [PubMed] [Google Scholar]
- 31.Eisenberger P, McCall SL. X-ray parametric conversion. Phys Rev Lett. 1971;26:684–88. [Google Scholar]
- 32.Yoda Y, Suzuki T, Zhang X, Hirano K, Kikuta S. X-ray parametric scattering by a diamond crystal. J Synchrotron Radiat. 1998;5:980–82. doi: 10.1107/S0909049597020232. [DOI] [PubMed] [Google Scholar]
- 33.Adams B, Fernandez P, Lee WK, Materlik G, Mills DM, Novikov DV. Parametric down conversion of X-ray photons. J Synchrotron Radiat. 2000;7:81–88. doi: 10.1107/S0909049599015113. [DOI] [PubMed] [Google Scholar]
- 34.Nazarkin A, Podorov S, Uschmann I, Förster E, Sauerbrey R. Nonlinear optics in the angstrom regime: hard X-ray frequency doubling in perfect crystals. Phys Rev A. 2003;67:041804. [Google Scholar]
- 35.Bannett Y, Freund I. Two-photon X-ray emission from inner-shell transitions. Phys Rev Lett. 1982;49:539–42. [Google Scholar]
- 36.Tamasaku K, Sawada K, Nishibori E, Ishikawa T. Visualizing the local optical response to extreme-ultraviolet radiation with a resolution of λ/380. Nat Photonics. 2011;7:705–8. [Google Scholar]
- 37.Freund I, Levine BF. Parametric conversion of X-rays. Phys Rev Lett. 1969;23:854–57. [Google Scholar]
- 38.Freund I. Nonlinear X-ray spectroscopy. Opt Commun. 1972;6:421–23. [Google Scholar]
- 39.Arya K, Jha SS. Microscopic optical fields and mixing coefficients of X-ray and optical frequencies in solids. Pramana. 1974;2:116–25. [Google Scholar]
- 40.Hudis E, Shkolnikov PL, Kaplan AE. X-ray stimulated Raman scattering in Li and He. Appl Phys Lett. 1994;64:818–20. [Google Scholar]
- 41.Freund I, Levine BF. Surface effects in the nonlinear interaction of X-ray and optical fields. Phys Rev B. 1973;8:3059–60. [Google Scholar]
- 42.Anderson T, Tomov IV, Rentzepis PM. A high repetition rate picosecond hard X-ray system and its application to time-resolved X-ray diffraction. J Chem Phys. 1993;99:869–75. [Google Scholar]
- 43.Bargheer M, Zhavoronkov N, Gritsai Y, Woo JC, Kim DS, et al. Coherent atomic motions in a nanostructure studied by femtosecond X-ray diffraction. Science. 2004;306:1771–73. doi: 10.1126/science.1104739. [DOI] [PubMed] [Google Scholar]
- 44.Elsaesser T, Woerner M. Transient charge density maps from femtosecond X-ray diffraction. In: Gatti C, Macchi P, editors. Modern Charge-Density Analysis. New York: Springer; 2012. pp. 697–714. [Google Scholar]
- 45.Deisenhofer J, Epp O, Miki K, Huber R, Michel H. Structure of the protein subunits in the photosynthetic reaction centre of Rhodopseudomonas viridis at 3 Å resolution. Nature. 1985;318:618–24. doi: 10.1038/318618a0. [DOI] [PubMed] [Google Scholar]
- 46.Chapman HN, Fromme P, Barty A, White TA, Kirian RA, et al. Femtosecond X-ray protein nanocrystallography. Nature. 2011;470:73–77. doi: 10.1038/nature09750. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Freund I, Levine BF. Optically modulated X-ray diffraction. Phys Rev Lett. 1970;25:1241–45. [Google Scholar]
- 48.Eisenberger PM, McCall SL. Mixing of X-ray and optical photons. Phys Rev A. 1971;3:1145–51. [Google Scholar]
- 49.Woo JWF, Jha SS. Inelastic scattering of X-rays from optically induced charge-density oscillations. Phys Rev B. 1972;6:4081–82. [Google Scholar]
- 50.Freund I. Nonlinear X-ray diffraction: determination of valence electron charge distributions. Chem Phys Lett. 1972;12:583–88. [Google Scholar]
- 51.Lindenberg AM, Kang I, Johnson SL, Missalla T, Heimann PA, et al. Time-resolved X-ray diffraction from coherent phonons during a laser-induced phase transition. Phys Rev Lett. 2000;84:111–14. doi: 10.1103/PhysRevLett.84.111. [DOI] [PubMed] [Google Scholar]
- 52.Cavalleri A, Wall S, Simpson C, Statz E, Ward DW, et al. Tracking the motion of charges in a terahertz light field by femtosecond X-ray diffraction. Nature. 2006;442:664–66. doi: 10.1038/nature05041. [DOI] [PubMed] [Google Scholar]
- 53.Chen J, Chen WK, Tang J, Rentzepis PM. Time-resolved structural dynamics of thin metal films heated with femtosecond optical pulses. Proc Natl Acad Sci USA. 2011;108:18887–92. doi: 10.1073/pnas.1115237108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Breidbach J, Cederbaum LS. Universal attosecond response to the removal of an electron. Phys Rev Lett. 2005;94:033901. doi: 10.1103/PhysRevLett.94.033901. Used many-body ab initio methods to monitor attosecond dynamics following impulsive core ionization. [DOI] [PubMed] [Google Scholar]
- 55.Young L, Kanter EP, Krässig B, Li Y, March AM, et al. Femtosecond electronic response of atoms to ultra-intense X-rays. Nature. 2010;466:56–61. doi: 10.1038/nature09177. [DOI] [PubMed] [Google Scholar]
- 56.Doumy G, Roedig C, Son S, Blaga CI, DiChiara AD, et al. Nonlinear atomic response to intense ultrashort X-rays. Phys Rev Lett. 2011;106:083002. doi: 10.1103/PhysRevLett.106.083002. [DOI] [PubMed] [Google Scholar]
- 57.Fang L, Hoener M, Gessner O, Tarantelli F, Pratt ST, et al. Double core-hole production in N2: beating the Auger clock. Phys Rev Lett. 2010;105:083005. doi: 10.1103/PhysRevLett.105.083005. Demonstrates the first experimental observation of single-site DCHs using the LCLS. [DOI] [PubMed] [Google Scholar]
- 58.Hoener M, Fang L, Kornilov O, Gessner O, Pratt ST, et al. Ultraintense X-ray induced ionization, dissociation, and frustrated absorption in molecular nitrogen. Phys Rev Lett. 2010;104:253002. doi: 10.1103/PhysRevLett.104.253002. [DOI] [PubMed] [Google Scholar]
- 59.Cryan JP, Glownia JM, Andreasson J, Belkacem A, Berrah N, et al. Auger electron angular distribution of double core-hole states in the molecular reference frame. Phys Rev Lett. 2010;105:083004. doi: 10.1103/PhysRevLett.105.083004. [DOI] [PubMed] [Google Scholar]
- 60.Glownia JM, Cryan J, Andreasson J, Belkacem A, Berrah N, et al. Time-resolved pump-probe experiments at the LCLS. Opt Express. 2010;18:17620–30. doi: 10.1364/OE.18.017620. [DOI] [PubMed] [Google Scholar]
- 61.Drescher M, Hentschel M, Kienberger R, Uiberacker M, Yakovlev V, et al. Time-resolved atomic inner-shell spectroscopy. Nature. 2002;419:803–7. doi: 10.1038/nature01143. [DOI] [PubMed] [Google Scholar]
- 62.Goulielmakis E, Loh Z, Wirth A, Santra R, Rohringer N, et al. Real-time observation of valence electron motion. Nature. 2010;466:739–43. doi: 10.1038/nature09212. [DOI] [PubMed] [Google Scholar]
- 63.Li W, Zhou X, Lock R, Patchkovskii S, Stolow A, et al. Time-resolved dynamics in N2O4 probed using high harmonic generation. Science. 2008;322:1207–11. doi: 10.1126/science.1163077. [DOI] [PubMed] [Google Scholar]
- 64.Li W, Jaro-Becker AA, Hogle CW, Sharma V, Zhou X, et al. Visualizing electron rearrangement in space and time during the transition from a molecule to atoms. Proc Natl Acad Sci USA. 2010;107:20219–22. doi: 10.1073/pnas.1014723107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Zhou X, Ranitovic P, Hogle CW, Eland JHD, Kapteyn HC, Murnane MM. Probing and controlling non-Born-Oppenheimer dynamics in highly excited molecular ions. Nat Phys. 2012;8:232–37. [Google Scholar]
- 66.Zhou X, Lock R, Li W, Wagner N, Murnane MM, Kapteyn HC. Molecular recollision interferometry in high harmonic generation. Phys Rev Lett. 2008;100:073902. doi: 10.1103/PhysRevLett.100.073902. [DOI] [PubMed] [Google Scholar]
- 67.Buth C, Santra R, Young L. Electromagnetically induced transparency for X-rays. Phys Rev Lett. 2007;98:253001. doi: 10.1103/PhysRevLett.98.253001. [DOI] [PubMed] [Google Scholar]
- 68.Rohlsberger R, Wille H, Schlage K, Sahoo B. Electromagnetically induced transparency with resonant nuclei in a cavity. Nature. 2012;482:199–203. doi: 10.1038/nature10741. [DOI] [PubMed] [Google Scholar]
- 69.Gadzuk JW. Core level spectroscopy: a dynamics perspective. Phys Scr. 1987;35:171–80. [Google Scholar]
- 70.Rohringer N, Santra R. X-ray nonlinear optical processes using a self-amplified spontaneous emission free-electron laser. Phys Rev A. 2007;76:033416. [Google Scholar]
- 71.Rentzepis PM. Direct measurements of radiationless transitions in liquids. Chem Phys Lett. 1968;2:117–20. [Google Scholar]
- 72.Eckhardt G, Hellwarth RW, McClung FJ, Schwarz SE, Weiner D, Woodbury EJ. Stimulated Raman scattering from organic liquids. Phys Rev Lett. 1962;9:455–57. [Google Scholar]
- 73.Penzkofer A, Laubereau A, Kaiser W. High intensity Raman interactions. Prog Quantum Electron. 1979;6:55–140. [Google Scholar]
- 74.Glatzel P, Bergmann U, Yano J, Visser H, Robblee JH, et al. The electronic structure of Mn in oxides, coordination complexes, and the oxygen-evolving complex of photosystem II studied by resonant inelastic X-ray scattering. J Am Chem Soc. 2004;126:9946–59. doi: 10.1021/ja038579z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 75.Champion P, Ziegler L, editors. XXII International Conference on Raman Spectroscopy (ICORS 2010); College Park, MD: Am. Inst. Phys; 2010. [Google Scholar]
- 76.Gel’mukhanov F, Ågren H. Resonant X-ray Raman scattering. Phys Rep. 1999;312:87–330. [Google Scholar]
- 77.Nordgren J, Bray G, Cramm S, Nyholm R, Rubensson J, Wassdahl N. Soft X-ray emission spectroscopy using monochromatized synchrotron radiation. Rev Sci Instrum. 1989;60:1690–96. doi: 10.1103/PhysRevLett.60.1759. [DOI] [PubMed] [Google Scholar]
- 78.Ament L, van Veenendaal M, Devereaux T, Hill J, van den Brink J. Resonant inelastic X-ray scattering studies of elementary excitations. Rev Mod Phys. 2011;83:705–67. [Google Scholar]
- 79.Roslyak O, Mukamel S. Spontaneous and stimulated coherent and incoherent nonlinear wave-mixing and hyper-Raleigh scattering. Lectures of Virtual University on Lasers. 2010 http://www.mitr.p.lodz.pl/evu/lectures/mukamel.pdf.
- 80.Cook DB. Handbook of Computational Quantum Chemistry. New York: Dover; 2005. [Google Scholar]
- 81.Tretiak S, Mukamel S. Density matrix analysis and simulation of electronic excitations in conjugated and aggregated molecules. Chem Rev. 2002;102:3171–212. doi: 10.1021/cr0101252. [DOI] [PubMed] [Google Scholar]
- 82.Nozières P, Dominicis CTD. Singularities in the X-ray absorption and emission of metals. III. One-body theory exact solution. Phys Rev. 1969;178:1097–107. [Google Scholar]
- 83.Nozières P, Gavoret J, Roulet B. Singularities in the X-ray absorption and emission of metals. II. Self-consistent treatment of divergences. Phys Rev. 1969;178:1084–96. [Google Scholar]
- 84.Roulet B, Gavoret J, Nozières P. Singularities in the X-ray absorption and emission of metals. I. First-order Parquet calculation. Phys Rev. 1969;178:1072–83. [Google Scholar]
- 85.Langreth DC. Singularities in the X-ray spectra of metals. Phys Rev B. 1970;1:471–77. [Google Scholar]
- 86.Mahan GD. Excitons in metals: infinite hole mass. Phys Rev. 1967;163:612–17. [Google Scholar]
- 87.Campbell L, Hedin L, Rehr JJ, Bardyszewski W. Interference between extrinsic and intrinsic losses in X-ray absorption fine structure. Phys Rev B. 2002;65:064107. [Google Scholar]
- 88.Heyl M, Kehrein S. X-ray edge singularity in optical spectra of quantum dots. Phys Rev B. 2012;85:155413. [Google Scholar]
- 89.Mukamel S. Multiple core-hole coherence in X-ray four-wave-mixing spectroscopies. Phys Rev B. 2005;72:235110. Derives closed expressions for coherent four-wave mixing signals, including the use of an electron-boson model. [Google Scholar]
- 90.Roslyak O, Bennett KC, Mukamel S. 2012 Submitted manuscript. [Google Scholar]
- 91.Dhar L, Rogers JA, Nelson KA. Time-resolved vibrational spectroscopy in the impulsive limit. Chem Rev. 1994;94:157–93. [Google Scholar]
- 92.Tanimura Y, Mukamel S. Two-dimensional femtosecond vibrational spectroscopy of liquids. J Chem Phys. 1993;99:9496–503. [Google Scholar]
- 93.Blank DA, Kaufman LJ, Fleming GR. Direct fifth-order electronically nonresonant Raman scattering from CS2 at room temperature. J Chem Phys. 2000;113:771–78. [Google Scholar]
- 94.Kubarych KJ, Milne CJ, Lin S, Astinov V, Miller RJD. Diffractive optics-based six-wave mixing: heterodyne detection of the full ξ(5) tensor of liquid CS2. J Chem Phys. 2002;116:2016–42. [Google Scholar]
- 95.Li YL, Huang L, Miller RJM, Hasegawa T, Tanimura Y. Two-dimensional fifth-order Raman spectroscopy of liquid formamide: experiment and theory. J Chem Phys. 2008;128:234507. doi: 10.1063/1.2927311. [DOI] [PubMed] [Google Scholar]
- 96.Zschornack GH. Handbook of X-Ray Data. New York: Springer; 2007. [Google Scholar]
- 97.Krause MO, Oliver JH. Natural widths of atomic K and L levels, KαX-ray lines and several KLL Auger lines. J Phys Chem Ref Data. 1979;8:329–38. [Google Scholar]
- 98.Patterson B. Tech Rep. SLAC Natl. Accel. Lab.; Menlo Park, CA: 2010. Resource letter on stimulated inelastic X-ray scattering at an XFEL. http://slac.stanford.edu/pubs/slactns/tn04/slac-tn-10-026.pdf. [Google Scholar]
- 99.Zholents A, Penn G. Obtaining two attosecond pulses for X-ray stimulated Raman spectroscopy. Nucl Instrum Methods A. 2010;612:254–59. [Google Scholar]
- 100.Zholents A. Next-generation X-ray free-electron lasers. IEEE J Sel Top Quantum Electron. 2012;18:248–57. [Google Scholar]
- 101.van den Brink J, van Veenendaal M. Correlation functions measured by indirect resonant inelastic X-ray scattering. Europhys Lett. 2006;73:121–27. [Google Scholar]
- 102.Ma Y, Wassdahl N, Skytt P, Guo J, Nordgren J, et al. Soft-X-ray resonant inelastic scattering at the C K edge of diamond. Phys Rev Lett. 1992;69:2598–601. doi: 10.1103/PhysRevLett.69.2598. [DOI] [PubMed] [Google Scholar]
- 103.Schuelke W. Electron Dynamics by Inelastic X-Ray Scattering. New York: Oxford Univ. Press; 2007. [Google Scholar]
- 104.Abbamonte P, Graber T, Reed JP, Smadici S, Yeh C, et al. Dynamical reconstruction of the exciton in LiF with inelastic X-ray scattering. Proc Natl Acad Sci USA. 2008;105:12159–63. doi: 10.1073/pnas.0801623105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 105.Abbamonte P, Finkelstein KD, Collins MD, Gruner SM. Imaging density disturbances in water with a 41.3-attosecond time resolution. Phys Rev Lett. 2004;92:237401. doi: 10.1103/PhysRevLett.92.237401. [DOI] [PubMed] [Google Scholar]
- 106.Glatzel P, Bergmann U. High resolution 1s core hole X-ray spectroscopy in 3D transition metal complexes: electronic and structural information. Coordin Chem Rev. 2005;249:65–95. [Google Scholar]
- 107.Biggs JD, Zhang Y, Healion D, Mukamel S. Two-dimensional stimulated resonance Raman spectroscopy of molecules with broadband X-ray pulses. J Chem Phys. 2012;136:174117. doi: 10.1063/1.4706899. Presents the first simulation of two-dimensional time-domain stimulated X-ray Raman signals. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 108.Tanaka S, Mukamel S. Coherent X-ray Raman spectroscopy: a nonlinear local probe for electronic excitations. Phys Rev Lett. 2002;89:043001. doi: 10.1103/PhysRevLett.89.043001. Presents the first simulation of coherent, wave-vector-matched frequency-domain X-ray Raman signals. [DOI] [PubMed] [Google Scholar]
- 109.Tanaka S, Mukamel S. Probing exciton dynamics using Raman resonances in femtosecond X-ray four-wave mixing. Phys Rev A. 2003;67:033818. [Google Scholar]
- 110.Tanaka S, Volkov S, Mukamel S. Time-resolved X-ray Raman spectroscopy of photoexcited polydiacetylene oligomer: a simulation study. J Chem Phys. 2003;118:3065–78. [Google Scholar]
- 111.Mukamel S, Wang H. Manipulating quantum entanglement of quasiparticles in many-electron systems by attosecond X-ray pulses. Phys Rev A. 2010;81:062334. [Google Scholar]
- 112.Rahav S, Roslyak O, Mukamel S. Manipulating stimulated coherent anti-Stokes Raman spectroscopy signals by broad-band and narrow-band pulses. J Chem Phys. 2009;131:194510. doi: 10.1063/1.3259653. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 113.Harbola U, Mukamel S. Coherent stimulated X-ray Raman spectroscopy: attosecond extension of resonant inelastic X-ray Raman scattering. Phys Rev B. 2009;79:085108. [Google Scholar]
- 114.Schweigert IV, Mukamel S. Probing valence electronic wave-packet dynamics by all X-ray stimulated Raman spectroscopy: a simulation study. Phys Rev A. 2007;76:012504. [Google Scholar]
- 115.Biggs JD, Voll JA, Mukamel S. Coherent nonlinear optical studies of elementary processes in biological complexes: diagrammatic techniques based on the wavefunction versus the density matrix. Philos Trans R Soc A. 2012;370:3709–27. doi: 10.1098/rsta.2011.0219. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 116.Healion D, Zhang J, Biggs JD, Govind N, Mukamel S. Entangled valence electron-hole dynamics revealed by stimulated attosecond X-ray Raman scattering. J Phys Chem Lett. 2012;3:2326–31. doi: 10.1021/jz300981w. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 117.Martin RL. Natural transition orbitals. J Chem Phys. 2003;118:4775–77. [Google Scholar]
- 118.Andrews DL, Thirunamachandran T. On three-dimensional rotational averages. J Phys Chem. 1977;67:5026–33. [Google Scholar]
- 119.Abramavičius D, Mukamel S. Coherent third-order spectroscopic probes of molecular chirality. J Chem Phys. 2005;122:134305. doi: 10.1063/1.1869495. [DOI] [PubMed] [Google Scholar]
- 120.Healion D, Biggs J, Mukamel S. Manipulating one- and two-dimensional stimulated-X-ray resonant-Raman signals in molecules by pulse polarizations. Phys Rev A. 2012;86:033429. [Google Scholar]
- 121.Schweigert IV, Mukamel S. Probing interactions between core-electron transitions by ultrafast two-dimensional X-ray coherent correlation spectroscopy. J Chem Phys. 2008;128:184307. doi: 10.1063/1.2839859. [DOI] [PubMed] [Google Scholar]
- 122.Healion DM, Schweigert IV, Mukamel S. Probing multiple core-hole interactions in the nitrogen K-edge of DNA base pairs by multidimensional attosecond X-ray spectroscopy: a simulation study. J Phys Chem A. 2008;112:11449–61. doi: 10.1021/jp803824a. [DOI] [PubMed] [Google Scholar]
- 123.Ernst R, Bodenhausen G, Wokaun A. Principles of Nuclear Magnetic Resonance in One and Two Dimensions. Oxford, UK: Clarendon; 1987. [Google Scholar]
- 124.Zhang Y, Biggs JD, Healion D, Govind N, Mukamel S. Core and valence excitations in resonant X-ray spectroscopy using restricted excitation window time-dependent density functional theory (REW-TDDFT) J Chem Phys. 2012;137:194306. doi: 10.1063/1.4766356. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 125.Salén P, van der Meulen P, Schmidt HT, Thomas RD, Larsson M, et al. Experimental verification of the chemical sensitivity of two-site double core-hole states formed by an X-ray free-electron laser. Phys Rev Lett. 2012;108:153003. doi: 10.1103/PhysRevLett.108.153003. [DOI] [PubMed] [Google Scholar]
- 126.Tashiro M, Ehara M, Fukuzawa H, Ueda K, Buth C, et al. Molecular double core hole electron spectroscopy for chemical analysis. J Chem Phys. 2010;132:184302. [Google Scholar]
- 127.Mukamel S, Oszwaldowski R, Abramavičius D. Sum-over-states versus quasiparticle pictures of coherent correlation spectroscopy of excitons in semiconductors: femtosecond analogs of multidimensional NMR. Phys Rev B. 2007;75:245305. [Google Scholar]
- 128.Schweigert IV, Mukamel S. Double-quantum-coherence attosecond X-ray spectroscopy of spatially separated, spectrally overlapping core-electron transitions. Phys Rev A. 2008;78:052509. Presents the first simulation of X-ray double-quantumcoherence signals, which depend on the coupling between spatially separated core transitions. [Google Scholar]
- 129.Cervetto V, Helbing J, Bredenbeck J, Hamm P. Double-resonance versus pulsed Fourier transform two-dimensional infrared spectroscopy: an experimental and theoretical comparison. J Chem Phys. 2004;121:5935–42. doi: 10.1063/1.1778163. [DOI] [PubMed] [Google Scholar]
- 130.Zhuang W, Abramavičius D, Mukamel S. Dissecting coherent vibrational spectra of small proteins into secondary structural elements by sensitivity analysis. Proc Natl Acad Sci USA. 2005;102:7443–48. doi: 10.1073/pnas.0408781102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 131.Li Z, Abramavičius D, Mukamel S. Probing electron correlations in molecules by two-dimensional coherent optical spectroscopy. J Am Chem Soc. 2008;130:3509–15. doi: 10.1021/ja0774414. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 132.Abramavičius D, Voronine DV, Mukamel S. Double-quantum resonances and exciton-scattering in coherent 2D spectroscopy of photosynthetic complexes. Proc Natl Acad Sci USA. 2008;105:8525–30. doi: 10.1073/pnas.0802926105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 133.Mukamel S, Oszwaldowski R, Yang L. A coherent nonlinear optical signal induced by electron correlations. J Chem Phys. 2007;127:221105. doi: 10.1063/1.2820379. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 134.Dutoi AD, Cederbaum LS, Wormit M, Starcke JH, Dreuw A. Tracing molecular electronic excitation dynamics in real time and space. J Chem Phys. 2010;132:144302. doi: 10.1063/1.3353161. [DOI] [PubMed] [Google Scholar]
- 135.Moiseyev N. Non-Hermitian Quantum Mechanics. New York: Cambridge Univ. Press; 2011. [Google Scholar]
- 136.Burke PG, Berrington KA. R-Matrix Theory of Atomic and Molecular Processes. Bristol: IOP; 1993. [Google Scholar]
- 137.Whitenack DL, Wasserman A. Density functional resonance theory of unbound electronic systems. Phys Rev Lett. 2011;107:163002. doi: 10.1103/PhysRevLett.107.163002. [DOI] [PubMed] [Google Scholar]
- 138.Tian P, Keusters D, Suzaki Y, Warren WS. Femtosecond phase-coherent two-dimensional spectroscopy. Science. 2003;300:1553–55. doi: 10.1126/science.1083433. [DOI] [PubMed] [Google Scholar]
- 139.Scheurer S, Mukamel S. Design strategies for pulse sequences in multidimensional optical spectroscopies. J Chem Phys. 2001;115:4989–5004. [Google Scholar]
- 140.Brinks D, Stefani FD, Kulzer F, Hildner R, Taminiau TH, et al. Visualizing and controlling vibrational wave packets of single molecules. Nature. 2010;465:905–8. doi: 10.1038/nature09110. [DOI] [PubMed] [Google Scholar]
- 141.Morita N, Yajima T. Ultrahigh-time-resolution coherent transient spectroscopy with incoherent light. Phys Rev A. 1984;30:2525–36. [Google Scholar]
- 142.Beach R, Hartmann SR. Incoherent photon echoes. Phys Rev Lett. 1984;53:663–66. [Google Scholar]
- 143.Schlawin F, Dorfman KE, Fingurhut BF, Mukamel S. Manipulation of two-photon fluorescence spectra of chromophore aggregates with entangled photons: a simulation study. Phys Rev A. 2012;86:023851. [Google Scholar]
- 144.Rahav S, Mukamel S. Multidimensional attosecond photoelectron spectroscopy with shaped pulses and quantum optical fields. Phys Rev A. 2010;81:063810. [Google Scholar]
- 145.Shwartz S, Harris SE. Polarization entangled photons at X-ray energies. Phys Rev Lett. 2011;106:080501. doi: 10.1103/PhysRevLett.106.080501. [DOI] [PubMed] [Google Scholar]
- 146.Richter M, Mukamel S. Ultrafast double-quantum-coherence spectroscopy of excitons with entangled photons. Phys Rev A. 2010;82:013820. doi: 10.1103/PhysRevA.82.013820. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 147.Stolow A, Bragg AE, Neumark DM. Femtosecond time-resolved photoelectron spectroscopy. Chem Rev. 2004;104:1719–58. doi: 10.1021/cr020683w. [DOI] [PubMed] [Google Scholar]
- 148.Stolow A. Femtosecond time-resolved photoelectron spectroscopy of polyatomic molecules. Annu Rev Phys Chem. 2003;54:89–119. doi: 10.1146/annurev.physchem.54.011002.103809. [DOI] [PubMed] [Google Scholar]
- 149.Oana CM, Krylov AI. Cross sections and photoelectron angular distributions in photodetachment from negative ions using equation-of-motion coupled-cluster Dyson orbitals. J Chem Phys. 2009;131:124114. doi: 10.1063/1.3231143. [DOI] [PubMed] [Google Scholar]
- 150.Hudock HR, Levine BG, Thompson AL, Satzger H, Townsend D, et al. Ab initio molecular dynamics and time-resolved photoelectron spectroscopy of electronically excited uracil and thymine. J Phys Chem A. 2007;111:8500–8. doi: 10.1021/jp0723665. [DOI] [PubMed] [Google Scholar]
- 151.Wollenhaupt M, Assion A, Baumert T. Femtosecond laser pulses: linear properties, manipulation, generation and measurement. In: Träger F, editor. Springer Handbook of Lasers and Optics. New York: Springer; 2007. pp. 937–83. [Google Scholar]
- 152.Wilson KC, Lyons B, Mehlenbacher R, Sabatini R, McCamant DW. Two-dimensional femtosecond stimulated Raman spectroscopy: observation of cascading Raman signals in acetonitrile. J Chem Phys. 2009;131:214502. doi: 10.1063/1.3263909. [DOI] [PubMed] [Google Scholar]
- 153.Rai N, Lakshmanna A, Namboodiri V, Umapathy S. Basic principles of ultrafast Raman loss spectroscopy. J Chem Sci. 2012;124:177–86. [Google Scholar]
- 154.Brodard P, Matzinger S, Vauthey E, Mongin O, Papamical C, Gossauer A. Investigations of electronic energy transfer dynamics in multiporphyrin arrays. J Phys Chem A. 1999;103:5858–70. [Google Scholar]
- 155.Banerji N, Bhosale SV, Petkova I, Langford SJ, Vauthey E. Ultrafast excited-state dynamics of strongly coupled porphyrin/core-substituted-naphthalenediimide dyads. Phys Chem Chem Phys. 2011;13:1019–29. doi: 10.1039/c0cp01544j. [DOI] [PubMed] [Google Scholar]
- 156.Mukamel S. Controlling multidimensional off-resonant Raman and infrared vibrational spectroscopy by finite pulse band shapes. J Chem Phys. 2009;130:054110. doi: 10.1063/1.3068548. [DOI] [PubMed] [Google Scholar]


