Multiscale Macromolecular Simulation: Role of Evolving Ensembles

Abstract

Multiscale analysis provides an algorithm for the efficient simulation of macromolecular assemblies. This algorithm involves the coevolution of a quasiequilibrium probability density of atomic configurations and the Langevin dynamics of spatial coarse-grained variables denoted order parameters (OPs) characterizing nanoscale system features. In practice, implementation of the probability density involves the generation of constant OP ensembles of atomic configurations. Such ensembles are used to construct thermal forces and diffusion factors that mediate the stochastic OP dynamics. Generation of all-atom ensembles at every Langevin timestep is computationally expensive. Here, multiscale computation for macromolecular systems is made more efficient by a method that self-consistently folds in ensembles of all-atom configurations constructed in an earlier step, history, of the Langevin evolution. This procedure accounts for the temporal evolution of these ensembles, accurately providing thermal forces and diffusions. It is shown that efficiency and accuracy of the OP-based simulations is increased via the integration of this historical information. Accuracy improves with the square root of the number of historical timesteps included in the calculation. As a result, CPU usage can be decreased by a factor of 3-8 without loss of accuracy. The algorithm is implemented into our existing force-field based multiscale simulation platform and demonstrated via the structural dynamics of viral capsomers.

I. Introduction

A focus of interest in theoretical and computational nanosciences is to predict the behavior of macromolecular assemblies such as viruses using their N -atom description and Newton’s equations of motion.¹ Molecular dynamics (MD) has been widely used to achieve such simulations. However, the simulation time for nanometer scale assemblies has been limited to tens or sometimes few hundred nanoseconds.^{2, 3} While an advantage of N-atom approaches is that, given an inter-atomic force field, they offer the possibility of calibration-free modeling, they are limited by the system size, simulation timestep and hardware requirements. Recently, billion atom MD simulations have been accomplished.^4–6 However, these simulations neglect one or more of Coulomb interactions, bonded forces, and rapidly fluctuating hydrogen atoms. All the latter are central to biomolecular structure and dynamics. Thus, all-atom simulation of large macromolecular assemblies remains a computational challenge.^{7, 8}

Standard MD packages include CHARMM,⁹ GROMACS,¹⁰ and NAMD.¹¹ Interest in large systems has stimulated the development of MD algorithms that take advantage of computational efficiencies enabled by parallel and graphical processor unit implementations.^{12, 13} A variety of coarse-grained approaches including bead, shape-based,^{14, 15} rigid region decomposition,¹⁶ and symmetry constrained^17–19 models, as well as principal component analysis^{20, 21} and normal mode analysis guided approaches²¹ have been introduced to reduce the computational burden of large system simulations, but they do so at the expense of losing atomic scale resolution.

We have undertaken a deductive multiscale approach that folds the physics underlying the existence of slowly evolving variables into the computations for large systems.^22–25 These variables, denoted space warping order parameters (OPs),^{26, 27} describe coherent, overall structural changes of the system. Furthermore, mathematical reformulation of the underlying molecular physics simultaneously captures high frequency atomic fluctuations and evolves the coarse-grained state. More precisely, we start with the N-atom Liouville equation and obtain Langevin equations for stochastic OP dynamics.²⁸ Since specifying the coarse-grained variables leaves great uncertainty in the detailed all-atom state, quasi-equilibrium ensemble of all-atom configurations consistent with the instantaneous state of the OPs is generated. This ensemble is used with Monte Carlo (MC) integration to construct factors (forces and diffusions) in the Langevin equations needed to advance the OPs to the next timestep. Such an approach yields a rigorous way to transfer information between variables on different space-time scales, avoiding the need to make and calibrate phenomenological expressions for evolving the state of OPs. This scheme has been implemented as the Deductive Multiscale Simulator (DMS) software system (denoted SimNanoWorld in previous publications).^{22, 29} DMS is used to capture polyalanine folding from a linear to a globular state,²⁷ Ostwald’s ripening in nanocomposites,³⁰ nucleation/front-propagation and disassembly pathways involving the structure and stability of virus capsids,^{31, 32} counter-ion induced transition in viral RNA and stability of RNA-protein complexes over a range of salinity and temperatures.²⁶ Result from DMS simulations are comparable to those from conventional MD (notably NAMD), but the former is faster and more statistically significant as it is derived from evolving ensembles of all-atom configurations.²⁹ The objective here is to further accelerate these calculations while maintaining accuracy and all-atom resolution.

The Langevin model of Brownian motion has been extensively used to describe the dynamics of particles in a heat bath under conditions near equilibrium.³³ Several MC techniques have been used to numerically integrate ordinary and general Langevin-type equations.³⁴ Their applicability depends on the magnitude of Langevin timesteps relative to that of velocity autocorrelation functions decay. Similarly, there are MC schemes based on the independent single-variate velocity and displacement distribution functions.³⁵ Other extensively used numerical integrations schemes include ones proposed by Gunsteren and Berendsen,³⁵ Brooks-Brunger-Karplus, and the Langevin impulse integrator.³⁶ The accuracy of these schemes ranges from first to second order. These schemes present a general numerical procedure for integrating Langevin equations. However, they are not meant to explicitly address the coevolution of slow structural variables with an ensemble of rapidly fluctuating ones, as is the case here.

The purpose of this study is not to discover a new Langevin integrator. Rather, we introduce a procedure that effectively enhances the size of aforementioned quasi-equilibrium ensembles by using configurations from earlier times (i.e., as ones move back in “history”) and simultaneously accounts for the dynamical OP and noise characteristics. In this way, statistical error for the numerical integration of factors in the Langevin equations is reduced. As a result, one can perform a multiscale simulation which still provides all-atom detail, but now with less stringent limitations on the Langevin timestep for OP evolution. With this, enhanced numerical efficiency of multiscale simulations is achieved without compromising with accuracy. Computational cost of Langevin OP simulations is mediated by the characteristic OP time, size of the all-atom ensemble for MC integration, and number of historical ensembles considered in extended MC sampling. Contributions from these three factors are evaluated to obtain a range of parameters that imply optimal simulation efficiency.

In the following, we review our OP based multiscale methodology and extend discussions on the use of dynamical ensembles to enhance the sample size for MC computation of thermal average forces (Sect. II). This algorithm is numerically demonstrated for all-atom simulations of Human Papillomavirus16 (HPV16) capsomers (Sect. III). Interplay between several numerical parameters is studied to identify those providing simulation accuracy as well as efficiency. Simulations with such parameters are used to investigate contrasting long-time behavior of different capsomer constructs. Conclusions are drawn in Sect. IV.

II. Methodology

In this section various components of our deductive multiscale approach are discussed. A central element of our multiscale analysis is the construction of OPs for describing the coarse-grained features of a macromolecular assembly. An OP mediated model captures the separation in timescales between the coherent (slow) and non-coherent (fast) degrees of freedom. In effect, OPs filter out the high frequency atomistic fluctuations from the low frequency coherent modes. This property of OPs enables them to serve as the basis of a multiscale approach for simulating the dynamics of macromolecular systems. Here, our methodology is outlined and discussion is extended on a dynamical ensemble enhancement scheme to accurately compute factors in the Langevin equation for OP dynamics.

A. Order Parameters

Consider a macromolecular assembly described via the positions of its N constituent atoms labeled i = 1,⋯ N. Let the i-th atom in the system be moved from its original position ${\stackrel{\rightharpoonup }{r}}_i^0$ via

$${\stackrel{\rightharpoonup }{r}}_i=\sum _k{\stackrel{\rightharpoonup }{\Phi }}_k{U}_{ki}+{\stackrel{\rightharpoonup }{\sigma }}_i,$$ (1)

where the ${\stackrel{\rightharpoonup }{\Phi }}_k\text{and}{U}_{ki}\equiv U_k({\stackrel{\rightharpoonup }{r}}_i^0)$ are k-th OP and basis function respectively. For example, the use of k have been taken to be products of Legendre polynomials in the X, Y, Z Cartesian directions, i.e., $U_k({\stackrel{\rightharpoonup }{r}}_i^0)=U_{k_1}(X_i^0)U_{k_2}(Y_i^0)U_{k_3}(Z_i^0)$.²³ ${\stackrel{\rightharpoonup }{r}}_i^0$ is the reference position of atom i which, through the OPs and the Eq. (1) is deformed into the instantaneous position r⃑_i. Since we seek a dimensionality reduction, the number of Φ⃑_ḵ is much less than the number N of atoms. Given a finite truncation of the k sum in Eq. (1), there will be some residual displacement (denoted σ⃑_i) for each atom in addition to the coherent deformation generated by the k sum.

An explicit expression for the Φ⃑_k is obtained by minimizing the mass-weighted square residual with respect to the Φ⃑_k.²³ One obtains

$${\stackrel{\rightharpoonup }{\Phi }}_k=\frac{\sum _{i=1}^N{m}_i{U}_{ki}{\stackrel{\rightharpoonup }{r}}_i}{{\mu }_k};{\mu }_k=\sum _{i=1}^N{m}_i{U}_{ki}^2,$$ (2)

where m_i is the mass of atom i. Inclusion of m_i in developing Eq. (2) gives Φ⃑_k the character of a generalized center-of-mass. For example, if U_ki is independent of i then Φ⃑_k is proportional to the center-of-mass of the assembly. A subset of OPs defined in this way constitutes a strain tensor accounting for compression-extension-rotation, while others describe more complex deformations such as tapering, twisting, bending and their various combinations.^{26, 27} The µ_k serve as effective masses associated with each OP, implying the spatial scale they capture. The masses primarily decrease with increasing complexity of U_ki.²⁶ Thus, OPs with higher k probe smaller regions in space. In summary, a model based on this set of OPs simultaneously probes structure over a diverse range of spatial scales via different orders in k.

B. Deductive Multiscale Approach

Eq. (2) implies that for a given set of atomic positions the corresponding OPs are uniquely defined. However, the converse is not true, i.e., there exist multiple all-atom configurations consistent with a given set of Φ⃑_k. Thus, an OP-based theory of macromolecular assemblies is statistical in character since specifying the coarse-grained variables leaves great uncertainty in the detailed all-atom state. To address this issue, the theory should provide an algorithm for evolving the coarse-grained variables and another for coevolving the probability of the detailed all-atom states. This conceptual framework has been shown to yield stochastic equations for the propagation of the slow OPs and those for constructing the coevolving ensemble of all-atom configurations.

The description adapted starts with the probability density ρ of the N atomic positions and momenta Γ. However, this formulation masks the underlying hierarchical organization of a macromolecular assembly. To address this, here, ρ is hypothesized to depend on Γ both directly, and via a set of OPs, indirectly. This “unfolding” of the N-atom probability density makes the multiple dependencies of ρ on Γ and time t explicit. With this ansatz, a perturbation analysis of the Liouville equation yields sets of coupled Langevin equations for the OPs

$$\frac{d{\stackrel{\rightharpoonup }{\Phi }}_k}{dt}=\sum _{k\text{'}}{\stackrel{\rightharpoonup }{\stackrel{\rightharpoonup }{D}}}_{kk\text{'}}{\stackrel{\rightharpoonup }{f}}_{k\text{'}}+{\stackrel{\rightharpoonup }{\xi }}_k,$$ (3)

²⁸ where the diffusivity factors ${\stackrel{\rightharpoonup }{\stackrel{\rightharpoonup }{D}}}_{kk}$ are related to the correlation function of OP momenta Π⃑_k via

$${\stackrel{\rightharpoonup }{\stackrel{\rightharpoonup }{D}}}_{kk\text{'}}=\frac{1}{{\mu }_k{\mu }_{k\text{'}}}\underset{-\infty }{\overset{0}{\int }}dt\langle {\stackrel{\rightharpoonup }{\Pi }}_{k\text{'}}(t){\stackrel{\rightharpoonup }{\Pi }}_k\rangle .$$ (4)

²⁸ Π⃑_k is the value of the OP momentum for a given N-atom configuration, Π⃑_k'(t) is advanced in time through Newtonian mechanics, and the 〈⋯〉 implies thermal average over configurations. Variance of noise ξ⃑_k is bound by ${\stackrel{\rightharpoonup }{\stackrel{\rightharpoonup }{D}}}_{kk}$. The thermal average force f⃑_k is given by

$$f_{k\alpha }=-\frac{\partial F}{\partial {\Phi }_{k\alpha }};\alpha =X,Y,Z$$ (5)

²² for OP-constrained Helmholtz free-energy F, where

$$F=-\frac{1}{\beta }\text{ln}Q(\Phi ,\beta ),$$ (6)

Q(Φ, β) = ∫ dΓ^* Δ(Φ − Φ^*)e^−βH* is the partition function constructed from configurations consistent with the set of Φ⃑_k (denoted Φ collectively). Eq. (3) implies overall structural dynamics through evolution of the OPs. It has been implemented as the DMS nanosystem simulator for the case of a single system²⁹ and more recently for a set of interacting subsystems.³⁷

A commonly used approach for treating far-from-equilibrium systems involves projection operators.^{35, 38–40} It is very general in the sense that no approximations are made in arriving at an equation for the reduced probability of a subset of variables (OPs in our case). However, this kinetic equation requires construction of a memory function, which usually can only be constructed using extensive MD simulations or experimental data. This is numerically expensive for N-atom problems except when the memory functions have short relaxation times.³⁸ In our analysis, the OPs of interest are much slower than the characteristic rate of atomistic fluctuations, and therefore the relaxation times are typically short relative to characteristic times of OP dynamics.²⁸ Under these conditions, our multiscale approach leads to the same set of Langevin equations as those from projection operators. However, the multiscale approach is more direct; we do not start with the projection operators and eventually resort to perturbation methods for constructing memory functions. Rather we make an ansatz that the N-atom probability density has multiple (initially unspecified) space-time dependencies, and analyze the resulting Liouville equation.²⁵

While several coarse-grained modeling approaches account for large-scale processes, important all-atom features of an assembly can be lost.⁴¹ However, processes like the interaction of an antibody with a viral capsid can depend sensitively on atomic structure.^{39, 40} To capture such details, in DMS, an ensemble of all-atom configurations consistent with the^{42, 43} instantaneous OPs description is constructed. To accomplish this, residuals σ⃑_i are constructed by changing those Φ⃑_k that do not contribute to the k-sum (Eq. (1)). By definition, OPs with higher k probe smaller regions in space. Consequently, they account for small-scale incoherent displacement of each atom in addition to coherent deformations generated by the other, lower k, OPs. Short MD (NAMD) runs are performed starting with configurations from this residual-generated ensemble to arrive at an enriched ensemble that is consistent with a given set of OPs (Φ). This procedure for generating ensembles is called hybrid sampling. Further details are provided elsewhere.²²

Given an all-atom structure at time t=0, a set of space warping OPs is constructed via Eq. (2). Then, an ensemble of all-atom configurations consistent with this set of OPs is generated via the aforementioned hybrid sampling scheme. This ensemble is then employed to compute factors (thermal average forces f⃑_k and diffusion coefficients ${\stackrel{\rightharpoonup }{\stackrel{\rightharpoonup }{D}}}_{kk\text{'}}$) that mediate the Langevin Φ⃑_k dynamics. The f⃑_k are expressed in terms of atomic forces F⃑_i via

$${\stackrel{\rightharpoonup }{f}}_k=\langle {\stackrel{\rightharpoonup }{f}}_k^m\rangle ;{\stackrel{\rightharpoonup }{f}}_k^m=\sum _{i=1}^N{U}_{ki}{\stackrel{\rightharpoonup }{F}}_i.$$ (7)

²⁸

The atomic forces F⃑_i computed for each member of an OP-constrained ensemble of atomic configurations are used to calculate the macroscopic force (or OP forces) ${\stackrel{\rightharpoonup }{f}}_k^m$. MC integration averaging of ${\stackrel{\rightharpoonup }{f}}_k^m$ over the ensemble is carried out to obtain the thermal average force f⃑_k. Short MD runs (~1 ps) are performed on configurations from this ensemble to calculate the OP velocity correlation functions needed to construct the ${\stackrel{\rightharpoonup }{\stackrel{\rightharpoonup }{D}}}_{kk\text{'}}$ (Eq. (4)). Using these f⃑_k and ${\stackrel{\rightharpoonup }{\stackrel{\rightharpoonup }{D}}}_{kk\text{'}}$, the OPs are evolved in time via the Langevin equation. The evolved OPs are used to generate a new ensemble of atomic configurations and the cycle repeats. Thus, OPs constrain the ensemble of atomic states (Eqs. (1)–(2)), while the latter determine the diffusion factors (Eq. (4)) and thermal average forces (Eq. (7)) that control OP evolution (Eq. (3)). With this, the two way transfer of structural information that couples microscopic motions to large-scale structural dynamics is captured. Also, accounting for the dynamically changing ensemble of atomistic configurations consistent with the evolving set of OPs provides statistical significance to DMS predictions.

C. Role of Dynamical Ensembles

A factor limiting the efficiency of the above algorithm is the need to generate a sufficiently rich all-atom ensemble at every OP timestep. If the ensemble is too small, statistical errors in the thermal forces and diffusion factors can misdirect the evolution and therefore limit the size of the Langevin timestep Δt needed to advance the system from a given time t to t + Δt. Thus, to increase the Δt, larger ensembles are required. This would then increase the computational expenditure of the multiscale simulation. Here, we address this issue by constructing ensembles from timesteps in the history prior to t to effectively enhance the ensemble needed to proceed to t + Δt. This is accomplished in a manner that accounts for the coevolution of the all-atom ensemble with the OPs as follows.

Let t be the present time and t_h be a time N_hΔt in the past (t_h = t − N_hΔt). Consider the integration of Eq. (3) from a time t_h to t + Δt. The result is

$${\stackrel{\rightharpoonup }{\Phi }}_k(t+\Delta t)={\stackrel{\rightharpoonup }{\Phi }}_k(t_h)+\underset{t_h}{\overset{t+\Delta t}{\int }}dt\text{'}(\sum _{k\text{'}}{\stackrel{\rightharpoonup }{\stackrel{\rightharpoonup }{D}}}_{kk\text{'}}{\stackrel{\rightharpoonup }{f}}_{k\text{'}}+{\stackrel{\rightharpoonup }{\xi }}_k).$$ (8)

Investigation of the ${\stackrel{\rightharpoonup }{\stackrel{\rightharpoonup }{D}}}_{kk\text{'}}$ (Eq. (4)) shows that the diagonal factors dominate when the U_ki are orthogonalized.²⁸ With this Eq. (8) becomes,

$${\stackrel{\rightharpoonup }{\Phi }}_k(t+\Delta t)={\stackrel{\rightharpoonup }{\Phi }}_k(t_h)+\underset{t_h}{\overset{t+\Delta t}{\int }}dt\text{'}({\stackrel{\rightharpoonup }{\stackrel{\rightharpoonup }{D}}}_{kk}{\stackrel{\rightharpoonup }{f}}_k+{\stackrel{\rightharpoonup }{\xi }}_k).$$ (9)

In a simple lowest order method N_h is taken to be 0. Here, we take N_h > 0 to fold historical ensemble information into the timestepping algorithm as follows. Breaking the integration interval into 1 N_h + 1 segments of length Δt yields

$${\stackrel{\rightharpoonup }{\Phi }}_k(t+\Delta t)={\stackrel{\rightharpoonup }{\Phi }}_k(t_h)+\sum _{j=0}^{N_h}\underset{t_h+j\Delta t}{\overset{t_h+(j+1)\Delta t}{\int }}dt\text{'}({\stackrel{\rightharpoonup }{\stackrel{\rightharpoonup }{D}}}_{kk}{\stackrel{\rightharpoonup }{f}}_k+{\stackrel{\rightharpoonup }{\xi }}_k).$$ (10)

Since the thermal average forces depend on the OPs, which to a good approximation change slowly, the first term inside the integral can be approximated via a simple rectangle rule. With this the thermal average force contribution becomes

$$\sum _{j=0}^{N_h}\underset{t_h+j\Delta t}{\overset{t_h+(j+1)\Delta t}{\int }}dt\text{'}({\stackrel{\rightharpoonup }{\stackrel{\rightharpoonup }{D}}}_{kk}{\stackrel{\rightharpoonup }{f}}_k)=\Delta t\sum _{j=0}^{N_h}{({\stackrel{\rightharpoonup }{\stackrel{\rightharpoonup }{D}}}_{kk}{\stackrel{\rightharpoonup }{f}}_k)}_{t=t_h+j\Delta t},$$ (11)

Such discretization applies provided $\Delta t<\sum _{j=0}^{N_h}{(f_{k\alpha })}_{t=t_h+j\Delta t}/\sum _{j=0}^{N_h}{(f_{k\alpha }^{\text{'}})}_{t=t_h+j\Delta t};\alpha =X,Y,Z$.⁴⁴ Since the force ξ fluctuates rapidly around zero, integration of the stochastic term is taken to follow the Ito formula.⁴⁵ When ξ is white noise, one obtains

$$\sum _{j=0}^{N_h}\underset{t_h+j\Delta t}{\overset{t_h+(j+1)\Delta t}{\int }}dt\text{'}({\stackrel{\rightharpoonup }{\xi }}_k)=\Delta t^{1/2}\sum _{j=0}^{N_h}{({\overline{\xi }}_k)}_{t=t_h+j\Delta t},$$ (12)

where $\langle {\stackrel{\rightharpoonup }{\xi }}_k\rangle =0\text{and}\frac{1}{2}\underset{-\infty }{\overset{0}{\int }}dt\langle {\stackrel{\rightharpoonup }{\xi }}_k(t){\stackrel{\rightharpoonup }{\xi }}_k(0)\rangle ={\stackrel{\rightharpoonup }{\stackrel{\rightharpoonup }{D}}}_{kk}$. Thus, the fact that the ensemble is changing over history as manifest in the diffusion and forces is accounted for. With this, the discretrization algorithm becomes

$${\stackrel{\rightharpoonup }{\Phi }}_k(t+\Delta t)={\stackrel{\rightharpoonup }{\Phi }}_k(t_h)+\Delta t\sum _{j=0}^{N_h}{({\stackrel{\rightharpoonup }{\stackrel{\rightharpoonup }{D}}}_{kk}{\stackrel{\rightharpoonup }{f}}_k)}_{t=t_h+j\Delta t}+\Delta t^{1/2}\sum _{j=0}^{N_h}{({\stackrel{\rightharpoonup }{\xi }}_k)}_{t=t_h+j\Delta t}.$$ (13)

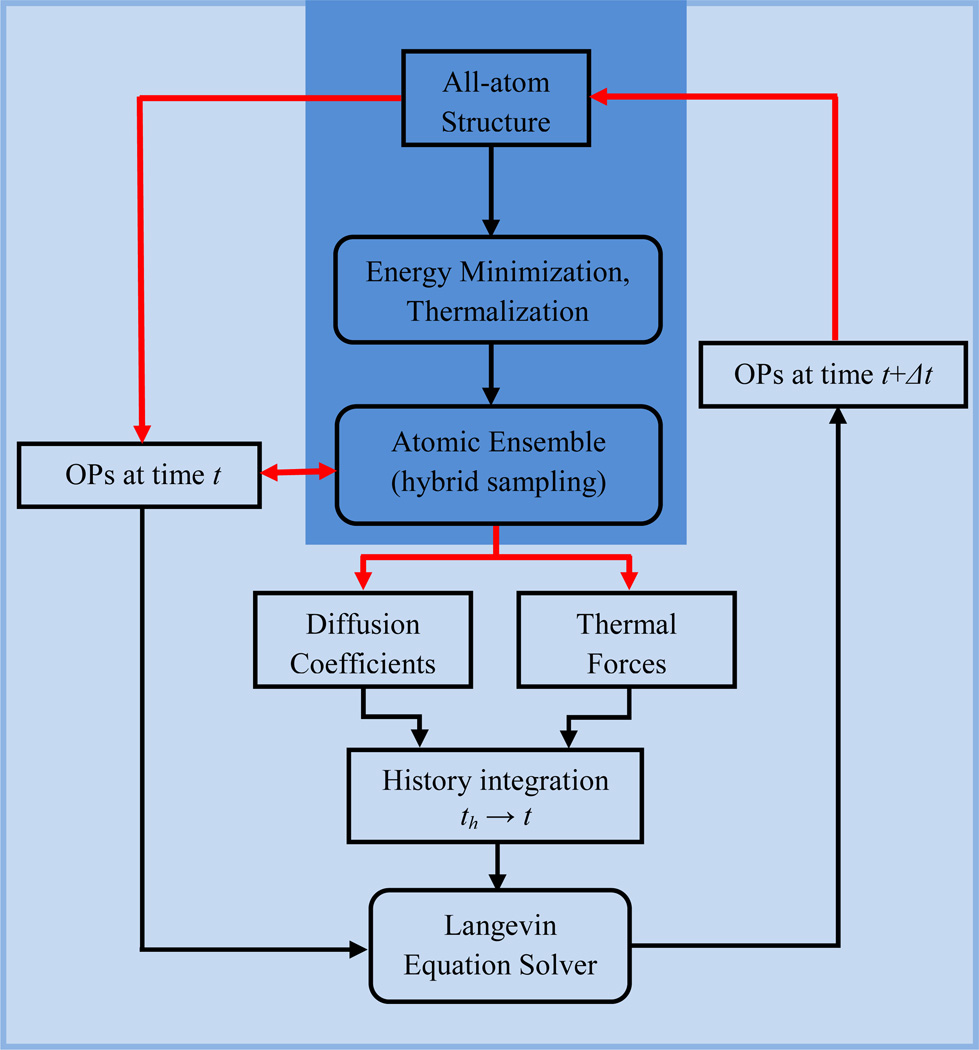
This is the basis of our history enhanced multiscale algorithm that is implemented in DMS via the workflow of Fig. 1. To arrive at Eq. (13) it has been assumed that the Langevin timestep is constant. This framework can be easily generalized to address adaptive timestepping. Furthermore, we demonstrate the method using a simple Langevin integrator. In a follow-on work, this workflow will be implemented to higher-order numerical integration schemes.

Fig. 1.

Workflow illustrating computational implementation of history enhanced DMS. Boxes indicating computations with all-atom details are presented in deep blue, while those involving OPs are shown in light blue.

An error analysis of the above approach is now considered. To simplify this analysis, and as observed for the demonstration system here, the diffusion factors are approximately constant in the interval t_h to t. With this, Eq. (13) becomes

$${\stackrel{\rightharpoonup }{\Phi }}_k(t+\Delta t)={\stackrel{\rightharpoonup }{\Phi }}_k(t_h)+\Delta t{\stackrel{\rightharpoonup }{\stackrel{\rightharpoonup }{D}}}_{kk}\sum _{j=0}^{N_h}{({\stackrel{\rightharpoonup }{f}}_k)}_{t=t_h+j\Delta t}+\Delta t^{1/2}\sum _{j=0}^{N_h}{({\stackrel{\rightharpoonup }{\xi }}_k)}_{t=t_h+j\Delta t}.$$ (14)

Using the definition of Δt, the second term in Eq. (14) takes the form $(t-t_h){\stackrel{\rightharpoonup }{\stackrel{\rightharpoonup }{D}}}_{kk}{\stackrel{\rightharpoonup }{f}}_{\mathit{\text{eff}}}$, where

$${\stackrel{\rightharpoonup }{f}}_{\mathit{\text{eff}}}=\frac{1}{N_h}\sum _{j=0}^{N_h}{({\stackrel{\rightharpoonup }{f}}_k)}_{t=t_h+j\Delta t}.$$ (15)

Dividing f⃑_k into ${\stackrel{\rightharpoonup }{f}}_k^{\infty }$ and g⃑k, where ${\stackrel{\rightharpoonup }{f}}_k^{\infty }$ is calculated from a very large ensemble the sum in Eq. (15) becomes

$${\stackrel{\rightharpoonup }{f}}_{\mathit{\text{eff}}}=\frac{1}{N_h}\sum _{j=0}^{N_h}{({\stackrel{\rightharpoonup }{f}}_k^{\infty }+{\stackrel{\rightharpoonup }{g}}_k)}_{t=t_h+j\Delta t}.$$ (16)

The sum of the ${\stackrel{\rightharpoonup }{f}}_k^{\infty }$ is of O(N_h) as the ${\stackrel{\rightharpoonup }{f}}_k^{\infty }$ change coherently on the timescale of OP evolution. In contrast, the g⃑_k contribution is a sum of random factors of fluctuating sign and zero mean since g⃑_k represents the MC error associated a finite ensemble. Therefore, the latter is of the order $O(N_h^{1/2})$. The magnitude of the g – terms divided by that of the f^∞ – terms is thus of $O(N_h^{-1/2})$. Next, let N_e be the number of all-atom configurations in the ensemble used to calculate thermal average forces at a given timestep. The MC integration error is $O(N_e^{-1/2})$.³⁴ Thus, assuming the ensembles at each timestep are statistically independent (shown below), the error in the history enhanced ensemble is O((N_eN_h)^−1/2). Since ensemble errors in the thermal average forces misdirect the OP evolution, the $O(N_e^{-1/2})$ error implies a limit on the Langevin timestep which is improved by a factor of $N_h^{1/2}$ when history enhancement is used (i.e., upper bound on the value of Δt in Eq. (13) increases by $N_h^{1/2}$ with increase in the number of history terms (N_h) in the associated f_k-summation). Overall accuracy of the history enhancement method also reflects the limit on (a) Δt due to the characteristic time of OP evolution and (b) N_h due to the need for periodic refreshment of reference structure, ${\stackrel{\rightharpoonup }{r}}_i^0$, (denoted re-referencing) for “on-the-fly” OP definition during a DMS run. The interplay of these factors is investigated in the next section in the context of obtaining optimal simulation parameters for numerical efficiency.

III. Results and Discussion

Here, DMS implementation of the history enhanced Langevin algorithm (Sect. II) is demonstrated via all-atom simulations of HPV16 capsomers in 0.3M NaCl solution. The T=1 L1 HPV16 Virus-Like Particle (VLP) contains 12 pentamers joined by “attacking arms” that stabilize it via strong hydrophobic interactions.⁴⁶ Each pentamer is composed of five L1 protein monomers. A C-terminal of the L1 protein consists of four helical regions h2, h3, h4 and h5 that maintain intra- and inter-pentameric connectivity. While h2, h3 and h5 are responsible for L1 protein folding and pentameric stability, h4 maintains inter-pentamer organization and, thereby, overall T=1 structure.⁴⁶ It has been experimentally shown that h4-truncated L1 proteins successfully form stable pentamers but fail to organize into a T=1 VLP, while h2,h3,h4 truncation prevents stable pentamer formation.⁴⁶ We simulate the expansion and consequent stability of a h4-truncated pentamer when it is isolated from the rest of the VLP. Simulations presented include 24 5ns DMS runs with different ensemble sizes (N_e) and number of history timesteps (N_h); a 5ns MD run for benchmarking results of these DMS runs; and 30–40ns DMS runs of complete, h4-truncated and h2,h3,h4-truncated pentamer showing contrasting long-time behaviors of respective structures. These systems contain 3–4×10⁴ atoms. Further details of conditions used for these simulations are provided in Table I.

Table 1.

Input parameters for the NAMD and DMS simulations.

Parameter	Values
Temperature	300K
Langevin damping	5
Timestep	1fs
fullElectFrequency	2fs
nonbondedFreq	1fs
Box size	160Å × 160Å × 160Å
Force-field parameter	par_all27_prot_na.prm
1-4scaling	1.0
Switchdist	10.0 Å
Cutoff	12.0 Å
Pairlistdist	20.0 Å
Stepspercycle	2
Rigid bond	Water

In the following, first, data from NAMD simulations are used to introduce the history enhanced MC scheme for computing thermal average forces. Effect of correlations between dynamical ensembles on the MC error analysis is discussed. Then, the history enhanced approach is used with DMS to understand the effects of Langevin timestep (Δt), ensemble size (N_e) and number of historical ensembles (N_h) on simulation accuracy and performance. An optimal set of simulation parameters (Δt, N_e and N_h) is obtained and used to simulate long-time behaviors of three pentamer constructs.

A. Relationship Between Ensemble Size and Langevin Timestepping: Implications for the history method from MD Results

The magnitude of Langevin timestepping Δt depends explicitly on the spatio-temporal scale of motion the associated OPs capture. For example, OPs capturing the overall motion of a macromolecular assembly change much more slowly than ones describing changes in individual macromolecule. Consequently, Δt for simulating a macromolecule is much less than that for the entire assembly.

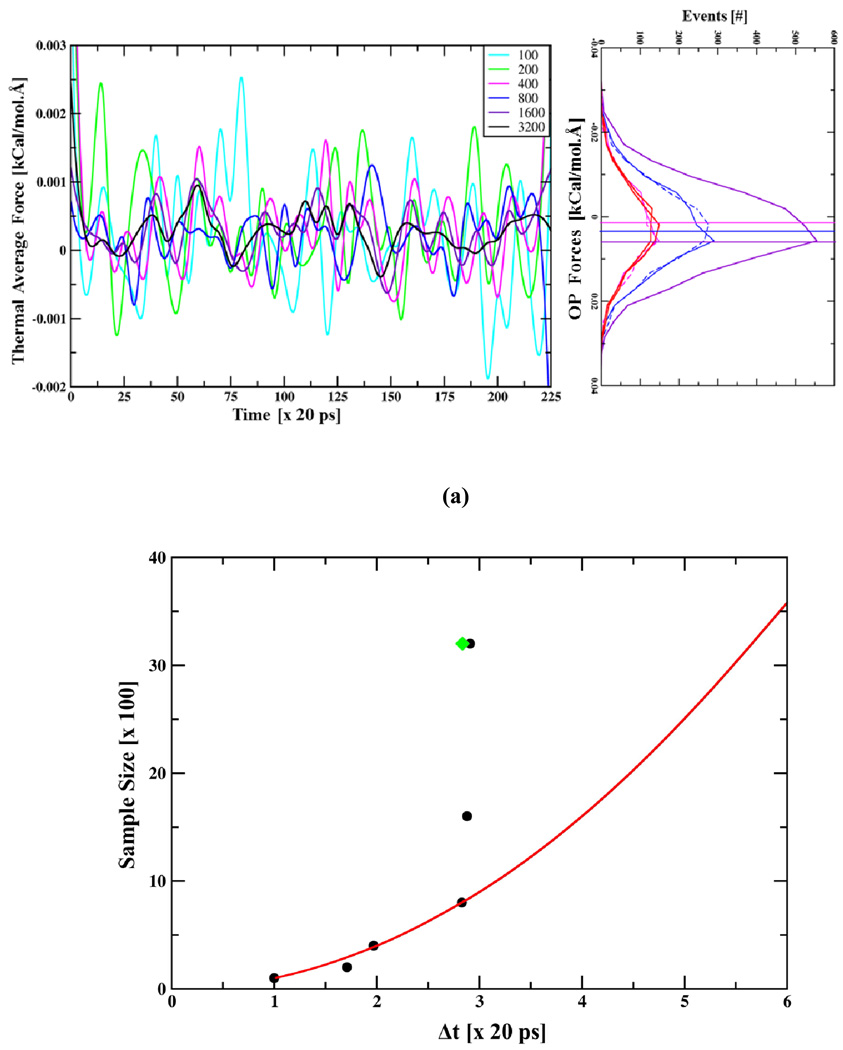
Consider the case of an isolated HPV pentamer. Its degrees of freedom are constrained inside a T=1 VLP. When all other pentamers in the capsid are removed instantaneously, this pentamer initially expands and then stabilizes to a new state. A 5ns MD simulation is performed that captures an early phase of this expansion. Here, this trajectory is used to investigate the rate of OP dynamics and compute an optimal timestep (Δt) for their Langevin evolution. Under friction dominated conditions (Eq. (3)), the rate of change of OPs is directly correlated to the thermal average forces.²² These forces, in turn, are statistical in nature and require sufficient averaging to accurately predict OP dynamics. For example, if the ensemble is too small, statistical errors in the thermal forces and diffusion factors can misdirect the evolution and therefore limit the size of the Langevin timestep Δt. Therefore, the optimal value of Δt for accurately capturing OP evolution should reflect the dynamical nature of thermal average forces, which in turn depend on size of the ensemble used. To understand this effect, structures are chosen every 20ps form the 5ns MD trajectory, constant OP ensembles are generated via hybrid sampling (Sect. II-B), and thermal average forces are computed using ensembles of different sizes (N_e) keeping N_h=0 (Fig. 2(a)).

Fig. 2.

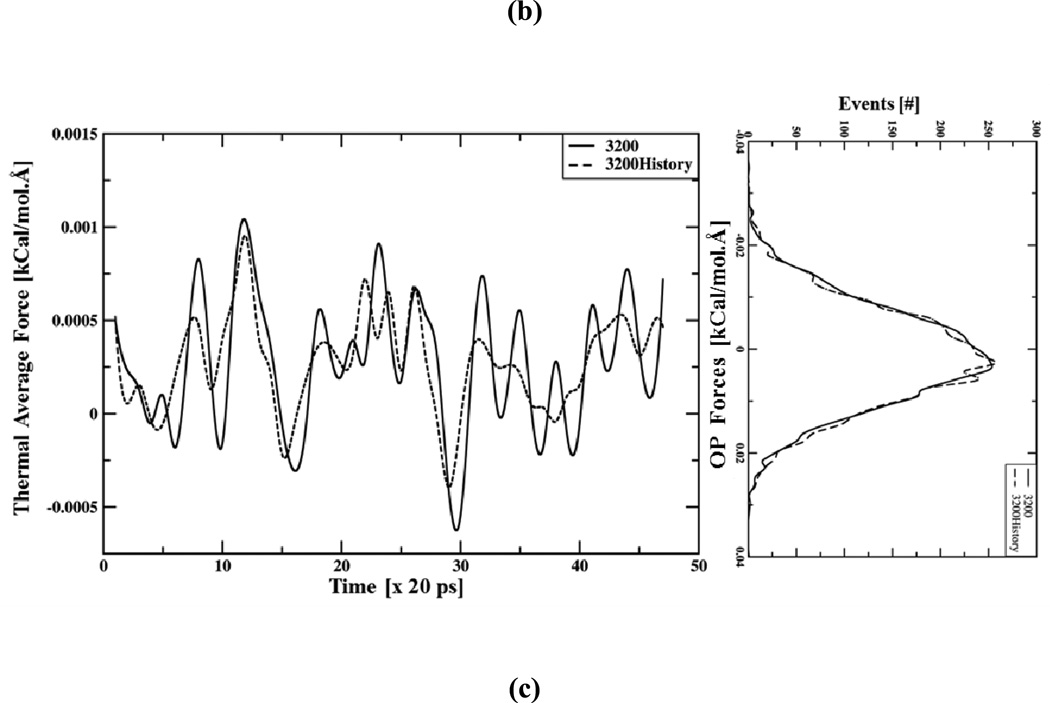
(a) Time evolution of thermal average forces (f_k with k₁=1, k₂=0 and k₃=0), constructed every 20ps using all-atom ensembles of sizes 100 to 3200. Averaging over larger ensembles yields more coherent thermal forces. (left) Line histograms showing distribution of associated OP forces ($f_{100}^m$) are shifted from their correct values when the ensemble size decreases. Data for this plot is obtained from the all-atom ensemble at 2.5 ns. (b) Optimal Langevin timestep Δt computed using $f_k/f_k^{\text{'}}$ versus ensemble size N_e (N_h = 0), showing as N_e grows Δt increases as O($N_e^{1/2}$) N_e till the maximum timestep limit is reached. Using history enhanced thermal average forces with N_e=400 and N_h= 8 similar step-size as for N_e=3200 and N_h = 0 (Fig. 2(b) (green point)) is obtained. (c) History enhanced thermal average forces versus time showing they are in agreement with those computed from N_e=3200, N_h=0 ensembles for the entire 5ns trajectory.(left) Line histograms showing distribution of OP forces for ensembles constructed using N_h=4, N_e=800. This distribution is in agreement with those from large non-history ensembles (N_h=0, N_e=3200) and other history enhanced ensembles (Fig. S2). Positively peaked distribution of these forces implies overall expansion of the pentamer.

At a given point in time, consider generation of all-atom ensembles with N_e varying over a range of values from 100 to 3200. While atomic forces in these ensembles show no clear trend (Fig. S1 in Supporting Information) (even though the underlying structures are dramatically different), OP forces (${\stackrel{\rightharpoonup }{f}}_k^m$, Eq. (7)) constructed from the same ensembles are peaked about a given value (Fig. 2(a)–(b)). Such peaks suggest strong thermal average forces; this induces coherence in large-scale dynamics.²² In the present context, positively peaked OP forces results in positive thermal average forces. Langevin evolution using these forces increases magnitude of the corresponding OP, thereby implying overall expansion of the pentamer. This suggests that the thermal average forces are an effective measure of coherence in subtle trends of the inter-atomic forces manifested in our OP-constrained ensembles. Their construction enables self-consistent transfer of structure and dynamics information from the atomic to the larger-scales.

Well resolved peaks in the distribution of OP forces suggest that many of the atomistic configurations in the ensemble contribute to similar OP forces. Such configurations are restricted to those consistent with instantaneous OP values. Together, these imply a modest size atomistic ensemble is sufficient for computing thermal average forces (${\stackrel{\rightharpoonup }{f}}_k=\langle {\stackrel{\rightharpoonup }{f}}_k^m\rangle$). However, generating these modest ensembles is still computationally expensive. Thus, practical sampling limits impose statistical errors in thermal average forces. As ensemble size decreases, the g-term in Eq. (16) increases. These g contributions randomly shift the numerically computed average forces around their correct values (Fig. 2(a)). To preserve accuracy of the predicted OP dynamics using such incomplete forces, the Langevin timestep should be reduced. This is because an erroneous thermal average when applied throughout a large timestep can take the system far away from its correct evolution pathway. But, over a sequence of small timesteps, these random errors tend to cancel (See below, Sect. III-C). However, this implies loss of multiscale simulation efficiency.

Here, we introduce a procedure that uses N_h ensembles from timesteps in the history prior to a given time t to effectively enhance the ensemble needed to proceed to t + Δt. Consequently, a slowly evolving ensemble is accounted for as a collection of small, less compete ones each of which captures some of the instantaneous influence of the evolving OP. With this history algorithm, statistical error in the MC integration of thermal average forces (resulting from lack of complete ensembles) is reduced and therefore numerical restrictions of Δt decreases limiting it to those values inherent in the accurate OP dynamics.

A rough estimate of maximum allowed Δt value can be obtained using the forces in Fig. 2(a) and their ratio with their derivatives, i.e., $\Delta t<\left(\frac{f_{k\alpha }}{f_{k\alpha }^{\text{'}}}\right)$ when N_h=0. This is shown as a function of ensemble size in Fig. 2(b). As ensemble sizes increases from 100 to 800 the required time step increases as $O(N_e^{1/2})$, as expected from the statistical arguments of Sect. II. Larger ensemble size removes numerical noise making the force more coherent. Consequently, the numerical timestep increases and reaches a limit implied by the characteristic timescale of OP evolution. For the present example, approximately a timestep Δt of ~60ps is achievable using a sample size N_e of 800 or more. However, generating such ensembles is computationally expensive for the macromolecular assemblies of interest. To address this, a composite ensemble of size 3200 is obtained by sampling 400 structures over 8 timesteps (i.e., using N_h=8 and N_e=400) in the history of a given time t. The population distribution of the history enhanced OP forces is in agreement with those from a large ensemble at a given time (Fig. 2(c)). Furthermore, the history enhanced thermal average forces are in agreement with those computed from N_e=3200, N_h=0 ensembles for the entire 5ns trajectory (Fig. 2(c)). Using the history enhanced thermal average forces implies that the characteristic Langevin timestep is increased from 20 to 60ps (Fig. 2(b) (green point)), i.e., $\Delta t\left(\frac{f_{k\alpha }}{f_{k\alpha }^{\text{'}}}\right)\to 20\text{ps}$ when N_e=400 and N_h=0, but when N_h=8 keeping N_e fixed $\sum _{j=0}^{N_h}{(f_{k\alpha })}_{t=t_h+j\Delta t}/\sum _{j=0}^{N_h}{(f_{k\alpha }^{\text{'}})}_{t=t_h+j\Delta t}\to 60\text{ps}$. Thus, the limiting OP timestep of 60ps obtained using N_e=3200 is recovered via N_e of 400 enhanced over 8 history steps. Other combinations of N_h and N_e that reproduce similar results are shown in the Supporting Information (Fig. S2). This analysis is valid only if all-atom ensembles used in the history enhancement are mutually uncorrelated, as shown in the following.

B. Applicability of the Multiscale Approach and Correlation Between Ensembles

The OP velocity autocorrelation function provides a criterion for the applicability of the present multiscale approach. If the reduced description is complete, i.e., the set of OPs considered do not couple strongly with other slow variables, then the correlation functions decay on a time scale much shorter than the characteristic time(s) of OP evolution. However, if some slow modes are not included in the set of OPs, then these correlation functions can decay on timescales comparable to those of OP dynamics. This is because the missing slow modes, now expressed through the all-atom dynamics, couple with the adopted set of OPs. The present approach fails under such conditions. For example, putting the lower limit of integral in Eq. (4) to −∞ is not a good approximation and the decay may not be exponential; rather it may be extremely slow so that the diffusion factor diverges. Consequently, atomistic ensembles required to capture such long-time tail behavior in correlation functions are much larger than those for capturing a rapid decay. In Fig. S3 it is seen that the velocity autocorrelation function decays on a scale of >10ps when an OP Φ_k with k₁=1, k₂=0 and k₃=0 (Eqs. (1)–(2)), implying extension-compression along the X-axis is missing, but on a scale of ~1ps when it is included. Here, such situations are avoided via an automated procedure of understanding the completeness of the reduced description and adding the OPs when needed (discussed briefly in Sect. SI1 of Supporting information).²⁶ Adapting this strategy ensures that the OP velocity autocorrelation functions decay on timescales orders of magnitude shorter than those characterizing coherent OP dynamics, and thus the present multiscale approach applies. Consequently, the history enhanced multiscale method allows one to use larger timesteps (i.e., 10ps or more versus <1ps, to account for the long-time tails, for the demonstration problem).

The present OP velocity autocorrelation functions decay on the ps timescale. Thus, multiple 1ps NAMD trajectories are used to compute OP velocities, correlations within which are ensemble averaged to construct the diffusion factors (Eq. (4)). Adapting this procedure is computationally practical as the timescale of decay is orders of magnitude shorter than that characterizing coherent OP dynamics. This procedure could be further optimized in two ways to make autocorrelation functions decay even faster. (a) OP force autocorrelation functions can be used to construct friction coefficients between OPs.³⁵ This matrix of friction factors can then be inverted to obtain the diffusion matrix ${\stackrel{\rightharpoonup }{\stackrel{\rightharpoonup }{D}}}_{kk\text{'}}$. Since the OP force autocorrelation functions decay faster than those for the OP velocities (Fig. S4), shorter MD runs are required to obtain the statistics for computing these functions. Thus, one saves computational time. (b) Since the OPs are constructed using orthonormalized polynomial basis functions, they mix overall rotational with extension-compression modes. This Coriolis-type coupling can be minimized to facilitate greater separation in scales between the slow and fast degrees of freedom, thereby possibly allowing more rapid decay of the autocorrelation functions. One way of achieving this separation is to cast the OPs in terms of Eckart internal, rather than Cartesian, coordinates.⁴⁷ Within this framework, there is no coupling between vibrational and rotational degrees of freedom at equilibrium. Related techniques involving a translating and rotating internal coordinate system are found to resolve molecular vibrations using only normal modes; translation and rotation are treated as vibrational motions with zero frequency.^47–49 In a similar way, use of the Eckart frame could result in correlation functions with shorter decay times, and therefore greater computational efficiency. In a related ongoing work, the idea of constructing OPs to capture deformations with respect to an evolving reference structure (not a fixed one ${\stackrel{\rightharpoonup }{r}}_i^0$ in Eq. (2)) is exploited. This dynamical reference configuration makes the associated OPs slower, thereby increasing the timescale separation with atomic fluctuations and reducing the decay time.

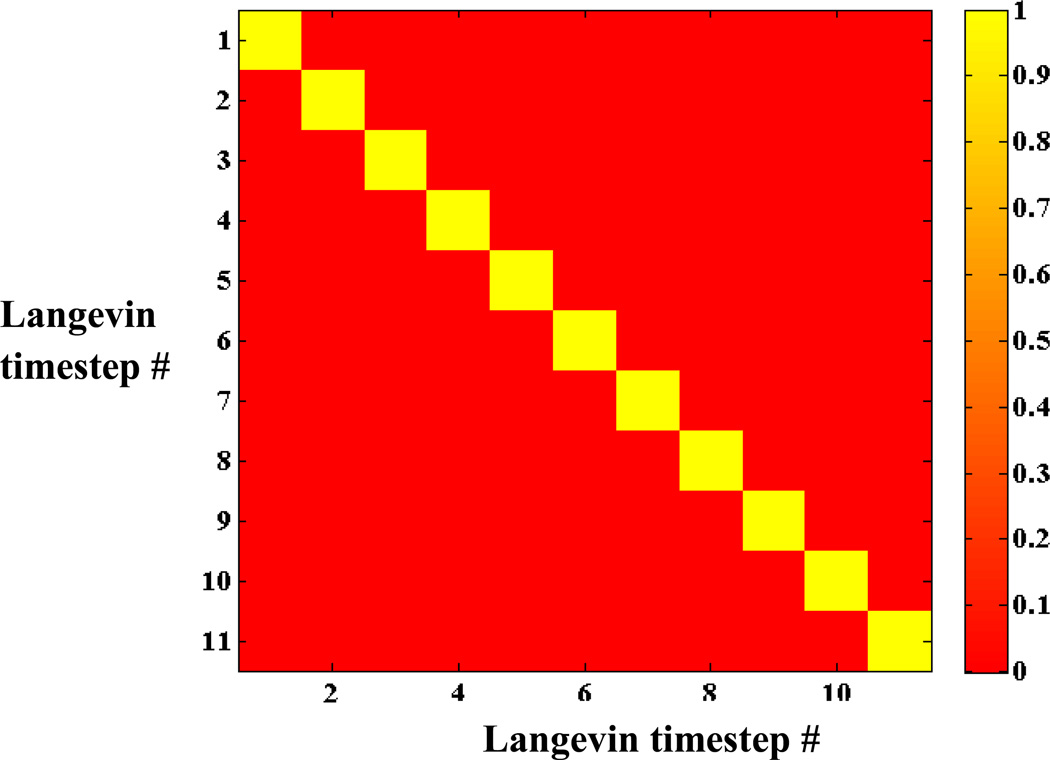
In any practical computation, the ensembles created are incomplete. Correlation of information between these ensembles must be considered in evaluating the history method. If the ensembles of all-atom configurations constructed at consecutive Langevin timesteps are very similar then using both adds no additional information to the net history enhanced (two-timestep) ensemble. Thus, for ensemble enhancement to be beneficial, the incomplete all-atom ensembles from consecutive timesteps should be uncorrelated. This is seen to be the case for the present example (Fig. 3) where ensembles characterizing OPs at discrete intervals of time are independent. Since ensembles involved in the MC integration are uncorrelated, the convergence of the thermal average forces is expected to be ∝(N_eN_h)^1/2. In this way, a large slowly varying ensemble can be accounted for via multiple atomistically uncorrelated smaller ones, each of which captures some of the instantaneous influence of the evolving OP. Here, the correlation coefficient between all-atom ensembles at two different Langevin timesteps is defined in terms of the covariance of the atomic forces obtained at these time points divided by the product of their standard deviations.⁴⁴

Fig. 3.

Correlation between atomic forces (projected along the ray from the center of mass), obtained every 20ps, from configurations of constant OP ensembles of size 1600. Near-zero correlation between ensembles characterizing OPs at discrete intervals of time imply that they are statistically independent.

When sufficiently large Boltzmann ensembles are constructed at every Langevin timestep, thermal average forces between consecutive Langevin timesteps should be correlated (Fig. S5), i.e., these OP forces depend on OPs which change only slightly from one Langevin step to another. However, finite sampling size introduces random ensemble error “noise” and reduces the correlation between the OP forces (Fig. S6). This also underlies the shifting distribution of OP force peaks as observed in Fig. 2(a). To address this ensemble noise we integrate historical information as follows.

C. Ensemble Size and Langevin Timestepping: A History Enhanced Multiscale Simulation Analysis

The history algorithm is implemented in DMS as per the workflow of Fig. 1. The first few loops in this workflow is executed considering N_h = 0. During these steps, the use of small but computationally practicable ensembles limit Δt to small values. As the number of loops exceeds N_h, the Langevin equation is integrated using the history method (Eq. (13)). Thus, the effective ensemble size and hence Δt is increased without loss of simulation accuracy.

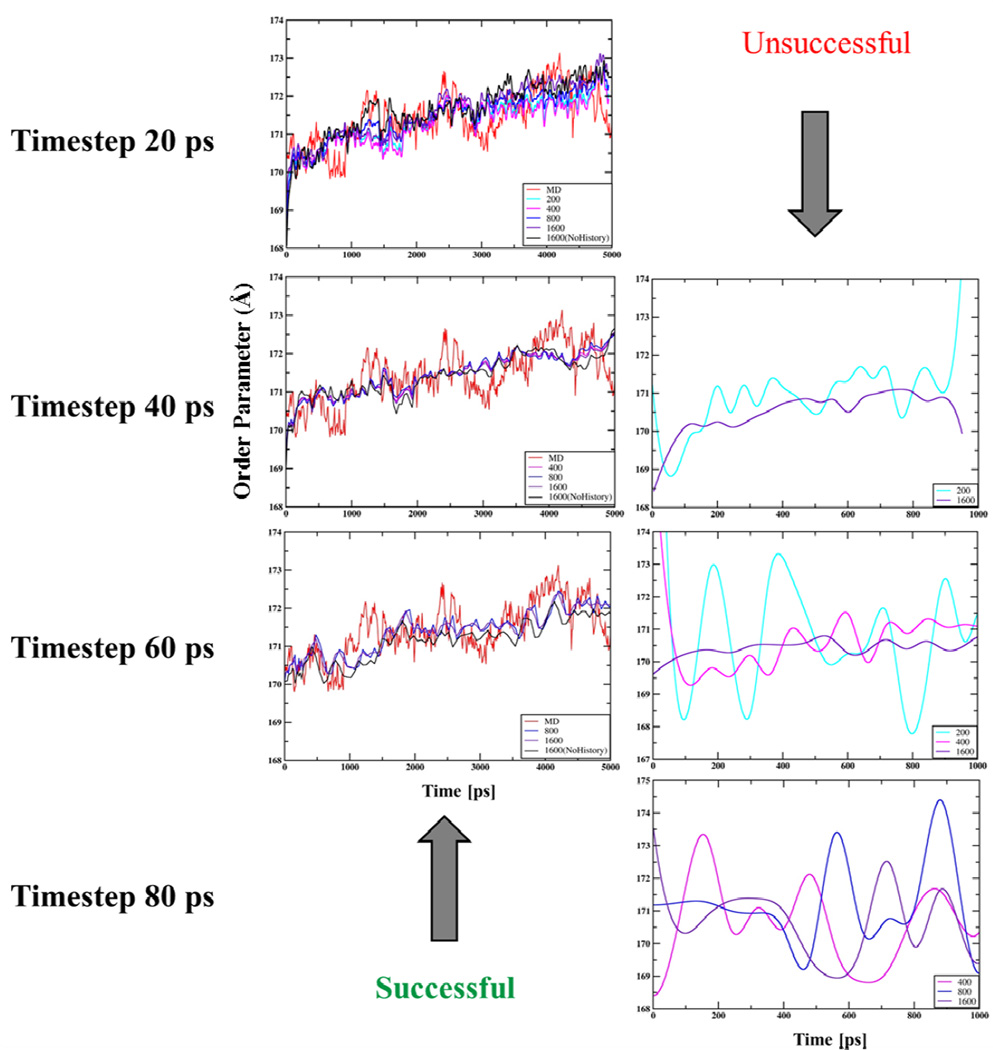
Multiscale simulation results using different timesteps and sample sizes (Changing N_h for a given Ne) are compared to those from the 5ns MD trajectory of the L1-pentamer expansion as discussed above. Limits on these parameters as obtained from the MD analysis (Sect. III-A) are Δt ~60ps and N_e > 800 when N_h=0 (Fig. 2(b)). DMS trajectories generated using ensemble of size 200 (N_e=200, N_h =0) to 1600 (N_e =200, N_h =8) are successful in reproducing NAMD results when Δt is 20ps (Fig. 4). This implies, statistical errors in incomplete thermal average forces when applied over a sequence of small timesteps cancels out, thereby reproducing results similar to those using more complete forces and larger timesteps. The result is also consistent with the fact that using ensembles of 200 or more configurations suffice to attain forces that imply Δt of 20ps (Fig. 2(b)). As the timestep increases, only runs with larger history ensemble sizes reproduce the MD derived OP trajectory. With smaller ensembles, statistical errors in the thermal forces and diffusion factors misdirect the OP evolution when the Langevin timestep is large. This is reflected in artificial overshoot and undershoot observed in the OP evolution (Fig. 4). Structurally, such behavior of OPs creates an abrupt increase in the amplitude as well as frequency of large scale motions, thereby evolving the system far away from its free-energy minimizing pathway. The timestep of 60ps is achieved using an ensemble of 1600 configurations (N_e=200 and N_h=8). This step-size is the maximum that can be used respecting the limit $\Delta t<\sum _{j=0}^{N_h}{(f_{k\alpha })}_{t=t_h+j\Delta t}/\sum _{j=0}^{N_h}{(f_{k\alpha }^{\text{'}})}_{t=t_h+j\Delta t}$ (Fig. 2(b)), and thereby reflects the characteristic timescale of OP evolution as imposed by the thermal regime of motion. Overshoots and undershoots in OP dynamics also appear as the Langevin timestep exceeds the characteristic time of OP evolution. However, in such cases, further increase in ensemble size (even an infinite ensemble) does not suffice to restore the OP dynamics since error from the numerical integration algorithm with $\Delta t<\sum _{j=0}^{\infty }{(f_{k\alpha })}_{t=t_h+j\Delta t}/\sum _{j=0}^{\infty }{(f_{k\alpha }^{\text{'}})}_{t=t_h+j\Delta t}$ is unacceptably large for the rectangular scheme used here (Eq. (13)).

Fig. 4.

Benchmarking of DMS simulated OP (Φ_100X) evolution against those from conventional NAMD trajectories. DMS trajectories using ensemble sizes (200 (N_e =200, N_h =0) to 1600 (N_e =200, N_h =8)) are consistent with MD when Δt is 20ps. As Δt increases to 40 and 60ps DMS trajectories generate only using larger ensembles succeed in reproducing MD results. For the same Δt, DMS trajectories with smaller ensemble size suffer from statistical errors in the thermal forces and diffusion factors that misdirect OP evolution. For Δt >60ps (e.g., 80ps) all DMS trajectories fail to reproduce MD results as under simulated conditions $\sum _{j=0}^{\infty }{(f_{k\alpha })}_{t=t_h+j\Delta t}/\sum _{j=0}^{\infty }{(f_{k\alpha }^{\text{'}})}_{t=t_h+j\Delta t}<80\text{ps}$.

There is a limit on the number of history timesteps, N_h, to be included in the Langevin integration that arises from our OP construction procedure (Eqs. (1)–(2)). These OPs are defined to describe the large scale dynamics as deformations of a fixed reference structure ${\stackrel{\rightharpoonup }{r}}_i^0$. However, the reference structure occasionally must be changed to accurately capture a structural transition. This is implied by the evolution of an appropriate reference structure on a timescale much greater than that characteristic of the OPs (Fig. S7(a)). For example, while the OPs change every Langevin timestep, typically the reference structure, and therefore the polynomials U change every 30 timesteps or more (Figs. S7(b)). Every time the reference structure changes, OPs are redefined in terms of the new reference. The history integration should not include time points beyond this re-referencing limit, as the very definition of OPs, OP forces and velocities are different across such reference structure transitions. Thus, for the case studied here N_h<= 30.

In summary, to capture the expansion of a h4-truncated pentamer the ensemble size N_e without the history enhancement must be greater than 800. It has been shown, using a maximum of 8 history steps and minimum of 200 structures per Langevin timestep, result of the equivalent non-history ensemble can be recovered. Consequently, in comparison with a non-history (N_h = 0) calculation with small N_e (200) and short Δt (e.g., 20ps), the history simulation with same N_e enables larger Δt (e.g., 60ps), and is therefore 3 times faster. Alternatively, if N_e is increased to 800 or 1600 for improving Δt keeping N_h = 0, then again the history formulation provides a speed-up of 4–8 over the non-history calculation as the considerable computational time for constructing sufficiently large ensembles is reduced. DMS without history enhancement is an order of magnitude faster than conventional MD.²⁹ With history the speed is enhanced by 3–8 folds. However, DMS is more appropriately comparable with ensemble MD as an ensemble of size, e.g., 1600 is constructed every Langevin timestep. Furthermore, this efficiency is size dependent and has been shown to increase as system size increases.^{28, 29}

D. Dependence of Simulation Parameters on System Characteristics: Demonstration via Stable and Unstable HPV Pentamer Constructs

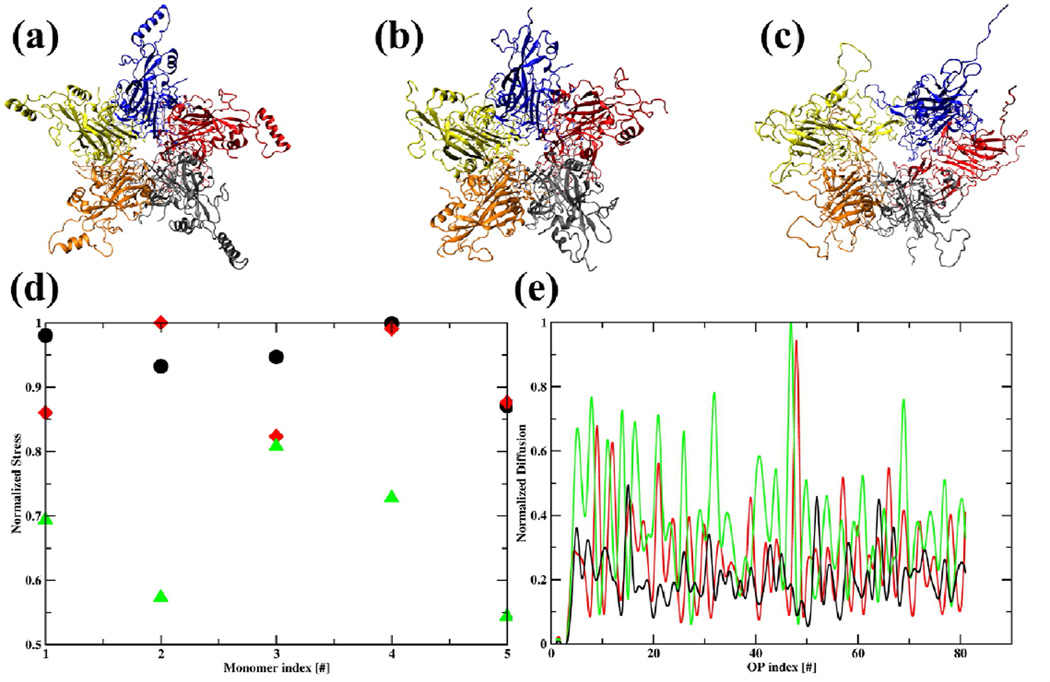
The history enhanced Langevin scheme is used to simulate three HPV pentamer systems (1) complete, (2) h4-truncated and (3) h2, h3, h4-truncated pentamers. While the first two structures initially expand and then remain stable, the third has weak intra-pentameric connections and thereby expands more extensively (Figs. 5(a)–(c) and S8). As a result for the third system, the stress on selected monomers is reduced by ~50% (Fig. 5(d)). Variations in large scale motion are reflected in the timescale of OP evolution characterizing the three systems. For example, the complete and h4-truncated pentamers remain bound (both in simulation and in experiments), and gradually approach an expanded equilibrium state. This transition is simulated using a Langevin timestep of 60ps. In contrast, the h2, h3, h4-truncated pentamer is unstable. It demonstrates significant large scale motions, however does not immediately split into monomers as there are secondary hydrophobic interactions that support a transient long-lived state. The diffusion coefficients for system 3 are greater than those for 1 and 2 (Fig. 5(e)). This reflects the higher level of fluctuations is system 3. Consequently, the Langevin timestep required for numerical stability is reduced to 40ps. Furthermore, a larger number of OPs are required, reflecting the importance of shorter scale fluctuations. The increased number of OPs decreases the number of residual degrees of freedom and therefore the required ensemble size decreases also. Nonetheless, the computational efficiency is still improved via history ensemble enhancement, but the net advantage is somewhat diminished.

Fig. 5.

Snapshots of (a) complete (b) h4-truncated and (c) h2,h3,h4-truncated HPV pentamers after 30ns of DMS simulation showing the first two structures are fairly stable but the third one is unstable and expands extensively. (d) Stress on L1-monomer during pentamer expansion showing system 3 releases ~50% of initial stress while 2 releases a maximum of 10 % relative to the most stable system 1. αβ component of stress tensor for monomer i with volume Ω is $(\sum _j\frac{1}{2}{m}_i{v}_i^{\alpha }{v}_i^{\beta }-\frac{1}{2}\sum _{j\ne i}\frac{d{V}_{ij}(r_{ij})}{d{r}_{ij}}\frac{r_{ij}^{\alpha }{r}_{ij}^{\beta }}{r_{ij}})/\Omega$, as computed using a continuum theory formulation of virus capsids;⁵⁰ here j = 1,5. The principal component of this stress tensor with largest magnitude is normalized over the three systems and presented here. (e) Diffusion coefficients computed from OP velocity autocorrelation functions (Eq. 4) versus the 3³ OPs used in DMS simulations. Diffusion coefficient for system 3>2>1 for most of the OPs. Thus, the allowed Δt follows reverse order.

IV. Conclusion

The simulation of many-atom systems like supramolecular assemblies can be greatly accelerated using multiscale techniques. However, these techniques require the construction of ensembles of all-atom configurations in order to compute diffusions and thermal average forces for advancing the coarse-grained variables (OPs in our case). As the approach yields the co-evolution of the OPs with the quazi-equillibrium distribution of all-atom configurations, it is effectively an ensemble MD method and thereby achieves statistically significant results. However, constructing such ensembles increases the computational burden, resulting in loss of efficiency. This difficulty stems from the use of ensembles which do not represent the space of all-atom configurations adequately. As a result, the coarse-grained state of the system will be somewhat misdirected in a given Langevin timestep, limiting the timestep size required to maintain the accuracy. It was shown here that this difficulty can be overcome using ensemble from previous timesteps. This requires that the latter are integrated into the computation in a manner which respects the changing nature of the ensembles over the past time period. Thus, ensemble from the evolution history cannot simply be added into a larger ensemble attributed to only one time.

In the history method presented here, it was shown that an acceleration of multiscale simulation of a factor of 3–8 over simulations which ignore history can be attained. The size of the allowed timestep increases with the number of timepoints included in the integration over history. The relation between Langevin timestep, ensemble size and re-referencing needed to sustain numerical accuracy and efficiency was established. The above points were demonstrated using three viral capsomers with different C-terminal truncations (thereby structural stability). While efficiency of the computations has some limits that depend on system detail, we expect the history enhanced approach appears to have broad applicability.