Effects of Muscle Vibration on Multi-finger Interaction and Coordination

Abstract

The purpose of this study was to investigate the effects of changes in the proprioceptive signals induced by muscle vibration on multi-finger interaction and coordination. We hypothesized that unintended force production by non-instructed fingers (enslaving) would increase with muscle vibration while synergy indices during steady-state force production would drop. The framework of the uncontrolled manifold hypothesis was used to quantify indices of multi-finger synergies stabilizing total force during steady-state force production and anticipatory changes in these indices (anticipatory synergy adjustments, ASAs) in preparation to a quick force pulse production with and without hand muscle vibration at 80 Hz. The dominant hands of twelve healthy right-handed subjects were tested under three conditions: no vibration, vibration of the palmar surface of the hand, and vibration of the forearm applied over the flexor muscles. There were no significant effects of vibration on maximal voluntary force. The magnitude of enslaving was larger during vibration of the hand compared to the other two conditions. During steady-state force production, strong synergies stabilizing total force were seen in all three conditions; however, indices of force-stabilizing synergies were lower during vibration of the hand. Prior to the force pulse initiation, the synergy index started to drop earlier and over a larger magnitude without vibration compared to either vibration condition. Effects of vibration on enslaving and synergy index may be due to diffuse reflex effects of the induced afferent activity on alpha-motoneuronal pools innervating the extrinsic flexor compartments. We conclude that multi-finger synergies are not based on signals from muscle receptors. The smaller synergy indices and ASAs may reflect supraspinal effects of the vibration-induced afferent activity, in particular its interactions with trans-thalamic loops.

Introduction

Multi-finger action can be characterized by two groups of phenomena. The first group reflects the fact that fingers are not independent force and movement generators. When a finger produces force (or movement) voluntarily, other fingers of the hand also show force (movement) production; this phenomenon has been addressed as lack of individuation or enslaving (Kilbreath and Gandevia 1994; Li et al. 1998; Zatsiorsky et al. 2000; Schieber and Santello 2004).

The second group, multi-finger synergies, is related to the fact that most (possibly all) natural multi-digit actions are redundant (Latash et al. 2003; Zatsiorsky and Latash 2004, 2008). This means that the number of elemental mechanical variables (those produced by individual digits) is higher than the number of task-related constraints. The classical problem of motor redundancy (Bernstein 1967) has been recently addressed within the principle of abundance (Gelfand and Latash 1998; Latash 2012). According to this principle, the central nervous system (CNS) organizes redundant sets of elemental variables into synergies characterized by a specific structure of across-trials variance, which can be analyzed within the uncontrolled manifold (UCM) hypothesis (Scholz and Schöner 1999). Such synergies stabilize (reduce variance of) potentially important performance variables. This means that the amount of variance that does not affect a performance variable (“good variance” or variance within the uncontrolled manifold, V_UCM) is higher than variance affecting that variable (“bad variance” or variance orthogonal to the UCM, V_ORT). Synergies have been quantified with an index (ΔV) reflecting the normalized differences between V_UCM and V_ORT, both per degree-of-freedom in the corresponding sub-spaces.

During steady-state force production tasks, strong multi-finger synergies have been demonstrated stabilizing the total force (Shim et al. 2005; Gorniak et al. 2007). When a person produces a quick change in the total force, the synergy index shows a drop in preparation to the quick action – anticipatory synergy adjustment (ASA, Olafsdottir et al. 2005; Shim et al. 2006). The likely purpose of ASAs is to attenuate synergies stabilizing a performance variable in preparation to its quick change; otherwise, the CNS would have to fight those synergies.

There is no agreement on the neural mechanisms involved in synergies. Several schemes have been offered including pure feed-forward control (Goodman and Latash 2006), optimal feedback control (Todorov and Jordan 2002), a scheme with central back-coupling loops (Latash et al. 2005), and schemes that unite the ideas of synergies with those of equilibrium-point (EP) hypothesis (Martin et al. 2009; Latash 2010). In this study we explore the potential role of proprioceptive information and reflex loops in phenomena of finger interaction and multi-finger synergies with the help of high-frequency, low-amplitude muscle vibration.

Muscle vibration produces a very high level of activity in the primary endings of muscle spindles (Brown et al. 1967; Roll and Vedel 1982; Cordo et al. 1998) as well as high activity in various cutaneous and subcutaneous receptors. This unusual barrage of the CNS by action potentials from peripheral sensory organs leads to a host of sensory-motor events, which include reflex contraction of muscles (tonic vibration reflex, Eklund and Hagbarth 1966) both in the area of vibration application and in relatively remote areas of the body (Gurfinkel and Latash 1979), kinesthetic illusions (commonly the muscle directly subjected to vibration is perceived as being stretched, Lackner and Levine 1979; Roll et al. 1989), postural disturbances (vibration-induced fallings, Eklund and Hagbarth 1967; Hayashi et al. 1981), and interactions with other reflexes, partly due to the increased presynaptic inhibition of primary afferent projections on alpha-motoneurons (Gillies et al. 1969; Desmedt and Godaux 1978). Vibration can involve neural structures that participate in the performance of such common tasks as vertical posture and locomotion (Gurfinkel et al. 1998; Selionov et al. 2009). To our knowledge, effects of vibration on finger interaction and multi-finger synergies have not been studied. Based on the described effects of vibration, we formulate the following three hypotheses.

First, we expect muscle vibration to spread to all the compartments of the extrinsic hand muscles and lead to an overall increase in the excitability of alpha-motoneurons innervating those compartments. As a result, any additional central excitation is expected to lead to relatively higher activation of all the compartments leading to higher force produced by fingers that are not instructed to produce force (enslaved fingers). So, our Hypothesis-1 is that enslaving effects will increase under muscle vibration.

Second, the distortion of the activity of peripheral sensory endings can be expected to lead to lower synergy indices in schemes that rely on the functioning of feedback loops from those endings. In particular, models that unite the ideas of synergic control and equilibrium-point control may be expected to malfunction under vibration given the importance of the tonic stretch reflex loops in the EP-hypothesis (Feldman 1986). Hence, we expect lower synergy indices during accurate multi-finger steady-state force production tasks (Hypothesis-2).

Hypothesis-2 is also corroborated by several recent studies of patients with disorders of neural loops that involve the thalamus, such as those with Parkinson’s disease (Park et al. 2012) and olivo-ponto-cerebellar atrophy (Park et al. 2013). Those patients show significantly reduced indices of multi-finger synergies and significantly delayed and reduced ASAs in preparation to a self-paced force pulse production. The vibration-induced unusual patterns of sensory signals to the thalamus may be expected to interfere with brain loops through this major “middle-man” of the brain resulting in synergy changes resembling those in the mentioned groups of patients. Hence, our Hypothesis-3 is that ASAs will be reduced under muscle vibration.

We tested the three hypotheses using vibration applied, in different series, to the hand or to the forearm. We used the two vibration sites to explore sensitivity of the indices of finger interaction and coordination to the vibration of the intrinsic and extrinsic muscles. Since vibration spreads through the tissues and may be expected to recruit sensory endings in many muscles, this was an exploratory manipulation.

Methods

Subjects

Twelve right-handed healthy subjects (five females; height: 157.5 ± 4.8 m, mass: 58.1 ± 7.8 kg, age: 28.4 ± 1.9 years, and seven males; height: 173.9 ± 7.8 m, mass: 73.8 ± 10.3 kg, age: 28.6 ± 5.6 years) volunteered to participate in this study and were tested with their dominant hand only. Hand dominance was determined on the basis of their natural hand preference for writing and eating. The subjects gave written informed consent according to the procedure approved by the Office for Regulatory Compliance of the Penn State University.

Apparatus

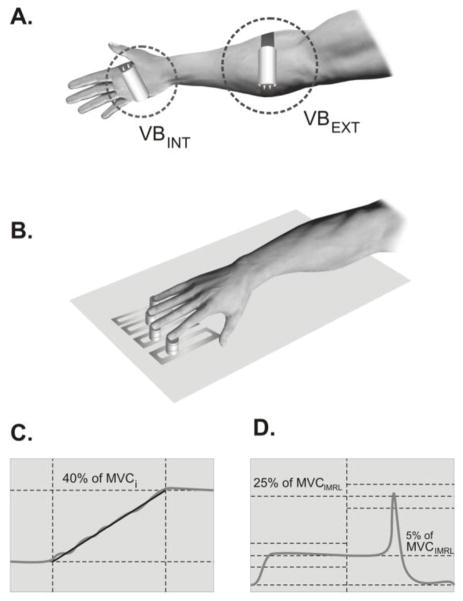
The vertical forces applied by the fingertips were measured with four force transducers (Nano-17, ATI industrial Automation, Garner, NC) mounted on an aluminum panel sitting on a wooden board (Figure 1). Sensors were spaced 3.0 cm apart in the medio-lateral direction and adjusted in the anterior-posterior direction to ensure comfortable positioning given the hand anatomy. Each sensor was covered with sandpaper to increase the friction at the contact point with the finger. The force signals were digitized with a 16-bit analog-to-digital converter at a sampling rate of 500 Hz and processed with a customized LABVIEW program.

Figure 1.

The experimental setup, the placement of the vibrators, and the feedback screens used in the tasks.

An electromechanical vibrator (Dynatronic, France) enclosed in a plastic housing accommodating a DC motor with an eccentric on the shaft was used to generate vibration. The control unit was used to set the vibration frequency. The weight, length and diameter of the vibrator were 100 g, 6 cm, and 3 cm, respectively. The vibrator was affixed to the skin over the target muscle groups by elastic straps to ensure that the vibrator kept the same position without slipping (sliding) out of place.

Experimental Procedures

The subject sat in a chair; the upper arm was positioned at approximately 45 degrees of abduction and 45 degrees of flexion whereas the elbow was at approximately 45 degrees of flexion with the wrist pronated. The 19″ computer monitor was positioned about 0.7 m in front of the subject to provide real-time visual feedback. The task-specific force feedback was displayed on the screen at a resolution of 1024 × 780 pixel and a refresh rate of 25 Hz. Before each trial initiation, subjects were asked to place the four fingertips on the corresponding sensors and remain relaxed; the sensor signals were set to zero so that only active vertical forces were measured. Total duration of the experiment was approximately 1 hour. Subjects were given 1-min rest intervals between conditions and between tasks.

Vibration Conditions

Three conditions were used: no vibration (VB_NO), vibration applied over the intrinsic hand flexors (VB_INT), and vibration applied over the extrinsic hand flexors (VB_EXT). In the VB_INT condition, the vibrator was placed on the palmar surface of the hand. During the VB_EXT condition, the vibrator was placed over the antero-medial side of forearm, distal to the elbow. Vibration was turned on 30 s before the initiation of each trial. It remained off during the rest periods. The order of the three vibration conditions was randomized across subjects. Under each vibration condition, the frequency was set at 80 Hz; this frequency was selected based on the high sensitivity of the primary spindle endings to mechanical vibration (Roll et al. 1989). At this frequency, the reported vibration amplitude was about 0.8 mm (Wierzbicka et al. 1998).

Experimental Tasks

The experiment involved three tasks: 1) maximal voluntary contraction (MVC); 2) single-finger accurate force ramp production, and 3) four-finger steady-state force production followed by a quick force pulse.

In the MVC task, subjects were instructed to press as hard as possible with all four fingers. The feedback was provided on the total force. The subjects had 8 s to reach the maximum force level. Three trials at the MVC task were performed under each of the three vibration conditions. The maximal total force (MVC_TOT) and the individual finger forces (MVC_i; i = I, Index; M, Middle; R, Ring; L, Little) were computed at the time of MVC_TOT. These values were used to set target force levels in further tasks.

During the single-finger accurate ramp force production trials, the subject was asked to press with one finger (i) and follow with that finger’s force the template consisting of three segments; 4-s horizontal line at 0% of MVC_i, 12-s slanted line from 0% to 40 % of MVC_i and 4-s horizontal line at 40 % of MVC_i. Subjects were instructed to pay no attention to possible force production by non-task fingers while keeping all fingers on the sensors during trials. The task was performed twice by each of the fingers as the task finger.

The third task required the subject to produce a steady-state force level while pressing naturally with all four fingers followed by a quick force pulse to a target. The screen showed the initial force level (5% of MVC_TOT) and the target force level (at 25±5 % of MVC_TOT). Over the first 5 s, the subject was required to match the initial force level. After 5 s, the cursor showing the total force crossed a vertical line, after which time the subjects were instructed to produce a force pulse into the target at a self-selected time (within 5 s). Eight practice trials were given prior to data collection. Then, the subject performed 20 trials with 10-s intervals between the trials. In cases of obvious errors (e.g., slow force drift prior to the force pulse, multiple peaks during the pulse, and peak force outside the target window), the trial was rejected and additional trials (up to ten) were performed.

Data Analysis

The force data were processed off-line using MATLAB. The signals were low-pass filtered at 10 Hz with a fourth-order, zero-lag Butterworth filter.

Enslaving matrix

The force data from the single-finger accurate force ramp production task were used to construct the enslaving matrix (E) that reflects unintended force production by non-task fingers (Zatsiorsky et al. 2000). The elements of the 4×4 E matrix (Eq. 1) were computed as the regression coefficients from linear regression analysis between individual finger forces and F_TOT over the ramp duration (Eq. 2). The first and last 1-s intervals of the ramp were excluded to avoid edge effects. The diagonal and non-diagonal elements of the matrix represent changes in the task-finger and non-task finger forces, respectively.

$$E=\left[\begin{array}{cccc}{k}_{I,I}& k_{I,M}& k_{I,R}& k_{I,L}\\ k_{M,I}& k_{M,M}& k_{M,R}& k_{M,L}\\ k_{R,I}& k_{R,M}& k_{R,R}& k_{R,L}\\ k_{L,I}& k_{L,M}& k_{L,R}& k_{L,L}\end{array}\right]$$ (1)

$${\text{F}}_{i,j}={\text{a}}_i+{\text{k}}_{i,j}•{\text{F}}_{\mathit{TOT},j},$$ (2)

where i,j ∈ {I,M,R,L}; j stands for the task finger. We quantified the total amount of enslaving using an index EN, which was computed as the average of the off-diagonal entries of E.

Multi-finger force stabilizing synergy

We quantified co-variation of commands to fingers (multi-finger force stabilizing synergy) within the framework of the uncontrolled manifold (UCM) hypothesis (Scholz and Schöner 1999; reviewed in Latash et al. 2002). The hypothetical commands to fingers were defined as finger modes (m_i). The E matrix was used to compute a mode vector (m) based on forces of individual fingers (F) (Eq.3).

$$\mathbf{m}={[\mathbf{E}]}^{-1}\mathbf{F};\mathbf{F}={[{\text{f}}_{\text{I}},{\text{f}}_{\text{M}},{\text{f}}_{\text{R}},{\text{f}}_{\text{L}}]}^{\text{T}}$$ (3)

For each subject and each condition, the across-trials variance in the mode space was quantified within two subspaces, the UCM (three-dimensional) and its orthogonal complement (one-dimensional), V_UCM and V_ORT. A synergy index (ΔV) that indicates the relative amount of V_UCM in the total variance, V_TOT, was computed as:

$$\mathrm{\Delta }V=\frac{V_{\mathit{UCM}}/3-V_{\mathit{ORT}}/1}{V_{\mathit{TOT}}/4}$$ (4)

where each variance index is computed per dimension in the corresponding space. ΔV > 0 is interpreted as a sign of a synergy stabilizing the total force; larger positive values of ΔV are interpreted as a stronger synergy. For details on this analysis see Latash et al. 2001. As ΔV could range from 1.33 (all variance is within the UCM) to −4 (all variance is in the subspace orthogonal to UCM), the ΔV values were subjected to Fisher’s z-transformation with adjusted boundaries prior to applying parametric statistical analyses:

$$\mathrm{\Delta }{V}_Z=0.5log\left(\frac{4+\mathrm{\Delta }V}{1.33-\mathrm{\Delta }V}\right)$$ (5)

Two exclusion criteria for the force pulse production trials were applied: a) trials where the peak force (F_peak) deviated from the target level by more than ±5%; and b) trials with the time to F_peak over 1 s. All the accepted trials (79% overall) were aligned with respect to t₀ before computing variance components and ΔV as described earlier.

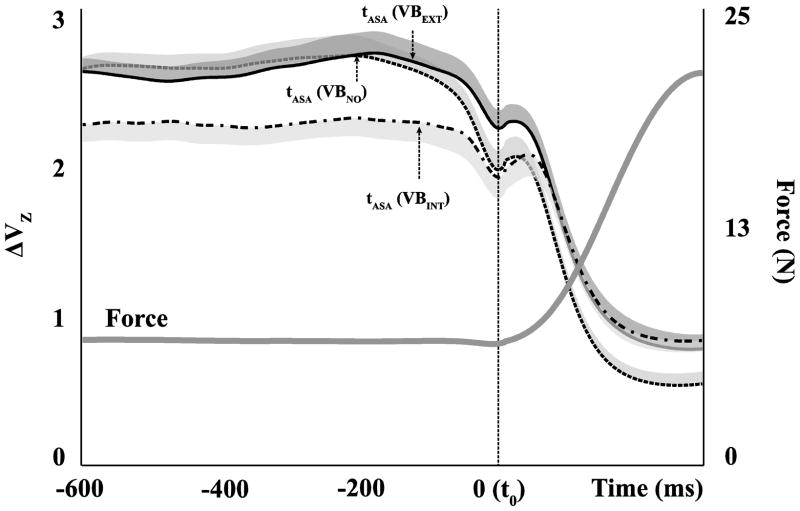
The time of initiation of F_TOT change (t₀) was defined as the time when the first derivative of force (dF/dt) reached 5% of its peak value in that particular trial. The steady state (SS) was defined as the period 600–400 ms before t₀. Anticipatory synergy adjustments (ASA) were quantified with two indices, the time of initiation of the ΔV drop (t_ASA), and the change in the synergy index (ΔΔV_Z) between steady state (SS) and t₀. The mean and standard deviation (SD) of ΔV_Z were computed over SS; tASA was defined as the time when ΔV_Z dropped below its average steady-state value by more than 2SDs.

Statistics

Standard methods of descriptive statistics were used; the data are presented in the text as means ± standard errors. ANOVAs with repeated measured were used to analyze the effect of vibration condition on the main outcome variables. Factors were Finger (4 levels: I, M, R, L), Variance (two levels: V_UCM and V_ORT), and VB-Condition (3 levels: VB_NO, VB_INT, VB_EXT). Mauchly’s sphericity test was used to confirm the assumptions of sphericity, and the sphericity violations were corrected by the Greenhouse-Geisser estimation. Significant effects were further explored using pairwise comparisons with Bonferroni corrections. In addition, variables with computational boundaries were transformed using Fisher’s z-transformation according to the upper and lower limits of each variable. The nominal level of significance was set at p < 0.05.

RESULTS

General performance

During the maximal voluntary contraction (MVC) tasks, the vibration did not induce any significant changes in the peak forces (F_[2,11] = 1.25, p = 0.31). On average, the MVC_TOT forces were 89.68±38.53 N, 88.20±39.20 N, and 86.69±39.16 N in the VB_NO, VB_INT, and VB_EXT conditions, respectively. During the multi-finger quick force pulse production tasks, the percentage of rejected trials was about 21%. There were no differences across the three conditions in the number of rejected trials (F_[2,11] = 1.59, p = 0.23). The average time to peak force in the quick force pulse production was 0.147±0.019 s, 0.146±0.020 s, and 0.146±0.015 s in the VB_NO, VB_INT, VB_EXT conditions, respectively. No differences across the conditions were observed (F_[2,11] = 0.08, p = 0.92). Thus, we conclude that the overall performance was not affected significantly by muscle vibration.

Enslaving (EN)

During the single-finger ramp force production tasks, non-task fingers produced unintended finger forces (enslaving). The enslaving index (EN) was larger in the VB_INT condition (0.097±0.016) as compared to the other two conditions (Fig. 2). These findings were supported by a two-way repeated-measure ANOVA, Finger (four levels: Index, Middle, Ring, and Little) ×Vibration (three levels), which showed significant main effect of Vibration (F_[2,11] = 7.89, p < 0.01) without a significant Finger × Vibration interaction. Pairwise comparisons revealed that EN for VB_EXT and VB_NO < EN for VB_INT (p < 0.05). While there was a tendency for EN to be higher in the VB_EXT condition compared to the VB_NO condition (0.086±0.028 vs. 0.073±0.018), this effect was under the significance level (p = 0.94). In addition, the main effect of Finger was significant (F_[3,11] = 52.09, p < 0.001). In particular, the ring and little fingers showed larger EN than the index and middle fingers across the conditions (Fig. 2). Pairwise comparisons confirmed that EN_I < EN_M < EN_R, EN_L (p < 0.05).

Figure 2.

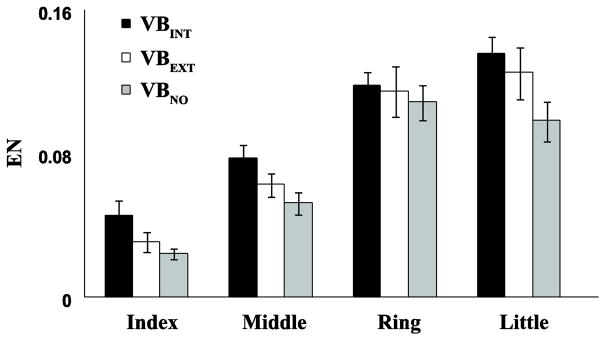
Finger force enslaving (EN) of the index, middle, ring, and little fingers during vibration applied to the hand (VB_INT, filled bar), to the forearm (VB_EXT, open bars), and in the no-vibration condition (VB_NO, gray bars). Average values across subjects are presented with standard error (SE) bars.

Multi-finger synergies at the steady state

Two components of finger mode variance, V_UCM and V_ORT, were quantified per degree-of-freedom at the steady state (−600 ms to −400 ms in Fig. 3). There was no significant difference in V_UCM among the three conditions (F_{[2, 11]} = 0.96, p = 0.35), while the main effect of Vibration on V_ORT was significant (F_{[2, 11]} = 10.49, p < 0.05). In particular, V_ORT for the VB_INT condition was larger than for the other two conditions (p <0.05) (Fig. 3).

Figure 3.

The two components of variance, V_UCM (black line) and V_ORT (gray line), during vibration applied to the hand (VB_INT, dash-dot line), to the forearm (VB_EXT, solid line), and in the no-vibration condition (VB_NO, dashed line). V_UCM and V_ORT were quantified per degree-of-freedom, and the average across subjects values are presented. The times of ASA initiation are shown with the arrows corresponding to a drop in ΔV_Z (see Figure 4).

Figure 4 shows the time-profile of z-transformed synergy index (ΔV_Z) averaged across subjects with standard error shades. During steady-state force production ΔV > 0, resulting in the high ΔV_Z values in all conditions. The magnitude of the synergy index at the steady-state was significantly higher in the VB_EXT and VB_NO conditions compared to the VB_INT condition (Fig. 4; F_[2,11] = 4.52, p <0.05). Pairwise comparisons confirmed the lower ΔV_Z values under VB_INT (p < 0.05).

Figure 4.

The total force (solid gray line, average across conditions) and synergy index (black line, z-transformed synergy index, ΔV_Z) during vibration applied to the hand (VB_INT, dash-dot line), to the forearm (VB_EXT, solid line), and in the no-vibration condition (VB_NO, dashed line) during the discrete quick force production tasks. Averages (with standard error shades) across subjects are presented for ΔV_Z.

Anticipatory synergy adjustments

The synergy index (ΔV_Z) dropped prior to the initiation of the force pulse in all three conditions (Fig. 4). These anticipatory synergy adjustments (ASAs) were quantified with two indices, the time of the ASA initiation (t_ASA, see Methods) and the difference in the synergy index between steady-state and t₀ (ΔΔV). Under the vibration conditions, the ASAs started later (t_ASA values for VB_EXT: −0.131± 0.085 s, for VB_INT: −0.124 ± 0.096 s, and for VB_NO: −0.211 ± 0.096 s) and led to a smaller change in the synergy index, (ΔΔV values for VB_EXT: 0.392 ± 0.251, for VB_INT: 0.328 ± 0.263, and for VB_NO: 0.641 ± 0.285). A main effect of Vibration was significant on both t_ASA and ΔΔV (F_[2,11] = 3.71, p < 0.05 for t_ASA; F_[2,11] = 4.53, p < 0.05 for ΔΔV). Pairwise comparisons confirmed the smaller t_ASA and larger ΔΔV in the VB_NO condition (p < 0.05).

The changes in the two variance components, ΔV_UCM (V_UCM at t₀ – V_UCM at t_ASA) and ΔV_ORT (V_ORT at t₀ – V_ORT at t_ASA), were quantified in order to examine the relative contributions of changes in V_UCM and V_ORT to the ASAs. Throughout the three vibration conditions, during ASAs V_UCM decreased in 27 out of 36 cases (mean change ± SD, −0.002± 0.017 N² for VB_NO, −0.012±0.034 N² for VB_EXT, and −0.013±0.017 N² for VB_INT), while V_ORT increased in 34 out of 36 cases (0.006±0.007 N² for VB_NO, 0.004±0.004 N² for VB_EXT, and 0.009±0.014 N² for VB_INT). These findings were supported by ANOVA, Variance (two levels: V_UCM and V_ORT) ×Vibration (3 levels), which showed a significant main effect of Variance (F_[1,11] = 5.82, p < 0.05) without a significant Variance × Vibration interaction (F_[2,11] = 0.83, p = 0.45). There was no significant difference in both ΔV_UCM and ΔV_ORT across the conditions (F_[2,11] = 1.19, p = 0.33).

Discussion

The three hypotheses formulated in the Introduction have been generally supported. In particular, muscle vibration led to larger indices of unintentional finger force production (enslaving, Li et al. 1998; Zatsiorsky et al. 2000), smaller indices of force-stabilizing multi-finger synergy (reviewed in Latash et al. 2007), and smaller anticipatory synergy adjustments (ASAs, Olafsdottir et al., 2005). There were, however, significant differences in the effects of vibration between the two sites of its application. Namely, vibration applied to the hand (VB_INT) produced stronger effects on the outcome variables as compared to vibration applied to the forearm (VB_EXT). Further we discuss implications of the findings for hypotheses on the origins of the phenomena of finger interaction and coordination.

On the origin of vibration effects on finger interaction

Limited finger individuation or enslaving has been demonstrated in a variety of tasks involving finger movement and force production (Kilbreath and Gandevia 1994; Li et al. 1998; Zatsiorsky et al. 2000; Schieber and Santello 2004; Kim et al. 2006; van Duinen and Gandevia 2011). A number of peripheral and central (neural) factors have been invoked to account for the phenomena of enslaving. These range from the peripheral coupling between fingers, to the action of multi-tendon extrinsic hand muscles, and to the overlapping cortical representations of the fingers (reviewed in Schieber and Santello 2004; van Duinen and Gandevia 2011). Changes in indices of enslaving with specialized practice (Slobounov et al. 2002) and neurological disorders (Park et al. 2012, 2013) have contributed to the growing evidence for the importance of neural mechanisms in enslaving.

The effects of muscle vibration are many and varied. Vibration produces high levels of activity of the spindle primary endings (as well as other receptors) resulting in both motor and perceptual effects. Motor effects include, in particular, involuntary tonic muscle activation (tonic vibration reflex, TVR) that can be seen in both the muscle group subjected to vibration and remote muscles (Eklund and Hagbarth 1966; Latash and Gurfinkel 1979). In addition, vibration produces strong presynaptic inhibition of the terminals of primary muscle afferents on alpha-motoneurons resulting in effective suppression of monosynaptic reflexes (Gillies et al. 1969). Perceptual effects of vibration include illusions of motion that may lead to perception of anatomically impossible joint configurations (Craske 1977; Lackner and Taublieb 1984). Hypotheses on the neural mechanisms involved in the various vibration-induced sensorimotor phenomena include effects of vibration on both sensory signals and the efference copy (Feldman and Latash 1982a,b) and involvement of the central pattern generator for locomotion (Gurfinkel et al. 1998; Selionov et al. 2009).

Under both vibration conditions, VB_EXT and VB_INT, the vibration likely affected muscle spindles in the extrinsic flexors. During VB_EXT, the vibration spread through the tissue directly to the muscle fibers; it was likely to have larger effects on muscle compartments closer to the surface of the forearm such as those in flexor digitorum superficialis (FDS) compared to flexor digitorum profundis (FDP). During VB_INT, the vibration was acting on the tendons of the extrinsic flexors and could be expected to lead to more uniform effects in all the compartments of both FDS and FDP. Only VB_INT, but not VB_EXT, was expected to affect spindle activity in the intrinsic hand muscles. Overall, one could expect VB_INT to be a more effective stimulus for spindle endings in the hand muscles, which is compatible with our findings of stronger effects on VB_INT on indices of finger interaction and coordination.

The broad spectrum of the effects of vibration allows offering several mutually non-exclusive interpretations for the observed changes in the enslaving and synergy indices. In the absence of vibration, voluntary force production by a finger leads to recruitment of motor units that belong to FDP compartments that produce force in all the fingers of the hand (enslaving). Larger effects are typically seen in the instructed fingers as compared to non-instructed fingers (Zatsiorsky et al. 2000) suggesting that the excitation is more focused on the compartment serving the instructed finger. The vibration-induced high activity of the primary spindle afferents is expected to produce widespread excitatory effects on the alpha-motoneuronal pools of all the muscles subjected to vibration and all their compartments. When a voluntary effort directed at a finger occurs during vibration, the voluntarily produced excitation to alpha-motoneurons driving non-target compartments may be expected to sum up with the vibration-induced excitation and lead to recruitment of a larger number of motor units in those compartments resulting in relatively larger enslaving effects as observed in our experiment.

In addition, the vibration-induced widespread excitatory effects on all the compartments of the extrinsic finger flexors may be expected to contribute to positive co-variation of finger forces across trials. This positive co-variation interferes with the high negative co-variation, which is a signature of a force-stabilizing synergy, observed in the absence of vibration. As a result, a drop in the synergy index was observed in our study under the VB_INT condition. We can suggest only a speculative explanation why no such effect was observed under the VB_EXT condition. Note that deep finger flexor tendons are attached at the distal phalanges making this muscle the primary focal agonist during fingertip force production tasks. The vibration applied to the forearm surface could be not very effective for spindles of those deep muscles. In contrast, vibration of tendons is a proven effective method of muscle spindle activation; so, the VB_INT condition could in fact be optimal for excitation of spindle endings in the extrinsic deep flexors (compare to strong effects of vibration of the Achilles tendon compared to the same vibration applied over the belly of the triceps surae, Eklund 1972; Lackner and Levine 1979).

While vibration led to smaller indices of multi-finger synergies, these synergies were present across all three conditions (Figure 4). This observation suggests that multi-finger synergies during pressing tasks are not crucially dependent on loops involving muscle spindles and other sensory endings sensitive to vibration. This conclusion is compatible with hypotheses that synergies are based on feed-forward processes (Goodman and Latash 2006) as well as with those based on short-latency back-coupling loops within the central nervous system (Latash et al. 2005). A similar conclusion has recently been reached in another study (Zhou et al. 2013).

Possible involvement of subcortical structures in synergies

Vibration-induced signals from proprioceptors are likely to reach many levels of the central nervous system including supraspinal structures. Such effects are corroborated by the mentioned kinesthetic illusions produced by vibration as well as by the profound vibration effects on vertical posture (Eklund 1972). In particular, these signals are likely to reach the ventroposteriorlateral nucleus of the thalamus via the dorsal column pathway and brain stem nuclei. At the thalamic level, interactions with loops involving the basal ganglia and the cerebellum are highly likely. A series of recent studies have shown that subcortical disorders such as Parkinson’s disease and olivo-ponto-cerebellar atrophy are associated with larger indices of enslaving, lower synergy indices during multi-finger action, and smaller ASAs (Park et al. 2012, 2013). These findings are qualitatively similar to the main results of the current study. In other words, our subjects behaved under the vibration conditions as if they had suddenly developed a mild form of parkinsonism.

Note that overall patterns of performance, as reflected in such indices as MVC forces and time to peak of the force pulses, did not show significant changes under vibration, while patterns of finger interaction and coordination did. A similar discrepancy has been reported in the mentioned study of patients with early-stage Parkinson’s disease who showed major changes in the indices of finger interaction and coordination and only minor changes in the characteristics of overall multi-finger actions (Park et al. 2012). In contrast, patients after cortical stroke show a dramatically different picture: Their overall patterns of multi-joint movements are strongly affected on the contralesional side, while the structure of variance in the joint configuration space (similar to the synergy index in our study) is relatively unchanged (Reisman and Scholz 2003).

Taken together, the observations in patients with various disorders and the results of the current study corroborate the earlier hypothesis that, while general patterns of movements may be defined by cortical mechanisms, patterns of coordination within a redundant system depend more on the functioning of subcortical circuits (Park et al. 2012). This hypothesis is consistent with ideas on the role of distributed processing modules in the control of voluntary actions advanced by Houk (2005).