Effect of Prestimulus Alpha Power, Phase, and Synchronization on Stimulus Detection Rates in a Biophysical Attractor Network Model

Abstract

Spontaneous oscillations measured by local field potentials, electroencephalograms and magnetoencephalograms exhibit a pronounced peak in the alpha band (8–12 Hz) in humans and primates. Both instantaneous power and phase of these ongoing oscillations have commonly been observed to correlate with psychophysical performance in stimulus detection tasks. We use a novel model-based approach to study the effect of prestimulus oscillations on detection rate. A previously developed biophysically detailed attractor network exhibits spontaneous oscillations in the alpha range before a stimulus is presented and transiently switches to gamma-like oscillations on successful detection. We demonstrate that both phase and power of the ongoing alpha oscillations modulate the probability of such state transitions. The power can either positively or negatively correlate with the detection rate, in agreement with experimental findings, depending on the underlying neural mechanism modulating the oscillatory power. Furthermore, the spatially distributed alpha oscillators of the network can be synchronized by global nonspecific weak excitatory signals. These synchronization events lead to transient increases in alpha-band power and render the network sensitive to the exact timing of target stimuli, making the alpha cycle function as a temporal mask in line with recent experimental observations. Our results are relevant to several studies that attribute a modulatory role to prestimulus alpha dynamics.

Introduction

Alpha oscillations are a prominent feature of spontaneous cortical activity and manifest themselves as a clear peak in power spectra of electroencephalogram (EEG) (Berger, 1929; for review, see Klimesch et al., 2007), magnetoencephalogram (MEG) (Cohen, 1972; Hari and Salmelin, 1997), and local field potential (LFP) recordings (Bollimunta et al., 2008) in human and primate cortex. In the past, the rhythm was believed to be of exclusively thalamic origin (Andersen and Andersson, 1968). More recently however, cortical sources of alpha oscillations have also been found (Bollimunta et al., 2008). The alpha rhythm has commonly been observed during spontaneous and prestimulus conditions, where its power is either positively (Linkenkaer-Hansen et al., 2004; Zhang et al., 2008) or negatively (Thut et al., 2006; Hanslmayr et al., 2007; Romei et al., 2008) correlated with psychophysical performance, e.g., stimulus detection. LFP recordings have revealed that the laminar origin of the oscillatory source is likely to be a distinguishing factor between these two modulatory effects (Bollimunta et al., 2008, 2011; Mo et al., 2011).

In addition, the phase of alpha oscillations at the stimulus onset has also been found to modulate psychophysical performance (Busch et al., 2009; Mathewson et al., 2009), and as a result, the alpha cycle has been associated with a transition between relatively high and low excitation states. Consistently with this idea, cortical pyramidal cell activity has indeed been shown to be modulated by the phase of alpha oscillations (Haegens et al., 2011).

Despite this pronounced role of alpha in perception, little is known about the underlying neural mechanisms. Here, we adopt a computational approach to examine the effect of prestimulus alpha conditions on the performance of weak stimulus detection, which to the best of our knowledge has not been done before. To this end, we adapt our previously developed cortical attractor network model (Lundqvist et al., 2006), which exhibits two types of attractor states (Djurfeldt et al., 2008; Lundqvist et al., 2010). The default state operates as an attractor and manifests itself by unspecific low-rate firing with population oscillations in the alpha band. An external stimulus can transiently switch the network to an active state where one of several coding attractors is visited. Due to mechanisms of neural fatigue these attractors have finite life-time (Lundqvist et al., 2006). Their activation is accompanied by elevated firing in the corresponding neural ensemble and population oscillations in the gamma range. Our stimulus induced change of state is thus congruent with discrete firing rate changes (Bathellier et al., 2012) and stimulus induced alpha to gamma transitions (Fries et al., 2008) observed in vivo. We interpret the activation of a stimulated coding attractor as successful stimulus detection and study how the phase, power, and synchronization of ongoing alpha oscillations modulate performance.

Materials and Methods

Network model.

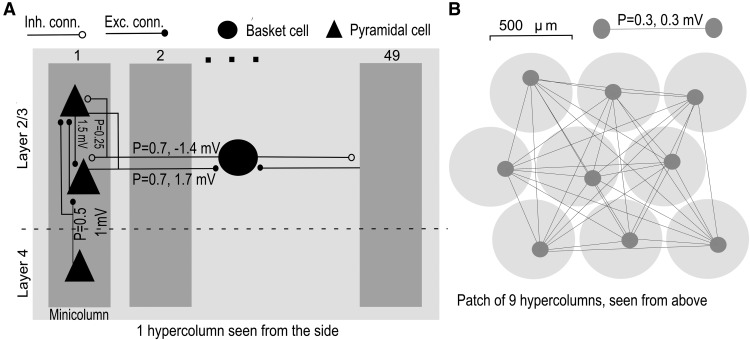
We used our biophysically detailed network model of cortical layer 2/3 (Lundqvist et al., 2006, 2010; Djurfeldt et al., 2008), implemented with version 7.1 of the parallel NEURON simulator (Carnevale and Hines, 2006). Analogously to our recent studies (Lundqvist et al., 2011, 2012), we removed the regular spiking nonpyramidal cells because they did not have any qualitative impact on the phenomena studied here and were not involved in generating the oscillatory dynamics. The model had a modular organization with hypercolumns and minicolumns (Fig. 1A). These minicolumns do not necessarily correspond to anatomical columns but rather to local subgroups of cells that tend to be connected (Yoshimura et al., 2005; Kampa et al., 2006) and coactive (Bathellier et al., 2012). Each layer 2/3 portion of a minicolumn contained 30 pyramidal cells (Peters and Yilmaz, 1993). Each minicolumn also included a rudimentary layer 4, with five pyramidal cells transmitting simulated sensory input in a feedforward fashion to layer 2/3. The connectivity was defined in terms of the probability of a cell in the presynaptic population to be connected to a cell in the postsynaptic population. Layer 4 cells were randomly connected to the layer 2/3 pyramidal cells in the same minicolumn with the probability P = 0.5, whereas the layer 2/3 cells formed recurrent connections (P = 0.25) within each minicolumn. All connections formed from one cell onto itself were removed. Every hypercolumn contained 49 such minicolumns and a cortical patch was composed of 16 hypercolumns. Within each hypercolumn there was a pool of 49 basket cells providing nonselective feedback inhibition across minicolumns. Within a given hypercolumn pyramidal cells could connect to all basket cells (with probability P = 0.7). The basket cells turn could connect to all pyramidal cells (P = 0.7). The local connectivity thus followed a scheme where layer 2/3 pyramidals sharing the same layer 4 input tended to form local assemblies, which were nonspecifically targeted by feedback inhibition (Yoshimura et al., 2005; Kampa et al., 2006). The hypercolumns were defined by the extent of this feedback inhibition and thus ∼0.5 mm in diameter (Yuan et al., 2011). Within this volume, the inhibitory feedback produced coherent alpha oscillations during the default state of the network and gamma oscillations during the active coding state.

Figure 1.

Network setup and connectivity. A, A detailed connectivity of a single hypercolumn, containing 49 minicolumns. B, A sketch of the long-range connectivity within a cortical patch, consisting of several hypercolumns (16 in a full patch). The numbers on the arrows specify the connectivity probabilities (see Materials and Methods) and postsynaptic potential size at resting potential of the postsynaptic cell.

Nonoverlapping cell assemblies were stored by means of selective long-range excitatory connections (Muir et al., 2011) between minicolumns belonging to separate hypercolumns (Fig. 1B). These connections were set up offline before simulations ensuring that each pattern contained one minicolumn from every hypercolumn.

In a control study, we used two connected cortical patches, one acting as a sensory patch and the other as an associative patch. They were identical copies with the only difference that the sensory patch connected with feedforward connections to the associative patch. Pyramidal cells in a minicolumn in the sensory patch only connected to pyramidal cells in the twin minicolumn in the associative patch (P = 0.1, 0.7 mV excitatory postsynaptic potential; EPSP). The distance between the patches was 1 cm.

In the detection tasks, 6 of 16 minicolumns belonging to a distributed cell assembly were selectively stimulated for 30 ms via layer 4 input cells. The latter were activated by Poisson spike trains and emitted 2–3 spikes during the 30 ms of stimulation. The minicolumns were spread out on a 2-D square grid (Fig. 1B). All conduction delays were calculated assuming a conduction speed of 0.5 m/s. Synaptic conductances and connectivity were set to comply with biological data (Thomson et al., 2002; cf. Lundqvist et al., 2006).

Cell and synapse model.

The cells included in the model network were pyramidal cells and soma targeting basket cells assumed to correspond to fast spiking cells. The neuron model was multicompartmental and conductance-based, following the Hodgkin–Huxley and Rall formalisms. The pyramidal cells were adapting, regular spiking and had six isopotential compartments (soma, basal dendritic, initial segment, and three apical dendritic). Interneurons were fast spiking with three compartments (soma, dendritic, and initial segment). The potential E in a compartment was calculated by integrating the currents:

where c_m is the capacitance of the membrane, g_m is the membrane leak conductance, and E_leak is the equilibrium potential of the leak current. Further, g_core is the conductance between connected compartments, which is dependent on compartmental cross section (equal for basal and apical dendrites, smaller for initial segment). g_ext is a nonspecific excitatory conductance with reversal potential E_ext, affecting the resting potential. I_channels is the active currents from the different ionic channels in the membrane of the compartment, including voltage-dependent Na⁺, K⁺, and Ca²⁺ channels as well as Ca²⁺-dependent K⁺ channels. I_syn is the current through glutamatergic and GABA-ergic synapses on the compartment. To avoid that all neurons have identical activation properties, which might contribute to potential spurious synchronization artifacts, we introduced moderate variability to some parameters (conductance of Na⁺ and K⁺ channels were normally distributed with 2% SD, Ca²⁺ conductance of Ca²⁺-dependent K⁺ channels, and compartment size were normally distributed with 10% SD). Pyramidal cells were strongly adapting due to the Ca²⁺-dependent K⁺ channels. The decay time constant for the Ca²⁺ was 1 s.

Pyramidal-to-pyramidal connections had both AMPA and voltage-dependent NMDA components, pyramidal to basket cell connections were purely AMPA-mediated whereas the inhibitory cells formed GABA_A-type synapses. The inhibitory basket cells connected to the soma whereas pyramidal cells targeted the second dendritic compartment. Time constants for the different synapses were τ_AMPA = 6 ms, τ_GABA = 6 ms and τ_NMDA = 150 ms. All pyramidal-to-pyramidal connections were depressing. Depression was multiplicative (Tsodyks et al., 1998), decreasing the synaptic conductance of the synapse by 25% with each incoming spike and decaying back to the initial conductance with the time constant of 700 ms.

Each pyramidal and basket cell received an independent noisy excitatory input through a low-conductance AMPA synapse activated by a simulated Poisson spike train with an average firing rate of 300 s⁻¹ (here called excitatory noise input). This source alone made the pyramidal cells spike at the rate of ∼1 s⁻¹. For complete cell parameters, synapse and model equations see Silverstein and Lansner (2011), where the same neuron as well as synapse models were used. For connectivity, cell numbers and noise input settings, however, please refer to this paper.

Bistability.

The network operated in a bistable regime (Amit and Brunel, 1997; Lundqvist et al., 2010) with two distinct activity states corresponding to attractors in the system. The default ground-state attractor exhibited characteristics of a fixed-point attractor. The coding attractors, on the other hand, had inherently finite life-times as a result of cellular adaptation and synaptic depression (Lundqvist et al., 2006). In consequence, firing rates in the coding state never reached a steady-state fixed-point-they built up at the onset and, after reaching a peak value they dropped off again. In this light, the term attractor is used in a loose sense and is motivated by the model's conceptual origin in and resemblance to a sparse and modular Hopfield network with a minicolumn in the model being represented by one nonspiking abstract model unit.

The bistable regime is present for a specific balance between excitation and inhibition (Amit and Brunel, 1997) but it does not require fine-tuning in the presented network (Lundqvist et al., 2010). The noncoding ground state was the default state of the network with all pyramidal cells active at a very low rate (∼0.1 s⁻¹), i.e., lower than for isolated cells only receiving excitatory noise input. This was a result of the feedback inhibition in the network. Following an external stimulation the network could visit the coding state, where one of the distributed cell assemblies, containing a single minicolumn in every hypercolumn, had significantly increased firing rates. The remaining 48 minicolumns in each hypercolumn belonging to other assemblies had reduced rates instead. We tested the upper limit of the bistability by progressively increasing excitatory synaptic weights until the network started to spontaneously activate the stored assemblies without any stimulation. The specific criterion adopted to verify whether the network's operating point did not exceed the upper limit was the lack of any activations throughout three 20 s simulations run with different random seeds, which implied that the ground state retained stability. The lower limit, on the other hand, was defined as the level of recurrent excitation below which even strong stimulation of all minicolumns in a pattern failed to elicit an activation of that pattern according to our criteria (see below, Detection rate). The bistability ratio, a measure of how robust the bistable dynamics was to permutations of the recurrent connectivity, was then defined as the upper limit of recurrent excitation divided by the lower limit. The weights set for the simulated detection tasks implied that the network operated approximately halfway between the upper and lower limit of the bistable range. The presented results did not depend on the exact weight setting as long as the network's operating point was above the lower limit and not too close to the upper limit to avoid its crossing when the excitatory noise input level was increased.

Detection rate.

To categorize a stimulus as detected (hit) or undetected (miss) we examined the distribution of spikes generated in layer 2/3 cells. The necessary condition for a hit was the activation of all the minicolumns in the partially stimulated cell assembly. The activation criterion for each minicolumn was the generation of at least 40% of all spikes from pyramidal cells in the respective hypercolumn within any sliding window of 150–200 ms in the period up to 500 ms after stimulation. The criterion was defined to optimally balance specificity and sensitivity, and to provide reliable early detection. The detection rate was defined as the percentage of successfully identified, i.e., detected, stimulations averaged over a set of 5 simulations. In each 100 s simulation 50 stimulations were applied at an average rate of 0.5 s⁻¹. To avoid the effect of entrainment of slower oscillations due to previous stimulations, a random temporal jitter drawn from zero-mean normal distribution with the SD of 0.3 ms was added to interstimulus intervals. In addition, we verified that the alpha phase at stimulation times was uniformly distributed. In the reminder of the paper, we use the term trial to refer to a time interval spanning an arbitrary period before and after a single stimulus. This way our simulation can be conceptualized as a series of 50 trials.

Synthetic local field potentials and their spectral analysis.

LFPs were estimated by calculating the average soma potential for all cells in a local population, i.e., one hypercolumn, similarly to the approach adopted by Ursino and La Cara (2006). They were produced at the sampling frequency of 1 kHz. Alpha oscillations were extracted from LFPs using a bandpass finite-impulse response filter in the forward and reverse directions to avoid any phase distortions. Then peaks and troughs were identified by inspecting local signal gradients. An analytic representation of the alpha rhythm was obtained by applying a Hilbert transform, which allowed for estimating its instantaneous phase and amplitude envelope.

To quantify the consistency of alpha phases corresponding to hits, Φ_h(k)^α(k = 1,.., N_h), and misses, Φ_m(k)^α(k = 1,.., N_m), a phase-locking index (PLI) was used (Lachaux et al., 1999):

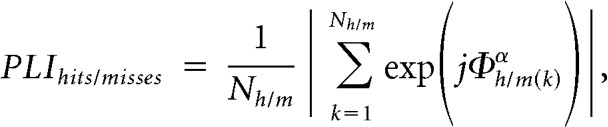where N_h/m is the number of stimulations classified as detected or undetected, respectively. In addition, a Rayleigh test for circular uniformity was applied. A PLI measure was also applied to quantify instantaneous phase consistency between hypercolumnar alpha oscillations.

The power spectra of LFP trials were obtained using the multitaper method (Thomson, 1982) with a family of orthogonal tapers produced by Slepian functions (Slepian and Pollak, 1961). For the broad alpha frequency range (8–14 Hz), the time window was set to fit 8 cycles (as a result, it was in the range from 0.6 s for the taper centered at 14 Hz to 1.0 s for the taper at 8 Hz) and the number of tapers amounted to 3. Overall, the time-bandwidth product was kept at 2.

Results

We used a previously developed network model with a hypercolumnar and minicolumnar structure, where competing cell assemblies were stored by long-range connections across hypercolumns (Fig. 1). Upon brief 30 ms stimulations these cell assemblies could produce a short-lived (∼300 ms) response in terms of elevated firing rates and gamma-like oscillations. Our focus was on prestimulus conditions favorable to the activation of such stimulated assemblies, associated here with successful detections of weak external stimuli. Before the stimulation onset the system was in its default ground state accompanied by alpha oscillations generated by the reciprocal interaction between recurrently connected pyramidal and basket cells, and manifested in the synthetic LFP (see Materials and Methods). Spiking of pyramidal cells receiving excitatory noise input activated the connected basket cells, which then in turn terminated the activity of the original pyramidal cells via inhibitory feedback. This interaction repeated in a cyclic fashion at the rate of ∼10 Hz. The rate was determined to some degree by the decay time constant of inhibition. More importantly however, it depended on how fast excitatory noise input reactivated the pyramidal cells and how quickly pyramidal cells activated the basket cells (Brunel and Wang, 2003).

Here we focused on functional consequences of the ongoing oscillatory dynamics. We studied the effect of oscillatory phase, power, and synchronization in the alpha band on the network's performance in detecting incoming stimuli. To this end we run 100-s-long simulations, each with 50 weak and brief external stimuli at the mean rate of 0.5 Hz.

Alpha phase at stimulus onset modulates detection rate

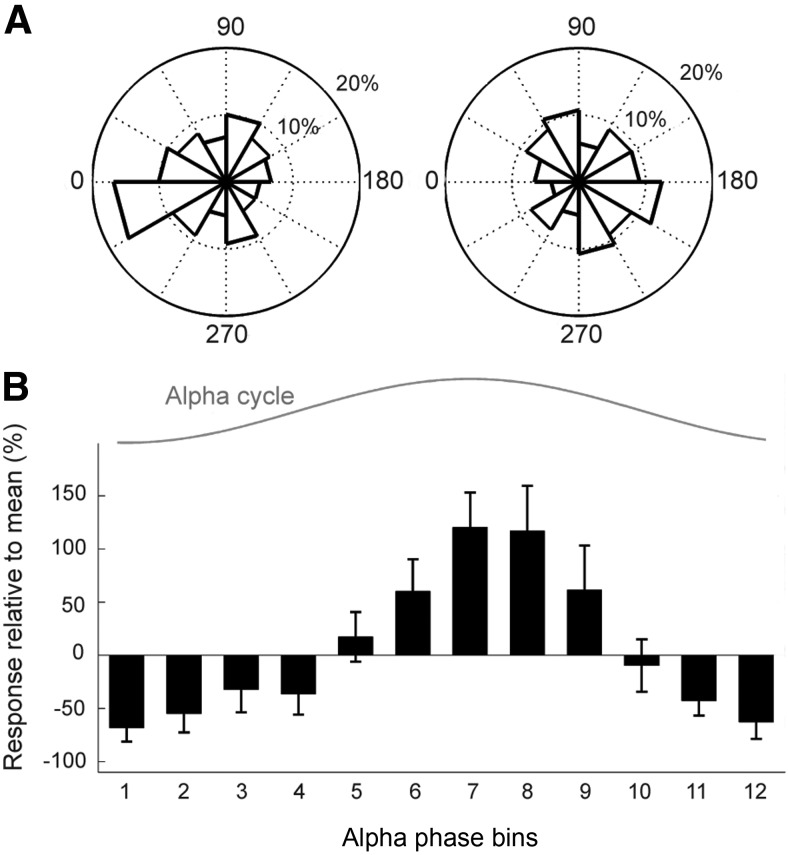
We closely examined the alpha rhythm dynamics in our network at the stimulus onset. We observed that the distribution of alpha phases corresponding to detected stimuli was concentrated near the trough of the alpha cycle (PLI_hits = 0.19; Rayleigh test, p = 0.048) whereas the alpha phases of undetected stimuli were distributed more broadly (PLI_misses = 0.10; p = 0.216, null hypothesis about uniformity could not be rejected) with the mean phase close to the peak of the alpha cycle (Fig. 2A). To obtain mechanistic insights into the observed phase modulation we dismantled the network by removing long-range excitatory recurrent connections, crucial for the attractor dynamics, and studied individual disconnected hypercolumns. A weak input in the form of a single synaptic event leading to a 1.5 mV EPSP was applied to all layer 2/3 pyramidal cells within one arbitrary minicolumn in each hypercolumn at different alpha phases, closely following a uniform distribution. Having inspected the spiking pattern in the alpha period subsequently to this stimulation, we observed that the number of spikes within an interval of one alpha cycle was strongly modulated by the phase of stimulation, as quantified by the linear-circular correlation coefficient of 0.95 (p < 0.004; Fig. 2B). We concluded that the long-range connections, although underlying the nonlinear attractor dynamics and critical for coordinated assembly activations, were not the key factor accounting for the observed phase effects. The main determinants were instead related to the nature of the ongoing alpha oscillations with windows of firing followed by windows of inhibition where the majority of cells were far below firing threshold. Because the time scale of the oscillation (∼100 ms) was much longer than the duration of the EPSPs (∼10 ms for he AMPA transmitted signal dominating the amplitude of the EPSP), presynaptic spiking events occurring around the inhibitory phase, i.e., the cycle trough, had limited impact on postsynaptic spiking activity.

Figure 2.

Modulatory effect of prestimulus alpha phase. A, Circular distribution (count presented as percentage; phase in degrees) of the alpha-rhythm phase at the time of stimulation for hits (left) with PLI_hits = 0.19 (null hypothesis about uniform phase distribution was rejected in Rayleigh test, p = 0.048) and misses (right) with PLI_hits = 0.10 (null hypothesis could not be rejected, p = 0.216). B, Spiking response to stimulation at different alpha phases, a relative change in the number of spikes elicited within the poststimulus interval of one alpha cycle with respect to the average number over all alpha phase bins (12 bins of the size of 30 degrees).

Dichotomous effect of alpha power on detection rate

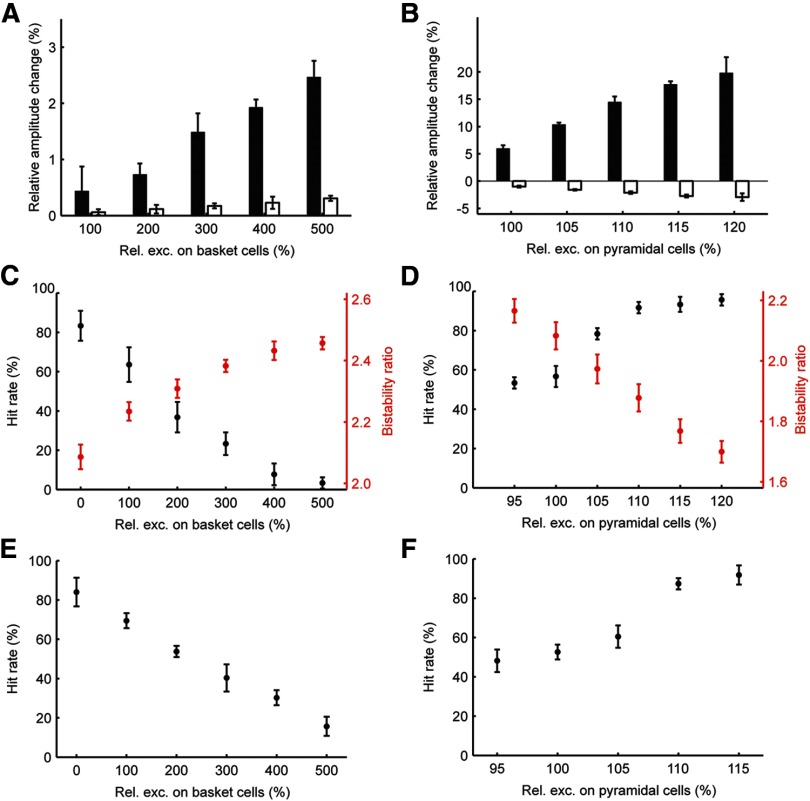
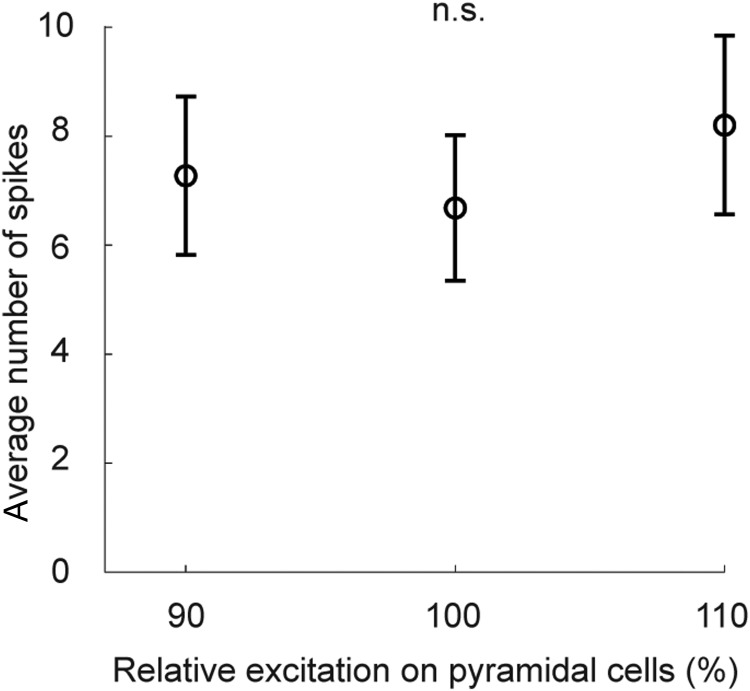
We found three simple mechanisms for modulating the power of alpha oscillations in the network: (1) by increased excitatory noise input to basket cells, or (2) to pyramidal cells, or (3) by synchronization of the oscillators across the network. In this section we deal with the first two. As a result of increasing the excitatory noise input to basket cells and making them more excitable, they fired in larger numbers in each oscillatory cycle, hence deepening the trough of the alpha cycle (Fig. 3A) due to the stronger synchronized inhibitory effect on the pyramidal cells. Analogously, strengthening the background excitation to the pyramidal population increased the number of pyramidal cells firing in each cycle, which deepened the wave trough as, again, more basket cells were recruited (Fig. 3B). These two ways of modulating alpha-band power had opposite effects on the observed detection rate: stronger diffuse excitation on the pyramidal population increased detection rate, whereas the opposite was observed when basket cells received elevated excitation (Fig. 3C,D). To investigate the mechanisms underlying these detection rate modulations we dismantled the network again and examined isolated hypercolumns. We then provided single 1.5 mV EPSPs to a single population, i.e., minicolumn, and studied its response at different levels of alpha power, generated by varying noise excitation onto pyramidal cells. However, we did not note any significant differences (repeated-measures ANOVA over 10 simulations; Fig. 4 illustrates the mean and SD of the number of generated spikes for three excitation levels) and concluded therefore that the reported detection rate modulations by alpha power could not be explained by response properties of individual minicolumns. Instead, they were found to depend on the nonlinear attractor dynamics. We observed that increasing the excitatory noise on basket cells stabilized the default ground state, whereas the opposite effect was obtained when the stronger noise input was applied to pyramidal cells (Fig. 3C,D). In other words, the network's operating point was shifted either further away or closer to the limit where individual cell assemblies would activate spontaneously, thus decreasing or increasing, respectively, the chance for a weak stimulation to activate the corresponding cell assembly.

Figure 3.

Detection rate modulation by alpha power. Alpha power could be enhanced by increased excitatory noise input on either basket cells (A) or pyramidal cells (B). In both cases, the alpha troughs are deepened by recruitment of more basket cells. The modulation of both troughs and peaks is shown as the relative percentage change with respect to the values corresponding to the lowest level of noise excitation. C, Enhancing alpha power by increasing excitatory noise on basket cells stabilizes the ground state (shown in red), as reflected by the rising bistability ratio (see Materials and Methods), and decreases detection rates (black). D, Enhancing alpha power by increasing excitatory noise on pyramidal cells destabilizes the ground state (red) and enhances detection rates (black). All error bars correspond to SDs of the means obtained in 250 trials. The same trends for hit rate modulation by the level of noise excitation on basket cells (E) and pyramidal cells (F) were obtained in a two-patch network (see Materials and Methods).

Figure 4.

Response properties of single minicolumns as a function of excitatory noise input to pyramidal cells. There is no statistical difference (null hypothesis cannot be rejected in a repeated-measures ANOVA test) between the average number of spikes generated in a single minicolumn at different levels of noise excitation (90, 100, and 110% of the nominal level) onto pyramidal cells. The mean number of spikes over 250 trials (stimulations) is depicted along with its SD.

Because stimulus detection is likely to involve the coactivation of multiple areas in vivo, we next tested whether similar behavior would occur in a hierarchy of two identical, connected cortical patches (see Materials and Methods, Network model). The lower-level “sensory” patch was activated by weak stimuli and had feedforward connections onto the higher-level “associative” patch. Detection was then tested in the associative patch during simultaneous excitatory noise manipulations to both patches. The same type of dichotomous behavior of alpha power and detection rate depending on the underlying mechanism of alpha-band power modulation was observed (Fig. 3E,F).

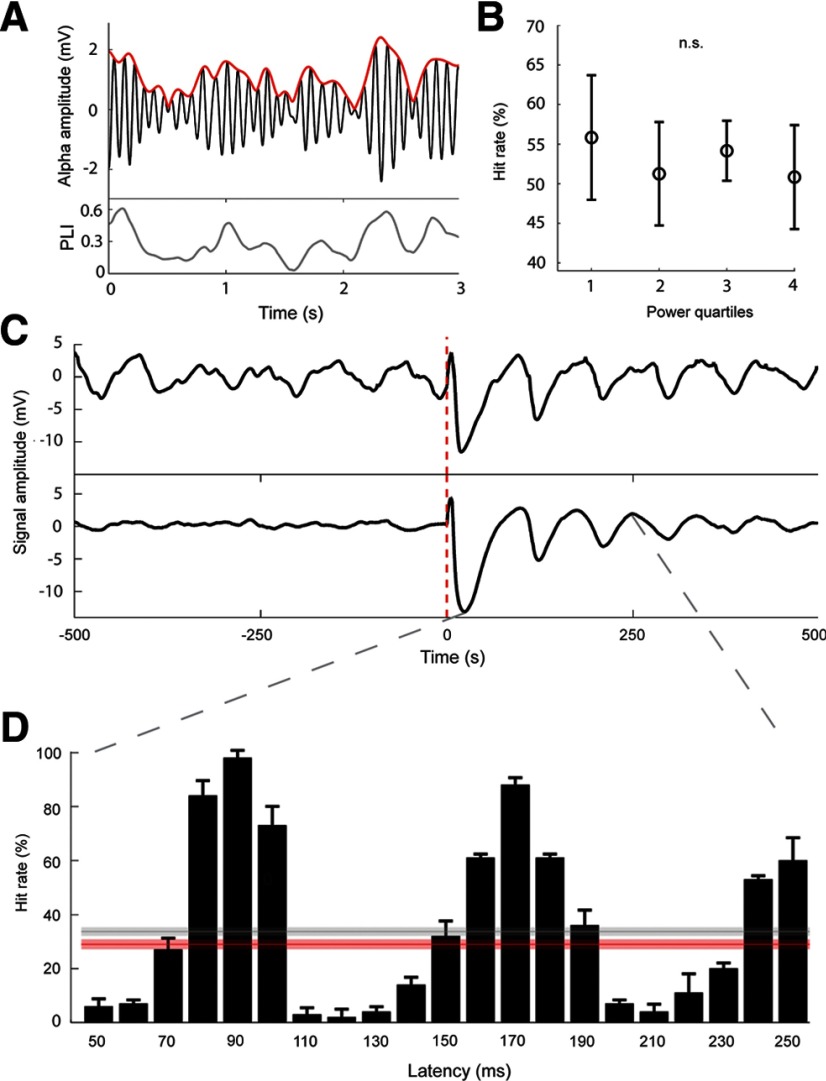
Reset signal synchronizes the network and provides a temporal mask for detection

The third mechanism modulating the alpha-band power in the ground state was synchronization of individual hypercolumns, acting as weakly coupled alpha oscillators. Increased phase synchronization implied enhanced amplitude of the alpha rhythm in the LFP averaged over the entire patch. Spontaneous fluctuations in alpha power occurred over the course of a single simulation and strongly correlated with the phase consistency (quantified with instantaneous PLI as discussed in Materials and Methods) among hypercolumnar alpha oscillators (Fig. 5A; Pearson's r = 0.83, p = 0.001). We investigated whether these spontaneous power fluctuations affected the detection rate by dividing trials into quartiles based on the prestimulus alpha-band power (200 ms time window ending at the stimulus onset) and calculating hit rates in each quartile (Fig. 5B). As a result, we did not find any significant modulatory effect (repeated-measures ANOVA over 5 simulations, overall 250 trials). We hypothesized that this was related to the alpha-phase dependence of detection rates mentioned earlier and that synchronization could modulate this effect without altering the average detection rate. This line of reasoning led us to another experiment, where weak external signals in the form of single 2.5 mV EPSPs were synchronously (within a 5 ms window) delivered to all pyramidal cells in the network at ∼5 s intervals. This resulted in a transiently enhanced alignment of the phases of the hypercolumnar alpha generators, since the cells were simultaneously forced toward the preferred spiking phase of the ongoing oscillations, which in turn led to alpha-band power bursts in the spatially averaged LFP. The effect of the phase reset was particularly apparent when a trial average was compared with a single-trial signal (Fig. 5C). Next, we stimulated single attractor cell assemblies following this reset at varying latencies ranging from 50 to 250 ms, probing the following alpha cycles. In line with our results on spontaneous fluctuations of the alpha-band phase synchronization, the overall detection rate averaged over different latencies was comparable to the performance level obtained with no reset (Fig. 5D, gray and red lines, respectively). However, we observed a strong modulatory effect of the stimulus latency on the detection rate, which corresponded to the alpha time scale. In particular, the network exhibited enhanced sensitivity to the stimuli applied around the time of postentrainment alpha peaks so that the increased detection performance was observed for two short windows of opportunity within the first 200 ms following the global reset: 80–100 ms and 160–180 ms, and suppressed detection rate was reported for the other latencies (Fig. 5D).

Figure 5.

Transient alpha phase alignment as a temporal mask for stimulus detectability. A, Alpha amplitude spontaneously fluctuates over the course of a trial (here 3 s interval is shown in the top) and is highly correlated (Pearson's r = 0.83, p = 0.001) with instantaneous interhypercolumn phase consistency (quantified using PLI and shown in the bottom). B, There is no statistical evidence for a modulatory effect of the spontaneous alpha-band power fluctuations on the hit rate. Null hypothesis about the equality of mean hit rates (shown with SDs, 250 trials) corresponding to different prestimulus alpha power quartiles cannot be rejected (repeated-measures ANOVA). C, A nonspecific stimulus applied to all pyramidal cells in the network at t = 0 resets and temporally aligns the phases of the ground-state oscillations in the network, resulting in a temporary enhancement of alpha amplitude seen in a single LFP trial (top) and reset-triggered LFP average over 250 trials (bottom). D, When a target stimulus is applied with a certain delay following the reset signal at t = 0, a strong detection rate modulation by this latency is observed (bars). The performance peaks correspond to the postreset alpha peaks. The average rate (gray line) is comparable with the mean rate in the control case without any reset signals (red line). The shaded areas illustrate the SDs of the corresponding average hit rates obtained over a set of five simulations, each consisting of 50 trials.

Discussion

We used a bistable attractor model to investigate the effect of prestimulus alpha oscillations on the stimulus detection performance. The alpha oscillations were generated in the default attractor state of the network characterized by low-rate diffuse activity and associated with the network's readiness to process incoming stimuli (Djurfeldt et al., 2008; Lundqvist et al., 2010). Following a selective stimulus the network could transiently visit the coding state, manifested as elevated spiking activity of the stimulated cell assembly at the expense of other assemblies embedded in the network. During the activation period, lasting ∼300 ms, the network instead produced gamma oscillations (Lundqvist et al., 2011, 2012). This is in line with the view that alpha controls access to the knowledge system and that alpha is attenuated for 200–500 ms after a stimulus which requires retrieval of memory content (Klimesch, 2012). Such assembly activations were viewed as hits in a simulated stimulus detection paradigm and we found that both phase and power of the ongoing alpha oscillations modulated the network's performance. An increase in prestimulus alpha-band power could either enhance or suppress the detection probability depending on the mechanism underlying the power modulation. Additionally, we observed that phase synchronization following an external reset signal could transiently boost the aforementioned phase effects.

Model simplifications

In an attempt to unify a large body of experimental findings we used a simplified network model. Here we discuss the extent and implications of our simplifications. Most importantly, the model only accounts for layers 2/3 in a single cortical patch. We concentrated on layer 2/3 when simulating stimulus detection for several reasons. First, stimulus-evoked firing has been reported to be sparser and carry more information about stimuli in the superficial layers (Sakata and Harris, 2009). Second, these layers appear as the main drivers of stimulus-evoked activity (Binzegger et al., 2009; Weiler et al., 2008). Thirdly, superficial recordings have revealed discrete, stimulus-evoked dynamics already in the early stages of cortical processing (Kenet et al., 2003; Bathellier et al., 2012), which also motivated us to use an attractor network. Finally, stimulus driven transitions from alpha to gamma oscillations, observed in our network and believed to reflect active cortical processing, are specific to layers 2/3 (Fries et al., 2008; Buffalo et al., 2011). In early sensory areas, the deep layers exhibit oscillations in the alpha frequency range even after such transitions. This deep alpha-band activity likely reflects pulsed inhibition involving the thalamo-cortical loop (Lorincz et al., 2009). Although we did not include this loop in the model, alpha oscillations have been reported to be coherent within a cortical column, i.e., between the superficial and deep layers (Bollimunta et al., 2008). Adding the deep layers should therefore have similar dynamical impact as increasing the drive on the interneurons in our network causing an increase in pulsed inhibition.

Here, we focused on stimulus detection in a single cortical patch. Because detection processes in vivo are likely to involve global activation of multiple cortical areas, we also demonstrated that our results translated to the case where two connected cortical patches were used without any loss of generality. In consequence, it can be expected that more elaborate networks of networks should display similar dynamics as long as each subnetwork is similar to the one presented here.

Alpha power modulations

Experimentally, prestimulus alpha power displays both positive (Linkenkaer-Hansen et al., 2004; Zhang et al., 2008) and negative (Hanslmayr et al., 2007; Romei et al., 2008) correlations with psychophysical performance. The combined use of LFP and multiunit recordings in monkeys has provided a possible explanation for these seemingly conflicting results (Bollimunta et al., 2008, 2011; Mo et al., 2011) with the cortical and laminar origin of alpha generation playing a central role. When the alpha was mainly produced in the deeper layers, as in low-level sensory cortices, alpha power had an inhibitory effect (Bollimunta et al., 2008, 2011). In the inferior temporal cortex, however, alpha was generated in the superficial layers and positively correlated with increased excitability (Bollimunta et al., 2008; Mo et al., 2011).

In our network, alpha oscillations were generated by rhythmic inhibition from the interneuron cell population, as arguably occurs in vivo (Klimesch et al., 2007; Jensen and Mazaheri, 2010; Haegens et al., 2011). By increasing tonic diffuse excitation on the inhibitory or excitatory populations, we obtained, respectively, negative or positive correlation between detection rate and the alpha-band power. Both these manipulations increased alpha power but had opposite effects on the stability of the ground-state attractor. Higher excitatory noise on the basket cells rendered the ground-state dynamics more stable (Amit and Brunel, 1997), thus making it more difficult to activate the cell assemblies. When the diffuse excitation on the pyramidal cells was upregulated, a less stable ground state facilitated the activation of a stimulated assembly. Alpha power was then positively correlated with pyramidal firing rates, consistently with the alpha generated in the inferior temporal cortex (Mo et al., 2011). In the case of a suppressive effect of alpha power on detection rate, we observed on the other hand that alpha power was negatively correlated with pyramidal firing rates, in accordance with recent experimental findings (Haegens et al., 2011). Attentional modulation could produce both phenomena by long-range excitatory connections generally targeting either pyramidal or inhibitory interneuron cells. The model predicts the presence of a population of fast spiking interneurons, which are phase-locked to ongoing alpha oscillations and phase-shifted relative to adjacent pyramidal cells. Furthermore, these cells should exhibit increased firing rates during periods of enhanced alpha power, regardless of whether the effect is inhibitory or excitatory. A reduction in alpha-band power as a result of active processing should however always be correlated with an increase in firing rates in a specific subset of pyramidal cells.

To the best of our knowledge, the modulatory effect of prestimulus alpha power on detection rates has not been previously modeled. However, in a related computational study by Jones et al. (2009), modulations of stimulus event-related potentials by alpha-band power were simulated. In addition, Rajagovindan and Ding (2011) obtained an effect of inverted U-shape dependence of evoked responses on prestimulus alpha power in their theoretical model, in line with some experimental evidence (Linkenkaer-Hansen et al., 2004; Zhang and Ding, 2010). Their model was constructed based on the assumption that alpha-band power modulates gain in a cortical network. We did not observe an inverted U-shape effect in our study but it could potentially be obtained by a combination of the inhibitory and excitatory effects described above.

Alpha phase as a temporal mask

On the micro-scale, the alpha cycle reflects periods of high and low excitability (Schroeder and Lakatos, 2009; Haegens et al., 2011). In our network, the means of the broadly distributed alpha phases corresponding to the time of stimulation differed by almost half a cycle between hits and misses, consistent with experimental results on the effect of alpha phase on stimulus detection probability (Busch et al., 2009; Mathewson et al., 2009; Busch and VanRullen, 2010).

The phase modulations observed in experimental data have fuelled discussions about functional implications of the alpha rhythm, which is hypothesized to provide timed (Klimesch et al., 2007) or pulsed inhibition (Haegens et al., 2011; Mathewson et al., 2011). Combined with the early finding that internal oscillations can become entrained to external stimuli (Adrian and Matthews, 1934), it has inspired the hypothesis that the brain can build up “attention energy” to rhythmic stimuli (Large and Jones, 1999). This idea has gained support from studies providing a regular chain of entraining stimuli followed by target stimuli at different time lags, presumably arriving at different phases of the entrained rhythm. The latency of the target stimuli had indeed a strong effect on the probability of its detection (Jones et al., 2002; Mathewson et al., 2010), as reflected in the enhanced hit rate for lags of ∼80 ms and suppressed for others. In our simulations, a reset signal caused the enhancement of alpha power due to global synchronization of the weakly coupled oscillators. This amplified the effect of the preferred alpha phase for hits demonstrated for the no-reset condition. The rate of detection of target stimuli applied 80–90 ms after the reset significantly increased, whereas for the other latencies around this peak it was suppressed below the no-reset control case. In consequence, we view such a reset signal as a powerful attentional gating mechanism that transiently applies a temporal mask. Such mask would be useful when the timing of relevant incoming stimuli is known, as during active sensory exploration, e.g., voluntary saccades. Interestingly, saccades have been shown to be phase-locked to alpha-like oscillations during free viewing (Ito et al., 2013). This part of our study also relates to a recent visual detection experiment in humans where a task irrelevant flash stimulus was followed by a rhythmic fluctuation in performance, likely due to entrainment of an 8 Hz rhythm (Landau and Fries, 2012). In our simulations, we also observed several peaks in the detection rate following the reset signal, closely matching the entrained rhythm.