Abstract
Motivation: By capturing various biochemical interactions, biological pathways provide insight into underlying biological processes. Given high-dimensional microarray or RNA-sequencing data, a critical challenge is how to integrate them with rich information from pathway databases to jointly select relevant pathways and genes for phenotype prediction or disease prognosis. Addressing this challenge can help us deepen biological understanding of phenotypes and diseases from a systems perspective.
Results: In this article, we propose a novel sparse Bayesian model for joint network and node selection. This model integrates information from networks (e.g. pathways) and nodes (e.g. genes) by a hybrid of conditional and generative components. For the conditional component, we propose a sparse prior based on graph Laplacian matrices, each of which encodes detailed correlation structures between network nodes. For the generative component, we use a spike and slab prior over network nodes. The integration of these two components, coupled with efficient variational inference, enables the selection of networks as well as correlated network nodes in the selected networks.
Simulation results demonstrate improved predictive performance and selection accuracy of our method over alternative methods. Based on three expression datasets for cancer study and the KEGG pathway database, we selected relevant genes and pathways, many of which are supported by biological literature. In addition to pathway analysis, our method is expected to have a wide range of applications in selecting relevant groups of correlated high-dimensional biomarkers.
Availability: The code can be downloaded at www.cs.purdue.edu/homes/szhe/software.html.
Contact: alanqi@purdue.edu
1 INTRODUCTION
With the popularity of high-throughput biological data such as microarray and RNA-sequencing data, many variable selection methods—such as lasso (Tibshirani, 1996) and elastic net (Zou and Hastie, 2005)—have been proposed and applied to select relevant genes for disease diagnosis or prognosis. Nevertheless, these approaches ignore invaluable biological pathway information accumulated over decades of research; hence, their selection results can be difficult to interpret biologically and their predictive performance can be limited by a small sample size of expression profiles. To overcome these limitations, a promising direction is to integrate expression profiles with rich biological knowledge in pathway databases. Because pathways organize genes into biologically functional groups and model their interactions that capture correlation between genes, this information integration can improve not only the predictive performance but also interpretability of the selection results. Thus, a critical need is to integrate pathway information with expression profiles for joint selection of pathways and genes associated with a phenotype or disease.
Despite their success in many applications, previous sparse learning methods are limited by several factors for the integration of pathway information with expression profiles. For example, group lasso (Yuan and Lin, 2007) can be used to utilize memberships of genes in pathways via a 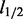 norm to select groups of genes, but they ignore pathway structural information. An excellent work by Li and Li (2008) overcomes this limitation by incorporating pathway structures in a Laplacian matrix of a global graph to guide the selection of relevant genes. In addition to graph Laplacians, binary Markov random field priors can be used to represent pathway information to influence gene selection (Li and Zhang, 2010; Stingo and Vannucci, 2010; Wei and Li, 2007, 2008). These network-regularized approaches do not explicitly select pathways. However, not all pathways are relevant, and pathway selection can yield insight into underlying biological processes. A pioneering approach to joint pathway and gene selection by Stingo et al. (2011) uses binary Markov random field priors and couples gene and pathway selection by hard constraints—for example, if a gene is selected, all the pathways it belongs to will be selected. However, this consistency constraint might be too rigid from a biological perspective: an active gene for cancer progression does not necessarily imply that all the pathways it belongs to are active. Given the Markov random field priors and the nonlinear constraints, posterior distributions are inferred by a Markov Chain Monte Carlo (MCMC) method (Stingo et al., 2011). But the convergence of MCMC for high-dimensional problems is known to take a long time.
norm to select groups of genes, but they ignore pathway structural information. An excellent work by Li and Li (2008) overcomes this limitation by incorporating pathway structures in a Laplacian matrix of a global graph to guide the selection of relevant genes. In addition to graph Laplacians, binary Markov random field priors can be used to represent pathway information to influence gene selection (Li and Zhang, 2010; Stingo and Vannucci, 2010; Wei and Li, 2007, 2008). These network-regularized approaches do not explicitly select pathways. However, not all pathways are relevant, and pathway selection can yield insight into underlying biological processes. A pioneering approach to joint pathway and gene selection by Stingo et al. (2011) uses binary Markov random field priors and couples gene and pathway selection by hard constraints—for example, if a gene is selected, all the pathways it belongs to will be selected. However, this consistency constraint might be too rigid from a biological perspective: an active gene for cancer progression does not necessarily imply that all the pathways it belongs to are active. Given the Markov random field priors and the nonlinear constraints, posterior distributions are inferred by a Markov Chain Monte Carlo (MCMC) method (Stingo et al., 2011). But the convergence of MCMC for high-dimensional problems is known to take a long time.
To overcome these limitations, we propose a new sparse Bayesian approach, called Network and NOde Selection (NaNOS), for joint pathway and gene selection. NaNOS is a sparse hybrid Bayesian model that integrates conditional and generative components in a principled Bayesian framework (Lasserre et al., 2006). For the conditional component, we use a graph Laplacian matrix to encode information of each network (e.g. a pathway) and incorporate it into a sparse prior distribution to select individual networks. For the generative component, we use a spike and slab prior distribution to choose relevant nodes (e.g. genes) in selected networks. For this hybrid model, we do not impose the hard consistency constraints used by Stingo et al. (2011). Furthermore, the prior distribution of our model does not contain intractable partition functions. This enables us to give a full Bayesian treatment over model parameters and develop an efficient variational inference algorithm to obtain approximate posterior distributions for Bayesian estimation. As described in Section 3, our inference algorithm is designed to handle both continuous and discrete outcomes.
Simulation results in Section 4 demonstrate superior performance of our method over alternative methods for predicting continuous or binary responses, as well as comparable or improved performance for selecting relevant genes and pathways. Furthermore, on real expression data for diffuse large B cell lymphoma (DLBCL), pancreatic ductal adenocarcinoma (PDAC) and colorectal cancer (CRC), our results yield meaningful biological interpretations supported by biological literature.
2 MODEL
In this section, we present the hybrid Bayesian model, NaNOS, for network and node selection. First, let us start from the classical variable selection problem. Suppose we have N independent and identically distributed samples 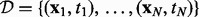 , where
, where 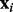 and ti are the explanatory variables and the response of the i-th sample, respectively. The explanatory variables can be various biomarkers, such as gene expression levels or single-nucleotide polymorphisms. Following the tradition in variable selection, we normalize the values of each variable so that its mean and standard deviation are 0 and 1, respectively. The response can be certain phenotype or disease status. We aim to predict the response vector
and ti are the explanatory variables and the response of the i-th sample, respectively. The explanatory variables can be various biomarkers, such as gene expression levels or single-nucleotide polymorphisms. Following the tradition in variable selection, we normalize the values of each variable so that its mean and standard deviation are 0 and 1, respectively. The response can be certain phenotype or disease status. We aim to predict the response vector 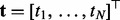 based on the explanatory variables
based on the explanatory variables 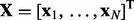 and to select a small number of variables relevant for the prediction. Because the number of variables (e.g. genes) is often much bigger than the number of samples, the prediction and selection tasks are statistically challenging.
and to select a small number of variables relevant for the prediction. Because the number of variables (e.g. genes) is often much bigger than the number of samples, the prediction and selection tasks are statistically challenging.
To reduce the difficulty of variable selection, we can use valuable information from networks, each of which contains certain variables as nodes and represents their interactions. For example, biological pathways cluster genes into functional groups, revealing various gene interactions. Based on M networks, we organize the explanatory variables 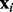 into M subvectors, each of which comprises the values of explanatory variables in its corresponding network. If a variable (i.e. a gene) appears in multiple networks (i.e. pathways), we duplicate its value in these networks. Note that networks here are exchangeable with graphs; we can use them to represent not only biological pathways but also linkage disequilibrium structures for genetic variation analysis.
into M subvectors, each of which comprises the values of explanatory variables in its corresponding network. If a variable (i.e. a gene) appears in multiple networks (i.e. pathways), we duplicate its value in these networks. Note that networks here are exchangeable with graphs; we can use them to represent not only biological pathways but also linkage disequilibrium structures for genetic variation analysis.
Our model is a Bayesian hybrid of conditional and generative models based on a general framework proposed by (Lasserre et al., 2006). The conditional component selects individual networks via ‘discriminative’ training, the generative component chooses relevant nodes in the selected networks and the two models are glued together through a joint prior distribution, so that the selected networks can guide node selection and, in return, the selected nodes can influence network selection.
Specifically, for the conditional model, we use a Gaussian data likelihood function for the continuous response
| (1) |
where  are regression weights, each of which represents the contribution of the corresponding node to the response, and τ is the precision parameter. For the unknown variance τ, we assign an uninformative diffuse Gamma prior,
are regression weights, each of which represents the contribution of the corresponding node to the response, and τ is the precision parameter. For the unknown variance τ, we assign an uninformative diffuse Gamma prior, 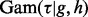 with
with 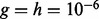 .
.
For the binary response, we use a logistic likelihood
| (2) |
where 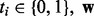 are classifier weights and
are classifier weights and 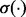 is the logistic function [i.e.
is the logistic function [i.e. 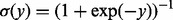 ]. Based on the M networks, we partition
]. Based on the M networks, we partition  into M groups, so that
into M groups, so that 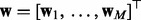 where
where 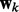 are the weights for the explanatory variables in the k-th network.
are the weights for the explanatory variables in the k-th network.
To incorporate the topological information of a network, we use its normalized Laplacian matrix representation. Specifically, given an adjacent matrix 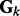 that represents the edges (i.e. interactions) between nodes in the k-th network, the normalized Laplacian matrix
that represents the edges (i.e. interactions) between nodes in the k-th network, the normalized Laplacian matrix 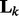 is defined as
is defined as
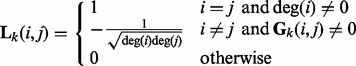 |
where 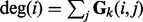 is the degree of the i-th node in the k-th network.
is the degree of the i-th node in the k-th network.
Based on the graph Laplacian matrices, we design the following mixture prior over 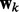 to select relevant networks:
to select relevant networks:
| (3) |
where 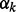 is a binary variable indicating whether the k-th network is selected,
is a binary variable indicating whether the k-th network is selected, 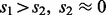 and
and 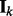 is an identity matrix. We set the hyperparameters s1 and s2 based on cross-validation (CV) in our experiments. To make sure
is an identity matrix. We set the hyperparameters s1 and s2 based on cross-validation (CV) in our experiments. To make sure 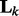 is strictly positive-definite, we add a diagonal matrix
is strictly positive-definite, we add a diagonal matrix 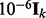 to
to 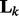 . In (3),
. In (3), 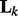 captures the correlation information between nodes in the k-th network. Note that if we replace
captures the correlation information between nodes in the k-th network. Note that if we replace 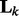 by
by 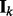 in the slab component, the prior
in the slab component, the prior 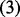 becomes a simple generalization of the classical spike and slab prior (George and McCulloch, 1997) for group selection. When
becomes a simple generalization of the classical spike and slab prior (George and McCulloch, 1997) for group selection. When 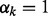 , the k-th network is selected and the elements of
, the k-th network is selected and the elements of 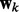 are encouraged to be similar to each other due to the Laplacian matrix
are encouraged to be similar to each other due to the Laplacian matrix 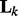 ; when
; when 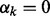 , because s2 is close to zero, the corresponding Gaussian prior prunes
, because s2 is close to zero, the corresponding Gaussian prior prunes 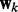 . We use a Bernoulli prior distribution to reflect the uncertainty in
. We use a Bernoulli prior distribution to reflect the uncertainty in 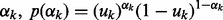 where
where 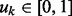 is the selection probability. Without any prior preference over selecting or pruning the k-th network, we assign a uniform prior over uk:
is the selection probability. Without any prior preference over selecting or pruning the k-th network, we assign a uniform prior over uk: 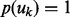 [i.e.
[i.e.  where
where 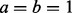 ].
].
To identify relevant nodes, we introduce a latent vector 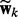 in the generative model for each network k, which is tightly linked to
in the generative model for each network k, which is tightly linked to 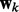 as explained later. We use a spike and slab prior:
as explained later. We use a spike and slab prior:
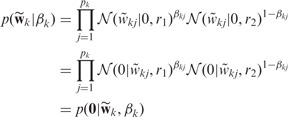 |
(4) |
where pk is the number of nodes in the k-th network, 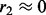 and
and 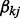 is a binary variable indicating whether to select the j-th node in the k-th network. We give
is a binary variable indicating whether to select the j-th node in the k-th network. We give 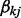 a Bernoulli prior,
a Bernoulli prior, 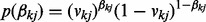 , and a uniform prior over vkj:
, and a uniform prior over vkj: 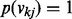 (i.e.
(i.e.  where
where 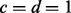 ). As shown above, the spike and slab prior
). As shown above, the spike and slab prior 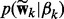 has the same form as
has the same form as 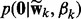 , which can be viewed as a generative model—in other words, the observation
, which can be viewed as a generative model—in other words, the observation 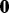 is sampled from
is sampled from 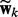 . This view enables us to combine the sparse conditional model for network selection with the sparse generative model for node selection via a principled hybrid Bayesian model.
. This view enables us to combine the sparse conditional model for network selection with the sparse generative model for node selection via a principled hybrid Bayesian model.
Specifically, to link the conditional and generative models together, we introduce a prior on 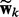 :
:
| (5) |
where the variance λ controls how similar 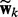 and
and 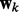 are in our joint model. For simplicity, we set
are in our joint model. For simplicity, we set 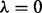 so that
so that 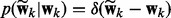 where
where 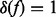 if f = 0 and
if f = 0 and 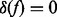 otherwise. The graphical model representation of the joint model is given in Figure 1.
otherwise. The graphical model representation of the joint model is given in Figure 1.
Fig. 1.
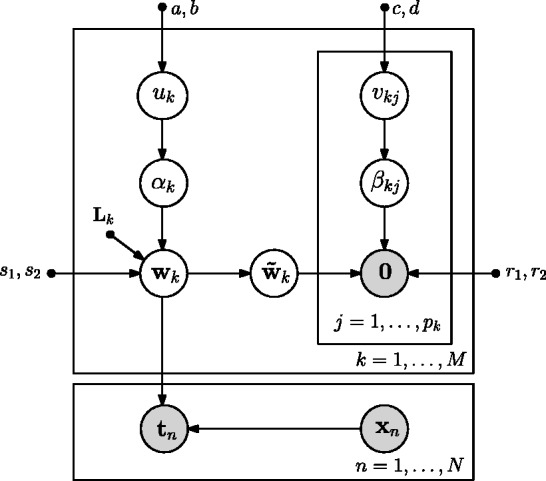
The graphical model representation of NaNOS
The network and node selections are consistent with each other in a probabilistic sense. If a network is pruned, all its node are removed. Because 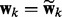 is enforced by the prior
is enforced by the prior 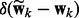 , when
, when 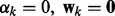 implies
implies 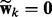 . As a result, the spike component in (4) will be selected for all the nodes in the k-th network (i.e.
. As a result, the spike component in (4) will be selected for all the nodes in the k-th network (i.e. 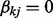 for
for 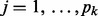 ) with a higher probability than the slab component. On the other hand, it is easy to see that if one or multiple nodes in a network are selected, then this network will be selected too. Note that if a node appears in multiple networks and is selected, our model will not force all the networks that contain this node to be chosen. The reason is that we duplicate the value of this node in the networks and treat their corresponding regression or classification weights as separate model parameters.
) with a higher probability than the slab component. On the other hand, it is easy to see that if one or multiple nodes in a network are selected, then this network will be selected too. Note that if a node appears in multiple networks and is selected, our model will not force all the networks that contain this node to be chosen. The reason is that we duplicate the value of this node in the networks and treat their corresponding regression or classification weights as separate model parameters.
3 ALGORITHM
In this section, we present the variational Bayesian algorithm for model estimation. Specifically, we develop the variational updates to efficiently approximate the posterior distribution of weights  , the network-selection indicators
, the network-selection indicators 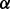 , the node-selection indicators
, the node-selection indicators 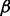 , the network- and node-selection probabilities
, the network- and node-selection probabilities  and
and  and the precision parameter τ for regression. Based on the posteriors of
and the precision parameter τ for regression. Based on the posteriors of 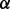 and
and 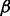 , we can decide which networks and nodes are selected.
, we can decide which networks and nodes are selected.
For regression, based on the model specification in Section 2, the posterior distribution of our model is
 |
(6) |
where 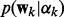 and
and 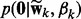 are defined in (3) and (4),
are defined in (3) and (4), 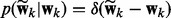 and Z is the normalization constant. For classification, the posterior distribution is similar to (6), except that we replace the Gaussian likelihood (1) by the logistic function (2) and remove the precision parameter τ and its prior for regression in (6).
and Z is the normalization constant. For classification, the posterior distribution is similar to (6), except that we replace the Gaussian likelihood (1) by the logistic function (2) and remove the precision parameter τ and its prior for regression in (6).
Classical Markov chain Monte Carlo methods can be applied to approximate the posterior distribution. However, given the high dimensionality of the parameters (e.g.  and α), it would take a long time for a sampler to converge. In practice, it is even difficult to judge the sampler’s convergence. Thus, we resort to a computationally efficient variational approximation to (6).
and α), it would take a long time for a sampler to converge. In practice, it is even difficult to judge the sampler’s convergence. Thus, we resort to a computationally efficient variational approximation to (6).
Specifically, we approximate the exact posterior distribution in (6) by a factorized distribution: Q(θ) = 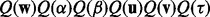 , where
, where 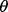 denotes all the latent variables. Note that, for classification, we do not have
denotes all the latent variables. Note that, for classification, we do not have 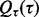 . Because we set
. Because we set 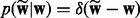 , we do not need a separate distribution
, we do not need a separate distribution 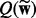 . To solve
. To solve 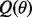 , we minimize the Kullback-Leibler (KL) divergence between the exact and approximate posterior distributions of
, we minimize the Kullback-Leibler (KL) divergence between the exact and approximate posterior distributions of 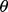 :
:
| (7) |
Applying coordinate descent for the minimization of (7), we obtain efficient updates for the variational distributions as described in the following sections. The updates are iterative: we update one of the variational distributions at a time while having all the other variational distributions fixed, and iterate these updates until convergence. Because these updates monotonically decrease the value of the KL divergence (7), which is lower bounded by zero, they are guaranteed to converge in terms of the KL value (Bishop, 2006).
3.1 Regression
The variational distributions for regression have the following forms:
| (8) |
| (9) |
| (10) |
| (11) |
| (12) |
| (13) |
Their parameters are iteratively updated as follows:
| (14) |
| (15) |
| (16) |
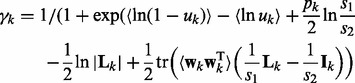 |
(17) |
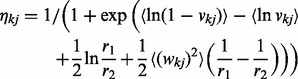 |
(18) |
| (19) |
| (20) |
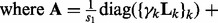
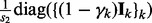
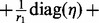
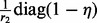 [note that
[note that 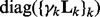 is a block-diagonal matrix],
is a block-diagonal matrix], 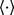 means expectation over the corresponding variational distribution, and the required moments in the above equations are
means expectation over the corresponding variational distribution, and the required moments in the above equations are
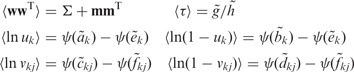 |
where 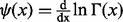 ,
, 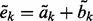 and
and 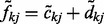 .
.
3.2 Classification
Compared with regression, the classification task is more challenging. Because of the logistic function (2), we cannot directly solve the variational distribution 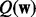 . Therefore, we use a lower bound proposed by (Jaakkola and Jordan, 2000) to replace the logistic function in the joint distribution:
. Therefore, we use a lower bound proposed by (Jaakkola and Jordan, 2000) to replace the logistic function in the joint distribution:
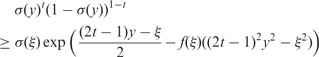 |
(21) |
where 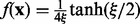 , and
, and 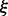 is a variational parameter. Note that the equality is achieved when
is a variational parameter. Note that the equality is achieved when 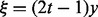 . Because the logarithm of the lower bound (21) is quadratic in
. Because the logarithm of the lower bound (21) is quadratic in 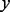 , it essentially converts the logistic function into a Gaussian form so that the variational inference becomes tractable.
, it essentially converts the logistic function into a Gaussian form so that the variational inference becomes tractable.
Combining the maximization of the lower bound (21) with the minimization of the KL divergence (7), we obtain the variational updates for classification. They are the same as those for the regression task, except for that 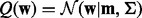 , now we have
, now we have
| (22) |
where 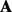 is the same as in the regression.
is the same as in the regression.
In addition, maximization of the lower bound of the logistic function gives the update for the variational parameter 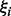 :
:
| (23) |
3.3 Computational cost
The computational cost of the proposed algorithm is dominated by (14) for regression and (22) for classification. For both cases, it takes 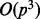 for matrix inversion to obtain
for matrix inversion to obtain  and
and 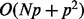 to obtain
to obtain  for each iteration. Thus, the total cost is
for each iteration. Thus, the total cost is 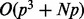 and, for most applications where
and, for most applications where 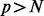 , it simplifies to
, it simplifies to 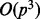 .
.
4 EXPERIMENTS
In this section, we apply NaNOS to synthetic and real gene expression data to select pathways (i.e. networks) and genes (i.e. nodes), and provide biological analysis of our results. We also compare NaNOS with alternative methods, including lasso (Tibshirani, 1996), elastic net (Zou and Hastie, 2005), group lasso (Jacob et al., 2009; Yuan and Lin, 2007), the network-constrained regularization approach [Li and Li (2008), henceforth ‘LL’] and the sparse Bayesian model with the classical spike and slab prior (George and McCulloch, 1997). For lasso and elastic net, we used the Glmnet software package (www-stat.stanford.edu/∼tibs/glmnet-matlab/). For group lasso, we treat each pathway as a group. To handle genes appearing in multiple pathways (i.e. groups), we first duplicated their expression levels for each group—as suggested by (Jacob et al., 2009)—and then used the SLEP software package (www.public.asu.edu/∼jye02/Software/SLEP/) for group lasso estimation. For the spike and slab model, we implemented variational inference similar to our updates in Section 3. Just as NaNOS, all these software packages use the Gaussian likelihood for regression and the logistic likelihood for classification. We used the default configuration of these software packages for the maximum number of iterations, initial values and the threshold for convergence. To tune regularization weights in lasso, group lasso and the LL approach, we conducted thorough 10-fold CV on training data (i.e. not using the test data) using a large computer cluster. The CV grids on the free parameters are summarized here: for lasso, 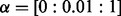 ; for elastic net,
; for elastic net, 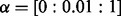 and
and 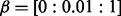 ; for group lasso (both regression and logistic regression),
; for group lasso (both regression and logistic regression), 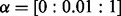 ; and for the LL approach,
; and for the LL approach, 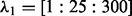 and
and 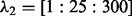 (we also did a second-level CV after we pruned the range of
(we also did a second-level CV after we pruned the range of 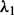 and
and 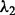 values based on the first-level CV). Finally, for NaNOS, the CV grids are
values based on the first-level CV). Finally, for NaNOS, the CV grids are 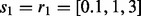 and
and 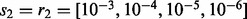 .
.
On the synthetic data for which we knew the true relevant pathways, we also compared NaNOS with a popular tool for gene set enrichment analysis (GSEA) (Mootha et al., 2003; Subramanian et al., 2005). We treated each pathway as a set, used GSEA’s default configuration and applied its suggested criterion false discovery rate (FDR) 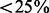 to discover enriched pathways. We then identified all the genes in these enriched pathways as target genes. Because GSEA cannot provide predictions on responses
to discover enriched pathways. We then identified all the genes in these enriched pathways as target genes. Because GSEA cannot provide predictions on responses  , we did not include it for comparison on the real data.
, we did not include it for comparison on the real data.
4.1 Simulation studies
We first compare all the methods on synthetic data in the following three experiments.
Experiment 1. We followed the first and second data generation models used by Li and Li (2008). Specifically, we simulated expression levels of 200 transcription factors (TFs), each controlling 10 genes in a simple tree-structured regulatory network, and assumed that four pathways—including all of their genes—have effect on the response  . We sampled the expression levels of each TF from a standard normal distribution,
. We sampled the expression levels of each TF from a standard normal distribution, 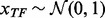 and the expression level of each gene that this TF regulates from
and the expression level of each gene that this TF regulates from 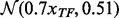 . This implies a correlation of
. This implies a correlation of 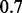 between the TF and its target genes.
between the TF and its target genes.
For the first model with the continuous response, we designed a weight vector for each pathway, 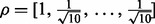 , corresponding to the TF and 10 genes it regulates, and then sampled
, corresponding to the TF and 10 genes it regulates, and then sampled  as follows:
as follows:
where 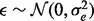 and
and 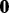 is a vector of all zeros.
is a vector of all zeros.
The second model is the same as the first one, except that the genes regulated by the same TF can have either positive or negative effect on the response  . Specifically, we set
. Specifically, we set
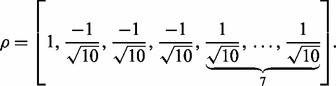 |
For the first and second models, the noise variance was set to be 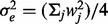 so that the signal-to-noise ratio was
so that the signal-to-noise ratio was 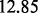 and
and 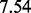 , respectively.
, respectively.
For the binary response, we followed the same procedure as for the continuous response to generate expression profiles  and the parameters
and the parameters  . Then we sampled
. Then we sampled  from (2).
from (2).
For each of the settings, we simulated 100 samples for training and 100 samples for test. We repeated the simulation 50 times. To evaluate the predictive performance, we calculated the prediction mean-squared error for regression and the error rate for classification. To examine the accuracy of gene and pathway selection, we also computed sensitivity and specificity and summarized them in the 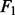 score, F1 = 2 >
score, F1 = 2 > 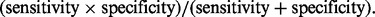 The bigger the
The bigger the 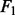 score, the higher the selection accuracy.
score, the higher the selection accuracy.
All the results are summarized in Figure 2, in which the error bars represent the standard errors. For all the settings, NaNOS gives smaller errors and higher 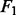 scores for gene selection than the other methods, except that, for classification of the samples from the second data model, NaNOS and group lasso obtain the comparable
scores for gene selection than the other methods, except that, for classification of the samples from the second data model, NaNOS and group lasso obtain the comparable 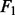 scores. All the improvements are significant under the two-sample t-test (P < 0.05). We also show the accuracy of group lasso, GSEA and NaNOS for pathway selection in Figure 5. Again, NaNOS achieves significantly higher selection accuracy. Because the LL approach was developed for regression, we did not have its classification results. While the LL approach uses the topological information of all the pathways, they are merged together into a global network for regularization. In contrast, using a sparse prior over individual pathways, NaNOS can explicitly select pathways relevant to the response, guiding the gene selection. This may contribute to its improved performance.
scores. All the improvements are significant under the two-sample t-test (P < 0.05). We also show the accuracy of group lasso, GSEA and NaNOS for pathway selection in Figure 5. Again, NaNOS achieves significantly higher selection accuracy. Because the LL approach was developed for regression, we did not have its classification results. While the LL approach uses the topological information of all the pathways, they are merged together into a global network for regularization. In contrast, using a sparse prior over individual pathways, NaNOS can explicitly select pathways relevant to the response, guiding the gene selection. This may contribute to its improved performance.
Fig. 2.

Prediction errors and 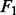 scores for gene selection in Experiment 1. ENet, S
scores for gene selection in Experiment 1. ENet, S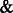 S and GLasso stand for elastic net, the spike and slab model and group lasso, respectively; Data 1 and 2 indicate the first and second data generation models
S and GLasso stand for elastic net, the spike and slab model and group lasso, respectively; Data 1 and 2 indicate the first and second data generation models
Fig. 5.
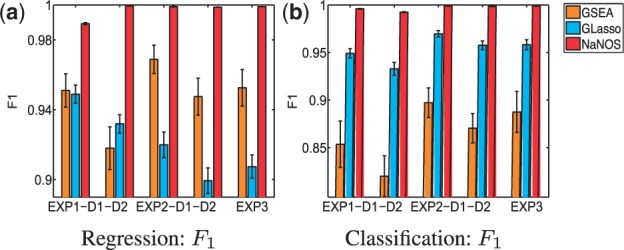
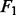 scores for pathway selection. ‘EXP’ stands for ‘Experiment’ and ‘D’ stands for ‘Data model’
scores for pathway selection. ‘EXP’ stands for ‘Experiment’ and ‘D’ stands for ‘Data model’
Experiment 2. For the second experiment, we did not require all genes in relevant pathways to have effect on the response. Specifically, we simulated expression levels of 100 TFs, each regulating 21 genes in a simple regulatory network. We sampled the expression levels of the TFs, the regulated genes and their response in the same way as in Experiment 1, except that we set
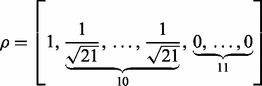 |
for the first data generation model and
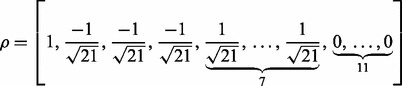 |
(24) |
for the second data generation model. Note that the last 11 zero elements in 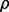 indicate that the corresponding genes have no effect on the response
indicate that the corresponding genes have no effect on the response  , even in the four relevant pathways.
, even in the four relevant pathways.
The results for both the continuous and binary responses are summarized in Figures 3 and 5. For regression based on the first data model, NaNOS and LL obtain the comparable 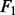 scores; for all the other cases, NaNOS significantly outperforms the alternative methods in terms of both prediction and selection accuracy (P < 0.05).
scores; for all the other cases, NaNOS significantly outperforms the alternative methods in terms of both prediction and selection accuracy (P < 0.05).
Fig. 3.

Prediction errors and 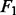 scores for gene selection in Experiment 2
scores for gene selection in Experiment 2
Experiment 3. Finally, we simulated the data as in Experiment 2, except that we replaced 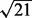 in the denominators in (24) with
in the denominators in (24) with 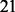 , to obtain a weaker regulatory effect of the TF. Again, as shown in Figures 4 and 5, NaNOS outperforms the competing methods significantly.
, to obtain a weaker regulatory effect of the TF. Again, as shown in Figures 4 and 5, NaNOS outperforms the competing methods significantly.
Fig. 4.

Prediction errors and 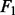 scores for gene selection in Experiment 3
scores for gene selection in Experiment 3
4.2 Application to expression data
Now we demonstrate the proposed method by analyzing gene expression datasets for the cancer studies of DLBCL (Rosenwald et al., 2002), CRC (Ancona et al., 2006) and PDAC (Badea et al., 2008). We used the probeset-to-gene mapping provided in these studies. For the CRC and PDAC datasets in which multiple probes were mapped to the same genes, we took the average expression level of these probes. We used the pathway information from the KEGG pathway database (www.genome.jp/kegg/pathway.html) by mapping genes from the cancer studies into the database, particularly in the categories of Environmental Information Processing, Cellular Processes and Organismal Systems.
4.2.1 Diffuse large B cell lymphoma
We used gene expression profiles of 240 DLBCL patients from an uncensored study in the Lymphoma and Leukemia Molecular Profiling Project (Rosenwald et al., 2002). From 7399 probes, we found 752 genes and 46 pathways in the KEGG dataset. The median survival time of the patients is 2.8 years after diagnosis and chemotherapy. We used the logarithm of survival times of patients as the response variable in our analysis.
We randomly split the dataset into 120 training and 120 test samples 100 times and ran all the competing methods on each partition. The test performance is visualized in Figure 6a. NaNOS significantly outperforms lasso, elastic net and group lasso. Although the results of the LL approach can contain connected subnetworks, these subnetworks do not necessarily correspond to (part of) a biological pathway. For instance, they may consist of components from multiple overlapped pathways. In contrast, NaNOS explicitly selects relevant pathways. Four pathways had the selection posterior probabilities larger than 0.95 and they were consistently chosen in all the 100 splits. Two of these pathways are discussed below.
Fig. 6.
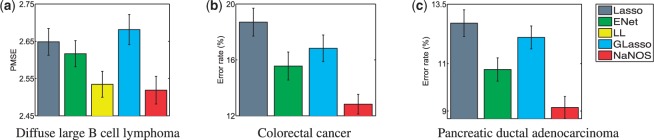
Predictive performance on three gene expression studies of cancer
First, NaNOS selected the antigen processing and presentation pathway. The part of this pathway containing selected genes is visualized in Figure 7a. A selected regulator CIITA was shown to regulate two classes of antigens MHC I and II in DLBCL (Cycon et al., 2009). The loss of MHC II on lymphoma cells—including the selected HLA-DMB, -DQB1, -DMA, -DRA, -DRB1, -DPA1, -DPB1 and -DQA1—was shown to be related to poor prognosis and reduced survival in DLBCL patients (Rosenwald et al., 2002). The selected MHC I (e.g. HLA-A,-B,-C,-G) was reported to be absent from the cell surface, allowing the escape from immunosurveillance of lymphoma (Amiot et al., 1998). And the selected Ii/CD74 and HLA-DRB were proposed to be monoclonal antibody targets for DLBCL drug design (Dupire and Coiffier, 2010).
Fig. 7.
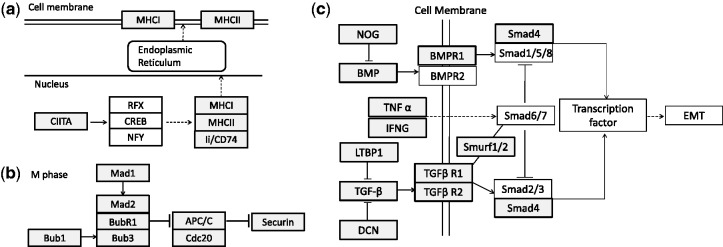
Examples of part of identified pathways. (a) The antigen processing and presentation pathway for DLBCL; (b) the cell cycle pathway for CRC; (c) the TGF-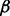 signaling pathway for PDAC. Shaded and unshaded boxes indicate selected and not selected genes, respectively
signaling pathway for PDAC. Shaded and unshaded boxes indicate selected and not selected genes, respectively
Second, NaNOS chose cell adhesion molecules (CAMs). Adhesive interactions between lymphocytes and the extracellular matrix (ECM) are essential for lymphocytes’ migration and homing. For example, the selected CD99 is known to be overexpressed in DLBCL and correlated with survival times (Lee et al., 2011), and LFA-1 (ITGB2/ITGAL) can bind to ICAM on the cell surface and further lead to the invasion of lymphoma cells into hepatocytes (Terol et al., 1999).
4.2.2 Colorectal cancer
We applied our model to a CRC dataset (Ancona et al., 2006). It contains gene expression profiles from 22 normal and 25 tumor tissues. We mapped 2455 genes from 22 283 probes into 67 KEGG pathways. The goal was to predict whether a tissue has the CRC or not and select relevant pathways and genes.
We randomly split the dataset into 23 training and 24 test samples 50 times and ran all the methods on each partition. The test performance is visualized in Figure 6b. Again, based on a two-sample t-test, NaNOS outperforms the alternatives significantly (P < 0.05). Three out of the four pathways with the selection posterior probabilities larger than 0.95 are discussed below. They were selected 20, 50 and 50 times in the 50 splits.
First, NaNOS selected the cell cycle pathway. This selection is consistent with the original result by Ancona et al. (2006). As shown in Figure 7b, NaNOS selected mitotic spindle assembly related genes. Specifically, Bub1 and Mad1 may regulate the checkpoint complex (MCC) containing Mad2, BubR1 and Bub3. The upregulated MCC may in turn inhibit ability of APC/C to ubiquitinate securin and further lead to mitotic event extension in CRC (Menssen et al., 2007). NaNOS also chose cyclin/CDK complexes, among which CycD/CDK4 overexpression is found in mouse colon tumor and CDK1, CDK2, CycE are increased in human CRC (Vermeulen et al., 2003; Wang et al., 1998). NaNOS further identified the minichromosome maintenance (MCM) complex—including MCM2 and MCM5—which are biomarkers for the CRC stage identification (Giaginis et al., 2009). Moreover, the selected TP53 and c-Myc are known to be closely related to CRC (Menssen et al., 2007).
Second, NaNOS chose the intestinal immune network for IgA production. A greatly increased level of IgA—as a result of long-term intestinal inflammation—can increase the chance of CRC (Rizzo et al., 2011) and serve as an effective biomarker for early diagnosis of CRC (Chalkias et al., 2011). Also, selected chemkines in this pathway, such as CXCR4 and CXCL12, may contribute to CRC progression (Sakai et al., 2012).
Third, NaNOS selected the cytokine–cytokine receptor interaction pathway as well as several well-known CRC-related molecules in this pathway. For instance, CXCL13 is a biomarker for stage II CRC prognosis (Agesen et al., 2012), CXCL10 dramatically increases with CRC progression (Toiyama et al., 2012) and IL10 secreted by CRC cells can accelerate tumor proliferation and be used for the prognosis of CRC progression (Toiyama et al., 2010).
4.2.3 Pancreatic ductal adenocarcinoma
This cancer dataset includes expression profiles from 39 PDAC and 39 normal subjects (Badea et al., 2008). By mapping 2781 genes from 54 677 probes into KEGG pathways, we obtained 67 pathways. Our goal was to predict whether a subject has the pancreatic cancer and select relevant pathways and genes. We randomly split the dataset into 39 training and 39 test samples 50 times and ran all the methods on each partition. The test performance is visualized in Figure 6c. Based on a two-sample t-test, NaNOS significantly outperforms lasso, elastic net and group lasso.
To investigate the sensitivity of NaNOS to the structural noise in the pathway database, we randomly chose 20, 50, 80 and 100% edges in each pathway and removed them. We tested NaNOS for each case and reported the average test error rate in the new Figure 8. As expected, the error rate of NaNOS gradually increases with more edges being removed because less topological information in pathways is available. But NaNOS still consistently outperformed all the alternative methods such as elastic net, the second best method on this dataset. This experiment demonstrates (i) that by exploiting subtle correlation information embedded in the pathway topology, NaNOS can boost its modeling power and predictive performance, and (ii) that NaNOS is robust to small perturbation in pathway topology.
Fig. 8.
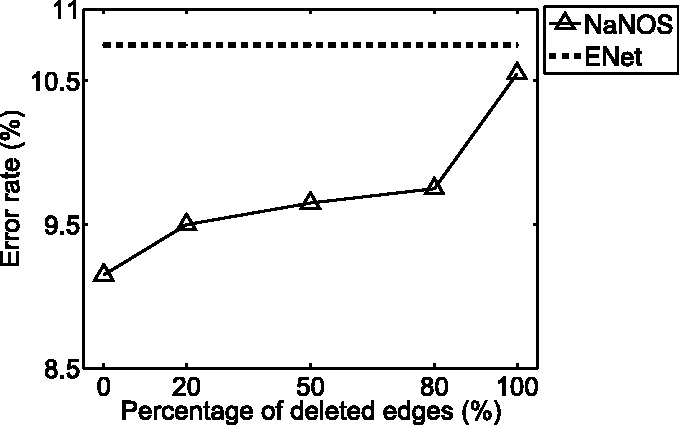
The predictive performance of NaNOS when the pathway structures are inaccurate. When more edges are randomly selected and removed from each pathway, the performance of NaNOS degrades smoothly, but still better than the competing methods
We also examined the impact of the important prior distributions on pathway and gene selection probabilities 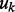 and
and 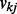 . As described in Section 2, we used the uniform priors [i.e. the Beta(1,1) prior] over
. As described in Section 2, we used the uniform priors [i.e. the Beta(1,1) prior] over 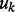 and
and 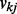 , indicating no prior preference over selecting a pathway or gene or not. The average test error based on the uninformative priors is
, indicating no prior preference over selecting a pathway or gene or not. The average test error based on the uninformative priors is 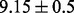 , as visualized in Figure 6c. If we change the prior to an informative one, Beta(1,10) (mean
, as visualized in Figure 6c. If we change the prior to an informative one, Beta(1,10) (mean 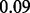 and standard deviation
and standard deviation 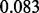 ) that strongly prefers sparsity, then the average test error increases slightly to
) that strongly prefers sparsity, then the average test error increases slightly to 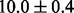 . This minor increase in error may stem from the oversparification caused by the sparsity prior that are overconfident (suggested by a small variance). Now if we use another informative prior Beta(10,1) (mean
. This minor increase in error may stem from the oversparification caused by the sparsity prior that are overconfident (suggested by a small variance). Now if we use another informative prior Beta(10,1) (mean 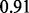 and standard deviation
and standard deviation 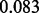 ) that strongly prefers dense—instead of sparse—estimation, then the average test error increases to
) that strongly prefers dense—instead of sparse—estimation, then the average test error increases to 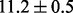 . This relatively larger error increase is exactly what we expected because now the wrong dense prior aims to select most pathways and genes. What is important is that, no matter which of these two informative priors we chose, NaNOS consistently outperformed lasso and group lasso in Figure 6c. Between these two extreme cases, if we use an uninformative or weak sparse prior [e.g. Beta(0.5,0.5)], we find that similar prediction error rates were obtained for NaNOS as in Figure 6c. The above analysis indicates that NaNOS is robust to the prior choice.
. This relatively larger error increase is exactly what we expected because now the wrong dense prior aims to select most pathways and genes. What is important is that, no matter which of these two informative priors we chose, NaNOS consistently outperformed lasso and group lasso in Figure 6c. Between these two extreme cases, if we use an uninformative or weak sparse prior [e.g. Beta(0.5,0.5)], we find that similar prediction error rates were obtained for NaNOS as in Figure 6c. The above analysis indicates that NaNOS is robust to the prior choice.
In addition to using the even splitting strategy with the same number of training and test samples, we also tested the performance of all the algorithms in another setting with more training samples—specifically, 62 training and 16 test samples. We repeated the random partitioning 50 times. The average error rates for NaNOS, elastic net, lasso and group lasso are 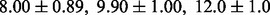 and
and 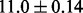 , respectively. Again, the two-sample t-test indicates that NaNOS outperforms the alternative methods significantly (P < 0.05).
, respectively. Again, the two-sample t-test indicates that NaNOS outperforms the alternative methods significantly (P < 0.05).
Three out of the five pathways with the selection posterior probabilities larger than 0.95 are discussed below. They were selected 35, 50 and 50 times in the 50 splits.
The first selected pathway was the transforming growth factor beta (TGF-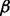 ) signaling pathway. It is essential in epithelial-mesenchymal transition (EMT)—a critical component for developmental and cancer processes—and related to PDAC (Krantz et al., 2012). The selected part of this pathway is visualized in Figure 7c. It shows that IFNG, TNF-
) signaling pathway. It is essential in epithelial-mesenchymal transition (EMT)—a critical component for developmental and cancer processes—and related to PDAC (Krantz et al., 2012). The selected part of this pathway is visualized in Figure 7c. It shows that IFNG, TNF-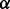 , LTBP1, DCN, TGF-
, LTBP1, DCN, TGF-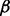 and its receptor TGF-
and its receptor TGF-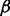 R1 were selected. The TGF-
R1 were selected. The TGF-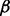 ligand—via its receptor—propagates the signal through phosphorylation of Smads including the selected Smad 4, which in turn translocate into the nucleus and interact with Snail TFs to regulate EMT (Krantz et al., 2012). The selected BMP ligand (i.e. BMP2) is bound to BMP R1 and R2 receptors to activate Smad1, which is in a protein complex including Smad4. Gordon et al. (2009) showed that in PANC-1 cell line, this protein complex mediates EMT partially by increasing the activity of MMP-2.
ligand—via its receptor—propagates the signal through phosphorylation of Smads including the selected Smad 4, which in turn translocate into the nucleus and interact with Snail TFs to regulate EMT (Krantz et al., 2012). The selected BMP ligand (i.e. BMP2) is bound to BMP R1 and R2 receptors to activate Smad1, which is in a protein complex including Smad4. Gordon et al. (2009) showed that in PANC-1 cell line, this protein complex mediates EMT partially by increasing the activity of MMP-2.
The second identified pathway was ECM–receptor interaction. It is associated with desmoplastic reaction, a hallmark in PDAC (Shields et al., 2012). In this pathway, NaNOS selected the integrin receptors—including ITGB1, ITGA2, ITGA3, ITGA5, ITGA6—and the ECM proteins—collagens including COL1A1 and COL1A2, and laminins including LAMC2 and LAMB3. Important interactions among them were revealed in a previous study by Weinel et al. (1992).
The third chosen pathway was CAMs. CAMs are pivotal in pancreatic cancer invasion by mediating cell–cell signal transduction and cell–matrix communication (Keleg et al., 2003). In this pathway, the selected molecules include calcium-dependent cadherin family molecules (CDH2, CDH3) and neural-related molecules (MAG); both of them have shown to be related to PDAC (Kameda et al., 1999; Keleg et al., 2003).
5 DISCUSSION
As shown in the previous section, the new Bayesian approach, NaNOS, outperformed the alternative sparse learning methods on both simulation and real data by a large margin. Now we discuss three factors that may contribute to the improved performance of NaNOS.
First, the spike and slab prior (3) and its generalization (4) in NaNOS separate weight regularization from the selection of variables (pathways or genes). Both the (generalized) spike and slab prior and elastic net can be viewed as mixture models in which one component encourages the selection of variables and the other helps remove irrelevant ones. However, unlike the elastic net where the weights over 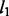 and
and 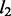 penalty functions are fixed, the spike and slab prior has the selection indicators over these two components estimated from data. When a variable is selected, the model has a Gaussian prior over its value (i.e. weight) that is equivalent to a
penalty functions are fixed, the spike and slab prior has the selection indicators over these two components estimated from data. When a variable is selected, the model has a Gaussian prior over its value (i.e. weight) that is equivalent to a 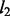 regularizer (as in ridge regression) and does not shrink the value of the selected variable as
regularizer (as in ridge regression) and does not shrink the value of the selected variable as 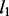 penalty would do. By contrast, lasso or elastic net, with a fixed mixture weight, has sparsity penalty over both pruned and selected variables, which can greatly shrink the values of selected variables and hurt predictive performance.
penalty would do. By contrast, lasso or elastic net, with a fixed mixture weight, has sparsity penalty over both pruned and selected variables, which can greatly shrink the values of selected variables and hurt predictive performance.
Second, NaNOS incorporates correlation structures encoded in pathways for variable selection. Specifically, it uses pathway structures into the extended spike and slab prior distribution to explicitly model the detailed relationships between correlated genes. In contrast, lasso and elastic net do not use this valuable correlation information in their models. By comparing prediction accuracies of NaNOS when 0 and 100% edges are removed from pathways (Fig. 8), we can see that the detailed correlation information captured by the pathway topology can greatly improve modeling quality.
Third, NaNOS has the capability of selecting both relevant pathways and genes due to its two-layer sparse structure. By contrast, with 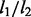 penalty, group lasso encourages the selection of all the genes in chosen pathways, leading to dense estimation. This may be undesirable in practice and deteriorate the predictive performance of group lasso. NaNOS enhances the flexibility of group lasso by conducting sparse estimation at both the pathway (or group) and gene levels. Meanwhile, our Bayesian estimation effectively avoids overfitting, a problem often plaguing flexible models.
penalty, group lasso encourages the selection of all the genes in chosen pathways, leading to dense estimation. This may be undesirable in practice and deteriorate the predictive performance of group lasso. NaNOS enhances the flexibility of group lasso by conducting sparse estimation at both the pathway (or group) and gene levels. Meanwhile, our Bayesian estimation effectively avoids overfitting, a problem often plaguing flexible models.
NaNOS has been applied to joint pathway and gene selection in this article. Inspired by the seminal works in (Chuang et al., 2007; Fröhlich et al., 2006; Srivastava et al., 2008; Zycinski et al., 2013), we can use NaNOS in a variety of biomedical applications where there are abundant high-dimensional biomarkers of individual samples and other information sources—for example, the gene ontology (GO) and protein–protein interaction networks information—that capture correlation in the high-dimensional space. Here we discuss two approaches to apply NaNOS when we have only GO or other group information without network topology. The first approach is to compute some distance or similarity scores between genes based on the GO information [e.g. following the approach by Srivastava et al. (2008)] and then estimate the network topology based on a network learning method, for example, graphical lasso (Friedman et al., 2008). With the estimated network topology, we can compute the graph Laplacian matrices and apply NaNOS to select genes and groups of genes. The second approach is to directly use the group membership information in NaNOS by replacing the graph Laplacian matrices with identity matrices. This approach becomes useful when we even do not have any information available to learn the network topology. As shown in Figure 8, even when all the edges were removed and we had only group information, NaNOS still outperformed the second best method, elastic net, in terms of prediction accuracy.
Funding: This work was supported by NSF IIS-0916443, NSF CAREER Award IIS-1054903, and the Center for Science of Information (CSoI), an NSF Science and Technology Center, under grant agreement CCF-0939370.
Conflict of Interest: none declared.
REFERENCES
- Agesen T, et al. ColoGuideEx: a robust gene classifier specific for stage II colorectal cancer prognosis. Gut. 2012;61:1560–1567. doi: 10.1136/gutjnl-2011-301179. [DOI] [PubMed] [Google Scholar]
- Amiot L, et al. Loss of HLA molecules in B lymphomas is associated with an aggressive clinical course. Br. J. Haematol. 1998;100:655–663. doi: 10.1046/j.1365-2141.1998.00631.x. [DOI] [PubMed] [Google Scholar]
- Ancona N, et al. On the statistical assessment of classifiers using DNA microarray data. BMC Bioinformatics. 2006;7:387. doi: 10.1186/1471-2105-7-387. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Badea L, et al. Combined gene expression analysis of whole-tissue and microdissected pancreatic ductal adenocarcinoma identifies genes specifically overexpressed in tumor epithelia. Hepatogastroenterology. 2008;55:2016–2027. [PubMed] [Google Scholar]
- Bishop CM. Pattern Recognition and Machine Learning (Information Science and Statistics) Secaucus, NJ: Springer-Verlag New York, Inc.; 2006. [Google Scholar]
- Chalkias A, et al. Patients with colorectal cancer are characterized by increased concentration of fecal hb-hp complex, myeloperoxidase, and secretory IgA. Am. J. Clin. Oncol. 2011;34:561–566. doi: 10.1097/COC.0b013e3181f9457e. [DOI] [PubMed] [Google Scholar]
- Chuang H, et al. Network-based classification of breast cancer metastasis. Mol. Syst. Biol. 2007;3:140. doi: 10.1038/msb4100180. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cycon K, et al. Alterations in CIITA constitute a common mechanism accounting for downregulation of MHC class II expression in diffuse large B-cell lymphoma (DLBCL) Exp. Hematol. 2009;37:184–194. doi: 10.1016/j.exphem.2008.10.001. [DOI] [PubMed] [Google Scholar]
- Dupire S, Coiffier B. Targeted treatment and new agents in diffuse large B cell lymphoma. Int. J. Hematol. 2010;92:12–24. doi: 10.1007/s12185-010-0609-6. [DOI] [PubMed] [Google Scholar]
- Friedman J, et al. Sparse inverse covariance estimation with the graphical lasso. Biostatistics. 2008;9:432–441. doi: 10.1093/biostatistics/kxm045. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fröhlich H, et al. International Joint Conference on Neural Networks. Los Alamitos, CA, USA: IEEE Computer Society; 2006. Kernel based functional gene grouping; pp. 3580–3585. [Google Scholar]
- George EI, McCulloch RE. Approaches for bayesian variable selection. Statistica Sinica. 1997;7:339–373. [Google Scholar]
- Giaginis C, et al. Clinical significance of MCM-2 and MCM-5 expression in colon cancer: association with clinicopathological parameters and tumor proliferative capacity. Dig. Dis. Sci. 2009;54:282–291. doi: 10.1007/s10620-008-0305-z. [DOI] [PubMed] [Google Scholar]
- Gordon K, et al. Bone morphogenetic proteins induce pancreatic cancer cell invasiveness through a Smad1-dependent mechanism that involves matrix metalloproteinase-2. Carcinogenesis. 2009;30:238–248. doi: 10.1093/carcin/bgn274. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jaakkola TS, Jordan MI. Bayesian parameter estimation through varational methods. Stat. Comput. 2000;10:25–37. [Google Scholar]
- Jacob L, et al. Proceedings of the 26th International Conference on Machine Learning. New York: 2009. Group lasso with overlap and graph lasso; pp. 433–440. [Google Scholar]
- Kameda K, et al. Expression of highly polysialylated neural cell adhesion molecule in pancreatic cancer neural invasive lesion. Cancer Lett. 1999;137:201–207. doi: 10.1016/s0304-3835(98)00359-0. [DOI] [PubMed] [Google Scholar]
- Keleg S, et al. Invasion and metastasis in pancreatic cancer. Mol. Cancer. 2003;2:14. doi: 10.1186/1476-4598-2-14. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Krantz S, et al. Contribution of epithelial-to-mesenchymal transition and cancer stem cells to pancreatic cancer progression. J. Surg. Res. 2012;173:105–112. doi: 10.1016/j.jss.2011.09.020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lasserre J, et al. IEEE Computer Society Conference on Computer Vision and Pattern Recognition. Vol. 1. Washington, DC, USA: IEEE Computer Society; 2006. Principled hybrids of generative and discriminative models; pp. 87–94. [Google Scholar]
- Lee S, et al. Clinicopathologic characteristics of CD99-positive diffuse large B-cell lymphoma. Acta. Haematol. 2011;125:167–174. doi: 10.1159/000322551. [DOI] [PubMed] [Google Scholar]
- Li C, Li H. Network-constrained regularization and variable selection for analysis of genomics data. Bioinformatics. 2008;24:1175–1182. doi: 10.1093/bioinformatics/btn081. [DOI] [PubMed] [Google Scholar]
- Li F, Zhang N. Bayesian variable selection in structured high-dimensional covariate space with applications in genomics. J. Am. Stat. Assoc. 2010;105:1202–1214. [Google Scholar]
- Menssen A, et al. c-MYC delays prometaphase by direct transactivation of MAD2 and BubR1: identification of mechanisms underlying c-MYC-induced DNA damage and chromosomal instability. Cell Cycle. 2007;6:339–352. doi: 10.4161/cc.6.3.3808. [DOI] [PubMed] [Google Scholar]
- Mootha VK, et al. PGC-1α-responsive genes involved in oxidative phosphorylation are coordinately downregulated in human diabetes. Nat. Genet. 2003;34:267–273. doi: 10.1038/ng1180. [DOI] [PubMed] [Google Scholar]
- Rizzo A, et al. Intestinal inflammation and colorectal cancer: a double-edged sword? World J. Gastroenterol. 2011;17:3092–3100. doi: 10.3748/wjg.v17.i26.3092. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rosenwald A, et al. The use of molecular profiling to predict survival after chemotherapy for diffuse large-B-cell lymphoma. N. Engl. J. Med. 2002;346:1937–1947. doi: 10.1056/NEJMoa012914. [DOI] [PubMed] [Google Scholar]
- Sakai N, et al. CXCR4/CXCL12 expression profile is associated with tumor microenvironment and clinical outcome of liver metastases of colorectal cancer. Clin. Exp. Metastasis. 2012;29:101–110. doi: 10.1007/s10585-011-9433-5. [DOI] [PubMed] [Google Scholar]
- Shields M, et al. Biochemical role of the collagen-rich tumour microenvironment in pancreatic cancer progression. Biochem. J. 2012;441:541–552. doi: 10.1042/BJ20111240. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Srivastava S, et al. A novel method incorporating gene ontology information for unsupervised clustering and feature selection. PLoS One. 2008;3:12. doi: 10.1371/journal.pone.0003860. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stingo FC, Vannucci M. Variable selection for discriminant analysis with Markov random field priors for the analysis of microarray data. Bioinformatics. 2010;27:495–501. doi: 10.1093/bioinformatics/btq690. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stingo FC, et al. Incorporating biological information into linear models: A Bayesian approach to the selection of pathways and genes. Ann. Appl. Stat. 2011;5:1978–2002. doi: 10.1214/11-AOAS463. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Subramanian A, et al. Gene set enrichment analysis: a knowledge-based approach for interpreting genome-wide expression profiles. PNAS. 2005;102:15545–15550. doi: 10.1073/pnas.0506580102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Terol M, et al. Expression of beta-integrin adhesion molecules in non-Hodgkin’s lymphoma: correlation with clinical and evolutive features. J. Clin. Oncol. 1999;17:1869–1875. doi: 10.1200/JCO.1999.17.6.1869. [DOI] [PubMed] [Google Scholar]
- Tibshirani R. Regression shrinkage and selection via the lasso. J. R Stat. Soc., B. 1996;58:267–288. [Google Scholar]
- Toiyama Y, et al. Loss of tissue expression of interleukin-10 promotes the disease progression of colorectal carcinoma. Surg. Today. 2010;40:46–53. doi: 10.1007/s00595-009-4016-7. [DOI] [PubMed] [Google Scholar]
- Toiyama Y, et al. Evaluation of CXCL10 as a novel serum marker for predicting liver metastasis and prognosis in colorectal cancer. Int. J. Oncol. 2012;40:560–566. doi: 10.3892/ijo.2011.1247. [DOI] [PubMed] [Google Scholar]
- Vermeulen K, et al. The cell cycle: a review of regulation, deregulation and therapeutic targets in cancer. Cell Prolif. 2003;36:131–149. doi: 10.1046/j.1365-2184.2003.00266.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang Q, et al. Altered expression of cyclin D1 and cyclin-dependent kinase 4 in azoxymethane-induced mouse colon tumorigenesis. Carcinogenesis. 1998;19:2001–2006. doi: 10.1093/carcin/19.11.2001. [DOI] [PubMed] [Google Scholar]
- Wei Z, Li H. A Markov random field model for network-based analysis of genomic data. Bioinformatics. 2007;23:1537–1544. doi: 10.1093/bioinformatics/btm129. [DOI] [PubMed] [Google Scholar]
- Wei Z, Li H. A hidden spatial-temporal Markov random field model for network-based analysis of time course gene expression data. Ann. Appl. Stat. 2008;2:408–429. [Google Scholar]
- Weinel R, et al. Expression and function of VLA-α2, -α3, -α5 and –alpha6-integrin receptors in pancreatic carcinoma. Int. J. Cancer. 1992;52:827–833. doi: 10.1002/ijc.2910520526. [DOI] [PubMed] [Google Scholar]
- Yuan M, Lin Y. Model selection and estimation in regression with grouped variables. J. R Stat. Soc., B. 2007;68:49–67. [Google Scholar]
- Zou H, Hastie T. Regularization and variable selection via the elastic net. J. R Stat. Soc., B. 2005;67:301–320. [Google Scholar]
- Zycinski G, et al. Knowledge Driven Variable Selection (KDVS) a new approach to enrichment analysis of gene signatures obtained from high-throughput data. Source Code Biol. Med. 2013;8:2. doi: 10.1186/1751-0473-8-2. [DOI] [PMC free article] [PubMed] [Google Scholar]


