Abstract
Motivation: Mass spectrometry (MS) instruments and experimental protocols are rapidly advancing, but de novo peptide sequencing algorithms to analyze tandem mass (MS/MS) spectra are lagging behind. Although existing de novo sequencing tools perform well on certain types of spectra [e.g. Collision Induced Dissociation (CID) spectra of tryptic peptides], their performance often deteriorates on other types of spectra, such as Electron Transfer Dissociation (ETD), Higher-energy Collisional Dissociation (HCD) spectra or spectra of non-tryptic digests. Thus, rather than developing a new algorithm for each type of spectra, we develop a universal de novo sequencing algorithm called UniNovo that works well for all types of spectra or even for spectral pairs (e.g. CID/ETD spectral pairs). UniNovo uses an improved scoring function that captures the dependences between different ion types, where such dependencies are learned automatically using a modified offset frequency function.
Results: The performance of UniNovo is compared with PepNovo+, PEAKS and pNovo using various types of spectra. The results show that the performance of UniNovo is superior to other tools for ETD spectra and superior or comparable with others for CID and HCD spectra. UniNovo also estimates the probability that each reported reconstruction is correct, using simple statistics that are readily obtained from a small training dataset. We demonstrate that the estimation is accurate for all tested types of spectra (including CID, HCD, ETD, CID/ETD and HCD/ETD spectra of trypsin, LysC or AspN digested peptides).
Availability: UniNovo is implemented in JAVA and tested on Windows, Ubuntu and OS X machines. UniNovo is available at http://proteomics.ucsd.edu/Software/UniNovo.html along with the manual.
Contact: kwj@ucsd.edu or ppevzner@ucsd.edu
Supplementary information: Supplementary data are available at Bioinformatics online.
1 INTRODUCTION
De novo peptide sequencing by tandem mass (MS/MS) spectrometry is a valuable alternative to MS/MS database search. In contrast to the database search approach that utilizes the information from proteome, the de novo sequencing approach attempts to identify peptides only using the information from the input spectrum. Hence, most de novo sequencing algorithms are based on the prior knowledge of the fragmentation characteristics (e.g. ion types and their propensities) of MS/MS spectra (Frank, 2009; Frank and Pevzner, 2005; Ma et al., 2003).
The fragmentation characteristics are highly dependent on the fragmentation method used to generate the spectrum. Among several fragmentation methods available, the collision-induced dissociation (CID) is the most commonly used method. Accordingly, the fragmentation characteristics of CID have been well studied compared with recently introduced fragmentation methods, such as electron transfer dissociation (ETD) and higher-energy collisional dissociation (HCD) (Barton and Whittaker, 2009; Breci et al., 2003; Huang et al., 2005; Johnson et al., 1987; Tabb et al., 2004; Wysocki et al., 2000). As a result, many de novo sequencing algorithms have been introduced for CID spectra; for example, PEAKS (Ma et al., 2003) and PepNovo+ (Frank, 2009; Frank and Pevzner, 2005) are the state of the art de novo sequencing tools for CID spectra.
Other fragmentation methods like ETD and HCD have a great potential for de novo sequencing. For example, for highly charged spectra, ETD provides better fragmentation and thus is better suited for de novo sequencing than CID (Swaney et al., 2008; Zubarev et al., 2008). Also, more complete fragmentation of peptide ions (especially in low mass regions) in HCD provides a better chance to obtain more accurate de novo reconstructions than CID (Chi et al., 2010; Olsen et al., 2007). Furthermore, modern mass spectrometers (e.g. LTQ-Orbitrap Velos) allow the generation of paired spectra (e.g. CID/ETD or HCD/ETD spectral pairs). Since CID (or HCD) and ETD spectra provide complementary information for peptide sequencing (Datta and Bern, 2009; He and Ma, 2010; Savitski et al., 2005), such spectral pairs (or even triplets) enable more accurate de novo sequencing.
Several de novo sequencing algorithms were recently presented to take advantage of those new fragmentation methods. For instance, Liu et al. (2010) proposed a de novo sequencing algorithm for ETD spectra, which is used by PEAKS. For HCD spectra, Chi et al. (2010) introduced a de novo sequencing tool, pNovo, that not only takes advantage of the high precision peaks in HCD spectra but also uses the information of abundant immonium and internal ions. In case of spectral pairs, Savitski et al. (2005) proposed a greedy algorithm (for CID/ECD spectral pairs) that significantly boosts the performance of de novo sequencing. Datta and Bern (2009) presented Spectrum Fusion, a de novo sequencing algorithm for CID/ETD spectral pairs. Spectrum Fusion constructs a combined spectrum from the input CID/ETD spectral pair using a Bayesian Network. It generates multiple de novo sequences using the combined spectrum and score them by the scoring function in ByOnic (Bern et al., 2007). He and Ma (2010) also presented a de novo sequencing algorithm, ADEPTS, for CID/ETD spectral pairs. Given a CID/ETD spectral pair, ADEPTS first finds 1000 candidate de novo sequences from each spectrum, using PEAKS. The total 2000 candidate sequences are then rescored against the input spectral pair, and the best-scoring peptide is reported.
While the above tools perform well for the spectra generated from the fragmentation method(s) that each tool targeted, they often generate inferior results for the spectra from other fragmentation methods. Moreover, if alternative proteases (e.g. LysC or AspN) are used for protein digestion, these tools may produce suboptimal results because different proteases often generate peptides with different fragmentation characteristics (Kim et al., 2010).
In case of the database search approach, Kim et al. (2010) recently introduced a universal algorithm MS-GFDB that shows a significantly better peptide identification performance than other existing database search tools such as Mascot + Percolator (Käll et al., 2007; Perkins et al., 1999). However, a universal de novo sequencing tool is still missing.
We present UniNovo, a universal de novo sequencing tool that can be generalized for various types (i.e. the combinations of the fragmentation method and the protease used to digest sample proteins) of spectra. The scoring function of UniNovo is easily trainable using a training dataset consisting of thousands of annotated spectra. All information needed for de novo sequencing are learned from the training dataset, and the running time for training is <5 h in a typical desktop environment. Currently, UniNovo is trained for CID, HCD and ETD spectra of trypsin, LysC or AspN digested peptides. We show that the performance of UniNovo is better than or comparable with PepNovo+, PEAKS and pNovo for various types of spectra.
One of the biggest challenges in de novo sequencing is to estimate the error rate of the resulting de novo reconstructions. Unlike MS/MS database search tools that commonly uses the target-decoy approach (Elias and Gygi, 2007; Nesvizhskii, 2010) to estimate the statistical significance of the peptide identifications, de novo reconstructions have rarely been subjected to a statistical significance analysis in the past.
Several de novo sequencing tools report the error rate of amino acid predictions (e.g. confidence scores in PEAKS), but this is often not sufficient because the overall quality of the sequence cannot be easily determined by the error rates of individual amino acid predictions. To our knowledge, only PepNovo+ reports the empirical probability that the output peptide is correct. PepNovo+ predicts the probabilities using logistic regression with multiple features of the reconstructions such as length and score, which are extracted from a training dataset consisting of hundreds of thousands of annotated spectra (Frank, 2009). However, PepNovo+ does not include an automated training procedure (that would allow to easily extend PepNovo+ for newly emerging mass spectrometry approaches) and is currently trained only for CID [Extending PepNovo+ beyond CID spectra requires training complex boosting-based re-ranking models for predicting peak ranks and rescoring peptide candidates. PepNovo+ training includes several manual steps and the availability of a very large corpus of training spectra (Ari Frank, personal communication, October 5, 2012)]. Thus, in case of non-CID fragmentation methods, it remains unclear how to obtain accurate error rate estimation for de novo reconstructions.
UniNovo estimates the probability that each reported reconstruction is correct, using simple statistics that are readily obtained from a small training dataset. We demonstrate that the estimation is accurate for all tested types of spectra (including CID, HCD, ETD, CID/ETD and HCD/ETD spectra of trypsin, LysC or AspN digested peptides). This allows UniNovo to automatically filter out low quality spectra.
2 METHODS
Similar to Kim et al. (2009a), we first describe the algorithm on a simplified model that assumes the following:
the masses of amino acids are integers (e.g. the mass of Gly is 57).
the m/z (mass to charge ratio) of peaks (in spectra) are integers.
the intensity of all peaks is 1.
only N-terminal charge 1 ions are considered (e.g. b, c, or
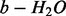 ions, but not y-ion series).
ions, but not y-ion series).the parent mass (the mass of the precursor ion) of a spectrum equals to the mass of the peptide that generated the spectrum.
While such a simplified model is impractical, we chose to introduce our algorithm on this model for better understanding of the algorithm on a more complex and realistic model. The algorithm on a more realistic model is described in the Supplementary section S2.
2.1 Terminology and definitions
Let A be the set of amino acids with (integer) masses m(a) for 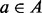 . A peptide
. A peptide
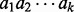 is a sequence of amino acids, and the mass of a peptide is the total mass of amino acids in the peptide. We represent a peptide
is a sequence of amino acids, and the mass of a peptide is the total mass of amino acids in the peptide. We represent a peptide 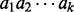 with mass n by a Boolean vector
with mass n by a Boolean vector 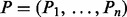 , where
, where 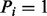 if
if 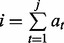 for
for 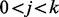 , and
, and 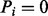 otherwise. If
otherwise. If 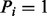 , we call a mass i a fragmentation site. For example, suppose there are two amino acids A and B with masses 2 and 3, respectively. Then, the peptide ABBA has the mass of
, we call a mass i a fragmentation site. For example, suppose there are two amino acids A and B with masses 2 and 3, respectively. Then, the peptide ABBA has the mass of 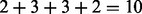 and is represented by a Boolean vector (0,1,0,0,1,0,0,1,0,0). The fragmentation sites of this peptide are, thus, 2, 5 and 8.
and is represented by a Boolean vector (0,1,0,0,1,0,0,1,0,0). The fragmentation sites of this peptide are, thus, 2, 5 and 8.
A spectrum is a list of peaks, where each peak is specified by an m/z. We represent a spectrum of parent mass n by a Boolean vector 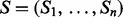 , where
, where 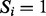 if the peak of m/z i (or simply the peak i) is present and
if the peak of m/z i (or simply the peak i) is present and 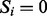 otherwise (Representing peptides and spectra as vectors allows us to represent the generation of spectra from peptides by simple vector operations.).
otherwise (Representing peptides and spectra as vectors allows us to represent the generation of spectra from peptides by simple vector operations.).
A peptide-spectrum match (PSM) is a pair 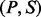 formed by a peptide P and a spectrum S. Given an integer δ called an ion type and a PSM
formed by a peptide P and a spectrum S. Given an integer δ called an ion type and a PSM 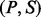 , we say a peak i is a δ-ion peak (with respect to P) if
, we say a peak i is a δ-ion peak (with respect to P) if 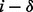 is a fragmentation site, that is,
is a fragmentation site, that is, 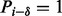 . In this model, the ion type can be any integer. In the connection to the experimental MS/MS spectra, ion types can represent common singly charged N-terminal ions; for example, the ion types 1 and −27 represent b and a ions, respectively.
. In this model, the ion type can be any integer. In the connection to the experimental MS/MS spectra, ion types can represent common singly charged N-terminal ions; for example, the ion types 1 and −27 represent b and a ions, respectively.
Given an integer f called a feature and a spectrum S, we say that a peak i satisfies f if another peak i + f is present in the spectrum, that is, 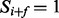 . For instance, a peak 30 satisfies a feature
. For instance, a peak 30 satisfies a feature 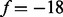 , if
, if 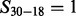 . In experimental spectra, various ions are often observed along with neutral losses (e.g. b-ion and
. In experimental spectra, various ions are often observed along with neutral losses (e.g. b-ion and 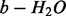 -ion) or with related ions (e.g. b-ion and a-ion). A feature describes the relation (the shift of m/z values in this simplified model) between two peaks that may correspond to a neutral loss or a mass gain/loss between related ions. For example, since we are dealing with only charge 1 ions, a water loss (from any ions) is represented by the feature
-ion) or with related ions (e.g. b-ion and a-ion). A feature describes the relation (the shift of m/z values in this simplified model) between two peaks that may correspond to a neutral loss or a mass gain/loss between related ions. For example, since we are dealing with only charge 1 ions, a water loss (from any ions) is represented by the feature 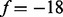 , and the mass gain from a-ion to b-ion is represented by the feature
, and the mass gain from a-ion to b-ion is represented by the feature 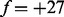 . The possible interpretations of selected features are found in Supplementary Tables S5–S37 in the Supplementary section S12.
. The possible interpretations of selected features are found in Supplementary Tables S5–S37 in the Supplementary section S12.
2.2 Peptide-spectrum generative model
We model how a peptide P of mass n generates a spectrum S. Apart from a 1-step generative model in Bandeira et al. (2008) or Kim et al. (2009a), we introduce a more adequate 2-step probabilistic model in which the dependency between different ions can be described.
Assume that we are given the set of ion types (the ion type set Δ) and the set of features (the feature set F). For simplicity, we consider the case where only one ion type 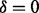 is in Δ and one feature f is in F. Given a peptide P, a partial-spectrum s is generated per each element Pi of P as follows: The probability that
is in Δ and one feature f is in F. Given a peptide P, a partial-spectrum s is generated per each element Pi of P as follows: The probability that 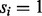 is given by α if
is given by α if 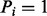 or by β otherwise (the first generation step). This first step can be characterized by a
or by β otherwise (the first generation step). This first step can be characterized by a 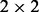 matrix called the ion type matrix (Fig. 1). When
matrix called the ion type matrix (Fig. 1). When 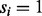 , the probability that
, the probability that 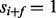 (i.e. the peak i satisfies f) is given by μ if
(i.e. the peak i satisfies f) is given by μ if 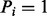 or ν otherwise (the second generation step). The second step is characterized by the feature-ion type matrix (Fig. 1) (Given
or ν otherwise (the second generation step). The second step is characterized by the feature-ion type matrix (Fig. 1) (Given 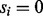 , the probability that
, the probability that 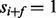 is assumed to be 0.). The second step can describe the dependency between different ions (or an ion and its neutral loss) from the same fragmentation site. If multiple ion types and multiple features are considered, the ion type matrix should be defined per ion type, and the feature-ion type matrix per ion type and per feature. The spectrum S is generated by taking elementwise OR operation for the generated partial-spectra s.
is assumed to be 0.). The second step can describe the dependency between different ions (or an ion and its neutral loss) from the same fragmentation site. If multiple ion types and multiple features are considered, the ion type matrix should be defined per ion type, and the feature-ion type matrix per ion type and per feature. The spectrum S is generated by taking elementwise OR operation for the generated partial-spectra s.
Fig. 1.

(a) The generation of a partial-spectrum s for Pi. One ion type 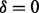 and one feature f are considered. The probability that
and one feature f are considered. The probability that 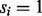 is given by α if
is given by α if 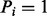 or by β otherwise. When
or by β otherwise. When 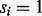 , the probability that
, the probability that 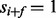 (i.e., the peak i satisfies f) is given by μ if
(i.e., the peak i satisfies f) is given by μ if 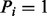 or by ν otherwise. The spectrum is generated by taking elementwise OR operation for generated partial-spectra for all elements of P. (b) The calculation of the fragmentation probability vector
or by ν otherwise. The spectrum is generated by taking elementwise OR operation for generated partial-spectra for all elements of P. (b) The calculation of the fragmentation probability vector 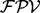 from a spectrum S (without knowing the peptide P that generated S). We consider one ion type
from a spectrum S (without knowing the peptide P that generated S). We consider one ion type 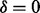 and two features f1 and f2. The events ‘a peak satisfies f1’ and ‘a peak satisfies f2’ are assumed to be independent. To derive
and two features f1 and f2. The events ‘a peak satisfies f1’ and ‘a peak satisfies f2’ are assumed to be independent. To derive 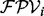 , first we examine which features the peak i satisfies in the spectrum S. Denote the features the peak i satisfies by H. Second, given H, we calculate the probability that
, first we examine which features the peak i satisfies in the spectrum S. Denote the features the peak i satisfies by H. Second, given H, we calculate the probability that 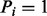 [using the probabilities given in ion type matrix and feature-ion type matrix—see the equation (1)]
[using the probabilities given in ion type matrix and feature-ion type matrix—see the equation (1)]
2.3 Training UniNovo
Since the ion type matrices and feature-ion type matrices fully describe the generation of a spectrum, in the training step, UniNovo learns these matrices from the training dataset (a set of PSMs). To define these matrices, the ion type set Δ and the feature set F should be formed. Using the offset frequency function introduced in Dancik et al. (1999), we collect frequently observed ion types and form the ion type set Δ. To form the feature set F, we define the feature frequency function with which one can count how many times each possible feature is observed in the training dataset (see the Supplementary section S1.2). Using the feature frequency function, we collect frequently observed features and form the feature set F. From here on, we only consider ion types in the ion type set Δ and features in the feature set F.
Next UniNovo learns the ion type and feature-ion type matrices that characterize the generative model of the PSMs in the training dataset. For example, 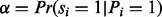 can be empirically determined if partial-spectra s are given. However, it is not clear how to decompose a spectrum S into partial-spectra s (since partial spectra may share peaks in the spectrum). As a compromise, we learn
can be empirically determined if partial-spectra s are given. However, it is not clear how to decompose a spectrum S into partial-spectra s (since partial spectra may share peaks in the spectrum). As a compromise, we learn 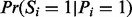 for estimation of α. Other probabilities are also empirically determined similarly by substituting the partial-spectra by the spectrum.
for estimation of α. Other probabilities are also empirically determined similarly by substituting the partial-spectra by the spectrum.
We emphasize that all the above probabilities can be learned from a small set of PSMs (e.g. 5000 PSMs per charge state are often sufficient to avoid overfitting; see the Supplementary section S15) even if there are many ion types in Δ and features in F because each probability is associated to an individual ion type or a combination of an ion type and a feature, not a combination of multiple ion types and multiple features.
Lastly, we compute the probability that a random element of a peptide vector is a fragmentation site, i.e., 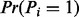 [When masses of amino acids are rounded to integers,
[When masses of amino acids are rounded to integers, 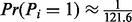 . However, if we consider more accurate amino acid masses (for the spectra of high resolution), this probability should be learned from the training dataset.]. This probability is called the prior fragmentation probability and denoted by p. The detailed description of UniNovo training is given in the Supplementary section S1.
. However, if we consider more accurate amino acid masses (for the spectra of high resolution), this probability should be learned from the training dataset.]. This probability is called the prior fragmentation probability and denoted by p. The detailed description of UniNovo training is given in the Supplementary section S1.
2.4 How to infer fragmentation sites from a spectrum
Given a spectrum S of parent mass n, our goal is to predict the fragmentation sites of the (unknown) peptide P that generated S. For simplicity, assume that there exists a single ion type 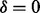 is in the ion type set Δ (but multiple features in the feature set F). Given a peak i, define H as the set of features that the peak i satisfies. Then the fragmentation sites are predicted by solving the following Bayesian inference problem.
is in the ion type set Δ (but multiple features in the feature set F). Given a peak i, define H as the set of features that the peak i satisfies. Then the fragmentation sites are predicted by solving the following Bayesian inference problem.
Fragmentation inference problem: Given the set of features H and Pi such that 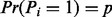 (the prior fragmentation probability), derive the posterior probability
(the prior fragmentation probability), derive the posterior probability 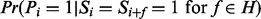 .
.
Since we assumed that there is only one ion type, we have only one ion type matrix. On the other hand, per each feature we have a feature-ion type matrix. Let 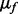 and
and 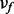 denote μ and ν associated to the feature f, respectively. If we can assume that all features are independent (i.e., the events ‘
denote μ and ν associated to the feature f, respectively. If we can assume that all features are independent (i.e., the events ‘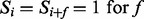 ’ are independent for
’ are independent for 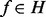 ), we obtain
), we obtain
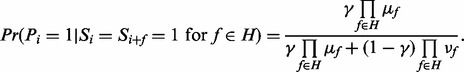 |
(1) |
where 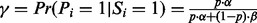 (see the Supplementary section S3 for derivation). Denote the obtained probability in (1) as
(see the Supplementary section S3 for derivation). Denote the obtained probability in (1) as 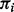 . We define a fragmentation probability vector (
. We define a fragmentation probability vector (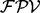 ) as a vector with n elements such that
) as a vector with n elements such that
| (2) |
for  , and
, and 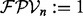 (see Fig. 1b).
(see Fig. 1b). 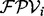 is an estimated probability that
is an estimated probability that 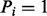 (see Supplementary Figs S3 and S4, blue bars). We use
(see Supplementary Figs S3 and S4, blue bars). We use 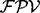 for the generation of de novo reconstructions.
for the generation of de novo reconstructions.
The equation (1) is based on a simplified model in which a single one ion type and multiple independent features are used. However, some features are known to be strongly dependent on each other (e.g. a feature describing a single water loss and a double water losses), and usually multiple ion types are present in the ion type set. Thus, in practice, per each peak, UniNovo automatically selects a small number of features (<10 out of thousands of features in the feature set) that are weakly correlated yet effective to determine the ion type of the peak. Assuming that the selected features are mutually independent, 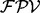 is calculated per ion type using the equation (1), and then the final
is calculated per ion type using the equation (1), and then the final 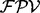 is given by a weighted summation of the
is given by a weighted summation of the 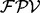 ’s of different ion types. Note that there are many possible combinations of features due to the large number of all the features in the feature set (even if the number of the features to calculate
’s of different ion types. Note that there are many possible combinations of features due to the large number of all the features in the feature set (even if the number of the features to calculate 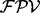 per peak is <10). Since different combinations of features are selected for different peaks, UniNovo is able to use more diverse relations between different ions as compared with other tools that typically use fixed dependencies between ions (e.g. PepNovo). The detailed description and an example of the feature selection method and the calculation of
per peak is <10). Since different combinations of features are selected for different peaks, UniNovo is able to use more diverse relations between different ions as compared with other tools that typically use fixed dependencies between ions (e.g. PepNovo). The detailed description and an example of the feature selection method and the calculation of 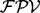 are given in the Supplementary section S3.
are given in the Supplementary section S3.
2.5 Generating de novo reconstructions
To generate de novo reconstructions, we first construct a spectrum graph (Dancik et al., 1999). Given a spectrum S of parent mass n from an unknown peptide P, the spectrum graph 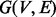 is defined as a directed acyclic graph whose vertex set V consists of 0 (the source), n (the sink) and integers i such that
is defined as a directed acyclic graph whose vertex set V consists of 0 (the source), n (the sink) and integers i such that 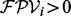 . Two vertices i and j are connected by an edge
. Two vertices i and j are connected by an edge 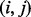 if j – i equals to the mass of an amino acid or the total mass of multiple amino acids (a mass gap). Any path from 0 (the source) to n (the sink) in a spectrum graph corresponds to a peptide (possibly containing mass gaps). We say that a vertex i is correct if
if j – i equals to the mass of an amino acid or the total mass of multiple amino acids (a mass gap). Any path from 0 (the source) to n (the sink) in a spectrum graph corresponds to a peptide (possibly containing mass gaps). We say that a vertex i is correct if 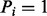 and an edge
and an edge 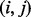 is correct if both vertices i and j are correct. We also say that a path r is correct if all vertices in r are correct. The length of a reconstruction is defined by the total number of amino acids and mass gaps in the reconstruction.
is correct if both vertices i and j are correct. We also say that a path r is correct if all vertices in r are correct. The length of a reconstruction is defined by the total number of amino acids and mass gaps in the reconstruction.
To score a de novo reconstruction, we use an additive (i.e., the score of a path is the sum of scores of vertices of the path) log likelihood ratio scoring [similar to Dancik et al. (1999)]. Given a vertex i, let 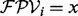 . The likelihoods of the following two hypothesis for the outcome
. The likelihoods of the following two hypothesis for the outcome 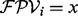 are tested: (i) the vertex i is correct and (ii) the vertex i is incorrect. Let
are tested: (i) the vertex i is correct and (ii) the vertex i is incorrect. Let 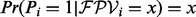 . Then, we have
. Then, we have
| (3) |
The score of the vertex i with 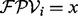 is defined by
is defined by 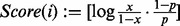 where
where  denotes the rounding to the nearest integer. Given a path r, the score of the path r is defined by
denotes the rounding to the nearest integer. Given a path r, the score of the path r is defined by 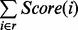 .
.
Since an additive scoring is used, top scoring reconstructions can be efficiently generated using a dynamic programming as in Dancik et al. (1999). We did not exclude symmetric paths in the spectrum graph that usually correspond to incorrect reconstructions. Considering only the antisymmetric paths would further enhance the performance of UniNovo (Chen et al., 2001).
After generating the reconstructions, a probability that each reconstruction is correct (termed the accuracy of the reconstruction) is predicted, using Hunter’s bound (Hunter, 1976) (see the Supplementary section S4 for the definition of the accuracy of reconstructions). Hunter’s bound can be calculated from relatively simple statistics that are readily learned from a small set of PSMs (about 5000 PSMs). Supplementary Figures S2 and S3 (green bars) in the Supplementary section S9 show that the accuracy of a reconstruction is a conservative estimate of the empirical probability of the reconstruction being correct.
3 RESULTS
3.1 Datasets
To benchmark UniNovo, we used 13 different datasets with diverse fragmentation methods (CID/ETD/HCD), digested with diverse proteases (trypsin, LysC and AspN), and having diverse charge states (see Table 1). We re-analyzed the spectral datasets (original datasets) from Albert Heck’s and Joshua Coon’s laboratories that were previously analyzed in Kim et al. (2010), Swaney et al. (2010) and Frese et al. (2011). The CID and ETD spectra in these original datasets were acquired in a hybrid linear ion trap/Orbitrap mass spectrometers (high MS1 resolution and low MS2 resolution). The HCD spectra have high MS1 and MS2 resolution. All spectra in the original datasets were identified by MS-GFDB (ver. 01/06/2012) (Kim et al., 2010) at 1% peptide-level FDR without allowing any modification except the carbamidomethylation of Cys (C + 57) as a fixed modification [In the Supplementary section S13, we also re-analyzed the dataset reported in Kim et al. (2009b) that contains doubly charged CID spectra identified using Sequest (Eng et al., 1994) and PeptideProphet (Keller et al., 2002).]. Out of all identified spectra, we selected 1000 spectra (or pairs of spectra) from distinct peptides randomly and formed the 13 datasets listed in Table 1. The unselected identified spectra (about 5000 to 20 000 spectra depending on the type of spectra) were used for the training of UniNovo. The peptide contained in the training dataset were not contained in the above 13 datasets. See the Supplementary section S10 for the detailed description of these datasets.
Table 1.
Summary of the datasets used for benchmarking
| Dataset | CID2 | CIDL2 | CIDA2 | ETD2 | ETD3 | ETDL3 | ETDL4 | ETDA3 | ETDA4 | HCD2 | HCD3 | CID/ETD2 | CID/ETD3 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Fragmentation | CID | CID | CID | ETD | ETD | ETD | ETD | ETD | ETD | HCD | HCD | CID/ETD | CID/ETD |
| Charge | 2 | 2 | 2 | 2 | 3 | 3 | 4 | 3 | 4 | 2 | 3 | 2 | 3 |
| Enzyme | Tryp | LysC | AspN | Tryp | Tryp | LysC | LysC | AspN | AspN | Tryp | Tryp | Tryp | Tryp |
| Average pep. length | 12.6 | 11.4 | 12.3 | 12.5 | 16.4 | 12.5 | 18.7 | 12.8 | 18.9 | 10.5 | 14.5 | 12.3 | 17.1 |
| UniNovo | * | * | * | * | * | * | * | * | * | * | * | * | |
| PepNovo+ | * | * | * | N/A | N/A | N/A | N/A | N/A | N/A | * | * | N/A | N/A |
| PEAKS | * | * | * | * | * | * | * | * | * | * | * | N/A | N/A |
| pNovo | N/A | N/A | N/A | N/A | N/A | N/A | N/A | N/A | N/A | * | * | N/A | N/A |
Note: Number of spectra (or spectral pairs) is 1000 for each dataset. While UniNovo is applicable to all datasets, other tools are only applicable to (or optimized for) datasets marked by ‘*’. PEAKS was not tested for HCD datasets.
3.2 Benchmarking UniNovo
We benchmarked UniNovo, PepNovo+ (ver. 3.1 beta) (Frank, 2009), PEAKS (ver. 5.3, online) (Ma et al., 2003) and pNovo (ver. 1.1) (Chi et al., 2010) using the datasets in Table 1. For each tool, we generated N de novo reconstructions per each spectrum for 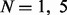 and 20. We say that a spectrum is correctly sequenced if at least one of N reconstructions generated from the spectrum is correct. To evaluate the performance of each tool, the number of correctly sequenced spectra and the average length of correct reconstructions were measured for each tool (Since mass gaps are allowed for reconstructions, often multiple correct reconstructions were reported for a spectrum. To calculate the average length of correct reconstructions, only the top scoring correct reconstruction was counted per a spectrum.).
and 20. We say that a spectrum is correctly sequenced if at least one of N reconstructions generated from the spectrum is correct. To evaluate the performance of each tool, the number of correctly sequenced spectra and the average length of correct reconstructions were measured for each tool (Since mass gaps are allowed for reconstructions, often multiple correct reconstructions were reported for a spectrum. To calculate the average length of correct reconstructions, only the top scoring correct reconstruction was counted per a spectrum.).
For UniNovo, the maximum number of mass gaps in a reconstruction was set to 2. UniNovo was tested for all datasets. For PepNovo+, also N top scoring reconstructions were generated per spectrum. PepNovo+ was used for CID2, CIDL2, CIDA2, HCD2 and HCD3 datasets. In case of PEAKS, we first generated 500 top scoring reconstructions per each spectrum. Then, for each reconstruction we converted amino acids with the local confidence <30% into mass gaps. Such conversion is adopted because PEAKS generates reconstruction without mass gaps while UniNovo and PepNovo+ generate reconstructions with up to two mass gaps. In this procedure, multiple reconstructions without mass gaps were often converted into the same reconstruction with mass gaps. The score of a converted reconstruction is defined as the highest score of the reconstructions before conversion. Out of the converted reconstructions, N top high scoring (distinct) ones were chosen and used for further analysis. PEAKS was tested for all datasets except for HCD2 and HCD3 datasets. For pNovo, N top scoring reconstructions were generated per a spectrum (pNovo also generates reconstructions without mass gaps. However, the conversion of reconstructions as in PEAKS could not be applied to pNovo because pNovo does not report any local score.). Only HCD2 and HCD3 datasets were analyzed by pNovo. The parameters of each tool for each dataset is provided in the Supplementary section S8.
We also indirectly compared UniNovo with MS-GFDB (Kim et al., 2010), as both tools were developed to analyze diverse types of spectra. We replaced the scoring function of UniNovo with that of MS-GFDB and generated reconstructions using the replaced scoring method. More precisely, the spectrum graph was generated by MS-GFDB per each spectrum, and the reconstructions were generated by UniNovo on that spectrum graph (instead of the spectrum graph generated by UniNovo). This generation method is specified by MS-GFDBScore. All experimental parameters for MS-GFDBScore were the same as for UniNovo.
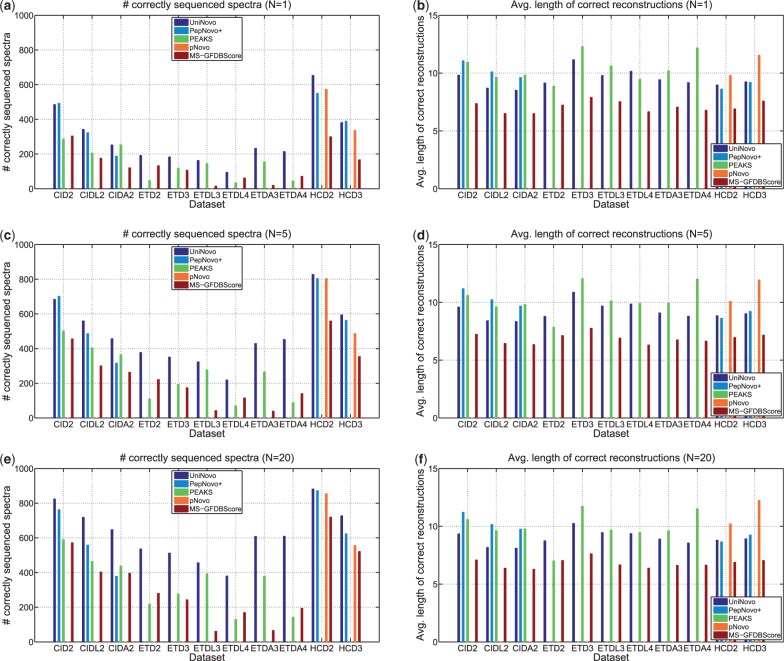
Figure 2 shows the comparison results for different datasets. UniNovo found the largest number of correctly sequenced spectra among all the tested tools in most datasets. In particular, for ETD spectra, UniNovo reported significantly more correctly sequenced spectra than PEAKS. For example, in case of ETD2 or ETDL4 dataset, the number of correctly sequenced spectra was more than twice for UniNovo than for PEAKS.
Fig. 2.
Comparison of de novo sequencing tools [as well as a database search tool MS-GFDB (Kim et al., 2010) tweaked for de novo sequencing]. Per each spectrum, N top scoring reconstructions were generated by UniNovo, PepNovo+ (Frank, 2009; Frank and Pevzner, 2005), PEAKS (Ma et al., 2003), pNovo (Chi et al., 2010) and MS-GFDBScore. MS-GFDBScore provides UniNovo with MS-GFDB’s scoring function. The number of reported reconstructions per a spectrum (N) is set to 1, 5 and 20. A reconstruction is correct if all the fragmentation sites of the reconstruction are correct, and a spectrum is classified as correctly sequenced if at least one of the reconstructions generated from the spectrum is correct. Figures on the left side (a, c and e) show the number of correctly sequenced spectra in each dataset, and figures on the right side (b, d and f) show the average length of the correct reconstructions
For CID spectra, UniNovo and PepNovo+ showed similar results. When N = 1, UniNovo and PepNovo+ found about the same number of correctly sequenced spectra in CID2 and CIDL2 datasets, but UniNovo found about 35% more correctly sequenced spectra than PepNovo+ in CIDA2 dataset.
While trypsin and LysC-digested peptides generate the spectra of similar fragmentation characteristics, AspN-digested peptides generate spectra with distinct fragmentation propensities. UniNovo worked well with AspN-digested peptides, but PepNovo+ showed suboptimal results for the spectra of AspN-digested peptides [Training of the parameters for the Bayesian network of PepNovo (Frank and Pevzner, 2005) for the CID spectra of AspN- or LysC-digested peptides would lead to better results; however, as mentioned above, the re-ranking models of PepNovo+ (Frank, 2009), which are crucial for the superior performance of PepNovo+ for CID tryptic spectra (see the Supplementary section S14), cannot be readily trained.]. The length of correct reconstructions for PepNovo+ was slightly longer than for UniNovo.
The results on HCD spectra also demonstrate that UniNovo finds the largest number of correctly sequenced spectra in general. The reconstructions reported by pNovo were, however, longer than those by UniNovo (and PepNovo+) by two to three amino acids. This suggests that UniNovo still has room for improvement for HCD spectra (e.g. introducing features better reflecting the high mass resolution and information from immonium or internal ions).
The results from UniNovo were superior to MS-GFDBScore in both terms of the number of correctly sequenced spectra and the average length of the correct reconstructions in all datasets.
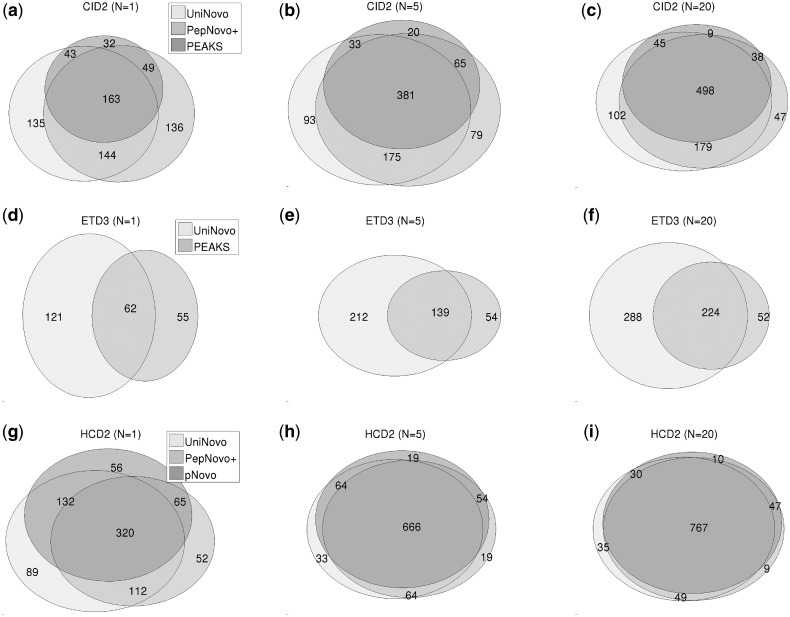
For each dataset, we drew the Venn diagrams of the correctly sequenced spectra (Fig. 3 and Supplementary Figs S5–S12) to see the overlaps of the spectra between different tools. For all datasets, the overlaps between different tools increase as N grows, as expected. Relatively small overlaps are observed for ETD spectra (as compared with CID or HCD spectra). It indicates that UniNovo may have been using some valuable features of ETD spectra missed by PEAKS (and vice versa) and suggests that combining UniNovo and PEAKS results may potentially lead to a promising de novo sequencing approach.
Fig. 3.
The Venn diagrams of the correctly sequenced spectra for CID2 (a–c), ETD3 (d–f) and HCD2 (g–i) datasets. For all datasets, the overlaps between different tools increase as N grows, as expected. Relatively small overlaps are observed for ETD spectra when compared with CID or HCD spectra. The Venn diagrams for other datasets are found in Supplementary Figures S5–S12 in the Supplementary section S11
While the above results measure the sequence level accuracy, they do not directly show the amino acid level precision or recall. To measure the amino acid level precision and recall, the top scoring reconstruction was generated per spectrum for each tool (i.e. N = 1). For this experiment, MS-GFDB was not tested, and the reconstructions of PEAKS were not converted using the local confidence. From the generated reconstructions, the number of (predicted) fragmentation sites and the number of correct fragmentation sites are counted. Also, since the spectra are annotated, we can count the number of all fragmentation sites in test sets. The precision and recall are defined by
| (4) |
| (5) |
Figure 4 shows the precision and recall values of the tested tools for different datasets. For all datasets, UniNovo showed the highest precision value. But the recall values of UniNovo tended to be lower than others in particular for CID spectra. For ETD2 and ETDL4 datasets, UniNovo had higher precision and recall than PEAKS. These observations are consistent with the sequence level results above; higher precision of UniNovo resulted in more accurate reconstructions, and lower recall resulted in shorter reconstructions.
Fig. 4.
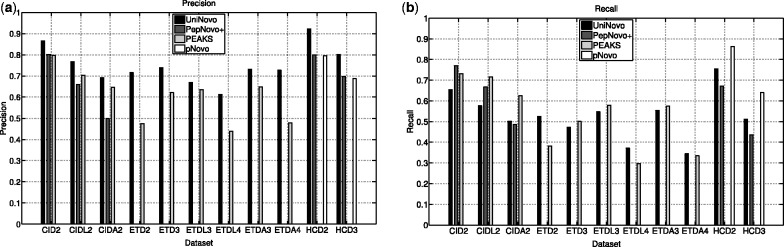
Comparison of de novo sequencing tools in terms of amino acid level precision (a) and recall (b). The definitions of precision and recall are given in (4) and (5), respectively
Both the sequence level and amino acid level results suggest that specific types of spectra are more suitable for de novo sequencing than others. For instance, in general, HCD spectra generated more accurate and longer reconstructions (or higher precision and recall in amino acid level) than ETD spectra. Further evaluation of the scoring function (i.e., spectrum graph) of UniNovo for different spectrum types is found in the Supplementary section S14, where we also compared the spectrum graphs from UniNovo, PepNovo and MS-GFDB for CID2 dataset.
3.3 De novo sequencing of paired spectra
UniNovo also can be used to sequence paired spectra (e.g. CID/ETD spectral pairs). Given multiple spectra from the same precursor ion, UniNovo first generates a spectrum graph from each of the spectra and next merges the spectrum graphs into a combined spectrum graph, on which the reconstructions are generated (refer to the Supplementary section S5 for the spectrum graph merging algorithm).
To benchmark UniNovo in de novo sequencing of paired spectra, CID/ETD2 and CID/ETD3 datasets were analyzed by UniNovo. From CID/ETD2 dataset, two additional datasets were generated: CID/etd2 and cid/ETD2 datasets. CID/etd2 dataset was formed by taking only CID spectra, and cid/ETD2 dataset by taking only ETD spectra in CID/ETD2 dataset. CID/etd3 and cid/ETD3 datasets were generated similarly. For each dataset, we generated 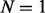 , 5 and 20 top scoring reconstructions.
, 5 and 20 top scoring reconstructions.
The results are shown in Figure 5. When precursor ions were doubly charged, the performance boost from the paired spectra was very modest. For 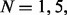 and 20, UniNovo reported 5% more correctly sequenced spectral pairs in CID/ETD2 datasets than in CID/etd2 dataset. The average length of correct reconstructions for CID/ETD2 dataset was slightly longer than for CID/etd2 dataset.
and 20, UniNovo reported 5% more correctly sequenced spectral pairs in CID/ETD2 datasets than in CID/etd2 dataset. The average length of correct reconstructions for CID/ETD2 dataset was slightly longer than for CID/etd2 dataset.
Fig. 5.
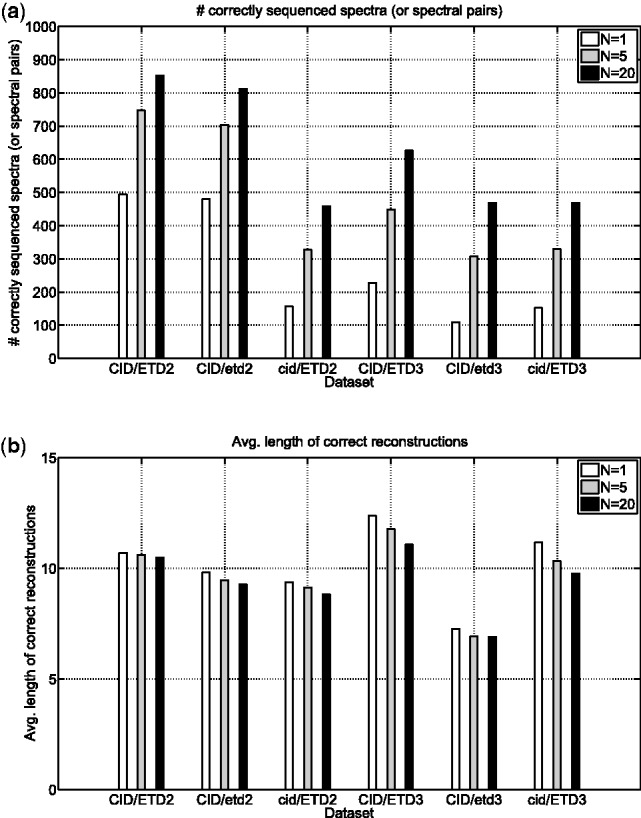
De novo sequencing of paired spectra. CID/ETD spectral pairs were analyzed by UniNovo (in CID/ETD2 and CID/ETD3 datasets). To see if the spectral pairs are beneficial for de novo sequencing, CID/etd2 (cid/ETD2) dataset was generated from CID/ETD2 dataset by collecting only CID (ETD) spectra in CID/ETD2 dataset. Likewise, CID/etd3 and cid/ETD3 datasets were generated from CID/ETD3 dataset. (a) the number of correctly sequenced spectra (or spectral pairs), (b) the average length of correct reconstructions for each dataset. The spectral pairs resulted in more accurate and longer reconstructions, in particular for triply charged spectral pairs
In contrast, for triply charged spectra, the use of paired spectra was highly beneficial for generating more accurate reconstructions. For example, when N = 1, UniNovo reported 100 and 50% more correctly sequenced spectral pairs in CID/ETD3 dataset than in CID/etd3 and cid/ETD3 datasets, respectively. The length of correct reconstructions typically increases by 1–2 amino acids by using the CID/ETD paired spectra.
3.4 De novo sequencing with quality filtering
Given a set of reconstructions generated from a spectrum, UniNovo estimates the probability that at least one reconstruction in the set is correct (i.e., a probability that the spectrum is correctly sequenced) based on the accuracies of reconstructions. The estimated probability is called the set accuracy (When multiple de novo reconstructions are reported, it is important to guarantee that one of them is correct.). Denote the set of reconstructions by 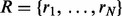 . If the events ‘ri is correct’ for
. If the events ‘ri is correct’ for 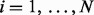 are independent, the set accuracy is simply given by
are independent, the set accuracy is simply given by 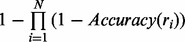 . However, since the reconstructions are often similar to each other, the dependency between reconstructions should be taken into account. To model this dependency, we assume Markov property between the events ‘ri is correct’ for
. However, since the reconstructions are often similar to each other, the dependency between reconstructions should be taken into account. To model this dependency, we assume Markov property between the events ‘ri is correct’ for 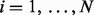 and compute the set accuracy. The derivation of the set accuracy is given in the Supplementary section S6.
and compute the set accuracy. The derivation of the set accuracy is given in the Supplementary section S6.
When the parameter N is set, one may want to choose N reconstructions with the highest accuracies to maximize the set accuracy. However, such a selection often results in a set of short reconstructions (because short reconstructions have relatively high accuracies). Since short reconstructions are not very useful in many cases (e.g. in follow-up homology searches), UniNovo uses a greedy algorithm to select long and accurate reconstructions. The inputs to the algorithm are the parameters SetAccuracyThreshold and N. The algorithm tries to form an output set of N reconstructions of set accuracy higher than SetAccuracyThreshold while maximizing the minimum length of the reconstructions (see the Supplementary section S7 for the description of the algorithm). If UniNovo fails to generate a set of N reconstructions with the set accuracy higher than SetAccuracyThreshold, it filters out the query spectrum.
We set 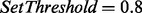 and reanalyzed the datasets in Table 1. The maximum number of mass gaps per each reconstruction was set to 10. For each dataset, we measured the number of unfiltered spectra (termed qualified spectra) and the percentage of qualified spectra that were correctly sequenced (which is expected to be 80% since
and reanalyzed the datasets in Table 1. The maximum number of mass gaps per each reconstruction was set to 10. For each dataset, we measured the number of unfiltered spectra (termed qualified spectra) and the percentage of qualified spectra that were correctly sequenced (which is expected to be 80% since 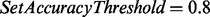 ). The average length of correct reconstructions was also measured.
). The average length of correct reconstructions was also measured.
The results are given in Figure 6. For all datasets, the number of qualified spectra increases sharply as the number of reconstructions N grows (Fig. 6a). For example, UniNovo reported only few qualified spectra (<5) from CIDA2 dataset when N = 1. When N = 20, it reported >900 qualified spectra from the same dataset. In contrast to the dramatic changes in the number of qualified spectra, the percentage of qualified spectra that were correctly sequenced hardly changed across the datasets and the values of N (Fig. 6b). As expected, the percentage was around 80% for all cases (including the datasets containing CID/ETD spectral pairs), which shows that the set accuracy reported by UniNovo is reliable. Figure 6c shows the average length of correct reconstructions. As N decreases, the average length also decreases. This is because shorter reconstructions (with higher accuracies) are chosen by UniNovo when N is small to achieve high set accuracy.
Fig. 6.
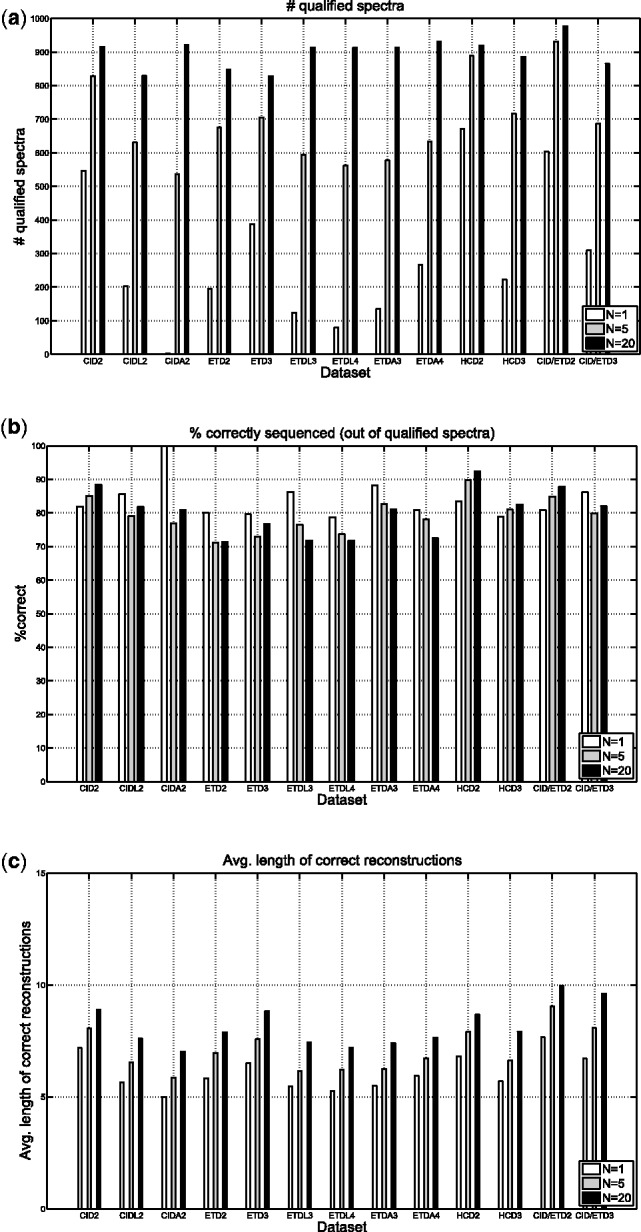
De novo sequencing with qualify filtering of spectra. Given a spectrum, if the parameter SetAccuracyThreshold is set, UniNovo attempts to achieve set accuracy (an estimated probability of the spectrum being correctly sequenced) exceeding SetAccuracyThreshold. If it fails to generate such a set, the spectrum is filtered out. An unfiltered spectrum is called a qualified spectrum. We set 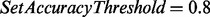 . (a) the number of qualified spectrum, (b) the percentage of qualified spectra that were correctly sequenced, (c) the average length of correct reconstructions
. (a) the number of qualified spectrum, (b) the percentage of qualified spectra that were correctly sequenced, (c) the average length of correct reconstructions
4 CONCLUSION
We presented a universal de novo sequencing tool UniNovo that works well for various types of spectra. UniNovo can be easily trained for different types of spectra using only thousands of PSMs that typically can be obtained from a single MS/MS run. The experimental results show that UniNovo generates accurate and long de novo reconstructions from spectra of CID, ETD, HCD and CID/ETD fragmentation methods and spectra of trypsin, LysC or AspN digested peptides. We also showed that UniNovo is better than or comparable with other state of the art tools.
As pointed out by Ma and Johnson (2011), de novo sequences not only are valuable for the analysis of the novel peptides that are not present in proteome databases but also can facilitate the homology-based database searches. Since the reconstructions reported by UniNovo contain mass gaps representing the total mass of multiple amino acids [termed gapped peptides (Jeong et al., 2011; Kim et al., 2009b)], MS-BPM algorithm (Ng et al., 2011) can be used for fast exact or homology searches (UniNovo MS-BPM). MS-BPM enables searches against a sequence database using gapped peptides as queries. Currently MS-BPM takes gapped peptides generated by MS-GappedDictionary (Jeong et al., 2011) (MS-GappedDictionary
MS-BPM). MS-BPM enables searches against a sequence database using gapped peptides as queries. Currently MS-BPM takes gapped peptides generated by MS-GappedDictionary (Jeong et al., 2011) (MS-GappedDictionary MS-BPM). However, the reconstructions from UniNovo are usually longer than those from MS-GappedDictionary (8–9 versus 5–6). Since the search time of MS-BPM strongly depends on the length of gapped peptides—the longer gapped peptides, the shorter search time—the running time of UniNovo
MS-BPM). However, the reconstructions from UniNovo are usually longer than those from MS-GappedDictionary (8–9 versus 5–6). Since the search time of MS-BPM strongly depends on the length of gapped peptides—the longer gapped peptides, the shorter search time—the running time of UniNovo MS-BPM is smaller than MS-GappedDictionary
MS-BPM is smaller than MS-GappedDictionary MS-BPM by an order of magnitude in a blind search against the IPI Human proteome database ver.3.87 (Kersey et al., 2004) (data not shown).
MS-BPM by an order of magnitude in a blind search against the IPI Human proteome database ver.3.87 (Kersey et al., 2004) (data not shown).
Supplementary Material
ACKNOWLEDGEMENT
We are grateful to Albert Heck and Joshua Coon for making their spectral datasets available. We are also thankful to Ari Frank, Sunghee Woo and Nuno Bandeira for helpful discussion.
Funding: The research was supported by the National Center for Research Resources of NIH via grant P-41-RR24851.
Conflict of Interest: none declared.
References
- Bandeira N, et al. Multi-spectra peptide sequencing and its applications to multistage mass spectrometry. Bioinformatics. 2008;24:i416–i423. doi: 10.1093/bioinformatics/btn184. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Barton SJ, Whittaker JC. Review of factors that influence the abundance of ions produced in a tandem mass spectrometer and statistical methods for discovering these factors. Mass Spectrom. Rev. 2009;28:177–187. doi: 10.1002/mas.20188. [DOI] [PubMed] [Google Scholar]
- Bern M, et al. Lookup peaks: a hybrid of de novo sequencing and database search for protein identification by tandem mass spectrometry. Anal. Chem. 2007;79:1393–1400. doi: 10.1021/ac0617013. [DOI] [PubMed] [Google Scholar]
- Breci LA, et al. Cleavage n-terminal to proline: analysis of a database of peptide tandem mass spectra. Anal. Chem. 2003;75:1963–1971. doi: 10.1021/ac026359i. [DOI] [PubMed] [Google Scholar]
- Chen T, et al. A dynamic programming approach to de novo peptide sequencing via tandem mass spectrometry. J. Comput. Biol. 2001;8:325–337. doi: 10.1089/10665270152530872. [DOI] [PubMed] [Google Scholar]
- Chi H, et al. pNovo: de novo peptide sequencing and identification using HCD spectra. J. Proteome Res. 2010;9:2713–2724. doi: 10.1021/pr100182k. [DOI] [PubMed] [Google Scholar]
- Dancik V, et al. De novo peptide sequencing via tandem mass spectrometry. J. Comput. Biol. 1999;6:327–342. doi: 10.1089/106652799318300. [DOI] [PubMed] [Google Scholar]
- Datta R, Bern M. Spectrum fusion: using multiple mass spectra for de novo peptide sequencing. J. Comput. Biol. 2009;16:1169–1182. doi: 10.1089/cmb.2009.0122. [DOI] [PubMed] [Google Scholar]
- Elias JE, Gygi SP. Target-decoy search strategy for increased confidence in large-scale protein identifications by mass spectrometry. Nat. Methods. 2007;4:207–14. doi: 10.1038/nmeth1019. [DOI] [PubMed] [Google Scholar]
- Eng JK, et al. An approach to correlate tandem mass spectral data of peptides with amino acid sequences in a protein database. J. Am. Soc. Mass Spectrom. 1994;5:976–989. doi: 10.1016/1044-0305(94)80016-2. [DOI] [PubMed] [Google Scholar]
- Frank A. A ranking-based scoring function for peptide-spectrum matches. J. Proteome Res. 2009;8:2241–2252. doi: 10.1021/pr800678b. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Frank A, Pevzner P. PepNovo: de novo peptide sequencing via probabilistic network modeling. Anal. Chem. 2005;77:964–973. doi: 10.1021/ac048788h. [DOI] [PubMed] [Google Scholar]
- Frese CK, et al. Improved peptide identification by targeted fragmentation using CID, HCD and ETD on an LTQ-Orbitrap velos. J. Proteome Res. 2011;10:2377–2388. doi: 10.1021/pr1011729. [DOI] [PubMed] [Google Scholar]
- He L, Ma B. ADEPTS: advanced peptide de novo sequencing with a pair of tandem mass spectra. J. Bioinform. Comput. Biol. 2010;8:981–994. doi: 10.1142/s0219720010005099. [DOI] [PubMed] [Google Scholar]
- Huang Y, et al. Statistical characterization of the charge state and residue dependence of low-energy CID peptide dissociation patterns. Anal. Chem. 2005;77:5800–5813. doi: 10.1021/ac0480949. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hunter D. An upper bound for the probability of a union. J. Appl. Probab. 1976;13:597–603. [Google Scholar]
- Jeong K, et al. Gapped spectral dictionaries and their applications for database searches of tandem mass spectra. Mol. Cell. Proteomics. 2011;10 doi: 10.1074/mcp.M110.002220. M110.002220. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Johnson RS, et al. Novel fragmentation process of peptides by collision-induced decomposition in a tandem mass spectrometer: differentiation of leucine and isoleucine. Anal. Chem. 1987;59:2621–2625. doi: 10.1021/ac00148a019. [DOI] [PubMed] [Google Scholar]
- Käll L, et al. Semi-supervised learning for peptide identification from shotgun proteomics datasets. Nat. Methods. 2007;4:923–925. doi: 10.1038/nmeth1113. [DOI] [PubMed] [Google Scholar]
- Keller A, et al. Empirical statistical model to estimate the accuracy of peptide identifications made by ms/ms and database search. Anal. Chem. 2002;74:5383–92. doi: 10.1021/ac025747h. [DOI] [PubMed] [Google Scholar]
- Kersey PJ, et al. The international protein index: an integrated database for proteomics experiments. Proteomics. 2004;4:1985–1988. doi: 10.1002/pmic.200300721. [DOI] [PubMed] [Google Scholar]
- Kim S, et al. Spectral dictionaries. Mol. Cell. Proteomics. 2009a;8:53–69. doi: 10.1074/mcp.M800103-MCP200. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kim S, et al. Spectral profiles, a novel representation of tandem mass spectra and their applications for de novo peptide sequencing and identification. Mol. Cell. Proteomics. 2009b;8:1391–1400. doi: 10.1074/mcp.M800535-MCP200. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kim S, et al. The generating function of CID, ETD, and CID/ETD pairs of tandem mass spectra: Applications to database search. Mol. Cell. Proteomics. 2010;9:2840–2852. doi: 10.1074/mcp.M110.003731. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu X, et al. Better score function for peptide identification with ETD MS/MS spectra. BMC Bioinformatics. 2010;11(Suppl. 1):S4. doi: 10.1186/1471-2105-11-S1-S4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ma B, Johnson R. De novo sequencing and homology searching. Mol. Cell. Proteomics. 2011 doi: 10.1074/mcp.O111.014902. O111.014902. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ma B, et al. PEAKS: powerful software for peptide de novo sequencing by tandem mass spectrometry. Rapid Commun. Mass Spectrom. 2003;17:2337–2342. doi: 10.1002/rcm.1196. [DOI] [PubMed] [Google Scholar]
- Nesvizhskii AI. A survey of computational methods and error rate estimation procedures for peptide and protein identification in shotgun proteomics. J. Proteomics. 2010;73:2092–123. doi: 10.1016/j.jprot.2010.08.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ng J, et al. Blocked pattern matching problem and its applications in proteomics. RECOMB 2011. 2011 Vancouver, Canada, pp. 298–319. [Google Scholar]
- Olsen JV, et al. Higher-energy c-trap dissociation for peptide modification analysis. Nat. Methods. 2007;4:709–712. doi: 10.1038/nmeth1060. [DOI] [PubMed] [Google Scholar]
- Perkins DN, et al. Probability-based protein identification by searching sequence databases using mass spectrometry data. Electrophoresis. 1999;20:3551–3567. doi: 10.1002/(SICI)1522-2683(19991201)20:18<3551::AID-ELPS3551>3.0.CO;2-2. [DOI] [PubMed] [Google Scholar]
- Savitski MM, et al. Proteomics-Grade de novo sequencing approach. J. Proteome Res. 2005;4:2348–2354. doi: 10.1021/pr050288x. [DOI] [PubMed] [Google Scholar]
- Swaney DL, et al. Decision tree-driven tandem mass spectrometry for shotgun proteomics. Nat. Methods. 2008;5:959–964. doi: 10.1038/nmeth.1260. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Swaney DL, et al. Value of using multiple proteases for Large-Scale mass Spectrometry-Based proteomics. J. Proteome Res. 2010;9:1323–1329. doi: 10.1021/pr900863u. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tabb DL, et al. Influence of basic residue content on fragment ion peak intensities in Low-Energy Collision-Induced dissociation spectra of peptides. Anal. Chem. 2004;76:1243–1248. doi: 10.1021/ac0351163. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wysocki VH, et al. Mobile and localized protons: a framework for understanding peptide dissociation. J. Mass Spectrom. 2000;35:1399–1406. doi: 10.1002/1096-9888(200012)35:12<1399::AID-JMS86>3.0.CO;2-R. [DOI] [PubMed] [Google Scholar]
- Zubarev RA, et al. Electron Capture/Transfer versus collisionally Activated/Induced dissociations: Solo or duet? J. Am. Soc. Mass Spectrom. 2008;19:753–761. doi: 10.1016/j.jasms.2008.03.007. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.