Skip to main content
NCBI home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2013 Jun 17;7(7):6129–6137. doi: 10.1021/nn4019619

Quantification of Nanoparticle Dose and Vesicular Inheritance in Proliferating Cells

Huw D Summers †,*, Martyn R Brown †, Mark D Holton †, James A Tonkin †, Nicole Hondow ‡, Andrew P Brown ‡, Rik Brydson ‡, Paul Rees †
PMCID: PMC3722614  PMID: 23773085

Abstract

graphic file with name nn-2013-019619_0008.jpg

Assessing dose in nanoparticle–cell interactions is inherently difficult due to a complex multiplicity of possible mechanisms and metrics controlling particle uptake. The fundamental unit of nanoparticle dose is the number of particles internalized per cell; we show that this can be obtained for large cell populations that internalize fluorescent nanoparticles by endocytosis, through calibration of cytometry measurements to transmission electron microscopy data. Low-throughput, high-resolution electron imaging of quantum dots in U-2 OS cells is quantified and correlated with high-throughput, low-resolution optical imaging of the nanoparticle-loaded cells. From the correlated data, we obtain probability distribution functions of vesicles per cell and nanoparticles per vesicle. Sampling of these distributions and comparison to fluorescence intensity histograms from flow cytometry provide the calibration factor required to transform the cytometry metric to total particle dose per cell, the mean value of which is 2.4 million. Use of the probability distribution functions to analyze particle partitioning during cell division indicates that, while vesicle inheritance is near symmetric, highly variable vesicle loading leads to a highly asymmetric particle dose within the daughter cells.

Keywords: nanoparticle dose, electron microscopy, flow cytometry, nanoparticle inheritance

The accurate determination of dose when studying nanoparticle–cell interactions is essential for quantitative particle toxicology and pharmacology.1,2 With nanoscale particulates, this is far from straightforward as the complex and varied mechanisms of interaction with cells mean that the exposure dose does not directly correlate to quantity of particles actually internalized.3 A layer of complexity comes from the multivariate nature of these interactions, with nanoparticle diameter, morphology, surface area, surface charge, and surface chemistry/coating all influencing the dispersion of the nanoparticles and subsequent cellular uptake and response.4−6 The standard dose concentration formulation of weight per unit volume of cell delivery solution does not account for any of these parameters as it quantifies only the totality of material rather than the discrete structural units of which the dose is composed. The fundamental dose measure must therefore always be the particle number internalized per cell or even the number internalized to a specific organelle per cell. This raises serious challenges to metrology as nanoscale measurement is required, under experimental conditions, that is, of nanoparticle concentration and dispersion within cell culture medium for in vitro assays (exposure dose) and of nanoparticle concentration within cellular tissue (i.e., dose delivered). The cellular internalization of nanoparticles has been extensively studied,7−12 but while quantification of total exposure dose is routinely reported, there are fewer studies on intracellular quantification and distribution at the single particle level. There are reports on cytoplasmic versus vesicle-bound particles,13 plentiful instances of descriptive EM, and a few comprehensive, statistically robust studies of particle count.14,15 Here, we demonstrate that calibration of cytometry techniques by electron microscopy-based nanoparticle (NP) counts in cell sections enables quantification of NPs internalized by endocytosis in tens of thousands of cells at a time.

Progressing further, even when a reliable and accurate measure of nanoparticle dose has been established, the prediction of dose–response characteristics still requires knowledge of the biological processes which determine the pharmacokinetics of nanotoxins and nanopharmaceuticals. More specifically, when endocytosis and exocytosis control particle uptake and expulsion,8,9,16,17 particles are commonly encapsulated within intracellular vesicles which can only be viewed as the effective unit of dose18 if the vesicles are not expelled or fused over the time scale of the measurement19 or that biological degradation within such vesicles has not had time to alter the physiochemical properties of the particles.20−22 Regardless of the temporal stability of vesicles, in proliferating cells, the dose will exhibit abrupt and significant dilution due to cell division.23 It is this process of nanoparticle inheritance which we report on here. The evolution of particle dose across cell generations must be appreciated if accurate toxicological models are to be developed.24 In nanomedicine, dose dilution upon mitosis is a crucial determinant of therapeutic efficacy, especially as much of the effort in this area is focused on cancer medicine where rapid cell proliferation is a hallmark of the disease.25 Consideration of nanoparticle inheritance leads to an important question—what is the unit of inheritance? While it is particle dose that we wish to quantify, for endocytically active cells, it is actually NP-loaded vesicles that are directly inherited. These nanoparticles are secondary, indirectly passing to daughter cells as vesicular cargo. Our previous studies of nanoparticle inheritance, using fluorescent nanoparticles (quantum dots) to quantify dose, indicated a marked asymmetry in the partitioning of fluorescence between daughter cells.26 This asymmetry has also been reported in other studies.27 Our measurements of vesicle partitioning, however, present a more ambiguous picture in which the inherited vesicle asymmetry is not as marked.18 In this paper, we show that this important discrepancy can be resolved by proper consideration of the appropriate metric for dose—the nanoparticle. That knowledge of particle number, plus the form of its vesicular packaging within the cell, is required for accurate prediction of dose kinetics.

Arguably, the most ideal technique to address nanoparticle dose quantification, in terms of spatial resolution, is three-dimensional (3-D) imaging using electron microscopy (EM) to provide a direct measure of particle size, localization, and count throughout the volume of the cell. This is technically possible but is a highly specialist technique requiring extensive expertise and, even with careful sampling, is challenging and time-consuming to implement for mass cell analysis or under cell culture conditions.14,15 The practical technology, commonly applied for nanoparticle dose assessment, is high-throughput optical cytometry (automated microscopy or flow cytometry). This is widely available and capable of rapid, mass measurement of cells28 but cannot deliver individual nanoparticle counts owing to the diffraction-limited resolution of optical/UV imaging techniques. To bridge these approaches, there is a need for calibration studies linking low-throughput, high spatial resolution nanoscale measurements to surrogate quantifiers of dose that have lower spatial resolution but which are suitable for high-throughput measurement, such as particle fluorescence29 or magnetic moment quantification.30 In this paper, we present a series of such calibration measurements, relating full 3-D EM imaging of quantum dot nanocrystals within a U-2 OS, osteosarcoma cell line, to fluorescence-based dose quantification by flow cytometry. The approach is based on statistical sampling of low-throughput nanoscale EM measurement sets to construct probability distribution functions (PDFs) of quantum dot (QD) particle dose. These are then calibrated to optical measurement sets and used to generate much larger computational data sets from which simulated fluorescence distributions can be validated by comparison to experiment.

Results

Intercellular Dose Variation

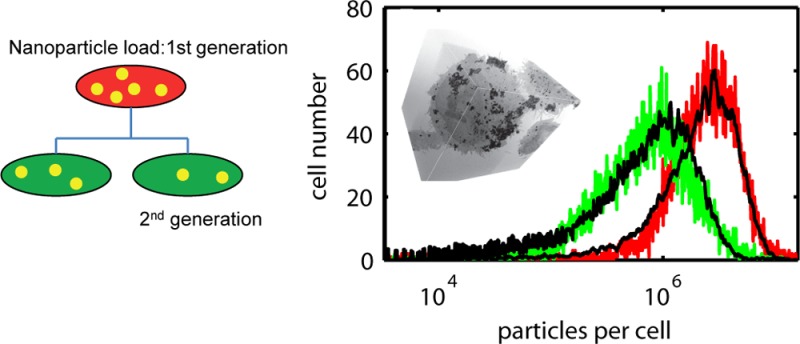
Robust measurement of nanoparticle dose within cells relies on large data sets to obtain statistical accuracy and requires data on >103 cells; for this, we use rapid-throughput flow cytometry. The starting point is measurement of particle dose per cell, identified by the integrated fluorescence from the quantum dots encapsulated within the cells, in this case by endocytosis. A typical fluorescence intensity histogram from 10 000 cells is shown in Figure 1A. The cell culture had been exposed to a 10 nM concentration of quantum dots for 1 h, following which the excess nanoparticles were removed with a series of washes; after a further 24 h incubation period, cells were fixed and prepared for measurement (see Methods section). In previous studies using this quantum dot system, the fluorescence intensity proved to be stable over 70 h following encapsulation within cells.18 There is marked variation in the cellular fluorescence with the distribution showing a standard deviation of 0.68 relative to the mean. To understand this heterogeneity, we need to consider the distribution of QD particles taken up by cells, and as we have previously shown, uptake here is driven by endocytosis so the count metric is the number of nanoparticle-loaded vesicles per cell (the term “vesicle” is used here as a general term for a membrane-bound, intracellular organelle; that is, no distinction is made between early endosome, late endosome, or lysosome). To achieve this, we use imaging cytometry to provide spatial information on the localization of quantum dots within cell vesicles. A representative panel of cell images (31 from 5000) is shown in Figure 1B. Automated image masking using the QD fluorescence signal and subsequent automated counting of mask spots provides a count of nanoparticle-loaded vesicles per cell image, the histogram of which is shown in Figure 1C (red circles). The probability distribution function has an overdispersed form and is well-described by a Polya distribution function (solid line) with mean μ = 7 vesicles per cell and overdispersion factor b = 0.25 (see Methods section for details on the mathematical form of this particular PDF function). It is clear that the dose heterogeneity seen at the whole cell level is in part due to a marked variation in the number of vesicles per cell which ranges from 0 to >30.

Figure 1.

Figure 1

Open in a new tab

(A) Histogram of quantum dot fluorescence intensity per cell, 24 h after endocytic uptake of the dots (10 nM concentration, 1 h exposure), showing a marked variation in individual cellular dose. (B) Cell optical images (fluorescence overlay on bright-field images) confirming the variation in dose and indicating the spatial location of particle-loaded vesicles. (C) Measured probability distribution of vesicles per cell (red circles) can be fitted by an overdispersed Polya distribution function (black line).

Intracellular Particle Dose and Packaging

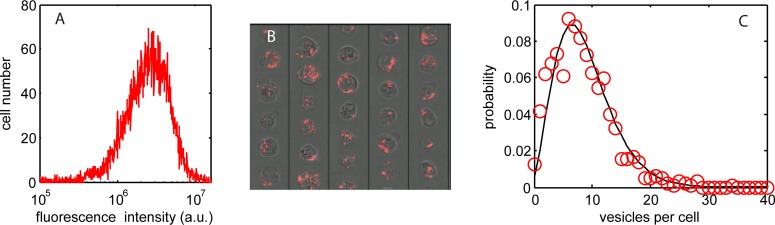
To probe within the cellular vesicles requires sub-micrometer resolution imaging, and so for this we use electron microscopy. A set of transmission electron microscope (TEM) images of vesicles within a cell section, typically 100 nm thick, are shown in Figure 2A. The high density inorganic quantum dots contain atomically heavy elements (Cd, Se, and Zn) and are crystalline, producing strong image contrast (both mass–thickness and diffraction) such that the particles are easily discriminated as dark ∼10–15 nm regions (black spots) in the bright-field TEM image. Counts of particle number per vesicle section for 391 vesicles taken from 102 cells are collated in the histogram in Figure 2B.

Figure 2.

Figure 2

Open in a new tab

(A) TEM images from a single cell sections, 100 nm thick; top left image shows the complete cell section, while other images show a selection of vesicles within the cell with a large range of quantum dot loading (10 nM dose, 1 h exposure followed by 24 h incubation); the bottom right-hand section has been falsely colored to indicate the results of the QD counting algorithm; blue spots correspond to isolated QDs, red spots refer to QDs in contact with other nanoparticles. (B) Measured probability distribution of quantum dots per vesicle section (red circles; 102 cells and 391 vesicles) fitted with a biexponential function (black line).

The most striking aspect of the images is the 3 decade range in the encapsulated number of particles per vesicle section; the frequency of which displays a biexponential distribution (fitting parameter values given in the Methods section). Analyses of the causative processes which underlie this number distribution are beyond the scope of this paper; however, we note that TEM studies of the quantum dot dispersion in cell culture media indicate a similar form for the size distribution of particle agglomerates.31 This suggests a direct transfer of agglomerates into the cells through an endocytic internalization processes that is independent of (agglomerate) size. The biexponential, probability distribution function in Figure 2B (solid line) enables prediction of the particle dose across a set of vesicles. A typical in vitro cytometry assay involves measurement of 10 000 cells, each with many nanoparticle-loaded vesicles (typically 5–30 vesicles per cell), and so knowledge of the probability distribution function is essential for accurate prediction of dose.

In addition to vesicle counts, the optical microscopy images provide a surrogate measure of particle number through the total fluorescence intensity per vesicle section. Thus a comparison of the electron and optical microscopy can be made using the QD particle number histogram shown in Figure 2B and the distribution of fluorescence intensity per vesicle section. This is presented as a cumulative frequency distribution in Figure 3 for sample sets of 391 TEM images and 690 fluorescence images. The integrated fluorescence intensity is calculated from the image set shown in Figure 1 using the masked areas to identify individual nanoparticle-loaded vesicles. An absolute correlation of fluorescence intensity to QD particle number is not possible due to the different transverse sampling of the electron and optical microscopy; the microtome sections for TEM are ∼100 nm thick while the imaging cytometer has a depth of field of ∼1 μm (objective lens NA = 0.75, λQD = 705 nm). However, the form of the two data sets can be compared, and this shows a close correspondence, indicating that the distribution in fluorescence intensity per vesicle optical section does correlate to a variation in individual nanoparticle number per vesicle EM section.

Figure 3.

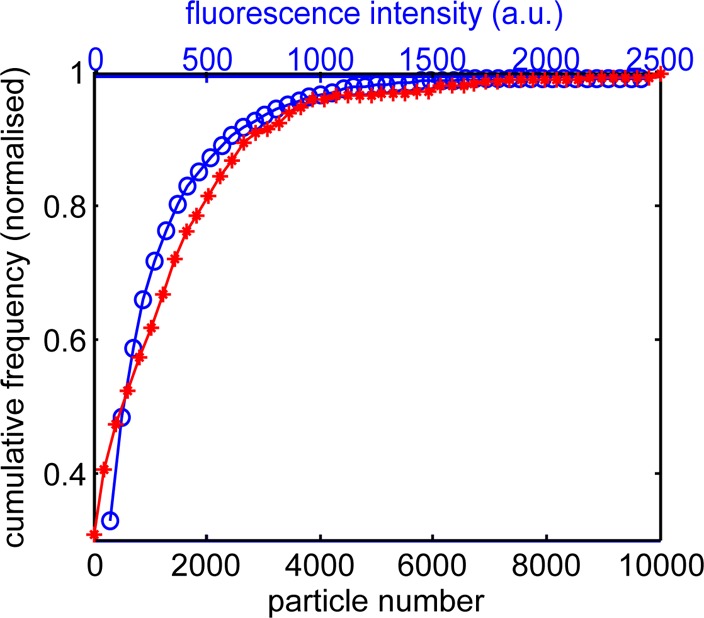
Figure 3

Open in a new tab

Cumulative frequency distribution of QD particles per vesicle measured by TEM (red stars and lower x-axis; taken from the data presented in Figure 2) and QD fluorescence intensity per vesicle measured by flow cytometry (blue circles and top x-axis; taken from the data presented in Figure 1).

Calibration of Cellular Dose

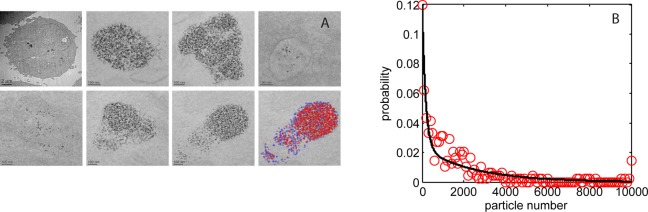
The results presented in Figure 2 detail the nanoparticle number per vesicle in ∼100 nm thick cell sections; therefore, to obtain the total particle dose per cell for a complete calibration of the quantum dot fluorescence, the TEM data from 2-D sections have to be related to the whole cell volume. To estimate the sampling fraction within the subvolume of a cell, we use serial block face backscattered electron imaging in a scanning electron microscope (SEM) containing an in-chamber microtome that slices a resin-mounted block of cells with accurate conformation of successive 2-D images of the exposed cell surfaces. This allows full 3-D image reconstructions from a group of cell sections.32Figure 4A shows a 2-D representation of such a 3-D reconstruction in which agglomerations of quantum dots can be seen, both on the outer cell membrane and internally within membrane-bound vesicles. The serial section thickness used to slice the cells by the SEM microtome is the same as for the TEM analysis (ca. 100 nm), and simulations of the electron penetration (Casino Flight simulator v2.42; further details in the Supporting Information) predict an interaction volume of ∼170 nm and a maximum backscattered electron emission depth of ∼70 nm (i.e., comparable to or less than the section thickness). Area analysis of the particle content in each of the 100–150 individual sections across whole cells and within the total cell volumes provides an estimate of the fraction of the total quantum dot content to be found within a typical 2-D section. The resolution of the backscattered electron imaging (the pixel size was limited to be 17 × 17 nm and the voxel size 17 × 17 × 100 nm) is not sufficient to resolve single QD particles within dense agglomerates, and so we use the total area of QD clusters as the metric for quantification. Figure 4B shows a histogram of the percentage of QD area within a single section to that summed across all cell sections; the data are an amalgamation of 453 sections taken from three cells; the mean value is 0.67% of the total cell area exposed in a section, which implies a 2-D to 3-D multiplying factor of 150. As the TEM images of the QD particle-loaded vesicles are a randomly selected set, both in terms of the transverse position of the cell section and the cell identity, we can use this mean value multiplying factor to scale the QD particle count PDFs and make an approximate conversion of the section-based particle counts to a whole cell particle number.

Figure 4.

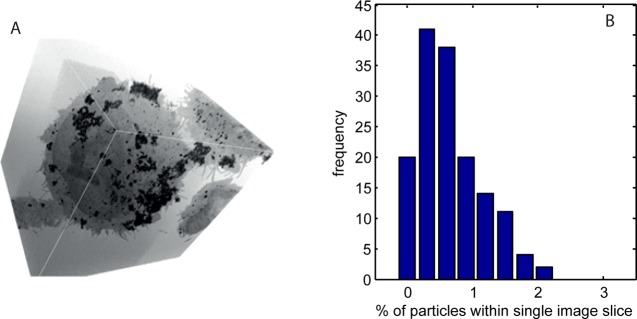
Figure 4

Open in a new tab

(A) Two-dimensional representation of a 3-D reconstruction of a series of serial block face SEM images of a QD-loaded cell; QDs on, and those encapsulated within, the cell can be identified and distinguished. (B) Frequency distribution of QD area fraction within a single 2-D image slice of a cell (the “loading” is expressed as a percentage of total cell area exposed in each respective slice). The mean area loading is 0.67%.

Given the variability in both QD particles per vesicle section and vesicles per cell, it is essential that population-wide, statistical measures are used to quantify the dose, for probabilistic approaches are the only robust option when the individual quantities are subject to such large variation. We therefore use random sampling of the PDFs shown in Figures 1 and 2 and the 2-D to 3-D conversion factor above to obtain frequency distributions of vesicles per cell and of particles per vesicle and from these construct the predicted particle dose across a large population of cells. The predicted dose for a population of 10 000 cells, obtained from sampling of the PDFs, is shown in Figure 5 (solid black line).

Figure 5.

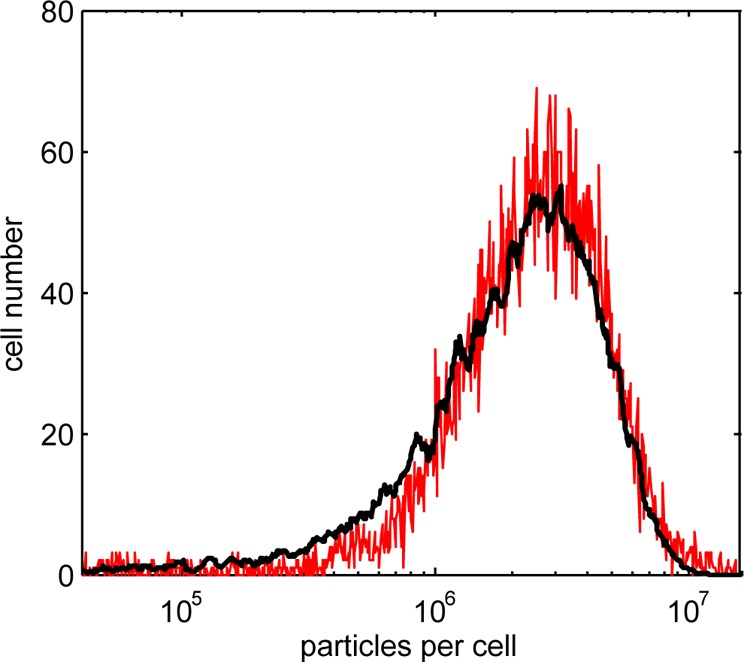
Figure 5

Open in a new tab

Predicted (black line) and measured (red line) frequency distributions of QD particles per cell (measured data are scaled by calibration factors obtained from the optical vesicle count and TEM-based particle count data).

The cytometry data provide a measure of the “whole cell” fluorescence which is a good surrogate of total particle number for QDs with stable emission. A single scaling factor is introduced to transform the arbitrary measurement base of fluorescence unit to a count of particles per cell. The predicted dose distribution is in excellent agreement with the measured data (Pearson coefficient, r = 0.96), thus confirming the validity of the statistical sampling approach to correlate individual particle counts to whole cell fluorescence measurement. The calibrated distribution has a mean dose of ∼2.4 million QD particles per cell. Counts of nanoparticles (targeted for endocytic uptake) per cell have been reported for a range of cell types, using direct counting from EM images,14,15 measurement of cell magnetization in the case of magnetic particles,13,33,34 and by atomic spectroscopy;35 values reported span the range of 103–107 per cell. Thus our results are within the bounds previously reported and provide further evidence that, on average, extremely high numbers of QD particles targeted for endocytic uptake are internalized per cell.

Dose Inheritance

Having confirmed the validity and accuracy of dose prediction from knowledge of QD particles per vesicle and vesicles per cell, the evolution of this dose in a proliferating cell population can be analyzed. Specifically, we model the dilution and partitioning of particle dose into daughter cells that occurs within a further 24 h time period. This is compared to measured dose distributions obtained from flow cytometry measurements taken at 24 and 48 h after exposure and constructed from the fluorescence intensity histograms using the x-axis scaling factor already reported. The dose inheritance is modeled using a binomial partitioning probability to decide which daughter inherits each vesicle.18,36 This is done for all vesicle-enclosed particle clusters used in the construction of the 24 h dose profile in Figure 5; that is, random sampling of the predicted dose for a population of 10 000 cells using a binomial portioning probability distribution generates the number of parent vesicles to be inherited by each daughter:

graphic file with name nn-2013-019619_m001.jpg 1
graphic file with name nn-2013-019619_m002.jpg 2

where B is the probability of daughter 1 inheriting d vesicles from a parent containing n vesicles when the mean inheritance probability is p; d′ is the number of vesicles inherited by daughter 2. Previous work on this cell line indicates that the mean cell cycle time is 20.5 h,23 and so there will be a small percentage of the population which progresses through two rounds of division within the 24 h time period (individual cells are assumed to be randomly distributed throughout the cell cycle at the 24 h time point). To account for this occurrence, a second round of binomial partitioning is imposed on 17% of the daughter cells. Predicted and measured distributions are shown in Figure 6A for a p value of 0.55; that is, the best fit is obtained with only a slight asymmetry in the mean probability of vesicle inheritance; however, this results in a much wider dose distribution of QD particles per cell because of the large variation in QD loading per vesicle. The importance of random inheritance is shown by Figure 6B, which depicts the expected dose in the case of strict 50:50 splitting of particle dose (i.e., p = 0.50). Systematic, symmetric partitioning maintains the distribution shape and moves it to half of the parent dose, it is clear that this is not in agreement with the present experimental evidence.

Figure 6.

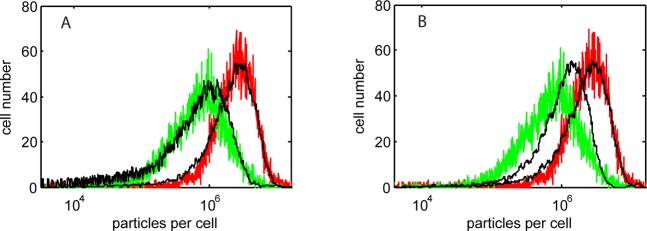
Figure 6

Open in a new tab

(A) Measured (colored lines) and predicted (p = 0.55) (black lines) frequency distributions of QD particle load per cell, 24 h (red experiment curve) and 48 h (green line) post-loading (10 nM concentration, 1 h exposure). Notably, in the predicted curve, the vesicles per cell were sampled with only a slight asymmetry of inheritance, but because of the large variation in QD loading per vesicle, this results in a much wider dose distribution of QD particles per cell. (B) Experimental data shown with predictions assuming strict 50:50 partitioning of particles between daughter cells. Clearly, this does not fit the experimental observations.

The reduction in peak value and the increased width of the dose distribution at 48 h is due to dispersion (driven by unequal partitioning of nanoparticles between daughter cells), stemming from two sources: the randomness of vesicle inheritance (given by the binomial partitioning above) and the variability in particle load of each vesicle (Figure 2). The inheritance variability is shown in Figure 7A, which plots the distribution of the partitioning fractions used in modeling the vesicle inheritance. Binomial partitioning of low numbers of vesicles (typically <30) leads to a wide range of inherited dose as the variance in binomial trials is proportional to √n. The particle-loaded vesicle inheritance variability is shown in Figure 7B, which is a scatter plot of the particle inheritance as a function of nanoparticle-loaded vesicle inheritance; that is, uniform loading of the vesicles would give equal fractions and produce a straight line at 45° to the axes. The large heterogeneity in the numbers of particles loaded into each vesicle and the relatively low number of loaded vesicles per cell can lead to a marked difference in the fraction of QD-loaded vesicles and thus particles inherited. The Pearson correlation coefficient of the data sets is 0.71, indicating a positive but imprecise relation between the inheritance of particle-loaded vesicles and of total particle number. The variance of particle load per vesicle introduces an asymmetry as excessively high (or low) loaded vesicles skew the fraction of particles inherited, especially at low parent vesicle number where the influence of outliers becomes significant.

Figure 7.

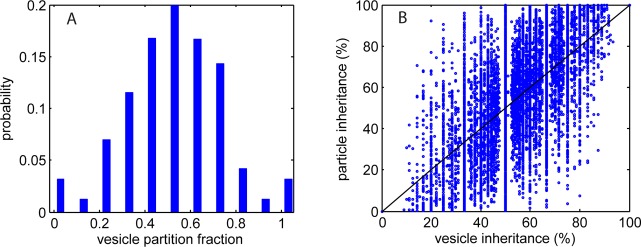
Figure 7

Open in a new tab

Statistics of predicted particle inheritance. (A) Probability distribution of vesicle partitioning fraction inherited by daughter cells. There is only a slight asymmetry to this, suggesting that the vesicles are inherited in a near random manner (i.e., a near 50:50 split on cell division). (B) Dot-plot of % of particles inherited versus % of nanoparticle-loaded vesicles inherited. There is a nonlinear relationship because of the variation in particle load within measured vesicles (Figure 2). The solid black line highlights the condition of equality in fraction of vesicles and of particles inherited (uniform loading of vesicles).

Conclusions

We have shown that through the use of limited cell sampling using high-resolution EM a calibration can be made, relating large population, cytometric measurements of fluorescence to exact quantum dot particle dose taken up by endocytosis. The statistical profile of particle dose is captured in probability distribution functions describing the variance of particle number within intracellular vesicles and of loaded vesicle number per cell. This probabilistic approach allows us to quantify at the fundamental level of particles per cell and maintain the capacity to analyze the 104 cells or more required to fully account for the biological heterogeneity displayed within a cell colony. The calibration indicates that substantial numbers of nanoparticles per cell are internalized by endocytosis, and this has implications for the design of in vitro assays. Typical pharmacology assays contain milliliter volumes of particle dispersions, at nanomolar concentration and a total particle number of ∼1012; with mean particle loads of 106 per cell in populations of ∼106 cells, this implies severe depletion of the nanoparticle reservoir and a highly nonlinear supply dynamic. The results also highlight the large variability present in nanoparticle–cell interactions, leading to a wide range of particle number per vesicle and so per cell, and show that near random partitioning of vesicles into daughter cells following cell division dictates the dispersion of particle dose.

In our experiments, the internalization of the nanoparticles occurs through endocytosis, as is the case for the majority of nanoparticle–cell studies. This loading process leads to particle encapsulation within organelles (endosomes) and the need to distinguish between the number of nanoparticles and the way in which they are packaged in the cell. While endosomes are dynamic organelles that can be exocytosed, fused, or matured into lysosomes, particle encapsulation is nonetheless particularly relevant when studying the impact of cell division upon dose; here the prediction of inherited dose must take into account the vesicles as well as the particles. Our analysis shows that a highly asymmetric inheritance of particle numbers by daughter cells can occur despite near symmetric partitioning of vesicles, and that this asymmetry is driven by the presence of extreme events in the loading process which lead to marked variation in the number of particles per vesicle. Regardless of the reason for the variation in vesicle packing, anomalous organelles then weigh the inherited particle fraction in daughter cells. Thus the process of dose dilution looks very different according to whether particle number or vesicle number is tracked through mitosis.

These studies pave the way for predictive modeling of nanopharmacology. The approach outlined allows us to relate the absolute dose level of a nanotherapeutic (particle number) and its formulation (intracellular packaging) to biomarkers of cell status, measured on the standardized, high-throughput platform of flow cytometry. It can also take into account the influences of cell cycle and proliferation on nanotherapeutic pharmacokinetics and pharmacodynamics, which are important arbiters of therapeutic outcome in diseases such as cancer. For example, nanoparticulate drug formulations could be fluorescently labeled and this labeling then used in conjunction with flow cytometry to track the exact dose across a population of cells as they progress through the cell cycle and proliferate under the influence of the therapeutic agent.

Methods

Cell Culture and QD Loading

U-2 OS (ATCC HTB-96) cells were maintained in McCoy’s 5a medium (Sigma M8403) supplemented with 10% fetal calf serum (FCS), 1 mM glutamine, and antibiotics and incubated at 37 °C in an atmosphere of 5% CO2 in air, in 25 cm2 cell culture flasks. Cells were loaded with commercially available targeted nanocrystals using the Qtracker 705 cell labeling kit (10 nM) (Invitrogen (Q25061MP)). Qtracker reagents A and B were premixed and then incubated for 5 min at room temperature. Fresh full growth medium (2 mL) was added to the tube and vortexed for 30 s. This labeling solution was then added to the cells and incubated for 1 h at 37 °C. After the 1 h period, the cells were washed twice with fresh media to remove any free quantum dots from the cell media and then reincubated at 37 °C in fresh media. To prepare for flow analysis, samples were incubated in FACS buffer (PBS/0.2% BSA/0.05% sodium azide) for 30 min before resuspension in 200 mL of PBS and storage in a refrigerator at 4 °C until later data acquisition on the flow cytometer.

Electron Microscopy

The quantum dot exposed cells (exposed for 1 h and incubated for a further 24 h) were harvested and placed in fixative (2% glutaraldehyde and 2% formaldehyde in 100 mM PIPES buffer), washed in a buffer, then spun into pellets, and fixed in 2% osmium tetroxide. Following dehydration by a series of ascending strength alcohols and washing with dry acetone, the specimens were infiltrated with Spurr’s resin which was polymerized at 60 °C for 24 h. Sections were cut from the polymerized block with a nominal thickness of 100 nm using an ultramicrotome (Leica Ultracut E) and placed on a copper grid (Agar Scientific). No conventional heavy metal stain (uranyl acetate or lead citrate) was used. Transmission electron microscopy (TEM) was then conducted on an FEI Tecnai F20 microscope operating at 200 kV and fitted with a Gatan Orius SC600A CCD camera. A total of 102 cells within one randomly selected thin section of the cell pellet was fully examined such that all membrane-bound quantum dots within each cell were identified and imaged. The images of the encapsulated quantum dots were processed to identify individual quantum dots using scripts in MATLAB, enabling quantification of numbers of quantum dots per vesicle. Section thickness was confirmed to be ∼100 nm using electron energy loss spectra recorded in a FEI CM200 FEG-TEM operating at 197 kV and fitted with a Gatan Imaging filter (GIF-200).

Whole cell information was collected from a resin block containing cells exposed to QDs for 1 h and prepared as described above, using a Gatan 3-View system32 installed on a FEI Quanta FEG250 ESEM operating at an accelerating voltage of 3.8 kV and with a water vapor pressure of 0.64 Torr (85 Pa). The ultramicrotome inside the SEM was used to cut sections from the polymerized block at nominal slice thickness of 100 nm, with serial backscattered imaging of the exposed block face recorded over an area of 69.014 μm × 69.014 μm with a pixel size of 17 × 17 nm, a 15 μs dwell time, a 30 μm objective aperture inserted, and at the manufacturer’s spot size setting of 3.5. A through thickness stack of 320 images was recorded over ∼25 h. The image stack was compiled and analyzed using Fiji image analysis software37 to select only image (sub)stacks of fully sectioned cells for 3-D reconstruction. Reconstructions were produced using the Imaris software with a voxel size of 17 nm × 17 nm × 100 nm.

Flow Cytometry

Cell images were acquired using an Imagestream100 cell analyzer (Amnis Corporation). A 488 nm wavelength laser was used to excite quantum dot fluorescence, which was collected with a 40×, 0.75 objective lens, using the 660–735 nm spectral detection channel. A subset of 1 × 104 cells taken from the larger cultured cell population was imaged for each sample and analyzed using the manufacturer’s software. Gating of the acquired data to ensure focused images of viable cells reduced the analyzed population to 5000 cells. Line-scan gradients were used to select cells within the focal plane, and gating on two-dimensional plots of cell area and aspect ratio were used to select viable cells. The system and peak image analysis algorithms were used to identify intensity clusters and calculate their number, assuming a discrimination level of intensity at twice the intensity of the background. Spot counting accuracy was confirmed by manual verification of confocal images. The sampling and gating procedures ensure that nanoparticle-loaded vesicles are only counted in healthy cells.

Statistical Modeling

Measured distributions of nanoparticles per vesicle and of particle-loaded vesicles per cell were fitted with statistical distributions to obtain probability distribution functions. The probability, Pn, of finding n particles in a cellular vesicle is described by a biexponential decay function of the form

graphic file with name nn-2013-019619_m003.jpg

with parameter values of, a1 = 0.103, b1 = 6 × 10–3, a2 = 0.017, b2 = 4 × 10–4. The probability, Pv, of finding v loaded vesicles in a cell is described by a Polya distribution of the form

graphic file with name nn-2013-019619_m004.jpg

with μ = 7 and b = 0.25. This is an overdispersed form of a Poisson distribution with mean, μ; b is a dispersion factor which broadens the distribution (b = 0, corresponds to a Poisson curve). To simulate a flow cytometry intensity histogram, the vesicle count PDF is randomly sampled to produce vesicle numbers for a simulated population of 10 000 cells; the particle number PDF is then randomly sampled to provide the nanoparticle dose in each vesicle.

Acknowledgments

This work was supported by the Engineering and Physical Sciences Research Council, U.K. under Grants EP/H008683/1 Swansea and EP/H008578/1 Leeds. The authors would like to thank the EPSRC for funding (EP/H008683/1 Swansea and EP/H008578/1 Leeds); A. Warley, K. Brady, and F. Winning (Centre for Ultrastructural Imaging, King’s College, London, U.K.) for pelleting and sectioning the cells for TEM analysis; T. Starborg (Wellcome Centre for Cell Matrix Research, University of Manchester) for performing the serial block face sectioning and imaging using Gatan’s 3-View package; A.G. Monteith and N. Wilkinson (Gatan U.K.) for facilitating access to the 3-View facility at Manchester and for help with the subsequent image processing.

Supporting Information Available

Modeled electron penetration using CASINO V2.42 (see Drouin et al., Scanning 2007, 29, 92–101, for further detail); movies reconstructing 3-D cell profiles from EM cell section images; and magnified images of the TEM section of Figure 2A. This material is available free of charge via the Internet at http://pubs.acs.org.

The authors declare no competing financial interest.

Supplementary Material

nn4019619_si_001.avi (52.8MB, avi)
nn4019619_si_002.mpg (44.5MB, mpg)
nn4019619_si_003.pdf (260.3KB, pdf)
nn4019619_si_004.pdf (208.4KB, pdf)

References

  1. Characterising the Potential Risks Posed by Engineered Nanoparticles, DEFRA governmental report, DEFRA Publications: London, 2007. [Google Scholar]
  2. Novel Materials in the Environment: The Case of Nanoparticles, Report from Royal Commission on Environment Pollution, TSO: Norwich, U.K., 2008. [Google Scholar]
  3. Wittmaack K. Excessive Delivery of Nanostructured Matter to Submersed Cells Caused by Rapid Gravitational Settling. ACS Nano 2011, 5, 3766–3778. [DOI] [PubMed] [Google Scholar]
  4. Hardman R. A Toxicological Review of Quantum Dots: Toxicity Depends on Physiochemical and Environmental Factors. Environ. Health Perspect. 2005, 1142, 165–172. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Albanese A.; Chan W. C. W. Effect of Gold Nanoparticle Aggregation on Cell Uptake and Toxicity. ACS Nano 2011, 5, 5478–5489. [DOI] [PubMed] [Google Scholar]
  6. Nell A. E.; Mädler L.; Velegol D.; Xia T.; Hoek E. M. V.; Somasundaran P.; Klaessig F.; Castranova V.; Thompson M. Understanding Biophysicochemical Interactions at the Nano–Bio Interface. Nat. Mater. 2009, 8, 543–557. [DOI] [PubMed] [Google Scholar]
  7. Chithrani B. D.; Ghazani A. A.; Chan W. C. W. Determining the Size and Shape Dependence of Gold Nanoparticle Uptake into Mammalian Cells. Nano Lett. 2006, 6, 662–668. [DOI] [PubMed] [Google Scholar]
  8. Zhang S.; Li J.; Lykotrafitis G.; Bao G.; Suresh S. Size-Dependent Endocytosis of Nanoparticles. Adv. Mater. 2008, 20, 1–6. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Iversen T.-G.; Skotland T.; Sandvig K. Endocytosis and Intracellular Transport of Nanoparticles: Present Knowledge and Need for Future Studies. Nano Today 2011, 6, 176–185. [Google Scholar]
  10. Rajan S. S.; Liu H. Y.; Vu T. Q. Ligand-Bound Quantum Dot Probes for Studying the Molecular Scale Dynamics of Receptor Endocytic Trafficking in Live Cells. ACS Nano 2008, 2, 1153–1166. [DOI] [PubMed] [Google Scholar]
  11. Huang J.; Bu L.; Xie J.; Chen K.; Cheng Z.; Li X.; Chen X. Effects of Nanoparticle Size on Cellular Uptake and Liver MRI with Polyvinylpyrrolidone-Coated Iron Oxide Nanoparticles. ACS Nano 2010, 4, 7151–7160. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Davda J.; Labhasetwar V. Characterization of Nanoparticle Uptake by Endothelial Cells. Int. J. Pharm. 2002, 233, 51–59. [DOI] [PubMed] [Google Scholar]
  13. Krpetić Z.; Saleemi S.; Prior I. A.; Seé V.; Qureshi R.; Brust M. Negotiation of Intracellular Membrane Barriers by TAT-Modified Gold Nanoparticles. ACS Nano 2011, 5, 5195–5201. [DOI] [PubMed] [Google Scholar]
  14. Elsaesser A.; Taylor A.; Yanés G. S.; McKerr G.; Kim E.-M.; O’Hare E.; Howard C. V. Quantification of Nanoparticle Uptake by Cells Using Microscopical and Analytical Techniques. Future Med. 2010, 5, 1447–1457. [DOI] [PubMed] [Google Scholar]
  15. Brandenberger C.; Muhlfeld C.; Ali Z.; Lenz A.-G.; Schmid O.; Parak W. J.; Gehr P.; Rothen-Rutishauser B. Quantitative Evaluation of Cellular Uptake and Trafficking of Plain and Polyethylene Glycol-Coated Gold Nanoparticles. Small 2010, 6, 1669–1678. [DOI] [PubMed] [Google Scholar]
  16. Jiang X.; Röcker C.; Hafner M.; Brandholt S.; Dörlich R. M.; Nienhaus G. U. Endo- and Exocytosis of Zwitterionic Quantum Dot Nanoparticles by Live HeLa Cells. ACS Nano 2010, 4, 6787–6797. [DOI] [PubMed] [Google Scholar]
  17. Dombu C. Y.; Kroubi M.; Zibouche R.; Matran R.; Betbeder D. Characterization of Endocytosis and Exocytosis of Cationic Nanoparticles in Airway Epithelium Cells. Nanotechnology 2010, 21, 355102. [DOI] [PubMed] [Google Scholar]
  18. Summers H. D.; Rees P.; Holton M. D.; Brown M. R.; Chappell S. C.; Smith P. J.; Errington R. J. Statistical Analysis of Nanoparticle Dosing in a Dynamic Cellular System. Nat. Nanotechnol. 2011, 6, 170–174. [DOI] [PubMed] [Google Scholar]
  19. Murphy R. F. Maturation Models for Endosome and Lysosome Biogenesis. Trends Cell Biol. 1991, 1, 77–82. [DOI] [PubMed] [Google Scholar]
  20. Sun Y. H.; Liu Y. S.; Vernier P. T.; Liang C. H.; Chong S. Y.; Marcu L.; Gundersen M. A. Photostability and pH Sensitivity of CdSe/ZnSe/ZnS Quantum Dots in Living Cells. Nanotechnology 2006, 17, 4469–4476. [Google Scholar]
  21. Mancini M. C.; Kairdolf B. A.; Smith A. M.; Nie S. Oxidative Quenching and Degradation of Polymer-Encapsulated Quantum Dots: New Insights into the Long-Term Fate and Toxicity of Nanocrystals in Vivo. J. Am. Chem. Soc. 2008, 130, 10836–10837. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Lin C.-H.; Chang L. W.; Chang H.; Yang M.-H.; Yang C.-S.; Lai W.-H.; Chang W.-H.; Lin P. The Chemical Fate of the Cd/Se/Te-Based Quantum Dot 705 in the Biological System: Toxicity Implications. Nanotechnology 2009, 20, 215101. [DOI] [PubMed] [Google Scholar]
  23. Errington R. J.; Brown M. R.; Silvestre O.; Njoh K. L.; Chappell S. C.; Khan I.; Rees P.; Wilks S. P.; Smith P. J.; Summers H. D. Single Cell Nanoparticle Tracking To Model Cell Cycle Dynamics and Compartmental Inheritance. Cell Cycle 2010, 9, 1–10. [DOI] [PubMed] [Google Scholar]
  24. Kim J. A.; Aberg C.; Salvati A.; Dawson K. A. Role of Cell Cycle on the Cellular Uptake and Dilution of Nanoparticles in a Cell Population. Nat. Nanotechnol. 2011, 7, 62–68. [DOI] [PubMed] [Google Scholar]
  25. Hanahan D.; Weinberg R. A. The Hallmarks of Cancer. Cell 2000, 100, 57–70. [DOI] [PubMed] [Google Scholar]
  26. Brown M. R.; Summers H. D.; Rees P.; Chappell S. C.; Silvestre O. F.; Khan I. A.; Smith P. J.; Errington R. J. Long-Term Time Series Analysis of Quantum Dot Encoded Cells by Deconvolution of the Autofluorescence Signal. Cytometry, Part A 2010, 77A, 925–932. [DOI] [PubMed] [Google Scholar]
  27. Hoshino A.; Hanaki K.; Suzuki K.; Yamamoto K. Applications of T-Lymphoma Labeled with Fluorescent Quantum Dots to Cell Tracing Markers in Mouse Body. Biochem. Biophys. Res. Commun. 2004, 314, 46–53. [DOI] [PubMed] [Google Scholar]
  28. Shapiro H. M. Practical Flow Cytometry, 4th ed.; Wiley: New York, 2003. [Google Scholar]
  29. Schweiger C.; Hartmann R.; Zhang F.; Parak W. J.; Kissel T. H.; Rivera-Gil P. Quantification of the Internalization Patterns of Superparamagnetic Iron Oxide Nanoparticles with Opposite Charge. J. Nanobiotechnol. 2012, 10, 28. [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Lartigue L.; Wilhelm C.; Servais J.; Factor C.; Dencausse A.; Bacri J.-C.; Luciani N.; Gazeau F. Nanomagnetic Sensing of Blood Plasma Protein Interactions with Iron Oxide Nanoparticles: Impact on Macrophage Uptake. ACS Nano 2012, 6, 2665–2678. [DOI] [PubMed] [Google Scholar]
  31. Hondow N.; Brydson R.; Wang P.; Holton M. D.; Brown M. R.; Rees P.; Summers H. D.; Brown A. Quantitative Characterization of Nanoparticle Agglomeration within Biological Media. J. Nanopart. Res. 2012, 14, 977. [Google Scholar]
  32. Denk W.; Horstmann H. Serial Block-Face Scanning Electron Microscopy To Reconstruct Three-Dimensional Tissue Nanostructure. PLoS Biol. 2004, 2, e329. [DOI] [PMC free article] [PubMed] [Google Scholar]
  33. Wilhelm C.; Gazeau F.; Roger J.; Pons J. N.; Bacri J. C. Interaction of Anionic Superparamagnetic Nanoparticles with Cells: Kinetic Analyses of Membrane Adsorption and Subsequent Internalisation. Langmuir 2002, 18, 8148–8155. [Google Scholar]
  34. Jaetao J. E.; Butler K. S.; Adolphi N. L.; Lovato D. M.; Bryant H. C.; Rabinowitz I.; Winter S. S.; Tessier T. E.; Hathaway H. J.; Bergemann C.; et al. Enhanced Leukemia Cell Detection Using a Novel Magnetic Needle and Nanoparticles. Cancer Res. 2009, 69, 8310–8316. [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Adolphi N. L.; Huber D. L.; Bryant H. C.; Monson T. C.; Fegan D. L.; Lim J.-K.; Trujillo J. E.; Tessier T. E.; Lovato D. M.; Butler K. S.; et al. Characterisation of Single-Core Magnetite Nanoparticles for Magnetic Imaging by SQUID Relaxometry. Phys. Med. Biol. 2010, 55, 5985–6003. [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Bergeland T.; Widerberg J.; Bakke O.; Nordeng T. W. Mitotic Partitioning of Endosomes and Lysosomes. Curr. Biol. 2001, 11, 644–651. [DOI] [PubMed] [Google Scholar]
  37. Schindelin J.; Arganda-Carreras I.; Frise E.; Kaynig V.; Longair M.; Pietzsch T.; Preibisch S.; Rueden C.; Saalfeld S.; Schmid B.; et al. Fiji: An Open-Source Platform for Biological-Image Analysis. Nat. Methods 2012, 9, 676–682. [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

nn4019619_si_001.avi (52.8MB, avi)
nn4019619_si_002.mpg (44.5MB, mpg)
nn4019619_si_003.pdf (260.3KB, pdf)
nn4019619_si_004.pdf (208.4KB, pdf)

Articles from ACS Nano are provided here courtesy of American Chemical Society

RESOURCES