Abstract
We studied the equilibrium conformations of a ‘zinc porphyrin tweezer’ composed of two carboxylphenyl-functionalized zinc tetraphenyl porphyrin subunits connected by a 1,4 butyndiol spacer, which was suspended inside the amphiphilic regions of 1,2-distearoyl-sn-glycero-3-phosphocholine (DSPC) liposomes. By combining phase-modulation two-dimensional fluorescence spectroscopy (2D FS) with linear absorbance and fluorimetry, we determined that the zinc porphyrin tweezer adopts a mixture of ‘folded’ and ‘extended’ conformations in the membrane. By fitting an exciton-coupling model to a series of data sets recorded over a range of temperatures (17 – 85 °C) and at different laser center wavelengths, we determined that the folded form of the tweezer is stabilized by a favorable change in the entropy of the local membrane environment. Our results provide insights toward understanding the balance of thermodynamic factors that govern molecular assembly in membranes.
Keywords: Two-dimensional electronic spectroscopy, DSPC liposomes, exciton-coupled dimers, binary mixture, entropy and enthalpy of folding
I. Introduction
The properties of biological macromolecular complexes are to a great extent influenced by non-covalent interactions between proteins, nucleic acids, sugars, and lipids 1-5. These interactions take many different forms. For example, proteins that bind to nucleic acids utilize hydrogen bonding and stacking between amino acid side chains and bases. The chromophore arrays of photosynthetic complexes are held in specific three-dimensional arrangements through their contacts with proteins, and through direct interactions between pigments. The folding of many proteins is driven, not only by the formation of favorable non-covalent bonds between amino acids, but also by the increasing entropy of water liberated from contacts with hydrophobic surfaces.
Significant work in molecular biology has focused on developing a better understanding of the various contributions to the stability of specific macromolecular complexes 6-8. The function of such systems often relies on their ability to exist in different conformational states. For example, the fidelity of DNA replication is thought to involve rapid interconversion between two conformational end-states of the DNA polymerase – primer-template DNA complex; a ‘proofreading’ conformation and a processive ‘polymerization’ conformation 9. Studies that seek to understand the mechanisms of such processes must determine the identities of the end-states, their relative stabilities, and the kinetics of their interconversion. A significant experimental challenge is to separate signals from the different end-states so that structural, thermodynamic and kinetic parameters can be accurately ascertained.
Changes in stability associated with the formation of a macromolecular complex are often governed by a delicate balance between large and opposing changes in enthalpy and entropy 1, 6, 8. Contributions to the enthalpy depend on direct interactions between components of the complex, in addition to contacts between the solvent and those components that become more or less solvent-exposed. Entropic contributions are due to changes in conformational degrees of freedom of the components (i.e., translational, rotational, vibrational, etc.), as well as those of solvent molecules, which may be tightly bound to exposed component surfaces. For our current purposes, we consider the dimerization reaction between two monomers . In this case, the free energy of association can be partitioned into enthalpic and entropic terms reflecting solvent-solvent interactions, monomer-monomer interactions, and monomer-solvent interactions, allowing for different mechanisms to lead to dimer stability. For example, dimer formation might be driven by favorable monomer-monomer enthalpic interactions, sufficient to offset the loss of entropic degrees of freedom of the ‘free’ monomer subunits. Alternatively, a favorable change in the solvent entropy upon dimerization might be large enough to compensate for the disruption of otherwise stable enthalpic contacts between solvent and exposed monomer surfaces.
In earlier work 10, one of us (TFM) found that dimeric esters of TPP linked by acyclic C2 symmetric 1,5-, 1,7- and 1,9-diols formulated in highly uniform unilamellar liposomes (DSSC, φave = 26±5.1 nm) exhibited strong circular dichroism (CD) signals at room temperature. These observations suggested the presence of organized bilayer-TPP structures supported by lipid bilayer-TPP interactions, or bilayer-constrained TPP-TPP interactions. Moreover, even simple long-chain naphthamides, when formulated in liposomes, exhibited complex temperature-dependent CD spectra 11-12 suggesting the assembly of multi-chromophore structures.
Two-dimensional electronic spectroscopy (2D ES) is a method that probes the correlations between successive electronic transitions, and it has been used to investigate energy transfer pathways in photosynthetic protein-pigment complexes 13-16, conjugated polymers 17 and semiconductors 18-19. In principle, 2D ES experiments are sensitive to the relative orientations of resonantly excited electronic transition dipole moments of coupled multi-chromophore systems, suggesting its general application as an analytical tool for structural elucidation. Recently, a fluorescence-detected version of 2D ES, called two-dimensional fluorescence spectroscopy (2D FS), was used to elucidate the conformation of a self-assembled magnesium meso tetraphenylporphyrin (MgTPP) dimer in a biological membrane 20-21. Subsequent extension of the method to ultraviolet wavelengths made it possible to solve the solution conformation of a dinucleotide of the fluorescent adenine analogue 2-aminopurine (2-AP) 22.
In previous 2D FS experiments performed on MgTPP chromophores embedded in the amphiphilic regions of 1,2-distearoyl-sn-glycero-3-phosphocholine (DSPC) liposomes, we found that self-assembled MgTPP dimers formed relatively open “T-shaped” structures, suggesting that the association process was driven primarily by an increase in the entropy of the local membrane environment (i.e., the monomer-solvent entropy term) 21. However, those experiments were not sufficient to determine the values of the different contributions to the free energy of dimerization. Measurements performed over a range of temperatures should yield separately the enthalpic and entropic contributions to dimer assembly. Moreover, by using a dimer consisting of two chemically tethered monomers instead of the previously studied self-assembled dimer, it is possible to work under dilute solute conditions to minimize the perturbation of solvent-solvent interactions, and to avoid the process of higher-order aggregation.
In this paper, we present 2D FS experiments on a chemically tethered dimer – a ‘zinc porphyrin tweezer’ [herein designated as (ZnTPP)2], which was synthesized by coupling two zinc 5-(p-carboxylphenyl)-10,15,20-triphenylporphyrin subunits using a 1,4 butyndiol spacer (see Fig. 1A). We studied the zinc porphyrin tweezer (ZnTPP)2 in the same DSPC liposomes as in our previous experiments on the self-assembled magnesium porphyrin dimer 20-21, and we expect both systems to exhibit similar enthalpic and entropic interactions with the local membrane environment. We combined a broad range of experimental data obtained from 2D FS experiments, linear absorption, and fluorimetry, which we compared to dimer conformation models based on the exciton coupling between the porphyrin subunits. Our results indicate that the zinc porphyrin tweezer adopts a mixture of ‘extended’ and ‘folded’ conformations in the membrane, and that the relative populations of these two states are temperature-dependent. By performing these experiments over a range of temperatures, we separately determined the relevant enthalpic and entropic contributions to the overall free energy change of the folding process.
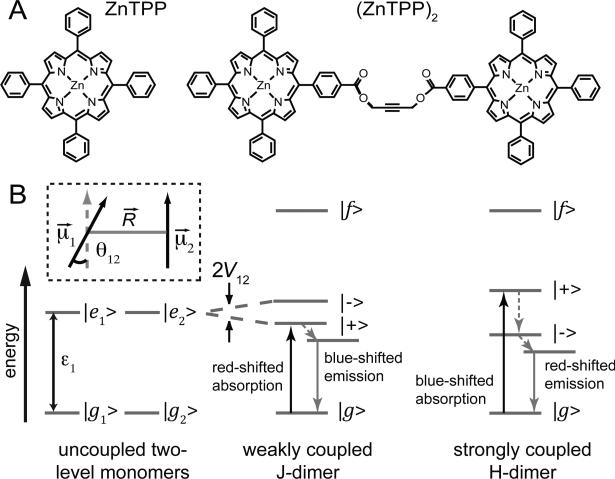
Figure 1.
(A) Structures of the chromophores used in this study, zinc tetraphenylporphyrin (ZnTPP) and a covalently linked dimer of ZnTPP (ZnTPP)2. (B) Energy level diagrams of two degenerate two-level molecules. Electronic coupling results in a four-level dimer with a single ground state |g〉, two non-degenerate singly-excited states |±〉, and a doubly-excited state |f〉. For a ‘weakly coupled J-dimer’ (i.e., with a head-to-tail dipole arrangement), the |+〉 state is shifted to lower energy. The situation is juxtaposed for a ‘strongly coupled H-dimer’ (i.e., a side-by-side dipole arrangement). Because transitions involving the |+〉 state are favored, absorption is red-shifted for a J-dimer, while it is blue-shifted for an H-dimer. After excited state relaxation, emission occurs from the lowest-energy singly-excited state, which is lower in energy for the H-dimer than the J-dimer due to the H-dimer's stronger coupling. Therefore, fluorescence from the H-dimer occurs on the red edge of the emission line shape while emission from the J-dimer occurs on the blue edge of the emission line shape.
II. Experimental Methods
A. Preparation of the (ZnTPP)2 dimer
1,4-Butanediol, but-2-yn-1,4-diol, zinc acetate dihydrate, and dicyclohexylcarbodiimide (DCC) were purchased from Sigma Aldrich (Milwaukee, WI) and used as received. Dry dichloromethane (DCM) and tetrahydrofuran (THF) were prepared by passage over activated alumina or molecular sieves under an argon atmosphere. 1H NMR spectra were recorded on Varian Mercury 400 or Jeol ECA 500 MHz spectrometers. Samples were measured in CDCl3 solution (referenced to residual solvent, δ = 7.24 ppm). Accurate mass spectra measurements were made using an Agilent 6230 time of flight mass spectrometer (TOFMS). TLC was carried out on aluminum plates thin-coated with silica (0.1 mm, EM Merck) and visualized under UV-light (254 nm).
Dimer (TPP)2 was prepared using a modification of the procedure of Nakanishi and coworkers 23. To a solution of 5-p-carboxyphenyl)-10,15,20-triphenylporphyrin (2.2 equiv), prepared as previously described, 24 in DCM (approximately 0.1-0.2 M) and DCC (2.2 equiv) was added but-2-yn-1,4-diol (1 equiv) and the mixture was stirred at room temperature until TLC of a sample of the mixture showed absence of starting material (overnight). The mixture was diluted with DCM (10 volumes), washed with NaHCO3 (aqueous, saturated) and dried over Na2SO4. Removal of the volatiles under reduced pressure gave a residue that was subjected to flash chromatography (silica, hexane: ethyl acetate) to provide pure TPP-diester (TPP)2 with TOFMS and NMR data consistent with the assigned structure.
A solution of (TPP)2 in DCM (0.1 M) was stirred rapidly with excess zinc acetate dihydrate (Zn(C2H3O2)2•2H2O) overnight at room temperature 23. The mixture was filtered and concentrated to give a highly colored residue that was purified by flash chromatography to give (ZnTPP)2 with TOFMS and NMR data consistent with the assigned structure.
Control experiments were performed using zinc meso tetraphenylporphyrin (ZnTPP) as a monomer, which was purchased from Sigma Aldrich and used as received. We prepared porphyrin / liposome samples using DSPC as the lipid according to established procedures 20, 25. We prepared samples containing the zinc porphyrin tweezer using a 30:1 DSPC : (ZnTPP)2 molar ratio, and samples containing monomeric ZnTPP using the ratios 20:1 and 70:1 DSPC : ZnTPP. Before performing our measurements, we annealed each liposome sample by heating it to 70 °C and allowing it to slowly cool back to room temperature (23 °C). We prepared solution phase samples by dissolving (ZnTPP)2 or ZnTPP in spectroscopic grade chloroform.
B. Differential Scanning Calorimetry (DSC)
We performed DSC measurements using a TA instruments DSC 2920. We prepared a 30:1 DSPC : (ZnTPP)2 liposome sample in addition to a control blank DSPC liposome sample using the procedures described above. The samples were centrifuged for 5 minutes at 5000 RPM and the supernatant liquid equal to 96% of the total volume was removed. The resulting samples (weighing ~ 10 mg) were placed in aluminum hermitic pans and crimped shut. An empty pan was used as a reference and the temperature was scanned from 10 °C to 80 °C at a rate of 10 °C / minute. After performing an initial run to anneal the sample, we recorded data on the second consecutive run.
C. Linear Absorption and Fluorescence Spectroscopy
We measured the linear absorption spectra of our samples using a Cary 3E UV-visible spectrophotometer, which was equipped with a computer-interfaced temperature control system. There was significant non-resonant background underlying the Q(0,0) line shpae (~ 600 nm), which was due to the strong B- (Soret) band transition (~ 430 nm). To obtain the line shapes used for our data analysis, we performed a background subtraction by fitting a line to the blue-edge (513 – 538 nm) and to the red-edge (650 – 700 nm) of the Q(0,0) and Q(0,1) features, and by subtracting this fit from the raw data. We recorded fluorescence spectra using a Jobin-Yvon FluoroMax-3 spectrofluorometer, which was equipped with a manual temperature control system. Fluorescence spectra were measured by exciting, in separate experiments, the blue and the red edges of the Q(0,0) band (596 and 602 nm), the Q(0,1) band (551 and 570 nm), and the B-band (418 and 452 nm).
D. Two-Dimensional Fluorescence Spectroscopy
The 2D FS instrumentation and method is described in detail elsewhere 20-21, 26. Briefly, the sample was resonantly excited using a sequence of four phase-modulated collinear femtosecond optical pulses. The ensuing nonlinear excited state populations were phase-synchronously detected by monitoring fluorescence. The laser pulses were prepared using two optical parametric amplifiers (OPAs), which were driven with the output of a 250 kHz amplified Ti:Sapphire oscillator (Coherent, RegA 9000, pulse energy ~ 10 μJ). The tunable output of each OPA was passed through a pair of SF10 prisms (double pass geometry) for pre-dispersion compensation, and subsequently directed into a Mach-Zehnder interferometer (MZI). The input of each MZI was split, and the resulting two beams were each passed through an acousto-optic Bragg cell (AOBC), which imparted a continuous phase sweep to the pulse. The relative beam paths were controlled using a retro-reflective mirror that was mounted to a computer-interfaced optical delay stage, and the beams were recombined and made collinear at the exit beam-splitters. The output of one of the MZIs was passed through an additional computer-interfaced delay stage before it was combined at a beam-splitter with the output of the other MZI, to create a train of four collinear pulses with controllable inter-pulse time delays. The AOBCs were detuned from each other such that the relative phase of pulses 1 and 2 was swept at 8 kHz and the relative phase of pulses 3 and 4 was swept at 5 kHz. A replica of each pulse pair was spectrally filtered using a monochromator and detected using an avalanche photodiode (APD). The 8 and 5 kHz reference signals created from the first and second pulse pairs, respectively, were input to a custom-built waveform mixer, which generated sum (13 kHz) and difference (3 kHz) sidebands. These waveforms were used as references for lock-in detection of the fourth-order population signals, analogous to the nonrephasing (NRP) and rephrasing (RP) signals measured in 2D ES 20-21, 26. To collect a 2D FS spectrum, the delays between pulses 1 and 2 (designated t21 = τ) and between pulses 3 and 4 (t43 = t) were scanned from 0 to 250 fs, while the delay between pulses 2 and 3 (t32 = T) was held fixed. The cosine and sine projections of the 13 and 3 kHz signals were thus recorded, and the Fourier transform of the resulting 2D interferogram, with respect to the variables τ and t, yielded the 2D FS spectrum. For all of the experiments discussed in this paper, we set T = 0. Before each series of experiments, the pulse durations and delay stage positions at which the pulses were maximally overlapped were determined through second harmonic generation autocorrelation using a beta barium borate (BBO) crystal. Before each data set, the phase calibrations of the lock-in amplifiers were adjusted to maximize the cosine projection of the signal at the time origin.
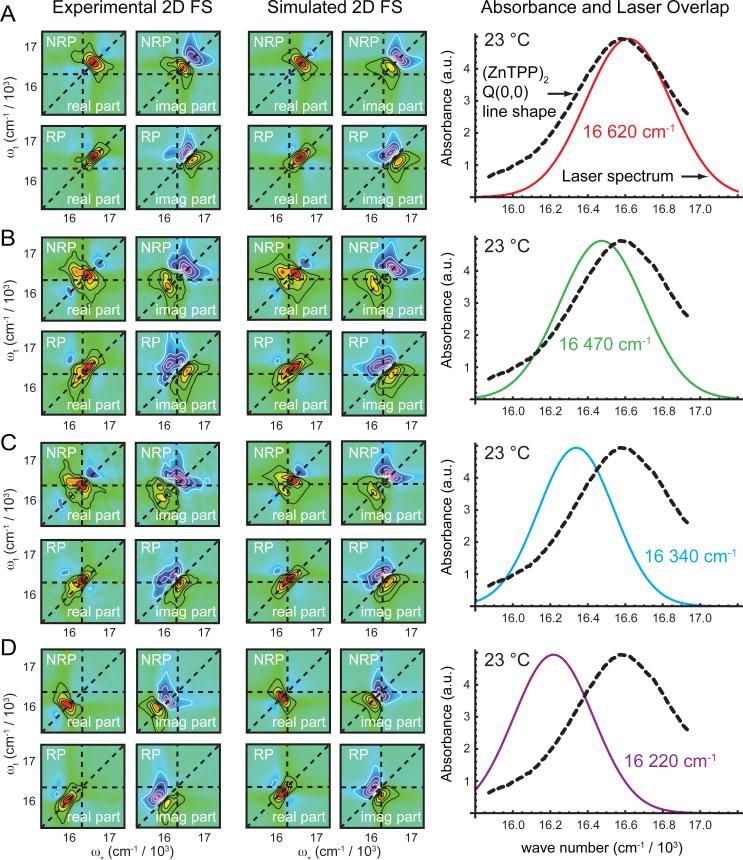
For all of our 2D FS measurements, we circulated the sample through a quartz flow cell using a peristaltic pump. The fluorescence was spectrally filtered, and detected using an APD. We used various filters and filter combinations for different experiments, which were a 610 – 680 nm band-pass filter (Chroma HQ645/75m), a 620 nm long-pass filter (Omega 3RD 620LP), a 635 nm long-pass filter (Chroma HQ635LP), a 645 nm long-pass filter (Chroma HQ645LP), and the above 620 nm long-pass filter combined with a 650 nm short-pass filter (ThorLabs FE S0650). The temperature was controlled by circulating water from a heat bath through a copper block in which the sample flow cell was mounted. The heat bath was calibrated by measuring the temperature of a blank sample using a thermocouple. For our temperature-dependent measurements, we annealed the liposome samples as described above, before recording successive data sets in order of increasing temperature at 23, 28, 46, 63, 72, and 85 °C. After reaching the highest temperature, the sample was slowly cooled to 17 °C for the final sets of measurements. At each temperature, we recorded 2D fluorescence spectra with the laser spectrum centered at four different frequencies: 16 620, 16 470, 16 340 and 16 220 cm-1.
E. Molecular Modeling Calculations
We performed thermodynamic calculations on the zinc porphyrin tweezer in the ‘folded’ and ‘extended’ conformations based on the Universal Force Field (UFF) 27. The UFF was used for optimizations of model structures for the ‘folded’ and ‘extended’ conformations. Subsequently, enthalpies and entropies of these conformations were computed in the harmonic approximation using UFF Hessian matrices. The UFF model was designed to provide consistent accuracy across the periodic table and yields rather accurate structure predictions for organic molecules 27 as well as transition-metal complexes 28. While the UFF model lacks parameterization to correctly describe planar Zn-porphyrin complexes, we expect it to provide useful estimates for differences in thermodynamic parameters between ‘folded’ and ‘extended’ conformations. All calculations were performed using the TURBOMOLE suite of programs 29.
III. Modeling Linear Absorption and 2D FS Data
A. Exciton-Coupled Four Level Dimer Model
Models that we previously used to simulate linear absorption and 2D FS spectra of metal porphyrin dimers, which depend on dimer conformation, are described in detail elsewhere 20-22. For the current study, we used the coupled two-dipole model 21, 30 with some additional modifications. Here, each monomer subunit of the zinc porphyrin tweezer supports a single ground state accessible electronic transition |en〉 ← |gn〉, with electric dipole transition moment (EDTM) μn [n ∈ {1,2}], and energy ε1 (see Fig. 1B). The effect of coupling between transitions is to create a four-level system consisting of a common ground state |g〉, two singly excited states |±〉 with ε± = ε1 ± V12, and a doubly excited state |f〉 with εf ≅ 2ε1. The symmetric and anti-symmetric singly excited states have wave functions delocalized among the monomer sites, which are related to the site basis according to . We used the point-dipole approximation to calculate the electronic coupling between EDTMs of each monomer
| (1) |
In Eq. (1), R12 is the vector connecting the centers of the EDTMs, and ε0 is the vacuum permittivity. The collective EDTMs that mediate transitions between ground and singly excited states are given by μ± = (1/2)[μ1 ± μ2], and between singly excited states and doubly excited states by μ±f = ±μ±. The intensities of the transitions between the various levels depend on the relative orientations of the dipoles within the complex. For example, the amplitudes of the ground state allowed transitions are given by I± = |μ|2 (1 ± cosθ12), where |μ|2 is the square magnitude of the monomer EDTM, and θ12 is the relative dipole angle. We note that an ‘H-type’ side-by-side configuration (i.e., ↑↑) with θ12 = 0 has the majority of its oscillator strength carried by the higher energy (blue-shifted) transition, whereas a ‘J-type’ head-to-tail configuration (i.e., →→) has the majority of its oscillator strength carried by the lower energy (red-shifted) transition. The effect of non-zero θ12 is to partition some intensity to the otherwise ‘dark’ transition. Moreover, the conformation of the dimer affects its emission spectrum. As illustrated in Fig. 1B, a weakly coupled J-dimer results in fluorescence on the blue edge of the emission line shape, while a strongly coupled H-dimer leads to self-quenching and relatively weak fluorescence on the red edge of the emission line shape.
We performed a series of 2D FS measurements with the laser spectrum centered at different wavelengths, ranging from the peak of the Q(0,0) absorption band to its red shoulder. For all of these measurements, we observed that the peaks of the 2D FS spectra shifted systematically with changing laser center wavelength, suggesting that the Q(0,0) line shapes were inhomogeneously broadened. To account for static disorder, we included in our model a correction based on the spectral overlap between the laser and components of the absorption spectrum 22. We modeled the laser spectrum g(ω) and individual spectral features anm(ω), due to a transition bridging the mth and nth state, as Gaussians
| (2) |
and
| (3) |
In Eqs. (2) and (3), ωL is the center frequency of the laser spectrum, σ1 is the standard deviation of the component of the absorption line shape that results in the shift, and σL (≈ 220 cm-1) is the standard deviation of the laser spectrum. For a given transition, we determined the simulated 2D FS spectrum from the spectral overlap function g(ω) · anm (ω). We thus adjusted the transition center frequency according to
| (4) |
and we adjusted the weight of the transition, which was determined by the laser amplitude, according to
| (5) |
We used the above model to calculate the center frequency for each 2D FS feature, assuming a Gaussian line shape with line width characterized by its phenomenological dephasing time τ. In addition to the correction given by Eq. (5), we applied the usual contributions to the signal from each coherence pathway, weighted according to the rotational average of the sequence of transition dipole moments involved in that pathway, 〈μ1μ2μ3μ4〉. We assumed that the orthogonal Qx and Qy EDTMs on each porphyrin monomer could be represented by one “effective” EDTM (discussed further in Results). We therefore modeled the linear absorption spectrum according to
| (6) |
where a0 is a baseline offset, δ is the intensity, σlin is the spectral line width, and the parameters μ, θ12, and ε± are defined above.
B. Fitting Procedures
We used our temperature-dependent linear absorption and 2D FS data sets, taken at four different laser center wavelengths, to constrain the structural parameters that determine the zinc porphyrin tweezer conformations. The fitting procedure involved a 16-parameter nonlinear global optimization, which we performed using the aid of the software package KNITRO 31. As we discuss further below, we determined from our fluorimetry and spectrally filtered 2D FS experiments that our data could not be modeled in terms of a single dimer conformation. We concluded that there must be two structures present in the membrane, one ‘folded’ conformation, which we modeled as an H-dimer, and one ‘extended’ conformation, which we modeled as a J-dimer. We used the model described above to simultaneously fit the linear absorption spectrum and both real and imaginary parts of the RP and NRP spectra, with the laser center frequency set to 16 620 cm-1 and 16 470 cm-1. The configurations that optimized these fits to our data also yielded spectra that matched our 2D FS measurements recorded with laser center frequency set to 16 340 cm-1 and 16 220 cm-1. Nevertheless, when the laser was significantly detuned from the Q(0,0) absorption maximum, as was the case with 16 340 cm-1 and 16 220 cm-1 excitation, the model slightly underestimated the extent to which the peaks were red-shifted towards the laser center frequency. For this reason, we only included in our optimizations the linear absorption and the 2DFS spectra with the laser center frequency tuned to 16 620 cm-1 and 16 470 cm-1.
We performed the following procedure to obtain optimized solutions for a mixture of H- and J-dimer species. The H- and J-dimer conformations were each characterized by five variables: i) the electronic coupling strength VH(J), ii) the relative dipole angle of the two monomers θH(J), iii) the phenomenological dephasing time τH(J), iv) the fluorescence quantum yield of the doubly excited state relative to the singly excited states ΓH(J), and v) the line shape overlap parameter σH(J). In addition, six parameters characterized the collective system: vi) the linear spectrum baseline offset a0, vii) the linear spectrum intensity δ, viii) the linear spectrum line width σlin, ix) the monomer transition energy ε1, x) the ratio b of H-dimer to J-dimer conformational populations, and xi) the ratio d of H-dimer to J-dimer fluorescence quantum yields. Initially, we calculated the linear absorption and 2D spectra for independent H- and J-dimer conformations. We treated these single species spectra as basis functions from which we obtained the linear spectrum of the mixture taking a linear combination of the two, weighted by the relative population of the H-dimer to that of the J-dimer. We thus obtained the 2D spectrum of the mixture by weighting the 2D spectrum of the H-dimer by its relative population and its relative fluorescence quantum yield, and combining this with the spectrum of the J-dimer.
We optimized the sixteen model parameters to find a global minimum of the least-squares cost function , which we constructed as follows.
| (7) |
| (8) |
| (9) |
In Eq. (7), NRP(RP)sim(exp)(ωτ, ωt) is the simulated (experimental) NRP (RP) signal at frequencies (ωτ, ωt). In Eq. (8), is the simulated (experimental) linear spectrum. In Eq. (9), is for the simulated and experimental spectra using 16 220 (16 470) cm-1 excitation, and n is a weighting factor used to make the contribution of to the cost function comparable to that of . We set n = 10 000 in order to fit our data taken at 17, 23, 28, 46, and 63°C. For the fits to data taken at 72 and 85 °C, we increased the value of n to 20 000 and to 50 000, respectively, in order to maintain a good fit to the linear spectrum. We first minimized the cost function for the room temperature (23 °C) data set to find an optimized sixteen-parameter solution. For the remaining temperature data sets, we fixed the parameters ε1, VH, VJ, θH, θJ and d to their room temperature values. We then varied the remaining parameters to minimize the cost function.
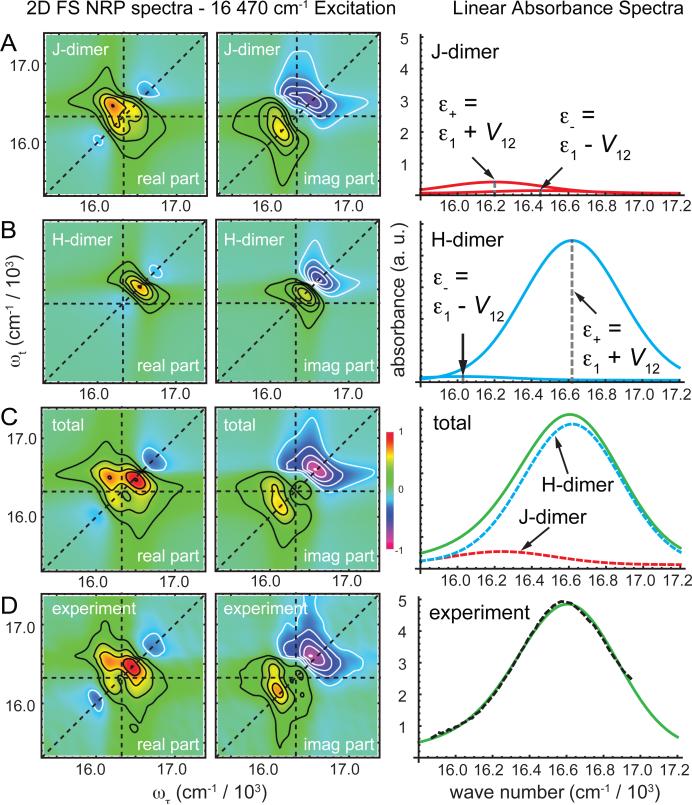
In Fig. 2, we show an example of simulated spectra obtained from the fitting procedure described above. For brevity, we show here only the 2D FS NRP spectra under 16 470 cm-1 excitation. However, we performed all of our optimizations by minimizing the cost function [Eq. (9)], which used as simultaneous constraints the linear absorbance, RP and NRP 2D FS spectra obtained with laser center frequency tuned to 16 620 and 16 470 cm-1. RP and NRP 2D FS spectra were routinely combined to obtain the total correlation spectra 21.
Figure 2.
Binary mixture decomposition analysis based on minimization of the cost function described by Eq. (9). Simulated contribution to 2D FS NRP and linear absorbance spectra are shown for (A) the J-dimer, (B) the H-dimer, and (C) the combined components of the mixture. (D) The experimental 2D FS and linear absorbance are to be compared to the simulated spectra shown in (C).
IV. Results
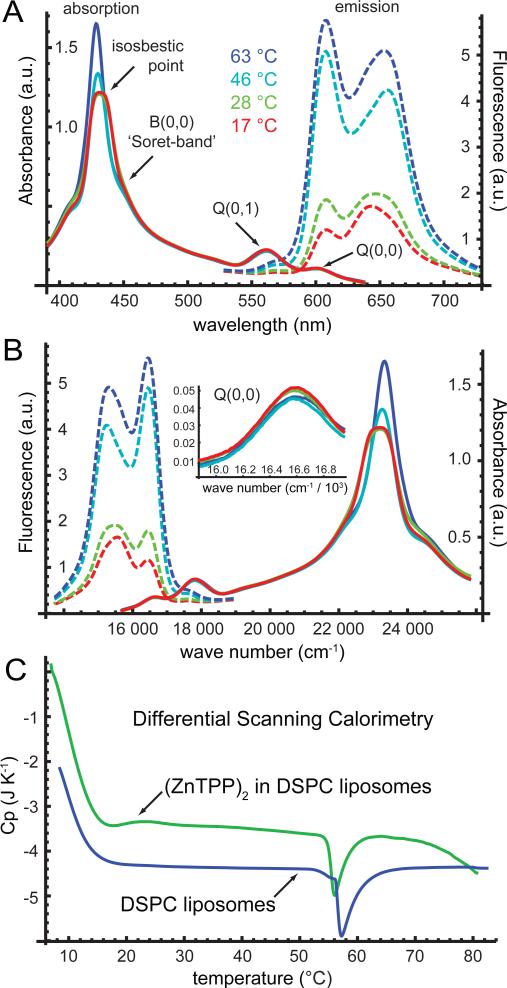
In Fig. 3, we present temperature-dependent absorption and fluorescence spectra of the DSPC liposome / (ZnTPP)2 system. We recorded the absorption spectra over the range 400 – 650 nm and observed the three characteristic features associated with metal porphyrins in solution 32. These are the Q(0,0)- and Q(0,1)-bands centered at 600 nm and 560 nm, respectively, and the B-band centered at 430 nm. We recorded fluorescence spectra by exciting the blue-edge of the B-band at 420 nm, and we observed two major features centered at ~ 610 and 650 nm. We performed these measurements at temperatures ranging from 17 – 85 °C.
Figure 3.
(A) The linear absorption (solid curves) and fluorescence spectra (dashed curves) of the zinc porphyrin tweezer (ZnTPP)2 in DSPC liposomes are shown for different temperatures, ranging from 17 °C to 63 °C. The spectra are plotted versus wavelength. However, the B-band narrows and blue-shifts at elevated temperatures, while the low-energy fluorescence band red-shifts at elevated temperatures. A single isosbestic point occurs in the B-band close to ~ 440 nm. (B) The same spectra shown in the preceding panel are plotted versus wave number. The inset shows an expanded view of the Q(0,0) band, which is the absorption band excited in our 2D FS measurements. The Q(0,0) band broadens slightly at elevated temperatures, but does not change shape significantly. (C) Differential scanning calorimetry data are shown for DSPC liposome samples prepared in the absence and presence of the (ZnTPP)2 dimer. The gel-to-liquid-crystal phase transition occurs near 57 °C in DSPC 33.
The fluorescence line shapes of the liposome / (ZnTPP)2 system were broad and asymmetric for all of the temperatures we investigated, suggesting that they might be a superposition of two bands. This is to be compared to the relatively narrow and symmetric line shapes of monomeric ZnTPP in solution, and at low concentration in liposomes. When we selectively excited the liposome / (ZnTPP)2 system on the red-edge of the absorption bands [i.e., the B-band at 452 nm and the Q(0,1)-band at 570 nm], we found that the blue-edge of the emission spectrum was enhanced. Conversely, when we excited on the blue-edge of the absorption bands, the red-edge of the emission spectrum was enhanced. Moreover, both the B-band and the fluorescence line shapes were sensitive to temperature. We observed that the blue-edge of the B-band and the red-edge of the emission line shape became increasingly more pronounced as the temperature was raised, and that a single isosbestic point was present in the absorption spectrum of the B-band. These observations further suggest the existence of two equilibrium populations of species with blue-edge excitation correlated to red-edge emission, and red-edge excitation correlated to blue-edge emission. While these temperature-dependent changes of the spectral line shapes were significant, the Q(0,0) and Q(0,1) features exhibitd very little sensitivity to temperature (see Fig. 3B, inset). We further note that the DSPC liposome system undergoes a gel-to-liquid-crystal phase transition close to ~ 57 °C 33. We determined by differential scanning calorimetry (DSC) that the transition temperature was shifted only slightly (~2 °C) by the presence of the (ZnTPP)2 chromophore (see Fig. 3C).
In chloroform solution, the 2D FS spectra of (ZnTPP)2 exhibited only a single diagonal feature, similar to those observed from monomeric ZnTPP. In low viscosity solvents, the (ZnTPP)2 molecule can adopt a broad distribution of conformations, so that the exciton-coupling strength under these conditions is small compared to the spectral width of dynamic site energy disorder. However, depending on experimental conditions, the 2D spectra of (ZnTPP)2 in DSPC liposomes exhibited multiple diagonal peaks and off-diagonal cross peaks. This suggested that interactions between the dimer and its local membrane environment resulted in preferred dimer conformations, which were reflected by specific couplings between the electronic transitions of the porphyrin residues. Thus the strengths of the electronic couplings in the membrane / (ZnTPP)2 system were comparable to the spectral width of site energy disorder.
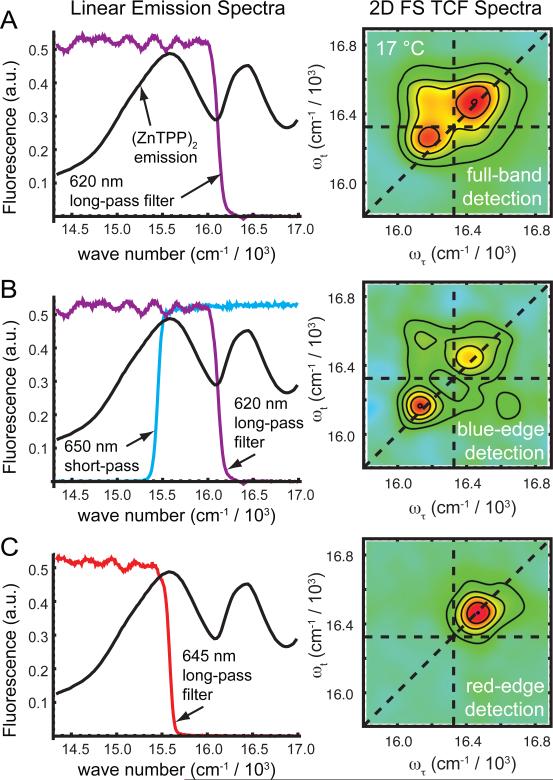
In order to test whether two major sub-populations of (ZnTPP)2 conformations existed in our samples, we performed 2D FS experiments in which the lowest-energy emission band was spectrally filtered to selectively detect signals from different species. Figure 4 summarizes the results of these measurements, which were carried out at 17 °C with the laser center frequency set to 16 470 cm-1 (607 nm). When we collected the entire low-energy emission band (using a 620 nm long-pass filter), we observed in the 2D FS total correlation function (TCF) spectrum well-separated blue- and red-shifted diagonal peaks (relative to the monomer), in addition to a cross peak positioned above the diagonal (see Fig. 4A). However, when we selectively detected the blue-edge of the emission band (using a 620 nm long-pass filter in combination with a 650 nm short-pass filter), the intensity of the red-shifted diagonal peak was enhanced relative to that of the blue-shifted feature (see Fig. 4B). Finally, when we isolated the red-edge of the emission band (using a 645 nm long-pass filter), we observed only the blue-shifted diagonal feature in the 2D FS spectrum (see Fig. 4C).
Figure 4.
Spectral selection of conformational sub-populations by 2D FS. (A) Left panel: The transmission spectrum of a 620 nm long-pass filter (purple) is shown superimposed with the emission spectrum (black) of (ZnTPP)2 in DSPC liposomes at 23 °C while exciting at 570 nm near the red edge of the Q(0,1) band. This filter passes the majority of the lowest-energy emission band. Right panel: The real part of the 2D FS total correlation function (TCF) spectrum is shown, which was obtained using the 620 nm long-pass filter. For these data, the laser center frequency was 16 470 cm-1 (607 nm). The dashed horizontal and vertical lines indicate the monomer transition energy. (B) Left panel: The transmission spectra of the 620 nm long-pass filter (purple) and a 650 nm short-pass filter (blue) are shown superimposed with the emission spectrum. This filter combination passes mostly the blue-edge of the emission line shape. Right panel: The 2D FS spectrum obtained using this filter combination has an enhanced red-shifted feature. (C) Left panel: A 645 nm long-pass filter (red) passes mostly the red side of the emission line shape. Right panel: The 2D FS spectrum obtained with this filter exhibits an enhanced blue-shifted feature. The 2D spectra appear to be very different depending on whether the blue-edge or the red-edge of the emission line shape is detected.
The observations summarized in Fig. 4 serve to illustrate an important principle of fluorescence-detected 2D optical coherence spectroscopy. While the 2D optical spectrum provides information about exciton coupled Q(0,0) transitions resonant with the laser spectral bandwidth (~ 16 200 – 16 700 cm-1), the signal can be selectively filtered by monitoring different regions of the emission line shape. We see that by detecting either the blue-edge or the red-edge of the lowest energy emission band (spanning the range 14 300 – 16 000 cm-1), we obtained two qualitatively different sets of 2D optical spectra. These results are consistent with our temperature-dependent fluorimetry measurements (see Fig. 3, and associated discussion), as they show that fluorescence occurring on the blue-edge of the emission line shape is correlated to red-edge absorption of the Q(0,0) feature (Fig. 4B), and conversely that red-edge emission is correlated to blue-edge absorption (Fig. 4C). Furthermore, these data provide strong support for our conjecture that the zinc porphyrin tweezer (ZnTPP)2 adopts two very different conformations in DSPC liposomes, i.e., a weakly coupled J-dimer and a strongly coupled H-dimer with distinct absorption and emission properties, as illustrated in Fig. 1B.
As we discussed above, we modeled the system in terms of a mixture of ‘extended’ and ‘folded’ conformations, which can be described as an electronically coupled H- and J-dimer, respectively, in the coupled two-dipole model. This model assumes that each ZnTPP monomer supports just a single “effective” EDTM, and it neglects relatively minor contributions to the electronic spectra due to the presence of orthogonally polarized degenerate Qx and Qy transitions within the planes of the ZnTPP macrocycles. Supporting this approximation, in our previous 2D FS theoretical modeling of self-assembled MgTPP dimers 21, we found that most extended conformations gave rise to predominantly red-shifted absorption, which can be reasonably approximated as a four-level J-dimer, while most folded conformations gave rise to predominantly blue-shifted absorption, which can be approximated as a four-level H-dimer (see Fig. 1B).
Because the spectral width of the Q(0,0) feature of the (ZnTPP)2 / liposome system was broader than the laser spectrum, we performed a series of 2D FS measurements in which the laser was progressively tuned across the absorption band (see Fig. 5, right column). These 2D data served to fully characterize the exciton-split spectral features underlying the linear Q(0,0) absorption line shape. Figure 5 summarizes the results of our measurements carried out at 23 °C, although we performed the same set of measurements at seven different temperatures spanning 17 – 85 °C. When the laser was tuned close to the Q(0,0) absorption maximum (16 620 cm-1, 602 nm), the 2D spectra exhibited a single diagonal feature, which was blue-shifted relative to the monomer transition energy (Fig. 5A). When the laser was detuned just to the red of the Q(0,0) maximum (16 470 cm-1, 607 nm), the 2D spectra exhibited an intense blue-shifted diagonal peak, a relatively weak red-shifted diagonal peak, and an intense cross peak above the diagonal (Fig. 5B). For the above two laser excitation frequencies, a 620 nm long-pass filter was sufficient to shield the detector from scattered laser light. Upon further detuning of the laser toward the red side of the absorption maximum, it was necessary to use a 635 nm long-pass filter to remove scattered laser light from the detection path. We found that as we progressively detuned the laser toward the red-edge of the Q(0,0) maximum, the red-shifted peaks in the 2D spectra became correspondingly enhanced. At the same time, the effect of using the red-shifted emission filter was to enhance the blue-shifted features in the 2D spectra, as we previously discussed (see Fig. 4). When the laser was further detuned to 16 340 cm-1 (612 nm), the two effects tended to cancel, leaving the relative intensities of the peaks nearly unchanged from the prior laser setting, while their absolute positions were somewhat shifted (Fig. 5C). Finally, when the laser was detuned to 16 220 cm-1 (617 nm, still using a 635 nm long-pass filter), we observed in the 2D spectra an intense red-shifted diagonal peak and a weak cross peak above the diagonal (Fig. 5D).
Figure 5.
Laser center frequency-dependence of 2D spectra, and optimized fits. Right column: The linear absorbance spectrum of the Q(0,0) band of the (ZnTPP)2 dimer in DSPC liposomes at 23 °C is shown (dashed black curve), superimposed with Gaussian fits to the laser spectrum at four different center frequencies, as indicated. Left and center columns: (A) Experimental and simulated 2D FS spectra are shown for the laser center frequency set to 16 620 cm-1. The simulated spectra were obtained by simultaneously fitting the linear absorbance spectrum and the 2D spectra using both 16 620 and 16 470 cm-1 excitation. (B) Experimental and simulated 2D FS spectra are shown for the laser center frequency set to 16 470 cm-1. (C) Experimental and simulated 2D FS spectra corresponding to 16 340 cm-1 excitation. The simulated spectra were determined using the same parameters obtained from the fit to the data shown in panels (A) and (B), however the parameter d (ratio of H- to J-dimer fluorescence quantum yield) was adjusted to reflect the necessary change of the emission filter (discussed in text). (D) Experimental and simulated 2D FS spectra corresponding to 16 220 cm-1 excitation. These simulated spectra were determined using the same parameters as those used to simulate the 2D spectra shown in panel (C).
We performed model optimizations to the full set of temperature-dependent 2D FS and linear absorption data, assuming a binary mixture of H- and J-dimer species, as described in the Methods Section. For each of the 2D data sets that employed different laser excitation frequencies, we simulated the 2D spectra using the same sets of values for the model parameters (listed in Table 1), with one exception. For the cases with the laser frequency tuned to 16 340 cm-1 and 16 220 cm-1, we allowed for a change in the parameter d, which described the ratio of detected fluorescence from the H-dimer relative to the J-dimer, from 0.0079 to 0.198. This change reflects the fact that for the experiments carried out with the laser tuned to 16 340 and 16 220 cm-1, our use of the red-shifted detection filter (relative to the one used for 16 620 and 16 470 cm-1 excitation) resulted in a larger fraction of the detected fluorescence emanating from the H-dimer. Taking this experimental difference into account, we assumed that all other properties of the system were unchanged relative to those in experiments carried out with the laser tuned to 16 620 and 16 470 cm-1. The simulated 2D FS spectra obtained using these parameters are shown along with the corresponding experimental data in Fig. 5.
Table 1.
Optimized parameter values
| Temp (°C) | 17 | 23 (RT) | 28 | 46 | 63 | 72 | 85 |
| VH (cm-1)a | b | 295 | |||||
| θH (°)c | 18 | ||||||
| τH (fs)d | 71 | 62 | 65 | 66 | 66 | 67 | 68 |
| Γ H e | 0.94 | 1.33 | 1.48 | 1.04 | 1.02 | 0.90 | 0.63 |
| σH (cm-1)f | 354 | 374 | 384 | 393 | 416 | 431 | 413 |
| VJ (cm-1)g | -123 | ||||||
| θJ (°) | 52 | ||||||
| τJ (fs) | 69 | 65 | 69 | 71 | 72 | 71 | 69 |
| Γ J | 0.38 | 0.58 | 0.59 | 0.57 | 0.49 | 0.40 | 0.46 |
| σJ (cm-1) | 57 | 50 | 50 | 50 | 60 | 50 | 50 |
| σ lin h | 354 | 374 | 384 | 393 | 416 | 431 | 413 |
| ε1 (cm-1)i | 16325 | ||||||
| bj | 8.56 ±0.07 | 10.31 ±0.06 | 10.40 ±0.06 | 12.46 ±0.07 | 13.81 ±0.08 | 19.59 ±0.08 | 21.69 ±0.06 |
| d k | 0.0079 |
Electronic coupling strength. Parameters with subscript H refer to the H-dimer species.
Empty boxes indicate that a given parameter was fixed at its room temperature value when performing the fit at another temperature.
Relative dipole angle of the two monomers.
Phenomenological dephasing time.
Fluorescence quantum yield of doubly-excited state relatively to singly-excited states.
Line shape overlap parameter.
Parameters with subscript J refer to the J-dimer.
Linear spectrum line width.
Monomer transition energy.
Ratio of H-dimer to J-dimer conformational popultions. Error bars determined according to the method of Lott et al. 20
Ratio of H-dimer to J-dimer fluorescence quantum yields.
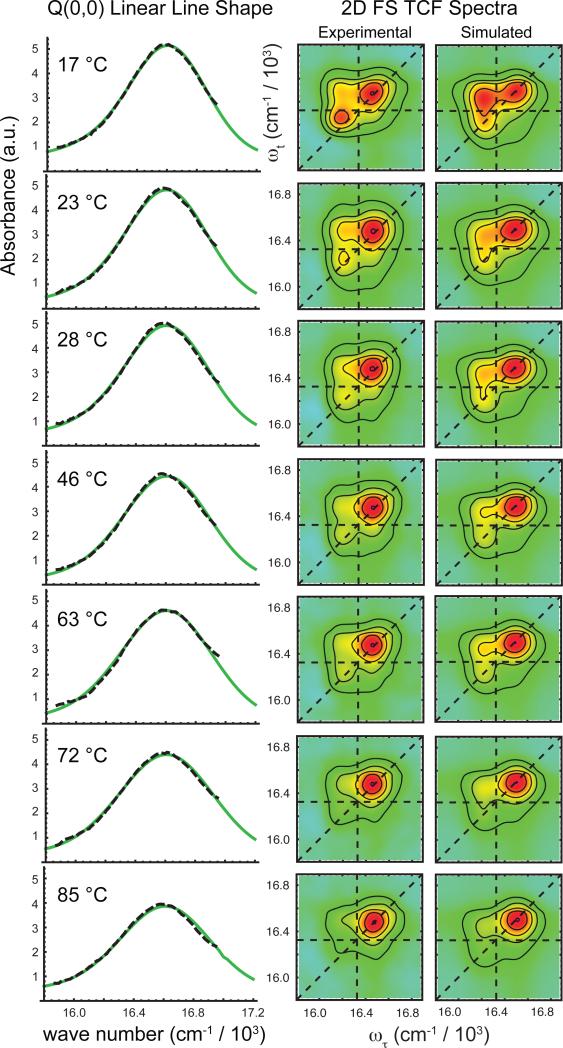
The results of our multi-parameter optimization over the complete range of temperatures investigated are summarized in Table 1, and a comparison between simulated and experimental data (for 607 nm excitation only) are shown in Fig. 6. The optimized values reported for each temperature are solutions corresponding to the minimized cost function . The most striking change with temperature occurs in the parameter b, the relative population of H- to J-dimer (shown in bold font in Table 1). Error bars for b were determined according to a procedure we developed previously,20 which we discuss further below (see Discussion Section). We emphasize that our best attempts to model these data using only a single dimer conformation were unsuccessful. Nevertheless, the full range of experimental data could be readily fit to the binary mixture model.
Figure 6.
Temperature-dependent 2D FS and linear absorption data, and optimized fits. Left column: The linear absorption spectrum of the Q(0,0) band of (ZnTPP)2 dimers in DSPC liposomes (dashed black) is overlaid with its optimized fit (green) for each of the seven temperatures investigated. Right column: The real part of the 2D FS total correlation spectra is compared to its optimized fit for each temperature. As the temperature is increased, the red-shifted diagonal peak and the above diagonal cross peak decrease in intensity, corresponding to a loss in the relative population of J-dimer conformation. These temperature-dependent changes in the 2D spectral line shapes are consistent with those observed in the B-band of the linear absorption spectra.
We note that the optimized room temperature solution exhibits a smaller exciton splitting for the J-dimer than for the H-dimer. This makes physical sense because the porphyrin residues are likely to be separated by a larger distance in the ‘extended’ conformation than in the ‘folded’ conformation (see Fig. 7A). This is also consistent with our experimental observation that selective excitation of the blue-edge of the Q(0,0) band (favoring excitation of the H-dimer) leads to red-edge emission, which follows from the fact that the larger coupling strength of the H-dimer places its lowest-energy singly-excited state at a lower energy than that of the J-dimer (see Fig. 1B for energy level diagrams that illustrate this). Immediately after the H-dimer is excited, nonradiative relaxation to the lowest energy singly-excited state followed by solvation results in a larger fluorescence Stokes-shift than that of the corresponding J-dimer.
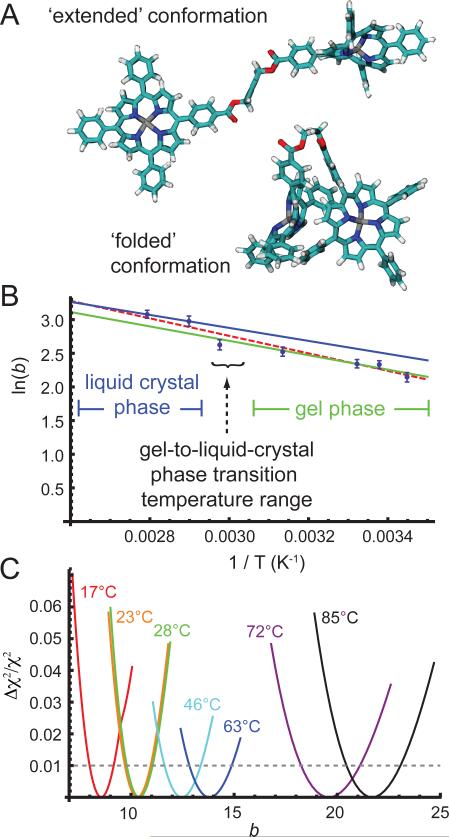
Figure 7.
(A) Models of ‘extended’ and ‘folded’ conformations of the zinc porphyrin tweezer from the UFF structure optimizations. (B) Van't Hoff plot of the parameter ln(b) versus inverse temperature, where b is the ratio of H- to J-dimer population. Blue points with error bars are the values of b obtained from the optimizations to the linear absorption and 2D FS spectra over the full range of temperatures shown in Fig. 6. The linear fits to these points (green and blue lines) yield the standard state changes in entropy and enthalpy associated with the ‘extended’-to-‘folded’ conformational transitions in the gel and liquid-crystal phases, respectively. See Table 2 for values. (C) The relative deviation of the cost function from the optimized reference value is plotted as a function of the parameter b. Cross-sections of the cost function at each temperature have minima corresponding to the optimized value bref. The cross-section curvatures indicate the sensitivity of the optimizations to the uncertainty Δb = b – bref. Trust intervals were directly read out from these plots based on the approximately 1% relative error associated with the experimental data quality (indicated by the dashed horizontal black line).
The 2D FS spectra reveal significant changes with temperature, despite the fact that they were obtained by exciting in the Q(0,0) band, where the linear absorption spectrum changes very little (Fig. 3B, inset). The temperature-dependent changes in the 2D FS spectra follow very closely to those seen in the B-band of the linear absorption spectrum, with the relative intensity of the blue-shifted peak increasing with raising temperature. All of these changes are consistent with an increase in the population of H-dimer at elevated temperatures, which is reflected by the temperature-dependence of the parameter b (see Table 1).
V. Discussion
The parameter b is the ratio of H- to J-dimer population, and is therefore equal to the equilibrium constant for the process by which the ‘extended’ conformation is converted into the ‘folded’ one. In Fig. 7B, we present our results in the form of a Van't Hoff plot – i.e., the natural logarithm of b versus the inverse temperature. The error bars associated with the values of b are also shown in Fig. 7B. Our determination of these uncertainties was based on a procedure we previously demonstrated for self-assembled porphyrin dimers, for which the data quality is very similar to that of the current study.20 For each temperature, the relative deviation of the cost function from the optimized reference value was determined as a function of the parameter b. In Fig. 7C are shown temperature-dependent cross-sections of the cost function over a range of values of b in the vicinity of the optimized value bref. Trust intervals were directly read out from these plots, based on the approximately 1% relative error associated with the experimental data quality (as indicated by the horizontal dashed line).
Taking error bars into account, the data shown in Fig. 7B can be fit very well to a line over the full range of temperatures we investigated (17 – 85 °C), with the exception of the point corresponding to 63 °C. This was the only data set recorded at a temperature in the vicinity of the gel-to-liquid-crystal phase transition of the DSPC liposome, which occurs near 57 °C. We note that the data presented in Fig. 7B show a slight discontinuity close to the phase transition temperature.
Each of the linear fits to the data shown in Fig. 7B has slope and y-intercept proportional to, respectively, the standard state changes in enthalpy and entropy of the monomer association process:
| (10) |
We thus obtained values of and for the gel and the liquid crystal phases separately, as well as the values that result from considering the full range of temperatures. These results are listed in Table 2. For both the gel and the liquid crystal phases, we find and . For comparison, the enthalpy change upon breaking a single hydrogen bond in liquid water is 11 kJ mol-1 34.
Table 2.
Thermodynamic Parameters
| ΔSa° (J mol-1 K-1) | ΔHa° (kJ mol-1) | |
|---|---|---|
| Gel phasea | 49 ± 8 | 9 ± 2 |
| Liquid crystal phaseb | 48 ± 22 | 8 ± 8 |
| All pointsc | 56 ± 3 | 10.9 ± 0.9 |
Fit to 17, 23, 28 and 46 °C data points.
Fit to 72 and 85 °C data points.
Fit to 17, 23, 28, 46, 63, 72 and 85 °C data points.
It is useful to decompose the thermodynamic parameters into contributions resulting from monomer-monomer and monomer-solvent interactions: and . We have assumed that contributions resulting from solvent-solvent interactions are negligible due to the low concentration of the porphyrin in the membrane. Since the association process is expected to lead to favorable contacts between the porphyrin residues, we may conclude that (considering the approximate values of and ), where the equality holds in the limit . Thus, the association process is opposed by the disruption of favorable enthalpic interactions between previously exposed porphyrin surfaces and the acyl chains of the membrane. The change in monomer-solvent enthalpic interactions upon association must therefore be larger in magnitude than the corresponding change in monomer-monomer interactions. The entropy change of the association process can be understood in a similar fashion. Because the porphyrin residues are connected together by a flexible linker, we expect the monomer-monomer entropy change of association to be small and negative, as relatively little conformational freedom is lost by the dimer in this process. Thus, the observed positive entropy change of association must be dominated by the monomer-solvent term: , where the equality holds in the limit . We therefore conclude that in both the gel and liquid crystal phases, the association process is largely driven by the increase in entropy of acyl side chains, which are liberated from their contacts with the porphyrin surfaces when the dimer folds. This membrane-facilitated association process is analogous to the hydrophobic effect that drives the folding of many proteins, in which folding is driven by the increase in entropy of water molecules that are liberated when the surfaces of the protein are buried.
We attempted to obtain rough estimates for the values of and by performing simple force field computer calculations. We carried out energy minimizations for the models of the ‘extended’ and ‘folded’ conformations of the zinc porphyrin tweezer using the Universal Force Field (UFF) (shown in Fig. 7A). From these calculations, we obtained the values and , which in turn allowed us to estimate and ., respectively. Since UFF fails to correctly predict the planar Zn-porphyrin coordination, the enthalpy estimates should be treated with caution. However, the entropy of the conformational change arises primarily from vibrational frequency changes in the flexible linker, for which UFF is expected to provide useful estimates.
The results of the current study provide further insights to, and are consistent with, the results of our previous experiments on self-assembled MgTPP dimers in DSPC liposomes 20-21. In that work, we observed that monomers of MgTPP could spontaneously assemble into dimers, which adopted an open T-shaped structure within the membrane. The T-shaped conformation of the self-assembled porphyrin dimer did not form a compact structure to maximize porphyrin-porphyrin stacking interactions, suggesting that the association process was not driven by the direct interactions between porphyrin monomers. There would be a significant entropic cost to the association of the monomers, which in contrast to our current work were not linked together. Furthermore, there is a sizable enthalpic cost to bury the porphyrin surfaces, which could otherwise interact favorably with the acyl side chains. It is therefore very likely that the self-assembly of MgTPP dimers in DSPC liposomes is also driven by an increase in entropy of the acyl chains, which are liberated from their local contacts with the porphyrin residues, similar to protein assembly in membranes 35-36.
It is important to reconsider at this stage the validity of the point-dipole approximation that we have implemented to model our data. Although the point-dipole model is proven to be useful to describe electronic coupling in a variety of chemical systems, its accuracy is questionable when the inter-chromophores separation is very small. We believe that the approach we have outlined could be applied in future studies to experimentally test the accuracy of higher levels of electronic structure theory and the limitations of point-dipole models.
The experiments presented in this paper illustrate a significant advantage of fluorescence-detected 2D electronic spectroscopy – different contributions to the nonlinear signal can be separated based on their fluorescence properties, such as emission wavelength (demonstrated here), fluorescence lifetime, or polarization. A particularly interesting application of this principle would involve placing a Förster resonance energy transfer (FRET) ‘acceptor’ chromophore on a molecule that binds to the ‘donor’ chromophore being excited. For example, the donor chromophore could be a pair of fluorescent nucleic acid base analogs such as 2-aminopurine (2-AP) dinucleotide incorporated into DNA 22, 37, and the FRET acceptor chromophore could be placed on a protein that binds to DNA. Recording 2D FS spectra while using filters to collect either fluorescence directly from the 2-AP dinucleotide labeled DNA or from the FRET acceptor labeled protein would allow one to separately measure the 2D FS spectra of local DNA conformations in the unbound and bound states, respectively.
VI. Conclusions
Using linear absorption, fluorescence and 2D FS, we studied the equilibrium conformations of a dimer composed of two ZnTPP residues connected by a flexible linker – i.e., a ‘zinc porphyrin tweezer’, which was suspended within the amphiphilic regions of a liposome membrane. We determined that the porphyrin tweezer exists within the membrane as a mixture of ‘extended’ and ‘folded’ conformations. This was accomplished using a novel approach to 2D FS in which the fluorescence was spectrally filtered to select signals from different components of the mixture. By fitting the linear absorption and 2D FS spectra over a series of temperatures, we determined the values of the enthalpy and entropy changes associated with the conformational transition between ‘extended’ and ‘folded’ states. Our results indicate that the enhanced stability of the folded state at elevated temperatures is driven by an increase in entropy of the membrane acyl chains, which are liberated from their local contacts with porphyrin surfaces when the dimer folds. Future work on this system will investigate the excited state relaxation pathways of the zinc porphyrin tweezer within its local membrane environment, the kinetics of interconversion between conformational sub-states, and the relationship between conformational transitions and spectral diffusion.
ACKNOWLEDGEMENT
We acknowledge helpful discussions with Prof. Peter H. von Hippel, Dr. Neil P. Johnson, and Prof. Marina Guenza of the Department of Chemistry, University of Oregon. We thank V. Spasojevic for preparation of TPP dimers.
Funding Sources
This material is supported by grants from the Office of Naval Research (Grant N00014-11-0193 – to AHM) and from the National Science Foundation, Chemistry of Life Processes Program (CHE-1105272 – to AHM). TFM is grateful for funding from NIH (AI100776-01). The TOFMS was purchased with funds provided by NIH (1S10RR025636-01). Support was also provided as part of the Center for Excitonics, an Energy Frontier Research Center funded by the US Department of Energy, Office of Basic Sciences [DE-SC0001088 to A.P.-O., D.R. and A.A.-G.] A. A.-G. also thanks the generous support of the Corning foundation. JRW is a Rosaria Haugland UO Predoctoral Research Fellow.
Footnotes
Author Contributions
The manuscript was written through contributions of all authors. All authors have given approval to the final version of the manuscript.
REFERENCES
- 1.Tanford C. The Hydrophobic Effect. 2 ed. John Wiley & Sons; New York: 1980. p. 233. [Google Scholar]
- 2.McGaughey GB, Gagné M, Rappé AK. π-Stacking Interactions. J. Biol. Chem. 1998;273:15458–15463. doi: 10.1074/jbc.273.25.15458. [DOI] [PubMed] [Google Scholar]
- 3.Steinberg IZ, Scheraga HA. Entropy Changes Accompanying Association Reactions of Proteins. J. Biol. Chem. 1963;238:172–181. [PubMed] [Google Scholar]
- 4.Finkelstein A, Janin J. The Price of Lost Freedom: Entropy of Bimolecular Complex Formation. Protein Engineering. 1989;3:1–3. doi: 10.1093/protein/3.1.1. [DOI] [PubMed] [Google Scholar]
- 5.Schenning APHJ, Hubert DHW, Feiters MC, Nolte RJM. Control of Aggregation and Tuning of the Location of Porphyrins in Synthetic Membranes as Mimics for Cytochrome P450. Langmuir. 1996;12:1572–1577. [Google Scholar]
- 6.von Hippel PH. From “Simple” DNA-Protein Interactions to the Macromolecular Machines of Gene Expression. Annu. Rev. Biophys. Biomol. Struct. 2007;36:79–105. doi: 10.1146/annurev.biophys.34.040204.144521. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.von Hippel PH. Protein-DNA Recognition: New Perspectives and Underlying Themes. Science. 1994;263:769–770. doi: 10.1126/science.8303292. [DOI] [PubMed] [Google Scholar]
- 8.Spolar RS, Record MT. Coupling of Local Folding to Site-Specific Binding of Proteins to DNA. Science. 1994;263:777–784. doi: 10.1126/science.8303294. [DOI] [PubMed] [Google Scholar]
- 9.Datta K, Johnson NP, von Hippel PH. DNA Conformational Changes at the Primer-Template Junction Regulate the Fidelity of Replication by DNA Polymerase. Proc. Nat. Acad. Sci. 2010;107:17980–17985. doi: 10.1073/pnas.1012277107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Molinski TF, Makarieva TN, Stonik VA. (-)-Rhizochalin is a Dimeric Enantiomorphic (2R)-Sphingolipid. Analysis of Pseudo-C2 Symmetric bis-2-Amino-3-Alkanols by CD. Angew. Chem. Int. Ed. 2000;39:4076–4079. [PubMed] [Google Scholar]
- 11.Dalisay DS, Quach T, Nicholas GN, Molinski TF. Amplification of Cotton Effects of a Single Chromophore through Liposomal Ordering. Stereochemical Assignment Plakinic Acids (I-J) from Plakortis. Angew. Chem. Int. Ed. 2009;48:4367–4371. doi: 10.1002/anie.200900888. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Dalisay DS, Quach T, Molinski TF. Liposomal Circular Dichroism. Assignment of Remote Stereocenters in Plakinic Acids K and L from a Plakortis - Xestospongia Sponge Association. Org. Lett. 2010;12:1524–1527. doi: 10.1021/ol100249v. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Brixner T, Stenger J, Vaswani HM, Cho M, Blankenship RE, Fleming GR. Two-Dimensional Spectroscopy of Electronic Couplings in Photosynthesis. Nature. 2005;434:625–628. doi: 10.1038/nature03429. [DOI] [PubMed] [Google Scholar]
- 14.Collini E, Wong CY, Wilk KE, Curmi PMG, Brumer P, Scholes GD. Coherently Wired Light-Harvesting in Photosynthetic Marine Algae at Ambient Temperature. Nature. 2010;463:644–647. doi: 10.1038/nature08811. [DOI] [PubMed] [Google Scholar]
- 15.Abramavicius D, Palmieri B, Voronine DV, Šanda F, Mukamel S. Coherent Multidimensional Optical Spectroscopy of Excitons in Molecular Aggregates; Quasiparticle Versus Supermolecule Perspectives. Chem. Rev. 2009;109:2350–2408. doi: 10.1021/cr800268n. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Ginsberg NS, Cheng Y-C, Fleming GR. Two-Dimensional Electronic Spectroscopy of Molecular Aggregates. Acc. Chem. Res. 2009;42:1352–1363. doi: 10.1021/ar9001075. [DOI] [PubMed] [Google Scholar]
- 17.Collini E, Scholes GD. Coherent Intrachain Energy Migration in a Conjugated Polymer at Room Temperature. Science. 2009;323:369–373. doi: 10.1126/science.1164016. [DOI] [PubMed] [Google Scholar]
- 18.Zhang T, Kuznetsova I, Meier T, Li X, Mirin RP, Thomas P, Cundiff ST. Polarization-Dependent Optical 2D Fourier Transform Spectroscopy of Semiconductors. Proc. Nat. Acad. Sci. 2007;104:14227–14232. doi: 10.1073/pnas.0701273104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Stone KW, Gundogdu K, Turner DB, Li X, Cundiff ST, Nelson KA. Two-Quantum Two-Dimensional Fourier Transform Electronic Spectroscopy of Biexcitons in GaAs Quantum Wells. Science. 2009;324:1169–1173. doi: 10.1126/science.1170274. [DOI] [PubMed] [Google Scholar]
- 20.Lott GA, Perdomo-Ortiz A, Utterback JK, Widom JR, Aspuru-Guzik A, Marcus AH. Conformation of Self-Assembled Porphyrin Dimers in Liposome Vesicles by Phase-Modulation 2D Fluorescence Spectroscopy. Proc. Nat. Acad. Sci. 2011;108:16521–16526. doi: 10.1073/pnas.1017308108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Perdomo-Ortiz A, Widom JR, Lott GA, Aspuru-Guzik A, Marcus AH. Conformation and Electronic Population Transfer in Membrane-Supported Self-Assembled Porphyrin Dimers by 2D Fluorescence Spectroscopy. J. Phys. Chem. B. 2012;116:10757–10770. doi: 10.1021/jp305916x. [DOI] [PubMed] [Google Scholar]
- 22.Widom JR, Johnson NP, von Hippel PH, Marcus AH. Solution Conformation of 2-Aminopurine (2-AP) Dinucleotide Determined by Ultraviolet 2D Fluorescence Spectroscopy (UV-2D FS). New Journal of Physics. 2013;15:025028–1-16. doi: 10.1088/1367-2630/15/2/025028. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Huang X, Rickman BH, Borhan B, Berova N, Nakanishi K. Zinc Porphyrin Tweezer in Host−Guest Complexation: Determination of Absolute Configurations of Diamines, Amino acids, and Amino alcohols by Circular Dichroism. J. Am. Chem. Soc. 1998;120:6185–6186. doi: 10.1002/(SICI)1521-3765(20000117)6:2<216::AID-CHEM216>3.0.CO;2-1. [DOI] [PubMed] [Google Scholar]
- 24.Matile S, Berova N, Nakanishi K, Novkova S, Philipova I, Blagoev B. Porphyrins: Power Chromophores for Structural Studies by Exciton-Coupled Circular Dichroism. J. Am. Chem. Soc. 1995;117:7021–7022. [Google Scholar]
- 25.MacMillan JB, Molinski TF. Long-Range Stereo-Relay: Relative and Absolute Configuration of 1,n-Glycols from Circular Dichroism of Liposomal Porphyrin Esters. J. Am. Chem. Soc. 2004;126:9944–9945. doi: 10.1021/ja047741a. [DOI] [PubMed] [Google Scholar]
- 26.Tekavec PF, Lott GA, Marcus AH. Fluorescence-Detected Two-Dimensional Electronic Coherence Spectroscopy by Acousto-Optic Phase Modulation. J. Chem. Phys. 2007;127:214307. doi: 10.1063/1.2800560. [DOI] [PubMed] [Google Scholar]
- 27.Rappé AK, Casewit CJ, Colwell KS, Goddard WA, III, Skiff WM. UFF, a Full Periodic Table Force Field for Molecular Mechanics and Molecular Dynamics Simulations. J. Am. Chem. Soc. 1992;114:10024–10035. [Google Scholar]
- 28.Rappé AK, Colwell KS, Casewit CJ. Application of a Universal Force Field to Metal Complexes. Inorg. Chem. 1993;32:3438–3450. [Google Scholar]
- 29.TURBOMOLE V6.3 2011, a development of University of Karlsruhe and Forschungszentrum Karlsruhe GmbH. ( http://www.turbomole.com)
- 30.Kasha M, Rawls HR, El-Bayoumi MA. The Exciton Model in Molecular Spectroscopy. Pure Appl. Chem. 1965;11:371–392. [Google Scholar]
- 31.Byrd RH, Nocedal J, Waltz RA. KNITRO: An Integrated Package for Nonlinear Optimization. In: di Pillo G, M. R., editors. Large-Scale Nonlinear Optimization. Springer-Verlag; 2006. pp. 35–59. [Google Scholar]
- 32.Gouterman M. Optical Spectra and Electronic Structure of Porphyrins and Related Rings. In: Dolphin D, editor. The Porphyrins: Physical Chemistry, Part A. III. Academic Press; New York: 1979. pp. 1–156. [Google Scholar]
- 33.Zein M, Winter R. Effect of Temperature, Pressure and Lipid Acyl Chain Length on the Structure and Phase Behaviour of Phospholipid–Gramicidin Bilayers. Phys. Chem. Chem. Phys. 2000;2:4545–4551. [Google Scholar]
- 34.Walrafen GE, Fisher MR, Hokmabadi MS, Yang W-H. Temperature Dependence of the Low- and High-Frequency Raman Scattering from Liquid Water. J. Chem. Phys. 1986;85:6970–6982. [Google Scholar]
- 35.Doxastakis M, Sakai VG, Ohtake S, Maranas JK, de Pablo JJ. A Molecular View of Melting in Anhydrous Phospholipidic Membranes. Biophys. J. 2007;92:147–161. doi: 10.1529/biophysj.106.089631. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Sintes T, Baumgärtner A. Protein Attraction in Membranes Induced by Lipid Fluctuations. Biophys. J. 1997;73:2251–2259. doi: 10.1016/S0006-3495(97)78257-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Jose D, Datta K, Johnson NP, von Hippel PH. Spectroscopic Studies of Position-Specific DNA “Breathing” Fluctuations at Replication Forks and Primer-Template Junctions. Proc. Nat. Acad. Sci. 2009;106:4231–4236. doi: 10.1073/pnas.0900803106. [DOI] [PMC free article] [PubMed] [Google Scholar]