PKPD modelling of the interrelationship between mean arterial BP, cardiac output and total peripheral resistance in conscious rats

Abstract

Background and Purpose

The homeostatic control of arterial BP is well understood with changes in BP resulting from changes in cardiac output (CO) and/or total peripheral resistance (TPR). A mechanism-based and quantitative analysis of drug effects on this interrelationship could provide a basis for the prediction of drug effects on BP. Hence, we aimed to develop a mechanism-based pharmacokinetic-pharmacodynamic (PKPD) model in rats that could be used to characterize the effects of cardiovascular drugs with different mechanisms of action (MoA) on the interrelationship between BP, CO and TPR.

Experimental Approach

The cardiovascular effects of six drugs with diverse MoA, (amlodipine, fasudil, enalapril, propranolol, hydrochlorothiazide and prazosin) were characterized in spontaneously hypertensive rats. The rats were chronically instrumented with ascending aortic flow probes and/or aortic catheters/radiotransmitters for continuous recording of CO and/or BP. Data were analysed in conjunction with independent information on the time course of drug concentration using a mechanism-based PKPD modelling approach.

Key Results

By simultaneous analysis of the effects of six different compounds, the dynamics of the interrelationship between BP, CO and TPR were quantified. System-specific parameters could be distinguished from drug-specific parameters indicating that the model developed is drug-independent.

Conclusions and Implications

A system-specific model characterizing the interrelationship between BP, CO and TPR was obtained, which can be used to quantify and predict the cardiovascular effects of a drug and to elucidate the MoA for novel compounds. Ultimately, the proposed PKPD model could be used to predict the effects of a particular drug on BP in humans based on preclinical data.

Introduction

Persistent elevation of BP is a risk factor for heart failure and is one of the major causes of cardiovascular disease (Graham et al., 2007). This risk continuously increases with the level of BP. Even small changes in BP, i.e. 10–20 mmHg, can have a relatively large effect (EMEA, 2004). BP regulation by the CVS is well characterized, and the homeostatic principles of the CVS are thoroughly understood. Briefly, mean arterial pressure (MAP) equals the product of cardiac output (CO) and total peripheral resistance (TPR). This relationship has been well established for many years and is based on Ohm's law, when applied to fluid flow. MAP is maintained within narrow limits by various regulatory feedback systems such as the renin–angiotensin–aldosterone system (RAAS) and the baroreflex system (Cleophas, 1998). In contrast to the detailed understanding of the physiological regulation of BP, the mechanisms underlying the desired or undesired drug effects on BP are often less clear. This is a major drawback because a quantitative understanding of the pharmacological effects of (novel) drugs on BP control is pivotal with regard to drug efficacy and safety. Moreover, understanding these effects early on in preclinical development would help to predict the expected magnitude of haemodynamic effects in humans.

To date, no models exist that provide an integrated description of the effects of drugs on the interrelationship between MAP, CO and TPR. A mechanism-based pharmacokinetic-pharmacodynamic (PKPD) modelling approach is uniquely suited to provide quantitative insights into the action of a drug on the CVS because it clearly distinguishes drug-specific effects from system-specific effects (Danhof et al., 2007; Ploeger et al., 2009). This would enable the prediction and extrapolation of treatment effects to later stages of development using a translational modelling approach and, thereby, facilitate the drug development process and help in the selection of suitable compounds (Danhof et al., 2007).

Following the concepts proposed by Van der Graaf et al. (1999) and Van Schaick et al. (1997), we hypothesize that by challenging the CVS with a variety of compounds, the rate and feedback parameters of the CVS can be quantified and a clear distinction can be made between drug- and system-specific parameters that govern the pharmacological effect. A crucial factor is that the ‘training set’ of selected compounds acts on the same system, but with different target sites and time courses of effect. We have selected a training set of six antihypertensive compounds with different, but well described effects on CO and/or TPR: enalapril, fasudil, amlodipine, prazosin, propranolol and hydrochlorothiazide (HCTZ) to challenge the CVS. The first four compounds have their primary effect on TPR; whereas the latter two compounds have their primary effect on CO (Ram et al., 1981; Cleophas, 1998; Masumoto et al., 2001). An overview of the mechanisms of action (MoA) of these compounds can be found in Table 1. In addition to making sure that enough compounds are tested, another important aspect of the experimental design is the selection of endpoints to monitor the drug effects on the CVS. Measuring BP is common practice, but it represents a ‘secondary’ PD parameter, as BP depends on both CO and TPR. At present, measuring CO has not been integrated into daily practice due to the difficulties associated with invasive instrumentation procedures (Doursout et al., 2001). Still, from a mechanistic point-of-view, these data are pivotal for a quantitative understanding of the dynamics of the system, especially as, due to the homeostatic feedback mechanisms, the effects on the underlying parameters CO and TPR may be much larger than the effects on BP (Brands et al., 2000). Finally, monitoring BP during the onset and offset of the drug effects provides the information needed to quantify the parameters of a dynamical system as this information can only be derived when the system is not in equilibrium. The offset phase can be especially informative as it provides information on the question if and how fast the system returns to its initial state.

Table 1.

Selected compounds to challenge the CVS with the aim of distinguishing system- from drug-specific parameters and their mechanism of action

Compound	Class	Mechanism of action	Primary effect
Enalapril	ACE inhibitor	ACE inhibitors competitively inhibit ACE, preventing the conversion of angiotensin I to angiotensin II, a potent vasoconstrictor that also stimulates release of aldosterone. Decreased levels of angiotensin II lead to decreased total peripheral resistance that is unassociated with reflex stimulation of the heart (Frohlich, 1989).	TPR
Fasudil	Rho-kinase inhibitor	Rho-kinase inhibits myosin light chain phosphatase activity and plays a key role in Ca2+ sensitization and hypercontraction of vascular smooth muscle cells. Rho-kinase inhibitors decrease total peripheral resistance (Masumoto et al., 2001).	TPR
Amlodipine	Calcium channel blocker	Amlodipine is a dihydropyridine that blocks voltage gated calcium channels and selectively inhibits Ca2+ influx into vascular smooth muscle cells. Calcium antagonists act by decreasing total peripheral resistance to lower arterial pressure. As a consequence, reflex tachycardia, increased cardiac output, and increased plasma catecholamine and plasma renin activity are commonly seen, particularly with the initial dose and with short-acting dihydropyridines (Michalewicz and Messerli, 1997; Perez-Reyes et al., 2009).	TPR
Prazosin	Selective α1 adrenoceptor blocker	Prazosin is a quinazoline derivative that is a specific and selective competitive antagonist of α1 adrenoceptors on vascular smooth muscle cells. Prazosin reduces BP by reducing elevated peripheral resistance and has little effect on cardiac function (Reid et al., 1987).	TPR
Propranolol	β-Adrenoceptor blocker	Propranolol is a non-selective β blocker. It antagonizes the action of noradrenaline and adrenaline at all β-adrenoceptors. Propranolol decreases cardiac output and heart rate with a reflex rise in total peripheral resistance (Ebadi, 2008).	CO
HCTZ	Diuretic	Diuretics cause blood volume contraction and lower venous pressure, which decreases cardiac filling and, by the Frank–Starling mechanism, decreases ventricular stroke volume (Levick, 2003).	CO

In this investigation, we describe the development of a mechanism-based PKPD model that integrates a quantitative description of the physiology of the interrelationship between BP, CO and TPR and the pharmacological effects of cardiovascular drugs using data from preclinical experiments with a training set of six antihypertensive drugs. Ultimately, this quantitative pharmacology model could be used to predict clinical responses to novel pharmacological agents.

Methods

Animals

Experiments were conducted on male spontaneously hypertensive rats (SHR) (Taconic Farms, Germantown, NY, USA) in accordance with approved Novartis Animal Care and Use Committee protocols (which have been accredited and conform to international animal welfare standards) and the Guide for the Care and Use of Laboratory Animals. At the time of study, rats' ages ranged from 21–45 weeks and body weights ranged from 269 to 490 g. Rats were housed on a 12 h light/dark cycle (light: 0600–1800 h), kept at room temperature, 22°C, and were provided with normal chow (Harlan Teklad 8604; Indianapolis, IN, USA) and water ad libitum. The total number of rats used was 12 (10 in Study 1 and 2 in Study 2). All studies involving animals are reported in accordance with the ARRIVE guidelines for reporting experiments involving animals (Kilkenny et al., 2010; McGrath et al., 2010).

Experimental procedures

The effects of a training set of compounds were obtained in two studies. In Study 1, detailed profiles of the time course of the effects on MAP and HR were obtained after repeated dosing. In Study 2, information on the effect on MAP and CO was obtained following a single administration of a range of different doses. The combined information from both studies was crucial to the identification of the system-specific model characterizing the interrelationship between MAP, CO and TPR.

For the recording of BP (Study 1), a sterile gel-filled catheter/radiotransmitter (PA-C40, Data Sciences International, St. Paul, MN, USA) was surgically implanted under isoflurane anaesthesia into a femoral artery (catheter tip residing in the lower abdominal aorta) and a s.c. pocket or directly into the abdominal aorta. Depth of anaesthesia was based on the inhaled concentration of isoflurane (2–2.5%) and the absence of a pedal reflex.

Arterial BP was recorded for 15 s every 10 min as detailed previously (Bazil et al., 1993). For BP and CO measurements (Study 2), rats were surgically instrumented with both an ascending aortic flow probe and a femoral arterial catheter/radiotransmitter (Figure 1). Rats were anaesthetized with isoflurane, tracheally intubated and artificially ventilated. A precalibrated 2.5 or 3.0 mm transit-time volumetric flow probe (2.5PS or 3PS, Transonic Systems Inc., Ithaca, NY, USA) was placed around the ascending aorta via an incision at the right second intercostal space. The flow probe connector was tunnelled s.c. to the mid-scapular region where it was attached to the skin by a cutaneous button. The ribs were approximated with sutures, air was removed from the chest and the chest wound closed in layers. Ketoprofen and penicillin G were administered for analgesia and infection prophylaxis. The rat was extubated and allowed to recover for approximately 2 weeks. Thereafter, the catheter/radiotransmitter was implanted as described earlier.

Figure 1.

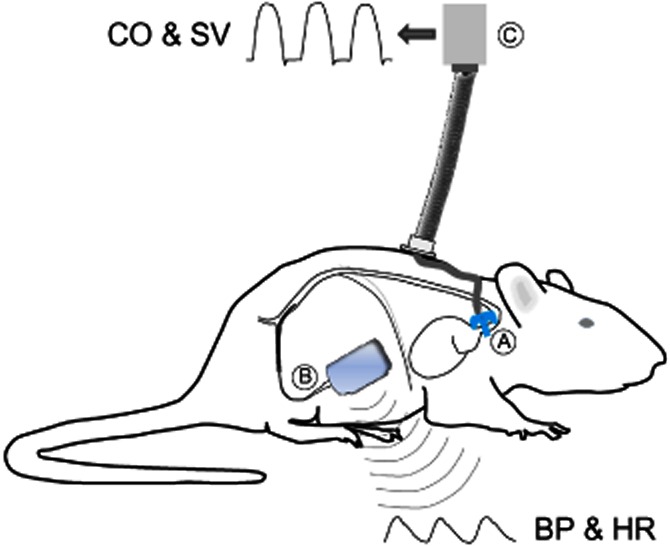
Experimental animal instrumentation. Rats in Study 2 were surgically instrumented with both an ascending aortic flow probe (A) and a femoral arterial catheter/radiotransmitter (B). CO was measured by connecting the flow probe to the flow meter via a cable and electrical swivel (C), which allowed the animal to remain fully mobile. MAP, heart rate, stroke volume, CO and TPR were derived for all beats averaged over consecutive 2 min intervals.

In Study 2, rats were used repeatedly for up to 6 months with sufficient washout between consecutive experiments. For continuous recording of CO, a tether cable was attached to the flow probe connector and a flow meter (Model T402, Transonic Systems Inc.) via an electrical swivel (Dragonfly Research & Development, Ridgeley, WV, USA). The digitized flow and telemetred pressure signals were analysed by a Ponemah data acquisition system (Data Sciences International). MAP, heart rate, stroke volume, CO and TPR were derived for all beats averaged over consecutive 2 min intervals.

Experimental design

Two different studies were conducted (Table 2). In Study 1, rats were treated once daily for 6 days with a single dose of drug (enalapril, fasudil, amlodipine or propranolol); SHR, n = 5 per drug. In Study 2, rats received single injections of four different doses of each drug (amlodipine, prazosin or HCTZ) on 4 separate days.

Table 2.

Study overview

Study	Measures	Study designs	Compound	Dose	Number of rats
1 Multiple dosing study	MAP	Days −1–0 : baseline (not included in analysis) Day 1 : baseline Days 2–3 : vehicle Days 4–9 : active treatment (once daily) Days 10–15: washout	Enalapril	30 mg·kg−1 p.o	5
			Fasudil	30 mg·kg−1 p.o	5
			Amlodipine	10 mg·kg−1 p.o	5
			Propranolol	1 mg·mL−1 in drinking water	5
2 Single administrations of different doses on separate days	MAP, CO (and TPR)	Day 1: vehicle Days 2–5: a different dose each day	Amlodipine	0.3, 1, 3, 10 mg·kg−1 p.o.	2
			Prazosin	0.04, 0.2, 1, and 5 mg·kg−1 p.o.	2
			HCTZ	0.1, 0.3, 1, 3 mg·kg−1 p.o.	2

In Study 1, rats were telemetred and, after 2 weeks recovery, received 1 week of daily, oral dosing of saline (dosing training), then baseline data were collected during 3 days of no treatment. Subsequently, rats were treated with vehicle for 2 days before treatment with active drug, which was administered once daily for 6 days at 1100 h. Thereafter, washout data were collected for 6 days.

In Study 2, flow cables were connected to the flow probes by 0700 h and disconnected after 1700 h. Baseline data were collected between 0800 and 1000 h each day. Rats were dosed at 1000 h and all data were continued to be collected until 1700 h. Thereafter, only MAP and HR data were obtained until the flow probes were reconnected the next morning.

Compounds

In Study 1, enalapril maleate (Sigma-Aldrich, St. Louis, MO, USA; E6888,), fasudil mono HCl (LC Laboratories, Woburn, MA, USA; MAF-4660) and amlodipine besylate (Lek Pharmaceuticals d.d., Verovskova, Ljubljana, Slovenia) were prepared for administration at 5 mL·kg⁻¹ by oral gavage. (±)-Propranolol HCl (Sigma-Aldrich, P0884) was dissolved in drinking water at 1 mg·mL⁻¹. Enalapril maleate, fasudil and amlodipine were homogenized in 0.5% methylcellulose (MC; Fisher Scientific, Pittsburgh, PA, USA).

In study 2, prazosin HCl (Sigma-Aldrich, P7791), amlodipine besylate and HCTZ (H2910, Sigma-Aldrich) were prepared for administration at 2 mL·kg⁻¹ by oral gavage. Prazosin and amlodipine were homogenized in 0.5% MC, whereas HCTZ was dissolved in NaOH and diluted with filtered water (vehicle was water adjusted to pH 11).

Data analysis

The interrelationship between MAP, CO and TPR is expressed in the formula: MAP = CO × TPR (Levick, 2003). On the basis of this relationship, a model was developed to depict the time course of the effects on MAP, CO and TPR (Figure 2). The model was defined by two linked turnover equations involving CO and TPR (Equation 1). Turnover models are also called indirect response models and can be used to describe hysteresis, that is the delay between a perturbation and a response (Dayneka et al., 1993). Examples of applications of this type of model can be found in the modelling of the homeostatic features of the release of endogenous compounds such as hormones or proteins (Gabrielsson and Weiner, 2000), or in the modelling of pharmacological responses such as drug-induced hypothermia (Zuideveld et al., 2001).

Figure 2.

Cardiovascular model to describe the change in mean arterial BP after administration of different compounds acting on CO and TPR. MAP equals the product of CO and TPR (MAP = CO × TPR). Effects on CO and TPR are described by two linked turnover equations. In these equations K_in__CO and K_in__TPR represent the zero-order production rate constants of CO and TPR; and k_{out_CO} and k_out__TPR represent the first-order dissipation rate constants of CO and TPR. When MAP increases as a result of a stimulating effect on CO or TPR, the values of CO and TPR will decrease as a result of the action of the different feedback mechanisms regulating the CVS. In this model, the magnitude of feedback on CO and TPR is represented by FB1 and FB2.

(1)

In these equations, K_{in_CO} and K_{in_TPR} represent the zero-order production rate constants and k_{out_CO} and k_{out_TPR} represent the first-order dissipation rate constants of CO and TPR, respectively. These hypothetical production and dissipation rate constants reflect the rate of change in CO and TPR. FB1 and FB2 are constants representing the magnitude of the negative feedback of MAP on CO and TPR. Following the criteria for statistical significance as specified in the section ‘Computation’, linear relationships between MAP and the production rate constants of CO and TPR were the most parsimonious relationships that captured the feedback mechanism adequately.

Initially, the circadian rhythm in BP was described as the sum of a maximum of 10 harmonics with different periods (Equation 2). The number of cosine functions was systematically reduced following the criteria for statistical significance (section ‘Computation’).

(2)

In this equation, amp represents the amplitude, t the time and HOR the horizontal displacement over time. From a mechanistic point-of-view, it is expected that the circadian rhythm in BP is a result of a circadian rhythm in CO and/or TPR as these are the primary drivers of MAP. However, as no 24 h measurements could be obtained for CO and TPR, the circadian rhythm was included in the model on MAP. Before pharmacological intervention (at baseline), MAP oscillates around its baseline value, which equals the product of the baseline values of CO and TPR (BSL_CO and BSL_TPR).

Before pharmacological intervention, the system is in a steady state, or dynamic equilibrium in mathematical terminology, denoting that MAP, CO and TPR do not change over time and are equal to their baseline values. As is common practice for turnover models (Dayneka et al., 1993), steady state conditions are described by the following equations (Equation 3) in which K_in is expressed in terms of BSL and k_out,

(3)

In the experiments, TPR was derived (Equation 1) from the directly measured MAP and CO. In contrast, in the modelling, the baseline values of MAP (BSL_MAP) and BSL_TPR were estimated and BSL_CO was derived from these parameters for reasons of model stability.

The system was functionally characterized by challenging the CVS with six different drugs with different MoA. Drug effects (EFF) were assumed to influence the production rates of either CO or TPR according to equation 4.

(4)

During pharmacological intervention TPR and CO can be calculated using Equation 5, where TPR_ss and CO_ss represent TPR and CO at steady state.

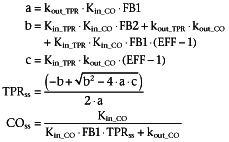(5)

Linear E_max and sigmoid E_max models were evaluated to depict the drug effects on CO and TPR. The effects of all compounds were best depicted by E_max models (Equation 6):

(6)

In this equation, E_max and EC₅₀ represent the maximum effect and the concentration resulting in a half-maximal effect, respectively, and C equals the drug concentration in plasma, which varies with time. Using the time course of the drug plasma concentrations, that is the PK, rather than the dose or exposure, as a predictor for the PD has the advantage that it enables a better indication of the time course of the drug effect. As the PK was not measured in these experiments, predicted plasma concentration versus time profiles were derived from the literature (Table 3). However, experimental conditions and formulations were different in these literature studies as compared with the experiments described in this paper. Therefore, for some compounds, PK parameters, for example the absorption rate, were estimated based on other known PK parameters and the effect on BP (Table 3). In that case, PK and PD parameters were estimated simultaneously.

Table 3.

Specification of the PK models to determine the pharmacokinetics of the six selected compounds, enalapril, fasudil, amlodipine, prazosin, propranolol and HCTZ to challenge the CVS

Compound	PK model	Literature model	Comments	Species
Enalapril	2-compartmental model with Michaelis-Menten elimination	(Lin et al., 1988)	Data read out from the manuscript and a 2- compartmental model with Michaelis-Menten elimination was optimized in NONMEM	Sprague-Dawley rats
Fasudil	1-compartmental model	(Ikegaki et al., 2001): Non-compartmental analysis	Ka and lag-time were derived from the reported half-life, AUC and Cmax using Berkeley Madonna	Wistar-Kyoto rats
Amlodipine	1-compartmental model	(Stopher et al., 1988): Non-compartmental analysis	Ka was derived from the reported half-life, Vd, F and Tmax using Berkeley Madonna	Sprague-Dawley rats
Prazosin	1-compartmental model	(Hamilton et al., 1985): 1-compartmental model	CL, Vd; scaled to rat using allometric scaling. Ka was estimated	New Zealand white rabbits
Propranolol	3-compartmental model	(van Steeg et al., 2010): 3-compartmental model	Absorption described as an infusion with a fixed duration of 24 h. Ka was estimated	Wistar-Kyoto rats
HCTZ	1-compartmental model	(Asdaq and Inamdar, 2009): 1-compartmental model	Reported: Ke, Ka, Vd, AUC -> F was calculated from these parameters	Wistar-Kyoto rats

The PK models were based on literature models. The adjustments required to account for the differences in experimental conditions and formulations in these literature studies as compared with the experiments described in this paper are described in the ‘Comments’ column.

CL, clearance; F, bioavailability; K_a, absorption rate; K_e, elimination rate; Vd, distribution volume.

Assumptions

The PK and PD models were based on the assumptions described in Table 4.

Table 4.

Model assumptions

No.	Assumption	Clarification
1	Compounds selectively influence either CO or TPR.	Although some compounds may have a combined mechanism of action, i.e. have an effect on both CO and TPR, it was assumed that only including the direct/primary effect was sufficient for identifying the system. Therefore, any changes observed in the other parameters were assumed to be a result of the feedback (indirect/secondary effect).
2	All compounds influence the production rates of CO or TPR rather than the dissipation rates.	This assumption is based on the MoA of the selected compounds (Table 1).
3	For compounds for which the maximum effect was not observed, complete inhibition (i.e. Emax = 1) was assumed at infinite concentrations to ensure identification of the EC50.	To evaluate the validity of this assumption, the influence of different values of the Emax (i.e. Emax = 0.8) on the estimates of the system parameters was tested. This was done for one of the compounds (amlodipine).
4	The PK do not differ between rat strains and can be scaled between rabbit and rat on the basis of an allometric function (West et al., 1999; Anderson and Holford, 2009).	Although published information on the PK of all selected compounds was available, the PK was often evaluated in different rat strains and, for prazosin, even in a different species (rabbit).

Influence of the selection of compounds on the system parameters

An adequate selection of compounds to challenge the functioning of the CVS was thought to be pivotal to successfully quantifying the parameters of the CVS model. The compounds were selected to have different mechanisms and durations of action as this provides the maximum potential to identify the model that is to distinguish system- and drug-specific parameters. Furthermore, we expected that a combined analysis of data from the six compounds would enable accurate and precise quantification of all system parameters. To determine whether the model obtained is truly system-specific, the influence of selectively omitting the data of one of the six compounds on the values of the system parameters was examined. If omission of these data does not lead to significant changes in these parameter estimates, this indicates that the model is truly drug-independent. In this analysis, the estimates of the system parameters obtained with these six sub-models were compared with those of the model based on all compounds.

System properties

Simulations were performed to investigate if the profiles of the time course of the drug effect on MAP, CO and TPR are different for compounds with an influence on either CO or TPR. The typical profiles of MAP, CO and TPR versus time and of CO versus TPR are referred to as signature profiles. Pertinent differences in signature profiles for compounds with either an effect on CO or TPR indicate whether the drug-independent model can be applied to investigate the site of action (CO or TPR) of new compounds with an unknown MoA on BP. The responses on CO, TPR and MAP were simulated after triggering the model by enhancing TPR or inhibiting CO. The stimulation and inhibition functions were analysed for a hypothetical constant rate infusion for 100 h to ensure that the drug effect is in steady state.

Computation

The data from Studies 1 and 2 were simultaneously analysed using the non-linear mixed-effects modelling approach implemented in NONMEM (version 7.1.0; Icon Development Solutions, Ellicott City, MD, USA). The models were compiled using Digital Fortran (version 6.6C3, Compaq Computer Corporation, Houston, TX, USA) and executed on a personal computer equipped with an AMD Athlon 64 processor 3200 + under Windows XP. The results from the NONMEM analysis were subsequently analysed using the statistical software package S-Plus for Windows (version 6.2 Professional, Insightful Corp., Seattle, WA, USA). The simulations were carried out using Berkeley Madonna (version 8.3.5, Berkeley Madonna Inc., University of California, Berkeley, CA, USA). Parameters were estimated using the first-order conditional estimation method with interaction between the two levels of stochastic effects (FOCE interaction). Random effects were included as exponential terms reflecting log normal distributions of model parameters. The residual variability was explored with proportional and additive error models. Goodness-of-fit was determined using the minimum value of the objective function defined as minus twice the log-likelihood. For nested models, a decrease of 10.8 points in the objective function (MVOF; corresponding to P < 0.001 in a chi-squared distribution) by adding an additional parameter was considered significant. The goodness-of-fit was also investigated by visual inspection of the plots of individual predictions and the diagnostic plots of (weighted) residuals. In addition, a visual predictive check was performed in which the median and the 90% interquartile range of data, simulated with the developed model, were plotted together with the observations.

Results

Model development

The CVS model as expressed by Equations 1–6, and graphically represented in Figure 2 was used to simultaneously analyse the data from Studies 1 and 2. To characterize the circadian variation in the baseline, the amplitudes of five harmonics of the circadian rhythm were quantified. Amp₁, amp₃, amp₄, amp₅ and amp₇ were estimated to be 3.17, −2.03, 1.15, 1.63 and 1.28 mmHg, respectively. Amp₂, amp₆, amp₈, amp₉ and amp₁₀ were fixed to 0, implying that these harmonics did not contribute to the circadian rhythm. In Study 1, BSL_MAP was allowed to vary between individual rats [inter-individual variability (IIV) ]. Study 2 provided information to estimate IIV on both BSL_MAP and BSL_TPR. The residual errors of MAP and TPR were best described by additive residual error models, whereas the residual error of CO was best described by a proportional error model. The dissipation rate of CO (k_{out_CO}) was found to be very high and could not be estimated accurately. Therefore, this parameter was fixed to a high value (99 1·h⁻¹) prior the other model parameters were estimated. The effects of all of the compounds were best described by E_max models. However, for amlodipine, fasudil, enalapril and HCTZ, it was not possible to identify both drug effect parameters, E_max and EC₅₀, independently and accurately. This was due to the fact that the E_max was not observed. Therefore, E_max was fixed to 1 for these compounds assuming that complete inhibition of K_in can be reached for infinite concentrations. For these compounds, the drug effects could have also been depicted as a linear concentration–effect relationship. However, these models were not applicable as the inhibition of K_in exceeded 100% during parameter optimization. In addition, adding a sigmoidicity parameter to the E_max models did not result in an improvement in the goodness-of-fit for all compounds.

In general, the model adequately described the data (Figures 3 and 4). However, for HCTZ, the effect of a dose of 1 mg·kg⁻¹ was under-predicted, but the effects of the higher and lower doses of HCTZ were adequately under-described (Figure 4B). This could indicate that the PD model selected, an E_max model with the value of E_max fixed to 1, was not optimal. However, this effect model could not be further optimized as the dose range selected was not large enough to cover the complete range from no effect to maximal effect.

Figure 3.

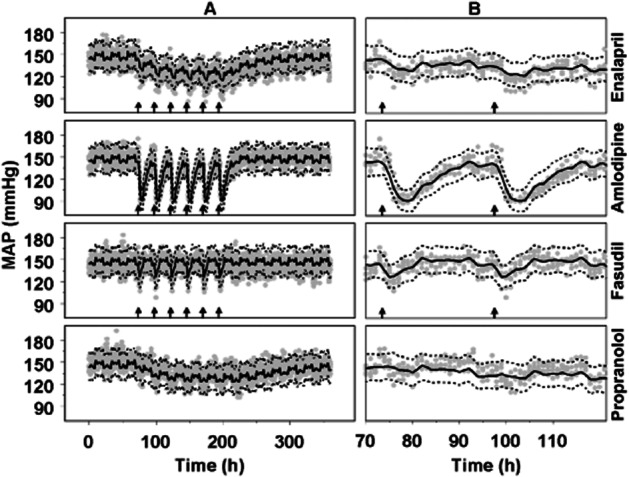
Visual predictive check of the description of the data from the repeated dosing Study 1 by the developed drug-independent CVS model. (A) Full-time scale; (B) Expansion of the responses to first two administrations of each drug. The grey dots represent the observations in SHR after administration of enalapril (30 mg·kg⁻¹ po) and amlodipine (10 mg·kg⁻¹ p.o.), fasudil (30 mg·kg⁻¹ p.o.) and propranolol (1 mg·mL⁻¹ in drinking water); n = 5 SHR per drug. The continuous lines represent the predicted median and the dashed lines represent the predicted lower and upper limit of the 90% prediction interval. The arrows indicate the six daily administrations of each drug.

Figure 4.

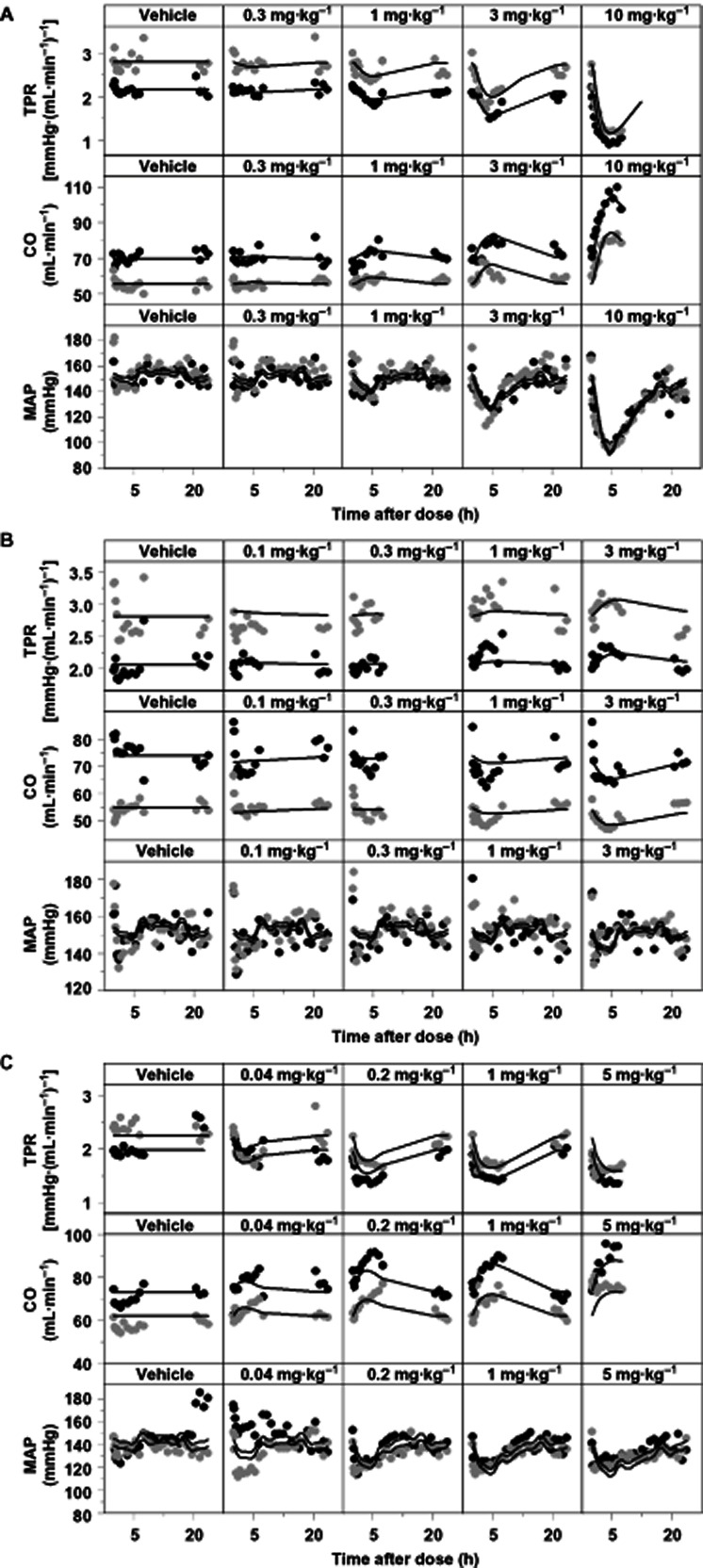
Depictions of the effects of amlodipine (A), HCTZ (B) and prazosin (C) on CO, TPR and MAP by the drug-independent CVS model. Data are from Study 2 in which vehicle and a different dose of amlodipine (0.3, 1, 3 and 10 mg·kg⁻¹ p.o.), HCTZ (0.1, 0.3, 1 and 3 mg·kg⁻¹ p.o.) or prazosin (0.04, 0.2, 1 and 5 mg·kg⁻¹ p.o.) was administered on separate days. The grey and black dots represent the observations of two different rats. The continuous lines represent the individual prediction by the developed drug-independent CVS model after the administration of amlodipine.

All system parameters could be estimated accurately as all SEMs were less than 50% of the parameter estimates (Table 5). Fixing E_max to 1 for amlodipine, fasudil, enalapril and HCTZ did not have a significant influence on the estimates of the system parameters [results shown for amlodipine after fixing the E_max of amlodipine to the arbitrarily selected value of 0.8 (instead of 1) in Table 5]. In addition, all drug-specific parameters could be estimated accurately, except for the EC₅₀ of prazosin (CV: 110%; Table 6). For this compound, the EC₅₀ and E_max were estimated simultaneously. Fixing E_max to 1, as was done for four other compounds, resulted in a more precise estimate of the EC₅₀, but the goodness-of-fit was less reliable as indicated by a significant increase in the MVOF. All correlations between system-specific parameters were less then 0.95, except for the correlation between k_{out_TPR} and FB2 (−0.984).

Table 5.

The system parameter values from the drug-independent model to describe the CVS

Parameter	Value	SE	CV	LLCI	ULCI	Value when Emax of amlodipine was fixed to 0.8 instead of 1
BSL_TPR (mmHg·mL−1·min−1)	2.32	0.132	5.69	2.06	2.58	2.32
BSL_MAP (mmHg)	147	1.38	0.939	144	150	147
kout_CO (1·h−1)	99 FIXED
kout_TPR (1·h−1)	0.260	0.129	49.6	0.00716	0.513	0.308
FB1 (1·mmHg−1)	0.00378	0.000148	3.92	0.00349	0.00407	0.00382
FB2 (1·mmHg−1)	0.00492	0.00101	20.5	0.00294	0.00690	0.00468

SE, SE of parameter estimate; CV, coefficient of variation; LLCI, lower limit of 95% CI; ULCI, upper limit of 95% CI.

Table 6.

The drug-dependent parameter values estimated by the drug-independent model to describe the CVS

Parameter	Value	SE	CV	LLCI	ULCI
Amlodipine
Emax	1 fixed
IC50 (ng·mL−1)	185	26.2	14.2	134	236
Fasudil
Emax	1 fixed
IC50 (ng·mL−1)	321	60.3	18.8	203	439
Propanolol
Emax	0.335	0.0624	18.6	0.213	0.457
IC50 (ng·mL−1)	9.82	3.8	38.7	2.37	17.3
Enalapril
Emax	1 fixed
IC50 (ng·mL−1)	2410	373	15.5	1679	3141
HCTZ
Emax	1 fixed
IC50 (ng·mL−1)	12 300	780	6.34	10 771	13 829
Prazosin
Emax	0.213	0.0158	7.42	0.182	0.244
IC50 (ng·mL−1)	0.133	0.146	109.8	−0.15	0.4

SE, SE of parameter estimate; CV, coefficient of variation; LLCI, lower limit of 95% CI; ULCI, upper limit of 95% CI.

Influence of the selection of compounds on the system parameters

None of the parameters changed significantly when data from one of the six compounds were selectively omitted, with the exception of the value of the parameter FB1, which was found to be dependent on the presence of the amlodipine data (Figure 5). FB1 changed from 0.00379 [confidence interval (CI): 0.00348–0.00410] to 0.00454 (CI: 0.00418–0.00490) 1·mmHg^–1.

Figure 5.

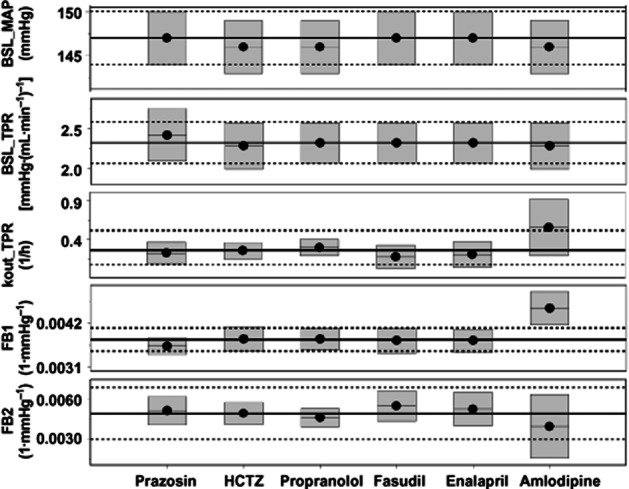
Evaluation of the drug-independence of the CVS model developed. Six different compounds, prazosin, HCTZ, propranolol, fasudil, enalapril and amlodipine, were used to estimate the system parameters of the CVS model. To determine if the system parameters were truly drug-independent, the model was re-evaluated after omitting the different compounds one by one. The continuous black lines represent the parameter estimates of the model including all compounds and the dashed lines represent the 90% CIs around these parameter estimates. The black lines with a black dot and the grey boxes represent the parameter estimates and the 90% CIs around these parameter estimates after omission of one of the compounds. When the grey boxes overlap with the area between the dotted lines, parameters are not significantly different and the model is independent of that compound. Therefore, the parameter estimate of FB1 is dependent on the presence of the amlodipine data.

System properties

Clear differences were found between the signature profiles of MAP, CO and TPR after simulating drug effects on CO and TPR. It was found that an increase in MAP can only be obtained by stimulating CO or TPR, and not by an overshoot of the feedback. Specifically, the simulation showed that inhibiting CO or TPR always results in a decrease in MAP, which demonstrates that feedback cannot be stronger than the primary effect (Figure 6). In addition, the delay in response was longer when the drug effect was on CO as compared with on TPR (Figure 6C).

Figure 6.

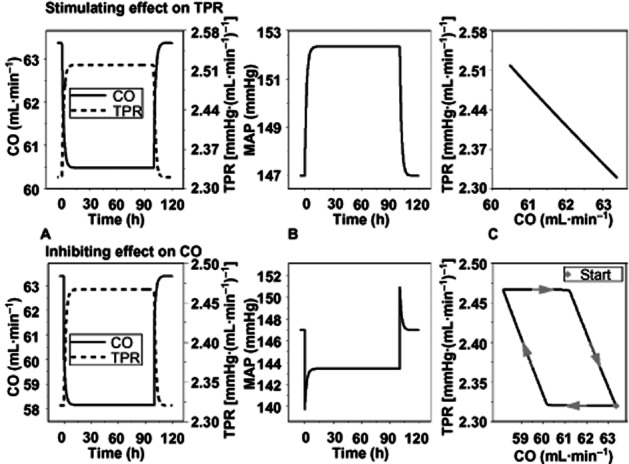
System properties of the CVS. The system properties of the CVS were investigated by simulating the effects on CO, TPR and MAP after stimulating TPR (upper panel) or inhibiting CO (lower panel). Both perturbations result in visually comparable effects on CO and TPR (A). However, the response of the MAP is in the opposite direction (B) indicating that the model can be used to identify the site of action. In addition, the hysteresis plot shows that an effect on TPR results in an immediate effect on CO as a result of feedback, whereas, an effect on CO results in a delayed response of TPR as a result of feedback (plot C).

Discussion

A mechanism-based PKPD model was developed to describe drug effects on the interrelationship between MAP, CO and TPR using data from preclinical experiments with a training set of six compounds with diverse effects on BP. Several models that describe the physiology of the CVS in great detail have been published, such as the Guyton and Coleman model (Guyton et al., 1972), which has provided the basis for the understanding of long-term BP control (Montani and Van Vliet, 2009). However, to date no models exist that integrate a quantitative description of the physiology of the CVS and the effect of cardiovascular drugs on the relationship between MAP, CO and TPR except for a model that was postulated by Francheteau et al. (1993). This model provides a description of the effect of dihydropyridine drugs on the relationship between MAP, CO and TPR. As several key model parameters of the Francheteau model were not identifiable, this is not a truly mechanism-based model, in the sense that drug- and system-specific properties were indistinguishable. An important feature of a mechanism-based PKPD model is that both the drug-specific and the system-specific model parameters are identifiable and quantifiable on data sets from preclinical or clinical studies (Danhof et al., 2007). This enables a reliable prediction of cardiovascular drug effects and becomes especially relevant when elucidating the variation between biological systems (i.e. between species) or between individuals (Danhof et al., 2007). Therefore, the model developed is the first mechanism-based model that can be applied to determine the effects of cardiovascular drugs with different MoA on the interrelationship between MAP, CO and TPR.

The model developed was based on a number of assumptions. One assumption was that only taking the primary/direct effects of the compounds on either CO or TPR into consideration was sufficient for identifying the system. For compounds like amlodipine and fasudil, this assumption can be justified, because these compounds primarily influence TPR. The change in CO, which is observed after administration of these compounds, is thought to be a secondary effect, which is triggered by the feedback mechanisms of the CVS. For compounds like enalapril and propranolol, the MoA is less clear as these compounds influence both CO and TPR albeit with different magnitudes and on different time scales (Table 1). Because the aim of this study was to develop a drug-independent model to describe the operation of the CVS, an accurate description of the system, based on all drug effects, was considered more important than the best possible description of the individual effects of the different compounds.

Another assumption was that all compounds influence the production rates rather than the dissipation rates of CO or TPR. This assumption was based on the MoA of the different compounds. The compounds that have a primary effect on TPR all influence smooth muscle cell contraction rather than causing relaxation. Therefore, if it is assumed that contraction is equivalent to production, modelling of the drug effect on the production rather than the dissipation rate mechanistically makes sense. The two compounds that influence CO, HCTZ and propranolol have quite different MoAs (Table 1). HCTZ, a diuretic, decreases ventricular stroke volume by decreasing cardiac filling. On the other hand, propranolol reduces sympathetically mediated stimulation of left ventricular contractility and heart rate. Therefore, from a mechanistic point-of-view, both compounds are thought to also influence the production rather than the dissipation rates. As the MoA of HCTZ and propranolol are quite different, it might be expected that the delay in response, as reflected by k_{out_CO}, would be different for these compounds. However, for both compounds, this delay was too short for it to be quantified accurately. Therefore, both the effects of HCTZ and propranolol could be adequately described by the model if k_{out_CO} was fixed to a high value of 99 1 h⁻¹. Although k_{out_CO} could not be quantified, the data did contain information about the rate of change in CO, which was high as fixing this parameter to a lower value resulted in an erroneous description of the HCTZ and propranolol data (results not shown). The exact value of k_{out_CO} is only relevant when examining the effect on shorter time scales than those investigated in the present studies, that is, seconds instead of minutes or hours. In addition, in theory, adding one or more compounds with an effect on the dissipation rate would provide additional information for identification of the system parameters. However, from a mechanistic point-of-view, it is difficult to find compounds with an effect on the k_out of CO or TPR. For example, enalapril influences the k_out of angiotensin I as it inhibits ACE. This effect, however, translates into an inhibition of the k_in of angiotensin II, which in turn leads to vasodilatation. The current model, therefore, describes the effect of enalapril on the k_in of TPR. Moreover, from a data-driven point-of-view, including compounds with an effect on k_out will only add additional information for quantification of the system parameters when the dose range selected is large enough to reach the E_max (Sharma and Jusko, 1996; 1998). In in vivo investigations, however, attainment of the maximum drug effect is not always feasible for safety reasons. Moreover, in situations where rapid adaptation occurs, it may be impossible experimentally to reach the E_max (Porchet et al., 1988). An interesting feature of the model developed is that it can be extended to more detailed levels without having to change the structure of the model. For example, the system can be described in more detail by assessing CO in terms of heart rate and stroke volume. In addition, including more information on the different feedback mechanisms could lead to a model that distinguishes the effects of different classes of antihypertensive drugs in more detail. The feedback mechanisms currently included in the model are likely to reflect the acute compensatory mechanisms (such as the baroreceptor reflex) better than the long-term compensatory mechanisms (such as RAAS) as the baroreflex system is active within minutes to hours to days whereas the RAAS is active within hours to days to weeks. To evaluate whether the model can be used to predict long-term effects on the CVS, long-term studies of days or weeks with CO measurements are required.

The assumptions made regarding the use of PK models derived from published results may have a large impact on the PK profiles. Therefore, the PK models were descriptive and the PK and drug-specific PD parameters may not represent ‘true’ values. Therefore, these estimates should only be interpreted in the context of this model. This was considered acceptable, as system-specific parameters, which are of primary interest in this research, are considerably less sensitive to changes in PK than drug-specific parameters. This is explained by the fact that drug-specific parameters are directly dependent on the PK of a specific drug, whereas the values of system-specific parameters are determined by the data of all compounds.

Previously, it was hypothesized that two aspects of the experimental design were pivotal for successfully quantifying the parameters of the CVS model: (i) the selection of the training set of compounds to challenge the functioning of the CVS and (ii) measuring both MAP and CO during the on- and offset phases of the drug effects. The correlations between some drug- and system-specific parameters were high (results not shown). However, evaluating whether the model was indeed drug-independent has demonstrated that the combination of compounds selected was adequate to develop a drug-independent model as only the parameter FB1, that is one of the five system-specific parameters, changed when the data of one of the six compounds (amlodipine) were omitted (Figure 5). To evaluate the importance of measuring both MAP and CO during the on- and offset phases of the drug effects, a retrospective sensitivity analysis was performed, using the parameters estimated from the model developed (Appendix 1). This sensitivity analysis demonstrated that measuring both MAP and CO during the on- and offset phases provided the pertinent information to quantify the system parameters. This is in agreement with the accuracy of the estimates of all the system-specific parameters. However, the values of k_out__TPR and FB2 were strongly correlated (−0.984) indicating that there was not enough information to estimate both parameters independently. This was confirmed by the sensitivity analysis, which showed that both parameters are most sensitive to the data collected during approximately the same period after drug administration and during the offset phase of the drug effects for compounds influencing TPR (Appendix 1: Figure 7). For compounds that influence CO, these peaks are more distinct (results not shown), which indicates that the information used to estimate these parameters was mainly obtained from the compounds that have an effect on CO. In the present study, only two compounds that have a primary effect on CO were included, that is propranolol and HCTZ, and CO was measured only after administration of HCTZ. To distinguish these parameters, detailed MAP and CO measurements from more compounds with an influence on CO are required. This should be taken into consideration when the model is applied for simulation purposes. Measuring CO provided an indication of the magnitude of the counteracting effects on TPR and CO underlying the effect on BP. Because MAP is the primary regulated haemodynamic variable, the effects of a drug on TPR and CO were disproportionately greater than those reflected by MAP alone. This indicates that a small pharmacological effect observed on MAP may mask much larger therapeutic benefits or, conversely, an increased risk of cardiovascular disease. Based on estimates of the residual error, the model is qualified to distinguish changes in MAP, CO and TPR larger than 7.6 mmHg, 4.3 mL·min⁻¹ and 0.5 mmHg/(mL·min⁻¹), respectively, from noise. This indicates that the model can be used to identify clinically relevant changes in BP. In conclusion, the rigorous experimental design was sufficient to provide the data to describe the interrelationship between MAP, CO and TPR in a quantitative and mechanism-based manner.

Figure 7.

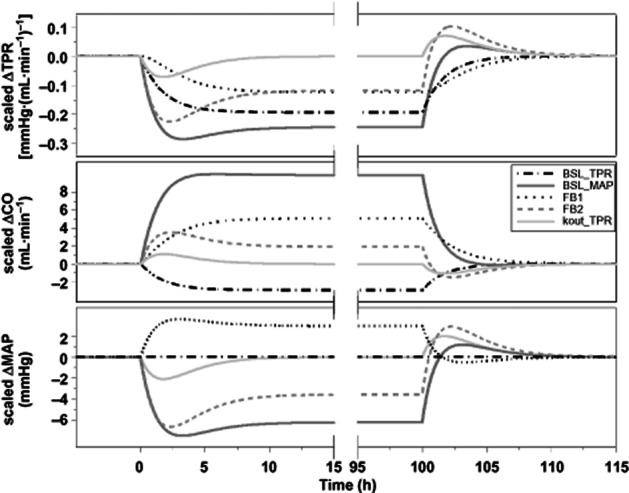
Sensitivity analysis. Influence of a 0.1% increase in the values of the system parameters of the drug-independent model (BSL_TPR, BSL_MAP, k_{out_TPR}, FB1 and FB2) on the dynamic behaviour of the CVS parameters MAP, CO and TPR. In this sensitivity analysis, an inhibitory effect of a drug (an on/off response; constant infusion during 100 h) on TPR was simulated.

The CVS model developed can be applied to estimate drug-specific parameters for new compounds, but this requires an accurate estimation of the PK. Recently, novel approaches have been proposed to accurately characterize PK without influencing the PD in preclinical PKPD investigations, e.g. the PK can be measured after completion of the PD part of the study (Bender et al., 2009) or the PK and PD can be measured on different days during the study (Viberg et al., 2012). In addition, the model developed can be applied to identify the site of action of new compounds influencing MAP through an unknown MoA; as in a simulation experiment it was shown that distinct differences exist between the signature profiles of compounds with an effect on CO and those that effect TPR (Figure 6). In this context, the model developed could provide key information for drug development, in that it can be used to predict whether the underlying MoA of compounds will have desired or undesired effects on BP. The model can also be applied to test hypotheses; for example, hypotheses on multiple sites of action can be evaluated by including drug effects on multiple parameters in the model. It should be noted that the set of system parameters identified is specific for SHR. Drug effects on MAP, CO and TPR may vary considerably in other (normotensive) rat strains due to physiological differences (Pinto et al., 1998). Consequently, applications of the present model, using the identified set of system parameters, are limited to this rat strain. However, an advantage of a mechanism-based model is that it allows the accurate extrapolation between different rat strains and from one species to another (Danhof et al., 2008; Ploeger et al., 2009) as the structure of the model is expected to be the same in all species. Therefore, an ultimate application of this drug-independent model would be to facilitate the prediction of the clinical response to newly developed compounds based on their preclinical data. Before our model can be applied for that purpose, the predictability of a long-term BP effect should be evaluated and the model should be scaled to human and validated using human MAP and CO measurements.

Glossary

Amp

amplitude

BSL_CO

baseline value of cardiac output

BSL_MAP

baseline value of MAP

BSL_TPR

baseline value of total peripheral resistance

C,

drug concentration in plasma

CO

cardiac output

E_max

maximum effect

FB1

negative feedback of mean arterial pressure on cardiac output

FB2

negative feedback of mean arterial pressure on total peripheral resistance

HCTZ

hydrochlorothiazide

HOR

horizontal displacement

IIV

inter-individual variability

K_{in_CO}

zero-order production rate constant of cardiac output

K_{in_TPR}

zero-order production rate constant of total peripheral resistance

k_{out_CO}

first-order dissipation rate constant of cardiac output

k_{out_TPR}

first-order dissipation rate constant of total peripheral resistance

MAP

mean arterial pressure

MC

methylcellulose

MoA

mechanisms of action

MVOF

minimum value of the objective function

PD

pharmacodynamics

PK

pharmacokinetics

PKPD

pharmacokinetic–pharmacodynamic

RAAS

renin–angiotensin–aldosterone system

SHR

spontaneously hypertensive rats

T

time

TPR

total peripheral resistance

Appendix: Sensitivity analysis, evaluation of the experimental design

An adequate experimental design was thought to be pivotal to distinguish drug- from system-specific parameters in this investigation. By showing how the dynamic behaviour of the system responds to changes in parameter values, a sensitivity analysis enables identification of the part of the experimental protocol that provides the pertinent information to quantify the parameters and to distinguish one parameter from another. Using the parameter estimates of the developed model, a retrospective parameter sensitivity analysis was performed in Berkeley Madonna (version 8.3.5, Berkeley Madonna Inc., University of California, Berkeley, CA, USA) to determine how ‘sensitive’ the developed model is to changes in the values of the parameters of the model.

First, a simulation was performed with all system parameters fixed at their estimated values [S(t,x₀)], while assuming an inhibiting drug effect on TPR during a constant drug infusion of 100 h to ensure that the drug effect is in steady state. Subsequently, simulations were performed after 0.1% increments in the system parameters (0.1% is the standard in Berkeley Madonna) [S(t,x)]. Finally, for each parameter, the sensitivity [S(t)] was calculated according to equation 7.

(A1)

The sensitivity [S(t)] in change from baseline for MAP, CO and TPR was evaluated for all system parameters ( Figure 7). This figure shows that the on- and offset phases of the drug effect contained complementary information; as in both phases, the peaks of the values of the different parameters of the PD system (BSL_TPR, BSL_MAP, k_{out_TPR}, FB1 and FB2) occurred at different time points relative to each other. In addition, the three biomarkers of the CVS, MAP, CO and TPR also contained complementary information regarding the dynamics of the system. For example, the peaks of the two feedback parameters, FB1 and FB2, occurred almost simultaneously when examining the sensitivity in MAP, whereas when looking at the sensitivity in CO and TPR, the peaks occurred relatively later. Therefore, measuring CO provided the pertinent information to distinguish these parameters.

Conflict of interest

None.