Abstract
Both microwave absorption and magnetocaloric effect (MCE) are two essential performances of magnetic materials. We observe that LaFe11.6Si1.4C0.2H1.7 intermetallic compound exhibits the advantages of both giant microwave absorption exceeding −42 dB and magnetic entropy change of −20 Jkg−1K−1. The excellent electromagnetic wave absorption results from the large magnetic loss and dielectric loss as well as the efficient complementarity between relative permittivity and permeability. The giant MCE effect in this material provides an ideal technique for cooling the MAMs to avoid temperature increase and infrared radiation during microwave absorption. Our finding suggests that we can integrate the giant microwave absorption with magnetic refrigeration in one multifunctional material. This integration not only advances our understanding of the correlation between microwave absorption and MCE, but also can open a new avenue to exploit microwave devices and electromagnetic stealth.
The extensive development and use of the electronic devices have created a new kind of problem called electromagnetic interference (EMI). To suppress the serious EMI problem, it is becoming very urgent to design and fabricate the electromagnetic compatibility (EMC) devices, which can ensure that equipment items will not interfere with or prevent each other's correct operation through spurious emission. For achieving sufficient EMC, researchers have long been involved in exploiting microwave absorbing materials (MAMs) due to their prospective applications in electronic devices, military affairs such as airplanes, steamboats, tanks, microwave darkrooms, and even broadband electromagnetic cloaking1,2. Up to date, various MAMs composed of magnetic loss powders such as ferrite, nickel, cobalt, and dielectric loss materials such as carbon nanotubes (CNTs) and conducting polymers have been fabricated3,4,5,6,7,8. Two approaches, either making electromagnetic wave disappearance by interference(Figure 1(a)), or absorbing electromagnetic wave effectively and converting electromagnetic energy into heat, are generally adopted for microwave loss. Unfortunately, the temperature increment and infrared radiation of MAMs due to the conversion of electromagnetic energy into heat will seriously hamper the application of microwave devices and electromagnetic stealth(Figure 1(b)). Therefore, it is interesting to explore whether MAMs can be refrigerated during microwave absorption (Figure 1(c)).
Figure 1. The scheme of microwave incident on an absorbing layer.
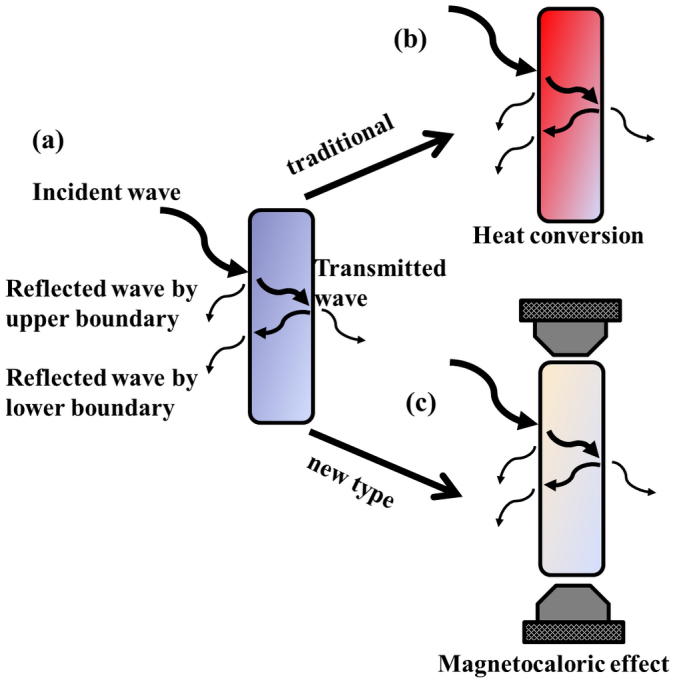
Two approaches, either making electromagnetic wave disappearance by interference (a), or absorbing electromagnetic wave effectively and converting electromagnetic energy into heat, are generally adopted for microwave loss (b). A prototype of magnetic cooling MAMs during microwave absorption (c).
Compared with traditional gas-compression/expansion refrigeration, magnetic refrigeration exhibits the advantages of high energy efficiency and environment friendliness9,10,11,12,13. The discovery of a giant magnetic entropy change in La(Fe1−xSix)13 intermetallic compounds gives rise to interest in searching for novel magnetic refrigerants14,15. Both microwave absorption and magnetocaloric effect (MCE) are two essential performances of magnetic materials. Meanwhile, to our knowledge, microwave properties of these novel magnetic refrigerants have never been reported. According to the Snoek limit16, the product of the high frequency susceptibility, 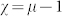 , and the resonance frequency,
, and the resonance frequency, 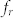 , is proportional to the saturation magnetization,
, is proportional to the saturation magnetization, 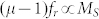 , where
, where 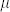 is permeability. In addition, the upper limit of magnetic entropy change is determined by the relation of
is permeability. In addition, the upper limit of magnetic entropy change is determined by the relation of 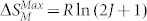 , where R is the gas constant and J is the total angular momentum of the magnetic ion. The high saturation magnetization is thus one of prerequisites for achieving both high frequency permeability and giant magnetic entropy change. Among the rare-earth-Fe intermetallic compounds, LaFe13-xSix intermetallics have the most abundant Fe concentration, and consequently possesses high saturation magnetization.
, where R is the gas constant and J is the total angular momentum of the magnetic ion. The high saturation magnetization is thus one of prerequisites for achieving both high frequency permeability and giant magnetic entropy change. Among the rare-earth-Fe intermetallic compounds, LaFe13-xSix intermetallics have the most abundant Fe concentration, and consequently possesses high saturation magnetization.
Here, we present the microwave absorption and magnetic entropy change of LaFe11.6Si1.4C0.2H1.7 intermetallic compound. LaFe11.6Si1.4 C0.2H1.7 intermetallic compound shows a metallic behavior with resistivity value of 3.8  at room temperature. The MAM must contain a sufficient quantity of free charge carriers in order to interact with microwave radiation. In order to reduce the eddy current loss induced by electromagnetic wave, the MAM sample was mixed metallic powders with insulating paraffin wax. To satisfy the microwave devices application above room temperature, the Curie temperature up to 330 K is achieved by the addition of interstitial atoms C and H. In the case of LaFe11.6Si1.4C0.2H1.7 intermetallic compound, Fe atoms occupy two sites, 8b and 96i, the Curie temperature is determined by the overall exchange interaction between Fe(8b)-Fe(8b), Fe(8b)-Fe(96i) and Fe(96i)-Fe(96i) atoms. Our previous neutron diffraction work demonstrated that the bond-length of Fe(8b)-Fe(96i) is very short, resulting a negative exchange interaction between Fe(8b) and Fe(96i), and consequently weakens the overall exchange interaction. The addition of interstitial atoms C and H leads to an expansion of the bond-length of Fe(8b)-Fe(96i) and a change in sign of Fe(8b)-Fe(96i) exchange interaction from negative to positive17. Therefore, the overall exchange interaction between Fe-Fe atoms and the Curie temperature are significantly enhanced by the introduction of interstitial atoms C and H. We observe that this intermetallic compound exhibits the advantages of both giant microwave absorption exceeding −42 dB and magnetic entropy change of −20 Jkg−1K−1. The value of RL for LaFe11.6Si1.4C0.2H1.7/paraffin wax is comparable with that of the most common used microwave absorber, carbonyl iron (35 dB) and conventional ferrite MAMs (30 dB)18,19. Our finding suggests that we can integrate the microwave absorption with magnetic refrigeration in one multifunctional material. This integration not only gives us a deeper insight into the effect of intrinsic magnetic properties on the performances of microwave absorption and MCE, but also provides a new possibility for solving the bottleneck of microwave devices and electromagnetic stealth.
at room temperature. The MAM must contain a sufficient quantity of free charge carriers in order to interact with microwave radiation. In order to reduce the eddy current loss induced by electromagnetic wave, the MAM sample was mixed metallic powders with insulating paraffin wax. To satisfy the microwave devices application above room temperature, the Curie temperature up to 330 K is achieved by the addition of interstitial atoms C and H. In the case of LaFe11.6Si1.4C0.2H1.7 intermetallic compound, Fe atoms occupy two sites, 8b and 96i, the Curie temperature is determined by the overall exchange interaction between Fe(8b)-Fe(8b), Fe(8b)-Fe(96i) and Fe(96i)-Fe(96i) atoms. Our previous neutron diffraction work demonstrated that the bond-length of Fe(8b)-Fe(96i) is very short, resulting a negative exchange interaction between Fe(8b) and Fe(96i), and consequently weakens the overall exchange interaction. The addition of interstitial atoms C and H leads to an expansion of the bond-length of Fe(8b)-Fe(96i) and a change in sign of Fe(8b)-Fe(96i) exchange interaction from negative to positive17. Therefore, the overall exchange interaction between Fe-Fe atoms and the Curie temperature are significantly enhanced by the introduction of interstitial atoms C and H. We observe that this intermetallic compound exhibits the advantages of both giant microwave absorption exceeding −42 dB and magnetic entropy change of −20 Jkg−1K−1. The value of RL for LaFe11.6Si1.4C0.2H1.7/paraffin wax is comparable with that of the most common used microwave absorber, carbonyl iron (35 dB) and conventional ferrite MAMs (30 dB)18,19. Our finding suggests that we can integrate the microwave absorption with magnetic refrigeration in one multifunctional material. This integration not only gives us a deeper insight into the effect of intrinsic magnetic properties on the performances of microwave absorption and MCE, but also provides a new possibility for solving the bottleneck of microwave devices and electromagnetic stealth.
Results
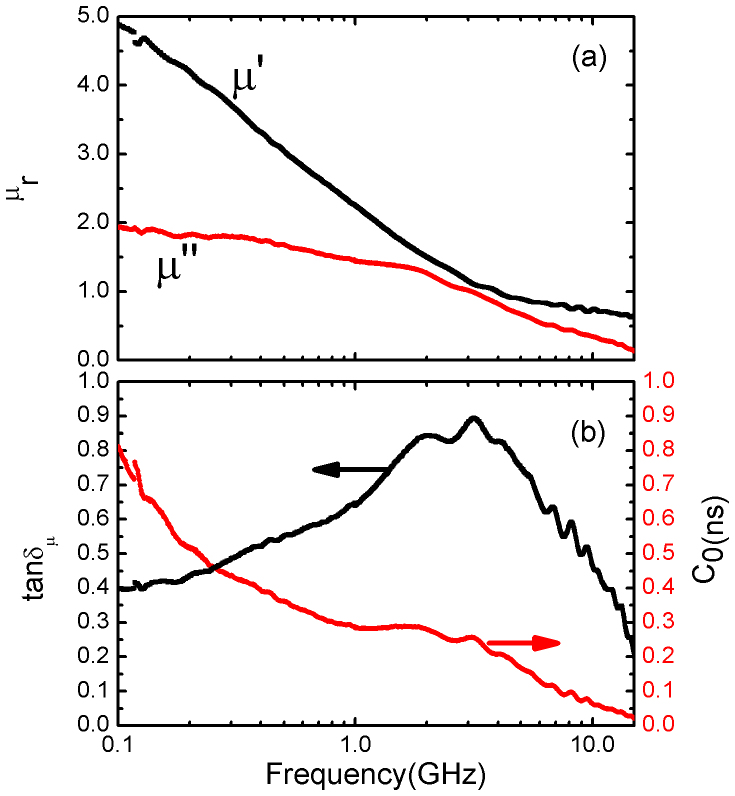
Figures 2(a) and 2(b) illustrates the frequency dependence of relative complex permeability 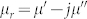 magnetic loss tangent
magnetic loss tangent 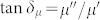 of the LaFe11.6Si1.4C0.2H1.7/paraffin wax, respectively. Both the real part (μ′) and the imaginary part (μ″) of relative complex permeability(
of the LaFe11.6Si1.4C0.2H1.7/paraffin wax, respectively. Both the real part (μ′) and the imaginary part (μ″) of relative complex permeability(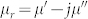 ) for the sample of LaFe11.6Si1.4C0.2H1.7/paraffin wax exhibit a relaxation behavior and decreases from 4.9 to 1.0, and from 1.9 to 1.0 as frequency increase up to 3.2 GHz, respectively (Figure 2(a)). The magnetic loss tangent
) for the sample of LaFe11.6Si1.4C0.2H1.7/paraffin wax exhibit a relaxation behavior and decreases from 4.9 to 1.0, and from 1.9 to 1.0 as frequency increase up to 3.2 GHz, respectively (Figure 2(a)). The magnetic loss tangent 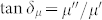 increases first with frequency, reaches a broad peak value of 0.89 at 3.2 GHz, and decreases with further increasing frequency (Figure 2(b)). It is known that the microwave magnetic loss of magnetic materials originates mainly from hysteresis, domain wall resonance, eddy current effect and the natural ferromagnetic resonance. Since almost no hysteresis loops can be observed from the magnetization curves measured during increasing and decreasing magnetic field processes (as will mention latter), the hysteresis loss resulted from irreversible magnetization is negligible. In our study, the permeability was measured over a frequency range of 0.1–15.0 GHz, the contribution of domain wall resonance is neglected since it occurs usually in the 1–100 MHz range. The eddy current loss is related to the diameter of particles d and the electric conductivity
increases first with frequency, reaches a broad peak value of 0.89 at 3.2 GHz, and decreases with further increasing frequency (Figure 2(b)). It is known that the microwave magnetic loss of magnetic materials originates mainly from hysteresis, domain wall resonance, eddy current effect and the natural ferromagnetic resonance. Since almost no hysteresis loops can be observed from the magnetization curves measured during increasing and decreasing magnetic field processes (as will mention latter), the hysteresis loss resulted from irreversible magnetization is negligible. In our study, the permeability was measured over a frequency range of 0.1–15.0 GHz, the contribution of domain wall resonance is neglected since it occurs usually in the 1–100 MHz range. The eddy current loss is related to the diameter of particles d and the electric conductivity 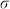 , which can be expressed by
, which can be expressed by 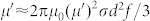 , where
, where 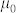 is the permeability of vacuum. If the magnetic loss only results from eddy current loss, the value of C0 (
is the permeability of vacuum. If the magnetic loss only results from eddy current loss, the value of C0 (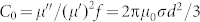 ) should be a constant with varying frequency20. The values of C0 significantly decrease with increasing frequency from 0.1 to 15.0 GHz, suggesting the magnetic loss is not related to eddy current (Figure 2(b)). Therefore, the very broad peak of magnetic loss is mainly caused by the natural ferromagnetic resonance.
) should be a constant with varying frequency20. The values of C0 significantly decrease with increasing frequency from 0.1 to 15.0 GHz, suggesting the magnetic loss is not related to eddy current (Figure 2(b)). Therefore, the very broad peak of magnetic loss is mainly caused by the natural ferromagnetic resonance.
Figure 2.
(a) Frequency dependence of relative complex permeability 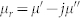 ; and (b) magnetic loss tangent
; and (b) magnetic loss tangent 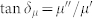 of the LaFe11.6Si1.4C0.2H1.7/paraffin wax.
of the LaFe11.6Si1.4C0.2H1.7/paraffin wax.
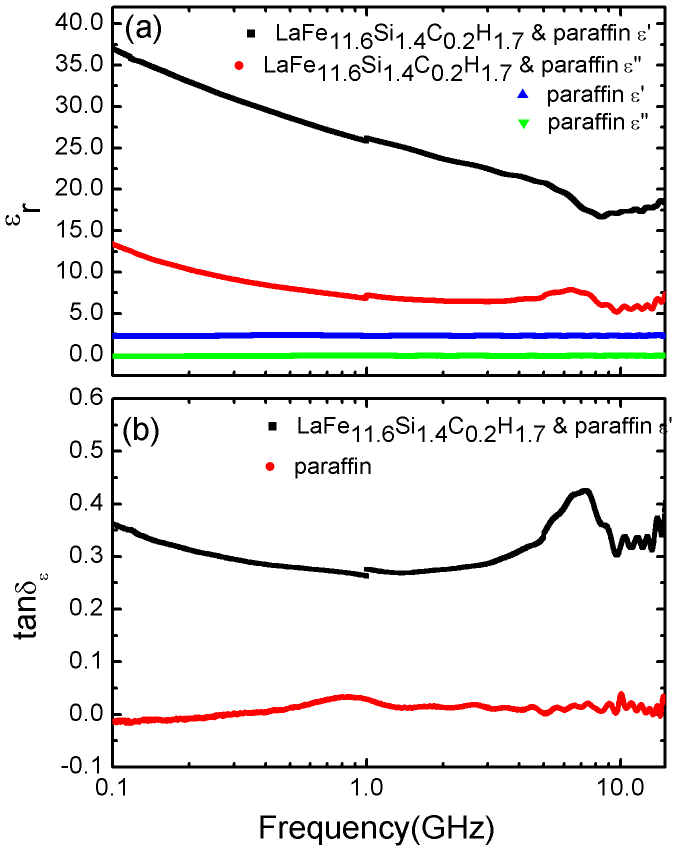
It is known that the real permittivity (ε′) is an expression of polarization ability of a material which mainly arises from dipolar polarization and interfacial polarization at microwave frequency21. The imaginary permittivity (ε″) follows the relation 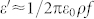 according to free-electron theory, where
according to free-electron theory, where 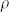 is the resistivity22. Both the real part ε′ and the imaginary part ε″ of relative complex permittivity (
is the resistivity22. Both the real part ε′ and the imaginary part ε″ of relative complex permittivity (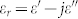 ) for the sample of LaFe11.6Si1.4C0.2H1.7/paraffin wax are expected to decrease with increasing frequency (Figure 3(a)). The dielectric loss tangent
) for the sample of LaFe11.6Si1.4C0.2H1.7/paraffin wax are expected to decrease with increasing frequency (Figure 3(a)). The dielectric loss tangent 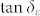 keeps almost constant of 0.35 in the frequency range of 0.1–5.0 GHz, and reaches a maximum value of 0.46 around 8.2 GHz (Figure 3(b)). For comparison, the data of paraffin wax were also plotted in Figures 3(a) and 3(b). The dielectric loss for paraffin wax is about at least one order of magnitude smaller and can be ignored. Although the fundamental understanding of what determines the dielectric loss tangent has still not been established8, we can concluded the displacement current by free carriers in LaFe11.6Si1.4C0.2Hδ is main source of dielectric loss in this composite compound. The large values of the dielectric loss owing to highly conductive LaFe11.6Si1.4C0.2Hδ are favorable for improving the microwave absorption properties. By comparing the frequency-dependence of dielectric loss with magnetic loss, the peak of
keeps almost constant of 0.35 in the frequency range of 0.1–5.0 GHz, and reaches a maximum value of 0.46 around 8.2 GHz (Figure 3(b)). For comparison, the data of paraffin wax were also plotted in Figures 3(a) and 3(b). The dielectric loss for paraffin wax is about at least one order of magnitude smaller and can be ignored. Although the fundamental understanding of what determines the dielectric loss tangent has still not been established8, we can concluded the displacement current by free carriers in LaFe11.6Si1.4C0.2Hδ is main source of dielectric loss in this composite compound. The large values of the dielectric loss owing to highly conductive LaFe11.6Si1.4C0.2Hδ are favorable for improving the microwave absorption properties. By comparing the frequency-dependence of dielectric loss with magnetic loss, the peak of 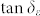 occurs usually in higher frequency range.
occurs usually in higher frequency range.
Figure 3.
(a) Frequency dependence of relative complex permittivity 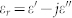 , and (B) dielectric loss
, and (B) dielectric loss 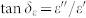 of the LaFe11.6Si1.4C0.2H1.7/paraffin wax. For comparison, the data of paraffin were also plotted.
of the LaFe11.6Si1.4C0.2H1.7/paraffin wax. For comparison, the data of paraffin were also plotted.
To further confirm the magnetic loss and dielectric loss, the reflected loss (RL) of the sample was investigated. According to the transmission line theory, for a single layer absorber with a backed metal plate, the RL were simulated from the electromagnetic parameters at various sample thicknesses by means of the following expressions23,24.
where f is the frequency of the electromagnetic wave, d is the thickness of the sample, c is the velocity of light, Z0 is the impedance of air, and Zin is the input impedance of the sample.
The RL curves are governed by the contribution of electromagnetic wave interference from interface and by the microwave absorption. Considering the incident electromagnetic wave reflected by both the upper and lower boundaries of a thin film, the path difference of the reflected waves must be calculated in order to determine the condition for interference (figure 1(a)). According to the quarter-wave length matching model, the reflected wave and the incident wave will be out of phase by 180° at a certain frequency point, and cancel each other for the thickness of the sample satisfying the quarter-wavelength thickness relation25.
where 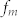 is the peak frequency of RL, tm is the thickness of the sample.
is the peak frequency of RL, tm is the thickness of the sample.
When the sample thickness satisfies the quarter or three-quarter of wave-length criteria, a peak or two peaks of RL appear (Figure 4). The optimal reflectivity loss of RL = −42.5 dB is reached at 2.7 GHz for 7.00 mm thickness. Since the RL is mainly deterined by the incident electromagnetic wave reflected by both the upper and lower boundaries of a thin film, its peak is sharper than theat of magnetic loss as shown in Figure 2(c).
Figure 4. Frequency- and thickness- dependence of refection loss (RL) for the LaFe11.6Si1.4C0.2H1.7/paraffin wax samples with different thickness.
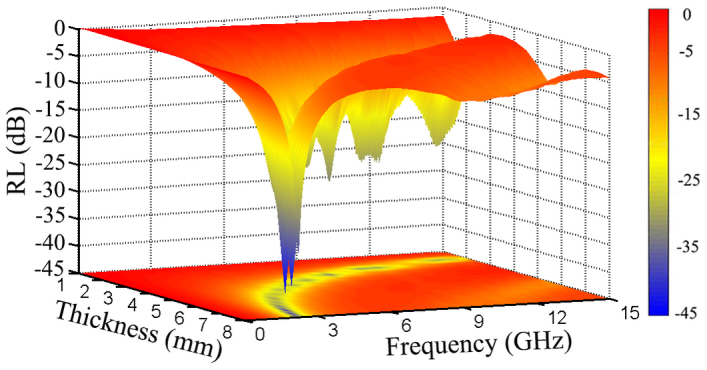
In addition, as shown in the projection of RL in the basal plane, the peaks of RL obviously shift to lower frequencies with increasing the sample thickness. The RL value of −20 dB is comparable to the 99% of electromagnetic wave absorption according to Eqs. (1) and (2), and thus “RL < −20 dB” is considered as an adequate electromagnetic absorption at a microwave frequency. For our samples, the RL < −20 dB can be obtained in the 2.0–12.0 GHz range for the absorber thickness of 2.5–8.3 mm. Moreover, owing to the large magnetic loss tangent and dielectric loss tangent, a considerably large RL = −10 dB can be obtained in whole frequency range of 0.1–15 GHz and thickness of 1.0–8.3 mm, suggesting that this compound is an excellent candidate for MAMs. An effective MAMs need to satisfy the impedance matching condition,  .
.
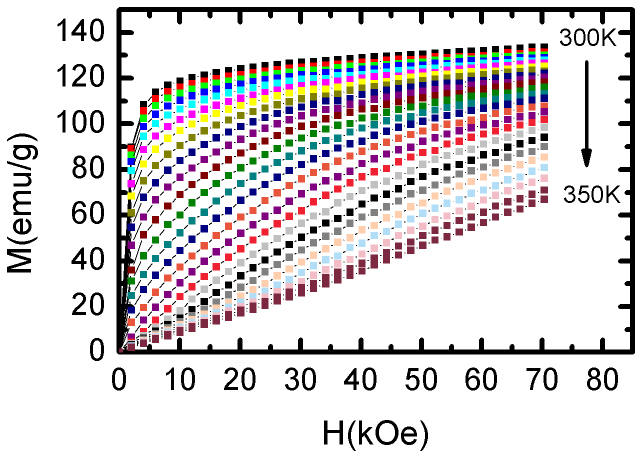
The large magnetic loss and dielectric loss are favorable for excellent broadband EMC application. Unfortunately, the conversion of electromagnetic energy into heat will increase the MAMs temperature, which restricts the miniaturization and rapid increase in frequencies of electric devices. Moreover, the increase in MAMs temperature leads to infrared radiation since infrared light includes most of the thermal radiation emitted by objects near room temperature. The infrared radiation of MAMs will seriously hamper their application for electromagnetic stealth. Magnetic refrigeration based on MCE is a promising technique for cooling the MAMs during microwave absorption. To understand the MCE, we measured the isothermal magnetization curves of LaFe11.6Si1.4C0.2H1.7 in the temperature range of 300–350 K with an interval of 2 K. Owing to the low anisotropy field, the magnetization curve at room temperature increases sharply with applied field (Figure 5). Moreover, we also observed that almost no hysteresis loops can be discerned from the magnetization curves measured either during heating and cooling processes or during increasing and decreasing magnetic field processes. No hysteresis loops is advantageous for the application of magnetic refrigeration10.
Figure 5. Isothermal magnetization curves of LaFe11.6Si1.4C0.2H1.7 in the temperature range of 300–350 K with an interval of 2 K.
At temperature T, the magnetic entropy change due to applied field H can be calculated from the isothermal curves by the Maxwell relation
Figure 6 displays magnetic entropy change 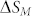 as a function of T and H of LaFe11.6Si1.4C0.2H1.7. From the calculated
as a function of T and H of LaFe11.6Si1.4C0.2H1.7. From the calculated 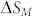 as a fuction of T and H, a giant magnetic entropy change of −20 Jkg−1K−1 can be achieved at temperature around 330 K and applied field of 70 kOe. It is noteworthy that the MCE is not only governed by the magnetic entropy change, but also the refrigeration capacity (RC). The RC can be calculated by integrating the area under
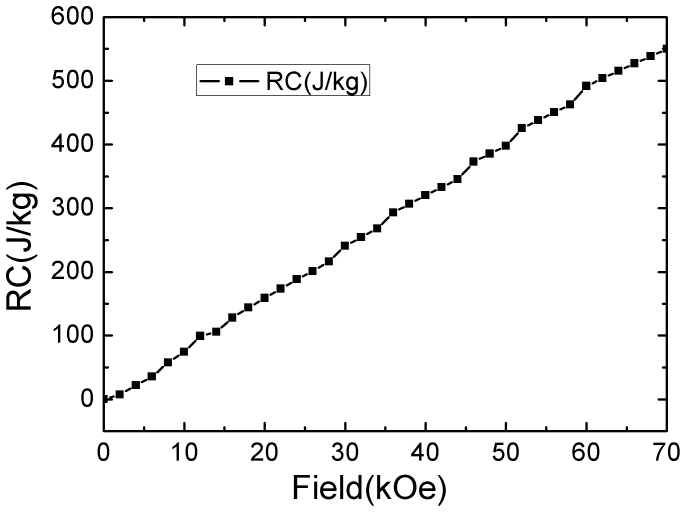
as a fuction of T and H, a giant magnetic entropy change of −20 Jkg−1K−1 can be achieved at temperature around 330 K and applied field of 70 kOe. It is noteworthy that the MCE is not only governed by the magnetic entropy change, but also the refrigeration capacity (RC). The RC can be calculated by integrating the area under 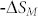 vs
T curves within the temperature range at half-maximum of the peak. The RC was observed to increase with applied field (Figure 7).
vs
T curves within the temperature range at half-maximum of the peak. The RC was observed to increase with applied field (Figure 7).
Figure 6. Magnetic entropy change 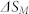 as a function of T and H of LaFe11.6Si1.4C0.2H1.7.
as a function of T and H of LaFe11.6Si1.4C0.2H1.7.
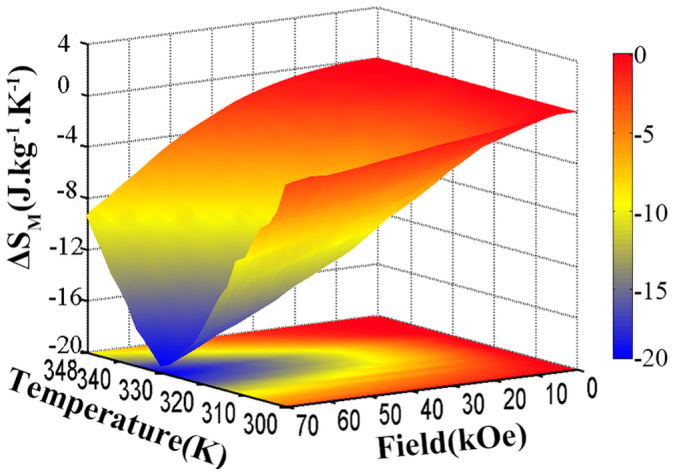
Figure 7. Field-dependence of refrigeration capability RC of LaFe11.6Si1.4C0.2H1.7.
Discussion
In order to demonstrate the useful cooling power above room temperature, Zimm et al. constructed a rotary magnetic refrigerator through a 15 kOe Nd2Fe14B permanent magnet. They found that the peak cooling capacity of LaFeSiH compares favorably with that of Gd26. Although the value of 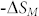 = 7.5 Jkg−1K−1 at 20 kOe is smaller than that of La(Fe1-xSix)Hy reported by Fujita et al.27, the value of RC = 158 J/kg owing the broad peak of magnetic entropy change of our sample suggests that LaFe11.6Si1.4C0.2H1.7 compound is also a promising magnetic refrigerant.
= 7.5 Jkg−1K−1 at 20 kOe is smaller than that of La(Fe1-xSix)Hy reported by Fujita et al.27, the value of RC = 158 J/kg owing the broad peak of magnetic entropy change of our sample suggests that LaFe11.6Si1.4C0.2H1.7 compound is also a promising magnetic refrigerant.
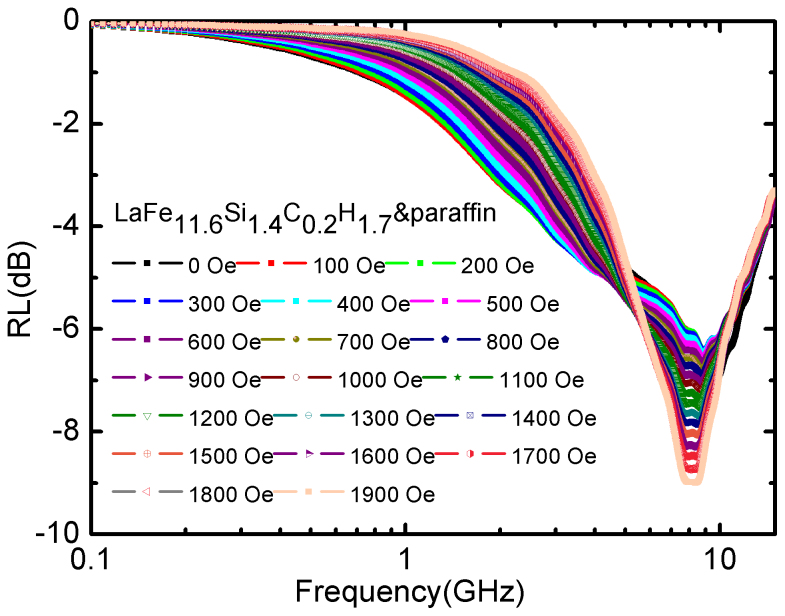
One may further concern whether the reflection loss is reduced by the applied field during magnetic refrigeration process. Figure 8 illustrates the reflection loss for the sample with thickness of 2.0 mm measured in the applied field ranging from 0 to 1900 Oe. Since the applied magnetic field may decrease magnetic permeability at low frequency range, the reflection loss is slightly reduced with increasing applied field. However, a slight enhancement of the reflection loss with increasing applied field was observed for the frequency range of 3.0–10 GHz. Therefore, for our sample, the applied field for magnetic refrigeration does not reduce the reflection loss seriously in the frequency range of 3.0–15.0 GHz.
Figure 8. Field-dependence of reflection loss RL of for the LaFe11.6Si1.4C0.2H1.7/paraffin wax samples with thickness of 2.0 mm.
In conclusion, we have demonstrated that LaFe11.6Si1.4C0.2H1.7 has both excellent microwave absorption and giant magnetic entropy change around ambient temperature. The excellent electromagnetic wave absorption results from the large magnetic loss and dielectric loss as well as the efficient complementarity between relative permittivity and permeability. The giant MCE effect in this material provides an ideal technique for cooling the MAMs to avoid temperature increase and infrared radiation during microwave absorption. A prototype of magnetic cooling MAMs during microwave absorption is illustrated in Figure 1(c). To our knowledge, the results of giant microwave absorption of −42 dB and magnetic entropy change of −20 Jkg−1K−1 in one multifunctional material have never been reported. Our finding suggests that we can integrate the microwave absorption with magnetic refrigeration in one multifunctional material. This integration not only advances our understanding of the correlation between microwave loss and MCE, but also can open a new avenue to exploit microwave devices and electromagnetic stealth.
Methods
The LaFe11.6Si1.4C0.2 samples were prepared by arc-melting by appropriate proportions of Fe–C alloy, La, Fe, and Si with the purity better than 99.9 wt.%. The heat treatment was carried out in a quartz tube of high vacuum at 1373 K for 7 days. The bulk LaFe11.6Si1.4C0.2 sample was crushed into small particles (<1.5 mm), and then hydrogenated at 523 K in a hydrogen atmosphere of ~0.6 MPa for a long time until saturation. Then, extraction of hydrogen to some extent from the saturated hydride was performed under a vacuum better than 5 × 10−4 Pa at 250°C for different lengths of time. The hydrogen content was calculated from the variation of the sample weight before/after hydrogen absorption (desorption) and the weight was measured by an electronic analytical balance (AND GR-202) with a readability of 0.01 mg and a repeatability of 0.02 mg in the range 0–42 g. The weight of absorbed hydrogen was about 0.21 wt.% by weighing the mass before and after hydrogenation, and then the hydrogen content x was estimated to be 1.7. The method of hot extraction was generally used to determine the hydrogen content28,29. Powder x-ray diffraction data were obtained using Cu Ka radiation at room temperature. The lattice expansion as compared to the LaFe11.6Si1.4C0.2 compound is 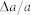 = 1.1%, which is corresponding to
= 1.1%, which is corresponding to 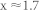 as previous report28. The hydrogen content obtained by weighing the mass before and after hydrogenation is consistent with the result estimated from lattice expansion. All magnetic measurements were performed on a commercial MPMS-7 type superconducting quantum interference device magnetometer.
as previous report28. The hydrogen content obtained by weighing the mass before and after hydrogenation is consistent with the result estimated from lattice expansion. All magnetic measurements were performed on a commercial MPMS-7 type superconducting quantum interference device magnetometer.
The measurement scheme of magnetic and dielectric spectra is shown in Figure 9. For magnetic and dielectric spectra measurements, the LaFe11.6Si1.4C0.2H1.7 was ground to powders with grain size of 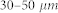 , then mixed homogenously with paraffin wax at the mass ratio of 4:1. The LaFe11.6Si1.4C0.2H1.7/paraffin wax samples were finaly pressed into the toroidal-shaped samples of 7.00 mm outer diameter and 3.04 mm inner diameter with the thickness from 2.0 to 8.3 mm. The scattering parameters of the toroidal samples that correspond to the reflection (S11 and S22) and transmission (S21 and S12) were measured by a vector network analyzer (Agilent N5224A) using a coaxial transmission–reflection method in the frequency range of 0.1–15.0 GHz. The toroids tightly fit into the coaxial measurement cell. Full two-port calibration was initially performed on the test setup in order to remove errors due to the directivity, source match, load match, isolation and frequency response in both the forward and reverse measurements. The complex permeability (μr) and permittivity (εr) were determined from the scattering parameters using the Nicolson models30.
, then mixed homogenously with paraffin wax at the mass ratio of 4:1. The LaFe11.6Si1.4C0.2H1.7/paraffin wax samples were finaly pressed into the toroidal-shaped samples of 7.00 mm outer diameter and 3.04 mm inner diameter with the thickness from 2.0 to 8.3 mm. The scattering parameters of the toroidal samples that correspond to the reflection (S11 and S22) and transmission (S21 and S12) were measured by a vector network analyzer (Agilent N5224A) using a coaxial transmission–reflection method in the frequency range of 0.1–15.0 GHz. The toroids tightly fit into the coaxial measurement cell. Full two-port calibration was initially performed on the test setup in order to remove errors due to the directivity, source match, load match, isolation and frequency response in both the forward and reverse measurements. The complex permeability (μr) and permittivity (εr) were determined from the scattering parameters using the Nicolson models30.
Figure 9. The measurement scheme of magnetic and dielectric spectra.
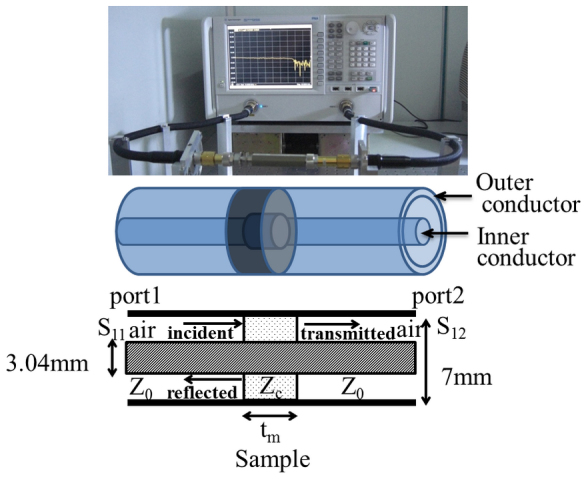
Coaxial line and sample.
Author Contributions
Z.H.C. planned the experiments. N.N.S. and Y.J.K. carried out the microwave and magnetic entropy changes experiments. H.Z. prepared the sample. H.T.Y. and X.Q.Z. setup the microwave measurements. B.G.S. explained the magnetocaloric effect. All the co-authors contributed to the analysis and discussion for the results. Z.H.C. wrote the paper with the input from all the co-authors.
Acknowledgments
This work was supported by the National Basic Research Program of China (973 program, Grant Nos. 2012CB933102, 2011CB921801 and 2010CB93420) and the National Natural Sciences Foundation of China (11174351, 11274357, 11034004, and 51021061).
References
- Vinoy K. J. & Jha R. M. Radar Absorbing Materials, Kluwer Academic Publishers, Boston, MA (1996). [Google Scholar]
- Shin D. et al. Broadband electromagnetic cloaking with smart metamaterials. Nature Commun. 3, 1213 (2012). [DOI] [PubMed] [Google Scholar]
- Che R. et al. Microwave absorption enhancement and complex permittivity and permeability of Fe encapsulated within Carbon nanotubes. Adv. Mater. 16, 40 (2004). [Google Scholar]
- Li B. W. et al. Enhanced microwave absorption in nickel/hexagonal-ferrite/polymer composites. Appl. Phys. Lett. 89, 132504 (2006). [Google Scholar]
- Liu J. R. et al. Magnetic and electromagnetic wave absorption properties of α-Fe/Z-type Ba-ferrite nanocomposites. Appl. Phys. Lett. 88, 062503 (2006). [Google Scholar]
- Lagarkov A. N. et al. High-frequency behavior of magnetic composites. J. Magn. Magn. Mater. 321, 2082 (2009). [Google Scholar]
- Srivastava R. K. et al. Ni filled flexible multi-walled carbon nanotube–polystyrene composite films as efficient microwave absorbers. Appl. Phys. Lett. 99, 113116 (2011). [Google Scholar]
- Liu L. et al. Microwave Loss in the High-Performance Dielectric Ba(Zn1/3Ta2/3)O3 at 4.2 K. Phys. Rev. Lett. 109, 257601 (2012). [DOI] [PubMed] [Google Scholar]
- Pecharsky V. K. & Gschneidner Jr K. A. Giant magnetocaloric effect in Gd5Si2Ge2. Phys. Rev. Lett. 78, 4494 (1997). [Google Scholar]
- Provenzano V., Shapiro A. J. & Shull R. D. Reduction of hysteresis losses in the magnetic refrigerant Gd5Ge2Si2 by the addition of iron. Nature (London) 429, 853 (2004). [DOI] [PubMed] [Google Scholar]
- Tegus O., Bruck E., Buschow K. H. J. & de Boer F. R. Transition-metal-based magnetic refrigerants for room temperature applications. Nature 415, 150–152 (2002). [DOI] [PubMed] [Google Scholar]
- Liu J. et al. Giant magnetocaloric effect driven by structural transitions. Nature Mater. 11, 620 (2012). [DOI] [PubMed] [Google Scholar]
- Moya X. et al. Giant and reversible extrinsic magnetocaloric effects in La0.7Ca0.3MnO3 films due to strain. Nature Mater. 12, 52 (2013). [DOI] [PubMed] [Google Scholar]
- Hu F. X. et al. Influence of negative lattice expansion and metamagnetic transition on magnetic entropy change in the compound LaFe11.4Si1.6. Appl. Phys. Lett. 78, 3675–3677 (2001). [Google Scholar]
- Shen B. G. et al. Recent progress in exploring magnetocaloric materials. Adv. Mater. 21, 4545–4564 (2009). [Google Scholar]
- Snoek J. L. Gyromagnetic resonance in ferrites. Nature 160, 90 (1947). [DOI] [PubMed] [Google Scholar]
- Wang F. W. et al. Strong interplay between structure and magnetism in the giant magnetocaloric intermetallic compound LaFe11.4Si1.6: a neutron diffraction study. J. Phys.: Condens. Matter 15, 5269 (2003). [Google Scholar]
- Mu G. et al. Microwave absorption properties of hollow microsphere/titania/M-type Ba ferrite nanocomposites. Appl. Phys. Lett. 91, 043110 (2007). [Google Scholar]
- Harris V. G. Modern Microwave Ferrites. IEEE Trans on Magn. 48, 1075 (2012). [Google Scholar]
- Wu M. Z. et al. Microwave magnetic properties of Co50/(SiO2)50 nanoparticles. Appl. Phys. Lett. 80, 4404 (2002). [Google Scholar]
- Watts P. C. P., Hsu W. K., Barnes A. & Chambers B. High permittivity from defective multiwalled carbon nanotubes in the X-Band. Adv. Mater. 15, 600 (2003). [Google Scholar]
- Ramo S., Whinnery J. R. & Duzer T. V. Fields and Waves in Communication Electronics Wiley, New York 1984. [Google Scholar]
- Naito Y. & Suetake K. Application of ferrite to electromagnetic wave absorber and its characteristics. IEEE Trans. Microwave Theory Tech. 19, 65 (1971). [Google Scholar]
- Davalos A. L. & Zanette A. Fundamentals of Electromagnetism. Springer Verlag, Berlin 1999.
- Wadhawan A., Garrett D. & Perez J. M. Nanoparticle-assisted microwave absorption by single-wall carbon nanotubes. Appl. Phys. Lett. 83, 2683 (2003). [Google Scholar]
- Zimm C. et al. Design and performance of a permanent-magnet rotary refrigerator. Inter. J. Refrigeration 29, 1302 (2006). [Google Scholar]
- Fujita A., Fujieda S., Hasegawa Y. & Fukamichi K. Itinerant-electron metamagnetic transition and large magnetocaloric effects in La(FexSi1-x)13 compounds and their hydrides. Phys. Rev. B. 67, 104416 (2003). [Google Scholar]
- Lyunina J. et al. Multiple Metamagnetic Transitions in the Magnetic Refrigerant La(Fe,Si)13Hx Phys. Rev. Lett. 101, 77203 (2008). [DOI] [PubMed] [Google Scholar]
- Chen Y. F. et al. Magnetic properties and magnetic entropy change of LaFe11.5Si1.5Hy interstitial compounds. J. Phys.: Condens. Matter. 15, L161 (2003). [Google Scholar]
- Nicolson A. M. & Ross G. F. Measurement of intrinsic properties of materials by time-domain techniques. IEEE Transactions on Instrumentation and Measurement. IM19, 377–382 (1970). [Google Scholar]