Skip to main content
PMC home page
Scientific Reports logoLink to Scientific Reports
. 2013 Jul 26;3:2288. doi: 10.1038/srep02288

Whole-cell phase contrast imaging at the nanoscale using Fresnel Coherent Diffractive Imaging Tomography

Michael W M Jones 1, Grant A van Riessen 1,a, Brian Abbey 1, Corey T Putkunz 2, Mark D Junker 1, Eugeniu Balaur 1, David J Vine 3, Ian McNulty 4, Bo Chen 2,7, Benedicta D Arhatari 1, Sarah Frankland 5,8, Keith A Nugent 2,7, Leann Tilley 5, Andrew G Peele 1,6
PMCID: PMC3724183  PMID: 23887204

Abstract

X-ray tomography can provide structural information of whole cells in close to their native state. Radiation-induced damage, however, imposes a practical limit to image resolution, and as such, a choice between damage, image contrast, and image resolution must be made. New coherent diffractive imaging techniques, such Fresnel Coherent Diffractive Imaging (FCDI), allows quantitative phase information with exceptional dose efficiency, high contrast, and nano-scale resolution. Here we present three-dimensional quantitative images of a whole eukaryotic cell by FCDI at a spatial resolution below 70 nm with sufficient phase contrast to distinguish major cellular components. From our data, we estimate that the minimum dose required for a similar resolution is close to that predicted by the Rose criterion, considerably below accepted estimates of the maximum dose a frozen-hydrated cell can tolerate. Based on the dose efficiency, contrast, and resolution achieved, we expect this technique will find immediate applications in tomographic cellular characterisation.

X-ray Coherent Diffractive Imaging (CDI) is currently under intensive development for a wide range of applications in the materials1,2,3 and biological sciences4,5, due in part to its ability to provide spatial resolution beyond the limits imposed by image-forming optics6. The short wavelength and element specific interaction of X-rays with matter may be exploited to characterise intracellular features7,8,9,10 with minimal sample preparation. In applications involving CDI of biological samples, the ultimate resolution limit will generally be determined by radiation damage rather than the coherent power of available light sources11,12. In the context of cellular imaging, it is therefore crucial to optimise the sensitivity and dose efficiency of the technique.

Historically, CDI could only be applied to small isolated samples due to the limits imposed by sampling of the diffracted wavefield13,14. Recent modifications to the standard CDI algorithm including Fresnel CDI (FCDI)15,16 and ptychography17 overcome the issue, allowing the CDI method to be applied to objects of arbitrary size. FCDI utilises illumination with known phase curvature to provide additional redundancy, providing more reliable, unique image reconstruction and increased tolerance to partial coherence from a single probe position15,18,19, while ptychography involves collecting data from multiple overlapping probe positions, significantly increasing image quality20. Ptychographic plane-wave CDI has been applied to biological samples20,21,22 and has demonstrated a very good compromise between dose (2.5 × 108 Gy) and resolution (60 nm) when applied to three-dimensional imaging of a bacteria cell23. However, the required imaging dose predicted by the Rose criterion for a resolution of 60 nm is only 106 Gy11. Ptychographic FCDI has also been demonstrated for several applications and has been shown to deliver the advantages of both of the techniques it combines without significantly adding to the experimental complexity24,25,26. In particular, this method has been demonstrated with known test samples in two-dimensions24 and three-dimensions25.

To demonstrate the viability of ptychographic FCDI for whole-cell three-dimensional imaging, a red blood cell (RBC) infected with the malaria parasite Plasmodium falciparum at the trophozoite life-cycle stage was used as a sample. During the blood stage of the P. falciparum life cycle, the parasite catabolizes hemoglobin breaking it down to amino acids and releasing free heme, which is toxic to the organism. The malaria parasite detoxifies the heme by crystallizing it to form malaria pigment or hemozoin27. The variation in structure and density between the high-density hemozoin and the low-density hemoglobin provides an ideal test for high contrast biological imaging in three dimensions. From the data presented here, the lower limit of delivered dose required for three-dimensional images at a defined contrast and the achieved spatial resolution of 70 nm is evaluated. Additionally, by recovering a three-dimensional map of the complex transmission function of the sample, the complex refractive index in each volume element of the cell may be determined, which facilitates the identification of ultracellular features through image segmentation.

Results

Ptychographic FCDI diffraction data were collected from a total of 79 individual projections spanning 124.5 degrees at an X-ray energy of 2.5 keV. At each projection angle, the sample was scanned through the beam to collect data from nine overlapping areas of the sample. Supplementary Figure S1 depicts an example set of diffraction data. The total accumulated imaging dose is less than 2.35 × 108 Gy. Retrieval of the complex sample transmission function for each projection was performed using the NADIA software library (NADIA Software Project http://www.coecxs.org/joomla/index.php/research-and-projects/nadia-software-project.html) and the 3-D volume reconstruction was carried out by algebraic reconstruction tomography (ART) based on the Kaczmarz algorithm28. Segmentation was performed based on the measured refractive index parameters described below and volume rendering was done using the Amira software package. Three-dimensional images of the phase reconstruction of the transmission function of the sample at two orthogonal angles are shown in Figure 1 a) and b).

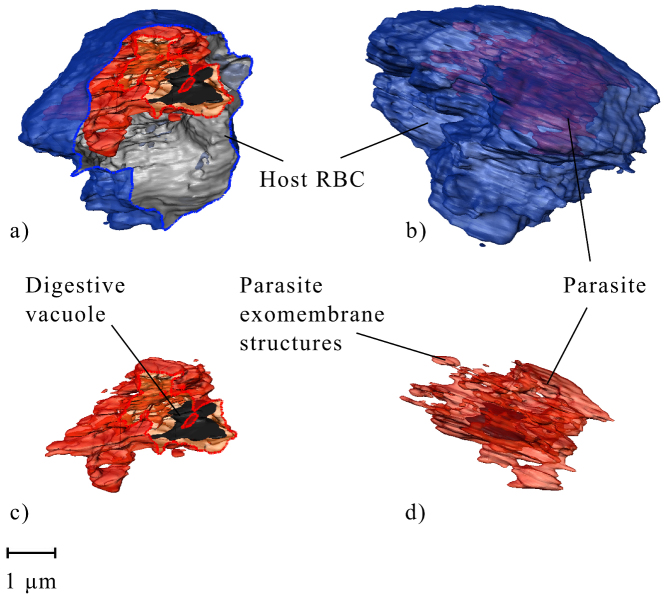
Figure 1. Three-dimensional rendering of the reconstructed phase of the sample shown at two orthogonal angles.

Figure 1

Open in a new tab

The whole infected red blood cell (blue), with the parasite (red) and the parasite's digestive vacuole (black) are illustrated in orthogonal views a) and b). Views c) and d) show the surface renderings of the parasite and the digestive vacuole corresponding to a) and b) respectively to highlight the parasite's exomembrane structures. These are areas where the parasite extends into the host cell and likely correspond to components of the exomembrane system such as the tubulovesicular network. The scale bar is equal to 1 μm.

Three regions are indentified corresponding to the host RBC (rendered in blue), the intraerythrocytic parasite (rendered in red), and the hemozoin-containing digestive vacuole (rendered in black). The advantages of the 3D volume reconstruction process are evident by comparing projections of the reconstructed 3D volume (Figure 1) with an individual two-dimensional ptychographic image (Figure 2b). The features are best appreciated by examining a rotation of the rendered 3D model (Supplementary Video). The parasite has an amorphous shape as described previously for trophozoite stage parasites29. Regions of the surface of the parasite show extensions into the RBC cytoplasm, highlighted in the surface rendering of the parasite and digestive vacuole with the host RBC removed in Figure 1 c) and d). These likely correspond to components of the exomembrane system of the parasite, such as the tubulovesicular network30. The host RBC is deformed from the classical biconcave disc shape of uninfected RBCs reflecting the substantial reorganisation of the host cell by the intraerythrocytic parasite31.

Figure 2. Line profiles through one projection angle with exposure times of 20, 10, 5, 2, and 1 second per ptychographic point (a).

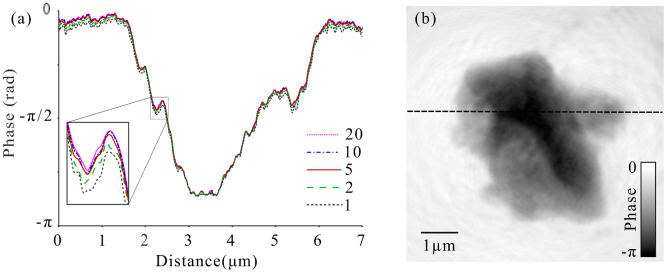
Figure 2

Open in a new tab

The results indicate little change for between 20 and 5 seconds, with 1 and 2 seconds of exposure per point (dotted black and dashed green lines respectively), leading to significant variations in the reconstructed phase values (see inset). From this result we can extrapolate that 5 seconds of exposure time per point would yield images of similar quality, with one fifth of the present acquisition time using the experimental configuration described in the methods section.

Quantitative measurements of the complex refractive index taken from the tomograms were used to isolate the three different compartments comprising the host red blood cell, the parasite, and the parasite's digestive vacuole. Values for the decrement from unity of the real part of the complex refractive index, δ, were measured to be 2.2 ± 0.7 × 10−5, 3.9 ± 0.4 × 10−5, and 5.2 ± 0.4 × 10−5 respectively. At 2.5 keV, these values are in agreement with the tabulated values32 for hemozoin, a significant proportion of the digestive vacuole (C34H32O4N4Fe1, density 1.45 g/cm3)33 with a value of δ = 5.12 × 10−5, and haemoglobin, contained in the red blood cell (C738H1166N812O203S2Fe1, density = 0.38 g/cm3)34 with a value of δ = 1. 35 × 10−5. The parasite itself contains many protein based compounds, and was therefore modelled as empirical protein (C30H50O10S1), however, the density of the parasite changes during the life cycle stage34. For the given composition and life cycle stage, the measured value of δ for the parasite implies that the density is equal to 1.1 g/cm3. The higher density of the cytoplasm of this trophozoite stage parasite compared with the host cell may reflect the high density of ribosomes at this stage35.

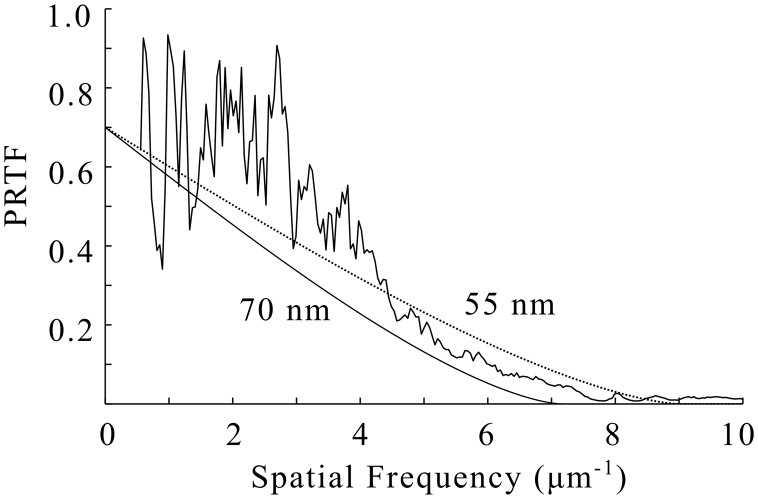
While the numerical aperture of the diffracted signal (related to the scattering strength of the sample11) sets a theoretical upper limit on the resolution, it is the extent to which this data can be accurately phased which practically determines the image resolution in CDI8. One method that is often used in determining the spatial resolution of the reconstructed images is to calculate the Phase Retrieval Transfer Function (PRTF). The PRTF is estimated by calculating the ratio of the intensity of the phased diffraction pattern to the measured intensity2. In this case, a projection through the transmission function of the entire reconstructed volume was created, which was propagated to the detector plane using the Fresnel propagator36. This was compared with the measured intensity data for the same projection angle after the incident illumination had been subtracted. This measurement of the resolution of the entire reconstructed volume therefore takes into account slice artefacts and artefacts arising from the limited angular scan range. As a comparison, the PRTF is shown alongside the theoretical modulation transfer function (MTF) for comparable conventional optics with 70% efficiency and an Abbé resolution equal to 55 and 70 nm in Figure 3. We conclude from this analysis that the spatial resolution in the three-dimensional image lies between 55 and 70 nm.

Figure 3. Resolution of the reconstructed volume: The PTRF (Ireconstructed/Imeasured) as a function of the spatial frequency.

Figure 3

Open in a new tab

Also displayed are the theoretical MTF with 70% efficiency for Abbé resolutions equal to 55 and 70 nm. The measured PTRF falls between these values, indicating resolution of better than 70 nm in the image. The reconstructed image was taken as a maximum intensity projection through the 3D volume and was compared to diffraction data from the same rotation angle. At low spatial frequencies, the beamstop on the zone plate masks the diffraction data and was therefore not included.

Putkunz et al.26 showed that by using many overlapping probe positions in FCDI, more accurate phasing of the diffraction data is possible while the total dose delivered to the sample can be greatly reduced without reducing the quality of the reconstructed image. To examine this result in the context of cellular tomography, we reconstructed images from diffraction data obtained with exposure times ranging from 1 s to 20 s per position in a ptychographic series at one particular projection angle. Line profiles through the reconstructed phase are shown in Figure 2, together with an example reconstruction in which their position in the sample is indicated. The similarities in the profiles show that the quality of the image is consistent between the datasets with exposure times of 5 s, 10 s, and 20 s, with an effective dose of between 6.0 × 105 and 2.4 × 106 Gy, in line with previously reported results26. This provides confirmation that 3D cellular diffractive imaging can be realised using ptychographic FCDI with a lower dose than (full-field) transmission X-ray microscopy (TXM) due to the inherent phase sensitivity of the former and the lack of attenuating optics between the sample and detector37. We note that Scanning Transmission X-ray Microscopy (STXM) also has no post-sample optics. High resolution STXM tomography is technically challenging, quantification generally demands increased dose, and the small depth of focus of zone plate optics limits sample thickness39. FCDI is also limited by sample thickness, albeit though different mechanisms, but this can be partially overcome by tailoring the experimental geometry to the sample thickness. Additionally, unlike STXM, the resolution of CDI is not limited by the NA of the optics15. Based on the analysis above, we can extend the hypothetical dose reduction to the whole dataset, yielding a 3D reconstruction with similar quality with a dose of 4.7 × 107 Gy, approaching the minimum required dose for imaging at the estimated spatial resolution reported by Howells et al. of approximately 106 Gy11. This result compares favourably in terms of dose and resolution to transmission X-ray microscopy (TXM), where a dose of up to two orders of magnitude greater may be required to achieve a similar resolution38. Our analysis shows that sub-70 nm imaging resolution can be achieved for thick, whole cells by ptychographic FCDI with an X-ray dose considerably below the tolerable maximum determined for frozen hydrated specimens11. While image resolution for such samples is expected to be ultimately limited to about 10 nm by radiation induced damage11, it is clear that coherent X-ray flux available from synchrotron based light sources will impose a practical limit on the achievable resolution12. Recent advances however, which include the coherent properties of the source19,39 combined with emerging detector technologies40, offer the possibility of allowing 3D cellular FCDI data to be acquired in less than one minute.

Discussion

We have demonstrated whole-cell ptychographic FCDI tomography with high contrast and dose efficiency to sub 70 nm resolution. High contrast in the three-dimensional map of refractive index made it possible to identify structures internal to the cell through segmentation, such as the ribosome- and membrane-rich parasite volume with a higher density than the host cell, but a lower density than the parasite's digestive vacuole (which houses crystals of hemozoin). Additionally, the analysis shows that a similar quality reconstruction can be achieved with a dose approaching the minimum dose required for imaging at the resolution achieved in the present work11, two orders of magnitude less than TXM38, and leading not only to lower damage sustained by the sample, but also decreasing the acquisition time substantially. Combined with recent advances in partial coherence and pink beam methods39 these results offer the possibility to reduce the acquisition time to several seconds, allowing the possibility of statistical numbers of biological samples to be imaged in a reasonable time frame. This therefore increases the value of the technique to the biological sciences. Extending to frozen hydrated samples in the water window, a similar result with respect to resolution and dose should be achievable11. Indeed, the increased available contrast between carbon containing proteins and the background38 could result in a lower dose while maintaining high contrast images.

Methods

Our experiment was conducted at Beamline 2-ID-B at the Advanced Photon Source41 using an in vacuo imaging endstation42 that permits a sample to be rotated and translated through a diverging beam formed via a Fresnel zone plate (FZP). We used a 2.5 keV X-ray beam to coherently illuminate a 160 μm FZP with nominal outer zone width of 30 nm, and placed the sample within the diverging beam. At this energy the focal length is 9.81 mm. All but the first order diffracted beam was blocked by a combination of a 40 μm central beam stop at the zone plate and a 10 μm order sorting aperture (OSA) positioned near the focal plane.

P. falciparum was cultured in vitro and mature stage-infected red blood cells were harvested and fixed in 0.01% paraformaldehyde before being freeze-dried for 30 minutes. The sample was mounted on a gold electron microscopy grid covered with formvar. While this assisted the sample location process, the tilt range was limited to 124.5 degrees. The sample was initially placed as close as practical to the focus of the diverging beam to maximize the number of incident photons. At high tilt angles, geometrical constraints led to the sample being positioned further downstream. Over the entire tilt range, the sample was placed between 375 μm and 650 μm downstream of the focus where the illumination diameter was between 6 μm and 11 μm. This variation has the benefit of introducing a form of phase-diversity into the three-dimensional reconstruction, which has been shown to reduce artefacts due to the structure in the illumination associated with the zone plate26. Ptychographic diffraction data in a 3 × 3 array with a 1.5 μm step size were collected at 84 projection angles uniformly spaced over 124.5 degrees. At each ptychographic position, 10 one-second exposures were summed to increase the signal to noise ratio and dynamic range in the data, while every third projection angle consisted of the sum of 50 one-second exposures per ptychographic position, which assists the ‘bootstrapping’ process43. An additional 15 projections were taken at the greatest incident angles to reduce tilt increment to ameliorate the effect of the projected increase in substrate thickness. Five additional projections were taken about normal incidence. Of the 104 projections measured, 25 were discarded due to poor reconstruction quality, typically due to uncontrolled sample movement during data acquisition, resulting in the total accumulated imaging dose of less than 2.35 × 108 Gy.

Diffraction data were collected on a cooled charge-coupled device detector (Princeton MT-MTE) cropped to 1150 × 1150 square pixels each with a 13.5 μm side length placed 83 cm downstream of the sample. The corresponding pixel size in the sample plane due to the numerical aperture of the detector is 26 nm. The actual resolution of reconstructed image depends on the signal-to-noise ratio at large angles in the diffraction pattern. Based on Abbé theory44 and the numerical aperture (NA) of the detector (defined here to be one half of the detector acceptance angle) we find a theoretical resolution limit of Γ = 0.82λ/NA ≈ 42 nm.

Each projected angle is reconstructed individually enforcing phase and amplitude complex constraints45 using the NADIA software library (NADIA Software Project http://www.coecxs.org/joomla/index.php/research-and-projects/nadia-software-project.html). To increase the speed of convergence of the reconstruction algorithms, the transmission function from each projection was used to bootstrap the subsequent projections, leading to a faster, more reliable convergence for each projection43, as illustrated by Peterson et al.25. Using this method, projections with 50 exposures per ptychographic position were reconstructed with 2000 iterations of the ER phase retrieval algorithm, while the remaining projections were reconstructed with 400 iterations. The individual projections were coarsely aligned before sinograms were created. Jitter in the sinograms was corrected using the iterative method that does not require fiducial markers inserted within the specimen described by Abbey et al. (Abbey, B. et al. Iterative Marker-Free Alignment Method for Low Quality Tomography Data, unpublished data). The tomograms were then reconstructed using the algebraic reconstruction tomography (ART) algorithm based on the Kaczmarz algorithm28. Due to the relatively high number of projections, qualitative convergence of the algorithm was achieved within 10 iterations. Segmentation based on the measured refractive indices of each reconstructed voxel, as described in the results section, and volume rendering was done using the Amira software package.

Author Contributions

M.W.M.J., G.A.V.R., B.A., C.T.P., M.D.J., B.C., E.B., D.J.V., I.M. designed and performed experiments, M.W.M.J., G.A.V.R., B.A., C.T.P., A.G.P., K.A.N., L.T., S.F., M.D.J., B.C. wrote the manuscript, M.W.M.J., B.A., C.T.P., B.D.A. analysed data, M.W.M.J., G.A.V.R., L.T., A.G.P. interpreted data, and S.F. prepared samples.

Supplementary Material

Supplementary Information

Supplementary Info - Figure S1

srep02288-s1.pdf (447.6KB, pdf)
Supplementary Information

Supplementary Video

Download video file (3.1MB, mov)

Acknowledgments

The authors acknowledge support from the Australian Research Council Centre of Excellence for Coherent X-ray Science. We acknowledge travel funding provided by the International Synchrotron Access Program (ISAP) managed by the Australian Synchrotron and funded by the Australian Government. Use of the Advanced Photon Source is supported by the U.S. Department of Energy, Office of Science, and Office of Basic Energy Sciences, under Contract No. DE-AC02-06CH11357.

References

  1. Miao J., Charalamous P., Kirz J. & Sayre D. Extending the methodology of X-ray crystallography to allow imaging of micrometre-sized non-crystaline specimens. Nature 400, 342–344 (1999). [Google Scholar]
  2. Chapman H. N. et al. High-resolution ab initio three-dimentional x-ray diffraction microscopy. Journal of the Optical society of America A 23, 1179–1200 (2006). [DOI] [PubMed] [Google Scholar]
  3. Luu M. B. et al. Multi-wavelength elemental contrast absorption imaging. Optics Express 19, 25969–25980 (2011). [DOI] [PubMed] [Google Scholar]
  4. Mancuso A. P., Yefanov O. M. & Vartanyants I. A. Coherent diffractive imaging of biological samples at synchrotron and free electron laser facilities. Journal of Biotechnology 149, 229–237 (2010). [DOI] [PubMed] [Google Scholar]
  5. Jiang H. et al. Quantitative 3D imaging of whole, unstained cells by using X-ray diffraction microscopy. PNAS 107, 11234–11239 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Nugent K. A. Coherent methods in the X-ray sciences. Advances in Physics 59, 1–99 (2010). [Google Scholar]
  7. Williams G. J. et al. High-resolution X-ray imaging of Plasmodium falciparum-infected red blood cells. Cytomety A 73, 949–957 (2008). [DOI] [PubMed] [Google Scholar]
  8. Shapiro D. et al. Biological imaging by soft x-ray diffraction microscopy. PNAS 102, 15343–15346 (2005). [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Mancuso A. P. et al. Internal structure of an intact Convallaria majalis pollen grain observed with X-ray Fresnel coherent diffractive imaging. Optics Express 20, 26778–26785 (2012). [DOI] [PubMed] [Google Scholar]
  10. Beckers M. et al. Chemical contrast in soft X-ray ptychography. Physical Review Letters 107, 208101 (2011). [DOI] [PubMed] [Google Scholar]
  11. Howells M. R. et al. An assessment of the resolution limitation due to radiation-damage in X-ray diffraction microscopy. Journal of Electron Spectroscopy and Related Phenomena 170, 4–12 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Bergh M., Huldt G., Timneanu N., Maia F. R. N. C. & Hajdu J. Feasibility of imaging living cells at subnanometer resolutions by ultrafast X-ray diffraction. Quarterly Reviews of Biophysics 41, 181–204 (2008). [DOI] [PubMed] [Google Scholar]
  13. Sayre D. Some implications of a theorem due to Shannon. Acta Crystallographica 5, 843 (1952). [Google Scholar]
  14. Bates R. H. T. Fourier phase problems are uniquely solvable in more than one dimension 1. underlying theory. Optik 61, 247–262 (1982). [Google Scholar]
  15. Abbey B. et al. Keyhole coherent diffractive imaging. Nature Physics 4, 394–398 (2008). [Google Scholar]
  16. Williams G. J. et al. Fresnel coherent diffractive imaging. Physical Review Letters 97, 0255061–0255064 (2006). [DOI] [PubMed] [Google Scholar]
  17. Rodenburg J. M. et al. Hard X-ray lensless imaging of extended objects. Physical Review Letters 98, 034801 (2007). [DOI] [PubMed] [Google Scholar]
  18. Williams G. J., Quiney H. M., Peele A. G. & Nugent K. A. Coherent diffractive imaging and partial coherence. Physical Review B 75, 104102–104107 (2007). [Google Scholar]
  19. Clark J. N., Huang X., Harder R. & Robinson I. K. High-resolution three-dimensional partially coherent diffractive imaging. Nature Communications 3, 993 (2012). [DOI] [PubMed] [Google Scholar]
  20. Giewekemeyer K. et al. Ptychographic coherent x-ray diffractive imaging in the water window. Optics Express 19, 1037–1050 (2011). [DOI] [PubMed] [Google Scholar]
  21. Giewekemeyer K. et al. Quantitative biological imaging by ptychographic x-ray diffraction microscopy. PNAS 107, 529–534 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Dierolf M. et al. Ptychographic X-ray computed tomography at the nanoscale. Nature 467, 436–440 (2010). [DOI] [PubMed] [Google Scholar]
  23. Wilke R. N. et al. Hard X-ray imaging of bactirial cells: nano-diffraction and ptychographic reconstrcuction. Optics Express 20, 19232–19254 (2012). [DOI] [PubMed] [Google Scholar]
  24. Vine D. J. et al. Ptychographic Fresnel coherent diffractive imaging. Physical Review A 80, 0638231–0638235 (2009). [Google Scholar]
  25. Peterson I. et al. Nanoscale Fresnel coherent diffraction imaging tomography using ptychography. Optics Express 20, 24678–24685 (2012). [DOI] [PubMed] [Google Scholar]
  26. Putkunz C. T. et al. Phase-Diverse Coherent Diffractive Imaging: High Sensitivity with Low Dose. Physical Review Letters 106, 013903 (2011). [DOI] [PubMed] [Google Scholar]
  27. Goldberg D. E. Hemoglobin degradation in Plasmodium-infected red blood cells. Seminars in Cell Biology 4, 355–361 (1993). [DOI] [PubMed] [Google Scholar]
  28. Gordon R., Bender R. & Herman G. T. Algebraic reconstruction techinques (ART) for three-dimensional electron microscopy and X-ray photography. Journal of Theoretical Biology 29, 471–481 (1970). [DOI] [PubMed] [Google Scholar]
  29. Hanssen E. et al. Cryo transmission X-ray imaging of the malaria parasite. P. falciparum. Journal of Structural Biology 173, 161–168 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Haldar K. & Mohandas N. Erythrocyte remodeling by malaria parasites. Current Opinion in Hematology 14, 203–209 (2007). [DOI] [PubMed] [Google Scholar]
  31. Bannister L. H., Hopkins J. M., Margos G., Dluzewski A. R. & Mitchell G. H. Three-dimensional ultrastructure of the ring stage of Plasmodium falciparum: Evidence for export pathways. Microscopy and Mcroanalysis 10, 551–562 (2004). [DOI] [PubMed] [Google Scholar]
  32. Henke B. L., Gullikson E. M. & Davis J. C. X-ray interactions: photoabsorption, scattering, transmission, and reflection at E = 50–30000 eV, Z = 1–92. Atomic Data and Nuclear Data Tables 54, 181–342 (1993). [Google Scholar]
  33. Pagola S., Stephens P. W., Bohle D. S., Kosar A. D. & Madsen S. K. The structure of malaria pigment β-haematin. Nature 404, 307–310 (2000). [DOI] [PubMed] [Google Scholar]
  34. Hanssen E. et al. Soft X-ray microscopy analysis of cell volume and hemoglobin content in erythrocytes infected with asexual and sexual stages of Plasmodium falciparum. Journal of Structural Biology 177, 224–232 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Bozdech Z. et al. The transcriptome of the intraerythrocytic developmental cycle of Plasmodium falciparum. PLoS Biology 1, 85–100 (2003). [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Quiney H. M., Peele A. G., Cai Z., Paterson D. & Nugent K. A. Diffractive imaging of highly focused X-ray fields. Nature Physics 2, 101–104 (2006). [Google Scholar]
  37. Kaulich B., Thibault P., Gianoncelli A. & Kiskinova M. Transmission and emission x-ray microscopy: operation modes, contrast mechanisms and applications. Journal of Physics: Condensed Matter 23, 083002 (2011). [DOI] [PubMed] [Google Scholar]
  38. Larabell C. A. & Le Gros M. A. X-ray tomography generates 3-D reconstructions of the yeast, Saccharomyces cervisiae, at 60-nm resolution. Molecular Biology of the Cell 15, 957–962 (2004). [DOI] [PMC free article] [PubMed] [Google Scholar]
  39. Chen B. et al. Diffraction imaging: The limits of partial coherence. Physical Review B 86, 235401 (2012). [Google Scholar]
  40. Doering D. et al. Development of a compact fast CCD camera and resonant soft x-ray scattering endstation for time-resolved pump-probe experiments. Review of Scientific Instruments 82, 073303 (2011). [DOI] [PubMed] [Google Scholar]
  41. McNulty I. et al. A beamline for 1–4 keV microscopy and coherence experiments at the Advanced Photon Source. Review of Scientific Instruments 67, 3372 (1996). [Google Scholar]
  42. Vine D. J. et al. An in-vacuum x-ray diffraction microscope for use in the 0.7–2.9 keV range. Review of Scientific Instruments 83, 033703 (2012). [DOI] [PubMed] [Google Scholar]
  43. Putkunz C. T. et al. Fresnel coherent diffraction tomography. Optics Express 18, 11746–11753 (2010). [DOI] [PubMed] [Google Scholar]
  44. Born M. & Wolf E. Principles of Optics: Electromagnetic Theory of Propagation, Interference and Diffraction of Light. 7 edn, (Cambridge University Press, 1999). [Google Scholar]
  45. Clark J. N. et al. Use of a complex constraint in coherent diffractive imaging. Optics Express 18, 1981–1993 (2010). [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Information

Supplementary Info - Figure S1

srep02288-s1.pdf (447.6KB, pdf)
Supplementary Information

Supplementary Video

Download video file (3.1MB, mov)

Articles from Scientific Reports are provided here courtesy of Nature Publishing Group

RESOURCES