Two-stage case–control designs for rare genetic variants

Abstract

The search for the association of rare genetic variants with common diseases is of high interest, yet challenging because of cost considerations. We present an efficient two-stage design that uses diseased cases to first screen for rare variants at stage-1. If too few cases are found to carry any variants, the study stops. Otherwise, the selected variants are screened at stage-2 in a larger set of cases and controls, and the frequency of variants is compared between cases and controls by an exact test that corrects for the stage-1 ascertainment. Simulations show that our new method provides conservative Type-I error rates, similar to the conservative aspect of Fisher’s exact test. We show that the probability of stopping at stage-1 increases with a smaller number of cases screened at stage-1, a larger stage-1 continuation threshold, or a smaller carrier probability. Our simulations also show how these factors impact the power at stage-2. To balance stopping early when there are few variant carriers versus continuation to stage-2 when the variants have a reasonable effect size on the phenotype, we provide guidance on designing an optimal study that minimizes the expected sample size when the null hypothesis is true, yet achieves the desired power.

Introduction

The frequency spectrum of genetic variants influencing susceptibility of common diseases ranges widely from common to rare variants. Despite debates about common versus rare variants associated with common diseases (Reich and Lander 2001; Pritchard and Cox 2002), genome-wide association studies (GWAS) have yielded reproducible associations of common variants with a broad range of diseases (Manolio et al. 2008). Nonetheless, the odds ratios (ORs) associated with common variants have been modest at best, often in the range of 1.1–1.5, suggesting little clinical utility per se. Because of this, and the purging effect of natural selection, the effects of rare variants might be much larger, with more immediate clinical utility (Bodmer and Bonilla 2008).

The hypothesis surrounding rare variants is that a significant proportion of inherited susceptibility for common disease is due to the summation of the effects of a series of low-frequency variants (e.g., frequencies ranging 0.1–1%) with dominant effects (dominant because most variants occur as heterozygous). It is also speculated that the variants act independent of each other, representing a variety of different genes. Although individually, or summed, the ORs for rare variants are larger than those for common GWAS SNPs (which have minor allele frequencies >5%), say ORs on the order of 2–5 for rare variants, the penetrance is too low (much less than 50%) to demonstrate familial clustering of disease that appears as a standard Mendelian segregation pattern, and too low to have reasonable power to be detected by pedigree linkage analyses (Bodmer and Bonilla 2008).

In the search for the association of rare variants with common disease, a typical strategy is to first screen candidate genes in a set of diseased cases, preferably enriched for rare variants by selecting on disease diagnosis at a young age, or strong family history, anticipating that the frequency of causal variants will be higher in selected cases than unaffected controls (Bodmer and Bonilla 2008). Any rare variants detected in cases are then evaluated for their frequency in an appropriate set of controls. However, this two-stage process—screening for rare variants in cases, and then screening selected variants in controls—leads to an “ascertainment” bias that can inflate the probability of a false-positive association, well illustrated by Li and Leal (Li and Leal 2009). The bias comes from using the same set of cases to screen for rare variants at stage-1 and then comparing with controls at stage-2. For example, if the true variant frequency is rare in the population, and without association with disease, then the two-stage process eliminates comparisons of cases that have low variant frequencies, only bringing forward to the second stage samples for which cases have an unusually high frequency of the rare variants, biasing upward the frequency among cases, while leaving the controls to be unbiased. Li and Leal (Li and Leal 2009) found that the amount of increase in Type-I error rate caused by the ascertainment bias depends on the number of cases screened in stage-1, the ratio of cases to controls in stage-2, the number of underlying variant sites, linkage disequilibrium among the different sites, and the variation in the frequency of variants over different sites.

The ascertainment bias can be avoided by either using a completely different set of cases to compare with controls at stage-2, or correcting for the ascertainment bias. Because cases can be limited, particularly if selected for a young age at diagnosis or for a strong family history of disease, correcting for ascertainment bias offers an appealing strategy to efficiently use the cases.

The purpose of this paper is to present an efficient two-stage design that uses some (or all) of the cases to screen for rare variants at stage-1, and then compares the frequency of variants among cases versus controls at stage-2 by an exact test that corrects for the stage-1 ascertainment. The algorithm to compute the exact test is presented in the methods section, along with a variety of simulation scenarios to evaluate the Type-I error rate and power of the proposed methods. Results show that the ascertainment-corrected exact test does not have the inflated Type-I error rates that others find when not correcting for ascertainment (Li and Leal 2009). Simulations to evaluate power, however, illustrate the impact on the power of the stage-1 design criteria. Guidance is provided for designing two-stage studies in order to achieve a reasonable balance between stopping at stage-1 because of too few variants detected among cases, versus continuing to stage-2 to achieve desired power when the causal variants have an effect on disease susceptibility. To achieve this, we present an optimal design that minimizes the expected sample size when the null hypothesis of no differential carrier frequency between cases and controls is true, while maintaining the desired power after accounting for the chance of stopping at stage-1.

Statistical methods

Because we assume rare variants with a dominant effect, so that almost all subjects that carry a particular variant are heterozygous, we describe our methods according to carrier probabilities, instead of allele frequencies. This is merely a matter of convenience, because we could describe carriers as either heterozygous or homozygous (if the variants are not rare), or as homozygous carriers (for a recessive effect). We use Table 1 to illustrate our notation for data summarized by carrier status after completing both stage-1 and stage-2. When multiple variants are measured, we combine across all variants so that a subject is a “carrier” if at least one variant is found, otherwise a non-carrier. Stage-1 data has x₁₁ carriers among n_d,1 cases, but continuation to stage-2 requires x₁₁ ≥ t, where t is the specified threshold of the required minimum number of carriers. The stage-2 sample has x₂₁ carriers among n_d,2 cases, and x₃₁ carriers among n_c controls. To account for screening for a minimum number of carriers among cases in stage-1, we need to consider the probability of stopping early at stage-1, based on the binomial density, which depends on the probability that a case is a carrier (p_d), t, and n_d,1:

$$P(\text{stop};t,p_d,n_{d,1})=\sum _{x=0}^{t-1}\left(\begin{array}{c}{n}_{d,1}\\ x\end{array}\right)p_d^x{(1-p_d)}^{n_{d,1}-x}.$$ (1)

Furthermore, we can conceptualize the analysis of the complete data set as a partially truncated binomial. The truncated binomial for stage-1 is

$$P(x_{11};t,p_d,n_{d,1})=\frac{\left(\begin{array}{c}{n}_{d,1}\\ x_{11}\end{array}\right)p_d^{x_{11}}{(1-p_d)}^{n_{d,1}-x_{11}}}{1-P(\text{stop};t,p_d,n_{d,1})}$$

Note that this denominator correction is similar to that used for ascertainment correction for pedigree analyses; Thomas and Gart (1971) give a nice summary of the link between the truncated binomial distribution and classical methods for ascertainment correction of pedigree segregation analyses. The stage-2 data are simply a product of binomial distributions, with p_d the carrier probability among cases and p_c the carrier probability among controls. The resulting log likelihood is

$$lnL=(x_{11}+x_{21})log(p_d)+(x_{12}+x_{22})log(1-p_d)+x_{31}log(p_c)+x_{32}log(1-p_c)-log[1-P(\mathit{stop};t,p_d,n_{d,1})]$$

The first two lines of lnL represent the usual log likelihood for case–control data: the first line combines the cases from stages 1 and 2. The third line of lnL is the correction for using threshold t at stage-1 to decide whether to continue to stage-2. Although one could test the null hypothesis that p_d = p_c with a likelihood ratio statistic, its distribution is not likely to be well approximated by a chi-square distribution when any of the cell counts in Table 1 are small, as expected for rare variants (particularly the count of carriers among controls). Hence, we derived an algorithm to compute exact p values that account for the truncation in stage-1.

Table 1.

Table of counts for data after completing Stage-2

	Carrier	Non-carrier	Total
Cases
Stage-1	x11	x12	nd,1
Stage-2	x21	x22	nd,2
Controls	x31	x32	nc
Total	c1	c2	n

Exact p values for 2-stage design

If there were no stopping at stage-1 (i.e., threshold t = 0), then one could combine the cases from both stages to construct a 2 × 2 table, and compute the usual Fisher’s exact test to compare the carrier frequency between cases and controls. Fisher’s exact test is based on enumerating all possible contingency tables with fixed margins, and assigning to each table its null probability based on the hypergeometric distribution. To allow for truncation, we need to remove tables that are not possible according to the threshold, and restandardize the remaining probabilities to sum to 1. A brief outline of our algorithm is as follows:

1. enumerate all possible 3 × 2 tables with fixed margin totals and compute their hypergeometric probabilities; exclude 3 × 2 tables for which x₁₁ < t;

2. collapse the remaining 3 × 2 tables by summing the counts for cases from stage-1 and stage-2, to create 2 × 2 tables;

3. for the 3 × 2 tables that map into a collapsed 2 × 2 table, sum the probabilities of the 3 × 2 tables to compute the probability of the collapsed 2 × 2 table;

4. standardize the probabilities of 2 × 2 tables to sum to 1; and

5. compute desired statistical tests on the enumerated 2 × 2 tables.

Some details about implementation of this algorithm are provided to help with understanding. Because we want to keep all enumerated tables in computer memory, it is helpful to first count the number of possible enumerated 3 × 2 contingency tables with fixed margins. This is achieved by a recursive equation (2.1), or an approximation (3.2), of Gail and Mantel (1977). To enumerate all possible 3 × 2 contingency tables, we use a modification of the algorithm by Saunders (1984). Our modifications included translation from Fortran77 to C, and forcing enumeration of all tables, even multiple tables that are in the same “equivalence class”. Equivalence class tables occur when there are ties in the row margin totals; permuting rows does not change row totals for these tied rows, or column totals. So, to gain computational efficiency, Saunder’s algorithm computes only one representative table from an equivalence class, its probability, and its multiplicity. The probability for the entire equivalence class is the multiplicity times the probability. For our purposes, however, when collapsing a 3 × 2 table into a 2 × 2 table, different 3 × 2 tables within an equivalence class can give different 2 × 2 tables, so we need to be careful about handling multiplicities when collapsing tables. That is, even though all 3 × 2 tables within an equivalence class have the same probability, after collapsing, their resulting 2 × 2 tables will not necessarily have equivalent probabilities, because they have different values in the 2 × 2 tables.

After all 3 × 2 tables are enumerated, along with their probabilities, we exclude 3 × 2 tables that have cell count x₁₁ < t. The retained 3 × 2 tables are then transformed to 2 × 2 tables by summing the first two rows that correspond to the cases from the first and second stages, hence creating the “usual” 2 × 2 tables for cases and controls. The probabilities of the resulting 2 × 2 tables are computed as follows. First, the 2 × 2 tables are grouped into identity classes (i.e., all 2 × 2 tables in an identity class are the same). The probability for an identity class is computed as the sum, over all tables in an identity class, of the hypergeometric probabilities that correspond to the original 3 × 2 tables. However, these probabilities do not yet sum to 1.0, because of excluding some 3 × 2 tables. Hence, the final step is to standardize the identity class probabilities by dividing each by the sum of probabilities over all identity classes. This later step adjusts the truncation at stage-1.

After enumerating the possible 2 × 2 tables that adhere to the first-stage exclusion, and their corresponding probabilities, a number of methods can be used to compute exact p values (Agresti 1992). A two-sided exact p value for the usual Pearson’s chi-square statistic for a 2 × 2 table merely sums the exact probabilities for which the chi-square statistic for an enumerated table is at least as large as the observed chi-square statistic, summing over all possible m enumerated tables,

$$p{\text{value}}_{\text{chi}2}=\sum _{i=1}^{m}I[{\chi }_1^2\ge {\chi }_{\text{obs}}^2]p_i,$$ (2)

where $I[{\chi }_i^2\ge {\chi }_{\text{obs}}^2]$ has value 1 if ${\chi }_i^2\ge {\chi }_{\text{obs}}^2$, 0 otherwise, for the ith enumerated table, and p_i is the probability of the table. To compute a one-sided exact test that favors a higher frequency of variants in cases than controls, we used a “signed” chi-square statistic. Consider the 2 × 2 table in Table 2. The sign of (ad–bc) indicates direction with +1 favoring cases over controls. Hence, a one-sided exact test is computed as

$$p{\text{value}}_{\text{chi}1}=\sum _{i=1}^{m}I\left[\right({\text{sign}}_i\times {\chi }_i^2)\ge ({\text{sign}}_{\text{obs}}\times {\chi }_{\text{obs}}^2\left)\right]p_i.$$ (3)

Table 2.

2 × 2 Table for case–control carrier status

Status	Carrier	Non-carrier
Cases	a	b
Controls	c	d

For p values analogous to Fisher’s exact tests, the two-sided p value is based on whether the probability of an enumerated table is equal to or smaller than the probability of the observed table,

$$p{\text{value}}_{\text{Fisher}2}=\sum _{i=1}^{m}I[p_i\le p_{\text{obs}}]p_i.$$ (4)

The one-sided Fisher’s exact test p value, in the direction of cases having more variants than controls, is based on the 2 × 2 table count a (the number of cases carrying the variant):

$$p{\text{value}}_{\text{Fisher}1}=\sum _{i=1}^{m}I[a_i\ge a_{\text{obs}}]p_i.$$ (5)

Simulation methods

We used simulations to evaluate the statistical properties of the two-stage design, including the probability of stopping at stage-1, Type-I error rate, and power. These properties depend on the sample sizes of the two stages, the threshold t for the minimum number of case carriers at stage-1, and the carrier probabilities among cases (p_d) and among controls (p_c). Although there are many scenarios that can give rise to the same values of p_d and p_c, they are mathematically equivalent in terms of their statistical properties. Nonetheless, to provide a sense of realism to our simulations, we parallel the simulation scenarios of Li and Leal (2009).

Type-I error

To evaluate the Type-I error rate, we performed simulations for four scenarios. Scenario-1 was for a single variant with carrier frequency of either 0.01 or 0.05. Scenario-2 was also for a single variant per subject, but incorporated heterogeneity as follows. We assumed a heterogeneous population composed of 20 subpopulations, with the carrier frequency varying over the subpopulations from 0.01 to 0.09, at equal increments (i.e., 0.0042). Each subject was randomly assigned to one of the 20 subpopulations, and the corresponding carrier frequency was used to simulate carrier status.

Scenario-3 allowed multiple independent rare variants per subject (i.e., multiple different causal variants per subject). We assumed 20 independent variants with carrier frequencies equally spaced between 0.005 and 0.01 (i.e., increments of 0.0005). Each subject was simulated to carry any number of the rare variants according to the 20 independent Bernoulli trials with differing carrier probabilities. A subject was considered a carrier if the subject had any of the 20 variants. This is equivalent to Li and Leal’s “collapsing” method (Li and Leal 2008), a common way to combine carriers of different variants within a candidate gene, or set of candidate genes.

Scenario-4 was based on simulations from a coalescent model using the ms software (Hudson 2002). Following the approach of Li and Leal (2009), we used scaled mutation rates N_eμ = 4 or 12, with an effective sample size (N_e) of 10,000, which yielded segment lengths with an average of 80 and 100 variants, respectively, with 20–30 of the variants having frequencies less than 0.01. To perform the simulations, we generated 100 batches of 10,000 haplotypes for a given scaled mutation rate. For each simulation, we randomly selected a batch of haplotypes. We then determined which markers would be selected to be the rare variants based on the allele frequencies in the batch of 10,000 haplotypes; only markers with frequencies less than 0.01 were candidates to be the rare variants. We selected the number of rare variants (M) to be either 5 or 10. Next, we sampled two haplotypes with replacement from the batch to create subjects, and then randomly assigned case/control status. The total number of variants per subject, summed over the five or ten preselected markers, was recorded. A subject was considered a carrier if the variant sum exceeded zero.

For each scenario, we simulated genotype data for total sample sizes of 400, 1,000, and 2,000, with an equal number of cases and controls. For each of these sample sizes, we allowed 50, 100, or all cases to be evaluated at stage-1, with the remaining cases and all controls evaluated at stage 2. Table 3 illustrates the study designs evaluated. All simulations were continued until 10,000 samples were obtained for stage-2 analyses, based on the stage-1 threshold set at 0, 1, 2, or 3. For all simulations, we report the probability of stopping at stage-1 based on the total number of simulated datasets that stopped at stage-1 divided by the total number of simulations required to obtain 10,000 simulations accepted for stage-2.

Table 3.

Study designs evaluated

Stage-1	Stage-2		Total
No. of cases	No. of cases	No. of controls
50	150	200	400
50	450	500	1,000
50	950	1,000	2,000
100	100	200	400
100	400	500	1,000
100	900	1,000	2,000
200	0	200	400
500	0	500	1,000
1,000	0	1,000	2,000

Power

For power simulations, the carrier status of multiple rare variants was simulated for two scenarios. In Scenario-5, we simulated either 10 or 20 variant sites with equal frequencies that were independently distributed in the population, with equal effect sizes (i.e., OR per allele). Hence, subjects could carry more than one variant.

Scenario-6 simulations were for multiple rare variants (M = 10 or 20) “competing” for disease, such that a subject could carry no more than one variant. This causes the variant sites to be weakly negatively correlated, because carrying one variant excludes the possibility of carrying any other variants. This approach was taken because it is frequently observed that diseased subjects carry only one variant, yet the site of the variant can differ across different diseased subjects (e.g., multiple mutations in BRCA1 or BRCA2 genes responsible for hereditary breast cancer). For Scenario-6, the population probability of carrying a variant at site i out of M possible sites, was modeled as,

$$P(c_i=1)=P(\text{any})P(c_i=1\mid \text{any})$$

where c_i has values 1 or 0 according to carrier status at site i, and “any” means a subject carries any of the possible M variants (i.e., Σc_i = 1). The conditional probability P(c_i = 1|any) was chosen to be skewed and sum to 1,

$$P(c_i=1\mid \text{any})=2i/[M(M+1)].$$

With P(any) = 0.05, the population carrier frequencies varied from 0.0009 to 0.009 for M = 10, and from 0.0002 to 0.005 for M = 20. For P(any) = 0.02, the population carrier frequencies varied from 0.0004 to 0.004 for M = 10, and from 0.000095 to 0.0019 for M = 20.

For both power scenarios, genotypes were simulated conditional on case–control status, using Bayes’ formulas. That is,

$$P(g\mid y)=\frac{P(y\mid g)P(g)}{{\sum }_{g}P(y\mid g)P(g)},$$

where y has values of 1 for case and 0 for control, P(y|g) is the logistic function for disease penetrance, and P(g) is the population unconditional probability of the genotype g. For the logistic function,

$$P(y\mid g)=\frac{e^{{\beta }_o+\beta x(g)}}{1+e^{{\beta }_o+\beta x(g)}},$$

β_o is the intercept, chosen to provide a specified population disease prevalence (either 0.01 for a rare disease or 0.10 for a common disease), β represents the log OR for a specific coding of genotypes, and x(g) represents how the genotypes were coded in the model. For Scenario-5, x(g) is the count of the number of rare variants across all sites (ranging from 0 to twice the number of variant sites), and β is the per-allele log OR. For Scenario-6, we assigned ORs for each of M sites by assigning the most frequent carrier site a smaller OR and the least frequent carrier site a higher OR; ORs in between were stepped up in equal increments. We allowed two ranges of ORs: from 1.2 to 3 to emulate moderate effects and from 2 to 5 to emulate strong effects.

Results

Stopping early

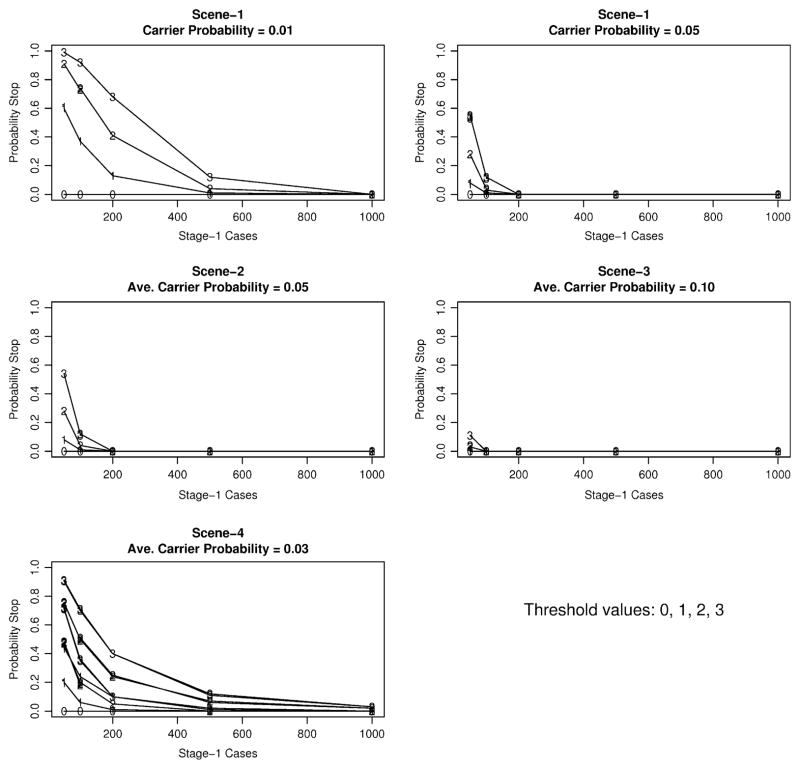
Detailed simulation results for each scenario are available as supplemental tables upon request, so here we summarize the main results across the different simulation scenarios. Figure 1 presents simulation results on the probability of stopping at stage-1 according to carrier probabilities, continuation thresholds, and the number of cases evaluated at stage-1. For Scenario-1, the carrier probability was fixed to either 0.01 or 0.05. For Scenarios 2–4, the carrier probability was allowed to vary, so we present in Fig. 1 the average probability over all simulations (little variability for Scenarios 2–3; larger variability for Scenario-4 that depended on the mutation rate and the number of variant sites). Figure 1 illustrates that the probability of stopping at stage-1 increases with a smaller number of cases screened at stage-1, a larger continuation threshold, or a smaller carrier probability.

Fig. 1.

Stopping probability at stage-1 for simulation scenarios 1–4 according to number of cases screened at stage-1 (x-axis) and continuation threshold (labels 0–3 in panels). Carrier probability is the probability of cases in stage-1 carrying any variant. The larger number of lines in scene-4 represents the different mutation rates and the number of variant sites

Type-I error rates

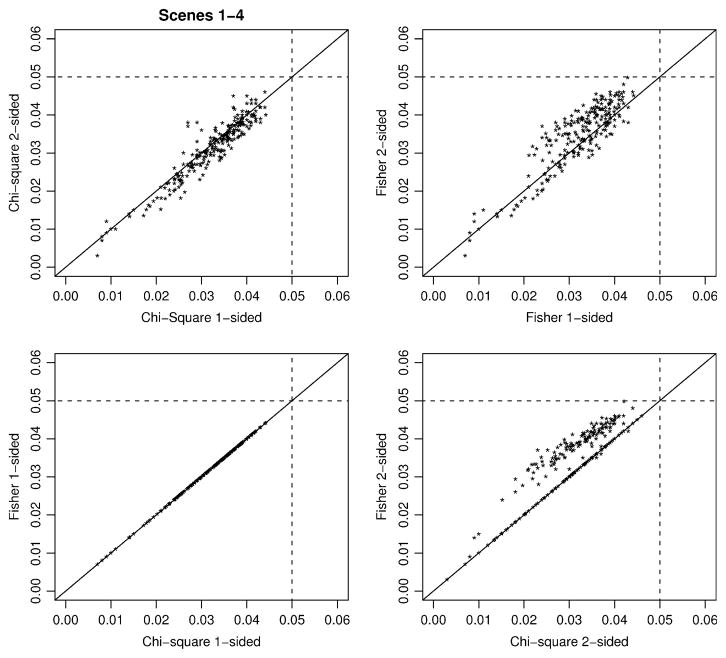
Case–control comparisons are computed only for the simulated datasets that qualify for stage-2. For Type-I error rates, it makes sense to describe error rates conditional on continuation to stage-2, because p values are reported in this matter. Figure 2 presents a summary of all the Type-I error rates for Scenarios 1–4 as pairwise plots of the four exact statistical tests given in expressions 2–5: exact chi-square two-sided (Chi2) and one-sided (Chi1), and exact Fisher two-sided (Fisher2) and one-sided (Fisher1). This figure illustrates that both the chi-square and Fisher exact tests have Type-I error rates less than the nominal value of 0.05, sometimes quite conservative, which occurs when cell counts are small due to sample size combined with small carrier probabilities. The exact distributions for the one-sided versus two-sided chi-square statistics are generally quite similar to each other, in contrast to the one-sided Fisher test being more conservative than the two-sided version. Figure 2 also illustrates that the one-sided versions of the Fisher and chi-square statistics were identical, in contrast to the two-sided chi-square statistic slightly more conservative than the Fisher two-sided test. Because of the general similarity of the Fisher and chi-square statistics, we focus on the Fisher test for power comparisons.

Fig. 2.

Type-I error rates over all simulation scenarios 1–4 for Chi-square exact tests and Fisher’s exact tests, accounting for ascertainment based on stage-1 screening of cases

Power

Because power depends on the probability of not stopping at stage-1 and then rejecting the null hypothesis at stage-2, we focus primarily on unconditional power,

$${\text{Power}}_{\text{unconditional}}=[1-P(\text{stop}\mid \text{alt})]{\text{Power}}_{\text{conditional}},$$ (6)

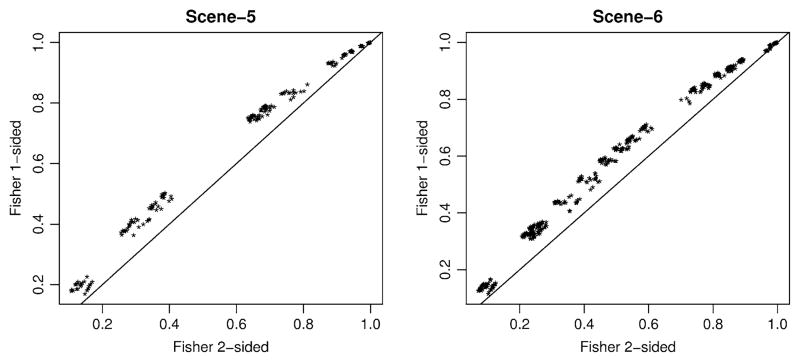
in contrast to conditional power that depends only on the statistical comparisons performed at stage-2. This allows us to evaluate the stage-1 design criteria (number of cases screened and continuation threshold) on the overall power. In contrast, the conditional power based only on stage-2 comparisons can appear overly optimistic by not recognizing that a study could have high probability of stopping early at stage-1. However, to choose between the one-sided versus two-sided Fisher test, we first compared the conditional power of these two tests over all simulations for Scenarios 5 and 6. Figure 3 illustrates that the one-sided test was uniformly more powerful than the two-sided test for all power simulations, despite the more conservative nature of the one-sided version. Hence, we focus on the one-sided Fisher test for the remaining comparisons.

Fig. 3.

Conditional power over simulation scenarios 5–6 for Fisher’s exact tests, accounting for ascertainment based on stage-1 screening of cases

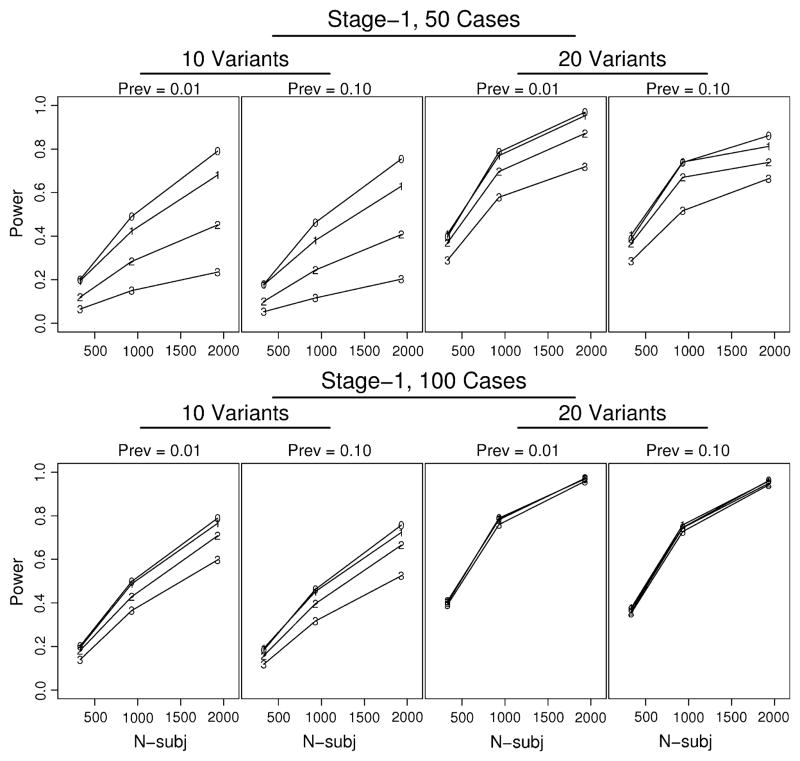
A number of our simulation factors influence the unconditional power, including the design criteria at stage-1 (i.e., the choice of threshold and the number of cases screened), the disease prevalence, the effect size (in terms of OR for carrier status), the carrier frequency, and the total sample size. Furthermore, scenario-5 allowed subjects to carry multiple independent variants, so the more variants, the greater the risk. In contrast, scenario-6 allowed subjects to carry only one variant, so increasing the number of variants did not have a large impact on power. To illustrate our main findings, we present in Fig. 4 simulation results from scenario-5, with an OR = 2. The top four panels, with only 50 cases screened at stage-1, illustrate that the unconditional power dramatically decreased as the threshold increased from zero to three; this impact was larger when only 10 variants were simulated in contrast to 20 variants. Increasing the number of variants increased both the probability of carrying any variant and the disease risk. The bottom four panels of Fig. 4 illustrate greater unconditional power and less influence of the threshold when a larger number of cases are screened at stage one. For the columns of panels in Fig. 4, prevalence alternates between 0.01 and 0.10; there was slightly greater power for smaller disease prevalence, albeit inconsequential. Similar results were found for an OR = 5, and for scenario six (results not shown).

Fig. 4.

Unconditional power for representative simulations (scenario-5, OR = 2) illustrating impact on power of threshold at stage-1 (labels 0–3 in panels), number of cases screened at stage-1 (50 in top panels; 100 in bottom panels), disease prevalence (Prev), and number of variants (10 or 20). x-axis “N-subj” is the total number of subjects

Design considerations

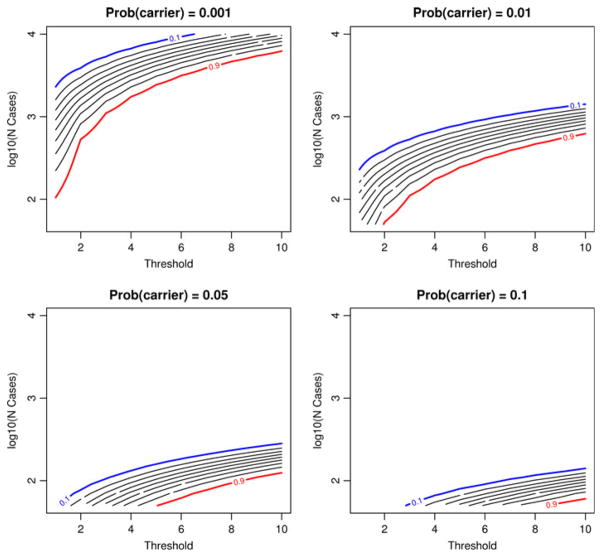
Our simulation results indicate that choosing too few cases (n_d,1) at stage-1, or too large a continuation threshold (t), decreases the chance of continuing to stage-2. To further evaluate the impact of stage-1 design criteria on the probability of stopping early, we used the binomial density to compute the probability of stopping early (expression 1). Figure 5 illustrates the probability of stopping early as it depends on the carrier probability, the threshold, and the number of cases screened at stage-1. Because the stopping probabilities varied broadly, Fig. 5 plots the number of cases on the log10 scale, and the stopping probabilities are given as contour lines, in step-sizes of 0.10. The lines are bracketed by 0.10 (blue line) and 0.90 (red line). The panels in Fig. 5 illustrate that when the carrier frequency is quite small (0.001), there is an extremely high probability of stopping early, even with over 1,000 cases. If the carrier frequency is 0.01, then screening 200–400 cases with a small threshold would likely assure only a small chance of stopping early, although larger thresholds increase the probability of stopping early with less than 200 cases. If the carrier frequency is at least 0.05, then screening 100 cases with a threshold of 1–4 would likely suffice.

Fig. 5.

Contour plots of the probability of stopping at stage-1 according to the continuation threshold (x-axis) and the number of cases screened at stage-1 (y-axis). The lines represent stopping probability contours in increments of 0.1, ranging from 0.1 (blue line) to 0.9 (red line)

Stopping early is good when the null hypothesis is true, but bad when the alternative hypothesis is true. Hence, it is desirable to choose a combination of n_d,1 and t that maximize the chance of stopping early under the null, but minimize the chance under the alternative. Quality-control studies and clinical trials often use two-stage designs, and we adopt their approach by defining a design to be optimal if it achieves the desired unconditional power while minimizing the expected sample size under the null hypothesis. As an approximation, we use the following strategy to find an optimal design. For a specified carrier frequency among controls (p_c) and OR, the probability that a case would be a carrier is

$$p_d=p_c\text{OR}/[1+p_c(\text{OR}-1)].$$

Conditional power can be determined by usual methods to compute power for two binomials, once the total sample size N and the desired Type-I error rate, α, are specified. Recognizing that unconditional power will be less than conditional power, we consider a range of N such that conditional power is larger than the desired power. For example, if the desired unconditional power is 90%, we determine N to achieve conditional power of 91–99%, in steps of 1%. For each value of N, we evaluate the probability of stopping under both the null and alternative hypotheses for all combinations of n_d,1 < N/2 and t ≤ n_d,1. From this information, we can compute expected sample sizes, under the null, for all possible designs,

$$E[N\mid \text{null}]=n_{d,1}P(\text{stop}\mid \text{null})+N[1-P(\text{stop}\mid \text{null})],$$

as well as the unconditional power (expression 6). The optimal design is then determined by finding the minimum of E[N|null] among all designs that have unconditional power at the desired level. Similar to E[N|null], we also compute the expected sample size under the alternative.

For illustrative examples, we considered two scenarios. For the first, we assumed that the carrier frequency among controls is 0.01, and for the second, 0.05. For both scenarios, we desired unconditional power of 90% for an OR = 5. Table 4 presents optimal designs for these two scenarios, along with the stopping probabilities and expected sample sizes under the null and alternative hypotheses. For Design-1, 1,058 total subjects are required, with 144 cases screened at stage-1. If at least four of these stage-1 cases carry variants, then the study proceeds to stage-2 to screen all cases and controls. When the null hypothesis is true, there is a 94% chance of stopping at stage-1, in contrast to only 8% chance if the alternative is true. The expected total sample size is 196.48 if the null is true, but 984.24 if the alternative is true. Design-2, for a carrier frequency of 0.05, requires 37 cases at stage-1, but a threshold of 5 to continue to stage-2.

Table 4.

Optimal design options for OR = 5

Design parameters	Design-1	Design-2
Prob carrier, controls	0.01	0.05
Total N	1,058	274
Powerconditional	0.98	0.99
Powerunconditional	0.90	0.90
Stage-1 cases (nd,1)	144	37
Stage-1 threshold (t)	4	5
P(stop|null)	0.94	0.96
P(stop|alt)	0.08	0.09
E[N|null]	196.48	45.52
E[N|alt]	984.24	252.48

Discussion

We present an efficient two-stage design that uses some, or even all, of the cases to screen for rare variants at stage-1, and then compares the frequency of variants among cases versus controls at stage-2. Our developed exact test corrects for the stage-1 ascertainment, providing unbiased, or even conservative, Type-I error rates. This two-stage exact test is similar in spirit to Fisher’s exact test for contingency tables, and in fact is identical to Fisher’s exact test when there is no stopping rule for stage-1 (i.e., threshold t = 0). Although we evaluated an exact chi-square statistic, it was quite close to the Fisher’s exact test for our simulations, suggesting that Fisher’s one-sided exact test, corrected for ascertainment, is a good choice.

Our simulations, and analytic evaluations, showed how the probability of stopping at stage-1 increases with a smaller number of cases screened at stage-1, a larger continuation threshold, or a smaller carrier probability. Our simulations also showed how these factors impact the unconditional power—the probability of not stopping times the conditional power at stage-2. Other factors which influenced our simulated power, as expected, were disease prevalence, the assumed genetic architecture (i.e., number of causal variants; single vs. multiple causal variants), the magnitude of effect size, and the total sample size.

There is a trade-off between stopping early when the null hypothesis is true, implying few cases that carry any variants, versus continuation to stage-2 when the alternative hypothesis is true. Stopping early can reduce sequencing efforts, reducing costs of a study, but at the price of potentially missing true causal variants. We propose choosing a combination of the number of cases screened at stage-1 and the continuation threshold in order to minimize the expected sample size when the null hypothesis is true, yet assure the desired unconditional power.

Our proposed strategies offer practical solutions to design and analyze studies that first screen disease cases for genetic variants, and then screen selected variants in a larger number of cases and controls if a sufficient number of variants are detected at the first stage. The simplicity of the proposed two-stage design is appealing, although greater efficiency could be achieved by screening sequentially only one case at a time. Although sequential screening might be impractical when assaying a relatively small number of candidate genes because batch assays are more efficient, sequential screening might offer greater benefits for costly whole genome sequencing.

Software

The software “trex” (for truncated exact test) is available from our Mayo web site: http://mayoresearch.mayo.edu/mayo/research/schaid_lab/software.cfm.

Hudson’s ms software: http://home.uchicago.edu/~rhudson1/source.html.