Anticipation in feedback-delayed manual tracking of a chaotic oscillator

Abstract

Manual tracking of non-chaotic targets, with and without feedback delay, as well as discrete prediction of chaotic maps have each been demonstrated by humans. Feedback-delayed tracking of chaotic targets, on the other hand, has not been well investigated. To this end, 10 participants were asked to track a chaotically moving target presented on a computer display by means of controlling a similar on-screen object using a pressure sensitive tablet and hand-held stylus. The participants were given delayed visual feedback of their own movements. Task success subsequently required anticipation on the part of the participant. Using 6 values of delay from 20 ms to 1 s, evidence shows that a) participants are able to synchronize with a chaotic target, even with some amount of applied delay, b) task performance varies systematically with applied delay, and c) this same systematic dependence is predicted for systems exhibiting anticipating synchronization.

Introduction

To synchronize one’s own movements to the motions of the surrounding environment, one must appropriately control the movement of, for example, one’s limbs. In the instance of manual tracking, the task demands that the motion of the hand becomes synchronized with the motion of a target. Thus, synchronization tasks and motor control are intricately linked.

Investigation into the ability of humans to synchronize with a dynamical system has, for the most part, developed along two major axes. First, the time series presented to a participant may be discrete or continuous¹, e.g. a metronome (Repp, 2005) or smooth oscillation (Vercher and Gauthier, 1992). Second, the underlying system may be regularly periodic (Voss et al, 2007) or chaotic (Neuringer and Voss, 1993; Smithson, 1997; Heath, 2002). Stochastic signals are another option at this point, but for the moment we restrict ourselves to periodic and chaotic signals (i.e. deterministic signals).

These two dimensions outline four areas of synchronization research, such as continuous- periodic (Voss et al, 2007) and discrete-chaotic (Stephen et al, 2008). In all of these cases, humans are able to synchronize in some respect with the time series presented to them (for a particularly non-human case, see Saigusa et al, 2008). That synchronization exists, however, is not an adequate description of the results of the foregoing line of inquiry–some form of anticipation is nearly always observed as well. An anticipatory ”systematic error” has been well documented in at least the discrete tasks (Fraisse, 1984; Radil et al, 1990; Aschersleben and Prinz, 1995) and explicit investigations show anticipatory ability in both discrete and continuous ones as well (Metzger and Theisz, 1994; Foulkes and Miall, 2000).

Delayed feedback puts participants into a position where they must anticipate in order to succeed at a task (Vercher and Gauthier, 1992; Foulkes and Miall, 2000; Voss et al, 2007). This anticipation-engendering property of delay is reminiscent of a phenomenon in dynamical systems known as anticipating synchronization (Voss, 2000). State-based synchronization of two dynamical systems x and y may not only be complete (y(t) ≈ x(t)) or lagged (y(t) ≈ x(t − τ)), but also anticipating (y(t) ≈ x(t + τ)). A class of unidirectionally coupled systems that often results in anticipating synchronization is shown in Equation 1.

$$\dot{\mathbf{x}}=f(\mathbf{x})\dot{\mathbf{y}}=g(\mathbf{y})+k(\mathbf{x}-{\mathbf{y}}_{\tau })$$ (1)

where f (x) and g(y) are the intrinsic dynamics of x and y, k is a coupling strength, and y_τ = y(t − τ) or in other words, the state of y delayed by τ in some unit of time. The vectors x and y themselves are states of a master and slave system, respectively.

The similarity between Equation 1 and many synchronization tasks involving delay invites direct comparison (as in Stepp and Frank, 2009; Voss et al, 2007). Therefore, this particular study has three aims. First, to show that synchronization to a continuous-chaotic oscillator is possible. Second, to show that there is a systematic dependence of synchronization behavior on applied delay. Third, to link performance of feedback-delayed synchronization tasks by humans to the phenomenon of anticipating synchronization.

Methods

Participants

Ten (5 female and 5 male) undergraduate and graduate students at the University of Connecticut participated in this study. Of the 10, 9 were right handed and 1 left handed. Right and left handedness was defined by the hand with which the participant preferred to draw. Participants gave informed consent and, in the case of undergraduates, received class credit for their voluntary participation. The study was approved by the University of Connecticut Institutional Review Board, and conducted in accordance with the Declaration of Helsinki.

Design

Each participant viewed a computer display (39 cm diagonal, 1280×800 pixel resolution) at a distance of approximately 65 cm from screen to eye. A pressure sensitive tablet (18 cm diagonal) sat 30 cm in front of the same display. Participants held a 14 cm stylus in their dominant hand that they could position on the tablet in order to interact with the display. The tablet and stylus were visible to the participant, and the background color of the display was set to a light gray color.

Trials, each lasting 80 s, were organized into 3 blocks of 6 for a total of 18. In general, there was a 2–3 second gap between each trial, although participants were able to rest between trials whenever they wished. During each trial a 20×20 pixel blue square, the target, moved along a chaotic ellipsoid trajectory. The on-screen s_x and s_y coordinates of the trajectory were generated by the x₁ and x₂ dimensions of a ”chaotic spring” system specified by Equation 2.

$${\dot{x}}_1=x_2{\dot{x}}_2=-{\left(2\pi \right(\frac{x_3}{\alpha }+\beta \left)\right)}^2{x}_1{\dot{x}}_3=-x_4-x_5{\dot{x}}_4=x_3+a{x}_4{\dot{x}}_5=b+x_5(x_3-c)$$ (2)

This particular system maintains an elliptical oscillation, at the same time varying chaotically in both amplitude and frequency. Therefore, the trajectories produced are chaotically hard to predict, but remain trackable by naive participants. Dimensions x₃, x₄, and x₅ comprise a standard Rössler oscillator. This chaotic system then drives the stiffness of a simple harmonic oscillator, dimensions x₁ and x₂. For all trials, a = b = 0.1, c = 14, α = 100, and β = 0.3. The system described by Equation 2 is then a straightforward extension of simpler systems that might produce more common circular or linear trajectories.

At the beginning of each trial, a 160 s time series was simulated from initial conditions x₁ = 1, x₂ = 0, x₄ =3.432, x₅ = 20.9, and x₃ taken from a uniform distribution on the interval [18.5, 19.5]. The first 80 s of this time series was truncated in order to remove any transient behavior. Lastly, x₁ and x₂ were mapped to on-screen coordinates s_x and s_y by the mappings in Equation 3 and Equation 4.

$$s_x=\frac{(s_{\mathit{\text{width}}}-2s_{\mathit{\text{x pad}}})(x_1-\text{min}{x}_1)}{\text{max}(x_1-\text{min}{x}_1)}+s_{\mathit{\text{x pad}}}$$ (3)

$$s_y=\frac{(s_{\mathit{\text{height}}}-2s_{\mathit{\text{y pad}}})(x_2-\text{min}{x}_2)}{\text{max}(x_2-\text{min}{x}_2)}+s_{\mathit{\text{y pad}}}$$ (4)

where s_{x pad} = 0.25s_width and s_{y pad} = 0.45s_height.

While the simulation was displayed on-screen, participants used the stylus and tablet to control a 10×10 pixel green square with the instruction to keep the green square in contact with the blue, ideally overlapping². The movement of the stylus, however, was delayed before being displayed to the participant. Delays were randomized within each block from the set τ = {20, 200, 400, 600, 800, 1000} ms. Horizontal and vertical coordinates of the undelayed tablet input, i.e. the movement of the hand, were captured as y₁ and y₂, respectively. As such, the data collected parallel the states x and y of the master–slave system described in Equation 1. Coupling, and subsequently synchronization, is considered to be between the hand and target. The delayed movements of the participant’s green square play the same supporting role as does y_τ from Equation 1.

Data Analysis

For the purpose of analysis, the first dimension of the target time series, x₁, was compared to the first dimension of the participant time series, y₁. These two dimensions correspond to the horizontal movements of each. To determine both the level of synchrony, ρ, and amount of phase shift, τ^*, between x₁ and y₁ we used the maximum of the cross-correlation between the two (Stepp and Frank, 2009).

For each trial, these two quantities were calculated according to Equation 5.

$$\rho =\text{xcorr}({\tau }^{*})=\text{max xcorr}(h),$$ (5)

where xcorr(h) is the normalized cross correlation function of x₁ and y₁ with lags from the interval h = [−40, 40].

Results

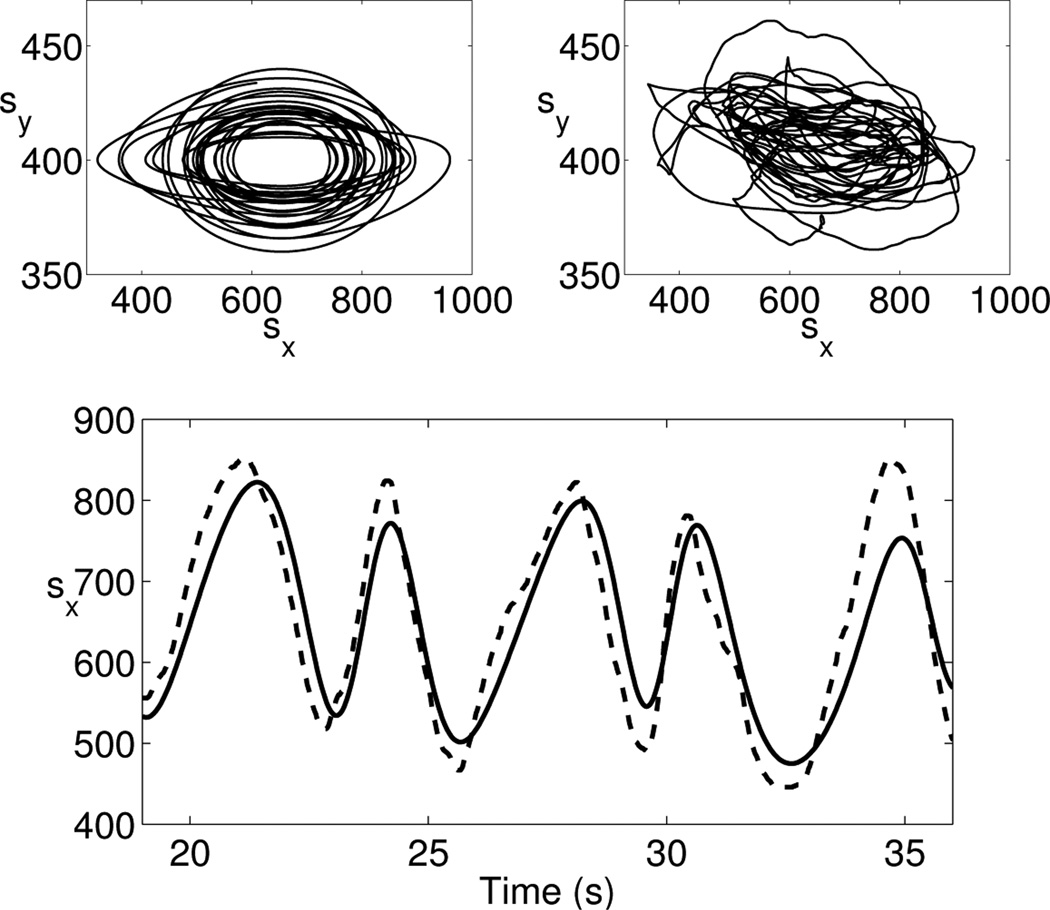
In general, participants reported experiencing only three different delays: no delay, small delay, and large delay. Participants also consistently reported trailing behind the target even when motions of the hand were clearly anticipatory. Figure 1 shows typical target and participant time series over a single 80 s trial.

Fig. 1.

Typical time series for both target (top left) and participant (top right). In this particular trial, the target time series was generated with x₃(0) = 18.6386, and the participant’s response was subjected to a delay of τ = 400 ms. The bottom panel contains a plot of the evolution of target (solid) and participant (dashed) together in time. A slight negative phase shift is evident, owing to the fact that the participant’s stylus is leading the target by approximately 180 ms on average.

Each participant produced three blocks of six time series such that each τ condition was repeated three times. While the first block was considered practice and not analyzed, the second two blocks were analyzed using the methods above to generate a ρ and τ^* measure for each trial. Participants in similar tasks (Miall and Jackson, 2006) have shown adaptation across many trials. In the case of the current task, however, differences between participant performance in block 2 and 3 are negligible. As such, analyses below are conducted using mean values per participant. Given our two measures, we may examine the effect of τ on each in turn.

Dependence of synchronization on delay

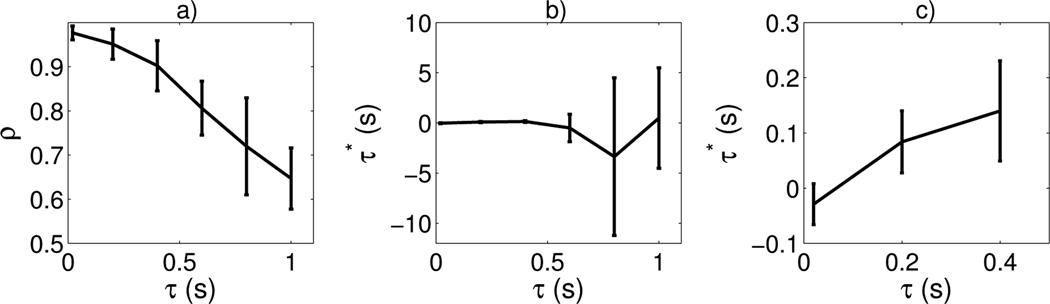
As expected, participants attained higher synchrony for smaller delays than for larger delays. Maximum cross correlations between hand and target (ρ above) ranged from 0.98 (SD = 0.016) at 20 ms delay to 0.65 (SD = 0.070) at 1000 ms delay. Performance measures for all delay conditions is plotted in Figure 2a. All pairwise comparisons (paired-sample t-tests) between τ conditions are significant at α = 0.02. Less trivial than decrease in performance with τ is the particular shape of the curve. Dependence of ρ on τ shows a significant cubic trend, F(1,9) = 5.40, p = 0.045. Differences between ρ values are smallest for small and large τ values.

Fig. 2.

a) Dependence of maximum cross correlation, ρ, on delay, τ. The value of ρ represents the highest correlation between participant and target, allowing for an arbitrary phase shift. Note that the negative slope doubles after 400 ms. b) Dependence of phase shift, τ^*, on delay, τ. For τ ≥ 600 ms, phase shifts are most likely artifacts of using Eq. 5 on time series which are not well correlated. c) Dependence of τ^* on τ ≤ 400, highlighting a linear regime

Dependence of phase shift on delay

At 20 ms delay, participants’ phase shifts are significantly negative, t(9) = −2.48, p = .035, meaning that their hands were trailing the motion of the target. At 200 and 400 ms, however, phase shifts are significantly positive, identifying anticipation by the hand in those conditions, t(9) = 4.74, p = .0011 and t(9) = 4.88, p < .001, respectively. Up to this point, τ^* varies roughly linearly with τ, R₂ = .54, F(2,27) = 32.42, p < .001 with τ as a predictor (b = 0.44, p < .05). At delays of 600 ms and above, however, variability across participants becomes quite large and any systematic dependence of phase shift on τ, as well as significance of either positive or negative shifts, disappear. Phase shifts for each τ condition are plotted in Figure 2b.

Discussion

This study set out to show that synchronization between hand and continuous-chaotic oscillator–even with applied delay–is possible, to show a systematic dependence of synchronization behavior on that delay, and to link that behavior to similar behavior within the phenomenon of anticipating synchronization. The results above immediately apply to the first two aims, showing that participants can indeed track chaotic movements and that their ability to do so depends systematically on applied delay. The particular form of this dependence leads to consideration of the third aim. Before addressing this last point, however, there are several elements of the first two worth examining more closely.

Anticipation of the target

It is clear that participants were able to behave in anticipation of the target in the 200 and 400 ms τ conditions. Phase shifts in these conditions are significantly positive. As described earlier, positive phase shifts of this sort denote anticipation. In the 20 ms condition, however, participants trailed the target, a somewhat unintuitive result given the existence of anticipation in conditions with much greater delay. At 600 ms delay and beyond, participants cease to reliably lead or trail the target. This is the first hint that there may be a critical τ at some point between 400 and 600 ms.

Is there a critical value of τ?

It is not only the fact of anticipation that is of interest, but the existence of a systematic dependence of both synchronicity and phase shift on delay. Several properties distinguish themselves in Figure 2. There are qualitative differences present in each graph between τ ≤ 400 ms and τ ≥ 600 ms. First considering the measure of synchronicity in Figure 2a, this boundary separates regions of small and large variability, as well as regions of small and large changes between adjacent τ conditions. In other words, values of ρ at τ ≤ 400 are relatively high, cluster more tightly across participants, and do not differ greatly from one τ to another. On the other hand, values of ρ at τ ≥ 600 are decreasing rapidly and are highly variable across participants.

Similar differences exist in Figure 2b. Values of τ^* at τ ≤ 400 also exhibit drastically lower variability than at τ ≥ 600. More interesting from the view of anticipatory systems is that the τ conditions for which participants were able to anticipate the target were also below this threshold, except for the very smallest tau condition, 20 ms.

In answer to the question posed by this section, it appears that there is a critical value, or region of values, 400 < τ_c < 600 ms. Properties of ρ and τ^* below this region are distinctly different from those above it. Further experiments should examine the space between 400 and 600 ms using a higher resolution, in order to find just how sharply defined this critical region is. For instance, Vercher and Gauthier (1992) performed a similar experiment, albeit with a non-chaotic target, using 10 values of τ from 0 to 450 ms. In that study no critical value of τ was discovered, which fits well with the observations above. It is expected that if τ values greater than 450 ms were used, a change in behavior would be observed similar to the one described here.

It is also expected that the particular critical τ suggested here is a function of target (Equation 2) as well as participant dynamics. That is, for any instantiation of a master and slave system coupled in the way presented above, there should be a corresponding τ_c.

Properties of τ^* above and below τ_c

Below the supposed critical time delay τ_c, values of τ^* show a linear relationship with τ. This region is plotted alone in Figure 2c. A linear relationship such as this is particularly interesting when one considers the task. As τ increases, so does each participant’s τ^*. It is not the case, however, that participants anticipate by exactly τ or greater (i.e., the slope the line in Figure 2c is less than one). The combination of these two facts amounts to the interesting result: participants demonstrate the ability to anticipate more than they actually do at a particular value of τ. Being specific, a participant tracking in the 200 ms condition will anticipate the target by some time τ₁, even having demonstrated in the 400 ms condition that he or she is capable of anticipating by τ₂ > τ₁. Participants anticipate by an amount relative to τ, not by the greatest of their ability. Values of τ^* above τ_c become two orders of magnitude more variable (mean SD = 0.058 for τ < τ_c, mean SD = 2.2 for τ > τ_c). That is, participants cease to perform reliably at these larger τ values.

Similarity to simulated anticipating synchronization

The similarity between this task and the delay coupling arrangement of Equation 1 was outlined at the start. The task put to participants is to minimize the difference between the current position of the target and the past position of the hand-held stylus. Participants must change their behavior in the present in order to synchronize two states separated by time. To successfully do so requires anticipation of the target.

Anticipating synchronization, following Equation 1, has stability that is dependent on the compatibility of f and g as well as the two parameters k and τ (Pyragas and Pyragiene, 2008; Stepp and Turvey, in press; Toral et al, 2003; Voss, 2000). Simulations which span combinations of k and τ show very similar relationships between ρ and τ as those seen in Figure 2a, as well as linear relationships between τ^* and τ (Voss, 2000). For two systems that are not perfectly matched (i.e. f ≠ g), the profile of Figure 2a is just what is expected for nearly constant k and varying τ (see Stepp and Turvey, in press).

The existence of a critical time delay, τ_c, is also fully expected. In simulated anticipating synchronization, such a delay tends to separate high ρ from low, positive τ^* from negative, and stability from instability (Stepp and Turvey, 2008, in press; Voss, 2000). That is, just the sort of behavior seen in the analyses above. Thus, there is at least an empirical link between manual tracking with delayed feedback and the phenomenon of anticipating synchronization. For the present task, this may not be surprising provided that the task itself so closely mirrors the dynamics of Equation 1. Particularly striking, however, is the fact that participants exhibit a τ^* according to a linear relationship with τ, rather than some higher phase-shift that they are clearly able to attain. This is notable, as a participant might have deviated from behavior predicted by anticipating synchronization, but did not.