Spatial-temporal disease mapping of illicit drug abuse or dependence in the presence of misaligned ZIP codes

Abstract

Geo-referenced data often are collected in small, administrative units such as census enumeration districts or postal code areas. Such areas vary in geographic area and population size and may change over time. In research into drug-related health issues within the United States, U.S. Postal Service ZIP codes represent a commonly used unit for data collection, storage, and spatial analysis because of their widespread availability in health databases through patient contact and billing information. However, the ZIP code was developed for the specific purpose of delivering mail and may be changed at any time, and its design and development does not take into consideration problems that may arise in data collection, analysis, and presentation in health studies. In this paper, we propose a spatial hierarchical modeling approach to quantify trends within ZIP-code based counts when some fraction of ZIP codes change over the study period, that is, when the data are spatially misaligned across time. We propose a data vector approach and adjust the spatial auto-correlation structure within our Bayesian hierarchical model to provide inference for our misaligned data. We motivate and illustrate our approach to explore spatio-temporal patterns of amphetamine abuse and/or dependence in Tracy, California over the years 1995-2005. Uncertainty associated with misaligned data is modeled, quantified, and visualized. The approach offers a framework for further investigation into other risk factors in order to more fully understand the dynamics of illicit drug abuse or dependence across time and space in imperfectly measured data.

Background

Geo-referenced data often are collected and reported within small, administrative units such as census enumeration or postcode areas. It is well known that the choice of geographic unit in such data can affect the interpretation of maps and the results of spatial analysis, a phenomenon known as the Modifiable Areal Unit Problem (MAUP) or the Change of Support Problem (COSP), the geographical manifestation of the so-called “ecologic fallacy” of interpreting associations observed in aggregated data as estimates of individual-level associations. In research into drug-related health issues within the United States, U.S. Postal Service ZIP codes represent a commonly used unit for data collection, storage, and spatial analysis because of their widespread availability in health databases through patient contact and billing information (Stallings et al. 1997; Cicero et al. 2007a; Cicero et al. 2007b; Bierut et al. 2008). However, the ZIP code was developed for the specific purpose of delivering mail and can change whenever necessary, so its design and development do not take into consideration problems that may arise in data collection, analysis, and presentation in health studies.

Some common problems arising when using ZIP code data in health studies is the fact that true spatial boundaries of ZIP codes are generally not known; some geographic areas represented by a ZIP code are not contiguous (Beyer et al. 2008); ZIP code areas do not nest within other administrative areas such as counties or census tracts; some ZIP codes represent large businesses or organizations with no residents; and ZIP codes are not required to be stable over time. To avoid such problems, the US Census Bureau produced a new ZIP code topology called the ZIP Code Tabulation Area (ZCTA) and provided boundary files for such areas to facilitate the use of ZCTAs within geographic information systems.

Several researchers have explored problems associated with using ZIP codes and ZCTAs for the spatial analysis of epidemiological data (Grubesic and Matisziw 2006) and warned of spatial mismatch and representational errors. In addition to these technical differences between ZIP codes and ZCTAs, spatiotemporal mismatches of ZIP codes across time points make many methods of spatiotemporal analysis difficult or impossible to apply since most rely on a spatially fixed set of geographic units. Generally, in a spatio-temporal analysis of health and disease, changing geographic units are handled in one of the following ways:

1. When point-level data are available, the exact locations may be mapped and analyzed directly, thereby avoiding impact of the changing geographic units (Diggle et al. 2009).

2. Data from multiple time points may be linked to a mid-point geographic mapping system (Manda et al. 2009). This approach works best in cases where there are relatively few changes in the maps across time points and the data have a high level of completeness.

3. Data from multiple time points are projected to a common geographic regional system (Paul et al. 2008) which does not change in the study period.

4. Changing geographic units are projected on an artificial uniform grid unit system with a collection of regions having exactly the same shape and size (Lipton and Banerjee 2007).

5. Geographic units may be filtered for those that have common boundary definitions over time (Gruenewald and Remer, 2006).

Obviously only the first solution precludes the possibility that biases may arise due to changes in spatial reference frames over time. The remaining solutions may introduce biases into statistical models of spatial data when changing geographic areas are linked to mid-points (#2), projected onto a common regional system (#3) or set of common artificial geographic areas (#4), or some geographic areas are excluded from analysis (#5). This type of systematic biases is due to the errors in the location information of the data and exists in statistical estimates of parameters of interest.

This paper proposes another approach that handles the changing ZIP code problem. The approach is motivated particularly by the growing literature within public health and prevention research that focus on the spatio-temporal patterns of drug misuse. With varying analysis units (e.g. ZIP code) across time points, estimates of spatio-temporal patterns of drug misuse are biased. The main purpose of this paper is to estimate the effect of misaligned data units on the overall spatio-temporal pattern of amphetamine abuse within one city in California. The remainder of this paper is organized as follows. The Methods section describes the dataset and the underlying research question of interest, i.e., the spatio-temporal distribution pattern of amphetamine misuse in Tracy, California for the years 1995-2005. We next define our approach using hierarchical Bayesian models implemented within WinBUGS (Spiegelhalter et al. 2003) and its spatial analysis extension GeoBUGS (Thomas et al. 2004). The Results section reports the results of our application of the chosen model providing quantitative and visual output addressing the key spatio-temporal changes in amphetamine misuse in Tracy during the study period. The Conclusions and Discussion section summarizes our major findings and presents avenues for future research.

Methods

Data

Our data are comprised of ZIP code summaries from the city of Tracy, California for years 1995 to 2005, during which the annual audited Hospital Discharge Data (HDD) were available from the Medical Information Reporting for California System, California Office of Statewide Health Planning and Development. Of special interest are the counts of amphetamine abuse or dependence within hospital discharges. The City of Tracy is in San Joaquin County, California, located in the Central Valley, east of the San Francisco Bay Area (Figure 1a). During the 1980s this area experienced a dramatic increase in arrests for sales, possession and use, and manufacturing of methamphetamine, a non-prescription form of amphetamine used primarily for recreational purposes. The Central Valley of California played a key role in this increasing trend, mainly because many domestic laboratory operations producing methamphetamine were located in this rural area. Corresponding increases in incidence and prevalence of amphetamine abuse/dependence were observed in the HDD records at the same time, noting that there is no separate category for methamphetamine abuse in the HDD records. Between Year 2001 and 2003, the study area experienced a sudden increase in hospital discharges related to amphetamine abuse/dependence, during which the rate increased from 4 to 8 per 10,000 population (Figure 2).

Figure 1.

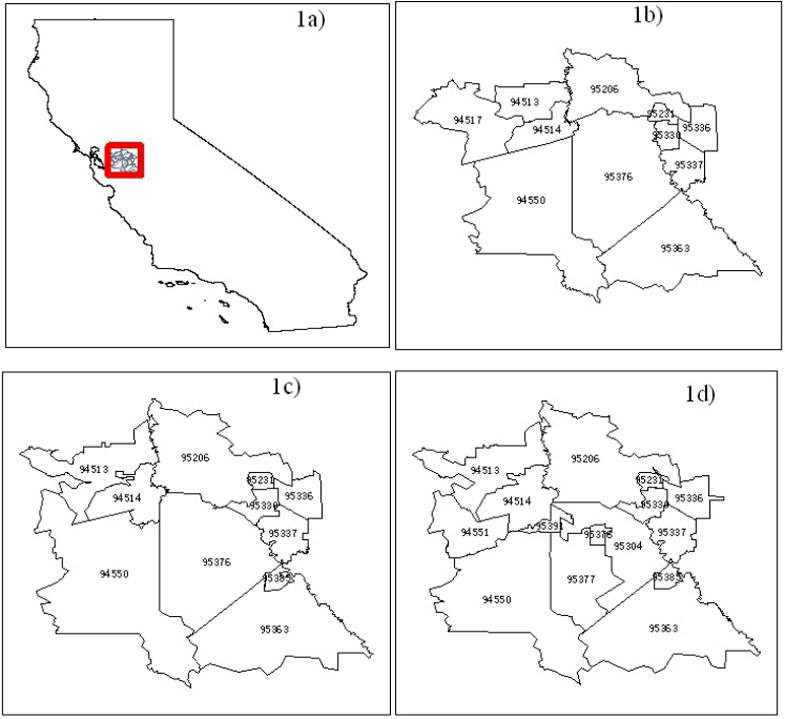
Study area and the changing ZIP codes in Years 1995, 2000, and 2005.

Figure 2.

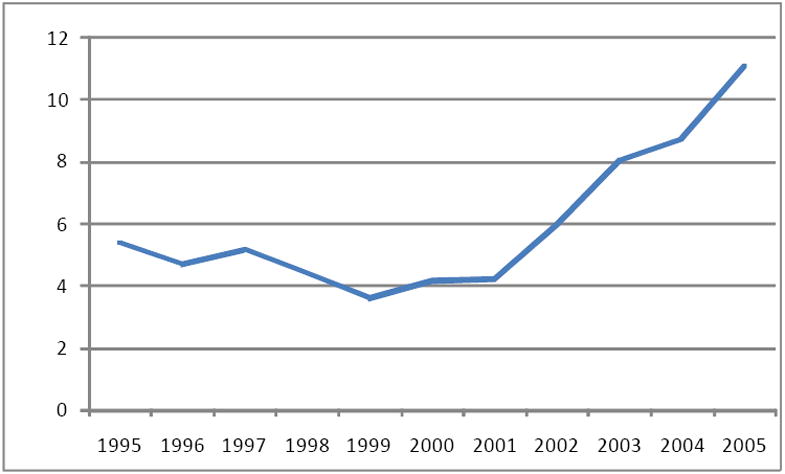
Hospital discharges related to amphetamine abuse/dependence per 10,000 population in Tracy, CA, 1995 – 2005.

Concurrently, the US Postal Service redesigned mail delivery routes in the same area due to rapid population growth. As a result, the ZIP code boundaries in Tracy underwent major changes in our 11-year study period (Figures 1b-1d). Basically, the change in ZIP code boundaries takes one of several forms. First, new ZIP codes were created (e.g., 95394, 95304, 95377 in the year 2002) due to rapid population growth. Secondly, ZIP codes were removed due to rezoning of mail delivery routes (e.g., 94517 in year 1999). Also, ZIP codes went through significant size changes (either increase or decrease of over 8% of their original area). Table 1 summarizes the different changes in ZIP code areas within our study area during the 11-year study period. Taken together, these changes introduce significant challenges in determining temporal trends in small-area rates of amphetamine misuse and dependence.

Table 1.

Type of Misalignment in the Tracy Amphetamine HDD data

Year	Number of ZIP codes	New	Size Increase	Size Decrease	Removal
1995	11
1996	11
1997	11		2	3
1998	12	1	1	1
1999	11		3	2	1
2000	11		1
2001	11
2002	14	3	3	1
2003	14
2004	15	1		1
2005	15

Spatio-temporal Disease Mapping with Bayesian Hierarchical Models

Crude maps based on local rates often feature large outlying risk estimates for small areas where the population density is sparse and a single amphetamine-related discharge could result in very high local rates. Such maps also fail to incorporate any similarity between relative risks in nearby or adjacent regions. In response to these problems, Bayesian methods for small area analysis and disease mapping have become fairly standard in the public health literature due to their ability to provide precise model-based estimates of local rates utilizing both local and neighboring observations. Such methods are often called “hierarchical” because they partition variation in complex statistical models of spatio-temporal association into simpler components (Carlin and Louis 2000).

Briefly, Bayesian hierarchical modeling involves two stages. At the first stage, a likelihood model is specified conditional on the region-specific random effects, and then a prior model over the space of possible random effects is specified at the second stage. Using software packages such as WinBUGS/GeoBUGS we can obtain a sample of observations from the joint posterior of all model parameters which forms the cornerstone of Bayesian inference. This set of posterior samples of parameter values provides the necessary elements for posterior estimates of predicted outcomes and local rates which, in turn, provide the information necessary to create maps to visualize high- and low-risk areas. The strength of the Bayesian methods in spatio-temporal disease mapping lies in that an appropriately-tailored Bayesian approach is capable of incorporating spatial assumptions and helping smooth the noisy maps by borrowing information from neighbors for those mapping units with small populations.

More specifically, most Bayesian models for spatio-temporal disease mapping take the form of Poisson regression model

$$Y_{i,t}\mid {\mu }_{i,t}~\mathit{Poisson}(E_{i,t}\exp ({\mu }_{i,t}))$$ (1)

where Y_i,t denotes the count of amphetamine-related discharges in spatial unit i at time point t. It is assumed that this count follows a Poisson distribution conditional on the space- and time-specific mean of the distribution. E_i,t denotes the expected number of the discharges (assuming all regions have the same underlying risk), which is fixed and proportional to the corresponding known population of the spatial unit i at time t. Hence exp(μ_i,t)may be interpreted as the relative risk of residing in spatial unit i at time point t: regions with exp(μ_i,t) > 1 will have greater counts than expected, and regions with exp(μ_i,t) < 1 will have fewer than expected. Following standard generalized linear models, the log-relative risk, μ_i,t, is modeled linearly as

$${\mu }_{i,t}={X^{’}}_{i,t}\beta +{\theta }_{i,t}+{\varphi }_{i,t}$$ (2)

This is a linear combination of fixed covariate effects and random effects which may take account of spatial and/or temporal correlation. Here X’_i,t is a matrix containing space- and time-specific covariates, and β is a vector of fixed effects. θ_i,t and ϕ_i,t denote a pair of random intercepts capturing spatially unstructured heterogeneity and spatial dependence, respectively. The typical way to impose this structure is to assume that θ_i,t ’s are i.i.d. Gaussian variables with mean 0 and variance 1/τ and ϕ_i,t ∣ ϕ_j≠i,t ~ N (μ_ϕi,t, σ²_ϕi,t), i=1,…, N[t] where

$${\mu }_{{\varphi }_{i,t}}=\frac{{\displaystyle \sum _{j\ne i}{w}_{\mathit{ij},t}{\varphi }_{\mathit{ij},t}}}{{\displaystyle \sum _{j\ne i}{w}_{\mathit{ij},t}}}\mathrm{and}{\sigma }_{{\varphi }_{i,t}}^2=\frac{1}{\lambda {\displaystyle \sum _{j\ne i}{w}_{\mathit{ij},t}}},$$

where weights w_ij,t are fixed constants defining spatial neighbors within time t. With this structure, the θ_i,t ’s capture heterogeneity among regions and the ϕ_i,t ’s capture spatial dependence or autocorrelation between regions. In practice, a common choice is to let w_ij,t = 0 unless areas i and j are adjacent, in which case w_ij,t = 1. This distribution for the spatial dependence random effects is called a conditionally autoregressive specification, which for brevity is typically written in vector notation as ϕ ~ CAR(λ). A fully Bayesian model specification is completed by adding prior distributions on β,τ , and λ. Without prior expectations about direction and magnitude of the covariate effects, a vague but proper prior distribution is put on the regression coefficients β. Typically, one assigns conjugate prior distributions for τ and λ via Gamma(a, b) distributions with mean a / b and variance a / b² . In practice, small values of a and b are chosen to represent large prior variance (little prior precision). Waller and Gotway (2004, Chapter 9) provide additional details and applications of disease mapping models.

Turning to our data, we find that instead of regular data matrices with rows and columns indicating spatial and temporal units respectively, the data in this project take an irregular form with varying numbers (and shapes) of spatial units at each time point. That is to say, for each t = 1, 2, …, T, the total number of spatial units, N[t], is different and, in some cases, the same ZIP code refers to a different spatial region at different time points. Hence the standard CAR disease mapping model (1) cannot be applied directly here. To solve the problem,, rather than treating each year as a replicate of observations of the same (fixed) set of regions, we “stack” each year’s data vector Y_1,tY_2,t,…,Y_N[t],t on top of the previous year’s data Y_1,t−1Y_2,t−1,…,Y_{N[t−1],t−1} so that the whole data form a vector of size ${\displaystyle \sum _{t=1}^{T}N[t]}$. In this manner, the two-dimensional data matrix Y_i,t is reduced to one-dimensional vector Y_i+J[t] for each unit i in year t, with $J[t]={\displaystyle \sum _{k=1}^{t-1}I[k]}$, the total number of spatial units from the first year in the study period to the previous year t-1 and J[1]=0. By rearranging the data this way, it is possible to investigate the spatio-temporal disease mapping problem for misaligned data with varying number and shapes of units across years without directly addressing the complex task of mapping one year’s regions into those of adjacent years. It would be ideally better to control for both temporal autocorrelation for a given place AND spatial autocorrelation within any given year. But the temporal autocorrelation is very difficult to define with changing units, so instead we allow for separate spatial relationships within each year and constrain these relationships to have common variance across years. Now the adjacency matrix needed in the CAR(λ) part of the model for the stacked data is block-diagonal with blocks representing the correlations of spatially adjacent units. That is, we simply define spatio-temporal adjacencies between observations rather than attempting to morph one year’s observations into those of another year using fixed spatial relationships. By rearranging the Tracy, CA, data (Table 1), instead of dealing with a dataset of 11 years with different number of units each year, we are handling a data vector of size 136 (total number of ZIP codes in the 11-year period) as if they were from a single year. Now the adjacency matrix in the CAR(λ) part of the model is block-diagonal with the first 11×11 block representing the Year 1995 spatial relations, and so on.

While the approach does not fully address the misalignment issues (Zhu et al. 2000; Gelfand et al. 2001; Zhu et al. 2003), the approach is straightforward to apply and flexible in that it is easy to add a time-dependent component f(t) in the fixed effects part X’_i,t β, so that a time-varying fixed effect can be estimated in addition to any other effects on possible covariates, a key aspect of the analysis.

After defining the basic family of models addressing our question of interest, the next step is to determine the model that best fits the data. For MCMC-based hierarchical models, Spiegelhater et al. (2002) proposed a convenient generalization of the Akaike Information Criterion (Akaike 1973) based on the posterior distribution of the deviance statistic

$$D(\vartheta )=-2\log p(\mathbf{y}\mid \mathbf{\theta })+2\log f(\mathbf{y}).$$

Here p(y ∣ θ) is likelihood function for the observed data vector y given the parameter vector θ , and f(y) is a standardizing function of data alone. In this approach the model fit is summarized by the posterior expectation of the deviance, D̄ = E_θ∣y (D), while model complexity is captured by the number of effective parameters p_D, which is defined as expected deviance minus deviance evaluated at the posterior expectations, i.e.

$$p_D=E_{\theta \mid y}(D)-D(E_{\theta \mid y}(\theta ))=\overline{D}-D(\overline{\theta })$$

The deviance information criterion (DIC) is then defined as the summation of fit and complexity, i.e.

$$\mathrm{DIC}=\overline{D}+p_D=2\overline{D}-D(\overline{\theta })$$

and smaller values of DIC indicate a better-fitting model.

To select a model which best describes the random effects correlation structure, consideration needs to be taken to check another criterion

$$\alpha =\frac{\mathit{sd}(\varphi )}{\mathit{sd}(\varphi )+\mathit{sd}(\theta )},$$

where sd(.) is empirical marginal standard deviation. Hence α is the proportion of variability in the random effects that is due to spatial dependence. Larger values (near 1) suggest a dominating spatial dependence, while smaller values (near 0) suggest a negligible one. Recall that we specified the same gamma prior distribution for τ and λ , i.e., α = 1/2.

Results

We applied the models above to the Tracy data. As a starting point and to assess the amount and type of inter-region associations, no covariates other than the type of misalignment were considered. The various types of misalignment in ZIP code are described in Table 1 and the Data section above. Two parallel sampling chains were run with overdispersed initial values. Convergence was assessed by checking the trace plots of the samples, autocorrelation functions, the Gelman-Rubin convergence statistic (Gelman and Rubin 1992) and Monte Carlo standard errors (Spiegelhatler et al. 2003). For each model, we generated 100,000 samples and treated the first 50,000 Markov Chain Monte Carlo (MCMC) iterations as a burn-in period.

Assessing overall fit, Table 2 lists deviance summaries for four models fit to the Tracy amphetamine data. A comparison of DIC values shows that the models incorporating random effects (Models II, III, and IV) fit much better than a model with only fixed effects (Model I) suggesting the presence of residual correlation. Also included in Model IV are time-dependent intercepts as fixed effects. The number of effective parameters in Model I is equal to the number of covariates since all parameters are independent of each other, while adding correlated random effects to Models II through IV makes the number of effective parameters far less than the total number of model parameters due to “borrowing of strength” across individual-level parameters in hierarchical models and correlation between neighboring values. Model II contributes 73 extra parameters, and Model III (with stronger restriction of spatial dependence) contributes 82 extra parameters to Model I. Model II has a slightly lower DIC value than Model IV.

Table 2.

Deviance Summaries for the Four Hierarchical Models

Model		D̄	D(ϑ̄)	pD	DIC
I	Fixed effects only	1000.10	985.14	14.96	1015.06
II	Fixed and heterogeneity	695.09	606.87	88.27	783.32
III	Fixed and dependence	712.53	616.16	96.36	808.89
IV	Full model	696.15	605.95	90.20	786.35

Turning to the proportion of variance criterion, we find that fitting data with the full model yields a posterior distribution for α with mean 0.408, median 0.429, and a 95% credible interval (0.0524, 0.714). This indicates that approximately 40% of excess variability is due to spatial dependence, while the remaining 60% is due to unstructured random noise. This confirms that Model IV (full model with both spatial dependence and spatial heterogeneity) is the best among the candidate models even though it does not have the smallest DIC value.

In Table 3, we summarize posterior statistics for the time-varying intercepts, the effects of different type of misalignment in ZIP code, and the precision parameters for spatial and unstructured random effects for Model IV. The columns in the table are posterior mean (Mean), standard deviation (S.d.), Monte Carlo error (MC error), 2.5^th percentile, median, and 97.5^th percentile of the posterior samples (labeled as 2.5%, Median, and 97.5%, respectively), while the difference between the last two items is the 95% credible interval, and relative risk (RR) computed as the exponential of corresponding posterior mean. As explained in the “Methods” section, regions (or time periods) with RR>1 are where (or when) disease counts are higher than expected. In Table 3, RR is expressed as percentages, so the difference between the RR and 100% is interpreted as impact (either positive or negative) of the time periods or type of misalignment to the RR.

Table 3.

Posterior estimates of model parameters

	Parameter	Mean	S.d.	MC error	2.5%	Median	97.5%	RR(%)
Time-varying Intercepts By years	1995	-0.289	0.155	0.0026	-0.592	-0.290	0.015	74.8
	1996	-0.339	0.159	0.0025	-0.662	-0.338	-0.038	71.3
	1997	-0.049	0.167	0.0033	-0.380	-0.048	0.280	95.3
	1998	-0.294	0.169	0.0031	-0.631	-0.291	0.032	74.8
	1999	-0.641	0.194	0.0035	-1.027	-0.641	-0.261	52.7
	2000	-0.330	0.157	0.0024	-0.633	-0.332	-0.018	71.7
	2001	-0.270	0.154	0.0024	-0.576	-0.269	0.032	76.4
	2002	-0.037	0.156	0.0033	-0.346	-0.036	0.268	96.5
	2003	0.227	0.140	0.0028	-0.055	0.229	0.500	125.7
	2004	0.289	0.133	0.0027	0.029	0.290	0.549	133.6
	2005	0.489	0.127	0.0029	0.237	0.490	0.737	163.2
Effect of misalignment	increase	0.060	0.218	0.0041	-0.370	0.061	0.488	106.3
	decrease	-0.406	0.222	0.0046	-0.850	-0.406	0.029	66.6
	new	-0.202	0.176	0.0036	-0.546	-0.203	0.144	81.6
	removal	0.183	0.311	0.0052	-0.432	0.182	0.797	120.0
Precision	Spatial	148.0	359.8	16.55	1.640	9.146	1092.0	----
	Noise	34.93	161.6	7.38	4.031	7.584	413.1	----

For the fixed effects of time-varying intercepts and misalignment effects, the sign (positive or negative) and the size of the parameters indicate the direction and magnitude of the time effects. The intercepts can be interpreted as the logarithm of the relative risk of amphetamine abuse or dependence hospital discharge over the entire city at different years after adjusting for the random noise and the spatial dependence structure. Over the 11-year study period, Year 1999 had the lowest RR (47.3% lower than expected), and Year 2005 had the highest RR (63.2% in excess of expected). These values represent a unique aspect of our modeling approach and could not be assessed without this analysis.

Of special interest in the table are the effects of different types of misalignment. Of the four types of ZIP code misalignment, i.e., size increase, size decrease, newly created ZIP codes, or removal of a ZIP code, size decrease has a marginally negative impact on the relative risk. Of those ZIP codes undergoing size decrease, the relative risk is 33% lower than the average of all the ZIP codes across the 11-year study period. Inclusion of the misalignment types in the model allows us to claim reduced biases in the estimates of the change of amphetamine abuse or dependence. A detailed inspection into the types of misalignment reveals that size decrease mainly occurred during the 1997 – 1999 period when small ZIP codes in the outskirts of the city changed boundaries. It is unclear whether the decreasing trend in standardized incidence ratio (ratio of observed counts to expected counts) was due to the population or other socio-economic change in these ZIP codes. But a reasonable conjecture is that ZIP codes undergoing size decrease are those where rapid growth among low risk populations takes place.

Turning to temporal trends, Figure 3 plots the posterior mean and the credible intervals (difference between the 2.5^th and 97.5^th percentile of the posterior estimates) of the time intercepts at each year. The temporal change is obvious in the plot. While there is an overall increasing trend throughout the 11-year period, Year 1999 has the lowest mean intercept and the highest variability in the estimate (the widest credible interval shown in the figure).

Figure 3.

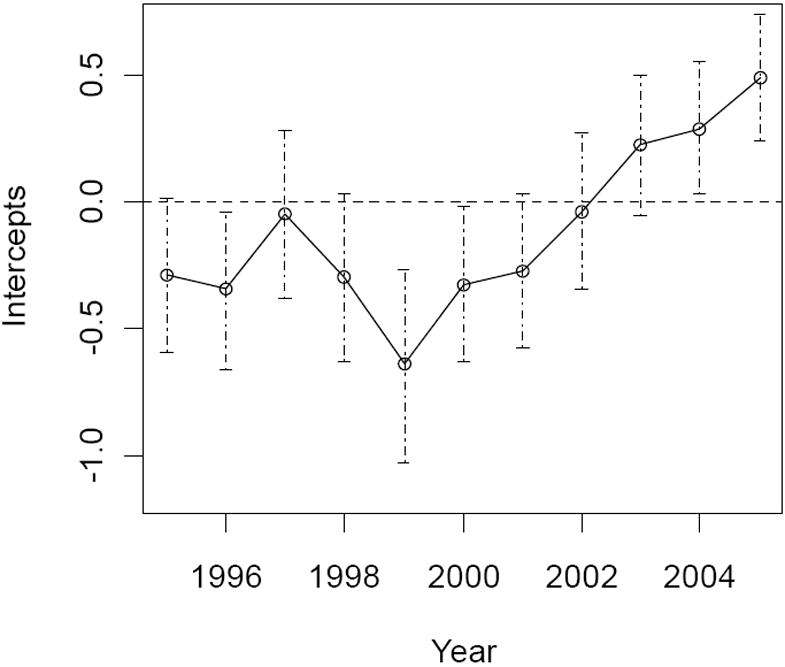
Intercepts and the credible intervals in the study period

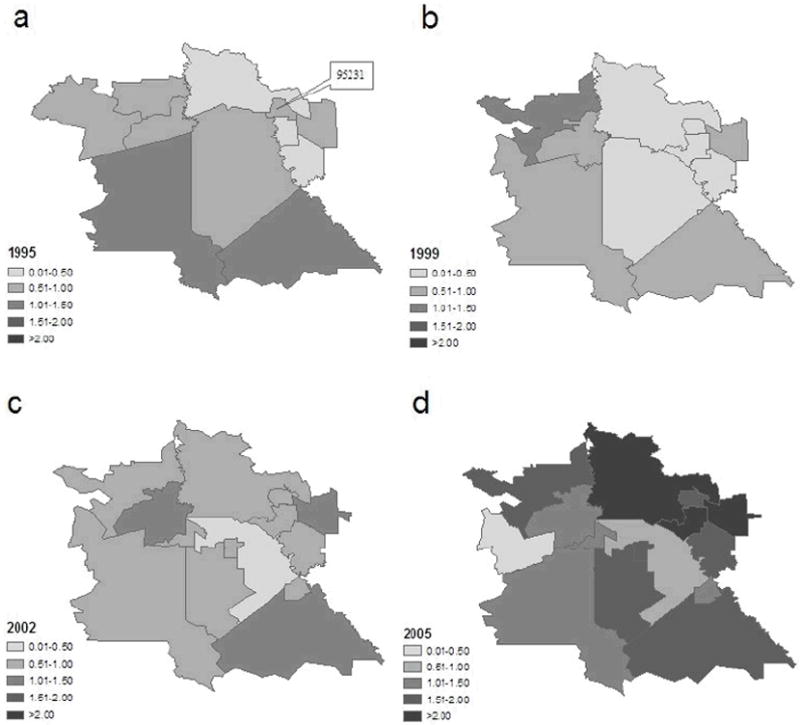
Figure 4 maps the crude standardized incidence ratio of amphetamine abuse or dependence HDD in the study area for the beginning and the ending years 1995 and 2005, and the lowest year 1999 and a middle year 2002. The standardized incidence ratio (SIR) is the crude ratio of observed counts to expected counts. As described in the Methods section, expected counts are thought of as fixed and proportional to the known population. No covariate or random effect is considered in their calculation. The value 1 serves as a reference value where observed and expected counts are the same. Areas with SIR>1 have larger observed counts than expected. Shift of the spatial distribution pattern is clear in these maps – in the beginning of the study period, the crude SIR is higher in the southern/southeastern part of the city; in Year 2005, the higher SIR areas move to the north. Overall, the SIR increases steadily (i.e., the maps become darker) during the study period.

Figure 4.

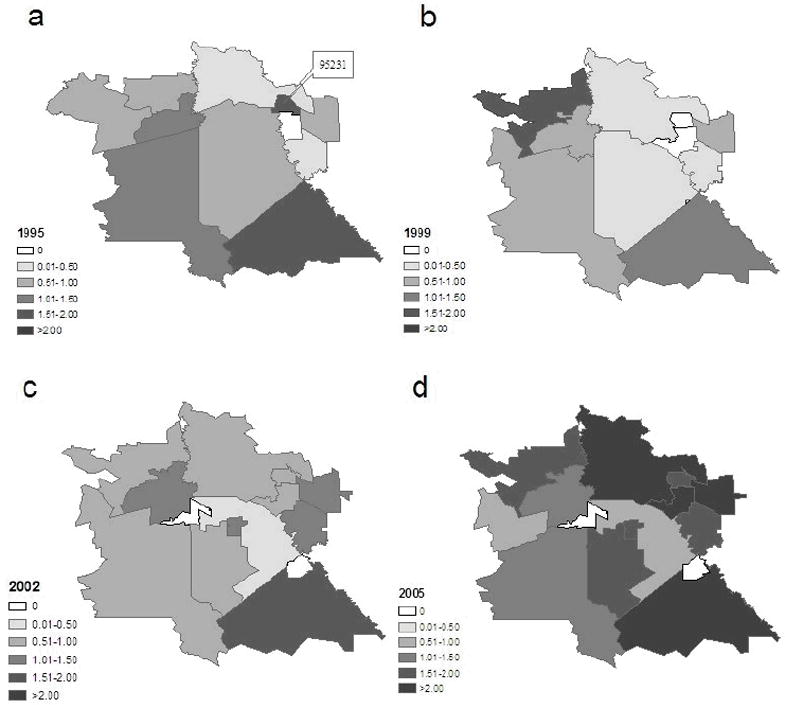
Crude standard incidence ratio (SIR) in Tracy in Years 1995, 1999, 2002, and 2005

Some extreme values do exist. A small ZIP code (95385) in the southeast part of the city observed amphetamine abuse/dependence over 8 times higher than expected in years 2001 and 2004 (not shown on the maps). In the maps of 1999, 2002, and 2005, several small ZIP codes are shown to have SIR = 0, indicating the locations where there were no observed disease counts. Since the crude maps were developed without consideration of covariate or spatial dependence structure, it is typical to observe the sort of high variability shown in Figure 4, representing statistical imprecision due to the limited data informing each local estimate.

Figure 5 presents the maps of the model-based median fitted incidence ratio of amphetamine abuse or dependence HDD in the study area for the same time points as in Figure 4. The fitted incidence ratio is also represented by the local measure of relative risk at each ZIP code, calculated as the exponential of μ_i in equation (2). This index accounts for information on all three aspects of the fixed effects, the unstructured heterogeneity random effect, and the spatial dependence effect. The overall increasing trend remains clear in the maps (i.e., the maps become darker). The figure clearly shows characteristic Bayesian “borrow of information” where local estimates represent a compromise between the estimate based on the limited local data alone, and data from surrounding areas. The result is “shrinkage” of the crude rate toward the average rate of the neighboring areas. In particular, no ZIP code is now assigned a value of exactly zero. Instead, the small ZIP codes with the crude SIR=0 now have estimates more similar to their nearby regions. The extremely high values of over 8 in ZIP code 95385 for the years 2001 and 2004 have been substantially reduced to 0.94 in 2001 and 0.67 in 2004 (not shown on the map). The high values in the northern part of the city remain high in Year 2005. There also appears to be some tendency for local clustering of similar values, the outcome of the CAR(λ) component of the model. For example, in 1995, the crude SIR in a small ZIP code 95231 in northeastern part of the study area is 1.71 (Figure 4), but the fitted SIR is changed to 0.91 (Figure 5) due to lower levels in the neighbors.

Figure 5.

Fitted standard incidence ratio (SIR) in Tracy in Years 1995, 1999, 2002, and 2005

Figure 6 reveals patterns of variability in the fitted SIR. Mapped here are credible intervals (difference between the 97.5^th percentile and the 2.5^th percentile of the posterior estimates) of the fitted SIR values. As the overall fitted SIR values increase over time (Figure 5), the variability is also increasing somewhat (maps appear darker), as we would expect for the Poisson likelihood. This variability is smallest for high-population ZIP codes, even if the areas of the ZIP codes are small, such as ZIP code 95376 in Year 2005. For areas with smaller population density (e.g. ZIP code 95385 in Year 2005), the variability in the SIR estimates is the highest.

Figure 6.

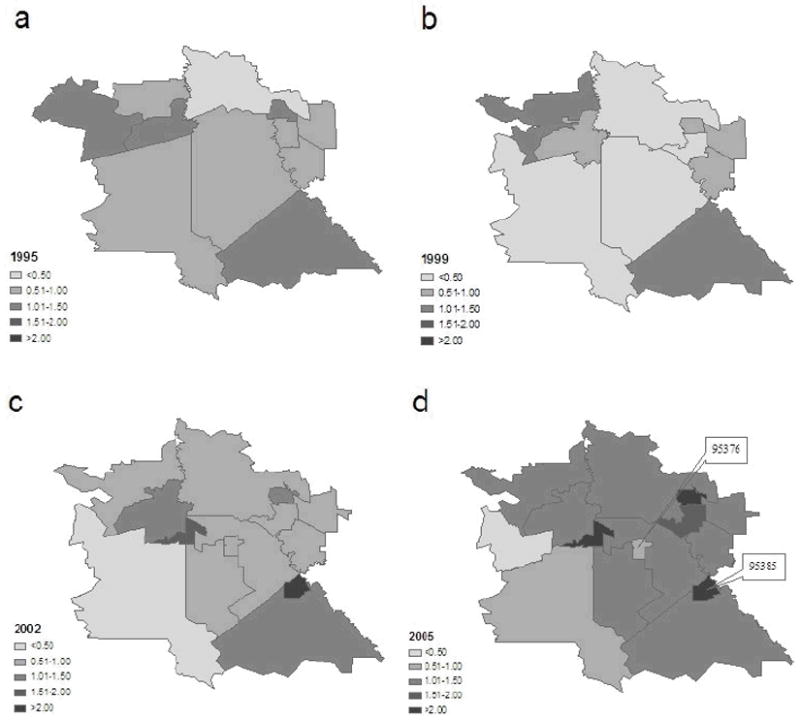
Width of credible intervals of SIR in Tracy in Years 1995, 1999, 2002, and 2005

Conclusions and Discussion

In this paper we develop a method to handle a common problem of misaligned spatial data units in small area rate estimation. A typical spatio-temporal approach treats the data as a regular matrix with rows and columns indexing spatial and temporal units. In a misaligned data set where the number and shape of spatial unit changes across time points, the data are no longer a regular matrix with fixed number of columns in each row. Instead, we propose a data vector approach and adjust the spatial auto-correlation structure in the Bayesian hierarchical model to reach estimates for the misaligned data. A three-level Bayesian hierarchical modeling approach is presented in this paper to model the spatio-temporal pattern of amphetamine abuse or dependence in Tracy, California. The first level defined the likelihood of the occurrence of amphetamine abuse or dependence following a Poisson distribution. Level 2 modeled the logarithm of relative risk as a linear combination of three components which accounted for fixed effects of ZIP code misalignment and time-dependent intercepts, random effects of unstructured heterogeneity and spatial dependence, allowing both extra-Poisson variation and spatial correlation, respectively, in our observed counts. At level 3, non-informative hyperprior distributions were assigned to the precision parameters for the random effects. Using the Deviance Information Criterion, we compared four models that included/excluded the two random terms and selected the full model including both unstructured and spatial dependence random effects as the model with the best fit. The ZIP code level random effects included both a spatial dependence and an unstructured heterogeneity effect, indicating the value of a Bayesian hierarchical framework where different formats of random effects and fixed effects are considered.

Compared to conventional statistical inference models, which derive point and interval estimates for parameters, hierarchical Bayesian modeling can produce full inference in parameters by taking into account heterogeneity effects, spatial autocorrelation, and covariate effects. A hierarchical Bayesian approach is effective in estimating spatial crude risks from data with high variability and uncertainty, and extracts realistic spatial and temporal trends from noisy data. As seen in our analysis, the use of small units can cause unstable risk estimates due to small local sample sizes and result in noisy maps. The model-based smoothing induced by our approach helps reduce local noise and visualize the underlying spatial and temporal patterns. The Bayesian modeling approach we applied here demonstrated that the approach behaves as expected since the fitted SIR map based on the posterior estimates preserves the high-risk areas while smoothing out variability in low-population areas.

A major contribution of the current study is to demonstrate the feasibility of handling misaligned ZIP codes through hierarchical spatio-temporal models in the area of illicit drug abuse or dependence. Biases induced by artificial rezoning of ZIP codes are estimated and in the study area of Tracy, California, the time-dependent amphetamine abuse or dependence rate estimates would have been lower if not corrected for ZIP code misalignment. Uncertainty associated with misaligned data is modelled, quantified, and visualized. The Bayesian hierarchical modelling approach provides the methodology to incorporate complex data with spatial dependence. Freely available software such as WinBUGS/GeoBUGS enables wider use of the developed methods.

Future work should include local covariates to explore the impact of spatial and temporal variations in risk factors as potential explanatory variables in defining the observed patterns. Given the framework developed here, adding confounding variables will involve expanding the X matrix in equation (2) to include the variables, and then the coefficient vector β will include both time intercepts and the fixed effects of those variables. It will be feasible to revise the code and add extra terms for covariates. In addition, we may also wish to model spatial and temporal variations in the strength of association with certain covariates as in geographically weighted regression or varying coefficient models (Waller et al. 2007). In both cases, the basic structure above provides the framework for such extensions and a basis for many further analyses.