Predictions of diotic tone-in-noise detection based on a nonlinear optimal combination of energy, envelope, and fine-structure cues

Abstract

Tone-in-noise detection has been studied for decades; however, it is not completely understood what cue or cues are used by listeners for this task. Model predictions based on energy in the critical band are generally more successful than those based on temporal cues, except when the energy cue is not available. Nevertheless, neither energy nor temporal cues can explain the predictable variance for all listeners. In this study, it was hypothesized that better predictions of listeners' detection performance could be obtained using a nonlinear combination of energy and temporal cues, even when the energy cue was not available. The combination of different cues was achieved using the logarithmic likelihood-ratio test (LRT), an optimal detector in signal detection theory. A nonlinear LRT-based combination of cues was proposed, given that the cues have Gaussian distributions and the covariance matrices of cue values from noise-alone and tone-plus-noise conditions are different. Predictions of listeners' detection performance for three different sets of reproducible noises were computed with the proposed model. Results showed that predictions for hit rates approached the predictable variance for all three datasets, even when an energy cue was not available.

INTRODUCTION

Detecting signals in noise is important for everyday activities, such as detecting speech in background noise and discriminating sounds in noisy environments. People with hearing loss have difficulty communicating in background noise even when using hearing aids. Thus, it is essential to understand how people with normal hearing can detect signals in noise in order to help design more effective hearing-aid devices. Tone-in-noise detection has been studied for decades as a stepping stone to find the cues that listeners use to detect more complex sounds in noise.

In early tone-in-noise detection studies, noise waveforms were generated randomly for each trial such that no waveform was tested twice (Blodgett et al., 1958, 1962; Dolan and Robinson, 1967). Detection performance was averaged across listeners and waveforms. However, Gilkey et al. (1985) found that detection performance varied among listeners and waveforms by inspecting the detection performance for a set of pre-generated waveforms. Because these waveforms were stored and could be “reproduced” exactly, they were referred to as reproducible noises. Using reproducible noise waveforms it is possible to compare each listener's detection performance for individual waveforms and to make detailed tests of different model predictions.

In detection tests, listeners' performance is described by the proportion of correct identification of tone presence for tone-plus-noise waveforms (hit rate), and the proportion of “tone present” responses for noise-alone waveforms (false-alarm, FA rate). The set of hit and FA rates for a given ensemble of reproducible noise maskers has been referred to as a detection pattern (Davidson et al., 2006).

In order to identify the cues used by listeners to detect a tone in noise in the diotic condition, several single-cue models based on energy or temporal cues have been used to predict listeners' detection patterns. In each model, a set of decision variables (DVs) that represent a particular feature of the corresponding reproducible waveforms is compared with the listeners' detection patterns. A description of several models in the literature is presented below. In particular, several commonly used energy and temporal cues and their performance in predicting listeners' detection patterns are described.

The critical-band model (CB; Fletcher, 1940) focuses on energy within a critical bandwidth of the tone frequency, whereas the multiple-detector model (MD; Gilkey and Robinson, 1986) considers energy within and outside a critical bandwidth. Although these energy-based models provide satisfactory predictions of the detection patterns, the CB model fails at predicting the roving-level stimulus condition, in which the level of stimulus is randomly varied for each trial (Kidd et al., 1989). Because the CB model predictions are based on the absolute energy within one filter bandwidth and stimulus levels are not fixed in each trial, “tone presence” would be predicted for a high-level noise-alone stimulus. The MD model is robust for roving-level noises and yields significantly better predictions than the CB model for most listeners in the wideband condition; however, the MD model computations involve fitting to the data (Davidson et al., 2009a). Fitting the data was avoided in this study in order to achieve a generic model for different types of stimuli and to prevent the risk of over-fitting the data, i.e., adjusting the parameters of variables for individual listeners to better match each detection pattern. In addition, the MD model is not applicable for waveforms whose bandwidths are smaller than one critical bandwidth, because this model requires comparison of energy in different frequency bands. Thus, the CB model was used to describe the energy cue in this study.

Two types of temporal cues are robust to the roving-level condition: envelope and fine-structure. The envelope-slope model (ES; Richards, 1992; Zhang, 2004; Davidson et al., 2006) examines the changes in envelope fluctuations. Adding a tone to a narrowband noise results in a decrease in envelope fluctuations, thus lower values of the DV for the ES model indicate a tone-plus-noise waveform. This model can be applied to wideband noises because the output of narrowband cochlear filters is analyzed in the model computation.

The phase-opponency model (PO; Carney et al., 2002), based on fine-structure, i.e., the fast fluctuations in the stimulus, uses responses from a coincidence detector that receives inputs from two model auditory-nerve fibers to predict tone presence. Because the two auditory-nerve fibers are tuned to frequencies symmetrically located around the tone frequency and have phase responses that differ by 180° at the tone frequency, the addition of a tone to a noise waveform yields fewer spike responses from the coincidence detector. Therefore, a lower value of the DV for the PO model indicates a tone-plus-noise waveform. In addition to the ES and PO models, the Dau et al. (1996a) and Breebaart et al. (2001) template-matching models also use temporal cues. In these models, detection results are based on comparing the internal test waveform representation with the pre-stored waveform representation in the template. However, previous studies have shown that these template-matching models do not yield predictions that were significantly correlated to the detection patterns for the ensemble of reproducible waveforms used in this study (Davidson et al., 2009a). Thus, the ES and PO models were used to evaluate the temporal features of the stimulus waveforms in this study.

Although previous studies have reported that correlations between predictions of some diotic models and listeners' detection patterns are statistically significant, the amounts of variance in the detection patterns that are explained by these models are substantially lower than the predictable variance (Davidson et al., 2009a). The predictable variance is computed as the squared mean of the correlations between detection patterns of individuals and those of the average listener (the mean of the detection patterns from individual listeners). Detection patterns differ for each listener; the predictable variance describes the proportion of the variation in detection patterns that is common among all listeners. Thus, the predictable variance is used as a benchmark for model predictions.

The goal of this study was to test the hypothesis that significantly better predictions for diotic detection could be obtained by using models that combine different cues, i.e., multiple-cue models. Given that different cues represent different features of a waveform, it is reasonable to argue that the combination of different cues can capture more information about a waveform than any single cue. Davidson et al. (2009b) reported that a multiple-cue model, based on a linear combination of envelope and fine-structure cues, results in poor predictions of listeners' detection patterns. However, energy and temporal cues are correlated, and a simple linear combination of cues is ineffective in characterizing the interaction among cues (Davidson et al., 2009a).

In this study, a nonlinear multiple-cue model was proposed to predict listeners' detection patterns, where the model takes into account the statistical correlations among energy and temporal cues in cue combination. The likelihood ratio test (LRT) is an optimal detector for a two-alternative (binary) hypothesis testing (Van Trees, 1968) and is thus a useful tool for tone-in-noise detection data. The LRT-based detection model has previously been used by Siebert (1970), Colburn (1973), and Heinz et al. (2001) to predict frequency, interaural time, and level discrimination data, respectively, based on model auditory-nerve responses. In this study, the DV of the nonlinear multiple-cue model was computed as the logarithmic likelihood ratio of cue values given tone-plus-noise and noise-alone waveforms. Distributions of the values of single cues were computed from a set of randomly generated noise-alone and tone-plus-noise waveforms that was different from the reproducible waveforms used for the detection task. Because of the difference between the covariance matrices of cue values for noise-alone and tone-plus-noise waveforms, the expression for the DV is a quadratic function in terms of cue values, implying a nonlinear combination of cues. In addition, the DV also includes cross-products of single cues that characterize the pair-wise interactions between cues.

In summary, a nonlinear cue-combination model which optimally combines energy, envelope, and fine-structure cues is presented in this study. It was shown that model predictions based on the nonlinear multiple-cue model improved significantly compared with those based on single-cue or linear multiple-cue models.

DESCRIPTION OF DATA

The diotic detection data was obtained from three previous experiments (Evilsizer et al., 2002; Davidson et al., 2006; Davidson et al., 2009b). Tone frequency was 500 Hz in all three datasets, and listeners were tested at tone levels near their detection threshold (i.e., an overall d′ = 1). In the first two studies, the same set of 25 reproducible noise waveforms was used, and eight listeners were tested. The duration of the noise waveforms was 300 ms, and the sound level was 40 dB sound pressure level (SPL). Both narrowband (452–552 Hz) and wideband (100–3000 Hz) noises were tested. The spectral content of the narrowband waveform was matched to the corresponding frequency range of the wideband waveform. In the third study, 50 equal-energy reproducible noise waveforms with 100-ms duration, 40 dB SPL, and narrower bandwidth (475–525 Hz) were used (baseline and control stimulus sets as described by Davidson et al., 2009b). Six listeners were tested in that study. In the present study, this dataset based on equal-energy stimuli was useful to test whether model predictions depended more on temporal cues in the absence of the energy cue.

In all studies, listeners responded whether they perceived a tone after each single-interval trial of a noise-alone or tone-plus-noise waveform. Detection patterns were described in terms of hit and FA rates, based on listeners' responses of “tone presence” (details of the experiments can be found in Evilsizer et al., 2002; Davidson et al., 2006; and Davidson et al., 2009b).

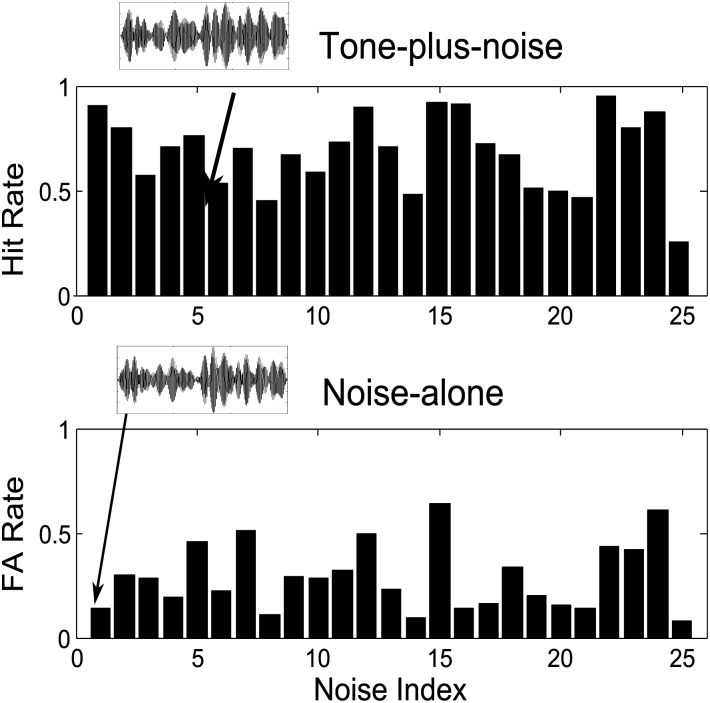
Figure 1 shows the detection pattern of the average listener (i.e., the average detection pattern across all individual listeners) for the 100-Hz bandwidth waveforms in the Evilsizer et al. (2002) and Davidson et al. (2006) studies. The detection patterns were consistent over the course of the experiment and were also significantly correlated across listeners. The goal of this study was to predict the variation in the average listener's detection pattern across the set of reproducible noises. Because the detection patterns were significantly correlated among individual listeners, these listeners were assumed to be using similar cues for tone-in-noise detection. Model predictions of the response of the average listener focused on explaining the common variance across listeners' performance while ignoring individual differences, which cannot be accounted for by a single model. The quality of the prediction was described as the proportion of variance in the detection pattern that was explained by a given model.

Figure 1.

The detection pattern of the average listener comprises hit and FA rates for each 100-Hz bandwidth reproducible waveform averaged across eight individual listeners. The x axis shows the index of the reproducible noise waveforms. The insets show examples of tone-plus-noise (top) and noise-alone (bottom) waveforms (data from Evilsizer et al., 2002; and Davidson et al., 2006).

METHODS

It was hypothesized that better predictions of reproducible-noise detection patterns could be achieved using nonlinear multiple-cue models that consider statistical correlations among different cues. First, the energy, envelope, and fine-structure cues used in the cue combination step will be introduced. Next, the statistical correlations between energy and temporal cues are examined for the three datasets. Last, both the nonlinear LRT-based multiple-cue and the linear multiple-cue models will be described.

Energy and temporal cue models

The CB (Fletcher, 1940) model, which is based on energy within a critical bandwidth of the target frequency, was used in the current study. The DV was computed as the root mean square (RMS) of a fourth-order gamma-tone filtered waveform (centered at 500 Hz) for all three datasets: $CB={\left\{{\int }_{T}G{\left[x(t)\right]}^{2}dt/T\right\}}^{1/2}$, where x(t) indicates the stimulus waveform, and G(.) represents the response of the gammatone filter.

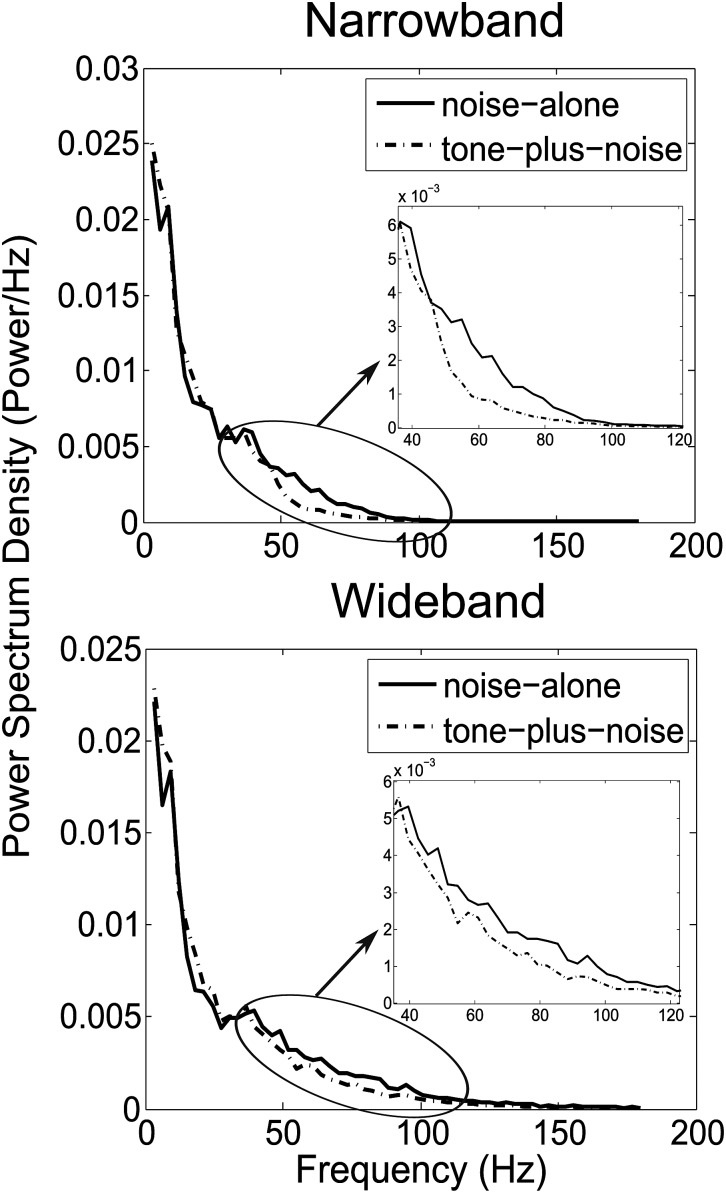
Two temporal models were used: the ES (Richards, 1992; Zhang, 2004; Davidson et al., 2006) and PO (Carney et al., 2002) models. DVs of the ES model were based on changes in envelope fluctuations. The envelope was computed from the Hilbert transform of a fourth-order gamma-tone filtered stimulus (centered at 500 Hz). The DV value is reduced by addition of the tone for the ES model because envelope fluctuation decreases. Figure 2 illustrates the averaged distribution of envelope energy for noise-alone (solid lines) and tone-plus-noise (dotted lines) stimuli in the frequency domain. The insets show enlarged views of the circled frequency region that yield the largest differences in the envelope magnitude between noise-alone and tone-plus-noise stimuli. The ES model was modified in the current study to emphasize this frequency range by substituting the low-pass envelope filter (cutoff frequency at 250 Hz) with a sixth-order bandpass envelope filter centered at 120 Hz (Q = 1). The computation of the modified ES cue is

$$\text{ES}={\int }_T\left|H\left[G\left(x(t)\right)\right]-H\left[G\left(x(t+\Delta t)\right)\right]\right|dt/{\left\{{\int }_{T}H{\left[G\left(x(t)\right)\right]}^{2}dt/T\right\}}^{1/2},$$

where x(t) indicates the stimulus waveform, G(.) represents the response of the gammatone filter, and H(.) is the envelope extracted using the Hilbert transform. The bandpass envelope filter, which is similar to physiological and psychological modulation filters, was applied to extract frequency components in the range illustrated. In addition, this filter attenuated low frequencies, which contain more energy but less information about the presence of the tone. The modified ES model, compared with the original ES model, could predict 20% and 10% more of the variance in hit and FA rates, respectively, for the average listener's narrowband detection patterns; whereas predictions from the modified ES model explained 10% less of the variance for the wideband hit rates than the original ES model, with no change in the FA rates (Davidson et al., 2009a).

Figure 2.

Envelope power spectrum density of noise-alone (solid lines) and tone-plus-noise (dotted lines) stimuli in narrowband (top) and wideband (bottom) conditions. Insets show an enlarged view of the circled frequency range where the largest difference of the envelope spectral energy between these two stimuli is observed.

The PO model extracts fine-structure information from the stimuli using a coincidence detector that receives inputs from two model auditory-nerve fiber responses: $PO={\int }_T{A}_{N1}\left[x(t)\right]\cdot A_{N2}\left[x(t)\right]dt$, where x(t) indicates the stimulus waveform, and A_N1 and A_N2 denote auditory-nerve models with two different characteristic frequencies. Because tone responses from the two model auditory-nerve fibers differ in phase by 180°, low DV values for the PO model indicate tone-plus-noise waveforms.

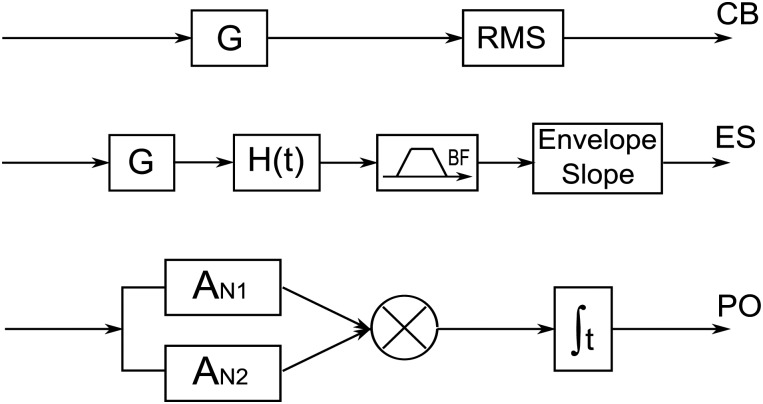
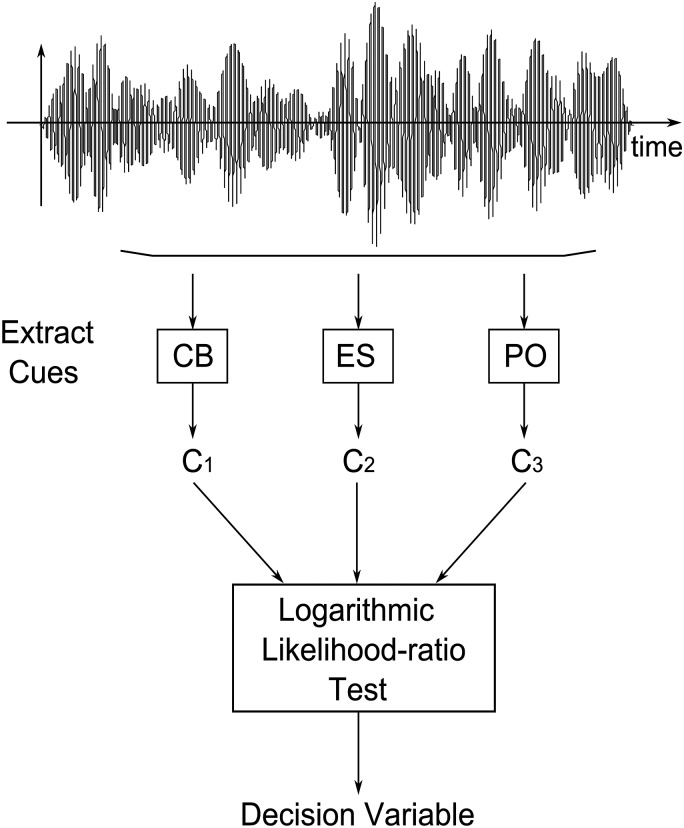
Figure 3 shows the three models that extract the single cues used in this study: the energy cue (the CB model), envelope cue (the ES model), and fine-structure cue (the PO model).

Figure 3.

A schematic diagram of the CB, ES, and PO models used to extract energy and temporal cues. In the CB model, DV was computed as the root mean square (RMS) of a fourth-order gamma-tone filtered waveform (center frequency 500 Hz, bandwidth equaled one critical bandwidth of tone frequency). In the ES model, the envelope of a waveform was computed using a Hilbert transform of a gamma-tone filtered waveform, and the DV was calculated as the slope of a band-pass filtered envelope. In the PO model, responses from two model auditory-nerve fibers that differed in phase by 180 degrees in response to the tone were applied to a coincidence detector, and the DV was computed as the integral of the coincidence detector responses.

Statistical correlations between energy and temporal cues

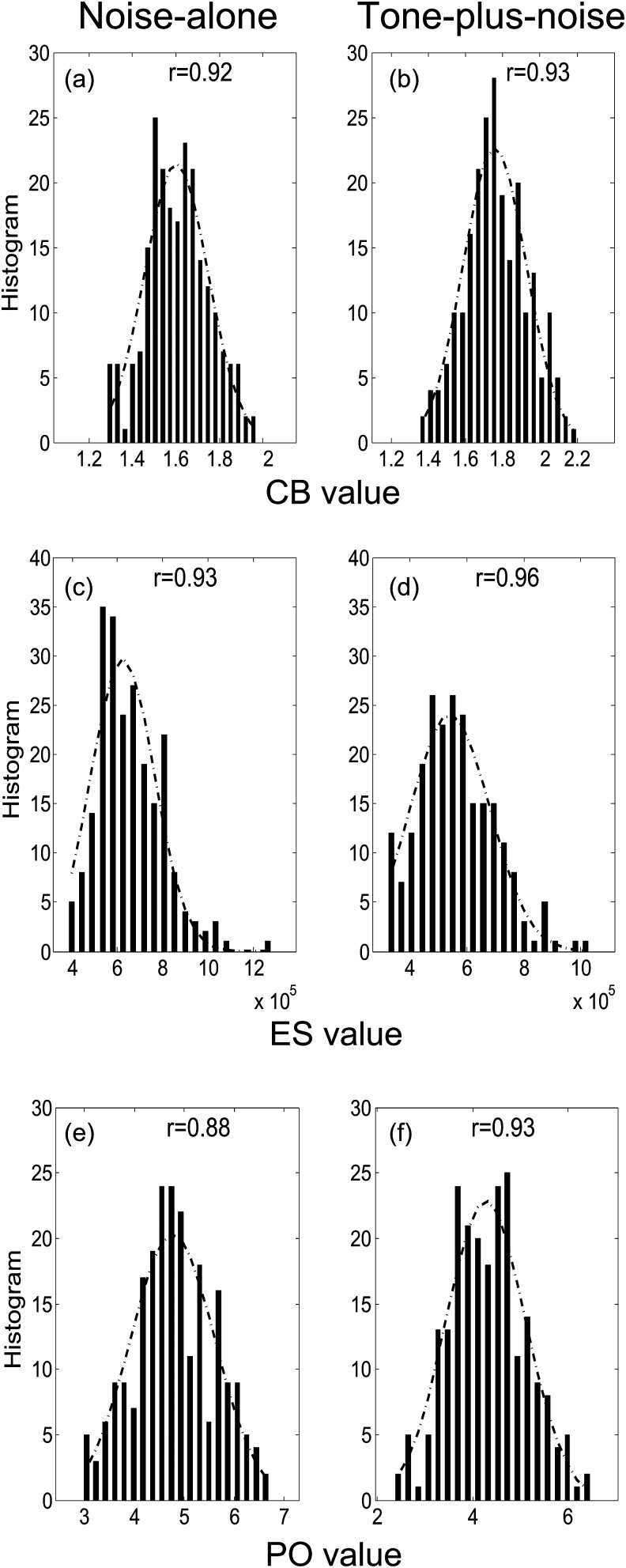
In order to investigate the relationship among different cues, the dependencies between pairs of cues were analyzed by computing the Pearson product-moment correlation coefficients between the DVs (Neter et al., 1996). Table TABLE I. shows the correlations of DVs for tone-plus-noise and noise-alone reproducible waveforms for the three conditions; bold values indicate DV pairs that are significantly correlated (p < 0.05, t-test). For the computations in Table TABLE I., the tone level was matched to the average listener's threshold. The two temporal DVs (ES and PO) were correlated in each dataset; the energy (CB) and temporal DVs were also correlated, except for the fine-structure cue in some conditions (Table TABLE I.). Furthermore, both energy and temporal DVs had distributions that were approximately Gaussian. In Fig. 4, the distributions of each DV are shown for large sets (n = 200) of randomly generated 100-Hz bandwidth noise-alone and tone-plus-noise waveforms, and the dotted lines show the corresponding Gaussian fits. The correlation between the DV distribution and the fitted Gaussian curve is shown at the top of each panel. The distribution of hits for the ES cue is slightly asymmetric; however, the correlation between the distribution and its Gaussian fit is high (r = 0.93). Distributions of cue values for randomly generated 2900- and 50-Hz equal-energy waveforms were also approximately Gaussian (not shown). In addition, further analysis was done to investigate whether the statistical distributions of cue values were Poisson-like. Results showed that the mean values were significantly different from the variance of the distributions for each cue, thus the cues did not have Poisson distributions.

TABLE I.

Correlations between energy and temporal DVs for three datasets. The bold values indicate that two DVs are significantly correlated (p < 0.05, r > 0.40 for n = 25 and r > 0.28 for n = 50), and n denotes the number of waveforms in each study.

	2900-Hz waveforms (n = 25)				100-Hz waveforms (n = 25)				50-Hz waveforms (n = 50)
	Envelope (ES)		Fine-structure (PO)		Envelope (ES)		Fine-structure (PO)		Envelope (ES)		Fine-structure (PO)
Name of cues	Hit	FA	Hit	FA	Hit	FA	Hit	FA	Hit	FA	Hit	FA
Energy (CB)	0.69	0.60	0.36	0.58	0.55	0.48	0.15	0.35	0.55	0.52	0.51	0.19
Envelope (ES)	__	__	0.48	0.74	__	__	0.48	0.79	__	__	0.75	0.65

Figure 4.

DV distributions for 200 randomly generated narrowband noise-alone (left column) and tone-plus-noise (right column) waveforms. The x axis shows the cue values and the y axis shows the number of instances in each bin in the histogram (20 bins in total). The label onthe x axis shows the model names. Panels in each row show the distributions of the DVs for the CB (panel a and b), ES (panel c and d), and PO (panel e and f) cues. In each panel, the dotted line represents a Gaussian fit to the DV distribution, and the r value at the top indicates the correlation between the DV distribution and the Gaussian fit.

Decision variable of the nonlinear LRT-based multiple-cue model

The DV of the test waveform was calculated from the logarithmic LRT of its cue values assuming the test waveform belonged to noise-alone ($x=N$) and tone-plus-noise ($x=S$) categories. Eq. 1 shows the nonlinear combination of energy and temporal cues, in which $\mathbf{c}={[c_1,c_2,c_3]}^T$ denotes the vector of cue values for the test waveform, $c_1$ denotes the energy cue (CB), $c_2$ denotes the envelope cue (ES), and $c_3$ denotes the fine-structure cue (PO), and n represents the number of cues (n = 3 in this study):

$$\begin{array}{c}D\left(\mathbf{c}\right)=\log \left(\frac{P\left(\mathbf{c}|S\right)}{P\left(\mathbf{c}|N\right)}\right)\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\text{and}\\ P\left(\mathbf{c}|x\right)=\frac{1}{\sqrt{{\left(2\pi \right)}^n\det \left({\mathbf{\Sigma }}_{x,r}\right)}}\exp \left(-\frac{1}{2}{\left(\mathbf{c}-{\mathbf{\mu }}_{x,r}\right)}^T{{\mathbf{\Sigma }}_{x,r}}^{-1}\left(\mathbf{c}-{\mathbf{\mu }}_{x,r}\right)\right)\hspace{0.17em},\\ \text{where}\hspace{0.17em}x\in \left\{S,N\right\},\hspace{0.17em}\text{and}\hspace{0.17em}{\mathbf{\mu }}_{x,r}=E\left[{\mathbf{c}}_{x,r}\right],\hspace{0.17em}\text{and}\hspace{0.17em}{\mathbf{\Sigma }}_{x,r}=E\left[\left(\mathbf{c}-{\mathbf{\mu }}_{x,r}\right){\left(\mathbf{c}-{\mathbf{\mu }}_{x,r}\right)}^T\right]\hspace{0.17em}.\end{array}$$ (1)

$P(\mathbf{c}\hspace{0.17em}|\hspace{0.17em}x)$ represents the conditional probability of cue values (c) given that the testing waveform belongs to category x (x = N or x = S). Because the single-cue DVs were correlated and their values had Gaussian distributions (Fig. 4), the conditional probability was computed using a multivariate Gaussian distribution. The term of ${\mathbf{\mu }}_{x,r}$ denotes the expected value of the cue vector (${\mathbf{c}}_{x,r}$) for category x computed from the randomly generated waveforms, where r indicates the randomly generated waveforms. The covariance matrix ${\mathbf{\Sigma }}_{x,r}$ characterizes the statistical correlations among different cues; ${\mathbf{\Sigma }}_{S,r}$ and ${\mathbf{\Sigma }}_{N,r}$ are different because the correlations among different cues vary for noise-alone and tone-plus-noise waveforms. Given that $P(\mathbf{c}\hspace{0.17em}|\hspace{0.17em}S)$ and $P(\mathbf{c}\hspace{0.17em}|\hspace{0.17em}N)$ have multivariate Gaussian distributions, the logarithmic LRT in Eq. 1 can be described as

$$D\left(\mathbf{c}\right)=\frac{1}{2}\log \left(\frac{\det \left({\mathbf{\Sigma }}_{N,r}\right)}{\det \left({\mathbf{\Sigma }}_{S,r}\right)}\right)\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}-\frac{1}{2}{\left(\mathbf{c}-{\mathbf{\mu }}_{S,r}\right)}^T{\mathbf{\Sigma }}_{S,r}^{-1}\left(\mathbf{c}-{\mathbf{\mu }}_{S,r}\right)+\frac{1}{2}{\left(\mathbf{c}-{\mathbf{\mu }}_{N,r}\right)}^T{\mathbf{\Sigma }}_{N,r}^{-1}\left(\mathbf{c}-{\mathbf{\mu }}_{N,r}\right)\hspace{0.17em}.$$ (2)

On the right-hand side of Eq. 2 a quadratic function in terms of the cue values was obtained because ${\mathbf{\Sigma }}_{S,r}$ and ${\mathbf{\Sigma }}_{N,r}$ are different. Thus, the current model is a nonlinear combination of different cues.

The logarithmic likelihood-ratio test is an optimal detector for a two-alternative detection problem (Van Trees, 1968). This test can be interpreted as testing whether the waveform is more likely to contain a tone or not. Specifically, because the prior probabilities of given noise-alone or tone-plus-noise waveforms are equal [$P(N)=P(S)$], a DV with a value greater than zero suggests that the current waveform is a tone-plus-noise stimulus; a DV with a value less than zero suggests that the current waveform is a noise-alone stimulus. The nonlinearity of the LRT model is guaranteed as long as the covariance matrices from noise-alone and tone-plus-noise waveforms are different. Assuming that the two covariance matrices were the same, then the first term in Eq. 2 would be zero and the second-order term of cue values would cancel out; thus, this equation would become a linear combination of cue values, as

$$D(\mathbf{c})=\left({\mathbf{\mu }}_{S,r}^T-{\mathbf{\mu }}_{N,r}^T\right){\mathbf{\Sigma }}^{-1}\mathbf{c}+\frac{1}{2}{\mathbf{\mu }}_{N,r}^T{\mathbf{\Sigma }}^{-1}{\mathbf{\mu }}_{N,r}-\frac{1}{2}{\mathbf{\mu }}_{S,r}^T{\mathbf{\Sigma }}^{-1}{\mathbf{\mu }}_{S,r},$$ (3)

where Σ = ${\mathbf{\Sigma }}_{S,r}$ = ${\mathbf{\Sigma }}_{N,r}$. Furthermore, pair-wise interactions between single cues are guaranteed as long as the cues are correlated. Another case to consider is the assumption that the covariance matrices from noise-alone and tone-plus-noise waveforms are different but single cues are uncorrelated (i.e., the covariance matrices are diagonal). In that case, Eq. 2 would reduce to

$$D(\mathbf{c})=\frac{1}{2}\log \left(\frac{\det ({\mathbf{\Sigma }}_{N,r})}{\det ({\mathbf{\Sigma }}_{S,r})}\right)-\frac{1}{2}{\displaystyle \sum _i\frac{{\left(c_i-{({\mathbf{\mu }}_{S,r})}_i\right)}^2}{{({\mathbf{\Sigma }}_{S,r})}_{\mathit{i}\mathit{i}}}}+\frac{1}{2}{\displaystyle \sum _i\frac{{\left(c_i-{({\mathbf{\mu }}_{N,r})}_i\right)}^2}{{({\mathbf{\Sigma }}_{N,r})}_{\mathit{i}\mathit{i}}}},$$ (4)

where c_i is the ith cue, (${\mathbf{\Sigma }}_{S,r}$)_ii and (${\mathbf{\Sigma }}_{N,r}$)_ii are the (i,i)th entries of the covariance matrix of the tone-plus-noise and noise-alone waveforms. The DV described by Eq. 4 is still nonlinear, but fails to capture the interactions between cues. Equations 3, 4 serve to illustrate features of the full LRT model, which includes both a nonlinear combination of cues and the interactions between pairs of single cues. Figure 5 shows a schematic diagram of the computation of the DV for the nonlinear LRT-based multiple-cue model.

Figure 5.

This schematic diagram illustrates the strategy for computing the nonlinear combination of cues. The DV is computed by combining energy and temporal cues using the nonlinear LRT-based multiple-cue model. Single cues are computed from the waveform (as in Fig. 3), and combined with a logarithmic likelihood-ratio test [shown in Eq. 1, where c₁, c₂, and c₃ denote the cue values).

Decision variable of the linear multiple-cue model

The DVs for a linear multiple-cue model were also computed using a weighted sum of energy and temporal cues. Performance of the linear and nonlinear cue-combination models was compared. Equation 5 illustrates the linear combination (LC) of energy and temporal cues, in which $c_1$ denotes the energy cue (CB), $c_2$ denotes the envelope cue (ES), and $c_3$ denotes the fine-structure cue (PO) for the test waveform. The weights corresponding to each cue are designated as $w_{1,x,r}$, $w_{2,x,r}$, and $w_{3,x,r}$; x denotes the waveform category, and any term with the subscript r is computed from a large set of randomly generated waveforms.

$$\begin{array}{c}DV=D_S-D_N,\\ D_x=w_{1,x,r}{c}_1+w_{2,x,r}{c}_2+w_{3,x,r}{c}_3\hspace{0.17em},\\ \text{where}\hspace{0.17em}x\in \left\{S,N\right\},\hspace{0.17em}\hspace{0.17em}{w}_{i,x,r}={\left[{\left({\mathbf{\Sigma }}_{x,r}\right)}_{\mathit{i}\mathit{i}}\right]}^{-1},\hspace{1em}\text{and}\hspace{0.17em}\hspace{0.17em}i=1,2,3\hspace{0.17em}.\end{array}$$ (5)

For each cue, the weight equals the inverse of the variance of the cue values, which corresponds to the inverse of the (i,i)th entry in the covariance matrix ${\mathbf{\Sigma }}_{x,r}$. Assuming that listeners used a combination of energy and temporal cues in the detection task, this linear combination would yield an optimal estimation of the combined cue value if the energy and temporal cues were uncorrelated (Yuille and Bulthoff, 1996); however, energy and temporal cues are typically correlated (Davidson et al., 2009a).

Given that the test waveform category was unknown during the detection task, the DV was computed as the difference between the combined cues for tone-plus-noise and noise-alone conditions. A DV with a value greater than zero suggests that the current waveform is a tone-plus-noise stimulus; a DV with a value less than zero suggests that the current waveform is a noise-alone stimulus.

RESULTS

It was hypothesized that if a listener used a particular cue-combination rule to detect a tone in noise, then DVs computed from that particular rule would be strongly correlated to the listener's detection pattern. In this section, predictions from single-cue and multiple-cue models were evaluated by computing the squared Pearson product-moment correlation coefficient between DVs and the z-score of listeners' detection patterns. In the following figures, each bar shows the proportion of predicted variance (squared correlation between detection patterns and hit or FA rates) for the average listener. The length of the error bar shows the standard deviation of the predicted proportion of variance across individual listeners.

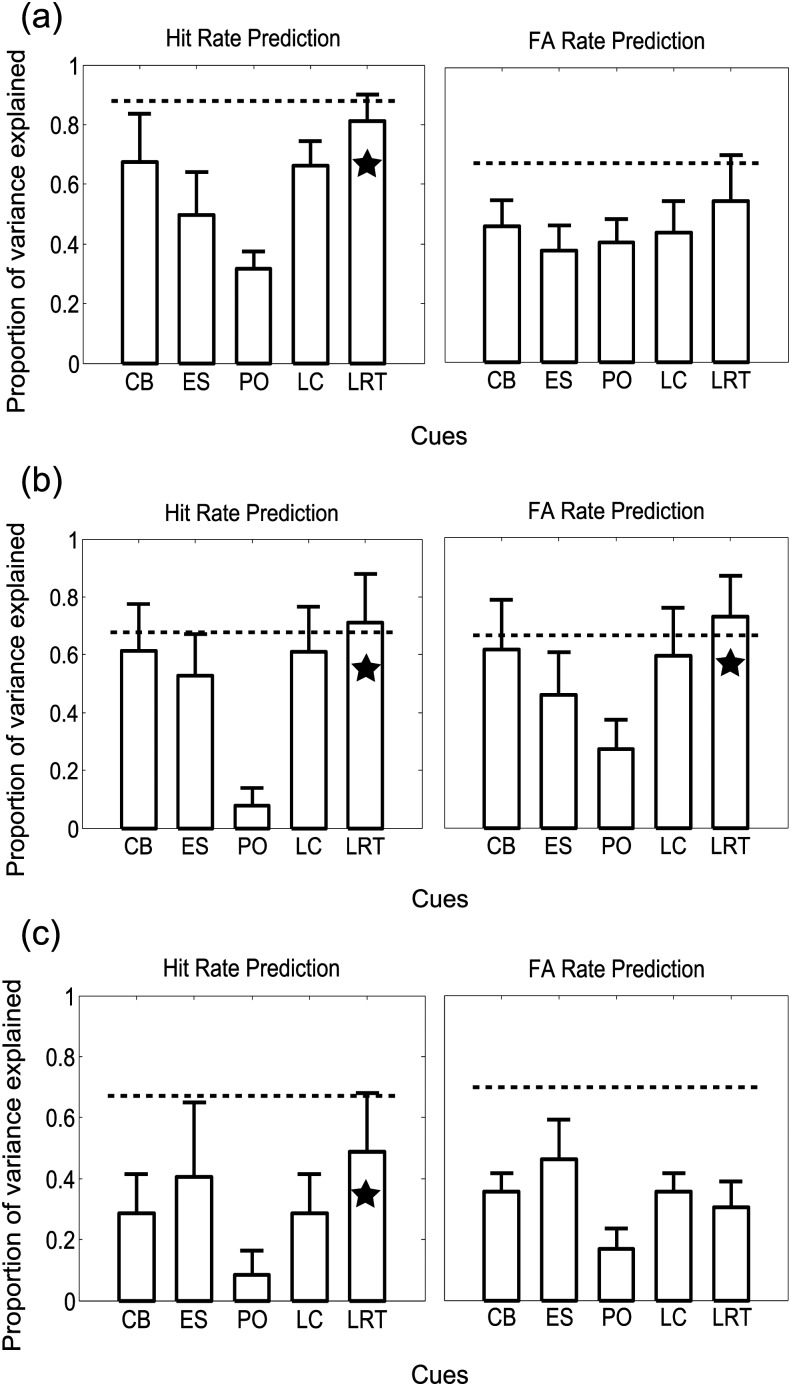
Figure 6a shows predictions based on the energy (CB) and temporal (ES and PO) single-cue models, as well as the linear (LC) and nonlinear (LRT) multiple-cue models for the 2900-Hz bandwidth waveforms. Predictions from the CB model alone were the best among the three single-cue models for both hit and FA rates. For multiple-cue models, predictions based on the LC model were similar to those of the CB model. However, predictions based on the LRT model approached the predictable variance (squared mean of the correlations between detection patterns of individuals and those of the average listener) for both hit and FA rates.

Figure 6.

The proportion of variance explained by single-cue and multiple-cue models of the average listener for the (a) 2900-Hz bandwidth, (b) 100-Hz bandwidth, and (c) 50-Hz bandwidth waveforms. The x axis shows the names of different models (CB: energy cue, ES: envelope cue, PO: fine-structure cue, LC: linear combination of three cues, LRT: nonlinear logarithmic likelihood ratio test combination of three cues). The stars indicate that multiple-cue model predictions were significantly improved compared with predictions from any single-cue model (p < 0.05, n = 25 for 2900- and 100-Hz waveforms, n = 50 for 50-Hz equal-energy waveforms). The y axis shows the proportion of variance explained by different models. The length of the error bar shows the standard deviation of the predicted proportion of variance across individual listeners. The dotted lines indicate the predictable variance for hit and FA rates.

Model predictions based on the energy and temporal single-cue models, as well as the linear (LC) and nonlinear (LRT) multiple-cue models for the 100-Hz bandwidth waveforms are shown in Fig. 6b. Similar to the results for the 2900-Hz bandwidth waveforms, predictions based on the CB model alone were the best among the three single-cue models for both hit and FA rates, and predictions based on the LC model were similar to those of the CB model. Furthermore, predictions based on the LRT model met the predictable variance for both hit and FA rates.

For the 50-Hz bandwidth equal-energy waveforms, Fig. 6c shows model predictions based on the energy and temporal single-cue models, as well as the linear (LC) and nonlinear (LRT) multiple-cue models. In contrast to the previous two datasets, the energies of the noise-alone and tone-plus-noise waveforms in this dataset were equalized, in an effort to remove the energy cue. Model predictions of hit and FA rates based on the ES model were the best among the three single-cue models. Similar to the other two datasets, predictions based on the LC model were close to those of the CB model.

Model predictions for waveforms from the three datasets suggested that for tone-in-noise detection listeners may use a nonlinear combination of energy and temporal cues that takes into account the statistical correlations of the three cues. In order to test whether predictions from the LRT or LC model were significantly better than those of single-cue models, an incremental F-test was carried out to analyze the model predictions. In Fig. 6, bars with stars indicate that the nonlinear (LRT) model significantly improved predictions (p < 0.05, n = 25 for 2900- and 100-Hz waveforms, n = 50 for 50-Hz equal-energy waveform). For example, for the 2900-Hz bandwidth waveforms, the single-cue CB, ES, and PO models were able to predict 68%, 50%, and 32% of the variance of hit rates, respectively. By combining all three cues with the nonlinear (LRT) model, 81% of the variance in the detection patterns could be predicted, and this amount of predicted variance was significantly greater than that from any of the single-cue models. For the LRT model, the amounts of predicted variance of hit rates for all noise bandwidths were significantly greater than those based on any of the single-cue models. The error bars indicate the standard deviation of model predictions across individual listeners. Although the difference between LRT and ES cue is not as large as in Fig. 6a and Fig. 6b, 50 waveforms were used in Fig. 6c while 25 waveforms were used in Fig. 6a and Fig. 6b. Thus, the improvement of LRT over ES is statistically significant (p = 0.03). In addition, the amount of predicted variance of FA rates for the 100-Hz bandwidth waveform was also significantly greater than those based on any of the single-cue models, whereas amounts of predicted variance of FA rates for the 2900- and the 50-Hz bandwidth equal-energy waveforms were not significantly greater than those based on the best single-cue model. In contrast, the amount of predicted variance of the LC model was not significantly greater than those of single-cue models; LC predictions were similar in quality to the CB predictions across all datasets and for both hits and FAs (Fig. 6).

DISCUSSION

In this study, model predictions for diotic detection based on three different single cues (the CB, ES, and PO models) and combinations of these cues (the LC and LRT models) were tested with detection patterns for three different sets of reproducible noise waveforms. The LRT model provided significantly better predictions of hit rates than any of the single-cue models for all three datasets and of FA rates for the 100-Hz bandwidth waveforms. Using the LRT-based detection model to predict listeners' detection performance is not new. Siebert (1970), Colburn (1973), and Heinz et al. (2001) used a similar strategy to predict frequency, interaural time, and level discrimination data from model auditory-nerve fibers. However, these linear models predicted listeners' discrimination thresholds using Possion-distributed model auditory-nerve responses; whereas, in the current study, the Gaussian-distributed cue values yielded a nonlinear cue-combination model to predict listeners' detection patterns.

Alternative models based on envelope cues

For all three datasets studied here, the envelope slope cue was robust in predicting listeners' detection patterns. Wojtczak and Viemeister (1999) showed that the envelope cue was also important for understanding intensity increment discrimination and amplitude-modulation detection experiments. They found that a decision variable based on the ratio between the maximum of the envelope and its minimum could explain the linear relationship between the intensity increment discrimination and amplitude-modulation detection thresholds. A similar max/min statistic was tested on the current datasets; however, this model's predictions were not significantly correlated to listeners' performance. In addition, envelope energy, computed as the sum of the energy in the non-zero frequency components, did not explain a significant amount of listeners' performance. Thus, a decision variable based on envelope fluctuations, such as that used in the ES model (Richards, 1992), outperformed other envelope-based variables for detailed predictions of performance in tone-in-noise detection tasks.

Dau et al. (1997) extended their “effective” signal processing model (Dau et al., 1996b) with a modulation filter bank and predicted thresholds for modulation detection and masking with random noises. Results from their study are consistent with auditory tuning to both audio and modulation frequency. They also showed that a bank of bandpass modulation filters predicted the trends of listeners' thresholds across many signal and masking conditions, whereas predictions using low-pass modulation filters (Viemeister, 1979) failed. Consistent with the implications of Dau et al., (1997) that envelope cues are processed in different modulation frequency bands, the ES model with a bandpass modulation filter was used in the current study. However, only one bandpass modulation filter was required here, because lower or higher modulation frequencies did not provide information about the difference between noise-alone and 500-Hz tone-plus-noise stimuli (Fig. 2). It was shown that this modified ES model yielded better predictions of listeners' detection results than the original ES model.

In addition, frozen noise stimuli were used in the Dau et al. (1996b) study of detection in noise. In that study, listeners' thresholds for detecting sinusoids of different durations, onset times, onset phases, or frequencies were predicted by their effective model (without modulation filters) (Dau et al., 1996a). Direct comparisons between their results and the results presented here are difficult. In their three-interval forced-choice test, the same frozen noise was used in all intervals, providing the potential for detailed comparisons across intervals. Their model structure, which utilizes a comparison between noise-alone and tone-plus-noise representations, is appropriate for such a task. However, in the datasets analyzed here, a single frozen noise-alone or tone-plus-noise stimulus was presented in a one-interval forced-choice task, and the noise for each trial was selected from an ensemble of waveforms. The models applied here were appropriate for this single-interval task; these models involved comparisons of cues for a single trial to distributions of cue values, but not the cues for a particular waveform. Furthermore, the waveforms studied here consisted of tone and noise waveforms that were gated simultaneously, whereas Dau et al. (1996b) stimuli were short-duration tones presented at a delay during a longer masking noise, making direct comparisons across the studies difficult.

For single-cue models, the “multiple-look” strategy (Viemeister and Wakefield, 1991) suggests that listeners might extract cues from short durations of the whole waveform in detection and discrimination tests. A similar strategy was tested in the current study by segmenting waveforms into equal-duration epochs. However, predictions based on the multiple-epoch scheme were not significantly different from those based on the single-epoch scheme for either single-cue or multiple-cue models. Thus, results presented above were all based on the single-epoch scheme.

Linear vs nonlinear cue combination

Davidson et al. (2006; 2009a) used different single-cue models to predict listeners' detection performance for the three datasets used in the current study, however, none of the single-cue models could explain the predictable variance. In another study focused on the 50-Hz bandwidth equal-energy waveforms, Davidson et al. (2009b) pointed out that that a linear combination of the two cues could not explain listeners' detection patterns and suggested the future consideration of models based on nonlinear combinations of cues. Results from these three studies motivated the nonlinear LRT-based multiple-cue model that was tested in this study. Because DVs were computed from a logarithmic likelihood ratio of cue values given noise-alone and tone-plus-noise waveforms, the degree of similarity between the covariance matrices under these conditions determined whether the combination of cues was linear or nonlinear. In the current study, the covariance matrices for noise-alone and tone-plus-noise conditions were different. For the three datasets tested, model predictions of hit rates based on the nonlinear LRT model were significantly better than those based on any of the single-cue models, whereas predictions of FA rates were significantly better for the 100-Hz bandwidth waveform but not for the other two datasets.

In order to understand the difference between the LRT model and the linear cue-combination model, the weights of the different cues in the models [Eq. 2] were inspected (see the Appendix). Recall, that for the linear model the weights are based on the reliability of each single cue (the inverse of the variance), thus higher weights are assigned to more reliable cues. Inspection of weights for the linear cue-combination model showed that CB was the dominant cue and PO had the least significant weight.

Note that for the LRT model the predictions for hit and FA rates were computed with the same model, in which the weights were computed from the distributions of cue values, i.e., the same covariance matrices were used to provide weights for both hits and FAs. For the LRT model, the relationships between different single cues were determined by computing their covariance. Thus, in addition to single cues, pairs of single cues also contributed to the DV in the LRT model. For the 100-Hz bandwidth waveforms, CB, ES, and PO single cues were assigned approximately equal positive weights, whereas the pairs of CB and ES, and ES and PO cues were assigned approximately equal negative weights that were less than the positive weights. For the 2900-Hz bandwidth waveforms, the weight for the CB cue was twice as large as for the ES cue and for the pair of CB and ES cues, and these three weights dominated the weighting matrix. The higher weight for the CB cue was not surprising, because this cue explained more variance than the ES or PO cues for both the 100- and 2900-Hz waveforms (Fig. 6). However, for the 50-Hz equal-energy waveforms, even though the CB cue was outperformed by the ES cue in single-cue model predictions, the significantly smaller variance of the CB cue resulting from the equal-energy waveforms yielded a higher weight to the CB cue in the LRT model. Similarly, consistent with the robustness of the ES cue for the single-cue predictions, it was assigned a higher weight than the PO cue. In addition, the weighting matrix of individual listeners was similar to that of the average listener, suggesting that the assumption that listeners used a similar strategy for tone detection in these experiments was reasonable.

Consideration of the equal-energy predictions

Further analysis for the CB cue of the 50-Hz bandwidth equal-energy waveforms showed that small energy differences between waveforms were introduced when the waveforms were passed through the gammatone filter used to calculate DVs of the CB model. Although model predictions from the CB model explained around 30% of the variance in the detection patterns, the absolute size of the energy differences was negligible (Davidson et al., 2009a). Inspection of the DVs from the CB model showed that average sound level difference among fifty tone-plus-noise and noise-alone waveforms was 0.1 and 0.2 dB, respectively. Thus, the predictions achieved by the CB model for the narrowband equal-energy condition are likely to be an artifact of the correlation between cues. In addition, the envelope cue was able to explain a significant amount of the variance in the detection pattern, confirming the robustness of the envelope cue, as in previous studies (Kidd et al., 1989; Richards, 1992; Zhang, 2004; Davidson et al., 2009a).

Model predictions based on the LRT model for the 2900- and the 100-Hz bandwidth waveforms were close to the predictable variance; however, predictions for the 50-Hz bandwidth equal-energy waveforms were lower than the predictable variance. Based on the analysis from the weighting strategy above, the CB cue dominated the weighting matrix for the 50-Hz dataset. However, the CB cue was not as effective as the ES cue for the equal-energy waveforms [Fig. 6c]. Thus, listeners may use alternative strategies to the optimal LRT-based method for the equal-energy narrowband waveforms.

Future directions

Given that predictions based on the LRT model were most consistent with listeners' detection patterns, it is interesting to ask whether LRT-type processing is observed along the auditory pathway. Because the auditory nerve is the only path from the inner ear to the brain, the nonlinear response of the auditory nerve contains all information available to the central nervous system. Inspection of auditory-nerve (AN) model responses (Zilany et al., 2009) would be a necessary first step. Rate, synchrony and fluctuation of the post-stimulus time histogram (PSTH) computed from model responses could represent the energy, fine-structure, and envelope cues of the stimulus. However, given that both on- and off-frequency AN fibers would respond to the stimuli, it would be interesting to investigate an optimal way to combine these cues.

In addition, responses from higher levels in the brain, such as the cochlear nuclei and inferior colliculus (IC), are also likely to convey information observed from the LRT model. In particular, the IC is a nearly obligatory pathway from the lower brainstem nuclei to higher processing centers. Analysis of IC model responses (Nelson and Carney, 2004) could be tested with responses from the LRT model.

Last, internal noise (Spiegel and Green, 1981) was not included in the current signal-processing type model. However, internal noise could be introduced in physiological models as an additive or multiplicative noise to further understand the difference of detection performance among individual listeners.

SUMMARY

In this study, model predictions for diotic detection based on three different single cues (the CB, ES, and PO models) and combinations of these cues (the LC and LRT models) were tested with detection patterns for three different sets of reproducible noise waveforms. The LRT model, which is an optimal combination of energy and temporal cues, provided significantly better predictions of hit rates than any of the single-cue models or the LC model for all three datasets and of FA rates for the 100-Hz bandwidth waveforms.

APPENDIX: WEIGHTS FOR THE NONLINEAR CUE-COMBINATION MODEL

The weights for the LRT nonlinear cue-combination model are shown in Tables 2, 3, TABLE IV. for 100- and 2900-Hz bandwidth waveforms and for the 50-Hz bandwidth equal-energy waveforms. In each table, the diagonal entries indicate weights for single cues (e.g., CB, ES, and PO), and the off-diagonal entries indicate weights for two cues (e.g., CB-ES, CB-PO, and ES-PO). Note that the weights are symmetric along the diagonal entries and the weight matrix is normalized to have a sum of one.

TABLE II.

Weights for 100-Hz bandwidth waveforms.

Weights for Cues	CB	ES	PO
CB	7.30	−6.26	1.41
ES	−6.26	8.40	−8.16
PO	1.41	−8.16	11.34

TABLE III.

Weights for 2900-Hz bandwidth waveforms.

Weights for cues	CB	ES	PO
CB	0.43	0.11	−0.00
ES	0.11	0.17	0.07
PO	−0.00	0.07	0.05

TABLE IV.

Weights for 50-Hz bandwidth equal-energy waveforms.

Weights for cues	CB	ES	PO
CB	1.03	−0.01	0.01
ES	−0.01	−0.11	−0.00
PO	0.01	−0.00	0.05