Abstract
Distortion-product otoacoustic emissions (DPOAEs) were measured in rabbits as time waveforms by employing a phase-rotation technique to cancel all components in the final average, except the 2f1-f2 DPOAE. Subsequent filtering allowed the DPOAE waveform to be clearly visualized in the time domain. In most conditions, f2 was turned off for 6 ms, which produced a gap so that the DPOAE was no longer generated. These procedures allowed the DPOAE onset as well as the decay during the gap to be observed in the time domain. DPOAEs were collected with L1 = L2 = 65-dB sound pressure level primary-tone levels for f2/f1 ratios from 1.25 to 1.01 in 0.02 steps. Findings included the appearance of complex onsets and decays for the DPOAE time waveforms as the f2/f1 ratio was decreased and the DPOAE level was reduced. These complexities were unaffected by interference tones (ITs) near the DPOAE frequency place (fdp), but could be removed by ITs presented above f2, which also increased DPOAE levels. Similar outcomes were observed when DPOAEs were measured at a sharp notch in the DPOAE level as a function of the f2 primary tone frequency, i.e., DP-gram. Both findings were consistent with the hypothesis that the DPOAE-ratio function, and some notches in the DP-gram, are caused by interactions of distributed DPOAE components with unique phases.
INTRODUCTION
Distortion-product otoacoustic emissions (DPOAEs) recorded in the ear canal are commonly believed to consist of two distinct components (e.g., Kim, 1980; Shera and Guinan, 1999; Kalluri and Shera, 2001). This concept assumes that one component, which is referred to as the “overlap” or “distortion” component, is generated near f2 at a basilar-membrane (BM) locus where the f1 and f2 primary tones mix within the cochlea's nonlinearity. This f2 distortion component then travels to the DPOAE frequency place (fdp), and is reflected via a linear coherent reflection mechanism to give rise to the secondary DPOAE reflection component.
It has also been recognized by many investigators (e.g., Kemp, 2002; Shera, 2003; Shera and Guinan, 2008) that DPOAE generation is, in fact, a distributed process involving the interaction of numerous wavelets most likely emanating from a region at and basal to f2, where the f1 and f2 primary-tone traveling-wave (TW) envelopes overlap on the BM. Evidence supporting the distributed nature of DPOAEs is not new (see review in Martin et al., 2010). However, the results of a relatively recent series of studies by Martin and colleagues (Martin et al., 2009, 2010, 2011) in humans, in both normal and noise-damaged rabbits, and in several common laboratory species demonstrated that significant DPOAE components are apparently generated at BM loci that can be much more broadly distributed than has been generally supposed, i.e., up to approximately two octaves basal to the f2 primary-tone site. In addition, these investigators were only able to reliably measure a reflection component arising from fdp in humans, while this component was extremely small or absent in rabbits, rats, and chinchillas (Martin et al., 2011). The lack of the reflection component in laboratory animals makes it even more difficult to explain some common DPOAE phenomena without invoking the distributed nature of DPOAE generation.
One of the main strategies used to reach the above conclusions involved obtaining DPOAE level/phase maps and DP-grams either in the presence or absence of a third or interference tone (IT) placed at one-third octave (1/3-oct) or more above f2. The vector difference between these two conditions was then computed to reveal emission components that were removed by the IT. These “basal components” could be relatively large and supported the notion that DPOAEs originate from a distributed region with significant contributions from BM regions above f2.
One potential objection to this interpretation of the findings based on the use of ITs is the possibility that the apparent basal components were somehow generated by the complex interactions associated with the simultaneous presence of three pure tones (i.e., f1, f2, IT) in a nonlinear system. In fact, Fahey et al. (2000) termed this possibility a “catalyst mechanism” and ascribed much of the suppression/enhancement effects observed above f2 by Martin et al. (1999, 2003) to such a process. However, the more recent experiments described above by Martin et al. (2010, 2011) largely ruled out the possibility that catalyst components were responsible for the observed findings, especially when results from the various control experiments involving comparisons between normal and noise-damaged ears were considered (see Fig. 6 in Martin et al., 2010). Nevertheless, it would be more satisfying if it were possible to demonstrate the actual existence of distributed DPOAE components without relying upon the IT paradigm.
The present manuscript describes the outcomes of experiments in which DPOAE time waveforms were collected using a modification of the method described by Whitehead et al. (1996), whereby the measured DPOAE is visualized in the time domain. With this approach, at narrow f2/f1 ratios, abrupt variations in the time-waveform magnitude and phase, hereafter referred to as “complexities,” could be observed at the DPOAE onset, or in the decay of the DPOAE when the f2 primary tone was turned off. The importance of these findings is that since no IT was present under these conditions, previous objections to basal components based upon the effects of an IT do not apply to time-domain measures. Consequently, the most likely explanation for these waveform complexities was the interaction of distributed DPOAE components generated along the BM at different distances from f2.
The observations reported here are in agreement with findings by other investigators, who have proposed a role for distributed DPOAE components in contributing to a variety of DPOAE phenomena including the inverted “U” form of the commonly observed f2/f1 ratio function (e.g., Fahey et al., 2006), notches in DP-grams (e.g., Fahey et al., 2008), and the observation that under certain circumstances DPOAEs appear to be traveling, unexpectedly, in a reverse direction from the cochlear base to the apex (e.g., Ren, 2004; de Boer et al., 2008; He et al., 2008, 2010; Vestenik and Gummer, 2012).
METHODS
Subjects
Four female rabbits (3 to 4 kg) served as experimental subjects. All subjects exhibited normal cochlear function in both ears as measured by DP-grams, which were comparable to those in our laboratory's extensive normative DPOAE database for the rabbit. Subjects were first habituated to being confined in a standard Plexiglas rabbit holder, and after the habituation period, they were tested while awake in a sound-attenuated chamber. The VA Loma Linda Healthcare System's Institutional Animal Care and Use Committee approved all rabbit-study protocols.
DPOAE measures
DP-gram methods utilized for rabbits were highly similar to those described previously (Martin et al., 2010, 2011). Briefly, for all subjects, DP-grams as a function of the f2 frequency (f2/f1 = 1.25) were measured in 0.1-octave steps at various L1,L2 levels to establish normal baseline DPOAEs. The equipment used to measure DPOAEs consisted of a PC-based platform (PXI chassis, model 1062Q, National Instruments, Austin, TX) fitted with a processor (model Core 2 Duo 8801 @ 2.53 GHz, Intel, Santa Clara, CA) running a commercial operating system (Windows XP, Microsoft Corp., Redmond, WA). The PXI chassis was equipped with a two-channel digital-signal processing board (model NI-PXI-4461, National Instruments), two ear-speakers (model ER-2, Etymotic Research, Inc., Elk Grove Village, IL), and a low-noise microphone assembly (model ER-10A, Etymotic Research, Inc.). A development environment (labview 2010, National Instruments) was used to create custom software that generated the two primary tones, i.e., f1 and f2, and simultaneously measured the level of the ear-canal sound pressure. For DP-grams, a fast-Fourier transform (FFT) was performed upon a time-domain average of four 92.9-ms samples (4096 points at 44.1 kHz) obtained during four successive 110-ms stimulus presentations. Each stimulus presentation was ramped on and off with a cosine function for 4.54 ms, with a delay of 5.67 ms after the end of the ramp, before sampling began. From the FFT of the time-domain average, the 2f1-f2 DPOAE and associated noise-floor (NF) levels were measured. The NF was based on the average (n = 8) of frequency bins on both sides of the DPOAE-frequency bin, excluding the first bin on either side of the DPOAE frequency.
DPOAE time waveform techniques
DPOAE time waveforms were collected with L1 = L2 = 65-dB sound pressure level (SPL) primary tones for f2/f1 ratios ranging from 1.25 to 1.01 in 0.02 steps. The procedures for obtaining DPOAE time waveforms were highly similar to those for obtaining DPOAE onset latencies originally described in detail by Whitehead et al. (1996). In the original Whitehead et al. study, the primary focus was to measure the delay from the onset of the primary-tones until the DPOAE waveform could be detected in the ear canal. Although these features were still retained in the present approach, the emphasis here was to detect the appearance of complexities in the emission's time waveform. This ability was enhanced by a modification of the original technique whereby f2 was turned off at 5 ms, and then turned back on at 11 ms after the initial onset of the primary tones. This allowed the visualization of complexities in the waveforms as various DPOAE components decayed during the 6-ms gap, and a replication of the onset portion of the waveform once f2 was turned back on.
Each waveform was based upon a time-domain average (4096 points) of 1024 successive 33-ms stimulus presentations. To more accurately measure DPOAE latency, each stimulus presentation was ramped on and off with a Blackman-Harris function for 0.1 ms, with a 10-ms delay between each stimulus. In contrast to the methods utilized for the DP-gram, the sample rate was increased from 44.1 to 132.3 kHz with the same number of sample points. This change decreased the sample duration from ∼93 to ∼31 ms. The higher sample rate along with the shorter ramp length allowed a reduction in the stimulus duration from 110 to 33 ms. This procedure decreased the frequency resolution when performing a FFT on the data, but it increased the time-domain resolution, and decreased the time necessary to collect each DPOAE waveform.
The basic paradigm to obtain the DPOAE time waveforms was based on a phase-rotation technique in which the phases of the f1 and f2 primaries were systematically rotated between stimulus presentations, i.e., in the present case, by 45° and 90°, respectively. The phase rotations (n = 1024) were arranged to give equal numbers of in-phase and 180° out-of-phase presentations, so that the primary tones and their harmonics, and all DPOAEs, except the one of interest, were canceled in the final average (see Table I in Whitehead et al., 1996). The phase-rotation process uncovered the raw 4096-point DPOAE-time waveform, which contained low- and high-frequency noise and, infrequently, small remnants of the primary-tones as well. Although the short 0.1-ms ramps utilized increased spectral splatter, the total energy of the splatter at the frequency of the DPOAE of interest was minimal and transient compared to the overall level of the measured DPOAE. Also, these spectral components were not phase-locked to the DPOAE frequency, because of the phase-rotational techniques utilized, so they largely canceled in the final time average (see Fig. 1 in Whitehead et al., 1996). During the course of the Whitehead et al. (1996) study, an entire series of different ramp lengths was investigated, and it was found that a short ramp length of 0.1 ms was not problematic, and, in fact, was very useful in visualizing the onset of the DPOAE waveform.
In the stimulus to the ear canal, there was often a slight “bulge” or “overshoot” when both primary-tone stimuli were turned on, and a small “aftertone” of the f2 speaker when it was turned off that lasted for approximately 2 ms [see Figs. 1I, 2E]. These effects were due to ringing of the Etymotic ER-2 speakers for some of the frequencies used. To be certain that this ringing was not responsible for the complexities observed in the data, several different control experiments were performed. In the worst-case scenario, the aftertone was approximately equal to a 45-dB SPL f2 primary combined with a 65-dB SPL f1 primary. Since this combination could conceivably produce a DPOAE, even at narrow f2/f1 ratios where complexities were routinely observed, we measured the level of the DPOAE that could possibly be produced by presenting the L1,L2 levels that would be present when f1, f2, or both f1 and f2 were turned off, i.e., L1,L2 = 45,65, L1,L2 = 65,45, and L1 = L2 = 45 dB SPL. Only the condition where f2 was turned off made a significant DPOAE at narrow ratios. The time-domain DPOAE waveforms with f1, f2, or both f1 and f2 turned off were then collected and in all cases no appreciable differences were observed in the resulting DPOAE complexities similar to those described below. In addition, subtraction of the onset stimulus from the steady-state stimulus revealed that the slight bulge or overshoot could have momentarily increased the primary-tone level by < 1 dB, a level highly unlikely to be responsible for large onset complexities. Finally, the DPOAE time-domain waveforms at several primary frequencies were collected that did not exhibit appreciable stimulus ringing or corresponding onset bulges and, again, the results obtained exhibited highly similar complexities.
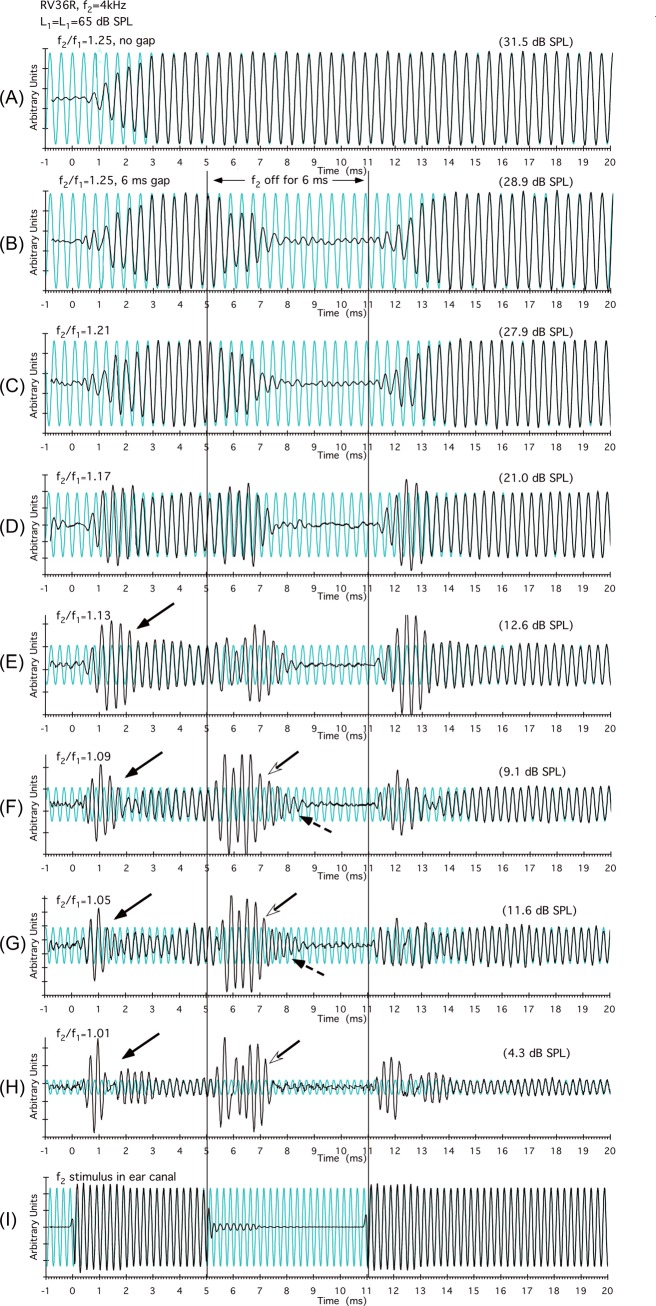
Figure 1.
(Color online) DPOAE time waveforms observed for a typical f2/f1-ratio series for the R ear of rabbit RV36. In particular, at the narrow ratios (f2/f1 = 1.13 to 1.01) shown in panels (E)–(H), short-latency onset complexities (black arrows) were observed around 0.5 to 1.5 ms. At about 1.5 ms, the overall amplitude of the waveform decreased, which is consistent with the notion that longer-latency f2 components were now canceling the early onset of basal-DPOAE components with shorter latencies. At the offset of f2 [open arrowheads in panels (F)–(H)], as the canceling short-latency basal components decayed, a large component presumably generated nearer to f2 became apparent. These more apical components required approximately 3.5 ms to decay [dashed arrows in panels (F) and (G)] representing a latency more consistent with the f2 = 4 kHz cochlear location than the initial 0.5-ms complexity observed as the primary tones were turned on. The bottom trace in panel (I) demonstrates that there was little ringing of the f2 stimulus in the ear canal, but control experiments demonstrated that it did not affect the results (see Sec. 2C above). Vertical lines at 5 and 11 ms in this and subsequent figures indicate the offset and onset of f2, respectively. Note that for clarity the DPOAE time waveforms are plotted on arbitrary magnitude scales so that the largest component is full scale. Consequently, DPOAE levels cannot be directly compared across experimental conditions. However, values in parentheses at the top right of each plot indicate the level of the corresponding DPOAE at steady state in dB SPL for all time waveforms in each figure.
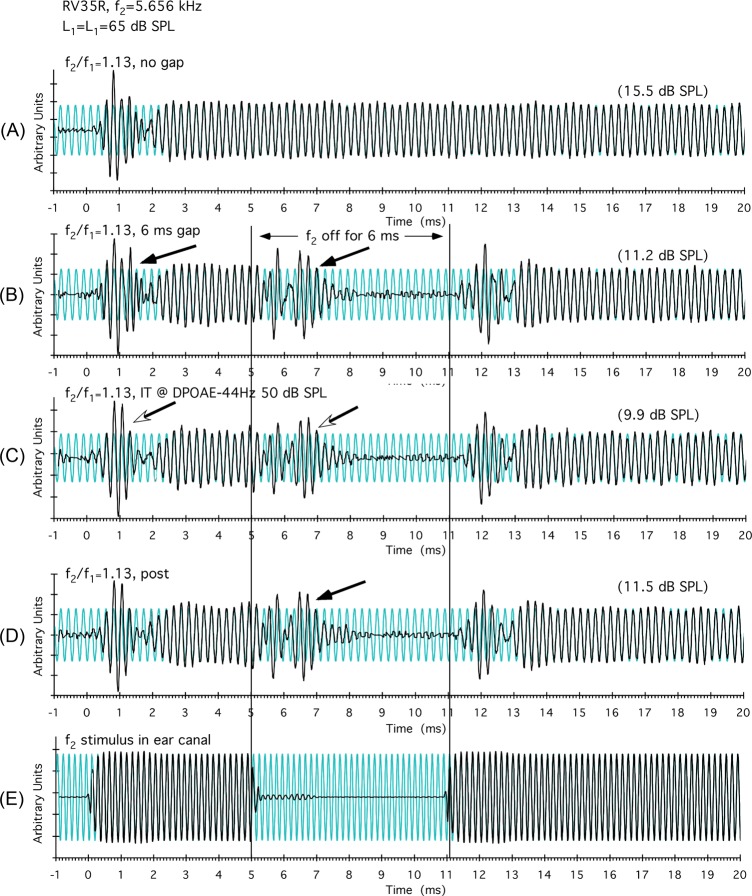
Figure 2.
(Color online) Results for the R ear of rabbit RV35 demonstrating that complexities observed in the DPOAE time waveforms are not due to reflection components from fdp. In panel (A), an onset complexity was present that disappeared as the DPOAE time waveform reached steady state after about 2.5 ms. In panel (B), when f2 was turned off at 5 ms, a complexity was observed as the canceling of distributed components diminished allowing one group of emission components to dominate. In panel (C), the complexities were unaffected when a 50-dB SPL IT was placed 44 Hz below fdp. In a post-condition shown in panel (D), in the absence of the IT, the waveform complexities (black arrow) were essentially identical to the initial [panel (B)] and IT conditions [panel (C)] displayed above indicating that reflection components from fdp were not responsible for the observed waveform complexities, and that the basis of their origin must lie elsewhere.
To “clean up” the DPOAE time waveform, an FFT was computed, and low-frequency pass spectral editing was performed to remove any residual primaries and high-frequency noise by setting the appropriate bins in the FFT to zero. The time waveform was then recovered by an inverse FFT (IFFT) operation. The custom labview-based DPOAE software accomplished this entire filtering procedure automatically, which could be visualized in real time by moving a sliding curser to the frequency on the spectrum where low-pass filtering was initiated. By moving the cursor back and forth, it was relatively straightforward to appreciate when the filtering began to introduce new waveforms into the data, which was generally when the curser got to within 100 Hz or less above the DPOAE frequency. Due to the large number of time averages and the care taken in collecting the data, primary-tone remnants were generally not a problem in this particular data set. Consequently, the filtering was performed largely to remove high-frequency components that make the waveform appear “noisy” [see Fig. 1(C) vs 1(D) in Whitehead et al., 1996]. Generally, this filtering was accomplished by starting just below the f2 frequency for the wider f2/f1-ratio values, and several hundred hertz above the f2 frequency for the narrower ratios.
After this manual filtering, both the filtered and unfiltered time waveforms were written to an output file, and transferred to a spreadsheet (Microsoft, Excel for the Macintosh, v11) for final analysis in which the time waveforms were high-pass filtered to remove low-frequency components, and then plotted. Both waveforms were separately analyzed to confirm that the IFFT-filtering process did not alter the basic features of the waveform with respect to either phase or magnitude. The spreadsheet was designed to subtract the acoustic delay so that actual DPOAE latencies could be appreciated on the time axis (i.e., abscissa). The spreadsheet also allowed the user to set a region on the time axis over which a sinusoid was synthesized, so that it was in-phase and of equal amplitude to the DPOAE waveform in that region. In the present study, this specified region was usually set to 15 to 20 ms after the onset of the primary tones, thus representing a point in time where the DPOAE had reached a steady-state level. Based upon an FFT of the data, the level of the DPOAE was measured in dB SPL, and this value is shown in parentheses at the right top of each plot over the DPOAE steady-state region. The reference sinusoid allowed one to compare the DPOAE steady-state phase and magnitude with the DPOAE phase and level at earlier regions of the time waveform.
IT techniques
For ITs presented above f2, the tones were digitally generated and mixed on the f1 channel. To cancel most of the IT and the other DPOAEs made by the interaction of the IT with either primary in the time average, its phase was rotated 11° with each presentation. For the ITs presented above f2, any remnant of this tone after averaging was also nulled by the filtering techniques described above. However, the use of the IFFT strategy to filter the time-domain data did not permit tones below the DPOAE frequency to be reduced by these procedures without also filtering out the DPOAEs being measured. Nevertheless, the ITs presented 44 Hz below the fdp were generally presented at a lower level than the higher-frequency ITs. This approach was necessary, because at higher levels, the tail of the IT envelope on the BM begins to affect DPOAE generation near f2 (Martin et al., 2011). Since the IT phase was unrelated to all the other signal phases, simple time averaging reduced these tones to a level that essentially eliminated them from the DPOAE time waveform.
RESULTS
Effects of f2/f1 ratio on DPOAE time waveforms
For the right (R) ear of rabbit RV36, Fig. 1 illustrates a typical f2/f1-ratio series in which DPOAEs are shown as waveforms in the time domain. In panel (A), the DPOAE waveform is depicted for the optimal f2/f1 ratio of 1.25 for the rabbit, where both f1 and f2 remain on throughout the measurement period. In this case, as soon as the DPOAE waveform was identified, it was approximately in-phase with the steady-state waveform synthesized in the background. It is clear that the earliest components occurred at around 0.5 ms and reached a steady state at approximately 3 ms after the onset of the primary tones. In panel (B), the data were collected again, but f2 was turned off starting at 5 ms for a period of 6 ms. At the 1.25 f2/f1 ratio, no complexities were observed either at the onset of the DPOAE time waveform or when f2 was turned off, i.e., the waveform remained largely in phase with the steady-state signal and either ramped up or down in a gradual fashion. Most notable in subsequent plots is that as the f2/f1 ratio decreased and the DPOAE level diminished (numbers in parentheses at top right for each panel), short-latency complexities were revealed at about 0.5 to 1 ms [solid black arrows in Figs. 1E, 1F, 1G, 1H] near the onset of the DPOAE time waveforms. It should be emphasized that all rabbits showed similar complexities at narrow f2/f1 ratios. The short latency of these waveform perturbations is consistent with them representing the more basal, i.e., high-frequency, DPOAE components that theoretically should arrive back at the ear-canal microphone first. When f2 was turned off, as indicated in the region demarcated by the two vertical black lines between 5 and 11 ms, large-magnitude complexities became apparent in the time-domain waveforms [open arrowheads in Figs. 1F, 1G, 1H]. These offset complexities are consistent with the emergence of longer-latency components generated closer to f2 that were initially canceled in the onset, and then revealed after more basal components responsible for the cancellation decayed in the offset. Note the long latencies of about 3.5 ms of some components [dashed arrows in Figs. 1F, 1G] measured from the offset of f2 (vertical black line at 5 ms). If DPOAE generation was restricted to a narrow region around f2, rather than distributed, then, theoretically, these “offset” latencies (dashed arrows) should be equal to their initial onset-latency counterparts (black arrows) at approximately 0.5 to 1 ms. Overall, these simple time-domain DPOAE waveforms provide compelling evidence for the interaction of distributed DPOAE components arising from distinct cochlear loci, with the complexity of the waveform depending upon the extent to which different components are either in-phase or out-of-phase, i.e., either adding to or canceling one another.
DPOAE time waveform complexities are not reflection components from fdp
One possibility, which would complicate the above interpretation that time-domain complexities provide evidence of distributed DPOAE sources, is that these complexities could conceivably be caused by emission components generated near f2 interacting with those reflected from the fdp. Such interactions, however, seem unlikely because rabbits do not exhibit reflection components arising from fdp (Martin et al., 2011). In any case, the plots of Fig. 2 for the R ear of rabbit RV35 depict the results of an experiment that essentially excludes this possibility. In Fig. 2A, a short-latency DPOAE component was clearly visible around 0.5 to 1.5 ms that disappeared as the waveform reached a constant steady-state level. When the f2 at 5.656 kHz was turned off at 5 ms, as shown in Fig. 2B, two complexities were observed (black arrows), i.e., the initial onset one and another component appearing during the gap similar to those shown in Figs. 1F, 1G, 1H. In Fig. 2C, when a 50-dB SPL IT was introduced at 44 Hz below fdp, no obvious change in the DPOAE waveform was apparent in that both DPOAE complexities (open arrow heads) remained nearly identical to those that were present without the near-fdp IT, as illustrated in Fig. 2B. This outcome indicates that the complexities in the DPOAE waveforms observed at narrow f2/f1 ratios were not produced by the interaction of DPOAE components generated near f2 with those reflected from fdp. Following the above manipulations, the DPOAE complexities could be replicated as indicated by the black arrow in Fig. 2D, and these were nearly identical to those initially measured in Fig. 2B, thus attesting to the stability of these observations.
Effects of ITs basal to f2 on DPOAE time waveform complexities
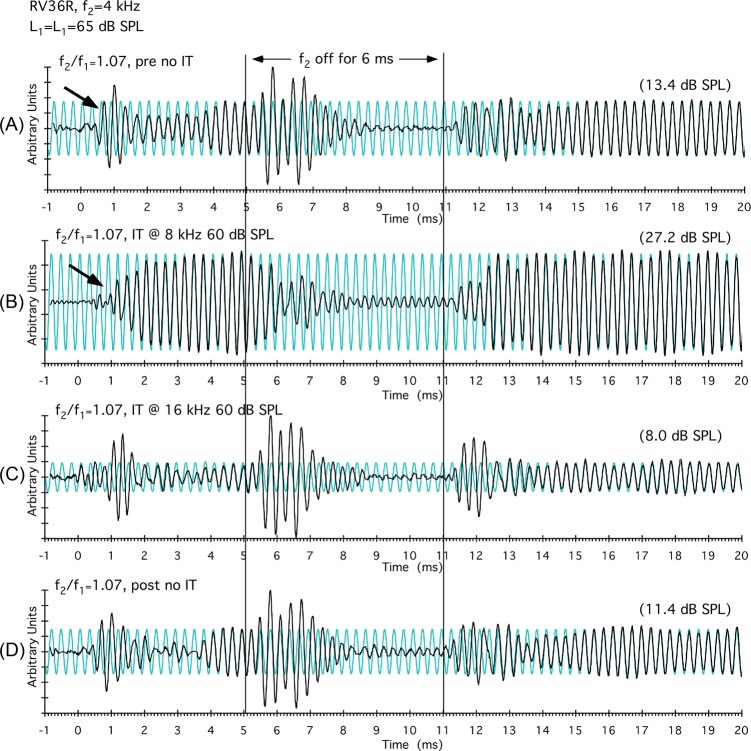
To test the hypothesis that DPOAE time-waveform complexities were based upon the interaction of f2 components with those generated more basally, ITs were introduced at various distances above a 4-kHz f2 during data collection, and the results are illustrated in Fig. 3 for the R ear of rabbit RV36. In Fig. 3A, an onset complexity is clearly visible (black arrow) as well as an offset complexity when f2 was turned off (vertical line at 5 ms). When a 60-dB SPL IT was placed at 8 kHz, the onset-related component [black arrow in Fig. 3B] was largely eliminated, the complexity produced by turning f2 off was also substantially altered, and the DPOAE level increased from approximately 13 to 27 dB SPL. In the next condition shown in Fig. 3C, the frequency of the IT was increased to 16 kHz. In this instance, the DPOAE waveform and magnitude was relatively similar to that shown in Fig. 3A, where there was no IT present. In combination, these results suggest that DPOAE components in the 8-kHz range, which were approximately an octave above f2, were interacting to produce the obvious waveform complexities. However, at 16 kHz, the IT apparently removed few, if any, distributed DPOAE components contributing to the time-waveform complexities, thus demonstrating that the frequency location of the IT was important. In sum, as might be expected, distributed components from different cochlear locations contribute differentially to the overall time waveform, depending on their magnitude and phase. The trace in Fig. 3D, without an IT, again demonstrates the stability of the initial findings shown in Fig. 3A.
Figure 3.
(Color online) Results from the R ear of rabbit RV36 demonstrating that DPOAE time waveform complexities originate from a restricted BM region above f2. In panel (A), DPOAE complexities at the onset of the primaries (black arrow at around 1 ms) and offset of f2 (vertical line at 5 ms) are easily appreciated. In panel (B), an 8-kHz IT presented an octave above the f2 = 4-kHz frequency removed these complexities. However, in panel (C), when the IT was increased another octave in frequency to 16 kHz, little effect of the IT was observed. After these manipulations, it was still possible, as seen in panel (D), to reasonably replicate the initial DPOAE time waveform, thus demonstrating the stability of the results. These findings are consistent with the suggestion that at an octave above f2, the IT removed DPOAE components originating basal to f2 that were responsible for the short-latency complexity. As these basal components diminished when f2 was turned off at 5 ms [as seen in panels (A), (C), and (D)], DPOAE components generated nearer f2 dominated to produce the large offset component.
Notches in DP-grams can result from cancellation of distributed DPOAE components
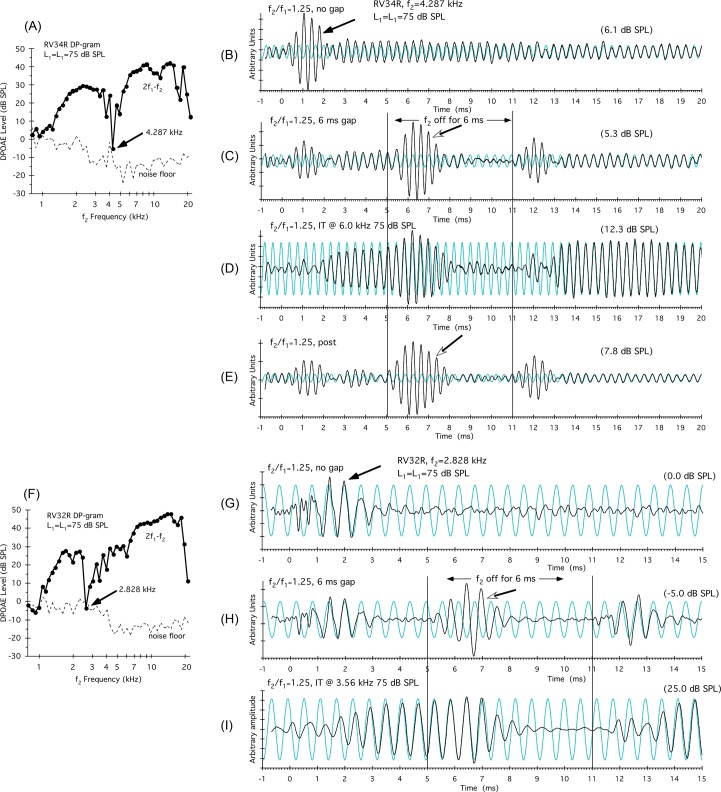
Rabbit DP-grams at higher primary-tone levels often show sharp notches. One explanation for such notches invokes a distributed-source hypothesis whereby two regions of emission components that are approximately 180° out-of-phase with one another produce the notch-like cancellation. Figure 4A illustrates the DP-gram for the R ear of rabbit RV34 obtained with equal-level primaries at L1 = L2 = 75 dB SPL. In this instance, a very sharp notch (black arrow) was apparent at 4.287 kHz, where the DPOAE level approached the corresponding NF (dashed line). To the right of this plot are shown DPOAE time waveforms [Figs. 4B, 4C, 4D, 4E] obtained at a standard f2/f1 ratio of 1.25, with the f2 frequency placed at the frequency of the notch, i.e., at 4.287 kHz. In Fig. 4B, a large onset complexity (black arrow) was observed before the DPOAE waveform reached a steady-state level for the remainder of the 20-ms measurement period. When f2 was turned off at 5 ms, as shown in Fig. 4C, a large DPOAE waveform (open arrowhead) emerged. This waveform was in-phase with the synthesized DPOAE frequency (i.e., the faint sinusoidal function in the background), but of a different phase to the onset waveform. These findings support the notion that the DP-gram notch resulted from the cancellation of two groups of out-of-phase DPOAE components. As illustrated in Fig. 4D, when a 75-dB SPL IT was placed above f2 at 6 kHz, the depth of the notch (not shown), along with the onset component, was reduced, and the DPOAE level increased from about 6 to 12 dB SPL. These findings suggest that one region of DPOAE components responsible for the cancellation was generated in the 6-kHz region and above, and was influenced by the 6-kHz IT. As in previous examples, when the IT was turned off, the original DPOAE time waveform was replicated as shown in Fig. 4E.
Figure 4.
(Color online) Examples of notches in the DP-grams for two different rabbits that can also be attributed to the cancellation of two groups of distributed DPOAE components. The DP-gram shown in panel (A) for the R ear of rabbit number RV34 was elicited by 75-dB SPL equal-level primary tones, and illustrates a deep notch at 4.287 kHz. DPOAE time waveforms shown in panels (B)–(E) were collected with the f2-primary tone set to the frequency of the notch. In panel (B), a DPOAE-onset component (black arrow) disappeared after about 2 ms, leaving a low-level DPOAE of about 6.1 dB SPL. When f2 was turned off in panel (C) at 5 ms, a DPOAE complexity was observed that was mostly in-phase with the synthesized steady-state DPOAE at 15 ms (fine background trace), which was in turn of a different phase to the onset response. In panel (D), an IT at 6 kHz eliminated the onset component and resulted in a much higher-level DPOAE of 12.3 dB SPL. In panel (F) the DP-gram for the R ear of rabbit RV32 showed a similar notch at the lower frequency of f2 = 2.828 kHz. DPOAE time waveforms shown in panels (G)–(I) were again collected with the f2-primary tone set to this lower notch frequency. In panel (G), the onset complexity emerged around 1 ms and then descended into the NF by around 3.5 ms. In panel (H), when the f2 was turned off at 5 ms, a complexity arose that was close to 180° out-of-phase with the initial onset complexity. In panel (I), an IT presented above f2 at 3.56 kHz eliminated the complexities and brought the DPOAE up out of the NF to approximately 25 dB SPL. These findings provide evidence for instances when sharp notches in DP-grams can be attributed to the cancellation of two groups of DPOAE components that are approximately 180° out-of-phase.
Figure 4F illustrates a similar notch also obtained with equal-level primaries at L1 = L2 = 75 dB SPL for a different subject (R ear of rabbit RV32) at a lower frequency (f2 = 2.828 kHz). Again, to the right of this plot are shown DPOAE time waveforms obtained at a standard f2/f1 ratio of 1.25, with the f2 frequency placed at the frequency of the notch, i.e., at 2.828 kHz. In Fig. 4G it is easy to appreciate the onset complexity (black arrow), which then rapidly decreased into the NF for this particular notch. In Fig. 4H, when f2 was turned off at 5 ms, a complexity arose, which was close to 180° out-of-phase with the onset complexity (open arrow). And, when the f2 tone was turned back on at 11 ms, the original onset complexity re-emerged with its original phase largely intact. As illustrated in Fig. 4I, when a 75-dB SPL IT was placed above f2 at 3.56 kHz, the depth of the notch (not shown), along with the onset component, was again reduced, and the DPOAE level increased from out of the NF, at approximately 0 to −5 dB SPL, to 25 dB SPL. These examples demonstrate that in some instances notches in rabbit DP-grams apparently arise from the cancellation of two out-of-phase regions of distributed DPOAE components, one region presumably generated near f2, and the other well basal to this BM location.
Hypothesized role of distributed DPOAE components in producing DPOAE time waveform complexities
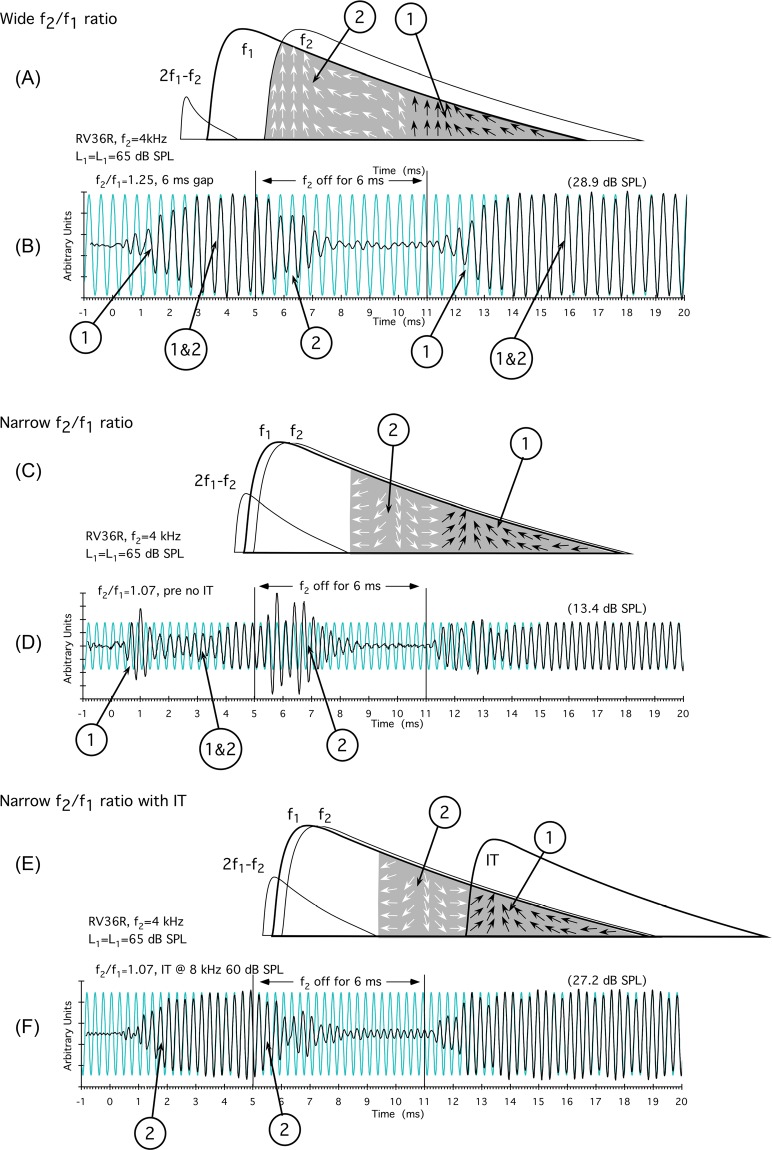
The cartoon in Fig. 5A is designed to represent the optimal f2/f1-ratio (i.e., 1.25) situation in the rabbit where TW envelopes are maximally separated. In this instance, the phase of basal DPOAE components (1, small black arrows) was similar to that of more apically generated components (2, small white arrows), and the majority of components add in-phase to produce the DPOAE measured in the ear canal. In the corresponding DPOAE-waveform data shown Fig. 5B for rabbit RV36, it is hypothesized that basal components (1) appeared first, thus accounting for the gradual onset of the time waveform. At steady-state (1&2), both basal and more apical DPOAE components added in-phase, and no complexities were observed. When f2 was turned off basal components diminished first leaving long-latency apical components (2) to decay. Subsequently, when f2 was turned back on at 11 ms, the onset process repeated.
Figure 5.
(Color online) Cartoons and representative time waveforms for wide [(A),(B)], narrow [(C),(D)], and narrow [(E),(F)] f2/f1 ratios in the presence of an IT illustrating how the interaction of distributed DPOAE components can give rise to observed complexities in DPOAE time waveforms. For the schematic in panel (A), at the optimal f2/f1 ratio, apical (#2, white arrows) and basal (#1, black arrows) DPOAE components are largely in-phase. In the time-domain data of panel (B), shorter latency basal components arose at #1 and added to longer latency more apical components (#1&2), but because they were largely in-phase, no complexities were apparent. Likewise, when f2 was turned off, shorter latency basal components decayed first leaving the long-latency apical components at #2 to decay gradually. The onset process repeated when f2 was turned back on at 11 ms. As shown in the narrow f2/f1-ratio diagram of panel (C), phase varies rapidly and apical components at #2 are mostly out-of-phase with those generated more basally at #1. In panel (D), onset complexities occurred in the time-domain waveforms when basal components at #1 appeared first. At narrow ratios, as f2 components added out-of-phase in #1&2, the waveform decreased in amplitude. When f2 was turned off, a large offset complexity was observed composed largely of longer latency apical components as indicated at #2, since canceling short latency more basal components had died out. In the bottom panel, also at narrow f2/f1 ratios, the diagram in panel (E) illustrates that the introduction of an IT sufficiently basal to the primary tones leaves mostly apically generated DPOAE components at #2. In this instance, the DPOAE time waveform in panel (F) was similar to the condition when all components were in-phase at standard f2/f1 ratios as shown above in panel (B). #1: Region of time waveform largely composed of DPOAE components generated considerably basal to f2; #2: Region of time waveform dominated by DPOAE components generated more apically closer to f2; #1&2: Region of time waveform where distributed components are added together with the results dependent upon their phase (see text for more details).
In the schematic of Fig. 5C, the f1 and f2 TW envelopes are drawn to illustrate the situation for a very narrow f2/f1 ratio of 1.07. At these narrow ratios, it is postulated that more apical components (2, white arrows) are largely out-of-phase with basal DPOAE components (1, black arrows). In the time-domain data shown in Fig. 5D for the same rabbit, basal components appeared early (1), giving rise to an onset complexity that was then largely canceled (1&2) by out-of-phase components arising more apically. When f2 was turned off, a large offset component consisting of mostly apical DPOAE wavelets (2) was observed.
In the illustration in Fig. 5E, an IT was introduced that “removed” basal DPOAE components (1) and left primarily apical elements. In the time-domain results shown in Fig. 5F, again, for rabbit RV36, the IT eliminated the onset complexity, and a gradual ramp up to a steady-state level was observed for more apical DPOAE components (2). When f2 was turned off, these same apical generators (2) decayed without exhibiting as much of an offset component as the one observed in Fig. 5D. The lack of an offset response can be explained by the fact that in this situation the DPOAE was at a relatively steady-state level and not in cancellation, since the IT removed the interfering basal components.
DISCUSSION
The present report details the findings of a series of experiments in rabbits that utilized a modification of the DPOAE onset-latency method originally described by Whitehead et al. (1996) to demonstrate complexities in DPOAE time waveforms that are consistent with the interaction of distributed DPOAE components. In these studies, at narrow f2/f1 ratios, short-latency onset complexities were observed in the DPOAE time waveforms. When f2 was turned off at 5 ms after the onset of the primary tones, and on again at 11 ms, a large DPOAE component was revealed throughout a significant portion of the 6-ms “off” period, which was consistent with the decay of basal components that previously were canceling the emission sources nearer to f2. The onset complexities cannot be the result of a catalyst mechanism, because only f1 and f2 were present. When an IT was introduced at a frequency basal to f2, both onset and offset complexities were eliminated as shown in Fig. 3B. It would be extremely difficult to invent a scenario where the IT somehow generated a component that canceled these complexities. Consequently, the overall findings provide corroborating time-domain evidence for the interaction of distributed DPOAE components, some of which could be removed by an IT. These findings supporting the existence of distributed DPOAE components are also relevant to several DPOAE phenomena debated in the emissions literature as addressed below. However, before addressing these issues, it is necessary to comment on how widely distributed basal DPOAE components might arise considering the majority of cochlear models restrict DPOAE generation principally to a BM region where the primary-tones overlap near the peak of the f2 TW.
Reconciling BM data with widely distributed DPOAE generation
It is well recognized that the response of the BM to a tone is compressive and nonlinear at the characteristic frequency (CF) and linear at approximately 1/3 octave and above CF (e.g., Robles and Ruggero, 2001). This compressive nonlinearity at CF is now attributed to the cochlear amplification process based upon outer hair cell (OHC) motility (e.g., Ashmore, 2008). Thus, the BM response can be viewed as “active” and nonlinear near CF, and “passive” and linear away from CF. This notion raises the question of how DPOAEs can be generated at more than an octave above the region of BM nonlinearity. For DPOAEs to be produced at these supra-CF distances, presumably at least three conditions must be met. First, there needs to be evidence for displacement of the BM at such remote locations; second, there must be a distributed nonlinearity capable of generating distortion products (DPs); and third, any DPOAEs generated remotely and measurable in the ear canal must be able to move the BM and couple into fluid pressure by some mechanism.
Regarding the first requirement, there is ample evidence for remote BM vibrations originating from studies that directly measured BM displacements. For example, Robles and Ruggero (2001) in their Fig. 2(A) show vibrations at the 10-kHz place produced by either a 70-dB SPL, 2-kHz tone, which, in this case, was 2.3 octaves away from the CF, or by a 50-dB SPL, 3-kHz tone that was 1.7 octaves away from the same 10-kHz CF. Additional data from Rhode and Recio (2000) showed BM responses to 50-dB SPL stimuli at about 2 octaves from the CF [see their Figs. 5(A) and 11(A)]. The above findings, not to mention the tails of eighth-nerve fiber tuning curves, provide ample evidence for mechanical displacement, that in conjunction with a distributed nonlinearity could be responsible for the wide spread generation of DPOAE wavelets from BM regions considerably basal to f2. Interestingly, the levels at about 65 dB SPL and above at which the BM responds at these remote basal regions corresponds to levels where evidence for widely distributed DPOAE components is most prominent in rabbits and other species including humans (Martin et al., 1999, 2010, 2011).
Although still somewhat debatable, the mechanoelectrical transduction (MET) channels of the OHC stereocilia have been implicated as the source of the nonlinearity responsible for DPOAEs, thus providing a means for DPOAE generation whenever stereocilia bundles are deflected. The presumed role of METs in DPOAE generation is based upon a collection of studies demonstrating that neither BM nonlinearity, nor OHC motility, is required to obtain measurable DPOAEs. One notable example supporting the notion that stereocilia micromovements are intimately involved in the generation of DPOAEs is the demonstration that prestin-null mice (Liberman et al., 2004) still display DPOAEs at high primary-tone levels in the absence of OHC motility. It has also been demonstrated that DPOAEs are lacking in mutant Strc-/- mice when the horizontal top connectors between adjacent stereocilia tips are absent, even when all other measures of cochlear function are near normal (Verpy et al., 2008), again implicating the hair bundle as having a critical role in DPOAE generation.
Additionally, the early work of Whitehead et al. (1992b) showed that near-normal level DPOAEs were obtained from rabbit ears shortly after death, or after the administration of ethacrynic acid at mid- to high primary-tone levels, while those elicited by lower primary-tone levels disappeared. However, following complete destruction of the OHCs produced by dosing with gentamicin followed by ethacrynic acid, all measurable DPOAEs were eliminated. Similar findings in a series of studies by Avan and colleagues (Mom et al., 2001; Avan et al., 2003; Carvalho et al., 2004) demonstrated not only the existence of DPOAEs elicited by high primary-tone levels after various cochlear insults, but also that these DPOAEs retained a degree of frequency specificity. Together, these earlier findings support the more recent “molecular” studies demonstrating that the nonlinearity of the BM at CF is not essential for DPOAE generation. In these cases, DPOAEs exist when stimulus levels are sufficient to compensate for the lack of OHC amplification, i.e., the final stage of the OHC-feedback loop. Also, the fact that DPOAEs are robust in frogs, lizards, and chickens (e.g., Bergevin et al., 2008) representing species in which the BM response is substantially different, or absent, is also consistent with these suggestions. In summary, the above findings strongly suggest that passive linear movements of the BM can produce DPOAEs if these displacements are sufficient to open the MET channels.
Overall, then, there is ample evidence for at least two of the requirements necessary to support the notion that DPOAEs can be generated at remote locations more than an octave above CF. These include directly measured BM displacements remote from CF and a distributed nonlinearity (MET channels of the OHC stereocilia) responsible for distortion generation. However, it still can be argued, based upon BM stiffness well basal to CF, that these DPOAEs cannot move the BM and, thus couple into the cochlear fluids to appear as DPOAEs in the ear canal. It is generally assumed that stereocilia-based nonlinearities create DPs that are reverse transduced into mechanical distortions via OHC motility (Liberman et al., 2004), which provides the necessary link to provide this coupling. However, prestin-null mice demonstrate that at high stimulus levels, at least near CF, the stereocilia are sufficiently well coupled into the cochlear partition in the absence of OHC motility to drive the middle ear in reverse and produce DPOAEs. This ability of the stereocilia to drive the BM in the absence of OHC motility, of course, becomes more problematic at the octave distances discussed here where the BM in response to the much lower CF is presumably very stiff.
In the defense of basal DPOAE components, it is worth considering that BM measurements, in even the most pristine preparations, probably represent situations where some slight threshold shift exists due to the invasiveness of the surgery resulting, perhaps, in an underestimation of the levels of BM vibration remote from CF. Importantly, we have routinely observed that following noise-induced temporary threshold shifts, or the administration of ethacrynic acid, evidence for basal components such as suppression/enhancement above f2 exhibit protracted recovery times (Martin et al., 1999), thus demonstrating the lability and sensitivity of these phenomena. Most of our prior studies supporting the existence of basal DPOAE components (Martin et al., 1999, 2010, 2011) were performed in normal, awake, or lightly anesthetized animals where the most sensitive aspects of cochlear mechanics are still fully functional. It is also interesting to speculate that perhaps active hair-bundle motility may contribute to amplification in the mammalian cochlea (Nin et al., 2012). This amplification may provide a means for DPOAEs to move the BM and couple DPOAEs into the cochlear fluid in normal ears, even in regions where the BM response is linear. Obviously, the role of widely distributed DPOAE components needs further verification. However, if present, as the bulk of our findings obtained in a variety of species strongly supports, their existence may help explain a variety of cochlear phenomena.
Relevance to DP-gram notches
Experimental subjects used in laboratory studies can show prominent notches in their DP-grams when f1 and f2 are swept, or as primary-tone levels, i.e., L1 and L2, are systematically altered to obtain a DPOAE input/output or response-growth function. Early on, such sharp notches were typically observed to be associated with a 180°-phase difference in rabbits (Whitehead et al., 1992a) and gerbils (Mills et al., 1993; Mills and Rubel, 1994; Mills, 1997). Both sets of investigators attributed these notches to the interaction of two DPOAE sources. Mills (1997) specifically hypothesized the existence of an f2 source that was 180° out-of-phase with a more basal source as the explanation for these sharp nulls. More recently, it was shown that nulls or notches can arise within a single nonlinearity (Lukashkin and Russell, 1999; Lukashkin et al., 2002), thus inferring that two DPOAE sources might not be required to produce sharp nulls in the DPOAE frequency/level space.
Fahey et al. (2008) offered a similar singular nonlinearity explanation for the notches observed in rabbit DPOAE responses. In both of these instances, the conclusions were based on similarities between data derived from experimental models and data actually observed in live preparations, where DPOAE stimulus parameters were systematically manipulated. Interestingly, Lukashkin and Russell (2001) attributed the lack of similar sharp nulls in human DPOAEs to a modification in the operating point of the cochlear nonlinearity. It is important to note that in studies like those noted above, direct experimental tests aimed at ruling out the two-source hypothesis originally envisioned by Mills (1997) were lacking.
Martin et al. (2010, 2011) recently demonstrated in rabbits and other laboratory animals that there is little or no evidence of DPOAE components reflected from the fdp. These findings are consistent with the lack of any effect of an IT placed near fdp (see Fig. 2) on the DPOAE complexities observed in the DPOAE time waveforms. Consequently, the reflection source cannot be responsible for creating the observed DP-gram notches, at least in rabbits, and most likely in other laboratory species as well.
In the present study, similar sharp nulls in DP-grams were observed [e.g., Figs. 4A, 4F], and the mechanism for their existence revisited by examining DPOAEs in the time domain [Figs. 4B, 4G] collected at the notch. Under this condition, with f2 placed at the notch frequency, an onset complexity was observed [Figs. 4B, 4G] that subsequently diminished to result in a low-level, steady-state DPOAE time waveform. In this same situation, when f2 was turned off [Figs. 4C, 4H], a large waveform appeared that was out-of-phase with the initial short-latency onset component (compare phases of the two components to the synthesized background phase). These findings strongly suggest that the cancellation of two DPOAE components as originally proposed by Mills (1997) can explain the notch observed in the present circumstances. This conclusion is reinforced by the findings shown in Figs. 4D, 4I, where an IT placed above f2 largely eliminated the waveform complexities and increased the DPOAE level by approximately 6 to 25 dB SPL, depending upon the particular rabbit being tested. The results support the notion of distributed DPOAE components, with some generated near f2 and others generated more remotely, interacting with different phase relationships similar to the circumstances diagrammed in Figs. 5C, 5E. However, for these two sets of DP-gram primaries, the conditions are such that the two distributed DPOAE components were significantly out-of-phase for one rabbit [Fig. 4C], and almost exactly 180° out-of-phase with one another for the other subject [Fig. 4H]. Overall, these time-domain data, as well as an overwhelming amount of evidence reviewed in Martin et al. (2010) supporting the existence of basal DPOAE components, favor a multiple-source explanation for notches in the rabbit and other laboratory animal DP-grams.
Finally, in a single-source formulation, one would expect notches in DPOAEs to coincide with notches measured for DPs on the BM, since they would presumably originate from the same source. This was not the case for direct comparisons of BM DPs and ear-canal DPOAEs, although the correspondence was close (Rhode, 2007). In Shera and Guinan (2007), in their Figs. 2(A) and 2(B) comparing DPOAEs to intra-cochlear DPOAEs measured indirectly by interacting a probe tone with the primary 2f1-f2 DPOAE to produce a secondary DPOAE (see Whitehead et al., 1993; Shera and Guinan, 2007), there is a very pronounced notch in the ear-canal DPOAE near an f2/f1 ratio of 1.4 that is not in the inferred intra-cochlear DP. We have recently obtained similar discrepancies between notches in rabbit f2/f1-DPOAE ratio functions, and the inferred intra-cochlear DP ratio function (Stagner et al., 2013). Presumably, this outcome would be impossible to observe, if the notch was produced within a single saturating nonlinearity responsible for generating the primary DPOAE. Thus, cancellation appears to occur for distributed DPOAE components directed toward the ear canal, but not for mostly in-phase DPOAE components directed toward the fdp (see Sec. 4C below).
Relevance to the f2/f1-ratio function
A major finding of the present study was that as the f2/f1 ratio was decreased and the corresponding DPOAE magnitude diminished, complexities were observed at both the onset of the primary tones, and again when f2 was turned off [see Figs. 1E, 1F, 1G, 1H]. It was hypothesized that at narrow f2/f1 ratios, these observations resulted from interactions of distributed and largely out-of-phase DPOAE components [see Fig. 5C]. A long-standing debate in the literature concerns the factors responsible for the inverted U-shaped f2/f1-ratio function, especially the decrease in DPOAE magnitude as the f2/f1 ratio approaches 1. Potential explanations for this phenomenon, which were reviewed in Fahey et al. (2006), have included a second filter, suppression by the primary tones, cancellation due to a re-emission from the fdp, even-order nulling that produces a canceling of the DPOAE, and cancellation of the DPOAE due to multiple sources that add vectorially in the ear canal.
To address the second-filter hypothesis, Fahey et al. (2006) designed a study in rabbits where there would be minimal vector cancellation of multiple DPOAE sources. Consequently, with phase-cancellation minimized, if a second filter were operating, then the f2/f1-ratio function should still be apparent. In this experiment, DPOAEs were selected (e.g., f2-f1, f2-2f1, f2-3f1, f2-4f1) so that the f1 tone was not undergoing a rapid phase change at the site of DPOAE generation, because f1 was significantly lower in frequency than f2. Since none of these DPOAEs showed the classical bandpass shape, it was assumed that there was no second filter in operation. As a result, Fahey et al. (2006) concluded that in the normal situation the f2/f1-ratio function was a manifestation of “wave interference due to the vectorial summation of sources with rapidly changing phases.”
Shera and colleagues (Shera, 2003; Shera and Guinan, 2008) proposed a similar mechanism based on modeling results. In the model they proposed, as the f2/f1 ratio approached 1, phase cancellation occurred for DPOAE wavelets traveling in the backward direction toward the ear canal. Conversely, narrow f2/f1 ratios tend to cause forward traveling DPOAE wavelets to add more or less in-phase. This effect imparts “directionality” to the DPOAEs, so that the distortion “radiates” primarily in the forward direction toward fdp. The interplay of these two opposing factors eventually results in the reduction of DPOAE levels in the ear canal at narrow f2/f1 ratios when the tendency for in-phase forward-traveling wavelets dominates. Central to this formulation is the assumption that the bulk of all surviving DPOAE wavelets emerge due to phase interactions occurring within or near the peak of the TW (Shera, 2003).
The present findings also support the notion that the shape of the f2/f1-ratio function is determined by cancellation of multiple DPOAE components. At standard f2/f1 ratios of around 1.25 in the rabbit, backward-traveling wavelets are presumably largely in-phase. However, as the f2/f1 ratio is decreased, these wavelets assume differing phases depending upon their region of generation. Complexities appear in the DPOAE time-domain waveforms, because wavelets with short latencies (basal regions) arrive in the ear canal first before they eventually add with longer-latency components from apical regions to achieve a steady-state response. This formulation can be seen as a departure from the above notions in that the generation of the critical DPOAE wavelets does not seem to be confined to the peak regions of the TW. The present time-domain findings are consistent with previous findings in rabbit subjects (Martin et al., 2010, 2011) where interactions occur between DPOAE components generated near f2, and those produced substantially basal to this place. These suggestions are supported by the fact that in the time domain, DPOAE-onset latencies were on the order of 0.5 ms for f2 frequencies at 4 kHz (see Figs. 123). However, when f2 was turned off [e.g., Fig. 1F], latencies for the DPOAE to decay to NF levels were often as long as 3.5 ms. Presumably these long-latency components were generated much nearer the 4-kHz location. That components canceling from relatively remote locations can result in the f2/f1-ratio effect is further supported by the introduction of ITs above f2. In this situation, DPOAE time-waveform complexities were eliminated and the DPOAE magnitude increased [see Fig. 3B] when the IT was an octave above f2. Overall, the present findings support the notion that the f2/f1-ratio function results from vector cancellation of DPOAE sources; however, these components appear to be distributed along much of the extent of the overlap of the f1 and f2 TW envelopes. Perhaps the fundamental difference between the above findings and the model results (Shera, 2003) was the primary-tone levels utilized. Model findings were based upon “low stimulus levels” where DPOAE wavelets are confined largely to the peak of the TW. Since the present findings were collected with L1 = L2 = 65 dB SPL, which are relatively moderate primary levels in the rabbit, it may not be surprising that the DPOAE components were more widely distributed. Nevertheless, these components seem to be similar to the model results in that at narrow f2/f1 ratios, the distributed reverse-traveling components tend to be of different phases and thus cancel each other.
Relevance to IDWP
There has been considerable debate regarding the mode of reverse propagation of DPOAEs from their generation sites to the ear canal. Traditional views maintain that the DPOAE is propagated like the forward TW via a transverse pressure wave (e.g., Shera et al., 2006, 2007). This mode of travel requires that the latency be equal to substantially more than the one-way delay to the f2 place on the BM. Recently, Ren and colleagues (Ren, 2004; He et al., 2008, 2010) have conducted a number of experiments where they were unable to detect reverse-DPOAE TWs between the presumed DPOAE generation region and the stapes. However, they detected forward TWs and found that the stapes vibrated earlier than the BM. These investigators interpreted their findings as evidence for a reverse propagation via a compression wave. To replicate and extend the above findings, de Boer and associates (de Boer et al., 2008) performed similar experiments, and also obtained a negative-phase slope for the measured DPOAE indicating that the DPOAE was traveling from the cochlear base to apex. These investigators coined the term “inverted direction of wave propagation” (IDWP) for this phenomenon. The latter results corroborated those of Ren and associates mentioned above and appear to contradict classical views of cochlear mechanics.
To obtain a more detailed insight into this problem, Vetesnik and Gummer (2012) compared the data of Ren and colleagues (Ren, 2004; He et al., 2008, 2010) to simulations of their experiments in a nonlinear cochlear model of DPOAE generation. From this analysis, they concluded that the appearance of the IDWP for DPOAEs might have been due to the DPOAE being at least partially generated basal to the measurement site. If this were the case, then one would expect a negative-phase slope since the DPOAE TW would, in fact, be traveling toward the apex from their vantage point.
The present study supplies new experimental evidence that supports Vetesnik and Gummer's (2012) conclusion. At narrow f2/f1 ratios, where much of the data supporting IDWP were obtained, the present findings revealed complexities in the DPOAE time waveforms. The short latency of the DPOAE-onset complexities and the evidence for their distributed nature based upon the effects of the ITs presented above f2 demonstrate that in these narrow-ratio situations DPOAEs behave as widely distributed sources with many components generated well basal to f2. Thus, based upon modeling results and experimental evidence for the distributed generation of DPOAEs, this potentially confounding factor needs to be considered, or ruled out, before it can be concluded that an IDWP occurs in the cochlea. Finally, both the short-latency onset and longer offset complexities are consistent with distributed components interacting either in- or out-of-phase with corresponding latency differences due to remote sites of generation.
Conclusions
The present findings demonstrated complexities in DPOAE time waveforms as f2/f1 ratios were decreased both at the onset of the primaries and when f2 was turned off. The most reasonable explanation for these time-domain complexities was that they were based upon the interaction of distributed DPOAE components. This interpretation is reinforced by the fact that such complexities could be removed by the presentation of ITs above f2. However, the fact that they were apparent in the absence of a third tone (i.e., IT) supports a host of previous research (see Martin et al., 2010) demonstrating that catalyst effects of the IT are negligible, and that phenomena such as suppression/enhancement of DPOAE by ITs above f2 (Martin et al., 1999, 2003) represent the removal of DPOAE components and not their creation by the third tone. Additionally, distributed DPOAE components most likely play a significant role in creating the commonly observed f2/f1-ratio function and in the studies of Ren and associates may have also been confused for an IDWP effect. Finally, it was shown that notches in DP-grams can result from apparent cancellations of multiple DPOAE components and are not necessarily based upon nulling within the cochlear nonlinearity. Overall, it seems apparent that the distributed nature of DPOAE generation most certainly plays a role in many emission phenomena, and that this aspect of DPOAE generation deserves significant attention in future studies.
ACKNOWLEDGMENTS
This work was supported by the VA Loma Linda Healthcare System and by grants from NIH (Grant No. DC000613) and the Veterans Administration (VA/RR&D Grant Nos. C7107R and C6212L). The authors thank Alisa Hetrick for technical assistance.
References
- Ashmore, J. (2008). “Cochlear outer hair cell motility,” Physiol. Rev. 88, 173–210. 10.1152/physrev.00044.2006 [DOI] [PubMed] [Google Scholar]
- Avan, P., Bonfils, P., Gilain, L., and Mom, T. (2003). “Physiopathological significance of distortion-product otoacoustic emissions at 2f1-f2 produced by high- versus low-level stimuli,” J. Acoust. Soc. Am. 113, 430–441. 10.1121/1.1525285 [DOI] [PubMed] [Google Scholar]
- Bergevin, C., Freeman, D. M., Saunders, J. C., and Shera, C. A. (2008). “Otoacoustic emissions in humans, birds, lizards, and frogs: evidence for multiple generation mechanisms,” J. Comp. Physiol. A 194, 665–683. 10.1007/s00359-008-0338-y [DOI] [PMC free article] [PubMed] [Google Scholar]
- Carvalho, S., Mom, T., Gilain, L., and Avan, P. (2004). “Frequency specificity of distortion-product otoacoustic emissions produced by high-level tones despite inefficient cochlear electromechanical feedback,” J. Acoust. Soc. Am. 116, 1639–1648. 10.1121/1.1777873 [DOI] [PubMed] [Google Scholar]
- de Boer, E., Zheng, J., Porsov, E., and Nuttall, A. L. (2008). “Inverted direction of wave propagation (IDWP) in the cochlea,” J. Acoust. Soc. Am. 123, 1513–1521. 10.1121/1.2828064 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fahey, P. F., Stagner, B. B., Lonsbury-Martin, B. L., and Martin, G. K. (2000). “Nonlinear interactions that could explain distortion product interference response areas,” J. Acoust. Soc. Am. 108, 1786–1802. 10.1121/1.1308048 [DOI] [PubMed] [Google Scholar]
- Fahey, P. F., Stagner, B. B., and Martin, G. K. (2006). “Mechanism for bandpass frequency characteristic in distortion product otoacoustic emission generation,” J. Acoust. Soc. Am. 119, 991–996. 10.1121/1.2146088 [DOI] [PubMed] [Google Scholar]
- Fahey, P. F., Stagner, B. B., and Martin, G. K. (2008). “Source of level-dependent minima in rabbit distortion product otoacoustic emissions,” J. Acoust. Soc. Am. 124, 3694–3707. 10.1121/1.3003078 [DOI] [PMC free article] [PubMed] [Google Scholar]
- He, W., Fridberger, A., Porsov, E., Grosh, K., and Ren, T. (2008). “Reverse wave propagation in the cochlea,” Proc. Natl. Acad. Sci. U.S.A. 105, 2729–2733. 10.1073/pnas.0708103105 [DOI] [PMC free article] [PubMed] [Google Scholar]
- He, W., Fridberger, A., Porsov, E., and Ren, T. (2010). “Fast reverse propagation of sound in the living cochlea,” Biophys. J. 98, 2497–2505. 10.1016/j.bpj.2010.03.003 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kalluri, R., and Shera, C. A. (2001). “Distortion-product source unmixing: A test of the two-mechanism model for DPOAE generation,” J. Acoust. Soc. Am. 109, 622–637. 10.1121/1.1334597 [DOI] [PubMed] [Google Scholar]
- Kemp, D. T. (2002). “Exploring cochlear status with otoacoustic emissions—The potential for new clinical applications,” in Otoacoustic Emissions Clinical Applications, edited by Robinette M. S. and Glattke T. J. (Thieme, New York: ), pp. 1–47. [Google Scholar]
- Kim, D. O. (1980). “Cochlear mechanics: implications of electrophysiological and acoustical observations,” Hear. Res. 2, 297–317. 10.1016/0378-5955(80)90064-7 [DOI] [PubMed] [Google Scholar]
- Liberman, M. C., Zuo, J., and Guinan, J. J., Jr. (2004). “Otoacoustic emissions without somatic motility: Can stereocilia mechanics drive the mammalian cochlea?,” J. Acoust. Soc. Am. 116, 1649–1655. 10.1121/1.1775275 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lukashkin, A. N., Lukashkina, V. A., and Russell, I. J. (2002). “One source for distortion product otoacoustic emissions generated by low- and high-level primaries,” J. Acoust. Soc. Am. 111, 2740–2748. 10.1121/1.1479151 [DOI] [PubMed] [Google Scholar]
- Lukashkin, A. N., and Russell, I. J. (1999). “Analysis of the f2-f1 and 2f1-f2 distortion components generated by the hair cell mechanoelectrical transducer: Dependence on the amplitudes of the primaries and feedback gain,” J. Acoust. Soc. Am. 106, 2661–2668. 10.1121/1.428096 [DOI] [Google Scholar]
- Lukashkin, A. N., and Russell, I. J. (2001). “Origin of the bell-like dependence of the DPOAE amplitude on primary frequency ratio,” J. Acoust. Soc. Am. 110, 3097–3106. 10.1121/1.1417525 [DOI] [PubMed] [Google Scholar]
- Martin, G. K., Stagner, B. B., Chung, Y. S., and Lonsbury-Martin, B. L. (2011). “Characterizing distortion-product otoacoustic emission components across four species,” J. Acoust. Soc. Am. 129, 3090–3103. 10.1121/1.3560123 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Martin, G. K., Stagner, B. B., Fahey, P. F., and Lonsbury-Martin, B. L. (2009). “Steep and shallow phase gradients distortion product otoacoustic emissions arising basal to the primary tones,” J. Acoust. Soc. Am. 125, EL85–EL92. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Martin, G. K., Stagner, B. B., Jassir, D., Telischi, F. F., and Lonsbury-Martin, B. L. (1999). “Suppression and enhancement of distortion-product otoacoustic emissions by interference tones above f2. I. Basic findings in rabbits,” Hear. Res. 136, 105–123. 10.1016/S0378-5955(99)00119-7 [DOI] [PubMed] [Google Scholar]
- Martin, G. K., Stagner, B. B., and Lonsbury-Martin, B. L. (2010). “Evidence for basal distortion-product otoacoustic emission components,” J. Acoust. Soc. Am. 127, 2955–2972. 10.1121/1.3353121 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Martin, G. K., Villasuso, E. I., Stagner, B. B., and Lonsbury-Martin, B. L. (2003). “Suppression and enhancement of distortion-product otoacoustic emissions by interference tones above f2: II. Findings in humans,” Hear. Res. 177, 111–122. 10.1016/S0378-5955(03)00028-5 [DOI] [PubMed] [Google Scholar]
- Mills, D. M. (1997). “Interpretation of distortion product otoacoustic emission measurements. I. Two stimulus tones,” J. Acoust. Soc. Am. 102, 413–429. 10.1121/1.419763 [DOI] [PubMed] [Google Scholar]
- Mills, D. M., Norton, S. J., and Rubel, E. W. (1993). “Vulnerability and adaptation of distortion product otoacoustic emissions to endocochlear potential variation,” J. Acoust. Soc. Am. 94, 2108–2122. 10.1121/1.407483 [DOI] [PubMed] [Google Scholar]
- Mills, D. M., and Rubel, E. W. (1994). “Variation of distortion product otoacoustic emission with furosemide injection,” Hear. Res. 77, 183–199. 10.1016/0378-5955(94)90266-6 [DOI] [PubMed] [Google Scholar]
- Mom, T., Bonfils, P., Gilain, L., and Avan, P. (2001). “Origin of cubic difference tones generated by high-intensity stimuli: Effect of ischemia and auditory fatigue on the gerbil cochlea,” J. Acoust. Soc. Am. 110, 1477–1488. 10.1121/1.1390337 [DOI] [PubMed] [Google Scholar]
- Nin, F., Reichenbach, T., Fisher, J. N. A., and Hudspeth, J. A. (2012). “Contribution of active hair-bundle motility to nonlinear amplification in the mammalian cochlea,” Proc. Natl. Acad. Sci. U.S.A. 109, 21076–21080. 10.1073/pnas.1219379110 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ren, T. (2004). “Reverse propagation of sound in the gerbil cochlea,” Nat. Neurosci. 7, 333–334. 10.1038/nn1216 [DOI] [PubMed] [Google Scholar]
- Rhode, W. S. (2007). “Distortion product otoacoustic emissions and basilar membrane vibration in the 6–9 kHz region of sensitive chinchilla cochleae,” J. Acoust. Soc. Am. 122, 2725–2737. 10.1121/1.2785034 [DOI] [PubMed] [Google Scholar]
- Rhode, W. S., and Recio, A. (2000). “Study of mechanical motions in the basal region of the chinchilla cochlea,” J. Acoust. Soc. Am. 107, 3317–3332. 10.1121/1.429404 [DOI] [PubMed] [Google Scholar]
- Robles, L., and Ruggero, M. A. (2001). “Mechanics of the mammalian cochlea,” Physiol. Rev. 81, 1305–1352. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shera, C. A. (2003). “Wave interference in the generation of reflection- and distortion-source emissions,” in Biophysics of the Cochlea: Molecules to Models, edited by Gummer A. W. (World Scientific Press, Singapore: ), pp. 439–453. [Google Scholar]
- Shera, C. A., and Guinan, J. J., Jr. (1999). “Evoked otoacoustic emissions arise by two fundamentally different mechanisms: A taxonomy for mammalian OAEs,” J. Acoust. Soc. Am. 105, 782–798. 10.1121/1.426948 [DOI] [PubMed] [Google Scholar]
- Shera, C. A., and Guinan, J. J., Jr. (2007). “Cochlear traveling-wave amplification, suppression, and beamforming probed using noninvasive calibration of intracochlear distortion sources,” J. Acoust. Soc. Am. 121, 1003–1016. 10.1121/1.2404620 [DOI] [PubMed] [Google Scholar]
- Shera, C. A., and Guinan, J. J., Jr. (2008). “Mechanisms of mammalian otoacoustic emission,” in Active Processes and Otoacoustic Emissions, edited by Manley G. A., Fay R. R., and Popper A. N. (Springer, New York), pp. 305–342. [Google Scholar]
- Shera, C. A., Tubis, A., and Talmadge, C. L. (2006). “Four counter arguments for slow-wave OAEs,” in Auditory Mechanisms: Processes and Models, edited by Nuttal A. L., Ren T., Gillespie P., Grosh K., and de Boer E. (World Scientific Publishing, Singapore: ), pp. 449–457. [Google Scholar]
- Shera, C. A., Tubis, A., Talmadge, C. L., de Boer, E., Fahey, P. F., and Guinan, J. J., Jr. (2007). “Allen-Fahey and related experiments support the performance of cochlear slow-wave otoacoustic emissions,” J. Acoust. Soc. Am. 121, 1564–1575. 10.1121/1.2405891 [DOI] [PubMed] [Google Scholar]
- Stagner, B. B., Martin, G. K., and Lonsbury-Martin, B. L. (2013). “What you see is not what you get: DPOAEs versus intracochlear DPs,” Assoc. Res. Otolaryngol. Abstr. 36, 29. [Google Scholar]
- Verpy, E., Weil, D., Leibovici, M., Goodyear, R. J., Hamard, G., Houdon, C., Lefevre, G. M., Hardelin, J.-P., Richardson, G. P., Avan, P., and Petit, C. (2008). “Stereocilin-deficient mice reveal the origin of cochlear waveform distortions,” Nature 456, 255–259. 10.1038/nature07380 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vetesnik, A., and Gummer, A. W. (2012). “Transmission of cochlear distortion products as slow waves: A comparison of experimental and model data,” J. Acoust. Soc. Am. 131, 3914–3934. 10.1121/1.3699207 [DOI] [PubMed] [Google Scholar]
- Whitehead, M. L., Lonsbury-Martin, B. L., and Martin, G. K. (1992a). “Evidence for two discrete sources of 2f1-f2 distortion product otoacoustic emission in rabbit: I. Differential dependence on stimulus parameters,” J. Acoust. Soc. Am. 91, 1587–1607. 10.1121/1.402440 [DOI] [PubMed] [Google Scholar]
- Whitehead, M. L., Lonsbury-Martin, B. L., and Martin, G. K. (1992b). “Evidence for two discrete sources of 2f1-f2 distortion product otoacoustic emission in rabbit: II. Differential physiological vulnerability,” J. Acoust. Soc. Am. 92, 2662–2682. 10.1121/1.404382 [DOI] [PubMed] [Google Scholar]
- Whitehead, M. L., Lonsbury-Martin, B. L., and Martin, G. K. (1993). “Measurement of 2f1-f2 excitation at the distortion-frequency place in the cochlea using ear-canal distortion products,” Assoc. Res. Otolaryngol. Abstr. 16, 395. [Google Scholar]
- Whitehead, M. L., Stagner, B. B., Martin, G. K., and Lonsbury-Martin, B. L. (1996). “Visualization of the onset of distortion-product otoacoustic emissions, and measurement of their latency,” J. Acoust. Soc. Am. 100, 1663–1679. 10.1121/1.416065 [DOI] [PubMed] [Google Scholar]