The effect of overall level on sensitivity to interaural differences of time and level at high frequencies

Abstract

For high-frequency complex stimuli, detection thresholds for envelope-based interaural time differences (ITDs) decrease with overall level. Substantial heterogeneity is, however, evident among the findings concerning the rate at which thresholds decline with level. This study investigated factors affecting the influence of overall level on threshold ITDs. Thresholds were measured as a function of overall level for 4-kHz-centered “targets” in three experiments focusing, respectively, on stimulus-type (sinusoidally amplitude-modulated or “transposed” tones), modulation frequency, and details concerning low-pass noise used to mask low-frequency distortion products. Results indicated that (1) log-ITD thresholds decreased linearly with overall level; (2) slopes relating log-ITD thresholds to level did not depend significantly on stimulus type; (3) lower modulation frequencies produced greater dependencies of thresholds on overall level than did higher modulation frequencies; (4) the effect of overall level on threshold-ITDs was independent of the interaural configuration and levels of the low-pass noise maskers tested; (5) synchronously gating the low-pass noise and target produced a greater dependency of thresholds on the overall level of the target than did continuous or temporally “fringed” presentation of the noise. A fourth experiment showed that threshold interaural level differences were somewhat less affected by changes in overall level than were threshold ITDs.

INTRODUCTION

Several studies have investigated how human binaural performance depends upon the overall level of the stimuli employed. Most of those studies investigated the influence of overall level on listeners' sensitivities to changes in interaural time differences (ITDs). The strength of the effect of overall level can be expressed by the slope of the threshold ITD as a function of the overall level. Zwislocki and Feldman (1956) obtained threshold ITDs from six subjects for low-frequency pure tones while varying sensation level (SL) over a range of 80 dB. Overall, they found that threshold ITDs decreased when SL was increased from 10 to about 60 dB SL. Increases in SL beyond about 60 dB SL yielded no further decreases in threshold ITD. The results of later studies (e.g., Hershkowitz and Durlach, 1969; Smoski and Trahiotis, 1986), which also employed low-frequency, pure-tone stimuli, were consistent with those obtained by Zwislocki and Feldman.

In contrast to the homogeneity of the results obtained using low-frequency pure-tones, the results of experiments exploring the influence of overall level on threshold ITDs conveyed by high-frequency complex stimuli are less clear-cut (e.g., Nuetzel and Hafter, 1976; Smoski and Trahiotis, 1986; Dreyer and Oxenham, 2008; Bernstein and Trahiotis, 2008; Klein-Hennig et al., 2011).

Smoski and Trahiotis (1986) employed 4-kHz-centered narrow bands of noise and sinusoidally amplitude-modulated (SAM) tones and found that threshold ITDs for the noise bands decreased by a factor of about 6 when overall level was increased from approximately 35 dB SPL to 80 dB SPL. Over the same range of overall level, however, thresholds obtained with SAM tones decreased by a factor of about 25. These findings appear to differ from those of Nuetzel and Hafter (1976) who employed 3.6-kHz-centered SAM tones and observed that threshold ITDs decreased by a factor of only 1.7 as overall level was increased from 40 to 70 dB SPL.

Dreyer and Oxenham (2008) and Bernstein and Trahiotis (2008)1 obtained results consistent with those of Neutzel and Hafter (1976). The results of Dreyer and Oxenham (2008) and Bernstein and Trahiotis (2008) revealed that threshold ITDs for both 4-kHz-centered SAM tones and 4-kHz-centered transposed tones (see van de Par and Kohlrausch, 1997; Bernstein and Trahiotis, 2002) decreased by factors of between 1.4 and 1.8 as overall level was increased from 40 to 70 or from 55 to 85 dB SPL, with the decreases being slightly greater for the transposed as compared to SAM tones. Klein-Hennig et al. (2011) found that threshold ITDs measured with 4-kHz-centered SAM tones decreased by a factor of 4.0 when overall level was increased from 36 to 66 dB SPL, suggesting an effect of overall level on threshold ITDs smaller than that observed by Smoski and Trahiotis (1986) but larger than those observed in the other studies cited.

The apparent disparity among the results of studies employing high-frequency amplitude-modulated stimuli might stem from across-study differences in the details and types of stimuli employed and differences in the ranges of overall levels tested. Another factor that might have influenced the effect of overall level on threshold ITD is the presence or absence and nature of the low-frequency noise that accompanied the presentation of the high-frequency stimuli in the studies cited. Such noise is routinely used in order to impede subjects from discriminating changes in ITD on the basis of low-frequency distortion products rather than on the basis of changes in ITD within high-frequency “channels” of the auditory system. For example, Klein-Hennig et al. (2011) maintained a constant level of their low-pass noise while employing different overall levels of the high-frequency SAM-tones conveying the ITD. In contrast, Bernstein and Trahiotis (2008) maintained a constant dB difference between the overall level of their low-pass noise and the various levels of the high-frequency stimuli conveying the ITD.

The current study sought to determine whether and to what degree the relation between detection thresholds and overall level is affected by (1) the type of high-frequency stimulus employed (SAM or transposed) and the specific values of the parameters that define it (e.g., modulation frequency) and (2) details concerning accompanying low-frequency noise (e.g., its relative level, interaural configuration, and temporal gating).

METHODS

Subjects

Five normal-hearing subjects aged between 22 and 25 yr participated in the experiments. They received at least 4 h of training before collection of formal data commenced. The subjects were university students and received compensation on an hourly basis. Data are shown for only four of the subjects. The fifth subject was excluded because, for some conditions, valid thresholds (see procedure) could not be measured. In addition, when valid thresholds could be obtained from that subject, they were generally found to be highly variable.

Stimuli

Three different types of stimuli were employed. The first, ${\tilde{s}}_1$, was a SAM tone

$${\tilde{s}}_1\left(t\right)=\left[1+m\times \sin \left(2\pi f_{m}t\right)\right]\times \sin \left(2\pi f_{c}t\right),$$ (1)

where the frequency of the pure tone carrier (f_c) was 4 kHz, the modulation frequency (f_m) was either 128 Hz (default) or 32 Hz, and the modulation index (m) was 1 (i.e., the depth of modulation was 100%).

The second stimulus, ${\tilde{s}}_2$, was a transposed tone

$${\tilde{s}}_2\left(t\right)=\mathrm{HWR}\left(\sin \left(2\pi f_{m}t\right)\right)\times \sin \left(2\pi f_{c}t\right),$$ (2)

where “HWR” designates the operations of half-wave rectification and a second-order 500-Hz low-pass filtering that were applied to a 128-Hz (f_m) modulator tone. The resulting modulator was multiplied with a 4-kHz (f_c) carrier, according to the procedure described by van de Par and Kohlrausch (1997).

The third stimulus, ${\tilde{s}}_3$, was a pure tone of 128-Hz (f),

$${\tilde{s}}_3\left(t\right)=\sin \left(2\pi ft\right).$$ (3)

The signals $\tilde{s}$ were normalized by their respective root-mean-square (rms) values before multiplication with the desired amplitude factor A, in order to set the overall level to 30, 45, 60, 75, or 85 dB SPL,

$$s\left(t\right)=A\times \frac{\tilde{s}\left(t\right)}{\sqrt{\overline{{\tilde{s}}^2(t)}}}.$$ (4)

All stimuli were 300 ms in total duration and were gated simultaneously in both ears with 20-ms sine-squared ramps. If an ITD was applied, it was applied to the whole waveform prior to gating. If an interaural level difference (ILD) was applied, the level of both channels was changed without changing the sum of the left and right rms values, in order to reduce changes in the overall loudness resulting from the imposition of an ILD. This was achieved by applying the following formula:

$$s_l\left(t\right)=\frac{2\mathrm{s}\left(t\right)}{1+{10}^{\text{ILD}\left[\text{dB}\right]/20}};\hspace{1em}{s}_r\left(t\right)=\frac{2\mathrm{s}\left(t\right)}{1+{10}^{-\hspace{0.17em}\text{ILD}\left[\text{dB}\right]/20}}.$$ (5)

The effect of the constant rms was to track rather closely the “binaural amplitude increase/decrease functions” found by Keen (1972) to preservation constant loudness.

A diotic Gaussian noise, low passed at 1300 Hz, was added to the high-frequency stimuli in order to mask potential distortion products. It was produced by generating a broadband noise in the time domain, transforming it to the frequency domain, setting the power of all components above 1300 Hz to zero, and transforming the result back to the time-domain. Unless stated otherwise, the noise was presented continuously at a constant spectrum level equivalent to 25 dB SPL/Hz, yielding an overall level of 56 dB SPL.

Procedure

Threshold ITDs and threshold ILDs were each measured using a four-interval, two-alternative, forced-choice adaptive task. Each trial consisted of four 300-ms observation intervals, each separated by a 400-ms silent interval. The stimuli in the first and fourth intervals were diotic. The subject's task was to detect the presence of a right-leading ongoing interaural disparity that was presented with equal a priori probability in either the second or the third interval. The remaining interval contained a diotic stimulus. A “three-down one-up” rule was used to estimate the 79% correct point on the psychometric function (Levitt, 1971). The step-size for the adaptive track initially corresponded to a factor of 1.585 (for either ITD or ILD) and was reduced to a factor of 1.259 after two reversals and to a factor of 1.122 after four reversals. A run was terminated after 12 reversals and threshold was defined as the geometric mean of the ITD or ILD across the last eight reversals.

Conditions were blocked by overall level and all conditions within a block were run in pseudo-random order. Data collection began with the block of conditions with the highest level before moving onto the next lower level. Three consecutive estimates of threshold were obtained for each condition. Once all of the conditions had been visited, three more estimates of threshold were obtained for each condition but with the ordering of levels reversed. In this fashion, six estimates of threshold were obtained for each subject at each of the experimental conditions.2

The “final” threshold for each subject and condition was estimated by calculating the median value across the six estimates. For the conditions in which a threshold ITD was measured, a maximum ITD of 5 ms within an adaptive track was allowed. If subjects exceeded this value, the run was terminated and assigned the value “infinity.” Up to two irregular terminations of this type were possible in each condition without influencing the median. In the single case in which more than two runs were terminated irregularly by S3, no median value was derived, and the subject's data were removed from the mean across subjects for all levels using that stimulus condition. When individual subjects' results are plotted, the error bars indicate the lower and upper quartiles. This corresponds to the second and fifth rank from the sorted list of six thresholds for each condition. The median is, by definition, the mean of the third and fourth rank.

Apparatus

Stimuli were presented via Sennheiser HD 650 headphones (Sennheiser Electronic GmbH & Co. KG, Wedemark-Wennebostel, Germany) to subjects seated in a double-walled, sound-attenuating booth. Signal generation and presentation during the experiments were controlled via a computer using the AFC software package for matlab^®, developed at the Universität Oldenburg. The stimuli were generated digitally at a sampling rate of 48 kHz. The transfer function of the headphones was measured on an artificial ear (B&K 4153; Brüel & Kjær Sound & Vibration Measurement A/S, Nærum, Denmark) and equalized in order to obtain a flat (±1.5 dB) amplitude response between 0.1 and 10 kHz.

The stimulus generation and the equipment were tested by recording the response of the artificial ear to the stimuli as presented to the human listeners. Those measurements confirmed that overall level matched the desired value for all tested levels within ±1 dB. No distortion products, intermodulation products, or higher harmonics could be measured in the presence of the background noise. The background noise always had a spectrum level more than 50 dB below the level of the highest signal component, i.e., the carrier level. Measurements were performed for overall levels of 60, 75, and 85 dB SPL.

EXPERIMENTS

One data set with 44 conditions was collected and those conditions were non-exclusively grouped into four “experiments.” Three experiments were conducted in order to determine factors that influence the dependence of threshold ITD on overall level. The first experiment investigated the influence of stimulus type, i.e., a comparison of thresholds obtained using the SAM tone, the transposed tone, and the low-frequency pure tone, as described in Sec. 2. The second experiment investigated the influence of modulation frequency while the third investigated the influence of parameters of the accompanying low-pass noise. In a fourth experiment the dependence of threshold ILD was investigated for the three different types of stimuli.

Experiment 1: Level dependence of threshold ITDs for different types of stimuli

The dependence of threshold ITDs on overall level was tested for the three different stimuli described earlier: The SAM tone [Eq. 1], the transposed tone [Eq. 2], and the pure tone [Eq. 3]. The frequency of the pure tone was chosen to be 128 Hz and corresponded to the default modulation frequency of the two high-frequency waveforms. The levels of the stimuli employed were 30, 45, 60, and 75 dB SPL. Presentation of the two high-frequency waveforms was accompanied by the presentation of a continuous low-pass noise (see Sec. 2B).

Results

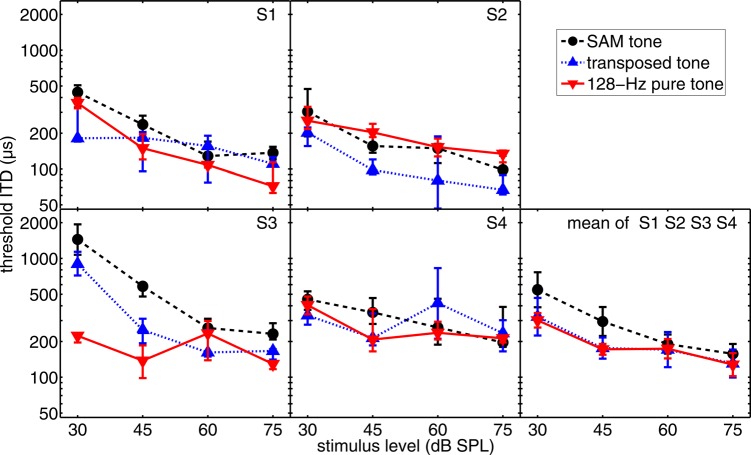
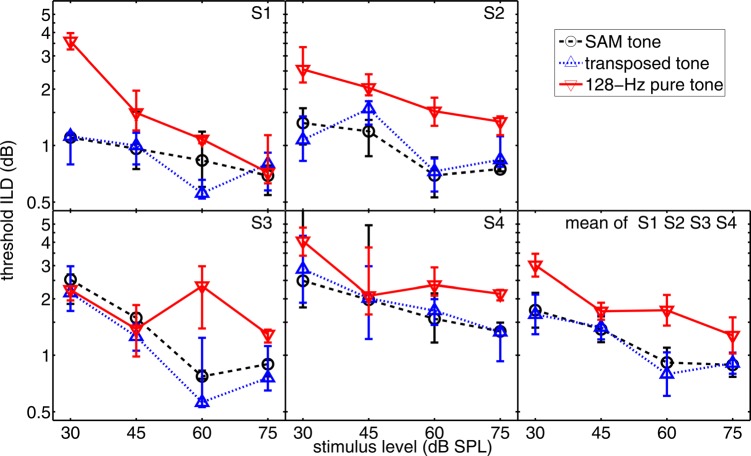
The four left-most panels of Fig. 1 show median threshold ITDs obtained from each of the four subjects (note the use of a logarithmically scaled ordinate). The remaining panel contains the geometric mean data (averaged across subjects' thresholds). In this panel the error bars indicate the geometric standard error across subjects' data.

Figure 1.

(Color online) Threshold ITD for different types of stimuli as a function of stimulus level. The SAM stimulus with f_m = 128 Hz is indicated by circles and a dashed line in this and all following figures. The transposed tone is marked by upward triangles and the pure tone by downward triangles. In the four left-most panels, the individual data of the four subjects are shown. The data points indicate the median and the error bars indicate the interquartile range from the six measurements of each condition. In the panel on the right-hand side the geometric mean across subjects is plotted, together with the geometric standard errors.

Visual inspection of Fig. 1 reveals that, for all four subjects, threshold ITDs generally decreased with increasing overall level. Substantial inter-individual differences are apparent in overall sensitivity, the shape of the functions, and the ordering of sensitivity among the three different stimulus types. Changes in threshold were not always strictly monotonic as a function of overall level, but for all subjects and conditions the threshold ITD obtained at 75 dB SPL were lower than those obtained at 30 dB SPL. Within the mean data, the steepest decrease in threshold with overall level is observed for the SAM tones (circles, dashed line).

A repeated-measures two-way analysis of variance (ANOVA) on the log-ITD data revealed a significant (assuming α = 0.05) main effect of level [F(3,6) = 8.76; p < 0.001]. There was no significant effect of stimulus type [F(2,6) = 2.6; p = 0.09] and no interaction between stimulus type and level [F(6,6) = 0.29; p = 0.94]. The proportions of variance accounted for (ω²) were determined for the two significant main effects (Hays, 1973): Level accounted for 37% of the total variance in the data, stimulus type accounted for 7%, and the interaction of the two factors accounted for 2%, indicating that the influence of presentation level is stronger than the choice of stimulus type. The total variance accounted for by the two factors including their interaction was 46%. A post hoc pair-wise comparison (Bonferroni) revealed a significant (p = 0.03) difference only between threshold ITDs for SAM stimuli and pure tone thresholds.

Experiment 2: Level dependence of threshold ITDs for different modulation frequencies

Two different modulation frequencies (128 and 32 Hz) were employed for the SAM stimulus. In addition to the overall levels tested in Experiment 1, the stimuli were also presented at a level of 85 dB SPL. The continuous low-pass noise accompanied the presentation of the stimuli.

Results

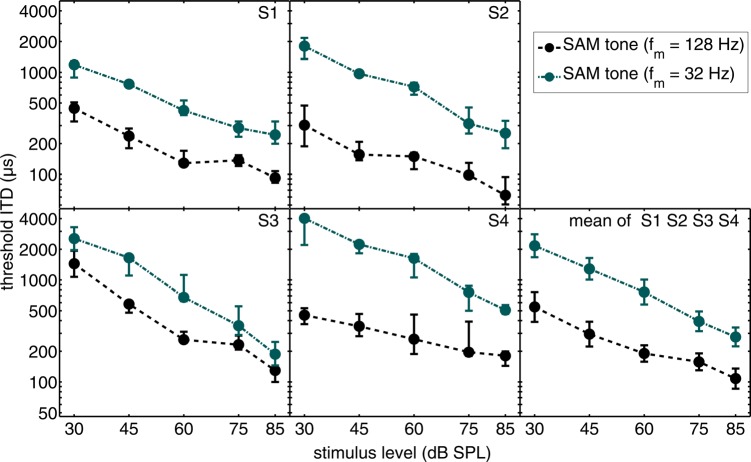
Figure 2 shows threshold ITDs for Experiment 2 in the same format as Fig. 1. For all subjects, the data reveal an essentially linear relation between log threshold ITD and overall level, as was observed for the 128-Hz SAM stimuli in Experiment 1. In addition, threshold ITDs obtained with a modulation frequency of 32 Hz were found to be uniformly larger than their counterparts obtained with a modulation frequency of 128 Hz. A repeated-measures two-way ANOVA on log-ITD indicated a significant main effect of modulation frequency [F(1,4) = 35; p < 0.001] and level [F(4,4) = 11; p < 0.001]. Level accounted for 39% of the total variance in the data, and modulation frequency accounted for 31%. The total variance accounted for by the two factors including their interaction was 73%. At an overall level of 30 dB SPL, the mean threshold ITD is about five times as large as that obtained at 85 dB SPL for the 128-Hz condition and about eight times as large as that obtained at 85 dB SPL for the 32-Hz condition. It is interesting to note that, for overall levels of 30, 45, and 60 dB SPL, the ratio of the mean threshold ITD obtained at 32 Hz and the mean threshold ITD obtained at 128 Hz is 4.0, which is precisely the ratio between the periods of the two modulation frequencies. Thus, the threshold ITDs obtained at any of these three overall levels correspond to identical threshold interaural phase differences for the two modulation frequencies. The relation was not maintained, however, for overall levels of 75 and 85 dB SPL, where the ratio dropped to 2.1 and 2.3, respectively.

Figure 2.

(Color online) Threshold ITD of SAM tones for different modulation frequencies as a function of stimulus level. The data are plotted in the same format as Fig. 1. The SAM stimulus with f_m = 128 Hz is again indicated by a dashed line and the stimulus with f_m = 32 Hz is indicated by a dashed-dotted line.

Experiment 3: Level dependence of threshold ITDs for different parameters of the accompanying low-pass noise

In this experiment, the dependence of threshold ITD on the overall level of 4-kHz-centered SAM tones (f_m = 128 Hz) was investigated while varying values of three parameters of the low-pass noise that accompanied the stimuli. Recall that, in the previous two experiments, the noise was presented continuously with an overall level of 56 dB SPL. The three parameters in this experiment were (a) the interaural configuration, (b) the gating, and (c) the overall level of the noise.

Effects arising from changes in the interaural configuration of the noise were assessed by measuring threshold ITDs for the SAM tone when the low-pass noise was presented continuously and its interaural configuration was diotic or was interaurally uncorrelated. The interaural configuration of the noise was varied parametrically with stimulus levels of 30 or 60 dB SPL.

The influence of different types of gating was explored by measuring threshold ITDs when the noise was (1) continuous, (2) gated synchronously with the SAM tone, (3) gated on 50 ms before and off 50 ms after the SAM tone (referred to as fringed condition), or (4) was absent altogether. In these conditions stimulus levels of 30 or 60 dB SPL were used. As a result of an error in the measurement protocol, the condition without low-pass noise was not measured for S1 and S3 at 30 dB SPL.

Effects resulting from changes in the spectrum level of the low-pass noise were explored by measuring threshold ITDs with a noise level relative to the signal level (the overall noise level was 4 dB lower than the target level) and comparing the results to those obtained to corresponding conditions in which the level of the noise was held constant at 56 dB SPL (Experiment 1). Threshold ITDs were measured separately for the 4-kHz-centered transposed and SAM tones (f_m = 128 Hz) at levels of 30, 45, 60, and 75 dB SPL, thus the corresponding relative noise levels were +26, +11, −4, and −19 dB, respectively.

Results

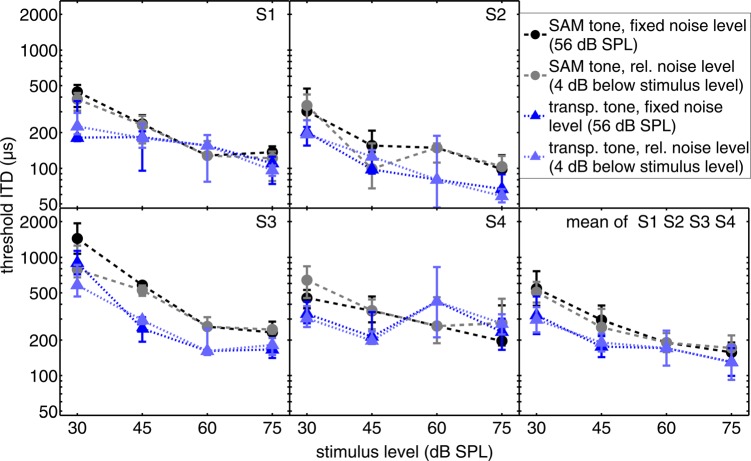
Figure 3 displays the results obtained with variations of the interaural configuration [Fig. 3a] and gating of the low-pass noise [Fig. 3b]. A repeated-measures two-way ANOVA on the data shown in Fig. 3a revealed that threshold ITDs did not differ significantly [F(1,1) = 0.17 p = 0.68] for the two interaural configurations of the noise.

Figure 3.

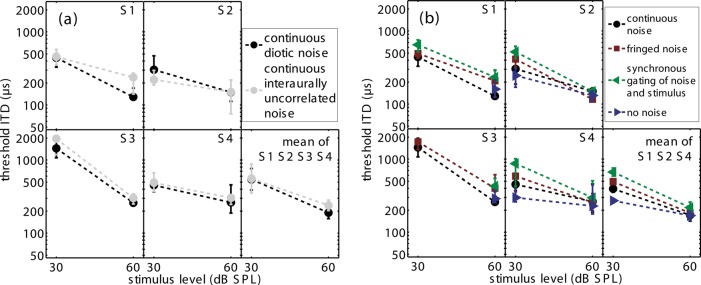
(Color online) Threshold ITD of SAM tones with f_m = 128 Hz for different configurations of the low-frequency noise at a stimulus level of 56 dB SPL. The data are plotted in the same format as before. (a) Threshold ITDs obtained with different interaural configurations of the low-frequency noise. The diotic condition is plotted in black and the condition with interaurally uncorrelated noise is plotted in gray. (b) Threshold ITDs obtained with noises gated in different manners are indicated by different symbols (circles: Continuous; square: Gated on/off 50 ms before/after the stimulus; leftward triangle: Gated on/off together synchronously with stimulus; rightward triangle: No noise). Subject S3 could not detect the lateralized target at 30 dB if the noise was gated synchronously with the stimulus and was, therefore, excluded from the calculation of the mean data.

Figure 3b displays the threshold ITDs for the four different gating conditions of the low-pass noise. When the noise was gated on and off synchronously with the high-frequency SAM tone, subject S3 was unable to perform the task at a stimulus level of 30 dB SPL. Because the conditions in which the low-pass noise was absent were only measured for S2 and S4 at both stimulus levels of 30 and 60 dB SPL, only their data were entered into a repeated-measures two-way ANOVA used to evaluate the data in Fig. 3b. The only significant effect was the main effect of level [F(1,3) = 18.6; p = 0.003]. No significant main effect of gating [F(3,3) = 1.4; p = 0.30] and no significant interaction between level and gating [F(3,3) = 0.8; p = 0.53] was found.

The results of the ANOVA notwithstanding, a visual inspection of Fig. 3b suggests that, when considered in isolation, the data obtained when the level was 30 dB SPL reveal systematic effects on threshold ITD of the type of gating of the low-pass masking noise that was employed. In fact, pairwise, one-tailed t-tests computed separately for the data of subjects S2 and S4 revealed that, for both subjects: (1) Threshold ITDs were significantly smaller in the absence of the low-pass masking noise as compared to when the noise was either temporally fringed (p = 0.003 for S2; p = 0.011 for S4) or when it was gated synchronously with the target (p = 0.002 for S2; p = 0.017 for S4); (2) threshold ITDs obtained in the continuous noise condition were significantly smaller than those obtained when the noise was gated synchronously with the target (p = 0.049 for S2; p = 0.037 for S4). No significant differences were found among the different noise gating conditions when the level of the target was 60 dB SPL.

Figure 4 shows threshold ITDs of SAM (circles) and transposed tones (upward triangles) for two different conditions each: (1) When the overall level of the low-pass masker was 4 dB below the overall level of the signal (dark symbols) and (2) when the level of the low-pass masking noise was held constant at 56 dB SPL (light-colored symbols). It is apparent that the level of the low-frequency noise, over the range of values tested, did not influence the threshold ITD [two-way repeated-measures ANOVA: F(3,3) = 0.07; p = 0.86 for SAM and F(3,9) = 0.00; p = 0.99 for transposed tones]. For both types of stimuli and for all four subjects the two different noise-level conditions result in very similar threshold ITDs at all levels. As shown in Experiment 1, there appears to be some difference between the thresholds obtained with the two different stimulus types, but those differences were not statistically significant [two-way repeated-measures ANOVA: F(1,3) = 2.8; p = 0.11 for absolute noise levels and F(1,3) = 2.5; p = 0.13 for relative noise levels].

Figure 4.

(Color online) Threshold ITD of SAM and transposed tones for different levels of the low-frequency noise as a function of stimulus level. The data are plotted in the same format as Fig. 1. The two dark plotted conditions represent measurements re-plotted from Fig. 1 measured with a constant absolute noise level (56 dB SPL). The two lighter plotted conditions were measured with a constant relative noise level of (4 dB below signal level). For the 60 dB signal level, where both the constant noise and the relative noise have a level of 56 dB, the same data is utilized for both conditions.

Experiment 4: Level dependence of threshold ILDs

In Experiment 4, the same stimuli and general procedures were employed as in Experiment 1 with the exception that threshold ILDs, rather than threshold ITDs, were measured as a function of the overall level.

Results

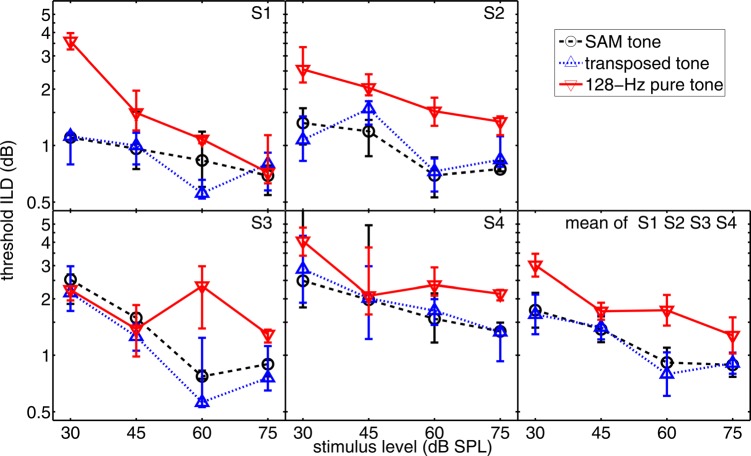
The plots in Fig. 5 display threshold ILD as a function of stimulus level for the same three stimuli employed in Experiment 1. Figure 5 reveals that the 128-Hz pure-tone stimuli (downward triangles, solid lines) generally yielded the highest thresholds among the three types of stimuli tested. This is opposite to the data shown in Fig. 1 showing (with the exception of S2) that the 128-Hz pure-tone yielded among the lowest threshold ITDs. Figure 5 further reveals that threshold ILDs obtained with SAM tones (circles, dashed lines) and transposed tones (upward triangles, dotted lines) were quite similar.

Figure 5.

(Color online) Threshold ILD for different types of stimuli as a function of stimulus level. The data are plotted in the same format as Fig. 1 with the exception that open, rather than closed, symbols are employed.

The results of a two-way repeated measures ANOVA revealed that both main effects were statistically significant. Overall level [F(3,6) = 9; p < 0.001] accounted for 33% of the variance and stimulus type [F(2,6) = 8.4; p = 0.001] for 20%. The total variance accounted for by the two factors including their interaction was 57%. Post hoc pair-wise comparisons (Bonferroni) revealed that threshold ILDs for SAM and transposed tones were not significantly different (p = 0.78), while pure tone threshold ILDs were significantly higher compared to either SAM or transposed tone (p = 0.001).

SUMMARY OF RESULTS AND DISCUSSION

The discussion will focus primarily on threshold ITDs obtained with high-frequency complex stimuli, for which only the envelope conveys the interaural cues. Only a brief comparison to the threshold ILDs measured is included. As in Sec. 1, for high-frequency complex stimuli, the results of previous studies are somewhat inconsistent with regard to the influence of overall level on the discrimination of ITDs (Nuetzel and Hafter, 1976; Smoski and Trahiotis, 1986; Bernstein and Trahiotis, 2008; Dreyer and Oxenham, 2008; Klein-Hennig et al., 2011). Over the relatively large 55-dB range of levels employed in the current study, the data obtained with each of the two types of stimuli exhibit a linear relation between log threshold ITD and overall level. Figure 6 depicts linear fits (with a logarithmic ordinate) applied to the data obtained in the current study and to the data obtained by Nuetzel and Hafter (1976); Smoski and Trahiotis (1986); Bernstein and Trahiotis (2008); Dreyer and Oxenham (2008), and Klein-Hennig et al. (2011). Each of the individual data sets in the plot has been normalized to the fitted thresholds at 85 dB SPL. Figure 6 reveals the large disparities in the slope of the functions relating threshold ITD to overall level that characterize the data across the various studies.

Figure 6.

(Color online) Normalized threshold ITDs for SAM tones as a function of stimulus level. Mean data from Fig. 2 (two conditions; circles) are re-plotted together with mean threshold ITD data obtained in earlier studies. Fits of the current studies threshold ITD data are shown as dashed lines (for f_m = 128 Hz) and dashed-dotted lines (f_m = 32 Hz). Fits to the threshold ITD data of other studies are plotted as solid lines.

The data of Smoski and Trahiotis (1986) have to be considered with care, because the threshold ITD of 25 μs they obtained at 80 dB SPL is much lower than thresholds reported in the other studies referenced above. Because Smoski and Trahiotis' high-frequency stimuli were not accompanied by low-pass masking noise, the possibility remains that the small threshold ITD they observed may have resulted from their subjects' use of low-frequency distortion. In Experiment 2, the 32-Hz modulation frequency resulted in higher threshold ITDs than did the modulation frequency of 128 Hz. This outcome is consistent with the results of earlier investigations that employed high-frequency SAM stimuli (e.g., Henning, 1974; Nuetzel and Hafter, 1981; Bernstein and Trahiotis, 2002). More importantly, this experiment revealed that lower modulation frequencies appear to result in stronger level dependencies (greater slope). The two steepest functions in Fig. 6 (disregarding the one corresponding to Smoski and Trahiotis, 1986) correspond to the data obtained by Klein-Hennig et al. (2011), who employed a modulation frequency of 50 Hz and to the data obtained in the current study using SAM tones having a modulation frequency of 32 Hz.

It remains unclear what mechanism or mechanisms are responsible for the greater level dependency observed at lower rates of modulation (as observed in Figs. 26). One potential mechanism may involve an interaction between peripheral bandpass filtering and the level-dependent compression that characterizes basilar membrane motion (Lopez-Poveda et al., 2003). In order to understand how such an interaction may operate, consider the SAM tones centered at 4 kHz that were employed in this study. At the output of an auditory filter centered at the carrier frequency, the relative attenuation of the sidebands of the stimuli would be greater at a modulation frequency of 128 Hz than at 32 Hz. This would result in there being a relative reduction in depth of modulation at the output of the filter at the higher of the two modulation frequencies. As a consequence, the peak-to-trough ratio of the envelope at the output of the filter would be lower at a modulation frequency of 128 Hz than at a modulation frequency of 32 Hz. As the level of the stimulus is increased, basilar membrane compression would be expected to “fill in” the troughs of the envelope to a greater extent at 128 Hz than would be the case at 32 Hz, counteracting potential gains in sensitivity to ITD that might come about as a result of the increase in level, per se. Based on these assumptions, the expectation would be that a smaller level dependency is observed at a modulation frequency of 128 Hz than at a modulation frequency of 32 Hz, as seen in the data.

Another mechanism that may contribute to the greater level dependency at a modulation rate of 32 Hz than at 128 Hz might involve the putative “envelope low-pass filter.” The overall decline of sensitivity to envelope ITDs with increasing modulation frequency is commonly accounted for via the inclusion of a stage of processing consisting of a 150-Hz low-pass envelope filter (e.g., Bernstein and Trahiotis, 2002). Now, if it were the case that the effective low-pass cutoff of the envelope low-pass filter decreased with increasing level, then, for modulation frequencies approaching the nominal cutoff of the filter (e.g., 128 Hz), increasing the overall level would be expected to result in an effective reduction in the “internal” depth of modulation, once again, counteracting potential gains in sensitivity to ITDs that might come about as a result of the increase in level, per se. For modulation frequencies well below the nominal cutoff of the envelope low-pass filter (e.g., 32 Hz), such a migration of the cutoff of the envelope low-pass filter with level would be expected to have essentially no effect. Such a process, if operative, could explain the smaller level dependency observed for the 128-Hz modulation frequency as compared to the 32-Hz modulation frequency at high levels. Evaluation of the two potential explanations offered here for the different level dependencies observed at low and high rates of modulation must await the results of future experiments specifically targeted to assess their validity.

The data obtained in Experiment 3 showed that different temporal configurations of the low-frequency noise that accompanied the presentation of the high-frequency “target” stimuli also influenced the relation between threshold ITD and overall level. Gating the noise, rather than presenting it continuously resulted in a somewhat, albeit not significantly higher level dependence. The change in level dependence brought about by changes in the gating of the noise is, perhaps, a manifestation of binaural “interference.” When the noise is gated synchronously, binaural interference is expected to be maximal (see, e.g., Bernstein and Trahiotis, 1995). It can be assumed that this effect would be particularly strong if the noise were presented at a fixed overall level because the relative influence of the noise would then be higher at lower levels of the target [see Fig. 3b]. This is a likely reason for the strong level dependence observed by Klein-Hennig et al. (2011) shown as diamonds in Fig. 6, who employed a gated noise presented at a fixed level. This would also explain why the data of Klein-Hennig et al. reveal an even greater level dependence with a modulation frequency of 50 Hz than do the data from the current study that were obtained with an even lower modulation frequency of 32 Hz but with continuous noise, in contrast to the previously identified trend of decreasing level dependence with increasing modulation rate.

The finding that threshold ITDs do not differ significantly for the two interaural configurations of the continuous noises (diotic vs binaurally uncorrelated) is consistent with Nuetzel and Hafter's (1976) results. They also found that there was no differential effect on threshold ITDs of these two interaural configurations of the low-pass noise.

A direct comparison of the normalized threshold ITDs and normalized threshold ILDs reveals that the dependence on overall level is generally weaker in the case of the latter. Data obtained by Rowland and Tobias (1967) and by Stellmack et al. (2004) reveal an increase by a factor of about 1.5 to 2.0 when reducing the level over a range of 30 to 40 dB. The results of the current study are consistent with these earlier findings in that they also reveal an increase in threshold ILDs by a factor of 2 when the overall level is reduced over a similar range of 45 dB.

It is important to determine whether and to what degree observations of decreases in threshold ITDs with increasing level are influenced by information conveyed via “off-frequency” auditory channels as opposed to being manifestations of increased within-channel sensitivity. Bernstein and Trahiotis (2008) found that, despite an overall increase in threshold-ITDs, level dependencies of the type observed in this study remain even when the target stimuli are presented within “notched noises” designed to reduce substantially the effectiveness of “off-frequency” information. Therefore, while information in off-frequency channels contributes to overall sensitivity, the primary determinant of the level dependencies observed here likely stems from changes of “within-channel” sensitivity. Such changes could, for example, occur via the “recruitment” with increasing level of “high-threshold” on-frequency auditory-nerve fibers.

CONCLUSIONS

The results of the experiments conducted in this study suggest that the heterogeneity of the findings of several earlier studies regarding overall level and envelope-based threshold ITDs stem from the operation of several factors. Specifically, the results indicate that:

• (1)For all of the target stimuli tested, log-ITD thresholds decreased linearly with overall level;
• (2)slopes relating log-ITD thresholds to level did not depend significantly on stimulus type;
• (3)for stimuli centered at 4 kHz, lower modulation frequencies appeared to produce somewhat greater dependencies of thresholds on overall level than did higher modulation frequencies;
• (4)for stimuli centered at 4 kHz, the effect of overall level on threshold ITD was independent of the interaural configuration and levels of the low-pass noise tested;
• (5)for stimuli centered at 4 kHz, gating the low-pass noise coincidentally with the target produced a greater dependency of thresholds on overall level of the target than occurred when the noise was presented continuously or temporally fringed.

Taken together these five observations, especially observations 3, 5, qualitatively address all of the across-study differences considered in Sec. 1 that could reasonably be expected to affect the influence the overall level has on threshold ITDs conveyed by the envelopes of high-frequency stimuli. Future studies should examine the reasons for modulation frequency dependence, and potentially further investigate the level dependent influence of binaural interference on threshold ITDs.

Finally, the results of Experiment 4 in which threshold ILDs were measured indicated that they were somewhat less affected by changes in the overall level than were threshold ITDs.

Although beyond the scope of the current study, it would be of interest to (1) investigate how the outcomes observed in the behavioral experiments reported here might be used to constrain and/or augment quantitative models of binaural hearing and (2) employ similar stimuli to reveal potential neurophysiological correlates of the empirical behavioral results.