Quantitative comparison of alternative methods for coarse-graining biological networks

Abstract

Markov models and master equations are a powerful means of modeling dynamic processes like protein conformational changes. However, these models are often difficult to understand because of the enormous number of components and connections between them. Therefore, a variety of methods have been developed to facilitate understanding by coarse-graining these complex models. Here, we employ Bayesian model comparison to determine which of these coarse-graining methods provides the models that are most faithful to the original set of states. We find that the Bayesian agglomerative clustering engine and the hierarchical Nyström expansion graph (HNEG) typically provide the best performance. Surprisingly, the original Perron cluster cluster analysis (PCCA) method often provides the next best results, outperforming the newer PCCA+ method and the most probable paths algorithm. We also show that the differences between the models are qualitatively significant, rather than being minor shifts in the boundaries between states. The performance of the methods correlates well with the entropy of the resulting coarse-grainings, suggesting that finding states with more similar populations (i.e., avoiding low population states that may just be noise) gives better results.

INTRODUCTION

Discrete-time Markov models and their continuous time counterparts, master equation models, are powerful tools for modeling many biological processes. These models consist of a set of states and a matrix of transition probabilities (or, equivalently, transition rates) between every pair of states. For example, Markov state models are an increasingly popular means of describing molecular processes, ranging from the folding and function of small proteins^{1, 2, 3, 4, 5, 6} to conformational changes in large cellular machines.^{7, 8} These models consist of a set of conformational states—each containing a set of rapidly mixing conformations—and a transition probability matrix (T) specifying the probabilities for jumping between every pair of states in some fixed time interval, called the lag time of the model. These models are typically constructed by running extensive molecular dynamics simulations, finely clustering the resulting data to identify states, and inferring a transition probability matrix from a transition count matrix (C) obtained by counting the number of transitions observed between every pair of states within one lag time.

Markov models and master equations can quantitatively describe many processes; however, they are often far too complex to understand. For example, Markov state models of protein folding that are capable of quantitative agreement with experiment often require tens of thousands of conformational states. Examining each of these states and the probabilities of jumping between them would be a daunting task. Therefore, it is often desirable to coarse-grain these models to obtain a more manageable state-space—say, with 10–100 states. Building such coarse-grained models may require sacrificing some of the original model's quantitative accuracy. However, they can greatly facilitate the formulation of new hypotheses that can then be tested with the original model and, ultimately, via experiment. A number of methods have been developed for building such coarse-grained models, raising the question of which method is the best.

Here, we employ Bayesian model comparison⁹ to quantitatively assess the relative merits of a number of methods for coarse-graining Markov state models: the Bayesian agglomerative clustering engine (BACE),¹⁰ the hierarchical Nyström expansion graph (HNEG),^{11, 12} the most probable paths (MPP) algorithm,¹³ Perron cluster cluster analysis (PCCA),^{14, 15, 16} and a more robust variant of PCCA that is called PCCA+.¹⁷ We also apply a number of other metrics to assess how different the outputs of these various methods really are and what qualities lead to better performance. We focus on Markov state models for conformational changes in three example proteins (Fig. 1), however, the results should generalize to other applications of Markov models and master equation models.

Figure 1.

Structures of the 1-residue alanine dipeptide (all-atom), the 35-residue villin headpiece (ribbon),¹⁸ and the 263-residue β-lactamase (ribbon).¹⁹ Structures were drawn with PyMOL.²⁰

METHODS

PCCA

Motivation: PCCA was one of the earliest methods presented for coarse-graining Markov state models.^{14, 15, 16} The development of PCCA was motivated by the idea that there should be a separation of timescales between slow transitions between different free energy basins and more rapid equilibration within a single basin. If such a separation exists, states within the same free energy basin should have relatively high transition probabilities to one another compared to much lower transition probabilities to states in other free energy basins. As a result, the transition probability matrix should have a block structure (where each block corresponds to a set of states in the same basin). This block structure can be identified from the spectral decomposition of the transition probability matrix.

Overview of the method: Given an initial Markov model with N states, one first chooses a number M (with M < N) of coarse-grained states to create (the choice of M is discussed below). One then solves for the M largest eigenvalues/eigenvectors of the original transition probability matrix. Each eigenvalue (λ_i) corresponds to the fraction of the total population that does not undergo some dynamic process, which is described by the corresponding eigenvector (q_i). Specifically, it is a process in which transitions occur between states with positive eigenvector components and states with negative eigenvector components. The first eigenvalue (λ₀) and its corresponding eigenvector are always ignored as they simply describe the equilibrium properties of a system rather than any dynamic process. Subsequent eigenvectors are used to coarse-grain the state space, as described below.

Procedure:

1. Initially assume that all of the original states are merged into one coarse-grained state.

2. Identify the coarse-grained state with the largest spread in the components of the eigenvector corresponding to the next largest eigenvalue (λ₁ > λ₂ > ⋯ > λ_N).

3. Split that coarse-grained state into two by separating states from the original model with positive eigenvector components from those with negative components.

4. Repeat steps 2 and 3 until the desired number of coarse-grained states is achieved.

Choosing the number of states: The number of coarse-grained states (M) has often been chosen based on the existence of a gap in the eigenvalue spectrum of the transition probability matrix.^{14, 15, 16, 22} Specifically, a large gap separating the M − 1 largest (i.e., slowest timescale) eigenvalues from the remaining eigenvalues suggests the existence of M free energy basins that are separated by large free energy barriers (compared to smaller internal barriers). However, the choice of M is generally very subjective. There is often a continuum of eigenvalues, so more recently it has become common to treat the number of states as an adjustable parameter.

Code: PCCA is implemented in the MSMBUILDER package,^{23, 24} available at https://simtk.org/home/msmbuilder, and the EMMA package,²⁵ available at https://simtk.org/home/emma.

PCCA+

Motivation: PCCA+ was developed to correct for some of the pitfalls of PCCA.¹⁷ Specifically, states that do not strongly participate in a given eigenmode will have eigenvector components near zero, and the sign can vary depending on finite sampling effects. Therefore, PCCA will arbitrarily group these states with either the group of states with positive eigenvector components or the group of states with negative eigenvector components. This can lead to compounding errors as PCCA sequentially considers each eigenvector. PCCA+ aims to avoid such errors by simultaneously considering all the relevant eigenvectors to identify the best set of coarse-grained states.

Overview of the method: Like PCCA, PCCA+ uses the eigenspectrum of the transition probability matrix to identify the underlying block structure. However, instead of considering each eigenvector sequentially, PCCA+ identifies a set of indicator-functions that serve as a basis set for q₁ to q_M. These functions must be either 0 or 1 for each of the original states, so they can be interpreted as membership functions for M coarse-grained states. By considering the M − 1 eigenvectors simultaneously instead of sequentially, it is hoped that PCCA+ can better deal with states that do not participate strongly in some of the eigenmodes.

Procedure:

1. For each state j, construct a vector v_j where element i is the entry for that state in the eigenvector q_i.

2. Use the Gram-Schmidt algorithm to identify a set of M representative states that have the most distinct vectors from {v_j}.

3. Assign each of the remaining states to the representative state that its v_j is most similar to.

4. Refine the coarse-graining by moving states to alternative coarse-grained states to maximize either the metastability or the crispness. The crispness is a measure of how much more likely a state is to be part of the coarse-grained state it is assigned to than any other coarse-grained state (see Ref. 21 for details).

Choosing the number of states: The number of states is chosen in the same manner as for PCCA.

Code: PCCA+ is implemented in the MSMBUILDER package,^{23, 24} available at https://simtk.org/home/msmbuilder, and the EMMA package,²⁵ available at https://simtk.org/home/emma.

HNEG

Motivation: One issue with PCCA and PCCA+ is that they tend to identify poorly sampled states as being kinetically distinct from their neighbors.¹² Therefore, these states are often preserved in the coarse-grained model even though manual inspection strongly suggests that they are likely just improbable excursions from more thoroughly sampled states—for example, the state may be observed only once (or a few times), only have transitions to/from one other state, and be extremely structurally similar to the single state it transitions to/from. HNEG attempts to solve this problem by placing more emphasis on well-sampled states than poorly sampled states.^{11, 12} Physically, this is done by trying to identify the bottoms of free energy basins (which are better sampled than other regions of conformational space since they have higher statistical weight) and then assigning other regions of conformational space to the basin bottom they can transition to most easily (suggesting they belong to that basin).

Overview of the method: Formally, HNEG is based on the Nyström method and its multilevel extensions, which allow us to approximate the transition probability matrix with its dominant submatrix. Using the Nyström approximation, the eigenvectors of the submatrix A containing the most common states (i.e., where the entries of A are significantly larger than those of B or C) are shown to contain the same sign structure as the eigenvectors of the whole transition probability matrix P:¹¹

$$P=\left[\begin{array}{cc}\hfill A& \hfill B\\ \hfill B^T& \hfill C\end{array}\right].$$ (1)

That is, the components of the eigenvectors of the two matrices have the same sign, suggesting that both provide insight into the same set of underlying free energy basins. Therefore, we can obtain the state decomposition based on the eigenvectors of the submatrix A using PCCA or PCCA+. In order to define the boundary between A and C, a multiscale procedure is used, as described below.

Procedure:

1. Sort the original N states (where s_i is a state and p_i is its population) from the most populated to the least populated: {s₁, s₂, …, s_N} with $p_{s_1}>p_{s_2}>\cdots >p_{s_N}$, where $p_{s_i}=n_{s_i}/n_{total}$, $n_{s_i}$ is the number of conformations in state s_i and n_total is the total number of conformations. Next, we divide these N states into m super-level-sets: P₁, P₂, …, P_m. Each super level (P_i) consists of a set of most populated states ({$s_1,s_2,...,s_{n_i}$}), where n_i is the number of states in the super level P_i and ${\sum }_{j=1}^{n_i}{p}_{s_j}\le P_i$. Typically, P_m is less than 1, so that the least populated states are ignored until the final stages of the algorithm.

2. Apply PCCA to each super-level-set.

3. Arrange the resulting groupings of states as a graph with edges pointing from groupings in one super-level-set P_i to those in the next set with higher populations (P_{i + 1}). An edge is added if a pair of groupings in adjacent super-level-sets have nonempty intersections (i.e., share one or more common states).

4. Assign all states to leaf-nodes—groupings with no edges pointing to more highly populated nodes that correspond to a basin of attraction—by assigning all groupings to the grouping in the next super-level-set they have the highest transition probability to.

5. Assign the states that reside between P_m and 1 to the leaf-node they have the highest transition probability to.

6. Consider all states assigned to the same leaf-node (i.e., attraction basin) to the same coarse-grained state.

Choosing the number of states: There are many possible choices of the super-level-sets, each of which could result in different coarse-grainings (and even different numbers of coarse-grained states). How best to make these choices is still an open research question and the answer is likely system-dependent since the topology of the free energy landscapes will vary for different proteins. Currently, we suggest varying the super-level-sets systematically to produce a large number of lumpings and then selecting the optimal one using the Bayes factor criteria. For example, one may construct super levels by selecting different values of P₁ and P_m, or different number of levels m.¹¹ This helps guide the selection of the number of coarse-grained states; however, there is still some subjectivity since PCCA is applied to each level set. Another potential drawback is that the user has less control over the final number of states than in other methods.

Code: The HNEG code is available for download at https://simtk.org/home/hneg.

BACE

Motivation: The BACE method was also developed to place more emphasis on better sampled states so that poorly sampled states do not dominate the coarse-grained model. This is done in a formal (and automated) fashion by drawing on Bayesian statistics. Physically, BACE identifies coarse-grained states by finding sets of states that have the same kinetics (i.e., transition probabilities to other states), within statistical uncertainty. This is a reasonable way to find coarse-grained states because two states in the same free energy basin should have to cross the same free energy barriers when transitioning to other states.

Overview of the method: BACE will only separate two states into different coarse-grained states if there is clear statistical support for their being in different basins of attraction. States that are clearly similar based on the statistics gathered are grouped together and highly uncertain states are grouped with their most similar neighbor. Formally, the similarity between two states is quantified by the BACE Bayes factor

$$\begin{array}{cc}& \log \frac{P\left(\mathrm{different}\right|C)}{P\left(\mathrm{same}\right|C)}\approx {\widehat{C}}_i\mathcal{D}(p_i\Vert q)+{\widehat{C}}_j\mathcal{D}(p_j\Vert q),\hfill \end{array}$$ (2)

where C is the transition count matrix, ${\widehat{C}}_i$ is the number of transitions observed from state i, $\mathcal{D}(p_i\Vert q)={\sum }_k{p}_{ik}\log \frac{p_{ik}}{q_k}$ is the relative entropy between probability distribution p_i and q, p_i is a vector of maximum likelihood transition probabilities from state i ($p_{ij}=\frac{C_{ij}}{{\widehat{C}}_i})$, and $q=\frac{{\widehat{C}}_i{p}_i+{\widehat{C}}_j{p}_j}{{\widehat{C}}_i+{\widehat{C}}_j}$ is the vector of expected transition probabilities from combining states i and j.

Procedure:

1. Calculate the BACE Bayes factor for every pair of connected states using Eq. 2.

2. Identify the pair of states with the smallest Bayes factor (i.e., the states that are most likely to have come from the same underlying distribution) and merge them by summing their transition counts.

3. Update the Bayes factors comparing the new merged state and every other state it is connected to, again using Eq. 2.

4. Repeat steps 2 and 3 until only two states remain.

Choosing the number of states: For a model with N states, BACE will construct a series of coarse-grained models with M = N − 1, N − 2, …, 2 states. There are a number of ways to choose which of these models warrant further investigation, depending on the users’ objective. The best way to choose is by tracking the Bayes factor between the two most similar states as BACE progressively merges states together. A model with M coarse-grained states may be of particular interest if there is a large increase in this Bayes factor when performing the next merger into M − 1 states because this jump suggests that two very similar states will be merged if one coarse-grains further. One could also choose M such that no two states have a Bayes factor above some threshold to ensure a certain level of statistical confidence.

Code: The BACE code is available through the MSMBUILDER package^{23, 24} at https://simtk.org/home/msmbuilder and https://sites.google.com/site/gregoryrbowman/.

MPP

Motivation: Like HNEG, the MPP algorithm aims to find states that are at the bottoms of free energy basins and then assign other states to the basin they are most likely to fall into.¹³

Overview of the method: For each state, the MPP algorithm finds the path a molecule starting in that state is most likely to take (the most probable path). A state is then grouped with the most probable state along its most probable path.

Procedure: The algorithm works as follows:

1. Calculate the most probable path for each of the initial states (i).

   1. Initialize the path to [i].
   2. Find the state (k) that the last state in the path (j) has the highest transition probability to (k = argmax_m(T_jm)), where T is the transition probability matrix). Only allow k = j if T_jj > Q_min, where Q_min is a user-defined parameter specifying the minimum allowable self-transition probability for the end-state of a most probable path.
   3. Update the most probable path to [i, …, j, k] by adding k.

2. Assign each state to the most probable state along its most probable path.

3. Group all the states assigned to the same end state to the same coarse-grained state.

Choosing the number of states: The number of coarse-grained states produced by this algorithm can be varied by adjusting Q_min. We chose Q_min to force the number of coarse-grained states to match HNEG. One could also choose Q_min based on physical considerations and allow the algorithm to automatically determine the number of coarse-grained states.

Code: The MPP code is not currently available on the web.

Model and simulation details

The model for the 1-residue alanine dipeptide was taken from Ref. 11. It has 5000 states and a lag time of 9 ps. The model was built with the data from Ref. 26 using MSMBUILDER 1.0.²³ Nine hundred seventy five simulations were performed with GROMACS.²⁷ Each trajectory is 20 ps long, with conformations stored every 0.1 ps. Further details on the model construction and validation are available in Ref. 11.

The model for the 35-residue villin headpiece was taken from Ref. 28. It has 10 000 states and a lag time of 15 ns. The model was built with the data from Ref. 29 using MSMBUILDER 1.0.²³ Five hundred simulations were performed with GROMACS deployed on the Folding@home distributed computing environment.^{27, 29, 30} The Amber03 force field³¹ and Tip3p explicit solvent were used. Each trajectory is up to 2 μs long, with conformations stored every 50 ps. Further details on the model construction and validation are available in Ref. 28.

The model for the 263-residue β-lactamase was taken from Ref. 32. It has 5152 states and a lag time of 2 ns. The model was built with the data from Ref. 32 using MSMBUILDER 2.0.^{23, 24} One thousand simulations were performed with GROMACS deployed on the Folding@home distributed computing environment.^{27, 29, 30} The Amber03 force field³¹ and Tip3p explicit solvent were used. Each trajectory is up to 320 ns long, with conformations stored every 100 ps. Further details on the model construction and validation are available in Ref. 32.

The coarse-grained models for the alanine dipeptide, villin, and β-lactamase have 5, 83, and 21 states, respectively. These are the numbers of states selected with the HNEG method and were chosen because of the physical motivation this method provides for choosing the number of coarse-grained states and because tuning the number of states is more straightforward with the other methods.

For HNEG, we selected 100 different super-level-sets for the alanine dipeptide system ({P₁, P₂, …, P_m}), where P₁ = 0.2. We varied P_m to be P_m ∈ {0.80, 0.82, …, 0.96, 0.98}. For each pair of (P₁, P_m), we generated super-level-sets with m levels by equally dividing between P₁ and P_m, where m ∈{2, 4, 6, …, 16, 18, 20}. For villin and β-lactamase, we selected 400 super-level-sets. Specifically, P₁ ∈ {0.20, 0.25} and P_m ∈ {0.50, 0.55, 0.60, …, 0.85, 0.90, 0.95}. For each pair of (p₁, p_m), m ∈{2, 4, 6, …, 36, 38, 40}.

RESULTS

To assess the relative performance of the coarse-graining methods examined here, we applied each of them to a range of systems from the 1-residue alanine dipeptide to the 263-residue protein β-lactamase. We chose to include the alanine dipeptide as part of our test set because it is small enough to sample thoroughly and is often used as a test case for new methods. Another reason it is a favorite test case is that there are two primary degrees of freedom, so one can meaningfully assess the performance of a method by examining projections of the free energy surface onto these order parameters. However, we do not take advantage of this property here since all of the methods perform reasonably well on this system. We also applied each method to a model of the folding of the 35-residue villin headpiece protein. This protein is far more complex than the alanine dipeptide but still small enough to sample thoroughly (albeit with extensive computational resources), so it provides a more realistic test system. Finally, we have applied each method to a model of dynamics within the folded state of the 263-residue protein β-lactamase. This model is of interest for our purposes because we certainly do not sample structures that are representative of the entire conformational space. With 80 μs of simulation, we observe many local fluctuations from the crystallographic structure that are of interest for understanding aspects of protein function like allosteric communication. However, β-lactamase folding and unfolding occur on seconds and slower timescales, so we do not observe these large-scale conformational changes. Given how diverse these data sets are in terms of the specific application and the amount of sampling, we expect trends from this range of systems to be representative of the type of performance one can expect for other systems.

To make a fair comparison between different methods, we built models with the same number of coarse-grained states with each method. In general, it is difficult to choose an “optimal” number of coarse-grained states. For example, one of the standard methods for choosing the number of coarse-grained states depends on the presence of a gap in the eigenvalue spectrum of the transition probability matrix that suggests a separation of timescales between intrastate relaxation and interstate transitions. However, complicated protein systems often do not have such a gap. The appropriate number of coarse-grained states may also depend on the degree of temporal and spatial coarse-graining one desires. Each of the methods used in this work comes with its own recommendations for how to choose the final number of states, so it may be possible to build better models with a particular method than the one presented here by following those proscriptions. However, we did not want to bias the results in favor of any particular method by allowing it to use more adjustable parameters (i.e., states and transition probabilities between them). Therefore, we used the HNEG method to determine the number of coarse-grained states to be used in all of the methods. We chose HNEG for this purpose because it chooses a physically meaningful number of coarse-grained states. It is also more difficult to vary the number of states generated by the HNEG method than the other methods used in this work.

In Subsections 3A, 3B, 3C, 3D, we first use Bayesian model comparison to quantitatively assess the relative performance of the methods examined here. We then apply a number of metrics for comparing two models to determine how similar or different the outputs from the various methods really are from one another. Finally, we measure some physical parameters of the models to gain some insight into what properties distinguish the best models from the rest.

Quantitative comparison of model performance

Bayesian model comparison based on Bayes factors is a powerful method of model selection. The main idea is to determine which of the two models is most consistent with the original data by comparing how likely each is to have generated that data. Formally, this is accomplished with a Bayes factor

$$\begin{array}{c}\hfill \frac{P\left(L_1\right|C)}{P\left(L_2\right|C)},\end{array}$$ (3)

where L₁ and L₂ are two coarse-grainings—or lumpings—of a Markov model and C is a transition count matrix specifying the number of transitions observed between every pair of states. This comparison integrates over all possible transition probability matrices between the coarse-grained states and all possible equilibrium probabilities of the original states. Therefore, the comparison captures both the thermodynamics and kinetics of each model. Such quantitative comparisons are crucial because the complexity of most real-world Markov models renders a qualitative assessment of a coarse-graining's validity impossible.

Instead of presenting Bayes factors, we actually present the log of the evidence for different models (log (P(L|C))) to facilitate the comparison of many different models. The log of a Bayes factor can be written as the difference between the logs of the evidences for two models:

$$\begin{array}{c}\hfill \log \frac{P\left(L_1\right|C)}{P\left(L_2\right|C)}=\log P\left(L_1\right|C)-\log P\left(L_2\right|C).\end{array}$$ (4)

Models with larger (less negative) evidence are more likely to explain a given set of observations. To calculate the evidence, we use the method from Ref. 9.

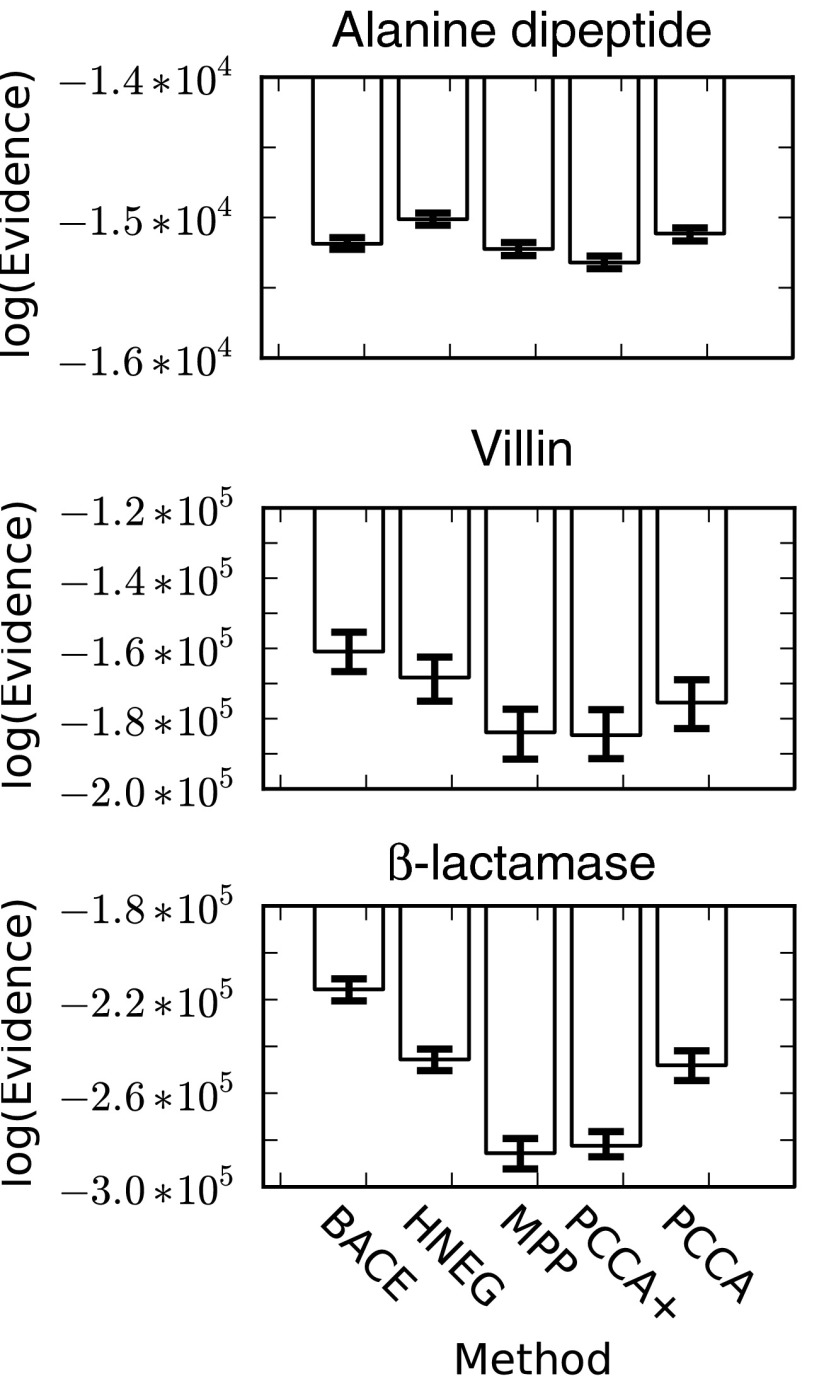
Comparison of the evidence for each method across a range of systems demonstrates that BACE and HNEG routinely provide the best models (Fig. 2). That is, the evidence for models from these methods is generally larger (less negative) than for models built with other methods. HNEG provides the best performance for the alanine dipeptide. However, the relative rankings of the different methods for the alanine dipeptide are not necessarily representative of their relative performance on more complex systems, highlighting the need to compare methods on a range of systems. BACE actually provides the best performance for both the villin headpiece and β-lactamase. In fact, the gap in performance between BACE and the other methods increases as the proteins examined become more complicated (or are less well sampled). This result is consistent with the fact that BACE explicitly accounts for finite sampling effects (i.e., statistical uncertainty). More generally, the fact that both BACE and HNEG perform so well is consistent with the fact that both were developed to deal with poorly sampled states that have been proposed to mislead other methods.

Figure 2.

The log  of the evidence for coarse-grained models built with different methods. The mean value from 100 bootstrapped samples is reported (bars) with 68% confidence intervals (error bars). Larger (less negative) numbers indicate better results. The large magnitudes are comparable to those found in Refs. ⁹, ¹⁰ and arise from the products of a large number of small probabilities in the likelihood function.

The rankings of the other methods are relatively consistent across the different proteins examined here. For example, PCCA is generally the third best method, though it slightly outperforms BACE on the alanine dipeptide. The fact that BACE and PCCA perform so similarly on the alanine dipeptide is consistent with the fact that this is the best sampled system, where BACE would benefit least from its ability to deal with statistical uncertainty. More surprising is that PCCA generally outperforms the newer PCCA+ method that was intended to provide more robust results. PCCA+ and MPP are close behind the other methods for the alanine dipeptide but perform less well for the more complicated systems.

Alternative methods yield very different models

While there is clearly a statistically significant difference between the performance of many of the methods, it is less clear whether this implies that they provide significantly different physical pictures. For example, one could imagine that all the models are essentially the same but with slight differences in where they draw the boundaries between coarse-grained states.

To determine how different coarse-grained models are from one another, we developed an overlap function for comparing two coarse-grainings. The main idea is to determine what fraction of the equilibrium population of some set of initial states are assigned to the “same” coarse-grained state in two different coarse-grained models. We calculate the overlap as follows:

1. Use the stable marriage algorithm³³ to match coarse-grained states from model L₁ with coarse-grained states in model L₂ to maximize their total overlap (${\sum }_{M_1,M_2}P(M_1,M_2)$ where M₁, M₂ is a pair of coarse-grained states, one from each model, and P(M₁, M₂) is the total equilibrium probability of all the original states that are in both M₁ and M₂). Every state in each model does not have to be paired with a state in the other model. For example, a coarse-grained state M₁ in L₁ may encompass two coarse-grained states M₂₁ and M₂₂ in L₂ (where P(M₂₁) > P(M₂₂)), in which case M₁ will be matched with M₂₁ while M₂₂ remains unpaired.

2. The overlap is then ${\sum }_{M_1,M_2}P(M_1,M_2)$.

The overlap will approach 1 for two coarse-grainings that are essentially the same and approach 0 for two models that are very different.

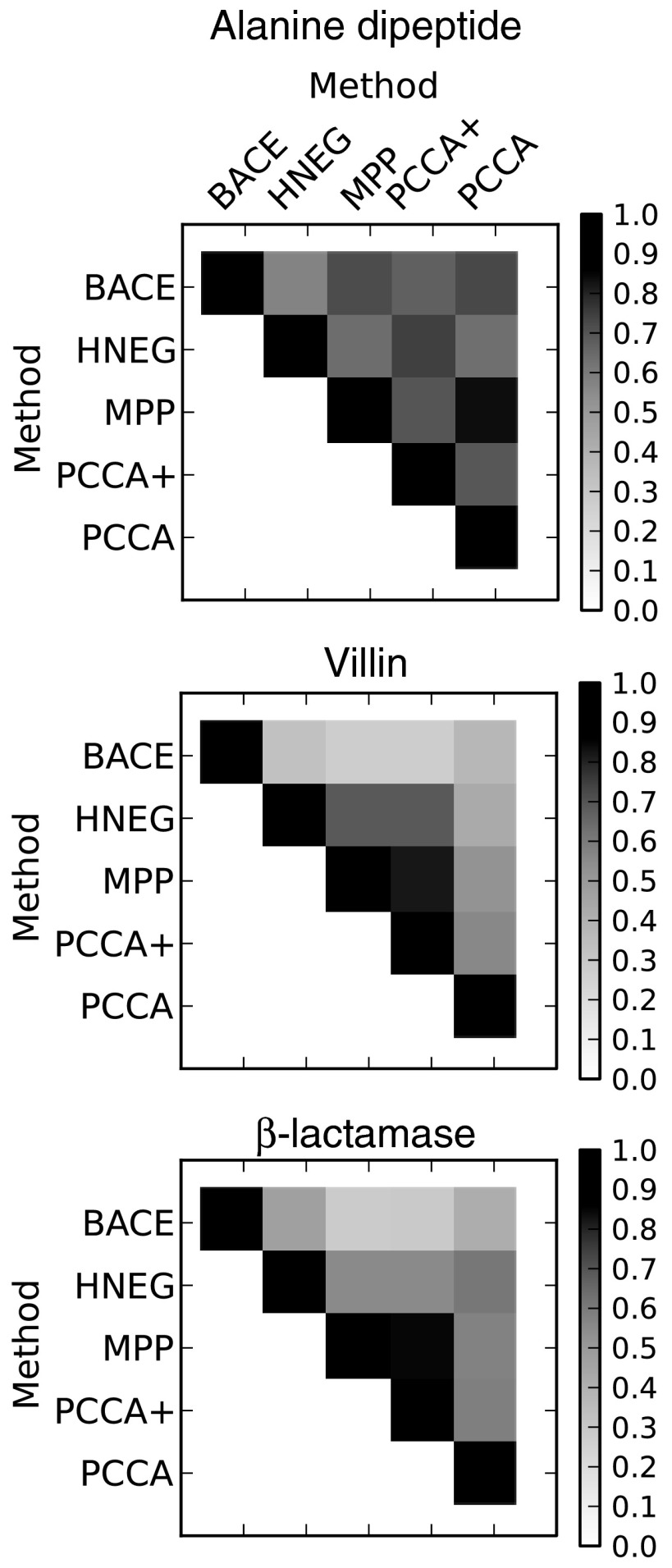
Application of this overlap function shows that the coarse-grainings generated by different methods can be quite different from one another (Fig. 3). In general, models that performed more similarly (as judged by Bayesian model comparison) have greater overlap. BACE has relatively little overlap with any of the other methods for villin and β-lactamase, consistent with the gap in the performance between them. For example, the maximum overlap between BACE and any of the other methods is 0.29 for villin, so at least 71% of the equilibrium population is assigned to different groupings when comparing BACE to other models. PCCA+ and MPP often have very similar performance and the overlap between them is generally quite high.

Figure 3.

The overlap between coarse-grained models built with different methods. The mean value from 100 bootstrapped samples is reported. Larger numbers indicate greater similarity.

The overlap between the results from different methods also tends to be greater for the simpler or better sampled proteins. For example, the overlap between the alanine dipeptide results is generally the highest. Meanwhile, the overlap between the β-lactamase results is generally the lowest. This trend is consistent with the idea that the main feature distinguishing the better methods from the worse ones is how they deal with poorly sampled states.

The mutual information between two models provides another perspective on their similarities and differences. In general, the mutual information is a measure of how much information one random variable contains about another. An important advantage of the mutual information over our overlap function is that it can capture nonlinear dependencies. However, it is less straightforward to interpret. Following Ref. 11, the mutual information between two models is defined as

$$\begin{array}{c}\hfill I(L_1,L_2)=\sum _{M_1\in L_1}\sum _{M_2\in L_2}P(M_1,M_2)\log \left(\frac{P(M_1,M_2)}{P\left(M_1\right)P\left(M_2\right)}\right),\end{array}$$ (5)

where M_i is a coarse-grained state in model L_i, P(M₁, M₂) is the total equilibrium population of the original states that are assigned to M₁ in model L₁ and M₂ in model L₂, and P(M_i) is the total equilibrium population of the original states that are assigned to M_i in model L_i. Models with larger mutual information are more similar.

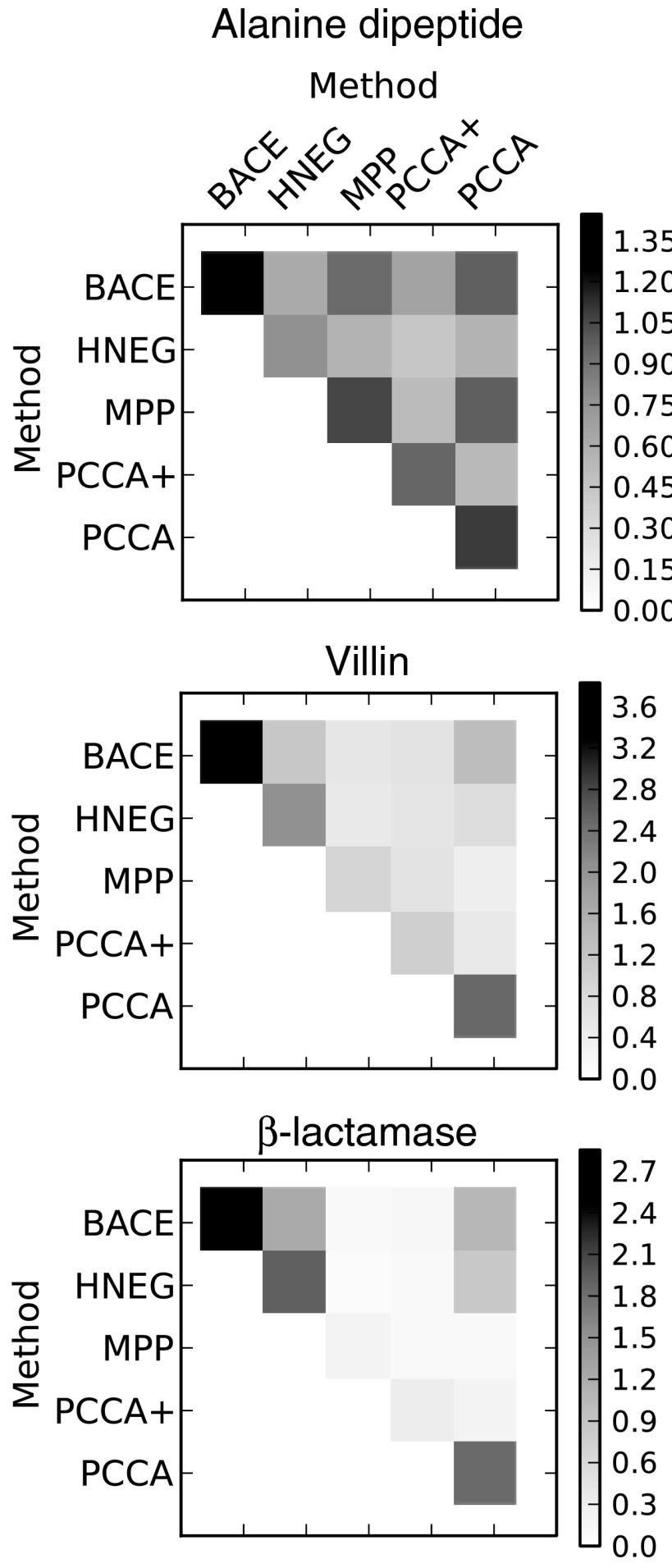
Examining the mutual information between models from the various methods provides a similar picture to that from our overlap function (Fig. 4). However, identifying the similarities and differences is somewhat more challenging since the mutual information between models must be judged relative to the self-information of each of them (along the diagonal). For example, the mutual information between the PCCA+ and MPP models for villin is low compared to that between BACE and PCCA, but the PCCA+ and MPP models are actually more similar because the mutual information between them is very close to the self-information of either model. This can be corrected by normalizing the mutual information by the joint entropy, as was done in Ref. 34.

Figure 4.

The mutual information between coarse-grained models built with different methods. The mean value from 100 bootstrapped samples is reported. Larger numbers indicate greater similarity.

Avoiding rare states improves models

Examining the mutual information between different models also provides quantitative support for previous observations that avoiding rare states leads to better coarse-grainings. The self-information along the diagonals in Fig. 4 is equivalent to the entropy of the equilibrium populations of the coarse-grained states. This entropy will be larger for models with more equally populated states. By cross-referencing with the evidences presented in Fig. 2, one can see that the best performing methods also tend to give rise to models with higher entropies. Therefore, we conclude that part of the explanation for the worse performing methods is that they are identifying poorly sampled sets of states as being distinct from other states. In reality, it is likely that the apparent kinetic differences between these states are due to finite sampling rather than a true difference.

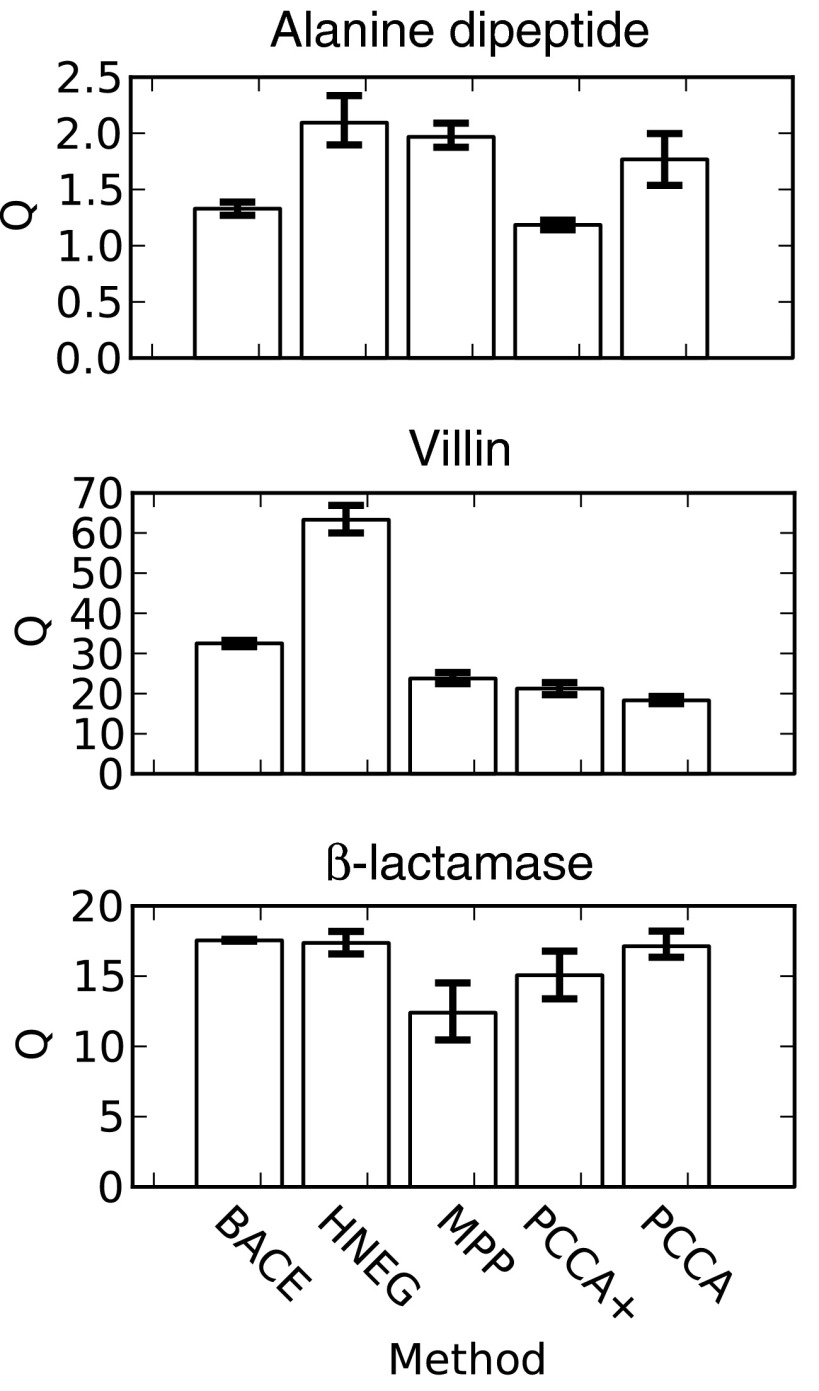
Other physical quantities that have been used as surrogates for model quality do not necessarily correlate as well with the results of Bayesian model comparison. For example, maximizing the metastability (Q = ∑_iT_ii) has previously been used as a strategy for refining coarse-grained models.^{23, 26} However, the metastability does not correlate well with the performance of the methods for all of the systems examined here (Fig. 5). For example, HNEG models routinely have one of the highest metastabilities even though BACE often gives better results according to the other metrics used in this work. The high metastability of HNEG models is not surprising since this method is designed to deal with rare states using a multilevel analysis that starts by identifying basins of attraction (i.e., the bottoms of free energy basins) and then merging less populated neighboring states into these basins.

Figure 5.

The metastability of coarse-grained models built with different methods. The mean value from 100 bootstrapped samples is reported (bars) with 68% confidence intervals (error bars).

Kinetics

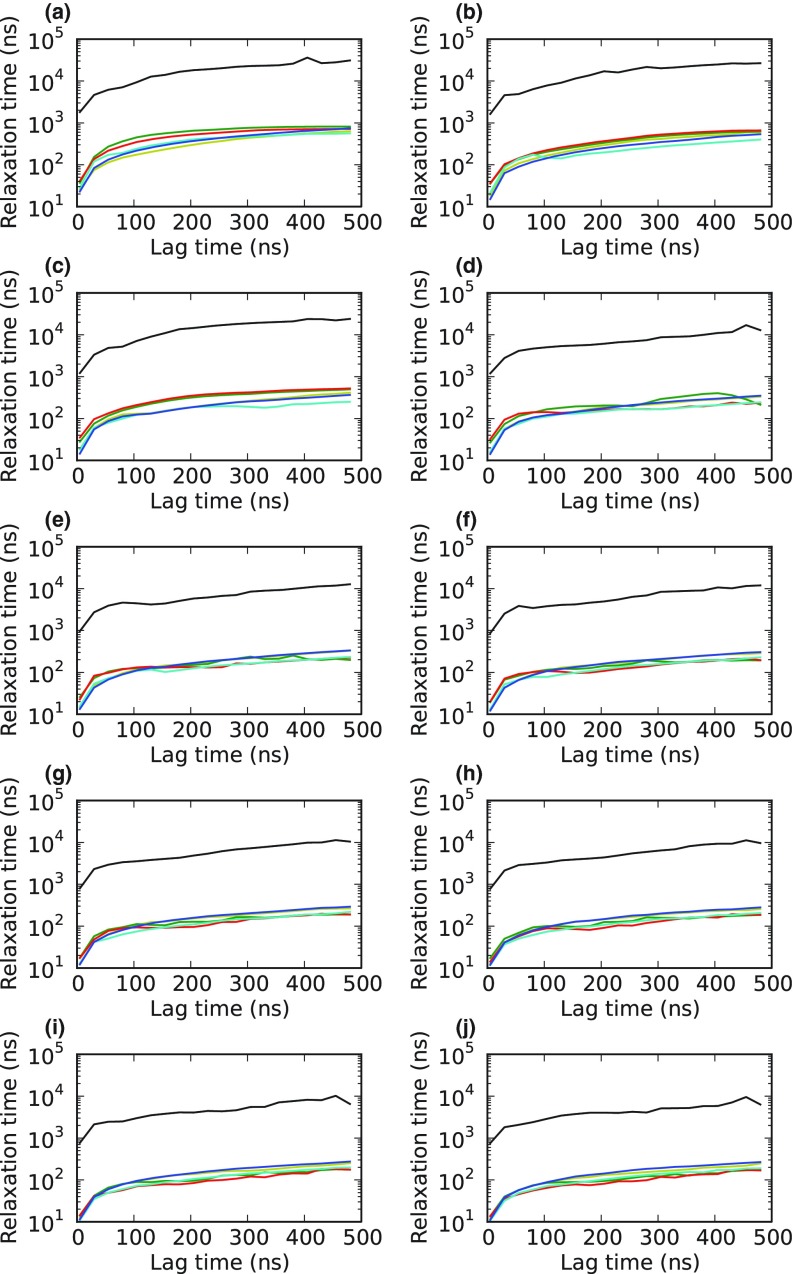
The various coarse-grained models appear to give very similar kinetics by standard measures, such as their relaxation (or implied) timescales (Fig. 6). All of the coarse-grained models exhibit significantly accelerated kinetics relative to the original model. These accelerated kinetics are due to two factors: (i) poorly sampled states in the original model prior to coarse-graining¹² and (ii) assuming rapid equilibration within large, coarse-grained states. The relaxation timescales of all the coarse-grained models are relatively similar. In fact, PCCA+ and MPP even appear to give somewhat better results, in that their slowest relaxation timescales level-off at somewhat shorter lag times (or observation intervals). However, further analysis reveals that other methods are actually preferable.

Figure 6.

The 10 slowest relaxation timescales from the slowest (a) to the fastest (j) for the original villin model before coarse-graining (black) and coarse-grainings from BACE (blue), HNEG (yellow), MPP (green), PCCA+ (red), and PCCA (cyan).

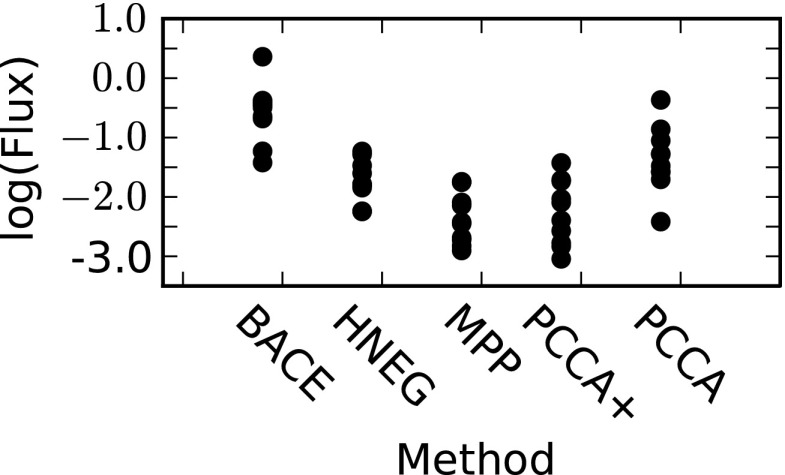
Examining the equilibrium flux between states corresponding to each relaxation timescale reveals that BACE actually gives the most reliable kinetics (Fig. 7). The equilibrium flux (F_n) corresponding to the nth relaxation timescale (or eigenvalue of the transition probability matrix) is given by

$$\begin{array}{c}\hfill F_n={\Vert {\varphi }_n\Vert }^2,\end{array}$$ (6)

where ϕ_n is the nth π-normalized left eigenvector of the transition probability matrix and ‖ ‖ denotes the L2-norm.³⁵ This flux will be low for poorly sampled transitions and higher for well-sampled transitions. BACE gives the highest fluxes (followed by PCCA), demonstrating that it identifies the most statistically reliable transitions.

Figure 7.

The interstate flux for the 10 slowest relaxation timescales for each of the villin coarse-grained models. Fluxes were calculated from a transition probability matrix with a lag time of 100 ns based on the apparent leveling off of the relaxation timescales at this lag time (which indicates Markovian behavior²²).

CONCLUSIONS AND FUTURE PERSPECTIVE

We have employed Bayesian model comparison to quantitatively assess the relative performance of some of the most recently developed and most commonly used methods for coarse-graining Markov state models on a variety of systems. We find that BACE and HNEG routinely outperform alternative methods, with BACE performing particularly well for less well sampled models. PCCA typically provides the third best performance, followed by PCCA+ and MPP. We also demonstrate that the various methods can yield quite different models by comparing their output with metrics like the overlap function presented here and the mutual information. Finally, we show that models that avoid low population states that may be artifacts of finite sampling give improved performance.

In the future, it will be interesting to assess whether these results extend to other settings, such as multi-body systems like ligand-binding. The above analysis is based on models of single-body processes like folding and functional dynamics. Markov models have also proved useful for studying multi-body systems like ligand-binding and protein-protein interactions though.^{32, 36, 37, 38} Constructing Markov models for these processes is challenging because one must capture both the protein's conformational changes and the heterogeneous timescales of ligand dynamics due to interactions with the protein. Furthermore, the formation of a protein-ligand or protein-protein complex is often coupled with protein conformational changes that further complicate the system's kinetics. The performance of the coarse-grained methods examined here may be quite different for these more complicated scenarios, and new methods may even be required.