The Temporal Evolution of Feedback Gains Rapidly Update to Task Demands

Abstract

Recent theoretical frameworks such as optimal feedback control suggest that feedback gains should modulate throughout a movement and be tuned to task demands. Here we measured the visuomotor feedback gain throughout the course of movements made to “near” or “far” targets in human subjects. The visuomotor gain showed a systematic modulation over the time course of the reach, with the gain peaking at the middle of the movement and dropping rapidly as the target is approached. This modulation depends primarily on the proportion of the movement remaining, rather than hand position, suggesting that the modulation is sensitive to task demands. Model-predictive control suggests that the gains should be continuously recomputed throughout a movement. To test this, we investigated whether feedback gains update when the task goal is altered during a movement, that is when the target of the reach jumped. We measured the visuomotor gain either simultaneously with the jump or 100 ms after the jump. The visuomotor gain nonspecifically reduced for all target jumps when measured synchronously with the jump. However, the visuomotor gain 100 ms later showed an appropriate modulation for the revised task goal by increasing for jumps that increased the distance to the target and reducing for jumps that decreased the distance. We conclude that visuomotor feedback gain shows a temporal evolution related to task demands and that this evolution can be flexibly recomputed within 100 ms to accommodate online modifications to task goals.

Introduction

A prominent theory of motor control, termed optimal feedback control (OFC), postulates that the sensorimotor control system produces smooth and adaptable movements by setting the appropriate feedback gains, which vary as a function of time, to the task being performed (Todorov and Jordan, 2002; Scott, 2004; Todorov, 2004). OFC determines the best possible feedback gains for any task so as to minimize a cost function that depends on measures such as accuracy and energy. The consequence of OFC is not to eliminate variability, but to constrain it in task-relevant dimensions while allowing it to accumulate in task-irrelevant dimensions (Todorov and Jordan, 2002). Therefore, OFC makes certain predictions that the feedback gains will vary both with the task and throughout the movement. The task variation of feedback gain has been demonstrated in a variety of studies investigating different features of movement. For example, appropriate modulation of reflex gains is seen across the two arms when controlling a single object (Diedrichsen, 2007; Dimitriou et al., 2012; Omrani et al., 2013), during reaching movement to specific target shapes (Knill et al., 2011; Nashed et al., 2012), and according to environmental variability (Franklin and Wolpert, 2008). OFC also suggests that the feedback gains should vary throughout a movement as, for example, the increased energetic cost of reaching the target starts to outweigh the cost of missing the target close to the end of a movement (Liu and Todorov, 2007). However, the within movement temporal evolution of the gains has received little investigation. Here we investigated the degree to which the feedback gains of the system vary throughout the movement and whether they can be updated during a movement to varying task demands.

Rapid corrective responses to reaching errors result from muscle-stretch-dependent motor responses (Kimura and Gomi, 2009; Kurtzer et al., 2009) and rapid visuomotor responses responding to shifts in the visual location of the hand (Brenner and Smeets, 2003; Sarlegna et al., 2003; Saunders and Knill, 2003, 2005). We examined whether the size of one of these two components, the visuomotor response, is modulated throughout a movement. It has been shown previously that the rapid component of the visuomotor response is involuntary in nature (Franklin and Wolpert, 2008), similar to other visuomotor responses to target or background motion (Day and Lyon, 2000; Gomi et al., 2006). The magnitude of the visuomotor response for a fixed size of visual perturbation is measured and termed the gain as it corresponds to the ratio of input-output responses. We specifically examined and demonstrate that the involuntary visuomotor feedback responses vary in gain during a movement. Moreover, because the results demonstrate that the feedback response decreases rapidly toward the end of a movement independently of movement length, we can elicit different sized visuomotor responses for the same limb posture for different target locations. This allowed us to examine whether the sensorimotor control system rapidly updates feedback responses to changes in the task goal that occur during the reach. Specifically, we examined whether there were changes, and if so over what time course, in the gain of the visuomotor response when the target was either jumped to be closer or further away from the hand.

Materials and Methods

Subjects.

Eight subjects (3 females) took part in the first experiment (mean age, 24.5 ± 4.3 years). Ten subjects (4 females) participated in the second experiment (mean age, 26.8 ± 6.2 years), 5 of whom had already participated in the first study. Another 10 subjects (4 females) took part in the third experiment (mean age, 22.3 ± 2.8 years) 4 of whom had participated in either the first and/or the second experiment. All participating subjects were naive as to the purpose of the study. No qualitative differences in results were seen between subjects who had encountered the experimental paradigm previously and those who had not. All subjects were neurologically healthy, right-handed as determined by the Edinburgh handedness questionnaire (Oldfield, 1971), and gave their informed consent before participating. The study was approved by the institutional ethics committee.

Experimental apparatus and setup.

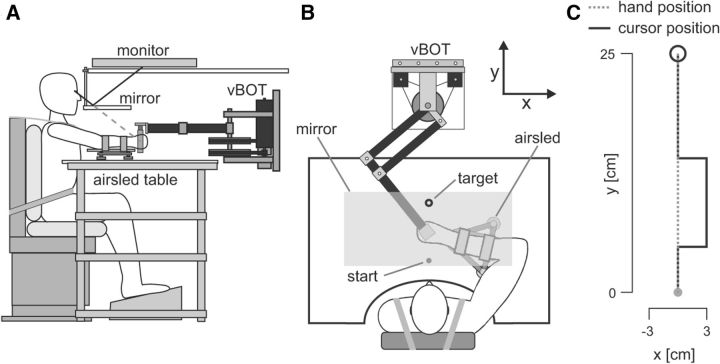
Subjects were firmly strapped into an adjustable chair in front of a robotic rig. The subjects' right arm rested on an air sled and they grasped the handle of a vBOT robotic interface with the right hand (Fig. 1A,B). The vBOT manipulandum is a custom-built planar robotic interface that can measure the position of the handle and generates forces on the hand (Howard et al., 2009). A six-axis force transducer (ATI Nano 25; ATI Industrial Automation) measured the endpoint forces applied by the subject at the handle. The position of the vBOT handle was calculated from joint-position sensors (58SA; IED) on the motor axes. Position and force data were sampled at 1 kHz. Visual feedback was provided using a computer monitor mounted above the vBOT and projected into the plane of the movement via a mirror (Fig. 1A). This virtual reality system covers the manipulandum, arm, and hand of the subject, thus preventing direct visual feedback of the arm (Fig. 1B). Full details of the robotic manipulandum and virtual reality setup have been described previously (Howard et al., 2009). The exact onset time of any visual stimulus presented to the subject was determined using the video card refresh signal and was confirmed using an optical sensor.

Figure 1.

Experimental paradigm. A, Subjects were seated with their right forearm resting on an air sled. They grasped the handle of a robotic manipulandum (vBOT) with their right hand. Direct view of their right arm was prevented by a mirror through which visual feedback from the monitor was overlaid in the plane of movement. B, The subjects' task was to make forward-reaching movements from a start point (filled gray circle) located ∼20 cm in front of the chest to a target (black circle) placed directly across the start point (i.e., on the y-axis). C, Throughout the study, a visual cursor was presented to the subject as a representation of their hand location. On probe trials, the cursor could jump either right or left by 3 cm (i.e., perpendicular to the principal axis of movement) for 250 ms (black trace). During these trials, the physical location of the hand (gray dotted trace) was constrained to move in a straight line toward the target by a mechanical channel produced by the vBOT. These trials were used to measure the magnitude of the visuomotor feedback response (which we term “gain”).

Three individual experiments were performed. In all experiments, subjects made forward-reaching movements from a start circle (1.6 cm diameter circle located ∼20 cm in front of their chest) to a target (2.0 cm diameter circle) located directly in front of the start position (Fig. 1B). The instantaneous location of the subject's hand was visually presented to the subject as a yellow circle of 1 cm diameter, hereafter referred to as the “cursor.”

Electromyography.

In the second and third experiments, surface electromyography (EMG) was recorded from six muscles actuating the right limb, the posterior deltoid, pectoralis major, triceps lateralis, triceps longus, biceps brachii, and brachioradialis, using the Delsys Bagnoli (DE-2.1 Single Differential Electrodes) system. Before attaching the electrodes, the skin was cleansed with alcohol and rubbed with an abrasive gel. The electrodes were then coated with conductive gel and attached to the skin using double-sided tape. A single ground electrode was placed just proximal to the wrist of the right forearm. The location for each electrode was chosen to maximize the signal-to-noise ratio while avoiding crosstalk. In particular, each electrode was positioned over the belly of the muscle, while the signal (and noise) was viewed to ensure a high-quality signal. The electrode for the pectoralis major muscles was located on the upper portion of the muscle close to the clavicle. The EMG signals were band-pass filtered online through the EMG system (20–450 Hz) and sampled at 2 kHz. The EMG signals were aligned with the force and position signals using a signal from the serial port that was recorded on a channel with the EMG. This signal was changed at the onset and offset of any perturbation to ensure that the correct timing was achieved over the period of interest.

Probe trials.

To assess the gain of the visuomotor feedback response during the experiments, probe trials with perturbations similar to those described previously (Franklin and Wolpert, 2008; Franklin et al., 2012) were used. On random probe trials, the cursor representing hand position was shifted instantaneously either to the right or left by 3 cm or unperturbed (i.e., along the x-axis; Fig. 1C, solid black line). The unperturbed probe trials provided a baseline for comparison with the perturbation trials. These visual perturbations occurred only once on each trial and lasted for 250 ms, after which the cursor returned to reflect the physical location of the hand. Therefore, to reach the target, a response to the perturbation was not needed. The duration of the visual perturbation (250 ms) was chosen based on two considerations. Our previous work has shown that the force responses ramps up over ∼150 ms (Franklin and Wolpert, 2008). Therefore, to have a stable measure of the magnitude, we wanted the perturbation to last at least 150 ms. For shorter perturbations, the force responses will be due to both the onset and offset of the perturbation, making interpretation difficult. Second, we wanted to minimize required voluntary responses that might start to play a role for longer perturbations, specifically for perturbations that were maintained, for example, to the end of the movement. As a compromise between these considerations, 250 ms was selected for the perturbation length.

During all probe trials, the hand was mechanically constrained to move along the straight path between the start point and the target by a physical channel generated by the vBOT. The mechanical channel was implemented as a one-dimensional spring with a stiffness of 5000 N m⁻¹ and damping of 2 N m⁻¹ s acting laterally to the line from the start to the target (Scheidt et al., 2000; Milner and Franklin, 2005; Smith et al., 2006). This allowed us to use the force transducer to measure any lateral forces produced against the channel wall in response to a shift in the cursor position. The perturbation trials were randomly applied during movements in a blocked fashion so that one of each perturbation type was applied within a block of trials, with half of all trials in a block being unperturbed.

Although feedback gain estimates could be obtained using either channel trials or measuring the hand motion in unconstrained movements, there are pros and cons for each method. The use of a mechanical channel to measure feedback gains is the most appropriate tool (due in part to its higher accuracy). However, there are three concerns about this method. Although the application of a channel during the movement may induce small errors between the desired motion (slightly curved) and the actual motion (straight), possibly leading to the production of stretch reflex responses (Crevecoeur et al., 2012), the calculation of our visuomotor response subtracts the responses on two physically identical channel trials (only differing in the visual presentation), therefore removing any such stretch reflex response from our estimate of the visuomotor feedback gain. The second possible confound is that prevention of the visuomotor response from physically moving the arm could induce an error between the planned motion (of the corrective response) and the actual hand location (straight movement to the target), which could potentially produce stretch reflex responses. However, these could only be produced after the hand was expected to move from the visuomotor response at least 200 ms from the onset of the visual perturbation (150 ms force onset; Franklin and Wolpert, 2008) plus a 25 ms loop delay (Pruszynski et al., 2008) plus a 25 ms neuromechanical delay (Ito et al., 2004). Moreover, such short latency stretch responses do not exhibit condition dependency on the time scales of these experiments, so the true delay to any response that could demonstrate condition dependancy would be 235 ms (60 ms loop delay (Pruszynski et al., 2008, 2011; Nashed et al., 2012), which is beyond the time frame analyzed in this study. Finally, channel trials are known to lead to a small amount of decay in the reflex response (Franklin and Wolpert, 2008; Franklin et al., 2012). Indeed, in terms of the predictions of OFC, the response should eventually be abolished because feedback responses are not required due to the transitory nature of visuomotor probes. However, because we only used channel trials on occasional movements, the decay was small across the experiment. More importantly, because we only compared the response on channel trials across conditions, any decay cannot bias our results.

Experimental paradigms

Experiment 1: time course of visuomotor feedback gain.

Previous studies have shown that perturbations of the visual location of the hand lead to corrective motor responses (Saunders and Knill, 2003, 2004; Bagesteiro et al., 2006) that are involuntary (i.e., reflex) in nature (Franklin and Wolpert, 2008). Experiment 1 examined how the gain of the visuomotor response varies at different distances throughout a movement. Subjects performed two separate experimental sessions on separate days. In one session, they made forward-reaching movements to a “near” target located 17.5 cm distal to the start point (Fig. 2A, inset). In the other session, subjects made movements to a “far” target located 25 cm distal to the start point (Fig. 2B, inset). The order of the sessions was counterbalanced across subjects. There were 1281 trials in each session, 641 of which were unperturbed trials and 640 of which were probe trials. On the probe trials, the visual location of the hand was perturbed at one of seven possible locations along the movement. Specifically, in either session, the visual perturbation could begin at 5%, 20%, 32.6%, 46.5%, 66.5%, 85%, or 95% of the movement distance (y-distance) to the target (Fig. 2A,B, insets). The precise perturbation onset locations were chosen so that three of the perturbation locations were at the same physical location for the two target locations (i.e., across experimental sessions); that is, the physical hand positions for cursor perturbations for the far target at 32.6%, 46.5%, and 66.5% were the same as the perturbations at 46.5%, 66.5%, and 95% for the near target. There were 40 repetitions of each visual perturbation type in each experimental session: 2 (left/right cursor perturbation) × 7 (perturbation onset locations) × 40 (repetitions) = 560. In total, there were 640 perturbation trials in each session, because subjects also underwent 80 trials in which their hand path was constrained by the force channel in the absence of any visual perturbations (i.e., the “zero-perturbation” condition). Perturbation trials were randomly interleaved among the unperturbed trials. On the unperturbed trials, the cursor always reflected the position of the hand and no forces were applied to the hand by the robotic manipulandum. On these trials, the subjects were free to move between the start and the target position using any trajectory.

Figure 2.

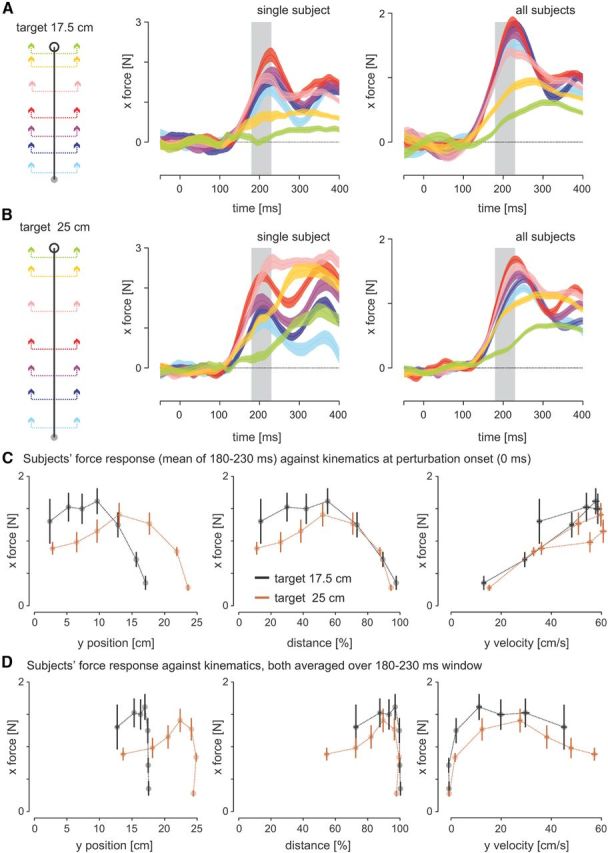
Time course of visuomotor gain. A, Left: Subjects made forward-reaching movements to the near target (17.5 cm), whereas on random trials, the visual location of the hand was perturbed either left or right at one of seven locations during movement. Middle: Different colors correspond to the different perturbation onset locations during reaching. Lateral forces exerted on the force channel in response to perturbations of the visual location of the hand during movement to a “near” target for a single subject. Responses to left and right perturbations are combined for each perturbation location with appropriate sign so that corrective forces are positive. Zero time indicates the onset of the visual perturbation and the gray background represents the reflex time window for force. Right: Mean lateral forces exerted on the channel across all subjects. B, Lateral force responses to cursor perturbations when reaching to a “far” (25 cm) target. C, Magnitude of lateral forces over the involuntary time window in A and B averaged across subjects separately for movements to the near (black trace) and far (brown trace) target. In the left panel, magnitudes are plotted as a function of absolute position from the start point; in the middle panel, the magnitudes are plotted as a function of percentage distance to the target; and in the right panel, the magnitudes are plotted as a function of the forward velocity, where each of these measures is determined at the time of perturbation onset. The error bars (both vertical and horizontal) represent the SEM. During reaching to either target, the visuomotor reflex gain was highest during the middle of movement and then decreased sharply as the hand neared the target. Higher initial gains were observed when reaching to the near target compared with the far target. D, The magnitude of lateral forces over the involuntary time window in A and B for movements to the near (black trace) and far (brown trace) target plotted as a function of the mean absolute position from the start point, percentage of distance to the target, and forward velocity over the same involuntary time window (180–230 ms).

Trials were self-paced; subjects initiated a trial by placing the cursor within the start circle for 500 ms. On each trial, tones were used to indicate when the movement should be initiated and also to indicate the required movement duration. Specifically, on each trial, five beeps were played. The intervals between the first three beeps were always 600 ms and subjects were instructed to initiate their movement on the third beep. They were required to reach the target on the fourth beep and the interval between the third and fourth beep varied depending on the experimental condition: 420 and 600 ms for movements of 17.5 and 25 cm, respectively. These durations were chosen to promote similar peak speeds across target locations. Subjects were required to remain at the target until the fifth beep, which occurred 600 ms after the fourth beep. Subjects were then free to return to the start point to initiate the next trial. A trial was considered successful if subjects did not overshoot the target and initiated movement between 80 ms before and 120 ms after the third beep and reached the target between 120 ms before and 80 ms after the fourth beep. On successful trials, the subjects received positive feedback (e.g., “good”) and a counter increased by one unit. However, within the successful trials, subjects were told that their movement was “great” if they initiated movement between 40 ms before to 60 ms after the third beep and reached the target between 60 ms before and 40 ms after the fourth beep. Other messages were provided visually at the end of each trial to inform the subjects of their performance (“too fast,” “overshot target,” “started too early,” or “started too late”). Specifically, if subjects left the start >80 ms before the third beep, the feedback was “started too early,” whereas if they left the start later than 120 ms after to the third beep, the feedback was “started too late.” If subjects entered the target >80 ms before the fourth beep, the feedback was “too fast,” whereas if they entered the target later than 120 ms after to the fourth beep, the feedback was “too slow.” Similarly, if the position of the cursor exceeded the distance of the movement by more than the target radius, feedback was “overshot the target.”

Experiment 2: simultaneous target perturbations.

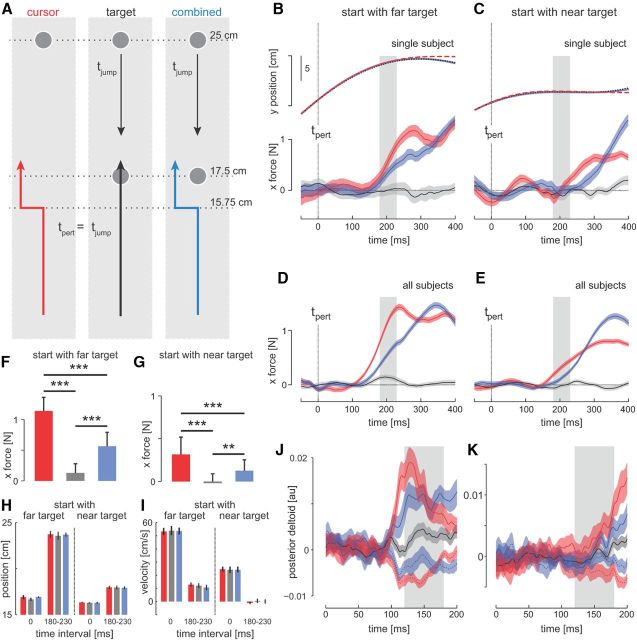
In Experiment 2, we examined whether the gain of rapid visuomotor responses modulated in response to intramovement changes in the target position. On each trial, subjects had to move to either the “near” target (17.5 cm from start) or to the “far” target (25 cm from start). On random trials, the cursor was perturbed either left or right (probe trials), the target jumped to the other location (near to far or vice versa), or both of these perturbations occurred simultaneously (Fig. 3A, inset). The cursor perturbations and target jumps started when the hand was 15.75 cm from the start position. All trials with cursor displacements and/or target jumps used the mechanical channel (as in the probe trials) to assess the visuomotor response.

Figure 3.

Simultaneous target and visual hand location perturbations. In Experiment 2, subjects made forward-reaching movements to a target that was initially set 25 cm away (far target) or 17.5 cm away (near target). A, Experimental protocol of movements to the far target. On random trials, one of three probe trial types was applied. On these perturbation trials, either only the cursor was perturbed (red trace, left), only the target was perturbed from the far to the near location (black trace, middle), or both the target and cursor were perturbed (blue trace, right). The onset of all three perturbations occurred at the same distance of movement to the target (15.75 cm) (t_pert = t_jump). B, Hand position and lateral forces for single subject responses to visual perturbations for the three perturbation conditions during movements to the far target. C, Hand position and lateral forces for single subject responses during movements to the near target in which the target could jump to the far location. D, E, Force responses to visual perturbations averaged across subjects. Zero time indicates the onset of the perturbations (t_pert), shading represents the SEM, and gray rectangles indicate the visuomotor reflex time window. F, G, Averaged forces over the reflex time window. Error bars represent 1 SD. Significant difference from the post hoc tests are indicated (***p < 0.001, ** p < 0.01). Little if any lateral forces were produced in response to target perturbations alone (gray bar). There was a reduction in force magnitude when cursor perturbations were accompanied by a concurrent target perturbation (blue bar smaller than red) regardless of the direction of target displacement. H, I, Position and velocity across subjects for the three perturbation conditions at the time of the perturbation onset (time 0 ms) and over the response interval (180–230 ms). J, K, Electromyographic responses in the posterior deltoid to the three perturbation conditions during movements to the far and near targets. The responses are shown for cursor perturbations to the left (solid red trace), cursor perturbations to the right (dotted red trace), combined cursor perturbation to the left and target jump (solid blue trace), combined cursor perturbation to the right and target jump (dotted blue trace), and only target jumps (black trace). Responses are averaged across subjects and shaded regions represent SEM. The gray rectangle indicates the reflex time window for EMG (120–180 ms after perturbation onset).

There were 641 unperturbed trials and 640 perturbation trials in this experiment. For each initial target location, there were 80 “zero perturbation” trials, 80 target jumps, 40 × 2 (right/left) cursor-only perturbations, and 40 × 2 (right/left) cursor with target jumps. On the trials in which the target was jumped, an additional 400 ms was added to the third interstimulus interval to account for the additional motor correction required to reach the target. On these trials, no feedback was provided about the accuracy of the movement duration. All other experimental conditions were identical to Experiment 1.

Experiment 3: delayed cursor perturbations.

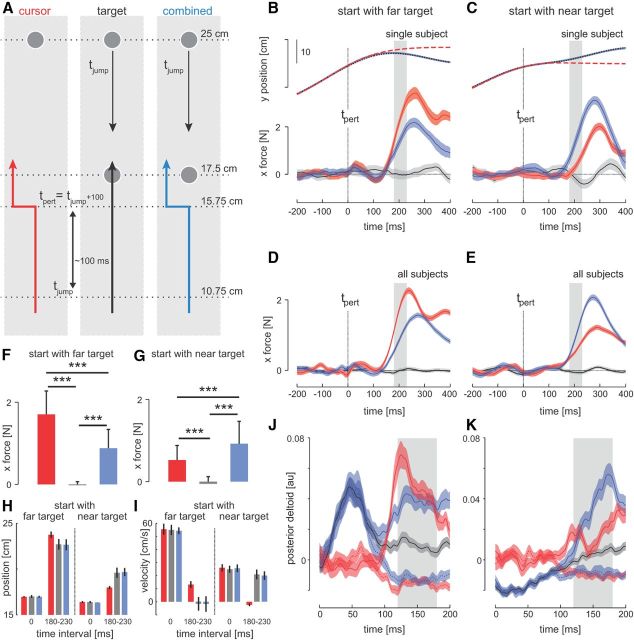
Experiment 3 was identical to Experiment 2 except that the target jumped at 10.75 cm, 5 cm before any cursor perturbations, corresponding approximately to a 100 ms advance (Fig. 4A, inset).

Figure 4.

Delayed cursor perturbations. A, Experimental protocol of movements to the far target. On random trials, one of three probe trial types was applied. On these perturbation trials, either only the cursor was perturbed (red trace, left), only the target was perturbed from far to the near location (black trace, middle), or both the target and cursor was perturbed (blue trace, right). The onset of all target jumps occurred when subjects had moved 10.75 cm distance (at time t_jump), whereas cursor perturbations occurred when subjects had moved 15.75 cm to the target (at time t_pert). This led to an approximately 100 ms delay between the target jump and the cursor perturbation (t_pert = t_jump + ∼100 ms). B, Hand position and lateral forces for a single subject for movements to the far target. C, Hand position and lateral forces for a single subject for movements to the near target in which the target could jump to the far location. D, E, Force responses to visual perturbations averaged across subjects. Zero time indicates the onset of the cursor perturbations (t_pert), shading represents the SEM, and gray rectangles indicate the visuomotor reflex time window. F, G, Averaged forces over the reflex time window. Error bars represent 1 SD. Significant difference from the post hoc tests are indicated (***p < 0.001, ** p < 0.01). There was a reduction in force magnitude during movements to the far target when cursor perturbations were preceded by a target jump to the near location. However, there was an increase in force magnitude to cursor perturbations during movements to the near target when the cursor perturbation was preceded by a target jump to the far location. H, I, Position and velocity across subjects for the three perturbation conditions at the time of the perturbation onset (time 0 ms) and over the response interval (180–230 ms). J, K, Electromyographic responses in the posterior deltoid to the three perturbation conditions during movements to the far and near targets. The responses are shown for cursor perturbations to the left (solid red trace), cursor perturbations to the right (dotted red trace), combined cursor perturbation to the left and target jump (solid blue trace), combined cursor perturbation to the right and target jump (dotted blue trace), and only target jumps (black trace). Responses are averaged across subjects and shaded regions represent SEM. The gray rectangle indicates the reflex time window for EMG (120–180 ms after perturbation onset).

Data analysis

The first five trials of each experimental condition for each subject were considered as familiarity trials and were not included in the analyses. The remaining data were analyzed using MATLAB R14. Force and kinematic data were low-band-pass filtered with a fifth-order, zero-phase-lag Butterworth filter with a 40 Hz cutoff. To get a single force response measure for each cursor perturbation location, the force responses to left and right cursor perturbations occurring at the same location along the y-axis were combined across pairs of individual trials (for a more detailed description, see Franklin and Wolpert, 2008). The magnitude of the force response (visuomotor gains) was examined (data not shown) for each perturbation condition as a function of the trial block number for all three experiments to determine whether the gains of the visuomotor response changed throughout the experiment. As expected from our previous work (Franklin and Wolpert, 2008; Franklin et al., 2012), these gains were initially high at the very beginning of the experiment, decreasing rapidly within the first five blocks and then remaining consistent (with a small decrease) throughout the rest of the trials. This very slow decrease suggests a slow reoptimization of the responses; however, because the force responses were maintained consistently above zero, we suggest that our results tap into the normal feedback behavior before it was extinguished by experience. To avoid any undue influence of the initial high gain trials at the beginning of the experiment, only the results from the last 35 blocks (blocks 6–40) were used in any of the analyses and results. Analysis of the remaining feedback responses throughout all three experiments demonstrated that the responses were maintained throughout the experiments with only 0.29 N decrease on average between the initial two and final two blocks. Because all perturbation conditions were pseudorandomly mixed, any decay would not affect the results because they compared across conditions.

EMG data were high-pass filtered with a fifth-order, zero-phase-lag Butterworth filter with a 30 Hz cutoff and then rectified. All EMG data were aligned to the onset of the perturbation. For each muscle individually, a baseline EMG trace was subtracted from the relevant EMG trace of each visual perturbation trial. The baseline EMG trace was the average EMG response across all “zero perturbation” trials in an experimental session (n = 80). To examine the rapid response (i.e., “reflex”), the average postperturbation EMG (120–180 ms) and force (180–230 ms) were calculated (Franklin and Wolpert, 2008). Only data from the above involuntary response time windows were used for statistical analyses, which were conducted using the general linear model in SPSS to perform ANOVAs. If a significant main effect was found, Tukey's honest significant difference post hoc test was used to examine differences. Statistical significance was considered at the p < 0.05 level for all statistical tests. Specifically, each data point used for statistical analysis represented the average across the reflex time window of a single perturbation trial for EMG and pairs of trials for force (combined leftward and rightward cursor perturbation trials). All statistical tests on the EMG data were performed on unscaled and unsmoothed subject data. For plotting purposes only (Fig. 3, Fig. 4), the EMG was scaled, smoothed, and averaged across subjects (but not across muscles). To do this for a particular muscle, a single scalar was calculated for each subject and used to scale the muscle's EMG traces for all trials for that subject. The scalar was chosen so that the mean (across trials) of the EMG data averaged over the period −50 to 50 ms relative to the onset of the perturbation was equal across subjects (and set to the mean over all the subjects). This put each subject on an equal scale to influence any response seen in the data. Before averaging, the individual muscle traces were initially smoothed using a 10 point (5 ms) moving average. The baseline EMG was then subtracted from all conditions (mean EMG during the zero cursor perturbation and no target jump condition: 80 trials). Once averaged across all subjects, the mean and SEM were determined for each condition and the mean muscle activity was then smoothed using a 10 point (5 ms) moving average before plotting.

To analyze visuomotor responses to cursor perturbations in Experiment 1 (Fig. 2), an ANOVA was performed for each target location (“far” and “near”) individually with the seven cursor perturbation onset locations as a fixed factor. Subjects were entered as a random factor. Force data from Experiment 2 (Fig. 3) were also analyzed independently for each initial target location because target perturbations were expected to have different effects in the two cases. For each initial target location, perturbation type (cursor only, target only, or target and cursor perturbations) was used as a fixed variable in an ANOVA that also included subjects as a random factor. The same ANOVA design was used for analyzing the force data from Experiment 3 (Fig. 4). To examine reflex EMG responses, a separate ANOVA was performed for each muscle and target location for Experiment 2 (Fig. 3) and Experiment 3 (Fig. 4). Each ANOVA had perturbation type as a fixed variable (two “perturbation type” levels: only cursor or target and cursor) using subjects as a random variable. The EMG values were calculated as the difference in integrated EMG over the interval 120–180 ms after the cursor perturbation between the leftward and rightward cursor perturbations. These values were calculated on a block by block basis throughout the experiment for each subject separately.

Results

In our study, right-handed subjects made forward-reaching movements to either a “near” or “far” target while grasping the handle of a robotic manipulandum with their right hand. On random probe trials, the cursor, representing the visual location of the hand, was perturbed either left or right of the physical hand location by 3 cm for 250 ms. During these probe trials, the hand was mechanically constrained to move in a straight line toward the target. In the first experiment, we perturbed the cursor at one of seven different locations during movement to examine the evolution of the gain of the rapid visuomotor response during a reach. In two subsequent experiments, the target jumped from the near to the far location or vice versa during the reach. The cursor was either perturbed simultaneously with the target jump (Experiment 2) or ∼100 ms later (Experiment 3). Modifying the end goal of the motor task (i.e., target location) allowed us to determine whether the gain of the visuomotor response adapted appropriately and rapidly to changes in the task goals.

Time course of visuomotor feedback response

In Experiment 1, subjects made movements to either the near or far target in two separate experimental sessions. We perturbed the visual location of the hand cursor at different locations throughout the movement (Fig. 2A,B, left). By measuring the force response, the differences in force produced against the channel wall for leftward and rightward perturbations, we could assess how the gain of the visuomotor reflex (reflective of the gain of the visuomotor response) evolved during a movement. Figure 2A shows the mean force response for each cursor perturbation location for reaching movements to the near target. Both the single subject (middle column) and group means (right column) demonstrate strong differences in feedback gains for the seven different perturbation locations. The visuomotor gains were largest for perturbations occurring near the middle of movement (red and purple traces) and decreased as the hand neared the target (yellow and green trace). For reaches to the far target, a similar pattern of responses was seen both for the single subject and group mean (Fig. 2B).

Figure 2C shows the force responses averaged over the 180–230 ms time window (Fig. 2A,B, gray area corresponds to the involuntary response; Franklin and Wolpert, 2008) against movement distance (Fig. 2A,B, left), movement percentage (Fig. 2A,B, middle), and movement velocity (Fig. 2A,B, right) at the time of the perturbation onset for both the near (Fig. 2A,B, black) and far targets (Fig. 2A,B, brown). Two ANOVAs, one for each target location, yielded a significant main effect of perturbation location on the magnitude of the reflex force responses for both the near target (F_(6,42.062) = 13.4, p < 0.001) and the far target (F_(6,42.007) = 13.2, p < 0.001). Post hoc tests were then performed to examine specific differences in the gains of the visuomotor response for different locations in the movements. For movements to the near target (Fig. 2C, black trace), the gain of the visuomotor response increased slightly from the beginning of the movement to the middle (46.5% > 5%: p = 0.01), but started to reduce in gain by 66.5% (p = 0.001 compared with 46.5%), decreasing significantly by 85% of the movement distance (p < 0.001 compared with all previous perturbation locations). This gain was further decreased by 95% of the movement distance (95% < 85%, p = 0.015). For movements to the far target (Fig. 2C, brown trace), the visuomotor gain rose over the first four locations (e.g., 46.5% > 5%: p < 0.001) and then decreased toward the end of the movement (e.g., 45% > 95%: p < 0.001) such that the final gains were smaller than those at the beginning of the movements (5% > 95%: p < 0.001).

The position of the hand changes during the perturbation and for late perturbations could even be stationary at the target for some of the measurement time. To investigate how the kinematics at the time of the force measurement affects the gain, we show the same data as in Figure 2C but with the kinematics (x-axis) computed as the average of position, percentage distance, and velocity over same time period as we averaged the force (180–230 ms). For the responses plotted as a function of these kinematics at the time of the response (Fig. 2D), multiple levels of feedback gain (force) can be seen for identical positions or velocities (at the end of the movements). This strongly supports the idea that the responses are produced as a function of the state of the limb at the time of the perturbation. Therefore, when reaching to either target, the evolution of the visuomotor response shows a similar profile: a relatively high gain around the middle of movement and then a decrease in gain toward the end of the movement (Fig. 2C). Our experimental design included three perturbations for the two movement distances that occurred when the hand was in the same physical location (8, 11.5, and 16.5 cm). However, these correspond to different percentages of the movement depending on the target location: for the near target, they correspond to 46.5%, 66.5%, and 95%, whereas for the far target, they correspond to 32.6%, 46.5%, and 66.5%. A separate ANOVA was performed for each perturbation location, which indicated no significant difference in force magnitude between the initial two perturbation locations (F_(1,7) = 4.96, p = 0.061, and F_(1,7) = 0.58, p = 0.47, respectively), but a significant difference at 16.5 cm, with responses for the near target being significantly less than for the far target (F_(1,7).007 = 17.2, p = 0.004). This result suggests that the gain of the visuomotor reflex was not primarily modulated by the actual physical location of the hand (Fig. 2C, left), but instead depended strongly on how close to the endpoint of the movement the perturbation occurred (Fig. 2C, middle) and was strongly related to the velocity of the movement at the time of the perturbation (Fig. 2C, right).

Simultaneous target perturbations

Experiment 1 demonstrated that the gains of the visuomotor responses are highest around the middle of movement, decreasing sharply toward the end of the movement, with the lowest responses observed when the hand was closest to the target. In Experiment 2, we examined whether the gain of the visuomotor response was preplanned or if it could be updated in real time if the location of the target changed. Most trials involved a simple reach to a fixed target. We used three types of probe trial (Fig. 3A, left) to assess the visuomotor response to the target jumping between locations (far to near or vice versa). We used probe trials with a hand cursor perturbation alone as in Experiment 1 (Fig. 3A, red line), a target jump alone (black line), or the simultaneous combination of both a target jump and cursor perturbation (Fig. 3A, blue line). These trials were randomly interleaved, with all perturbations starting when the hand was 15.75 cm from the starting location, and the hand was constrained in a mechanical channel. The target could either start at the far location (Fig. 3, left) or at the near location (Fig. 3, right). If the visuomotor response could update instantly to changes in the task, then from the results of Experiment 1, perturbing the target from the far to the near location (i.e., bringing the target closer to the cursor) would be expected to cause a decrease in the gain of the visuomotor response. Conversely, target jumps from the near to the far location would be expected to cause an increase in the visuomotor response.

When the initial target position was located at the far target (Fig. 3, left) for the target jump only condition, as expected, little if any lateral forces were produced (Fig. 3B, D, black traces for a single subject and group mean, respectively). This demonstrates that target jumps alone do not cause changes in the lateral forces that could confound our feedback gain measurements. As expected from Experiment 1, the cursor perturbations alone produced large force responses to the perturbation because the onset of the perturbation occurred at 63% of the total distance to the target (red trace). The condition in which the cursor perturbation occurred simultaneously with the target jump (blue) resulted in a decreased response compared with the cursor perturbation alone. The kinematics across all three conditions were virtually identical for the periods of interest (Fig. 3B, Fig. 3H,I, top traces). Note that for a far to near target jump, the hand can actually pass the new target location before returning in a corrective movement. We compared the average force responses across the 180–230 ms interval (Fig. 3B,D, gray bars) for the three conditions (Fig. 3F). This showed a significant main effect of perturbation type on the magnitude of the force response (F_(2,18) = 172, p < 0.001), with post hoc tests indicating that the response to cursor perturbations alone (red) were significantly higher than both other conditions (p < 0.001) and the response during simultaneous target jump and cursor perturbations were significantly higher than responses during target perturbations alone (Fig. 3F, blue vs gray bars, p < 0.001).

In contrast to our prediction, a similar decrease in visuomotor gain was also seen when the target was perturbed from near to the far (Fig. 3C,E). An ANOVA indicated a significant effect of perturbation type of the gain of the visuomotor response (F_(2,18) = 21.4, p < 0.001). Post hoc tests indicated that the gain of the response to cursor perturbations alone (Fig. 3G, red) were significantly higher than the other two perturbation types (p < 0.001) and forces during target perturbations alone (Fig. 3G, gray) were significantly lower than those of the combined cursor perturbation and target jump condition (p = 0.005). These results suggest that, rather than the predicted update of the rapid visuomotor response to the new target location, the combination of target jump and cursor perturbation results in a nonspecific decrease in the visuomotor gain for either direction of target jump.

Similar effects were found in the muscular activity. Figure 3J, K shows the mean rectified EMG for the posterior deltoid muscle to the three probe types, with the leftward and rightward cursor perturbation for the cursor alone (red) and combined target and cursor trials (blue) shown as solid and dashed lines, respectively. Target jump alone (gray) produced little change in EMG activity for this muscle. We computed a measure of muscular response that was the difference in EMG for leftward and rightward cursor perturbations integrated over the 120–180 ms interval. When the target was initially in the far location (Fig. 3J), the responses to the combined target jump and cursor perturbations (blue traces) were smaller than the responses to the cursor perturbations alone (red traces) in the posterior deltoid (F_(1,780) = 18.059, p < 0.001). Similar results were also found for the pectoralis major (F_(1,780) = 70.265, p < 0.001), triceps longus (F_(1,780) = 45.376, p < 0.001), and triceps lateralis (F_(1,780) = 34.075, p < 0.001). When the target was initially in the near location (Fig. 3K), similar results were obtained in the posterior deltoid, with smaller levels of muscle responses to the combined cursor and target perturbations than to the cursor perturbation by itself (F_(1,782) = 28.015, p < 0.001). Again, these differences were also found in the pectoralis major (F_(1,782) = 15.676, p < 0.001). Therefore, the results demonstrate that when the target was jumped simultaneously with the cursor perturbation, the result was a decrease in the visuomotor responses both in force and muscle activity at involuntary latencies regardless of the direction of the target jump.

Delayed cursor perturbations

Because simultaneous target jumps produced an inhibition in the visuomotor reflex gains, Experiment 3 examined target jumps that occurred ∼100 ms before cursor perturbation to determine whether the visuomotor responses would rapidly update to changes in the task. Similar to Experiment 2, the position of the target was jumped along the principal axis of movement (either from the near to the far target or from the far to near target), after which the visual location of the hand was perturbed (Fig. 4A). Although the kinematics were almost identical at the time of the cursor perturbation (Fig. 4B,H,I), they had changed by the time we measured the force response in the condition where the target jump occurred ∼100 ms before the cursor perturbation. Similar to Experiment 2, in the far to near target jump, the hand could actually pass the revised target location before returning in a corrective movement.

As expected, when the initial target position was located at the far target in the target jump only condition, little or no lateral forces were produced (Fig. 4B,D). This finding demonstrates that target jumps alone do not cause changes in the lateral forces that could confound our feedback gain measurements even when they occur in advance of the cursor perturbations. In the cursor perturbation only condition, large responses in the force to the cursor perturbation were seen (red traces). However, when target jumped before the cursor perturbation, there was a smaller response produced in the force (blue trace) compared with the cursor perturbation alone condition (red trace). We compared the average force responses across the 180–230 ms interval (Fig. 4B,D, gray bar) for the three conditions (Fig. 4F). An ANOVA confirmed a significant effect of perturbation type on the magnitude of the forces produced at reflex latencies (F_(2,18) = 76.4, p < 0.001), with post hoc comparisons showing that forces produced in response to cursor perturbations after the target jump were significantly smaller than responses to cursor perturbations alone (p < 0.001) and larger than responses to target jumps alone (p < 0.001).

In cases in which the target was perturbed from the near to far location (Fig. 4C,E), the opposite responses were found. When the target jump preceded the cursor perturbation, the responses to the cursor perturbation (Fig. 4C,E, blue trace) was much larger than to the cursor perturbation alone (Fig. 4C,E, red trace). An ANOVA confirmed a significant effect of perturbation type on the gain of the visuomotor response (Fig. 4G, F_(2,18) = 22.3, p < 0.001) during the involuntary interval. Post hoc tests indicated that gain was significantly higher when cursor perturbations occurred just after a target perturbation compared with cursor perturbations only or target jumps (p < 0.001). When the cursor was perturbed just after the target, there was an increase in the visuomotor gain compared with the case in which no target perturbation preceded the cursor perturbation (Fig. 4C,E,G, blue vs red traces).

In Experiment 2, the kinematics in the response measurement time window were the same for all trial types (Fig. 3B,C, gray, and H,I). However, in the delayed perturbation experiment, there were differences in the kinematics in this time window that depended on trial type (Fig. 4B,C, gray, and H,I). The results of Experiments 1 and 2 show that the gain was not purely determined by kinematics during the time response window, because different gains can be seen for the same kinematics. However, to confirm that the changes in reflex gain in the delayed perturbation experiment were due to online replanning and not simply a consequence of the differences in kinematics seen for the different trial types, we performed additional analyses on individual trials for the cursor (red) and combined (blue) trials.

For each trial, we calculated the average position and velocity of the hand in the response time window (180–230 ms). In the condition in which the target was initially at the near location, for the combined trials, the hand moved on average farther and was faster compared with the cursor only trials (Fig. 4H,I, blue vs red trial types). However, natural movement variability led to considerable overlap in the distributions of the kinematics for these two trial types. This allowed us to determine whether trials that were matched for kinematics for these two trial types had different gains.

We selected probe trials for the combined and the cursor only trials that were matched for position and velocity. For each subject, we chose pairs of trials from these two trial types that differed by <1 cm in position and by <2 cm/s in velocity. We selected as many such pairs as we could from the data, which yielded 76 pairs of trials across the subjects (with 8 of the 10 subjects contributing samples to this dataset). Comparing the positions and velocity showed that these datasets were well matched for position (mean ± SD of 5.71 ± 0.82 and 5.79 ± 0.79 cm for cursor only and combined, respectively) and for velocity (8.07 ± 4.56 and 8.31 ± 4.61 cm/s, respectively) and neither differed significantly between the trial types (both p > 0.5). However, even in these datasets matched for kinematics, the reflex gain for the combined trials (mean ± SEM of 1.05 ± 0.13 N) was significantly larger (t₁₅₀ = 4.6083, p < 0.0001) than for the cursor only (0.35 ± 0.09 N) condition. This confirms that the changes in reflex gain in this condition of the delayed perturbation experiment are due to online replanning and not to differences in kinematics. Examining the distributions of the kinematics for the condition in which the target was initially at the far location showed that the distributions did not have sufficient overlap to perform this matched dataset analysis. However, we also performed additional tests for both conditions.

For each of the initial target locations (near or far), an ANCOVA with covariates of the position and velocity, random factors of subjects, and a main factor of trial type (two levels: combined and cursor only conditions) were performed on the reflex gain data. This allowed us to determine whether the particular velocity or position on a given trial explains the difference in the force responses seen across these two trial types in each condition. For both the initial near target and the initial far target conditions, the ANCOVA found a significant main effect of trial type (F_(1,92.91) = 17.00, p < 0.001 and F_(1,55.923) = 44.96, p < 0.001, respectively), indicating that these differences were significant independent of any linear effect of position and velocity at the time of the response. This provides further evidence in support of online control of reflex gains in our task.

The task-dependent changes in the force responses were mirrored by similar changes in the muscle activity (Fig. 4J,K). The traces are aligned with the cursor perturbation so that on the target conditions (blue and black), the target has jumped 100 ms earlier. Therefore, the early difference between the blue and black curves and the red ones reflect rapid responses to the target jump. We computed a measure of muscular response that was the difference in EMG for leftward and rightward cursor perturbations integrated over the 120–180 ms interval. When the target was initially in the far location (Fig. 4J), the responses to the combined target jump and cursor perturbations (blue traces) were smaller than responses to the cursor perturbations alone (Fig. 4J, red traces) in the posterior deltoid (F_(1,789) = 18.1, p < 0.001), as well as for the triceps lateralis (F_(1,789) = 7.85, p < 0.005) and triceps longus (F_(1,789) = 28.1, p < 0.001). When the target was initially in the near location (Fig. 4K), the responses to the combined target jump and cursor perturbations (Fig. 4K, blue traces) were larger than responses to the cursor perturbations alone (Fig. 4K, red traces) in the posterior deltoid (F_(1,780) = 27.5, p < 0.001). Similar differences were also found in the triceps lateralis (F_(1,780) = 40.5, p < 0.001) and triceps longus (F_(1,780) = 20.2, p < 0.001). These results demonstrated rapid task-appropriate adaptation in the involuntary visuomotor feedback responses when the target shifted position 100 ms in advance of the perturbations of the visual location of the hand.

Discussion

By applying perturbations at a variety of points throughout a movement, we determined the time course of the visuomotor feedback response. We found significant modulation of the feedback gain that was largest in the middle of the movement and decreased sharply toward the end of the movement regardless of the movement extent. To determine whether these feedback responses can rapidly update to changes in the task goal, we examined the gains in response to jumps in the target location during movement. Based on the modulation seen to static targets, we predicted that the gains should increase for target jumps that increased the distance to the target but decrease to jumps that decreased the distance. Gains measured synchronously with a target jump showed a nonspecific reduction that did not depend on the jump direction. However, the visuomotor gain measured 100 ms after the target jump showed an appropriate goal-related dissociation with a respective reduction and increase in gain when the target jumped closer to or further from the hand.

OFC models predict a time-varying positional gain that depends on the estimated location of the hand p and target p*, with the feedback force given by F = K(t)*(p*(t) − p(t)) (Liu and Todorov, 2007). For simplicity, we assume that K(t) is a 2 × 2 matrix made by multiplying a scalar gain k(t) by the 2 × 2 identity matrix. Although our technique visually perturbs the hand lateral to the direction of movement and measures the lateral restoring force, it is able to measure the gain k(t) directly. When the hand is moving toward the target and a distance d away (y-direction) the visual perturbation of a lateral distance s leads to a feedback force F = k(t)*[−s; d]. Therefore, the component that we measured using the mechanical channel is −k(t)*s. Because s was fixed in all of our perturbations, we measured k(t) directly. Note that if k(t) is not time varying, our measure of the visuomotor response would be independent of the distance between the hand and the target.

The modulation of the visuomotor gain to static targets showed that the gain depends on the distance to the target. Specifically, the gain was highest around the middle of movement and decreased rapidly as the hand neared the target. This pronounced decrease toward the end of the movement occurred as a function of the distance to the target rather than depending on the distance moved. These effects are in agreement with the predictions of OFC models. For example, Liu and Todorov (2007) modeled reaching movement to a fixed target with time-varying feedback gains on the hand position, velocity, and acceleration so as to match the kinematics of the movement. Although they did not measure the feedback gains directly, they estimated the feedback gains that best explained the kinematics. They suggested that the gains controlling position were high around the middle of movement and then decreased sharply as the hand neared the target (Fig. 3A in Liu and Todorov, 2007). According to the OFC model, when the hand is near the target, feedback responses are primarily determined by the need to stop the movement (i.e., damping) and therefore the feedback gain controlling position is relatively low. This prediction matches our measured gains, which showed a rapid reduction toward the end of the movement (Fig. 2C). In addition, when lateral target perturbations occurred early in a movement rather than later, subjects made weaker corrections (Liu and Todorov, 2007). This was interpreted as there being sufficient time to correct for errors at the earlier stages of movement. These predictions of the feedback gains are supported by our results showing that the measured gains were low early in the movements, especially for movements to the far target.

We also measured change in reflex gain in response to target location jumps to examine whether updating within a movement occurs and, if so, the time needed to recompute new gains. Measuring the gains at the time of the jump (so that visual information about the jump is synchronous with the onset of the visuomotor perturbation, which lasts 250 ms) showed that there was a reduction of gain regardless of the direction of target displacement (Fig. 3). We suggest that this reduction of the visuomotor gain may be a response to increased uncertainty in the state of the limb. This supports our proposed distinction in the adaptation of feedback gains to uncertainty (Franklin et al., 2012); that is, when the uncertainty occurs in the sensory feedback, the feedback gains should decrease (Ariff et al., 2002; Körding and Wolpert, 2004; Izawa and Shadmehr, 2008; Braun et al., 2009), but when the uncertainty occurs in the internal model of the dynamics, an increase in the feedback responses should be seen (Franklin et al., 2012). In contrast, measuring the visuomotor gains 100 ms after the target jump showed that the gains now appropriately dissociated as a function of the direction of the jump. As predicted by the static target experiments, we found that the perturbations bringing the target closer to the hand resulted in a decrease in visuomotor gain and perturbations that took the target away from the hand lead to an increase in gain (Fig. 4). Therefore, after target perturbation, the reflex gains were rapidly updated to reflect the new distance to the target. This demonstrates a remarkable ability by the CNS to rapidly adjust reflex gains online within a 100 ms timeframe given the changes in the task goal. Previous studies have demonstrated that reflex responses can be adjusted for a task goal before movement (Diedrichsen, 2007; Franklin and Wolpert, 2008; Kimura and Gomi, 2009; Kurtzer et al., 2009; Pruszynski et al., 2011; Dimitriou et al., 2012; for review, see Pruszynski and Scott, 2012) and that feedback gains can be gradually learned so as to be appropriate for the environmental dynamics (Kimura et al., 2006; Franklin et al., 2007; Wagner and Smith, 2008; Kimura and Gomi, 2009; Ahmadi-Pajouh et al., 2012). This time course of this change (100 ms) is similar to that seen for the rapid update in stretch reflex latency when targets are presented to a stationary subject (Yang et al., 2011). In a related study (Mutha et al., 2008), stretch reflex perturbations were elicited 100 ms after a target jump by perturbing either with or against the target jump. Although the measured responses varied during the short and long latencies with the claim that visual input does not produce responses within this time interval, this is the exact interval over which visual input from target jumps (Brenner and Smeets, 2003; Diedrichsen et al., 2004), cursor jumps (Saunders and Knill, 2004; Franklin et al., 2008), and background shifts (Saijo et al., 2005) affects the motor output. The design of the current study, in which the feedback probe was orthogonal to shifts in the target (task goal), allowed the measurement of the feedback gain to be performed independently. Our study therefore is the first evidence for the rapid updating of the feedback response within a movement to changes in the task goal based on new sensory information.

Our results are consistent with the framework of model-predictive control (for review, see Lee, 2011). In model-predictive control, rather than compute the set of time-varying feedback gains once before movement, the feedback optimization is repeatedly performed throughout the movement. At each step of the control loop, the optimal feedback gains for the rest of the movement are calculated, but only the first step is taken and then the optimal feedback gains are recalculated. Such a technique allows changes in task goals or errors that accumulate due to noise or errors in calculation of gains to be taken into account in an efficient manner. In essence, this method allows continuous replanning of the remainder of the movement, but only the initial part of any plan is ever executed. However, it is important to note that our experiment cannot distinguish between online reoptimization of feedback control and precomputing several feedback solutions (for possible target positions) and then switching between them if the target jumps. Nevertheless, both of these control strategies lead to online modification of the feedback gains, albeit through different mechanisms.

To calculate the optimal gains requires both an estimate of the current state of the limb as well as the location of the target relative to the limb. Recent work suggests that the posterior parietal cortex is well placed to perform such calculations (Desmurget and Grafton, 2000; Mulliken et al., 2008). There have been several studies implicating this region in the rapid updating and correction of movements (Desmurget et al., 1999; Pisella et al., 2000; Della-Maggiore et al., 2004) and, more recently, it has been proposed that the parietal cortex is involved in state estimation in combination with the cerebellum, which forms the forward model (Wolpert et al., 1998; Mulliken et al., 2008; Shadmehr and Krakauer, 2008). In this framework, the cerebellum predicts the next state of the limb (based on the previous motor output and state estimates), which is combined in the posterior parietal cortex with the sensory feedback thereby providing an optimal estimate of the current state. There have been several studies supporting the involvement of the cerebellum in such forward modeling (for review, see Franklin and Wolpert, 2011). For example, the misreaching seen in humans when transcranial magnetic stimulation is applied over the cerebellum is consistent with the cerebellum being involved in the process of estimating the limb state from the motor command (Miall et al., 2007). When transcranial magnetic stimulation was applied, subjects produced movements that appeared to use the limb state 140 ms in the past, as if relying on purely delayed sensory inputs. Moreover, it is possible that internal models underlying state estimation exist at many levels in the sensorimotor hierarchy. For example, it has been proposed that even muscle spindles can act as predictors, because their outputs correlate best with kinematic states 100–150 ms in the future (Dimitriou and Edin, 2010).

We have shown here that the visuomotor feedback gains vary as a function of the movement to the target in a manner congruent with OFC, with higher gains in the middle of movements and low gains as the hand approaches the target. Moreover, we have demonstrated that the sensorimotor system is able to rapidly recompute visuomotor reflex gains to accommodate online changes to the task goal during reaching, whereas nonspecific inhibition occurs immediately in response to the target jump. These studies demonstrate not only the modulation of feedback within movements, but that these feedback gains are rapidly updated based on sensory feedback available within the movement itself, which is consistent with model-predictive control.