Thermodynamic framework for identifying free energy inventories of enzyme catalytic cycles

Abstract

Pauling’s suggestion that enzymes are complementary in structure to the activated complexes of the reactions they catalyze has provided the conceptual basis to explain how enzymes obtain their fantastic catalytic prowess, and has served as a guiding principle in drug design for over 50 y. However, this model by itself fails to predict the magnitude of enzymes’ rate accelerations. We construct a thermodynamic framework that begins with the classic concept of differential binding but invokes additional terms that are needed to account for subtle effects in the catalytic cycle’s proton inventory. Although the model presented can be applied generally, this analysis focuses on ketosteroid isomerase (KSI) as an example, where recent experiments along with a large body of kinetic and thermodynamic data have provided strong support for the noncanonical thermodynamic contribution described. The resulting analysis precisely predicts the free energy barrier of KSI’s reaction as determined from transition-state theory using only empirical thermodynamic data. This agreement is suggestive that a complete free energy inventory of the KSI catalytic cycle has been identified.

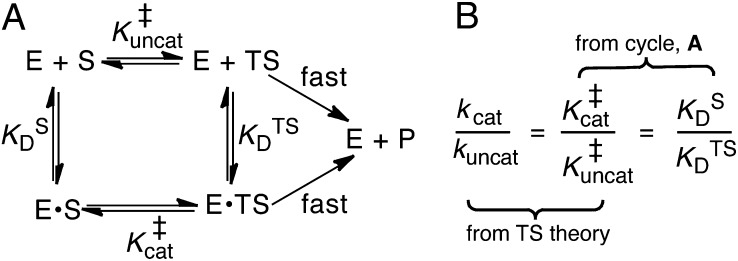
Enzymes are generally viewed as devices that use protein architecture to precisely position several key functional groups and electrostatic partners with respect to the substrate (1–4). This structure-based approach is complemented by thermodynamic models, which provide abstract but quantitative descriptions of these interactions, including those that escape visual intuition. In particular, the model shown in Fig. 1, first advanced by Kurz (5), has served as a dominant paradigm for conceptualizing enzyme catalysis for 50 y. This thermodynamic cycle formalizes Pauling’s hypothesis that enzymes are complementary in structure to the transition states of the reactions they catalyze (6, 7) and, combined with physical models to describe the enzyme–transition state interactions, it can help determine what leads to enzymes’ catalytic effects (8).

Fig. 1.

Kurz’s model of enzymatic catalysis. (A) The rate of a chemical reaction [either enzymatic (cat) or uncatalyzed (uncat)] is dictated by a pseudoequilibrium constant, K^‡. E, enzyme; S, substrate; TS, transition state. K_D is a dissociation constant. (B) Using transition-state theory, the ratio of the rate constants (known as the “rate enhancement”) is equal to the ratio of the K^‡s, and the thermodynamic cycle implies that the ratio of dissociation constants equals .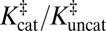

According to an elementary formulation of transition-state theory (TST), a rate constant, k, is determined by the position of a pseudoequilibrium (represented by K^‡) to the activated complex (9). In this depiction, chemical reactions are treated as equilibria between ground states and transition states (Fig. 1A). An enzyme’s accelerated rate (k_cat >> k_uncat) is represented by a relatively large value of 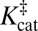compared with 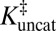(Fig. 1B). This implies that the enzyme must bind its cognate transition state very tightly, so the enzyme’s dissociation constant to the transition state 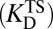is very small (2, 5). In this model, the overall rate constants are taken to be proportional to K^‡. By solving the thermodynamic cycle of Fig. 1A, one obtains

where k_cat and k_uncat are the enzyme-catalyzed and uncatalyzed unimolecular rate constants, respectively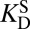, and and 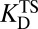are dissociation constants of the enzyme to substrate and transition state, respectively. Eq. 1 implies that the rate enhancement (the ratio of the enzymatic and uncatalyzed rate constants) is equal to the differential binding factor of the transition state. Despite its great conceptual power, Eq. 1 seems to fall short of accounting for actual enzymes’ catalytic power. Whereas it is often asserted that inhibitors serve as analogs of transition states (10–14), the differential binding factors for good inhibitors are normally around 10^3–7 (13–15), much smaller than the fantastic rate enhancements (k_cat/k_uncat) on the order of 10^5–17 (10–12) achieved by natural enzymes. Kurz’s simple model has been a useful tool for rationalizing why tight-binding inhibitors sometimes resemble the transition states of their target enzymes’ reactions (10), but it has been less useful for understanding the origin of enzyme catalysis. Indeed, the fact that rate ratios for enzymes can sometimes be accurately calculated by computational methods such as empirical valence bond (16, 17) or quantum mechanics/molecular mechanics simulation (18), but are nearly always strikingly larger than empirically determined binding ratios, is a persistent puzzle and has been met with a number of different reactions. Many have conceded (and in some cases, shown) that inhibitors are not equivalent to the transition states of chemical reactions but rather are only crude simulacra (10, 12, 19, 20). Others have proposed that there are dynamical contributions to catalysis that cannot be recapitulated in an equilibrium thermodynamic picture (21–23). A third possibility is that the thermodynamic cycles that are commonly used to bring binding effects to bear on catalysis are incorrect or incomplete (17, 24).

In the present work, we argue for the third case. In laying out this argument, we extend the classical thermodynamic framework for the reaction catalyzed by ketosteroid isomerase (KSI) that incorporates insights from recent studies (25–27). This analysis of KSI reveals that subtle processes other than differential binding are at work in KSI’s catalytic cycle; when these processes are accounted for, one can obtain an estimate for the activation barrier that is consistent with kinetics (28) and computation (16, 29). This model effectively bridges the divide between the rate ratio and the binding ratio, without invoking dynamic factors.

Background on KSI

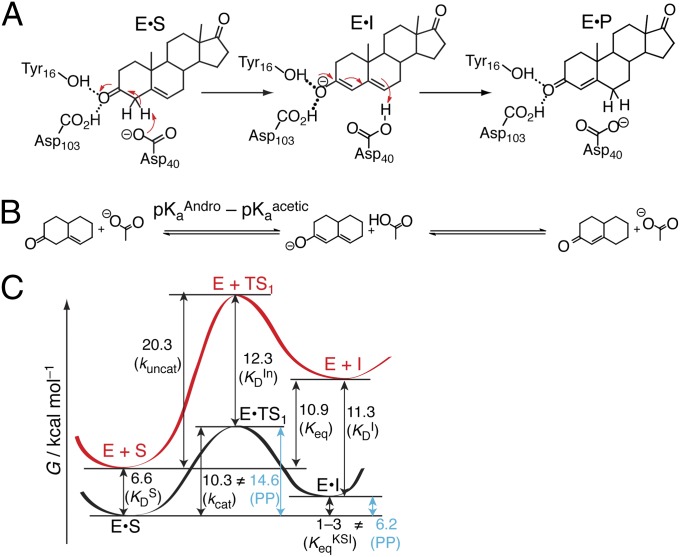
KSI is among a class of enzymes that elicit the ability to abstract protons (30) from an apparently nonacidic carbon acid (5-androsten-3,17-dione, pK_a = 12.7; ref. 31) using a weak general base (Asp40, pK_a = 3.75; ref. 32), as shown in Fig. 2A. These pK_as and all other thermodynamic parameters that will be used in this analysis are compiled in Table S1. KSI is a highly proficient enzyme, because in its absence the isomerization of androstene proceeds about a trillion times more slowly (11). In the following, the uncatalyzed reaction will refer to the “chemically filtered” reference reaction—that is, the nonenzymatic reaction that proceeds by the same mechanism (17). In KSI’s case, this corresponds to the slow acetate-catalyzed isomerization of androstene in solution (Fig. 2B), which involves a high-energy dienolate intermediate (33). In KSI, this intermediate is strongly stabilized by an oxyanion hole (OAH) in the active site (34). The OAH consists of a tyrosine (Tyr16) and a protonated aspartic acid (Asp103) that donate hydrogen bonds to the carbonyl oxygen of androstene (35). Tyr16 is very close to two additional tyrosines (Tyr32, Tyr57), which form a hydrogen-bond network (35).

Fig. 2.

Chemical mechanism and energetics of KSI. (A) 5-Androsten-3,17-dione (androstene), the steroid substrate, is converted to the conjugated isomer, 4-androsten-3,17-dione, via the enolization (first step) and reketonization (second step) of the carbonyl. (B) The chemically filtered uncatalyzed enolization of androstene. Androstene is abbreviated with two rings. The ∆G° of the first reaction is proportional to 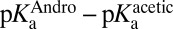according to Eq. 2. (C) Reaction coordinate diagram for the enolization of androstene (S) to the dienolate intermediate (I), either in KSI (black) or in solution (red). Numbers correspond to free energy differences in kcal⋅mol^–1. Black arrows correspond to measured quantities and are associated with the binding/rate constants in parentheses. Blue arrows correspond to quantities calculated by closing thermodynamic cycles that articulate Pauling’s paradigm (PP).

Fig. 2B introduces nomenclature conventions that will be used throughout the discussion: First, androstene, the steroid substrate, is abbreviated with only two (A and B) rings and, second, free energies of reaction (∆G°s) are expressed over arrows in terms of logarithmic equilibrium constants (i.e., pKs). Logarithmic equilibrium constants are linear with free energy, as expressed by Eq. 2:

The KSI-catalyzed and uncatalyzed isomerization of androstene share the same chemical mechanism, passing through a presumed dienolate intermediate (36, 37), so that the present analysis can focus on energetics. In Fig. 2C, an annotated reaction coordinate diagram for the first chemical step is given. ∆Gs (in kcal⋅mol^–1) for various processes associated with formation of the first transition state (TS₁) and the intermediate (I) are provided, as well as the associated binding/rate constants from which the ∆Gs are determined. As judged from interpreting chemical kinetics with TST, the free energy barrier of the first enzyme-catalyzed reaction is 10.3 kcal⋅mol^–1 (28, 38) (this barrier is evaluated from the “microscopic” rate constant for the process E•S → E•I, which is not the same as k_cat from the Michaelis–Menten model, which corresponds to E•S → E + P), which is substantially less than the barrier of the same reaction (20.3 kcal⋅mol^–1; ref. 33) occurring in solution with acetate as the base. [This barrier is based on the pseudo-unimolecular rate calculated from the bimolecular rate constant and the maximal base concentration.] Using the differential binding formalism (Fig. 1) and treating the binding constant of an inhibitor (E + In ⇌ E•In) as a model for transition-state binding (E + TS₁ ⇌ E•TS₁), a prediction for the enzyme-catalyzed activation barrier can be formulated by closing a thermodynamic cycle on the reaction coordinate diagram (blue arrow, Fig. 2C). This analysis uses the empirical values for 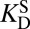, 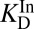(which stands in for 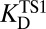), and 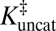as ingredients, which correspond to binding constants for substrate and inhibitor and the rate constant for the uncatalyzed solution reaction, respectively. The prediction from this calculation (represented by PP in Fig. 2C) is that the enzyme-catalyzed reaction would possess an activation barrier of 14.6 kcal⋅mol^–1—which is significantly higher than that observed. This disagreement is in fact very common and easy to rationalize on account of the fact that the inhibitor may only roughly recapitulate the energetics associated with the true transition state (19, 20).

In addition to stabilizing its transition state, KSI is also known to stabilize its dienolate intermediate. The “internal” equilibrium constant for KSI’s first reaction (i.e., the K_eq for E•S ⇌ E•I) has been experimentally shown to be between 0.01 and 0.3, implying the intermediate lies only 1–3 kcal⋅mol^–1 higher in free energy relative to the reactant in the active site (39, 40). In contrast, forming the intermediate is highly endergonic in solution, with a free energy change of 10.9 kcal⋅mol^–1. A Pauling-like formalism could also be applied to describe this effect. By combining the empirical values for 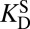, 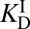(binding constants for substrate and intermediate, respectively), and K_eq for S ⇌ I in solution, one should in principle be able to estimate the K_eq for E•S ⇌ E•I (and therefore its ΔG°). This analysis furnishes a ΔG° of 6.2 kcal⋅mol^–1, which is again not in agreement with the measured value. This disagreement is more difficult to rationalize, because in this case the thermodynamic cycle is rigorous and does not use one molecule to act as a surrogate for something else. We hypothesized that this inconsistency is due to underlying processes inherent in the catalytic cycle that are not represented by binding effects, and so not captured by Kurz’s model. As we show in the following, these effects come to light upon using a detailed thermodynamic cycle (Fig. 3A).

Fig. 3.

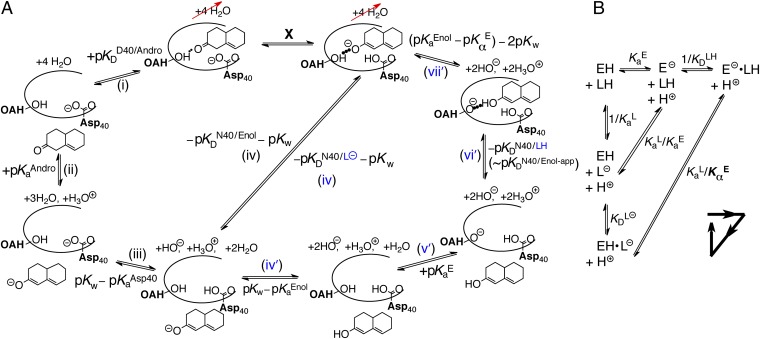
Thermodynamic model of enzyme-catalyzed intermediate formation. Steps that incorporate the effect of differential acidity are in blue. (A) Pathway X (E•S → E•I) can be dissected into a four-step or seven-step thermodynamic cycle. (i) Dissociation of androstene from KSI; (ii) solution deprotonation of androstene; (iii) solution protonation of general base Asp₄₀; (iv) binding of intermediate as a dienolate to KSI with a protonated general base (i.e., KSI^D40N) plus autoionization of water; (iv′) solution formation of dienol; (v′) solution deprotonation of oxyanion hole; (vi′) binding of intermediate as a dienol to KSI with a protonated general base; (vii′) internal proton transfer plus two autoionizations of water. The left-hand half-cycle uses 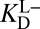to complete the cycle, and the full cycle uses 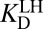. The right-hand half-cycle relates differential acidity to 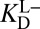and 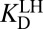. (B) Detailed treatment of step (iv), incorporating that both the active site and ligand can titrate protons. L, ligand. H implies protonated, ⊝ implies deprotonated. K_a, acid dissociation constant; K_D, ligand dissociation constant. The arrowed triangle shows the convention for the forward reaction direction. The new parameter, 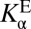, is a measure of the internal acidity of the enzyme active site.

Thermodynamic Cycle for KSI’s First Chemical Step

Fig. 3A shows how one can determine the free energy of an enzyme-actuated process by decomposing it into thermodynamically defined steps. In this case, X stands for the transformation under consideration, E•S → E•I, which is the first chemical step of the mechanism. To determine ΔG° of X, we write a thermodynamic cycle [black steps (i)–(iv)] starting with E•S, and proceed with processes that add up to form E•I. All of the steps (i)–(iv) have their ΔG°s independently defined by various empirical equilibrium constants.

Starting with the enzyme–substrate complex, in step (i) the substrate is removed from the enzyme’s active site. This dissociation constant is well-approximated by the Michaelis constant of KSI for a slow substrate (17 µM; ref. 41). Next, with androstene out of the enzyme, step (ii) ionizes androstene with water, which is energetically defined as the pK_a of androstene (12.7; ref. 31). In step (iii), the general base of KSI is neutralized by water, which is also described by its pK_a (3.75; ref. 32). Step (iv) is the favorable association of the intermediate dienolate to the enzyme active site with the general base protonated. The thermodynamics of this step is likened to the binding of the enolic intermediate to the Asp40Asn mutant of KSI (written as KSI^D40N), whereby the Asp40Asn background simulates the neutralized (i.e., protonated) general base present during this process. It is known that the dienol binds to KSI^D40N in (at least partially) the anionic form (36, 37). The observed binding is much tighter 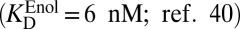than that of the substrate, which is qualitatively consistent with Pauling’s hypothesis. In black step (iv), we also regenerate the two water molecules using the autoionization constant of water. At this stage, we see that X closes a thermodynamic cycle whose overall free energy change must be identically zero:

Using the known values for the equilibrium constants and the relationship between equilibrium constants and free energy, Eq. 3 allows one to calculate ΔG°(X) to be 7.6 kcal⋅mol^–1. This is less endergonic than the uncatalyzed case by the differential binding of the intermediate over the substrate. However, the current treatment is far from recapitulating the observation that KSI renders ΔG°(X) to be 1–3 kcal⋅mol^–1 (40). The discrepancy is suggestive that certain processes are not being properly accounted for.

Introducing Internal Acidity, K_α

Let us reexamine step (iv) of Fig. 3A and ask a seemingly simple question: Does the experimental parameter (the binding constant of the dienol intermediate to KSI^D40N) properly represent the process being portrayed in step (iv)? Drawn in step (iv) is an ionized intermediate (dienolate) binding with a neutral enzyme to form a complex. However, in the actual binding experiment, the preponderant form of the intermediate (whose pK_a is 10.0) in solution is neutral (dienol). This complication will be encountered in any instance where both the enzyme (E; in this case KSI^D40N) and the ligand (L; in this case the steroid dienol) possess titratable moieties whose protonation statuses affect the binding interaction. Such a situation would arise in any enzyme catalyzing proton-transfer chemistry, and is treated in a general fashion in Fig. 3B. A priori, we consider the two binding modes on equal footing: binding of neutral ligand to ionized enzyme 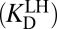and binding of ionized ligand to neutral enzyme 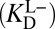. Moreover, the products of these binding equilibria can interconvert via an internal proton transfer (the long hypotenuse in Fig. 3B), and the reactants of these binding equilibria can interconvert as well via exchanging protons to bulk water (the short hypotenuse). We impose only that the active site accommodate one negative charge, and so a complex between ionized ligand and ionized enzyme is not considered (35).

In any real experiment of the binding constant of L, what can be measured is an “apparent” binding constant that represents the collective affinity of ligand to enzyme, without regard to protonation states or binding modes.

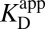does not correspond to any microscopic process in Fig. 3B. We can define conventional microscopic equilibrium constants for each elementary step under consideration, which are found located along the legs of the triangle in Fig. 3B. The equilibrium between E^–•LH and EH•L^– (the long hypotenuse of Fig. 3B) is referred to as the internal proton transfer. To describe this process, we will make an analogy to a different but related process along the inner hypotenuse. The proton exchange described by E^– + LH ⇌ EH + L^– is a canonical acid–base reaction, whose equilibrium position is dictated by the ratio of acid dissociation constants, .

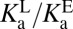The internal proton transfer between ligand and enzyme, E^–•LH ⇌ EH•L^–, also depends on the relative acidity of the enzyme and the ligand; but unlike the E^– + LH ⇌ EH + L^– process, the internal exchange does not involve transfer of protons to/through water, and possibly is influenced by the enzyme’s and ligand’s properties being altered upon binding. Therefore, it is incorrect to define the enzyme’s acidity in the EH• state with a standard K_a. Instead, we refer to the enzyme’s “internal acidity” with the symbol 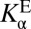(with a subscript α rather than the conventional a), and will use the ratio of 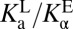to indicate the equilibrium position of the internal proton transfer.

By using the appropriate conservation equations and mass action expressions, we can derive expressions for the microscopic binding constants in terms of the apparent binding constant and the acidity constants:

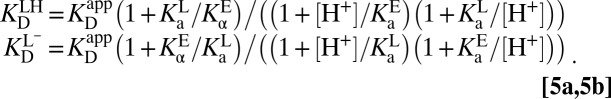This model is capable of reproducing the pH dependence of the apparent dissociation constant (42), and it also predicts (correctly) that the position of the internal proton transfer is largely invariant to pH (36). Fig. 3B shows that the internal proton transfer does not exchange protons with the bulk aqueous bath, and so must be independent of pH, excluding secondary effects resulting from pH-induced structural changes to the protein. The capacity of proteins to “self-buffer” an internal proton transfer against changes in external pH has been previously observed in green fluorescent protein, where the protonation state can be readily observed from the intrinsic chromophore (43). We take these observations as a validation of Eq. 5.

Defining Differential Acidity

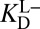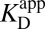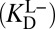Returning to the original context of Fig. 3A, it becomes apparent that one of the steps was not assigned a correct thermochemical description. The step that was written down as (iv) really corresponds (in light of Fig. 3B) to (in blue), and not the measured binding constant of we used initially. To convert from what is known to what is needed , one must have measures of the enzyme’s active site’s standard acidity to water 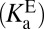and internal acidity to the ligand 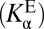, as prescribed by Eq. 5. The essential concept that we build upon is that these two acidities are empirically not equal; in fact, KSI’s active site is several orders of magnitude more acidic in the apo state. This feature (that is, 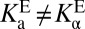) is what we describe with the term “differential acidity,” in analogy to differential binding (which implied ).

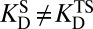A recent study detailed that Tyr57 (part of the OAH) in ligand-free KSI^D40N has an unusually low 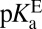of 6.3 ± 0.1, originally evidenced by ¹³C NMR studies of labeled tyrosines and confirmed by UV spectroscopic titration (26). Because tyrosine normally has a pK_a ∼10, this study highlighted how hydrogen-bond networks can severely perturb a residue’s acidity (35). With this additional knowledge in hand, the preponderant mechanism of ligand (intermediate) binding to KSI^D40N at pH 7.2 (the standard condition for this analysis) involves a neutral dienol and an ionized OAH given their pK_as of 10.0 and 6.3, respectively. Therefore, 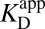is expected to be a good estimator of 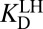, but very different from .

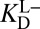Classical interpretations of acidity would posit that because 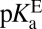is 6.3, a second acid whose pK_a is 6.3 would exist at the equivalence point with KSI, with each half-neutral/half-ionized. This picture would be true for the reaction E^– + LH ⇌ EH + L^–, but is incorrect for the reaction E^–•LH ⇌ EH•L^–, which is not strictly governed by pK_as. In fact, infrared spectroscopy studies have shown that a ligand of 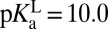is 30 ± 2% ionized at equilibrium when bound to the enzyme (27), so 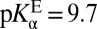, in agreement with the estimate of pK_α^E from a ligand-titration study (25). The fact that KSI’s active site is significantly more acidic in the apo state 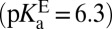than in the liganded state 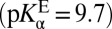in conjunction with the way that these terms enter into 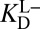(Eq. 5) demonstrates the subtle but significant effect the proton inventory exercises on the thermodynamic cycle.

Amending the Thermodynamic Model

As shown by the blue steps in Fig. 3A, eithe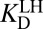r or can be used in 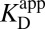’s place to complete the cycle. On one hand, we can simply substitute 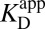with 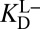[blue (iv)], which by Eq. 5b is 1,900-fold lower than 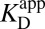at the common pH of 7.2. The factor by which 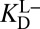differs from 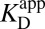depends dramatically on the enzyme’s two acidity parameters, as shown in Fig. S1. We recalculate the free energy change for intermediate formation [ΔG°(X)] using Eq. 3, except replacing the apparent affinity for the intermediate to KSI^D40N (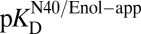, 8.2) with the affinity for the anionic intermediate to neutral KSI^D40N (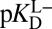, 11.5). This substitution leads to a ΔG°(X) of 3.0 kcal⋅mol^–1, which is in good agreement with the experimental value of the internal equilibrium constant (40).

Alternatively, we could use a lengthier thermochemical cycle, labeled with primes (′). After step (iii), the protonation states of the enzyme and the ligand can be swapped [blue steps (iv′) and (v′)], to allow for the ligand to bind under 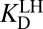[blue step (vi′)]. 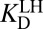is nearly identical to the apparent dissociation constant (1.3-fold larger), which makes sense because the preponderant means by which the complex is formed involves ionized enzyme and neutral ligand. Following the full cycle of Fig. 3A, we generate the following expression:

which gives the exact same result; however, it sets the stage for a conceptually useful approximation (see SI Discussion on the approximation’s range of validity). As noted previously, 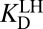is approximately the same as 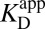. Applying this substitution and rearranging terms, Eq. 6 can be reexpressed as

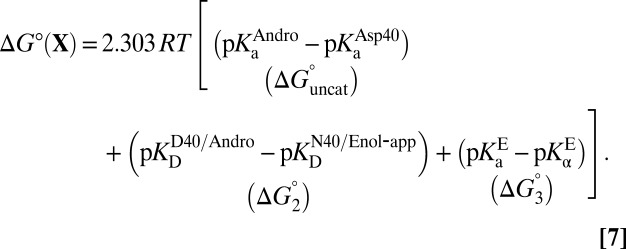Eq. 7 decomposes the free energy cost for catalyzed intermediate formation into three separate contributions. 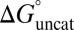is the uncatalyzed free energy cost for intermediate formation, given by the pK_a mismatch between acid and base. 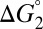, the contribution from differential binding, is responsible for 4.7 kcal⋅mol^–1 of intermediate stabilization. A new contribution 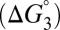from differential acidity extends that stabilization by an additional 4.6 kcal⋅mol^–1, implying a modification that is comparable to the energy of differential binding. The formulation in Eq. 7 shows that differential acidity directly affects the energetics of catalysis. It can further be shown using the right-hand half-cycle in Fig. 3A that the differential acidity 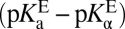equals the ratio of the two microscopic dissociation constants 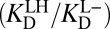. This ratio is independent of 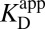according to Eq. 5; therefore, the differential acidity effect is completely orthogonal to the “actual” affinity of the inhibitor, and so is properly viewed as a separate contribution from differential binding. Importantly, this analysis demonstrates that a large alteration in the catalytic cycle’s energetics stems from the unusual pK_a of the oxyanion hole in KSI (26). Perturbed pK_as are fairly general features of enzyme active sites, and have been successfully related to catalysis in the serine proteases (44), although their functional relevance in general is an open question. We propose that perturbed pK_as in other enzyme active sites may have similar energetic consequences in their respective cases with the framework described.

Predicting KSI’s Rate Enhancement

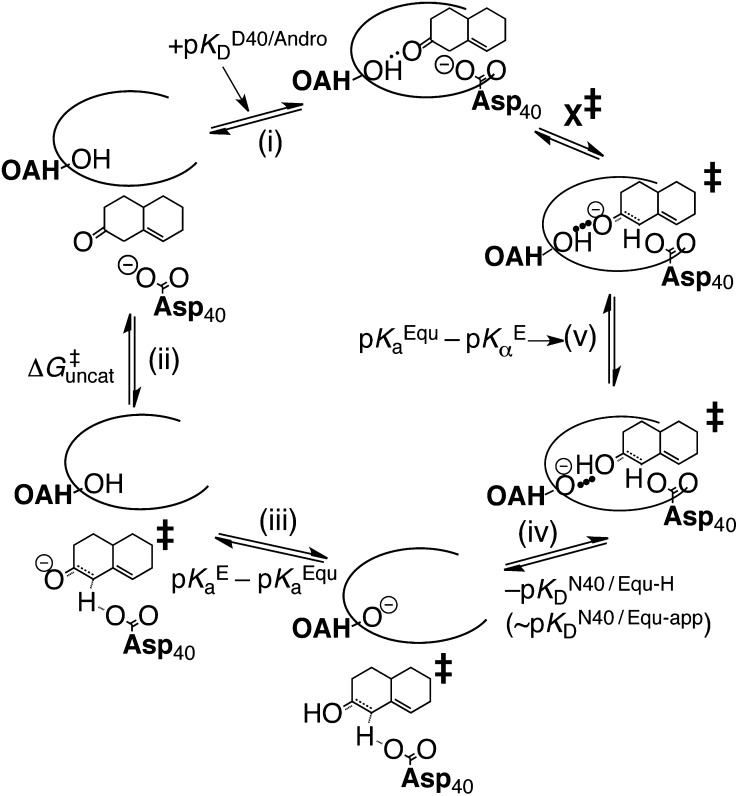
The analysis up to this point has been applied to the intermediate dienolate of KSI. However, the actual catalytic effect of KSI depends on the reduction of the activation barrier. In a more approximate fashion, a parallel thermodynamic treatment can be applied to the transition state (Fig. 4) by returning to the notion of using an inhibitor (equilenin) to serve as an analog for KSI’s transition state. The thermodynamic properties of equilenin are very similar to those of KSI’s chemical intermediate, and so a distinction between the two is not essential for this analysis. Fig. 4 treats the transition state essentially like the intermediate—a large assertion, albeit a common one (36, 37, 39–41)—which is at least supported by the fact that linear free energy analysis of KSI has demonstrated the transition state to be late along the reaction coordinate (45). The thermodynamic cycle shows a delineation of three contributions to process X^‡: the uncatalyzed component, a differential binding factor, and ∆G₃. Similar to Eq. 7, the thermodynamic cycle provides an approximation for ∆G^‡ as follows:

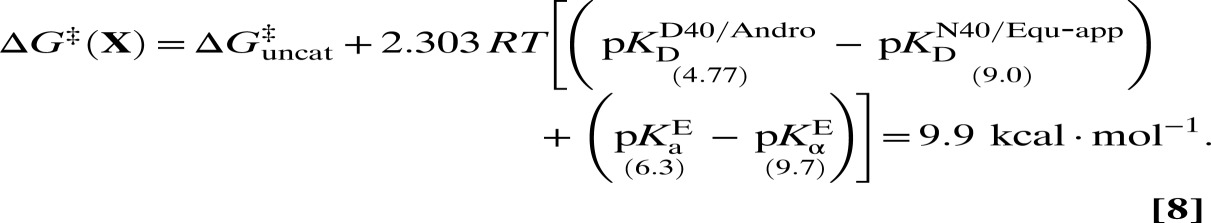Fig. 4.

Decomposition of X^‡, the barrier of KSI’s chemical reaction. (i) Dissociation of androstene from KSI; (ii) uncatalyzed formation of the transition state; (iii) solution protonation of the transition state and deprotonation of the oxyanion hole; (iv) binding of transition state to KSI; (v) internal proton transfer.

Eq. 8 provides an estimate for the free energy barrier that is in excellent agreement with transition-state theory, which furnishes the value of 10.3 kcal⋅mol^–1 (28). This estimate is in much better agreement than the estimate from the original analysis (14.6 kcal⋅mol^–1), resolving the discrepancy inspired by Fig. 2C. More broadly, by accounting for differential acidity, the thermodynamic model presented adequately bridges the gap between the binding ratio and the rate ratio of Eq. 1. This agreement is suggestive that a complete free energy inventory of the KSI catalytic cycle has been identified, providing an economic solution to a problem that has led others to more complex proposals (46).

Discussion and Conclusion

Differential acidity is typically not included in discussions about enzyme energetics, and we conjecture that this contribution could be significant in many other enzymes. The use of a careful thermodynamic decomposition of an enzyme-actuated process (such as Fig. 3A) over heuristic models (such as Fig. 1) may help reveal complexities in the proton/electron/atom inventory over the catalytic cycle, resulting in thermodynamic contributions that supplement the differential binding effect. KSI serves as an example to illustrate the usefulness of this framework, but the model’s general nature suggests that it could help identify free energy inventories for other enzymes as well. For the broad category of enzymes that catalyze proton transfer, a differential acidity effect will appear any time the active site and a ligand can exchange protons; then 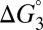manifests as a difference in acidities between the apo and liganded states of the enzyme (as in Fig. 3B). For electron-transfer chemistry, one can imagine redrawing Fig. 3B where K_as are replaced with reduction potentials; then 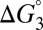would appear as a difference in electron affinities between the apo and liganded states of the enzyme.

Most widely discussed hypotheses concerning the origins of enzyme catalysis—electrostatic stabilization, entropy trapping, approximation, desolvation, and strong hydrogen bonds—are believed to be encompassed by differential binding and be captured by ∆G₂ (47). However, the present thermodynamic analysis suggests that these effects can only account for ∼55% of the total barrier reduction by KSI. Furthermore, it is important to point out that computer models of KSI’s catalytic cycle have been able to accurately reproduce its barrier reduction and intermediate stabilization (16, 29), meaning that ∆G₃ effects were implicitly accounted for in the different thermodynamic cycles used in those calculations. Identifying what physical interactions are responsible for differential acidity, and determining how its effect is borne out in a simulated reaction coordinate, is a new question that remains to future research.

At this stage, we can only speculate what physically underlies the differential acidity effect. One possibility is that the effect is primarily borne by the ligand; namely, the environment of the active site polarizes the electronic structure of the ligand in such a way as to modify its proton affinity. We do not favor this idea, because the equilibrium properties in the complexed state (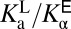) appear to be roughly consistent with one’s expectations: With tyrosine’s standard pK_a close to that of the ligand, finding the ligand present at 30% ionized (i.e., close to 50%) does not seem too extraordinary, and is inconsistent with the idea that the active site imposes a large perturbation onto the ligand’s electronic structure. Rather, what is more extraordinary is the 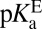of the oxyanion hole in the apo enzyme, an effect that has been attributed partially to the involvement of a bound water molecule in the hydrogen-bonding network (26). It is conceivable to imagine hydrophobically driven binding as a way of upsetting this delicate interaction, and so reverting the anomalously acidic oxyanion hole to a more normative state. Tuning of active-site properties with ordered water molecules has been discussed in KSI (48) and in general (49). We provisionally attribute the differential acidity effect to changes in the active site (i.e., water displacement) accompanying ligand binding, although it is difficult to trace this effect back to physical causes based on empirical thermodynamic parameters alone. This highlights the importance of framing the origin of catalysis question in terms of a well-defined thermodynamic cycle (17), and points to the need to turn to computational methods, which have been able to identify large acidity shifts in other systems (50, 51).

This work has further implications for enzyme engineering. For many natural enzyme systems, the barrier reduction (∆∆G^‡ = ∆G₂ + ∆G₃) as calculated from kinetics is more dramatic than the measured differential binding to a transition-state analog (∆G₂). Additionally, in the pursuit of catalytic antibodies and designed enzymes, a high affinity for transition-state analogs (∆G₂) has not necessarily translated to catalytic competence, ∆∆G^‡ (20, 52). We posit that some of these discrepancies could be due to ∆G₃ for systems that involve proton-transfer chemistry. In KSI, ∆G₃ amounted to a significant positive contribution, on par with the effect of tight binding to the transition state. However, for other regions of the acidity parameter space, differential acidity could have a deleterious effect and stymie the catalysis of less-optimized systems such as artificial enzymes (Fig. S1).

Some have contended that the lack of agreement between the binding ratio and the rate ratio (Eq. 1) results from dynamical nonequilibrium aspects of enzyme catalysis (21, 53). These theories are necessary for advancing our understanding of enzyme catalysis, because in many cases, activation barriers calculated from thermodynamic premises fail to match those measured by kinetics. However, simple thermodynamic models such as Fig. 1 continue to see use because they excel at providing insight, and they are often easier to translate into design principles. We found that by expanding on a classic thermodynamic analysis to include one additional effect, we were able to calculate the catalytic power of KSI in agreement with kinetics, suggesting that it may not be necessary to invoke dynamic arguments to explain one highly proficient enzyme’s catalysis (54). A detailed thermodynamic analysis has revealed that a static picture suffices to explain KSI’s catalytic power, and its energetics is fully consistent with the thermodynamics of chemical equilibrium.