Hearing the shape of a room

Seeing the shape of a room is not difficult for most people. Using a combination of stereo vision and parallax as we move around the room, we can resolve the position and angle of walls to determine the size and shape of the room we are in. However, suppose now that you are blind, or in a windowless room with no lights. It is still possible to get a sense of the size of the room by using sound. Clap your hands and the echoes will typically tell you if you are in a small office, a medium-sized classroom, or a large concert hall. However, is it possible to tell the shape of a room using sound alone? This is the question addressed by Dokmanić et al. (1) in PNAS.

Human hearing is particularly sensitive to the sound of objects and shapes. In the age of steam railways, “wheel-tappers” would check for cracks in railway carriage wheels by tapping with a hammer and listening to the echoes (2). In fiction, the character “Daredevil” (Marvel Comics 1964, movie release 2003) used acoustic “radar” to navigate the world. In reality, a small number of blind people are able to use echolocation to find their way around and locate objects by producing mouth clicks and listening to the returned echoes (3). The findings of Thaler et al. (4) suggest that brain regions normally used for vision can be adopted by such echolocation experts to process these click echoes. However, although these results suggest that sounds can be used to determine differences between shapes, they do not confirm whether or not it is possible to uniquely determine the shape of a room using sound alone.

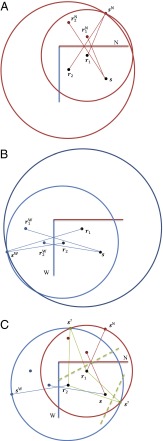
We can approach the problem of finding the location of reflective walls in a room by measuring the time between the sound being emitted from the loudspeaker and being picked up by the microphone, after reflection from one of the walls. In Fig. 1A we see a geometrical view of a 2D example, where we see the sound paths from the sound source s to the microphones r₁ and r₂ after reflection from the north wall (N). Much as we would see light images in a mirror, we can think of the reflections as creating an “image” s^N of the sound source s, and indeed images r₁^N and r₂^N of the microphones r₁ and r₂. By measuring the time delays, and hence the distances, from s to r₁ and r₂ via the wall reflection, solving for the points that match the measured distances will find the possible locations of the images, at the points where the circles cross. In Fig. 1A we see that one of these points where the circles cross is the true source image s^N, reflected in the north wall: with only two microphones there are two points where this happens, so an additional third (noncolinear) microphone will be needed to resolve this completely.

Fig. 1.

(A) Sound path from source s to microphones r₁ and r₂ reflected from the north wall (N). Source image s^N is one of two points that have the correct distances s − r₁ and s − r₂. This is also shown in B for the west wall (W). If the echoes from different walls are labeled together by mistake (C), we will get incorrect “ghost” source images (s^?), suggesting false walls that do not exist.

With additional walls, we would like to apply the same technique to find the images of the sound source in the other walls, and so find the remaining walls (Fig. 1B). However, with more than one wall, the situation is considerably more complex, because the reflections from different walls are not labeled to indicate the wall from which the echo has been reflected. The microphones will pick up a sequence of echoes, but we do not know which echo has been reflected from which wall. This type of ambiguity has an analogy in stereovision, where a repeating pattern, such as a grid or picket fence, can be locally “fused” to give illusions where the stereo depth is closer or farther away than the true stereo depth (5).

If the arrangement of microphones is small compared with the room dimensions, such as a microphone array with small diameter, then the echoes will cluster together in time. The echoes from the source to all microphones reflected via the closest wall (e.g., wall N) will arrive before all of the echoes reflected via the next-closest wall (e.g., wall W), and so on. The echoes can then be uniquely labeled and the shape of the room resolved (6).

However, in the general case the echoes from different walls may be intermingled, and this simple time-clustering approach is not possible. If we are unable to label the echoes we may get completely illusory (“ghost”) source images and, hence, false wall locations. To illustrate, Fig. 1C shows a situation where the reflection from s to r₁ via the north wall (N) has been mistakenly labeled together with the reflection from s to r₂ via the west wall (W). Here the apparent solution gives two false source images labeled s^?, neither of which correspond to a valid source images (s^N or s^W). These two ghost source images suggest two entirely false walls, as shown by the green dashed lines.

Dokmanić et al. (1) tackle this problem. Their approach is based on an interesting property of Euclidean distance matrices, the matrix of pairwise Euclidean distances r_i − r_j² between the microphones, as well as the distances s^α − r_i² between loudspeaker source images and each microphone. Using the fact that a Euclidean distance matrix for a point set in n-dimensional space has rank at most n + 2, the authors are able to reject the type of false-echo labelings that we see in Fig. 1C. Specifically, for a 3D room with a loudspeaker and at least four microphones, where the microphones are placed at random inside a region where they will pick up all first-order reflections from the loudspeaker, they show that the unlabeled echoes determine the room shape with probability 1. Dokmanić et al. also develop practical algorithms to find the room shape, and demonstrate it on finding the shape of a classroom, as well as stretching the model by attempting to find the shape of a more complex room (a cathedral portal) that does not satisfy the modeling assumptions. These promising results indicate that it is possible to find the shape of a room from a loudspeaker and a small number of microphones in an almost arbitrary arrangement, without the need for a special microphone array or soundfield microphone.

Dokmanić et al. (1) concentrate on first-order reflections from the walls. The authors are able to detect and eliminate second- and higher-order reflections from their calculation: these are not needed to estimate the wall locations. However, by extending this work to estimate additional reflections, it may be possible to measure the so-called plenacoustic function (7), the room impulse-response

It may be possible to “crowd-source” the shape of a room from the microphones on the many smartphones that are now carried around.

function between any two points in a room, perhaps using methods based on compressed sensing (8) or other sparsity-based techniques.

Although the present report (1) relies on control and knowledge of the loudspeaker sound source, with fixed microphones, it will be interesting to see if the technique can be extended to handle estimated sound sources and a small number of mobile microphones. We could speculate that, not only could the room shape be estimated from someone moving around talking into their mobile phone, as the authors suggest, but it may be possible to “crowd-source” the shape of a room from the microphones on the many smartphones that are now carried around.

As a final note, Dokmanić et al. (1) have released the code and data to reproduce the results of the report in their Reproducible Research Repository (http://rr.epfl.ch). Research in signal and image processing is often based on algorithms implemented in software, with many hidden complexities and adjustable parameters, such that it can be very difficult for other researchers to follow precisely what has been done just from the published report alone. Together with the group of Donoho et al. (9) at Stanford, the present group at Ecole Polytechnique Fédérale de Lausanne has been one of the leading actors promoting reproducible research in this field, setting an example for other researchers to follow.