Significance
We propose a highly compressed readout architecture for arrays of imaging sensors capable of detecting individual photons. By exploiting sparseness properties of the input signal, our architecture can provide the same information content as conventional readout designs while using orders of magnitude fewer output channels. This is achieved using a unique interconnection topology based on group-testing theoretical considerations. Unlike existing designs, this promises a low-cost sensor with high fill factor and high photon sensitivity, potentially enabling increased spatial and temporal resolution in a number of imaging applications, including positron-emission tomography and light detection and ranging.
Keywords: multiplexing, single-photon detection, superimposed codes
Abstract
Advances in solid-state technology have enabled the development of silicon photomultiplier sensor arrays capable of sensing individual photons. Combined with high-frequency time-to-digital converters (TDCs), this technology opens up the prospect of sensors capable of recording with high accuracy both the time and location of each detected photon. Such a capability could lead to significant improvements in imaging accuracy, especially for applications operating with low photon fluxes such as light detection and ranging and positron-emission tomography. The demands placed on on-chip readout circuitry impose stringent trade-offs between fill factor and spatiotemporal resolution, causing many contemporary designs to severely underuse the technology’s full potential. Concentrating on the low photon flux setting, this paper leverages results from group testing and proposes an architecture for a highly efficient readout of pixels using only a small number of TDCs. We provide optimized design instances for various sensor parameters and compute explicit upper and lower bounds on the number of TDCs required to uniquely decode a given maximum number of simultaneous photon arrivals. To illustrate the strength of the proposed architecture, we note a typical digitization of a 60 × 60 photodiode sensor using only 142 TDCs. The design guarantees registration and unique recovery of up to four simultaneous photon arrivals using a fast decoding algorithm. By contrast, a cross-strip design requires 120 TDCs and cannot uniquely decode any simultaneous photon arrivals. Among other realistic simulations of scintillation events in clinical positron-emission tomography, the above design is shown to recover the spatiotemporal location of 99.98% of all detected photons.
Photon detection has become an essential measurement technique in science and engineering. Indeed, applications such as PET, single-photon-emission computed tomography, flow cytometry, light detection and ranging (LiDAR), fluorescence detection, confocal microscopy, and radiation detection all rely on accurate measurement of photon fluxes. Traditionally, the preferred measurement device has been the photomultiplier tube (PMT), which is a high-gain, low-noise photon detector with a high-frequency response and a large area of collection. In particular, it behaves as an ideal current generator for steady photon fluxes, making it suitable for use in applications in astronomy and medical imaging, among others. However, they are bulky, require manual assembly steps, and have limited spatial resolution for PET. For these reasons, extensive research has focused on finding feasible solid-state alternatives that can operate at much lower voltages, are immune to magnetic effects, have increased efficiency, and are smaller in physical size (1). Recent designs have raised significant interest in the community, and their use as a replacement for PMTs in applications such as PET imaging (2), high-energy physics (3), astrophysics (4), LiDAR (5), and flow cytometry has been recently explored.
Silicon photomultiplier (SiPM) devices consist of 2D arrays of Geiger avalanche photodiode (APD) microcells. Devices built up from these microcells are characterized by the fraction of sensing area on the device (the fill factor) and the fraction of incident photons that cause charged APDs to fire (the detection quantum efficiency). The product of these two quantities gives the combined photon detection efficiency.
The compatibility of Geiger APDs with standard complementary metal-oxide semiconductor technology has enabled a number of different designs. For example, the digital silicon photomultiplier (6) adds processing circuitry to count the total number of photons hitting the sensor and records a time stamp at the onset of each significant burst. The resolution of the resulting sensor coincides with the size of the entire sensor (usually 3 × 3 mm in area), whereas the temporal sampling is limited to a single time stamp per pulse. Nevertheless, the sensor does achieve a very high fill factor (80%) and is, therefore, very sensitive. Note that in SiPM terminology the above tiling of microcells into larger atomic units is often referred to as a pixel. Throughout this paper, however, we use the term “pixel” to refer to individual Geiger APD microcells, because they represent the smallest resolvable element in our proposed design.
An alternative sensor design, the single photon avalanche diode array, aims at a high temporal resolution and registers the time of each pixel (APD) firing (7, 8). This is achieved by connecting each pixel to a high-performance time-to-digital converter (TDC), which records a time stamp in a memory buffer whenever a signal is detected on its input. Because of their relatively low complexity, especially compared with analog-to-digital converters, TDCs allow the sensor to achieve an extremely high temporal resolution. However, the spatial resolution of the sensor is severely compromised by the large amount of support circuitry between neighboring pixels, resulting in an extremely low fill factor of ∼1–5%.
Although promising, both designs show that current implementations highly underuse the full potential of these silicon devices: Owing to the restricted chip area a trade-off must be made between the spatiotemporal resolution and the fill factor. To improve this trade-off, we take advantage of the special properties present in settings with a low photon flux. In particular, we claim that, by taking advantage of the temporal sparsity of the photon arrivals, we can greatly increase the spatiotemporal resolution of the SiPM while maintaining simple circuitry and a high fill factor.
This claim is made possible by the combination of two ideas: (i) to use TDCs as the main readout devices and (ii) to exploit ideas from group testing to reduce the number of these devices. As a motivational example, consider three possible designs for an 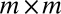 pixel grid. The first design, illustrated in Fig. 1A, corresponds to a design with a single TDC per pixel. This design can be seen as a trivial group test capable of detecting an arbitrary number of simultaneous firings, but at the cost of
pixel grid. The first design, illustrated in Fig. 1A, corresponds to a design with a single TDC per pixel. This design can be seen as a trivial group test capable of detecting an arbitrary number of simultaneous firings, but at the cost of 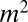 TDCs. When the photon flux is low, only a small number of pixels will typically fire at the same time†, thus causing most TDCs to be idle most of the time, and resulting in a very poor use of resources. The second design, shown in Fig. 1B, corresponds to the widely used cross-strip architecture in which rows and columns of pixels are each aggregated into a single signal. This design requires only
TDCs. When the photon flux is low, only a small number of pixels will typically fire at the same time†, thus causing most TDCs to be idle most of the time, and resulting in a very poor use of resources. The second design, shown in Fig. 1B, corresponds to the widely used cross-strip architecture in which rows and columns of pixels are each aggregated into a single signal. This design requires only 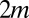 TDCs, but information from the TDCs can only be uniquely decoded if at most one pixel fired during the same time interval. Hinting at the power of more efficient group-testing designs, Fig. 1C shows a design in which pixels are numbered from 1 to
TDCs, but information from the TDCs can only be uniquely decoded if at most one pixel fired during the same time interval. Hinting at the power of more efficient group-testing designs, Fig. 1C shows a design in which pixels are numbered from 1 to 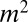 and in which a pixel i is connected to TDC j only if the j-th bit in the binary representation number i is one. This design is also capable of decoding up to a single pixel firing but requires only
and in which a pixel i is connected to TDC j only if the j-th bit in the binary representation number i is one. This design is also capable of decoding up to a single pixel firing but requires only 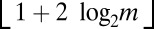 TDCs. The objective of this paper is to show that whenever the number of simultaneous firings is small, a significant reduction in the number of TDCs (and accompanying memory buffers) can be similarly attained by carefully selected designs. This reduces both the amount of overhead circuitry and the generated volume of data.
TDCs. The objective of this paper is to show that whenever the number of simultaneous firings is small, a significant reduction in the number of TDCs (and accompanying memory buffers) can be similarly attained by carefully selected designs. This reduces both the amount of overhead circuitry and the generated volume of data.
Fig. 1.
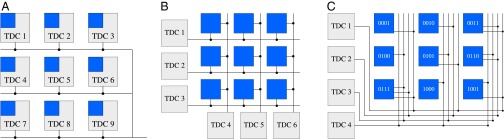
Three SiPM designs with (A) one TDC per pixel, (B) one TDC per row and column of pixels, and (C) one TDC per bit of the binary representation of each pixel number. The first design is capable of detecting any number of simultaneous hits, at the cost of a large number of TDCs. The other two can only uniquely decode up to a single pixel firing but require substantially fewer TDCs.
Contributions and Paper Organization
The main contributions of this paper are (i) the introduction of group testing to the design of interconnection networks in imaging sensors, combined with TDC readout; (ii) an architecture to time and locate photon arrivals; (iii) the explicit construction of highly optimized group testing matrices for a variety of conventional 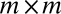 grid sizes; (iv) a comparison with alternative constructions; and (v) an extensive comparison with explicitly evaluated and optimized theoretical upper and lower bounds on the minimum number of TDCs required to decode an imaging sensor array.
grid sizes; (iv) a comparison with alternative constructions; and (v) an extensive comparison with explicitly evaluated and optimized theoretical upper and lower bounds on the minimum number of TDCs required to decode an imaging sensor array.
The paper is organized as follows. We start by reviewing the concept of group testing and construct the currently best-known group testing designs for a range of grid sizes. We then provide an extensive survey of constructions used to obtain upper and lower bounds on the minimum number of TDCs needed to guarantee recovery for 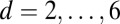 simultaneous hits. There, the results show that the designs generated earlier are within a factor two of the theoretical lower bounds. We then test the performance of the design on data generated using a realistic model of scintillation events arising in PET scanners. We conclude with a discussion on practical considerations in the implementation of the proposed design.
simultaneous hits. There, the results show that the designs generated earlier are within a factor two of the theoretical lower bounds. We then test the performance of the design on data generated using a realistic model of scintillation events arising in PET scanners. We conclude with a discussion on practical considerations in the implementation of the proposed design.
Throughout the paper we use the following notation: log is base e unless otherwise indicated; 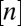 denotes the set
denotes the set  ; and
; and 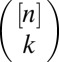 denotes the family of all subsets of
denotes the family of all subsets of 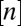 with k elements.
with k elements.
Group Testing
Group testing was proposed by Dorfman (9) to effectively screen large numbers of blood samples for rare diseases (see ref. 10 for more historical background). Instead of testing each sample individually, carefully chosen subsets of samples are pooled together and tested as a whole. If the test is negative, we immediately know that none of the samples in the pool is positive, saving a potentially large number of tests. Otherwise, one or more samples is positive and additional tests are needed to determine exactly which ones.
Since its introduction, group testing has been used in a variety of different applications including quality control and product testing (11), pattern matching (12, 13), DNA library screening (14–17), multiaccess communication (18), tracking of hot items in databases (19), and many others (10, 20). Depending on the application, group testing can be applied in an adaptive fashion in which tests are designed based on the outcome of previous tests, and in a nonadaptive fashion in which the tests are fixed a priori. Additional variations include schemes that provide robustness against test errors (21, 22) or the presence of inhibitors (23, 24), which cause false positives and negatives, respectively.
In our SiPM application, each pixel fires independently‡ according to some Poisson process and exactly fits in the probabilistic group-testing model (14). Nevertheless, because we are interested in guaranteeing performance up to a certain level of simultaneous firings, we will study the application from a combinatorial group-testing perspective. Furthermore, measurements are necessarily nonadaptive because they are hardwired in the actual implementation. No error correction is needed; the only errors we can expect are spurious pixel firings (dark counts) or afterpulses, but these appear indistinguishable from real firings and cannot be corrected for. The rate of these spurious pixel firings is usually much less than the signal rate, especially in our scintillation example (25).
Matrix Representation and Guarantees.
A group test can be represented as a binary  incidence matrix or code A with t the length or number of tests and n the size or number of items, or pixels in our case. An entry
incidence matrix or code A with t the length or number of tests and n the size or number of items, or pixels in our case. An entry 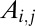 is set to one if item j is pooled in test i, that is, if pixel j is connected to TDC i, and zero otherwise. Given a vector x of length n with
is set to one if item j is pooled in test i, that is, if pixel j is connected to TDC i, and zero otherwise. Given a vector x of length n with 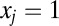 if item j is positive and zero otherwise, we can define the test vector y as
if item j is positive and zero otherwise, we can define the test vector y as 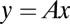 , where multiplication and addition are defined as logic and and or, respectively§. The columns
, where multiplication and addition are defined as logic and and or, respectively§. The columns 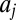 in A are called codewords, and for sake of convenience we allow set operations to be applied to these binary codewords, acting on or defining their support. As an illustration of the above, consider the following example:
in A are called codewords, and for sake of convenience we allow set operations to be applied to these binary codewords, acting on or defining their support. As an illustration of the above, consider the following example:
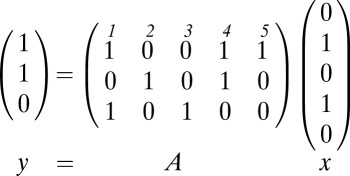 |
In this example pixels 1, 4, and 5 are connected to the first TDC, as represented by the first row of A. When pixels 2 and 4 fire, we sum (logical or) the corresponding columns and find that the first and second TDCs are activated, as seen in y.
For group testing to be effective we want to have far fewer tests than items 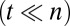 . This inherently means that not all vectors x can be reconstructed from y, so we will be interested in conditions that guarantee recovery when x has up to d positive entries.
. This inherently means that not all vectors x can be reconstructed from y, so we will be interested in conditions that guarantee recovery when x has up to d positive entries.
The weakest notion for recovery is d separability, which means that no combination of exactly d codewords can be expressed using any other combination of d codewords. A matrix is said to be  -separable if the combination of any up to d codewords is unique. This immediately gives an information-theoretic lower bound on the length t:
-separable if the combination of any up to d codewords is unique. This immediately gives an information-theoretic lower bound on the length t:
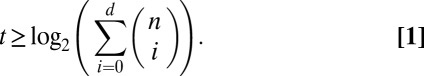 |
When d is small compared to n, this gives 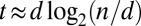 . A stronger criteria is given by d disjunctness. Given any two codewords u and v, we say that u covers v if
. A stronger criteria is given by d disjunctness. Given any two codewords u and v, we say that u covers v if 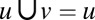 . Based on this, define A to be d-disjunct if no codeword in A is covered by the union of any d others. The concept of disjunctness of sets and codes has been proposed in a number of settings and such codes are also known as superimposed codes (26), or d-cover-free families (27). The advantage of d-disjunct codes is that the positive entries in any d-sparse vector x correspond exactly to those codewords in A that remain after discarding all codewords that have a one in a position where y is zero. This is unlike general separable matrices, where a combinatorial search may be needed for the decoding.
. Based on this, define A to be d-disjunct if no codeword in A is covered by the union of any d others. The concept of disjunctness of sets and codes has been proposed in a number of settings and such codes are also known as superimposed codes (26), or d-cover-free families (27). The advantage of d-disjunct codes is that the positive entries in any d-sparse vector x correspond exactly to those codewords in A that remain after discarding all codewords that have a one in a position where y is zero. This is unlike general separable matrices, where a combinatorial search may be needed for the decoding.
The central goal in group testing is to determine the smallest length t for which a matrix of size n can satisfy certain separability or disjunctness properties. Denote by 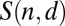 and
and 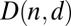 the set of all matrices A of size n that are d-separable, respectively d-disjunct. Then we can define
the set of all matrices A of size n that are d-separable, respectively d-disjunct. Then we can define 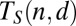 the smallest length of any
the smallest length of any 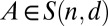 , and likewise for
, and likewise for 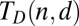 . As a further refinement in classification we define
. As a further refinement in classification we define 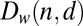 as all constant-weight d-disjunct matrices of size n, that is, those matrices whose columns all have the same weight or number of nonzero entries (note that the weights of any two matrices within this class can differ). The overlap between any two columns
as all constant-weight d-disjunct matrices of size n, that is, those matrices whose columns all have the same weight or number of nonzero entries (note that the weights of any two matrices within this class can differ). The overlap between any two columns 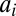 and
and 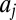 of a code is defined as
of a code is defined as 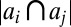 . Consider a constant-weight w code A with maximum pairwise overlap
. Consider a constant-weight w code A with maximum pairwise overlap
It is easily seen that it takes 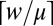 columns to cover another one, and therefore that
columns to cover another one, and therefore that
 |
We can then define 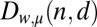 as the class of constant-weight codes of size n where the right-hand side of Eq. 2 equals d. As for all other classes, the actual disjunctness of the codes in
as the class of constant-weight codes of size n where the right-hand side of Eq. 2 equals d. As for all other classes, the actual disjunctness of the codes in 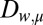 may still be higher. Summarizing, we have
may still be higher. Summarizing, we have
along with the associated minimum lengths 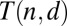 .
.
The above criteria are worst case in that they consider all possible combinations of d codewords. It is possible to relax this and require that combinations are recovered with a certain probability. Although we do not study such average-case behavior, it is evident from the numerical experiments that d-disjunct matrices can successfully recover combinations of many more than d codewords with high probability.
Matrix Construction.
In this section we discuss three methods for creating d-disjunct binary matrices. Given that the number of rows in the matrices correspond directly to the number of TDCs required to implement the design, it is crucial that this number is kept as small as possible. We apply the techniques to construct optimized matrices for the case where 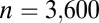 , corresponding to a
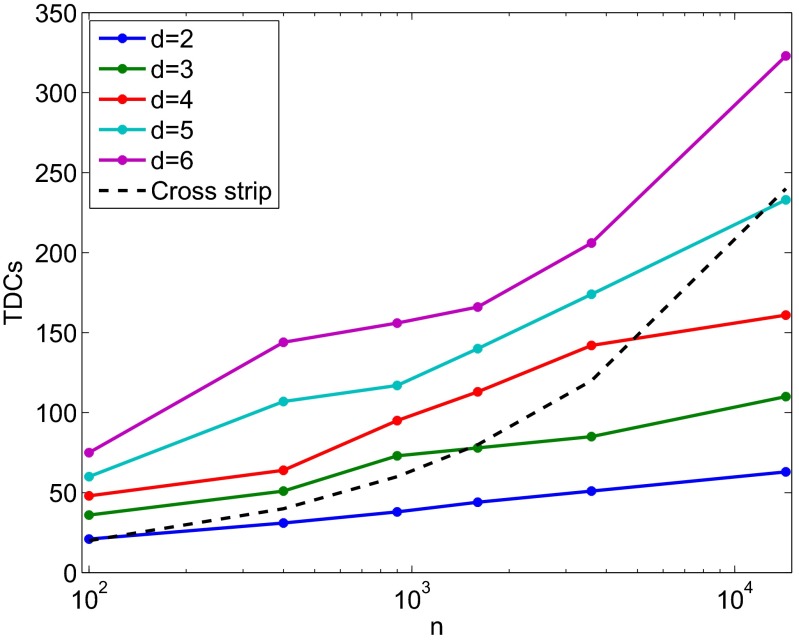
, corresponding to a 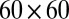 pixel array. Rows (l–n) in Table 1 show clear differences in the performance of the given construction methods. Fig. 2 compares the best constructions with the standard cross-strip design.
pixel array. Rows (l–n) in Table 1 show clear differences in the performance of the given construction methods. Fig. 2 compares the best constructions with the standard cross-strip design.
Table 1.
Upper and lower bounds on the minimum number of rows needed for a d-disjunct or 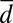 -separable matrix with
-separable matrix with 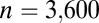 rows
rows
 |
2 | 3 | 4 | 5 | 6 | Ref. and comments |
| Upper bounds (theoretical) | ||||||
(a) 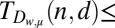
|
436 | 982 | 1,746 | 2,729 | 3,929 | Adaptation of 40 given in 3 |
(b) 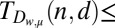
|
94 | 237 | 443 | 711 | 1043 | Ref. 27, proposition 2.1 with optimal w |
(c) 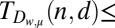
|
90 | 222 | 412 | 660 | 966 | Eq. 4 with optimal w |
(d) 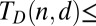
|
149 | 278 | 442 | 640 | 870 | Bernoulli (36, theorem 5) |
(e) 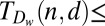
|
96 | 190 | 312 | 459 | 631 | Constant weight, groupwise cover |
(f) 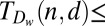
|
76 | 163 | 279 | 422 | 590 | Constant weight, Lovász local lemma |
(g) 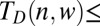
|
110 | 225 | 376 | 561 | 779 | Bernoulli, groupwise cover |
(h) 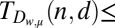
|
99 | 249 | 465 | 746 | 1,094 | Constant weight, pairwise overlap |
(i) 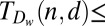
|
71 | 154 | 265 | 402 | 565 | Constant weight, groupwise cover (see 46) |
(j) 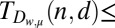
|
130 | 300 | 522 | 828 | 1,178 | Adaptation of 52, algorithm 1 |
(k) 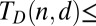
|
98 | 205 | 348 | 524 | 734 | Ref. 42, theorem 2.6 |
| Upper bounds (instances) | ||||||
(l) 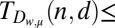
|
58 | 132 | 224 | 345 | 484 | Greedy search |
(m) 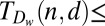
|
82 | 155 | 237 | 333 | 445 | Ref. 52, section 2; Supporting Information gives details |
(n) 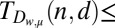
|
51 | 85 | 142 | 174 | 206 | Error-correction code-based |
| Lower bounds | ||||||
(o) 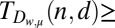
|
35 | 56 | 75 | 96 | 115 | Ref. 46, theorem 2 |
(p) 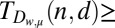
|
35 | 55 | 74 | 93 | 113 | Ref. 26, equation 5 and 36, equation 18 |
(q) 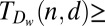
|
35 | — | — | — | — | Ref. 53, theorem 1 |
(r) 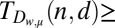
|
32 | 48 | 62 | 75 | 88 | Ref. 27, proposition 2.1 |
(s) 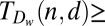
|
29 | 40 | 48 | 55 | 61 | Ref. 34, lemma 3.2 |
(t) 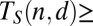
|
23 | 33 | 43 | 53 | 62 | Information theoretical lower bound |
Entries shown in boldface denote the best theoretical upper and lower bounds we could find for each of the given classes.
Fig. 2.
Comparison between the number of TDCs used for the best-known codes in Table 3 and a standard cross-strip design, for different numbers of pixels n. The cross-strip design connects each row and column to a single TDC, giving a 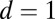 disjunct encoding. The number of TDCs in the cross-strip design grows as
disjunct encoding. The number of TDCs in the cross-strip design grows as 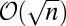 , much faster than the
, much faster than the 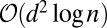 in group-testing matrices.
in group-testing matrices.
Greedy approach.
The greedy approach generates d-disjunct matrices one column at a time. For the construction of a constant-weight w matrix of length t the algorithms starts with 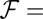 Ø and proceeds by repeatedly drawing, uniformly at random, an element F from
Ø and proceeds by repeatedly drawing, uniformly at random, an element F from 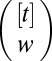 as a candidate column. Whenever the distance to all sets already in
as a candidate column. Whenever the distance to all sets already in 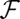 exceeds
exceeds 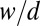 we add F to
we add F to  and continue the algorithm with the updated family. This process continues until either
and continue the algorithm with the updated family. This process continues until either  or a given time limit is reached.
or a given time limit is reached.
We applied the greedy algorithm to find d-disjunct matrices of size at least 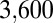 . For each value of d and length t, the algorithm was allowed to run for 12 h. Row (l) of Table 1 gives the minimum t for which the algorithm found a solution. Instances with fewer rows are very well possible; this strongly depends both on the choice of the initial few columns and the amount of time available.
. For each value of d and length t, the algorithm was allowed to run for 12 h. Row (l) of Table 1 gives the minimum t for which the algorithm found a solution. Instances with fewer rows are very well possible; this strongly depends both on the choice of the initial few columns and the amount of time available.
A further reduction in the code length could be achieved by checking disjunctness in a groupwise, rather than a pairwise, setting. However, the number of possible d subsets of columns to consider at each iteration grows exponentially in d, thereby rendering this approach intractable for even moderate values of d.
Designs based on error-correcting codes.
Excellent practical superimposed codes can be constructed based on error-correcting codes. Here, we discuss a number of techniques and constructions we used to generate the best superimposed codes known to us for a variety of pixel array sizes (i.e., for square 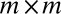 arrays with
arrays with 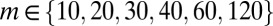 ). For comparison with other constructions, the results are summarized in Table 2, and row (n) of Table 1 for
). For comparison with other constructions, the results are summarized in Table 2, and row (n) of Table 1 for 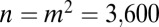 .
.
Table 2.
Overview of best-known constructions for d-disjunct matrices of size n
| d | t | Construction |
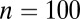 |
||
| 2 | 21 | st (21,8,7) |
| 3 | 36 | st (36,10,7) |
| 4 | 48 | st (48,8,5) |
| 5 | 60 | st (60,10,6) |
| 6 | 75 | 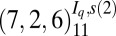 |
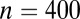 |
||
| 2 | 31 | st (31,8,7) |
| 3 | 51 | st (51,10,7) |
| 4 | 64 | c(65,9,3)s(1) |
| 5 | 107 | 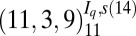 |
| 6 | 144 | 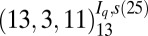 |
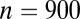 |
||
| 2 | 38 | st (38,8,7) |
| 3 | 73 | 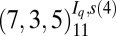 |
| 4 | 95 | 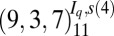 |
| 5 | 117 | 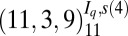 |
| 6 | 156 | 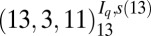 |
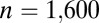 |
||
| 2 | 44 | st (44,8,7) |
| 3 | 78 | 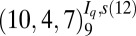 |
| 4 | 113 | 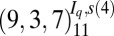 |
| 5 | 140 | 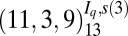 |
| 6 | 166 | 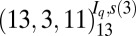 |
 |
||
| 2 | 51 | st (51,8,7) |
| 3 | 85 | 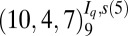 |
| 4 | 142 | 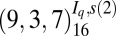 |
| 5 | 174 | 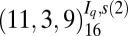 |
| 6 | 206 | 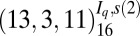 |
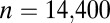 |
||
| 2 | 63 | 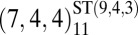 |
| 3 | 110 | 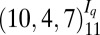 |
| 4 | 161 | 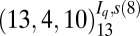 |
| 5 | 233 | 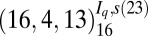 |
| 6 | 323 | 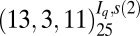 |
Codes from the Standard Table (28) are indicated by 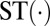 . The covering
. The covering 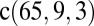 appears in the La Jolla Covering Repository (33) and was used in ref. 14. All other entries are
appears in the La Jolla Covering Repository (33) and was used in ref. 14. All other entries are 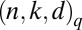 codes. Superscripts
codes. Superscripts 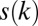 indicates a shortening of k steps with pivoting on zero entries; x indicates a greedy extension,
indicates a shortening of k steps with pivoting on zero entries; x indicates a greedy extension, 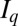 indicates concatenation with a
indicates concatenation with a 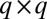 identity matrix. The
identity matrix. The 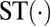 superscript indicates concatenation with a binary code from the Standard Table.
superscript indicates concatenation with a binary code from the Standard Table.
Binary codes.
The most straightforward way of obtaining d-disjunct superimposed codes is by simply taking constant-weight binary error-correction codes obeying Eq. 2, with overlap μ as given below. The on-line repository (28) lists the best known lower bound on maximum size 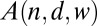 for constant weight w codes of length n and Hamming distance d (note the different use of n and d in this context). Given a code st (n,d,w) from this Standard Table, the overlap satisfies
for constant weight w codes of length n and Hamming distance d (note the different use of n and d in this context). Given a code st (n,d,w) from this Standard Table, the overlap satisfies 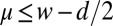 . Some codes are given explicitly, whereas others require some more work to instantiate. We discuss two of the most common constructions that are used to instantiate all but one of the remaining codes we use. The first construction consists of a short list of seed codewords
. Some codes are given explicitly, whereas others require some more work to instantiate. We discuss two of the most common constructions that are used to instantiate all but one of the remaining codes we use. The first construction consists of a short list of seed codewords 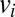 , along with a number of cyclic permutations. These permutations give rise to a permutation group
, along with a number of cyclic permutations. These permutations give rise to a permutation group 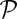 and the words in the final code are those in the union of orbits of the seed vectors:
and the words in the final code are those in the union of orbits of the seed vectors: 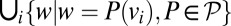 . The second construction shortens existing codes in one of two ways. We illustrate them based on the generation of the 2-disjunct code st (21,8,7) of size 100 from st (24,8,8). The first type of shortening consists of identifying a row i with the most ones and then selecting all columns incident to this row and deleting row i. This both reduces the weight and the length of the code by one, but preserves the distance, and in this case gives st (23,8,7) (note that shortenings do not in general lead to new optimal or best known codes). The second type of shortening identifies a row i with the most zero entries and creates a new code by keeping only the columns with a zero in the i-th row, and then removing the row. This construction does not affect the weight of the matrix, only the size and length. Repeating this twice from st (23,8,7) yields the desired st (21,8,7) code. Note that for constant-weight codes, the minimum number of ones in any given row is bounded above by
. The second construction shortens existing codes in one of two ways. We illustrate them based on the generation of the 2-disjunct code st (21,8,7) of size 100 from st (24,8,8). The first type of shortening consists of identifying a row i with the most ones and then selecting all columns incident to this row and deleting row i. This both reduces the weight and the length of the code by one, but preserves the distance, and in this case gives st (23,8,7) (note that shortenings do not in general lead to new optimal or best known codes). The second type of shortening identifies a row i with the most zero entries and creates a new code by keeping only the columns with a zero in the i-th row, and then removing the row. This construction does not affect the weight of the matrix, only the size and length. Repeating this twice from st (23,8,7) yields the desired st (21,8,7) code. Note that for constant-weight codes, the minimum number of ones in any given row is bounded above by 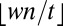 . This expression can be used to give a theoretical minimum on the number of rows by which we can shorten a code. In practice it may be possible to remove a substantially larger number of rows. Below we will frequently use shortening to obtain codes with smaller length. In these cases we only use the second type of shortening, based on zero entries.
. This expression can be used to give a theoretical minimum on the number of rows by which we can shorten a code. In practice it may be possible to remove a substantially larger number of rows. Below we will frequently use shortening to obtain codes with smaller length. In these cases we only use the second type of shortening, based on zero entries.
q-ary error-correction codes.
The Standard Table only lists codes with relatively small lengths and, consequently, limited sizes. To construct larger or heavier codes we apply a construction based on [maximal distance separable (MDS)] q-ary error-correcting codes, as proposed by Kautz and Singleton (26). Let 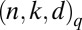 denote a linear q-ary code of length n, size
denote a linear q-ary code of length n, size 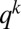 , and Hamming distance d. Each codeword in these codes consists of n elements taken from
, and Hamming distance d. Each codeword in these codes consists of n elements taken from 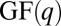 and differs in at least d locations from all other codewords. A binary superimposed code can be obtained from these q-ary codes by replacing each element with a corresponding column of a
and differs in at least d locations from all other codewords. A binary superimposed code can be obtained from these q-ary codes by replacing each element with a corresponding column of a  identity matrix
identity matrix 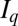 . That is, we map each element in
. That is, we map each element in 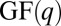 to a unique column of
to a unique column of 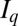 . For example, we map value k to the
. For example, we map value k to the 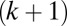 -st column of
-st column of 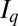 as follows:
as follows:
| q-ary | 2 | 0 | 1 | 2 | 1 | 1 | 0 | |
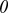 |
0 | 1 | 0 | 0 | 0 | 0 | 1 | |
| Binary | 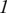 |
0 | 0 | 1 | 0 | 1 | 1 | 0 |
 |
1 | 0 | 0 | 1 | 0 | 0 | 0 |
The overlap between any two codewords of the resulting concatenated code is bounded by the length of the code n minus the distance d. Meanwhile, the weight is exactly the length. The disjunctness of the resulting code is therefore at least 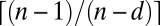 . As an aside, note that this construction requires an explicit set of codewords. This can be contrasted with q-ary error-correction codes, for which fast encoding–decoding algorithms often exist, and which do not require such an explicit representation.
. As an aside, note that this construction requires an explicit set of codewords. This can be contrasted with q-ary error-correction codes, for which fast encoding–decoding algorithms often exist, and which do not require such an explicit representation.
Existence of a large class of 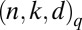 codes, including the well-known Reed–Solomon codes is shown by Kautz and Singleton (26) and Singleton (29). In MacWilliams and Sloane (ref. 30, chap. 11, theorem 9) cyclic MDS codes with
codes, including the well-known Reed–Solomon codes is shown by Kautz and Singleton (26) and Singleton (29). In MacWilliams and Sloane (ref. 30, chap. 11, theorem 9) cyclic MDS codes with 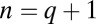 and
and 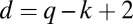 are shown to exist whenever
are shown to exist whenever 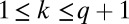 and q is a prime power. As a result, it can be concluded that, when expressed in group-testing notation, this concatenated code construction requires a length
and q is a prime power. As a result, it can be concluded that, when expressed in group-testing notation, this concatenated code construction requires a length 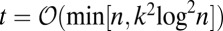 (20), compared with the best-known bound of
(20), compared with the best-known bound of 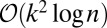 . Despite the slightly weaker bound, we shall see below that for small instances, the resulting codes are far superior to the random constructions used to yield the improved bound.
. Despite the slightly weaker bound, we shall see below that for small instances, the resulting codes are far superior to the random constructions used to yield the improved bound.
As an example, we used a concatenation of 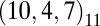 with
with 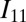 , denoted
, denoted 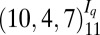 , to construct the 3-disjunct matrix of size
, to construct the 3-disjunct matrix of size 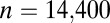 shown in Table 2. Most of the other codes obtained using this construction have an additional superscript
shown in Table 2. Most of the other codes obtained using this construction have an additional superscript  to indicate the application of k shortening steps. The 4-disjunct code of length
to indicate the application of k shortening steps. The 4-disjunct code of length  also has a superscript x to indicate extension of the code. In this case, the four shortening steps resulted in a
also has a superscript x to indicate extension of the code. In this case, the four shortening steps resulted in a  code, falling just short of the desired size of
code, falling just short of the desired size of  . The very structured nature of these concatenated codes means that many constant-weight vectors are not included, even if they may be feasible. We can therefore try to apply greedy search techniques to augment the code. For this particular case it was found to be relatively easy to add several columns, thus resulting in a code of desired size.
. The very structured nature of these concatenated codes means that many constant-weight vectors are not included, even if they may be feasible. We can therefore try to apply greedy search techniques to augment the code. For this particular case it was found to be relatively easy to add several columns, thus resulting in a code of desired size.
All of the q-ary codes appearing in Table 2 are Reed–Solomon codes, except for 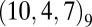 , which is a constacyclic linear code whose construction is given by ref. 31.
, which is a constacyclic linear code whose construction is given by ref. 31.
General concatenated codes.
As mentioned by Kautz and Singleton (26), it is possible to replace the trivial identity code by arbitrary d-disjunct binary matrices in forming concatenated codes, provided that the size of the matrix is at least equal to q. This construction is extensively used by D’yachkov et al. (32) to form previously unknown instances of superimposed codes. We also investigated this approach and found that the concatenation of the 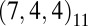 code with st (9,4,3) yielded our smallest 2-disjunct code of size 14,400. Likewise a 2-disjunct
code with st (9,4,3) yielded our smallest 2-disjunct code of size 14,400. Likewise a 2-disjunct 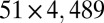 matrix can be obtained by concatenating
matrix can be obtained by concatenating 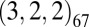 with st (17,6,5). The code given in Table 2 lists instead st (51,8,7), which yields a slightly smaller code with weight 7 instead of 15.
with st (17,6,5). The code given in Table 2 lists instead st (51,8,7), which yields a slightly smaller code with weight 7 instead of 15.
Theoretical Bounds
Given the codes constructed in the previous section, a natural question is to ask how much better we can do. In this section we summarize an extensive literature concerning theoretical bounds on the minimum number of pools required for a group-testing design of size n to be d-disjunct. The results include both upper and lower bounds on this minimum, and the models used also provide ways of generating matrices. The lower bounds show that the codes we constructed can be reduced by at most a factor of two. However, this reduction may be smaller in practice because matrices that reach the lower bound are not guaranteed to exist.
Asymptotic Bounds.
Bounds on the growth rate of 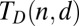 have been discovered and rediscovered in different contexts in information theory, combinatorics, and group testing (33, 34). In the context of superimposed codes, D’yachkov and Rykov (35) obtained the following bounds:
have been discovered and rediscovered in different contexts in information theory, combinatorics, and group testing (33, 34). In the context of superimposed codes, D’yachkov and Rykov (35) obtained the following bounds:
Ruszinkó (34) and Füredi (36) give an interesting account on the lower bound and provide simpler proofs. The lower bound was also obtained for sufficiently large d with 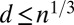 by Chaudhuri and Radhakrishnan (37) in the context of d-cover-free systems for system complexity, which was extended to the general case by Clementi et al. (38).
by Chaudhuri and Radhakrishnan (37) in the context of d-cover-free systems for system complexity, which was extended to the general case by Clementi et al. (38).
For the upper bound, it follows from the analysis of a greedy-type construction given by Hwang and Sós (39), that for 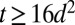 we have
we have
An efficient polynomial-time algorithm for generating similar constant-weight d-disjunct  matrices with
matrices with 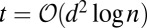 was given by Porat and Rothschild (20).
was given by Porat and Rothschild (20).
Nonasymptotic Results.
When working with particular values of d and n, constants in theoretic bounds become crucial. Most theoretical results, however, are concerned with growth rates and even if explicit constants are given, such as those in Eq. 3, they may be too loose to be of practical use.
In this section we are interested in the code length t required to guarantee the unique recovery of up to 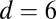 simultaneous firings on a
simultaneous firings on a 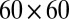 pixel array, that is
pixel array, that is 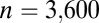 . We do this by studying the various models used to obtain upper and lower bounds on
. We do this by studying the various models used to obtain upper and lower bounds on 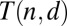 and numerically evaluating the original expressions, instead of bounding them. By optimizing over parameters such as weight or matrix size, we obtain the best numerical values for the bounds, as permitted by the different models. These will be used as a reference point to evaluate the quality of the codes given in Table 2.
and numerically evaluating the original expressions, instead of bounding them. By optimizing over parameters such as weight or matrix size, we obtain the best numerical values for the bounds, as permitted by the different models. These will be used as a reference point to evaluate the quality of the codes given in Table 2.
All bounds are evaluated using Sage (40) and summarized in Table 1 for 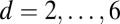 . We omit results for
. We omit results for 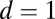 , which only requires the columns of the matrix to be unique.
, which only requires the columns of the matrix to be unique.
Upper bounds on 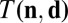 .
.
Constructing a d-disjunct binary  matrix, or providing an algorithm for doing so, immediately yields t as an upper bound for one of the
matrix, or providing an algorithm for doing so, immediately yields t as an upper bound for one of the 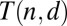 values. In the literature there are three main techniques to obtain d-disjunct matrices of various sizes; we discuss each of these in the following paragraphs.
values. In the literature there are three main techniques to obtain d-disjunct matrices of various sizes; we discuss each of these in the following paragraphs.
Sequential picking.
The construction given by Hwang and Sós (39) for obtaining an upper bound on 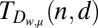 works as follows. Starting with a family of initially all good sets
works as follows. Starting with a family of initially all good sets 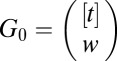 of a fixed weight w we pick a random element
of a fixed weight w we pick a random element  . After we make this choice we determine the family
. After we make this choice we determine the family 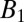 of sets in
of sets in 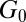 whose overlap with g is
whose overlap with g is  or more (this includes g itself). We then remove all of the bad items
or more (this includes g itself). We then remove all of the bad items 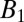 from
from  to get
to get 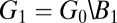 . We repeat the procedure, picking at each point a g from
. We repeat the procedure, picking at each point a g from 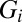 , determining
, determining 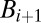 and forming
and forming 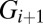 , until
, until 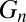 is empty. We can then form a
is empty. We can then form a  matrix A with the support of each column corresponding to one of the selected g. This matrix will be d-disjunct because, by construction, it has constant column weight w and satisfies Eq. 2 with overlap
matrix A with the support of each column corresponding to one of the selected g. This matrix will be d-disjunct because, by construction, it has constant column weight w and satisfies Eq. 2 with overlap 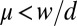 . For the number of rows in A, notice that the size of each
. For the number of rows in A, notice that the size of each 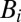 satisfies
satisfies
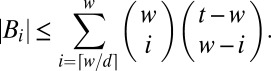 |
Because the size of the initial family  was
was 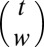 we have that
we have that
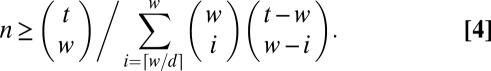 |
This can be turned into the upper bound on  shown in Eq. 3 by following the parameter choice and analysis given in ref. 39. Essentially the same argument was used earlier by Erdös et al. (27, proposition 2.1) to prove an alternative bound. Entries a–c in Table 1 are obtained respectively by optimizing Eq. 3, the bound given in (27) with optimal choice of w, and the smallest
shown in Eq. 3 by following the parameter choice and analysis given in ref. 39. Essentially the same argument was used earlier by Erdös et al. (27, proposition 2.1) to prove an alternative bound. Entries a–c in Table 1 are obtained respectively by optimizing Eq. 3, the bound given in (27) with optimal choice of w, and the smallest  satisfying Eq. 4 (see also ref. 41, p. 232).
satisfying Eq. 4 (see also ref. 41, p. 232).
Random ensemble.
An alternative to picking compatible columns one at a time is to draw an entire set of columns from a suitable distribution and check if the resulting matrix is indeed d-disjunct. An upper bound on the required number of rows is obtained by finding the smallest t such that the probability that the matrix does not satisfy d disjunctness is strictly bounded above by one.
Consider a  matrix A with entries drawn independent, identically distributed (i.i.d.) from the Bernoulli distribution; each entry takes on the value 1 with probability β and the value 0 with probability
matrix A with entries drawn independent, identically distributed (i.i.d.) from the Bernoulli distribution; each entry takes on the value 1 with probability β and the value 0 with probability 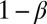 . For any column in A, the probability that it is covered by
. For any column in A, the probability that it is covered by 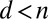 of the other columns is given by
of the other columns is given by
because each entry in the column is not covered by the union of the other d if and only if its value is 1, and the corresponding entries in the other d columns are all 0. Because we want to minimize the chance of overlap, we find the minimum with respect to β, giving 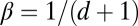 . By taking a union bound over all possible sets, we can bound the probability that at least one column in A is covered by some d others as
. By taking a union bound over all possible sets, we can bound the probability that at least one column in A is covered by some d others as
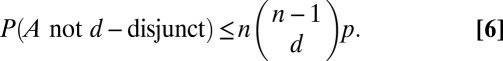 |
This setup forms the basis for the analysis given by D’yachkov and Rykov (35). In Table 1, row (d), we show the smallest t for which this probability is strictly less than one; for the optimal β, this is given by
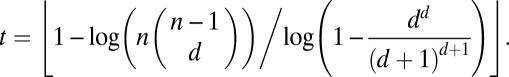 |
To construct matrices with constant-weight w, we can uniformly draw columns from  . The probability that a fixed column is covered by d others can be evaluated as follows. Let
. The probability that a fixed column is covered by d others can be evaluated as follows. Let  denote the number of ways we can cover a fixed set of w entries in a t-length vector with d columns, given that i entries have already been covered. With only a single column left, we first cover the remaining
denote the number of ways we can cover a fixed set of w entries in a t-length vector with d columns, given that i entries have already been covered. With only a single column left, we first cover the remaining  entries, leaving i entries to be freely selected in the remaining
entries, leaving i entries to be freely selected in the remaining 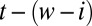 positions. This gives
positions. This gives
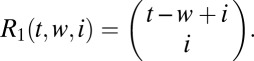 |
For 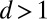 we can cover up to
we can cover up to 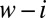 entries and cover the others using the remaining
entries and cover the others using the remaining 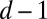 columns. Therefore,
columns. Therefore,
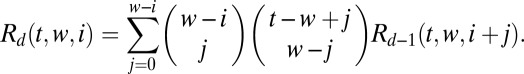 |
The probability that a column is covered by d others is then given by
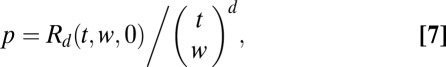 |
and we can again use the union bound given by Eq. 6. To determine the smallest possible t we start at 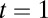 and double its value until the right-hand side of Eq. 6 is less than one and then use binary search to find the desired t. This is repeated for all suitable column weights w and row (e) of Table 1 lists the smallest value of t obtained using this procedure.
and double its value until the right-hand side of Eq. 6 is less than one and then use binary search to find the desired t. This is repeated for all suitable column weights w and row (e) of Table 1 lists the smallest value of t obtained using this procedure.
The use of the union bound in Eq. 6 ignores the fact that many of the columns and d sets are independent. To obtain sharper bounds for a similar problem, we follow Yeh (42) and apply Lovász local lemma (43), stated in ref. 44, corollary 5.1.2.
Lemma 1. (The Local Lemma, Symmetric Case).
Let
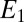 ,
, 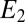 ,…,
,…,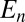 be events in an arbitrary probability space. Suppose that each event
be events in an arbitrary probability space. Suppose that each event
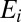 is independent of all other events
is independent of all other events
 except at most μ of them, and that
except at most μ of them, and that
 for all
for all
 . If
. If
then
 .
.
Working again with n columns drawn uniformly and independently from  , let
, let 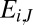 denote the event that column i is covered by the set J of d other columns. Any event
denote the event that column i is covered by the set J of d other columns. Any event 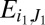 is independent from
is independent from 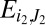 whenever
whenever 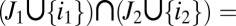 Ø, and the number of events μ that violate this condition is given by
Ø, and the number of events μ that violate this condition is given by
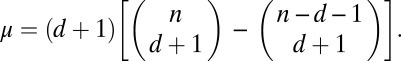 |
All we then need to do is find the smallest t for which, with an optimal choice of w, the condition in Eq. 8 is satisfied using p as given in Eq. 7. That is, find a t such that
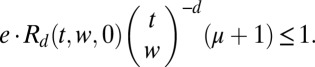 |
The results obtained by this method are given in row (f) in Table 1. We omit similar results obtained using a Bernoulli model, or the q-ary construction considered by Yeh (42), because they give larger values of t.
Random selection with postprocessing.
A third approach to generating d-disjunct matrices is to start with a 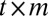 matrix with
matrix with 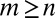 , drawn from a certain random ensemble, and randomly mark for deletion one of each pair of columns whose overlap is too large. Whenever the expected number of columns marked for deletion is strictly less than
, drawn from a certain random ensemble, and randomly mark for deletion one of each pair of columns whose overlap is too large. Whenever the expected number of columns marked for deletion is strictly less than 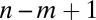 we can be sure that a d-disjunct
we can be sure that a d-disjunct  matrix exists and can be generated using this approach. (Note that some of the approaches described in the previous paragraph are a special case of this with
matrix exists and can be generated using this approach. (Note that some of the approaches described in the previous paragraph are a special case of this with 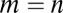 .) A variation on this approach is to pick a column and mark it for deletion if there exists any other d columns that cover it. Starting with the latter approach for the Bernoulli model with
.) A variation on this approach is to pick a column and mark it for deletion if there exists any other d columns that cover it. Starting with the latter approach for the Bernoulli model with 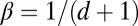 , a bound on the probability of a column being marked is found by applying a union bound to Eq. 5:
, a bound on the probability of a column being marked is found by applying a union bound to Eq. 5:
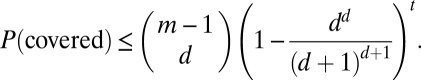 |
The expected number of columns marked is then bounded by
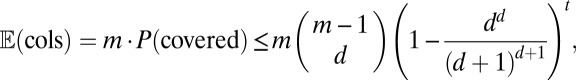 |
and the smallest t for which the left-hand side of this inequality is strictly less than  is given in row (g) of Table 1. A similar derivation based on constraints on the pairwise overlap of columns can easily be seen to yield
is given in row (g) of Table 1. A similar derivation based on constraints on the pairwise overlap of columns can easily be seen to yield
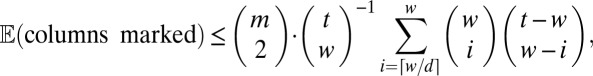 |
which leads to the results shown in row (h). The best results for 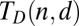 based on bounds of the probabilistic method in row (i) were obtained for groupwise covering of constant weight vectors, a model which was studied earlier by Riccio and Colbourn (45). For completeness we list in row (j) the results based on a random q-ary construction similar to the one we discussed earlier. A final method we would like to mention chooses
based on bounds of the probabilistic method in row (i) were obtained for groupwise covering of constant weight vectors, a model which was studied earlier by Riccio and Colbourn (45). For completeness we list in row (j) the results based on a random q-ary construction similar to the one we discussed earlier. A final method we would like to mention chooses 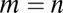 , but instead of removing marked columns, it augments the matrix with the identity matrix below all marked columns, thus fixing a (potential) violation of d-disjunctness by increasing the number of rows. The results of this method by Yeh (42) are presented in row (k).
, but instead of removing marked columns, it augments the matrix with the identity matrix below all marked columns, thus fixing a (potential) violation of d-disjunctness by increasing the number of rows. The results of this method by Yeh (42) are presented in row (k).
Remarks on the upper bounds.
Although different models may lead to the same growth rates in 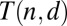 , there is a substantial difference in resulting values when numerically evaluated and optimized. The groupwise models easily outperform bounds based on pairwise comparison overlap. In addition there is a large gap between matrices with constant-weight columns, and those generated with i.i.d. Bernoulli entries, the former giving much more favorable results. The second approach given above, based on drawing fixed
, there is a substantial difference in resulting values when numerically evaluated and optimized. The groupwise models easily outperform bounds based on pairwise comparison overlap. In addition there is a large gap between matrices with constant-weight columns, and those generated with i.i.d. Bernoulli entries, the former giving much more favorable results. The second approach given above, based on drawing fixed  matrices is clearly outperformed by the third approach in which a
matrices is clearly outperformed by the third approach in which a 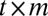 matrix is screened and reduced in size by removing columns that violate disjunctness or maximum overlap conditions, even if the Lovász local lemma is used to sharpen the bounds.
matrix is screened and reduced in size by removing columns that violate disjunctness or maximum overlap conditions, even if the Lovász local lemma is used to sharpen the bounds.
Lower Bounds on T(n,d).
Most of the lower bounds listed in Table 1 are derived using the concept of a private set. Let ℱ be a family of sets (the columns of our matrix A). Then T is a private set of 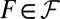 , if
, if 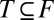 , and T is not included in any of the other sets in ℱ. For
, and T is not included in any of the other sets in ℱ. For 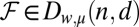 with length t, constant column weight w, and maximum overlap μ, it is easily seen that, by definition, each
with length t, constant column weight w, and maximum overlap μ, it is easily seen that, by definition, each 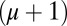 subset of
subset of 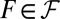 is private. The number of such private sets
is private. The number of such private sets 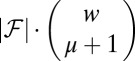 cannot exceed the total number of these sets,
cannot exceed the total number of these sets, 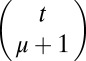 , and it therefore follows (26, 35) that
, and it therefore follows (26, 35) that
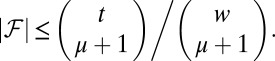 |
Based on this we can find the smallest t for which there are values w and μ obeying 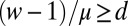 , such that the right-hand side of the above inequality exceeds the desired matrix size. This gives a lower bound on the required code length and the resulting values are listed in row (p) of Table 1. A slightly better bound on the same class of matrices follows from an elegant argument due to Johnson (46), and is given in row (o).
, such that the right-hand side of the above inequality exceeds the desired matrix size. This gives a lower bound on the required code length and the resulting values are listed in row (p) of Table 1. A slightly better bound on the same class of matrices follows from an elegant argument due to Johnson (46), and is given in row (o).
Ruszinkó (34) studies d disjunctness in constant-weight matrices without considering maximum overlap and provides the following argument. Let 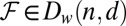 be a family of w subsets in
be a family of w subsets in 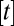 , such that no d sets in ℱ cover any other set. Moreover, assume that
, such that no d sets in ℱ cover any other set. Moreover, assume that 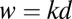 for some integer k. Any
for some integer k. Any 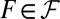 can be partitioned into d sets of length k, and it follows from the d-disjunctness of ℱ that at least one of these d subsets is private to F (otherwise it would be possible to cover F with d other columns). The key observation then, is that Baranyai’s theorem (47) guarantees the existence of
can be partitioned into d sets of length k, and it follows from the d-disjunctness of ℱ that at least one of these d subsets is private to F (otherwise it would be possible to cover F with d other columns). The key observation then, is that Baranyai’s theorem (47) guarantees the existence of 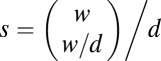 different partitions of F such that no subset in the partitions is repeated. Each of these s partitions contains a private set, so the total number of private sets is at least
different partitions of F such that no subset in the partitions is repeated. Each of these s partitions contains a private set, so the total number of private sets is at least 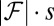 . Rewriting this gives
. Rewriting this gives
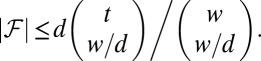 |
With proper rounding this can be extended to general weights w, giving the results shown in row (s). The results in rows (q) and (r) are also obtained based on private sets, but we will omit the exact arguments used here. Finally, an evaluation of the information-theoretic bound (1) is given in row (t).
Numerical Experiments
To illustrate the strength of the proposed design, we analyze the performance of some of the group-testing designs given in Table 2, by using them to decode scintillation events in a PET setting.
Simulation Parameters.
In PET, scintillation crystals are used to convert 511-kEv annihilation photons into bursts of low-energy (visible light) photons. We use the standard software package Geant4 (48, 49) to simulate this process for some 1,000 scintillation events for a 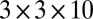 mm3 cerium-doped lutetium oxyorthosilicate crystal (7.4 g/cm3,
mm3 cerium-doped lutetium oxyorthosilicate crystal (7.4 g/cm3, 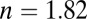 , absorption length = 50 m, scintillation yield = 26,000 photons/MeV, fast time constant = 40 ns, yield ratio = 1, resolution scale = 4.41) coupled to a
, absorption length = 50 m, scintillation yield = 26,000 photons/MeV, fast time constant = 40 ns, yield ratio = 1, resolution scale = 4.41) coupled to a 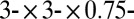 mm silicon sensor by 50 μm of optical grease (
mm silicon sensor by 50 μm of optical grease (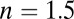 , absorption length = 50 m). For each event the simulation yields the location and arrival time of the low-energy photons relative to the start of the event.
, absorption length = 50 m). For each event the simulation yields the location and arrival time of the low-energy photons relative to the start of the event.
The silicon sensor is assumed to have a 70% fill factor and a quantum efficiency of 50% for blue photons. Once a photon is detected a pixel will be unable to detect a new photon for a known dead time, simulated to lie between 10 and 80 ns. We assume that each pixel takes up the same fraction of detector area and assign photons uniformly at random to a pixel. This increases the pixel firing rate by avoiding hitting dead pixels in high-flux regions, thereby making the decoding process more challenging. We do not model dark counts and cross-talk between pixels, because they would account to less than 1% of the total number of detected photons and therefore do not significantly affect the result.
In terms of pixel firings, we ignore the jitter in the time between an incident photon and the actual firing of a pixel. This assumption greatly simplifies the simulation and is not expected to have any significant influence on the results. The signal delays over the interconnection network between pixels and TDCs are assumed to be uniform, that is, the travel time of the signal from each pixel to any connected TDC is assumed to be the identical, and can therefore be set to zero without loss of generality. TDCs are further assumed to be ideal in the sense that they have no dead time; a time stamp is recorded whenever an event occurred during the sampling interval.
Decoding.
Pixel firings give rise to specific patterns of TDC recordings through the group-testing design embedded in the interconnection network. For each time window we can construct a binary vector with ones in positions corresponding to TDCs that recorded a time stamp during that interval, and zero for all other entries. Given such a test vector y, the decoding process starts by identifying all codewords 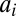 that are covered by y. When the group testing matrix A is a d-disjunct matrix, it immediately follows that whenever there are no more than d simultaneous firings, only the codewords corresponding to those pixels will be selected, and the decoding is successful. Whenever there are
that are covered by y. When the group testing matrix A is a d-disjunct matrix, it immediately follows that whenever there are no more than d simultaneous firings, only the codewords corresponding to those pixels will be selected, and the decoding is successful. Whenever there are 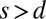 pixels that fired simultaneously, many more than s columns may be covered by y. At this point we use two of various possible decoding methods. The first is a groupwise method in which we return all feasible columns whenever none of them can be omitted to form y, or nothing otherwise. The second, individual decoding scheme returns all columns that have a one in a position where all other feasible columns have a zero (and therefore cannot be omitted). Finally, note that we only recover the pixels that fired when decoding of the corresponding column is successful, otherwise they are missed. Neither method has false positives.
pixels that fired simultaneously, many more than s columns may be covered by y. At this point we use two of various possible decoding methods. The first is a groupwise method in which we return all feasible columns whenever none of them can be omitted to form y, or nothing otherwise. The second, individual decoding scheme returns all columns that have a one in a position where all other feasible columns have a zero (and therefore cannot be omitted). Finally, note that we only recover the pixels that fired when decoding of the corresponding column is successful, otherwise they are missed. Neither method has false positives.
Results
In our simulations we considered sensors with both 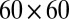 and
and 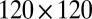 pixel arrays, and a variety of different pixel dead times and TDC interval lengths. Due to space limitations we can only show a select number of tables that are representative of the results. We describe any significant differences in the text and provide additional tables in Supporting Information.
pixel arrays, and a variety of different pixel dead times and TDC interval lengths. Due to space limitations we can only show a select number of tables that are representative of the results. We describe any significant differences in the text and provide additional tables in Supporting Information.
Table 3 shows the simulation results obtained using a 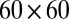 array with interconnection networks based on the superimposed codes from Table 2, with disjunctness ranging from 2 to 6. The pixel dead time and TDC interval length are chosen to be 20 ns and 40 ps, respectively. These times are somewhat strict because pixel dead times are typically longer and the TDC intervals shorter. Both choices cause an increase in the number of simultaneous photons per TDC sampling window, thereby making recovery more challenging. Although the maximum number of simultaneous firings reaches as high as 14, such events are exceedingly rare, with six or fewer simultaneous hits amounting to 97.7% of the total number of hits (hence the maximum
array with interconnection networks based on the superimposed codes from Table 2, with disjunctness ranging from 2 to 6. The pixel dead time and TDC interval length are chosen to be 20 ns and 40 ps, respectively. These times are somewhat strict because pixel dead times are typically longer and the TDC intervals shorter. Both choices cause an increase in the number of simultaneous photons per TDC sampling window, thereby making recovery more challenging. Although the maximum number of simultaneous firings reaches as high as 14, such events are exceedingly rare, with six or fewer simultaneous hits amounting to 97.7% of the total number of hits (hence the maximum 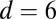 ). Decoding often remains successful beyond the disjunctness level of the interconnection network, although the probability of success decreases quickly with increasing numbers of simultaneous hits. Using groupwise decoding, it can be seen that even with a 4-disjunct interconnection network, more than 99% of all pixel firings are successfully recovered. For the
). Decoding often remains successful beyond the disjunctness level of the interconnection network, although the probability of success decreases quickly with increasing numbers of simultaneous hits. Using groupwise decoding, it can be seen that even with a 4-disjunct interconnection network, more than 99% of all pixel firings are successfully recovered. For the 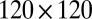 array, this number is slightly lower at 98.5% because fewer photons hit dead pixels, thus causing an increase in the number of firings and, consequently, a shift in the number of simultaneous hits. The results based on individual decoding are even better, attaining recovery rates of 99.98% and 99.93%, respectively.
array, this number is slightly lower at 98.5% because fewer photons hit dead pixels, thus causing an increase in the number of firings and, consequently, a shift in the number of simultaneous hits. The results based on individual decoding are even better, attaining recovery rates of 99.98% and 99.93%, respectively.
Table 3.
Decoding statistics for a 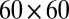 pixel array using a pixel dead time of 20 ns and TDC interval length of 40 ps
pixel array using a pixel dead time of 20 ns and TDC interval length of 40 ps
| No. simultaneous | No. of occurrences | Successfully decoded, % | ||||
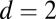 (51) (51) |
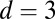 (85) (85) |
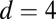 (142) (142) |
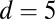 (174) (174) |
 (206) (206) |
||
| 1 | 1,021,073 | 100.000 | 100.000 | 100.000 | 100.000 | 100.000 |
| 2 | 419,174 | 100.000 | 100.000 | 100.000 | 100.000 | 100.000 |
| 3 | 192,232 | 44.015 | 100.000 | 100.000 | 100.000 | 100.000 |
| 4 | 87,389 | 2.289 | 89.808 | 100.000 | 100.000 | 100.000 |
| 5 | 38,526 | 0.026 | 44.271 | 99.574 | 100.000 | 100.000 |
| 6 | 16,126 | 0.000 | 7.590 | 96.366 | 99.895 | 100.000 |
| 7 | 6,186 | 0.000 | 0.404 | 84.481 | 99.208 | 100.000 |
| 8 | 2,216 | 0.000 | 0.000 | 59.206 | 94.540 | 99.549 |
| 9 | 725 | 0.000 | 0.000 | 27.448 | 83.586 | 97.793 |
| 10 | 231 | 0.000 | 0.000 | 7.792 | 59.307 | 91.342 |
| 11 | 70 | 0.000 | 0.000 | 1.429 | 30.000 | 71.429 |
| 12 | 17 | 0.000 | 0.000 | 0.000 | 5.882 | 70.588 |
| 13 | 6 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| 14 | 1 | 0.000 | 0.000 | 0.000 | 0.000 | 100.000 |
| Pixel firings missed: groupwise, individual, % | ||||||
| 32.571 | 9.636 | 0.833 | 0.135 | 0.025 | ||
| 19.145 | 2.381 | 0.012 | 0.000 | 0.000 | ||
Results shown correspond to the decoding of 1,000 sequential scintillation events. d, disjunctness; number of TDCs is given in parentheses in column headings. Total number of pixel firings, 3,145,990.
A more complete picture on the relationship between the number of pixel firings missed and the pixel dead time and TDC interval length is given in Table 4. Shown are the percentage of pixel firings missed for various pixel dead times and TDC interval lengths on a 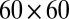 pixel array using individual decoding. As expected, smaller TDC intervals reduce the number of simultaneous hits and therefore lead to more uniquely decodable events. The results for the
pixel array using individual decoding. As expected, smaller TDC intervals reduce the number of simultaneous hits and therefore lead to more uniquely decodable events. The results for the 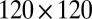 setting are similar, except for
setting are similar, except for 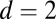 where the lowest recovery rate is 63.42%, compared with 78.98% for the
where the lowest recovery rate is 63.42%, compared with 78.98% for the 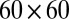 setting.
setting.
Table 4.
Percentage of pixel firings missed by individual decoding for various combinations of pixel dead time, TDC interval length, and disjunctness
| Dead time (no. of firings) | TDC interval, ps | No. simultaneous | Pixel firings missed, % | ||||
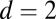 |
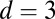 |
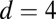 |
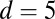 |
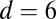 |
|||
| 10 ns (3.4 m) | 5 | 6 | 0.23 | 0.00 | 0.00 | 0.00 | 0.00 |
| 10 | 7 | 1.22 | 0.01 | 0.00 | 0.00 | 0.00 | |
| 20 | 11 | 5.80 | 0.18 | 0.00 | 0.00 | 0.00 | |
| 40 | 14 | 21.02 | 2.52 | 0.01 | 0.00 | 0.00 | |
| 20 ns (3.1 m) | 5 | 6 | 0.21 | 0.00 | 0.00 | 0.00 | 0.00 |
| 10 | 7 | 1.13 | 0.01 | 0.00 | 0.00 | 0.00 | |
| 20 | 11 | 5.33 | 0.17 | 0.00 | 0.00 | 0.00 | |
| 40 | 14 | 19.15 | 2.38 | 0.01 | 0.00 | 0.00 | |
| 40 ns (2.8 m) | 5 | 6 | 0.22 | 0.00 | 0.00 | 0.00 | 0.00 |
| 10 | 7 | 1.16 | 0.01 | 0.00 | 0.00 | 0.00 | |
| 20 | 11 | 5.46 | 0.19 | 0.00 | 0.00 | 0.00 | |
| 40 | 14 | 19.14 | 2.57 | 0.01 | 0.00 | 0.00 | |
| 80 ns (2.5 m) | 5 | 6 | 0.24 | 0.00 | 0.00 | 0.00 | 0.00 |
| 10 | 7 | 1.28 | 0.01 | 0.00 | 0.00 | 0.00 | |
| 20 | 11 | 6.03 | 0.21 | 0.00 | 0.00 | 0.00 | |
| 40 | 14 | 20.98 | 2.87 | 0.01 | 0.00 | 0.00 | |
Results shown correspond to the decoding of 1,000 sequential scintillation events on a  pixel array. The first three columns show the dead time (and total number of firings of rings in millions), TDC time interval, and maximum number of simultaneous hits.
pixel array. The first three columns show the dead time (and total number of firings of rings in millions), TDC time interval, and maximum number of simultaneous hits.
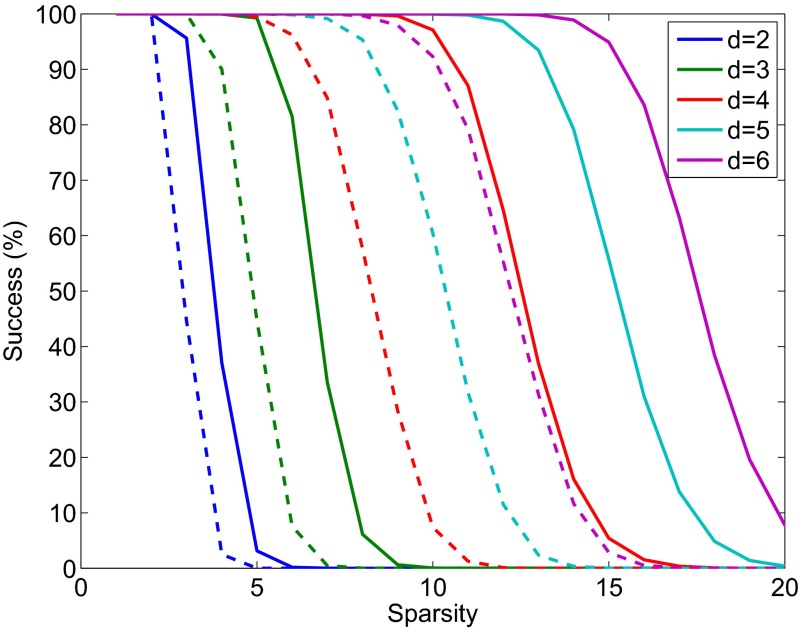
As seen, even when the number of simultaneous pixel firings exceeds the disjunctness of the group-testing design, it often remains possible to uniquely decode the resulting codeword, or at least a large fraction of the pixels included. To get more accurate statistics, we studied the decoding properties of randomly generated sparse vectors (corresponding to random pixel firing patterns) with the number of nonzero entries ranging from 1 to 20. For each sparsity level we decoded 10,000 vectors and summarize the success rates in Fig. 3. The plots show that recovery breaks down only gradually once the sparsity exceeds the disjunctness level of the matrix. Moreover, the plot shows that individual recovery far exceeds the success rate of groupwise decoding.
Fig. 3.
Percentage of successfully decoded pixels using individual (solid) and groupwise decoding (dashed) for a  array, as a function of sparsity level. For each sparsity level 10,000 random vectors were generated and decoded.
array, as a function of sparsity level. For each sparsity level 10,000 random vectors were generated and decoded.
Discussion
For the adaptation of the group-testing based design in hardware, a number of issues will need to be addressed. Among them, we expect the most important to be asynchronicity of the system, and we here discuss it in more detail. When the delay of the signal from one pixel to its incident TDCs is nonuniform due to difference in wiring lengths, it may happen that some of the TDCs record a time stamp in one interval and the remaining TDCs in another. As a consequence, it may be possible that the test vector y contains partial codewords. This complicates the decoding process: Groupwise decoding may fail more often, whereas individual decoding may now return false positives. Even with highly uniform delays between a pixel and its associated TDCs, it is possible to lose parts of the codeword when the signal arrival overlaps with the dead time of the receiving TDCs.
There are two main approaches of dealing with this problem. The first approach is to carefully choose wiring lengths and synchronize the logical signal generated by the pixel using a global clock across the chip to ensure uniform arrival of signals to the TDC digitizers. Such synchronization has been successfully implemented in clock design trees for central processing unit chips (50). The second approach is to consider bursts of consecutive events and decode the union of the corresponding test vectors as a whole. Although this reduces the chance of partial codewords, it also leads to a decrease in temporal resolution and an increase in the expected number of simultaneous firings. As a result, the second approach is useful only in settings where the photon flux is sufficiently low. Other methods would be needed to reduce or eliminate the problem of TDC dead time.
Supplementary Material
Acknowledgments
The authors thank the anonymous referees for providing several suggestions that greatly helped improve the paper. E.C., E.v.d.B., and C.S.-L. acknowledge support from the National Science Foundation via the Waterman Award, from the Broadcom Foundation, from Office of Naval Research Grant N00014-10-1-0599; and from Air Force Office of Scientific Research Multidisciplinary University Research Initiative Grant FA9550-09-1-06-43. C.S.-L. is partially funded by a Fulbright–National Commission for Scientific and Technological Research scholarship. P.D.O. acknowledges support through a Stanford Interdisciplinary Graduate Student Fellowship.
Footnotes
The authors declare no conflict of interest.
*This Direct Submission article had a prearranged editor.
†Throughout the paper, firing at the same time is to be understood as firing within the same TDC sampling interval.
‡This assumes that pixels have been shielded to avoid cross-talk.
§Addition using the logic OR gives 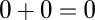 and
and 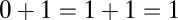 , whereas
, whereas 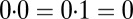 and
and 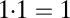 , as usual.
, as usual.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1216318110/-/DCSupplemental.
References
- 1.Renker D. Geiger-mode avalanche photodiodes, history, properties and problems. Nucl Instrum Methods Phys Res A. 2006;567(1):48–56. [Google Scholar]
- 2. Henseler D, Grazioso R, Zhang N, Schmand M (2009) SiPM performance in PET applications: An experimental and theoretical analysis. 2009 IEEE Nuclear Science Symposium Conference Record (IEEE, New York), pp 1941–1948.
- 3. Sefkow F (2007) The CALICE tile hadron calorimeter prototype with SiPM read-out: Design, construction and first test beam results. 2007 IEEE Nuclear Science Symposium Conference Record (IEEE, New York), Vol 1, pp 259–263.
- 4. Teshima M, Dolgoshein B, Mirzoyan R, Nincovic J, Popova E (2007) SiPM development for astroparticle physics applications. Proceedings of the 30th International Cosmic Ray Conference (Univ Nacional Autónoma de México, Mexico City), Vol 5, pp 985–988.
- 5.Aull BF, et al. Geiger-mode avalanche photodiodes for three-dimensional imaging. Lincoln Lab J. 2002;13:335–350. [Google Scholar]
- 6. Frach T, et al. (2009) The digital silicon photomultiplier —principle of operation and intrinsic detector performance. 2009 IEEE Nuclear Science Symposium Conference Record (IEEE, New York), pp 1959–1965.
- 7. Isaak S, Pitter MC, Bull S, Harrison I (2010) Design and characterisation of 16×1 parallel outputs SPAD array in 0.18 um CMOS technology. 2010 IEEE Asia Pacific Conference on Circuits and Systems (IEEE, New York), pp 979–982.
- 8. Markovic B, Tosi A, Zappa F, Tisa S (2010) Smart-pixel with SPAD detector and time-to-digital converter for time-correlated single photon counting. 2010 23rd Annual Meeting of the IEEE Photonics Society (IEEE, New York), pp 181–182.
- 9.Dorfman R. The detection of defective members of large populations. Ann Math Stat. 1943;14:436–440. [Google Scholar]
- 10. Du DZ, Hwang FK (2000) Combinatorial Group Testing and Its Applications (World Scientific Publishing, Singapore)
- 11.Sobel M, Groll PA. Group testing to eliminate efficiently all defectives in a binomial sample. Bell Syst Tech J. 1959;38:1179–1252. [Google Scholar]
- 12. Clifford R, Efremenko K, Porat E, Rothschild A (2007) k-mismatch with don’t cares. Proceedings of the 15th Annual European Conference on Algorithms (Springer, Berlin), pp 151–162.
- 13. Indyk P (1997) Deterministic superimposed coding with applications to pattern matching. Proceedings of the 38th Annual Symposium on Foundations of Computer Science (IEEE Computer Society, Washington, DC), pp 127–136.
- 14. Balding DJ, Bruno WJ, Knill E, Torney DC (1996) A comparative survey of non-adaptive pooling designs. Genetic Mapping and DNA Sequencing, eds Speed T, Waterman MS (Springer, Berlin), pp 133–154.
- 15. Du DZ, Hwang FK (2006) Pooling designs and nonadaptive group testing: Important tools for DNA sequencing. Series on Applied Mathematics (World Scientific, New York), Vol 18.
- 16. D’yachkov AG, Macula AJ, Rykov VV (2000) New Applications and Results of Superimposed Code Theory Arising from the Potentialities of Molecular Biology (Kluwer, Dordrecht, The Netherlands), pp 265–282.
- 17. Ngo HQ, Du DZ (2000) A survey on combinatorial group testing algorithms with applications to DNA library screening. Discrete Mathematical Problems with Medical Applications (Am Mathematical Soc, Providence, RI), Vol 55 of DIMACS Ser Discrete Math Theoret Comput Sci, pp 171–182.
- 18.Wolf JK. Born again group testing: Multiaccess communications. IEEE Trans Inf Theory. 1985;31:185–191. [Google Scholar]
- 19.Cormode G, Muthukrishnan S. What’s hot and what’s not: Tracking most frequent items dynamically. ACM Trans Database Syst. 2005;30:249–278. [Google Scholar]
- 20. Porat E, Rothschild A (2008) Explicit non-adaptive combinatorial group testing schemes. Automata, Languages and Programming, eds Aceto L, et al. (Springer, Berlin), Vol 5125 of Lecture Notes Comp Sci, pp 748–759.
- 21.Knill E, Bruno WJ, Torney DC. Non-adaptive group testing in the presence of errors. Discrete Appl Math. 1998;88:261–290. [Google Scholar]
-
22.Macula AJ. Error-correcting nonadaptive group testing with
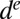 -disjunct matrices. Discrete Appl Math. 1997;80:217–222. [Google Scholar]
-disjunct matrices. Discrete Appl Math. 1997;80:217–222. [Google Scholar] - 23.De Bonis A, Ga\x{0327}sieniec L, Vaccaro U. Optimal two-stage algorithms for group testing problems. SIAM J Comput. 2005;34:1253–1270. [Google Scholar]
- 24. Farach M, Kannan S, Knill E, Muthukrishnan S (1997) Group testing problems with sequences in experimental molecular biology. Proceedings of Compression and Complexity of Sequences 1997, pp 357–367.
- 25. Castro IF, Soares AJ, Veloso JF (2009) Impact of dark counts in low-light level silicon photomultiplier multi-readout applications. 2009 IEEE Nuclear Science Symposium Conference Record (IEEE, New York), pp 1592–1596.
- 26.Kautz WH, Singleton RC. Nonrandom binary superimposed codes. IEEE Trans Inf Theory. 1964;10:363–377. [Google Scholar]
- 27.Erdös P, Frankl P, Füredi Z. Families of finite sets in which no set is covered by the union of r others. Israel J Math. 1985;51:79–89. [Google Scholar]
- 28. Brouwer AE Bounds for constant weight codes. Available at www.win.tue.nl/~aeb/codes/Andw.html.
- 29.Singleton RC. Maximum distance q-nary codes. IEEE Trans Inf Theory. 1964;10:116–118. [Google Scholar]
- 30. MacWilliams FJ, Sloane NJA (1977) The Theory of Error-Correcting Codes (North-Holland, Amsterdam)
- 31. Grassl M (2007), Bounds on the minimum distance of linear codes and quantum codes. Available at www.codetables.de.
- 32.D’yachkov AG, Macula AJ, Rykov VV. New constructions of superimposed codes. IEEE Trans Inf Theory. 2000;46:284–290. [Google Scholar]
- 33. Gordon D, et al. La Jolla Covering Repository. Available at www.ccrwest.org/cover.html.
- 34.Ruszinkó M. On the upper bound of the size of the r-cover-free families. J Comb Theory Ser A. 1994;66:302–310. [Google Scholar]
- 35.D’yachkov AG, Rykov VV. A survey of superimposed code theory. Problems Control Info Theory. 1983;14:1–13. [Google Scholar]
- 36.Füredi Z. On r-cover-free families. J Comb Theory Ser A. 1996;73:172–173. [Google Scholar]
- 37. Chaudhuri S, Radhakrishnan J (1996) Deterministic restrictions in circuit complexity. Proceedings of the twenty-eighth annual ACM symposium on Theory of Computing (Assoc for Computing Machinery, New York), pp 30–36.
- 38.Clementi AE, Monti A, Silvestri R. Distributed broadcast in radio networks of unknown topology. Theor Comput Sci. 2003;302:337–364. [Google Scholar]
- 39.Hwang FK, Sós VT. Nonadaptive hypergeometric group testing. Studia Sci Math Hungar. 1987;22:257–263. [Google Scholar]
- 40. Stein WA, et al. (2012) Sage Mathematics Software (Version 4.7.2). Available at www.sagemath.org.
- 41.De Bonis A, Vaccaro U. Constructions of generalized superimposed codes with applications to group testing and conflict resolution in multiple access channels. Theor Comput Sci. 2003;306:223–243. [Google Scholar]
- 42.Yeh HG. d-Disjunct matrices: Bounds and Lovász local lemma. Discrete Math. 2002;253:97–107. [Google Scholar]
- 43.Erdös P, Lovász L. (1975) Problems and results on 3-chromatic hypergraphs and some related questions. Infinite and Finite Sets II, eds. Hajnal A, Rado R, Sós VT. pp. 609–627. [Google Scholar]
- 44. Alon N, Spencer JH (1992) The Probabilistic Method (Wiley, New York), 2nd Ed.
- 45. Riccio L, Colbourn CJ (1998) An Upper Bound for Disjunct Matrices preprint.
- 46.Johnson SM. Improved asymptotic bounds for error-correcting codes. IEEE Trans Inf Theory. 1963;9:198–205. [Google Scholar]
- 47. Baranyai Zs (1973) On the factorization of exponential sized families of k-independent sets. Proceedings Colloquium Math Soc János Bólyai (North-Holland, Amsterdam), Vol 10, Infinite and Finite Sets.
- 48.Agostinelli S, et al. Geant4 – a simulation toolkit. Nuclear Instrum Methods Phys Res Sect A. 2003;506:250–303. [Google Scholar]
- 49.Rodrigues P, et al. Geant4 applications and developments for medical physics experiments. IEEE Trans Nucl Sci. 2004;51:1412–1419. [Google Scholar]
- 50.Restle PJ, et al. A clock distribution network for microprocessors. IEEE J Solid-State Circuits. 2001;36:792–799. [Google Scholar]
- 51.Cheng Y, Du DZ. New constructions of one- and two-stage pooling designs. J Comput Biol. 2008;15(2):195–205. doi: 10.1089/cmb.2007.0195. [DOI] [PubMed] [Google Scholar]
- 52.Eppstein D, Goodrich MT, Hirschberg DS. Improved combinatorial group testing algorithms for real-world problem sizes. SIAM J Comput. 2007;36:1360–1375. [Google Scholar]
- 53.Erdös P, Frankl P, Füredi Z. Families of finite sets in which no set is covered by the union of two others. J Comb Theory Ser A. 1982;33:158–166. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.