Acoustic echoes reveal room shape

Abstract

Imagine that you are blindfolded inside an unknown room. You snap your fingers and listen to the room’s response. Can you hear the shape of the room? Some people can do it naturally, but can we design computer algorithms that hear rooms? We show how to compute the shape of a convex polyhedral room from its response to a known sound, recorded by a few microphones. Geometric relationships between the arrival times of echoes enable us to “blindfoldedly” estimate the room geometry. This is achieved by exploiting the properties of Euclidean distance matrices. Furthermore, we show that under mild conditions, first-order echoes provide a unique description of convex polyhedral rooms. Our algorithm starts from the recorded impulse responses and proceeds by learning the correct assignment of echoes to walls. In contrast to earlier methods, the proposed algorithm reconstructs the full 3D geometry of the room from a single sound emission, and with an arbitrary geometry of the microphone array. As long as the microphones can hear the echoes, we can position them as we want. Besides answering a basic question about the inverse problem of room acoustics, our results find applications in areas such as architectural acoustics, indoor localization, virtual reality, and audio forensics.

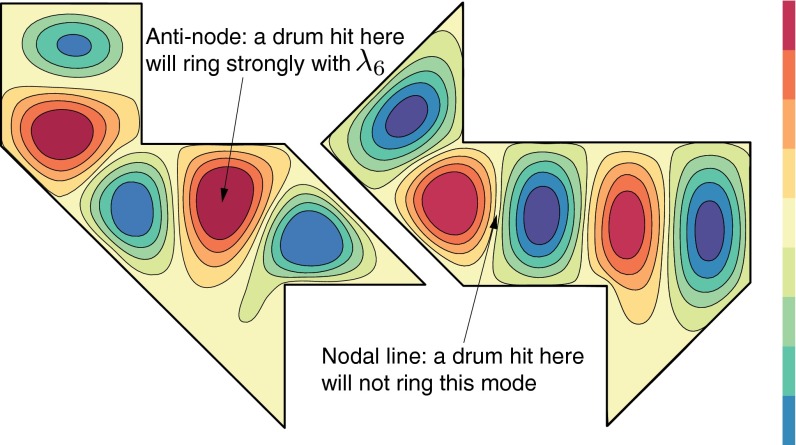
In a famous paper (1), Mark Kac asks the question “Can one hear the shape of a drum?” More concretely, he asks whether two membranes of different shapes necessarily resonate at different frequencies.* This problem is related to a question in astrophysics (2), and the answer turns out to be negative: Using tools from group representation theory, Gordon et al. (3, 4) presented several elegantly constructed counterexamples, including the two polygonal drum shapes shown in Fig. 1. Although geometrically distinct, the two drums have the same resonant frequencies.^†

Fig. 1.

Figure shows two isospectral drums (16). Although geometrically distinct, these drums have the same resonant frequencies. The standing waves corresponding to the eigenvalue 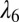are shown for both drums. It is clear that this mode will be excited with different amplitudes, depending on where we hit the drum. Extremes are nodes and anti-nodes.

In this work, we ask a similar question about rooms. Assume you are blindfolded inside a room; you snap your fingers and listen to echoes. Can you hear the shape of the room? Intuitively, and for simple room shapes, we know that this is possible. A shoebox room, for example, has well-defined modes, from which we can derive its size. However, the question is challenging in more general cases, even if we presume that the room impulse response (RIR) contains an arbitrarily long set of echoes (assuming an ideal, noiseless measurement) that should specify the room geometry.

It might appear that Kac’s problem and the question we pose are equivalent. This is not the case, for the sound of a drum depends on more than its set of resonant frequencies (eigenvalues)—it also depends on its resonant modes (eigenvectors). In the paper “Drums that sound the same” (5), Chapman explains how to construct drums of different shapes with matching resonant frequencies. Still, these drums would hardly sound the same if hit with a drumstick. They share the resonant frequencies, but the impulse responses are different. Even a single drum struck at different points sounds differently. Fig. 1 shows this clearly.

Certain animals can indeed “hear” their environment. Bats, dolphins, and some birds probe the environment by emitting sounds and then use echoes to navigate. It is remarkable to note that there are people that can do the same, or better. Daniel Kish produces clicks with his mouth, and uses echoes to learn the shape, distance, and density of objects around him (6). The main cues for human echolocators are early reflections. Our computer algorithms also use early reflections to calculate shapes of rooms.

Many applications benefit from knowing the room geometry. Indoor sound-source localization is usually considered difficult, because the reflections are difficult to predict and they masquerade as sources. However, in rooms one can do localization more accurately than in free-field if the room geometry (7–10) is known. In teleconferencing, auralization, and virtual reality, one often needs to compensate the room influence or create an illusion of a specific room. The success of these tasks largely depends on the accurate modeling of the early reflections (11), which in turn requires the knowledge of the wall locations.

We show how to reconstruct a convex polyhedral room from a few impulse responses. Our method relies on learning from which wall a particular echo originates. There are two challenges with this approach: First, it is difficult to extract echoes from RIRs; and second, the microphones receive echoes from walls in different orders. Our main contribution is an algorithm that selects the “correct” combinations of echoes, specifically those that actually correspond to walls. The need for assigning echoes to walls arises from the omnidirectionality of the source and the receivers.

There have been several attempts in estimating the room geometry from RIRs (12–14). In (13), the problem is formulated in 2D, and the authors take advantage of multiple source locations to estimate the geometry. In (14) the authors address the problem by 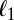-regularized template matching with a premeasured dictionary of impulse responses. Their approach requires measuring a very large matrix of impulse responses for a fixed-source–receiver geometry. The authors in (15) propose a 3D room reconstruction method by assuming that the array is small enough so that there is no need to assign echoes to walls. They use sparse RIRs obtained by directing the loudspeaker to many orientations and processing the obtained responses. In contrast, our method works with arbitrary measurement geometries. Furthermore, we prove that the first-order echoes provide a unique description of the room for almost all setups. A subspace-based formulation allows us to use the minimal number of microphones (four microphones in 3D). It is impossible to further reduce the number of microphones, unless we consider higher-order echoes, as attempted in (12). However, the arrival times of higher-order echoes are often challenging to obtain and delicate to use, both for theoretical and practical reasons. Therefore, in the proposed method, we choose to use more than one microphone, avoiding the need for higher-order echoes.

In addition to theoretical analysis, we validate the results experimentally by hearing rooms on Ecole Polytechnique Fédérale de Lausanne (EPFL) campus. Moreover, by running it in a portal of the Lausanne cathedral, we show that the algorithm still gives useful output even when the room thoroughly violates the assumptions of it being a convex polyhedron.

Modeling

We consider the room to be a K-faced convex polyhedron. We work in 3D, but the results extend to arbitrary dimensionalities (2D is interesting for some applications). Sound propagation in a room is described by a family of RIRs. An RIR models the channel between a fixed source and a fixed receiver. It contains the direct path and the reflections. Ideally, it is a train of pulses, each corresponding to an echo. For the mth microphone it is given by

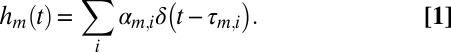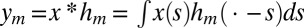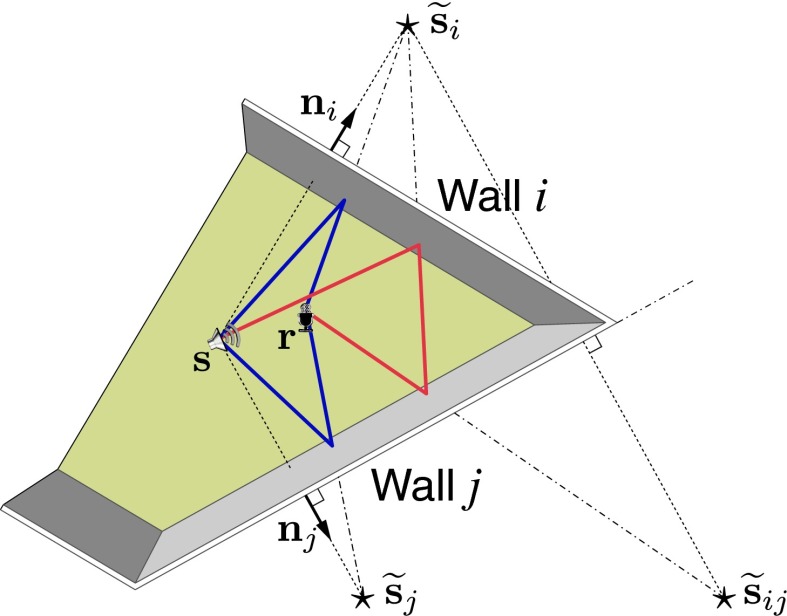
Microphones hear the convolution of the emitted sound with the corresponding RIR, . By measuring the impulse responses we access the propagation times 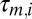, and these can be linked to the room geometry by the image source (IS) model (17, 18). According to the IS model, we can replace reflections by virtual sources. As illustrated in Fig. 2, virtual sources are mirror images of the true sources across the corresponding reflecting walls. From the figure, the image of the source with respect to the ith wall is computed as

where 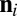is the unit normal, and 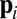any point belonging to the ith wall. The time of arrival (TOA) of the echo from the ith wall is 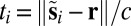, where c is the speed of sound.

Fig. 2.

Illustration of the image source model for first- and second-order echoes. Vector 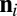is the outward-pointing unit normal associated with the ith wall. Stars denote the image sources, and 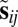is the image source corresponding to the second-order echo. Sound rays corresponding to first reflections are shown in blue, and the ray corresponding to the second-order reflection is shown in red.

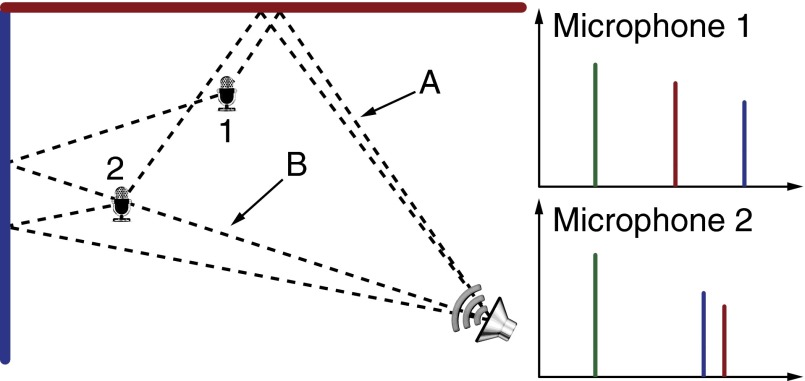
In a convex room with a known source, knowing the image sources is equivalent to knowing the walls—we can search for points instead of searching for walls. The challenge is that the distances are unlabeled: It might happen that the kth peak in the RIR from microphone 1 and the kth peak in the RIR from microphone 2 come from different walls. This is illustrated in Figs. 3 and 4. Thus, we have to address the problem of echo labeling. The loudspeaker position need not be known. We can estimate it from the direct sound using either TOA measurements, or differences of TOAs if the loudspeaker is not synchronized with the microphones (19–21).

Fig. 3.

Illustration of echo swapping. Microphone 1 hears the echo from the red wall before hearing the echo from the blue wall, because path A is shorter than path B. The opposite happens for microphone 2.

Fig. 4.

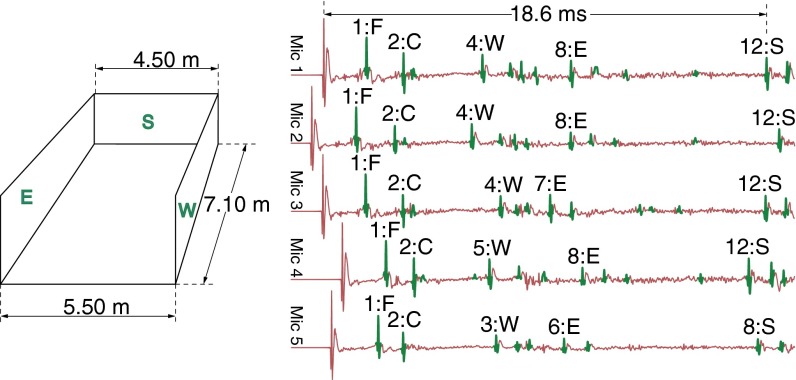
Actual room impulses responses acquired in a room sketched on the Left (see experiments for more details). First peak corresponds to direct propagation. Detected echoes are highlighted in green. Annotations above the peaks indicate the ordinal number of the peak, and the wall to which it corresponds (south, north, east, west, floor, and ceiling). We can see that the ordinal number of the W-peak changes from one impulse response to another (similarly for E and S). For larger microphone arrays this effect becomes more dramatic. We also see that some peaks do not correspond to walls. Our algorithm successfully groups peaks corresponding to the same wall, and disregards irrelevant peaks.

In practice, having a method to find good combinations of echoes is far more important than only sorting correctly selected echoes. Impulse responses contain peaks that do not correspond to any wall. These spurious peaks can be introduced by noise, nonlinearities, and other imperfections in the measurement system. We find that a good strategy is to select a number of peaks greater than the number of walls and then to prune the selection. Furthermore, some second-order echoes might arrive before some first-order ones. The image sources corresponding to second-order or higher-order echoes (e.g., Fig. 2) will be estimated as any other image source. However, because we can express a second-order image source in terms of the first-order ones as

and

we can eliminate it during postprocessing by testing the above two expressions.

Echo Labeling

The purpose of echo labeling is twofold. First, it serves to remove the “ghost” echoes (that do not correspond to walls) detected at the peak-picking stage. Second, it determines the correct assignment between the remaining echoes and the walls. We propose two methods for recognizing correct echo combinations. The first one is based on the properties of Euclidean distance matrices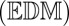, and the second one on a simple linear subspace condition.

EDM-Based Approach.

Consider a room with a loudspeaker and an array of M microphones positioned so that they hear the first-order echoes (we typically use 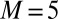). Denote the receiver positions by , 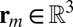and the source position by 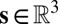. The described setup is illustrated in Fig. 5. We explain the 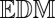-based echo sorting with reference to this figure. Let 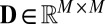be a matrix whose entries are squared distances between microphones, 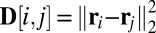, 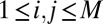. Here, 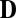is an 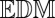corresponding to the microphone setup. It is symmetric with a zero diagonal and positive off-diagonal entries.

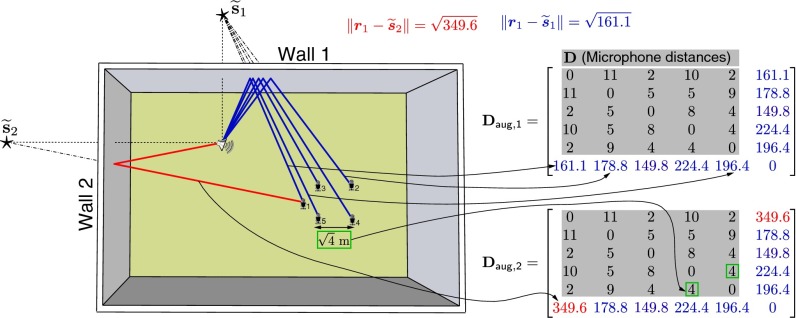
Fig. 5.

Illustration of 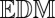-based echo sorting. Microphones receive the echoes from all of the walls, and we aim to identify echoes coming from a single wall. We select one echo from each microphone and use these echoes to augment the 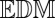of the microphone setup, 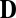. If all of the selected echoes come from the same wall, the augmented matrix is an 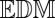as well. In the figure, 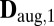is an 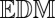because it contains the distances to a single point 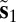; 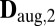contains a wrong distance (shown in red) for microphone 1, so it is not an 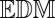. For aesthetic reasons the distances are specified to a single decimal place. Full precision entries are given in the SI Text.

If the loudspeaker emits a sound, each microphone receives the direct sound and K first-order echoes corresponding to the K walls. The arrival times of the received echoes are proportional to the distances between image sources and microphones. As already discussed, we face a labeling problem as we do not know which wall generated which echo. This problem is illustrated in Fig. 3 for two walls and in Fig. 4 for the whole room. Simple heuristics, such as grouping the closest pulses or using the ordinal number of a pulse, have limited applicability, especially with larger distances between microphones. That these criteria fail is evident from Fig. 4.

We propose a solution based on the properties of 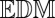s. The loudspeaker and the microphones are—to a good approximation—points in space, so their pairwise distances form an 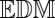. We can exploit the rank property: An 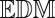corresponding to a point set in 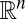has rank at most 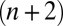(22). Thus, in 3D, its rank is at most 5. We start from a known point set (the microphones) and want to add another point—an image source. This requires adding a row and a column to 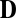, listing squared distances between the microphones and the image source. We extract the list of candidate distances from the RIRs, but some of them might not correspond to an image source; and for those that do correspond, we do not know to which one. Consider again the setup in Fig. 5. Microphone 1 hears echoes from all of the walls, and we augment 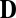by choosing different echo combinations. Two possible augmentations are shown. Here, is a plausible augmentation of 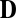because all of the distances correspond to a single image source, and they appear in the correct order. This matrix passes the rank test, or more specifically, it is an 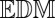. The second matrix, , is a result of an incorrect echo assignment, as it contains entries coming from different walls. A priori, we cannot tell whether the red echo comes from wall 1 or from wall 2. It is simply an unlabeled peak in the RIR recorded by microphone 1. However, the augmented matrix does not pass the rank test, so we conclude that the corresponding combination of echoes is not correct.

To summarize, wrong assignments lead to augmentations of 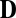that are not 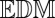s. In particular, these augmentations do not have the correct rank. As it is very unlikely (as will be made precise later) for incorrect combinations of echoes to form an 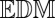, we have designed a tool to detect correct echo combinations.

More formally, let 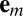list the candidate distances computed from the RIR recorded by the mth microphone. We proceed by augmenting the matrix 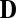with a combination of M unlabeled squared distances 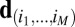to get ,

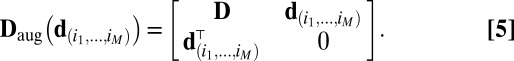The column vector 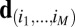is constructed as

with 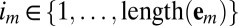. In words, we construct a candidate combination of echoes 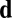by selecting one echo from each microphone. Note that 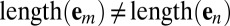for 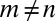in general. That is, we can pick a different number of echoes from different microphones. We interpret as an object encoding a particular selection of echoes .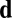

One might think of 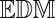as a mold. It is very much like Cinderella’s glass slipper: If you can snugly fit a tuple of echoes in it, then they must be the right echoes. This is the key observation: If 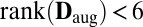or more specifically 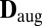verifies the 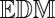property, then the selected combination of echoes corresponds to an image source, or equivalently to a wall. Even if this approach requires testing all of the echo combinations, in practical cases the number of combinations is small enough that this does not present a problem.

Subspace-Based Approach.

An alternative method to obtain correct echo combinations is based on a simple linear condition. Note that we can always choose the origin of the coordinate system so that

Let 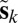be the location vector of the image source with respect to wall k. Then, up to a permutation, we receive at the mth microphone the squared distance information,

Define further 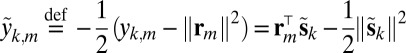. We have in vector form

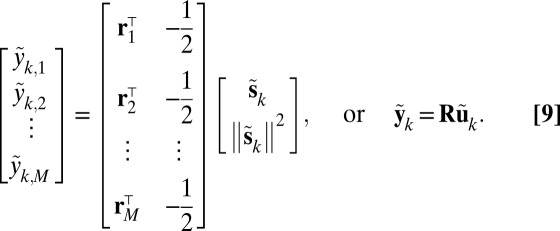Thanks to the condition 7, we have that

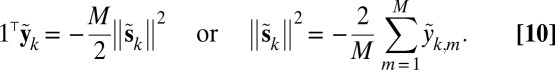The image source is found as

where 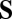is a matrix satisfying

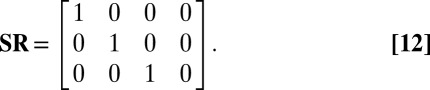These two conditions characterize the distance information. In practice, it is sufficient to verify the linear constraint

where 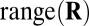is a proper subspace when 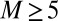. However, note that we can use the nonlinear condition 10 even if .

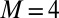Uniqueness.

Can we guarantee that only one room corresponds to the collected first-order echoes? To answer this, we first define the set of “good” rooms in which our algorithm can be applied. The algorithm relies on the knowledge of first-order echoes, so we require that the microphones hear them. This defines a good room, which is in fact a combination of the room geometry and the microphone array/loudspeaker location.

Definition 1:

(Feasibility). Given a room 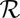and a loudspeaker position , we say that the point 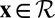is feasible if a microphone placed at receives all the first-order echoes of a pulse emitted from .

Our argument is probabilistic: The set of vectors 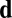such that 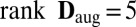has measure zero in 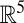. Analogously, in the subspace formulation, 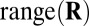is a proper subspace of 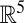thus having measure zero. To use four microphones, observe that the same is true for the set of vectors satisfying [10] in 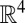. These observations, along with some technical details, enable us to state the uniqueness result.^‡

Theorem 1.

Consider a room with a loudspeaker and 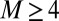microphones placed uniformly at random inside the feasible region. Then the unlabeled set of first-order echoes uniquely specifies the room with probability 1. In other words, almost surely exactly one assignment of first-order echoes to walls describes a room.

This means that we can reconstruct any convex polyhedral room if the microphones are in the feasible region. A similar result could be stated by randomizing the room instead of the microphone setup, but that would require us to go through the inconvenience of generating a random convex room. In the following, we concentrate on the 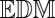criterion, as it performs better in experiments.

Practical Algorithm

In practice, we face different sources of uncertainty. One such source is the way we measure the distances between microphones. We can try to reduce this error by calibrating the array, but we find the proposed schemes to be very stable with respect to uncertainties in array calibration. Additional sources of error are the finite sampling rate and the limited precision of peak-picking algorithms. These are partly caused by unknown loudspeaker and microphone impulse responses, and general imperfections in RIR measurement. They can be mitigated with higher sampling frequencies and more sophisticated time-of-arrival estimation algorithms. At any rate, testing the rank of 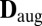is not a way to go in the presence of measurement uncertainties. The solution is to measure how close 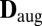is to an 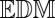. We can consider different constructions:

• (i) Heuristics based on the singular values of ;

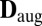• (ii) distance of 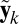from 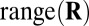(Eq. 13);

• (iii) nonlinear norm condition 10; and

• (iv) distance between 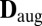and the closest .

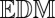The approach based on the singular values of 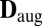captures only the rank requirement on the matrix. However, the requirement that 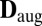be an 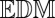brings in many additional subtle dependencies between its elements. For instance, we have that (23)

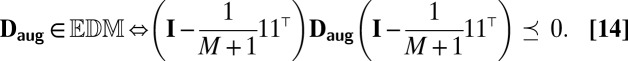Unfortunately [14], does not allow us to specify the ambient dimension of the point set. Imposing this constraint leads to even more dependencies between the matrix elements, and the resulting set of matrices is no longer a cone (it is actually not convex anymore). Nevertheless, we can apply the family of algorithms used in multidimensional scaling (MDS) (23) to find the closest between the points in a fixed ambient dimension.

Multidimensional Scaling.

As discussed, in the presence of noise the rank test on is inadequate. A good way of dealing with this nuisance (as verified through experiments) is to measure how close is to an 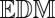. To this end we use MDS to construct the point set in a given dimension (3D) that produces the 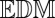“closest” to 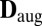. MDS was originally proposed in psychometrics (24) for data visualization. Many adaptations of the method have been proposed for sensor localization. We use the so-called “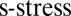” criterion (25). Given an observed noisy matrix 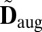, 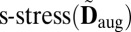is the value of the following optimization program,

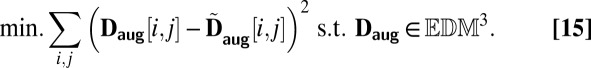By 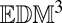we denote the set of 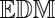s generated by point sets in 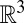. We say that 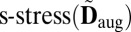is the score of the matrix 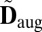, and use it to assess the likelihood that a combination of echoes corresponds to a wall. A method for solving [15] is described in the SI Text.

Reconstruction Algorithm.

Combining the described ingredients, we design an algorithm for estimating the shape of a room. The algorithm takes as input the arrival times of echoes at different microphones (computed from RIRs). For every combination of echoes, it computes the score using the criterion of choice. We specialize to constructing the matrix 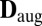as in (5) and computing the 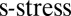score. For the highest ranked combinations of echoes, it computes the image-source locations. We use an additional step to eliminate ghost echoes, second-order image sources, and other impossible solutions. Note that we do not discuss peak picking (selecting peaks from RIRs) in this work. The algorithm is summarized as

• i) For every , ;

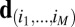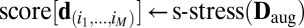• ii) sort the scores collected in ;

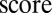• iii) compute the image source locations;

• iv) remove image sources that do not correspond to walls (higher-order by using step iii, ghost sources by heuristics); and

• v) reconstruct the room.

Step iv is described in more detail in the SI Text. It is not necessary to test all echo combinations. An echo from a fixed wall will arrive at all of the microphones within the time given by the largest intermicrophone distance. Therefore, it suffices to combine echoes within a temporal window corresponding to the array diameter. This substantially reduces the running time of the algorithm. As a consequence, we can be less conservative in the peak-picking stage. A discussion of the influence of errors in the image-source estimates on the estimated plane parameters is provided in (15).

Experiments

We ran the experiments in two distinctly different environments. One set was conducted in a lecture room at EPFL, where our modeling assumptions are approximately satisfied. Another experiment was conducted in a portal of the Lausanne cathedral. The portal is nonconvex, with numerous nonplanar reflecting objects. It essentially violates the modeling assumptions, and the objective was to see whether the algorithm still gives useful information. In all experiments, microphones were arranged in an arbitrary geometry, and we measured the distances between the microphones approximately with a tape measure. We did not use any specialized equipment or microphone arrays. Nevertheless, the obtained results are remarkably accurate and robust.

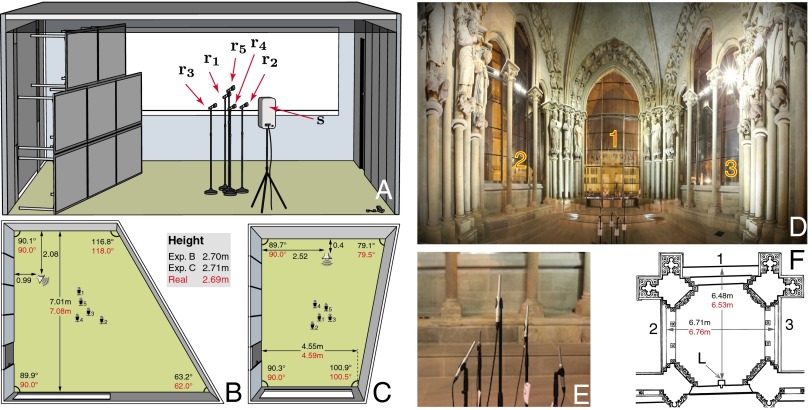
The lecture room is depicted in Fig. 6A. Two walls are glass windows, and two are gypsum-board partitions. The room is equipped with a perforated metal-plate ceiling suspended below a concrete ceiling. To make the geometry of the room more interesting, we replaced one wall by a wall made of tables. Results are shown for two positions of the table wall and two different source types. We used an off-the-shelf directional loudspeaker, an omnidirectional loudspeaker, and five nonmatched omnidirectional microphones. RIRs were estimated by the sine sweep technique (26). In the first experiment, we used an omnidirectional loudspeaker to excite the room, and the algorithm reconstructed all six walls correctly, as shown in Fig. 6B. Note that the floor and the ceiling are estimated near perfectly. In the second experiment, we used a directional loudspeaker. As the power radiated to the rear by this loudspeaker is small, we placed it against the north wall, thus avoiding the need to reconstruct it. Surprisingly, even though the loudspeaker is directional, the proposed algorithm reconstructs all of the remaining walls accurately, including the floor and the ceiling.

Fig. 6.

(A) Illustration of the room used in the experiment with a movable wall. (B and C) Two reconstruction results. Real values are indicated in red, and the estimated values are indicated in black. (D) Panoramic photo of the portal of the Lausanne cathedral. (E) A close up of the microphone array used in cathedral experiments. (F) Floor plan of the portal.

Fig. 6 D and F shows a panoramic view and the floor plan of the portal of the Lausanne cathedral. The central part is a pit reached by two stairs. The side and back walls are closed by glass windows, with their lower parts in concrete. In front of each side wall, there are two columns, and the walls are joined by column rows indicated in the figure. The ceiling is a dome ∼9 m high. We used a directional loudspeaker placed at the point L in Fig. 6F. Microphones were placed around the center of the portal. Alas, in this case we do not have a way to remove unwanted image sources, as the portal is poorly approximated by a convex polyhedron. The glass front, numeral 1 in Fig. 6F, and the floor beneath the microphone array can be considered flat surfaces. For all of the other boundaries of the room, this assumption does not hold. The arched roof cannot be represented by a single height estimate. The side windows, numerals 2 and 3 in Fig. 6F, with pillars in front of them and erratic structural elements at the height of the microphones, the rear wall, and the angled corners with large pillars and large statues, all present irregular surfaces creating diffuse reflections. Despite the complex room structure with obstacles in front of the walls and numerous small objects resulting in many small-amplitude, temporally spread echoes, the proposed algorithm correctly groups the echoes corresponding to the three glass walls and the floor. This certifies the robustness of the method. More details about the experiments are given in the SI Text.

Discussion

We presented an algorithm for reconstructing the 3D geometry of a convex polyhedral room from a few acoustic measurements. It requires a single sound emission and uses a minimal number of microphones. The proposed algorithm has essentially no constraints on the microphone setup. Thus, we can arbitrarily reposition the microphones, as long as we know their pairwise distances (in our experiments we did not “design” the geometry of the microphone setup). Further, we proved that the first-order echoes collected by a few microphones indeed describe a room uniquely. Taking the image source point of view enabled us to derive clean criteria for echo sorting.

Our algorithm opens the way for different applications in virtual reality, auralization, architectural acoustics, and audio forensics. For example, we can use it to design acoustic spaces with desired characteristics or to change the auditory perception of existing spaces. The proposed echo-sorting solution is useful beyond hearing rooms. Examples are omnidirectional radar, multiple-input–multiple-output channel estimation, and indoor localization to name a few. As an extension of our method, a person walking around the room and talking into a cellphone could enable us to both hear the room and find the person’s location. Future research will aim at exploring these various applications.

Results presented in this article are reproducible. The code for echo sorting is available at http://rr.epfl.ch.