Modelling the physics in iterative reconstruction for transmission computed tomography

Abstract

There is an increasing interest in iterative reconstruction (IR) as a key tool to improve quality and increase applicability of X-ray CT imaging. IR has the ability to significantly reduce patient dose, it provides the flexibility to reconstruct images from arbitrary X-ray system geometries and it allows to include detailed models of photon transport and detection physics, to accurately correct for a wide variety of image degrading effects. This paper reviews discretisation issues and modelling of finite spatial resolution, Compton scatter in the scanned object, data noise and the energy spectrum. Widespread implementation of IR with highly accurate model-based correction, however, still requires significant effort. In addition, new hardware will provide new opportunities and challenges to improve CT with new modelling.

1. Introduction

Computed tomography (CT) was introduced as a clinical imaging tool in the 1970s. Since then, it has seen impressive improvements in hardware and software. In the last decades, the number of detector rows has increased continuously, effectively turning multi detector row CT systems into cone beam CTs. To increase scanning speed, the rotation time has been reduced, reaching values below 300 ms per rotation, and the original approach of sequential circular scanning has been replaced by helical (spiral) orbits (Kalender 2006). In the last 20 years, flat-panel detectors have been introduced for planar and tomographic X-ray imaging (Kalender and Kyriakou 2007). These detectors are being used in dedicated CT applications, such as flexible C-arm CT systems for angiography and cardiac imaging, digital tomosynthesis for mammography and high resolution dental imaging. This evolution of the hardware was parallelled by new developments in image reconstruction software. New “exact” analytical reconstruction algorithms have been derived for CT with 2D detectors, moving along helical (Katsevich 2002, Noo 2003) and other, more exotic acquisition trajectories (Pack et al. 2004). In addition, as a side effect of these developments, new insight has been gained in reconstruction from truncated projection (Clackdoyle and Defrise 2010).

Although analytical reconstruction algorithms usually produce excellent images, there is a growing interest in iterative reconstruction. One important reason for this is a growing concern about the radiation doses delivered to the patients. Another reason is the higher flexibility and robustness of iterative algorithms, which will allow new CT designs that would pose problems for analytical reconstruction algorithms.

In iterative reconstruction (IR), one models the fact that there are a finite number of measured rays, whereas analytical methods are derived assuming a continuum of rays. In contrast to analytical reconstruction, iterative methods assume right from the start that the image to be reconstructed consists of a finite number of samples too. This is obviously an approximation, but it allows application of numerical methods to solve the reconstruction problem. The algorithms can be considered as a feedback mechanism, with a simulator of the CT-physics (re-projection) in the feedback loop. The feed forward loop updates the reconstruction image, based on deviations between the measured and simulated scans (this usually involves a backprojection). The output of the algorithms is very sensitive to the CT-simulator in the feedback loop; for accurate results, it is essential to use a sufficiently accurate simulator. There is more freedom in the feed forward loop, which can be exploited by algorithm designers to improve the (local or global) convergence properties (De Man and Fessler 2010).

This paper discusses the physics models that are used in the feedback loop. The basic model that is often used can be written as follows:

$$Y_i=b_i{e}^{-{\sum }_j{l}_{ij}{\mu }_j}+s_i+n_i,$$ (1)

where Y_i is the measured transmission sinogram value along projection line i, b_i is the corresponding value that would be measured in absence of attenuation (blank or air calibration scan), μ_j is the linear attenuation coefficient at voxel j, l_ij represents the effective intersection length of the projection line i with voxel j and s_i represents possible additive contributions, such as Compton scatter. The model is completed by assuming a probability distribution for the noise n_i. The index i combines all dimensions of the sinogram (including axial and transaxial detector position, view angle), the index j typically represents the three dimensions of the reconstruction volume. An alternative representation is

$$y_i=ln\left(\frac{b_i}{Y_i-s_i}\right)=\sum _j{l}_{ij}{\mu }_j+n_i^{\prime },$$ (2)

which takes the log-converted data as the input. A noise model for $n_i^{\prime }$ can be obtained by propagating the noise model for (1) through the logarithm. Many analytical algorithms and some iterative ones, such as the well-known SART algorithm (Andersen and Kak 1984, Byrne 2008), use the same weight for all data during the computations. This corresponds to assuming that $n_i^{\prime }$ is independent of i.

The models (1) and (2) have several limitations. They assume a monochromatic transmission source, prior knowledge of the scatter contribution and no detector crosstalk. They cannot accurately account for the finite sizes of the transmission source and the detector elements, and cannot model blurring effects due to continuous gantry rotation. Although these approximations are acceptable in many applications, there are also many cases where better models have significantly improved the final reconstruction.

Below we discuss various aspects of the physics model in iterative CT reconstruction. Section 2 discusses problems and opportunities of the discretisation, and section 3 shows how the models can be extended to take into account effects limiting the spatial resolution. Compton scatter in the scanned object is discussed in section 4. Section 5 analyses the complex noise characteristics of data from the energy-integrating X-ray detectors and presents ways to approximate it. Section 6 briefly discusses incorporation of the energy spectrum and section 7 shows how artifacts due to motion can be reduced or eliminated.

2. Discretisation

Any practical IR algorithm needs to make accurate approximations of the true, continuous nature of the object. Typically, the reconstructed object is represented as a weighted sum of a finite set of spatial basis functions, with a grid of cubic, uniform, non-overlapping voxels covering the reconstructed field of view being perhaps the most common and intuitive example of such a basis set. The reconstruction algorithm solves for the coefficients of this expansion, i.e., the attenuation (or density in polyenergetic reconstruction) of each uniform voxel in the grid. An alternative, but closely related expansion replaces the voxels with a set of spherically symmetric Kaiser-Bessel functions, known as “blobs” (Lewitt 1990, Matej and Lewitt 1996, Ziegler et al. 2006, Carvalho and Herman 2007). During the reconstruction, projections of the object are simulated either by tracing rays and computing intersection lengths with each basis function (for voxels, common choices are the ray-tracing algorithms of Siddon (1985) or Joseph (1982)), or by a “footprint”-based approach (De Man and Basu 2004, Ziegler et al. 2006, Long et al. 2010). Note that the system model assumed in iterative reconstruction (involving discretised object and detectors) is fundamentally different from the one used in the derivation of analytical algorithms (where the object is assumed continuous). This indicates that notions such as sufficient sampling (e.g., in the case of sparse acquisitions) may not directly translate from the analysis of analytical reconstruction to IR, as discussed in (Bian et al. 2013).

A host of new considerations for object discretisation is likely to arise with the growing interest in the application of iterative reconstruction to time-resolved CT imaging, such as in motion-compensated cardiac reconstruction (Isola et al. 2010, Isola et al. 2008), or perfusion imaging on slowly rotating cone-beam systems (Neukirchen et al., 2010). In motion-compensated reconstruction, a new strategy for computation of basis footprints to account for changes in sampling due to the motion field was shown to be necessary and developed for blob-based representation (Isola et al. 2008). Examples from cardiac emission tomography suggest that other object representations, such as deformable meshes (Brankov et al. 2004, Brankov et al. 2005) could provide an interesting alternative to conventional discretisation with voxels or blobs for modelling motion in IR. In perfusion imaging and other applications involving tracking contrast enhancement, IR is enabled by representing the time-varying attenuation (or density) at each location in the object as a superposition of a finite number of temporal basis functions (e.g., gamma-variate distributions) and then solving for the coefficients of this expansion (Neukirchen et al. 2010, Johnston et al. 2012). This essentially means that the reconstruction problem is now decomposed into a set of spatio-temporal basis functions, instead of the purely spatial basis functions discussed above. More details on the dynamic aspects of iterative reconstruction are given in section 7.

Here, we discuss some considerations regarding object discretisation in IR that arise regardless of the chosen method of re-projection. In particular we will review: i) artifacts due to inconsistencies caused by the discrete approximation of true continuous physical objects, ii) region-of-attention strategies to reduce the computational burden of using finely spaced basis functions, and iii) issues related to the use of discrete object and detector models in simulation studies of algorithm performance.

2.1. Discretisation artifacts in iterative reconstruction

The very fact that the object is discretised into a finite number of basis functions inherently leads to discrepancies between the measured projection data and the simulated re-projections estimated during the reconstruction (Zbijewski and Beekman 2004a, Pan et al. 2009, Herman and Davidi 2008). Finite-dimensional object representation is thus both a crucial enabler and a potential source of significant errors in reconstruction, as discussed in the general context of (linear) statistical inverse problems in (Kaipio and Somersalo 2007). As presented in (Zbijewski and Beekman 2004a) for cubic voxels, even in the case of “ideal” discretisation where each voxel represents the average attenuation (or density) of the continuous object within its volume, the simulated re-projection of such representation will be mismatched with the measured projections in areas corresponding to interfaces between tissues. Because IR algorithms seek to maximise the agreement between the re-projections and the measured data, these unintended mismatches may cause artifacts. Typically, such artifacts are most pronounced around sharp material boundaries and appear as edge overshoots and aliasing patterns. Figure 1 illustrates these effects for a simulation of a clinical fan-beam CT scanner. No artifacts attributable to object discretisation are present in the analytical (filtered backprojection or FBP) reconstruction onto a grid of “natural” voxels, given by de-magnified detector pixel size (figure 1(A)). Figure 1(B) shows the result of iterative reconstruction onto the same object grid, exhibiting the edge and aliasing artifacts explained above.

Figure 1.

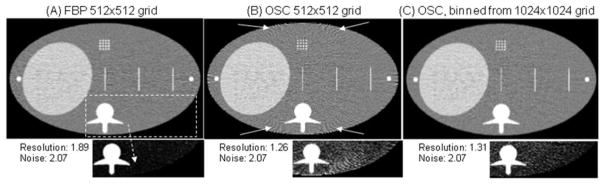
(A) FBP reconstruction from simulated projections of a digital abdomen phantom. Simulations were performed on a very fine (4096×4096) grid with 0.125 mm voxels and 16 rays traced per 2 mm detector bin. All reconstructions are presented on a 512×512 grid of 1 mm voxels (“natural” voxel size for this geometry with magnification of 2). Iterative unregularised Ordered Subset Convex (OSC) reconstruction on the 512×512 grid is shown in (B) at a noise level matching the FBP image (accomplished by low-pass filtering). Despite better resolution (FWHM of the line pattern), the OSC image is plagued by edge and aliasing artifacts caused by object discretisation. Artifacts are indicated by arrows; in each case, an image of a section of the phantom is also shown using a compressed gray scale to better visualise the artifacts. OSC reconstruction on a fine grid (1024×1024) followed by downsampling to the same grid as used for FBP is illustrated in (C). Gray scale range is 0.9–1.1 g/cm³ for full images and 1.0–1.02 g/cm³ for image details. Figure adopted from (Zbijewski and Beekman 2004a).

Intuitively, using many basis functions to represent the object (e.g., smaller voxels) should alleviate such discretisation-induced artifacts, as has been shown by Zbijewski and Beekman (2004a). In particular, it was demonstrated that while statistical reconstruction onto a voxel grid typical for analytical reconstruction results in severe edge artifacts (fig 1), reconstruction on twice as fine a grid followed by binning back onto the “natural voxels” is sufficient to remove most of the artifacts (1 (C)). The binning step mitigates the increased noise in the finely sampled reconstruction; this approach has been shown to outperform simple post-smoothing of the low resolution reconstructions in terms of the trade-off between artifact reduction and resolution (Zbijewski and Beekman 2004a). Reconstruction using finely sampled voxel basis has also been demonstrated to outperform an approach based on smoothing the measured projections (Zbijewski and Beekman 2006a), which intends to compensate for the blur introduced by discretisation and improve the match between measured and simulated projections (Kunze et al. 2005). Finally, even though basis functions such as the blobs are expected to show slightly less pronounced edge artifacts than square voxels (Matej and Lewitt 1996), such artifacts have still been observed in blob-based CT reconstructions (Ziegler et al. 2006). It has also been shown that, at least in some cases, voxel-based reconstruction on a fine grid outperforms blob-based reconstruction on a coarser grid in terms of edge artifact reduction (Zbijewski and Beekman 2006a). Some projection operators were demonstrated to be more immune to such artifacts than others (e.g., the trapezoidal separable footprint outperformed distance-driven projector in (Long et al. 2010) in this respect), but in general the root cause of the problem is using a finite number of basis functions to represent a continuous object (Pan et al. 2009), regardless of the particular form of the basis functions or projection operator. Iterative reconstruction is thus likely to typically require finer object discretisations than analytical reconstruction to minimise edge artifacts. Note that using more basis functions may degrade the conditioning of the reconstruction problem, so that judicious choice of regularisation may become increasingly important in constraining the solution. Furthermore, the edge and aliasing artifacts due to discretisation may occur alongside similar artifacts caused by the Gibbs phenomenon, where the reconstruction algorithm attempts to recover high frequencies lost in the detection process, compound by mismatches between the true blurring in the system and its model used by the reconstructor, as described in (Snyder et al. 1987) for emission tomography.

2.2. Non-uniform discretisation and other region-of-interest techniques

Using fine discretisations to reduce edge artifacts (or for any other purpose) may pose practical problems, because the reconstruction time increases with the size of the basis set used to represent the object (the number of elements in the reconstruction grid). This increase could be partly mitigated if computations on a fine reconstruction grid could be restricted only to those areas of the object where the improved discretisation is most likely to be beneficial (region-of-interest, ROI). One example where this approach could be applied is in reduction of Non-Linear Partial Volume effect (NLPV, also known as edge-gradient effect (De Man 2001)), in particular around metallic implants. NLPV is caused by inconsistencies in projection data arising from attenuation gradients occurring within the field of view of a single detector cell due to the logarithmic relationship between attenuation and measured intensity (Glover and Pelc 1980, Joseph and Spital 1981). NLPV is therefore an unavoidable result of using finite detector apertures, but can be alleviated if the reconstruction accounts for the process of formation of this artifact by finely discretising the object space (to better capture the image gradients) and by subsampling the detector cells (to capture the averaging of detected intensities across image gradients) (Stayman et al. 2013, Van Slambrouck and Nuyts 2012). Since the NLPV artifacts are most pronounced around high-intensity image gradients, e.g., around metallic implants, strategies where the object discretisation is made finer only in the vicinity of such structures were proposed (Stayman et al. 2013, Van Slambrouck and Nuyts, 2012). In (Van Slambrouck and Nuyts 2012), grouped coordinate ascent is employed to allow for sequential update (and associated faster convergence) of image regions with different discretisation. In (Stayman et al. 2013), a non-uniform reconstruction grid is applied within an algorithm where prior knowledge of the shape and composition of the implant (e.g., a CAD model) is used to recast the reconstruction objective function as estimation of the underlying anatomy and registration of the known implant. The discretisation of the known implant model is now easily decoupled from the discretisation on the underlying volume, allowing for significant upsampling of only the implant without incurring large computational cost.

The examples discussed above considered spatial basis functions that are most commonly used in iterative reconstruction of X-ray CT data, i.e., cubic voxels and blobs. Non-uniform discretisation could perhaps be achieved more naturally when using a polygonal mesh to represent the object (similar to finite-element analysis), as shown for emission tomography in (Brankov et al. 2004). The mesh is defined by its vertices, whose density is varied throughout the space based on the level of local image detail. This focuses the computations on the regions of highest detail, while also benefitting from a likely more compact object representation than in the case of voxel basis. It remains to be seen whether this approach could benefit IR in X-ray CT, where the image resolution and spatial detail in the reconstructed distributions is significantly higher than in emission tomography and the spectrum of detection and estimation tasks differ from those in emission tomography.

Another application benefitting from selective use of fine object discretisation is high resolution imaging of large body sites, such as the heart. In this case, high-resolution representation of only a selected ROI (e.g., the heart itself) is likely sufficient for diagnosis. Restricting the finely sampled iterative reconstruction only to this ROI would reduce computation, but cannot be achieved with standard IR algorithms because re-projections of the complete field of view are needed to compute the objective function. In (Ziegler et al. 2008), this limitation is overcome by using an initial analytical high resolution reconstruction of the complete volume (relatively computationally inexpensive) to compute projections of the volume without the ROI (masked out from the analytical reconstruction), which are then subtracted from the original data to yield projections of the ROI only, which are subsequently reconstructed with IR at high resolution. Related approaches using IR with two different voxel grids were proposed by Hamelin et al. (2007, 2010).

A situation where the complete object fills only a relatively small volume within the field-of-view (FOV) could also benefit from an approach that exploits region-of-interest discretisation. If the area of the FOV that does not contribute to the projections (i.e., air surrounding the object) can be identified inside the discretised volume through image processing techniques, the forward and back-projection could be limited only to those spatial basis functions that cover the object (attenuator), saving memory and computation time, especially if the forward and back-projector utilise pre-computed voxel footprints (Benson and Gregor 2006).

2.3. Discretisation in simulation studies

Development of reconstruction algorithms usually heavily relies on simulation studies, where projections of digital phantoms are computed and then reconstructed. Such simulation studies frequently rely on discrete representations of the object and the detector, mainly because of the flexibility of this approach in capturing the complexities of real anatomy compared to the alternative approach of analytical modelling. The assessment of reconstruction algorithms based on the results of such numerical simulations can however be biased due to the choice of the basis set used in the discretisation.

In (Goertzen et al. 2002), several phantoms were simulated using Siddon ray-tracing algorithm (Siddon 1985) and voxel image representation for a range of numbers of rays per projection pixel and voxel sizes. Filtered-back projection (FBP) reconstructions of these simulations were performed onto a voxel matrix of fixed sampling distance and examined for discretisation-induced artifacts. It was shown that to reduce discretisation-induced artifacts in the reconstructions of simulated data with realistic amounts of noise, the simulation grid sampling should be at least half of that of the reconstruction grid, and at least 4 rays should be traced per detector pixel (for the clinical CT system geometry with 1 mm). Note that the applicability of these criteria to more accurate CT simulators that include blurs due to detector aperture, focal spot size, and source-detector motion has not yet been explored in the literature.

Another form of bias caused by using discrete object and system models in numerical assessment of iterative reconstruction algorithms may arise from simply employing the same discretisation in the simulation of the test projection data as in the subsequent reconstructions, regardless of how fine that discretisation is. Having such a perfect match is sometimes referred to as the “inverse crime” (Herman and Davidi 2008, Kaipio and Somersalo 2007, Bian et al. 2013). While “inverse crime” simulations are sufficient for investigating stability, upper performance bounds, and theoretical aspects of a reconstruction algorithm (Bian et al. 2013, Sidky and Pan, 2008), they are likely to overestimate an algorithm’s performance compared to its behaviour with real data (Kaipio and Somersalo 2007). As mentioned above, such overestimation can be avoided when the discretisation in the simulation is finer than that assumed by the reconstructor, which usually involves a denser voxel grid, but often also denser detector sampling, depending on the chosen mechanism for forward projection (De Man et al. 2000, De Man et al. 2001, Nuyts et al. 1998, Zbijewski and Beekman 2004a, Elbakri and Fessler 2003a).

2.4. Summary

Discretisation of the object is an approximation that may significantly affect the output of simulations and iterative reconstruction algorithms. Artifacts are reduced by using finer discretisations, but the computation time increases accordingly. This can be mitigated by using non-uniform discretisations, using the finer grids only at the locations where it matters most. For realistic simulations, one should avoid committing the “inverse crime”.

3. Finite spatial resolution

Ignoring finite spatial resolution effects due to detector size, focal spot size, motion of the CT gantry, crosstalk and/or afterglow will result in loss of resolution, because the blurring of the data will propagate unhampered into the final reconstruction.

The implementation of a forward projection and backprojection often involves some interpolation, which in turn can yield some blurring effects. In analytical reconstruction, this causes a blurring of the reconstructed image, unless it is compensated by adjusting the ramp filter. In contrast, in iterative reconstruction, the blurring will be iteratively inverted, resulting in a sharper image. However, the true blurring is usually more severe than the blurring due to interpolation, and additional work is needed for a proper compensation.

3.1. Stationary PSF

An easy model is to assume a stationary point spread function, which is modelled either as a convolution in the projection domain (typically blurring the views, but not along the angles) or as a 3D convolution in image space. The blurring kernel is typically chosen to be Gaussian, with a different standard deviation in axial and transaxial directions. This model has been applied also as a sinogram precorrection method (Carmi et al. 2004, Rathee et al. 1992) and as a correction applied after reconstruction (Rathee et al. 1992, Wang et al. 1998). The precorrection method has the advantage that the known noise properties of the data can be taken into account (La Rivière 2006).

3.2. Voxel footprints

As mentioned above, a voxel footprint is the (position dependent) projection of a voxel on the detector. Projectors based on such a footprint usually take into account the geometry of the divergent beam and the finite detector size. Doing so, they account for the related blurring, which would be ignored when simple ray tracing were used. An additional advantage of footprint based (back)projectors is that they avoid the creation of Moiré patterns which are often produced by algorithms derived with straightforward discretisation (De Man and Basu 2004).

The footprint depends on the basis function assumed for the voxel. For traditional pixels, De Man and Basu (2004) proposed the “distance driven projector”, where the projection of a voxel is approximated with a rectangular profile both in transaxial and axial direction. Long et al. (2010) extended this to a trapezoidal shape, which enables more accurate modelling for projection lines obliquely intersecting the voxel grid. Examples of other basis functions are the blobs (Lewitt 1992) discussed above, and a related approach using Gaussian blobs, also called “sieve”, as proposed by Snyder and Miller (1985). Matej and Lewitt (1996) reported that the use of blobs results in less noisy images when compared to the traditional pixel grid. However, the width of the blob should be less than the spatial resolution of the data, otherwise overshoots near the edges are created. In these approaches, the blob or sieve could be regarded as a stationary resolution model, while the reconstructed image converges to the ideal image, convolved with the point spread function.

3.3. Detector crosstalk and afterglow

Detector crosstalk results in a blurring of adjacent detector signals within the same view. Detector afterglow causes blurring from the detector signal of a particular view into the signal of the same detector in the next view(s). It seems relatively straightforward to extend the footprint approach, which already models the finite detector size, to model the crosstalk between adjacent detectors as well. One can either convolve the computed sinogram views with a convolution kernel (Thibault et al. 2007), or enlarge the detectors into overlapping virtual detectors (Zeng et al. 2009a) during footprint computation. These techniques correspond to the following model (ignoring scatter, i.e. s_i = 0, see (2)):

$$Y_i=b_i{e}^{-{\sum }_d{g}_{id}{\sum }_j{l}_{dj}{\mu }_j},$$ (3)

where g represents the crosstalk kernel. This involves an approximation, because the blurring due to crosstalk and afterglow is between the detected photons, not between the attenuation values. Extending (1) with the crosstalk smoothing kernel g yields

$$Y_i=\sum _d{g}_{id}{b}_d{e}^{-{\sum }_j{l}_{dj}{\mu }_j}.$$ (4)

A maximum-likelihood algorithm for this model has been proposed by Yu et al. (2000) and was used in Feng et al. (2006) and Little and La Rivière (2012). In this last paper, reconstruction based on the non-linear model (4) did not outperform reconstruction using the linear model (3) in simulations with the FORBILD phantom. Kernel g can represent detector crosstalk as well as the effect of detector afterglow. However, because afterglow involves adjacent views, modelling it as blurring over angles is not compatible with the ordered subsets approach. Forthmann et al. (2007) discuss issues about the correct definition of kernel g for afterglow correction in dual focal spot CT systems.

Note that ML algorithms assume that Y_i in (4) is Poisson distributed. However, the afterglow and (at least part of) the crosstalk occur after the X-rays interacted with the detector, and therefore they cause noise correlations. It would be more accurate to assume uncorrelated noise before the smoothing kernel g is applied (La Rivière et al. 2006).

3.4. Finite source size

The finite size of the focal spot of the X-ray tube can be modelled by subsampling, i.e., by representing the source as a combination of point sources. Applying that to (4) results in

$$Y_i=\sum _d{g}_{id}{Y}_d^{\prime }\text{with}{Y}_i^{\prime }=\sum _s{b}_{is}exp\left(-\sum _j{l}_{ij}^s{\mu }_j\right),$$ (5)

where b_is represents the X-rays sent from the source in position s to detector i, and $l_{ij}^s$ is the beam geometry for that particular point source. Based on this model, reconstruction algorithms for maximum likelihood (Browne et al. 1995, Yu et al. 2000, Bowsher et al. 2002, Little and La Rivière 2012) and simultaneous algebraic reconstruction (SART) (Yu and Wang 2012) have been proposed. Browne et al. (1995) did not use a footprint approach, but represented the detectors by subsampling those as well, using ray tracing between all detector points and source points. Note that the apparent focal spot size may be different for different positions on the detector due to the anode angulation (La Rivière and Vargas 2008).

Because each point source has its own projection matrix, algorithms based on these models need to compute forward and backprojections for every point source in every iteration. For that reason, some authors use a simpler model, like (4), with a kernel g that is designed to include effects of the finite focal spot size as well (Feng et al. 2006). In 2D, this can be a good approximation if there are many views and small detectors, because then eccentric point source positions in one view will correspond with good accuracy to a central point source position in another view (La Rivière and Vargas 2008).

3.5. Fit a model to known resolution loss

Instead of modelling the physics accurately, some authors prefer to create a model that accurately mimics the effective resolution loss. One advantage is that this can be tuned with measurements or Monte Carlo simulations, including all possible effects contributing to resolution loss.

Feng et al. (2006) used the model of (4) for SPECT transmission scanning with sources of finite size. Michielsen et al. (2012) used a position dependent version of (4) to compensate for resolution loss due to tube motion in tomosynthesis. Zhou and Qi (2011) proposed to accurately measure the projection matrix, and then model it as a combination of sinogram blurring, ideal projection and image blurring. The combination of these three operators offers enough flexibility to obtain a good fit, while their sparsity allows fast computation times.

3.6. 2D simulation

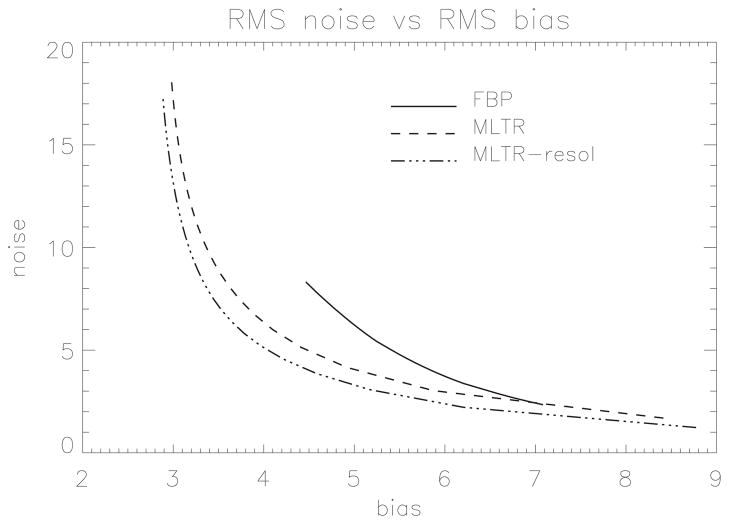
A 2D CT acquisition was simulated, assuming a perfect point source but detectors with finite width and suffering from significant cross talk: each detector detected 11.3% from the X-rays arriving in its neighbours. The focus-detector distance was 100 cm, the distance between focus and rotation centre was 55 cm, there were 300 detectors with a size of 1.5 mm. The acquisition consisted of 1000 views, with monochromatic 70 keV X-rays and 40000 photons sent to every detector. The object was a disk consisting of fat, containing 35 rings with soft tissue attenuation and two disks consisting of bone. To avoid the “inverse crime” during simulation, the object was represented in a matrix of 1952 × 1952 (pixel size 0.125 mm), and 5 rays per detector element were computed. The resulting sinogram was reconstructed in a matrix of 488 × 488 (pixel size 0.5 mm) with three algorithms: filtered backprojection (FBP), a maximum likelihood algorithm for transmission tomography without (MLTR) and with (MLTR-resol) resolution recovery using (4). The ML-algorithms did not use regularisation, and up to 40 iterations with 50 subsets each were applied. Simulations with and without Poisson noise were done. The phantom and two noisy reconstructions are shown in figure 2. The bias was estimated as the square root of the mean squared difference (RMS) between the noiseless images and the true object. The noise was estimated as the RMS between the noisy and noise-free images for each algorithm. A bias-noise curve was obtained by post-smoothing the FBP image with a Gaussian kernel with varying width, and by varying the iteration number for MLTR. The result is shown in figure 3. When compared to FBP, MLTR obtains lower bias for the same noise level, thanks to its more accurate noise model. Incorporation of the resolution model yields a further improvement. The iterative algorithms can reach lower bias levels than FBP, in particular when the finite resolution is modeled.

Figure 2.

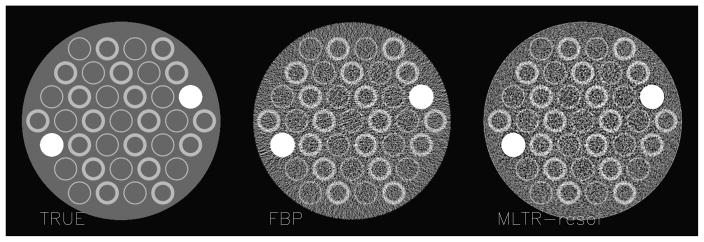
An example from the 2D simulation, showing the true attenuation image, and the reconstruction from FBP and from ML with resolution recovery in the presence of noise.

Figure 3.

The noise versus bias for FBP, MLTR and MLTR with resolution recovery. The curves are generated by varying the number of iterations for MLTR, and by varying the width of a Gaussian post-smoothing filter. RMS bias and noise are expressed as % of the background attenuation.

3.7. Summary

Accurate modelling of the finite resolution effects increases the computation time, because it requires multiple samples over the detectors and the focal spot. However, good results have been reported with approximate models that basically replace increased sampling with well-chosen smoothing operations during the computations. The use of such models improves the achievable tradeoff between bias and noise.

4. X-ray scatter

Detection of X-rays that have scattered in the object to be reconstructed can result in significant image quality degradation. Both management of scatter and correction of scatter-induced artifacts have been steadily growing in importance in X-ray CT. This is due to continuing increase of the axial coverage of modern multi-detector CT scanners and, perhaps more significantly, due to the introduction of large area digital solid-state detectors (e.g. flat-panel detectors, CCD cameras) for X-ray tomography and the rapid proliferation of such cone-beam CT (CBCT) devices in clinical, pre- clinical and material testing applications. Deleterious effects of X-ray scatter in CT reconstructions include cupping and streak artifacts, decreased contrast and resolution, and decreased image contrast-to-noise (Johns and Yaffe 1982, Joseph and Spital 1982, Glover 1982, Endo et al. 2001, Siewerdsen and Jaffray 2001, Kyprianou et al. 2005, Colijn et al. 2004, Zbijewski and Beekman 2006b).

While scatter can be partially mitigated by judicious selection of imaging geometry, e.g. by using long air gaps (Neitzel 1992, Siewerdsen et al. 2004), or by direct rejection with anti-scatter grids, the level of achievable scatter removal is often limited by other image quality considerations (e.g. the increase in dose needed to compensate for primary attenuation in a grid while maintaining full spatial resolution (Siewerdsen et al. 2004, Neitzel 1992, Kwan et al., 2005)), design constraints, and cost of devices (e.g. need of larger detectors and gantry when using gaps) and thus many volumetric CT systems will require additional software scatter correction.

In iterative statistical reconstruction, scatter is often included in the measurement model as an additive, known a priori term representing the mean amount of scatter per detector pixel (s_i in eq (1) and (2)). While accounting for the scatter is straightforward (especially for Poisson noise model (1), where the projection data is never log-corrected, and thus the additive nature of scatter is maintained throughout reconstruction), estimating the required mean scatter background accurately and efficiently remains challenging. A variety of scatter estimation techniques have been developed to aid correction in radiography and in analytical CT reconstruction, where a scatter estimate is typically subtracted from measured projections as a pre-processing step (Glover 1982). Iterative (statistical) methods have the potential to improve over simple subtraction-based scatter pre-correction because (i) they inherently better handle projection noise (and negative projection values) for cases with high scatter-to-primary ratios and low signal levels, and (ii) by its design, statistical reconstruction process consists of iterative computation of image estimates and their reprojections, which can be readily modified to incorporate simulation of scatter contribution from the latest image estimate instead of using a fixed guess for the scatter term. Despite these potential advantages, only few papers to date report on inclusion of scatter estimates in iterative reconstruction (Elbakri and Fessler 2003a, Zbijewski and Beekman 2006b, Jin et al. 2010, Wang et al. 2010, Evans et al. 2013), and future research is needed to evaluate the gains in image quality and identify clinical applications most likely to benefit from this approach. The following review summarises scatter estimation methodologies currently in use in CT imaging (a recent, more in-depth survey of scatter correction methodologies can be found in (Ruhrnschopf and Klingenbeck 2011a, 2011b), recognising that all of them could potentially be implemented in the iterative framework, but only a small subset has already been applied and validated in this context. Three broad categories of methods are considered: (i) scatter measurement techniques, (ii) analytical methods for estimating scatter from projection data, and (iii) simulation of the scatter component from an (intermediate) object/patient representation. The approaches in the first two categories are employed as pre-correction in analytical CT reconstruction, but could also provide a fixed scatter guess for statistical reconstruction. The approaches in the third category naturally fit in iterative reconstruction: the scatter estimates will improve with the improving quality of the successive image estimates. Considering also that very accurate simulation techniques exist (e.g. Monte Carlo), the combination of iterative reconstruction with scatter simulation is an attractive avenue for scatter correction.

4.1. Physical scatter measurements

Typically, experimental measurements of X-ray scatter exploit some form of beam blockers placed in front of the X-ray source and before the object. Detector signals directly behind the blocker are assumed to be mainly scattered photons (neglecting effects such as off-focal radiation and blocker penetration). Various experimental designs have been proposed, ranging from extrapolation of measurements in the shadow of tube collimators (Siewerdsen et al. 2006) to beam blocker arrays extending across the projection image. In the latter case, the main practical concern is to alleviate the need for a double scan (one with the blocker array to estimate scatter, one without the blocker array to measure the total signal everywhere in the detector plane). This can be achieved through acquisition of only a small subset of projections with the blocker in place and computation of the global scatter estimate by interpolation (Ning et al. 2004), by using blockers only in a first of a sequence of scans (prior scan - e.g. in the monitoring of radiation therapy treatment) (Niu et al. 2012), by employing moving blockers (Liu et al. 2005, Zhu et al. 2005, Jin et al. 2010, Wang et al. 2010), or by exploiting data redundancy in the design of blocker pattern (Niu and Zhu 2011, Lee et al. 2012). Novel variations on the concept of beam blocker measurements include a complementary method where a collimator (beam pass) creates pencil beams at the entrance to the object that induce negligible scatter and thus provide estimates of primary signal (Yang et al. 2012, Sechopoulos 2012), or using an array of semi-transparent (instead of opaque) blockers that modulate the primary distribution so that Fourier techniques can be used to separate scatter and primary signals (Zhu et al. 2006).

Scatter estimates obtained through the experimental methods described above can be included in statistical reconstruction as the background scatter term, which in this case remains fixed throughout the iterations. In addition, since iterative reconstruction methods are inherently better suited to handling scanning geometries with missing data (Zbijewski and Beekman 2004b, Bian et al. 2010), they could potentially be applied to projections obtained with beam blockers without the need for interpolation in blocker shadows, such as presented in (Jin et al. 2010, Wang et al. 2010) for the case of full rotation CBCT with moving beam stop array. Furthermore, statistical reconstruction methods can somewhat mitigate the increase in image noise that accompanies correction by simple subtraction of measured scatter estimates (Wang et al. 2010).

4.2. Analytical scatter models

Scatter estimation by means of computational models provides an alternative to direct physical measurements in that it does not require modifications to scanner equipment or increase in imaging dose. In their simplest form, such computational models represent the scatter fluence as a constant across the projection plane, assuming the same value for entire scan (Glover 1982) or different values for individual views (Bertram et al. 2005). A potentially more accurate approach models the scatter as a point spread function (kernel) applied to primary fluence and tries to estimate the scatter from projection data (scatter+primary) by deconvolution (Love and Kruger 1987, Seibert and Boone 1988). The knowledge of the scatter kernel is essential for this deconvolution; the kernels are usually assumed to depend on object thickness (estimated locally based on water equivalent projections) and are either measured (Li et al. 2008) or pre-simulated with Monte Carlo (MC) methods (Maltz et al. 2008, Sun and Star-Lack 2010). A somewhat related analytical model (Yao and Leszczynski 2009) separates the scatter distribution into object-dependent terms that are captured by the primary intensity, and terms which are independent of the object and thus can be pre-computed; primary is iteratively estimated from measured projection using this model. Other possible analytical approaches involve approximating the object by a simple ellipsoid, for which scatter can be either pre-computed or estimated at relatively low cost using MC simulations (Bertram et al. 2006), a hybrid method combining this approach with scatter kernels (Meyer et al. 2010), and algorithms utilising calibration scans to establish relationships between scatter properties of typical objects (e.g. spatial distribution of scatter-to-primary ratio) and some basic parameters accessible in projection images or raw reconstructions (e.g. local breast diameter) in a manner allowing for interpolation of a scatter estimate for any new projection dataset (Cai et al. 2011).

4.3. Iterative scatter estimation from reconstructions: Monte Carlo methods

Both the experimental and computational methods of scatter estimation described above suffer from a number of simplifying assumptions and thus yield approximate results. Despite this, remarkably accurate scatter correction can usually be achieved with such methods, largely due to the often smooth, slowly varying nature of scatter distributions. There is however growing evidence that under certain imaging conditions (e.g. high scatter-to-primary ratio, presence of an anti-scatter grid, or metal objects in the patient), significant heterogeneity may be introduced into the scatter distribution and thus more accurate scatter estimates may be needed to achieve complete artifact correction and maximise improvement of quantitative accuracy (Mainegra-Hing and Kawrakow 2010, Zbijewski et al. 2012). Monte Carlo simulations are a likely candidate to provide such high-fidelity estimates although computational load of calculations used to be a limitation. Compared to the analytical methods described above, MC-based approaches utilise reconstructed images or image estimates during iterative reconstruction instead of projections to compute scatter. Initial reconstruction is computed from scatter-contaminated data, segmented and employed for MC simulation of scatter (re-projection). The thus obtained scatter estimate is used to compute a new reconstruction with reduced level of scatter-induced artifacts and the process of MC scatter computation and reconstruction can be iterated until satisfactory correction has been obtained. This framework readily fits into the statistical reconstruction process, where image estimates are also obtained iteratively and computation of successive image updates (that can be used as input for MC scatter simulation) is an inherent part of the algorithm.

Until recently, the long computation times associated with low noise MC simulations remained the major limitation of MC-based scatter correction. Encouraging developments in MC acceleration suggest however that practical implementation of Monte Carlo scatter estimation is achievable. One approach to MC acceleration involves the application of the so-called variance reduction techniques (e.g. forced detection, Woodcock tracking, interaction splitting), which, when optimised for simulation of X-ray scatter, can potentially result in 10–100× reduction of computation time necessary to reach a given level of noise (Mainegra-Hing and Kawrakow 2010). Such methods can be further supplemented by techniques that exploit the smoothness of X-ray scatter fields (to the extent that the particular imaging scenario supports such assumption) to simplify or de-noise the MC simulations. For example, one can reduce the number of simulated photons and rely on either (i) model-based fitting of smooth surfaces in the projection plane to reduce the noise in the resulting scatter estimates (Colijn and Beekman 2004, Jarry et al. 2006), or on (ii) forcing the photons from each interaction to a fixed, small number of nodes in the projection plane and interpolating between them to obtain the complete distribution (Poludniowski et al. 2009). Furthermore, since the scatter varies slowly between the projections (angularly), one could either combine these approaches with simulating only a subset of projections, or exploit this angular smoothness by further reducing the number of tracked photons and fitting a smooth three dimensional scatter distribution to the stack of noisy MC-simulated projections (Zbijewski and Beekman 2006b, Bootsma et al. 2012). In (Zbijewski and Beekman 2006b), a 3D fit that included the angular dimension reduced simulation time by 3–4 orders of magnitude (depending on the desired simulation error) compared to fitting only in the projection plane; this level of acceleration may be difficult to achieve by methods that rely only on reducing the number of simulated projection angles. Poly-energetic statistical reconstruction (Elbakri and Fessler 2003a) was combined with accelerated MC utilising a combination of variance reduction, and de-noising by means of a three dimensional Richardson-Lucy fit (Richardson 1972, Lucy 1974) to provide scatter correction for cone-beam micro-CT (Zbijewski and Beekman 2006b). Estimation of water density was improved from 12% to 1% after 2 cycles of MC scatter correction. Another recently proposed acceleration strategy combines an analytical model of 1st-order scatter with a coarse MC simulation of the typically homogeneous higher-order scatter (Kyriakou et al. 2006). Advances in computer hardware are also likely to play an important role in reducing the computation times of MC scatter estimation to levels acceptable in clinical practice. One important recent development is the implementation of MC simulation of X-ray photon propagation on graphics processing units (GPUs) (Badal and Badano 2009). A 27-fold acceleration over single-CPU implementation has been reported, indicating the potential for fast simulation environment within standard desktop PC.

It is possible to combine some of the above mentioned methods to enable additional speed-ups of scatter re-projection. Also several very fast scatter estimation methods have been proposed for emission tomography that have not been tested yet in transmission CT. Potentially interesting are methods to accurately model effects of object non-uniformity on scatter re-projection S^nu when low noise scatter projections of uniform objects S^u are already known or can be calculated quickly and accurately with e.g. the above mentioned analytical methods (Li et al. 2008, Maltz et al. 2008, Sun and Star-Lack 2010, Bertram et al. 2006). Using Correlated Monte Carlo methods (Spanier and Gelbard 1969), such a scatter estimate can then be rapidly transformed to the scatter projection of a non-uniform object by scaling it with a ratio of MC simulations of the non-uniform object $S_{MC}^{nu}$ and the uniform object $S_{MC}^u$, both obtained with only a very low number photon tracks ( $S^{nu}=S^u\times S_{MC}^{nu}/S_{MC}^u$), but in which correlated noise partly cancels out during division, as has been shown for SPECT scatter modelling (Beekman et al. 1999).

All scatter correction methods that are based on simulation of scatter from reconstruction (re-projection) are potentially prone to errors due to truncation of the true object volume caused by limited field-of-view of the system, cone-beam artifacts, and the choice of the reconstructed region of interest. While some authors have shown that restricting the MC simulation only to the region of the object directly illuminated by the X-ray beam is sufficient for achieving accurate scatter estimates (Zbijewski and Beekman 2006b), there may be circumstances when significant portions of this irradiated volume cannot be reconstructed, e.g. for interventional C-arm systems which often exhibit lateral truncation. In such cases, a likely solution is some form of model-based, virtual “extension” of the reconstructed object during the MC simulation (Bertram et al. 2008, Xiao et al. 2010).

4.4. Summary

Modelling the scatter contribution is becoming more important due to the increasing detector size, and in particular for cases where no anti-scatter grids can be used. Ingenious hardware modifications have been invented for measuring the scatter. Analytical models have been proposed as well, and due to software and hardware improvements, it becomes feasible to estimate the scatter with accurate Monte Carlo simulation techniques during iterative reconstruction. Further improvements of accuracy and computation times are possible by combining complementary existing methods and by better exploiting the potential of iterative reconstruction.

5. Noise models and the energy spectrum

Noise models for X-ray CT measurements are important (Whiting 2002, Whiting et al. 2006) for statistical image reconstruction methods (particularly for low-dose scans), for performing realistic simulations of CT scans, for adding noise to CT measurements to “synthesise” lower dose scans, and for designing sinogram data compression schemes (Bae and Whiting 2001). For photon counting detectors, the measurements have simple Poisson distributions provided dead-time losses are modest (Yu and Fessler 2000, Yu and Fessler 2002), although pulse pileup can complicate modelling for detectors with multiple energy bins (“spectral CT”) (Taguchi et al. 2012, Srivastava et al. 2012, Heismann et al. 2012). However, for transmission imaging systems that use current integrating detectors, such as current clinical X-ray CT systems, the measurement statistics are considerably more complicated than for the ideal photon counting case. There are numerous sources of variability that affect the measurement statistics, including the following.

• Usually the X-ray tube current fluctuates slightly (but noticeably) around its mean value.

• For a given X-ray tube current, the number of X-ray photons transmitted towards a given detector element is a random variable, typically modelled by a Poisson distribution around some mean.

• The energy of each transmitted photon is a random variable governed by the source spectrum.

• Each transmitted photon may be absorbed or scattered within the object, which is a random process.

• X-ray photons that reach a given detector element may interact with it, or may pass through without interacting.

• An X-ray photon that interacts with the detector can do so via Compton scattering and/or photoelectric absorption.

• The amount of the X-ray photon’s energy that is transferred to electrons in the scintillator is a random variable because the X-ray photon may scatter within the scintillator and then exit having deposited only part of its energy,

• The energised electrons within the scintillator produce a random number of light photons with some distribution of wavelengths.

• The conversion of light photons into photoelectrons involves random processes.

• Electronic noise in the data acquisition system, including quantisation in the analog-to-digital converters that yield the final (raw) measured values, adds further variability to the measurements.

The following diagram summarises most of these phenomena.

The overall effect of all of these sources of variability is that (i) the raw data variance is not equal to the mean, and (ii) there can be negative apparent transmission values (after correcting for ADC offset and dark current) for low X-ray intensities. Both of these properties differ from the Poisson variates associated with counting statistics. We now examine these random variations in more detail to help develop statistical models for X-ray CT. (See also (Lei 2011: Ch. 5.2).) For simplicity, we focus on the situation where the X-ray source does not move but where we acquire repeated scans of an object. This scenario is useful for validating statistical models experimentally.

5.1. X-ray tube current fluctuations

Often X-ray CT systems include deliberate tube current modulation to reduce X-ray dose while maintaining image quality (Gies et al. 1999, Kalender et al. 1999, Greess et al. 2000, Hurwitz et al. 2009, Angel et al. 2009). In addition to these intentional changes in tube current, in practice the X-ray tube current fluctuates continuously like a random process. Therefore the number of transmitted photons fluctuates between projection views more than would be predicted by Poisson statistics alone. This fluctuation affects the entire projection view, leading to slight correlations between the measurements in a given view, even after correction using reference measurements. In contrast, most of the other random phenomena are independent from view to view and even from ray to ray, consistent with the usual assumption of independence used by image reconstruction algorithms. (The mean effect of these fluctuations can also be corrected using suitable statistical image reconstruction methods (Thibault 2007, Nien and Fessler 2013).) Much of the literature on noise statistics in X-ray imaging has been focused on radiography where there is only a single exposure so tube current fluctuations have been unimportant. For conciseness we also ignore these fluctuations here, though they may be worth further investigation in future work.

5.2. Transmitted photons

For a given tube current, the number of photons N_i transmitted towards the ith detector element is a random variable having a mean N̄_i that is proportional to the tube current. The mean N̄_i is ray dependent due to the geometrical factors relating emission from the X-ray source to the detector position including X-ray tube angulation and detector solid angle, as well as bowtie filters and the heel effect (Whiting et al. 2006). For a given tube current, it is widely hypothesised that the number of transmitted photons has a Poisson distribution, i.e.,

$$N_i~\text{Poisson}\{{\overline{N}}_i\},i.e.,\text{P}\{N_i=n_i\}={\text{e}}^{-{\overline{N}}_i}{({\overline{N}}_i)}^{n_i}/n_i!,n_i=0,1,\dots .$$ (6)

The variance of N_i equals its mean: Var{N_i} = N̄_i. It is also reasonable to assume that {N_i} are all statistically independent for a given tube current.

5.3. X-ray photon energy spectra

For practical X-ray sources, the transmitted photons have energies ε that are random variables governed by the source spectrum. Because of geometrical effects such as anode angulation (La Riviére and Vargas 2008) and bowtie filters (Toth et al. 2005), the X-ray photon energy distribution can be different for each ray. Let p_i(ε) denote the energy distribution for the ith ray, which has units of inverse keV. This distribution depends on the X-ray source voltage, which we assume to be a fixed value such as 120 kVp. (For certain scans that use fast kVp switching the spectrum varies continuously (Zou and Silver 2008, Xu et al. 2009) and it can be important to model this effect.) The energy of each of the N_i X-ray photons that are transmitted towards the ith detector is drawn independently (and identically for a given i) from the distribution p_i(ε).

5.4. X-ray photon interactions in the object

For an X-ray photon with energy ε that is transmitted towards the ith detector element, the survival probability that the photon passes through the object without any interactions in the object is given by the Lambert-Beer law:

$${\text{e}}^{-{\int }_{{\mathcal{L}}_i}\mu (\overrightarrow{\text{x}},\mathcal{E})\text{d}\ell },$$ (7)

where the line integral is along the path 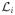between the X-ray source and the ith detector element, and μ(x⃗, ε) denotes the linear attenuation coefficient of the object at position x⃗ and for energy ε. The survival events for each photon are all statistically independent. Let M_i denote the number of X-ray photons that reach the ith detector element without interacting within the object. For a given tube current, the {M_i} are statistically independent Poisson random variables with mean

$${\text{E}}_{\mu }[M_i]={\overline{N}}_i{\rho }_i(\mu ),$$ (8)

where the survival probability of an X-ray photon is

$${\rho }_i={\rho }_i(\mu )={\int }_0^{{\mathcal{E}}_{max}}{\text{e}}^{-{\int }_{{\mathcal{L}}_i}\mu (\overrightarrow{\text{x}},\mathcal{E})\text{d}\ell }{\text{p}}_i(\mathcal{E})\text{d}\mathcal{E}.$$ (9)

For a polyenergetic source, we must consider the X-ray source spectrum because photons of different energies have different survival probabilities.

5.5. X-ray photon interactions in detector, scintillation, and photo-conversion

The ideal photon counting X-ray detector (PCXD) would count every (unscattered) X-ray photon that is incident on it, i.e., the recorded values would be {M_i}. In practice, when an X-ray photon is incident on a detector element, there are several possible outcomes. The photon may pass through the detector without interacting and thus fail to contribute to the recorded signal. Similar to (7), the probability of failing to detect is e^{−d_sμ_s(ε)} where d_s denotes the scintillator thickness and μ_s denotes its (usually large) linear attenuation coefficient. The scintillators used in X-ray detectors are usually high Z materials, so it is likely that the X-ray photon will transfer all of its energy to an electron in the scintillator by photoelectric absorption. It is also possible for the X-ray photon to undergo one or more Compton scatter interactions and then either exit the detector element or deposit its remaining energy in a final photoelectric absorption. These interactions are random phenomena and their distributions depend on the X-ray photon energy. For example, higher energy photons are more likely to escape the detector element without interacting.

For an incident X-ray photon of energy ε, the amount of its energy deposited within the detector is a random variable having a quite complicated distribution over the range from 0 to ε. The electrons that are energised by the X-ray photon can release their energy in several ways including emitting light photons and by interacting with other electrons, some of which in turn produce light photons. The number of light photons produced and the wavelengths of those photons depends on the type of electron interactions. Although it may be convenient to approximate the number of light photons as having a Poisson distribution, e.g., (Elbakri and Fessler 2003b), this can be only an approximation because the number of light photons has a maximum value that depends on ε.

Some of the light produced in a scintillator will reach the photosensitive surface of the photosensor (typically a photodiode (Boyd 1979, Takahashi et al. 1990)). Depending on the quantum efficiency of the photosensor, some fraction of these light photons will produce photoelectrons that contribute to the recorded signal.

Ideally, each X-ray photon interaction in a detector element would produce the same number, say K, photoelectrons (De Man et al. 2007, Iatrou et al. 2007); these would then be recorded with additional electronic noise, and (ignoring A/D quantisation) a reasonable measurement model would be the popular “Poisson+Gaussian” model (Snyder et al. 1993, 1995, Ma et al. 2012):

$$Y_i^{\text{raw}}~K\text{Poisson}\{{\text{E}}_{\mu }[M_i]\}+\text{N}({\mu }_{{\epsilon }_i},{\sigma }_{{\epsilon }_i}^2),$$ (10)

where μ_εi represents the dark current of the ith channel and ${\sigma }_{{\epsilon }_i}^2$ the electronic noise variance. In this case we correct the measurements for the dark current and gain K:

$$Y_i\triangleq (Y_i^{\text{raw}}-{\mu }_{{\epsilon }_i})/K$$

for which the moments are

$$\text{E}[Y_i]={\text{E}}_{\mu }[M_i],\text{Var}\{Y_i\}={\text{E}}_{\mu }[M_i]+{\sigma }_{{\epsilon }_i}^2/K^2.$$

The dispersion index of the corrected measurement Y_i, the ratio of its variance to its mean, would be

$$\frac{\text{Var}\{Y_i\}}{\text{E}[Y_i]}=1+\frac{{\sigma }_{{\epsilon }_i}^2}{K^2{\text{E}}_{\mu }[M_i]}.$$

Being larger than unity, this is called over dispersion.

In practice, the number of photoelectrons produced by an X-ray photon is a random variable whose distribution depends on ε. When M_i X-ray photons are incident on the ith detector element, let K_im denote the number of photoelectrons produced by the mth X-ray photon, for m = 1,…, M_i. We assume that {K_im} are statistically independent random variables with distributions

$${\text{P}}_{\mu }\{K_{im}=k\}={\int }_0^{{\mathcal{E}}_{max}}\text{P}\{K_{im}=k\mid {\mathcal{E}}_{im}=\mathcal{E}\}{\text{q}}_i(\mathcal{E};\mu )\text{d}\mathcal{E},$$ (11)

where ε_im denotes the energy of the mth X-ray photon incident on the ith detector element and where the energy distribution of X-ray photons that passed through the object without interacting is

$${\text{q}}_i(\mathcal{E};\mu )=\frac{{\text{p}}_i(\mathcal{E}){\text{e}}^{-{\int }_{{\mathcal{L}}_i}\mu (\overrightarrow{\text{x}},\mathcal{E})\text{d}\ell }}{{\int }_0^{{\mathcal{E}}_{max}}{\text{p}}_i({\mathcal{E}}^{\prime }){\text{e}}^{-{\int }_{{\mathcal{L}}_i}\mu (\overrightarrow{\text{x}},{\mathcal{E}}^{\prime })\text{d}\ell }\text{d}{\mathcal{E}}^{\prime }}=\frac{{\text{p}}_i(\mathcal{E}){\text{e}}^{-{\int }_{{\mathcal{L}}_i}\mu (\overrightarrow{\text{x}},\mathcal{E})\text{d}\ell }}{{\rho }_i(\mu )},$$ (12)

where ρ_i was defined in (9). The total number of photoelectrons produced in the ith photosensor is

$$K_i=\sum _{m=1}^{M_i}{K}_{im},i=1,\dots ,n_{\text{d}}.$$ (13)

The ideal electronic readout system would record the value of K_i for each detector element. One can show that the moments of K_i are

$${\text{E}}_{\mu }[K_i]={\text{E}}_{\mu }[M_i]{\text{E}}_{\mu }[K_{im}]$$ (14)

$${\text{Var}}_{\mu }\{K_i\}={\text{E}}_{\mu }[M_i]{\text{E}}_{\mu }[K_{im}^2].$$ (15)

Rearranging yields the following nonlinear relationship between the variance and the mean of K_i:

$${\text{Var}}_{\mu }\{K_i\}={\text{E}}_{\mu }[K_i]\left(\frac{{\text{E}}_{\mu }[K_{im}^2]}{{\text{E}}_{\mu }[K_{im}]}\right).$$ (16)

The parenthesised ratio quantifies the dispersion due to variability in the number of photoelectrons produced by each X-ray photon. This ratio is related to the reciprocal of the “statistical factor” or Swank factor derived in (Swank 1973) and investigated in (Ginzburg and Dick 1993, Blevis et al. 1998). The reciprocal is also related to the noise equivalent quanta (NEQ) (Whiting 2002: eqn. (6)).

The sum (13) greatly complicates statistical modelling of X-ray CT measurements, both because the number M_i of elements in the sum is a (Poisson) random variate, and the distribution of K_im is quite complicated. This makes it essentially intractable to find realistic log-likelihoods, even in the absence of electronic noise and quantisation. The value of K_im depends on how the X-ray photon interacts with the detector (photoelectric absorption, or one or more Compton scatter events or combinations thereof) and depends also on the energy ε. Thus the distribution of K_im is a mixture of numerous distributions. One simple model assumes every (recorded) X-ray photon has a single complete photoelectric absorption, and that the number of photoelectrons produced has a Poisson distribution whose mean is γε for some gain factor γ. Under this model, (11) “simplifies” to the following mixture distribution:

$${\text{P}}_{\mu }\{K_{im}=k\}={\int }_0^{{\mathcal{E}}_{max}}\frac{1}{k!}{(\gamma \mathcal{E})}^k{\text{e}}^{-\gamma \mathcal{E}}(1-{\text{e}}^{-d_{\text{s}}{\mu }_{\text{s}}(\mathcal{E})}){\text{q}}_i(\mathcal{E};\mu )\text{d}\mathcal{E},$$ (17)

where d_s and μ_s(ε) denote the thickness and linear attenuation coefficient of the scintillator. This model leads to the compound Poisson distribution considered in (Whiting 2002, Elbakri and Fessler 2003b). Even though this model is already complicated, it is still only an approximation because it ignores many effects; for example, lower energy X-ray photons are more likely to interact near the entrance surface of the scintillator, which is usually farthest from the photosensor so the optical gain is lowest. This depth dependence implies that the gain parameter γ should be a function of ε. Accurate modelling usually involves Monte Carlo simulations (Badano and Sempau 2006).

As a more tractable approach, Xu and Tsui (2007, 2009) proposed an exponential dispersion approximation (Jorgensen 1987) for which Var{K_i} = φ(E_μ[K_i])^p where p > 1 and φ > 0 is the dispersion parameter.

5.6. Electronic readout noise

Fluctuations in the leakage current of the photosensor and noise in the preamplifier input (Knoll 2000 p. 288), often called electronic noise, add additional variability to the recorded values. A reasonable model for the raw recorded values is

$$Y_i^{\text{raw}}={\alpha }_i(K_i+{\stackrel{\sim }{\epsilon }}_i),$$

where α_i is a scale factor that depends on the gain of the preamplifier and A/D converter, and ε̃_i is modelled as additive white Gaussian noise (AWGN) with mean ε̄_i and standard deviation σ_ε. The mean ε̄_i is related to the mean dark current of the photosensor and to the offset of the A/D converter; these factors can be calibrated so we assume ε̄_i is known. Similarly we assume that the gain α_i is known through a calibration process. We correct for these deterministic factors as follows:

$$Y_i\triangleq \frac{1}{{\alpha }_i}{Y}_i^{\text{raw}}-{\overline{\epsilon }}_i=K_i+{\epsilon }_i,$$ (18)

where now the (scaled) electronic noise is zero mean: ${\epsilon }_i~\text{N}(0,{\sigma }_i^2)$ and where now the standard deviation σ_i = σ_ε/α_i has units of “photoelectrons.” Clearly the statistics of Y_i are at least as complicated as those of K_i.

5.7. Post-log statistics

FBP and PWLS image reconstruction methods use the logarithm of the offset-corrected data (18):

$$y_i=log\left(\frac{b_i}{Y_i}\right),$$ (19)

where

$$b_i=\text{E}[N_i]{\text{E}}_0[K_{im}]$$ (20)

comes from an air scan or blank scan with no object present, with a high X-ray flux so that the SNR is large, and where E₀ denotes expectation when μ = 0. For a polyenergetic spectrum one must correct y_i for beam hardening.

Using a first-order Taylor expansion, the variance of the log sinogram y_i is approximately

$$\text{Var}\{y_i\}\approx \frac{1}{{\overline{Y}}_i^2}\text{Var}\{Y_i\},$$

where Ȳ_i ≜ E_μ[Y_i]. If Y_i had a Poisson distribution, then Var{Y_i} = Ȳ_i and Var{y_i} ≈ 1/Ȳ_i: More realistically, from (18) and (16):

$$\text{Var}\{Y_i\}=\text{Var}\{K_i\}+{\sigma }_i^2={\text{E}}_{\mu }[K_i]\left(\frac{{\text{E}}_{\mu }[K_{im}^2]}{{\text{E}}_{\mu }[K_{im}]}\right)+{\sigma }_i^2={\overline{Y}}_i\left(\frac{{\text{E}}_{\mu }[K_{im}^2]}{{\text{E}}_{\mu }[K_{im}]}\right)+{\sigma }_i^2.$$

A PWLS formulation should use weights that are the reciprocal of the variance of the log data:

$$w_i=\frac{1}{\text{Var}\{y_i\}}\approx \frac{{\overline{Y}}_i^2}{\text{Var}\{Y_i\}}=\frac{{\overline{Y}}_i^2}{{\overline{Y}}_i\left(\frac{{\text{E}}_{\mu }[K_{im}^2]}{{\text{E}}_{\mu }[K_{im}]}\right)+{\sigma }_i^2}.$$ (21)

For a counting detector the parenthesised term in the denominator is unity and there is no electronic noise ( ${\sigma }_i^2=0$), so the data-based weighting w_i = Ȳ_i ≈ Y_i is often used (Sauer and Bouman 1993). When electronic noise is important, often the parenthesised term in the denominator is ignored or assumed to be unity, leading to the weighting (Thibault et al. 2006 eqn. (18)):

$$w_i=\frac{{\overline{Y}}_i^2}{{\overline{Y}}_i+{\sigma }_i^2}\approx \frac{Y_i^2}{Y_i+{\sigma }_i^2}.$$ (22)

5.8. Other considerations

5.8.1. Compton scatter in object

The analysis above ignored the effects of X-ray photons that undergo Compton scatter within the object and reach the detector and are recorded. This effect positively biases the recorded values. It also affects the variance of the measurements, leading to further object-dependent nonlinearities in the relationship between mean and variance, even after correcting for scatter as described in section 4.

5.8.2. Quantisation noise

CT measurements are recorded by A/D converters with finite, discrete levels, so there is also quantisation noise in the measurements (Whiting 2002, De Man et al. 2007), as well as a finite dynamic range leading to the possibility of overflow. The variance due to quantisation noise can be absorbed in the electronic noise variance σ_i in (18). However, quantisation noise does not have a Gaussian distribution so developing an accurate log-likelihood is challenging (Whiting 2002).

5.8.3. Detector size

X-ray detectors have finite width, so the infinitesimal line integral in (7) is an approximation. The exponential edge-gradient effect (Joseph and Spital 1981) affects not only the mean recorded signal as described in section 3, but also its variance. Hopefully this effect on the variance is small because accounting for it seems to be challenging.

5.8.4. X-ray noise insertion and related work

Using a variety of simplified noise models, numerous methods have been proposed for adding “synthetic” noise to X-ray CT sinograms to simulate lower dose scans (Mayo et al. 1997, Frush et al. 2002, Karmazyn et al. 2009, Massoumzadeh et al. 2009, Benson and De Man 2010, Wang et al. 2012, Zabic et al. 2012).

5.9. Summary

The statistical phenomena in X-ray CT measurements are so complex (Siewerdsen et al. 1997) that it is unlikely that a highly accurate log-likelihood model will ever be practical. Instead, the field seems likely to continue using simple approximations such as the Poisson+Gaussian model (10) or the standard Poisson model (Lasio et al. 2007) for the pre-log data, or a WLS data-fit term (Gaussian model) with data-dependent weights (22) for the post-log data. Apparently these models are adequate because the Swank factors and the polyenergetic spectra often have fairly small effects on the statistics in practice. A model like (16) could be the basis for a model-weighted least squares cost function that has a weighting term that is a function of μ rather than a weighting term that is precomputed from the data as used in much previous work such as (Sauer and Bouman 1993, Fessler 1994). It is rather uncertain whether further refinements in statistical modeling could lead to noticeably improved image quality. Possibly the most important question is whether it would be beneficial to work with the raw measurements {Y_i} in (18) rather than the log measurements considered in (Sauer and Bouman 1993). The logarithm could become problematic at very low doses where the Y_i values can be very small or even non-positive due to photon starvation and electronic noise.

6. The energy spectrum

The polychromatic nature of standard X-ray sources not only complicates the noise statistics, if uncorrected it also leads to beam hardening and image artifacts (cupping and shadows) (McDavid et al. 1975, Brooks and Chiro 1976). Assuming that the scanned object consists of a single material with position dependent density (which can be zero to represent air), the monochromatic measurements (acquired at energy ε̃) can be modelled as

$$Y_i^m=b_i^{\stackrel{\sim }{\mathcal{E}}}exp\left(-{\mu }_{\stackrel{\sim }{\mathcal{E}}}{\int }_{{\mathcal{L}}_i}\rho (\overrightarrow{\text{x}})dl\right)\text{and}{y}_i^m=ln\frac{b_i^{\stackrel{\sim }{\mathcal{E}}}}{Y_i^m}$$ (23)

whereas for the polychromatic measurements one has

$$Y_i^p={\int }_{\mathcal{E}}{b}_i^{\mathcal{E}}exp\left(-{\mu }_{\mathcal{E}}{\int }_{{\mathcal{L}}_i}\rho (\overrightarrow{x})dl\right)d\mathcal{E}\text{and}{y}_i^p=ln\frac{{\int }_{\mathcal{E}}{b}_i^{\mathcal{E}}}{Y_i^p}$$ (24)

where ρ(x⃗) is the position dependent density of the material, μ_ε is the mass attenuation coefficient at energy ε, $b_i^{\stackrel{\sim }{\mathcal{E}}}$ is the monochromatic blank scan and $b_i^{\mathcal{E}}$ represent the polychromatic distribution of blank scan photons. Whereas $y_i^m$ is a linear function of the line integral ∫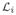ρ(x⃗)dl, $y_i^p$ is a nonlinear, but monotone, function of that integral, so one can derive analytically (if the spectrum is known) or with calibration measurements a function to convert $y_i^p$ to $y_i^m$. This is the basis of the so-called water correction (Herman 1979); (24) can also be used to implement a simple polychromatic projector, consisting of a single forward projection followed by a simple sinogram operation (Van Slambrouck and Nuyts 2012). When multiple materials are present, (24) can be extended by summing over all materials ζ:

$$Y_i^p={\int }_{\mathcal{E}}{b}_i^{\mathcal{E}}exp\left(-\sum _{\zeta }{\mu }_{\mathcal{E}}^{\zeta }{\int }_{{\mathcal{L}}_i}{\rho }^{\zeta }(\overrightarrow{\text{x}})dl\right)d\mathcal{E},$$ (25)

where ρ^ζ denotes the density map of the ζ’th material. In CT, the attenuation by a material is dominated by the Compton effect and photoelectric effect, and the energy dependence of these two functions is (almost) independent of the material. Consequently, the attenuation of a material as a function of the energy can be well modelled as a weighted combination of Compton scatter and photoelectric, or a set of two materials with sufficiently different behaviour (Alvarez and Macovski 1976). Thus, the sum in (25) can be restriced to the chosen pair of base materials.

If the material densities are known or can be estimated (e.g. from a first reconstruction), then (25) can be computed for the spectrum of the scanner and also for an ideal monochromatic beam, to estimate and correct for the beam hardening artifact. Alternatively, by putting constraints on the possible material combinations, the number of unknowns can be reduced to one value per image pixel, allowing direct reconstruction of ρ^ζ(x⃗), ζ ∈ {1, 2} from single energy data. Of course, less constraining is needed for dual energy CT data. Based on these ideas, numerous correction methods for analytical reconstruction have been proposed (Joseph and Spital 1978, Herman 1979, Herman and Trivedi 1983, Joseph and Ruth 1997, Hsieh et al. 2000, Yan et al. 2000, Kyriakou et al. 2010, Liu et al 2009). Naturally, the models and methods depend on whether the detector is current integrating or photon counting (Shikhaliev 2005). Other researchers have combined a model for the polyenergetic spectrum with the other models described above (object discretization, detector resolution, and measurement statistics) to develop model-based image reconstruction methods that “correct” for the polyenergetic spectrum during the iterations (De Man et al. 2001, Elbakri and Fessler 2002 and 2003a, O’Sullivan and Benac 2003, Lasio et al. 2007).

Alternatively, the polyenergetic spectra can be viewed as providing an opportunity to estimate object material properties, particularly when combined with multiple measurements, such as dual-energy scans (Alvarez and Macovski 1976, Clinthorne 1994, Sukovic and Clinthorne 2000, Fessler et al. 2002, O’Sullivan and Benac 2007, Maass et al. 2011, Semerci and Miller 2012) or detectors with multiple energy bins (“spectral CT”) (Xu et al. 2007, Xu et al. 2012). By using constraints, one can estimate more materials than measured energy bins (Mendonca et al. 2010, Long et al. 2011, Depypere et al. 2011, Long and Fessler 2012). This is an active area of research that will continue to spawn new models and image reconstruction methods as the detector technology evolves.

6.1. Summary

The energy dependence of photon attenuation makes pre-correction or modelling of the energy spectrum necessary to avoid beam hardening artifacts. However, it also creates opportunities for contrast enhancement and improved material identification.

7. Motion

In this section we focus on the specific challenge of performing iterative reconstruction in the presence of motion. While we describe most techniques in the context of the beating heart, many of them can also be applied to other types of motion, including breathing, contrast agent flow, peristaltic motion and involuntary patient motion.

Motion during a CT scan typically causes motion blur or degrades spatial resolution. Cardiac motion can have speeds on the order of 7cm/s (Ritchie et al. 1992). State-of-the-art CT scanners acquire cardiac CT data over time intervals on the order of 100ms. This corresponds to displacements as high as 7mm, which may lead to unacceptable blur of the sub-mm resolution images. In addition, motion during the scan causes mutually inconsistent projection measurements, resulting in streak artifacts. Figure 4 shows a typical motion-induced streak artifact for a coronary artery. In the next sections we will loosely use the term motion artifacts to include real artifacts as well as motion blur. Fast scanning offers the opportunity to image the heart at multiple time frames, providing functional information about wall motion, valves, ejection fraction, etc. This 4D imaging task has specific implications for the reconstruction algorithm, as will be discussed later.

Figure 4.

(a) Motion-induced streaking artifacts in a 0.35s CT scan of a coronary artery. Courtesy of Jed Pack (GE Global Research). (b) The Tam window defines the minimum data required for accurate helical cone-beam reconstruction.

The most fundamental way to avoid motion artifacts is to prevent or minimise motion. Beta-blockers are commonly administered prior to cardiac CT to reduce the heart rate and make the heart beat more regular. ECG gating is used to select the cardiac phase with least motion. ECG gating can be prospective: only a particular phase is scanned, or retrospective: only a specific phase is used for reconstruction. Depending on the heart rate and the specific part of the heart or coronary of interest, the end-diastolic or the end-systolic phase may be preferred.

CT technology has evolved dramatically in terms of scanning speed. State-of-the-art CT scanners have gantry rotation times in the range of 0.27s–0.35s. A half-scan reconstruction interval is about 200ms. Dual-source CT and multi-sector CT are two techniques to cut this interval in half, resulting in about 100ms effective acquisition interval. Reducing the rotation time even further is mechanically very challenging, given that a typical CT gantry weighs almost 1 ton, hence less costly algorithmic approaches are preferable if they can be effective.

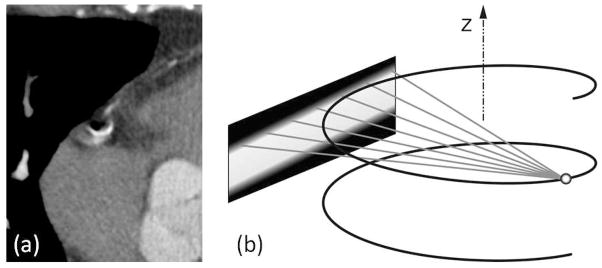
In the next sections we will discuss iterative reconstruction methods to minimise motion artifacts and maximise temporal resolution, by reducing the used temporal data interval or by modelling the motion.

7.1. Use as little data as possible

CT measurements often have significant redundancy. In 2D, a half-scan (a scan with a view interval of 180° + fan angle) is sufficient to accurately reconstruct a slice. A full-scan (a scan with 360° worth of data) has a number of conjugate rays that are not theoretically required, but contain useful information for noise reduction and resolution enhancement. Similarly in 3D helical scans, all measurements outside of the Tam-Danielsson window (Tam et al. 1998) are not required for exact reconstruction but still contain useful information. In FBP, redundant data is handled by projection domain or image domain weighting factors, such as Parker weighting (Parker 1982) and helical weighting (Wang et al. 1993). Iterative reconstruction typically uses either no preferential weights (such as in ART-type algorithms (Gordon et al. 1970)), treating all measurements equally, or statistical weights (such as in ML-type algorithms (Lange and Carson 1984, De Man et al. 2000) or weighted least squares approaches (Sauer and Bouman 1993, Sukovic and Clinthorne 2000)), emphasising more reliable data and de-emphasising less reliable data.

A straightforward extension to the traditional weighting approaches is to include a temporal weighting factor. The statistical weighting factors can be modulated based on the cardiac phase, such that data closer to the temporal phase of interest receives a higher weight, and data further from the temporal phase of interest receives a lower weight. The phase-weighted WLS cost function for example then becomes:

$$\text{PW}-\text{WLS}=\sum _{i}P(t_i,t_0)W_i{(y_i-{[A\mu ]}_i)}^2$$ (26)

where (precorrected and log-converted) measurement y_i occurs at time t_i and has statistical weight W_i, A is the projection matrix and μ the image, represented as a column matrix. The temporal weighting function P(t_i, t₀) can be made aggressive to completely eliminate the contribution of data that is far from the phase of interest and not required for reconstruction. This concept was successfully applied to a helical scan trajectory (Zeng et al. 2009b). The concept of the Tam window, originally invented in the context of analytic reconstruction, is applied to iterative reconstruction. Setting the weights to zero outside the Tam window (figure 4b) can dramatically reduce motion artifacts.

Using iterative reconstruction one can go a step further and reduce the data usage below the minimum amount needed for exact reconstruction. In (Tang et al. 2010) iterative reconstruction is performed based on a 90° view interval. However, to avoid image artifacts induced by the incomplete data, the authors use the half-scan FBP image as prior information and suggest that the final image should only sparsely differ from this prior image. The temporal resolution improvement prior image constrained compressed sensing (TRI-PICCS) weighting scheme is shown schematically in figure 5a. The corresponding optimisation problem is given by:

$$\text{PICCS}:min(\alpha {\Vert \nabla (\mu -\text{FBP})\Vert }_1+(1-\alpha ){\Vert \nabla (\mu )\Vert }_1)\text{subject}\text{to}\mid y-A\mu \mid <\epsilon$$ (27)

Figure 5.

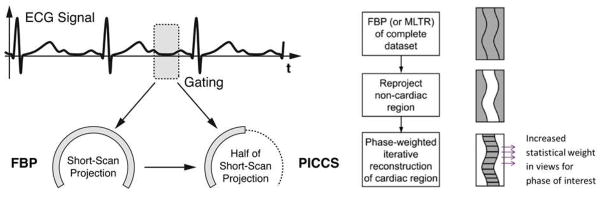
(a) The PICCS uses a short-scan FBP reconstruction as prior information for the iterative reconstruction based on only a portion of the short-scan. (b) In phase-weighted iterative reconstruction image increments are computed relative to FBP using increased statistical weights for the views corresponding to the phase of interest.

Figure 6a shows results for an in vivo animal dataset reconstructed with FBP showing significant motion artifacts and figure 6b shows the corresponding PICCS reconstruction, reducing motion artifacts.

Figure 6.

In vivo animal dataset scanned with GE 64-slice scanner (a) reconstructed with FBP from a short-scan interval and (b) reconstructed with TRI-PICCS. Reproduced from (Tang et al. 2010).

An earlier attempt to improve temporal resolution using sparse view sampling was proposed by De Man et al. (2003, 2005). The main idea is to use a slow gantry rotation, during which multiple cardiac cycles are acquired. Each cardiac phase then corresponds to a small number of views distributed across the full 360°. Using only the phasic data would result in very sparse view sampling, which would lead to severe view aliasing artifacts. Using all views would result in a blurred, not phase-specific image. Instead, an initial reconstruction was based on all views, ignoring phase information. An incremental image was then computed in the ML/MAP framework and modulating the weights based on the phase of interest. I.e., the airscan and the transmission scan were both artificially modulated, resulting in phase-specific low-artifact reconstructions. This process was repeated for 50 different cardiac phases resulting in a movie of a beating heart. Corresponding movies are downloadable from movie, see supplemental data. While noisy, this 4D dataset can serve as input for some of the approaches described in the next section. More recent compressed sensing technique (Sidky et al. 2006) may be better suited to deal with sparse view sampling and further enhance these results.

7.2. Motion modelling

The previous section described how to perform independent phasic reconstructions based on the smallest possible temporal interval. We now give an overview of methods that explicitly model the temporal variations in the reconstructed images.

The most basic approach is to reconstruct multiple frames and either constrain the relationship between consecutive frames using temporal basis functions or regularise the differences between consecutive frames using temporal neighbourhood priors. Since the difference between consecutive frames may be sparse, a sparsifying norm on this difference such as an L1 norm is a good candidate to incorporate in the cost function :

$$\text{Temp}-\text{WLS}=\sum _t\sum _i{W}_i{(y_i-{[A{\mu }^{(t)}]}_i)}^2+\sum _t\varphi ({\mu }^{(t)}-{\mu }^{(t+1)})$$ (28)

where μ^(t) is the image of frame t and ϕ can be any type of penalty function. In kinetic parameter iterative reconstruction (KPIR) (Yu et al. 2011), the reconstructed images are described by a kinetic model and the parameters of the kinetic model become the unknown in the reconstruction process. A second order model is given by :

$$\mu (\overrightarrow{x},t)=\mu (\overrightarrow{x},t_0)+{\frac{d\mu (\overrightarrow{x},t)}{dt}|}_{t=t_0}(t-t_0)+{\frac{d^2\mu (\overrightarrow{x},t)}{{dt}^2}|}_{t=t_0}\frac{{(t-t_0)}^2}{2},$$ (29)

where μ(x⃗, t₀), dμ/dt and d²μ/dt² are the parameters to be estimated for every voxel x⃗.

Figure 7 shows (left) a conventional iterative reconstruction with significant motion artifacts and (right) a reconstruction based on the KPIR method with a second order motion model with significantly reduced motion artifacts. While this method does model the change in attenuation over a time of a given voxel, it does not explicitly model object motion.

Figure 7.

Clinical lung CT scan reconstructed with FBP and KPIR (Courtesy of Zhou Yu (GE Healthcare)) : the conventional FBP reconstruction (left) shows a ghosting artifact near the heart wall and blurred vessels due to cardiac and respiratory motion. These artifacts are significantly reduced by KPIR (right).

The most realistic approach is to estimate the actual motion of the object, i.e. to compute motion vectors at every location, and incorporate these motion vectors in a joint time-resolved reconstruction. This is usually performed in three stages: first-pass reconstruction, motion vector estimation and time-resolved reconstruction. This was demonstrated for rigid head motion in (Bodensteiner et al. 2007, Nuyts et al. 2011). When performing motion compensated image reconstruction for non-rigid motion models, regularisation designs should consider resolution and noise effects (Chun and Fessler 2009, Chun and Fessler, 2012).

7.3. Summary

While many groups have researched the combination of motion and CT iterative reconstruction, this area still has a long way to go to completely eliminate motion artifacts, improve robustness, minimise dose and overcome computational hurdles.