Exploring the potential of protein-based pharmacophore models in ligand pose prediction and ranking

Abstract

Protein-based pharmacophore models derived from the protein binding site atoms without the inclusion of any ligand information have become more popular in virtual screening studies. However, the accuracy of protein-based pharmacophore models for reproducing the critical protein-ligand interactions has never been explicitly assessed. In this study, we used known protein-ligand contacts from a large set of experimentally determined protein-ligand complexes to assess the quality of the protein-based pharmacophores in reproducing these critical contacts. We demonstrate how these contacts can be used to optimize the pharmacophore generation procedure to produce pharmacophore models that optimally cover the known protein-ligand interactions. Finally, we explored the potential of the optimized protein-based pharmacophore models for pose prediction and pose rankings. Our results demonstrate that there are significant variations in the success of protein-based pharmacophore models to reproduce native contacts and consequently native ligand poses dependent on the details of the pharmacophore-generation process. We show that the generation of optimized protein-based pharmacophore models is a promising approach for ligand pose prediction and pose rankings.

Introduction

Pharmacophore models aim to reproduce the features of ligand-protein interactions that are most crucial for binding and biological activity. These models are used for virtual screening to identify potential new actives or for generating ligand alignments for subsequent QSAR simulations. Pharmacophore models are typically derived from analyzing the similarity of several known actives. A number of methods^1–5 have been developed to deduce structural features common to biologically active ligands that are hypothesized to be important for biological activity. If experimental information about the three-dimensional structure of the binding pocket is known, these data can guide the optimization of the pharmacophore model. In the program LigandScout⁶, for example, interactions between protein and ligand in an experimentally determined protein–ligand structure guide the pharmacophore selection process.

All previously described ligand-based pharmacophore models are dependent on the chemical features present in the known actives. Physicochemical features that are absent in the particular set of actives, but are important for the binding of structurally different ligands, will likely be neglected in the pharmacophore model. Alternatively, the binding site of the target protein can be used to generate a protein-based pharmacophore model without the inclusion of ligand information. These protein-based pharmacophore models are advantageous because a priori knowledge of active ligands is not required and the models are not biased by the chemical space of previously identified actives. Several approaches^7–9 have been developed to derive the protein-based pharmacophore models from ligand-free proteins. Molecular Interaction Fields (MIFs) are usually used as the first step in deriving pharmacophore models solely based on the protein structure¹⁰. To generate the MIFs, a 3D grid is projected onto the binding site of interest and the interaction energies at each grid point are computed between the protein and several molecular probes each with different physicochemical properties. Finally, pharmacophores can be derived from the MIFs via a variety of different methods. For example, the structure-based pharmacophore⁷ (SBP) method implemented in Discovery Studio uses clustering methods to convert LUDI¹¹ interaction fields into pharmacophore queries. It is possible that some critical protein-ligand interactions will be lost during the conversion from the MIFs to the pharmacophore models. However, the accuracy of protein-based pharmacophore models for reproducing the critical protein-ligand interactions has never been explicitly assessed.

In this study, we use known protein-ligand interactions from a large set of experimentally determined protein-ligand complex structures to assess the quality of the protein-based pharmacophores in reproducing these critical contacts. The rationale is that the known protein-ligand interactions need to be represented by the protein pharmacophore elements in order to correctly model critical protein-ligand interactions in studies utilizing those pharmacophore models. Consequently, a successful pharmacophore model should, ideally, cover all known interactions between a protein and its ligands.

We will first present our methodology to generate protein-based pharmacophore models based on interaction fields. We then will demonstrate how the pharmacophore generation procedure can be optimized to produce pharmacophore models that optimally cover the known protein-ligand interactions. Typically, the generated protein-based pharmacophore models will be curated to form the workable queries for virtual screening. Little attention has been paid to investigate the application of the protein-based pharmacophores for ligand pose prediction and pose rankings. In this study, we will explore the potential of using optimized protein-based pharmacophore models for pose prediction and pose rankings. We will show that there are significant variations in the success of protein-based pharmacophore models to reproduce native contacts and consequently native ligand poses dependent on the details of the pharmacophore-generation process.

Material and Methods

The overall procedure to generate and test optimal protein pharmacophore models is depicted in Figure 1. Different parameters are adjusted to optimally reproduce protein-ligand interaction contacts observed in x-ray complex structures. In the pose generation phase, the clique-detection and scoring function are subsequently optimized for the models selected in the previous optimization step. The details of this optimization procedure are discussed in the following sections.

Figure 1.

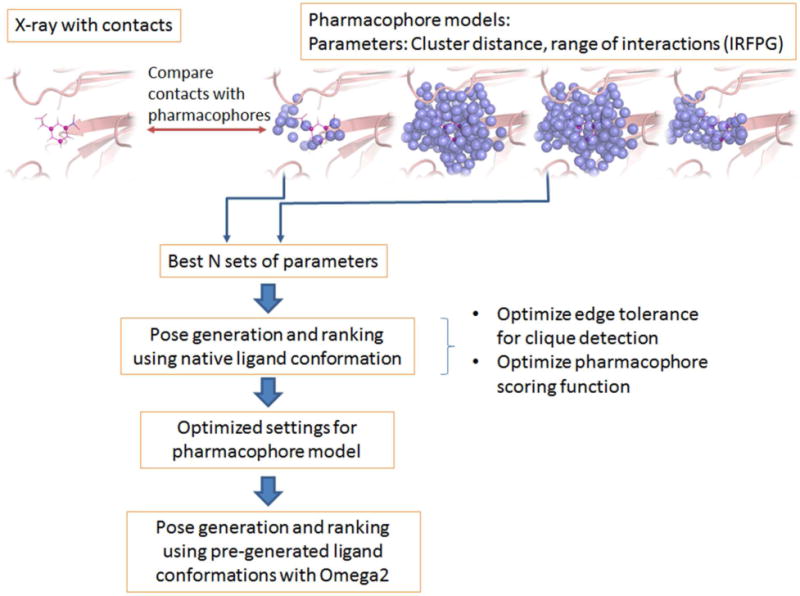
Overall procedure for pharmacophore model optimization and testing.

Data Set

The “core set” of the PDBbind^12–13 database (version 2007) was used for this study. The PDBbind database provides a “refined set” which consists of 1,300 protein-ligand complexes that were compiled particularly for docking/scoring studies. From the “refined set”, 210 protein-ligand complexes were non-redundantly sampled to form the so-called “core set”¹². It covers 70 different proteins, each of which contains three protein-ligand complexes with different binding affinities. This “core set” provides an ideal divergent set for our study. All the protein-ligand complexes in the PDBbind core set were pre-processed with the hydrogen atoms added and were therefore used directly without additional preparations. All the 210 protein-ligand complexes were used for the optimization of the protein-based pharmacophore generation program. However, due to various reasons, 20 protein-ligand complexes are excluded from the pose prediction and ranking study. A detailed reason for exclusion of those complexes can be found in the Supporting Information S1.

Protein pharmacophore generation

In this paper, the term “protein-based pharmacophores” and “protein pharmacophores” were used interchangeable. They both refer to the potential interaction sites for the ligand that could interact with the protein atoms in the binding site. They can be viewed as the negative or complimentary image of the protein binding site. There are four types of protein pharmacophores: hydrogen-bond donor/acceptor, hydrophobic, aromatic and ionic pharmacophores. In addition, the exclusive volume of the protein was also represented by so-called forbidden pharmacophores, representing the portion of the protein that would overlap with ligand atoms placed in this moiety.

To generate protein-based pharmacophore elements, a 3D grid with 0.4 Å spacing between grid points was placed in the binding site for each protein structure. The interaction potentials (hydrogen-bond donor/acceptor, hydrophobic, aromatic and ionic) between the protein atoms and probes representing hypothetical ligand atom were computed on each grid point. The interaction potentials for hydrogen-bonding and hydrophobic probes placed at the grid points were computed using a continuous form of the ChemScore^14–15 scoring function. The aromatic and ionic interactions were calculated using a functional form similar to ChemScore. The detailed equations are presented in the Supporting Information S2.

The pharmacophores were generated using the computed interaction energies with the probes on the 3D grid points. The hydrophobic pharmacophores were computed by a k-means clustering over all grid points with favorable hydrophobic scores. The hydrophobic pharmacophore element was then defined as the energy-weighted geometric center over all grid points of a particular cluster. The number of clusters, k, was adjusted until the minimum distance between a cluster center i and any other cluster center was on average smaller than a certain distance cutoff. Five cutoff values, 1.0 Å, 1.5 Å, 2.0 Å, 2.5 Å and 3.0 Å, were used. The influence of cluster distance on pose-prediction quality was investigated and will be discussed in the following sections.

Unlike hydrophobic pharmacophores, which represent the presence of several hydrophobic atoms in a hydrophobic moiety, hydrogen-bond, aromatic and ionic interactions are typically more specific interactions with an individual functional group of the protein. Therefore, k-means clustering to generate hydrogen-bond, aromatic and ionic pharmacophores was performed over the grid points associated with the same nearest functional group. For example, in generating a hydrogen-bond donor pharmacophore, the program iterates through all protein acceptors, and groups the grid points closest to the same acceptor into one patch. K-means clustering was then performed within this patch. Analogous to the generation of the hydrophobic pharmacophores, five different cutoff values were investigated throughout clustering.

In addition to k-means clustering, a scheme that simply defines one pharmacophore by the energy-weighted geometric center of a patch was tested for hydrogen-bonding, aromatic and ionic pharmacophores. In detail, the center of the pharmacophore was computed by

$$c={{\displaystyle \mathrm{\sum }}}_i{x}_i\cdot {\epsilon }_i.$$ (1)

The sum was over all grid points i associated with the same functional group, i.e. the grid points from the same patch. x_i and ɛ_i were the coordinates and interaction potential of each grid point, respectively.

In the pharmacophore generation process, the scoring function used to compute the interactions between protein atoms and probes was empirically derived. The interaction strength decreases with distance between protein atom and probe. The pharmacophore elements were derived using clustering of the grid points, which can shift the center of a cluster to larger distances compared to the optimal distance, i.e. maximum interaction strength, between protein and ligand atoms (Figure 2a). Thus, we limited the distance range of favorable interactions between protein and ligand probes for pharmacophore generation, i.e. minimum and maximum cutoffs were introduced to the scoring function (Figure 2b). We investigated how the identification of the pharmacophore elements was influenced by the allowed interaction range, which was named “interaction range for pharmacophore generation” (IRFPG) throughout the paper. The IRFPGs tested for different interaction types are listed in Figure 3.

Figure 2.

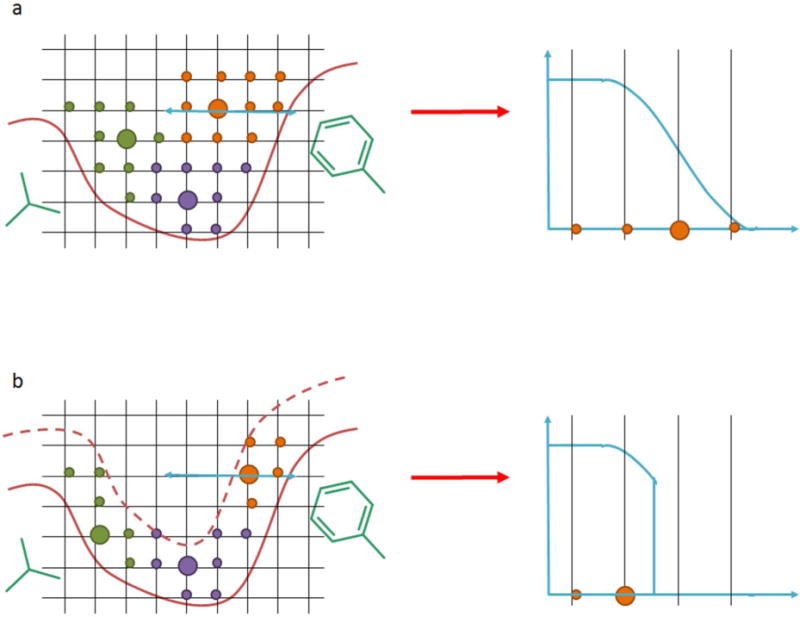
Example for influence of “interaction range for pharmacophore generation” (IRFPG) parameter on generation of hydrophobic pharmacophores. The hydrophobic grid points are shown as circles and color coded according to cluster membership. The cluster center is depicted as large circle and represents the pharmacophore. In a. the minimum and maximum range of hydrophobic interactions are following the values of the scoring function. In b. the maximum range of interaction is reduced compared to the maximum range of the scoring function.

Figure 3.

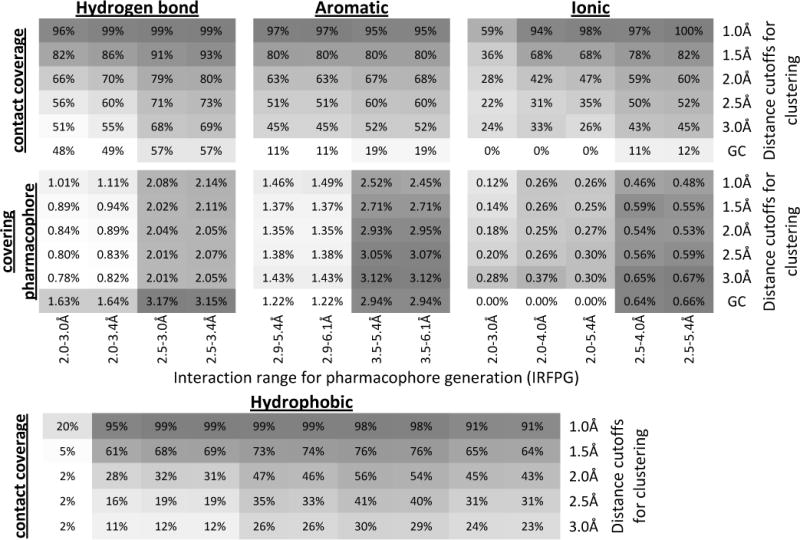
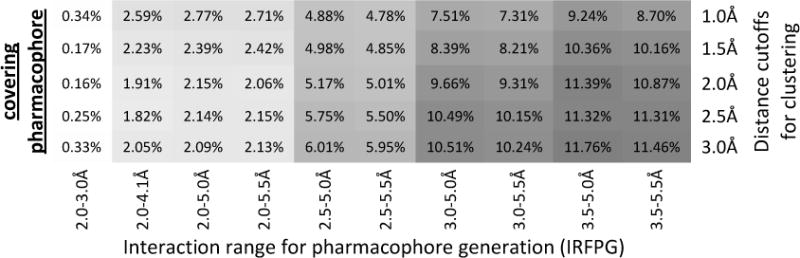
Heat map of the overall contact coverage rate and percentage of the covering pharmacophore for hydrogen-bonding, aromatic, ionic and hydrophobic pharmacophores. For each pharmacophore type, the upper panel shows the overall contact coverage rate and the lower panel shows the percentage of the covering pharmacophores. The results in each column are from the same IRFPG whereas the results in each row are from the same distance cutoffs for clustering. GC: energy-weighted geometric center.

Throughout the posing phase, ligand configurations that overlapped with the protein would be ranked lower or removed from the pool of potential poses. For this process, forbidden pharmacophore elements were determined that represented the residues forming the binding site. Those pharmacophores were generated by clustering over all grid points that are closer than 2 Å to a heavy atom of a protein residue. A cluster radius of 1.5 Å was chosen.

Protein-ligand contacts analysis

A protein-ligand contact map represents the localized interactions between the ligand and protein atoms such as hydrogen-bonding, aromatic interactions or hydrophobic contacts, but neglects long-range interactions, e.g. electrostatics. In a contact map the “contacts” points were positioned onto the ligand heavy atoms. Corresponding to the types of the pharmacophores, there were four types of protein-ligand contacts: hydrogen bonding, hydrophobic, aromatic, and ionic contacts. The identification of hydrogen bonding, hydrophobic and ionic atoms as well as the center of the aromatic ring were identical to those used to define the ligand pharmacophore elements described in the “ligand conformation and pharmacophore generation” section (see below). The same scoring function as described under “Protein pharmacophore generation” was used for calculating the interaction strength between the protein and ligand heavy atoms in an x-ray structure. If there was a favorable interaction, i.e. negative score, between a given ligand-protein atom pair, a contact was defined between both atoms and a contact point would be positioned onto the ligand heavy atom involved in that interaction. This procedure was performed on all x-ray complex structures of our curated database.

Contact coverage by the protein pharmacophores

As described in the section “Protein pharmacophore generation”, the IRFPG and the cluster distances are parameters that influence the location of the generated pharmacophore elements. Ideally, the generated protein pharmacophores should co-localize with the known ligand-protein contacts in the x-ray structure of the associated protein-ligand complex. Therefore, the degree to which the generated protein pharmacophores covered the known protein-ligand contacts was a valuable criterion for identifying the best set of parameters in the protein pharmacophores generation process (cf. Figure 1). In this study, the PDBbind core set was used as the training set to achieve this purpose.

We first generated the protein-ligand contact map for each complex from the core set as described in the section “Protein-ligand contacts analysis”. The protein-ligand contact maps were then matched onto the protein pharmacophore models to identify how well the contacts were reproduced by the pharmacophore elements. A contact was covered by the pharmacophore model if at least one protein pharmacophore element with the same interaction type was located within 1 Å of the contact. The pharmacophore element that covered a contact was named a “covering pharmacophore”. For identifying the optimal set of parameters, i.e. IRFPG values and cluster distances, during pharmacophore generation, two values were calculated for each setting:

$$\text{Contact}\text{coverage}\text{rate}=\frac{\text{Number}\text{of}\text{contacts}\text{being}\text{covered}}{\text{Total}\text{number}\text{of}\text{contacts}}$$

$$\text{Percentage}\text{of}\text{covering}\text{pharmacophores}=\frac{\text{Number}\text{of}\text{covering}\text{pharmacophores}}{\text{Total}\text{number}\text{of}\text{pharmacophores}}$$

The first measure determined the percentage of contacts the pharmacophore model was able to reproduce, whereas the second measured the enrichment of the covering pharmacophores in the pharmacophore model.

Ligand conformation and pharmacophore generation

In our study for prediction of native ligand poses, both the native conformer and low-energy conformers were used as inputs. The low-energy conformers were generated by Openeye Omega¹⁶. For each ligand, a maximum of 1,000 conformations were generated with the calculated internal energy no more than 15 kcal/mol above the energy of the ligand conformation with the lowest internal energy. Duplicate conformers were removed using a 0.2 Å root-mean-square deviation (RMSD) cutoff for ligands with zero to three rotatable bonds, a 0.3 Å cutoff for ligands with four to six rotatable bonds, and a 0.4 Å cutoff for all ligands with more than six rotatable bonds.

The in-house program clusterconformer was then used to generate the pharmacophore elements for each ligand conformation. Four types of pharmacophores were defined for each ligand: hydrogen-bond donor/acceptor, hydrophobic, aromatic and ionic pharmacophores. Hydrogen-bond pharmacophores are placed at the position of potential donor and acceptor groups of the ligand: Hydrogen-bond donors are polar hydrogen atoms bonded to oxygen, nitrogen and sulfur atoms, acceptors are oxygen, nitrogen and sulfur atoms with at least one lone pair. Ligand atoms (excluding hydrogen atoms) were defined to be hydrophobic if they were not hydrogen-bond donors or acceptors or directly bonded to a ligand’s donor or acceptor atoms. The hydrophobic atoms from each ligand conformation were clustered using hierarchical clustering with a minimum distance between cluster centers of 2.0 Å. Clustering was performed to reduce the number of hydrophobic ligand pharmacophores. This significantly reduced the cost of clique detection and consequently increased the efficiency of pose prediction. Aromatic pharmacophores were defined as centers of aromatic rings. Ionic groups included functional groups that were formally charged positive or negative, e.g. protonated amines or deprotonated carboxylic acids, and were placed at the centroids of the functional group.

Prediction of ligand poses

Our in-house program, PharmPose, was used to sample ligand poses in the generated pharmacophore model. The sampling process is based on a modified Bron-Kerbosch clique detection algorithm^17–18 that enumerates all possible multi-points (> = 3) matches of protein and ligand pharmacophores. First, the length of the edge between each pair of ligand pharmacophores was determined. The edge lengths were also determined for each protein pharmacophore pair. All ligand pharmacophore edges that matched the protein pharmacophore edges, based on the pharmacophore types (hydrogen bond donor/acceptor, hydrophobic, aromatic and ionic interactions) of their vertices and edge lengths, were identified. Throughout the matching process, a tolerance for the edge lengths was allowed, and the optimal value of this edge tolerance was studied as will be described in subsequent sections. The matching process can be represented by a graph in which each node represents a matching ligand-protein pharmacophore pair. The clique detection algorithm then identified all the completely connected subgraphs from this graph. The Kabsch algorithm¹⁹ was then used to spatially align the ligand pharmacophore elements to the matching protein pharmacophore in each clique, thus placing the ligand into the protein binding site. To avoid steric clashes between ligand and protein atoms, the number of heavy atoms of the ligand that were located within 1.3 Å to any of the forbidden pharmacophores was counted for each ligand pose. If more than 10% of the ligand’s heavy atoms overlapped with forbidden pharmacophores, the pose was rejected.

Pharmacophore-based pose ranking

The ligand poses sampled by PharmPose were scored and ranked using a simple geometric scoring function based on the matching pharmacophore pairs formed by each ligand pharmacophore and its closest protein pharmacophore of the same type:

$$S=w_{\text{hbond}}\ast {\displaystyle {\sum }_{\text{hbond}}f(r)+}{w}_{\text{hphob}}\ast {\displaystyle {\sum }_{\text{hphob}}f(r)+}{w}_{\text{arom}}\ast {\displaystyle {\sum }_{\text{arom}}f(r)+}{w}_{\text{ionic}}\ast {\displaystyle {\sum }_{\text{ionic}}f(r)}$$ (1)

Where w was the weighting factor ranging from −1.0 to 0.0 and was optimized as described in the following section.f(r) was a distance-dependent function that measures the spatial separation of protein and ligand pharmacophores of a matching pharmacophore pair:

$$f(r)=\{\begin{array}{cc}\begin{array}{c}1.0\\ 2\ast (1.0-r)\\ 0\end{array}& \begin{array}{c}r\le 0.5Å\\ 0.5Å<r\le 1.0Å\\ r>1.0Å\end{array}\end{array}$$ (2)

r was the distance between the ligand pharmacophore and its closest matching protein pharmacophore of the same type. It is noteworthy that equation 1 calculated the score of a pose based on all the ligand pharmacophores rather than only those involved in forming cliques.

Optimization of pose prediction and pose ranking

To identify optimal protein pharmacophore models for pose prediction, three pharmacophore models were chosen that were able to accurately reproduce native protein-ligand contacts. In the next step of optimization, we used clique detection and the pharmacophore-based scoring function to generate and rank poses, aiming to reproduce native binding modes (cf. Figure 1). In the clique detection process, the distance tolerance in the edge matching process is a critical parameter for both sampling accuracy and time efficiency. A larger edge tolerance will result in a higher number of matching edges and cliques. This search will generate a larger ensemble of sampled poses, which increases the probability of recovering a native-like pose. However, the computational efficiency suffers from larger edge-length tolerances, as the number of matching cliques will linearly increase with the number of the matching edges¹⁸.

In addition, variation in distance cutoffs throughout the k-means clustering was studied. The number of protein pharmacophores would become very large when a small distance cutoff is used. Consequently, a smaller edge tolerance is preferred to allow the completion of pose sampling within a reasonable amount of time. Therefore, a benchmark study was performed, using the native conformation of each ligand as the input, in order to achieve the best tradeoff between the sampling accuracy and time efficiency. Throughout this phase of pharmacophore optimization, the native ligand conformation was chosen to remove any uncertainty introduced by ligand conformations that do not resemble the native form. In detail, the ligand pharmacophores were generated for the native conformation of each ligand in the PDBbind core set following the method described in “ligand pharmacophore generation” section. This native ligand pharmacophore model was then matched onto different protein pharmacophore models (variation in IRFPG and cluster distance) with different edge tolerances. The poses sampled from each run were assessed for their RMSD to the native binding pose of the ligand. The CPU time needed for the whole process was also recorded for analyzing the efficiency of the process.

After determination of the optimal combination of pharmacophore model (IRFPG value and cluster distance) and edge tolerance for the reproducibility of native-like poses and sampling efficiency, the binding poses sampled from this model were scored by equation 1. All weighting factors were initially set to one. The performance of this equally-weighted scoring function was then evaluated on the top-100 ranked poses by its ability to reproduce the native-like poses for each protein-ligand complex in the PDBbind core set. The best pose RMSD, i.e. the minimal RMSD between the sampled poses to the native binding pose denoted as RMSD_min, was calculated. The average RMSD_min over the studied protein-ligand complexes was reported to assess the overall sampling performance. In addition, the percentages of complexes that were successfully predicted with poses within 1 Å, 2 Å and 3 Å RMSD to the native conformation were also used to evaluate the overall performance of pose generation and ranking.

The equally-weighted function assumed that each type of pharmacophore element contributed equally to protein-ligand interactions. However, as seen in many empirical scoring functions^{14, 20} used for docking, different types of interactions were weighted differently to better reproduce protein-ligand interactions. Therefore, a training process was performed to optimize the weights of the function in equation 1. To accelerate the optimization process, the top-1000 poses of each protein-ligand complex ranked by the equally-weighted function were used as the input data. A systematic optimization scheme was adopted: First, each pre-factor w in equation 1 was systematically altered from −1.0 to 0.0 with an increment of 0.1. This leads to 11⁴ different sets of pre-factors, each of which corresponds to a differently weighted scoring function. The poses were then re-scored and re-ranked by each of the scoring functions. The fitness of each function was assessed using the Receiver Operating Characteristic (ROC) curve. In detail, for each protein-ligand complex, the poses with a RMSD less than or equal to 2 Å to the native pose were labeled as active and those with RMSD beyond 2 Å were labeled as decoys. A ROC curve displaying the fraction of ranked actives at a given fraction of the ranked decoys was then plotted for each protein-ligand complex. The area-under-the-curve (AUC) was calculated for each curve. Finally, the average AUC over all the protein-ligand complexes was used to measure the fitness of each set of pre-factors.

Results and Discussion

Optimization of protein pharmacophore generation methodology

Protein pharmacophores derived from the protein binding site atoms without the inclusion of any ligand information have been used in various virtual screening studies^{7, 21}. The term “protein pharmacophores” refers to the functional groups of hypothetical ligands that potentially interact with the atoms of the protein binding site. In this perspective, pharmacophores can be viewed as the negative or complementary image of the protein binding site. In our approach, the elements of a protein pharmacophore were derived by computing the interaction energy between molecular probes placed on a 3D grid in the binding site with the protein residues, and subsequent clustering of proximate grid points with similar properties (see Material and Methods section for details). As mentioned in the Introduction, it has never been systematically investigated if the critical protein-ligand interactions observed in experimental structures are well preserved during this pharmacophore generation process. Therefore, in our study we assessed the quality of the pharmacophore models in reproducing the key protein-ligand interactions observed in protein-ligand complex structure of the PDBbind core set.

First, a contact map representing the known protein-ligand interactions was generated for each protein-ligand complex in the dataset. The protein pharmacophore models were then superimposed with the contact map to assess how well the protein-ligand interactions were reproduced by the pharmacophore models. As mentioned in the Materials and Methods section, the IRFPG and the cluster distance strongly influenced the location of the pharmacophore elements. Variation of these two parameters generated an ensemble of pharmacophore models which were assessed for the potential to reproduce the known contact maps. For hydrogen-bond and aromatic pharmacophore types, we tested four different IRFPG and six different cluster distances, resulting in a total of 24 sets of parameters for these two pharmacophore types (Figure 3). For hydrophobic and ionic pharmacophores, the utilized potential functions have a wider range of interactions. Therefore, ten and five different IRFPG values were tested for them, respectively. To measure the quality of the parameter sets for reproducing native contacts, two fitness values were calculated: the overall contact coverage rate, which measures how many of the known ligand-protein interactions are reproduced by a given pharmacophore model; and the percentage of the covering pharmacophores, which measures the enrichment of the covering pharmacophore in the given pharmacophore model. A 100% contact coverage rate of a pharmacophore model would indicate that the graph of known protein-ligand interactions is a sub-graph of the given pharmacophore model, i.e. there exists a clique in the set of pharmacophore elements that overlays with all native contacts within a certain distance uncertainty. Consequently, in pose prediction studies an exhaustive search using clique detection should be able to retrieve the native binding pose using such optimal pharmacophore models as long as the native ligand conformation can be reproduced. On the other hand, a high percentage of the “covering pharmacophore” would suggest a high enrichment of pharmacophore elements representing the key protein-ligand interactions. The predicted poses using such pharmacophore models would potentially have a higher true positive rate than the poses predicted from a model with lower covering pharmacophore rate. Therefore, an ideal pharmacophore model for pose prediction should have both a high contact coverage rate and a high percentage of covering pharmacophores.

The contact coverage rates and the percentage of the covering pharmacophores for the four pharmacophore types are shown in Figure 3. It is obvious from this heat map that variation in IRFPG has a significant impact on the quality of the pharmacophore model. It also demonstrates that the suggested optimal IRFPG value is very consistent across the different cluster distances. For example, with regards to hydrogen-bond pharmacophores, the highest contact coverage rates were observed for IRFPG equal to the range 2.5–3.4 Å, no matter which cluster distance was used. This is also true for ionic pharmacophores where the IRFPG of 2.5–5.4 Å gives the best contact coverage rates. For aromatic and hydrophobic pharmacophores, a slight variation of best IRFPG as a function of cluster distance was observed. However, including the percentage of covering pharmacophores in our consideration, the IRFPG of 3.5–5.4 Å and 3.5–6.1 Å are optimal for aromatic and 3.0–5.0 Å is the best choice for hydrophobic pharmacophores. Therefore, in the remainder of this paper all pharmacophore models were generated using these optimal IRFPG ranges; IRFPG of 3.5–6.1 Å was used for aromatic pharmacophores.

Figure 3 also shows that the contact coverage rate decreases with increasing cluster distances. This is not surprising, as a larger cluster distance will result in a sparser pharmacophore model. Such sparse models will less likely cover all known contacts. In parallel, the percentage of the covering pharmacophore does not change significantly with variation in cluster distance. This is a result of the compensatory effects of decreasing number of covering pharmacophores and decreasing total number of pharmacophores (Supporting Information S3).

It is noteworthy that, for hydrogen bond, aromatic and ionic pharmacophores, a method that defines the pharmacophores based on the energy-weighted geometric center (GC) of the grid points was also tested. This method resulted in the sparsest pharmacophore models and showed a significant drop in performance compared to models resulting from k-means clustering. Recently Tintori et al.⁹ reported the pharmacophore generation approach based on the MIFs calculated by the popular GRID²² program. They used several criterions to select the points of minimum energies on MIFs as the pharmacophore elements. Although our energy-weighted geometric center does not directly coincide with the minimum energy position, our results nevertheless suggest that using the minimum energy positions might be inadequate to cover the critical protein-ligand interactions.

In summary, considering both the contact coverage rate and the enrichment of the covering pharmacophores, it seems that a 1Å cluster distance is the best option for reproducing the native contacts, and consequently might be the optimal choice for subsequent pose prediction using protein-pharmacophore models. However, taking the absolute number of pharmacophores into consideration (Table 1), the 1Å cutoff might not be the optimal choice for clique detection as the computation efficiency decreases exponentially as the number of pharmacophores increases. For example, the number of hydrogen-bond pharmacophores generated using 1Å radius (554) is more than twice the number of pharmacophores generated using a 2Å radius (225). As will be shown in the next section, to achieve the same performance in pose prediction, the high density pharmacophore map generated using 1Å cutoff requires a much smaller edge tolerance and is more resource demanding than a sparser pharmacophore model.

Table 1.

The number of protein pharmacophores and number of contacts averaged over all protein-ligand complexes for each interaction type. Only the pharmacophore models generated using the optimal IRFPG (hydrogen-bond: 2.5–3.4 Å; hydrophobic: 3.0–5.0 Å; aromatic: 3.5–6.1 Å; ionic: 2.5–5.4Å) were shown. GC: energy-weighted geometric center.

Distance cutoff for clustering	Hydrogen-bond	Hydrophobic	Aromatic	Ionic
1.0Å	554	343	119	219
1.5Å	305	114	60	88
2.0Å	225	62	42	53
2.5Å	189	40	33	37
3.0Å	174	29	28	29
GC	79	N/A	9	7
Average number of contacts	4	10	1	0.4

Pharmacophore-based poses prediction and ranking using native conformation

Protein-based pharmacophore models are traditionally used for virtual screening purposes^7–9. Because the size of the pharmacophore model is typically quite large, a selection of pharmacophore points that are most critical for binding known ligands is usually needed to generate workable queries for virtual screening. On the other hand, protein-based pharmacophore models are, by definition, enriched with the information of potential interactions between other ligands with novel scaffold and the protein target. Consequently, another application of the protein-based pharmacophore models is to use them for ligand pose prediction and pose ranking. The use of the protein pharmacophores as “site points” for pose sampling in some pioneer docking programs^{11, 23–25} can be viewed as such application examples.

To explore the potentials and limits of our protein-based pharmacophore models for pose prediction and pose ranking, we investigated their ability in reproducing the native-like binding poses using the in-house program PharmPose. As described in the Materials and Methods section, PharmPose is based on a clique-detection algorithm^17–18. It enumerates all the possible multiple-points matches between ligand pharmacophores and protein pharmacophores. In this process, an edge tolerance that defines the uncertainty allowed for matching the distances of the pharmacophore edges significantly influences the accuracy and efficacy of pose prediction. For a model with a large number of pharmacophore elements, a small edge tolerance value may be necessary to reduce the possible number of matches between ligand and protein pharmacophores and lower the computational time for pose sampling. However, this reduction in sampling space might potentially cause a reduced probability to generate the native binding pose. Therefore, we screened different combinations of edge tolerance and cluster distance to identify the best combination for pose prediction.

To study the relationship between size of protein-based pharmacophore models and the edge tolerance, we performed a native pose-prediction study using the native ligand conformation as input. This approach removes any additional uncertainty in the pose prediction due to difficulties in pre-generating native-like ligand conformations. We first generated the pharmacophore features for each native ligand conformation in the PDBbind core set. The in-house program PharmPose was then used to sample all possible matches between the ligand pharmacophores and the corresponding protein-based pharmacophore models. To accelerate the pose sampling process, only hydrogen bonding and hydrophobic pharmacophores were used in the clique detection process. This can be substantiated by examining the average number of ligand-protein contacts found in the PDBbind core set (Table 1); on average only one aromatic interaction and less than one ionic interaction per protein-ligand complex is observed in the known protein-ligand complexes. Therefore, considering only hydrogen-bond and hydrophobic pharmacophores in the clique detection should be sufficient to generate native-like poses. The investigated settings for pharmacophore–model generation and edge tolerance are listed in Table 2. The average RMSD_min values, which measure the minimal RMSD between the sampled poses to the native binding pose, and the percentages of the protein-ligand complexes having native-like poses with an accuracy of 1Å, 2Å and 3Å RMSD, are also reported in Table 2. In general, for the same pharmacophore model, prediction accuracy increases as the edge tolerance increases. A larger edge tolerance results in a larger pool of predicted poses and therefore a higher probability for finding native-like poses. However, this increase in accuracy is accompanied by a reduction in the sampling efficiency measured by the average CPU time of pose generation per complex. For instance, for a pharmacophore model with a 1Å cluster distance for both hydrogen bond and hydrophobic pharmacophore generation, the required CPU time per complex increased five folds if the edge tolerance was increased from 0.05 Å to 0.10 Å. For a pharmacophore model with a larger cluster distance a larger edge uncertainty can be tolerated to achieve similar accuracy without losing efficiency. Overall, the pharmacophore models using a 2.0 Å cluster distance for hydrogen-bond and 1.5 Å for hydrophobic pharmacophore elements combined with an 0.30 Å edge tolerance seems to provide a good compromise between sampling accuracy and efficiency. For this setting, the models are able to find a pose within 3 Å RMSD of the native pose for all protein-ligand complexes and a pose within 2 Å RMSD to the native pose for 98% of the complexes. The average required CPU time is only 13 seconds. As a consequence, this setting will be used for the following studies.

Table 2.

Sampling accuracy and efficiency of pharmacophore-based pose prediction using the native ligand conformation as input. Pharmacophore models with three different cluster distances were assessed. For each pharmacophore model, several different values for edge tolerance were tested. The quality of pose sampling were measured by the RMSD_min averaged over all the protein-ligand complexes and the percentages of protein-ligand complexes that were successfully predicted with a ligand pose within 1Å, 2Å and 3Å RMSD to its native binding configuration (%comp < 1Å, 2Å and 3Å). The average number of poses per protein-ligand complex was also listed. The average CPU time measures the efficiency of the sampling process. All computations were run on a single core of a 2.5 GHz Quad-Core AMD2380 computer.

Pharmacophore model and pose sampling settings			Poses sampling results
Hydrogen-Bonding	Hydro-phobic	Edge tolerance (Å)	RMSDmin (Å)	%comp < 1Å	%comp < 2Å	%comp < 3Å	Average number of poses	CPU time (s)
1.0Å	1.0Å	0.05	1.27	45%	87%	96%	1030	8
		0.075	1.00	63%	95%	98%	2095	14
		0.08	0.93	69%	97%	99%	2724	28
		0.10	0.82	79%	98%	100%	4237	41
1.5Å	1.5Å	0.10	1.51	34%	79%	92%	429	3
		0.15	1.13	55%	90%	98%	1046	5
		0.20	0.94	70%	95%	99%	1987	10
		0.25	0.84	81%	97%	99%	3179	17
2.0Å	1.5Å	0.25	0.93	67%	96%	99%	2001	9
		0.30	0.83	76%	98%	100%	2837	13
		0.35	0.78	81%	98%	100%	3740	19

Given that our protein-based pharmacophore models are able to generate at least one pose within 2 Å RMSD to the native binding pose for 98% of the protein-ligand complexes, we asked the question whether the protein-based pharmacophore model can also provide sufficient information for ranking the native-like poses before nonnative-like poses. To address this question, we used a simple geometric scoring function (equation 1 in Materials and Methods section) to score and rank the predicted poses. Because the scoring process does not demand as many computational resources as the pose sampling process, the most detailed pharmacophore model generated with a 1 Å cluster distance for all pharmacophore types was used for scoring. The rationale is that the densest pharmacophore model provides the best description of the binding site contacts as demonstrated in the previous section (cf. Figure 3), and consequently should provide the largest amount of information for scoring.

As a preliminary test, we first ranked all poses with an equally-weighted scoring function in which all the pre-factors in equation 1 were set to one. We investigated the enrichment of native-like poses among the top-100 ranked configurations. Table 3 displays the ranking results measured by the RMSD_min and the percentage of complexes having native-like poses among the top-100 ranked poses. To demonstrate that the pharmacophore model does provide extra information throughout scoring, we also randomly selected 100 poses from the full ensemble of poses for each protein-ligand complex to serve as a negative control. As shown in Table 3, the equally-weighted scoring scheme clearly outperforms the randomly selected scheme in terms of RMSD_min, average rank of RMSD_min and the percentages of systems with generated poses within 1 Å and 2 Å RMSD to the native pose. This suggests that the simple pharmacophore-based scoring scheme does provide valuable information for pose ranking.

Table 3.

Pharmacophore-based pose ranking. RMSD_min: the minimal RMSD between the sampled poses to the native binding pose averaged over all the protein-ligand complexes. Average rank of RMSD_min: ranking of the best pose averaged over all the complexes. %comp < 1Å, %comp < 2Å, %comp < 3Å: percentage of the complexes with poses within 1 Å, 2 Å and 3 Å RMSD to the native pose. Exhaustive: no scoring process was used to rank the poses and the evaluation was over the full ensemble of generated poses. Randomly selected ranking scheme: 100 poses were randomly selected from the ensemble of poses for each protein-ligand complex to serve as a negative control for the other ranking schemes. Equally-weighted ranking scheme: all the weights in equation 1 were set to one. Optimized weights ranking scheme: weights in equation 1 were optimized to achieve a better discrimination between native-like and nonnative-like poses. For all ranking schemes (except ‘Exhaustive’) the top-100 ranked poses are considered.

Input conformer	Ranking scheme	RMSDmin(Å)	Average rank of RMSDmin	%comp < 1Å	%comp < 2Å	%comp < 3Å
Native	Exhaustive	0.83	N/A	76%	98%	100%
	Randomly selected	1.42	44	30%	81%	97%
	Equally-weighted	1.02	32	65%	91%	98%
	Optimized weights	0.93	32	68%	94%	99%
Omega	Exhaustive	1.20	N/A	49%	90%	97%
	Randomly selected	2.16	49	5%	48%	82%
	Optimized weights	1.80	42	19%	71%	87%

To further explore the potential of the simple pharmacophore-matching scoring function, we optimized the weights of this function to investigate whether such optimization can further improve the pose ranking quality. Starting from the top-1000 ranked poses for each system based on the equally-weighted scoring function, 11⁴ different sets of pre-factors in equation 1 were assessed for their ability to distinguish native-like poses (RMSD ≤ 2 Å) from non-native-like poses (RMSD > 2 Å) (see Materials and Methods section for detail). The fitness of each set of pre-factors was measured by the average AUC over all the protein-ligand complexes. The best average AUC value was obtained for the set of pre-factors with values w_hbond = −0.7, w_hphob = −0.4, w_arom = −0.6 and w_ionic = −0.6. It should be mentioned that on average there are more hydrophobic ligand-protein contacts than any of the other three types (Table 1). The lower pre-factor of the hydrophobic pharmacophore compared to the pre-factors of the other three pharmacophore types potentially balances the contribution of different interaction types to the final score. The performance of the optimized weights is reported in Table 3 for the top-100 ranked poses. The RMSD_min was lowered by about 0.1 Å and the percentage of the complexes with poses within 1 Å and 2 Å RMSD of the native configuration were both increased by 3% compared to the results from the equally weighted scoring function.

Pharmacophore-based poses prediction and ranking using multiple low-energy conformations

Using the native ligand conformation as input, we identified suitable sets of parameters for pose sampling and pose ranking. Typically, the native ligand conformation is not known as a prior to the pose prediction process. Thus, software is usually used to generate an ensemble of low-energy ligand conformations prior to pose sampling. Therefore, we repeated our pose prediction and ranking experiment using the low-energy ligand conformations generated with the software Openeye Omega¹⁶ as input.

We first performed an exhaustive search to generate all possible poses without scoring (Table 3). Comparing the results with those generated by using the native ligand conformation as input allows us to assess the influence of the input conformation on the quality of sampling native-like poses. Not surprisingly, the use of low-energy conformations introduced another source of inaccuracy into the pose-generation process and this significantly reduces the sampling accuracy comparing to the exhaustive search using native conformation: the RMSD_min decreased on average by 0.4 Å and the success rate of generating ligand pose within 1 Å, 2 Å and 3 Å RMSD to the native pose reduced by 27%, 8% and 3%, respectively. To better quantify the reason for this observed reduction in sampling accuracy, we assessed the relationship between best pose RMSD (RMSD_min) and Omega-generated conformations with lowest RMSD (Omega RMSD_best) to the native conformation for each protein-ligand complex (Figure 4, left). In general, a correlation between RMSD_min and the Omega RMSD_best was observed. As all pre-generated conformations are docked rigidly into the binding site using PharmPose, the lowest RMSD_min of each complex can only be greater than or equal to Omega RMSD_best. In other words, in the ideal situation where no additional inaccuracy is introduced throughout the posing process, all data points in Figure 4 left will lay on the y = x line and the average RMSD_min value will equal the value of the average Omega RMSD_best (0.73 Å). However, in such an ideal case, the average RMSD_min value using the native conformations as input would be zero; the observed average RMSD_min value using the native conformation as the input, however, was on average 0.83 Å. Adding this additional uncertainty value to the ideal y = x curve (resulting in the y = x + 0.83 Å line in Figure 4 left), demonstrates that the native pose for the majority of complexes can be reproduced with such an additional inaccuracy compared to the Omega RMSD_best value. The 23 compounds that are located outside of this region all have an Omega RMSD_best value below 1 Å (red points in Figure 4, left). For these outliers a good correlation between the RMSD_min using the Omega-generated conformation and the RMSD_min using the native conformations was observed (Figure 4, right). These observations mean that ligands whose native pose is difficult to reproduce using the Omega-generated conformations as input are also difficult to reproduce when the native conformation was provided as input. In conclusion, the average RMSD_min value when using the Omega-generated conformations can be largely explained as the sum of inaccuracies introduced through the pre-generation of ligand conformations and the pose-sampling process.

Figure 4.

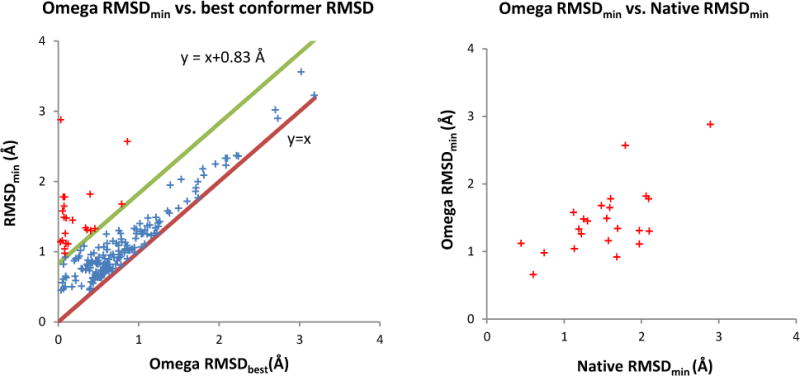
Analysis of the pose-sampling results using Omega-generated conformations as input. Left: Correlation between the RMSDs of best pose (RMSD_min) and the best omega-generated conformation (Omega RMSD_best) with respect to native pose and native conformation, respectively. In the ideal situation in which no additional inaccuracy will be introduced during the pose-sampling process, all points should locate on the ideal line of y = x. Estimated from the RMSD_min for using native conformations as input, the majority of complexes (blue crosses) fall into the region between the associated line of uncertainty (y = x + 0.83 Å) and the ideal line (y = x). Right: Correlation between the RMSD_min values of using native and Omega-generated conformations for the outliers that are located outside of the region defined by y = x + 0.83 Å and y = x (red crosses on left figure).

Finally, we assessed the quality of the optimized pharmacophore-based scoring function for ranking the poses generated using the Omega-generated conformations. The results for the top-100 ranked poses are reported in Table 3. Both the RMSD_min and the percentage of systems with native-like poses dropped significantly compared to the results obtained using the native conformation as input. These results are not surprising for two reasons: First, using Omega-generated conformations introduces additional uncertainty in the pose-generation process as discussed previously. Second, many more poses need to be ranked to identify native-like poses which presents a much harder problem for the pose-ranking process using Omega-generated conformations compared to the same process using only the native conformation. In the case that the native conformer was used, there are on average only 2837 poses per protein-ligand complex that need to be ranked. This number increased to over 800,000 per complex if multiple low-energy conformations were provided. To make the situation worse, the ensembles of poses using the Omega-generated conformations were more highly populated by non-native-like poses (> 3 Å) than native-like poses (data not shown). Given the difficulty of this ranking problem, the increased performance of the simple pharmacophore-based scoring scheme compared to the performance of the random selection of conformations suggests the usefulness of the protein-based pharmacophore models for pose ranking.

Comparison with molecular docking programs

Despite tremendous efforts, the identification of native-like binding poses as top-ranked configurations in a reasonable amount of computation time is still an unsolved issue^26–27. On the other hand, it has been shown that current docking programs are more mature in sampling native-like poses^27–28. Using the sampled docking poses, various approaches^29–30 can be applied to score those poses. In this study, we have assessed the potential of the protein-based pharmacophore models for pose prediction and ranking. Although a direct comparison with the current state-of-the-art docking programs is not an aim of this study, it is of interest to understand the potentials and limits of the protein-based pharmacophore models for pose generation and ranking compared with existing docking programs. Table 4 displays the results recently reported by Plewczynski et al. evaluating seven widely used docking programs on the PDBbind refined set²⁸. They used both the native conformer and ten omega-generated low-energy conformers as inputs in their evaluation. For each input ligand conformation, ten poses were generated from each docking program. To compare their results with ours, we recalculated the RMSD_min and the success rate of generating a ligand pose within 2 Å RMSD to the native configuration for the top-10 ranked poses sampled using the native conformation. It is encouraging to observe that our simple pharmacophore-based approach outperformed most of the tested docking programs. Using the Omega-generated conformations demonstrated that our approach also performs significantly better than three of the tested docking programs. Only three of the evaluated docking programs generated a success rate over 71% for docking the ligand within 2 Å RMSD to its native pose. Considering that only a simple pharmacophore-based scoring function was used in our study, a 71% success rate in posing the ligand within 2 Å to its native conformation is very encouraging. We recognized that the datasets used in our study are not exactly the same as used by Plewczynski et al.. However the “core set” we used is a subset non-redundantly sampled from the “refined set” used in Plewczynski et al.’s study. Furthermore, the average RMSD_min values generated by our pharmacophore models are also quite comparable to the results of four docking programs (Glide, GOLD, LigandFit and Surflex) evaluated by Li et al. on the PDBbind core set²⁷.

Table 4.

Comparison of PharmPose to seven docking programs evaluated by Plewczynski et al.²⁸. The results using native conformer as input were recalculated for the top-10 ranked poses to be comparable to that of Plewczynski et al.’s study. The RMSD_min was averaged over all the protein-ligand complexes.

	Native conformer		Omega-generated conformer
	RMSDmin (Å)	%comp < 2 Å	RMSDmin (Å)	%comp < 2 Å
Surflex	2.25	67%	1.30	86%
GOLD	1.75	71%	1.25	83%
eHiTs	N/A	N/A	1.65	72%
Glide	2.35	65%	1.85	70%
AutoDock	1.65	72%	2.95	66%
LigandFit	1.95	69%	2.15	64%
FlexX	3.10	56%	3.10	56%
PharmPose	1.70	74%	1.80	71%

Conclusions

Starting from the optimization of an empirically-based pharmacophore generation program, we have studied the potential of protein-based pharmacophore models for ligand pose prediction and ranking. After optimization of the pharmacophore generation process, the protein-based pharmacophore models were able to cover more than 95% of the experimentally known protein-ligand contacts. Using these optimized pharmacophore models, we first studied the quality of pose prediction with the native conformations of each ligand as input. For 98% of all protein-ligand complexes, a native-like binding pose could be generated, and using an optimized pharmacophore-based scoring function the native-like poses could be ranked within the top-100 for 94% of all systems. Using multiple low-energy conformations as input for pose prediction and ranking, a 71% success rate was achieved for predicting native-like binding pose within the top-100 ranked poses. Our studies demonstrate that significant variations in reproducing native contacts and as a consequence native ligand poses exist dependent on the details of generating protein pharmacophores. Thus, it is essential to tune the parameters of the underlying pharmacophore-generation process to obtain optimal performance in native-pose identification.

Our method’s results for pose generation and ranking are comparable in quality to widely used docking programs that are typically significantly more time-consuming than our method. Noticing that a fair comparison between different docking programs is quite difficult³¹, due to many influencing factors, we do not intend to draw any firm conclusions from such a comparison. However, this comparison inspires us to further explore the usefulness of protein-based pharmacophore models in pose predictions. We also want to emphasize that it is not the aim of our method to compete with existing docking methods per se as our simple pharmacophore-based scoring scheme is not comparable to more sophisticated scoring functions used in standard docking. We view our approach as a fast method to generate native-like poses and enrich those poses within the top-100 ranked poses. As a consequence, no attempts have been made to apply the method to virtual screening as important free-energy contributions such as ligand desolvation or entropy are not or only rudimentarily accommodated in the simple pharmacophore-scoring scheme. The future direction is to combine our protein-pharmacophore method with more sophisticated pose-optimization methods: For example, starting from the top-100 ranked poses, an optimization method combined with a more sophisticated scoring function might be able to further optimize the predicted poses and their ranking. This combination of fast pose generation, optimization and more time-consuming scoring could then also been applied to virtual screening applications as ultimate goal.