Abstract
Competitive adsorption of counterions of multiple species to charged surfaces is studied by a size-effect included mean-field theory and Monte Carlo (MC) simulations. The mean-field electrostatic free-energy functional of ionic concentrations, constrained by Poisson’s equation, is numerically minimized by an augmented Lagrangian multiplier method. Unrestricted primitive models and canonical ensemble MC simulations with the Metropolis criterion are used to predict the ionic distributions around a charged surface. It is found that, for a low surface charge density, the adsorption of ions with a higher valence is preferable, agreeing with existing studies. For a highly charged surface, both of the mean-field theory and MC simulations demonstrate that the counterions bind tightly around the charged surface, resulting in a stratification of counterions of different species. The competition between mixed entropy and electrostatic energetics leads to a compromise that the ionic species with a higher valence-to-volume ratio has a larger probability to form the first layer of stratification. In particular, the MC simulations confirm the crucial role of ionic valence-to-volume ratios in the competitive adsorption to charged surfaces that had been previously predicted by the mean-field theory. The charge inversion for ionic systems with salt is predicted by the MC simulations but not by the mean-field theory. This work provides a better understanding of competitive adsorption of counterions to charged surfaces and calls for further studies on the ionic size effect with application to large-scale biomolecular modeling.
1 Introduction
Electrostatic interactions play an important role in many complex systems, such as biological processes, soft matter material, nanofluids, and electrochemical devices [1–8]. Accurate and efficient modeling and computations of such interactions have been challenging due to the inhomogeneity, complicated geometry, multiple scales, and the nature of many-body interaction of an underlying charged system.
A common scenario of electrostatic interactions is a mixture of crowded mobile ions of multiple species with different valences and sizes in an electrolyte surrounding an external charged surface. Excluded-volume effects or size effects of such mobile ions, in particular effects of different ionic sizes, contribute significantly to the electrostatic free energy and forces, which in turn determine the structure and stability of an underlying system. For instance, the size of monovalent cations can influence the stability of RNA tertiary structures [9]; and differences in ionic sizes can also affect how mobile ions bind to nucleic acids [10, 11]. Concentrations of ions in an ion channel can reach as high as dozens of mol/L (about 30 mol/L in calcium and sodium channels), and the ionic sizes can affect the ion transport and channel selectivity [12]. Detailed density-functional theory calculations, Monte Carlo simulations, and integral equations calculations confirm some of these experimentally observed properties due to the non-uniformity of ionic sizes [13–17].
Historically, many theoretical studies of electrostatic interactions have been based on the classical, mean-field, Poisson–Boltzmann (PB) theory [18–21]. In particular, such a theory has been successfully applied in biomolecular modeling and colloidal science; see [1, 3, 8, 22, 23] and the references therein. In the PB theory, electrolytes are treated as ideal ionic gases, and the ionic concentrations are related to the electrostatic potential by the Boltzmann distributions. This theory, often very efficient, thus works well for monovalent ions, low surface charge densities, and high solvent dielectric coefficients. The mathematical form of the PB theory is the PB equation which is Poisson’s equation for the electrostatic potential with the equilibrium ionic concentrations given by the Boltzmann distributions via the potential. In a variational setting, such distributions result from the equilibrium conditions for a mean-field electrostatic free-energy functional of ionic concentrations where the potential is determined by Poisson’s equation [24–28]. Despite its success in many applications, the classical PB theory is known to fail in capturing the ion-ion correlations and ionic size effects, particularly for highly charged systems at molecular scales [29,30].
For years, attempts have been made to include ionic size effects, particularly nonuniform ionic size effects, into a PB-like efficient approach [26,31–37]. See also [38–45]. One of the key ideas has been to introduce the local concentration of solvent molecules, in addition to those of ions of multiple species, and to incorporate all the ionic and solvent molecular volumes in the entropic part of a mean-field electrostatic free-energy functional. If all linear sizes (including that of solvent molecules) are the same, such a free-energy functional can be derived using a lattice-gas model [32,35,36]. Moreover, there are explicit formulas, the generalized Boltzmann distributions, relating equilibrium ionic concentrations and the corresponding electrostatic potential. These distributions, together with Poisson’s equation, lead to the generalized PB equation for the case of a uniform ionic size [26, 27, 46]. For a system of three ionic species with two different ionic sizes, Chu et al. [34] derived a different size-modified PB equation from a similar lattice-gas model and applied this equation to study the ionic size effect in the binding of ions to DNA. For a general system, Tresset [36] derived an expression of the free energy with an effective volume fraction of free space, under the assumption that the ionic excluded volumes are dispersed from each other to a reasonable extent.
For the general case of multiple ionic species with different valences and sizes, Li [26] proposed and analyzed a semi-phenomenological free-energy functional of ionic concentrations with Poisson’s equation as a constraint for the electrostatic potential. This functional is obtained simply by using different individual ionic sizes instead of a uniform size in the previous functional derived from a lattice-gas model. Equilibrium conditions for the new and general free-energy functional are nonlinear algebraic equations for the equilibrium concentrations. It is shown that such conditions determine completely the dependence of equilibrium ionic concentrations on the corresponding electrostatic potential [26]. Explicit formulas of such dependence and hence Boltzmann-like distributions for the equilibrium concentrations, however, seem unavailable. Therefore, there is no explicit PB-like equation of the electrostatic potential in the general case.
Nevertheless, Zhou et al. [37] developed a robust numerical method for minimizing such a functional to obtain the equilibrium ionic concentrations and the corresponding electrostatic potential. The starting point there is to reformulate the variational problem as a constrained optimization problem [47, 48]. An augmented Lagrange multiplier method is then constructed and implemented to solve this constrained optimization problem. Extensive numerical results reported in [37] demonstrate that the new mean-field, size-effect included model can describe many detailed properties of ionic concentrations, including the stratification of concentrations, that have been predicted by other refined models but not by the classical PB theory; cf. [33,36]. In particular, it is found that the ionic valence-to-volume ratio is the key parameter in the stratification [37].
In this work, we study the ionic size or excluded volume effect to the structure of electrical double layer in the vicinity of a highly charged surface, using both the mean-field model and Monte Carlo (MC) simulations. Our goal is two-fold. First, we would like to understand how counterions with different valences and sizes compete in the adsorption to the charged surface, and how the ionic valence-to-volume ratio affect the ordering of ion packing near such a surface. Second, we would like to examine the validity of the mean-field theory with nonuniform size effects by comparing it with the MC simulations.
The adsorption of counterions to a charged surface is determined by the competition between the entropic and energetic contributions of an underlying system of electrolyte. The ionic size effect is quite significant in such adsorption, since the excluded volume of crowded ions reduces the mixed entropy, and thus increases the Helmholtz free energy of the total system. Concentrations of counterions can reach maximal values at the charged surface controlled by the ionic sizes. The competition of entropy and energy results in a stratification of counterions of different species in the electrical double layer, as revealed in both experimental investigations [49] and theoretical predictions [36,37,50,51]. For a low surface charge density, the electrostatic interaction dominates and the ions with higher valence are most likely to stay closest to the charged surface. For a highly charged surface, smaller counterions are stronger in competition to form the first layer of the stratification [16, 51]. Our mean-field numerical computations and MC simulations reproduce these results. In particular, our MC simulations validate the prediction by the mean-field theory of the role of ionic valence-to-volume ratios in the counterion stratification.
MC simulations treat an underlying system of electrolyte as a set of discrete particles and provide equilibrium properties of the system with statistical averages [52, 53]. Such simulations have been a standard tool in the study of structures of electrical double layer, if the geometry of the charged surface is not too complicated [16,51,54,55]. In MC simulations, ionic size and correlation effects are automatically included, and image charge effects can also be included [56–60]. Therefore, the correlation-induced phenomena, such as charge inversion and like-charge attraction, can be described by MC simulations [29,55].
Our simulation system consists of a spherical macroion immersed centrally in an electrolyte system. There are counterions of multiple species in the electrolyte. The entire system is assumed to be neutral in charge. The parameters of the system include the linear size of the simulation box, the radius and constant surface charge density of the macroion, and the valence, volume, and total number of each species of (micro) mobile ions. The same set of parameters are used in our MC simulations and mean-field computations. We use unrestrictive primitive models of ionic system, treating ions as hard spheres. Based on such a model, we use canonical ensemble MC simulations with Metropolis criterion. We plot the radial particle density function for each species of mobile ions. Such functions are compared with the corresponding equilibrium ionic concentrations predicted by our mean-field theory.
The rest of this paper is organized as follows: In Section 2, we introduce the mean-field theory and numerical method for nonuniform ionic size effects. In Section 3, we describe our method of Monte Carlo simulations. In Section 4, we present and discuss the results of our MC simulations and mean-field computations. Finally, in Section 5, we draw conclusions.
2 Mean-Field Theory and Method
We consider an electrolyte with M species of ions. For each i (1 ≤ i ≤ M), we denote by zi the valence and vi the volume of an ion of the ith species. We also denote by Ni the total number of ions of the ith species. The total number of all ions is . We assume that there is a spherical colloidal particle—a charged macroion—of radius R inside the electrolyte solution and that its charge effect is described effectively by a constant surface charge density, denoted σ. We assume the system charge neutrality
| (2.1) |
where z = 4πR2σ/e is the valence of the macroion and e is the elementary charge.
We assume that the entire system occupies the cubical region (−L/2, L/2)3 with the linear size L > 2R and that the macroion occupies the spherical region BR of radius R centered at the origin. Therefore all the ions are in the region Ω = (−L/2, L/2)3\BR. We denote by Γ = ∂BR the boundary of the sphere BR, i.e., the spherical surface of the macroion.
2.1 A mean-field theory with nonuniform size effects
For each i (1 ≤ i ≤ M), we denote by ci(r) the local concentration at a spatial point r ∈ Ω of ions of the ith species. The charge density of solution is then given by . All the concentrations ci(r) are constrained by
| (2.2) |
We also denote by v0 the volume of a solvent molecule. The local concentration c0 = c0(r) of the solvent molecules is defined by
For a given set of ionic concentrations c = (c1, …, cM ), a mean-field approximation of the electrostatic free energy is given by
| (2.3) |
The first part Fpot[c] is the electrostatic potential energy, defined by
| (2.4) |
where Φ is the electrostatic potential. It is determined by Poisson’s equation
| (2.5) |
together with the boundary condition
| (2.6) |
where ε0 is the vacuum permittivity, ε is the relative permittivity or dielectric coefficient of the solution, and n is the exterior unit normal at the boundary of Ω that consists of the spherical surface Γ and the boundary, Γbox, of the box (−L/2, L/2)3. We shall assume that ε is a constant in the entire solution region Ω. Notice that Φ is not an independent variable of the functional F[c].
The second part Fent[c] is the entropic contribution. It is given by [26,37]
| (2.7) |
where kB is the Boltzmann constant and T is the absolute temperature. Notice that the summation index starts from i = 0. Notice also that in the variational approach to the classical PB equation, the solvent entropy is not included and all the ionic linear sizes are replaced by the de Broglie wave length [24,25,27].
The set of equilibrium ionic concentrations c = (c1, …, cM ) is defined to minimize the free-energy functional (2.3), subject to the constraint (2.2). The equilibrium electrostatic potential is determined by the corresponding equilibrium ionic concentrations through Poisson’s equation (2.5) and the boundary condition (2.6).
Alternatively, we can introduce for each i the chemical potential μi for ions of the ith species, and add the following term
| (2.8) |
to the free energy F[c] in (2.3). The chemical potentials μi (i = 1, …, M ) can be regarded as Lagrange multipliers accounting for the constraint (2.2). With these chemical potentials, one minimizes the new, total electrostatic free-energy functional that now consists of all the integral terms in (2.4), (2.7), and (2.8), without the constraint (2.2).
Taking the variational derivative with respect to each concentration field ci(r) of the new, total free energy and setting it to 0, we obtain with suitable boundary conditions for Poisson’s equation (2.5) the conditions for equilibrium concentrations c1, …, cM [26]
| (2.9) |
In the special case that v0 = v1 = · · · = vM, one can solve this system of nonlinear algebraic equations to obtain explicit formulas of ci(r) = ci(Φ(r)) (i = 1, …, M). These are the generalized Boltzmann distributions. For the general case, it is known that the conditions (2.9) determine uniquely ci(r) = ci(Φ(r)) (i = 1, …, M ); but explicit formulas for such dependence seem unavailable. See [26,27].
2.2 A constrained optimization method
By integration by parts, Poisson’s equation (2.5), and the boundary conditions (2.6), we can rewrite the free-energy functional (2.3), which is the sum of Fpot[c] given in (2.4) and Fent[c] given in (2.7), as
where Φ solves the boundary-value problem of Poisson’s equation (2.5) and (2.6). Notice that the dependence of F on Φ is now explicitly indicated. One can verify mathematically that the minimization of F[c] defined in (2.3) over all c subject to (2.2) is equivalent to that of F[Φ, c] over all (Φ, c) subject to (2.2), (2.5), and (2.6).
Introduce the Bjerrum length lB = e2/(4πεε0kBT). Define Φ′ = eΦ/(kBT), and , σ′ = 4πlBσ/e, and ω′ = (4πlB)−1/3ω for ω = Γ, Γbox, or Ω. Then F [Φ, c] = εε0(kBT/e)2F′[Φ′, c′], where
| (2.10) |
and is defined similarly using the primed quantities. The constraint (2.2), Poisson’s equation (2.5), and the boundary condition (2.6) become now
| (2.11) |
| (2.12) |
| (2.13) |
respectively, where n′ is the unit exterior normal at the boundary of Ω′.
For simplicity, we will drop all the primes in what follows.
We apply an augmented Lagrange multiplier method [61, 62] to numerically minimize the functional F[Φ, c] defined in (2.10) subject to (2.11)–(2.13) (with all the primes dropped). Our method is an improved version of that developed in our previous work [37] for minimizing numerically a similar functional formulated using (E, c) instead of (Φ, c), where E = −∇Φ is the electric field. In the augmented Lagrange multiplier formulation, we solve the corresponding saddle-point problem
| (2.14) |
where Λ = (λ1, …, λM ) ∈ ℝM, s = (s1, …, sM ) ∈ ℝM with each si ≥ 0, and
The function Ψ is the Lagrange multiplier for Poisson’s equation (2.5). It satisfies the same boundary conditions as for Φ, cf. (2.13) (no primes). The numbers λ1, …, λM are the Lagrange multipliers for the constraint (2.11) (no primes). The last summation term is a penalty term. It is added to stabilize and accelerate our numerical iterations.
The solution (Φ, c, Ψ, Λ, s) to the saddle-point problem (2.14) is determined by the following equations:
| (2.15) |
| (2.16) |
| (2.17) |
| (2.18) |
Since both Φ and Ψ satisfy the same boundary conditions, Eq. (2.15) implies that they differ by an additive constant. We may choose this constant to be 0 and assume that Ψ = Φ in Ω. Notice that Eq. (2.16) is Poisson’s equation (2.12) (no primes) and Eq. (2.18) is the constraint (2.11) (no primes). As pointed out before, the nonlinear system of algebraic equations (2.17) has a unique solution c = (c1, …, cM ) but its explicit solution formulas seem unavailable [26].
The entire system of equations is equivalent now to the three sets of equations (2.16)–(2.18) with Ψ in (2.17) replaced by Φ. We solve these equations by the following algorithm:
Algorithm
-
Step 0
. Distribute the total surface charge 4πR2σ uniformly on the spherical surface by interpolation onto the nearest grids [37, 47]. Initialize Φ(0), , and . Choose a parameter γ > 1. Set l = 0.
-
Step 1
Solve Eq. (2.16) with ci replaced by , together with the boundary condition (2.13), to obtain the solution Φ(l+1).
-
Step 2
Use Newton’s method to solve Eq. (2.17) (where Ψ is replaced by Φ) with Φ, Λ, and s replaced by Φ(l+1), Λ (l), and s(l), respectively, to obtain the solution c(l+1).
-
Step 0Step 3. Update the Lagrange multipliers
Update the penalty parameters .
-
Step 4
Test convergence. If not, set l ← l + 1 and go to Step 1.
The parameter γ > 1 is used only for updating si (i = 1, …, M ). Various kinds of approximations can be used to solve the boundary-value problem of Poisson’s equation. For instance, we can use the periodic boundary condition instead, and apply the fast Fourier transform. In this case, we have the linear complexity in terms of the number of unknowns of resulting system of linear equations. We note that the matrix-vector multiplication can be avoided in Newton’s iteration scheme for solving the system (2.17) (with Ψ replaced by Φ), since the exact formula of the inverse of related Jacobian matrix can be obtained. See [37] for more details.
3 Monte Carlo Simulations
We consider the same system described in the previous section: A macroion occupying the sphere BR of radius R centered at the origin, with a constant surface charge density σ, is immersed in an electrolyte in the box (−L/2, L/2)3. There are M species of (micro) ions in the region Ω = (−L/2, L/2)3\BR. For each i (1 ≤ i ≤ M ), an ion of the ith species has valence zi and volume vi. The number of ions of the ith species is Ni; and the total number of all (micro) ions is . We use an unrestricted primitive model for our underlying electrolyte system; and apply the canonical ensemble Monte Carlo (MC) simulations with the Metropolis criterion [50,52,63–66].
In a primitive model of electrolytes, the mobile ions are represented by charged hard spheres and the solvent is modeled through its dielectric permittivity ε. We label all the (micro) ions by k = 1, …, N. We denote by ẑk and R̂k the valence and radius of the kth ion. If the kth ion is of the ith type (1 ≤ i ≤ M), then its valence is ẑk = zi and its volume is . For convenience, we label the spherical macroion by 0 and denote R̂0 = R, the radius of the macroion. We also denote its valence by ẑ0 = z = 4πR2σ/e.
For a given configuration of the system, the Hamiltonian is defined to be the work needed to bring all the ions from infinity to their current positions. It is the sum of all pairwise interaction energies between all the ions, including the macroion. We only consider the hard-sphere contribution and the Coulomb interaction. Therefore, we define the total potential energy of the system to be
where
| (3.1) |
Here, β = (kBT)−1, lB = e2β/(4πεε0) is the Bjerrum length, and rjk is the center-center distance between the jth and kth ions. Notice that, in the case rjk ≥ R̂j + R̂k, ujk is just the Coulomb interaction energy between the jth and kth ions in the solvent with the relative dielectric permittivity ε. We shall consider the water solvent at room-temperature and thus take lB = 7 Å.
Our MC simulations consist of a sequence of single-particle moves with the periodical boundary condition. In each move, we randomly select an individual particle (i.e., mobile ion). Let us assume that the selected particle is centered at p. We then randomly generate a positive number, denoted a, from the interval [0, Δmax] for some parameter Δmax > 0. We finally place the (center of) selected particle randomly on the sphere of radius a centered at p. We use the L-periodical boundary condition in each direction, so that all the ions remain in the region Ω of electrolyte. The parameter Δmax can change during the MC moves. The acceptance or rejection of the move is determined by the Metropolis criterion. We calculate the difference ΔU = Unew − Uold of the energies of the previous (old) and current (new) configurations. If ΔU ≤ 0, the move is accepted. Otherwise, it is accepted if exp (−βΔU) is greater than a randomly generated number in [0, 1].
The entire sequence of our MC moves are divided into three parts: acceleration, equilibration, and statistics. Typically, our simulation system consists of M = 3 or 4 ionic species; and the number of ions in each of these species can vary from 25 to 50 and to 200. With these parameters, we usually perform 12 × 105N MC moves in total, with the first 105N moves for acceleration, the next 105N moves for equilibrating the system, and the last 106N moves for statistics, where N is the total number of mobile ions.
We introduce a parameter l̃B to replace lB in the definition of interaction (3.1), and dynamically change l̃B in the first part of moves, a total of 105N of them, to speed up the thermal equilibration of the crowded system of particles. We generate a geometrical sequence of 105N terms with the first and last terms being 1 and lB = 7 Å, respectively. In the mth MC move with m ≤ 105N, the parameter l̃B is taken to be the mth term in the geometrical sequence. After the first 105N moves, we fix l̃B = lB for all of the rest MC moves. We run another 105N moves so that the system can reach an equilibrium.
Throughout the entire simulation, we keep the percentage of acceptance of MC moves between 20% and 50% by adaptively adjusting the value of the maximum length Δmax. Initially, we set Δmax = 2 Å. We then change it after every 100 moves. If the acceptance rate is larger than 50% in current 100 moves, we increase Δmax by multiplying it by 1.05 but always keep the new value of Δmax to be less than or equal to l̃B. If the acceptance rate is smaller than 20% in current 100 moves, we decease Δmax by multiplying it by 0.95, and we keep the new Δmax to be greater than 0.001 l̃B.
In the last part of MC moves, a total of 106N of them, we derive the production statistics and calculate the local radial particle density (RPD) for each ionic species. The RPD of the ith ionic species is defined by
| (3.2) |
where Ni(r, r + Δr) is the number of ions of the ith species whose centers are in the spherical shell between r and r + Δr, and the bracket 〈·〉 represents an ensemble average over the shell. Notice that the denominator in the definition (3.2) is the volume of the shell. We choose Δr to be 1 Å. In our implementation, we approximate 〈Ni(r, r + Δr)〉 in (3.2) by the total number of ions of the ith species that move (in the last part of moves for statistics) into the shell between r and r + Δr, multiplied by the total number Ni of ions of ith species, divided by the total number of moves (in the last part of moves) in which an ion of ith species is displaced.
We remark that the use of periodic boundary condition effectively introduces a spatial cut-off of the underlying system region. In principle this can affect the accuracy of the calculation of electrostatic interactions. However, we have tried simulations on boxes with different linear sizes and found almost no differences in the results. In fact, we find that averagely only in one out of 10, 000 moves an ion has to “leave” through one side of the box and “come back” to the box through the opposite side. The reason for this is that most of the ions are crowded around the charged sphere, away from the boundary of simulation box.
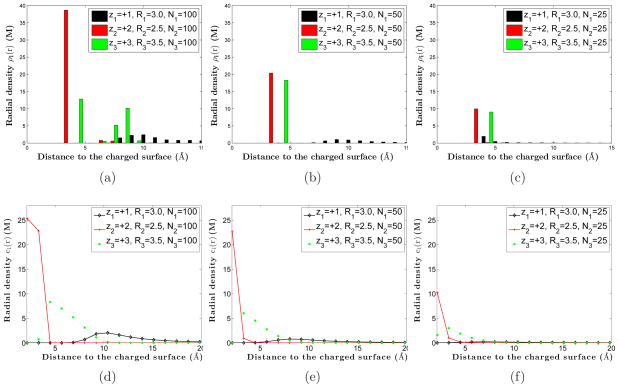
In Figure 1, we display our typical MC simulations results for two systems: one without salt and one with salt. Notice that the counterions with smaller valence-to-volume ratios have less possibility to be adsorbed to the charged surface.
Figure 1.
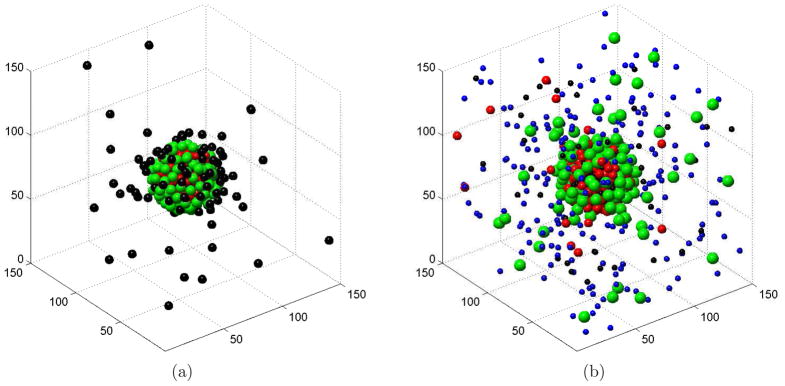
(Color online) Typical MC simulations of ions surrounding a highly charged macroion. (a) A salt free system composed of monovalent (black), divalent (red, or dark gray in print version), and trivalent (green, or light gray in print version) counterions, with radii 3 Å, 2.5 Å, and 3.5 Å, respectively. (b) A system of salt solvent with coions (blue, or dark in print version), and counterions of valences and radii +1 and 2 Å (black), +2 and 3 Å (red, or dark gray in print version), and +3 and 4 Å (green, or light gray in print version), respectively.
4 Results and Discussions
We set the linear size of our computational box (−L/2, L/2)3 to be L = 150 Å, and the radius of the spherical colloidal particle (the macroion) to be R = 15 Å. The Bjerrum length is set to be lB = 7 Å. The surface charge density σ ranges from −0.05 to −0.21 e/Å2. In our simulations, we investigate mixed solutions of three types of counterions, with their valences (z1, z2, z3) = (+1, +2, +3). We choose their radii to range from 1 Å to 4 Å. These are within the interval of physical interest. For example, the hydrated radii of monovalent hydrogen, sodium and potassium, divalent magnesium and calcium, and trivalent aluminum ions are 4.5, 2.25, 1.5, 4.0, 3.0, and 4.5 Å, respectively [67]. For salt electrolytes, we choose monovalent or divalent coions with radius 2 Å.
One of the main objectives of our study is to understand the competitive adsorption of counterions with different valences and sizes. Such property has been already investigated previously; see [16, 17, 50, 51, 63, 64, 68] and the references therein. Most of these studies found that the valence of counterion determines the competition in adsorption to a charged surface with a low surface charge density and that smaller ions are stronger in such competition for a high surface charge density. These conclusions result naturally from the competition between electrostatic attraction and entropic repulsion expressed in the free-energy functional (2.3), where the electrostatics dominates the free energy for the low surface charge density, and the entropy dominates otherwise. It has been recently found in our previous work [37] using the mean-field model described in the last section that the competition between different ions in adsorption to a charged surface can be in fact characterized by the ionic valence-to-volume ratios. Here, we use MC simulations to further explore this characterization and compare our results with those from mean-field calculations. In particular, we study a system with a crowded ionic population near a highly charged surface, as shown in Figure 1.
In what follows, for an ion of the ith species (1 ≤ i ≤ M), we denote by Ri its radius and by
its valence-to-volume ratio.
4.1 Crucial factors in the competition between counterions
We first study salt-free systems with monovalent, divalent and trivalent counterions: z1 = +1, z2 = +2, and z3 = +3. We investigate three different groups of such counterions with the following order of valence-to-volume ratios: α+2 > α+3 > α+1; α+3 > α+1 > α+2; and α+1 > α+2 > α+3. Here and below, we use α+i to denote the valence-to-volume ratio of the counterion with valence +i. We use the parameters:
Group 1: (R1, R2, R3) = (3.0, 2.5, 3.5) in Å, α+1 : α+2 : α+3 = 1 : 3.5 : 1.9;
Group 2: (R1, R2, R3) = (2.5, 3.5, 3.0) in Å, α+1 : α+2 : α+3 = 1.4 : 1 : 2.4;
Group 3: (R1, R2, R3) = (2.0, 3.0, 4.0) in Å, α+1 : α+2 : α+3 = 2.7 : 1.6 : 1.
For each group, we choose the same number of ions for each of the three different species: N1 = N2 = N3. Moreover, we select three different surface charge densities by setting N1 = N2 = N3 = 100, 50, and 25, respectively, and by using the charge neutrality (2.1). The corresponding surface charge densities of the macroions are −0.212, −0.106, and −0.053e/Å2, all in the regime of strong surface charge.
To report our MC simulations, we use bar plots, with each bar representing the radial density ρi(r) for the ith ionic species (1 ≤ i ≤ M ) as defined in (3.2). We choose the thickness of the spherical shell to be Δr = 1 Å. We also convert the unites number/volume to mol/L which is abbreviated M. To show our results of mean-field computations, we plot smooth curves of radial densities ci(r) for the ith ionic species (1 ≤ i ≤ M ) that are just the ionic concentrations in the radial direction. For each i the two quantities ρi(r) and ci(r) should be close to each other, in particular, if the shell size Δr is very small. However, since the solvent molecules are not explicitly included in our MC simulations but the concentration of solvent molecules is included in our mean-field model, the two quantities ρi(r) and ci(r) are not exactly the same.
The quantitative results of our MC simulations are illustrated in Figures 2–4, where in Figure 2 we also show our results of mean-field computations for comparison. Results in Figure 2 are obtained using Group 1 parameters, while those in Figure 3 and Figure 4 are obtained using Group 2 and Group 3 parameters, respectively. We observe clearly that counterions are adsorbed tightly to the highly charged surface, and near the surface layers of counterions of different species form, leading to the remarkable structure of stratification. Moreover, we find that the order of layering depends on the valence-to-volume ratio, instead of the valence or the size independently. Counterions with the largest valence-to-volume ratio forms the first layer closest to the charged surface, those with the second largest such ratio forms the second layer, and so on. When the surface charge density σ becomes smaller, the role of valence is more important in determining which ionic species form a layer closest to the surface. These results demonstrate that the selective adsorption and layer ordering in the stratification depend on the competition between energetics and entropy, and that the valence-to-volume ratio is an important parameter in such adsorption and layering for a highly charged surface.
Figure 2.
(Color online) The radial densities by MC simulations (a), (b), and (c), and by mean-field computations (d), (e), and (f) of the three species of counterions in Group 1: (z1, z2, z3) = (+1, +2, +3), (R1, R2, R3) = (3.0, 2.5, 3.5) in Å, and α+1 : α+2 : α+3 = 1 : 3.5 : 1.9. All three species have the same number of ions. This number is 100 in (a) and (d), 50 in (b) and (e), and 25 in (c) and (f), respectively. Hence the constant surface charge density decreases from (a) and (d), to (b) and (e), and to (c) and (f).
Figure 4.
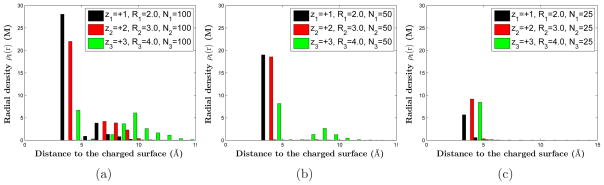
(Color online) The radial densities obtained by MC simulations of the three species of counterions in Group 3: (z1, z2, z3) = (+1, +2, +3), (R1, R2, R3) = (2.0, 3.0, 4.0) in Å, and α+1 : α+2 : α+3 = 2.7 : 1.6 : 1. All three species have the same number of ions. This number is 100 in (a), 50 in (b), and 25 in (c), respectively. Hence the constant surface charge density decreases from (a) to (b) and to (c).
Figure 3.
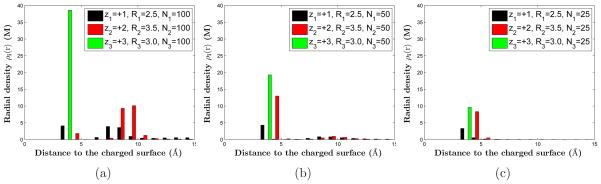
(Color online) The radial densities obtained by MC simulations of the three species of counterions in Group 2: (z1, z2, z3) = (+1, +2, +3), (R1, R2, R3) = (2.5, 3.5, 3.0) in Å, and α+1 : α+2 : α+3 = 1.4 : 1 : 2.4. All three species have the same number of ions. This number is 100 (a), 50 (b), and 25 (c), respectively. Hence the constant surface charge density decreases from (a) to (b) and to (c).
In Figure 2, we find a qualitative agreement of our size-effect included mean-field theory with the MC simulations. We note that the peaks of ionic densities close to the surface predicted by the MC simulations have a larger magnitude and are closer to the surface than those predicted by the mean-field theory.
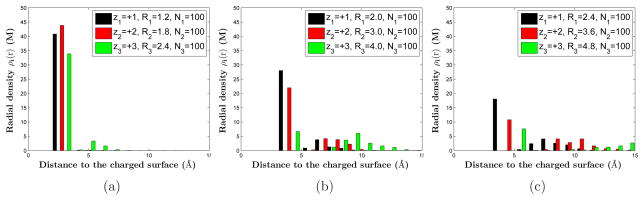
We now investigate the sensitivity of the ionic sizes with respect to the ionic structure in the vicinity of charged surface. We fix the surface charge density to be σ = −0.22e/Å2. We consider three species of counterions with valences zi = +i (i = 1, 2, 3) and number of ions N1 = N2 = N3 = 100. In Figure 5, we plot the ionic densities for various combinations of the ionic radii R1, R2, and R3. The radius of the trivalent counterion is decreased from 4 Å in Figure 5 (a) to 3.5 Å in Figure 5 (b) so that the divalent and trivalent species have almost the same valence-to-volume ratio. The radius of the monovalent ion is decreased from 2 Å in Figure 5 (b) to 1.5 Å in Figure 5 (c). In both cases, the species with the highest valence-to-volume ratio, i.e. the monovalent ionic species, remains the strongest in the competition to form the first layer closest to the charged surface. This indicates that the ionic competitive ability in adsorption is greatly improved by a slight decrease of its radius, which weakens the ionic entropic repulsion. From Figure 5 (b), we also find that when two species of counterions have close values of valence-to-volume ratios, the species with a higher valence will have a stronger ability of adsorption.
Figure 5.
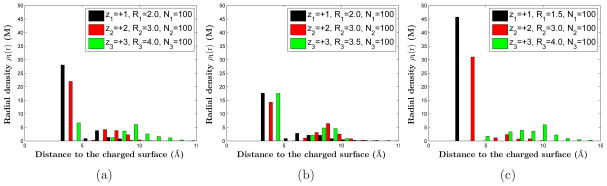
(Color online) MC simulations of the layering structure of ionic radial densities of three counterion species with the valences z1 = 1, z2 = 2, and z3 = 3, and numbers of ions in each species N1 = N2 = N3 = 100. The set of radii (R1, R2, R3) are different in the three plots. The corresponding valence-to-volume ratios are: (a) α+1 : α+2 : α+3 = 2.7 : 1.6 : 1; (b) α+1 : α+2 : α+3 = 1.8 : 1.1 : 1; (c) α+1 : α+2 : α+3 = 6.3 : 1.6 : 1.
Figure 5 (c) also illustrates an interesting phenomenon. With the decrease of the radius of monovalent ions, the concentration of the divalent ions, which have the second largest of the three valence-to-volume ratios, is increased. The trivalent ions which have the smallest valence-to-volume ratio are depleted in the vicinity of the surface. This can be interpreted that the more tightly binding of the monovalent ions to the surface decreases more the electrostatic energy contributed by divalent and trivalent ions. The effect of the valence-to-volume ratio is strengthened in the competition between the latter two species. This result demonstrates that the nonuniform ionic size effect plays a very important role in determining the properties of electrolyte solutions.
We now fix the numbers of ions N1 = N2 = N3 = 100, the surface charge density σ = −0.21e/Å2, the ratios of radii R1 : R2 : R3 = 2 : 3 : 4, and the order of valence-to-volume ratios α+1 > α+2 > α+3. We vary simultaneously the ionic radii of the three species of counterions by changing a common multiplier. We use three different sets with the radii of monovalent ions being 1.2, 2.0, and 2.4 Å, respectively. We study how the different ionic sizes affect the layering structure of counterions and how the competition in ionic adsorption is changed with the change of entropy. The corresponding results are plotted in Figure 6. It can be found that, with the increase of the ionic radii, the entropic contribution to the electrostatic free energy is increased, leading to the enhancement of the counterion repulsion. Moreover, the particle numbers of all the three ionic species in the layers closest to the surface are diminished. In the meantime, when ionic sizes are increased from small to large, the entropic contribution to the free energy becomes more significant. Hence, the valence-to-volume ratios give a clear characterization of stratification. In fact, the monovalent counterions, which has the smallest value of valence but largest valence-to-volume ratio, always forms the first layer closest to the surface. It is a further evidence that the competition between electrostatic energetics and entropy leads to the following limits: at the limit of the electrostatics domination the valence is the main indicator of the ordering of layers, while at the limit of the entropy domination the valence-to-volume ratio is the main indicator of layer ordering.
Figure 6.
(Color online) MC simulations of radial densities of three species of counterions with the valences z1 = 1, z2 = 2, and z3 = 3, and numbers of ions in each species N1 = N2 = N3 = 100. The radii R1, R2, R3 in the three plots differ by a common factor. (a) Small ionic radii. (b) Medium ionic radii. (c) Large ionic radii.
4.2 Systems with the presence of coions
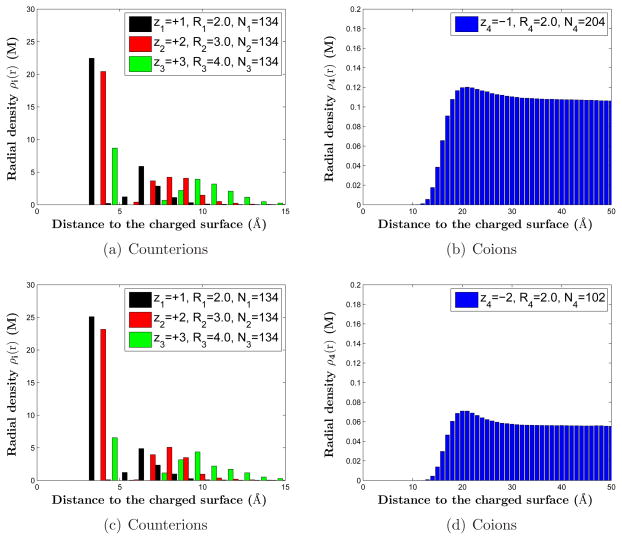
We now add coions in the system and study the effect of coions to the competitive adsorption and order of packing of counterions, in comparison with the salt-free systems. We consider two cases. In the first case, we add monovalent coions to the system. We assume that the radius of such a coion is R4 = 2 Å and that the total number of coions is N4 = 204. In the second case, we add divalent coions to the system. We assume that the radius of such a divalent coion is R4 = 2 Å and that the total number of such coions is N4 = 102. In both cases, we still have the monovalent, divalent, and trivalent counterions, with now their radii 2, 3, and 4 Å, respectively, and their total numbers N1 = N2 = N3 = 134. We also assume a high surface charge density σ = −0.21 e/Å2. The charge neutrality (2.1) is now satisfied with M = 4 species of counterions and coions. The system will have an averaged 100 mM concentration of monovalent coions in the first case and 50 mM concentration of divalent coions in the second case.
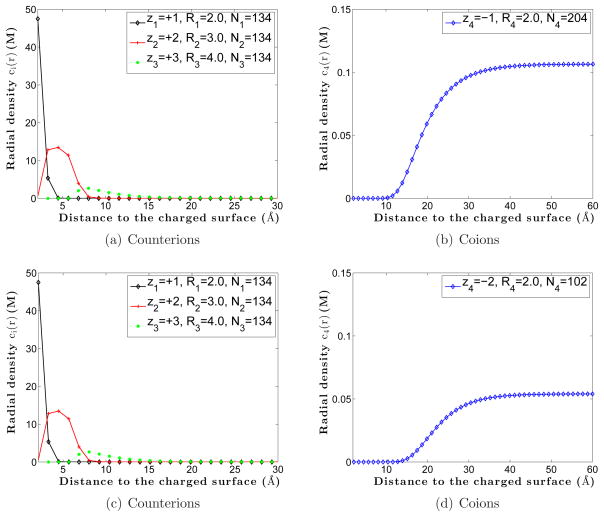
For these two systems with coions, we plot the radial densities of counterions and coions obtained by our MC simulations in Figure 7 and those obtained by our mean-field numerical computations in Figure 8. In comparison with those salt free systems, we find that the addition of coions slightly enhances the layering effect. The densities of all three counterions are increased. This has a minor influence to their layering order. It is clear that a qualitative agreement between mean-field calculations and MC simulations is reached on the competition of counterion adsorption.
Figure 7.
(Color online) MC simulations of counterion and coion radial densities. (a) and (b): systems with monovalent coions. (c) and (d): systems with divalent coions.
Figure 8.
(Color online) Counterion and coion radial densities from numerical computations based on the mean-field theory with the ionic size effect. (a) Radial densities of counterions for the system with monovalent coions. (b) Radial density of coions for the system with monovalent coions. (c) Radial densities of counterions for the system with divalent coions. (d) Radial density of coions for the system with divalent coions.
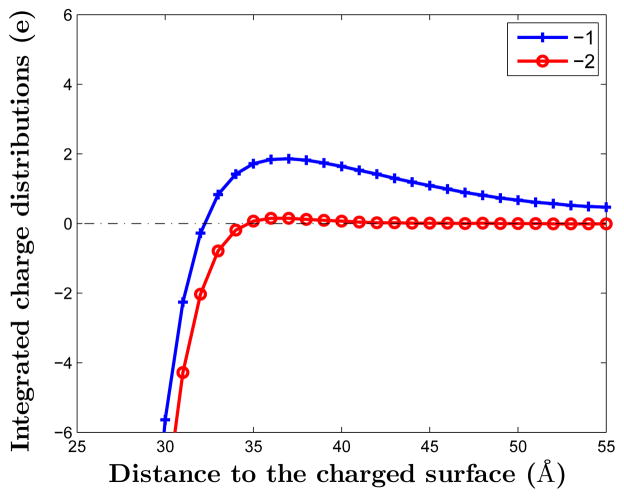
We observe from Figure 7 (b) and (d) that the coion density predicted by MC simulations is non-monotonic, while from Figure 8 (b) and (d) that the coion density predicted by the mean-field theory is monotonic. In Figure 9, we plot the total ionic charge density for each of the two systems obtained by our MC simulations. We find the over-charging of the system, i.e., the total charge density is above zero that corresponds to the charge neutrality [29, 69]. Interestingly, the over-charging of the monovalent-coion system is stronger than that in the divalent-coion system: the inverted charges of the monovalent-coion system and divalent-coion system are 1.86 e and 0.15 e, respectively. This is mainly due to the fact that it is easier to form anion-cation binding pairs in the divalent-coion system than in the monovalent-coion system. Thus the density of free counterions is decreased. In contrast, the mean-field theory can only produce a monotonic profile of the total charge density as proved mathematically in [26]. Therefore, the mean-field theory with the nonuniform size effect still fails in predicting the charge inversion.
Figure 9.
(Color online) MC simulations of the total charge density for the system with monovalent coions (marked −1) and that with divalent coions (marked −2).
5 Conclusions
In this work, we study the competition of multiple counterions of different valences and different sizes in binding to the surface of a spherical colloidal particle by both a mean-field theory and Monte Carlo (MC) simulations. The parameters of the underlying system of electrolyte include: the valences zi, radii Ri (or volumes vi), and numbers Ni of ions of ith species with i = 1, …, M, the radius R0 of a solvent molecule, the constant dielectric coefficient ε of the electrolyte, and the surface charge density σ. The entire system is assumed to be in charge neutrality. In the mean-field approach, we minimize a semi-phenomenological electrostatic free-energy functional of ionic concentrations constrained by Poisson’s equation. The electrostatic potential is not an independent variable of the functional. The different ionic sizes are described through the entropic contributions of ions and solvent molecules. The constrained free-energy minimization is realized numerically by an augmented Lagrange multiplier method. We also use an unrestricted primitive model and canonical ensemble Monte Carlo (MC) simulations with the Metropolis criterion to predict the ionic distributions around the charged surface.
Through our extensive MC simulations and mean-field computations, we have found the following:
For a low surface charge density, the adsorption of counterions with a higher valence is preferable. This agrees with previous studies in existing literature. For a highly charged surface, both of the mean-field theory and MC simulations show that the counterions bind tightly around the charged surface, forming stratification or layering of counterions of different species.
The ionic valence-to-volume ratios, instead of ionic valences alone, are the key parameters that determine the binding of counterions to the charged surface. Due to the ionic size effect, counterions with the largest valence-to-volume ratio form the first layer of stratification, while those with the second largest valence-to-volume ratio form the second layer, and so on. We shall call this the “criterion of valence-to-volume rations” in ionic stratification. Our MC simulations confirm the validity of this criterion that was discovered in our previous mean-field calculations [37].
Our MC simulations predict the charge inversion for ionic systems with salt. Moreover, we find that the over-charging is more significant for a system with monovalent coions than for a system with divalent coions. The mean-field theory, however, fails in predicting the charge inversion, since it does not include the ion-ion correlation.
In our mean-field computations, we have never found a case where our criterion of valence-to-volume ratios fails for the prediction of stratification of multiple counterions for highly charged surfaces. For MC simulations, we sometimes find the criterion does not work, when those ratios are too close and the surface charge is too low. In fact, the MC simulation reported in Figure 6 (b) of [51] for a low surface charge density contradicts our criterion.
While our mean-field theory and Monte Carlo simulations have both predicted the stratification of counterions near a highly charged surface and the crucial role of the ionic valence-to-volume ratios in such stratification, we have neglected several effects in our theory and methods.
First, in our MC simulations, we treat ions as hard spheres to describe the short-range repulsion in the van der Waals interactions between different kinds of ions of multiple valences and different sizes, and between the ions and the charged macroion. We have neglected the long-range attraction in such interactions that can contribute largely to the ion-ion correlations. For a highly charged surfaces, counterions are crowded near the surface; and the van der Waals attraction may not be as strong as the corresponding repulsion. While we have taken a rather common approach in MC simulations, we understand that including the attraction part of the van der Waals interactions is practically quite possible. We shall include such interaction in our subsequence works.
Second, in both of our mean-field treatment and MC simulations, we use a uniform dielectric coefficient for the ionic solution. This is only an approximation in the description of the dielectric properties of solvent, as the water in the proximity of a highly charged surface is not expected to behave like bulk solvent. In fact, the dielectric coefficient can depend on the ionic concentrations [13, 70, 71]. Such dependence is experimentally known to be continuous and linear; cf. Eq. (1) and Table 1 in [72]. Near the charged surface the dielectric coefficient is locally close to a constant; and the ion-ion interactions in such a region can be still modeled well by our interaction energy (3.1) but with a dielectric coefficient different from that in the bulk. We thus do not expect that this will significantly affect the competition of different counterions in the stratification. To further explore the detailed consequences of the concentration dependent dielectrics, we are currently extending our work to such dielectric systems.
Third, the size effect of solvent molecules is not directly included in our MC simulations. This makes our comparison between the mean-field theory and MC simulations only qualitative. There is clearly a need to develop models and algorithms to include the solvent molecular size effect in MC simulations of electrolyte systems.
We are currently working on to improve our theory and methods to include some of these effects. In the future, it is desirable to apply our efficient theory and methods to large-scale modeling of biomolecular systems in which nonuniform ionic size effects can be sometimes very important. On the theoretical development, it is also necessary to derive from statistical mechanics theory our mean-field, electrostatic free-energy functional that includes the nonuniform ionic size effect.
Acknowledgments
This work was supported by the US National Science Foundation (NSF) through grant DMS-0811259 (B.L. and J.W.), the US NSF Center for Theoretical Biological Physics (CTBP) through grant PHY-0822283 (B.L. and S.Z.), the National Institutes of Health through the grant R01GM096188 (B.L.), the Natural Science Foundation of China through grant NSFC-11101276 (Z.X.), the Chinese Ministry of Education through grant NCET-09-0556 (Z.X.), and the China Scholarship Council (S.Z.).
Contributor Information
Jiayi Wen, Email: j2wen@ucsd.edu.
Shenggao Zhou, Email: s4zhou@math.ucsd.edu.
Zhenli Xu, Email: xuzl@sjtu.edu.cn.
Bo Li, Email: bli@math.ucsd.edu.
References
- 1.Andelman D. Electrostatic properties of membranes: The Poisson–Boltzmann theory. In: Lipowsky R, Sackmann E, editors. Handbook of Biological Physics. Vol. 1. Elsevier; 1995. pp. 603–642. [Google Scholar]
- 2.Boroudjerdi H, Kim YW, Naji A, Netz RR, Schlagberger X, Serr A. Statics and dynamics of strongly charged soft matter. Phys Rep. 2005;416:129–199. [Google Scholar]
- 3.Davis ME, McCammon JA. Electrostatics in biomolecular structure and dynamics. Chem Rev. 1990;90:509–521. [Google Scholar]
- 4.Fogolari F, Brigo A, Molinari H. The Poisson–Boltzmann equation for biomolecular electrostatics: A tool for structural biology. J Mol Biol. 2002;15:377–392. doi: 10.1002/jmr.577. [DOI] [PubMed] [Google Scholar]
- 5.French RH, Parsegian VA, Podgornik R, Rajter RF, Jagota A, Luo J, Asthagiri D, Chaudhury MK, Chiang Y-M, Granick S, Kalinin S, Kardar M, Kjellander R, Langreth DC, Lewis J, Lustig S, Wesolowski D, Wettlaufer JS, Ching W-Y, Finnis M, Houlihan F, von Lilienfeld OA, van Oss CJ, Zemb T. Long range interactions in nanoscale science. Rev Mod Phys. 2010;82(2):1887–1944. [Google Scholar]
- 6.Levin Y. Electrostatic corrections: From plasma to biology. Rep Prog Phys. 2002;65:1577–1632. [Google Scholar]
- 7.McCammon JA. Darwinian biophysics: Electrostatics and evolution in the kinetics of molecular binding. Proc Nat Acad Sci USA. 2009;106:7683–7684. doi: 10.1073/pnas.0902767106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Sharp KA, Honig B. Electrostatic interactions in macromolecules: Theory and applications. Annu Rev Biophys Biophys Chem. 1990;19:301–332. doi: 10.1146/annurev.bb.19.060190.001505. [DOI] [PubMed] [Google Scholar]
- 9.Lambert D, Leipply D, Shiman R, Draper DE. The influence of monovalent cation size on the stability of RNA tertiary structures. J Mol Biol. 2009;390:791–804. doi: 10.1016/j.jmb.2009.04.083. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Bai Y, Travers K, Chu VB, Lipfert J, Doniach S, Herschlag D. Quantitative and comprehensive decomposition of the ion atmosphere around nucleic acids. J Amer Chem Soc. 2007;129:14981–14988. doi: 10.1021/ja075020g. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Bleam ML, Anderson CF, Record MTJ. Relative binding affinities of monovalent cations for double-stranded DNA. Proc Natl Acad Sci USA. 1980;77:3085–3089. doi: 10.1073/pnas.77.6.3085. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Eisenberg B. Crowded charges in ion channels. In: Rice SA, Dinner AR, editors. Adv Chem Phys. Vol. 148. 2011. pp. 77–223. [Google Scholar]
- 13.Howard JJ, Perkyns JS, Pettitt BM. The behavior of ions near a charged wall—dependence on ion size, concentration, and surface charge. J Phys Chem B. 2010;114:6074–6083. doi: 10.1021/jp9108865. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Kornyshev AA. Double-layer in ionic liquids: Paradigm change? J Phys Chem B. 2007;111:5545–5557. doi: 10.1021/jp067857o. [DOI] [PubMed] [Google Scholar]
- 15.Quesada-Pérez M, Martín-Molina A, Hidalgo-Álvarez R. Simulation of electric double layers with multivalent counterions: Ion size effect. J Chem Phys. 2004;121:8618–8626. doi: 10.1063/1.1798932. [DOI] [PubMed] [Google Scholar]
- 16.Valiskó M, Boda D, Gillespie D. Selective adsorption of ions with different diameter and valence and highly charged interfaces. J Phys Chem C. 2007;111:15575–15585. [Google Scholar]
- 17.Wang K, Yu Y-X, Gao G-H, Luo G-S. Density-functional theory and Monte Carlo simulation study on the electric double layer around DNA in mixed-size counterion systems. J Chem Phys. 2005;123:234904. doi: 10.1063/1.2137710. [DOI] [PubMed] [Google Scholar]
- 18.Chapman DL. A contribution to the theory of electrocapillarity. Philos Mag. 1913;25:475–481. [Google Scholar]
- 19.Debye P, Hückel E. The theory of electrolytes. I. Lowering of freezing point and related phenomena. Phys Zeitschr. 1923;24:185–206. [Google Scholar]
- 20.Fixman F. The Poisson–Boltzmann equation and its application to polyelecrolytes. J Chem Phys. 1979;70:4995–5005. [Google Scholar]
- 21.Gouy G. Constitution of the electric charge at the surface of an electrolyte. J Phys. 1910;9:457–468. [Google Scholar]
- 22.Grochowski P, Trylska J. Continuum molecular electrostatics, salt effects and counterion binding—A review of the Poisson–Boltzmann model and its modifications. Biopolymers. 2008;89:93–113. doi: 10.1002/bip.20877. [DOI] [PubMed] [Google Scholar]
- 23.Lu BZ, Zhou YC, Holst MJ, McCammon JA. Recent progress in numerical methods for the Poisson–Boltzmann equation in biophysical applications. Commun Comput Phys. 2008;3:973–1009. [Google Scholar]
- 24.Che J, Dzubiella J, Li B, McCammon JA. Electrostatic free energy and its variations in implicit solvent models. J Phys Chem B. 2008;112:3058–3069. doi: 10.1021/jp7101012. [DOI] [PubMed] [Google Scholar]
- 25.Fogolari F, Briggs JM. On the variational approach to Poisson–Boltzmann free energies. Chem Phys Lett. 1997;281:135–139. [Google Scholar]
- 26.Li B. Continuum electrostatics for ionic solutions with nonuniform ionic sizes. Nonlinearity. 2009;22:811–833. [Google Scholar]
- 27.Li B. Minimization of electrostatic free energy and the Poisson–Boltzmann equation for molecular solvation with implicit solvent. SIAM J Math Anal. 2009;40:2536–2566. [Google Scholar]
- 28.Reiner ES, Radke CJ. Variational approach to the electrostatic free energy in charged colloidal suspensions: General theory for open systems. J Chem Soc Faraday Trans. 1990;86:3901–3912. [Google Scholar]
- 29.Grosberg AY, Nguyen TT, Shklovskii BI. Colloquium: The physics of charge inversion in chemical and biological systems. Rev Mod Phys. 2002;74:329–345. [Google Scholar]
- 30.Vlachy V. Ionic effects beyond Poisson–Boltzmann theory. Annu Rev Phys Chem. 1999;50:145–165. doi: 10.1146/annurev.physchem.50.1.145. [DOI] [PubMed] [Google Scholar]
- 31.Borukhov I, Andelman D, Orland H. Steric effects in electrolytes: A modified Poisson–Boltzmann equation. Phys Rev Lett. 1997;79:435–438. [Google Scholar]
- 32.Borukhov I, Andelman D, Orland H. Adsorption of large ions from an electrolyte solution: A modified Poisson–Boltzmann equation. Electrochimica Acta. 2000;46:221–229. [Google Scholar]
- 33.Boschitsch AH, Danilov PV. Formulation of a new and simple nonuniform size-modified Poisson-Boltzmann description. J Comput Chem. 2012;33:1152–1164. doi: 10.1002/jcc.22946. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Chu VB, Bai Y, Lipfert J, Herschlag D, Doniach S. Evaluation of ion binding to DNA duplexes using a size-modified Poisson–Boltzmann theory. Biophys J. 2007;93:3202–3209. doi: 10.1529/biophysj.106.099168. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Kralj-Iglič V, Iglič A. A simple statistical mechanical approach to the free energy of the electric double layer including the excluded volume effect. J Phys II (France) 1996;6:477–491. [Google Scholar]
- 36.Tresset G. Generalized Poisson–Fermi formalism for investigating size correlation effects with multiple ions. Phys Rev E. 2008;78:061506. doi: 10.1103/PhysRevE.78.061506. [DOI] [PubMed] [Google Scholar]
- 37.Zhou S, Wang Z, Li B. Mean-field description of ionic size effects with nonuniform ionic sizes: A numerical approach. Phys Rev E. 2011;84:021901. doi: 10.1103/PhysRevE.84.021901. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Antypov D, Barbosa MC, Holm C. Incorporation of excluded-volume correlations into Poisson–Boltzmann theory. Phys Rev E. 2005;71:061106. doi: 10.1103/PhysRevE.71.061106. [DOI] [PubMed] [Google Scholar]
- 39.Bazant M, Storey BD, Kornyshev AA. Double-layer in ionic liquid: Over-screening versus crowding. Phys Rev Lett. 2011;106:046102. doi: 10.1103/PhysRevLett.106.046102. [DOI] [PubMed] [Google Scholar]
- 40.Bazant MZ, Kilic MS, Storey BD, Ajdari A. Towards an understanding of induced-charge electrokinetics at large applied voltages in concentrated solutions. Adv Colloid Interface Sci. 2009;152:48–88. doi: 10.1016/j.cis.2009.10.001. [DOI] [PubMed] [Google Scholar]
- 41.Bikerman JJ. Structure and capacity of the electrical double layer. Philos Mag. 33:384–397. [Google Scholar]
- 42.Eisenberg B, Hyon Y-K, Liu C. Energy variational analysis of ions in water and channels: Field theory for primitive models of complex ionic fluids. J Chem Phys. 2010;133:104104. doi: 10.1063/1.3476262. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Kilic MS, Bazant MZ, Ajdari A. Steric effects in the dynamics of electrolytes at large applied voltages. I. Double-layer charging. Phys Rev E. 2007;75:021502. doi: 10.1103/PhysRevE.75.021502. [DOI] [PubMed] [Google Scholar]
- 44.Kilic MS, Bazant MZ, Ajdari A. Steric effects in the dynamics of electrolytes at large applied voltages. II. Modified Poisson–Nernst–Planck equations. Phys Rev E. 2007;75:021503. doi: 10.1103/PhysRevE.75.021503. [DOI] [PubMed] [Google Scholar]
- 45.Lu B, Zhou Y. Poisson–Nernst–Planck equations for simulating biomolecular diffusion-reaction processes II: Size effects on ionic distributions and diffusion-reaction rates. Biophys J. 2011;100:2475–2485. doi: 10.1016/j.bpj.2011.03.059. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Silalahi ARJ, Boschitsch AH, Harris RC, Fenley MO. Comparing the predictions of the nonlinear Poisson–Boltzmann equation and the ion size-modified Poisson–Boltzmann equation for a low-dielectric charged spherical cavity in an aqueous salt solution. J Chem Theory Comput. 2010;6:3631–3639. doi: 10.1021/ct1002785. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Baptista M, Schmitz R, Dünweg B. Simple and robust solver for the Poisson–Boltzmann equation. Phys Rev E. 2009;80:016705. doi: 10.1103/PhysRevE.80.016705. [DOI] [PubMed] [Google Scholar]
- 48.Maggs AC, Rossetto V. Local simulation algorithms for Coulomb interactions. Phys Rev Lett. 2002;88:196402. doi: 10.1103/PhysRevLett.88.196402. [DOI] [PubMed] [Google Scholar]
- 49.Tulpar A, Van Tassel PR, Walz JY. Structuring of macroions confined between like-charged surfaces. Langmuir. 2006;22(6):2876–2883. doi: 10.1021/la0530485. [DOI] [PubMed] [Google Scholar]
- 50.Avendaño C, Gil-Villegas A. Monte Carlo simulations of primitive models for ionic systems using the Wolf method. Molecular Phys. 2006;104:1475–1486. [Google Scholar]
- 51.Taboada-Serrano P, Yiacoumi S, Tsouris C. Behavior of mixtures of symmetric and asymmetric electrolytes near discretely charged planar surfaces: A Monte Carlo study. J Chem Phys. 2005;123:054703. doi: 10.1063/1.1992484. [DOI] [PubMed] [Google Scholar]
- 52.Frenkel D, Smit B. Understanding molecular simulation: From algorithms to applications. Academic Press; New York: 2002. [Google Scholar]
- 53.Linse P. Simulation of charged colloids in solution. Adv Polym Sci. 2005;185:111–162. [Google Scholar]
- 54.Goel T, Patra CN, Ghosh SK, Mukherjee T. Effect of ionic size on the structure of cylindrical electric double layers: A systematic study by Monte Carlo simulations and Density Functional Theory. J Phys Chem B. 2011;115:10903–10910. doi: 10.1021/jp203779t. [DOI] [PubMed] [Google Scholar]
- 55.Wang ZY, Ma YQ. Insight from Monte Carlo simulations on charge inversion of planar electric double layers in mixtures of asymmetric electrolytes. J Chem Phys. 2010;133:064704. doi: 10.1063/1.3469795. [DOI] [PubMed] [Google Scholar]
- 56.Gan Z, Xu Z. Multiple-image treatment of induced charges in Monte Carlo simulations of electrolytes near a spherical dielectric interface. Phys Rev E. 2011;84:016705. doi: 10.1103/PhysRevE.84.016705. [DOI] [PubMed] [Google Scholar]
- 57.Kjellander R, Marcelja S. Correlation and image charge effects in electric double layers. Chem Phys Lett. 1984;112:49–53. [Google Scholar]
- 58.Messina R. Image charges in spherical geometry: Application to colloidal systems. J Chem Phys. 2002;117:11062. [Google Scholar]
- 59.Torrie GM, Valleau JP, Patey GN. Electrical double layers. II. Monte Carlo and HNC studies of image effects. J Chem Phys. 1982;76:4615. [Google Scholar]
- 60.Wang ZY, Ma YQ. Monte Carlo determination of mixed electrolytes next to a planar dielectric interface with different surface charge distributions. J Chem Phys. 2009;131:244715. doi: 10.1063/1.3276279. [DOI] [PubMed] [Google Scholar]
- 61.Bertsekas DP. Constrained Optimization and Lagrange Multiplier Method. Academic Press; New York: 1982. [Google Scholar]
- 62.Nocedal J, Wright S. Numerical Optimization. Springer–Verlag; New York: 1999. [Google Scholar]
- 63.Abbas Z, Ahlberg E, Nordholm S. Monte Carlo simulations of salt solutions: exploring the validity of primitive models. J Phys Chem B. 2009;113:5905–5916. doi: 10.1021/jp808427f. [DOI] [PubMed] [Google Scholar]
- 64.Bester M, Vlachy V. Monte Carlo study of mixed electrolytes in the primitive model. J Chem Phys. 1992;96:7656–7661. [Google Scholar]
- 65.Metropolis N, Rosenbluth AW, Rosenbluth MN, Teller AH, Teller E. Equation of state calculations by fast computing machines. J Chem Phys. 1953;21:1087–1092. [Google Scholar]
- 66.Valleau JP, Cohen LK. Primitive model electrolytes. I. Grand canonical Monte Carlo computations. J Chem Phys. 1980;72:5935–5941. [Google Scholar]
- 67.Kielland J. Individual activity coefficients of ions in aqueous solutions. J Am Chem Soc. 1937;59:1675–1678. [Google Scholar]
- 68.Guerrero-Garcia GI, Gonzalez-Tovar E, de la Cruz MO. Entropic effects in the electric double layer of model colloids with size-asymmetric monovalent ions. J Chem Phys. 2011;135:054701. doi: 10.1063/1.3622046. [DOI] [PubMed] [Google Scholar]
- 69.Quesada-Pérez M, González-Tovar E, Martín-Molina A, Lozada-Cassou M, Hidalgo-Álvarez R. Overcharging in colloids: Beyond the Poisson–Boltzmann approach. Chem Phys Chem. 2003;4:234–248. doi: 10.1002/cphc.200390040. [DOI] [PubMed] [Google Scholar]
- 70.Eigen M, Wicke E. The thermodynamics of electrolytes at higher concentration. J Phys Chem. 1954;58:702–714. [Google Scholar]
- 71.Kalcher I, Schulz JCF, Dzubiella J. Electrolytes in a nanometer slab-confinement: Ion-specific structure and solvation forces. J Chem Phys. 2011;133:164511. doi: 10.1063/1.3490666. [DOI] [PubMed] [Google Scholar]
- 72.Ben-Yaakov D, Andelman D, Podgornik R. Dielectric decrement as a source of ion-specific effects. J Chem Phys. 2011;134:074705. doi: 10.1063/1.3549915. [DOI] [PubMed] [Google Scholar]