Haploscope: a tool for the graphical display of haplotype structure in populations

Abstract

Patterns of linkage disequilibrium are often depicted pictorially by using tools that rely on visualizations of raw data or pairwise correlations among individual markers. Such approaches can fail to highlight some of the more interesting and complex features of haplotype structure. To enable natural visual comparisons of haplotype structure across subgroups of a population (e.g. isolated subpopulations or cases and controls), we propose an alternative visualization that provides a novel graphical representation of haplotype frequencies. We introduce Haploscope, a tool for visualizing the haplotype cluster frequencies that are produced by statistical models for population haplotype variation. We demonstrate the utility of our technique by examining haplotypes around the LCT gene, an example of recent positive selection, in samples from the Human Genome Diversity Panel. Haploscope, which has flexible options for annotation and inspection of haplotypes, is available for download at http://scheet.org/software.

INTRODUCTION

A haplotype is a configuration of alleles at neighboring sites along a chromosome. Because haplotypes provide the basic representation of genetic information across sites within individuals, tools for the analysis of haplotypic patterns are fundamental in diverse settings in population genetics and statistical genetics that require information on relationships among alleles across loci.

As part of the analysis of haplotype patterns, visualizations of haplotypic data provide a basis for identifying features of interest, such as regions of high correlation of allelic status across adjacent sites (regions of high linkage disequilibrium, or LD), regions in which haplotypes vary greatly among two or more sets of individuals, or regions in which haplotype diversity in a population is elevated or reduced. Production of convenient haplotype visualizations has posed a considerable challenge, however, owing both to the difficulty of summarizing high-dimensional data without discarding important information and to the multiplicity of components of a haplotype data set that are useful to represent. These components include: the spatial array of loci along a chromosome, the variety of genetic types possible at a site or series of sites, the differences in the occurrence of these types across individuals or groups of individuals, and the co-occurrence of haplotype properties with other genetic features that vary along the genome.

A number of approaches to haplotype visualization have been developed, providing different levels of emphasis on representing the raw data accurately and on visually highlighting specific features of interest, such as positive selection [Sabeti et al., 2002], pairwise LD [Barrett et al., 2005], haplotype “flow” [Conrad et al., 2006], and tag-SNP information [Zhang et al., 2002; Davidovich et al., 2007]. At one extreme, a Visual Haplotypes plot [http://gvs.gs.washington.edu/GVS] simply converts a data matrix of phased individual haplotypes at a collection of biallelic sites into a graphic by replacing the minor and major alleles at each site with distinct colors. This type of plot represents the raw data faithfully, but because no computations are performed to construct the graphic, it contains no information that is not already included in the raw data. Further, in the case in which the data matrix consists of haplotypes that have been statistically estimated rather than obtained empirically, the haplotype reconstruction is not certain, and a Visual Haplotypes plot does not illustrate this uncertainty. Other approaches, such as Haploview [Barrett et al., 2005], focus on displaying pairwise LD patterns. These approaches do perform some level of analysis, but their plots are limited to the display of pairwise relationships among genetic sites. Although the user can identify certain patterns among multiple sites by visual examination of entries in an upper-triangular matrix, it is generally difficult to use Haploview plots to uncover properties of haplotype structure that extend beyond marker pairs, such as relative frequencies of multilocus haplotypes. Haplotype bifurcation diagrams [Sabeti et al., 2002] are useful for visualizing the long frequent haplotypes that accompany positive selection, but they are not generally applicable to investigation of haplotype frequencies or haplotype composition across populations. Patterns of haplotype variation across populations can be examined using a technique that involves haplotype estimation, identification of common haplotype templates, and construction of mosaics of these templates in each phased individual haplotype [Conrad et al., 2006]; this method, however, involves a multi-step process that has not been formally automated for general use. An improvement on the issue of automation has recently been developed in the hapvisual software [Teo and Small, 2009]; however, because both the method of Conrad et al. [2006] and that of Teo & Small [2009] rely on fixed canonical templates, they are primarily useful for short regions over which relatively few transitions occur between templates in any given mosaic haplotype.

A feature shared by Visual Haplotypes, Haploview, hapvisual, and the methods of Sabeti et al. [2002] and Conrad et al. [2006] is that each can be viewed as algorithmic rather than statistical, relying on a visualization either of quantities deterministically computed from haplotypic data or of the raw haplotypes themselves. One fundamentally different approach to the display of haplotypes involves the application of a statistical model to locally summarize patterns of haplotype variation, followed by visualization of the estimated model parameters. In this type of model-based approach, the haplotype structure in a data set is treated as a single realization of an underlying model intended to describe key properties of the data while ignoring features that are not of interest. Model parameters are estimated from the data, and it is those estimates that are incorporated into a visualization of haplotype structure.

A model-based approach to haplotypic analysis and visualization was introduced by Jakobsson et al. [2008], who applied statistical summaries of haplotype variation as units of analysis in a genome-wide study of SNP variation from the Human Genome Diversity Panel (HGDP), using the cluster-based statistical model for haplotypes that has been implemented in fastPHASE [Scheet and Stephens, 2006]. This model approximates the local genealogy of chromosomes in a genomic neighborhood as a multifurcating tree of equally related clusters, where each of the clusters “cuts” the tree at a certain level identical across clusters, and where genealogies are treated as star-shaped beneath this cut so that all chromosomes are identical within a given cluster. Each sampled haplotype consists of a mosaic of these haplotype clusters, with cluster membership changing in the haplotype along the genome to accommodate changing local genealogies. The clustering process captures the LD structure in that cluster memberships at neighboring locations are correlated; within a cluster, however, the alleles at different SNPs are independent.

In their approach to visualization of the features of the clustering model, Jakobsson et al. [2008] obtained “membership frequencies” in each cluster for a given population at each genotyped site, and they plotted the spatial change in these frequencies as a function of genomic position. This visualization strategy was similar to those of Conrad et al. [2006] and Teo & Small [2009] in that all of these methods involved plots along the genome of relative frequencies of membership in haplotype clusters. Unlike the algorithmic methods of Conrad et al. [2006] and Teo & Small [2009], however, the model-based method of Jakobsson et al. [2008] used as its graphical unit estimated population-level conditional probabilities of haplotype cluster membership under the model, rather than displaying individual mosaics of common template haplotypes. A complementary visualization was subsequently developed by Browning & Weir [2010], relying on output from an alternative haplotype clustering model [Browning and Browning, 2007a]. While Jakobsson et al. [2008] arranged haplotype frequencies within populations, Browning & Weir [2010] displayed the relative frequencies of subpopulations arranged by haplotype cluster.

Here we present Haploscope, a software package that produces the model-based visualizations introduced by Jakobsson et al. [2008] and that, in addition, enables flexible renderings of model features directly produced by the statistical model for haplotype structure implemented in fastPHASE [Scheet and Stephens, 2006]. It can also be applied to certain output from other cluster-based models for haplotypes in populations (e.g. BEAGLE [Browning and Browning, 2007b]). The Haploscope perspective can represent both the spatial haplotype composition of a population along a chromosome, the change in this composition across genomic locations, the differences in haplotype composition between populations or subgroups of a population, and local levels of haplotype diversity and cluster membership. To simultaneously illustrate all of these aspects of haplotype variation, Haploscope sacrifices the property possessed, for example, by Visual Haplotypes, of precisely representing the raw data. Thus, Haploscope provides a visualization at the opposite extreme from Visual Haplotypes, highlighting features of haplotype structure through informative summaries.

ALGORITHM

To explicitly describe the graphical features of Haploscope, we briefly review the hidden Markov model for haplotype variation introduced by Scheet & Stephens [2006]. Let θ_km denote the frequency of an arbitrarily chosen allelic type (‘1’) in cluster k (1,…,K) at marker (m = 1,…,M), where K, a fixed constant identical at all markers, denotes the number of clusters, and M denotes the number of markers to be analyzed. Let z_im be the (hidden) unordered pair of clusters from which diploid individual i derived its data (unordered pair of alleles) at marker m, and let the set of all of these pairs across all markers be represented by z_i. We assume that z_i forms a Markov chain comprising two independent Markov chains for haploid processes (see [Rabiner, 1989] for a discussion). We obtain the likelihood of the model parameters θ, α, and r as a product over n individuals:

$$p(g;\theta ,\alpha ,r)={\prod }_{i=1}^{n}p(g_i;\theta ,\alpha ,r),$$

where

$$p(g_i;\theta ,\alpha ,r)=\sum p(g_i|z_i,\theta )p(z_i;\alpha ,r).$$

Here, g represents the complete genotype data at all markers for n individuals, g_i represents the complete genotype data for individual i, and r (probabilities of inter-marker jumps to a new cluster) and α (probabilities of clusters conditional on jumps) parameterize the transitions of z_i among clusters. The sum proceeds over all [K(K+1)/2]^M possible choices for the values in the vector z_i. Note that naïve evaluation of the sum is intractable; however, because z_i forms a Markov chain, the sum can be obtained with a Baum-Welch dynamic programming algorithm (see [Rabiner, 1989] for a review), which calculates all probabilities for all cluster configurations across markers using iterative computations based on results computed at adjacent markers. The model parameters θ, α, and r are estimated using an expectation-maximization algorithm.

In a Haploscope plot, haplotype clusters are represented as colors, and markers are depicted as vertical bars partitioned into colored segments that correspond to estimated population frequencies of the haplotype clusters. The frequency represented for cluster k at marker m in subpopulation s (1,…,S), where S is the total number of subpopulations, is

$$p_{km}(s)={\sum }_{i=1}^{n_s}{\sum }_{k\text{'}=1}^{K}p(z_{im}=\{k,k\text{'}\left\}\right|g_i,\theta ,\alpha ,r)\times 2^{I_{k=k\text{'}}}/(2n_s).$$

Here, I_{A} is 1 if A is true and 0 otherwise, and n_s is the number of sampled individuals in subpopulation s. The quantity p(z_im|g_i,θ,α,r) can be calculated from the joint probability of z_im and g_i, obtained from multiplying the forward and backward probabilities – e.g. p(g_i1,…,g_im,z_im|θ,α,r) and p(g_i(m+1,…,g_iM|z_im, θ,α,r) – and applying the constraint ${\sum }_{k=1}^K{p}_{km}(s)=1$. The frequencies {p_km(s)} are summarized “pointwise” by Haploscope at each marker m. The plots also depict the estimated parameters {r_m} (m = 2,…,M), the probabilities for the Markov chain to “jump” to a new cluster from marker m-1 to marker m, θ (the cluster-specific allele frequencies), and various summaries of haplotype and allele frequencies for different subgroups of the larger population to which the parameter estimation process is applied (e.g. distinct subpopulations or distinct phenotypic classes). Thus, Haploscope plots enable natural comparisons of LD and haplotype structure across groups.

EXAMPLE

Figure 1 shows an example of each of three types of haplotype cluster visualization generated by Haploscope for data from the Human Genome Diversity Panel [Li et al, 2008]. In Figure 1A and 1B, for each SNP surrounding the LCT gene (lactase), relative frequencies of haplotype clusters are displayed with colors on a thin vertical line. Each of K=30 colors depicts a distinct haplotype cluster, and the proportion of a line in a given color gives the frequency of a specific one of the 30 clusters. Moving across genomic regions, interpretation of cluster membership is conducted locally, as clustering patterns vary along the chromosome through the effects of historical recombination events that generate distinct genealogies at different sites. Different color patterns correspond to differences in haplotype composition across the range of markers.

Figure 1.

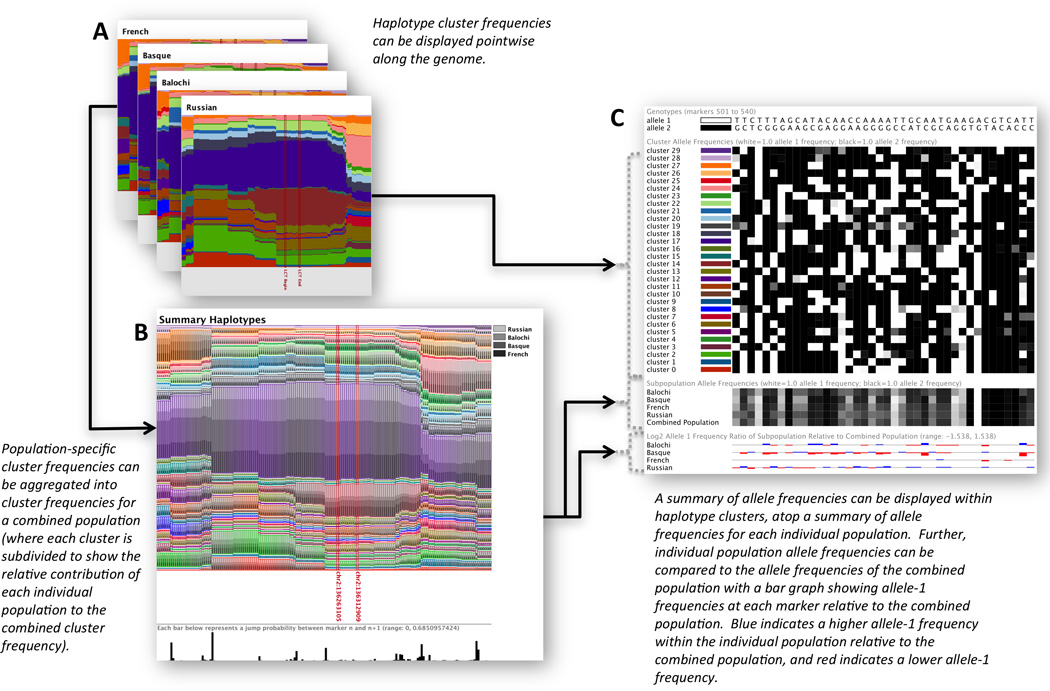
The summary haplotypes plot (Figure 1B) shows cluster frequencies averaged across selected subpopulations. Each cluster in this image is overlaid with varying shades of gray, each of which indicates the relative contribution to the sum across subpopulations of frequencies for that haplotype. This feature aids in the visual discovery of a haplotype cluster of interest (e.g. one that discriminates among populations, between cases and controls, or among groups of individuals classified by subphenotype). The black vertical bars below the plot in B represent probabilities of cluster jumps (r), and they can be interpreted as representing “recombination” rates in forming the mosaics of haplotype clusters inferred by fastPHASE from the genotype data of all members of the input collection of populations. The sizes of the bars have been normalized using the largest jump probability observed in the plot.

Finally, Haploscope can facilitate the inspection of the haplotype composition. For example, one group of parameters of the fastPHASE model of Scheet & Stephens [2006] is the set of cluster-specific allele frequencies, θ. When all allele frequencies within a cluster are near 0 or 1, little allelic variation exists in the cluster, and the entries of θ can be viewed as describing the ancestral haplotypes from which sampled haplotypes have derived. However, the components of θ can take any values between 0 and 1, representing uncertainty in the allelic configuration for that haplotype cluster. These frequencies and their deviations from 0 and 1 can be viewed with a heat map, as depicted in Figure 1C. The stacked colored bars running down the left side of this image correspond to the colors of the clusters generated in Figures 1A and 1B. The allele frequencies of each cluster used in fitting the model are displayed to the right of these color keys in a grayscale heat map, enabling a visual comparison of haplotype composition across clusters. White squares correspond to a frequency of 1 for allele 1 at a given marker and black corresponds to a frequency of 1 for allele 2. The genotypes for alleles 1 and 2 are listed above the heat maps for each marker position.

Below these cluster-specific allele frequencies, heat maps are displayed for summaries of allele frequencies for individual populations. These rows facilitate a high-level visual comparison of allele frequencies across populations. In the bar charts below these heat maps, each bar is vertically aligned with a genotype, depicting deviations in allele frequencies from those for the combined population. Specifically, the magnitude of the bar corresponds to a log₂ ratio of the allele-1 frequency for an individual subpopulation relative to the combined population. The color of the bar indicates the direction of deviation. The sizes of the bars are normalized using the largest allele frequency deviation observed across all markers and populations, as seen in the plots. These population-specific allele frequencies are not calculated from the raw data, but rather are model-based. That is, missing genotypes in the raw data would lead to uncertainty in sample allele frequencies, and we integrate out this uncertainty according to the model for LD. Specifically, we obtain the allele frequency for marker m in population s as

$$f_m(s)={\sum }_{k=1}^K{p}_{km}(s)\times {\theta }_{km}.$$

The overall frequency from which subpopulation-specific deviations are plotted is obtained as an equally weighted average of the subpopulation allele frequencies.

DISCUSSION

Haploscope images can complement population-genetic analyses. In Figure 1A, we have demonstrated the ability of Haploscope to visually illustrate a region of recent positive selection surrounding the LCT region. This region has been identified in numerous studies as the location of a recent selective sweep in populations of European descent, as long shared haplotypes have been found to surround alleles that likely confer lactase persistence [Bersaglieri et al., 2004; Voight et al., 2006]. Haploscope identifies this feature of the data, as it detects a predominant haplotype cluster that spans much of the LCT region. Further, Figure 1B shows that the predominant LCT haplotype cluster has higher frequency in the Basque and French populations than in the Balochi and Russian populations, a result compatible with the observation in the Basque and French populations of higher frequencies for the favored alleles [Bersaglieri et al., 2004].

Because our allele frequency calculations are model-based, our method can display results either from measured genotypes or from strictly-imputed genotype data, in which genotypes at certain markers are probabilistically imputed in all sampled individuals [Marchini et al., 2007; Servin and Stephens, 2007]. This application can be particularly useful, for example, to identify the source of an association signal at an imputed marker. An imputation-based association test at an individual marker is, in effect, a guided haplotype test, as single-marker association tests based on imputed data are driven by differences in haplotype frequencies between cases and controls. Thus, visual examination of subtle differences in haplotype frequencies among cases, controls, and a reference panel (as in Fig. 1A), in conjunction with knowledge of which haplotypes tend to carry a particular allele (as in Fig. 1C), can provide an explanation for associations observed at imputed markers.

Our software allows various options for generating images, enabling the user to specify subsets of populations to analyze, the range of marker positions to include in a graph, and the number and order of clusters. Cluster colors, graphical labels, and other features are also configurable. In addition, the images are exportable to high-resolution postscript files, a convenient file format for publication-quality images. The flexibility offered by Haploscope in the graphical representation provides investigators with the ability to report visually appealing and informative plots of haplotype structure. Haploscope and accompanying documentation with a tutorial are downloadable at http://scheet.org/software with a GNU GPL v3 license.