Fluorescence Methods to study DNA Translocation and Unwinding Kinetics by Nucleic Acid Motors

Abstract

Translocation of nucleic acid motor proteins (translocases) along linear nucleic acids can be studied by monitoring either the time course of the arrival of the motor protein at one end of the nucleic acid or the kinetics of ATP hydrolysis by the motor protein during translocation using pre-steady state ensemble kinetic methods in a stopped-flow instrument. Similarly, the unwinding of double-stranded DNA or RNA by helicases can be studied in ensemble experiments by monitoring either the kinetics of the conversion of the double-stranded nucleic acid into its complementary single-strands by the helicase or the kinetics of ATP hydrolysis by the helicase during unwinding. Such experiments monitor translocation of the enzyme along or unwinding of a series of nucleic acids labeled at one position (usually the end) with a fluorophore or a pair of fluorophores that undergo changes in fluorescence intensity or efficiency of fluorescence resonance energy transfer (FRET). We discuss how the pre-steady state kinetic data collected in these ensemble experiments can be analyzed by simultaneous global non-linear least squares (NLLS) analysis using simple sequential “n-step” mechanisms to obtain estimates of the macroscopic rates and processivities of translocation ad/or unwinding, the rate-limiting step(s) in these mechanisms, the average “kinetic step-size”, and the stoichiometry of coupling ATP binding and hydrolysis to movement along the nucleic acid.

1. Introduction

The ability to translocate processively and with biased directionality along a nucleic acid (NA) filament is central to the biological function of many enzymes involved in nucleic acid metabolism including DNA and RNA polymerases (1), helicases (2-4), chromatin remodelers (5-7), some nucleases (8, 9) and some restriction enzymes (10-12). These “molecular motors” all use the chemical potential energy obtained through the binding and hydrolysis of nucleoside triphosphates (NTP or dNTP) to perform the mechanical work of directional translocation along the NA filament. Helicases are also capable of the NTP-dependent unwinding of double-stranded nucleic acids (dsNA) (2, 3, 13, 14). An understanding of the translocation and unwinding mechanisms of these motor proteins requires quantitative kinetic information to obtain the rate constants, processivities, kinetic step-sizes, and ATP coupling stoichiometries associated with these processes.

Here, we describe the design and analysis of pre-steady state ensemble stopped-flow kinetic experiments (3, 6, 11, 12, 15-20) to probe either the mechanism of single-stranded nucleic acid (ssNA) translocation or of double-stranded nucleic acid (dsNA) unwinding by processive nucleic acid motor proteins using a simple sequential “n-step” kinetic model. The application of this methodology provides an accurate determination of macroscopic kinetic parameters such as the rate of net forward motion of the motor protein along the NA and the net efficiency at which the hydrolysis of ATP is coupled to this net forward motion. However, the estimates of microscopic kinetic parameters, such as the kinetic step size of translocation, can be inflated under some circumstances if non-uniform motion or persistent heterogeneity (static disorder) (21-24) occurs during translocation. We also compare the approach of analyzing the full time course of the kinetic reaction to a simpler “time to peak” analysis and show that the simpler method can grossly overestimate the rate of translocation under a number of circumstances.

2. Materials

The experiments discussed below are applicable to any NA motor that can translocate along ssNA or unwind dsNA substrates. Generally the solution conditions (i.e., buffer components, pH, temperature, etc.) that are used are those in which the motor enzyme is stable, well behaved, can interact with the NA substrate, and can function. Special consideration is needed when designing the NA substrates and selecting a trap for free motor enzyme.

2.1 ssNA and dsNA substrates

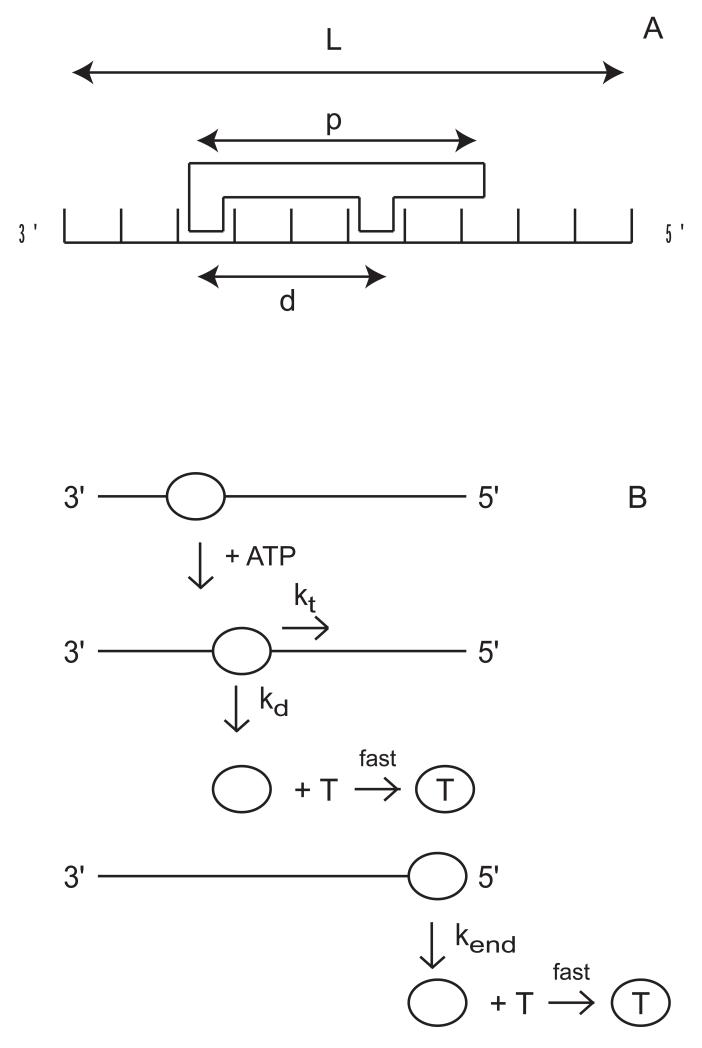
Three important features need to be considered when designing the fluorescent ssNA and dsNA substrates: length, base composition, and fluorophore. In order to determine the kinetic parameters for translocation along ssNA or unwinding of dsNA, experiments should be carried out with a series of NA substrates of different lengths. In our studies we generally start by testing 4 to 5 different lengths spanning the range from 25-124 nucleotides or base pairs. Since these nucleic acids are generally synthesized, the lengths are limited to be less than 150 nucleotides or base pairs.

When monitoring translocation along single-stranded DNA (ssDNA), we have used nucleic acids composed of a single base type, generally oligodeoxythymidylates (oligo(dT)) because these do not form internal base pairs and are the easiest oligodeoxynucleotides to synthesize. Similarly, oligouridylates (oligo(U)) could be used if one is studying single-stranded RNA (ssRNA) translocation.

When selecting a fluorophore for monitoring translocation along ssNA the fluorophore must yield a detectable fluorescent change upon interaction with the motor enzyme. A number of fluorescent dyes are commercially available as phosphoamadite derivatives and thus can be incorporated directly into the ssDNA using an automated oligodeoxynucleotide synthesizer. For translocation substrates the dye is usually placed at either the 3′- or 5′-end of the ssNA. We have found that Cy3 and Fluorescein have generally yielded good signal changes for the translocases that we have studied (17, 25-27). For DNA or RNA unwinding substrates the complementary strands are labeled with a FRET pair such as Cy3 and Cy5. Upon separation of the complementary strands, a change in FRET is detected.

2.2 Traps for free enzyme

All the experiments discussed below are performed as single-round kinetic experiments in that they monitor a single round of NA translocation or NA unwinding by an enzyme initially bound to the NA substrate before the initiation of the translocation or unwinding reaction. That is, any enzyme that dissociates during translocation or unwinding is prevented from re-initiating translocation or unwinding on the NA and any enzyme that is initially free in solution is prevented from binding the NA. This condition is essential if one is to apply the analysis in section 3.5 to extract the kinetic parameters for ssNA translocation or dsNA unwinding from the data. Single-round conditions can be maintained experimentally by including a trap for free enzyme in the reaction that prevents rebinding of enzyme to the NA substrate.

In principle any nucleic acid that binds to the motor enzyme can be employed such as a trap. In addition, we have often used the polyanion heparin which binds non-specifically to most nucleic acid binding proteins. For the enzymes we have studied we use heparin, obtained from porcine mucosa (available commercially), as a trap (17, 18, 25, 27, 28). Heparin is relatively inexpensive, has high solubility (~50mg/ml) in aqueous buffers, and spectroscopic assays are available for readily determining the concentration (29). The advantage of heparin is that the ATPase activity of the enzyme is not generally stimulated by heparin (27). This will allow for more straightforward and simple analysis of the ATPase activity of the motor protein that is associated with translocation or unwinding. The concentration of trap used for a given experiment needs to be empirically determined for a particular trap, enzyme and solution condition.

3. Methods

The kinetic models and associated equations used to analyze the ssNA translocation and dsNA unwinding experiments assume that no more than one molecular motor is bound to each NA substrate. Thus, the application of the kinetic models to the analysis of the data requires the experiments to be performed under these conditions. Generally, for experiments monitoring translocation along ssNA this is achieved by performing the experiments under conditions where the ssNA is in molar excess over the motor protein. For experiments monitoring dsNA unwinding, where the helicase generally initiates at a particular site, the relative concentration of dsNA to the concentration of motor protein will vary depending upon the system. As mentioned in section 2.2, analysis of the data collected in these experiments also assume single round or single turnover conditions, i.e., that any motor enzyme that is initially free in solution at the start of the reaction or that dissociates from the DNA during translocation or unwinding does not rebind to the DNA. This is accomplished experimentally by including a trap for free enzyme (e.g., heparin).

3.1 Monitoring the Kinetics of the Arrival of the Translocase at a Specific Site on ssNA

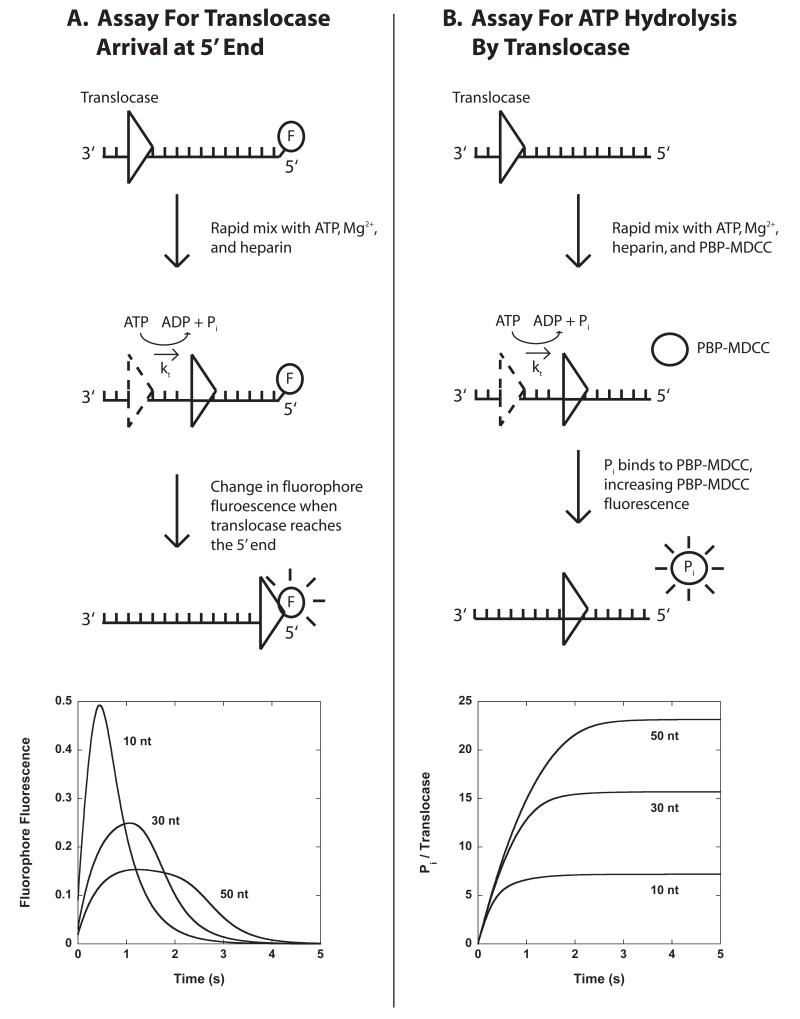
The first experimental method we discuss to study the kinetics of translocation of an enzyme along ssNA is a stopped-flow fluorescence approach first introduced by Dillingham et al.(30), and subsequently modified by Fischer et al. (16, 17, 27), is depicted in Figure 3.1A. For studies of ssDNA translocation, the method utilizes a series of oligodeoxthymidylates of varying lengths, L ((dT)_L), that have a fluorophore attached covalently to either the 3′ or 5′ end of the DNA. When the translocase reaches and interacts with the fluorophore a change in fluorescence signal occurs. In this way, one can monitor the time-dependent concentration of the translocase at the DNA end resulting from arrival of the translocase due to translocation from other sites on the DNA and dissociation of translocases from the end.

Figure 3.1.

Stopped-flow assays for monitoring the pre-steady state kinetics of enzyme translocation along ssNA. Panel A: A translocase is pre-bound to single-stranded ssNA labeled at the 5′-end with a fluorescent dye, then rapidly mixed with ATP, Mg²⁺, and heparin (protein trap) to initiate translocation. When the translocase nears the 5′-end of the ssNA the fluorescence of the dye is either quenched or enhanced. Example time courses are shown for three different lengths of DNA. Panel B: A translocase is pre-bound to ssNA and then rapidly mixed with ATP, Mg²⁺, heparin, and an excess concentration of fluorescently labeled phosphate binding protein (PBP-MDCC) to initiate translocation. As the translocase moves along the filament, ATP is hydrolyzed into ADP and inorganic phosphate (P_i). PBP-MDCC rapidly binds the P_i resulting in an increase in the PBP-MDCC fluorescence. Example time courses are shown for three different lengths of ssNA.

These experiments are performed by pre-incubating the translocase with ssNA in one syringe of the stopped-flow and initiating translocation by rapidly mixing the enzyme:ssNA complex with ATP, MgCl₂, and trap. When the experiments are performed as a function of ssNA length the resulting time courses can be analyzed using a sequential n-step model discussed in section 3.5 to determine the microscopic kinetic parameters associated with translocation of the enzyme along the NA. An example of time courses for translocation along ssDNA by the monomeric UvrD translocase is shown in Figure 3.2. Similar experiments could be performed for an RNA translocase with a series of fluorescently end-labeled ssRNA, such as oligouridylate (oligo(U)).

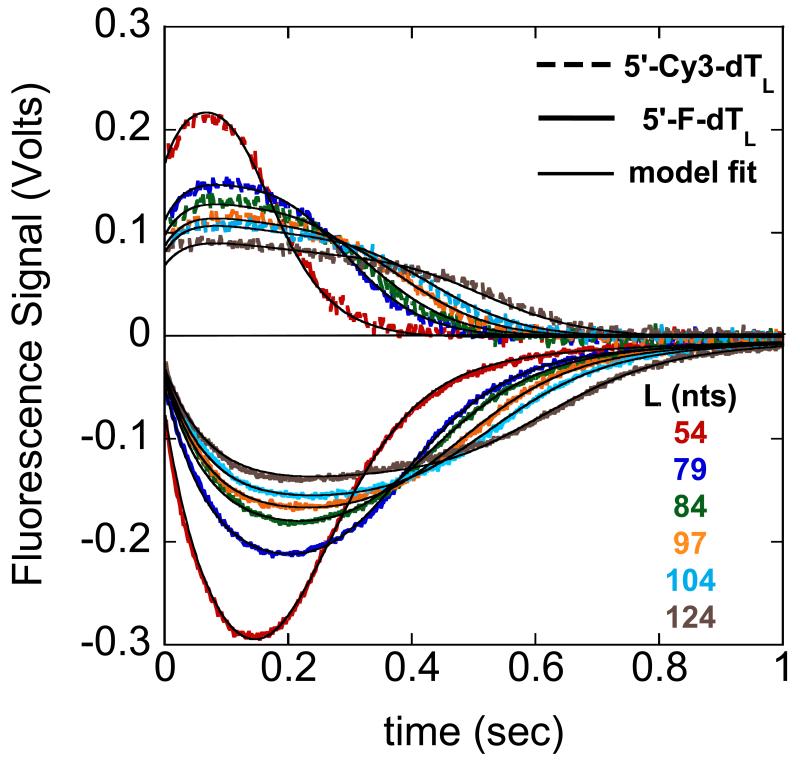
Figure 3.2.

UvrD translocation along single strand DNA labeled at the 5′-end with either fluorescein (F) or Cy3. UvrD is pre-incubated with excess DNA then rapidly mixed in the stopped-flow with ATP, MgCl₂, and heparin to initiate translocation (final conditions: 10mM Tris-HCl, pH 8.3, 20mM NaCl, 20%(v/v) glycerol, 25nM UvrD, 50nM DNA, 0.5mM ATP, 2mM MgCl₂, 4mg/ml heparin at 25°C). Heparin serves as a protein trap for UvrD, preventing UvrD from rebinding to the DNA, reinitiating translocation. The resulting fluorescence time courses for fluorescein (solid lines) and Cy3 (dashed lines) labeled single strand DNA of differing lengths is shown. The single strand DNA is composed of deoxythymidylates to avoid formation of secondary structures that may have an effect on translocation. The black curves are a global fit to both data sets using a n-step sequential model (27) yielding a value of m*k_t = (193 ± 1) nucleotides/second.

The directionality bias of translocation along the ssNA can be determined by comparing the time courses observed when the fluorophore is attached to the 3′ versus the 5′ end of the ssDNA (16, 17, 30). Specifically, characteristic changes in the fluorescence time course as a function of increasing NA length (e.g. an increase in both the time required to reach maximum (or minimum) fluorescence and the breadth of the fluorescence peak as shown in Figures 3.1A and 3.2) will occur if the translocation direction is biased toward the fluorophore. When translocation is biased away from the fluorophore, a length-independent time course, often described by a single exponential change in signal, will typically result (16, 17).

3.2 Monitoring the Kinetics of ATP Hydrolysis by the Translocase during Translocation

Enzyme translocation along ssNA can also be monitored by measuring the amount of ATP hydrolyzed by the enzyme during translocation. This approach also requires transient pre-steady state kinetic experiments rather than steady-state ATPase experiments since steady-state rates of ATP hydrolysis will generally be limited by other kinetic processes that are slower than protein translocation (e.g. dissociation and/or rebinding of protein to another NA molecule). The pre-steady state rate and extent of ATP hydrolysis by the translocase can be monitored, for example, by directly measuring the conversion of ATP to ADP using a radioactive assay (31, 32) or by monitoring the release of inorganic phosphate using a fluorescently labeled phosphate-binding protein (27, 33) as depicted in Figure 3.1B.

Analysis of a series of time courses of ATP hydrolysis during translocation performed as a function of ssNA length can be analyzed using a sequential n-step model (section 3.5) to estimate the ATP coupling stoichiometry during translocation. This analysis requires knowledge of the kinetic parameters obtained from independent analysis of translocation time courses using Method 3.1 to be used as constraints, due to parameter correlation in the n-step model (27).

3.3 Monitoring the Kinetics of dsNA Unwinding

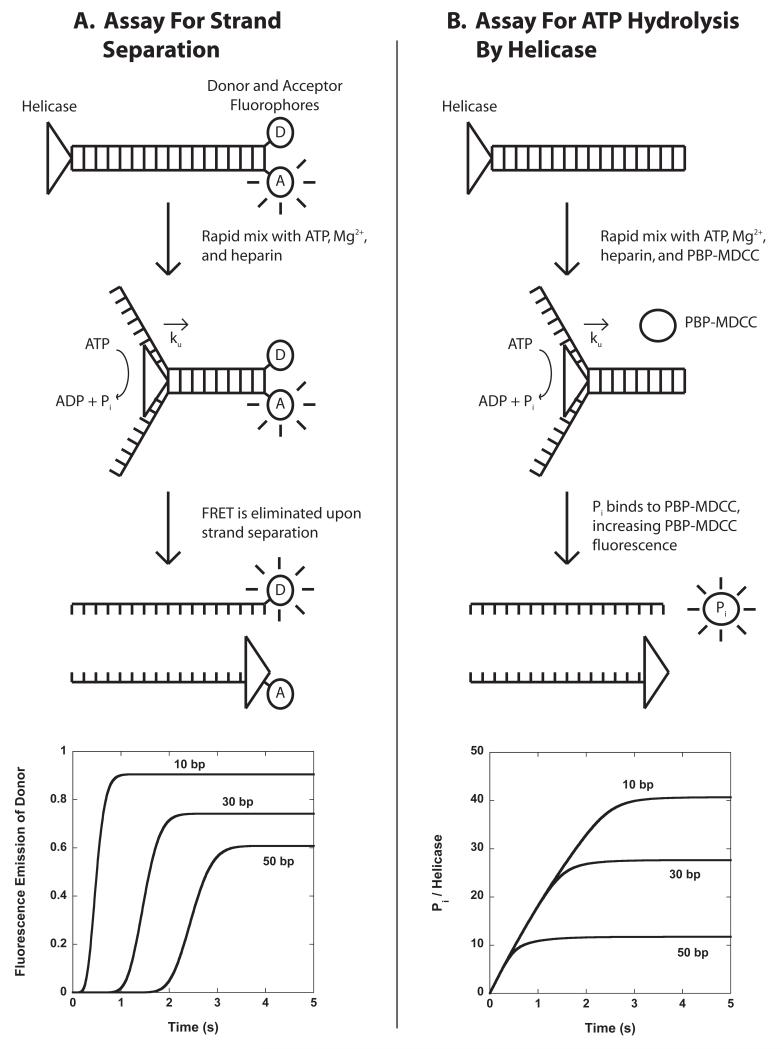
A generalized stopped-flow fluorescence based technique for monitoring the helicase catalyzed unwinding of dsDNA is depicted in Figure 3.3A (19, 34). This method employs a series of dsNA substrates, of varying lengths, L, that have donor and acceptor fluorophores attached covalently to either strand of the dsNA. In Figure 3.3A, the two fluorophores are shown adjacent to each other, in order to improve the fluorescence resonance energy transfer (FRET) between the two fluorophores, however alternate orientations are also possible. The FRET efficiency between the two fluorophores will decrease significantly upon unwinding of the duplex and subsequent separation of the two single strands. This decrease in FRET efficiency will result in an increase in the fluorescence intensity of the donor fluorophore and a decrease in the fluorescence intensity of the acceptor fluorophore, assuming only FRET changes occur. Quantitative analysis of a series of these time-courses performed as a function of L using Equation (10) allows one to estimate the microscopic kinetic parameters associated with translocation of the enzyme along the DNA. A subsequent estimate of the kinetic step size, m, can then be obtained from the analysis of the dependence of n on L through Equation (12). An example of time courses for unwinding of double-stranded DNA by the RecBC helicase (35) is shown in Figure 3.4.

Figure 3.3.

Stopped-flow assays for monitoring the pre-steady state kinetics of helicase catalyzed dsNA unwinding. Panel A: A helicase is pre-bound to dsNA labeled at the opposite end with donor and acceptor fluorophores. The close proximity of the two fluorophores results in large FRET between them. The helicase-dsNA complexes are then rapidly mixed with ATP, Mg²⁺, and heparin (protein trap) to initiate dsNA unwinding. When the helicase completely unwinds the dsNA, the two single strands separate and the FRET efficiency is dramatically decreased; this decrease in FRET efficiency will result in an increase in the fluorescence emission of the donor fluorophore and a decrease in the fluorescence emission of the acceptor fluorophore. Example time courses are shown for the unwinding of three different lengths of dsNA. Panel B: A helicase is pre-bound to dsNA and then rapidly mixed with ATP, Mg²⁺, heparin, and an excess concentration of fluorescently labeled phosphate binding protein (PBP-MDCC) to initiate translocation. As the helicase unwinds the dsNA, ATP is hydrolyzed into ADP and inorganic phosphate (P_i). PBP-MDCC rapidly binds the P_i resulting in an increase in the PBP-MDCC fluorescence. Example time courses are shown for the unwinding of three different lengths of dsDNA.

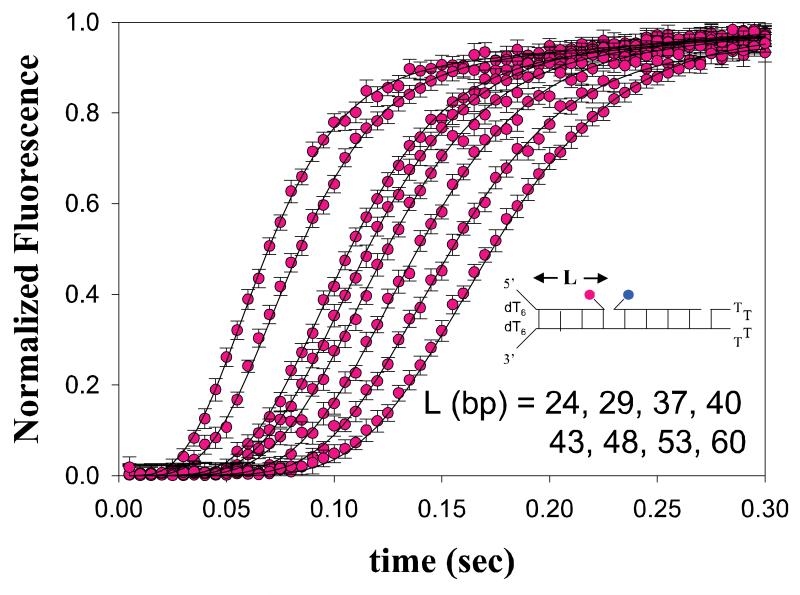
Figure 3.4.

Stopped-flow fluorescence time-courses of RecBC catalyzed DNA unwinding. 40 nM of DNA duplexes of varying length L are pre-incubated with 200 nM RecBC. DNA unwinding is initiated by rapid mixing with 10 mM ATP and 15 mg/mL heparin trap (20 mM Mops-KOH (pH 7.0 at 25°C), 30 mM NaCl, 10 mM MgCl₂, 1 mM 2-ME, 5% (v/v) glycerol). Each DNA substrate is labeled with Cy3 (pink) and Cy5 (blue) as indicated and DNA unwinding is observed by monitoring both Cy3 and Cy5 fluorescence simultaneously. Cy3 time-courses are shown and the data is described well by Scheme 3.2 using Equation 10 with an associated value of m*k_u = (372 ± 15) basepairs/second.

3.4 Monitoring the Kinetics of ATP Hydrolysis by the Helicase during Double-stranded DNA Unwinding

The helicase catalyzed unwinding of double-stranded DNA can also be monitored by measuring the amount of ATP hydrolyzed by the helicase during the unwinding reaction. As with measurements of ssNA translocation, the pre-steady state rate and extent of ATP hydrolysis by the helicase as it unwinds dsNA can be monitored using either a radioactive assay (31, 32) or a fluorescence-based assay (27, 33) as depicted in Figure 3.3B.

Analysis of a series of time courses of ATP hydrolysis during translocation performed as a function of dsNA length, L, can be analyzed using Equation (11) to determine estimates of the microscopic parameters c, k_a, k_end, and the macroscopic ATP coupling stoichiometry c/m. In this analysis, the values of the microscopic parameters obtained from the analysis of translocation time courses using Method 3.4 (k_u, k_d, k_end,) are used as fixed constraints in the application of Equation (10).

3.5 Sequential “n-step” Models for Analyzing Translocation and DNA Unwinding Time courses

3.5.1 Translocation along ssNA

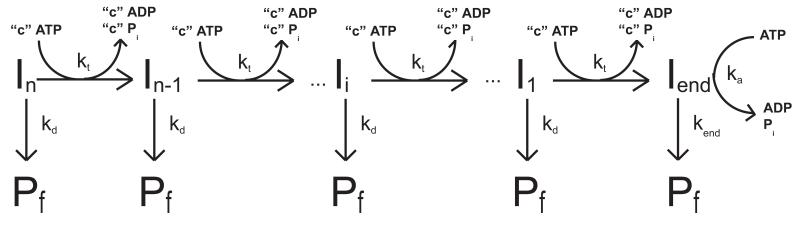
The sequential “n-step” kinetic mechanism shown in Scheme 3.1 has been used to model enzyme translocation and its coupling to ATP hydrolysis (16, 27). In this mechanism (16), depicted in Figure 3.5, a translocase with an occluded site size of b nucleotides and a contact size of d nucleotides binds with polarity to a ssNA molecule, L nucleotides long. The contact size, d, represents the number of consecutive nucleotides required to satisfy all contacts with the translocase and is thus less than or equal to the occluded site size. In this discussion we will assume that translocation along the ssNA is directionally biased from 3′ to 5′, but the results are equally applicable to a translocase which exhibits the opposite directional bias.

Scheme 3.1.

Figure 3.5.

Kinetic model for ATP-dependent protein translocation along a ssNA filament. Panel A: A cartoon depicting the binding of a translocase with a contact size d and occluded site size b to a ssNA filament of length L. As shown in this cartoon, the contact size, d, is always less than or equal to the occluded site size, b. Panel B: Cartoon showing the model used to describe enzyme translocation along a ssNA filament. The line segments represent the ssNA and the triangles represent the translocase. The translocase binds randomly, but with polarity, to the ssNA and upon binding and hydrolysis of ATP proceeds to translocate toward the 5′ end of the filament in discrete steps with rate constant k_t. The rate constant of dissociation during translocation is k_d. Upon reaching the 5′ end of the filament, the translocase dissociates with a rate constant k_end. Dissociated translocases bind to a protein trap, T, and are thereby prevented from rebinding the ssNA.

The translocase is initially bound i translocation steps away from the 5′-end, with concentration, I_i. The number of translocation steps, i, is constrained (1≤i≤n), where n is the maximum number of translocation steps needed for a translocase bound initially at the 3′ end to move to the 5′ end of the NA. In the discussion here we considered two initial binding states for the translocase: one in which all proteins initiate translocation from the same site on the ssNA (in this case at the 3′ end of the ssNA, which is n steps away from the 5′ end) and one in which the proteins initiate translocation from random binding sites on the ssNA.

Upon addition of ATP the translocase moves with directional bias along the ssNA via a series of repeated rate-limiting translocation steps each associated with the same rate constant, k_t. The rate constant for protein dissociation during translocation is k_d. The processivity of translocation along the NA can be defined as $P=\frac{k_t}{k_d+k_t}$. Between two successive rate-limiting translocation steps the enzyme moves m nucleotides, while hydrolyzing c ATP molecules. Therefore, c/m is defined as the macroscopic ATP coupling stoichiometry and corresponds to the average number of ATP molecules hydrolyzed per nucleotide translocated along the ssNA. Similarly the product m*k_t is the macroscopic translocation rate in units of nucleotides/second. When the translocase reaches the 5′-end of the NA it continues to hydrolyze ATP with rate constant k_a and dissociates from the NA with rate constant k_end. This hydrolysis of ATP at the end of the ssNA is not coupled to the physical movement of the enzyme along the ssNA and thus is referred to as futile hydrolysis (27, 33).

We note that, in general, k_t represents the rate constant for the rate-limiting step that occurs within each repeated translocation cycle and does not necessarily correspond to the rate constant for physical movement of the translocase along the ssNA (16). Similarly, the average number of nucleotides translocated between two successive rate-limiting steps, defined as the translocation “kinetic step-size” (m), can be larger than the length of ssNA traversed during hydrolysis of a single ATP.

Based on Scheme 3.1, the expressions in Equations (1) and (4) can be derived (16, 19) for the time-dependent accumulation of protein at the 5′ end of the ssNA. In these equations, L⁻¹ is the inverse Laplace transform operator, s is the Laplace variable (19) and the parameters k_t, k_d, k_end, c, k_a and n are as defined above and r is the initial (at time, t = 0) ratio of the probability of the translocase binding to any one binding position on the ssNA other than the 5′ end to the probability of the translocase binding to the 5′ end (16, 17). For the case where all the proteins are initially bound at the same position (in this case taken to be the 3′ end of the ssNA), the equation for the time-dependent accumulation of protein at the 5′ end of the ssNA is given by Equation (1).

$$f_{5^{\prime }}t=A^{\ast }{L}^{-1}\left[\frac{1}{k_{end}+S}{\left(\frac{k_t}{k_t+k_d+S}\right)}^n\right]$$ (1)

For the case where all the proteins are initially bound at random positions along the NA, the equation for the time-dependent accumulation of protein at the 5′ end of the NA is given by Equation (2).

$$f_{5^{\prime }}t=\frac{A}{1+n^{\ast }r}{L}^{-1}\left[\frac{1}{S+k_{end}}\ast \left(1+\frac{k_t{}^{\ast }r}{S+k_d}\left(1-{\left(\frac{k_t}{S+k_t+k_d}\right)}^n\right)\right)\right]$$ (2)

The scalar A in Equations (1) and (2) allows for conversion of the concentration of protein bound at the 5′ end of the NA into a signal that can be measured experimentally (e.g., a spectroscopic change) (16, 17, 27).

Similarly, Equations (3) and (4) are expressions for the time-dependent production of ADP or P_i, due to ATP hydrolysis by the translocases (16). In Equations (3) and (4), I(0) is the concentration of translocase initially bound to the NA (at time, t =0) and the scalar A allows for the conversion of the concentration of ADP (or P_i) produced by the translocase into a signal that can be measured experimentally. Equation (3) describes the ATP production occurring when all proteins are initially bound at the same position (e.g., the 3′ end of the NA) and Equation (4) describes the ATP production occurring when all the proteins are initially bound at random positions along the NA.

$$ADPt=A^{\ast }I0{}^{\ast }{L}^{-1}\left[\frac{1}{S}\left(\frac{c{}^{\ast }{k}_t{}^{\ast }\left(1-{\left(\frac{k_t}{k_t+k_d+S}\right)}^n\right)}{k_d+S}+\frac{k_a}{k_{end}+S}{\left(\frac{k_t}{k_t+k_d+S}\right)}^n\right)\right]$$ (3)

$$ADPt=\frac{A^{\ast }I0}{1+n^{\ast }r}{L}^{-1}\left[\frac{1}{S}\left(\frac{c^{\ast }{k}_t{}^{\ast }{r}^{\ast }\left(n{k}_d+S+k_t\left({\left(\frac{k_t}{k_t+k_d+S}\right)}^n-1\right)\right)}{k_d+S{}^2}+\frac{k_a\left(1+\frac{k_t{}^{\ast }r\left(1-{\left(\frac{k_t}{k_t+k_d+S}\right)}^n\right)}{k_d+S}\right)}{k_{end}+S}\right)\right]$$ (4)

The maximum number of translocation steps, n, for a NA of a length, L, is related to the translocation kinetic step-size, m, and the translocase contact size by Equation (5).

$$n=\frac{L-d}{m}$$ (5)

Equation (5) can be re-expressed as Equation (6) which allows for the determination of m from the experimentally determined dependence of L on n.

$$L=mn+d$$ (6)

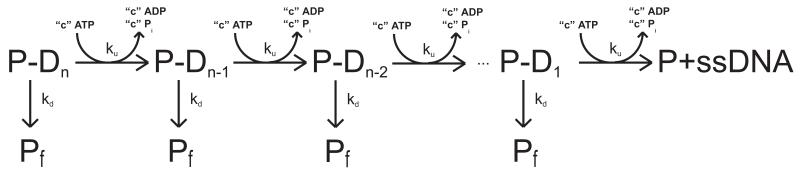
3.5.2 Unwinding of dsNA

The sequential “n-step” kinetic mechanism shown in Scheme 3.2 can been used to model helicase catalyzed dsNA unwinding and the coupling of this process to ATP hydrolysis (19). In this mechanism, a helicase binds to a unique site at one end of region of dsNA n basepairs long. Upon addition of ATP the helicase unwinds the dsNA through a series of repeated rate-limiting steps each associated with the same rate constant, k_u. The rate constant for protein dissociation during unwinding is k_d. An expression for the processivity of unwinding, identical to the expression for the processivity of k translocation, can be defined as $P=\frac{k_t}{k_d+k_t}$. Between two successive rate-limiting unwinding steps the enzyme unwinds m basepairs of the dsNA, while hydrolyzing c ATP molecules. As for the case of ssNA translocation, the ratio c/m is defined as the macroscopic ATP coupling stoichiometry and, in this case, corresponds to the average number of ATP molecules hydrolyzed per basepair of dsNA unwound. Similarly the product m*k_u is the macroscopic unwinding rate in units of basepairs/second. When the helicase completes the unwinding of all n basepairs of the dsNA, it may remain bound to one of the resulting ssNA strands and continue to hydrolyze ATP (futile hydrolysis) with rate constant k_a and dissociates from the DNA with rate constant k_end.

Scheme 3.2.

We note that, in general, k_u represents the microscopic rate constant for the rate-limiting step that occurs within each repeated unwinding cycle and does not necessarily correspond to the rate constant for physical movement of the helicase through the dsNA (16). Similarly, the average number of basepairs unwound between two successive rate-limiting steps, defined as the translocation “kinetic step-size” (m), can be larger than the length of dsNA traversed during hydrolysis of a single ATP.

Based on Scheme 3.2, the expression in Equation (7) can be derived (19) for the time-dependent formation of ssNA (or the corresponding decrease in the concentration of dsNA) resulting from the activity of the helicase.

$$ssDNAt=P^n\left(1-\frac{\Gamma n,k_u+k_{d}t}{\Gamma n}\right)$$ (7)

In this equation, the parameters P, k_u, k_d, and n are defined as above. Γ(n) is the Gamma function, defined in Equation (8), and Γ (n, (k_u+k_d)t) is the incomplete Gamma function, defined in Equation (9).

$$\Gamma n={\int }_0^{\infty }{r}^{n-1}{e}^{-r}dr=n-1!$$ (8)

$$\Gamma n,k_u+k_{d}t={\int }_{k_u+k_{d}t}^{\infty }{r}^{n-1}{e}^{-r}dr$$ (9)

When the unwinding reaction is monitored using a spectrophotometric assay, such as the FRET assay described in Method 3.3, then Equation (10) can be used.

$$ft=A^{\ast }{L}^{-1}\left[\frac{1}{S}{\left(\frac{k_u}{k_u+k_d+S}\right)}^n\right]$$ (10)

In Equation (10), L⁻¹ is the inverse Laplace transform operator, s is the Laplace variable (19) and the parameters k_u, k_d, and n are as defined above. The scalar A allows for the conversion of the formation of ssNA into a signal that can be measured spectrophotometrically.

Similarly, Equation (11) is the expression for the time-dependent production of ADP or P_i, due to ATP hydrolysis by the helicase during the unwinding of the dsNA.

$$ADPt=P-{D_{nt=0}}^{\ast }{L}^{-1}\left[\frac{1}{S}\left(\frac{c{}^{\ast }{k}_u{}^{\ast }\left(1-{\left(\frac{k_u}{k_u+k_d+S}\right)}^n\right)}{k_d+S}+\frac{k_a}{k_{end}+S}{\left(\frac{k_u}{k_u+k_d+S}\right)}^n\right)\right]$$ (11)

In Equation (11), L⁻¹ is the inverse Laplace transform operator, s is the Laplace variable (19) and the parameters k_u, k_d, k_end, k_a and n are as defined above. [P−D_n]_t=0 is the concentration of helicase initially bound to the dsNA (at time, t =0). The maximum number of unwinding steps, n, for a dsNA of length L is related to the kinetic step size, m, by Equation (12).

$$n=\frac{L}{m}$$ (12)

4. Notes

4.1

In preparing the trap for the motor enzyme, it is important to determine the concentration of trap that will be effective in trapping any free enzyme. This is especially true if heparin is used as the trap, since heparin preparations obtained commercially are not homogeneous and in our experience each new lot of heparin varies in its effectiveness. Trap effectiveness can be assayed most directly by monitoring the kinetics of enzyme binding to the ssNA or dsNA used in the translocation or unwinding experiments, respectively, in the presence of varying concentrations of the trap. The minimum concentration of the trap that can effectively compete with the NA for enzyme binding is the concentration that should be used in all experiments as the presence of trap may affect the kinetics of ssNA translocation or dsNA unwinding (see note 4.2).

4.2

It has been observed that the enzyme trap can often facilitate the dissociation of the motor enzyme from the NA substrate. We have observed this in our studies of E. coli UvrD using heparin as a trap (17). This can be determined by performing a series of experiments as a function of the trap concentration to see if the time courses change. In the case of UvrD, the only kinetic parameters affected by the heparin concentration are the rate constants for dissociation from internal sites and for dissociation from the 5′-end of the ssDNA (17), which increase with heparin concentration. If this situation occurs one the processivity will also be dependent on trap concentration due to the effect on the dissociation rate constant.

4.3

When monitoring motor enzyme translocation along ssNA a single set of fluorescent labled ssNA substrates is sufficient in obtaining an initial estimate of the macroscopic translocation rate (m*k_t). However, the microscopic parameters (k_d, k_t, r, m, n, d, and k_end) can be fluorophore dependent. This can result due to the different mechanisms by which the fluorophore intensities can be affected by the presence of the enzyme. In addition, the intensities of different fluorophores can be affected by the enzyme over different distances. In order to obtain fluorophore independent estimates of the macroscopic and microscopic kinetic parameters data should be collected from at least two sets of experiments using ssNA substrates labeled with different fluorescent probe. Simultaneous, global analysis of the resulting data together using the appropriate sequential n-step model yields fluorophore independent estimates of k_t, m, n, d, and r (17, 27).

4.4

Significant correlations can occur among the parameters in Equations (1) through (4). For this reason, it is always best to determine independently as many parameters as possible so that they can be constrained in the NLLS analysis to determine the remaining parameters. For example, the rate of dissociation during translocation (k_d in Scheme 3.1) can often be determined independently by monitoring the dissociation of enzyme during translocation along an infinitely long DNA (16, 17, 27).

4.5

As seen in Equations (7) and (10), it is the sum of k_u and k_d that dominate the kinetics of dsNA unwinding (19). This sum is often termed k_obs = k_u + k_d, and can be determined from the dependence of the kinetics of double-stranded DNA unwinding on DNA length, regardless of the processivity of the helicase (18-20).

4.6

We note that the presence of the fluorophore on the DNA can potentially influence the rate of translocation, unwinding, or the rate of dissociation near the fluorophore (17, 27). It is also possible that variations in the electrostatics of the NA molecule near its ends may contribute to differences in k_t and k_d at binding positions near the ends. Thus, for an enzyme that translocates in a 3′ to 5′ direction, the values for k_t and k_d obtained from fitting experimental time-courses obtained with NA labeled with a fluorophore at the 3′ end may not be the same as the values of k_t and k_d that apply in the absence of the fluorophore or to interior regions of the NA. Similarly, the value of k_end obtained from fitting experimental time-courses obtained with DNA labeled with a fluorophore at the 5′ end may not equal the value of k_end that applies in the absence of the fluorophore (16, 27).

4.7

The models (Scheme 3.1 and Scheme 3.2) presented here assume translocation and unwinding occur via a uniform repetition of irreversible rate-limiting steps, and ignores any non-uniformity in these processes. Our analysis of simulated kinetic data that includes non-uniformity has demonstrated that the values of the macroscopic translocation rate (mk_t), macroscopic unwinding rate (mk_u), and the coupling stoichiometry (c/m) obtained using these equations reliably reflect the actual input values used for the simulations regardless of the presence of any non-uniform motion of the motor protein. The estimates of the microscopic kinetic parameters, especially k_u, k_t, and m, will be affected by the presence of the non-uniformity, however. Generally, the estimate of m is increased by the presence of non-uniformity; because of this, the estimate of m should be considered an upper limit.

4.8

Use of the uniform sequential “n-step” model to analyze time courses of ssNA translocation obtained from experiments in which the translocase initiates at random positions along the NA requires inclusion of the r parameter in Equations (2) and (4). If the translocase has equal affinity for all potential binding sites on the DNA then r must have a value between 1 and m depending upon the specific details of the translocation mechanism near the end of the DNA (see (16) for more details). Thus, estimated values of r for which r > m may indicate a failure of the simple model to correctly describe the translocation process, regardless of the quality of the fits. In other words, r can serve as an indicator of potential non-uniformity in the translocation mechanism.

4.9

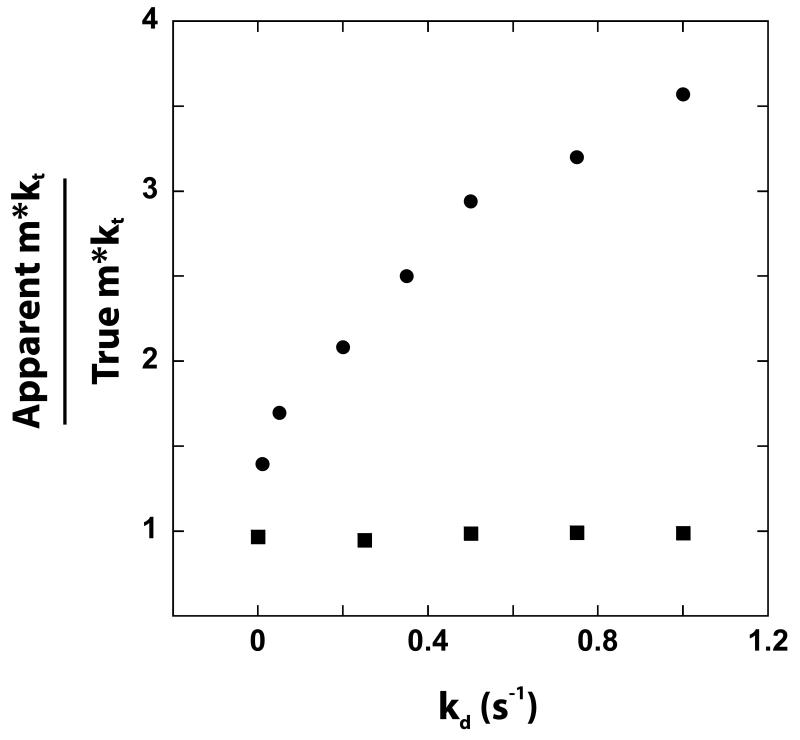
We note that an approximate analysis, which we refer to as the “time to peak fluorescence” analysis has been used to estimate the macroscopic translocation rate from data collected using Method 3.2. This approximate analysis is based upon the dependence on the length of the NA of the time required to reach the maximum (or minimum) fluorescence signal during a translocation time course (30, 36). We have examined the utility of this procedure by using it to analyze computer simulated translocation time courses and have determined that it does not generally provide a reliable estimate of even the macroscopic translocation rate; in fact, the procedure results consistently in an over-estimate of the rate for systems in which the enzyme can initiate translocation randomly along the ssNA. The exact magnitude of the overestimation is a function of the microscopic translocation rate (k_t in Scheme 3.1), the microscopic rate of dissociation during translocation (k_d in Scheme 3.1), and the microscopic rate of dissociation from the end of the DNA (k_end in Scheme 3.1). For example, as shown in Figure 4.1 (filled symbols), the ratio of the apparent macroscopic translocation rate (m*k_t) determined from the “time to peak” analysis to the true value used in the simulation is strongly dependent on the value of k_d in the simulation, with the overestimation of the rate increasing with increasing k_d. Similar results were obtained when either k_t or k_end was varied independently, while other simulation parameters were held constant (data not shown). We found that this method of determining the value of m*k_t was most accurate when the magnitude of k_t was much larger than the magnitude of k_end and when the processivity of translocation was sufficient for nearly all the translocating enzymes to reach the end of the NA. However, since such microscopic kinetic information is not known before the experiment is performed, and cannot be determined from the time to peak fluorescence analysis, use of this simplified analysis can result in incorrect quantitative conclusions.

Figure 4.1.

The dependence of the ratio of the apparent value of the macroscopic translocation rate (m*k_t) to the true value of m*k_t used in the simulation on the value of k_d used in the simulation. The apparent value of the m*k_t was determined from the dependence on the length of the DNA of the maximum fluorescence signal (i.e., population of protein bound at the end of the DNA) that occurs during the time course of protein translocation along the DNA (30). In the simulations used to generate these time courses, we used constant values of k_t = 30 steps/s, m = 1 nt/step, and k_end = 3 s⁻¹. Qualitatively similar results are obtained with other sets of parameters (data not shown).

On the other hand, if the translocase initiates from a unique position (e.g., from one end of the DNA), then our simulations indicate that the “time to peak” analysis returns an accurate estimate of the macroscopic translocation rate (open symbols in Figure 4.1).