Abstract
In the research reported here, we examined whether processing speed mediates the development of general intelligence (g) in adolescence. Using the Armed Services Vocational Aptitude Battery, a battery of 12 diverse cognitive tests, we assessed processing speed and g in a large sample of 13- to 17-year-olds obtained from the National Longitudinal Survey of Youth (N = 6,969). The direct effect of age on g was small compared with the total effect of age on g, which was almost fully mediated through speed. The results suggest that increases in g in adolescence can be attributed to increases in mental speed.
Keywords: intelligence, cognitive ability
Other things being equal, the more quickly a person produces the correct response, the greater is his intelligence. (Thorndike, Bregman, Cobb, & Woodyard, 1927, p. 24)
In the research reported here, we examined whether processing speed contributes to the development of general intelligence (g) in adolescence. Researchers calculate g by measuring variance common to mental tests. Such variance is strongly related to performance on IQ and other intelligence tests, which are said to be “g loaded.” Tests that are g-loaded are among the best predictors of success in school and work (Jensen, 1998, pp. 270–305). Processing speed refers to mental speed and is measured by reaction time, computing speed, and coding speed, as well as performance on other timed tasks. Faster processing speed predicts better performance on g-loaded tests (Jensen, 2006).
Processing speed and g both increase during adolescence (for reviews, see Jensen, 2006; Kail, 1991, 2000). From the ages of 12 to 18 years, adolescents show global increases in processing speed, as indicated by reaction times on tests of coding speed and naming speed, and in g, as indicated by performance on g-loaded tests. Together, these findings suggest that processing speed is a critical component in the development of g.
Although no single study modeling both constructs has linked processing speed to the development of g, processing speed has been linked to the development of fluid intelligence (e.g., Fry & Hale, 1996). Fluid intelligence refers to general reasoning ability, one of several specific cognitive abilities (Carroll, 1993). Such abilities are loaded with construct specific variance and are therefore imperfect estimates of g. They are further removed from g when they are estimated using only one test (e.g., Raven’s Matrices), as they have been in developmental studies of fluid intelligence (Fry & Hale, 1996; cf. Kail, 2007). A good estimate of g can be obtained only from the variance common to a diverse set of cognitive tests (Jensen & Weng, 1994).
In this study, we examined whether processing speed mediates the development of g between the ages of 13 and 17 years, using the 1997 National Longitudinal Survey of Youth (NLSY97). The NLSY97 included the computerized adaptive Armed Services Vocational Aptitude Battery (ASVAB), which consists of 12 cognitive tests. We estimated processing speed using the simple ASVAB tests of coding speed and computation speed, which have been widely used in similar research (Kail, 1991; Salthouse, 1996). We estimated g using the 10 other ASVAB tests, which measure diverse cognitive abilities (e.g., arithmetic reasoning, ability to assemble objects, and knowledge of words). Estimates of g made using the ASVAB are strongly related to performance on intelligence tests (Coyle & Pillow, 2008; Frey & Detterman, 2004).
Our study is the first to use structural equation modeling (SEM) to model relations among age, g, and processing speed in adolescence. Given prior research (Jensen, 2006; Kail, 1991, 2000), we predicted that age would be positively related to both g and processing speed, and that processing speed would be positively related to g. We further predicted that the relation between age and g would be attributable to processing speed. Such a finding would be the first direct evidence that mental speed mediates the development of g in adolescence.
Method
Subjects
Subjects were drawn from the NLSY97 (N = 8,984), which is administered by the U.S. Department of Labor (Hering & McClain, 2003, pp. 1–14). The NLSY97 is a nationally representative sample of U.S. youths who were born between 1980 and 1984. The sample used in our study consisted of 6,969 subjects who had complete ASVAB scores and were 13 to 17 years old at the time of testing (mean age = 14.99 years, SD = 1.39). Our sample included 1,365 thirteen-year-olds (705 males, 660 females), 1,415 fourteen-year-olds (738 males, 677 females), 1,434 fifteen-year-olds (731 males, 703 females), 1,468 sixteen-year-olds (725 males, 743 females), and 1,287 seventeen-year-olds (628 males, 659 females).
Processing speed and g
Processing speed and g were estimated using the ASVAB (Hering & McClain, 2003, pp. 82–84). The ASVAB includes two timed speed tests, which we used to estimate processing speed, and 10 untimed power tests, which we used to estimate g. The two speed tests are Coding Speed, in which respondents match numbers and words using a key, and Numerical Operations, in which respondents perform simple mathematical operations, most of which involve single-digit numbers (e.g., 3 + 3 = ?). Similar speed tests have been widely used to estimate processing speed (e.g., Kail, 1991; Salthouse, 1996).
The power tests are Arithmetic Reasoning, which measures the ability to solve mathematical word problems; Assembling Objects, which measures the ability to visualize how an object will look when its parts are assembled; Auto Information, which measures knowledge of automotive technology; Electronics Information, which measures knowledge of electronics; General Science, which measures knowledge of physical and biological sciences; Math Knowledge, which measures the ability to solve basic (mostly algebraic) math problems; Mechanical Comprehension, which measures knowledge of mechanical and physical principles; Paragraph Comprehension, which measures reading comprehension; Shop Information, which measures knowledge of wood- and metal-shop tools and practices; and Word Knowledge, which measures the ability to identify synonyms.
The power tests were presented on a computer using an adaptive procedure that calibrated item difficulty with ability level. The speed tests were presented on a computer using a nonadaptive procedure, in which items were presented in the same order to all subjects. The power tests were scored using item-response-theory statistics, with higher scores indicating better performance. The speed tests were scored using latencies for correct responses, adjusted for guessing and item presentation time. To facilitate interpretation, we standardized scores on all tests (M = 0, SD = 1) prior to analysis.
Statistics and mediation model
SEM with maximum likelihood estimation was used to estimate latent constructs (g and speed) and standardized path coefficients. The analysis estimated three effects: total effect (the unmediated effect of age on g before controlling for speed), direct effect (the mediated effect of age on g after controlling for speed), and indirect effect (the magnitude of mediation, or the difference between the total and direct effects). We used Sobel’s test to evaluate the significance of the indirect effect.1 We used four tests—chi-square, comparative fit index (CFI), root-mean-square error of approximation (RMSEA), and standardized root-mean residual (SRMR)—to evaluate model fit. Chi-square tests are sensitive to sample size and can show significant effects (indicating poor fit) with samples as large as ours; CFI and RMSEA are less sensitive to sample size. Following Kline’s (2005) procedure, we deemed model fit adequate for CFIs greater than .90, and for RMSEAs and SRMRs less than .10.
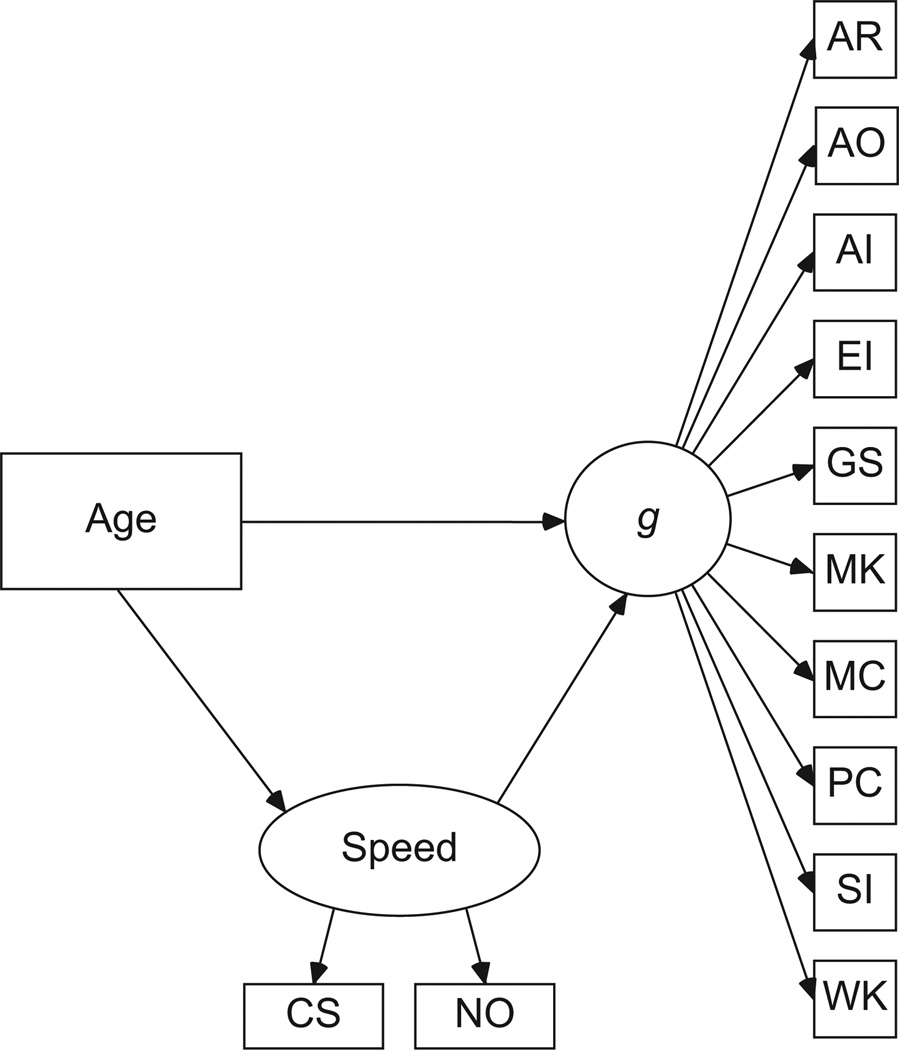
Because fit statistics and path coefficients can vary with different models of g (Coyle & Pillow, 2008), we tested the mediation model in four SEM analyses using different models of g. In Analysis 1, g was modeled as a first-order factor with no group factors (see Fig. 1 for an illustration of this model). In Analysis 2, g was modeled as a second-order factor with two group factors, one covering school-related abilities (Arithmetic Reasoning, General Science, Paragraph Comprehension, Math Knowledge, and Word Knowledge), and the other covering shop-related abilities (Auto Information, Assembling Objects, Electronics Information, Mechanical Comprehension, and Shop Information). Analysis 3 was conducted in the manner of the exploratory factor analysis used by Coyle and Pillow (2008). In this analysis, g was modeled as a second-order factor with three group factors: shop-related ability (Auto Information, Electronics Information, Mechanical Comprehension, and Shop Information), school-related ability (General Science, Paragraph Comprehension, and Word Knowledge), and math-related ability (Arithmetic Reasoning, Assembling Objects, and Math Knowledge). Analysis 4 was identical to Analysis 3 but included correlated errors among five pairs of tests (Auto Information–Shop Information, Assembling Objects–Mechanical Comprehension, Arithmetic Reasoning–Numerical Operations, Electronics Information– Mechanical Comprehension, and Numerical Operations–Math Knowledge). The correlated errors were identified using modification indices and involved tests that were meaningfully related to each other.
Fig. 1.
Mediation model estimating the direct effect of age on g and the indirect effect of age on g through speed (Analysis 1). Speed was assessed with two tests, and g was assessed with 10 tests. AR = Arithmetic Reasoning; AO = Assembling Objects; AI = Auto Information; EI = Electronics Information; GS = General Science; MK = Math Knowledge; MC = Mechanical Comprehension; PC = Paragraph Comprehension; SI = Shop Information; WK = Word Knowledge; CS = Coding Speed; NO = Numerical Operations.
Results
The results were consistent across all analyses (Table 1). As predicted, age was positively related to g (mean total effect = 0.29) and to speed (mean effect = 0.34), which was strongly related to g (mean effect = 0.77). Speed strongly mediated the effect of age on g in all analyses (Sobel zs ≥ 21.69). The direct effect of age on g (M = 0.04) was small compared with the total effect (M = 0.29). The total effect was almost fully explained by the indirect effect through speed (M = 0.26; 88% of the total effect). The best-fitting model was the three-factor model of g with correlated errors, for which all fit statistics except the chi-square test indicated adequate fit (Table 1, Analysis 4).2
Table 1.
Fit Statistics, Standardized Path Coefficients, and Mediation Effects From the Structural Equation Modeling Analyses
| Fit statistic | Path coefficient | Age → g | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Analysis | χ2 | CFI | RMSEA | SRMR | Age → g | Age → speed |
Speed → g |
Total effect | Indirect effect |
Sobel z |
| 1 (no group factors) | 8,262.33 (df = 63) | .88 | .14 | .06 | 0.05 | 0.34 | 0.76 | 0.30 | 0.26 | 21.69 |
| 2 (two group factors) | 6,394.16 (df = 61) | .91 | .12 | .06 | 0.01 | 0.33 | 0.75 | 0.26 | 0.25 | 22.35 |
| 3 (three group factors) | 5,530.64 (df = 60) | .92 | .11 | .05 | 0.04 | 0.34 | 0.78 | 0.31 | 0.26 | 21.73 |
| 4 (three group factors, correlated errors) | 3,237.94 (df = 55) | .95 | .09 | .04 | 0.04 | 0.33 | 0.79 | 0.30 | 0.26 | 25.35 |
Note: N = 6,969. All chi-square and Sobel tests were significant (ps < .01). All path coefficients were significant (ps < .01) except for the path from age to g in Analysis 2 (p = .41). CFI = comparative fit index; RMSEA = root-mean-square error of approximation; SRMR = standardized root-mean residual.
To determine whether g had mediated the effect of age on speed, we conducted additional SEM analyses in which we replaced the path from speed to g in the prior analyses with a path from g to speed. If g had mediated the effect of age on speed, then the indirect effect in these reverse-causality analyses should have been larger (as a percentage of the total effect) than the indirect effect in the prior analyses. But this was not the case: The indirect effect in the reverse-causality analyses (M = 0.22; 65% of the total effect) was consistently smaller than the indirect effect in the prior analyses (M = 0.26; 88% of the total effect).
Discussion
This study is the first to show that increases in processing speed almost fully mediate increases in g between the ages of 13 and 17 years. We estimated g using 10 diverse cognitive tests, and estimated processing speed using two common speed tests (Coding Speed and Numerical Operations). The mediating effect of speed on g was strong and consistent (Table 1). The direct effect of age on g was small compared with the total effect, which was almost fully explained by the indirect effect through speed (M = 88% of the total effect). Reverse-causality analyses, which tested whether g mediated the effect of age on speed, yielded weaker effects.
Our results confirm and extend previous findings on processing speed and cognitive development. Increases in processing speed in adolescence have been linked to improvements in reading comprehension, phonological awareness, mental rotation, spatial memory, verbal memory, and mental computation (Jensen, 2006; Kail, 1991, 2000). In the current study, increases in processing speed in adolescence were linked to increases in g, with speed almost fully mediating the effect of age on g. We found evidence for this mediating effect using a large sample of subjects and a diverse array of tests, which minimized sampling error.
The results also confirm and extend developmental research on processing speed and fluid intelligence, which reflects reasoning and problem-solving ability (Carroll, 1993). For example, in one developmental study, Fry and Hale (1996; cf. Kail, 2007) found that increases in fluid intelligence were related to working memory, which in turn was related to processing speed. However, in that study, fluid intelligence was measured using only Raven’s Progressive Matrices, an inductive reasoning test with homogeneous content (i.e., figural matrices). Because performance on Raven’s Matrices is not always strongly related to g (r = .42; Coyle & Pillow, 2008, Fig. 1A), it should not be regarded as a good measure of g, which can be accurately estimated only by using a broad spectrum of tests.
Although processing speed strongly mediated the development of g in our study, it may have done so indirectly through cognitive processes such as encoding, inhibition, or retrieval. These other cognitive processes have been found to be related to each other and to processing speed (Carroll, 1993). However, processing speed is assumed to broadly constrain cognitive development by limiting the speed of all cognitive processes (e.g., Kail, 1991). Thus, processing speed would also be expected to constrain the development of g, which reflects all cognitive processes (cf. Jensen, 2006; Kail, 2000).
Our findings are consistent with theories emphasizing the role of processing speed in children’s cognitive development (Jensen, 2006; Kail, 1991, 2000). These theories assume that increases in processing speed contribute to global improvements in cognition, which are observed as increases in g. Such improvements in cognition and g have been attributed to neural changes including increases in nerve conduction velocity, neuronal oscillations, and brain myelination (Jensen, 2011; Miller, 1994).
Our study is the first to show that processing speed almost fully mediates age-related increases in g during adolescence. Our findings extend the dictum of Thorndike et al. (1927, p. 24) quoted at the beginning of this article: Not only is faster mental speed related to higher levels of g, but mental speed also contributes significantly to the growth of g in adolescence.
Acknowledgments
We thank Steve McClaskie of National Longitudinal Surveys User Services for his help in identifying relevant variables in the National Longitudinal Survey of Youth, and Michelle Little for her suggestions on structural equation modeling.
Funding
This research was supported by the San Antonio Area Foundation, by University of Texas at San Antonio Faculty Research Awards and Development Leaves, by University of Texas Health Science Center at San Antonio General Clinical Research Center Grant M01-RR-01346, and by National Institute of Biomedical Imaging and Bioengineering Grant K01-EB006395.
Footnotes
Declaration of Conflicting Interests
The authors declared that they had no conflicts of interest with respect to their authorship or the publication of this article.
Sobel’s test is based on the ratio of an indirect effect over its standard error.
Because age differences in the relation between speed and g could have distorted the mediation effects, we examined whether age moderated this relation in a supplemental analysis. The analysis used the g from the best-fitting model (Table 1, Analysis 4). Fit was estimated using an unconstrained model in which speed-g relations were freely estimated at each age and a constrained model in which speed-g relations were equal across ages. A chi-square difference test for the models was not significant, χ2(4) = 2.18, p = .70, indicating that the relation between speed and g did not vary with age (β = 0.79, 0.78, 0.79, 0.76, and 0.78, for 13-, 14-, 15-, 16-, and 17-year-olds, respectively).
References
- Carroll JB. Human cognitive abilities: A survey of factor analytic studies. Cambridge, England: Cambridge University Press; 1993. [Google Scholar]
- Coyle TR, Pillow DR. SAT and ACT predict college GPA after removing g. Intelligence. 2008;36:719–729. [Google Scholar]
- Frey MC, Detterman DK. Scholastic assessment or g? The relationship between the Scholastic Assessment Test and general cognitive ability. Psychological Science. 2004;15:373–378. doi: 10.1111/j.0956-7976.2004.00687.x. [DOI] [PubMed] [Google Scholar]
- Fry A, Hale S. Processing speed, working memory, and fluid intelligence: Evidence for developmental cascade. Psychological Science. 1996;7:237–241. [Google Scholar]
- Hering J, McClain A, editors. NLSY97 user’s guide: A guide to rounds 1–5 data. Columbus: Ohio State University, Center for Human Resource Research; 2003. [Google Scholar]
- Jensen AR. The g factor: The science of mental ability. Westport, CT: Praeger; 1998. [Google Scholar]
- Jensen AR. Clocking the mind: Mental chronometry and individual differences. Amsterdam, The Netherlands: Elsevier; 2006. [Google Scholar]
- Jensen AR. The theory of intelligence and its measurement. Intelligence. 2011;39:171–177. [Google Scholar]
- Jensen AR, Weng LJ. What is a good g. Intelligence. 1994;18:231–258. [Google Scholar]
- Kail R. Developmental change in speed of processing during childhood and adolescence. Psychological Bulletin. 1991;109:490–501. doi: 10.1037/0033-2909.109.3.490. [DOI] [PubMed] [Google Scholar]
- Kail R. Speed of information processing: Developmental change and links to intelligence. Journal of School Psychology. 2000;38:51–61. [Google Scholar]
- Kail R. Longitudinal evidence that increases in processing speed and working memory enhance children’s reasoning. Psychological Science. 2007;18:312–313. doi: 10.1111/j.1467-9280.2007.01895.x. [DOI] [PubMed] [Google Scholar]
- Kline RB. Principles and practice of structural equation modeling. 2nd ed. New York, NY: Guilford Press; 2005. [Google Scholar]
- Miller EM. Intelligence and brain myelination: A hypothesis. Personality and Individual Differences. 1994;17:803–832. [Google Scholar]
- Salthouse TA. The processing-speed theory of adult age differences in cognition. Psychological Review. 1996;103:403–428. doi: 10.1037/0033-295x.103.3.403. [DOI] [PubMed] [Google Scholar]
- Thorndike EL, Bregman EO, Cobb MV, Woodyard E. The measurement of intelligence. New York, NY: Teachers College, Columbia University, Bureau of Publications; 1927. [Google Scholar]