Abstract
Neurofilaments are transported along axons in a rapid intermittent and bidirectional manner but there is a long-standing controversy about whether this applies to all axonal neurofilaments. Some have proposed that only a small proportion of axonal neurofilaments are mobile and that most are deposited into a persistently stationary and extensively cross-linked cytoskeleton that remains fixed in place for many months without movement, turning over very slowly. In contrast, others have proposed that this hypothesis is based on a misinterpretation of the experimental data and that, in fact, all axonal neurofilaments move. These contrary perspectives have distinct implications for our understanding of how neurofilaments are organized and reorganized in axons both in health and disease. Here, we discuss the history and substance of this controversy. We show that the published data on the kinetics and distribution of neurofilaments along axons favor a simple “stop and go” transport model in which axons contain a single population of neurofilaments that all move in a stochastic, bidirectional and intermittent manner. Based on these considerations, we propose a dynamic view of the neuronal cytoskeleton in which all neurofilaments cycle repeatedly between moving and pausing states throughout their journey along the axon. The filaments move infrequently, but the average pause duration is on the order of hours rather than weeks or months. Against this fluid backdrop, the action of molecular motors on neurofilaments can have dramatic effects on neurofilament organization that would not be possible if the neurofilaments were extensively cross-linked into a truly stationary network.
INTRODUCTION
“Stop and go” movement of neurofilaments in axons
Neurofilaments, which are the intermediate filaments of neurons, are space-filling cytoskeletal polymers that accumulate in axons during post-natal development. The principal known function of neurofilaments is to increase axonal cross-sectional area, thereby increasing the rate of propagation of the nerve impulse (Perrot et al. 2008). Radioisotopic pulse-labeling studies in vivo have demonstrated that neurofilament proteins are transported along axons and that they are among the slowest of axonally transported proteins, moving anterogradely at average rates of approximately 0.1–1 mm/day (Hoffman and Lasek 1975; Lasek et al. 1984) (see Fig. 1A & B)). In contrast, time-lapse fluorescence imaging of cultured neurons has demonstrated that neurofilament proteins actually move at fast rates in both anterograde and retrograde directions, and that the movements are also intermittent (Wang et al. 2000). To reconcile these observations, we have proposed that slow axonal transport is caused by rapid bidirectional movements interrupted by prolonged pauses (Brown 2000; Brown 2003; Brown 2009). According to this “stop and go” model, the cargoes of slow axonal transport are propelled by fast motors, but the average velocity is slow because they spend some of their time moving backwards and most of their time pausing.
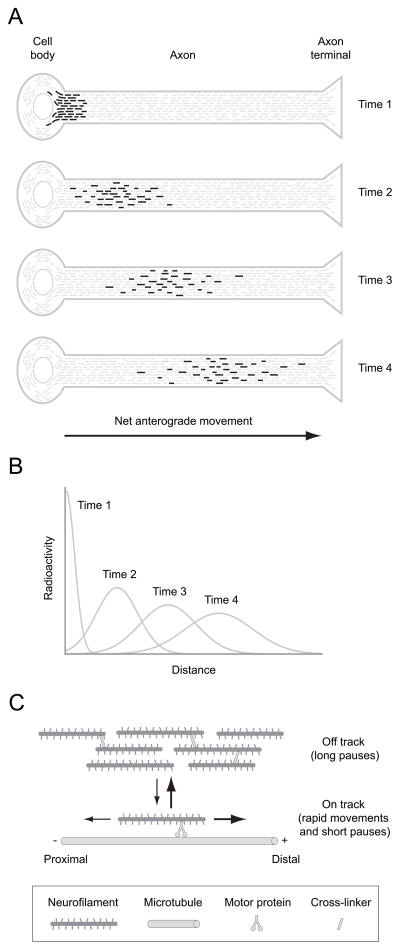
Figure 1. Axonal transport of neurofilaments.
A. Schematic diagram illustrating the movement of a pulse of radiolabeled neurofilaments along an axon in a radio-isotopic pulse labeling experiment, meant to be representative of axons in a long nerve such as the sciatic. To perform such an experiment, radioactive amino acids are injected into the vicinity of neuronal cell bodies. The radiolabeled amino acids become incorporated into newly synthesized proteins, generating a pulse of radiolabeled proteins that move out along the axons by the mechanisms of axonal transport. The most commonly used injection sites are the dorsal root ganglia, which labels sensory neurons, the anterior horn of the spinal cord, which labels motor neurons, and the eye, which labels retinal ganglion cells. This diagram shows a single axon but in reality these experiments are performed on nerves that contain thousands of axons that run in parallel, so the actual kinetics are a summation of the kinetics of many individual axons. The pulse of radiolabeled neurofilaments is sharp initially but spreads considerably over time due to the stochastic, intermittent and bidirectional nature of the movement. B. Schematic illustrating the distribution of the pulse of radiolabeled neurofilaments at the four time points shown in A. The neurofilaments form a symmetrical and slowly moving Gaussian wave that spreads as it propagates distally (Brown et al. 2005; Craciun et al. 2005; Hoffman et al. 1985; Hoffman and Lasek 1975; Hoffman et al. 1983; Jung and Brown 2009; Xu and Tung 2001). The average velocity is usually in the range 0.2–1.0 mm/day and depends on the age of the animal and the particular nerve being studied. C. Schematic diagram of the “stop and go” model of neurofilament transport. Neurofilaments are transported by motor proteins along microtubule tracks in a rapid intermittent manner, cycling between kinetically distinct on-track and off-track states. Neurofilaments in the on-track state engage in rapid bouts of movement interrupted by short pauses, whereas neurofilaments in the off-track state pause for prolonged periods without any movement. Off-track neurofilaments may be interconnected temporarily by cytoskeletal cross-linkers such as spectraplakins. The neurofilaments switch between forwards (anterograde) and backwards (retrograde) movement, but anterograde movements predominate, resulting in a net anterograde directionality.
Neurofilaments cycle between distinct short and long-term pausing states
Our kinetic analysis of neurofilament transport in axons of cultured neurons has revealed that neurofilaments cycle between two distinct kinetic states which we have termed “on-track” and “off-track” (Trivedi et al. 2007). Neurofilaments in the on-track state alternate between short bouts of movement interrupted by short pauses, whereas neurofilaments in the off-track state pause for longer periods of time without movement (Fig. 1C). The average pause times are about 20–30 seconds in the on-track state and about 1 hour in the off track state (Trivedi et al. 2007), and computational modeling predicts similar pause times in vivo (Jung and Brown 2009). The overall slow rate of neurofilament transport is due largely to the fact that these cargoes spend most of their time in the off-track pausing state. As the names of these states suggest, we have speculated that neurofilaments in the on-track and off-track states may differ in their proximity to microtubules, which are the tracks along which they move, but it is also possible that they differ in some other way that could influence their pausing behavior such as in their interaction with molecular motors or in the activity of those motors.
The polymer transport controversy
The axonal transport of neurofilament proteins has been no stranger to controversy. In the 1980s and 1990s there was considerable debate about the form in which these proteins move. Lasek and colleagues proposed that neurofilament proteins move in the form of assembled polymers (Lasek 1986; Lasek et al. 1984; Tytell et al. 1981) whereas Hirokawa and colleagues proposed that neurofilament polymers do not move and that these proteins are transported in the form of unassembled subunits (Okabe et al. 1993; Takeda et al. 1994; Terada et al. 1996). These hypotheses became known as the polymer and subunit transport models and they were hotly debated (Baas and Brown 1997; Hirokawa et al. 1997). The controversy was ultimately resolved by the direct observation of neurofilament polymer movement in axons of cultured neurons (Brown, 2000; Wang et al. 2000; Yan and Brown, 2005). This do not rule out the possibility that neurofilament proteins may also be transported in the form of unassembled subunits, but it is now generally accepted that neurofilament polymers are at least the principal cargo structures of neurofilament protein transport.
The stationary axonal cytoskeleton controversy
While it is now clear that neurofilament polymers move in axons, there is disagreement about whether they all move. This controversy originated more than 25 years ago, when Nixon and colleagues proposed that a significant proportion of axonally transported neurofilaments are deposited along axons into a persistently stationary and extensively cross-linked cytoskeleton (Nixon and Logvinenko 1986). According to this stationary axonal cytoskeleton hypothesis, the deposited neurofilaments remain fixed in place for many months without movement and turn over only very slowly. This hypothesis was challenged by Lasek and colleagues (1992), who proposed that it was based on a misinterpretation of the experimental data and that axons contain a single population of mobile neurofilaments which all move relentlessly at a slow average rate. Many years later, Nixon and colleagues responded to this criticism by repeating their earlier kinetic analysis in an improved manner and they claimed that their new findings supported their earlier conclusions (Yuan et al. 2009). In the following sections we explain the experimental basis for this controversy and then we summarize how we have used computational modeling to resolve it.
The original evidence for the stationary axonal cytoskeleton hypothesis
The stationary axonal cytoskeleton hypothesis was introduced to explain the distribution and axonal transport of neurofilaments in mouse optic nerve (Nixon and Logvinenko 1986), and has been explained in several review articles (Nixon 1991; Nixon 1992; Nixon 1998). In essence, the hypothesis was based on three principal lines of evidence:
The neurofilament transport waves are markedly asymmetric with a pronounced trailing edge. Radio-isotopic pulse labeling in mouse optic nerve generated a pulse of radiolabeled neurofilaments which formed a markedly asymmetric wave with a substantial trailing component, giving the impression that many radiolabeled neurofilaments were left behind as the wave propagated along the axon (Nixon and Logvinenko 1986). Nixon and colleagues proposed that this trailing component represented the progressive deposition of radiolabeled neurofilaments into a persistently stationary cytoskeleton during their transit along the axon.
The kinetics of neurofilament departure from a window of the optic nerve are biphasic. Nixon and colleagues analyzed the transit of a pulse of radiolabeled neurofilaments through a 9mm “window” of the mouse optic nerve, extending from the eye towards the brain (Nixon and Logvinenko 1986). The total amount of radioactivity in the nerve window increased during the first week as the pulse of radiolabelled neurofilaments entered the optic nerve from the eye, and then declined slowly over a period of many months as the neurofilaments gradually moved through the nerve window towards the nerve terminals. Importantly, the kinetics of this departure were found to be biphasic, with an initial rapidly declining phase followed by a later more slowly declining phase. The authors concluded that there were two distinct populations of axonal neurofilaments. They proposed that the initial more rapidly declining phase was due to the departure of a population of mobile neurofilaments from the nerve window and that the later more slowly declining phase was due to extremely slow degradation or mobilization of a population of persistently stationary neurofilaments which represented a substantial fraction of the total axonal neurofilaments.
Neurofilaments are distributed non-uniformly along axons. Nixon and colleagues reported that the neurofilament content of mouse retinal ganglion cell axons is not constant along the length of the optic nerve, but actually increases approximately two-fold in a proximal-to-distal manner (Nixon and Logvinenko 1986). Thus these axons contain about twice as many neurofilaments per cross-section in the distal optic nerve compared to more proximal locations. The authors proposed that this gradient was formed by the progressive deposition of mobile filaments into a stationary network during their transport along the axon, and they proposed that the existence of this gradient was evidence in support of their deposition model.
A challenge to the stationary axonal cytoskeleton hypothesis
The rebuttal of the stationary axonal cytoskeleton hypothesis by Lasek and colleagues (1992) was based on three key points:
The proteins of slow axonal transport can be resolved into two groups, termed Slow Components ‘a’ and ‘b’ (Black and Lasek 1979; Black and Lasek 1980). Slow component ‘a’ in mouse optic nerve is comprised predominantly of neurofilament proteins and tubulin, which move at average rates of less than 0.2 mm/day (Jung and Shea 1999), whereas Slow Component ‘b’ comprises several hundred different proteins, including actin, which move at average rates of about 1–2 mm/day (Lewis and Nixon 1988; Paggi et al. 1989). Due to the short length of the mouse optic nerve (about 11 mm from the eye to the superior colliculus) and the considerable amount of spreading of the transport waves, these two groups of proteins overlap and do not resolve fully before the faster moving Slow Component ‘b’ proteins reach the nerve terminals.
Some Slow Component ‘b’ proteins co-migrate with neurofilament proteins by one-dimensional (1D) gel electrophoresis due to their similar molecular mass. Most of the Slow Component ‘b’ proteins are cytosolic and can be separated from neurofilaments by detergent extraction because cytosolic proteins are generally soluble in non-ionic detergents whereas neurofilaments are insoluble. Alternatively, these proteins can be separated from the neurofilament proteins by 2D electrophoresis. Lasek and colleagues noted that Nixon and Logvinenko (1986) used total nerve protein, which contains both soluble and insoluble proteins, and 1D electrophoresis, which fails to separate neurofilament proteins from Slow Component ‘b’ proteins of similar size.
Pure neurofilament transport kinetics exhibit fairly symmetrical waves with no pronounced trailing edge. By analyzing neurofilament transport kinetics in mouse optic nerve using 2D electrophoresis, which separates neurofilament proteins from Slow Component ‘b’ proteins of similar size based on their charge, Lasek and colleagues concluded that there was no evidence for the selective retention of a sub-population of neurofilaments behind the wave peak. These authors also noted that this is similar to the transport behavior of neurofilaments in longer nerves, where Slow Components ‘a’ and ‘b’ are better resolved (Hoffman et al. 1985; Xu and Tung 2001).
Based on these observations, Lasek and colleagues proposed that the pronounced asymmetry of the neurofilament transport waves in the data of Nixon & Logvinenko (1986) was actually due to contamination of the neurofilament transport kinetics with faster moving Slow Component ‘b’ proteins that comigrate with neurofilament proteins by 1D electrophoresis. Furthermore, they proposed that the initial more rapidly declining phase of the biphasic decay kinetics in the data of Nixon & Logvinenko (1986) was actually due to Slow Component ‘b’ proteins, not neurofilament proteins. According to this hypothesis, the data of Nixon and Logvinenko [1986] did not represent pure neurofilament kinetics until most of the faster moving Slow Component “b” proteins had moved through the nerve window, i.e., after about 45 days (Fig. 2A, B and C). However, Lasek and colleagues did not reproduce the exact experimental conditions of Nixon & Logvinenko (1986). For example, they used different radioisotopically labeled amino acids, which can result in differential labeling of proteins depending on their amino acid composition, and they used different injection-sacrifice intervals. In addition, Lasek and colleagues used different approaches to analyze, quantify and display the data, making it hard to perform a direct side-by-side comparison of their data with the data of Nixon and colleagues.
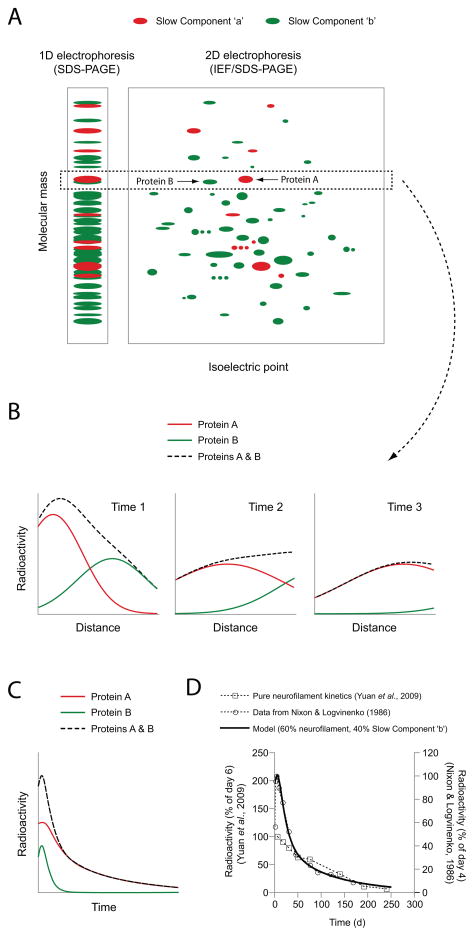
Figure 2. Contamination of the neurofilament transport kinetics in mouse optic nerve by Slow Component ‘b’ proteins.
A. Schematic diagram of hypothetical radiolabeled axonal proteins resolved by one dimensional (1D) gel electrophoresis, i.e. sodium dodecyl sulfate polyacrylamide gel electrophoresis (SDS-PAGE), or two dimensional (2D) gel electrophoresis, i.e. isoelectric focusing (IEF) in the first (horizontal) dimension and SDS-PAGE in the second (vertical) dimension. Slow Component ‘a’ proteins (which are relatively few) are shown in red and Slow Component ‘b’ proteins (which are relatively numerous) are shown in green. The box demarcated with the dashed line shows a hypothetical Slow Component ‘a’ protein, Protein A, and a hypothetical Slow Component ‘b’ protein of similar molecular mass, Protein B. These proteins comigrate using 1D electrophoresis, but can be resolved using 2D electrophoresis because they have different isoelectric points. B. Schematic representation of the distribution of a pulse of these radiolabeled proteins along a hypothetical short nerve (meant to be representative of the optic nerve) at three different time points. Radioactivity associated with Protein A, which moves more slowly (in Slow Component ‘a’), is shown in red. Radioactivity associated with Protein B, which is transported more rapidly (in Slow Component ‘b’), is shown in green. The dashed black line represents the sum of the radioactivity profiles for the two proteins and is representative of the profile that would be observed if the analysis was performed using 1D electrophoresis of total nerve protein, as in Nixon & Logvinenko (1986). C. Schematic representation of the time course of appearance and disappearance of radioactive protein in the entire nerve window over time. Note that Protein B, which moves in Slow Component ‘b’, enters and exits the nerve window more rapidly than Protein A. The decay kinetics of the individual proteins are monophasic, but the decay kinetics of the two proteins combined (dashed black line) is biphasic. The initially more rapidly declining phase corresponds to Protein B, which departs the nerve more rapidly, and the later more slowly declining phase corresponds to Protein A, which departs more slowly. D. The experimental data of Nixon and colleagues, as plotted in Li et al. (2012). The symbols represent the data for neurofilament protein M from Yuan et al. (2009) (open squares) and from Nixon & Logvinenko (1986) (open circles). Yuan et al. (2009) used a Triton-insoluble protein fraction, yielding pure neurofilament protein and monophasic decay kinetics. In contrast, Nixon & Logvinenko (1986) used total nerve protein (soluble and insoluble), yielding biphasic decay kinetics. The solid black line represents the output of the model, assuming contamination of the neurofilament protein kinetics with a hypothetical Slow Component ‘b’ protein (relative weighting of 60% neurofilament protein and 40% Slow Component ‘b’ protein). Note that the model shows good agreement with the biphasic decay kinetics of Nixon & Logvinenko (1986) at all times, and also with the monophasic decay kinetics of Yuan et al. (2009) at later times (>50 days), after the Slow Component ‘b’ proteins in the model have left the nerve window. Thus the biphasic decay kinetics of Nixon & Logvinenko (1986) can be explained by contamination of the neurofilament transport kinetics with faster moving Slow Component ‘b’ proteins.
A resolution to the controversy
To address the criticisms of Lasek and colleagues, Nixon and colleagues repeated their original experiments with some technical improvements (Yuan et al. 2009). First, they used a Triton-insoluble fraction of the optic nerve tissue for their analyses, effectively depleting soluble Slow Component ‘b’ proteins and enriching for insoluble protein complexes such as neurofilaments. Second, the authors confirmed the purity of the neurofilament protein bands on their polyacrylamide gels by using two-dimensional SDS-PAGE and peptide mapping (Yuan et al. 2009). The authors reported that the resulting kinetics were comparable to those obtained in their earlier study (Nixon and Logvinenko 1986), so they concluded that their new data confirmed the stationary axonal cytoskeleton model. Notably, the authors estimated that fewer than 10% of axonal neurofilaments are transported in a “stop and go” manner in mouse optic nerve and that greater than 90% are fixed in place for months without movement.
To evaluate this conclusion, we performed a direct comparison of the decay kinetics published by Nixon & Logvinenko (1986) and Yuan et al. (2009) (Li et al. 2012). Contrary to the conclusion of Yuan et al. (2009), this comparison indicates that the kinetics are actually very different. The two decay curves are not superimposable: the initial rapidly declining phase in the data of Nixon & Logvinenko (1986) is absent from the pure neurofilament kinetics of Yuan et al. (2009) (Fig. 2D). While the kinetics of Nixon & Logvinenko (1986) are biphasic, the kinetics of Yuan et al. (2009) are distinctly monophasic. Moreover, the pure neurofilament kinetics of Yuan et al. (2009) align well with the second phase of the Nixon & Logvinenko (1986) kinetics. These observations are consistent with the proposal of Lasek et al. (1992) that only the second phase of the biphasic decay kinetics of Nixon & Logvinenko (1986) corresponds to pure neurofilament kinetics and that the first (more rapidly declining) phase can be explained by contamination of the neurofilament kinetics with soluble Slow Component ‘b’ proteins that are similar in size to the neurofilament proteins and therefore not resolved by 1D electrophoresis.
Computational modeling of neurofilament transport in the mouse optic nerve
If the above critique of the stationary axonal cytoskeleton hypothesis is correct then it should be possible to explain the pure neurofilament kinetics of Yuan et al. (2009) in terms of a single population of neurofilaments moving in a “stop and go” manner. To test this, we have performed computational modeling of neurofilament transport in the mouse optic pathway (Li et al. 2012). The power of computational modeling is that it forces us to make our hypotheses explicit and enables us to ask in a quantitative way whether or not those hypotheses can explain the experimental data.
To simulate neurofilament movement, we used a kinetic model based on the “stop and go” motile behavior of neurofilaments in cultured neurons (Brown et al. 2005; Jung and Brown 2009; Trivedi et al. 2007). In this model the neurofilaments move linearly and independently along axons, cycling between distinct on-track and off-track states, as described above (Fig. 1C). The model is described in detail in the methods section of Li et al. (2012). The movement of the filaments is treated as a stochastic process, which means that the transitions between the moving and pausing states are described by probabilities. The probabilities were obtained directly from our kinetic measurements in cultured neurons, with no assumptions about the underlying molecular mechanism of movement. Neurofilaments which reached the end of the axon were assumed to be either degraded with a half life of 2 days, as observed in vivo (Garner 1988; Paggi and Lasek 1987), or to reverse direction, as we have observed in cultured neurons (Uchida and Brown 2004). Importantly, this model assumes that the “stop and go” motile behavior of neurofilaments in cultured neurons also occurs in vivo. We believe that this is a reasonable assumption that is supported by studies on other axonally transported cargoes, such as mitochondria and vesicles, which move with similar kinetics in vivo as they do in cultured neurons (Misgeld et al. 2007; Reis et al. 2012). Moreover, our computational modeling studies have demonstrated that the stop-and-go kinetics of neurofilament transport in cultured neurons can explain the kinetics of neurofilament transport in vivo in a variety of nerve cell types (Brown et al. 2005; Craciun et al. 2005; Jung and Brown 2009). Nevertheless, it will be important to verify this assumption experimentally when it becomes technically possible to do so.
Explaining the gradient in neurofilament content along optic nerve axons
As noted above, Nixon and Logvinenko [1986] reported that there is a proximal-to-distal gradient in neurofilament number along the optic nerve (Figs. 3A and 3B). According to the stationary axonal cytoskeleton hypothesis, this gradient is generated by a gradual deposition of neurofilaments into a stationary cytoskeleton during their movement along the axon, but our simulations indicate that such models actually generate a gradient of decreasing neurofilament number along the axon, exactly the opposite of what is observed experimentally. A simple alternative mechanism that does generate a gradient of increasing neurofilament content along these axons would be a gradient of decreasing transport velocity (Fig. 3C). In fact, a slowing of neurofilament transport along axons has been reported in the optic nerve (Jung and Shea 1999) and also in the sciatic nerve (Hoffman et al. 1985; Hoffman et al. 1983; Watson et al. 1989; Xu and Tung 2001). Remarkably, we found that such a gradient in neurofilament transport velocity can be explained by only a small increase in the proportion of the time that the filaments spend pausing (from ≈96% proximally to ≈98% distally), or alternatively by only a small decrease in the proportion of the time that they spend moving anterogradely (from ≈63% proximally to ≈58% distally) (Li et al. 2012). Thus subtle changes in pausing or directionality can have significant effects on neurofilament distribution and shallow gradients in these parameters can explain the proximal-to-distal gradient in neurofilament number along mouse optic nerve axons.
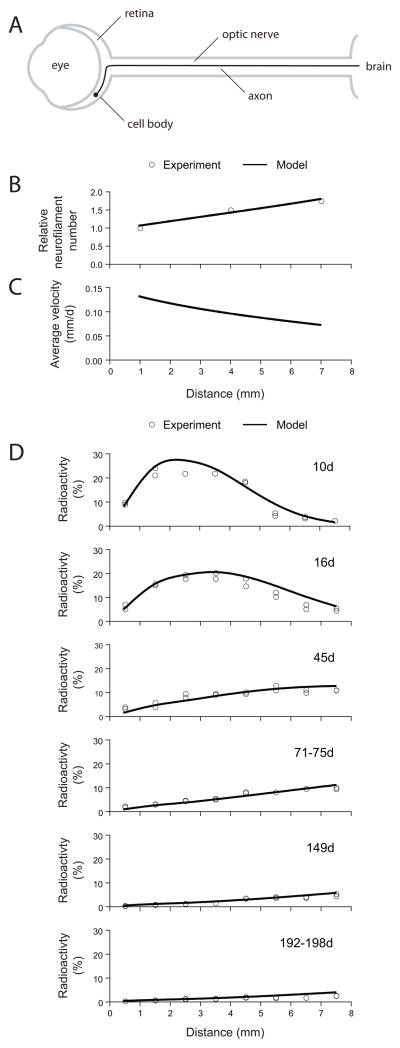
Figure 3. Computational modeling of neurofilament transport in the mouse optic nerve.
A. Schematic of the optic pathway from one eye. The axons of retinal ganglion cells course through the retina and emerge from the eye at the optic disk to form the optic nerve, which extends to the contralateral side of the brain. B. The gradient in neurofilament content along the mouse optic nerve. The experimental data (open circles) are from Nixon & Logvinenko (1986). The solid line represents the predictions of our computational model (from Li et al. 2012). C. The gradient in average neurofilament transport velocity that is required to explain the gradient in neurofilament content shown in B (from Li et al. 2012). D. The kinetics of neurofilament transport in the mouse optic nerve (from Li et al. 2012). The open symbols represent the experimental data from Yuan et al. (2009) for NFL and NFM, recalculated as described in Li et al. (2012), and the solid line represents the output of the “stop and go” model. The radioactivity at each time point is expressed as a percentage of the total radioactivity in the nerve window at day 10, as described in Li et al. (2012). Note that the model generates a symmetrical wave when the kinetic parameters are uniform (Brown et al. 2005; Craciun et al. 2005; Jung and Brown 2009), but the wave here is not perfectly symmetrical because of the gradient in the transport velocity.
Explaining the shape and velocity of the neurofilament transport wave
To analyze the transport kinetics, we simulated the movement of a pulse of radiolabeled neurofilaments along axons of retinal ganglion cells (Li et al. 2012). These axons course through the retina for an average distance of 1mm before emerging from the eye to form the optic nerve. We assumed that the pulse of radiolabeled amino acid lasted for 5 hours but we found that the precise duration had no significant effect on the shape or velocity of the wave by the time that it entered the optic nerve. As expected for a stochastic transport model with a net anterograde bias, the population adopted a Gaussian waveform that spread as it propagated along the axon, and this was independent of the shape of the starting pulse (Jung and Brown 2009). By analyzing the shape and location of the waves in the data of Yuan et al. (2009), we found that the average velocity of neurofilament transport slows by about 5-fold within the retina, and then by a further 2-fold along the length of the optic nerve. The magnitude of this slowing is broadly consistent with the experimental data of Jung & Shea (1999). Factoring in this slowing, the computational model displayed remarkably good agreement with the experimental data of Yuan et al. [2009] at all time points (Fig. 3D). Thus it is possible to explain the pure kinetics of neurofilament transport in mouse optic nerve by a simple “stop and go” model in which axons contain a single population of neurofilaments that all move stochastically in a rapid, intermittent and bidirectional manner.
Explaining the apparent retention of neurofilaments in the axons long after the wave peak has passed
Nixon and colleagues reported that a significant fraction of the radiolabeled neurofilaments in their radioisotopic pulse labeling experiments appeared to be retained in the optic nerve window behind the wave peak, giving rise to an apparently stable distribution of radiolabeled neurofilaments that remained constant between 71–75 days and 192–198 days after injection (Yuan et al. 2009). However, our analyses of the pure neurofilament transport kinetics of Yuan et al. (2009) indicate that this interpretation is incorrect; the radiolabeled neurofilaments remaining in the axon between 71–75 days and 192–198 days after injection are indeed distributed along the axon in a proximal-to-distal gradient, but the slope decreases continuously throughout this time period as the radiolabeled neurofilaments continue to exit the nerve window at its distal end (Fig. 3D; see also Fig. 6 in Li et al. 2012). The radiolabeled filaments depart slowly but continuously throughout this time period. If we consider the amount of radiolabeled neurofilament protein in the nerve window at day 10 to be 100%, then only 6% remains after 240 days. The explanation for this slow departure is that there is enormous spreading of the pulse of radiolabeled neurofilaments during the time course of the experiment. We have shown previously that this spreading is due in part to the bidirectional excursions of the neurofilaments, with a significant fraction of the neurofilaments moving backwards at any point in time (Brown et al., 2005; Jung & Brown, 2009). According to the stationary axonal cytoskeleton model, the radiolabeled neurofilament proteins that remain in the axon at later times represent a distinct population of stationary neurofilaments that are deposited behind the moving wave front (Yuan et al. 2009), but our modeling indicates that these neurofilaments are simply the tail end of a single population of moving neurofilaments that spreads considerably due to the stochastic, intermittent and bidirectional motile behavior.
Comparison to neurofilament transport kinetics in other nerves
It is important to note that radio-isotopic pulse labeling experiments in the sciatic nerve have also yielded broadly symmetrical neurofilament transport waves with no evidence of neurofilament deposition behind the advancing wave (Hoffman et al. 1985; Jung and Brown 2009; Xu and Tung 2001), and this also has been reported for Slow Component ‘a’ in phrenic and hypoglossal nerves (Lasek 1980; Lasek et al. 1984). Thus neurofilament transport in mouse optic nerve is not fundamentally different from other nerve cell types, and in all these cases the movement is consistent with the “stop and go” model. However, the optic nerve is distinct in two important ways. First, the average velocity of neurofilament transport is about 0.1–0.2 mm/day proximally, which is about 5 times slower than in the sciatic, phrenic and hypoglossal nerves. Second, the sciatic, phrenic and hypoglossal nerves are significantly longer than the optic nerve. In long nerves the pulse of radiolabeled neurofilaments spreads enormously, reaching many centimeters in width (Hoffman et al. 1985; Xu and Tung 2001). However, due to the short length of the optic nerve the entire wave exceeds the entire length of the nerve window within a week (see Fig. 3D), whereas the entire wave is fully contained within the excised portion of the mouse sciatic nerve for at least 2 months (Xu and Tung 2001). Thus the short length of the mouse optic nerve presents a particular challenge for radioisotopic pulse labeling studies.
Pausing or stationary: what’s the difference?
At first glance it may seem that the stationary axonal cytoskeleton hypothesis is not fundamentally different from the “stop and go” hypothesis. Both hypotheses consider that there are two distinct kinetic states for neurofilaments, one mobile and the other stationary, and both hypotheses recognize that the neurofilaments spend only a small proportion of their time in the mobile state. However, as Yuan et al. (2009) have observed, these models are actually fundamentally different. In the stationary axonal cytoskeleton model, <10% of the axonal neurofilaments are engaged in axonal transport and >90% are deposited in a persistently stationary cytoskeleton that remains fixed in place for many months without movement (Yuan et al. 2009). In contrast, our computational analyses have shown that all neurofilaments are engaged in axonal transport and that the experimental data are not consistent with the existence of a persistently stationary population. For example, our simulations of neurofilament transport in the optic nerve predict that the average neurofilament cycles on and off track more than 200 times over a period of 10 days, with average on and off track pause durations of about 20 seconds and 60 minutes, respectively (Li et al. 2012). Using the analytical solutions described in Jung & Brown (2009) we calculate that the probability of a neurofilament remaining paused off track for more than 12 hours is <0.001%. Thus the two models have very different implications for the mechanism of neurofilament transport and the dynamics of the axonal neurofilament array.
The importance of analyzing neurofilament transport on both fast and slow time scales
If neurofilaments cycle continuously between distinct on-track and off-track kinetic states, then it is reasonable to ask why these distinct kinetic states do not yield biphasic decay kinetics in the radioisotopic pulse labeling experiments of Yuan et al. (2009) (Fig. 2D). The explanation for this is that the rate of cycling is fast relative to the time scale of the pulse labeling experiments. The neurofilaments switch between on-track and off-track states on a time scale of minutes or hours, but this behavior averages out during their transport along axons and consequently they behave as a single population on a time scale of days and weeks. To resolve the on and off track pausing states, it is necessary to analyze the decay kinetics on a time scale of minutes or hours (Trivedi et al. 2007). While there is general agreement that axonal neurofilaments spend a large proportion of their time pausing, our analyses indicate that there is no persistently stationary population and that the vast majority of neurofilaments move over the course of several hours. Thus it is important to note that the “stop and go” model does not predict that all axonal neurofilaments are identical, but simply that any heterogeneities among the neurofilament population (for example, in terms of pausing behavior) are not persistent on the long time scales that are typical of most radioisotopic pulse labeling experiments.
The importance of resolving Slow Components ‘a’ and ‘b’
Our contention that the neurofilament transport kinetics of Nixon & Logvinenko (1986) were contaminated with faster moving Slow Component ‘b’ proteins which comigrate by one-dimensional SDS-PAGE depends on the assumption that there are Slow Component ‘b’ proteins in mouse optic nerve that have similar electrophoretic mobility to neurofilament proteins. In fact, it is known that several hundred Slow Component ‘b’ proteins are radiolabeled in pulse-labeling studies on retinal ganglion cells (Brady and Lasek 1982; Garner and Lasek 1982; Tytell et al. 1981), and some of these proteins do comigrate with neurofilament polypeptides on one-dimensional gels (Lasek et al. 1984; Lasek et al. 1992; Lewis and Nixon 1988; Shea et al. 1988). For example, in mouse optic nerve there are two structurally related Triton-soluble Slow Component ‘b’ proteins with apparent molecular weights of 197,000 and 200,000 which comigrate with the highest molecular weight neurofilament protein (neurofilament protein H) by one-dimensional SDS-PAGE. Radioisotopic pulse labeling studies have shown that these proteins form broad waves that move faster than neurofilament protein H, yet overlap considerably (Lewis and Nixon 1988). Moreover, these proteins could be separated by Triton-extraction, taking advantage of the insolubility of neurofilaments in the presence of non-ionic detergents. Lasek and colleagues have also described a Triton-soluble Slow Component ‘b’ protein with an apparent molecular weight of 70,000 which comigrates with neurofilament protein L (Lasek et al. 1992). Clearly, these Slow Component ‘b’ proteins would be expected to contaminate the neurofilament transport kinetics in pulse-labeling experiments if total nerve protein were separated by one-dimensional SDS-PAGE. By simulating the movement of Slow Component ‘b’ proteins in optic nerve, we confirmed that this can explain the discrepancy between the biphasic decay kinetics of Nixon & Logvinenko (1986) and the monophasic decay kinetics of Yuan et al. (2009) (Fig. 2D) (Li et al. 2012).
Neurofilament pausing in cultured neurons
In addition to their radio-isotopic pulse-labeling experiments, Yuan et al. (2009) also performed an analysis of neurofilament transport in cultured embryonic cortical neurons using live-cell time-lapse fluorescence microscopy. By tracking the movement of single neurofilaments in photobleached gaps along the axons, the authors confirmed the rapid, intermittent and bidirectional motility that we and others have reported previously (Ackerley et al. 2003; Roy et al. 2000; Uchida and Brown 2004; Wang and Brown 2001; Wang and Brown 2010; Wang et al. 2000). To analyze the neurofilament transport kinetics on longer time scales, the authors employed a variant of the fluorescence photoactivation pulse-escape technique of Trivedi et al. (2007). This method uses photoactivation or photoconversion to generate a pulse of fluorescent neurofilaments in the axons. Since the neurofilaments exit the activated region very rapidly when they move, the kinetics of departure are dictated largely by the pause times of the neurofilaments. Thus the pausing kinetics can be determined from the kinetics of departure of neurofilaments from the activated regions.
Instead of using a photoactivatable or photoswitchable fluorescent fusion protein, Yuan et al. (2009) used a conventional fluorescent fusion protein and created a pseudo-activated region by photobleaching the flanking regions. Using this approach, these authors found that the kinetics of neurofilament departure were slower in more neurofilament-rich proximal axonal regions and faster in more neurofilament-poor distal axonal regions. Thus the extent of neurofilament pausing varied inversely with axonal neurofilament content. In proximal axons, where the neurofilament content was highest, the authors claimed that there was no appreciable loss fluorescence from the pseudo-activated regions, implying that the neurofilaments were “unequivocally stationary”. To understand these data, it is important to note that the experiments were all performed by co-expressing GFP-tagged neurofilament protein L and untagged neurofilament protein M, which resulted in a marked increase in axonal neurofilament content that may have artificially increased the proportion of neurofilaments that are off track. Nevertheless, close inspection of the data shows that there was loss of neurofilament fluorescence even in the most neurofilament-rich axons. In fact, in two of the figures the fluorescence in proximal or highly expressing axons decreased by 30–40% within the first 30 minutes (see Figs. 3D & 6D in Yuan et al. 2009), which is comparable to the average rate of neurofilament departure that we have reported in cultured sympathetic neurons from superior cervical ganglia (35% lost within the first 30 minutes; Trivedi et al. 2007). In a third figure the fluorescence in a proximal axon decreased by about 30% over a period of 5 hours (see Fig. 5C in Yuan et al. 2009). This is within the range that we have observed for cultured neurons from dorsal root ganglia (Alami et al. 2009), which are neurofilament-rich axons that exhibit much greater off-track pausing than neurons from superior cervical ganglia. Based on these considerations, the kinetic analysis of neurofilament pausing by Yuan et al. (2009) appears to be broadly similar to previous reports in other nerve cell types, and we have shown that those kinetics can be fully explained in terms of the “stop and go” model (Alami et al. 2009; Trivedi et al. 2007).
Implications for neurofilament organization in axons
Over the past 25 years, the concept of a stationary axonal cytoskeleton has influenced how many researchers think about axonal cytoskeletons (e.g. Barry et al. 2007; LoPachin et al. 2004; LoPachin et al. 2005; Millecamps et al. 2007; Sunil et al. 2012; Yuan et al. 2009). Perhaps the willingness of researchers to adopt this concept has been influenced by electron micrographs of axons prepared by the rapid-freeze deep-etch method, which have given the impression that the axonal cytoskeleton is an extensively cross-linked network (Hirokawa 1982; Schnapp and Reese 1982). Indeed, the stationary axonal cytoskeleton hypothesis likens neurofilaments to static structural elements in a building, as if welded or cemented together (Yuan et al. 2009). However, biochemical and morphometric studies on neurofilaments have failed to demonstrate extensive or strong cross-linking interactions between neurofilaments or their sidearms (Brown and Lasek 1993; Price et al. 1988), and biophysical experiments suggest that neurofilament sidearms interact through long-range repulsive forces, and function more to space adjacent filaments apart rather than to link them together (Brown and Lasek 1993; Brown and Hoh 1997; Kumar et al. 2002; Price et al. 1988). Moreover, it is hard to reconcile the notion of an extensively cross-linked neurofilament network with the extraordinarily dynamic nature of axonal cytoplasm in which organelles and other axonally transported cargoes must continually push neurofilaments aside and apart as they move through the forest of cytoskeletal polymers that makes up axonal cytoplasm. Thus we must be cautious about inferring strength and mechanisms of interaction based on the appearance of neurofilament sidearm projections in electron micrographs. Certainly there are sure to be cross-links between neurofilaments, but there is no evidence that neurofilaments are extensively or stably interconnected in a manner that would preclude intermittent movement.
In conclusion, we believe that the experimental data favor a dynamic model of the axonal cytoskeleton in which the interactions between neurofilaments are mostly weak or reversible, allowing these cytoskeletal polymers to cycle freely between mobile and immobile states during their journey down the axon. Certainly the filaments spend most of their time not moving, but the average pause duration is on the order of hours rather than weeks or months. Against this more fluid backdrop, the regulated action of molecular motors or temporary cross-linkers on neurofilaments can have dramatic effects on neurofilament organization in ways that would not be possible if the neurofilaments were extensively cross-linked into a truly stationary network, and this may have important implications for the mechanisms by which neurofilaments are organized and reorganized in along axons both in health and disease.
Acknowledgments
We thank Atsuko Uchida and Paul Hoffman for helpful discussions and comments. This work was supported by a collaborative grant from the National Science Foundation to A.B. and P.J., and a grant from the National Institutes of Health to A.B.
References
- Ackerley S, Thornhill P, Grierson AJ, Brownlees J, Anderton BH, Leigh PN, Shaw CE, Miller CC. Neurofilament heavy chain side arm phosphorylation regulates axonal transport of neurofilaments. Journal of Cell Biology. 2003;161(3):489–95. doi: 10.1083/jcb.200303138. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Alami NH, Jung P, Brown A. Myosin Va increases the efficiency of neurofilament transport by decreasing the duration of long-term pauses. Journal of Neuroscience. 2009;29(20):6625–34. doi: 10.1523/JNEUROSCI.3829-08.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Baas PW, Brown A. Slow axonal transport: the polymer transport model. Trends in Cell Biology. 1997;7(10):380–384. doi: 10.1016/S0962-8924(97)01148-3. [DOI] [PubMed] [Google Scholar]
- Barry DM, Millecamps S, Julien JP, Garcia ML. New movements in neurofilament transport, turnover and disease. Experimental Cell Research. 2007;313(10):2110–20. doi: 10.1016/j.yexcr.2007.03.011. [DOI] [PubMed] [Google Scholar]
- Black MM, Lasek RJ. Axonal transport of actin: slow component b is the principal source of actin for the axon. Brain Research. 1979;171(3):401–13. doi: 10.1016/0006-8993(79)91045-x. [DOI] [PubMed] [Google Scholar]
- Black MM, Lasek RJ. Slow components of axonal transport: two cytoskeletal networks. Journal of Cell Biology. 1980;86(2):616–23. doi: 10.1083/jcb.86.2.616. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brady ST, Lasek RJ. The slow components of axonal transport: movements, compositions and organizations. In: Weiss DG, editor. Axoplasmic Transport. Berlin Heidelberg: Springer-Verlag; 1982. pp. 206–217. [Google Scholar]
- Brown A. Slow axonal transport: stop and go traffic in the axon. Nature Reviews Molecular Cell Biology. 2000;1:153–156. doi: 10.1038/35040102. [DOI] [PubMed] [Google Scholar]
- Brown A. Axonal transport of membranous and nonmembranous cargoes: a unified perspective. Journal of Cell Biology. 2003;160(6):817–21. doi: 10.1083/jcb.200212017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brown A. Slow axonal transport. In: Squire LR, editor. Encyclopedia of Neuroscience. Oxford: Academic Press; 2009. pp. 1–9. [Google Scholar]
- Brown A, Lasek RJ. Neurofilaments move apart freely when released from the circumferential constraint of the axonal plasma membrane. Cell Motility and the Cytoskeleton. 1993;26:313–324. doi: 10.1002/cm.970260406. [DOI] [PubMed] [Google Scholar]
- Brown A, Wang L, Jung P. Stochastic simulation of neurofilament transport in axons: the “stop-and-go” hypothesis. Molecular Biology of the Cell. 2005;16(9):4243–55. doi: 10.1091/mbc.E05-02-0141. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brown HG, Hoh JH. Entropic exclusion by neurofilament sidearms: a mechanism for maintaining interfilament spacing. Biochemistry. 1997;36(49):15035–40. doi: 10.1021/bi9721748. [DOI] [PubMed] [Google Scholar]
- Craciun G, Brown A, Friedman A. A dynamical system model of neurofilament transport in axons. Journal of Theoretical Biology. 2005;237(3):316–22. doi: 10.1016/j.jtbi.2005.04.018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Garner JA. Differential turnover of tubulin and neurofilament proteins in central nervous system neuron terminals. Brain Research. 1988;458(2):309–18. doi: 10.1016/0006-8993(88)90473-8. [DOI] [PubMed] [Google Scholar]
- Garner JA, Lasek RJ. Cohesive axonal transport of the slow component b complex of polypeptides. Journal of Neuroscience. 1982;12:1824–1835. doi: 10.1523/JNEUROSCI.02-12-01824.1982. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hirokawa N. Cross-linker system between neurofilaments, microtubules and membranous organelles in frog axons revealed by quick freeze deep etching method. Journal of Cell Biology. 1982;94:129–142. doi: 10.1083/jcb.94.1.129. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hirokawa N, Terada S, Funakoshi T, Takeda S. Slow axonal transport: the subunit transport model. Trends in Cell Biology. 1997;7(10):384–388. doi: 10.1016/S0962-8924(97)01133-1. [DOI] [PubMed] [Google Scholar]
- Hoffman PN, Griffin JW, Gold BG, Price DL. Slowing of neurofilament transport and the radial growth of developing nerve fibers. Journal of Neuroscience. 1985;5(11):2920–9. doi: 10.1523/JNEUROSCI.05-11-02920.1985. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hoffman PN, Lasek RJ. The slow component of axonal transport: Identification of major structural polypeptides of the axon and their generality among mammalian neurons. Journal of Cell Biology. 1975;66:351–366. doi: 10.1083/jcb.66.2.351. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hoffman PN, Lasek RJ, Griffin JW, Price DL. Slowing of the axonal transport of neurofilament proteins during development. Journal of Neuroscience. 1983;3(8):1694–700. doi: 10.1523/JNEUROSCI.03-08-01694.1983. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jung C, Shea TB. Regulation of neurofilament axonal transport by phosphorylation in optic axons in situ. Cell Motility and the Cytoskeleton. 1999;42:230–40. doi: 10.1002/(SICI)1097-0169(1999)42:3<230::AID-CM6>3.0.CO;2-A. [DOI] [PubMed] [Google Scholar]
- Jung P, Brown A. Modeling the slowing of neurofilament transport along the mouse sciatic nerve. Physical Biology. 2009;6(4):046002. doi: 10.1088/1478-3975/6/4/046002. [DOI] [PubMed] [Google Scholar]
- Kumar S, Yin X, Trapp BD, Hoh JH, Paulaitis ME. Relating interactions between neurofilaments to the structure of axonal neurofilament distributions through polymer brush models. Biophysical Journal. 2002;82(5):2360–72. doi: 10.1016/S0006-3495(02)75581-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lasek RJ. Axonal transport: a dynamic view of neuronal structures. Trends in Neurosciences. 1980;3:87–91. [Google Scholar]
- Lasek RJ. Polymer sliding in axons. Journal of Cell Science Supplement. 1986;5:161–179. doi: 10.1242/jcs.1986.supplement_5.10. [DOI] [PubMed] [Google Scholar]
- Lasek RJ, Garner JA, Brady ST. Axonal transport of the cytoplasmic matrix. Journal of Cell Biology. 1984;99:212s–221s. doi: 10.1083/jcb.99.1.212s. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lasek RJ, Paggi P, Katz MJ. Slow axonal transport mechanisms move neurofilaments relentlessly in mouse optic axons. Journal of Cell Biology. 1992;117:607–616. doi: 10.1083/jcb.117.3.607. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lewis SE, Nixon RA. Multiple phosphorylated variants of the high molecular mass subunit of neurofilaments in axons of retinal cell neurons: characterization and evidence for their differential association with stationary and moving neurofilaments. Journal of Cell Biology. 1988;107(6 Pt 2):2689–701. doi: 10.1083/jcb.107.6.2689. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li Y, Jung P, Brown A. Axonal transport of neurofilaments: a single population of intermittently moving polymers. Journal of Neuroscience. 2012;32(2):746–758. doi: 10.1523/JNEUROSCI.4926-11.2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- LoPachin RM, He D, Reid ML, Opanashuk LA. 2,5-Hexanedione-induced changes in the monomeric neurofilament protein content of rat spinal cord fractions. Toxicology and Applied Pharmacology. 2004;198(1):61–73. doi: 10.1016/j.taap.2004.03.002. [DOI] [PubMed] [Google Scholar]
- LoPachin RM, Jortner BS, Reid ML, Monir A. gamma-Diketone Central Neuropathy: Quantitative Analyses of Cytoskeletal Components in Myelinated Axons of the Rat Rubrospinal Tract. Neurotoxicology. 2005;26(6):1021–30. doi: 10.1016/j.neuro.2005.04.008. [DOI] [PubMed] [Google Scholar]
- Millecamps S, Gowing G, Corti O, Mallet J, Julien JP. Conditional NF-L transgene expression in mice for in vivo analysis of turnover and transport rate of neurofilaments. Journal of Neuroscience. 2007;27(18):4947–56. doi: 10.1523/JNEUROSCI.5299-06.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Misgeld T, Kerschensteiner M, Bareyre FM, Burgess RW, Lichtman JW. Imaging axonal transport of mitochondria in vivo. Nature Methods. 2007;4(7):559–61. doi: 10.1038/nmeth1055. [DOI] [PubMed] [Google Scholar]
- Nixon RA. Axonal transport of cytoskeletal proteins. In: Burgoyne RD, editor. The Neuronal Cytoskeleton. New York, NY: Wiley-Liss, Inc; 1991. pp. 283–307. [Google Scholar]
- Nixon RA. Slow axonal transport. Current Opinion in Cell Biology. 1992;4:8–14. doi: 10.1016/0955-0674(92)90052-e. [DOI] [PubMed] [Google Scholar]
- Nixon RA. The slow axonal transport of cytoskeletal proteins. Current Opinion in Cell Biology. 1998;10(1):87–92. doi: 10.1016/s0955-0674(98)80090-2. [DOI] [PubMed] [Google Scholar]
- Nixon RA, Logvinenko KB. Multiple fates of newly synthesized neurofilament proteins: evidence for a stationary neurofilament network distributed nonuniformly along axons of retinal ganglion cell neurons. Journal of Cell Biology. 1986;102(2):647–59. doi: 10.1083/jcb.102.2.647. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Okabe S, Miyasaka H, Hirokawa N. Dynamics of the neuronal intermediate filaments. Journal of Cell Biology. 1993;121:375–386. doi: 10.1083/jcb.121.2.375. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Paggi P, Lasek RJ. Axonal transport of cytoskeletal proteins in oculomotor axons and their residence times in the axon terminals. Journal of Neuroscience. 1987;7:2397–2411. [PMC free article] [PubMed] [Google Scholar]
- Paggi P, Lasek RJ, Katz MJ. Slow component B protein kinetics in optic nerve and tract windows. Brain Research. 1989;504:223–230. doi: 10.1016/0006-8993(89)91361-9. [DOI] [PubMed] [Google Scholar]
- Perrot R, Berges R, Bocquet A, Eyer J. Review of the multiple aspects of neurofilament functions, and their possible contribution to neurodegeneration. Molecular Neurobiology. 2008;38(1):27–65. doi: 10.1007/s12035-008-8033-0. [DOI] [PubMed] [Google Scholar]
- Price RL, Paggi P, Lasek RJ, Katz MJ. Neurofilaments are spaced randomly in the radial dimension of axons. Journal of Neurocytology. 1988;17:55–62. doi: 10.1007/BF01735377. [DOI] [PubMed] [Google Scholar]
- Reis GF, Yang G, Szpankowski L, Weaver C, Shah SB, Robinson JT, Hays TS, Danuser G, Goldstein LS. Molecular motor function in axonal transport in vivo probed by genetic and computational analysis in Drosophila. Molecular Biology of the Cell. 2012;23(9):1700–14. doi: 10.1091/mbc.E11-11-0938. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Roy S, Coffee P, Smith G, Liem RKH, Brady ST, Black MM. Neurofilaments are transported rapidly but intermittently in axons: implications for slow axonal transport. Journal of Neuroscience. 2000;20:6849–6861. doi: 10.1523/JNEUROSCI.20-18-06849.2000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schnapp BJ, Reese TS. Cytoplasmic structure in rapid frozen axons. Journal of Cell Biology. 1982;94:667–679. doi: 10.1083/jcb.94.3.667. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shea TB, Majocha RE, Marotta CA, Nixon RA. Soluble, phosphorylated forms of the high molecular weight neurofilament protein in perikarya of cultured neuronal cells. Neuroscience Letters. 1988;92(3):291–7. doi: 10.1016/0304-3940(88)90605-2. [DOI] [PubMed] [Google Scholar]
- Sunil N, Lee S, Shea TB. Interference with kinesin-based anterograde neurofilament axonal transport increases neurofilament-neurofilament bundling. Cytoskeleton (Hoboken) 2012 doi: 10.1002/cm.21030. [DOI] [PubMed] [Google Scholar]
- Takeda S, Okabe S, Funakoshi T, Hirokawa N. Differential dynamics of neurofilament-H protein and neurofilament-L protein in neurons. Journal of Cell Biology. 1994;127:173–185. doi: 10.1083/jcb.127.1.173. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Terada S, Nakata T, Peterson AC, Hirokawa N. Visualization of slow axonal transport in vivo. Science. 1996;273:784–788. doi: 10.1126/science.273.5276.784. [DOI] [PubMed] [Google Scholar]
- Trivedi N, Jung P, Brown A. Neurofilaments switch between distinct mobile and stationary states during their transport along axons. Journal of Neuroscience. 2007;27:507–516. doi: 10.1523/JNEUROSCI.4227-06.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tytell M, Black MM, Garner JA, Lasek RJ. Axonal transport: each major component reflects the movement of distinct macromolecular complexes. Science. 1981;214:179–181. doi: 10.1126/science.6169148. [DOI] [PubMed] [Google Scholar]
- Uchida A, Brown A. Arrival, reversal and departure of neurofilaments at the tips of growing axons. Molecular Biology of the Cell. 2004;15:4215–4225. doi: 10.1091/mbc.E04-05-0371. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang L, Brown A. Rapid intermittent movement of axonal neurofilaments observed by fluorescence photobleaching. Molecular Biology of the Cell. 2001;12:3257–3267. doi: 10.1091/mbc.12.10.3257. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang L, Brown A. A hereditary spastic paraplegia mutation in kinesin-1A/KIF5A disrupts neurofilament transport. Molecular Neurodegeneration. 2010;5:52. doi: 10.1186/1750-1326-5-52. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang L, Ho C-L, Sun D, Liem RKH, Brown A. Rapid movement of axonal neurofilaments interrupted by prolonged pauses. Nature Cell Biology. 2000;2(3):137–141. doi: 10.1038/35004008. [DOI] [PubMed] [Google Scholar]
- Watson DF, Hoffman PN, Fittro KP, Griffin JW. Neurofilament and tubulin transport slows along the course of mature motor axons. Brain Research. 1989;477(1–2):225–32. doi: 10.1016/0006-8993(89)91410-8. [DOI] [PubMed] [Google Scholar]
- Xu Z, Tung VW. Temporal and spatial variations in slow axonal transport velocity along peripheral motoneuron axons. Neuroscience. 2001;102(1):193–200. doi: 10.1016/s0306-4522(00)00449-8. [DOI] [PubMed] [Google Scholar]
- Yan Y, Brown A. Neurofilament polymer transport in axons. Journal of Neuroscience. 2005;25(30):7014–21. doi: 10.1523/JNEUROSCI.2001-05.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yuan A, Sasaki T, Rao MV, Kumar A, Kanumuri V, Dunlop DS, Liem RK, Nixon RA. Neurofilaments form a highly stable stationary cytoskeleton after reaching a critical level in axons. Journal of Neuroscience. 2009;29(36):11316–29. doi: 10.1523/JNEUROSCI.1942-09.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]