On Inclusion of Covariates for Class Enumeration of Growth Mixture Models

Abstract

In this article, we directly questioned the common practice in growth mixture model (GMM) applications that exclusively rely on the fitting model without covariates for GMM class enumeration. We provided theoretical and simulation evidence to demonstrate that exclusion of covariates from GMM class enumeration could be problematic in many cases. Based on our findings, we provided recommendations for examining the class enumeration by the fitting model without covariates and discussed the potential of covariate inclusion as a remedy for the weakness of GMM class enumeration without including covariates. A real example on the development of children’s cumulative exposure to risk factors for adolescent substance use was provided to illustrate our methodological developments.

Introduction

Growth mixture modeling (GMM; Muthen & Muthen, 2000; Muthen & Shedden, 1999; Nagin, 1999) has recently become a popular tool in longitudinal research. Despite its popularity, one of the oldest and most challenging task in GMM still is the extraction of correct number of the classes without much a priori knowledge (Tofighi & Enders, 2007). Although less noticed, an important consideration related to this task is whether covariates should be included in determination of the number of classes (Tofighi & Enders, 2007).

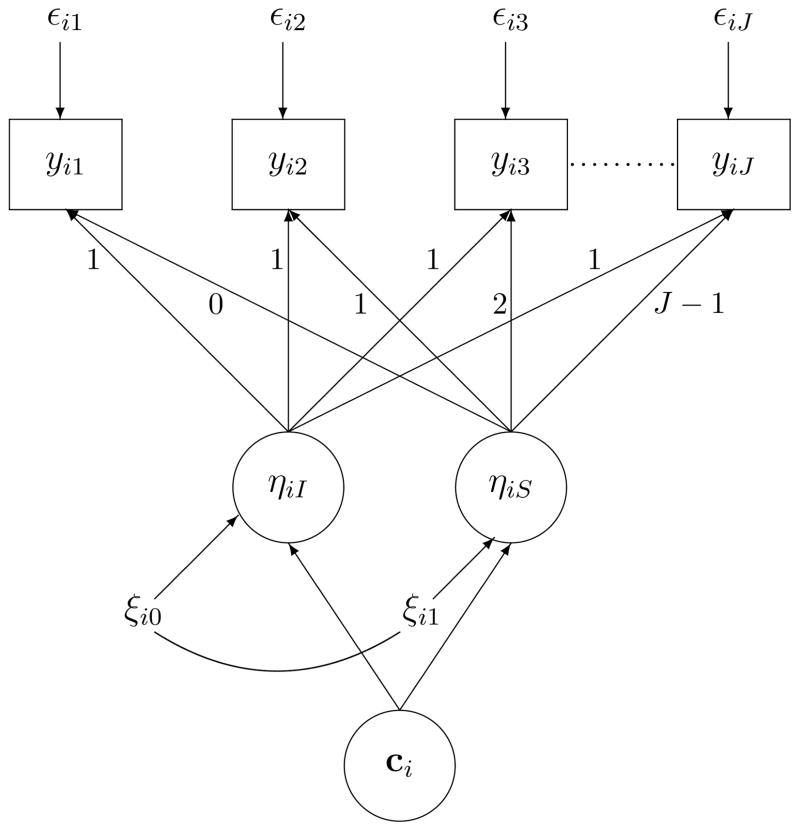
Today, most applications used GMM model without covariates to determine the number of classes. In this model, as the one illustrated in Figure 1, subjects (denoted by i in Figure 1) are assumed to belong to different classes (denoted by c_i, which includes c_i1, ···, c_iK, where c_ik = 1 if the ith subject falls in kth class and is zero otherwise) with distinct patterns of trajectories of outcomes over time (denoted by y_i1, y_i2, ···, y_iJ). Furthermore, within each class, the heterogeneity of outcome trajectories can be further explained by some growth factors such as the intercept and slope factors (denoted by η_iI and η_iS in Figure 1 respectively).

Figure 1.

Growth mixture model without covariates

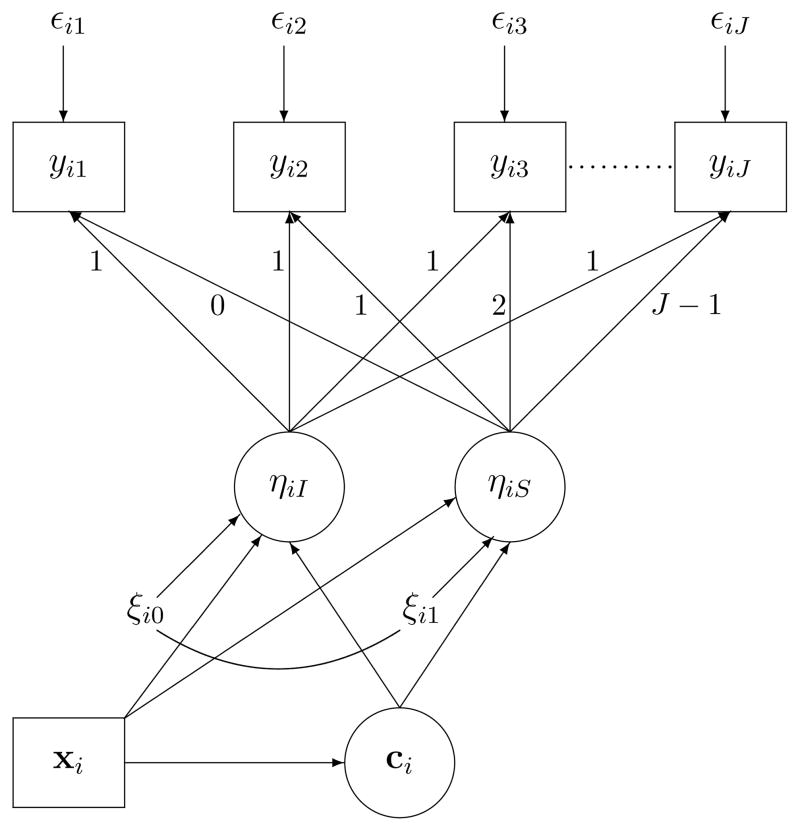
Muthen (2004) suggested that incorporating covariates may play an important role in enumerating classes. According to this suggestion, as illustrated in Figure 2, including covariates (denoted by x_i, which includes P covariates x_i1, ···, x_iP) into the GMM model above to predict the class membership and the growth factors within each class may be helpful for GMM class enumeration. However, few practice today followed the suggestion and included covariates in the stage of class enumeration even though the final model could have many substantive and statistical advantages by the inclusion (e.g., Muthen, 2004).

Figure 2.

Growth mixture model with covariates

Unquestionably, correct class enumeration is one key issue in GMM. To our knowledge, Tofighi and Enders (2007) may be the only existing study that has addressed the issue of covariate inclusion on class enumeration in the context of GMM and they found a detrimental effect of covariate inclusion on GMM class enumeration. It should be noticed that their simulation used a substantively more complex model than other models found in applied practice so that their conclusion may not be applicable to the more restricted models commonly-used in practice, the focus of this article.

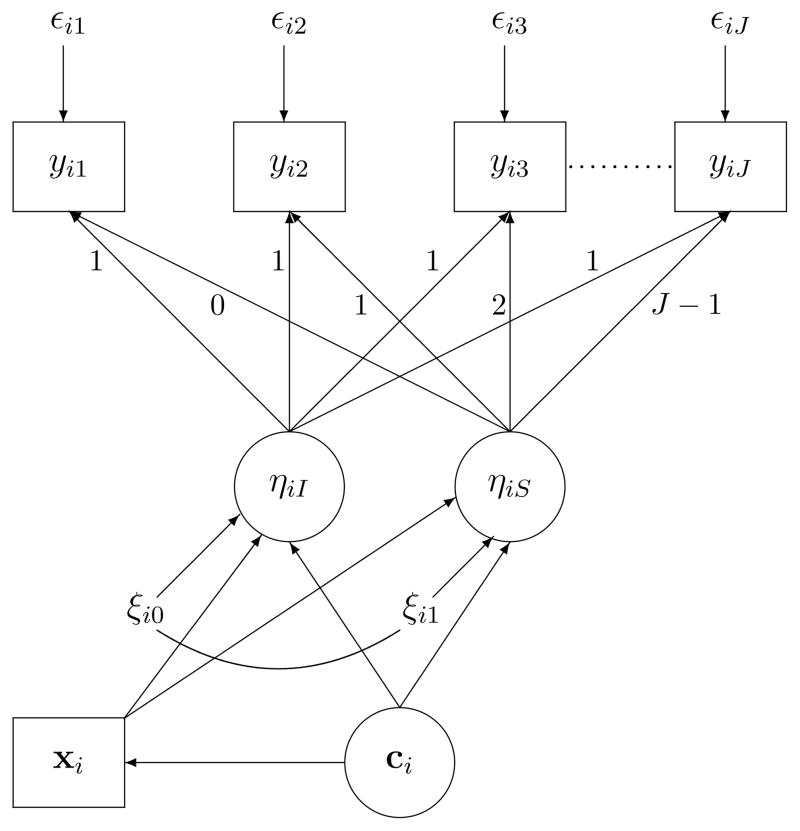
In this article, we investigate the issue of covariate inclusion and its implication to GMM class enumeration. We first use a real example to demonstrate that class enumeration with and without covariates could have different conclusions on the number of classes and explore this discrepancy from a statistical perspective. Then we introduce a new GMM data generation model as illustrated in Figure 3. Unlike in the fitting model in Figure 2, x_i is no longer treated as covariates, is now predicted by class membership c_i and could have different distributions across classes in this new data generation model. As demonstrated below, this new data generation model by its design allows easier manipulation of within-class distribution of x_i. Through this data generation model, we generate data with different distribution of x_i (e.g., binary, mildly nonnormal and severely nonnormal) within classes to assess the effects of (1) fitting models conditional on x_i when x_i is in fact predicted by class membership, and (2) omitting x_i when it is predicted by class membership and predicts growth factors, on class enumeration. The results of simulation will then be presented. Finally, implications of results are discussed with the real example we provided and conclusions are presented at the end of the article.

Figure 3.

Data generation model for our simulation studies

A Real Example

Our data is from the National Survey of Child and Adolescent Well-Being (see NSCAW, 2007 for detail) and the children in their middle childhood (aged from 6 to 10 at baseline-the first of four waves available) are selected. Our focus is the development of their cumulative exposure to risk factors for their adolescent substance use. We sum cumulative exposure to nine risk factors and form our risk index at each wave. We identify seven caregivers’ characteristics at baseline as covariates. They include age, employment status, substance abuse experience, education, marital status and ethnicity of caregivers as well as the indicator of whether biological mother is caregiver or not. We remove eleven cases having missing values on the covariates and obtain 1481 cases for the illustration here.

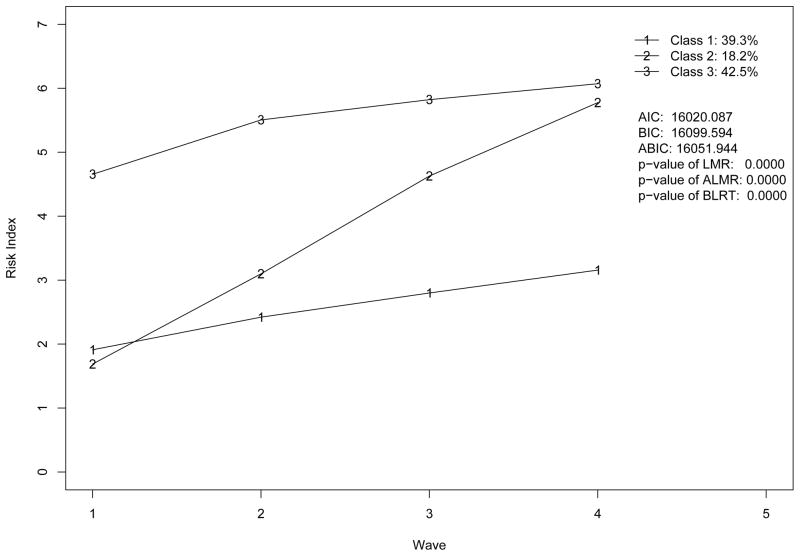
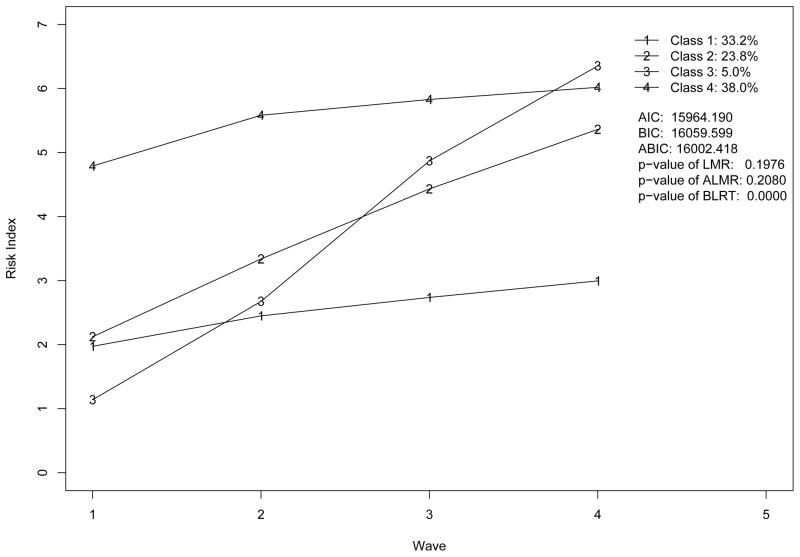
Excluding covariates as in Figure 1, we apply GMM model with the number of classes ranging from 2 to 5 to our risk indices across four waves. In this fitting model, we assume that the variances of residuals (ε_i1, ···, ε_iJ in Figure 1), the variances and covariances of growth factors (ξ_i0 and ξ_i1 in Figure 1) are invariant across classes. We obtain the following fit statistics for each model: AIC (Akaike, 1987), BIC (Schwartz, 1978), adjusted BIC (ABIC; Sclove, 1987), Lo-Mendell-Rubin likelihood ratio test (LMR; Lo et al., 2001), adjusted LMR likelihood ratio test (ALMR; Lo et al., 2001), and the bootstrap likelihood ratio test (BLRT; McLachlan, 1987; McLachlan & Peel, 2000)¹. By examining these statistics and parameter estimates, we exclude the two-class model due to bad fit and the five-class models due to improper solution. The plots of trajectories implied by three and four-class models are presented in Figure 4 and Figure 5 respectively. The results of analysis show that the parameter estimates of both models have no serious substantive problem. However, the model fit statistics in the two figures lead to a conflicting conclusion on the number of classes for the study. The information criteria, AIC, BIC, ABIC and BLRT, support the four-class model while LMR and ALMR support the three-class model.

Figure 4.

Trajectories by three-class GMM model without covariates.

Figure 5.

Trajectories by four-class GMM model without covariates.

Given this conflict, we add seven covariates to predict the class membership and the growth factors (as in Figure 2) and refit the three and four-class models. In both models, the effects of covariates on growth factors are assumed to be invariant across classes. For parsimony, we also simplify both models after inclusion of covariates and initial refitting as below. Throughout our modification, we use .05 alpha level to determine the significance of parameter estimates and the scaled χ² difference test (Satorra & Bentler, 2001) for model comparison. The covariate effects on growth factors whose estimates are not significant in both models will be evaluated by the scaled χ² difference test before removal of parameter. The covariates that have no significant prediction of any class membership in both models will also be tested for removal. In the final three and four-class models obtained by this modification, all seven covariates are retained. All of them have at least a significant prediction of class membership in both models. Among seven covariates, biological mother as caregiver or not, substance abuse experience and education of caregivers have significant covariate effects on growth factors in both models. Age of caregivers has a significant covariate effect on intercept factor in the final three-class model but not in the final four-class model. Ethnicity of caregivers has a significant covariate effect on intercept factor in both final models. However, its effect on slope factor is significant in the final four-class model but not significant in the final three-class model. Even though not significant in both models, we decide to keep them in the final models because no common parameters can be further reduced for both models.

With inclusion of covariates, the trajectories implied by the two models do not change much from Figure 4 and Figure 5. The fit statistics for the final three-class model with covariates are as follows: AIC = 15615.249, BIC = 15821.968, ABIC = 15698.076, and the p-values of LMR and ALMR both are less than .0001. For the final four-class model, AIC = 15564.452, BIC = 15829.475, ABIC = 15670.640, and the p-values of LMR and ALMR are 0.2119 and 0.2153 respectively. For both models, the p-values of BLRT may not be trustworthy as prompted by Mplus (Muthen & Muthen, 2006) and are ignored here. From AIC, BIC and ABIC, we see that the overall fit of both models improves after inclusion of covariates. As to class enumeration, fit indices still give inconsistent conclusion. LMR and ALMR still support the three-class solution. Unlike AIC or ABIC, BIC begins to support the three-class solution. If we weight BIC more in class enumeration (e.g., Jeffries, 2003; Jones & Nagin, 2007), the class enumeration conclusions with or without covariates diverge.

A Potential Problem in the Common Practice of GMM Class Enumeration

A common practice in GMM applications is to use GMM without covariates as in Figure 1 for class enumeration. This practice implicitly assumes that GMM without covariates would recover the correct number of classes no matter if covariates have impact on class membership or growth factors in population. However, this assumption may not hold always.

Let y_i = (y_i1 ···y_iJ)′ and η_i = (η_iI, η_iS, η_iQ)′, where η_iQ is the quadratic factor in GMM. Then the GMM data for the model in Figure 2 can be generated in this way (e.g., Muthen, 1998–2004). First, x_i, which can be different types of variables (e.g., categorical or nonnormal continuous variables), is generated from a distribution f₁(x_i); then c_i is generated from the multinomial distribution f₁(c_i|x_i) conditional on x_i; finally y_i is generated from a conditional normal growth model f(y_i|x_i, c_i). We denote this data generation scheme as Scheme 1.

The probability of the observation generated by Scheme 1 can be expressed as

$$f_1({\mathbf{y}}_i,{\mathbf{x}}_i,{\mathbf{c}}_i)=f({\mathbf{y}}_i\mid {\mathbf{x}}_i,{\mathbf{c}}_i)f_1({\mathbf{c}}_i\mid {\mathbf{x}}_i)f_1({\mathbf{x}}_i)=f({\mathbf{y}}_i\mid {\mathbf{x}}_i,{\mathbf{c}}_i)·\prod _k{\pi }_{ik}^{c_{ik}}·f_1({\mathbf{x}}_i)$$ (1)

where π_ik, the probability of ith case in kth class conditional on x_i, can be modeled as

$${\pi }_{ik}=\text{P}(c_{ik}=1\mid {\mathbf{x}}_i)=\frac{exp(a_k+{\sum }_p^P{b}_{kp}·x_{ip})}{{\sum }_{k}exp(a_k+{\sum }_p^P{b}_{kp}·x_{ip})}$$ (2)

with a_K = 0, b_Kp = 0, and a_k and b_kp as logit intercept and slope respectively (e.g., Muthen, 1998–2004), and f(y_i|x_i, c_i) can be expressed as

$$f({\mathbf{y}}_i\mid {\mathbf{x}}_i,{\mathbf{c}}_i)=\int f({\mathbf{y}}_i,{\eta }_i\mid {\mathbf{x}}_i,{\mathbf{c}}_i)d{\eta }_i=\int f({\mathbf{y}}_i\mid {\eta }_i,{\mathbf{x}}_i,{\mathbf{c}}_i)f({\eta }_i\mid {\mathbf{x}}_i,{\mathbf{c}}_i)d{\eta }_i.$$ (3)

In this article, we specify the within-class level-1 (outcomes) model f(y_i|η_i, x_i, c_i) in (3) as

$$y_{ij}^k={\eta }_{iI}^k+{\eta }_{iS}^k·t_j+{\eta }_{iQ}^k·t_j^2+{\epsilon }_{ij}^k(\text{assume}\text{no}\text{time}\text{varying}\text{covariates})$$ (4)

for class k, where j = 1, ···, J, t_j = (j − 1) is the time score at time j for all cases and ${\epsilon }_{ij}^k~N(0,{\psi }_j)$ is the normal distributed residual of $y_{ij}^k$, which is assumed to be independent across time. We specify the within-class level-2 (person-level) model f(η_i|x_i, c_i) in (3) as

$$\begin{array}{l}{\eta }_{iI}^k={\gamma }_{00}^k+{\gamma }_{10}^k{x}_{i1}+\cdots +{\gamma }_{P0}^k{x}_{iP}+{\xi }_{i0}^k\\ {\eta }_{iS}^k={\gamma }_{01}^k+{\gamma }_{11}^k{x}_{i1}+\cdots +{\gamma }_{P1}^k{x}_{iP}+{\xi }_{i1}^k\\ {\eta }_{iQ}^k={\gamma }_{02}^k\end{array}$$ (5)

for class k, where ${\gamma }_{00}^k,{\gamma }_{01}^k$ and ${\gamma }_{02}^k$ are the intercepts of the growth factors η_i in kth class, all other ${\gamma }_{ij}^k$s are the regression coefficients of η_i on x_i in kth class, and ${\xi }_{i0}^k$ and ${\xi }_{i1}^k$ are the multivariate normal distributed residuals of growth factors with a zero mean vector, $\text{Var}({\xi }_{i0}^k)={\sigma }_{00},\text{Var}({\xi }_{i1}^k)={\sigma }_{11}$ and $\text{Cov}({\xi }_{i0}^k,{\xi }_{i1}^k)={\sigma }_{01}$. As in Tofighi and Enders (2007), we specify no random error and no covariate effect for the quadratic factor in (5).

Scheme 1 is the assumption for the GMM fitting model with covariates as in Figure 2. However, there is a less obvious problem for Scheme 1. In application, if the data is really generated in this way, or in other words, if the data is really like what the GMM fitting model with covariates as in Figure 2 assumes, the fitting model with covariates would be a correctly specified model. However, at the same time, the fitting model without covariates as in Figure 1 in general could be misspecified in the within-class distribution (see Appendix I for detail). More importantly, this misspecification in the within-class distribution, if serious enough, could cause the fitting model without covariates as in Figure 1 enumerate a greater number of classes than the model with covariates would (e.g., Bauer & Curran, 2003, 2004; Tofighi & Enders, 2007) and pose problem to the common practice of class enumeration in GMM applications as we mentioned before.

Of course, we must mention that our conclusion above is only applied to the situation where the growth factors η_i as assumed in Figure 2 are influenced by x_i within classes in population. When x_i only predict the class membership under Scheme 1 and have no influence on the growth factors in (5) as assumed in some studies (e.g., Lubke & Muthen, 2007), the fitting models as in both Figure 1 and Figure 2 are correct and theoretically would have the same number of classes (see Appendix I for detail).

A New Data Generation Scheme

Before further investigation of the issue of the covariate inclusion or exclusion on GMM class enumeration, we introduce a second GMM data generation scheme (Scheme 2) which is implied by the data generation model in Figure 3. This data generation scheme is different from Scheme 1 and is defined as follows: first c_i is generated from a multinomial distribution f₂(c_i); then x_i is generated from some distribution (e.g., binary or some continuous distribution) given the membership c_i; then y_i is generated from the conditional normal growth model f(y_i|x_i, c_i) in (3).

The probability of observation generated in this way can be expressed as

$$f_2({\mathbf{y}}_i,{\mathbf{x}}_i,{\mathbf{c}}_i)=f({\mathbf{y}}_i\mid {\mathbf{x}}_i,{\mathbf{c}}_i)f_2({\mathbf{x}}_i\mid {\mathbf{c}}_i)f_2({\mathbf{c}}_i)=f({\mathbf{y}}_i\mid {\mathbf{x}}_i,{\mathbf{c}}_i)f_2({\mathbf{x}}_i\mid {\mathbf{c}}_i)·\prod _k{\pi }_k^{c_{ik}}$$ (6)

where π_k is the probability of ith observation in kth class, which is not conditional on anything. Due to the inclusion of f₂(x_i|c_i), Scheme 2 in (6) compared to Scheme 1 has an advantage that it is more convenient for us to manipulate the within-class distribution of x_i (e.g., mildly nonnormal and severely nonnormal) during GMM data generation. We will use Scheme 2 in simulation studies below to investigate the class enumeration issues.

Specifically, when the within-class distribution f₂(x_i|c_i) is normal in data generation, by integrating (6) over x_i as (A-3) in Appendix, we can see that the within-class distributions f₂(η_i|c_i) and f₂(y_i|c_i) corresponding to f₁(η_i|c_i) and f₁(y_i|c_i) in (A-3) respectively would be normal in the data and thus the fitting model without covariates x_i as in Figure 1 exactly matches the data by Scheme 2. By the same logic, when x_i include categorical variables or are nonnormally distributed within classes under Scheme 2, the fitting model without covariates x_i as in Figure 1 would be misspecified because the within-class normality assumption of η_i and y_i has been violated in the generated data. This misspecification in distribution may impair the class enumeration performance of the model as we mentioned before.

Theorectically, the population models implied by Scheme 1 and Scheme 2 can be transformed to each other in model form (see Appendix II). By these transformations, we can examine whether the population model by Scheme 2 can be reparameterized to a population model by Scheme 1 with an implementable model of membership prediction in form of (2) that is assumed by the fitting model with covariates. By this examination, we can determine the correctness of the fitting model with covariates when the data are in fact generated by Scheme 2. In fact, we observe from these tranformations that the fitting model as in Figure 2 in general may be misspecified for the data generated by Scheme 2 (except in some special cases as in our studies below; see Appendix II for detail). In GMM literature, in addition to misspecification in distribution, other sources of misspecification (e.g., misspecification in parameter class specificity, Bauer & Curran, 2004, Enders & Tofighi, 2008; misspecification of nonlinear relationships among observed and/or latent variables, Bauer & Curran, 2004) have been documented to have detrimental effect and lead to additional classes for GMM class enumeration. So the misspecification of the fitting model as in Figure 2 discussed here may impair its class enumeration performance.

Design of Simulation Studies

For each of the studies below, the data is generated by Scheme 2 with four levels of sample size (N = 200, 400, 1000N = 200, 400, 2000) and x_i only has a single variable for convenience of manipulation. For all these studies, the number of classes is set to 2 and the proportion of each class is 50 percent. For the distribution f(y_i|x_i, c_i) in (3), the parameters are as follows: $({\gamma }_{00}^1,{\gamma }_{01}^1,{\gamma }_{02}^1)=(28,2,-.5),({\gamma }_{00}^2,{\gamma }_{01}^2,{\gamma }_{02}^2)=(15,6,-.5),({\gamma }_{10}^1,{\gamma }_{11}^1)=({\gamma }_{10}^2,{\gamma }_{11}^2)=(1.897,0.948),{\psi }_j=27.5$, ψ_j = 27.5 for j = 1, ···, 7, and (σ₀₀, σ₀₁, σ₁₁) = (15, 3, 4). From these parameters, we can see that the residual variances of outcomes, the factor variances and covariances, and the effects of x_i on the growth factors are set to be invariant across classes in population model. Due to the difference on f₂(x_i|c_i), the within-class distribution of x_i, we design three studies for investigation.

Study I: Binary covariates

In this study, x_i is set to be a binary variable (0 or 1) with f₂(x_i = 1|c_i1 = 1) = .30 and f₂(x_i = 1|c_i2 = 1) = .70. As mentioned above, when x_i include categorical variables under Scheme 2, the fitting model without covariates x_i as in Figure 1 would be misspecified because η_i and y_i given c_i would not be normaly distributed in the generated data as assumed.

It is obvious that the joint distribution of the two binary variables, x_i and c_i, by Scheme 2 in this study can be summarized as a 2×2 cross table. This 2×2 cross table can be expressed by a f₂(x_i|c_i)f₂(c_i) as in our data generation as well as by an reparameterized f₁(c_i|x_i)f₁(x_i) with an implementable model of membership prediction in form of (2). Specifically, by (A-4) in Appendix II, the implied ḟ(x_i) would suggest that x_i unconditionally has 50 percent of chance to be either 0 or 1. The implied π̇_ik for the data can also be fully expressed by the model in (2) with a₁ = log(7/3), b₁ = log(9/49), a₂ = 0 and b₂ = 0. Given this reparameterization of the population model by Scheme 2 and the common f(y_i|x_i, c_i) in the two schemes, we believe that the fitting model with covariates as in Figure 2 would be an exact-fitting model for the generated data in this study.

Our setting in this study is substantively meaningful. Suppose now x_i = 1 denotes caregiver who is hispanic and x_i = 0 denotes caregiver who is not as in our NSCAW example. By Scheme 2, our setting states that the first class includes more children of non-hispanic caregivers while the second class includes more children of hispanic caregivers. Under Scheme 2 for our data generation, the hispanic origin of caregiver is not conceived as a covariate as in Figure 2. However, like in many equivalent models in literature (e.g., Lee & Hershberger, 1990; MacCallum et al., 1993), this difference of x_i in substantive meaning or diagrams (e.g., Figure 2 vs. Figure 3) does not prevent the data in this study to be well fitted by a fitting model as in Figure 2 where the hispanic origin of caregiver predicts the class membership of child as a covariate.

Furthermore, the parameters ( ${\gamma }_{10}^1,{\gamma }_{11}^1$) and ( ${\gamma }_{10}^2,{\gamma }_{11}^2$) would represent the effects of caregiver’s ethnicity on the intercept and slope factors within classes. In this article, we assume the two sets of parameters to be class-invariant. Of course, it is interesting to investigate how such within-class effect of caregiver’s ethnicity would affect the within-class nonnormality of outcomes and consequently the class enumeration performance of GMM fitting model without covariates included. For this investigation, we set two levels of effect of x_i within classes: low level vs. high level of effect of x_i within classes. In these two conditions, ( ${\gamma }_{10}^1,{\gamma }_{11}^1$) and ( ${\gamma }_{10}^2,{\gamma }_{11}^2$) in (5), which were set to be (1.897, 0.948) above, are further multiplied by 2 and 5 respectively.

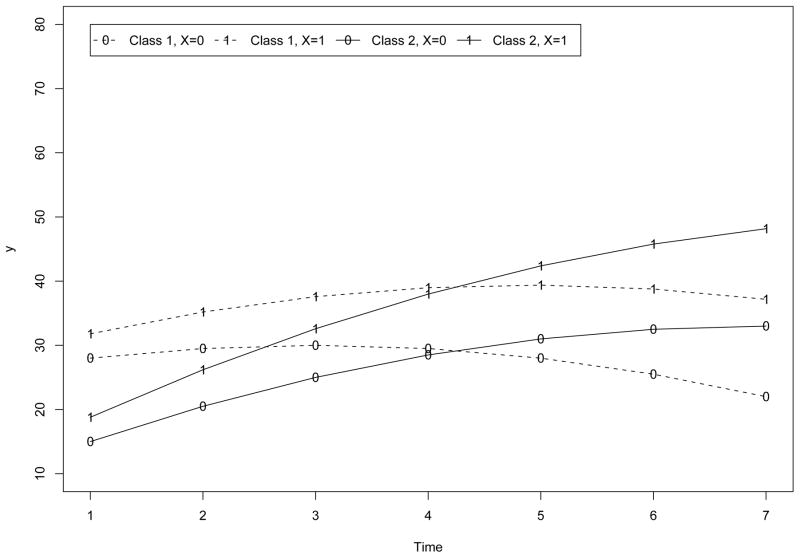
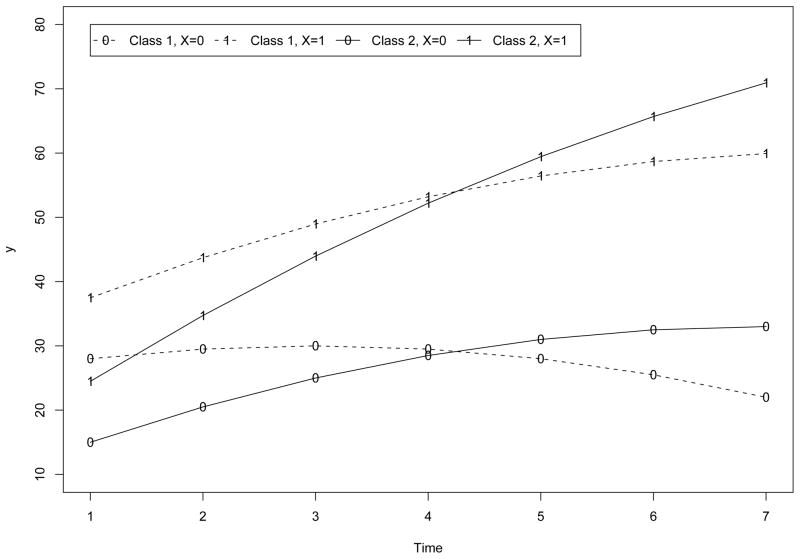
Statistically, the larger number is used for the multiplication, the more nonnormal distribution will result in each class. Substantively, the larger number is used for the multiplication, the more heterogeneity in the data the covariate would capture. In Figure 6 and Figure 7, we plotted the expected within-class trajectories of y_i (for both classes) in Study I when ( ${\gamma }_{10}^k,{\gamma }_{11}^k$) in (5) is multiplied by 2 and 5 respectively. From Figure 6 to Figure 7, the distance between the expected within-class trajectories of y_i increases in both classes. In term of Mahalanobis distance, the within-class distance increases from 1.23 to 7.71 in both classes from Figure 6 to Figure 7. On the other hand, despite the levels of effect of x_i, given x_i, the distance between the expected trajectories of y_i across classes (e.g., the trajectories of y_i across classes given x_i = 1 or the trajectories of y_i across classes given x_i = 0) holds constantly as 9.34.

Figure 6.

Trajectories under Low Level of Effect of x_i in Study I.

Figure 7.

Trajectories under High Level of Effect of x_i in in Study I.

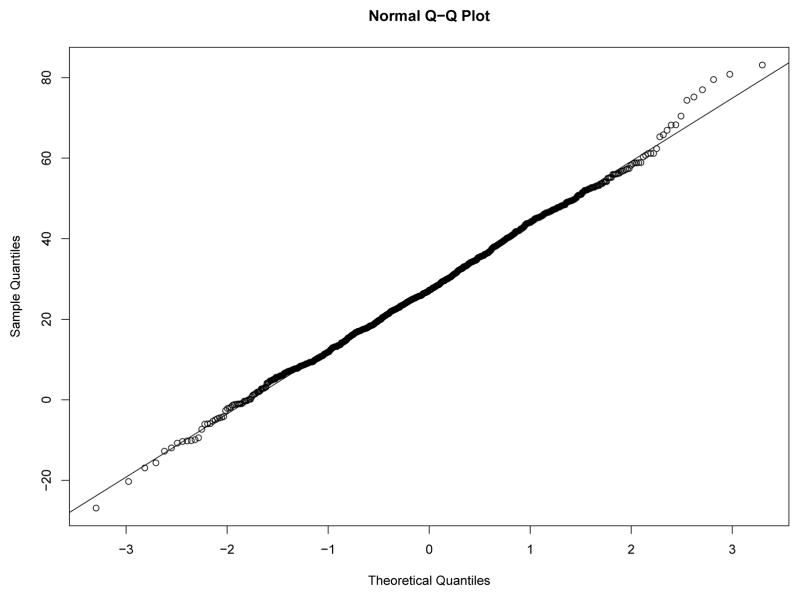
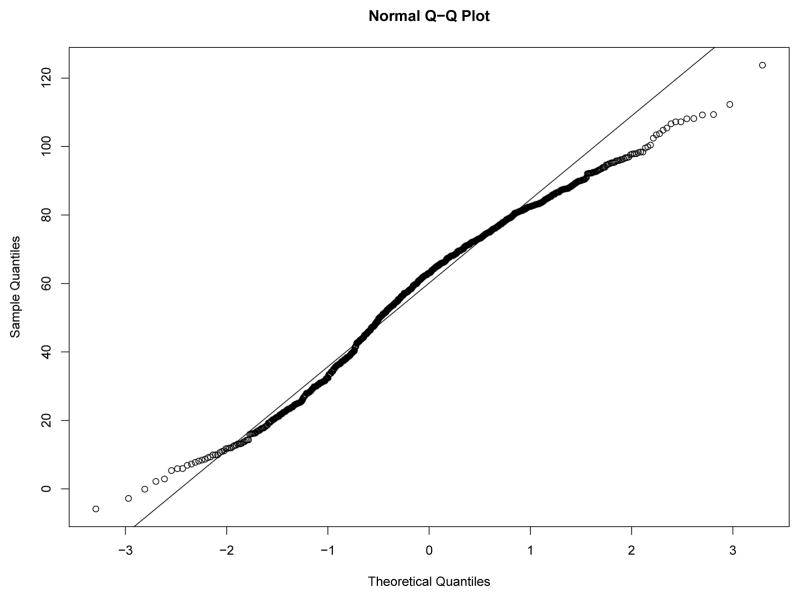
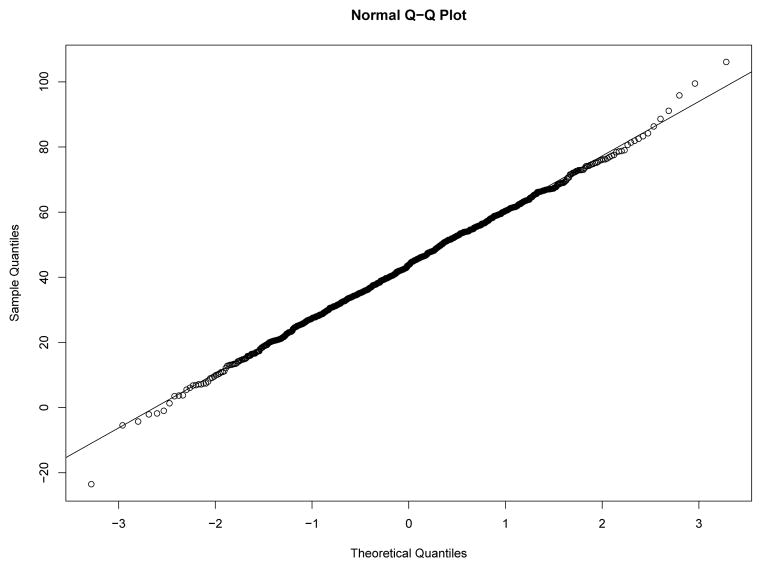
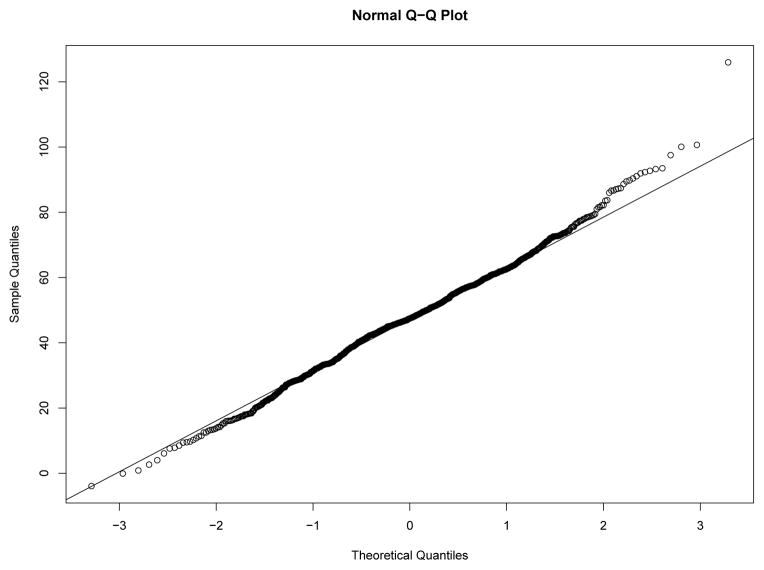
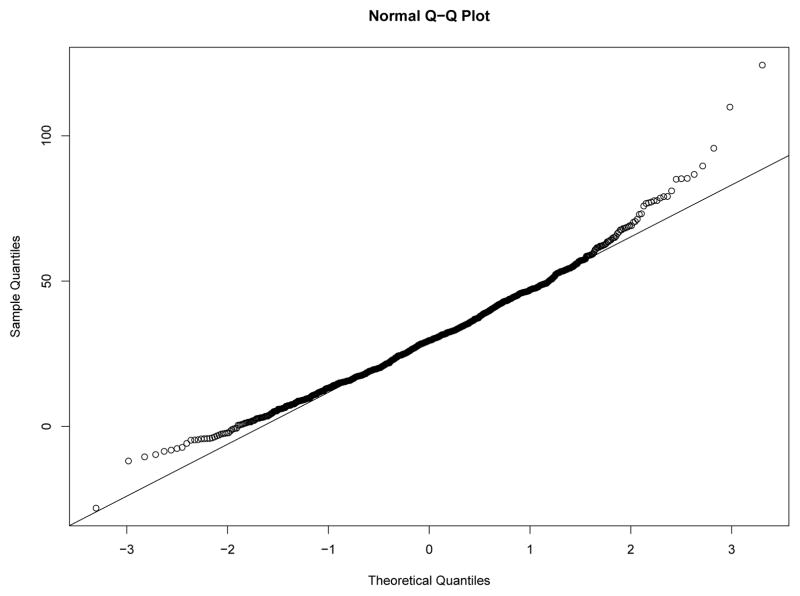
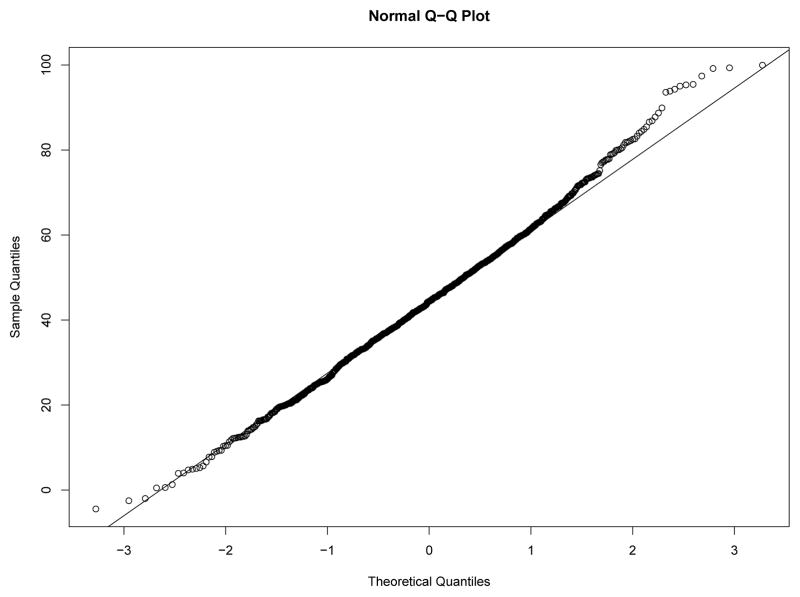
Our first study has 8 experimental conditions: two levels of effect of x_i within classes and four sample size levels. To verify the within-class nonnormality, we randomly selected a sample with N = 2000 under each level of effect of x_i and drawn the QQ-plots of y_i at Time 7 against standard normal distribution for each class in the two samples from Figures 8–11. We used y_i at Time 7 because at this time the nonnormality of y_i reaches its maximum across classes. In Figure 8 and Figure 9, under the low level of effect of x_i, the within-class distributions of y_i approximate the normal distribution well in sample against our expectation. Of course, under the higher level condition as shown in Figure 10 and Figure 11, the distributions depart from the normal one clearly. We calculated Mardia’s skewness and kurtosis test statistics (Mardia, 1974) for y_i in each class of both samples. With α = .05, Mardia’s skewness test statistic is significant for both classes under the high level of effect of x_i and is nonsignificant for both classes under the low level condition. For both samples, Mardia’s kurtosis test statistic is nonsignificant across classes.

Figure 8.

QQ-plot of y_i at Time 7 in Class 1 under Low Level of Effect of x_i

Figure 11.

QQ-plot of y_i at Time 7 in Class 2 under High Level of Effect of x_i

Figure 9.

QQ-plot of y_i at Time 7 in Class 2 under Low Level of Effect of x_i

Figure 10.

QQ-plot of y_i at Time 7 in Class 1 under High Level of Effect of x_i

Study II: Mildly nonnormal continuous covariates

In our second study, x_i is set to be a continuous variable. When c_i1 = 1, the distribution of x_i is set by the method of Flieshman (1978) to have a mean and variance equal to 1, and skewness and kurtosis equal to 1 and 3 respectively. When c_i2 = 1, the distribution of x_i is set to the same distribution but with a mean equal to δ. For this study, δ is set to 1, $\sqrt{2}$ or 2. As discussed before, when x_i is nonnormally distributed within classes under Scheme 2 as in this study, the fitting model without covariates as in Figure 1 would be misspecified because η_i and y_i given c_i would not be normally distributed in the generated data as assumed.

However, for the model with covariates as in Figure 2, the situation is different. When δ = 1, x_i is independent of c_i under Scheme 2 and their joint distribution in the generated data can be reparameterized by a f₁(c_i|x_i)f₁(x_i) in (1). Specifically, by (A-4), the implied ḟ(x_i) would suggest that x_i unconditionally has a single nonnormal distribution, the implied π̇_ik for the data becomes a constant, .50 and suggests that all parameters of the f₁(c_i|x_i) in (2) would be equal to zero. Clearly, the data in this condition can be correctly fitted by GMM models with covariates as in Figure 2 even though the class membership prediction would make the model unparsimonious. Furthermore, when $\delta =\sqrt{2}$ or 2, the joint distribution of x_i and c_i in the generated data may not be able to be reparameterized by a f₁(c_i|x_i)f₁(x_i) with an implementable model of membership prediction in form of (2). By (A-4), the implied ḟ(x_i) for the data is a nonnormal mixture. However, the implied π̇_ik would not be fully expressed by the model for class membership prediction in (2), and consequently GMM fitting model with covariates would not be a correctly specified model because its assumed model for membership prediction in (2) can not be satisfied in the generated data.

Let x_i denote the age of caregiver at baseline in our NSCAW example. Substantively, the setting of Scheme 2 in this study states that the average age of caregiver in the second class could be equal to or older than the one in the first class and this difference may result in further difference on the growth factors across classes. For our study, this simulated population would allows us to investigate the class enumeration performance of the model with covariates as in Figure 2 when age of caregiver in fact is predicted by class membership and the underlying population could be either correctly or incorrectly fitted by the model.

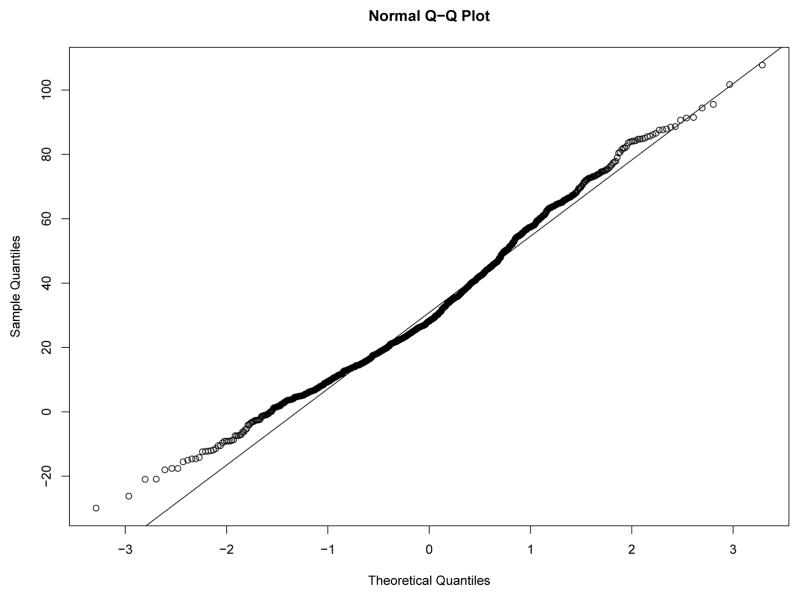
In this study, we have 12 experimental conditions: 3 levels of δ value and four sample size levels. We randomly selected a sample when N = 2000 and δ = 2 and drawn the QQ-plots of y_i at time 7 in Figure 12 and Figure 13. Two plots show that the within-class distributions of y_i approximate to the normal distribution somewhat against our expectation. Mardia’s skewness and kurtosis test statistics calculated from this sample also suggest that multivariate normality holds for both classes.

Figure 12.

QQ-plot of y_i at Time 7 in Class 1 when x_i has a mean equal to 1 and is mildly nonnormal within the class

Figure 13.

QQ-plot of y_i at Time 7 in Class 2 when x_i has a mean equal to 2 and is mildly nonnormal within the class

Study III: Severely nonnormal continuous covariates

In our third study, x_i follows chi square distribution within classes. When c_i1 = 1, ${\mathbf{x}}_i~{\chi }_1^2$ and when c_i2 = 1, ${\mathbf{x}}_i~{\chi }_{\delta }^2/\sqrt{\delta }$, where δ can be either of two values, 1 or 2. Like before, the fitting model without covariates as in Figure 1 would be misspecified in this study despite the value of δ because of the violation of normality assumption. Again, when δ = 1, x_i is independent of c_i under Scheme 2` and their joint distribution in the generated data can be reparameterized by a f₁(c_i|x_i)f₁(x_i) in (1). By (A-4), the implied ḟ(x_i) would suggest that x_i unconditionally has a single chi square distribution, the implied π̇_ik becomes a constant, .50 and and suggests that all parameters of the f₁(c_i|x_i) in (2) would be equal to zero, and the data can be correctly fitted by GMM model with covariates even though it may be unparsimonious. When δ = 2, the mean, variance, skewness and kurtosis of x_i in the second class are equal to $\sqrt{2}$, 2, $\sqrt{2}/2$ and 1.5 respectively while x_i in the first class follows a central chi square distribution with mean and variance equal to 1 and 2 respectively. For this condition, the joint distribution of x_i and c_i in the generated data may not be able to be reparameterized by a f₁(c_i|x_i)f₁(x_i) with an implementable model of membership prediction in form of (2). By (A-4), the implied ḟ(x_i) for the data is a chi square mixture, the implied π̇_ik may not be fully expressed by the model for class membership prediction in (2) and consequently GMM fitting model with covariates may not be correctly specified because its assumed model for membership prediction in (2) can not be satisfied in the generated data.

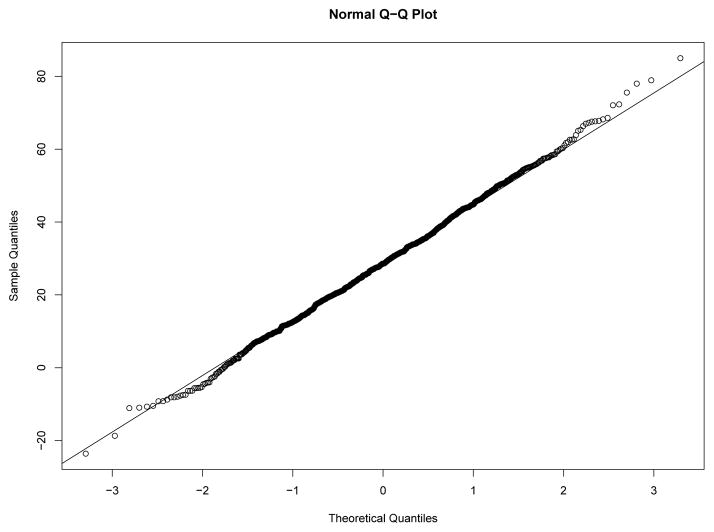
In this study, we have 8 experimental conditions: 2 levels of δ value and four sample size levels. We randomly selected a sample when N = 2000 and δ = 2 and drawn the QQ-plots of y_i at time 7 in Figure 14 and Figure 15. Two plots show that y_i in the first class departs from normal distribution while y_i in the second class approximate normal distribution somewhat. Mardia’s skewness test statistics calculated for the two classes also suggest that multivariate normality does not hold for the first class even though Mardia’s kurtosis test statistics are nonsignificant in both classes.

Figure 14.

QQ-plot of y_i at Time 7 in Class 1 when ${\mathbf{x}}_i~{\chi }_1^2$

Figure 15.

QQ-plot of y_i at Time 7 in Class 2 when ${\mathbf{x}}_i~{\chi }_2^2/\sqrt{2}$

Model fitting, fit indices and model evaluation

For each experimental condition above, 200 replications are generated by using R package. For each replication, two types of fitting models, GMM with covariates and GMM without covariates, are fitted using Mplus. In both types, the residual variances of outcomes, the factor variances and covariances, and the covariate effects on the growth factors (if covariates are included) are set to be invariant across classes. For both types, the number of classes specified ranges from one to five. When the number of classes specified is greater than or equal to 2, the number of sets of random starting values, the number of iteration for each of random starting value sets, and the number of solutions with the highest likelihood values selected and iterated in the final stage are set to 400, 40 and 20 respectively for all fitting models.

For model evaluation, we use all six fit statistics used for our NSCAW example. To save the computational time, the default method in Mplus is used to calculate the BLRT. In addition, as recommended by Muthen and Muthen (2006), we use 40 draws for the model with k classes in the initial stage followed by 10 optimizations in the final stage.

In GMM, for AIC, BIC and ABIC, a lower value represents an improvement of fit after controlling the increase of model complexity. For each replication and each type of fitting models (GMM with or without covariates), the lowest value of AIC, BIC or ABIC among the series of fitting models with one to five classes is used for that fit index to determine the number of classes. As to LMR, ALMR and BLRT (LRTs), the strategy is different. The p-values of these statistics are used to make a choice between k − 1 vs. k-class models. In practice, these values could shift from being significant to nonsignificant and then back to significant again (e.g., Nylund et al., 2007). As a result, we follow Nylund et al. (2007) and check the p-value of each of fit statistics sequentially from the model with two classes to the one with five classes. The process will stop and the model with k − 1 classes will be used for that fit index to determine the number of classes once its p-value for the model with k classes become nonsignificant (p > .05) for the first time during checking. For example, by this procedure, the two-class solution will be selected by LMR when the p-values of LMR are significant for both two and four-class models but not significant for the three-class model.

In our model evaluation, we treat local or improper solutions and failure of convergence equally. For example, if a fitting model with two classes fails to converge or converges to a local or improper solution in a replication, then an extremely large positive value will be given to AIC, BIC, ABIC and the p-values of LRTs for the two class model to prevent the number two from being enumerated by the model as the correct number of classes in that replication. For LRTs, when their p-values are prompted to be untrustworthy by Mplus, the extremely large positive number will also be given to the p-values of the corresponding fit indices for that model during model evaluation due to the same purpose.

Results

For our first study, we present the class enumeration results of different fit indices under the low and high level of effect of x_i in Table 1 and Table 2 respectively. The class enumeration results for our second study are presented in Table 3–Table 5 for δ = 1, $\sqrt{2}$ and 2 respectively. The class enumeration results for our third study are presented in Table 6 and Table 7 for δ = 1 and 2 respectively. In all these tables, for each experimental condition and each type of fitting models, the percentage of times at which a fit index indicated a specific number as the correct number of classes was given under that number of classes. Note that in all our studies, the correct number of class is two and has been bolded in all seven tables.

Table 1.

Percentage of times enumerated by the fit indices for different number of classes under the low level of effect of x_i in Study I.

# of Classes		Model w/o Covariates					Model with Covariates
		1	2	3	4	5	1	2	3	4	5
N=200	AIC	0	66.5	19.5	9.5	4.5	0	85.5	11.0	3.5	0
	BIC	17.0	83.0	0	0	0	0	100.0	0	0	0
	ABIC	0	76.5	15.0	7.0	1.5	0	89.0	8.5	2.5	0
	LMR	8.5	79.0	12.0	0.5	0	13.0	84.5	2.5	0	0
	ALMR	11.5	76.5	12.0	0	0	13.0	85.0	2.0	0	0
	BLRT	1.0	93.5	5.0	0.5	0	2.0	95.0	3.0	0	0
N=400	AIC	0	65.5	24.0	4.0	6.5	0	73.5	20.0	5.5	1.0
	BIC	0	100.0	0	0	0	0	100.0	0	0	0
	ABIC	0	89.5	9.5	1.0	0	0	95.5	4.0	0.5	0
	LMR	0	82.0	16.5	1.0	0.5	0.5	96.5	2.5	0.5	0
	ALMR	0	83.5	15.0	1.0	0.5	0.5	97.5	2.0	0	0
	BLRT	0	91.5	8.5	0	0	0	97.5	2.5	0	0
N=1000	AIC	0	65.5	19.5	8.0	7.0	0	80.5	16.0	2.0	1.5
	BIC	0	100.0	0	0	0	0	100.0	0	0	0
	ABIC	0	99.5	0.5	0	0	0	99.5	0.5	0	0
	LMR	0	80.5	17.5	2.0	0	0	96.5	3.5	0	0
	ALMR	0	81.5	17.0	1.5	0	0	97.5	2.5	0	0
	BLRT	0	90.0	10.0	0	0	0	96.5	3.5	0	0
N=2000	AIC	0	58.5	18.5	14.0	9.0	0	69.0	21.0	7.5	2.5
	BIC	0	100.0	0	0	0	0	100.0	0	0	0
	ABIC	0	99.0	1.0	0	0	0	99.0	1.0	0	0
	LMR	0	73.0	24.5	2.5	0	0	93.5	5.5	1.0	0
	ALMR	0	74.0	23.5	2.5	0	0	95.0	4.5	0.5	0
	BLRT	4.5	84.0	10.5	1.0	0	1.0	93.5	5.0	0.5	0

Table 2.

Percentage of times enumerated by the fit indices for different number of classes under the high level of effect of x_i in Study I.

# of Classes		Model w/o Covariates					Model with Covariates
		1	2	3	4	5	1	2	3	4	5
N=200	AIC	0	4.0	2.0	60.0	34.0	0	75.5	16.0	6.5	2.0
	BIC	3.0	91.5	1.0	4.5	0	0	100.0	0	0	0
	ABIC	0	7.0	2.5	62.5	28.0	0	78.5	14.5	6.0	1.0
	LMR	5.5	87.5	6.0	1.0	0	13.0	86.0	1.0	0	0
	ALMR	7.0	86.5	5.5	1.0	0	14.0	85.0	1.0	0	0
	BLRT	0	82.5	7.5	9.5	0.5	1.5	92.0	6.5	0	0
N=400	AIC	0	0.5	0	55.0	44.5	0	73.0	18.5	7.0	1.5
	BIC	0	59.5	0	40.5	0	0	100.0	0	0	0
	ABIC	0	1.0	0	87.5	11.5	0	92.5	7.0	0	0.5
	LMR	0	82.5	3.5	7.5	6.5	0	98.0	2.0	0	0
	ALMR	0	84.0	4.0	6.5	5.5	0	98.0	2.0	0	0
	BLRT	0	76.0	6.5	16.0	1.5	0	93.0	7.0	0	0
N=1000	AIC	0	0	0	56.5	43.5	0	68.0	21.5	9.0	1.5
	BIC	0	0	0	100.0	0	0	100.0	0	0	0
	ABIC	0	0	0	97.0	3.0	0	98.0	2.0	0	0
	LMR	0	77.5	0	14.0	8.5	0	98.0	2.0	0	0
	ALMR	0	82.0	0	12.0	6.0	0	98.0	2.0	0	0
	BLRT	0	44.5	19.5	33.0	3.0	1.5	89.5	8.5	0.5	0
N=2000	AIC	0	0	0	52.0	48.0	0	71.0	19.5	8.5	1.0
	BIC	0	0	0	100.0	0	0	100.0	0	0	0
	ABIC	0	0	0	98.5	1.5	0	100.0	0	0	0
	LMR	0	49.5	0	38.0	12.5	0	92.0	8.0	0	0
	ALMR	0	53.0	0	35.0	12.0	0	93.0	7.0	0	0
	BLRT	0	23.0	23.5	51.5	2.0	4.0	87.5	8.0	0.5	0

Table 3.

Percentage of times enumerated by the fit indices for different number of classes when δ = 1 in Study II

# of Classes		Model w/o Covariates					Model with Covariates
		1	2	3	4	5	1	2	3	4	5
N=200	AIC	0	56.5	21.5	14.5	7.5	0	53.5	22.5	17.0	7.0
	BIC	16.0	83.5	0.5	0	0	0	100.0	0	0	0
	ABIC	0	61.0	22.0	11.0	6.0	0	62.0	19.5	14.0	4.5
	LMR	8.5	77.0	14.0	0	0.5	22.0	72.5	4.5	1.0	0
	ALMR	8.5	78.5	12.5	0	0.5	23.5	72.0	3.5	1.0	0
	BLRT	2.0	85.0	13.0	0	0	4.0	89.5	6.5	0	0
N=400	AIC	0	55.0	29.5	11.0	4.5	0	49.0	23.0	17.5	10.5
	BIC	0	99.5	0.5	0	0	0	100.0	0	0	0
	ABIC	0	86.0	11.5	2.5	0	0	90.5	8.5	1.0	0
	LMR	0	75.0	22.0	3.0	0	1.0	85.0	13.5	0.5	0
	ALMR	0	77.5	20.0	2.5	0	1.0	86.5	12.0	0.5	0
	BLRT	0	87.5	11.5	1.0	0	1.5	94.0	4.5	0	0
N=1000	AIC	0	44.0	31.5	16.5	8.0	0	57.5	18.0	15.0	9.5
	BIC	0	100.0	0	0	0	0	100.0	0	0	0
	ABIC	0	91.0	8.5	0.5	0	0	97.0	2.5	0.5	0
	LMR	0	66.0	28.0	5.0	1.0	0	88.0	11.0	1.0	0
	ALMR	0	68.0	26.0	5.0	1.0	0	89.5	9.5	1.0	0
	BLRT	0	66.5	28.5	5.0	0	3.0	91.0	5.0	1.0	0
N=2000	AIC	0	37.5	34.5	20.5	7.5	0	60.0	19.0	10.5	10.5
	BIC	0	97.5	2.5	0	0	0	100.0	0	0	0
	ABIC	0	90.0	9.0	1.0	0	0	100.0	0	0	0
	LMR	0	67.5	27.5	5.0	0	0	85.0	14.5	0.5	0
	ALMR	0	68.5	27.0	4.5	0	0	85.5	14.0	0.5	0
	BLRT	8.0	60.0	29.5	2.5	0	4.0	91.0	5.0	0	0

Table 5.

Percentage of times enumerated by the fit indices for different number of classes when δ = 2 in Study II

# of Classes		Model w/o Covariates					Model with Covariates
		1	2	3	4	5	1	2	3	4	5
N=200	AIC	0.5	59.5	22.5	15.0	2.5	0	31.0	34.0	21.0	14.0
	BIC	13.5	86.5	0	0	0	0	97.0	3.0	0	0
	ABIC	0.5	66.0	21.0	10.5	2.0	0	36.5	34.5	18.0	11.0
	LMR	11.0	76.0	12.0	1.0	0	15.0	74.5	10.5	0	0
	ALMR	13.0	75.5	11.0	0.5	0	16.0	73.5	10.5	0	0
	BLRT	2.0	87.0	10.5	0.5	0	0	74.5	25.5	0	0
N=400	AIC	0	57.5	28.5	10.5	3.5	0	14.5	39.0	30.5	16.0
	BIC	0	99.5	0.5	0	0	0	86.5	13.5	0	0
	ABIC	0	85.0	14.0	1.0	0	0	33.0	48.5	15.0	3.5
	LMR	0	73.5	19.0	7.0	0.5	7.0	59.0	32.0	2.0	0
	ALMR	0	75.5	18.0	6.0	0.5	7.5	59.5	31.0	2.0	0
	BLRT	0	86.5	13.5	0	0	2.5	45.0	47.5	5.0	0
N=1000	AIC	0	40.5	36.0	15.5	8.0	0	0.5	24.5	46.5	28.5
	BIC	0	100.0	0	0	0	0	42.5	57.0	0.5	0
	ABIC	0	90.0	9.5	0.5	0	0	6.0	71.5	22.0	0.5
	LMR	0	69.5	27.5	3.0	0	1.0	16.5	63.0	18.5	1.0
	ALMR	0	70.0	27.5	2.5	0	1.0	16.5	63.5	18.0	1.0
	BLRT	0	66.0	30.0	4.0	0	5.0	9.0	60.5	25.5	0
N=2000	AIC	0	28.0	28.5	26.0	17.5	0	0	11.5	42.0	46.5
	BIC	0	99.0	1.0	0	0	0	1.0	91.0	8.0	0
	ABIC	0	84.0	16.0	0	0	0	0	57.5	42.5	0
	LMR	0	61.5	29.5	7.5	1.5	0	0	57.5	38.0	4.5
	ALMR	0	63.0	28.5	7.0	1.5	0	0	60.0	35.5	4.5
	BLRT	1.5	60.5	29.0	8.5	0.5	4.0	12.5	35.0	46.5	2.0

Table 6.

Percentage of times enumerated by the fit indices for different number of classes when δ = 1 in Study III

# of Classes		Model w/o Covariates					Model with Covariates
		1	2	3	4	5	1	2	3	4	5
N=200	AIC	3.5	22.0	38.0	25.5	11.0	0.5	59.0	20.5	13.0	7.0
	BIC	11.5	77.0	11.0	0.5	0	0.5	99.5	0	0	0
	ABIC	3.5	24.0	40.5	23.0	9.0	0.5	65.0	18.0	11.0	5.5
	LMR	13.0	63.0	20.0	3.5	0.5	16.5	79.5	4.0	0	0
	ALMR	13.5	64.0	20.5	2.0	0	17.0	79.0	4.0	0	0
	BLRT	3.5	45.5	48.5	2.5	0	4.5	91.0	4.5	0	0
N=400	AIC	0	7.5	32.5	39.5	20.5	0	58.5	23.5	10.5	7.5
	BIC	0	66.0	33.0	1.0	0	0	100.0	0	0	0
	ABIC	0	17.5	50.5	28.5	3.5	0	88.5	8.0	3.5	0
	LMR	1.0	60.5	29.0	9.0	0.5	1.5	87.0	11.0	0	0.5
	ALMR	1.0	62.5	27.5	8.5	0.5	2.0	87.5	10.0	0	0.5
	BLRT	0	23.5	59.0	17.5	0	0	94.5	5.0	0.5	0
N=1000	AIC	0	1.0	10.5	42.0	46.5	0	61.5	19.0	13.0	6.5
	BIC	0	17.5	74.5	8.0	0	0	100.0	0	0	0
	ABIC	0	2.5	38.5	52.5	6.5	0	97.5	2.5	0	0
	LMR	0	57.0	29.0	11.0	3.0	0	88.0	10.0	2.0	0
	ALMR	0	59.0	28.5	10.0	2.5	0	88.0	10.0	2.0	0
	BLRT	0	10.5	35.5	49.5	4.5	2.0	90.5	7.5	0	0
N=2000	AIC	0	0	1.0	33.0	66.0	0	53.0	24.5	14.0	8.5
	BIC	0	0.5	52.5	46.0	1.0	0	100.0	0	0	0
	ABIC	0	0	9.5	70.5	20.0	0	100.0	0	0	0
	LMR	0	41.5	30.5	19.5	8.5	0	83.0	17.0	0	0
	ALMR	0	42.0	31.0	19.5	7.5	0	83.5	16.5	0	0
	BLRT	3.0	3.5	18.0	59.0	16.5	4.0	89.5	6.5	0	0

Table 7.

Percentage of times enumerated by the fit indices for different number of classes when δ = 2 in Study III

# of Classes		Model w/o Covariates					Model with Covariates
		1	2	3	4	5	1	2	3	4	5
N=200	AIC	0.5	26.0	40.5	25.5	7.5	1.5	29.5	36.5	25.5	7.0
	BIC	15.5	77.5	7.0	0	0	1.5	90.5	8.0	0	0
	ABIC	0.5	30.5	43.5	21.0	4.5	1.5	31.5	40.0	21.0	6.0
	LMR	15.5	66.0	16.5	2.0	0	17.0	65.0	17.5	0.5	0
	ALMR	16.0	66.0	16.5	1.5	0	18.5	65.5	16.0	0	0
	BLRT	1.0	57.5	39.0	2.5	0	3.0	64.0	32.5	0.5	0
N=400	AIC	0.5	9.5	33.5	30.0	26.5	0	9.5	52.5	20.5	17.5
	BIC	0.5	70.5	29.0	0	0	0	74.0	26.0	0	0
	ABIC	0.5	24.0	51.5	19.0	5.0	0	14.0	71.5	11.5	3.0
	LMR	2.5	57.0	35.5	4.5	0.5	5.5	43.5	47.5	2.0	1.5
	ALMR	3.0	57.5	35.5	3.5	0.5	6.0	44.0	46.5	2.0	1.5
	BLRT	0.5	28.0	61.0	9.5	1.0	1.0	21.0	75.5	2.5	0
N=1000	AIC	0	0	9.5	52.0	38.5	0	0.5	47.5	31.5	20.5
	BIC	0	31.5	62.5	6.0	0	0	3.5	96.5	0	0
	ABIC	0	3.5	46.5	47.0	3.0	0	0.5	93.5	6.0	0
	LMR	0	47.0	33.0	18.0	2.0	0.5	10.0	77.5	12.0	0
	ALMR	0	48.0	33.0	17.0	2.0	1.0	10.0	78.0	11.0	0
	BLRT	0	6.0	41.0	50.5	2.5	2.0	15.5	73.5	9.0	0
N=2000	AIC	0	1.5	2.0	38.5	58.0	0	0	44.5	38.0	17.5
	BIC	0	5.0	59.0	35.0	1.0	0	0	99.5	0.5	0
	ABIC	0	2.0	15.5	74.0	8.5	0	0	90.0	10.0	0
	LMR	0	36.5	36.0	20.0	7.5	0	4.0	76.5	18.5	1.0
	ALMR	0	37.5	36.0	19.5	7.0	0	4.0	77.5	17.5	1.0
	BLRT	0	4.5	19.0	62.5	14.0	1.0	14.0	63.0	21.5	0.5

Performance of parameter recovery

Before the discussion of class enumeration, it is worthwhile to examine the parameter recovery performance of our correctly-specified models at first. In our first study, the two-class GMM fitting model with covariates is exactly specified in Table 1 and Table 2 despite the levels of effect of x_i. In our second and third studies, the two-class GMM fitting model with covariates would be correctly specified when δ = 1 as in Table 3 and Table 6. In both studies, the two-class GMM fitting model with covariates would be misspecified when $\delta =\sqrt{2}$ or 2. The GMM fitting model without covariates would be always misspecified in all studies.

In our studies, the correctly-specified GMM models perform well in parameter recovery. Across the three studies and the four sample size levels, the probabilities of the 95% confidence interval of parameters containing their population values over 200 replications range from .90 to .99 with three exceptions in our third study when N = 200. The three coverage exceptions are 88.5% for membership prediction by covariate (b₁ in equation 2), 86.5% for the covariate effect on intercept factors ( ${\gamma }_{10}^1$ and ${\gamma }_{10}^2$, which are assumed to be class-invariant), and 81% for the covariate effect on slope factor ( ${\gamma }_{11}^1$ and ${\gamma }_{11}^2$, which are assumed to be class-invariant too). Despite inclusion or exclusion of these three coverage probabilities, the median of the coverage probabilities across all parameters, all studies and all sample sizes would be 95%.

In addition to the coverage probabilities, the mean relative bias (MRB) of parameter estimates (see p. 352 of Bauer & Curran, 2003 for the definition) are also within the acceptable level (<10%, see Kaplan, 1989) in all cases and support a good performance of parameter recovery. The largest MRB (5.48%) happens to the estimates for σ₀₀ in our third study when N = 200 while all others are less than 5%. When N ≥ 400, the MRBs are less than 2.5% for all cases. For more information of parameter recovery, please refer to http://www.caldar.org/documents/li-hser-estimates.pdf, where the mean of estimates, the average standard errors, the MRBs, and the coverage probabilities over replications are listed for each parameter of the models across sample sizes.

Performance of GMM model without covariates

Unlike previous studies (e.g., Nylund, et al., 2007), we study the class enumeration performance of the GMM fitting model without covariates when it is not the correctly specified model. Across all seven tables, the degree of misspecification of the GMM fitting model without covariates varies. When the within-class nonnormality is minor as in Table 1, and Table 3-Table 5, BIC is the most robust index to the misspecification and detects the correct number of classes over 97.5 percent of times when N ≥ 400. In these tables, AIC performs poorly in general and ABIC detects the correct number of classes at majority of times but performs somewhat worse than BIC across the sample size levels (except N = 1000 and 2000 in Table 1). Among LRTs, BLRT performs well when N = 200. However, LRTs especially LMR and ALMR (LMRs) are relatively more sensitive and tend to accept more extra classes when N ≥ 400. This tendency of LMRs is similar to their performance in Nylund et al. (2007) when the GMM fitting model without covariates is correctly specified.

When the within-classes nonnormality become more severe as in Table 2, Table 6 and Table 7, BIC is more robust to the misspecification and more tends to reject extra classes than all other indices when N = 200. However, interestingly, in this condition, BIC, ABIC and BLRT begin to be less robust to misspecification than LMRs and ALMR when N ≥ 400 and tend to almost exclusively accept more classes than necessary when N ≥ 1000. In reverse, at this time, LMR and ALMR become more conservative and still detect the correct number of classes at a substantial percent of times. For example, in Table 2, when N = 2000 and BIC and ABIC almost exclusively support the four-class solution, LMRs still support the two-class solution around 50 percent of chance. Across the three tables, it seems that for the model without covariates LMRs are more sensitive to some minor misspecification (as in Table 1, Table 3-Table 5) but are less sensitive to some severe misspecification (as in Table 2, Table 6 and Table 7) than other indices.

Performance of GMM model with covariates

As discussed before, the fitting model with covariates included is the exactly specified model for the data in Table 1 and Table 2. In Table 3 and Table 6, when δ = 1 in the second class, the fitting model with covariates included are correctly specified but not the most parsimonious one. In the four tables, as expected, the fitting model with correct covariate inclusion clearly outperforms the one without covariates in recovering the correct number of classes across fit indices and Ns, no matter if the misspecification for the fitting model without covariates is minor (e.g., in Table 1 and Table 3) or severe (e.g., in Table 2 and Table 6) and no matter how BIC, ABIC and LMRs by the fitting model without covariates agree or disagree with each other. For example, in Table 2 and Table 6, due to severe misspecification of the model without covariates included, BIC, ABIC and LMRs tend to favor the model with more than two classes and may also give inconsistent conclusions on class enumeration when N ≥ 1000. However, with the correct inclusion of covariates, all fit indices (except AIC) tend to reject extra classes and consistently support two-class model.

Of course, variation among different fit indices also exists in this case. Across the four tables and Ns, BIC performs better than all other fit indices and almost exclusively favors the two-class model. In reverse, ABIC would exclusively favor the two-class model only when N ≥ 1000. In Table 1 and Table 2, when the model with covariates is the exactly specified model, LMRs perform very well when N ≥ 400. However, in Table 3 and Table 6, LMRs become less robust and accept more extra classes across Ns. Notice that the fitting model with covariates included is the correctly specified model but not the most parsimonious one in the two tables. The worse performance of LMRs in the two tables may be due to this reason. As to BLRT, it performs well in Table 1 and Table 3 when N ≥ 400 but tends to accept more extra classes in Table 2 and Table 6 when N increases.

Like its exclusion, covariate inclusion can bring misspecification to the fitting model too as in Table 4, Table 5 and Table 7. Consequently, as expected, the class enumeration by GMM model with covariates overall deviates from the correct number of class in the three tables (except BIC in Table 4). Furthermore, it is interesting to compare the class enumeration performance before and after the inclusion of covariates in this situation. In Table 4, where the misspecification before inclusion of covariates is relatively minor, BIC is robust to the misspecification after covariate inclusion, performs as well as before inclusion of covariates and almost exclusively favors the two-class model across Ns. Unlike BIC, after covariate inclusion, all other fit indices depart in various degrees from the two-class model across Ns. Compared to exclusion of covariates, inclusion of covariates in Table 4 is substantially detrimental to AIC and ABIC across Ns. For LRTs, this detrimental effect of covariate inclusion does not become obvious until N = 2000.

Table 4.

Percentage of times enumerated by the fit indices for different number of classes when $\delta =\sqrt{2}$ in Study II

# of Classes		Model w/o Covariates					Model with Covariates
		1	2	3	4	5	1	2	3	4	5
N=200	AIC	0	58.0	24.0	13.5	4.5	0	47.5	24.5	18.5	9.5
	BIC	16.5	83.5	0	0	0	0	99.5	0.5	0	0
	ABIC	0	65.0	22.5	9.0	3.5	0	54.0	23.5	16.5	6.0
	LMR	9.0	78.0	13.0	0	0	19.5	76.0	4.0	0.5	0
	ALMR	11.0	78.0	11.0	0	0	22.5	73.0	4.5	0	0
	BLRT	2.0	86.5	10.0	1.5	0	2.5	88.0	9.0	0.5	0
N=400	AIC	0	59.5	25.0	10.0	5.5	0	47.5	23.0	19.0	10.5
	BIC	0	100.0	0	0	0	0	100.0	0	0	0
	ABIC	0	85.5	12.0	5	0	0	80.5	14.0	4.0	1.5
	LMR	0	79.0	18.0	2.0	1.0	1.0	90.5	8.5	0	0
	ALMR	0	80.0	17.0	2.0	1.0	1.0	90.5	8.5	0	0
	BLRT	0	87.5	11.5	1.0	0	0.5	89.5	9.5	0.5	0
N=1000	AIC	0	42.5	31.0	17.0	9.5	0	16.5	23.5	37.0	23.0
	BIC	0	98.0	2.0	0	0	0	96.5	3.5	0	0
	ABIC	0	90.0	9.0	1.0	0	0	67.0	28.5	4.0	0.5
	LMR	0	69.0	25.0	5.5	0.5	0	71.5	24.5	3.5	0.5
	ALMR	0	69.5	24.5	5.5	0.5	0	72.5	24.0	3.5	0
	BLRT	0	64.0	31.0	5.0	0	4.0	57.0	34.0	5.0	0
N=2000	AIC	0	29.0	36.0	25.5	9.5	0	2.5	13.0	52.5	32.0
	BIC	0	98.0	2.0	0	0	0	93.0	6.5	0.5	0
	ABIC	0	87.0	13.0	0	0	0	44.5	44.0	11.5	0
	LMR	0	64.0	27.5	7.5	1.0	0	46.5	43.0	10.0	0.5
	ALMR	0	65.0	27.5	7.0	0.5	0	47.0	42.5	10.5	0
	BLRT	15.5	50.5	32.0	2.0	0	3.5	23.0	48.0	25.5	0

In Table 5, where the misspecification before inclusion of covariates is still minor and δ increases from $\sqrt{2}$ to 2, the robustness of BIC on longer holds. More severe misspecification after covariate inclusion is detrimental to all fit indices and they tends to depart from the two-class model when N ≥ 400. Of course, even in this situation, BIC is still relatively more conservative than all other fit indices in accepting more extra classes. In addition, in Table 5, despite the misspecification after covariate inclusion, LMRs are relatively more conservative than AIC, ABIC and BLRT in class enumeration across Ns.

Finally, in Table 7, where the misspecification before inclusion of covariates becomes relatively severe, all fit indices depart from the two-class model across Ns after covariate inclusion. In this table, when N ≤ 400, BIC performs better or equally well after inclusion of covariates and all other fit indices perform similarly before and after the inclusion. When N ≥ 1000, BIC and ABIC more tend to favor the three-class model and reject both the two and four-class models after inclusion of covariates than before the inclusion. This tendency also happens to LRTs even though they accept the two and especially four-class models more frequently than BIC and ABIC after covariate inclusion.

Discussion and Recommendation

In this article, our simulation studies investigated the class enumeration performance of two types of widely-used GMM fitting models under Scheme 2. Clearly, our data generation model by Scheme 2 structurally deviates from both fitting models. However, despite this deviation, through our study design, we generated our experimental conditions for the two types of fitting models by Scheme 2. That is, GMM fitting model without covariates is minorly misspecified as in Tables 1, Table 3–Table 5 while is severely misspecified as in Tables 2, Table 6 and Table 7. At the same time, GMM fitting model with covariates is correctly specified as in Tables 1–Table 3, and Table 6 while is misspecified as in Tables 4, Table 5, and Table 7. Even though our type of factorial design here with two levels of severity of misspecification in GMM fitting model without covariates and two levels of correctness of specification in GMM fitting model with covariates may not be very strict, it could allow us systematically investigate the strength of the two widely-used GMM fitting models in different experimental conditions and provides guidelines or recommendations for GMM class enumeration. In fact, this kind of study is clearly relevant in practice since either of the two widely-used GMM fitting models could be misspecified in real world and researchers generally don’t know whether they would be correctly specified or not in their applications. Of course, our design only includes a portion of potential factorial combinations for the two fitting models, the true data generation model in practice could be other than Scheme 2, and future studies are needed.

In this article, we studied the class enumeration performance of GMM fitting model without covariates when it is not the correctly specified model. Our findings for the model without covariates should be relevant to some existing literature. Nylund et al. (2007) suggested using BIC to narrow the number of potential models down, and then using BLRT and substantive interpretation to help guide the final choice. Although BLRT performs well in Nylund et al. (2007) when the fitting model without covariates is the correctly specified model, it performs poor in general in our studies when it is a misspecified one. Across seven tables, except when N = 200 and the misspecification is minor (e.g., in Table 1), BLRT performs worse than either BIC or LMRs.

As a result, unlike Nylund et al. (2007), we instead suggest to pay attention to the sample size and the discrepancy of class enumeration by BIC and LMRs. Our results show that BIC can outperform LMRs and reject extra classes when the mis-specification of GMM fitting model without covariates is minor (e.g., Table 1, Table 3–Table 5) or when the misspecification is severe and N = 200 (e.g., Table 2, Table 6 and Table 7). On the other hand, LMRs are more conservative than BIC and reject extra classes when the misspecification of the fitting model is severe and N is large (e.g., Table 2, Table 6 and Table 7). Thus, in a relatively large sample (e.g., N ≥ 1000 as in our NSCAW example), as long as LMRs enumerates a different (either less or more) number of classes from BIC, it is very likely that some misspecification (either minor or severe) exists in our fitting model for class enumeration. At this time, the less number of classes enumerated by BIC or LMRs should receive some attention. On the other hand, in a relatively small sample (e.g., N < 400), BIC would be more reliable than LMRs in general.

In this article, the class enumeration strategy for LMR, ALMR and BLRT we used is same as the one used by Nylund et al. (2007) for their Table 8. Our results by this strategy suggest that LMRs should be considered sequentially and independently and not be limited to the number of potential models narrowed down by BIC when the sample size is large and BIC enumerates a very different number of classes from LMR and ALMR. For example, in Table 2, when N ≥ 1000 and BIC exclusively detects four classes, the potential number of classes for LMR and ALMR would be limited to three, four or five and the correct number of classes, two, will be missed if they are not considered sequentially and independently.

Of course, we have to mention that even though a smaller number of classes enumerated by BIC or LMRs or an agreement of class enumeration between BIC and LMRs could be informative or helpful, they do not guarantee a correct solution for class enumeration. For example, in Table 6 and Table 7, when N = 2000, the percent of times LMRs favors the two-class model drops below 50. In other words, it is very likely that BIC and LMRs favor the same model with more than two classes or different models with more than two classes.

In practice, GMM fitting model without covariates is very likely to be misspecified. Even though inspecting BIC and LMRs as discussed above could be helpful in some cases, it can not be the complete story. Our studies demonstrate that there is another potential way to overcome the problem of GMM fitting model without covariates. That is inclusion of covariates for GMM class enumeration. We demonstrated in Appendix that GMM fitting models with or without covariates theoretically are not always consistent to the same population model as many applications assumed. This could cause class enumeration problems for the fitting model without covariates and lead to a better performance by the fitting model with covariates. We demonstrated this point by the results in Tables 1–3 and Table 6. In these tables, despite the severity of misspecification and the agreement or disagreement between BIC and LMRs by the model without covariates, the fitting model with correct covariate inclusion clearly outperforms the one without covariates in recovering the correct number of classes across fit indices and Ns. In practice, this consistent rejection of extra classes across fit indices could be a strong indication of beneficial effects of covariate inclusion. Our results also demonstrated the variation among different fit indices for class enumeration in this condition. Based on our results, we recommend BIC for class enumeration when inclusion of covariates leads fit indices to favor a less number of classes but does not provide a consistent conclusion across fit indices.

Of course, the inclusion of covariates could also bring some extra problems which would not happen to the model without covariates included. For example, in Table 4, Table 5 and Table 7, inclusion of covariates brings misspecification in membership prediction to the fitting model. In the three tables, the fitting model with or without covariates both are misspecified but are subject to different sources of misspecification. In Table 4 and Table 5, where the misspecification before inclusion of covariates is relatively minor, all fit indices after inclusion of covariates tend to accept more extra classes as N or the misspecification in membership prediction increases. In Table 7, where the misspecification before inclusion of covariates is relatively severe, all fit indices (except BIC when N ≤ 400) more tend to favor the three-class model and reject the two and four-class models after inclusion of covariates than before the inclusion. By our results, we suggest that comparison of class enumeration before and after inclusion of covariates in practice is a comparison of relative sensitivity of class enumeration to the two types of misspecification.

NSCAW example revisited

Given the findings above, we go back to our NSCAW example. In our example, without including covariates into the fitting model, BIC and ABIC both support a four-class solution while the p-values of LMR and ALMR are significant for the two and three-class models but are not significant for the four-class model. Given that our sample size is large (N = 1481), based on our findings above, it is likely that the more conservativeness of LMR and ALMR than BIC and ABIC in class enumeration in that example may results from some serious misspecification of the fitting model as in some of our tables (e.g., Table 2).

After inclusion of covariates as we described before, BIC shifts away from the four-class solution and favors the three-class model. Notice that in Table 4, Table 5 and Table 7, BIC is the index that least tends to accept extra classes after inclusion of covariates and should be recommended in this case. Like before inclusion of covariates, the p-values of LMRs are nonsignificant for the four-class model. Even though AIC and ABIC still support the four-class solution and are inconsistent with BIC and LMRs, the difference of AIC and ABIC between the three and four-class models reduce after inclusion of covariates.

All of these changes are in the direction of favoring the three-class model. However, as we discussed before, for this example, it would be safer for us to say that the beneficial effect of covariate inclusion makes the misspecification after inclusion become less serious to class enumeration than the one before inclusion. In our example, not all of fit indices support a smaller number of classes and give an consistent conclusion. Even though it is beneficial, the effect of covariate inclusion may not be complete or strong enough in our example as in our simulation studies. In fact, even when all fit indices become consistent after inclusion of covariates, the model with the selected number of classes may still be misspecified. For our example, whether a three-class model or a four-class model should be used as the basis of determining the number of classes still needs substantive knowledge to help us judge the interpretability of the trajectories and parameter estimates and to make final selection. In fact, if researchers cannot interpret a solution (either with or without covariates included; either with less or with more number of classes) favored by the statistical procedures above, the model becomes impractical and useless. For our example, combining our substantive judgment and our analysis above, we select the three-class solution for our data.

Limitations and implications

Throughout this article, we assumed the within-class normality for GMM fitting model without covariates. As we demonstrated, this assumption could cause a poor class enumeration performance for the fitting model when the within-class distribution is severely nonnormal in practice. Of course, in practice, some within-class distributions other than normal distribution can be specified by researchers for the GMM fitting model without covariates. For example, a fitting model with more general within-class distribution assumptions may take into account of the within-class nonnormality of the data in our Study III and perform well in class enumeration. However, we need notice that even that type of fitting model may not be able to include all possible within-class nonnormalities in practice. In this sense, even though the models with more general within-class distribution assumptions are needed, it may not be the complete solution for the fitting model without covariates.

In this article, we evaluate the covariate effect on GMM class enumeration and recommend some fit indices (e.g., BIC, LMRs) for practical use. Theoretically, the performance of these fit statistics requires that the sample size is large enough. Whether the beneficial effect of covariate inclusion or the robust class enumeration performance of some fit indices (e.g., BIC) still exist in some smaller sample size (e.g., N = 50 or N = 100) is an interesting question and need more studies in future.

Our studies demonstrate that misspecification caused by inclusion of covariates, like other sources of misspecification mentioned before, can lead GMM class enumeration away from the truth in practice. In general, including covariates into the fitting model would add more information to the fitting model than excluding them would. Our results may suggest that this is not absolutely true and including more incorrect information could be harmful too. Of course, as we mentioned before, the detrimental or beneficial effects of covariate inclusion still depend on the relative strength of the model with or without covariates to the class enumeration in application and are subject to substantive judgment finally. However, it leave a question that what is the mechanism that the misspecification causes this impairment. Future study on this question is needed.

In this article, we assume that the residual variances of outcomes, the factors variance and covariances, and the covariate effects on the growth factors (if covariates are included) are class-invariant in the GMM models for our example and simulation studies. We use this type of model due to its popularity. Tofighi and Enders (2007) studied inclusion of covariates for GMM class enumeration when models are much less restrictive. Given the very different level of class specificity of their population and fitting models, how well our conclusions on inclusion of covariates for GMM class enumeration in this article would be applicable to that type of models still need more future studies.

In this article, we only considered time-invariant covariates and ignored time-varying covariates. Like time-invariant covariates, inclusion of time-varying covariates may also influence the class enumeration. In our first study, we multiplied ( ${\gamma }_{10}^k,{\gamma }_{11}^k$) by 2 and 5. However, we didn’t do that when the covariate is continuous. Clearly, with different values of ( ${\gamma }_{10}^k,{\gamma }_{11}^k$), the nonnormality of x_i would have different impact on the nonnormality of y_i within classes. In addition, in this article, we fixed the mixing proportions to be equal across classes. Our conclusion may change when the mixing proportion of some classes are very small. Further research along this direction is needed.

Appendix

1. Let x_i = (x_i1, x_i2), where x_i1 includes all categorical covariates and x_i2 includes all continuous variables. For Scheme 1, we can reformulate

   $$\begin{array}{l}{f}_1({\mathbf{y}}_i,{\mathbf{x}}_i,{\mathbf{c}}_i)=f({\mathbf{y}}_i\mid {\mathbf{x}}_i,{\mathbf{c}}_i)·\prod _k{\pi }_{ik}^{c_{ik}}·f_1({\mathbf{x}}_i)\\ =f({\mathbf{y}}_i\mid {\mathbf{x}}_i,{\mathbf{c}}_i)·\frac{{\prod }_k{\pi }_{ik}^{c_{ik}}·f_1({\mathbf{x}}_i)}{{\sum }_{{\mathbf{x}}_{i1}}\{\int {\prod }_k{\pi }_{ik}^{c_{ik}}·f_1({\mathbf{x}}_i)d{\mathbf{x}}_{i2}\}}·\sum _{{\mathbf{x}}_{i1}}\left\{\int \prod _k{\pi }_{ik}^{c_{ik}}·f_1({\mathbf{x}}_i)d{\mathbf{x}}_{i2}\right\}\\ =f({\mathbf{y}}_i\mid {\mathbf{x}}_i,{\mathbf{c}}_i)·\frac{{\prod }_k{[{\pi }_{ik}{f}_1({\mathbf{x}}_i)]}^{c_{ik}}}{{\prod }_k{\left[{\sum }_{{\mathbf{x}}_{i1}}\{\int {\pi }_{ik}{f}_1({\mathbf{x}}_i)d{\mathbf{x}}_{i2}\}\right]}^{c_{ik}}}·\prod _k{\left[\sum _{{\mathbf{x}}_{i1}}\left\{\int {\pi }_{ik}{f}_1(x_i)d{\mathbf{x}}_{i2}\right\}\right]}^{c_{ik}}\\ =f({\mathbf{y}}_i\mid {\mathbf{x}}_i,{\mathbf{c}}_i)·\prod _k{\left(\frac{{\pi }_{ik}{f}_1({\mathbf{x}}_i)}{{\sum }_{{\mathbf{x}}_{i1}}\{\int {\pi }_{ik}{f}_1({\mathbf{x}}_i)d{\mathbf{x}}_{i2}\}}\right)}^{c_{ik}}·\prod _k{\left[\sum _{{\mathbf{x}}_{i1}}\left\{\int {\pi }_{ik}{f}_1({\mathbf{x}}_i)d{\mathbf{x}}_{i2}\right\}\right]}^{c_{ik}}\\ =f({\mathbf{y}}_i\mid {\mathbf{x}}_i,{\mathbf{c}}_i)·\stackrel{.}{f}({\mathbf{x}}_i\mid {\mathbf{c}}_i)·\prod _k{\stackrel{.}{\pi }}_k^{c_{ik}}\end{array}$$ (A-1)
   where ḟ(x_i|c_i) = Π_k[π_ikf₁(x_i)/Σ_xi1{∫ π_ikf₁(x_i)dx_i2}]^c_ik and π̇_k = Σ_xi1 {∫ π_ikf₁(x_i)dx_i2}. Notice that π̇_k is not conditional on x_i and for c_ik, there is only one element equal to 1 while all others are zeros. So for any ith observation,

   $$\stackrel{.}{f}({\mathbf{x}}_i\mid {\mathbf{c}}_i)=\frac{{\pi }_{im}{f}_1({\mathbf{x}}_i)}{{\sum }_{{\mathbf{x}}_{i1}}\{\int {\pi }_{im}{f}_1({\mathbf{x}}_i)d{\mathbf{x}}_{i2}\}}=\frac{{\pi }_{im}}{{\stackrel{.}{\pi }}_m}·f_1({\mathbf{x}}_i)$$ (A-2)

   where m is the value by which c_im = 1.

   From (A-1), we can see if we first sample x_i from some distribution and then sample c_i by (2) and y_i from f(y_i|x_i, c_i) in (3), we can obtain a same sample if we first sample c_i from a multinomial distribution with P(c_ik = 1) = π̇_k and then sample x_i from ḟ(x_i|c_i) conditional on c_i and y_i from f(y_i|x_i, c_i) conditional on c_i and x_i.

   In general, ḟ(x_i|c_i) by (A-2) will barely be normal for each class except in some special cases, for example, when f₁(x_i) is normal and π_im is a constant and does not vary with x_i. This within-class nonnormality of ḟ(x_i|c_i) could cause problem for the GMM fitting model without covariates as in Figure 1. Suppose that there is no direct path from x_i to y_i (time-varying covariates) in population. Then combining (A-1) with (3) and integrating (A-1) over x_i, the marginal distribution f₁(y_i, c_i), which the GMM fitting without covariates as in Figure 1 is based on, in the data by Scheme 1 can be obtained as

   $$\begin{array}{l}{f}_1({\mathbf{y}}_i,{\mathbf{c}}_i)=f_1({\mathbf{y}}_i\mid {\mathbf{c}}_i)f_1({\mathbf{c}}_i)\\ =\int f({\mathbf{y}}_i\mid {\eta }_i,{\mathbf{c}}_i)f_1({\eta }_i\mid {\mathbf{c}}_i)f_1({\mathbf{c}}_i)d{\eta }_i\\ =\int f({\mathbf{y}}_i\mid {\eta }_i,{\mathbf{c}}_i)\left\{\sum _{{\mathbf{x}}_{i1}}\left\{\int f({\eta }_i\mid {\mathbf{x}}_i,{\mathbf{c}}_i)\stackrel{.}{f}({\mathbf{x}}_i\mid {\mathbf{c}}_i)d{\mathbf{x}}_{i2}\right\}·\prod _k{\stackrel{.}{\pi }}_k^{c_{ik}}\right\}d{\eta }_i.\end{array}$$ (A-3)

   By (4) and (5), f(y_i|η_i, c_i) and f(η_i|x_i, c_i) are conditional normal. However, as mentioned before, ḟ(x_i|c_i) in general would be barely normal under Scheme 1. Then the within-class distribution f₁(η_i|c_i) and consequently f₁(y_i|c_i) by (A-3) in general will not be normal in the data by Scheme 1 except when ḟ(x_i|c_i) is normally distributed. On the other hand, in GMM application, the fitting model without covariates as in Figure 1 assumes the within-class distributions f₁(η_i|c_i) and consequently f₁(y_i|c_i) to be conditional normal in estimation. Thus, under Scheme 1, or in other words, if the data is really like what the GMM fitting model with covariates as in Figure 2 assumes, the GMM fitting model without covariates as in Figure 1 may be misspecified in the within-class distribution in general.

   Of course, there is one exception. When x_i only predict the class membership under Scheme 1 and has no influence on the growth factors in (5) as assumed in some studies (e.g., Lubke & Muthen, 2007), the distribution f(η_i|x_i, c_i) is independent of x_i in the data. Consequently, f₁(η_i|c_i) and f₁(y_i|c_i) in (A-3) are normal within classes no matter how x_i is distributed and the fitting models as in Figure 1 and Figure 2 are both correct for the data.

2. Comparing (A-1) and (6), it is clear that the population model implied by Scheme 1 can be transformed to the form of Scheme 2 in (6) with f₂(x_i|c_i) = ḟ(x_i|c_i) and π_k = π̇_k. On the other hand, for Scheme 2, we can reformulate

   $$\begin{array}{l}{f}_2({\mathbf{y}}_i,{\mathbf{x}}_i,{\mathbf{c}}_i)=f({\mathbf{y}}_i\mid {\mathbf{x}}_i,{\mathbf{c}}_i)f_2({\mathbf{x}}_i\mid {\mathbf{c}}_i)f_2({\mathbf{c}}_i)\\ =f({\mathbf{y}}_i\mid {\mathbf{x}}_i,{\mathbf{c}}_i)·\frac{f_2({\mathbf{x}}_i\mid {\mathbf{c}}_i)f_2({\mathbf{c}}_i)}{{\sum }_{\mathbf{c}}{f}_2({\mathbf{x}}_i\mid {\mathbf{c}}_i)f_2({\mathbf{c}}_i)}·\sum _{\mathbf{c}}{f}_2({\mathbf{x}}_i\mid {\mathbf{c}}_i)f_2({\mathbf{c}}_i)\\ =f({\mathbf{y}}_i\mid {\mathbf{x}}_i,{\mathbf{c}}_i)·\prod _k{\left(\frac{{\pi }_k{f}_2({\mathbf{x}}_i\mid k)}{{\sum }_k{\pi }_k{f}_2({\mathbf{x}}_i\mid k)}\right)}^{c_{ik}}·\sum _k{\pi }_k{f}_2({\mathbf{x}}_i\mid k)\\ =f({\mathbf{y}}_i\mid {\mathbf{x}}_i,{\mathbf{c}}_i)·\prod _k{({\stackrel{.}{\pi }}_{ik})}^{c_{ik}}·\stackrel{.}{f}({\mathbf{x}}_i)\end{array}$$ (A-4)

   where f₂(x_i|k) is the conditional probability of x_i given kth class under Scheme 2, π̇_ik denotes π_kf₂(x_i|k)/Σ_k π_kf₂(x_i|k), and ḟ(x_i) denotes Σ_k π_kf₂(x_i|k). Then comparing (A-4) and (1), it is clear that the population model implied by Scheme 2 can be transformed to the form of Scheme 1 in (1) with π_ik = π̇_ik and f₁(x_i) = ḟ(x_i).

   Moreover, in terms of Scheme 1 in (1), the implied unconditional distribution of x_i in the GMM data generated by Scheme 2 would be a mixture in general. However, π̇_ik, the implied probability of c_i given x_i in this type of the data, in general may not be completely expressed for all possible x_i by the model for class membership prediction in (2). When this is the case, the joint distribution of x_i and c_i by f₂(x_i|c_i)f₂(c_i) in the generated data can not be reparameterized into a f₁(c_i|x_i)f₁(x_i) with an implementable model of membership prediction in form of (2), and consequently the fitting model with covariates as in Figure 2 may be misspecified because its assumed model for membership prediction in (2) can not be satisfied in the generated data by Scheme 2.