Nature of Motor Control: Perspectives and Issues

Abstract

Four perspectives on motor control provide the framework for developing a comprehensive theory of motor control in biological systems. The four perspectives, of decreasing orthodoxy, are distinguished by their sources of inspiration: neuroanatomy, robotics, self-organization, and ecological realities. Twelve major issues that commonly constrain (either explicitly or implicitly) the understanding of the control and coordination of movement are identified and evaluated within the framework of the four perspectives. The issues are as follows: (1) Is control strictly neural? (2) Is there a divide between planning and execution? (3) Does control entail a frequently involved knowledgeable executive? (4) Do analytical internal models mediate control? (5) Is anticipation necessarily model dependent? (6) Are movements preassembled? (7) Are the participating components context independent? (8) Is force transmission strictly myotendinous? (9) Is afference a matter of local linear signaling? (10) Is neural noise an impediment? (11) Do standard variables (of mechanics and physiology) suffice? (12) Is the organization of control hierarchical?

1.0 INTRODUCTION: FOUR PERSPECTIVES

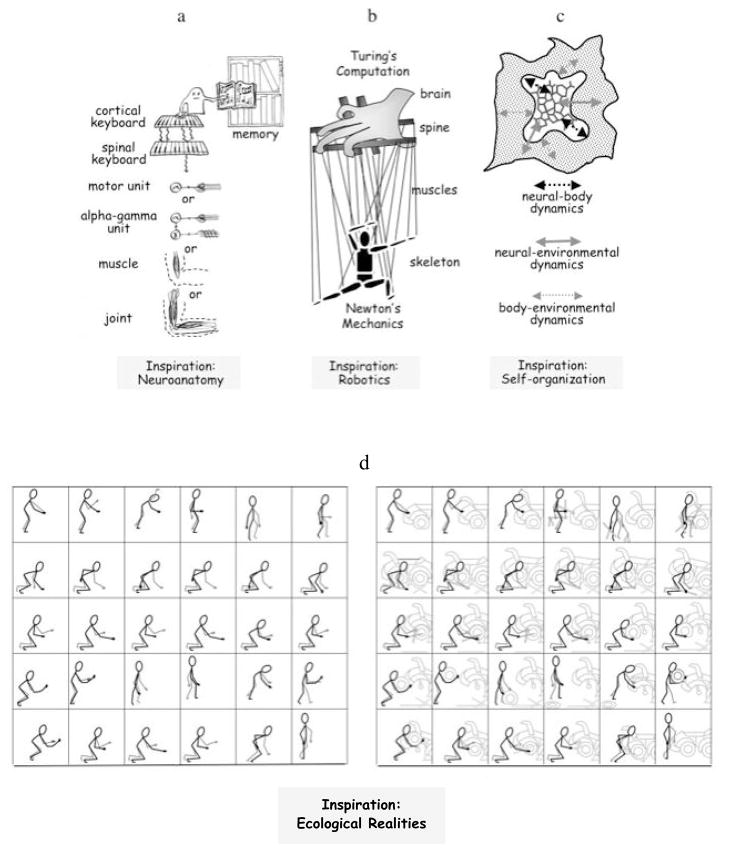
Figure 1 provides four images expressing four different perspectives of motor control. Figure 1a makes explicit a human-analogue as executive system, a library of motor scores, cortical and spinal keyboards on which to play out a retrieved score, and various possibilities for the physiological units by which the score might be realized. With minor adjustments (e.g., deleting the alpha-gamma link), Figure 1a portrays motor control as it might have been envisaged in the 19^th century.

Figure 1.

Four perspectives on motor control. See text for details. (Figure 1a is adapted with permission from Turvey, M.T., Fitch, H.L., & Tuller, B. (1982). The Bernstein perspective, I: The problems of degrees of freedom and context-conditioned variability. In J.A.S. Kelso (Ed.), Understanding human motor control. Hillsdale, New Jersey: Lawrence Erlbaum Associates. Figure 1b is adapted with APA permission from Turvey, M. T. (1990). Coordination. American Psychologist, 45, 938–953).

Figure 1b presents a more contemporary image—a coupling of Turing computation with Newtonian mechanics (see Loeb, 2001; Turvey, 1990). Within the marionette image, the hand is the brain, the control platform is the spine, the strings are the muscles, and the marionette is the skeleton. Explicit involvement of Turing computation decreases top-down; explicit involvement of Newtonian mechanics decreases bottom-up.

Figure 1c provides an image of three mutually influencing dynamical systems—namely, the nervous system, the body, and the environment—on which devolve responsibility for movement’s control (Chiel & Beer, 1997). In this image the embodiment of the nervous system is made explicit (neural-body dynamics), as are the embeddings of nervous system (neural-environment dynamics) and body (body-environment dynamics) in the task environment.

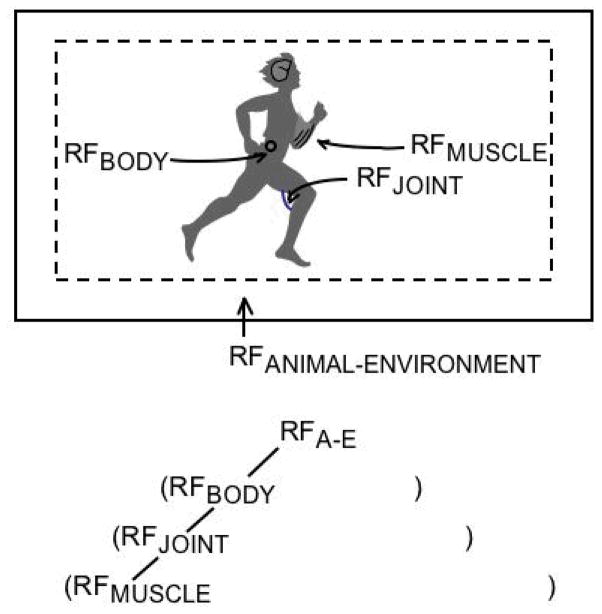
The rightward panel of Figure 1d is closely cognate with Figure 1c. It gives expression to the ecological perspective on control as a process distributed over the animal-environment system and not something residing in the animal or in the environment (Gibson, 1979; Fitch & Turvey, 1978). Let the term “event” refer to the larger system in which an agent or actor (any given animal) and its environment are co-participants. Then, in comparison to the leftward panel of Figure 1d (which shows movements without environmental referents), the rightward panel (which shows the event of changing a tire) expresses two principles. Stated abstractly, the first is that an agent controls the functional description of an event rather than the functional description of his or her own body; the second is that the appropriate observational perspective for a theorist of control is a perspective that encompasses events rather than agents only (Fowler & Turvey, 1978). Figure 1d brings to the forefront the ecological hypothesis that behavior is intrinsically functional rather than intrinsically mechanical and only extrinsically or secondarily functional (Reed, 1985). It highlights that actions are specific to function not to mechanism (see Section 2.6). Movements and postures are controlled and coordinated to realize functionally specific acts based on the perception of affordances (that is, possibilities for action, Gibson, 1979; Reed, 1985; Turvey, 1992).

In Figure 1a we begin with relatively concrete identifications of what is controlled and where control originates in terms of anatomical parts. In the progression from Figure 1a to Figure 1d, the ‘what’ and ‘where’ of control become increasingly less concrete and less expressible in anatomical terms.

Below, key issues in the theory of motor control are identified by way of posing, in question form, assumptions implicit in the perspective characterized in Figure 1a or its most immediate successor, the perspective characterized in Figure 1b. The issues are divided into two sets roughly according to the schema of Figure 1a. The first set covers the level of the executive and cortical keyboard and the second set covers the levels below.

2.0 EXECUTIVE LEVEL

2.1 Strictly neural?

Figure 1a represents a long-standing convention to think of movement control as essentially a neural matter. Control is primarily—perhaps solely—an enterprise of the central nervous system, with different aspects divided among different cortical, subcortical and spinal subsystems. A student of movement would be strongly inclined to this belief after reading a standard neuroscience text (e.g., Kandel, Schwartz, & Jessell, 2000; Purves, Augustine, Fitzpatrick, Katz, LaMantia, McNamara, & Williams, 2001).

Figure 1b suggests, albeit modestly, why control cannot be understood in a strict neural sense. The body must make an integral contribution. The kinematic chains constituted by bones and their mutual attachments through muscle, tendons, ligaments, and fascia abide by principles that are part and parcel of movement’s control. As Raibert and Hodgins (1993, p. 305) remarked: “Many researchers in neural motor control think of the nervous system as a source of commands that are issued to the body as “direct orders”. We believe that the mechanical system has a mind of its own, governed by the physical structure and the laws of physics. Rather than issuing commands, the nervous system can only make “suggestions” which are reconciled with the physics of the system and the task.”

Figures 1c and 1d go further in the not-strictly-neural direction. They highlight that comprehension of control and the development of a thoroughgoing theory requires inclusion of the body and the environment that embed the neural processes. In the image of Figure 1c, control resides within the triad of couplings: between nervous system and body, body and environment, and nervous system and environment. In Chiel and Beer’s (1997, p. 555) words: “The role of the nervous system is not so much to direct or to program behavior as to shape it and evoke the appropriate patterns of dynamics from the entire coupled system. As a consequence, one cannot assign credit for adaptive behavior to any one piece of this coupled system.”

And in Fowler and Turvey’s (1978, p. 13) words, with respect to the image supplied by Figure 1d: “Clearly, actors cannot achieve an aim to perform an act by generating all of the forces necessary to get the job done. Rather, they must contribute to the totality of extant forces just those muscular forces that will bend the character of an event in the right direction.” Or, synonymously, and in a more contemporary language, there is Warren’s (2006, p. 368) casting of the control problem: “From the agent’s perspective, the problem becomes one of tweaking the dynamics of the system in which it is embedded so as to enact stabilities for the intended behavior.”

2.2 A divide between planning and execution?

For the theorist, Figure 1a identifies issues of representation, selection, and translation. To elaborate, it identifies issues of (a) defining the representational form of motor scores or programs for movement (i.e., the language of the books in the library), (b) how programs are selected to satisfy a plan (i.e., how the human-analogue makes its choices befitting its goals), and (c) how time-independent programs are translated into time-dependent instructions (i.e., how the motor score becomes a sequence of cortical keys).

Responses to issues (a) – (c) have been shaped traditionally by the presumptions that the primary motor cortex contains a topographic map of the body with each point specifying muscular tension either for a single muscle or for a small collection of muscles (e.g., Fulton, 1938; but see Section 2.6). Accordingly it could be assumed that the patterning of activity in the primary motor cortex—the tune played on the cortical keyboard—is, for all intents and purposes, the planned movement. In the foregoing context of ideas, the plan and program selection constitute planning and the translation of selected programs into the cortical keyboard pattern constitutes execution.

In the context of Figure 1b, the scientific issues have been phrased in terms of the consequences for execution of the plan’s level of abstraction (e.g., Hollerbach, 1990a, 1990b). Consider an arm movement parallel to the sagittal plane. Planning could be in respect to the trajectory of the hand (the end point), or the angular motions of the shoulder, elbow and wrist, or the tensions in the muscles of the shoulder, elbow and wrist. The progression from planning trajectories to planning muscle states is one of decreasing abstraction/increasing detail. A plan expressed as an end-point trajectory places the most computational demands upon execution and the least computational demands on planning. To be implemented, a desired trajectory has to be mapped to joint motions, which in turn have to be mapped to joint torques. The implementation entails ill-defined processes of inverse kinematics and inverse kinetics addressed, theoretically, through conceptions from control theory and biomechanics (Hollerbach, 1990a, 1990b; Todorov, 2004). In contrast, the conceptions forming the theoretical framework for planning are closer to those of the information processing approach to cognitive psychology and the tradition of logicism (see Kirsch, 1991) in artificial intelligence.

The planning-execution conceptual divide is difficult to maintain in the perspective of Figures 1c and 1d. The singular dynamical, self-organizing language required to capture the time-evolution of neural, body, and environmental states incorporates preparing and doing (Beer, 1995). A central and challenging issue for the theory implied by Figure 3 is how to craft the dynamics of planning so as to express its continuous development and seamless transformation into the dynamics of execution (Erlhagen & Schöner, 2002).

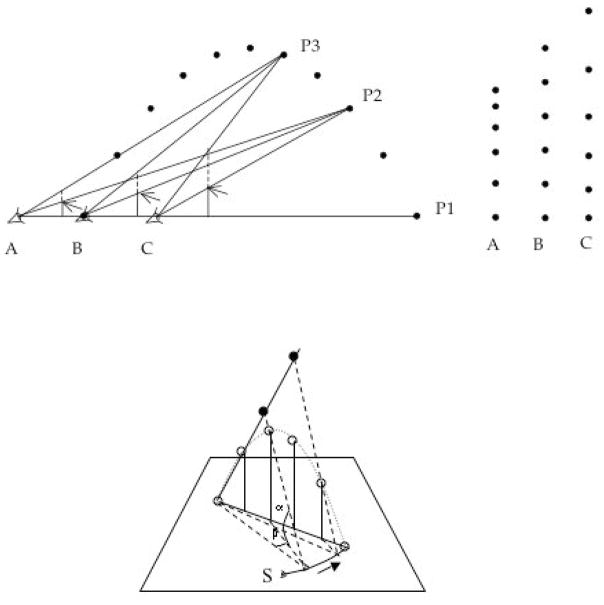
Figure 3.

(Top). So move as to keep the ball’s optical vertical acceleration constant. A ball is depicted traveling a parabolic path from right to left with its position P shown at equal temporal intervals. The ball is viewable from positions A, B, and C, where B is the location of the ball’s landing point. Lines connect three positions of the ball in flight (P1, P2, and P3) to the viewing positions (A, B, and C). Vertical lines, starting on the line to P1 and ending on the line to P3, identify image planes. Arrows indicate where the line to P2 intersects the image planes with a dashed segment above and a solid segment below each arrow. Relative to viewing positions A, B and C, dashed < solid for A, dashed = solid for B, and dashed > solid for C, meaning that, in the image plane, the ball is decelerating, of constant velocity, and accelerating, respectively. (The rightward array of points expresses the successive ball locations viewed from A, B, and C.) In summary, the ball will arrive at the eye if its optical image (the image on the plane) has zero acceleration. (From Michaels, C. F., & Zaal, F. T. J. M. (2002). Catching fly balls. In K. Davids, G. J. P. Savelsbergh, S. J. Bennett, and J. van der Kamp (Eds.), Interceptive actions in sport: Information and movement (pp. 172–183). London: Routledge. Reprinted with permission from Taylor and Francis Publishers.) (Bottom). So move as to linearize the ball’s optical trajectory. Applies to the case when the ball’s flight path is not in the catcher’s sagittal plane. In the figure, the catcher starts at S. The ball’s optical trajectory will be linear when the catcher runs on a path (identified by the arrow) such that tangents of the vertical angle α and the horizontal angle β change proportionally. (From McBeath, M. K., Shaffer, D. M., & Kaiser, M. K. (1995). How baseball outfielders determine where to run to catch fly balls. Science, 268, 569–573. Reprinted with permission from AAAS.)

2.3 Intelligent executive intervening often?

Historically, the lexicon of motor control theorists includes the word executive or synonyms thereof. In Figure 1a the executive is plainly portrayed and in Figure 1b it is implicit in the hand on the control platform. A distinct executive function often seems inevitable and a need to give it concrete form has led to suggestions that it is housed in prefrontal cortex.

The pertinent characteristic of an executive system is intelligence—the intelligence needed to make the right kinds of inferences and decisions, those that produce adaptive behavior. In consequence, building a theory of the executive is very much a matter of (a) identifying the forms and degrees of explicit knowledge with which to endow the executive, and (b) the degree to which the knowledgeable executive is responsible for specifying movement’s details. The conception of a very intelligent executive intervening frequently has been a common (although, perhaps, implicit) feature of accounts of motor control fashioned in the frameworks of Figures 1a and 1b.

In blunt terms, to endow the executive with knowledge is to take out one or more intelligence-loans (Kugler & Turvey, 1987). The loans are taken to ensure the requisite competence of the inference engine(s) and, thereby, the means of accounting for the adaptability of movement, but it is not readily apparent as to how the loans will be repaid. To repay such loans in full requires another kind of theory, one that explains the knowledge-like capability in a non-epistemic fashion.

The devolution of executive responsibilities and, perforce, a consequent reduction in executive knowledge, has been of some concern to movement theorists (e.g., Greene, 1969, 1972; Kugler, Kelso, & Turvey, 1980). Fundamentally, the concern is reducing executive degrees of freedom. In broader perspective, the concern is developing a theory of a minimally intelligent executive intervening minimally (Kugler et al., 1980). The desideratum is an understanding of movement control grounded, counter intuitively, in a theory of executive ignorance.

In Figure 1 the challenge for the executive in framing its commands is the complicated nature of the state spaces of the to-be-commanded subsystems and the mappings among them (Greene, 1972). The state spaces may not be known explicitly. (And even if they were known explicitly, it is questionable whether the executive would find such knowledge useful. The subsystem dynamics vary from moment to moment and from subsystem to subsystem.) In Greene’s words (1972): “The question therefore arises: which properties of mappings between these spaces remain invariant from instance to instance, and of these, which can be known by an executive subsystem that lacks explicit knowledge of the spaces?” For Greene a promising approach to the preceding question is to consider executive control as conducted in terms of equivalence classes—sets of functions that are logically reflexive, symmetric, and transitive. Prime examples are the family of all tunings and the family of all transition functions (with individual family members depicted in Figure 2). In principle, an executive could always activate standard members of the two families, with independent processes selecting those members of the families (those variants of the equivalent classes) most suited to the prevailing contexts. In this scheme, the executive would bring about felicitous outcomes in ignorance of the details (the tunings and transition functions) responsible for them.

Figure 2.

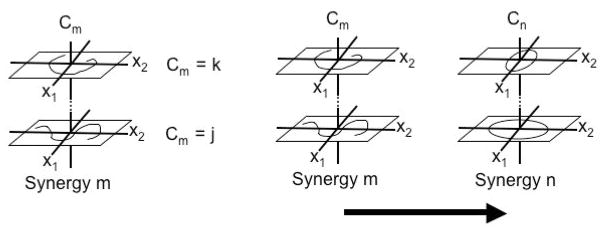
The family of tunings of a synergy (left) and the family of transitions between synergies (right) can be characterized, for simplicity, by means of control phase-space diagrams. (The xs are the phase variables, for example, position, velocity, and the Cs are the control parameters.) For a given synergy m the values assumable by its control parameter for the attainment of a specific function, invariant over circumstances, form an equivalence class. In the left panel, the change of C_m from j to k changes the space-time behavior but preserves the function. In the right panel, to achieve the desired behavior, two or more synergies must be serially coordinated. At issue is the type and timing of the transition. Here, the transition functions ensuring the circumstance-invariant requisite coordination of synergies assume values that form an equivalence class.

2.4 Analytic model(s)?

Internal models in various guises are hypothesized as the bases for controlling movement in each of its many aspects (e.g., Wolpert & Gharamani, 2000). They are proposed as the means for anticipating the upcoming consequences of movement (forward models) and for prescribing the dynamics (inverse models). These models are analytical. They are typically expressed in the perspective of Figure 1b. In that perspective they require, at a minimum, explicit and accurate knowledge of the (Newtonian) equations governing skeletal motion, the involved quantities (e.g., the body’s moments of mass distribution, its elastic, viscous, and creep coefficients, its reflex lags, etc.), and the quantitative relations that hold among the involved quantities.

Analytical models of control entail substantial intelligence-loans (of the kind identified in Section 2.3). Additionally, in adopting them one has to presume that the versatility of the movement system and its modes of control are addressable by known variables and governing equations. The presumption might hold for some highly restrained movements but its generality can be questioned.

The leading inspiration for analytical models is robotics in which the operational components, the actuators, do not have, as biological actuators do, a nested structure consisting of multiple redundant components and multiple (neural, metabolic, and mechanical) processes at indefinitely many length and time scales. For an analytic model of a biological movement system there is not a single inverse transformation but many. Explicit specification of joint torques would have to be succeeded by explicit solutions to the inverse problems of specifying individual muscles, motor units, EMG signals, motoneurons, synaptic potentials, and so on. The single inverse transformation from joint kinematics to joint kinetics in the robotics case would be, at best, a first step in the biological case.

Model-dependent (analytical, explicit) control can be proposed, in theory, within all four perspectives covered by Figures 1, but it need not be (see Ostry & Feldman, 2002). Formal analyses suggest that, to date, none of the data interpretations favoring a model-dependent control strategy have ruled out a model-independent control strategy (Mehta & Schaal, 2002). Within the context of Figures 1c and 1d, perhaps more so than in the other two contexts, there is pressure for comprehending a form of control that does not require explicit knowledge. An accurate analytical model of the interactive dynamics of nervous system, body, and environment, with their nonlinearities, nonstationarities, and nonobvious variables, is impractical, if not impossible. The requisite form of control, it would seem, has to be model-independent (non-analytical, implicit).

2.4.1 Possibility of unknowable (action) variables

Some rough intuitions about the implementation of model-independent control might be gleaned from efforts to bring about real time experimental control of dynamical (e.g., excitable, chaotic) systems that are only understood qualitatively (e.g., Christini, In, Spano, et al., 1997). There are procedures for estimating the necessary dynamics (expressed in “fake variables”, see below) from past observations of the system. But in the general case of assembling control on the fly, there is no time for a learning phase, no time for pre-control analysis. Dynamics must be determined in real time.

The latter notions present an interesting option for the elegant theory of executive ignorance. Assuming a form of Takens’ theorem (Takens, 1981) that extends reliably to real systems (Stark, 2000), one can raise the possibility of an executive that need have no knowledge of the movement system’s defining equations or the variables that they involve simply because no such static inventory of equations and variables exists. Roughly, Takens’ theorem is that an unknown system is (potentially) knowable through any measured variable, given that in any system of nonlinear interactions, every variable is affected by every other variable to greater or lesser degree. For a certain class of systems, pre-control analysis derives suitable time-lagged copies of the single measured variable (the copies are the “fake variables”) that yield the dimensions of the system’s dynamics and in terms of which a viable approximation to the system’s equations of motion can then be expressed (Abarbanel, 1996). Although the measured variable might be familiar, for example, joint angle θ, its time lagged form, θ + nT, is a nonlinear mixture that includes the measured variable itself and all of the system’s other dynamical quantities. A valuable theoretical exercise is addressing the question: To what extent can the idea of such variables, assembled on the spot, specific to the task, generalize to the problems of motor control?

2.5 Model-dependent (weak) anticipation?

Formalisms for forward/anticipatory models are derivative of Rosen’s (1985) definition paraphrased for present purposes as: the movement system contains a predictive model of itself and its inputs, which allows it to change at instant t in accord with the model’s predictions about t + T. If s is the elbow-joint system and i is its proprioceptive input, and s* and i* are their anticipated or predicted future states, then the forward modeling evolves the elbow-joint state according to (approximately):

$$s(t+T)=f[s(t),s^{\ast }(t+T),i(t),i^{\ast }(t+T)]$$

Model-based prediction via internal simulations has been referred to as weak anticipation (Dubois, 2000). It is contrasted with strong anticipation in which the anticipation is a property of the system itself rather than of a (symbol-manipulating) model of the system. In the strong case, anticipation is embedded in the system’s ordinary or physical mode of functioning.

Examples of efforts to identify strong anticipation are to be found in perception-action research. Proposed solutions to the problem of catching fly balls (the outfielder problem) are good instances. Figure 3 presents the two most prominent proposals. For both proposals, getting to the right place at the right time is not solved by prediction. It is solved in the ordinary manner of functioning: by continuously adapting action to information (Michaels & Zaal, 2002). For both proposals, the very ‘catchableness’ of a ball is made apparent only in the course of locomotion.

The strategy depicted in Figure 3 (top) accommodates the difficult case of catching a fly ball in the catcher’s sagittal plane. The significant optical variable is hypothesized to be the vertical optical acceleration of the ball’s projection onto the image plane. The catcher so behaves as to nullify this optical quantity. To elaborate, Figure 3 (top) suggests that catching a fly ball is a matter of adjusting one’s locomotion to keep the vertical velocity of the ball’s projection on the image plane constant (and not a matter of predicting and then running to where the ball will fall). The strategy depicted in Figure 3 (bottom) is restricted to cases in which the ball’s flight deviates from the sagittal plane, that is, when the ball has horizontal velocity with respect to the catcher. By this strategy, the ball will be caught if the would-be catcher’s locomotion continuously linearizes the ball’s optical trajectory.

Describing the prior two examples as instances of strong anticipation is to mislabel them, however, given that there is no explicit anticipation or prediction. They are more properly understood as examples of strong prospective control (Stepp & Turvey, 2007; Turvey, 1992). A similar lack of explicit anticipation or prediction seems to characterize the task of balancing a stick at the fingertip. Although it has been suggested that this task may well satisfy acceptable criteria for a forward model (Mehta & Schaal, 2002), closer inspection indicates that the skill is largely prediction-free and understandable in the more general language of learned adjustments (tuning) of Lévy flight dynamics (Cabrerea & Milton, 2004).

2.6 Preassembled movements?

The question posed raises issues continuous with those encountered in Section 2.2. The executive system of Figure 1a has at its disposal a library of recipes for movement. Given an intention, preassembled movements in the form of a program of instructions can be retrieved, singly or in combination, for implementation by the musculoskeletal system. In the context of Figure 1a and the traditional division of motor cortex into pre- and primary motor areas (Fulton, 1938) the posed question often translates into whether movements as such are coded in the primary area.

A straightforward answer has not been forthcoming given the lack of any clear understanding of the primary area’s organization and function (Graziano, Taylor, Moore, & Cooke, 2002). First, the textbook somatotopy (Gleitman, 1999; Kandell et al., 2000) does not hold beyond the major body divisions. In its detail, the body’s cortical map is fragmented with multiple intertwined regions rather than being ordered and segmented in accord with the body’s layout of muscles and joints (Sanes & Schieber, 2001). Second, every standard kinetic and kinematic descriptor of a moving limb examined so far seems to have a correlate in cortical neuronal activity (Scott, 2003). No single type of control information is preeminent. Correlates of spatial goals, end effector motion, joint motion, emg activity and spindle activity are all present, bringing into question the idea (often advanced in the perspective of Figure 1b) of a logically ordered time-evolution of sensorimotor transformations (from, say, spatial goals to emg activity). Third, putative hierarchical orderings of the many motor areas identified to date are questionable on grounds that most, if not all, of the areas project to the spinal cord in an intricate, intermingled fashion.

In response to an apparent absence of principle in the functional organization of motor cortex, research conducted with relatively high (25–150 μA) and prolonged (500 ms) cortical stimulation has suggested that the map is not of the body but of spatial locations near the body to which movements are directed (Graziano et al., 2002). The thesis, more broadly, is that the motor cortex’s control of movement “is organized in terms of behaviorally useful actions aimed toward a goal posture (Graziano et al., 2002, p. 354).” Examples are given in Figure 4. On elaboration, one can suppose that control is very much in the spirit of Figure 1: there is a stored set of postures from which any situation-specific limb posture, and the details of its realization, can be generated by a process of linear combination (e.g., Rosenbaum, Loukopoulos, Meulenbroek, Vaughan & Engelbrecht, 1995; see Rosenbaum et al. in the present volume).

Figure 4.

Examples of preassembled transformations of arm posture. For stimulation of specific cortical sites in a monkey’s right precentral gyrus, the left hand moves toward a specific final position indifferent to starting position. (From Graziano, M., Taylor, C., Moore, T., & Cooke, D. (2002). The cortical control of movement revisited. Neuron, 36, 349–362. Reprinted with permission from Elsevier Publishing.)

In an overlap of the perspectives conveyed by Figures 1b and 1c is found a different kind of answer to the question of whether there are preassembled movements. The focus (for the present, at least) is posture and locomotion and the central idea is that of a movement template: the simplest model exhibiting a given targeted behavior. Figure 5 identifies the philosophy and strategy (Full & Koditscheck. 1999; Holmes, Full, Koditscheck, Guckenheimer, 2006; see Full and Koditscheck in the present volume). For the target behavior of hopping, the template is a spring-loaded inverted pendulum (SLIP). The minimal morphology and physiology needed to embed or anchor the template is sought by asking what is essential to the implementation of the SLIP dynamics. On the flip side, the template itself is an instance of the derivation of simplicity from complexity, a condensing of degrees of freedom to derive a low dimensional form. The issue of executive intelligence (Section 2.3) and the Bernstein Problem are, in the terms of Figure 5, interpreted as realizing control policies for collapsing dimensions from anchor to template. In respect to the current topic of preassembled movements, the template-anchor approach promises a base set of templates. Ontologically, they are not of like kind with the motor scores retrieved by the executive of Figure 1a. They are abstractions of the stabilities or attractors of tasks, defined at the task level and generalized across species and, perforce, nervous systems.

Figure 5.

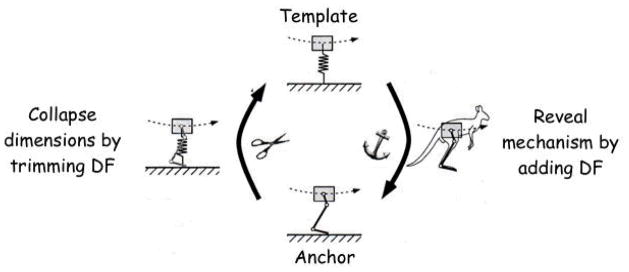
Relationship between template and anchor (see text for details). (After Full, R., & Koditscheck, D. (1999). Templates and anchors: Neuromechanical hypotheses of legged locomotion on land. Journal of Experimental Biology, 202, 3325–3332, with permission of the Company of Biologists.)

The latter assessment can be taken a step further. As underscored in the introduction, the strong implication of Figure 1d is that all movements are specific to the problems of realizing goals in ever-changing animal-environment settings. The foregoing implication is, perhaps, Bernstein’s (1967, 1996) most basic thesis expressed by him in the terms of a physiology of activity in opposition to the more conventional (in his day) physiology of reaction. The focus implicit in the tire-changing act depicted in the right panel of Figure 1d is abstract, task-specific organizations of movements, not a repertoire of preassembled movements (as might be inferred from the left panel of Figure 1d). It can be hypothesized that the many parallel and successive activities on view in the right panel of Figure 1d possess intrinsic dynamics (Kelso, 1995) with attractor states modified by optic, acoustic and haptic variables via their influences on the control parameters of those dynamics. In broad terms, the challenge posed is understanding how “Stable, adaptive behavior emerges from the dynamics of interaction between a structured environment and an agent with simple control laws, under physical and informational constraints (Warren, 2006, p. 358).”

3.0 LEVELS BELOW THE EXECUTIVE

3.1 Context-independent parts?

In Figure 1a, the executive produces movement by instructions sent to pieces of anatomy. This emphasis on anatomy in defining what is controlled follows from the Cartesian machine metaphor that has been the mainstay of theorizing on movement for over 350 years. Descartes advocated that all physical things (inanimate and animate) be explained in the way machines or automata are explained, through the properties of their independent parts. Accordingly, behind the control perspective of Figure 1a is the assumption that the function F executed by any given anatomical component C is implicated or entailed strictly by the component’s material composition and form. Subsystem functions are presumed to be context independent.

Functional units are the alternative to anatomical units. They are contingent—that is, context dependent—with no existence outside the larger system. They will not necessarily conform to scientifically convenient demarcations such as sensory/motor and brain/body/environment (Turvey, 2004). Whereas in the conception of anatomical components, C entails F, in the conception of functional units, F entails C. The latter direction of entailment is integral to the theory behind the perspective captured by Figure 1d and implicit in that portrayed by Figure 1c.

3.1.1 Muscular roles

Consider muscles, the frequently proposed prime targets of executive instructions. In vivo work-loops reveal that, depending upon the action context, muscles function as brakes, struts, tuners, meters, and springs as well as functioning as motors (Dickinson et al., 2000). They also function in less obvious ways for which we do not (as yet) have names (e.g., redistributing moments or finely tuning the ground reaction force, Kargo & Rome, 2002). One implication is that muscles in a single anatomical group (e.g., the muscles that swing a leg) do not necessarily share a common mechanical function (Ahn & Full, 2002). The implication, stated more generally, is that redundancy in a multiple muscle group may represent diversity in muscle function. If such is the case, then the coordination that characterizes a synergy or coordinative structure (see Kelso in the present volume) is not so much the coordination of individuals (muscles) as it is the coordination of roles (context-dependent functions).

3.1.2 Context-dependence of reflexes

The most hard-worked conception of an anatomical unit is the reflex: a stereotyped, context-independent response to a specific (or proper or adequate) stimulus. It served to ground notions of motor control throughout the past century despite the early cautionary remarks of Sherrington (1906). He noted that the interconnectedness of the nervous system’s many parts made the existence of a simple stereotyped reflex unlikely. In this regard it is noteworthy that, at best, reflexes exhibit a given probability of response to the adequate stimulus, instead of a uniquely expected one (Zehr & Stein, 1999).

The complex interactions among neural elements at multiple locations within the CNS and their ongoing changes during any functionally meaningful motor activity, makes it difficult to accept that reflexes conceptualized in strictly anatomical terms are a basic form of stimulus–response mechanism. Uncomplicated reflexes are highly influenced by oral instructions (Gurfinkel, Kots, Krinskiy et al. 1971, see below) and orientation of body segments (e.g., Sorensen, Hollands, & Patla, 2002). To be purposely redundant, instead of fixed responses, reflexes are context-dependent and probably functionally related.

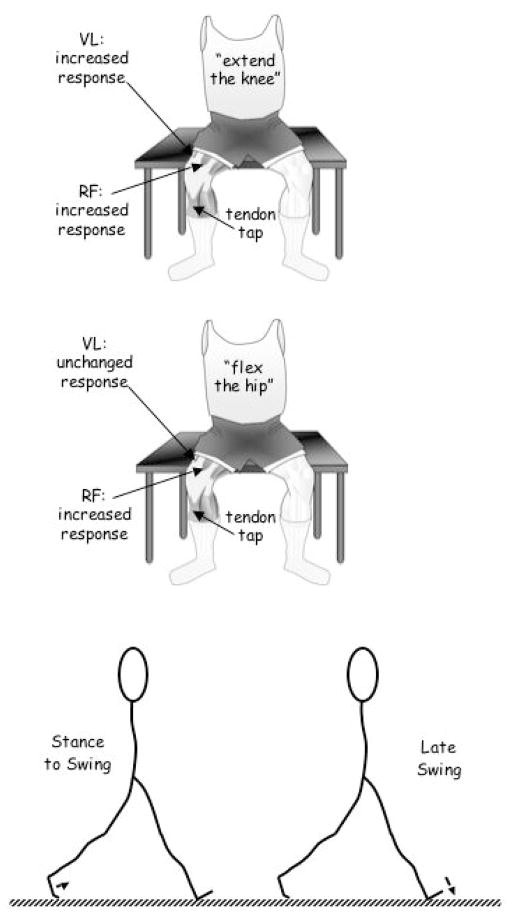
Gurfinkel, Kots, Krinskiy et al. (1971) provided a particularly important example of context dependence of reflexes (Figure 6 top two panels). On cue, participants extended a knee while surface electromyography (EMG) of the rectus femoris (two-joint) and vastus lateralis (one-joint) muscles were recorded. During the interval between the oral command and the observed EMG voluntary response, taps of the patellar tendon were applied at different times and the reflex EMG activity recorded. It was observed that the size (EMG amplitude) of the patellar reflex was greatest at 100 to 130 ms after giving the command to extend the knee. When the command given to the participants was to flex the hip, the same amplification of the reflex response was observed in the bi-articular rectus femoris muscle (that participates in the movement), but was absent in the vastus lateralis muscle that, as a single-joint muscle, cannot contribute to the solicited movement. The condition of the segmental apparatus of the spinal cord and, thus, the expected reflex response, seems to be dependent on the individual’s specific preparation for movement.

Figure 6.

The context dependency of reflexes. See text for details.

Similar context dependence of reflexes is observed during muscular and cutaneous afferent nerve stimulation. Stimulation of these afferents has been shown to induce complex excitatory and inhibitory effects on leg muscles that are dependent on postural orientation, the task or the phase of rhythmic movements (e.g., Haridas, Zehr, & Misiaszek, 2005; Zehr & Stein, 1999). For example, as communicated in Figure 6 (bottom panel) stimulation of the tibial nerve at the foot sole during the stance-to-swing phase of walking (before toe-off) produces dorsiflexion of the ankle, whereas stimulation of the same nerve during late swing (before heel strike) produces plantarflexion of the ankle (Zehr, Komiyama, & Stein, 1997). The observed changes in reflex responses reflect the complex neural interactions, producing context-dependent adaptations during human movements.

3.1.3 An unexpected lesson

Surprisingly, perhaps, contemporary inquiry into the functional nature of muscles and reflexes, the traditional staples of motor control theory, may turn motor control on its head. Muscles and reflexes are compelling examples of how context-dependence allows the very same parts (the same degrees of freedom) to implement different, multiple, and often higher-level functions. Both muscles and reflexes express a separation of two distinct characterizations of a functional subsystem, one descriptive, one interpretive. The subsystem can be described in terms of locally determined, intrinsic, descriptive properties and it can be described in terms of properties that are non-locally determined, relational, and interpretive—the properties it has by virtue of its role in the embedding system (McClamrock, 1995). The descriptive/interpretive distinction parallels the syntactic/semantic distinction in linguistic and computational theory, and the predicative/impredicative distinction in logic and complexity theory (Rosen, 1990, 2001). Coming to terms with the interpretive, semantic, impredicative status of muscles and reflexes is not likely within standard logical formulations. Rampant context-dependence may require radical rethinking of foundational assumptions in motor control. If F entails C, by what principles is C assembled? Theory and research within the perspectives of Figures 1c and 1d have taken preliminary steps toward answering such a question.

3.2 Only myotendinous force transmission?

Common assumptions are that muscles are functionally independent of one another and functionally independent of the tissues (the fascia) that envelop them. The corollary of these cognate assumptions is that the forces a muscle generates are transmitted solely via the muscle’s tendinous connection to bone. The fully dissected in situ muscle is the standard model for expressing the well-known dependencies of muscular force on muscle length and contraction velocity (Rack & Westbury, 1969). Under the standard conditions, measures of force at a muscle’s proximal and distal attachments are presumed equal. Demonstrations of different proximal and distal forces are suggestive of muscle dependence on surrounding tissues and they are suggestive of modes of force transmission additional to the myotendinous route (Huijing, 2003). Collectively, these additional modes compose myofascial force transmission. Fascia in different forms connects muscle fibers to muscle fibers, muscle to muscle, and muscle to bone, to yield possibilities for intramuscular, intermuscular, and extramuscular force transmissions, respectively.

The involvement of forces manifest in muscle-fascia complexes means that neighboring muscles are more functionally bound, more unified on strictly mechanical grounds, than heretofore considered. This potential simplification of control in the perspectives of Figures 1a and 1b is countered by the fact that joint postural stability may entail a coordination of stiffness coefficients over the intra-, inter-, and extra-muscular paths of force transmission (Huijing & Baan, 2002). Simplification would also seem to be countered by an additional form of context-dependency, namely, the muscle force generated for a given muscle length depends on the muscle’s position relative to neighboring muscles and compartment connective tissues (Huijing, 2003; Huijing & Baan, 2002; see Figure 7A). The need to take into account muscle’s fascial contexts renders the formal challenges of inverse dynamics all the more daunting.

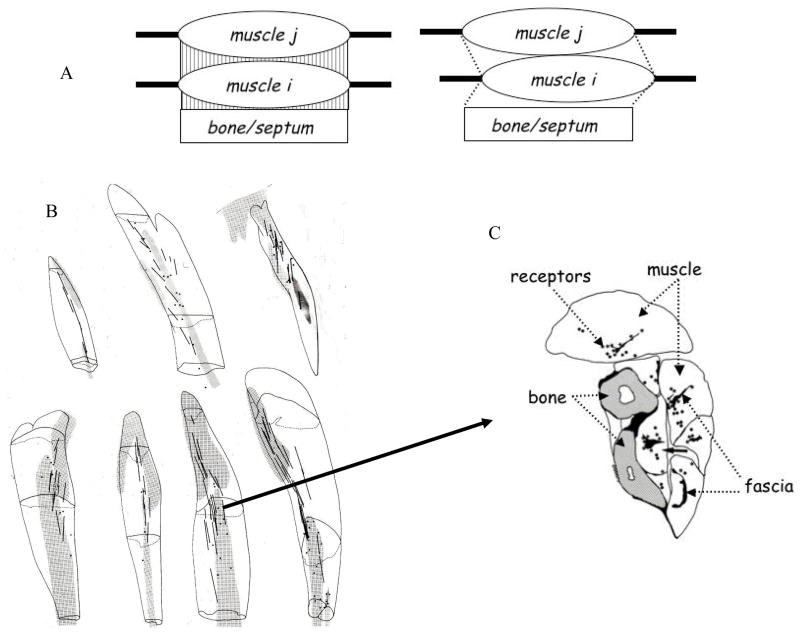
Figure 7.

A. Schematic of effects of changes in relative position of a muscle with respect to adjacent muscles and extramuscular connective tissue. (Based on Huijing, 2003.) B and C. Relation between mechanoreceptors and fascia in the antebrachial extensor muscles of the rat. The gray bands in the seven muscles are the sites of the mechanoreceptors. The location within the extensor digitorum communis muscle is shown in cross-sectional view; note the proximity of the mechanoreceptors to the fascia. (Figures B and C are taken from Figures 6.13 and 6.7D4 of Wal, 1988 and reproduced with the author’s permission.)

3.3 Afference as local, linear signaling?

The afference underwriting nonvisual perception of the body and its segments is typically depicted in terms of signals transmitted over non-interacting linear pathways from mechanoreceptors to spinal neurons to brain. The signals are typically understood as referring to the states of individual muscles, tendons, and ligaments. For purposes of movement control, these spatially and temporally separate signals must be organized in a manner that (a) informs about the states of the body as a unit, and (b) informs about the states of the limb segments relative to the body as a unit and relative to each other. The required organization of mechanoreceptor activity is typically presumed to be an achievement partly of the spinal neurons and primarily of the parietal lobe and cerebellum but there are few, if any, acceptable theories as to how they do so. Any account of the realization of (a) and (b) from linear signaling paths seems prone to intelligence borrowing. Perhaps the organization of afference has a different basis.

A starting point for a potential reconsideration is the functional architecture of mechanoreceptors as revealed by their three-dimensional spatial distribution and orientation in relation to muscle and fascia (e.g., Strasmann, Wal, Halata, & Drukker, 1990; Wal, 1988). A leading question is whether muscles as such represent the proper architectural units for understanding the organization of muscle spindles and Golgi tendon organs. As it turns out the answer is that they do not, for two cognate reasons: First, muscles as such are not the architectural units in the conveying of stresses, and second, spindles and Golgi tendon organs align with the lines of stress.

Figure 7B displays the arrangement of muscle spindles and Golgi tendon organs for the antebrachial extensor muscles of the rat. (It is an arrangement that conforms in essential details to the arrangement found for humans; Wal & Drukker, 1988). The arrangement suggests no common organizing principle when considered from the perspective of individual muscles but such a principle is suggested when a perspective is taken relative to connective tissue (of the regular dense collagen type). As both Figure 7B and Figure 7C show there is a strong spatial correlation between the morphological substrate of proprioception and the muscle-connective tissue architecture (Wal, 1988). And as Figure 7C highlights, the primary location of the mechanoreceptors is the transitional zones between collagenous connective tissue and muscle. An important reading of the anatomical findings manifest in Figure 7 is that the functional architectural units are not necessarily muscles but connective and muscular tissues organized in series (e.g., Wal & Drukker, 1988). This definition of the architectural unit (a) rationalizes the puzzling findings of spindle-rich versus spindle-poor muscles and spindle-rich versus spindle-poor regions within a muscle (e.g., Wal, 1988) and (b) undercuts the anatomical basis for the conventional division into joint and muscle receptors (Strasmann et al., 1990).

3.3.1 Biotensegrity and the mechanical behavior of the cell

In principle, the identified architectural unit opens the door on the hypothesis that, at the level of the body, tension distributions and their changes are registered—with the former related to postural states and the latter related to their transitions. The hypothesized registration is at a scale encompassing the proprioceptive substrate as a whole. The mechanical behavior of individual cells provides an introduction to the registration of global tension distributions.

Conventionally the cell is described as a composite of independent parts distinguished by their chemical functions. Unconventionally the cell is described as a biotensegrity structure: an intricate internal framework of interconnected tension-supporting components and isolated compression-bearing components that are in a constant balance of forces with their internal and external environments (Figure 8C). The contrast between the two views of the cell is schematized in Figures 8A and 8B. Due to this stable balance of forces, externally applied stresses propagate a long distance into the cytoplasm and to the nucleus (Hu et al, 2005). This instantaneous, long-distance propagation of forces (mimicking solid state matter) allows the coordination of local activities at different parts of the cell (Wendling et al., 2003). As forces propagate not only inside the cell but also from cell to cell, cells exposed to physiological stresses are continuously activated by subtle variations in the force balance, producing a concerted global response, instead of only local adaptations (Ingber, 2003b). Cell phenotypes, such as growth, differentiation, and apoptosis, emerge as a result of the distributed information flow (changes in tension distribution) inside this global structural network (Ingber, 2003b).

Figure 8.

(A) A conventional depiction of the cell as composed of separate parts. (B) A contemporary photo revealing the cell as a network of networks from the smallest (nuclear matrix) to the larger scales (intermediate filament network in the cytoplasm). (Reprint of Figure 7A in Forgacs, G. (1995). On the role of cytoskeletal filamentous networks in intracellular signaling; an approach based on percolation. Journal of Cell Science, 108, 2131–2143, with permission Company of Biologists.) (C) A tensegrity structure as the hypothesized basic architectural form for cells (and, possibly, the skeleto-muscular system).

3.3.2 Mechanoregulation of the musculoskeletal system

The structural organization of cells implicates a medium of support for a structured flow of information. This form of information propagation contrasts with diffusion signaling by cytoplasm soluble factors in the cell (and linear signal transmission by neural processes). Instead of local electrochemical transduction, requiring local context-independent decisions, mechanical forces are instantly (at the speed of sound) broadcast along the stress bearing elements, producing global context-dependent force-coupled responses. The architectural organization of the cell and, by analogy, the musculoskeletal system, suggests, therefore, that afferent signal processing and integration proceeds at the whole unit level. The basis of mechanoregulation is not activity at the level of individual receptors but activity at the level of the whole system, the level at which the force balance is established (Ingber, 2003a, 2003b).

On the basis of the preceding, it may be argued that afference within the musculoskeletal system may be less complicated than implied by conventional anatomical descriptions that fail to consider the system’s more global organization (e.g., internal force balance and three-dimensional architecture, see Figure 8C). Although multiple mechanoreceptors are active at multiple locations, rapid integration to a few degrees of freedom is possible given the force balance property allowed by the system’s architectural organization. The latter remarks may be taken as the basis for a biotensegrity hypothesis of the haptic perceptual system (Fonseca & Turvey, 2006)—the system by which the body and the environment adjacent to the body are perceived by the body.

3.4 Impeding neural noise?

Within the control perspectives of Figures 1a and 1b, movement variability is often viewed as the consequence of white neuromotor noise superimposed on, and impeding the implementation of, a deterministic prescription of muscle activation (e.g., the motor score). Variability about the mean is interpreted as problematic random variation—for the theorist who wishes to provide a thoroughgoing explanation and for the animal that needs to behave felicitously. Because movement variability is equated with randomness (noise), and because randomness and determinism are opposite concepts, movement variability and movement invariants (reflective of deterministic structure) are held as distinct and opposing facets of motor behavior.

Within this standard perspective, the mechanisms implementing motor control must overcome the undesirable effects of random noise. How the challenge is met is presumably reflected in the unvarying aspects of movements (e.g., their mean states). The tendency, therefore, is to focus primarily upon the invariants with the quantification of randomness a secondary concern conducted typically through measures such as standard deviation or root mean square variability. Reinforcing the standard perspective are implicit assumptions of conventional statistics—specifically, that moments of dependent measures exist, and, moreover, that the first and second moments (mean and variance, respectively) not only exist but are always meaningful descriptive quantities.

The emergence of nonlinear dynamics and fractals in mathematics and physics has led to an increasing appreciation of the fact that seemingly random behavior can emerge from non-random sources. There is also increasing recognition that what appears as white (unstructured, uncorrelated) noise in data collected from real, natural systems may possess structure in the form of correlation functions in the time and frequency domains—that is, the noise may be colored. The overall relevance of the latter ideas to the biological sciences has been well publicized (see Bassingthwaighte, Liebovitch, & West, 1994; Liebovitch, 1998; Traynelis & Jaramillo, 1998). Of even larger potential significance is the comprehension of (a) orderliness that would not appear in the absence of noise and (b) the manners in which noise enhances or initiates existing processes (e.g., Shinbrot & Muzzio, 2001).

Within the control perspectives represented by Figures 1c and 1d (as expressed through the dynamical systems approach to perception-action) the aforementioned concepts have been used to varying degrees to guide theory and research. Some authors have noted the typical benefits that chaotic variability—but not white noise—would provide biological systems, namely, controllability stemming from a blend of flexibility and stability. Other authors have suggested that variability functions in facilitating transitions between behavioral modes and that variability may have an exploratory, perceptual function (see Riley & Turvey, 2002, for summary).

A simple equation provides a synopsis of the foregoing remarks. In the commonly held point of view, a time series X(t) of any given motor behavior, with mean value μ and standard deviation σ, can be understood as satisfying

$$X(t)=M(t)+N(t).$$

In this equation, M(t) is the deterministic part (e.g., motor commands, motor program) and N(t) is the random part—the signal and the noise, respectively. The conventional interpretation of the equation is that the more closely N(t) approaches zero, the better is the fit of X(t) to the intended or ideal movement, embodied by M(t) (Newell & Corcos, 1993). In actuality the equation is open to several distinct interpretations reflecting variety in the composition of N(t) and in the relation of X(t) to N(t) (Riley & Turvey, 2002). For example, a finding that X(t) is correlated noise could be interpreted as evidence that (a) N(t) is correlated noise but of a different kind, (b) N(t) is random noise appended to a particular form of M(t), or (c) N(t) ≈ 0 and M(t) is a low-dimensional chaotic, or a piecewise-deterministic process.

What the above simple equation makes clear is that the measure of degree of randomness in a motor behavior X(t) is not, at the same time, a measure of the degree of randomness in the noise source N(t) acting on motor control. The theorist and experimenter must be circumspect in drawing inferences about N(t) from X(t). Indeed, a possible implication of finding that X(t) is correlated noise is that M(t) is random noise. Within the familiar Wing-Kristofferson formulation for repetitive timing tasks (e.g., tapping), colored X(t) is attributed to a (minimally) two-tiered random noise structure composed of a recurring central clock or timekeeper process that triggers a peripheral motor process (Wing & Kristofferson, 1973; Pressing, 1999). In the equation for X(t), M(t) and N(t) would represent these random clock and motor processes, respectively.

In sum, the status of noise in contemporary science suggests that movement variability should be treated respectfully as central to the study and understanding of motor control. Investigations of variability in postural and rhythmic behaviors have revealed crucial features of control, such as particular blends of noise and determinism (piecewise determinism). Most particularly they have suggested that more variable does not mean more random and that more controllable does not mean more deterministic, potentially important lessons that may apply quite generally to motor control (Riley & Turvey, 2002).

3.5 Standard variables?

In the implementation of the perspectives expressed in Figures 1a and 1b it is largely taken for granted that the variables of motor control, the controlled variables, are the familiar magnitudes of mechanics (e.g., force, velocity) and the identifiable states of physiological components (e.g., the electromyographic activity of muscles, the axon activity of alpha motoneurons). One implication of the discussion of analytical models (Section 2.4) is that the most obvious and most easily measured variables, the ones most convenient for describing a movement, are not necessarily the variables involved in the control of the movement. Arguably, the question of “How does a gymnast calculate forces and rates for hundreds of muscles with millisecond precision while whirling from one maneuver to the next?” is not addressable in the language of kinematic and kinetic variables. For an authority on temporal order in biology such as Winfree (1987, p. 253), the exactitude of the gymnast’s reproducible precision entails a flexibility that exceeds the exactitude enshrined in equations of motion. It is an exactitude best described and reasoned about abstractly in a geometric language devoid of standard geometric properties such as distance and angle. Winfree’s conjecture is that the reproducible precision of the gymnast is a topological exactitude. Recasting the temporal precision of the kinetics and kinematics of a gymnastic maneuver in such geometric terms exemplifies how obvious and familiar variables may obscure the non-obvious and unfamiliar variables that nature actually employs.

A well-known non-standard variable in motor control is λ—a kind of spatial threshold that seems resistant to interpretation in strictly mechanical or physiological terms. Whatever the scale of its application, λ defines a threshold below which movement elements are quiescent and at or above which movement elements are engaged. In the case of λ for a muscle, the movement elements are the motor units of the muscle; in the case of λ for a joint, the movement elements are the muscles of the joint. For an individual muscle, λ_muscle is a collective variable expressing current states of the central and peripheral nervous systems, multiple motor and sensory units, and properties of muscle tissue (Latash, 1993). For the body as a whole, λ_body is a collective variable encompassing all the constituent λ_muscle and λ_joint collective variables nested within it (Feldman, 1998; Feldman & Levin, 1995; and the chapter by Feldman and Levin in the present volume). The λ conception is scale invariant. At each of its manifest scales, it operates as the origin of a spatial reference frame—as depicted in Figure 9. To change origin is to produce forces in the manner understood for shifting physical frames of reference. The shifts at each scale must be tied together, an implied feature of the λ approach that has not been addressed. One promising presumption, after West (1999; see Section 4.0; and the chapter by West in the present volume), is that the required concinnity of scales—the adaptive fit of the scales to each other and to the system as a whole—is achieved by an allometric control principle based in a renormalization group relation.

Figure 9.

The generalized λ model: A nesting of reference frames (RF).

A further illustration of nonstandard variables is warranted. It reinforces the thesis of this section and related themes in Section 2.4. Balancing a stick on a finger or a pole on a horizontally displaceable cart is a problem of functionally stabilizing an unstable fixed point. The problem can be addressed in standard state variables but the human movement system may opt for another approach (Foo, Kelso & Guzman, 2000). A time-to-balance variable (τ balance) can be identified through the ratio between the stick’s current inclination to the vertical (θ) and that inclination’s first time derivative (dθ/dt). If the angular velocity is constant, then τ balance specifies the time remaining until the stick achieves the vertical orientation. Its time derivative, d(τ balance)/dt, is the angular deceleration of the stick in approaching that orientation. An assessment of the stick’s relation to the unstable fixed point for values of d(τ balance)/dt between 0 and 1.0 relative to hand velocity suggests that successful stick balancing (stabilizing the inverted pendulum) follows from keeping the derivative of τ balance between 0.5 and 1.0 at peak hand velocity (Foo et al., 2000). The upshot is a control law for the stick-balancing task written in terms of this nonstandard variable (Foo et al., 2000; Warren, 2006). An important question for motor control is what to make of such nonstandard variables and the control options they make possible.

3.6 Fixed meters?

This final question brings into sharp focus what could be, potentially, the deepest distinction between the perspectives communicated by Figures 1a and 1b on the one hand and Figures 1c and 1d on the other. A suitable starting point is the set of conventional proprioceptive meters, the muscle spindles and golgi tendon organs. The standard understanding is that these anatomically defined measuring instruments register muscle length, change in muscle length, rate of change in muscle length, muscle tension, and rate of change in muscle tension. It is commonly presumed that these are the measurement or metered primitives from which all the proprioceptive functions subserving movement are composed.

The taxonomy of agents (organisms, robots) proposed by Cariani (e.g., 1992) provides a framework in which the notion of a fixed set of meters can be evaluated. A non-adaptive agent is strictly reactive, unable to modify its meters and effectors. In contrast, the simplest adaptive agent can change the relation between its meters and its effectors. Both categories remain fixed but the mapping between them is docile, subject to change via the environment’s feedback. In Cariani’s taxonomy, the latter type of agent is an adaptive computational agent able to generate new combinations of existing primitives. It is combinatorially emergent (Bird, Layzell, Webster, & Husbands, 2003). The most adaptive agent is one that can go beyond combining the current givens by creating new givens, new primitives. Such an agent is creatively emergent (Bird et al., 2003).

The control perspectives of Figures 1a and 1b align more with the assumption of fixed meters and the capacity for combinatorial emergence. The robotics research that inspires the perspective of Figure 1b entails a designer responsible for (a) the explicit modeling of how relevant conditions of stimulation affect the prescribed sensors (meters) and (b) identifying a priori the precise nature of those relevant conditions (Bird et al., 2003). The control perspectives of Figures 1c and 1d are potentially less restrained. Their designers are undetermined. In theory, the entailed meters could be without fixed functional roles (the context-dependence discussed in Section 3.1) and open to developing attunement to the invariants of environments and tasks that are not identifiable a priori. In theory, the control perspectives of Figures 1c and 1d have the capacity for creative emergence.

Returning to the meters of proprioception, the principles of mechanoregulation identified in Section 3.3 suggest that the variables defined over the fascia net would exceed in number and type the standard inventory. Potentially, they share with the optical variables alluded to above (e.g., τ balance) their higher-order nature and specificity to control problems (Turvey & Carello, 1995). The issue of observables and meters in biology and complex systems most generally is a topic in its own right (Kugler & Turvey, 1987; Pattee, 1996; Rosen, 1978; Rosen, 2001). There is good reason to believe that it will bear significantly on future developments in motor control.

4.0 A HIERARCHICAL ORGANIZATION?

The images of Figures 1a and 1b suggest a possible hierarchical ordering—multiple levels of neuroanatomical structures and processes of control. The images of Figures 1c and 1d do not. For most students of motor control the intuitive interpretation of hierarchy is a flow of control from higher to lower levels with the higher as the primary sources of constraint and the lower alleviating the control burden by assuming responsibility for more elementary computation and processing. Less intuitive, more formal, interpretations dismiss the mere fact of levels as sufficient to identify a hierarchy (e.g., Turvey, Shaw & Mace, 1978). In purest form, a control hierarchy is a net with two or more levels of control constructed from divergent elements (e.g., node A dominates nodes B and C) and no reciprocity of control (B and C cannot dominate A). The known patterns of interconnectivity of neural components are consistent, at best, with a multiple levels interpretation of the hierarchical hypothesis (e.g., Section 2.6). In their details, they suggest that the CNS is more aptly described as heterarchical than hierarchical. A heterarchy abides by a control principle of circular transitivity: if A modulates B and B modulates C, then not only does A modulate C but C modulates A and B modulates A (Turvey et al., 1978). Fractal processes (Mandelbrot, 1983) provide a way to think about such patterns of control reciprocity.

4.1 Allometric control

Step-to-step fluctuations in human gait (e.g., Hausdorff, Purdon, et al. 1996), center-of-pressure fluctuations in prolonged quiet standing (Duarte & Zatsiorsky, 2001), and period fluctuations in finger tapping (Chen, Ding, & Kelso, 1997), exhibit long-range correlations. An implication of these findings is that motor control incorporates scaling giving rise to the novel hypothesis that motor control is allometric (B. West, 1999; B. West & Griffin, 1998).

The idea of allometric control is closely related to the power laws of allometry that relate biological properties, such as body mass and a characteristic metabolic variable or a characteristic length and a characteristic time (Calder, 1984). Animals are to be found at multiple mass, length and time scales. Allometric laws reveal that, despite the obvious variations in animals across scales, many relations between biological properties are scale invariant. For example limb frequency and metabolic cost are both found to scale as power functions of body size implying common size-independent mechanisms for timing and energy use. An allometric law reflects a general fractal (or scale-invariant) ordering principle that correlates species nearby and species far apart on the dimension of body size (B. West & Deering, 1995).

There are good reasons to suppose that the fractal ordering principle applies more widely. In particular, it might be expected to apply to the multiple allometric laws that span the spectrum of processes operating within an animal at short-time scales (e.g., skeletel muscle contraction) to those operating at long-time scales (life duration). The scaling of biological times (Lindstedt & Calder, 1981) suggests that the allometric laws governing biological functions of different durations exhibit interrelated scaling exponents. The implication is that scaling is a mechanism at the level of the individual animal that ensures the integrated function of the component biological structures and functions.

The observation that the variability of stride-intervals are long-range correlations rather than uncorrelated random deviations from a mean stride interval (e.g., Hausdorff, Peng, et al., 1996) invites a reexamination of the control of locomotion along allometric lines. The inverse power-law behavior of stride intervals (plotted against stride number) may be the resultant of possibly many processes interacting over a multiplicity of interdependent scales. In locomotion, a variety of proprioceptive loops act concurrently and interactively with a variety of optical flow and vestibular functions that are, in turn, concurrent and interactive with muscular, respiratory and metabolic functions. The allometric control hypothesis is that the many component functions at short and long time scales exhibit concinnity because of an underlying fractal (scale-invariant) process (B. West, 1999). Responding to the allometric hypothesis, and the experimental facts behind it, will challenge standard interpretations of hierarchical ordering and all four motor control perspectives depicted in Figure 1.