Abstract
Purpose
To develop a pharmacokinetic-pharmacodynamic disease progression (PK/PD/DIS) model to characterize the effect of etanercept in collagen-induced arthritis (CIA) rats on rheumatoid arthritis (RA) progression.
Methods
The CIA rats received either 5 mg/kg intravenous (IV), 1 mg/kg IV, or 5 mg/kg subcutaneous (SC) etanercept at day 21 post-disease induction. Effect on disease progression was measured by paw swelling. Plasma concentrations of etanercept were assayed by enzyme-linked immunosorbent assay (ELISA). PK profiles were fitted first; parameter estimates were applied to fit paw edema data for PD and DIS-related parameter estimation using ADAPT 5 software.
Results
The model contained a two-compartment PK model with Michaelis-Menten elimination. For SC administration, two additional mathematical functions for absorption were added. The disease progression component was an indirect response model with a time-dependent change in paw edema production rate constant (kin) assumed to be inhibited by etanercept.
Conclusions
Etanercept has modest effects on paw swelling in CIA rats. The PK and PD profiles were well described by the developed PK/PD/DIS model, which may be used for other anti-cytokine biologic agents for RA.
Keywords: arthritis, etanercept, model, pharmacodynamics, pharmacokinetics
INTRODUCTION
Rheumatoid arthritis (RA) is a chronic inflammatory autoimmune disease that affects about 0.6% of the world population (1,2). It is characterized by inflammation in the synovial membrane, cartilage and bone, where hyperplasia (increased vascularity) and infiltrate of immune cells are observed (3). Patients experience severe pain and swelling in the joints, and, eventually, it can lead to erosions of the inflamed sites, joint deformity, disability, and reduced life expectancy (4).
Surgery and medications can improve the condition of RA patients (1). Four main therapeutic categories used for RA are non-steroidal anti-inflammatory drugs (NSAID), disease-modifying anti-rheumatic drugs (DMARD), corticosteroids (CS), and biologic agents. The biologic agents, also called biologic response modifiers, are either antibodies or recombinant proteins that block the activities of inflammatory mediators or certain signaling molecules in RA. Examples of these mechanisms include blockade of pro-inflammatory cytokines, such as interleukin-1 (IL-1) and tumor necrosis factor-alpha (TNF-α), depletion of B-cells, and inhibition of the co-stimulatory pathway for T-cell activation (5).
Five of the nine currently approved biologic agents (including tocilzumab, an IL-6 antagonist approved in January 2010 by the FDA (6)) are TNF-α inhibitors (5): infliximab, etanercept, adalimumab, certolizumab, and golimumab (2). Due to its importance in promoting inflammation and joint destruction, TNF-α has been extensively studied as a therapeutic target for RA (3). During inflammation, activated macrophages secrete an elevated amount of TNF-α, which stimulates the secretion of other inflammatory cytokines, such as IL-1, IL-6, IL-8, and granulocyte-monocyte colony-stimulating factor (3). Specifically in RA, these cytokines increase expression of adhesion molecules, which drive more inflammatory cells into joints and also further stimulate cytokine production (3). These cytokines also stimulate activated macrophages and fibroblasts for the release of matrix metalloproteinases (MMPs), which are potent mediators for breaking up cartilage tissue (7), and receptor activator of NFκB ligand (RANKL), which plays an important role in bone-destroying osteoclast formation (8). As TNF-α is an early mediator of the subsequent immune cascade, its inhibition can effectively ameliorate inflammation and lessen further damage of bone tissue.
The first specific TNF-α inhibitor approved for RA is etanercept, a soluble dimeric fusion protein that consists of the ligand-binding portion of human 75 kDa (p75) TNFR and the constant (Fc) region of human IgG1 (9). It binds to both soluble TNF-α and TNF-β (lymphotoxin) (10), and its in vitro binding efficiency to TNF-α is approximately 1000-fold more than soluble monomeric TNFR (9). Etanercept can effectively neutralize TNF-α and block its pro-inflammatory activity, thereby improving physical function and preventing further joint damage in RA patients (11). A rat inflammation model has shown that etanercept can reduce disease severity when given subcutaneously or in a biodegradable polymer device (12). Despite its efficacy, the mechanisms of action of etanercept remain unclear, and there is limited information available regarding its PK/PD relationship.
Collagen-induced arthritis (CIA) is a well-established RA animal model that mirrors the human disease. We previously utilized this animal model to investigate the effects of dexamethasone and developed a mechanistic model that quantitatively measured the complexities among the important mediators and their influences on disease endpoints (13,14). Our ultimate goal is to develop a similar model with etanercept to mathematically describe the drug effect on immune responses and disease endpoints so that the pharmacology of etanercept can be better understood. The model reported in the current study describes effects of etanercept on paw edema in CIA rats and is a starting point for our purpose. It may be useful for designing future animal studies and facilitating development of a more advanced mechanistic PK/PD model.
MATERIALS AND METHODS
Drug
Etanercept (50 mg/mL, ~1 mL/package, Immunex Corporation (Thousand Oaks, CA)) was purchased from a local pharmacy. Etanercept was first diluted with injection solution composed of 10 mg/mL sucrose, 5.8 mg/mL sodium chloride, 5.3 mg/mL L-arginine hydrochoride, 2.6 mg/mL sodium phosphate monobasic monohydrate, and 0.9 mg/mL sodium phosphate dibasic anhydrous with pH of 6.3±0.2. Etanercept solution was stored at 2–8°C before use.
Animals
Fifty male Lewis rats, ages 6–9 weeks, were purchased from Harlan (Indianapolis, IN) and weight-matched to approximately 200 g. Animals were housed individually in the University Laboratory Animal Facility and acclimatized for 1 week under constant temperature (22°C), humidity (72%), 12-h light/12-h dark cycle. Rats had free access to rat chow and water. All protocols followed the Principles of Laboratory Animal Care (Institute of Laboratory Animal Resources, 1996) and were approved by the University at Buffalo Institutional Animal Care and Use Committee.
Induction of Collagen-Induced Arthritis in Lewis Rats
The induction of collagen-induced arthritis (CIA) in Lewis rats followed protocols; reagents were supplied by Chondrex, Inc. (Redmond, WA). Porcine collagen type II (2 mg/mL) in 0.05 M acetic acid was emulsified with incomplete Freund’s adjuvant (IFA; Sigma-Aldrich, St. Louis, MO) using an electric homogenizer (VirTis, Gardiner, NY) equipped with a small blade 10 mm in diameter. Equal volumes of collagen (2 mg/mL) and IFA were mixed in an ice water bath, adding the collagen dropwise to the IFA at the lowest speed setting. The homogenizer speed was increased to 30,000 rpm for 2.5 min then 0 rpm for 2.5 min, and a final mix at 30,000 rpm for 2.5 min. The emulsion was ready when it became a stiff white substance that congealed instead of dissipating when dropped in water. Ensuring proper time for the solution to cool in the ice bath is critical to prevent collagen degradation (2.5 min was used between homogenizations). Rats were anesthetized with ketamine/xylazine (75:10 mg/kg) and received 0.2 mL of collagen emulsion by intradermal injection at the base of the tail. Booster injections were given on day 7 of the study with 0.1 mL of emulsion at the same injection site (13).
Experimental Design
After evaluation of paw edema on day 20, 24 CIA rats with a paw volume increase of at least 50% in one or two paws were selected and randomly assigned to four groups for PK/PD study: vehicle control group (n=6), which received blank injection dosed IV; IV1 group (n=6), which received 1 mg/kg etanercept dosed IV; IV5 group (n=6), which received 5 mg/kg etanercept dosed IV; and SC5 group (n=6), which received 5 mg/kg etanercept dosed subcutaneously (SC). All four groups received injections on day 21. Serial blood samples for the blank and IV treatment groups were collected from the saphenous vein at post-dose 0.003 (5 min), 0.010 (15 min), 0.208 (30 min), 0.17 (4 h), 0.42 (10 h), 1, 3, 6, 8, 11, 14, 16, and 20 days, using EDTA as an anti-coagulant. For the SC treatment group, samples were taken at 0.17 (4 h), 0.42 (10 h), 1.25, 2, 2.4, 3, 3.38, 4, 6, 8, 11, 14, 16, and 20 days. All blood samples were centrifuged at 2000 g for 10 min at 4°C. Plasma fractions were immediately transferred into siliconized tubes on ice and stored frozen at −80°C.
Measurement of Edema and Body Weight
Edema was indicated by swelling of the rat hind paws (13). Two cross-sectional areas were determined with digital calipers (VWR Scientific, Rochester, NY), one area on the rat forefoot (paw) and the other at the ankle. Two measurements were made on each section, perpendicular to each other, to define the length and height of the ellipse from which the area was determined. Measurements were made side-to-side and top-to-bottom across the paw at the base of the last food pad. Measurements on the ankle were made side-to-side and front-to-back at a 45° angle across the ankle. The area contained in the ellipse is area = π · a/2 · b/2, where a is the length of the side-to-side measurements, and b is the other length. Edema was indicated by the sum of the paw and ankle area measures for each hind foot. Body weights were obtained from the day of collagen induction until the end of the study.
ELISA Methodology
Etanercept plasma concentrations were measured using an anti-human IgG ELISA kit (Bethyl Laboratories, Montgomery, TX). Rat plasma was diluted (1:500 or 1:50) by sample diluent before assay; otherwise, procedures followed the manufacturer’s instructions. The standard curve range was 7.8– 500 ng/mL and was fitted to a four-parameter logistic model. Quality control samples to test for between-assay variability, QC1 (250 ng/mL) and QC2 (50 ng/mL), contained etanercept in blank rat plasma. Use of this ELISA kit for detection of etanercept has been previously reported (12). The lower limit of quantification was 7.8 ng/mL with an interday coefficient of variation of approximately 15.7%.
Pharmacokinetic Model
Etanercept concentration-time profiles were described by compartment models. Several models were tested, and the models shown here were selected using the approach described in the “Model Fitting and Analysis” section. The equations for the final two-compartment model for both 1 and 5 mg/kg IV groups are shown below.
| (1) |
| (2) |
where A1 and A2 are amounts of drug in the central and peripheral compartments, CLD is the distribution clearance, V1 and V2 are volume of the central and peripheral compartments, and Vmax and Km are Michaelis-Menten constants.
A more complicated model was used for fitting the PK profile of 5 mg/kg SC etanercept group.
| (3) |
| (4) |
where CP = A1/V1 and:
| (5a) |
| (5b) |
where F is bioavailability for SC administration, Fr is fraction of SC dose that undergoes first-order absorption, τ is the time period of zero-order process, and ka is the first-order absorption rate constant. The plasma concentration-time profiles of the three treatment groups were fitted simultaneously, and the parameter estimates were then fixed and applied in the combined PK/PD model.
Pharmacodynamic Model
Many models were tested, including biophase and transduction models, but none gave better results than the selected model. Effects of etanercept on paw edema were described by a model based on a published dynamic model. Earp and Jusko proposed an empirical model to characterize the post-delay time course of paw edema ratio change in CIA rats (15):
| (6) |
| (7) |
where Paw is area of the measured paw divided by area at time zero for each specific rat paw in the study. The first-order rate constant kout describes the loss of edema. The production rate kin is a function of time starting at the onset time and dependent upon the degree of swelling, and tonset is a time delay in disease onset after collagen induction. The first-order rate constant Rdeg represents a negative feedback loop that reduces the production of response in the presence of paw edema and is controlled by the relative changes of paw edema compared with day 0.
In the current model, the effect of etanercept was described by type I basic indirect response model, which incorporates an inhibitory effect on the production of response (kin). Some modifications were added to the previous model:
| (8) |
| (9) |
In this model, Paw is the sum of ankle and paw size of a rat hind foot, not the ratio change compared with day 0. A zero-order rate constant accounting for the paw natural growth (kgrow) was added, and Rdeg represents a linear decline in the first-order rate constant kin and accounts for the natural remission of arthritis after disease onset. This type of basic disease progression model was previously introduced by Post et al. (16). Drug-related parameters include the capacity constant Imax (maximum loss of paw edema caused by etanercept) and sensitivity constant IC50 (etanercept concentration producing 50% of maximum inhibition). Since etanercept was given on day 21 after induction, the Imax function would only come into effect after day 21. For control rats, Imax=0 and the function becomes 1.
Model Fitting and Analysis
Noncompartmental analysis was performed by WinNonlin 5.0 software (Pharsight Corporation). Model fittings were performed by nonlinear regression analysis using the maximum likelihood algorithm in ADAPT 5 (17). All PK and PD data were naïve pooled before analysis. The PK profiles were first fitted, and the resulting parameter estimates were fixed and applied in the combined PK/PD model. The variance model used is
| (10) |
where Vi represents the variance of the ith data point, σ1 and σ2 are variance model parameters, and Yi is the ith model prediction. Model selection was based on the Akaike Information Criterion (AIC). Goodness-of-fit was assessed by the objective functions and by visual inspection of various diagnostic plots. Statistical analyses of paw edema measurements were performed using SPSS (SPSS Inc., Chicago, IL).
RESULTS
Pharmacokinetics
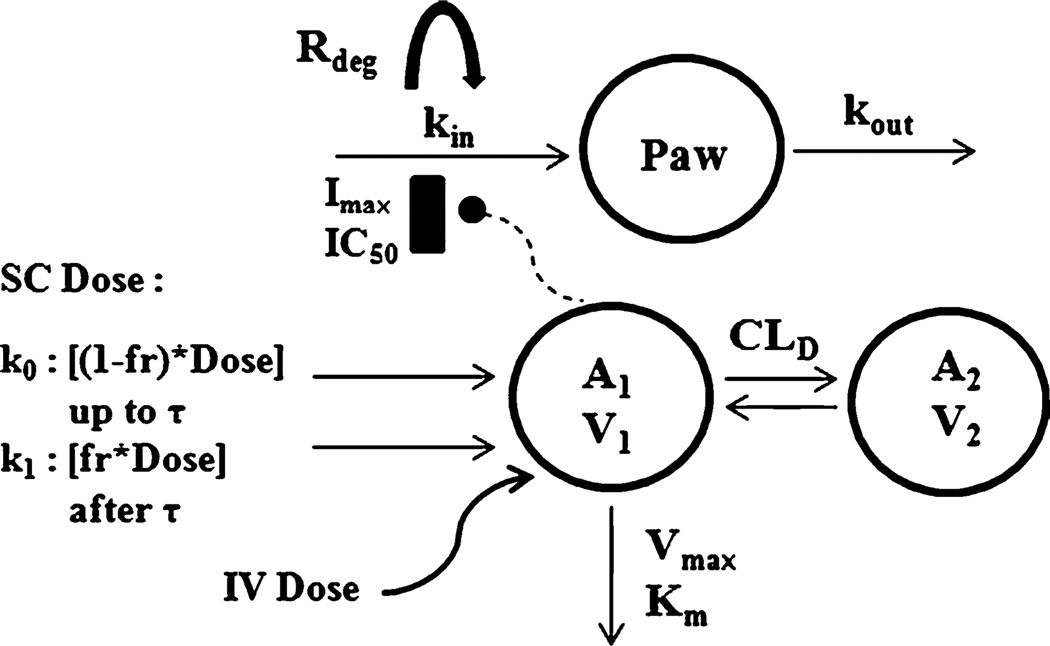
The structure of the final PK/PD model is shown in Fig. 1. Noncompartmental analysis of the PK profiles suggested that etanercept exhibits nonlinear PK in CIA rats, so saturable Michaelis-Menten elimination from plasma was assumed. An additional peripheral compartment appeared necessary to properly capture the profiles of the three treatment groups. Therefore, a two-compartment model with Michaelis-Menten elimination was used for 1 and 5 mg/kg IV etanercept. An additional linear elimination from plasma was also tested, but offered no improvement in fitting. For the 5 mg/kg SC etanercept group, a first-order input was initially added to the A1 compartment in attempt to fit the PK profile, but the absorption kinetics was more complicated. Addition of dual first-order (k1) and zero-order (k0) absorption processes allowed the model to adequately fit the SC PK profile. The use of this model for absorption kinetics of an SC protein has been reported (18).
Fig. 1.
Schematic of the PK/PD model for effect of etanercept on paw edema in CIA rats. Refer to Tables I and II for definitions of parameters.
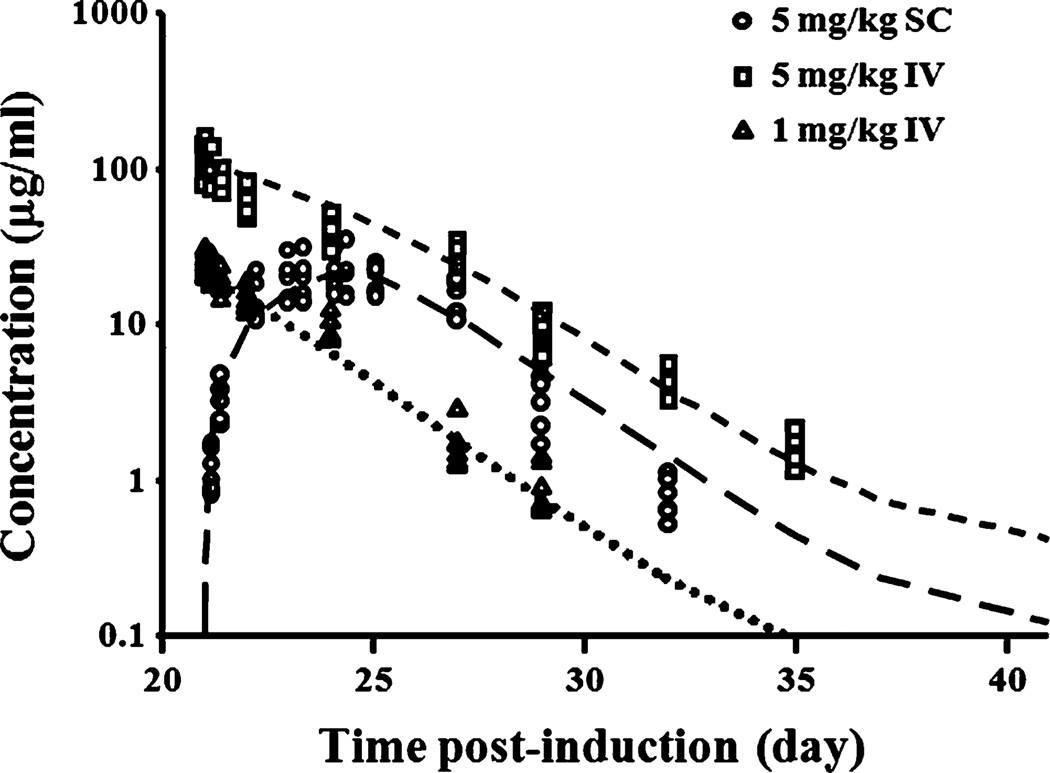
The time course of etanercept concentrations after IV and SC dosing are shown in Fig. 2. Etanercept concentrations decline in a biphasic manner after IV administrations, and there is a three-day absorption phase (day 21 to day 25 post-induction) for SC administration. Model fittings of the PK profiles are presented in Fig. 2, and parameter estimates are shown in Table I.
Fig. 2.
Plasma etanercept concentration vs. time profiles after 5 mg/kg SC (circles), 5 mg/kg IV (squares), and 1 mg/kg IV (triangles) administration in CIA rats (n=6). Curves depict model fittings.
Table I.
Pharmacokinetic Parameter Estimates for Etanercept in CIA Rats
| Parameter | Definition | Estimate | CV% |
|---|---|---|---|
| CLD (mL/day/kg) | Distributional clearance | 1.15 | 759 |
| V1 (mL/kg) | Volume of central compartment | 46.3 | 3.19 |
| V2 (mL/kg) | Volume of peripheral compartment | 53.9 | 1722 |
| Vmax (µg/day) | Capacity Michaelis-Menten constant | 1200 | 143 |
| Km (µg/mL) | Affinity Michaelis-Menten constant | 59.5 | 104 |
| ka (day−1) | First-order absorption rate constant | 1.41 | 72.4 |
| F | Bioavailability of SC administration | 0.42 | 7.93 |
| Fr | Fractional dose undergoing k1 process | 0.201 | 330 |
| T (day) | Time period for k0 process | 3 | FIXED |
CV% coefficient of variation percentage
The central volume (V1) was estimated to be 46.3 mL/kg, which is close to plasma volume, while V2 was 53.9 mL/kg. The Vmax and Km were estimated to be 1200 µg/day and 59.5 µg/mL, which suggested that nonlinearity mainly affects the high dose group. Bioavailability was estimated to be 42%, which is close to the AUC calculated value of 33%. The fraction of dose that undergoes the first-order k1 input process was estimated to be 0.201, which means most SC etanercept entered the circulation in a zero-order manner. The time period for the zero-order process was fixed to three days which, according to the SC PK profile, seemed reasonable, and the value stayed unchanged throughout all modeling trials.
Pharmacodynamics and Disease Progression
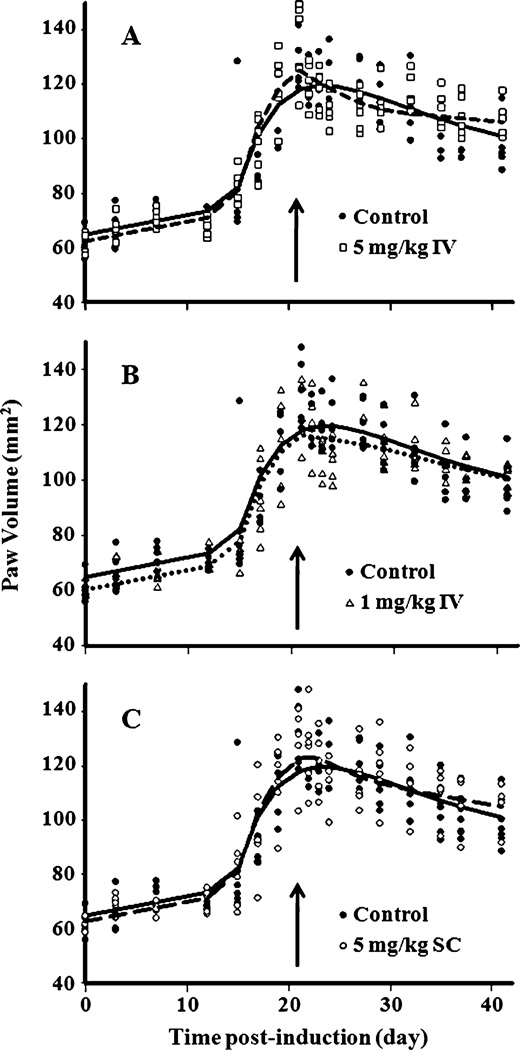
Model fittings for the paw edema data of the three treatment groups are displayed in Fig. 3A–C and the parameter estimates are listed in Table II. There was no significant difference in paw size among the four groups before day 21 (P>0.05). Significant differences (P<0.05) were found by the Student’s t-test in paw size change on specific days 22–27 in the 5 mg/kg IV group and only on days 22 and 24 for the 1 mg/kg IV and 5 mg/kg SC groups compared with control rats. However, analysis of AUC of paw edema time-course using ANOVA found no difference in the responses among the four groups (P>0.05). Therefore, single doses of etanercept have little or modest effects on paw edema in CIA rats. This is in agreement with the small value of the Imax (0.289). Most parameters were estimated quite precisely (with low CV%), except for IC50, which was around 22.7 µg/mL with CV of 166%. However, this value seemed reasonable considering that the decrease in paw edema is only observed when plasma concentrations of etanercept were above this value in all three groups. The value of tonset was estimated to be 14.5 days, which is close to the value reported (13.9 days) by Earp et al. (15). Since rate constant kgrow was added to describe the natural growth of the paw, the gradual increase in paw size from day 0 to day 15 was captured and estimated to be 0.718 mm2/day. Rate constants kout and Rdeg were estimated to be 0.137 and 0.128 day−1.
Fig. 3.
Time course of paw volumes in CIA rats (n=6) before and after (A) 5 mg/kg IV (squares), (B) 1 mg/kg IV (triangles), and (C) 5 mg/kg SC (open circles) etanercept administration on day 21 (arrow). Vehicle controls (closed circles) are shown in each figure for comparison. Curves depict model fittings.
Table II.
Pharmacodynamic Parameter Estimates for Etanercept in CIA Rats
| Parameter | Definition | Estimate | CV% |
|---|---|---|---|
| tonset (day) | Time of arthritis onset | 14.5 | 1.57 |
| kout (day−1) | Loss of edema rate constant | 0.137 | 8.38 |
| Rdeg (day−1) | Loss of production rate constant | 0.128 | 45.6 |
| kgrow (mm2/day) | Natural paw growth rate | 0.718 | 27.3 |
| Imax | Maximum inhibition on paw edema | 0.289 | 71.5 |
| IC50 (µg/mL) | Etanercept concentration for 50% max. inhibition | 22.7 | 166 |
| kin0,c (mm2/day) | Paw edema production rate at tonset for control | 11.9 | 9.46 |
| Paw0,c (mm2) | Paw size on day 0 for control | 64.8 | 3.02 |
| kin0,5mgSC (mm2/day) | Paw edema production rate at tonset for 5 mg/kg SC | 12.6 | 7.96 |
| Paw0,5mgSC (mm2) | Paw size on day 0 for 5 mg/kg SC | 62.8 | 3.05 |
| kin0,5mgIV (mm2/day) | Paw edema production rate at tonset for 5 mg/kg IV | 13.0 | 7.98 |
| Paw0,5mgIV (mm2) | Paw size on day 0 for 5 mg/kg IV | 62.4 | 3.06 |
| kin0,1mgIV (mm2/day) | Paw edema production rate at tonset for 1 mg/kg IV | 11.9 | 8.46 |
| Paw0,1mgIV (mm2) | Paw size on day 0 for 1 mg/kg IV | 60.2 | 3.12 |
CV% coefficient of variation percentage
DISCUSSION
Pharmacokinetics
Since its approval in 1998, etanercept has been used as a third-line agent in RA treatment and is prescribed for patients with moderate to severe RA, especially those who fail to respond to DMARD (9). Due to its satisfactory efficacy and safety properties in RA, etanercept has been often assessed for optimization of RA treatment, combinational therapy with other agents, and uses in other diseases (12,19,20). The PK properties of etanercept have been extensively investigated (21–23). These reports showed that etanercept exhibits a linear PK profile and is primarily metabolized through peptide and amino acid pathways with either recycling of amino acids or biliary and renal elimination in humans (22,24,25). The RA disease state does not alter its PK properties in humans or mice (22,23).
Unpublished studies in our lab demonstrated no significant difference in etanercept PK for healthy and CIA rats. Etanercept half-life calculated from the terminal slope from the three groups was around 1.2–1.9 days, which is different from the half-life in humans and mice (~4 days) (23). This may be because of the formation of autoantibodies, which accelerate elimination. Since etanercept is a fully humanized fusion protein, it may elicit an immunogenic response in rats. Although the occurrence is low in humans (26), these autoantibodies have been shown to appear 2 weeks after drug dosing in mice (27). The small value estimated for volume of the peripheral compartment (53.9 mL/kg) matches findings in humans, where minimal tissue penetration and distribution in other extracellular spaces (such as synovial fluid) are expected (22). The bioavailability after SC administration (33–42%) is smaller than in humans (58%) (22). This may be due to species differences in absorption from the SC injection site and local degradation. The Tmax observed for the SC group in this study was 3.37 days, which is longer than the reported value of 2.13 days in humans (22). It can be concluded that etanercept has a slower absorption rate but more rapid elimination in rats, so it is reasonable that a different PK model is necessary for rats. Indeed, a single first-order rate constant ka is sufficient to model the absorption phase after SC administration in humans (25), whereas a more complicated two-step mechanism was needed in rats. According to the model, 80% of the bioavailable dose first undergoes zero-order absorption (with τ=3 days) to reach the peak concentration, and then the rest undergoes a slower first-order process to enter the circulation. This behavior is quite common for SC macromolecules (18,28,29).
Another difference from humans is the nonlinear PK behavior in rats, as revealed by noncompartmental analysis and the PK model fitting results. Nonlinearity is unlikely due to recycling of Fcγ receptors (a common protective mechanism for monoclonal antibodies), since it has been shown that etanercept has poor binding affinity to FcRn (2). Instead, it may arise from the formation of autoantibodies to etanercept in rats, as discussed above. Another possibility is the receptor-mediated clearance, as etanercept is known to form complexes with TNF and stay in circulation for long periods of time in both humans and mice (2). The exact mechanisms and consequences of this “TNF-carrier effect” are not clear, but there is a possibility that the PK and/or PD of etanercept would somehow be affected.
Pharmacodynamics and Disease Progression
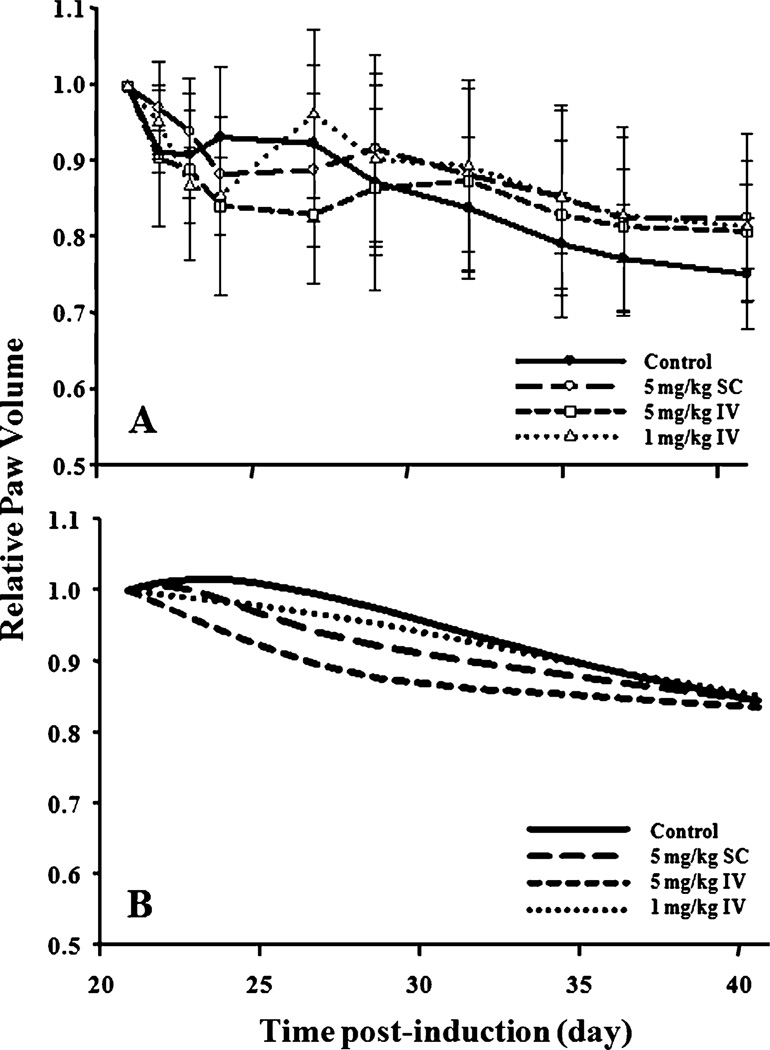
The modest effect of single-dose etanercept and the variation of paw edema in individual rats created challenges in this modeling effort. Since there is natural remission of the disease after the peak of response (as seen in the control group), it is difficult to distinguish the remission and the drug effects in the model, especially in this case of modest therapeutic effect. The current PD model was able to generate acceptable predictions for paw edema-time profiles for all groups (Fig. 3) and reasonable parameter estimates. Figure 4 presents a clearer picture of the etanercept effect on paw edema. Mean paw edema data after day 21 were normalized with values on day 21 for each group. The relative paw size versus time profiles for observed data and model predictions are shown. Not all rats exhibited peak paw edema on day 21, so these figures only demonstrate the overall tendency of the data and may not clearly indicate actual drug effects. As seen in Fig. 4B, the model over-predicted the duration of etanercept effect on paw edema. Observed paw edema versus time profiles of all three treatments superimposed with the control group somewhat earlier than model predictions. However, the model did capture the degree of reduction in paw edema well, with the order of 5 mg/kg IV>5 mg/kg SC>1 mg/kg IV. It also predicted that the profiles of the three treatment groups would merge with the controls after the drug effect. Considering the large inter-individual variability of disease state, disease onset time, and etanercept effects in CIA rats, the model predictions were acceptable.
Fig. 4.
Relative paw volume vs. time profiles after etanercept administration. Data were normalized with the paw size value at peak of edema (day 21). (A) Mean ± SD observed relative paw volume in the four groups. Symbols and curves are the mean values; the error bars are the standard deviations. (B) Predicted relative paw volumes in the four groups.
The current PD model was composed of a modified version of a previous model for paw edema in arthritic rats (15) and type I indirect response model (IDR). Addition of kgrow allows the fitting of the slight initial increase in paw edema. However, one should be cautious when interpreting this kgrow value, because it is a linear function and untenably assumes no limit (i.e. the paw will grow infinitely). A logistic-type model that anticipates an upper limit is a better choice for natural growth, but kgrow was sufficient for the timeframe of the current study. The disease state was modeled based on the disease progression extension of indirect response models by Post et al. (16). They posited that a time-dependent change in either synthesis or elimination can result in an ongoing deterioration in chronic degenerative disease. Our present model fitted actual paw data better than the previous model (15) using the relative paw ratio.
Use of IDR for describing activity of monoclonal antibodies is common (29,30). In our study, type I IDR (inhibition on kin) agrees mechanistically with the pharmacology, as etanercept blocks the activity of TNF molecules and thereby inhibits subsequent inflammatory responses. The resemblance of type I IDR for etanercept mechanism of action is as follows. The turnover of paw swelling is described by the kin and kout processes. Production of paw swelling in CIA rats is triggered by the immune consequences (i.e. activity of pro-inflammatory cytokines and infiltration of immune cells in the synovium) after collagen induction, and these processes are represented by the kin zero-order rate constant in the model. The initial conditions of kin were individually estimated for each control and treatment group, which was helpful in accounting for the intrinsic variation between the groups. First-order rate constant kout, on the other hand, describes the processes that diminish paw swelling (i.e. activity of anti-inflammatory cytokines). When etanercept is added, the functioning of TNF is hindered, and, hence, the drug-related parameters Imax and IC50 would cause a decrease in kin.
The parameter Rdeg captures the change of kin over time as the natural remission of the disease. Such phenomenon is common in both humans and animal models (8,31), although relapse of the disease occurs more often in humans. This is possibly due to the shift of activity of the T helper cell 1 (TH1) subset to T helper cell 2 (TH2) subset (31) where cytokines and mediators released by the TH1 subset are mostly pro-inflammatory, and those from TH2 subset elicit opposite effects (32). Since this phenomenon is complex and not fully understood, the use of a single first-order rate constant may oversimplify the situation. Nevertheless, it served as a useful tool for describing the time-profile of paw edema.
Our study demonstrated that a single dose of etanercept has a modest effect on paw edema in CIA rats. The reason is not likely due to the species difference in the structure of TNF, as TNF is known to be highly conserved across species (33). The efficacy of etanercept is also unlikely to be a problem, because the IC50 (22.7 µg/mL) was low, and numerous studies have proven its effectiveness (2,19). Partial reasons may be the time delay for emergence of response and the rapid elimination of the drug. This is supported by Roord et al. who found that a single-dose of SC etanercept (0.3 mg/kg) did not significantly reduce arthritic scores in AIA rats, but three repeated doses given every other day did (34). Hsu et al. also obtained the same results using 3 mg/kg SC etanercept following the same dosing regimen (20). Therefore, more doses of etanercept given to maintain effective concentrations may yield a more favorable decrease in paw edema. Our study involved collection of both PK and PD data from the same groups of animals simultaneously. The blood collection (with anesthesia) might create stress on animals. However, the PD profiles are consistent with our previous studies (13–15).
Although our model is able to account for the overall trend of the natural disease progression as well as the drug effects, there are some concerns that need to be addressed. In our PK analysis, the later etanercept concentrations that were below the quantification limit (BQL) were not included, and this may lead to biased parameter estimates if a late phase is missing (35–37). However, such concentrations are far below the IC50 and would have a negligible role in the pharmacodynamics. Our PD analysis adapted the naïve pooled approach, which does not allow consideration of intra-individual variability. This again may cause bias in the parameter estimation. Nonlinear mixed effects modeling would allow a better approach for more definitive studies than these exploratory assessments. Future work will seek more physiological and disease-related measurements (such as expression of cytokines) from the rats to explain more of the variability (covariate effects).
Our previous study with dexamethasone (Dex) showed the ability of the steroid to reduce paw edema to 60% of control values (13,14). This was attributed to Dex acting on three pro-inflammatory cytokines (TNF-α, IL-1β, IL-6) with TNF-α having the least contribution. This finding is confirmed in the present study where, with only inhibition of TNF-α, modest efficacy was observed in CIA rats.
CONCLUSIONS
A model describing the PK/PD, as well as the disease progression of paw edema in CIA rats was developed. The PK of IV etanercept was described by a two-compartment model with Michaelis-Menten elimination.The PK of SC etanercept required zero-order and first-order absorption processes, common with macromolecules. The PD effect of etanercept and disease progression on paw edema was characterized by type I IDR model (inhibition of production of response) combined with functions accounting for natural rat growth and natural remission of the disease after the peak response. Single doses of etanercept do not give a strong effect on paw edema in CIA rats, and multiple-dosing appears necessary. The modest effects of etanercept and the substantial inter-individual variability in rats complicated this modeling task. Our simplified model can capture both PK and PD of etanercept in CIA rats reasonably well and provide some insights of how a more mechanistic model could evolve. It serves as a basis for future studies where additions of new biomarkers and other disease endpoints will allow quantitative assessment of the PK/PD/DIS behaviors of cytokine blockers in RA animal models in a more mechanistic manner.
ACKNOWLEDGMENTS
This work was supported by funding from the UB Center for Protein Therapeutics, NIH Grant GM 24211, a fellowship for Ms. Lon from Amgen, Inc., and fellowship support for Dr. Liu from Hoffman-LaRoche Inc.
Contributor Information
Hoi-Kei Lon, Department of Pharmaceutical Sciences, School of Pharmacy & Pharmaceutical Sciences, University at Buffalo, Buffalo, New York 14260, USA.
Dongyang Liu, Department of Pharmaceutical Sciences, School of Pharmacy & Pharmaceutical Sciences, University at Buffalo, Buffalo, New York 14260, USA.
Qi Zhang, Department of Pharmaceutical Sciences, School of Pharmacy & Pharmaceutical Sciences, University at Buffalo, Buffalo, New York 14260, USA.
Debra C. DuBois, Department of Biological Sciences, University at Buffalo, Buffalo, New York 14260, USA
Richard R. Almon, Department of Biological Sciences, University at Buffalo, Buffalo, New York 14260, USA
William J. Jusko, Email: wjjusko@buffalo.edu, Department of Pharmaceutical Sciences, School of Pharmacy & Pharmaceutical Sciences, University at Buffalo, Buffalo, New York 14260, USA.
REFERENCES
- 1.Rheumatoid Arthritis. http://www.cdc.gov/arthritis/basics/rheumatoid.htm.
- 2.Tracey D, Klareskog L, Sasso EH, Salfeld JG, Tak PP. Tumor necrosis factor antagonist mechanisms of action: a comprehensive review. Pharmacol Ther. 2008;117:244–279. doi: 10.1016/j.pharmthera.2007.10.001. [DOI] [PubMed] [Google Scholar]
- 3.Choy EH, Panayi GS. Cytokine pathways and joint inflammation in rheumatoid arthritis. N Engl J Med. 2001;344:907–916. doi: 10.1056/NEJM200103223441207. [DOI] [PubMed] [Google Scholar]
- 4.Roy A, Mould DR, Wang XF, Tay L, Raymond R, Pfister M. Modeling and simulation of abatacept exposure and interleukin-6 response in support of recommended doses for rheumatoid arthritis. J Clin Pharmacol. 2007;47:1408–1420. doi: 10.1177/0091270007307573. [DOI] [PubMed] [Google Scholar]
- 5.Feely MG, Erickson A, O’Dell JR. Therapeutic options for rheumatoid arthritis. Expert Opin Pharmacother. 2009;10:2095–2106. doi: 10.1517/14656560903071043. [DOI] [PubMed] [Google Scholar]
- 6.Riley K. FDA approves new drug for rheumatoid arthritis. http://www.fda.gov/NewsEvents/Newsroom/PressAnnouncements/ucm197108.htm.
- 7.Shingu M, Nagai Y, Isayama T, Naono T, Nobunaga M. The effects of cytokines on metalloproteinase inhibitors (TIMP) and collagenase production by human chondrocytes and TIMP production by synovial cells and endothelial cells. Clin Exp Immunol. 1993;94:145–149. doi: 10.1111/j.1365-2249.1993.tb05992.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Klareskog L, Catrina AI, Paget S. Rheumatoid arthritis. Lancet. 2009;373:659–672. doi: 10.1016/S0140-6736(09)60008-8. [DOI] [PubMed] [Google Scholar]
- 9.Jarvis B, Faulds D. Etanercept: a review of its use in rheumatoid arthritis. Drugs. 1999;57:945–966. doi: 10.2165/00003495-199957060-00014. [DOI] [PubMed] [Google Scholar]
- 10.Gaffo A, Saag KG, Curtis JR. Treatment of rheumatoid arthritis. Am J Health Syst Pharm. 2006;63:2451–2465. doi: 10.2146/ajhp050514. [DOI] [PubMed] [Google Scholar]
- 11.Enbrel (etanercept) solution for subcutaneous use. http://www.enbrel.com/documents/ENBREL-Prescribing-Information.pdf.
- 12.Zanella JM, Burright EN, Hildebrand K, Hobot C, Cox M, Christoferson L, et al. Effect of etanercept, a tumor necrosis factor-alpha inhibitor, on neuropathic pain in the rat chronic constriction injury model. Spine (Phila Pa 1976) 2008;33:227–234. doi: 10.1097/BRS.0b013e318162340a. [DOI] [PubMed] [Google Scholar]
- 13.Earp JC, Dubois DC, Molano DS, Pyszczynski NA, Keller CE, Almon RR, et al. Modeling corticosteroid effects in a rat model of rheumatoid arthritis I: Mechanistic disease progression model for the time course of collagen-induced arthritis in Lewis rats. J Pharmacol Exp Ther. 2008;326:532–545. doi: 10.1124/jpet.108.137372. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Earp JC, Dubois DC, Molano DS, Pyszczynski NA, Almon RR, Jusko WJ. Modeling corticosteroid effects in a rat model of rheumatoid arthritis II: Mechanistic pharmacodynamic model for dexamethasone effects in Lewis rats with collagen-induced arthritis. J Pharmacol Exp Ther. 2008;326:546–554. doi: 10.1124/jpet.108.137414. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Earp JC, Dubois DC, Almon RR, Jusko WJ. Quantitative dynamic models of arthritis progression in the rat. Pharm Res. 2009;26:196–203. doi: 10.1007/s11095-008-9711-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Post TM, Freijer JI, DeJongh J, Danhof M. Disease system analysis: basic disease progression models in degenerative disease. Pharm Res. 2005;22:1038–1049. doi: 10.1007/s11095-005-5641-5. [DOI] [PubMed] [Google Scholar]
- 17.D’Argenio DZ, Schumitzky A, Wang X. ADAPT 5 user’s guide: Pharmacokinetic/Pharmacodynamic Systems Analysis Software. 2009 [Google Scholar]
- 18.Ramakrishnan R, Cheung WK, Farrell F, Joffee L, Jusko WJ. Pharmacokinetic and pharmacodynamic modeling of recombinant human erythropoietin after intravenous and subcutaneous dose administration in cynomolgus monkeys. J Pharmacol Exp Ther. 2003;306:324–331. doi: 10.1124/jpet.102.047191. [DOI] [PubMed] [Google Scholar]
- 19.Wiens A, Venson R, Correr CJ, Otuki MF, Pontarolo R. Meta-analysis of the efficacy and safety of adalimumab, etanercept, and infliximab for the treatment of rheumatoid arthritis. Pharmacotherapy. 30:339–353. doi: 10.1592/phco.30.4.339. [DOI] [PubMed] [Google Scholar]
- 20.Hsu YH, Chang MS. Interleukin-20 antibody is a potential therapeutic for experimental arthritis. Arthritis Rheum. doi: 10.1002/art.27689. [DOI] [PubMed] [Google Scholar]
- 21.Nestorov I. Clinical pharmacokinetics of TNF antagonists: how do they differ? Semin Arthritis Rheum. 2005;34:12–18. doi: 10.1016/j.semarthrit.2005.01.004. [DOI] [PubMed] [Google Scholar]
- 22.Zhou H. Clinical pharmacokinetics of etanercept: a fully humanized soluble recombinant tumor necrosis factor receptor fusion protein. J Clin Pharmacol. 2005;45:490–497. doi: 10.1177/0091270004273321. [DOI] [PubMed] [Google Scholar]
- 23.Filler SG, Solis NV, Guo J, Doellgast G, Ruiz-Garcia A, Pan WJ. Pharmacokinetics of murine p75-Fc fusion protein and MP6-XT22 anti-murine TNF-alpha mAb in mice. J Investig Dermatol Symp Proc. 2007;12:52–56. doi: 10.1038/sj.jidsymp.5650036. [DOI] [PubMed] [Google Scholar]
- 24.Korth-Bradley JM, Rubin AS, Hanna RK, Simcoe DK, Lebsack ME. The pharmacokinetics of etanercept in healthy volunteers. Ann Pharmacother. 2000;34:161–164. doi: 10.1345/aph.19126. [DOI] [PubMed] [Google Scholar]
- 25.Lee H, Kimko HC, Rogge M, Wang D, Nestorov I, Peck CC. Population pharmacokinetic and pharmacodynamic modeling of etanercept using logistic regression analysis. Clin Pharmacol Ther. 2003;73:348–365. doi: 10.1016/s0009-9236(02)17635-1. [DOI] [PubMed] [Google Scholar]
- 26.Anderson PJ. Tumor necrosis factor inhibitors: clinical implications of their different immunogenicity profiles. Semin Arthritis Rheum. 2005;34:19–22. doi: 10.1016/j.semarthrit.2005.01.005. [DOI] [PubMed] [Google Scholar]
- 27.Clinical Pharmacokinetics Review of BLA 98–0286 (Enbrel, TNFR:Fc) http://www.fda.gov/downloads/Drugs/DevelopmentApprovalProcess/HowDrugsareDevelopedandApproved/ApprovalApplications/TherapeuticBiologicApplications/ucm088681.pdf.
- 28.Mager DE, Jusko WJ. Receptor-mediated pharmacokinetic/ pharmacodynamic model of interferon-beta 1a in humans. Pharm Res. 2002;19:1537–1543. doi: 10.1023/a:1020468902694. [DOI] [PubMed] [Google Scholar]
- 29.Mould DR, Green B. Pharmacokinetics and pharmacodynamics of monoclonal antibodies: concepts and lessons for drug development. BioDrugs. 24:23–39. doi: 10.2165/11530560-000000000-00000. [DOI] [PubMed] [Google Scholar]
- 30.Dayneka NL, Garg V, Jusko WJ. Comparison of four basic models of indirect pharmacodynamic responses. J Pharmacokinet Biopharm. 1993;21:457–478. doi: 10.1007/BF01061691. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Luross JA, Williams NA. The genetic and immunopathological processes underlying collagen-induced arthritis. Immunology. 2001;103:407–416. doi: 10.1046/j.1365-2567.2001.01267.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Elenkov IJ. Glucocorticoids and the Th1/Th2 balance. Ann N Y Acad Sci. 2004;1024:138–146. doi: 10.1196/annals.1321.010. [DOI] [PubMed] [Google Scholar]
- 33.Soller JT, Murua-Escobar H, Willenbrock S, Janssen M, Eberle N, Bullerdiek J, et al. Comparison of the human and canine cytokines IL-1(alpha/beta) and TNF-alpha to orthologous other mammalians. J Hered. 2007;98:485–490. doi: 10.1093/jhered/esm025. [DOI] [PubMed] [Google Scholar]
- 34.Roord ST, Zonneveld-Huijssoon E, Le T, Yung GP, Koffeman E, Ronaghy A, et al. Modulation of T cell function by combination of epitope specific and low dose anticytokine therapy controls autoimmune arthritis. PLoS One. 2006;1:e87. doi: 10.1371/journal.pone.0000087. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Byon W, Fletcher CV, Brundage RC. Impact of censoring data below an arbitrary quantification limit on structural model misspecification. J Pharmacokinet Pharmacodyn. 2008;35:101–116. doi: 10.1007/s10928-007-9078-9. [DOI] [PubMed] [Google Scholar]
- 36.Beal SL. Ways to fit a PK model with some data below the quantification limit. J Pharmacokinet Pharmacodyn. 2001;28:481–504. doi: 10.1023/a:1012299115260. [DOI] [PubMed] [Google Scholar]
- 37.Duval V, Karlsson MO. Impact of omission or replacement of data below the limit of quantification on parameter estimates in a two-compartment model. Pharm Res. 2002;19:1835–1840. doi: 10.1023/a:1021441407898. [DOI] [PubMed] [Google Scholar]