Abstract
Microelectrophoresis based on the dynamic light scattering (DLS) effect has been a major tool for assessing and controlling the conditions for stability of colloidal systems. However, both the DLS methods for characterization of the hydrodynamic size of dispersed submicron particles and the theory behind the electrokinetic phenomena are associated with fundamental and practical approximations that limit their sensitivity and information output. Some of these fundamental limitations, including the spherical approximation of DLS measurements and an inability of microelectrophoretic analyses of colloidal systems to detect discrete charges and differ between differently charged particle surfaces due to rotational diffusion and particle orientation averaging, are revisited in this work. Along with that, the main prospects of these two analytical methods are mentioned. A detailed review of the role of zeta potential in processes of biochemical nature is given too. It is argued that although zeta potential has been used as one of the main parameters in controlling the stability of colloidal dispersions, its application potentials are much broader. Manipulating surface charges of interacting species in designing complex soft matter morphologies using the concept of zeta potential, intensively investigated recently, is given as one of the examples. Branching out from the field of colloid chemistry, DLS and zeta potential analyses are now increasingly finding application in drug delivery, biotechnologies, physical chemistry of nanoscale phenomena and other research fields that stand on the frontier of the contemporary science. Coupling the DLS-based microelectrophoretic systems with complementary characterization methods is mentioned as one of the prosperous paths for increasing the information output of these two analytical techniques.
Keywords: Colloidal system, dynamic light scattering, microelectrophoresis
INTRODUCTION
Zeta Potential represents a basic law of Nature, and it plays a vital role in all forms of plant and animal life. It is the force that maintains the discreteness of the billions of circulating cells, which nourish the organism. The stability of simple inorganic man–made systems is governed by these same laws.[1]
Surface charge of particles in sols has been used for centuries to regulate the stability of colloidal suspensions.[2] The ancient Egyptians used to render many colloids, from clays to inks, stable by electrostatic means, without being aware.[3–6] In 1857, Michael Faraday described the preparation of colloidal gold sols which are still stable and on display in the British Museum.[7] Although Faraday used different salt contents to control the electrostatic repulsion between the particles and, therefore, the extent of their aggregation (nowadays known as the “salting out” effect), neither was he aware that he had been indeed manipulating with the surface charge of the particles, although he was on the right track of explaining the cause of the stability of his sols. “There is probably some physical change in the condition of the particles, caused by the presence of the salt and such affecting media, which is not a change of the gold as gold, but rather a change of the relation of the surface of the particles to the surrounding medium,”[8] stands written in his extensive treatise. The Gouy-Chapman model of the particle-solution interface then postulated a separation of charges at the interface and the formation of the so-called double layer composed of counterions and co-ions, some of which are, as later pointed out by Stern, tightly bound to the surface and some of which are free to diffuse.
Built on the basis of this model, DLVO theory developed in 1940s by Derjaguin and Landau and Verwey and Overbeek, separately, explained the stability of colloids by invoking a balance between the repulsive electric double layer forces and the attractive, short-range van der Waals forces.[9,10] Ever since the propositions of this theory, it has been used as the theoretical basis in controlling the stability of colloidal dispersions for various technologies—foods, pharmaceutics, cosmetics, photography, electronics, agrochemicals, paints, building materials, etc. Opposing the exclusively attractive and short-range van der Waals interactions, the charged nature of suspended particles induces their repulsion and is a critical factor in controlling the stability of colloidal systems. As small particles tend to aggregate and phase separate due to their high interfacial free energies, ensuring relatively high surface charges on the particles is oftentimes a necessary precondition for keeping their colloidal suspensions stable. A measurable quantity used to control the intensity of the repulsive electrostatic interaction between the charged colloidal particles is zeta potential (ζ potential). Typically, ζ potential of± 15 mV is considered as the threshold for agglomeration, whereas ± 30 mV is considered as the limit above which the colloidal system becomes thoroughly stable. In between 15 and 30 mV, the system may be either agglomerated or dispersed.
To measure the distribution of ζ potential of suspended particles, an electric field is applied to the suspension. Electrophoretic mobility (μ) of the charged particles moving across the field is measured in terms of changes in the intensity of the scattered light caused by the light-scattering particles moving in the alternate electric field and is further used to calculate ζ potential of the particles according to Smoluchowski equation, in which η is the viscosity coefficient of the medium, ν is the electrophoretic velocity, ε is the dielectric constant of the medium, and E is the gradient of the electric field applied:
| (1) |
Since the measurement of the particle size typically presents the first step in characterization of colloids using DLS, the next section will deal with fundamentals of these measurements using the dynamic light scattering (DLS) effect, also known as photon correlation spectroscopy (PCS) and quasi-elastic light scattering (QELS), which is the technique on which this work will focus.
DYNAMIC LIGHT SCATTERING
Particles, micelles and molecules in suspension undergo Brownian motion, which is the random zigzag motion caused by collisions with solvent molecules that themselves are randomly moving owing to their thermal energy (Figure 1). The name for this ubiquitous random motion of particles in any given medium was given after the botanist who first observed this phenomenon with pollen grains “dancing” on the surface of the water. An essential feature of Brownian motion is that smaller and lighter particles are “kicked” further by the solvent molecules and, thus, experience more rapid zigzag motion. According to the classical kinetic gas theory, every particle in the suspension has an equal kinetic energy, Ek=mν2/2=3kT/2 (along a single axis thermal energy is equal to kT/2). So, with a decrease in size, the mass will get lower and the velocity will go up, and vice versa.
FIG. 1.

An example of Brownian motion: a dust particle is bombarded by air molecules (a) and randomly moves in space (b). Note that dust particles dispersed in air are also a form of colloidal systems, known as aerosol or smoke. Sols, gels, foams and latexes present other common form of colloids where solids, liquids, gases and macromolecules are dispersed in liquid (sols, foams, and saps) and solid phases (gels), respectively.
Hence, particles in suspension undergo random, Brownian motion, the velocity of which is proportional to the particle mass, which can be represented as the product of size and density. The DLS devices are built on the principle of extracting information about diffusion and size properties of dispersed colloidal entities exactly from this seemingly random, Brownian motion.
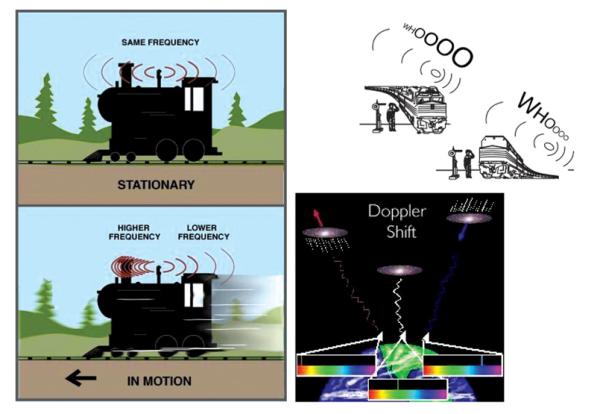
All materials are capable of scattering light (Tyndall effect) and only perfectly homogeneous systems, which neither pure liquids nor dust-free gases are, would be an exception to this rule. There are different types of scattering, depending on the size of the particle as the scattering entity: Rayleigh (when the particles are small compared to the wavelength of the light: <circa λ/20), Debye (when the particles are large and their refractive index is not significantly different from that of the dispersion medium), and Mie (when the particles are large and their refractive index is significantly different from that of the dispersion medium). For systems analyzable using the DLS method, Rayleigh scattering presents the dominant scattering mechanism. According to Rayleigh’s theory released in 1871, as an electromagnetic wave hits the particle, it induces oscillating dipoles in the particle, which then acts as a secondary source for the emission of the scattered radiation of the same wavelength as the incident light in all directions, provided that the particle is stationary with respect to the light source. Light scattered by a moving particle will experience a Doppler shift to slightly higher or lower frequencies depending on whether the particle is moving towards or away from the observer/detector. Illuminating particles or molecules in suspension with a monochromatic and coherent, laser light results in fluctuations of the intensity of the scattered light at a rate that is dependent on the particle size. Since the suspended particles are randomly moving back and forth with respect to the light source, time-dependent fluctuation of the intensity of the light scattered off the particles results, owing to the Doppler effect (Figure 2).
FIG. 2.
A set of drawings depicting the Doppler effect on which the DLS measurement device relies in determining the size of the dispersed particles. The Doppler effect occurs when the source of waves is moving relative to the detector. Red shifts to lower frequencies result when the source moves away from the detector, while blue shifts to higher frequencies occur when the source moves towards the detector, independently of the waves in question: electromagnetic (galaxies in the image) or mechanical waves of pressure (train whistle). (Figure available in color online.)
In the case of Rayleigh scattering, the intensity of light scattered from a particle is proportional to the square of the particle mass. Analysis of the intensity fluctuations resulting from the Doppler effect that the particles undergo in their Brownian motion yields the particle velocity and, hence, the particle size from the Stokes-Einstein relationship:
| (2) |
D is the measured translational diffusion coefficient [m2/s]; η is the viscosity coefficient of the medium [Ns/m2]; kb is the Boltzmann constant (1.38 × 10−23 J/K); T is the absolute temperature; and r is the Stokes or hydrodynamic radius of the particle. It is not the effective radius of a hydrated molecule in solution, as often mentioned. Rather it is the radius of a hard sphere that diffuses at the same rate as the molecule. The behavior of this sphere includes hydration and shape effects. Since most molecules are not perfectly spherical, the Stokes radius is smaller than the effective radius (or the rotational radius). A more extended molecule will have a larger Stokes radius when compared to a more compact molecule of the same molecular weight.
The translational diffusion coefficient (D) correspondingly depends not only on the size of the particle, but on multiple other factors, including the topology and chemical ordering of the particle surface as well as the ionic strength and the ionic composition of the medium. A direct consequence of this is that the particle size estimated using DLS turns out to be typically larger than that obtained during any of the electron microscopy analyses, during which the particle is looked at in isolation, away from its dynamic colloidal environment.[11]
Diffusion coefficient has [cm2s−1] units and represents a factor of proportionality in Fick’s law, representing the amount of substance diffusing across a unit area through a unit concentration gradient in unit time. As such, it does not depend on concentration of the particles, but presents a coefficient that describes how proportional concentration of the particles is to their flux. Typically, D of a compound is circa 104 times higher in air than in water. For example, CO2 in air has D=16 mm2/s, while in water its diffusion coefficient is only 0.0016 mm2/s. For biological molecules, D normally ranges from 10−11 to 10−10 m2/s. D also increases with both temperature and pressure. According to Einstein’s equation, where x is the mean Brownian displacement of a particle along a given axis after time t:
| (3) |
Combining the former two equations (Equations (2) and (3)), one can calculate that an uncharged particle with 1 nm in radius will travel 1.23 mm in an hour during its Brownian motion in water at 20°C, whereas an uncharged particle with 1 μm in radius will cross only 39 μm during the same period of time.
The DLS device measures D by looking at the Doppler shift of dispersed particles as they randomly move back and forth with respect to the light source. Distribution of the particle size and its average are calculated from the half-width of the peak on the scattering intensity versus light frequency curve (Figure 3). If one were to look at static scattering entities, only the natural width of the peak of intensity of the scattered light versus scattering frequency, ωo would remain. Smaller particles produce a more intensive Doppler effect than the bigger and less movable ones. So, the half-width of the peak of intensity of the scattered light versus scattering frequency, Δω1/2 is directly proportional to the diffusion coefficient of the particle and inversely to its size:
| (4) |
FIG. 3.
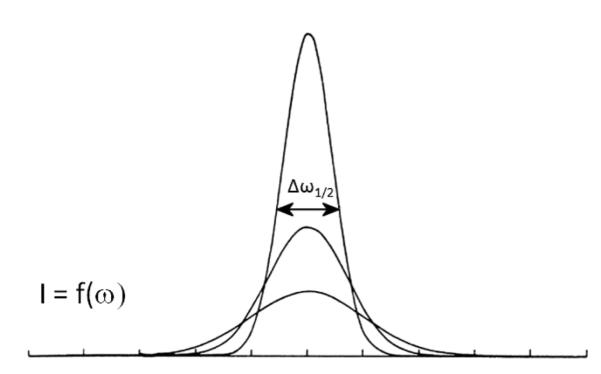
Light intensity versus frequency curve with the denoted half-width of the main peak from which the diffusion coefficient is calculated.
The raw function that the DLS device draws during the measurement is the correlation function versus time curve (G(τ)), and is related to the diffusion coefficient of the dispersed particles. In general, quasi-random physical events could be described with the use of correlation functions, mathematical constructs designed to reflect the average time spans during which the signals followed remain correlated. The characteristic of greatly damped phenomena that include diffusion is that correlation functions describing them decay approximately exponentially, with a distinctive time constant known as the “correlation time,” τ.
| (5) |
| (6) |
| (7) |
| (8) |
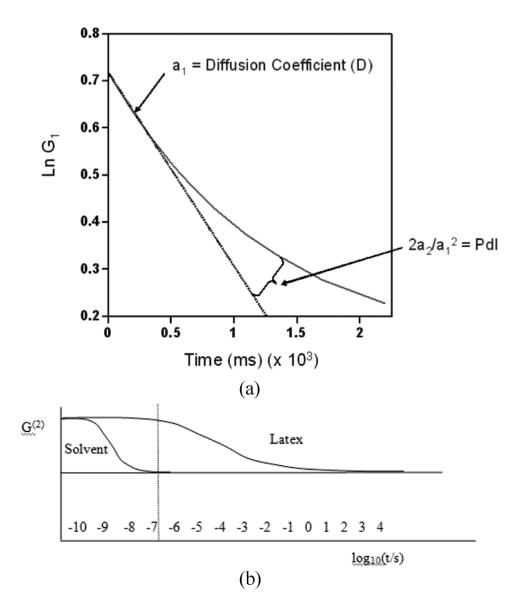
I is the scattered light intensity; t is the initial time; τ is the delay time; A is the amplitude or intercept of the correlation function; B is the baseline; D is the diffusion coefficient; q is the scattering vector magnitude; λo is the vacuum laser wavelength; n is the medium refractive index; θ is the scattering angle; and r is the hydrodynamic radius. This exponentially decaying curve falls to zero at time when the particle in its movement exceeds the wavelength of the laser light. The slope of the logarithm of this function (the so-called “first cumulant”) could be used to calculate the particle size, r, whereas the curvature indicates nonlinearity due to polydispersity and can be used to estimate its range (Figure 4).
FIG. 4.
Cumulants analysis used to calculate the average D and polydispersity index (PdI) from the logarithmic autocorrelation curve (a) and a comparison of two exponentially decaying autocorrelation curves, one for a suspension medium (pure water) and another one for a polymeric dispersion (b). Obviously, the scattering from rapidly diffusing solvent molecules remains correlated only for a very short time, inaccessible to the correlator. Reprinted with permission of Malvern Instruments, Ltd., www.malvern.com.[11]
EFFECT OF IMPURITIES ON THE PARTICLE SIZE
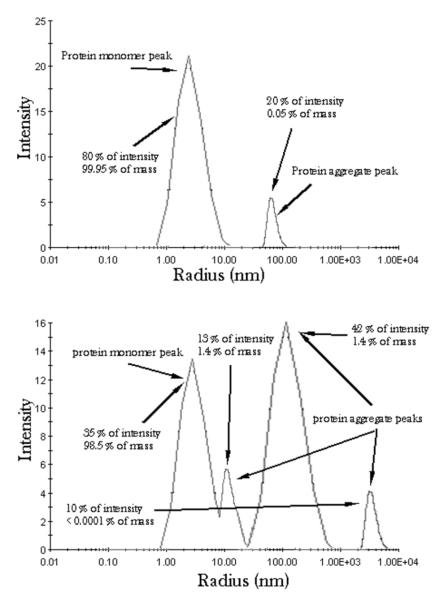
One of the essential factors that affect the quality and reliability of DLS analyses are impurities. The following example demonstrates the drastic influence that they may exert. Figure 5a shows the particle size distribution of a sample with the major peak at ~2 nm, derived from the light scattered off small colloidal particles, and a minor peak at ~80 nm, derived from the light scattered off aggregates of the small particles or relatively large impurities. Although this minor peak accounts for less than one-third of the overall scattered light, since intensity is directly proportional to the particle mass and the mass increases in proportion to r3, the total mass represented by this peak is only ~0.05% of the total. Figure 5b shows the size distribution of an even more impure/aggregated sample, where additional aggregate peaks are visible at ~10 nm and the ~4 μm. The largest aggregate (4% of intensity of the scattered light) in this case represents less than 1 ppm of the total mass. Also, the main peak at ~2 nm possesses a sharp shoulder at ~10 nm. Although the light intensity represented by the former peak is only 3.5 times higher than that of the latter peak, the scattering mass is more than 60 times greater for the former, 2 nm sized particles versus the latter, 10 nm ones. In general, because the scattering intensity is the function of r3, a particle with 1 nm in diameter will scatter 106 times less light than a particle with 10 nm in radius.
FIG. 5.
Particle size distribution curves expressed in terms of the intensity of the scattered light for two protein samples forming aggregates in suspension.
This sensitivity of DLS measurements to impurities is a seeming weakness that could be transformed into strength. Namely, protein solutions or suspensions tend to easily aggregate and repeated freezing/thawing cycles or prolonged aging frequently result in this undesired aggregation. When it comes to DLS analyses of protein solutions or suspensions, however, this technique can prove to be of great use in evaluating the stability of these systems. Since these large clumps of protein typically grow from trace amounts of markedly smaller precursor aggregates, DLS can present valuable means for detecting such segregation process long before apparent aggregation marked by visible particulates floating in the suspension has taken place. As such, DLS presents a valuable tool for assessing the stability of protein solutions or suspensions, especially since it allows for studying protein sols directly in their formulation buffers as well as at either very low or very high concentrations (0.01–100 mg/ml). Deviations of the highly concentrated samples from the ideal conditions due to the so-called “molecular crowding” effect, although, make the data analysis burdensome at times. The latter effect, common to intracellular environments, describes altering of the properties of macromolecules in highly concentrated solutions. It is associated with the protein molecules capturing solvent molecules and increasing the effective concentration and viscosity of the medium. This, in turn, often modifies the behavior of the proteins compared to the one evidenced in test-tube assays at lower concentrations.
SPHERICAL APPROXIMATION
The central fundamental problem that the DLS faces in analyzing the particle size is the spherical particle shape approximation that it employs. Although common sense thinking may prompt us to assume that elongation of particles will produce a bimodal distribution of sizes, any elongation will, in fact, produce a single peak at the sizes that would correspond to the averaged particle dimension. Hence, every elongated particle will not be detected as such, but rather as a spherical one with the diameter averaged over the three axes.[13] The reason is that in addition to Brownian, translational diffusion of suspended particles, they also undergo rotational diffusion around their axes. The latter form of diffusion contributes to randomization of the particle orientation, implying that any particle deviating from the spherical shape would be treated as an “ellipsoid of revolution,” which is characterized by its axial ratio, that is, the ratio of the single half-axis, a, to the radius of revolution, b. For this reason, it cannot be expected from elongated particles to produce multiple peaks, presumably one corresponding to their width and another to length. The aforementioned Stokes-Einstein relationship is thence used to calculate the mean particle size.
For a dispersion of rod-like particles, for example, the translational diffusion coefficient (Do) of the particle can be represented[14] by a linear combination of the diffusion coefficients parallel and perpendicular to the long axis of the rod, DII and DI:
| (9) |
For very diluted dispersions, particle interactions become negligible and the overall expression for the diffusion coefficient can be written in the following way:[15]
| (10) |
| (11) |
The length of the rod is represented with l; d is the diameter of the rod; and lef represents an effective average particle length. For rod-like particles with large aspect ratio, the last three terms within square brackets can be neglected.[16]
Hence, by knowing the shape and the dimensions of the particles, one can calculate the expected measured hydrodynamic radius using the spherical approximation applied by the device. In the example of 4 × 25 nm sized CdS rods, a difference was detected between the measured and the calculated values, and the authors concluded that the formation of dimers had had to take place in the suspension.[17] For one such deduction to be made, a priori information, typically coming from microscopic analyses, has to be obtained.
Whenever one works with elongated particles, one can also apply the hydrodynamic Brenner theory to estimate the hydrodynamic radius of the particle that will be given as the output by the device. Barbara Jachimska et al. have, thus, shown[18] that for the case of fibrinogen, which is known to have the length l=47.5 nm and the molecular volume ν=387 nm3, the other two dimensions can be calculated as 3.2 nm each. Hence, the aspect ratio, λ, would be 47.5/3.2=15. Assuming that a monolayer of water dipoles is adsorbed on each side of the molecule (proteins in general are strongly hydrated), and knowing that its thickness is 0.145 nm, the hydrodynamic width would be 3.2+2×0.145=3.5 nm. The effective aspect ratio, λ*, would, thus, be equal to 13.6. Then, one can apply Brenner equation:[19]
| (12) |
a1=1 and a2=0.11 for cylinders (rods); a1=11/12 and a2=0.31 for bend cylinders forming a semicircle (semitorus); and a1=11/12 and a2=1.2 for cylinders bent to form torus.[20] One can, thus, calculate the hydrodynamic radius (rh) for various a1 and a2, and by comparison with the size measurement outcomes infer which shape fits most the results obtained. In other words, as previously noticed, by knowing the molecular shape, one can deduce details regarding the shape of the aggregates or molecules in solution, but not vice versa.
In order to assess how self-assembly of colloidal entities proceeds over a reaction coordinate (time, concentration of a reactant, etc.), the decay rate (1/s) can be measured instead of the particle size and plotted against time or enzyme concentration. A mirrored sigmoidal curve reaching a plateau at lower decay rates would, thus, indicate attainment of a state of lower mobility, which the decay rate is the direct indicator of. As oftentimes fibers are assembled from the initial spheres, one would detect one such drop in the decay rate, that is, the mobility or the diffusion coefficient of the particles. Widening of the fibers or their elongation would correspond to the same drop. In general, translational diffusion coefficient (D) may be more appropriate to plot against time or concentration while following the protein self-assembly since particle size as a parameter becomes meaningless if we know that the spherical approximation fails.
SOURCES OF THE SURFACE CHARGE
As already mentioned, owing to charge separation effects, particles in suspension acquire surface charge, which is typically screened at a certain distance from the particle surface.[21] There are three sources of electrical charges on particle surfaces:
Ionization: Proteins are examples of particles with intrinsic surface charges primarily deriving from the protonation and deprotonation of acidic and basic side chains of amino acid residues. Also, ionization of the end amino and carboxyl groups determine the charge of the whole molecule and, thus, of its aggregates. Thus, proteins are normally positively charged at low pH values when amino group (−NH2) becomes and carboxyl group is also protonated . But at higher pH values, amino group and carboxyl group become deprotonated (−NH− and −COO−), so that the protein as a whole becomes negatively charged. In the case of hydrous metal oxide sols, hydroxyl groups (M–OH) become deprotonated at high pH values, transforming from —OH to O−,, thus, also contributing to the formation of negatively charged particle surface, whereas they become protonated, transforming from —OH to at low pH values. The same argument applies for the case of silica, typically negatively charged at neutral pH values. Metal ions on the metal oxide particle surface are likewise bound to OH groups owing to hydration effects and deprotonation of these groups is what makes these particles negatively charged. Similarly to silanol groups that render silica particles in aqueous media negatively charged, gold particles form a micelle-like sheet of oxide groups on their surface (refer to Figure 11), which makes covalent conjugation of various functional molecules thereto possible and makes them negatively charged too, unlike the typically positively charged silver particles under physiological conditions.
Adsorption of Species: The surface charge of many types of particles derives from selective adsorption of ions, such as metals, anions, protons or hydroxyl groups. Ions in general adsorb more easily on hydrophobic surfaces, such as lipids, rather than on hydrated ones, which include proteins and polysaccharides. Because cations are usually more hydrated than anions and, therefore, have a greater tendency to reside in the bulk aqueous medium, whereas bigger, less hydrated and more polarizing anions have the tendency to be specifically adsorbed, surfaces in contact with aqueous media are most often negatively charged. Owing to this effect, even oil droplets, alcohol monolayers and air bubbles in water are negatively charged, except under very acidic conditions.[22–25] The effect of increased interfacial tension between water and air/oil following the addition of electrolyte can also be interpreted by referring to light and more movable cations moving away from the water-air and water-oil interfaces more than anions and leaving the interfaces negatively charged. In the absence of surface-active species, the surface charge of metal oxides is solely due to adsorption/desorption of protons. Whether this proton adsorption/desorption equals protonation/deprotonation of discreet surface sites is still questionable, although it is accepted as such in most models. If surfactant ions are present, their adsorption will usually determine the surface charge. Finally, although adsorption of bipolar molecules does not contribute to the net surface charge, it does affect a rearrangement of the double layer composition, which indirectly leads to modified ζ potential of the particles.
Selective dissolution of ionic compounds: In these cases, it is either anions or cations comprising the particles that are preferentially dissolved,, thus, contributing to the imbalance in electroneutrality of the particle as a whole. Such is the case with AgI particles, which upon dissolution tend to preferentially release smaller and more mobile Ag+ ions into the solution and retain heavier and less mobile I− within the crystal lattice. Consequently, although the solubility product (aAg+aI−) for AgI is equal to 10−16, the point of zero charge (PZC) does not exist at pAg 8 but is displaced to pAg 5.5 (pI 10.5).
FIG. 11.
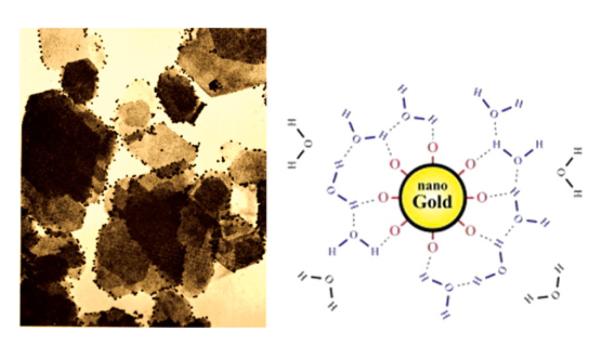
An electron micrograph showing negatively charged nano-sized gold particles adsorbed on electronegative plate-shaped kaolin crystals, and the scheme depicting the negatively charged surface structure of gold nanoparticles in water. Although kaolin platelets are negatively charged as a whole, their edges are electropositive and as such attract the gold particles onto them. Reprinted with permission from Riddick.[1] (Figure available in color online.)
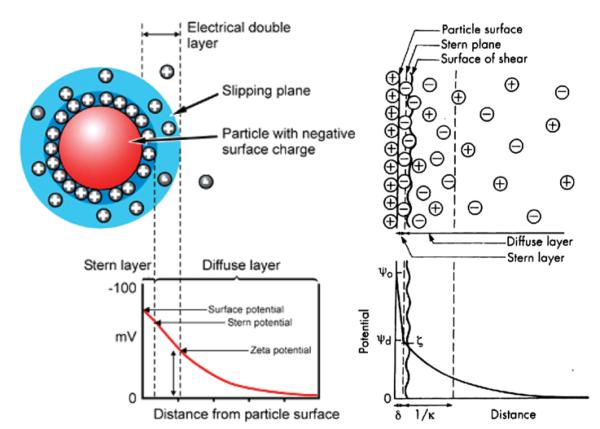
As shown in Figure 6a, ζ potential is actually a difference in electric potentials between that of the bulk and neutral liquid and that at a certain distance from the particle surface, corresponding to the so-called slipping or shear plane. The latter is the boundary of the sphere composed of both firmly adsorbed ions (Stern layer) and some of the diffusing ions surrounding the charged particle. Hence, the distance from the particle surface at which ζ potential is measured is further away from Stern layer. However, the exact location of the shear plane is an unknown feature of the electric double layer. Still, as can be seen from Figure 6b, ζ potential is normally taken to be just a bit lower than Ψd, which is the potential at the boundary of the Stern layer. Experiments have shown that even assuming that these two potentials are identical, especially for lyophobic surfaces, would not produce a significant error. Any differences between the two would most likely be pronounced at high surface potentials and high electrolyte concentrations due to the effect of compression of the diffusion layer of charges that leads to a higher slope of the surface potential versus distance curve between the Stern layer boundary and the slipping plane.
FIG. 6.
Distribution of counterions in the double layer surrounding a negatively charged colloidal particle. Reprinted from Shaw[28] (this article was published in Introduction to Colloid and Surface Chemistry, D. J. Shaw, © Elsevier [2003]). Stern layer of counterions is depicted as tightly bound to the charged particle surface. The electric potential at the boundary of the shear plane compared to the neutral medium at the distance that surpasses the Debye length (1/κ) equals ζ potential. (Figure available in color online.)
Strictly speaking, isoelectric potential is, thus, never the measure of the surface potential. Counterions are typically mostly present within this cloud of ions (composed of partly fixed ions in Stern layer and partly diffusing and replaceable ions outside of it but still within the shear plane) that moves together with the particle, thus, contributing to typically lower ζ potential compared to the surface potential. Still, sometimes it is the case that co-ions are dominant in this layer (either as (a) overlapping with or lying over the layer of counterions confined very close to the particle surface, or (b) due to specific adsorption in spite of the electrostatic repulsion), and in those cases ζ potential will be higher than the surface potential (Figure 7b). Also, sometimes, particularly when polyvalent ions act as counterions, this layer of counterions may be sufficiently strong to induce the reversal of charges (Figure 7a). This is why aluminum ions are frequently used to produce “salting out” aggregation effects. In that case, ζ potential would be of a different sign compared to the surface potential.
FIG. 7.
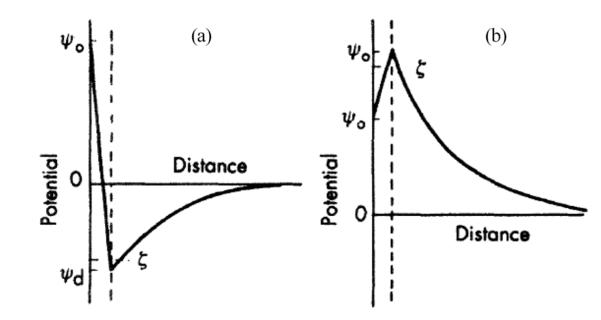
Examples of polyvalent ions adsorbed onto a charged particle and reversing its effective charge (a), and of specific adsorption of ions of the same charge as the particle, contributing to an effective increase of the effective charge (b). These are the two cases when the surface charge cannot be readily estimated from ζ potential—the presence of polyvalent ions (a) and specific adsorption that transcends the electrostatic repulsion (b). Reprinted from Shaw[28] (this article was published in Introduction to Colloid and Surface Chemistry, D. J. Shaw, © Elsevier [2003]).
To sum up, ζ potential should be, strictly saying, named voltage as it is effectively the electric potential difference and its units, Volts, denote that. It is the difference between the potential of the medium (considered as neutral) and the potential at a certain distance from the particle surface. This distance is normally taken to be beyond the Stern layer and at the boundary of the so-called shear/slipping plane. Another important boundary/layer is Debye length, which corresponds to the distance from the particle surface at which surface potential is completely screened and reaches zero. It normally, but not necessarily lies further away from the Stern layer and shear plane.
Just as one often confuses ζ potential with the surface charge, isoelectric point (the zero value of ζ potential, IEP in general or pI in case of proteins) is often confused with the point of zero (surface) charge (PZC). Whereas the former quantities correspond to certain distances from the particle surface, the latter are associated with the very particle surface. PZC is taken as equal to IEP only in the absence of ions that screen the charge on the particle surface. (This would ideally happen only in vacuum, which is, en passant, the only particle-medium interface which we can be literally called “surface”; everything else is an interface). Hence, a particle with the zero surface charge may have a non-zero value of ζ potential owing to the effect of double layer of charges surrounding it and, thus, may move in the electric field, whereas the particle at the IEP may not have zero surface charge and still be stationary in the electric field.
Smoluchowski equation typically used to convert the measured electrophoretic mobility to ζ potential has its limitations too. First of all, it is mainly applicable for medium thicknesses of the double layer and low-to-medium ionic strengths. It also applies only when the ratio of the double layer curvature to its thickness is so high that it can be assumed that the surface is almost flat. When the particle itself is small and the layer of ionic charges surrounding it is thin too, so that the given ratio is small and the charged particle could be treated as a point charge, Hückel equation, the conditions for which are mostly found at extremely low ionic strengths (I < 10−5 M for 10 nm sized particles) or nonpolar solvents, is applicable:
| (13) |
EFFECT OF IONIC STRENGTH
Ionic strength plays a role in screening ion-ion interactions (as well as the ones between charged colloidal particles) in the solution. Namely, surface charge density is equal to: σ=εκψo, where ε is the dielectric constant of the medium (inversely proportional to the ionic strength), ψo is the surface potential, and 1/κ is the length of the diffuse double layer of ions surrounding the particle surface. The latter can be divided to the Stern layer composed of adsorbed counterions and a diffuse layer of both counterions and co-ions, yielding as a sum the distance from the particle surface to the slipping plane, the electric potential at which corresponds to the measured ζ potential of the particle. The slipping plane separates the mobile fluid from the fluid that remains attached to the particle surface and moves together with it, similar to a cloud of charges, a part of which is bound to the particle and a part of which is of diffuse character. Another name for 1/κ is Debye length and is, as already noted, usually taken as the distance from the charged particle surface at which the electrical neutrality is reestablished. It can be represented as:
| (14) |
I is the ionic strength of the medium in mol/m3; ε0 is the permittivity of free space; εr is the dielectric constant of the medium; k is the Boltzmann constant; T is temperature in K; NA is the Avogadro number; e is the elementary charge. A simpler expression for Debye length when water is used the dispersion medium is the following:
| (15) |
The initially proposed model of charged particle surface in solution was by Helmholtz in 1850, and it merely described the charge on the particle surface as balanced by an equal charge in the liquid phase. Only the subsequent upgrade of this model by invoking the diffuse nature of layer of ions due to thermal motion and its double layer structure yielded the so-called Gouy-Chapman model. The addition of inert electrolyte compresses the diffuse layer of charged ions and co-ions around each of the dispersed and charged particles. Namely, a higher concentration of co-ions and counterions implies screening of the particle surface charge at a distance closer to the particle. (This explains why ζ potential drops upon the addition of electrolyte: ψo exponentially decays with the distance from the surface, and ζ potential is measured at some distance from the particle surface; as with the addition of electrolyte this potential decays faster, the ζ potential will correspondingly be lower.) In other words, 1/κ decreases, which entails either an increase in σ or a decrease in ψo, or both. For example, in the case of AgI particles whose potential depends on the concentration of silver and iodide ions in the solution, the addition of electrolyte and the corresponding drop in κ leads to adsorption of potential-determining silver or iodide ions which increases σ but keeps ψo constant. In case of an ionogenic surface, however, σ stays constant, but ψo drops.
As shown in Figure 8a, increasing ionic strength causes the double layer of ions around the charged particle surface to shrink owing to a higher concentration of ions in the dispersion. Consequently, the absolute value of ζ potential decreases at any given pH following an increase in the ionic strength, as shown in Figure 8b. IEP, on the other hand, is supposed to remain the same, provided the electrolyte is inert. However, as shown in Figure 9, van der Waals forces dominating at shorter particle-particle distances are not influenced by the change in the ionic strength. Note that ζ potential could be used in DLVO theory to calculate the interaction force or energy as a function of the distance between the particles based on the balance between the repulsive electrostatic and attractive van der Waals forces. Coagulation is a direct consequence of this interaction energy, and maximum coagulation rates, aggregate sizes and sedimentation rates all coincide with the pI/IEP for the given system.
FIG. 8.
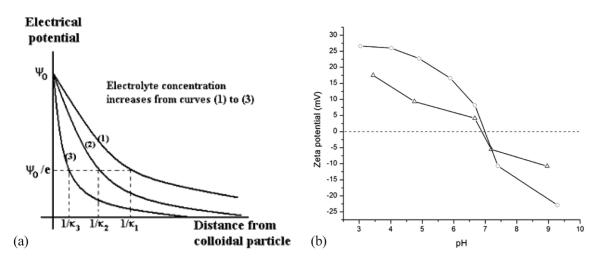
Compression of the electrical double layer following an increase in the ionic strength of the medium (a) and a ζ potential versus pH curve for a suspension of a recombinant protein in the absence of the background electrolyte (-o-) and in the presence of 150 mM KCl (-Δ-) (b).
FIG. 9.
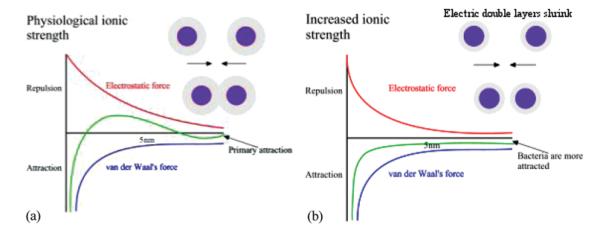
Van der Waals force remains unchanged while electrostatic field gets suppressed in the vicinity of the particle following an increase in the ionic strength of the dispersion medium. The local energy maximum existing at low ionic strengths (a) disappears at high ionic strengths (b), yielding an unstable colloidal (or cellular as in this example) suspension as the result. (Figure available in color online.)
It is well known that Nature disperses colloids almost exclusively on the negative side. Most cells and biological surfaces are, thus, negatively charged. One of the reasons behind the negative charge of biological surfaces is the lower mobility of OH− ions compared to that of protons, which makes the former more prone to adsorption on the particle surface. The effect of the ionic strength on destabilization of biological colloids is, therefore, such that they are primarily sensitive to the valence of the cation rather than to that of the anion. Critical coagulation concentration (ccc) of the cation can be calculated using the following empirical formula, where v is the valence of the cation:
| (16) |
So, for monovalent Na+ ccc=0.8 M; for divalent Ca2+ ccc=12.5 mM; and for trivalent Al3+ ccc=1 mM. Hence, 10 mM is the ionic strength high enough to induce rapid coagulation of colloidal dispersions if multivalent ions are present. Equation (16) gives a general picture, but needs to be readjusted for a specific material in question since some compounds are more sensitive to the “salting out” effect and some are less. Thus, for example, in the case of negatively charged As2S3 sols (where valence of the cation is decisive), ccc for NaCl is 50 mM, for ZnCl2 it is 0.7 mM, and for AlCl3 it is 0.1 mM, whereas for positively charged Fe(OH)3 (where valence of the anion is critical), ccc for NaCl is 9 mM, for K2SO4 it is 0.2 mM, and for K2Cr2O7 it is 0.2 mM. For the As2S3 sol, ccc values are in the ratio 1:0.015: 0.0018 as the counterion valence increases from 1 to 3, which is in agreement with the DLVO theory which states that the ratios should be 1:2−6:3−6 (1:0.0156:0.0014).
Schulze-Hardy rule has accordingly stated that ccc for a typical lyophobic (solvent-fearing, as opposed to lyophilic-solvent-loving) sol is extremely sensitive and inversely proportional to the valence of the counterion. Note that adding two or more electrolytes together to a colloid may have different effects on the colloidal stability. Thus, if ccc for a mixture of two electrolytes, A and B, corresponds to concentrations of the two components, ca and cb, whereas cccs of A and B taken separately are and , then the effects of the electrolytes are said to be additive if ; they are synergistic if ; antagonistic if . Note also that the addition of small amounts of a hydrophilic colloid to a hydrophobic sol may make the latter more sensitive to flocculation by electrolyte, which is the phenomenon known as sensitization.[29] Higher concentrations of the same hydrophilic colloid usually protect the hydrophobic sol from flocculation, and this phenomenon is called protective action. The fact that the stability of colloids tends to be sensitive to ionic strength of the background electrolyte also limits the pH ranges for which reliable ζ potential information can be collected because not only 2 > pH > 12 tends to dissolve many particles, but it also possesses intrinsically high ionic strengths.
Thomas Riddick, the originator of the idea that ζ potential of particles dispersed in blood could be used as a control parameter in treating various cardiovascular diseases that involve pathological coagulation, such as atherosclerosis, claimed that some salts act as coagulants and other as dispersants.[1] Aluminum salts and others that comprise divalent or trivalent cations, thus, act as coagulants for the negatively charged colloids (which most biological systems are), whereas potassium citrate acts as a dispersant. The former were in his classification named as 2:1 or 3:1 salts (because of having divalent or trivalent cations and monovalent anions), while the latter was named 1:3 (because potassium is monovalent and citrate is a trivalent ion). Figure 10 shows how this rule can be used to predict the direction in which ζ potential of a colloid will change upon the addition of a given salt. Hence, it is multivalent ions that play a decisive role in shifting the value of ζ potential in the direction of their valence. Thus, 3:1 and 2:1 salts will tend to shift the ζ potential in the +direction, and 1:2, 1:3 and 1:4 salts will shift it in the — direction. Recently, the same concept was invoked to explain the aggregation of cholesterol particles, pointing out that a control over ζ potential may be used to prevent the formation of pathological cholesteric deposits, including atherosclerotic plaque and gallstones.[30–32] These findings are on the line of Thomas Riddick’s invoking ζ potential to explain the “salting out” effect of ions on coagulation in blood, including the effect of thrombosis.[1] It is also worth noting that Nature never disperses its entities using exceptionally high negative ζ potential values. Human blood platelets, for example, have a ζ potential of −14±2 mV in their physiological environment,[33] which is right at the aforementioned threshold for dispersion/agglomeration. Human blood too is supersaturated with respect to more than one calcium phosphate phase, speaking in favor of Nature’s tendency to keep its systems in the states of metastability from which they can transition to any of the sides depending on the needs of the system. To keep its entities “at the edge” where they might interact but also be well dispersed, depending on the biological needs of the moment, is, thus, “Nature’s way,” the one symbolized by the Way, an epitome of simultaneous connection and separation, as has been elaborated by the author on different occasions.[34–37]
FIG. 10.
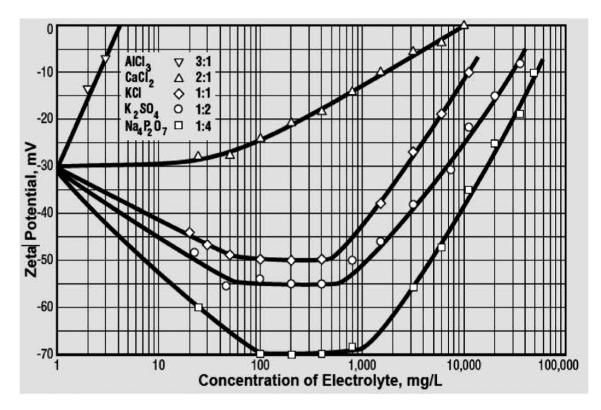
The effect of the type and concentration of electrolytes on ζ potential. Reprinted with permission from Zeta-Meter Inc.[38]
OTHER APPLICATIONS OF THE CONCEPT OF ζ; POTENTIAL IN BIOCHEMISTRY
That ζ potential is important in governing many interactions in the world of biochemistry can be seen from the increasing usage of this term in various biochemical contexts. It is known that enzyme-ligand binding is favored under conditions of electrostatic attraction, which is especially true for enzymatic reactions that rely on the acid/base conjugate mechanism.[39] Also, enzyme immobilization is known to depend not only on the chemical interaction specificity, but on the difference in the surface potentials between the enzyme molecule and the matrix carrier.[40] Electrostatic effects have been regularly relied on in the electrophoretic separation of peptides, and the protein adsorption has been shown to be directly dependent on the magnitude of the difference between the ζ potentials of the protein and the adsorbent.[41] Deviations of ζ potential of cells from the expected values have been used to conclude about their membrane abnormalities.[42] Charge on the cell membrane, originating from phosphoryl and carboxyl groups of macromolecules that constitute it,[43] can be manipulated to prevent cellular aggregation, which is an effect detrimental for cellular electrophoresis techniques.[44] It can also be assessed to differ between metabolically active and inactive cells,[45] as well as between rich, starved and dead ones.[46] Antibiotics have, thus, been shown to induce a rapid change in bacterial ζ potential,[47] and the same effect was observed on fungal cells following the application of antifungal drugs.[48] In fact, different bacterial strains could be distinguished between based on their specific electrophoretic response.[49] The role of ζ potential in viral-host interactions has been proposed as well,[50] and the transfection efficiency was said to be predictable by referring to the parameter of ζ potential.[51,52] The adhesion of pathogens residing in the oral cavity and binding to saliva has been shown to be governed by the surface charge attraction.[53,54] The membrane glycoproteins contribute to the negative charge of virus entities and cells at the physiological pH, and ζ potential of polioviruses was taken advantage of for the purpose of eliminating them from contaminated waters.[55] The same approach was used to flocculate blue-green algae in eutrophic lakes.[56] Flocculation of cells during their removal from fermentation broth has been also correlated with the parameter of ζ potential.[57]
Essentially, most biological structures carry a net negative charge,[58] and it was shown that medical implants for substitution of hard tissues carrying negative ζ potentials help in promoting bone regeneration and osseointegration.[59] This might also explain the recently shown good adhesion of cells onto positively charged apatite and poor adhesion and growth on negatively charged apatite surfaces.[60] It was similarly proposed that ζ potential could be used to predict the attachment of biomaterials to osteoblasts and bone.[61] Another study demonstrated that the nucleation and growth of calcium phosphates on the surface of 45S5 bioactive glass can be followed by assessing the temporal variations in ζ potential over time.[62] Evidence was also offered in support of an approach wherein the wound healing process could be assisted by endowing cells with relatively high ζ potentials.[63] Inorganic particles used as ingredients in skin care cosmetic products have been shown to accelerate skin permeability barrier recovery when they are provided with negative ζ potential values.[64] The sorption of nanoparticles applied for drug and gene delivery by the target cells can also be controlled using the ζ potential.[65] Changes in the ζ potential of cells incubated with nanoparticles have been taken as an indication of the vital role that the cell membrane charge plays in maintaining the cell endocytosis capacity.[66] It was, thus, shown that ζ potential of cells could be monitored to follow the internalization of nanoparticles; whereas the binding of positively charged nanoparticles on the cell plasma membrane shifts its ζ potential to more positive values, the subsequent internalization, mainly via vesicular-transport-based endocytosis, reestablishes the initial negative value.[67] This observation is in agreement with a similar change in the ζ potential of multilamellar liposomes consisting of phosphatidylcholine following their encapsulation of a drug.[68–70] Aging of drug-containing microcapsules and release of the entrapped drugs can also be correlated with specific ζ potential changes of the drug carriers.[71] Among many other particles conjugated with surface agents, ζ potential has been used to estimate the surface characteristics of calcium-phosphate/DNA complexes too. If DNA coats the particles, they carry a strong negative charge; if calcium phosphate is uncoated, the particle charge is only slightly negative.[72] A similar ζ potential shift from that of the core particle to that of the coating applies for all other core-shell systems.[73] Orientation of amphiphilic or bipolar molecules conjugated to the particle surface can also be assessed using ζ potential measurements.[74] Zeta potential shifts to positive values when carbohydrates become attached to the particle surface, and the interest in functionalizing nanoparticles for intracellular drug or gene delivery with sugars is connected with the finding that polysaccharides residing on the surface of Gram-negative bacteria have a role in enhancing cell penetration. Convenient for following the adsorption of species onto dispersed particles of interest, ζ potential analyses have also recently been used to detect binding of amelogenin nanospheres onto apatite crystals under various conditions[75] and correspondingly improve the understanding of the mechanism of amelogenesis, a biomineralization process during which a finely structured protein gel directs the growth of hierarchically ordered enamel crystals, the hardest material in the vertebrate body.[76] Finally, the brain itself, as a whole, has a specific ζ potential, which implies that the extracellular translational motion is governed by electrokinetic effects under this naturally occurring electric field in addition to diffusion and tissue tortuosity.[77]
ANALYZING COMPLEX CERAMICS
This section will deal with the main practical and fundamental challenges in the analysis of ceramic particles using DLS microelectrophoresis, and hydroxyapatite (HAP), the main mineral constituent of hard tissues, will be used as the example.[78]
The problem with analyzing HAP and other complex ceramics and minerals with respect to ζ potential is that at the mineral surface, changes in pH do not only shift the surface charge by changing the distribution of proton and hydroxyl groups hydrating the interface, but they also influence selective dissolution of the surface ions, which then induces rearrangement of the surface charge layers,, thus, oftentimes shifting the ζ potential values in unpredictable ways. Typically, HAP undergoes a shift in the ζ potential depending on the immersion time, which is an effect related to ion exchange between the hydrated layer around the material and the material surface, leading to dissolution and re-precipitation of new phases defined by the ionic composition of the solution, the material surface activity and the presence of additives.[79] This selective leaching of ions has been the source of great unpredictability and irreproducibility of the electrophoretic analyses of apatite powders. For HAP, the PZC in calcium-free solutions is said to occur at pH 7.3. For more alkaline solutions the surface should be negatively charged, whereas for more acidic solutions it should be positively charged. However, ions other than H+ and OH− can adjust the surface charge, and in calcium-containing solutions Ca2+ ions bind to the surface at pH > 7, leaving the surface neutral rather than negative.[80] As already said, HAP also undergoes dissolution depending on the pH and these dissolved ions can have a decisive effect on ζ potential of the particle. Consequently, whereas some studies report negatively charged particles in the entire pH range in which HAP is the stable phase (4–11),[81] others report IEP values at anywhere between 5 and 7.5, below which the particles become positively charged.[82,83] There are, however, reports[84] on IEP of HAP suspensions detected at pHs as high as 10.
In addition, HAP, like many other materials, has two types of crystal planes, each one of which carries a different charge: positive on a-planes and negative on c-planes. Zeta potential analyses are not able to differ between the two and often it happens that an electrostatic attraction that leads to specific adsorption is observed between two types of particles carrying the same net charge. In such cases, planes or edges of one of the particles carry the opposite charge compared to the particles as wholes, inducing the electrostatic attraction and adsorption to occur. One such example is shown in Figure 11. Similarly, streaming potential measurements of f potential of sapphire monocrystals yielded a difference equivalent to 2 pH units between the IEPs of different crystal planes, indicating the existence of a pH window within which different crystal planes would carry opposite charges.[85] Also, assuming a uniform distribution of surface charges is another approximation that is known to yield significant discrepancies whenever discrete or alternate charges, as in the case of HAP, comprise the surface.[86] Such finer levels of charge distribution could be analyzed only by means of techniques more sophisticated than colloidal electrophoresis.
Buffers do not necessarily need to be used when proteins are analyzed because proteins act as buffers per se through their titratable residues. If the experiments are carried out under atmospheric conditions, an amount of CO2 will be dissolved in the solution and will enter the equilibrium with carbonate ions that CO2 forms upon dissolution in water. Carbonate/bicarbonate system also has a buffering capacity and is, as such, utilized by living organisms, in addition to the intrinsic buffering capacity of proteins and phosphate species. Buffers are mixtures of weak acids or bases and their salts and their purpose is to resist drastic changes in pH produced by adding a strong acid or base to the system. The cause of their acting in such a way can be seen from the titration curve of a weak acid with a strong base (Figure 12a). The curve appears as a 90° rotated sigmoidal curve, and the range of stability of pH with the addition of the titrant presents the buffering range for that particular buffer. The middle of this range, the half-equivalence point, is equal to pKa of the given acid, so that the buffering range is usually taken as pH=pKa+−1. When HAP is analyzed, however, the use of buffers is recommended in order to eliminate the measurement error due to extensive pH fluctuations and instability. Tris and Bis-Tris are commonly used to stabilize the pH of organic and biological systems, and could be used in the 8.3±1 and 6.8±1 ranges of pH, respectively (note that HCl is the complementary acid for these two salts, which implies that Cl− ions are required for both Tris and Bis-Tris to act as buffers); glycine/HCl and glycine/KOH could be used as buffers in 2–4 and 10–12 ranges of pH, respectively; citric and phosphoric acids, which have three pKa values each present additional common options. However, it is vital to remember that components of buffers usually show specific adsorption and were thus, for example, excluded from the most extensive compilation of PZCs and IEPs up to date.[27]
FIG. 12.
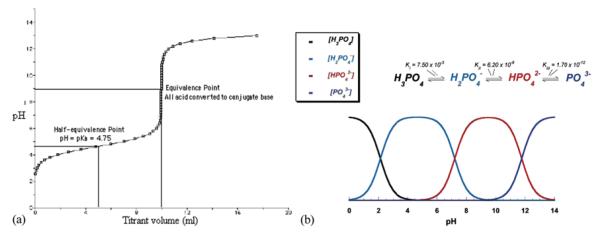
(a) The titration curve of a weak acid, acetic acid, with a strong base, NaOH, showing pH=pKa ±1 as the buffering range for the given acid/base pair. (b) The buffering capacity of phosphoric acid is strongest at the points of intersection of the curves that represent the amount of different phosphate species as the products of dissociation of phosphoric acid: pHs 2, 7, and 12. Reprinted from Dorozhkin.[90] (Figure available in color online.)
Although protonation/deprotonation reactions in solution are some of fastest ones and the same is expected to be the case for surface protonation/deprotonation, pH changes are often detected during sample incubation, suggesting that there might be analytically detrimental kinetic effects on the adsorption equilibrium. In the case of surfaces that undergo selective dissolution and possibly phase transitions of surface layers, as is the case with calcium phosphates, longer equilibration times may be required. The procedure used by Somasundaran et al. was, thus, to soak apatite powders in KNO3 solutions and age them as such overnight as well as to equilibrate the samples for 1 hour at any given pH.[87] Another main concern for calcium phosphates is their tendency to aggregate over time (namely, calcium phosphates particles are typically composed of smaller, nanosized subunits), which may affect the particle size and ζ potential values alike. Sodium hexametaphosphate (0.1 wt%) used in food industry as a deflocculant could be applied to stabilize dispersions of HAP and enable more reliable DLS measurements.[88] Prolonged ultrasonication (>30 minutes); bubbling of inert gases to eliminate the effects of surface-active CO2; extensive incubation to allow the sediments to settle down, with or without centrifugation; and the use of supernatants only are other measures routinely applied to obtain more reproducible and reliable results. Optimization of the solid-to-liquid weight ratios, typically recommended for DLS measurements to be in the range 5×10−5 to 5×10−3, presents another strategy for improving the measurement quality. Calcium carbonates share numerous properties with calcium phosphates, including the high mobility of the surface layer and a high tendency to undergo Ostwald ripening and agglomeration, which implies that in their case too, similarly to HAP and other calcium phosphates, great discrepancies between values for IEP/PZC reported in the literature exist.[89]
The size and shape of inorganic particles normally do not affect surface charge density, σ, but they do affect ζ potential since particles with the same surface charge but of different sizes and shapes will move with different velocities in the electric field; hence, their electrophoretic mobility, from which ζ potential is calculated, will be different. Typically, an increase in temperature leads to a drop in the ζ potential for inorganic samples, whereas an increase in pressure may have different effects depending on the chemical nature of the sample and its ionic environment.[91] A linear decrease in the PZC for alumina particles was observed in 10–40°C range with an increase in temperature, owing to the thermal desorption of protons from the particle/solution interface.[92] Also, although increasing ionic strength tends to push the ζ potential values closer to IEP at any given pH, the IEP itself is normally not subject to change following changes in the ionic strength. Unlike ζ potential, with surface charge density, σ, this trend follows the opposite direction: it increases following an increase in the concentration of an inert electrolyte. By definition, inert electrolyte is composed of ions that react with the surface only by a Coulombic force and do not get specifically adsorbed to it. This can be verified by evidencing no shift in the PZC/IEP at different electrolyte concentrations. Specific adsorption of cations leads to a shift in the PZC/IEP to lower values, and vice versa for anions. Any combination of Na+, K+ on the cation side and of Cl−, NO3−, and ClO4− on the anion side has been accepted as inert for metal oxides. However, although halide ions are usually inert with respect to metal oxides, they are potential determining for silver halides, which makes the term “inert electrolyte” very relative. Still, to these rules there are exceptions since a particular combination of the particle surface composition and the double layer ions may trigger specific adsorption and other counterintuitive effects that may follow. This can be exemplified by the case of dispersions of ice in water.[93] In those cases, whereas the IEP is detected at pH 3.0, the PZC is found at pH 7.0, which altogether with the evidenced shift in the IEP depending on the NaCl concentration directly implies complex specific adsorption of ions at the interface between water and water. The complexity and versatility of water as a dispersing medium with respect to the surface charge properties of the interfaces in it is, thus, also implicit.
ZETA POTENTIAL OF PROTEINS
Amino acids as basic building blocks of proteins are normally negatively charged at high pH values and positively charged at low pH values. Simply speaking, each amino acid has a carboxyl (−COOH) group at one of its ends and an amino (−NH2) group at another. In an acidic environment, the free ions are predominantly protons. With a plenty of protons surrounding the protein, −COOH group does not tend to dissociate to −COO− and H+, and, thus, remains neutral. In contrast, −NH2 group will tend to be protonated and, thus, become . Hence, the net charge of the molecule will be positive. At high pH values, hydroxyl ions will be the dominant ions in the solution. Thus, the protons from −COOH groups would readily be released into the solution to combine with free OH− ions and yield water. As a result, −COOH group will tend to dissociate into −COO− and H+. Protonation of −NH2 will be suppressed, however, and it will remain in neutral, NH2 form. So, the net charge will be negative (Figure 13).
FIG. 13.
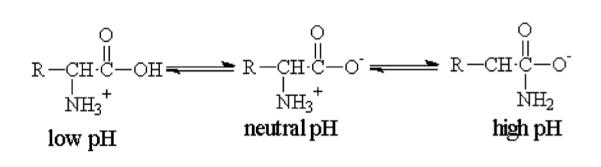
Dissociation of an amino acid depending on the pH.
This can be also described through La Chatelier’s principle. Namely, the dissociation constant for COOH ↔ COO− +H+ reaction is always constant. La Chatelier’s principle says that as concentration of any of the reactants is increased, all the concentrations will change so that the dissociation constant remains the same. The latter is given as:
| (17) |
So, as the concentration of protons is increased by lowering the pH, the concentration of COOH has to go up in order for the K to remain constant.
To calculate the isoelectric point (pI) of an amino acid, the following equation can be used in case when no protonation of the side chain takes place:
| (18) |
Alternatively, when the side chain is also titratable, the following equation is valid:
| (19) |
The same equation (Equation (19)) could be applied for estimating the pI of a protein molecule as a whole. In that case, pKa is the pK value of −COOH group at the C-terminal; pKb is the pK value of −NH2 group at the N-terminal; and pKr is the average pK value of the active acid and base groups in the side chains of the so-called titratable residues (the ones with acidic or alkaline side chains). In the case of polypeptides, pKa and pKb of amino acids other than the ones on terminals do not contribute to pI because their COOH and NH2 groups form peptide bonds.
To estimate the extent of dissociation of acid/base pairs of individual titratable side chains at any given pH, the Henderson-Hasselbalch equation can be used:
| (20) |
| (21) |
Note that pK of a compound is equal to pH at which one half of its molecules are protonated and the other half are not. Note also that since the Henderson-Hasselbalch equation does not account for the ionization of water itself, it is not useful for calculating pH of solutions of strong acids or bases (pH~1 or 14).
The general trend is that pK values of amino acids decrease with temperature: not much although, by ~0.05 to 0.2 units as the temperature is increased from 25 to 37°C. On one hand, this may be seen as a consequence of the fact that the pH of neutral water drops by ~0.2 units following the increase in temperature from 25 to 37°C. On the other hand, it can be, all by itself, treated as different depending on whether the protonation/deprotonation reaction is exothermic or endothermic, while referring to La Chatelier’s principle. Namely, according to Le Chatelier’s principle, raising the temperature of exothermic reactions pushes the system back towards the reactants, which is observed as a decrease in the equilibrium constant value (or an increase in the pK value), whereas raising the temperature of endothermic reactions pushes the system towards the products, which results in an increase in the equilibrium constant value (or a decrease in the pK). Empirically speaking, pKb decreases in all cases, whereas pKa may decrease, stay constant or increase following an increase in temperature. Thus, the overall effect of increasing temperature is typically a lower combined pK of the amino acid or a protein. And as pK values get lower, so does pI. This may explain why pI detected at 37°C is lower by almost 0.5 pH units relative to pI detected at 25°C. This also explains why pH of organic buffers, such as Tris/Bis-Tris, decreases following an increase in temperature. In case of Tris and other organic buffers, one often detects a change in the pH by 0.5 units following a transition from 25 to 37°C. Thus, pure aqueous Tris buffer at pH 6.8 at 25°C will exhibit pH 6.46 when heated to 37°C. In fact, as the temperature increases, pKa of Tris decreases at an approximate rate of 0.03 units/°C. In the case of phosphate buffers, this change is almost negligible. Thus, pH 7 buffer has pH 7.00 at 25°C and pH 6.98 at 37°C; pH 10 buffer has pH 10.00 at 25°C and pH 9.90 at 37°C; and pH 4 buffer has pH 4.00 at 25°C and pH 4.02 at 37°C.
However, notice also that a phosphate buffer with pH 7.00 at 25°C is neutral, whereas having pH 6.98 at 37°C means that it has become basic. This is why. Namely, dissociation of water to hydrogen (or hydroxonium, H3O+, strictly speaking, as free protons are always bound with hydrogen bonds to water molecule monomers, dimers or trimers) and hydroxyl ions is an endothermic process, capturing thermal energy from the surrounding. As one increases the heat content of the system by bringing the temperature up, one instigates more of the dissociation, according to La Chatelier’s principle. The effect of this is an increase of the dissociation constant of water, Kw, as temperature increases. Table 1 shows Kw values for water at different temperatures:
TABLE 1.
Equilibrium constants for dissociation of pure water and the neutral pH values at different temperatures
| T (°C) | Kw (mol2 dm−6) | pH |
|---|---|---|
| 0 | 0.114×10−14 | 7.47 |
| 10 | 0.293×10−14 | 7.27 |
| 20 | 0.681×10−14 | 7.08 |
| 25 | 1.008×10−14 | 7.00 |
| 30 | 1.471×10−14 | 6.92 |
| 40 | 2.916×10−14 | 6.77 |
| 50 | 5.476×10−14 | 6.63 |
| 100 | 51.3×10−14 | 6.14 |
This does not mean, however, that water with pH 6.77 at 40°C will be acidic. It means that neutral pH is 6.77 at 40°C. Water with pH 7 at 40°C will, thus, be basic. Namely, in the case of pure water, the number of free hydrogen ions and hydroxide ions is always balanced. Hence, pure water remains pH neutral at all temperatures, even though its pH changes with temperature.
In view of this, note that the real concentration of free protons as defined by Kw is subject to change even for the phosphate buffers following a change in temperature. Namely, although pH of the pH 7 phosphate buffer changes from 7.00 to 6.98 as temperature is increased from 25 to 37°C, pH of neutral water changes from 7.0 to 6.8 with the same temperature change. Hence, it can be said that concentration of free protons, in fact, decreases with increasing the temperature by about 0.2 pH units. On the other hand, Tris buffers exhibit a drop of about 0.5 pH units with an increase in temperature from 25 to 37°C. In view of the mentioned change in the pH of neutral water following this change in temperature, this drop accounts for only 0.3 instead of 0.5 pH units, and is, thus, almost similar in magnitude to the one exhibited by the pH 7 phosphate buffer, although in a different direction.
Zeta potential analyses of proteins may be significantly hampered due to high ionic strengths of the conductive media in which they are dissolved or suspended. The consequence of this is that destabilization and disintegration of the protein structure often occurs during the analysis owing to the electric field effect. Namely, high ionic strengths increase electrical conductivity of the dispersing medium, which makes the dissolved protein more prone to “cooking.” The magnitude of this effect varies depending on the sensitivity of a particular protein, which implies that there are no precisely defined standard operation procedures that would apply for proteins in general. Essentially, a tradeoff between the intensity of the electric field in which the charged particles or molecules move and susceptibility of the macromolecules analyzed has to be ensured. The higher the intensity of the field, the more precise is the measurement, but the higher are the chances that the protein will disintegrate too. As with every other method, a compromise between powerfulness and sensitivity needs to be found. Thus, many advanced measurement settings offer very intensive fields, thereby increasing the measurement precision for the relatively robust inorganic particles, but present imperfect solutions for the organics. Even Tris as a default organic buffer in biochemistry may disintegrate under these settings at conductivities as low as 1 mS/cm. High ionic strengths essentially either increase the surface tension of the solvent and intensify the hydrophobic forces, or increase the solubility of the nonpolar protein residues, thus, unbalancing the protein secondary and tertiary structures by different mechanisms. According to the Hofmeister series,[94–96] which was confirmed as valid for inorganic particles as well,[97] the following ions are arranged in the direction on their increasing destabilization (aggregation or unfolding) of proteins:
| (22) |
| (23) |
Be that as it may, to take pK values of all amino acids that comprise a protein into account when calculating its pI would be a mistake. Namely, as all amino acid residues except those at the C- and N-terminals have their amino and carboxyl groups involved in forming peptide bonds, only those with free acidic or basic side chains should be included in the intrinsic charge calculations. Only Cys/C, Asp/D, Glu/E, His/H, Lys/K, Arg/R, and Tyr/Y (and the amino- and carboxyl-termini of the peptide) amino acid residues, that is, only those containing the so-called titratable side chains are, thus, considered[98] (i.e, only the ones with acidic or basic side chains, as shown in Table 2), and many online algorithms[99] work on this principle. On the other hand, taking into account only these amino acids is again an approximation. Strictly speaking, a deeply buried residue may not necessarily undergo dissociation and, if that is so, it should be excluded from contributing to the intrinsic molecular charge. Since water is mostly excluded from the predominantly hydrophobic and nonpolar interior of the protein, and whenever present it occupies rigid positions in space where it contributes in highly directional hydrogen bonds, it is difficult to predict the extent of dissociation of buried charged side chains. This is however thought to be a rare case since the crucial role of hydrophobic forces in determining the active conformation of the protein dictates that it is energetically unfavorable to have a charged residue buried in the deep interior of the protein. The protein core is typically made up only of non-titratable, hydrophobic and neutral amino acids. The nonpolar residues such as Val/V, Leu/L, Ile/I, Met/M, and Phe/F are, thus, mostly found in the interior of the protein; the charged polar residues such as Arg/R, His/ H, Lys/K, Asp/D, and Glu/E are normally located on the protein surface, in contact with the aqueous solvent; and uncharged polar groups such as Ser/S, Thr/T, Gln/Q, and Tyr/Y may occur in the interior of the protein (typically as H-bonded, which mitigates their polarity), although they are still prevalently exposed on the surface, in contact with the water molecules. Still, the energetically unfavorable packing of charges may happen under certain conditions. Namely, charged residues could be packed inside of the protein as covalent bonds between -SH groups of two cystein residues, forming an S-S bond (disulfide bridge); as salt bridges where opposite charges neutralize each other; or as metal coordination complexes. On the other hand, the dielectric constant in the interior of the protein is 2–40 times less (ε=2–40) than in the bulk water (ε=80), which implies more intensive electric field effects to take place therein.[100] Also, it is worth noting that even residues with nonacidic or non-basic side chains can induce charge on their surface through polarization effects, weak bonding and coordination of ions. Furthermore, pK values for individual amino acid residues are empirically determined for amino acids alone and not as parts of a peptide chain, let alone folded into specific three-dimensional confirmations where they may be forming weak bonds with other residues. Just as increasing the length of an aliphatic chain decreases the frequency of C-C vibrations, a similar synergetic effect occurs herein as well. Amine groups in a chain would not possess the same pK values as in isolation; surrounding cationic amine groups will, for example, electrostatically suppress the protonation of the neighboring amines.[101] Increasing the length of a polyamine chain will, thus, decrease the protonated fraction of its amine group constituents. pK values of given acid-base pairs of titratable side chains of amino acid residues can vary by as much as several pH units depending on the microenvironment. For example, Asp/D residue in nonpolar environment or in close proximity to another Asp/D would attract protons more strongly than otherwise and, hence, have a higher pK.[102] pK values of amino acids also change depending on the ionic strength of the solution. Hence, pI values of proteins are subject to significant variations and are intrinsically determined by the content of the titratable residues and extrinsically by the adsorption of ionic species and the effect of the diffuse double layer of charges. Hence, pI values range from as low as less than 1.0 for pepsin to 4.9 for human serum albumin to 5.4 for human fibrinogen to 6.6 for collagen to 7.1 for human hemoglobin to 9.4 for ribonuclease A to 10.8 for histone to 11.0 for lysozyme to 12.1 for salmine in salmon.[102] Finally, ζ potential is a descriptive quality that is merely indicative of the surface charge of the particle.[27] Because the actual distance from the particle surface at which ζ potential is measured is unknown and depends on the nature of the particle and the suspension medium (it could be anywhere between the Stern layer and the Debye length, that is, the outer boundary of the diffuse layer), ζ potential is merely loosely indicative of the surface charge of the particle. Zeta potential versus pH curves can still be specific to different materials, which justifies the occasional use of the term “electrophoretic fingerprinting” (Figure 14).
TABLE 2.
pK values of the 20 biological amino acids, including those of the side chains of seven titratable residues
| Amino Acid | α-carboxylic acid | α-amino | Side chain |
|---|---|---|---|
| Alanine | 2.35 | 9.87 | |
| Arginine | 2.01 | 9.04 | 12.48 |
| Asparagine | 2.02 | 8.80 | |
| Aspartic Acid | 2.10 | 9.82 | 3.86 |
| Cysteine | 2.05 | 10.25 | 8.00 |
| Glutamic Acid | 2.10 | 9.47 | 4.07 |
| Glutamine | 2.17 | 9.13 | |
| Glycine | 2.35 | 9.78 | |
| Histidine | 1.77 | 9.18 | 6.10 |
| Isoleucine | 2.32 | 9.76 | |
| Leucine | 2.33 | 9.74 | |
| Lysine | 2.18 | 8.95 | 10.53 |
| Methionine | 2.28 | 9.21 | |
| Phenylalanine | 2.58 | 9.24 | |
| Proline | 2.00 | 10.60 | |
| Serine | 2.21 | 9.15 | |
| Threonine | 2.09 | 9.10 | |
| Tryptophan | 2.38 | 9.39 | |
| Tyrosine | 2.20 | 9.11 | 10.07 |
| Valine | 2.29 | 9.72 |
FIG. 14.
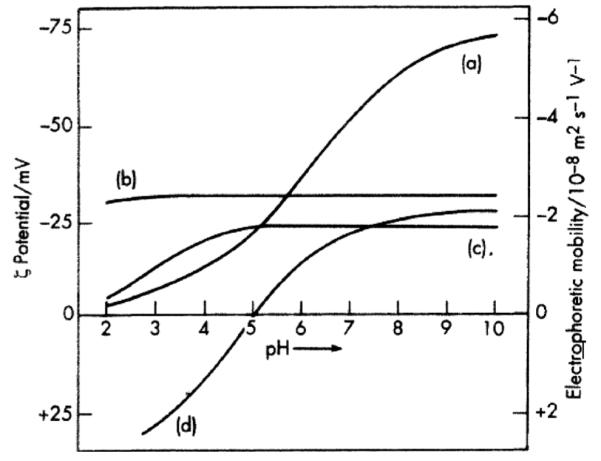
Zeta potentials and electrophoretic mobility of different compounds versus pH: hydrocarbon oil droplets (a), sulphonated polystyrene latex (b), arabic acid as carboxylated polymer (c), and serum albumin (d). Note that there are polymers (b), typically containing periodically arranged heavily charged, phosphorylated or sulphonated groups along their chains,[103] possessing linear and flat ζ potential versus pH curves. Reprinted from Shaw[28] (this article was published in Introduction to Colloid and Surface Chemistry, D. J. Shaw, © Elsevier [2003]).
From the raw electrophoretic mobility data, one can also estimate the effective (uncompensated) charge on molecules (Ne) as a function of pH and ionic strength, which is of interest in predicting the deposition propensity and interaction energy, kinetics and mechanisms on various interfaces. For that purpose, one uses Lorenz-Stokes relationship:[18]
| (24) |
η is viscosity [g(cm s)−1]; rh is the hydrodynamic radius [cm] (determined from the diffusion coefficient measured using DLS and the Stokes-Einstein relationship); and μ is the electrophoretic mobility [μm cm s−1 V−1]. This equation is considered to be more reliable than the titration method which typically tends to overestimate charge on molecules, presumably owing to ion exchange processes. If Ne is >10 (10–25, approximately), the surface charge is high and the aggregation of the protein is excluded for the given pH values. Also, it may imply that a significant rearrangement of the flexible parts of the tertiary structure of the molecule is expected to occur, in analogy with the behavior of polyelectrolyte chains. However, it is important to emphasize that this is the number of uncompensated and not total charges on the protein molecule/particle. As even in pure water free hydronium ions and hydroxyl groups form due to dissociation of water, there will always be ions screening the surface charge of the particle/molecule itself. The number of charges calculated from the electrophoretic mobility data will, thus, not account for the particle/molecule per se, regardless of the properties of the medium in which it is dispersed, but for the given particle/molecule and the ions adsorbed thereon and diffusing between the particle surface and the slipping plane. For, an essential principle of colloid chemistry is that both sides of an interface need to be referred to when describing and explaining any property emanating from it; or, as Ludwig Wittgenstein would have put it, “in order to draw a limit to thinking, we need to think both sides to this limit.”[104]
PRACTICAL LIMITATIONS OF ζ; POTENTIAL ANALYSES
Different specimens made up of an identical chemical composition typically give nonidentical ζ potential versus pH curves and yield different IEPs. Representing each single curve of this type as a narrow line, as is often seen in the literature, instead of a spread of values around each data point is, thus, quite misleading. When standard deviations of the error are not denoted in the graphs, one should imagine them in both X and Y directions for each data point. The bar along Y axis would originate from the inherent unrepeatability of ζ potential measurements, as caused by uncontrollable variations in: (a) the extent of particle aggregation and polydispersity (i.e., imperfect stability of even the most stable suspensions); (b) temperature; (c) concentration of the background inert electrolyte; (d) the type and concentration of impurities; (e) interatomic distances that affect the acidity of surface oxygen atoms. Moreover, the same Brownian motion on which the DLS device relies in measuring the particle size of a colloid is the source of an intrinsic error during the measurements of ζ potential. The DLS device, therefore, takes the average mobility of an ensemble of particles into account, which implies that the measurement error becomes more pronounced at high polydispersities. Spherical approximation mentioned in the previous section accounts for an additional source of uncertainty. Namely, when the particles are anisotropic with respect to their shape, the electrostatic force exerted during ζ potential measurements will depend on their orientation. However, an orientationally averaged mobility could be considered by assuming that the electric field is too low to align the rod-like particles. Still, due to high polydispersity, it is convenient to treat the particles as spheres, although in this approximation the absolute value of the ζ potential may change by a factor of 0.8–1.5 depending on the particle orientation.[105]
The bar along X axis, on the other hand, would originate from the error of pH measurements, which are said to be the main source of uncertainty in microelectrophoretic analyses.[27] Since the second decimal digit of pH values is usually uncertain and unstable, such mistakenly reported overly precise values should have been rounded to 0.1 pH unit. Although pH measurements are sometimes presented with the precision of the third decimal digit,[106] reports of PZCs/pIs with precision down to the second decimal digit are claimed to be due to carelessness and inaccuracy in estimation of the error rather than to extraordinary accuracy. pH values for solutions either partially or completely composed of nonaqueous solvents are also frequently reported based on the direct pH electrode output, without a prior normalization for the water content,[107] which is, however, known to be a complex and not perfectly clear procedure, particularly when nanosized domains of water/oil phases comprise the solvent.[108] Ethanol, for example, does not have pH even though a pH electrode will respond with a signal when immersed in it. However, pKa of ethanol is 15.9, which means that when dissolved in water, at pH 15.9 a half of its molecules will be in C2H5O− form and another half will exist as C2H5OH. Basically, pH of diluted ethanol solutions in water is practically the same as that of water; it can be calculated from two equilibriums—pKw (negative logarithm of the ion product for water: 14.00346 at 25°C) and pKa for ethanol (~15.9)—using Henderson-Hasselbalch equation.
How critical errors in pH measurements can be during the interpretation of microelectrophoretic data is demonstrated in Figure 15. According to Kosmulski, there are multiple reasons for this inevitable spread of pH values measured, starting from the trivial ones which include improper contact between the electrode and the solution, errors in calibration (old calibration buffers?), worn or defective electrodes, inadequate flow rate between the reference electrode and the solution on a clogged electrode, etc., but ending at some fundamental reasons that include the following:
pH is minus the logarithm of the activity of protons rather than of their concentration. Yet, at I > 10 mM, this difference is already higher than 0.1 pH units.
Nonbuffered systems can display fluctuations 1 pH unit wide, and very dilute dispersions (<10−6 M) are particularly sensitive to this effect. This effect may be mitigated by buffering the system, although a tradeoff exists there too. Namely, buffer components are usually surface-active and also the extensive addition of acid/base to adjust the pH would substantially modify the background ionic strength.
Most pH electrodes are very sensitive to Na+ and Li+ salts at pH > 12. Namely, every electrode in certain extent confuses these two ions for H+ ions, implying that in their presence the measured pH will be lower than the real.
For very concentrated dispersions, the solid surface acts as a buffer partially; however, the tendency of the system to be less stable and segregate then appears.
In suspensions, pH measurements are affected by the local gradient of the pH and shifting the electrode up and down can sometimes induce a difference in pH higher than 0.2 pH units. This is the consequence of the gradient of numerous physical properties of the medium, ranging from density to viscosity to pH, as one is moving away from or approaching the interface. A thin gel layer is, thus, present on the accurately responsive electrode; however, its degradation leading to erroneous measurements may result following long-term immersion in: hygroscopic or nonaqueous solutions; in HF acid below pH 4 or strongly alkaline solutions at elevated temperatures; in colloids comprising abrasive particles (SiO2, Al2O3, soil samples, etc.); or during storage in dry conditions.[109,110]
The standard pH scale is designed for room temperature, atmospheric pressure, I < 1 M, and water as the solvent. Using the pH electrode outside of this scale requires its calibration under the nonstandard conditions, for which, however, most limitations outlined above still apply.
FIG. 15.
To explain the discrepant data point in terms of the error in a ζ potential measurement solely, a broad margin of error has to be allowed. Yet, it can be explained by allowing relatively narrow margin of error in the pH.
In addition to temperature affecting the pH electrode calibration curve slope (Figure 16), every sample exhibits internal temperature-dependent chemical equilibriums, pre-disposing it to possess a unique pH versus temperature relationship.[112] Therefore, even though a pH electrode may be hypothetically perfectly calibrated, the pH-meter would be unable to correct pH values for temperature effects with a perfect precision. Then, the heat content is never uniformly distributed throughout the sample, which implies local variations in temperature, and different sensors in the system (such as pH electrode and thermocouple) will then respond to different environments. Every electrode also leaks some of its electrolyte content into the solution during a continuous measurement, thereby manifesting the general principle that there is no measurement without an interaction in which the measuring device modifies the properties of the measured system. The greater the leakage rate, the more precise the measurement, which reflects the general trend of all measurements: the greater the interference with the measured system, the more information will be gathered, but the more changes will be introduced in the system as well, which at the same time makes the measurement results less reliable. Finally, every electrode presents a foreign surface which can influence nucleation, and that becomes particularly critical when one works with metastable, lowly supersaturated systems. The latter will be increasingly exploited in future because many natural self-assembly processes, including biomineralization, occur exactly under conditions of low supersaturation when phase transformations are governed by subtle interactions conveyed by weak chemical forces.[113–115]
FIG. 16.
The scope of the temperature-induced pH measurement error for a range of temperatures, as calculated using the Nernst equation: E=Eo—2.3RT(−log[H+])/F, where E is the electric potential measured, Eo is the standard electric potential, R is the gas constant, T is the temperature, and F is the Faraday constant. Reprinted with permission from Queeney.[111] (Figure available in color online.)
The greater spread is typically found in the vicinity of the IEP because dispersions are inherently unstable in that range. Quite often, ζ potential values are immensely scattered in this range and interpolation based on arbitrarily connecting data points from +and – sides of the ζ potential versus pH curve is carried out; depending on the concaveness of the sigmoidal curve drawn, the IEP detected may vary significantly. Extrapolation is done when IEP is very low or very high and the ζ potential data are available only on the +or only on the – side (typically on the – side, as is the case with silicates). If all these effects account for the difference that is less than a single pH unit in terms of IEP, they are considered acceptable. If it is greater than a single pH unit, then impurities could be blamed. Impurities in suspension are normally concentrated on the particle surface, and tiny amounts thereof may be enough to drastically interfere with the ζ potential output. As for impurities, silicate and carbonate ions present the main ones, as they are present in water and other reagents and are also adsorbed from air and leach from parts of the device. The reason why distilled water at atmospheric conditions, typically used in the lab, is acidic rather than neutral (it has pH 5.7) is due to the effect of dissolution of carbon dioxide and the formation of carbonic acid and carbonate ions. The sorption of carbonates and silicates leads to an increase in the negative charge and, thus, a shift of IEP to lower values. Long contacts of dilute dispersions of metal oxides with neutral or basic solutions in glass containers at room temperature have been known to result in decreased pI owing to silica leaching out of the glassware and adsorbing onto the particle surface.[27] Storing colloids in plastic containers is known to minimize the presence of silica contaminants; however, it has been documented that rubber, polyethylene and Teflon all undergo chemical degradation over time and may significantly disrupt experimental reproducibility.[116] Typical distilled (de-ionized) water contains a few solutes at a level higher than 0.01 mM (a few ppm), a few dozens of solutes at a level higher than 1 nM, and hundreds of solutes at a level higher than 10 pM. Then, water under atmospheric conditions contains approximately 5 mM of dissolved gas, which adds up to a single gas molecule per each 3 nm (note that oils contain 10 times more than that). The effects of the dissolved gas on various chemical transformations in wet conditions are mostly unknown, except for the fact that their presence can be comparable to defects in a solid body.[117] There are many cases, however, in which the gas content significantly influences the reaction taking place in the system. For example, the first nucleation stage in precipitation of ferrites involves oxidation of ferric ions. The oxygen content of the solution can, thus, exert a critical effect on the kinetics of the overall process, the particle size, the microstructure and crystal stoichiometry of the precipitated powders, and, therefore, its properties, including the magnetic ones.[118] Yet, another example comes from the recent synthesis of vaterite in reverse micelles of SDS/hexane/water microemulsion.[119] The formation of calcium carbonate is in this case triggered by continuous purging of nitrogen gas through the microemulsion. This leads to a gradual removal of carbon dioxide bubbles, which are, however, unable to escape from the dispersed water phase and become trapped at the oil-water interface where they form a gas-water interface and provide a nucleation surface for the formation of vaterite crystals. Gas bubbles (strictly speaking, these are cavities, as bubbles are defined as possessing a boundary of a different phase beyond which the same phase as the one comprising the bubble exists) are known for their ability to intensify hydrophobic forces, as shown in the case of a 10-fold decrease in flocculation rates upon the removal of dissolved gas in a colloid system composed of paraffin and stearic acid.[120] Just as repeated adsorption/desorption of water during thawing/freezing cycles can induce denaturation of proteins, gaseous cavities can too disrupt their native conformations and, thus, affect ζ potential measurements, which explains why vortexing protein solutions and suspensions is not always recommended.[121] The effect of the gaseous content on pH measurements was evidenced before and invoked to explain variations in the measurement outcomes depending on the stirring rates.[122] As for recombinant proteins, for which the average purity is around 90 wt% (95 wt% is considered high purity), the effect of remnants of the purification and lyophilization processes, such as various types of silica beads or shorter polypeptide segments, can be a cause of variation of the results from one sample/batch to another. Another one of the rarely mentioned effects that leads to a shift in the ζ potential versus pH curves, including the extrapolated IEP, depends on whether an acid or base titration is carried out. Typically, an overlap of these two types of ζ potential versus pH curves results in a hysteresis instead of a perfect overlap. As pointed out by Kosmulski, “Reversibility of titration (acid titration vs. base titration) is not guaranteed, but this is seldom examined; that is, titration in only one direction is reported in most studies. The system tends to ‘remember’ its state from the past: this phenomenon is called hysteresis.”[27] This hysteresis loop also typically narrows as the titration rate decreases, presumably owing to leaving more time for the system to transform from a mildly metastable state to a state that lies closer to adsorption equilibrium.
PROSPECT OF COMBINATORIAL TECHNIQUES
DLS electrophoresis has found innumerable applications in the fields of colloid and soft chemistry. It has been used to characterize colloid dispersions and to gather crucial insights into the particle/solution interface parameters that promote the desired stabilization or phase segregation processes.[123] Deposition of oppositely charged layers has been routinely applied in multilayered thin film technologies,[124] and fabrication of nanoparticles with functionalized surfaces or complex core-shell structures routinely relies on ζ potential measurements.[125–127] Yet, one of the most prosperous paths for the future of this method lies in the possibility of its real-time coupling with other spectroscopic or microscopic methods, which would enrich the information content of the characterization outcomes. An upgrade of the DLS electrophoresis measurement apparatus with a gel permeation chromatographer, for example, enables differentiating between protein monomers and dimers, and gives indication of the protein conformation—globular, random coil or elongated, for example—by calculating the slope of the density versus molecular weight curves.[128] In fact, changes in the particle size and ζ potential in parallel are routinely followed to additionally support insights about the interaction of given entities, and a similar combinatorial principle could be applied with numerous other experimental techniques. Some of these methods that were used in combination with the DLS electrophoresis so as to gain more profound insights into the mechanisms of the investigated physicochemical transformations have been small angle x-ray scattering (SAXS),[129] circular dichroism (CD),[130] isothermal titration calorimetry,[131] microbalance, rheological, and conductivity analyzers,[132–137] flow fractionation technologies,[138] various infrared spectroscopies,[139,140] x-ray photoelectron spectroscopy,[141] nuclear magnetic resonance,[142] UV-vis spectroscopy,[143] electron spin resonance spectroscopy,[144] surface enhanced Raman spectroscopy,[145] a range of electron, optical, and atomic force microscopic techniques,[146–148] and many other. The main risk, however, is that the complemented methods may give contrasting and incompatible information. On one occasion, for example, the DLS indicated a sharp increase in the particle size following an increase in temperature, whereas this increase was absent in the complementary SAXS analyses.[149] Also, estimating the melting point of hemoglobin as the onset of change in the particle size due to aggregation yielded 38°C as the outcome, which is lower in comparison with the results of CD studies and unlikely to apply to physiological conditions.[150]
In parallel with miniaturization of critical boundaries in technological devices and functional materials that entails the progress in nanoscience and nanoengineering, the reaction systems and the characterization interfaces will tend to become smaller and finer as well.[151,152] Ultrafine streaming potential measurements of ζ potential in microfluidic devices, which are designed to offer in situ optimization of reaction conditions based on an ultrafast feedback from an array of characterization techniques,[153] ranging from various spectroscopic and microscopic analyses to microelectrophoretic ones, seem especially prospective in this context.[154–156]
To sum up, electrophoresis presents an invaluable and, yet, not perfectly quantifiable tool in controlling the interaction and stability of finely dispersed particles. Although electrostatic effects have been proposed as the first step in the merging of self-assembling peptide entities, it was also observed that the following steps dominated by molecular recognition interactions using more subtle forces and short ranges start to take over, exerting the decisive influences on the assembling systems.[157] The complexity of chemical systems utilized to yield advanced materials and assemblies is too high to allow for their control via long-range and nondirectional electrostatic forces. Probing static nanostructures at the fine scale is already an enormous challenge[158] and understanding the dynamic evolution of bio-nano-morphologies at an ultrafine scale and with respect to the short-range and highly directional weak forces stands forth as an even greater one.[2,159–161]
One example of how weak forces can have a decisive influence on the stability of colloidal systems, prevailing over the effect of electrostatic forces, comes from the frequently observed effect of thickening of colloidal dispersions following specific adsorption of phosphate ions onto the particle surface.[162] Namely, although one may expect the adsorbed multivalent phosphate ions to repulse each other and prevent particle-particle contact, it turns out that phosphate ions coating the particles engage in hydrogen bonding with each other, promoting interparticle attraction and aggregation. On the other hand, citrate ions specifically adsorbed on the particle surface undergo intramolecular hydrogen bonding between -OH and the free terminal carboxylic group, which prevents the formation of intermolecular and interparticle hydrogen bonds, resulting in steric repulsion and increased stability of the suspension. Also, the fact that cells whose surface is negatively charged display preferential uptake of negatively charged nanoparticles, rather than those that are positively charged[163] (as in concert with the already mentioned negative surface charge of most biological entities) indicates the prime role of molecular recognition interactions of subtler nature compared to the long-range electrostatic forces in the reign of soft- and bio- chemistry. Numerous other effects of attraction of likewise charged colloidal particles,[164–168] which may seem anomalous from the perspective of sole electrostatic interactions, can be understood only by referring to finer and more directional physicochemical forces. These examples provide arguments against the simple and straightforward application of the criterion of electrostatic repulsion in analyzing and predicting the conditions of colloid stability or aggregation propensity, while disregarding the interaction specificities on a fine, molecular scale.
SUMMARY
Fundamentals of two analytical methods that find pervasive usage in colloid chemistry, DLS, and microelectrophoresis, have been discussed, along with pointing out the main limitations of the two. Most importantly, the spherical approximation integrated in the measuring apparatus of DLS devices and the limited spatial sensitivity and an inability to fully discern double-layer effects from the surface charge ones in microelectrophoretic measurements stand forth as the critical limitations of the two. These two methods are now increasingly finding application in drug delivery, biotechnologies, nanoscience, and other research fields that stand on the frontier of the contemporary science and developing more precise equipment and better quantitative models for probing fine particles with respect to their dimensions and surface charge properties is a vital precondition for an ever greater presence thereof in the modern scientific arena. Also, upgrading or complementing the standard DLS settings with different spectroscopic and microscopic methods can be seen as a prospective path and some of these combinatory characterization techniques were mentioned in this work.
Acknowledgments
The author acknowledges the NIH grant DE021416 for support.
REFERENCES
- [1].Riddick TM. Control of Colloid Stability through Zeta Potential and Its Relationship to Cardiovascular Disease. Livingston; Wynnewood, PA: 1968. [Google Scholar]
- [2].Uskoković V. Reviews in Chemical Engineering. 2007;23:301–372. [Google Scholar]
- [3].Lyklema J. Fundamentals of Interface and Colloid Science. Morgan Kaufmann; San Francisco, CA: 2005. [Google Scholar]
- [4].Shchukin ED. Colloid and Surface Chemistry, Studies in Interface Science 12. Elsevier; Amsterdam: 2001. [Google Scholar]
- [5].Hiemenz PS, Rajagopalan R. Principles of Colloid and Surface Chemistry, Undergraduate Chemistry 14. CRC Press; Boca Raton, FL: 1997. [Google Scholar]
- [6].Ostwald CWW. An Introduction to Theoretical and Applied Colloid Chemistry. LLC; BiblioBazaar: 2009. [Google Scholar]
- [7].Lawandy NM. Applied Physics Letters. 2004;85:5040–5042. [Google Scholar]
- [8].Faraday M. Philosophical Transactions of Royal Society London. 1857;147:145–181. [Google Scholar]
- [9].Derjaguin BV, Landau L. Acta Physicochimica (URSS) 1941;14:633–662. [Google Scholar]
- [10].Verwey EJW, Overbeek JTG, Van Ness K, editors. Theory of the Stability of Lyophobic Colloids–The Interactions of Soil Particles Having an Electrical Double Layer. Elsevier; Amsterdam: 1948. [Google Scholar]
- [11].Malvern, Ltd. (2011) Dynamic Light Scattering (DLS) 2011 Retrieved from http://www.malvern.com/labeng/technology/dynamic_light_scattering/dynamic_light_scattering.htm.
- [12].Alliance Protein Laboratories Inc. Laser Light Scattering. 2010 Retrieved from http://www.ap-lab.com/light_scattering.htm (2010)
- [13].Rossi L, ten Hoorn JWMS, Melnikov SM, Velikov KP. Soft Matter. 2010;6:928–936. [Google Scholar]
- [14].Dhont JKG. An Introduction to the Dynamics of Colloids. Elsevier; Amsterdam: [Google Scholar]
- [15].Tirado MM, Martinez CL, de la Torre JG. Journal of Chemical Physics. 1984;81:2047–2052. [Google Scholar]
- [16].Dhont JKG. An Introduction to the Dynamics of Colloids. Elsevier; Amsterdam: 1996. [Google Scholar]
- [17].Connah M, Kaszuba M, Mattison K. Measuring Nanotube Length & Bundle Number Using Non-Invasive Dynamic Light Scattering. Malvern Instruments; Southborough, MA: 2009. [Google Scholar]
- [18].Wasilewska M, Adamczyk Z, Jachimska B. Langmuir. 2009;25:3698–3704. doi: 10.1021/la803662a. [DOI] [PubMed] [Google Scholar]
- [19].Norde W, Lyklema J. Journal of Colloid and Interface Science. 1978;66:266–284. [Google Scholar]
- [20].Adamczyk Z, Bratek A, Jachimska B, Jasinski T, Warszynski P. Journal of Physical Chemistry B. 2006;110:22426–22435. doi: 10.1021/jp063981w. [DOI] [PubMed] [Google Scholar]
- [21].Wilde PJ. Current Opinion in Colloid and Interface Science. 2000;5:176–181. [Google Scholar]
- [22].Takahashi M. Journal of Physical Chemistry B. 2005;109(46):21858–21864. doi: 10.1021/jp0445270. [DOI] [PubMed] [Google Scholar]
- [23].Han MY, Ahn HJ, Shin MS, Kim SR. Water Science and Technology. 2004;50(8):49–56. [PubMed] [Google Scholar]
- [24].Usui S, Healy TW. Journal of Colloid and Interface Science. 2001;240(1):127–132. doi: 10.1006/jcis.2001.7661. [DOI] [PubMed] [Google Scholar]
- [25].Kim JY, Song MG, Kim JD. Journal of Colloid and Interface Science. 2000;223(2):285–291. doi: 10.1006/jcis.1999.6663. [DOI] [PubMed] [Google Scholar]
- [26].Malvern, Ltd Zeta potential measurement using laser Doppler electrophoresis (LDE) 2010 Retrieved from http://www.malvern.de/LabGer/technology/zeta_potential/zeta_potential_LDE.htm.
- [27].Kosmulski M. Surface Charging and Points of Zero Charge, Surfactant Science Series 145. CRC Press; Boca Raton, FL: 2009. [Google Scholar]
- [28].Shaw DJ. Introduction to Colloid and Surface Chemistry. Butterworth Heinemann; Oxford, UK: 2003. [Google Scholar]
- [29].International Union of Pure and Applied Chemistry . Manual of Symbols and Terminology for Physicochemical Quantities and Units. Appendix II. Definitions, Terminology and Symbols in Colloid and Surface Chemistry. IUPAC; Washington, DC: 1971. [Google Scholar]
- [30].Uskoković V, Matijević E. Journal of Colloid and Interface Science. 2007;315(2):500–511. doi: 10.1016/j.jcis.2007.07.010. [DOI] [PubMed] [Google Scholar]
- [31].Uskoković V. Materials and Manufacturing Processes. 2008;23(6):620–623. [Google Scholar]
- [32].Uskoković V. Steroids. 2008;73:356–369. doi: 10.1016/j.steroids.2007.12.005. [DOI] [PubMed] [Google Scholar]
- [33].Tatsumi N, Tsuda I, Masaoka M, Imai K. Thrombosis Research. 1992;65(4–5):585–592. doi: 10.1016/0049-3848(92)90208-r. [DOI] [PubMed] [Google Scholar]
- [34].Uskoković V. Res Cogitans: Journal of Philosophy. 2009;6(1):286–400. [Google Scholar]
- [35].Uskoković V. Axiomathes: An International Journal in Ontology and Cognitive Systems. 2009;19:17–50. [Google Scholar]
- [36].Uskoković V. World Futures: Journal of General Evolution. 2009;65:241–269. [Google Scholar]
- [37].Uskoković V. Pragmatics & Cognition. 2011;19(3):562–589. [Google Scholar]
- [38].Zeta-Meter, Inc. Zeta Potential: A Complete Course in 5 Minutes. 2010 Retrieved from www.zeta-meter.com/5min.pdf.
- [39].Wade RC, Gabdoulline RR, Ludemann SK, Lounnas V. Proceedings of the National Academy of Sciences. 1998;95(11):5942–5949. doi: 10.1073/pnas.95.11.5942. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [40].Schultz N, Metreveli G, Franzreb M, Frimmel FH, Syldatk C. Colloids and Surfaces B. 2008;66(1):39–44. doi: 10.1016/j.colsurfb.2008.05.004. [DOI] [PubMed] [Google Scholar]
- [41].Cai K, Frant M, Bossert J, Hilderbrand G, Liefeith K, Jandt KD. Colloids and Surfaces B. 2006;50(1):1–8. doi: 10.1016/j.colsurfb.2006.03.016. [DOI] [PubMed] [Google Scholar]
- [42].Tokumasu F, Nardone GA, Ostera GR, Fairhurst RM, Beaudry SD, Hayakawa E, Dvorak JA. PLoS One. 2009;4(6):e5828. doi: 10.1371/journal.pone.0005828. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [43].Wilson WW, Wade MM, Holman SC, Champlin FR. Journal of Macrobiological Methods. 2001;43(3):153–164. doi: 10.1016/s0167-7012(00)00224-4. [DOI] [PubMed] [Google Scholar]
- [44].Klodzinska E, Szumski M, Dziuabkiewicz E, Hrynkiewicz K, Skwarek E, Janusz W, Buszewski B. Electrophoresis. 2010;31(9):1590–1596. doi: 10.1002/elps.200900559. [DOI] [PubMed] [Google Scholar]
- [45].Martinez RE, Pokrovsky OS, Schott J, Oelkers EH. Journal of Colloid and Interface Science. 2008;323(2):317–325. doi: 10.1016/j.jcis.2008.04.041. [DOI] [PubMed] [Google Scholar]
- [46].Soni KA, Balasubramanian AK, Beskok A, Pillai SD. Current Microbiology. 2007;56(1):93–97. doi: 10.1007/s00284-007-9046-z. [DOI] [PubMed] [Google Scholar]
- [47].Dealler SF. Journal of Antimicrobial Chemotherapy. 1991;28(3):470–473. doi: 10.1093/jac/28.3.470. [DOI] [PubMed] [Google Scholar]
- [48].Miyake Y, Tsunoda T, Minagi S, Akagawa Y, Tsuru H, Suginaka H. FEMS Microbiology Letters. 1990;57(3):211–214. doi: 10.1016/0378-1097(90)90067-z. [DOI] [PubMed] [Google Scholar]
- [49].Klodzinska E, Szumski M, Hrynkiewicz K, Dziubakiewicz E, Jackowski M, Buszewski B. Electrophoresis. 2009;30(17):3086–3091. doi: 10.1002/elps.200900186. (2009) [DOI] [PubMed] [Google Scholar]
- [50].Rowell RL, Fairhurst DS, Key, Morfesis A, Monahan IM, Mitchnick M, Shattock RA. Langmuir. 2005;21(22):10165–10171. doi: 10.1021/la050619k. [DOI] [PubMed] [Google Scholar]
- [51].Son KK, Tkach D, Patel DH. Biochimica and Biophysica Acta. 2000;1468(1–2):11–14. doi: 10.1016/s0005-2736(00)00312-6. [DOI] [PubMed] [Google Scholar]
- [52].Takeuchi K, Ishihara M, Kawaura C, Noji M, Furuno T, Nakanishi M. FEBS Letters. 1996;397(2–3):207–209. doi: 10.1016/s0014-5793(96)01136-2. [DOI] [PubMed] [Google Scholar]
- [53].Groenink J, Veerman EC, Zandvoort MS, Van der Mei HC, Busscher HJ, Amerongen AVN. Antonie Van Leeuwenhoek. 1998;73(3):279–288. doi: 10.1023/a:1001543514171. [DOI] [PubMed] [Google Scholar]
- [54].Weerkamp AH, Uyen HM, Busscher HJ. Journal of Dental Research. 1988;67(12):1483–1487. doi: 10.1177/00220345880670120801. [DOI] [PubMed] [Google Scholar]
- [55].Kondo Y, Morita Y, Yamada A, Kimura H. Microbiology and Immunology. 2004;48:599–605. doi: 10.1111/j.1348-0421.2004.tb03557.x. [DOI] [PubMed] [Google Scholar]
- [56].Taki K, Seki T, Mononobe S, Kato K. Water Science and Technology. 2008;57(1):19–25. doi: 10.2166/wst.2008.787. [DOI] [PubMed] [Google Scholar]
- [57].Pearson CR, Heng M, Gebert M, Glatz CE. Biotechnology and Bioengineering. 2004;87(1):54–60. doi: 10.1002/bit.20097. [DOI] [PubMed] [Google Scholar]
- [58].Ishijima SA, Okuno M, Mohri H. International Journal of Andrology. 1991;14(5):340–347. doi: 10.1111/j.1365-2605.1991.tb01102.x. [DOI] [PubMed] [Google Scholar]
- [59].Smeets R, Kolk A, Gerressen M, Driemel O, Maciejewski O, Hermanns-Sachweh B, Riediger D, Stein JM. Head and Face Medicine. 2009;5:13. doi: 10.1186/1746-160X-5-13. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [60].Boghak S, Bose S, Bandyopadhyay A. 2010 Society for Biomaterials Annual Meeting; Seattle, WA. 2010. (2010), poster #474. [Google Scholar]
- [61].Smith IO, Baumann MJ, McCabe LR. Journal of Biomedical Materials Research A. 2004;70(3):436–441. doi: 10.1002/jbm.a.30098. [DOI] [PubMed] [Google Scholar]
- [62].Lu HH, Pollack SR, Ducheyne P. Journal of Biomedical Materials Research. 2000;51(1):80–87. doi: 10.1002/(sici)1097-4636(200007)51:1<80::aid-jbm11>3.0.co;2-6. [DOI] [PubMed] [Google Scholar]
- [63].Beech JA. Bioelectromagnetics. 1997;18(5):341–348. doi: 10.1002/(sici)1521-186x(1997)18:5<341::aid-bem1>3.0.co;2-2. [DOI] [PubMed] [Google Scholar]
- [64].Fuziwara S, Ogawa K, Aso D, Yoshizawa D, Takata S, Denda M. British. Journal of Dermatology. 2004;151(3):557–564. doi: 10.1111/j.1365-2133.2004.06085.x. [DOI] [PubMed] [Google Scholar]
- [65].Schwegmann H, Feitz AJ, Frimmel FH. Journal of Colloid and Interface Science. 2010;347(1):43–48. doi: 10.1016/j.jcis.2010.02.028. [DOI] [PubMed] [Google Scholar]
- [66].Zhang Y, Yang M, Portney NG, Ciu D, Budak G, Ozbay E, Ozkan M, Ozkan CS. Biomedical Microdevices. 2008;10(2):321–328. doi: 10.1007/s10544-007-9139-2. [DOI] [PubMed] [Google Scholar]
- [67].Zhang Y, Yang M, Park J-H, Singelyn J, Ma H, Sailor MJ, Ruoslahti E, Ozkan M, Ozkan C. Small. 2009;5(17):1990–1996. doi: 10.1002/smll.200900520. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [68].Fatouros DG, Antimisiaris S,G. Journal of Colloid and Interface Science. 2002;251(2):271–277. doi: 10.1006/jcis.2002.8432. [DOI] [PubMed] [Google Scholar]
- [69].Matos C, de Castro B, Gameiro P, Lima JL, Reis S. Langmuir. 2004;20(2):369–377. doi: 10.1021/la034780b. [DOI] [PubMed] [Google Scholar]
- [70].Schlieper P, Medda PK, Kaufmann R. Biochimica and Biophysica Acta. 1981;644(2):273–283. doi: 10.1016/0005-2736(81)90385-0. [DOI] [PubMed] [Google Scholar]
- [71].Labhasetwar VD, Dorle AK. Journal of Microencapsulation. 1991;8(1):83–85. doi: 10.3109/02652049109021861. [DOI] [PubMed] [Google Scholar]
- [72].Sokolova V, Prymak O, Meyer-Zaika W, Colfen H, Rehage H, Shukla A, Epple M. Mat.-wiss. u. Werkstofftech. 2006;37:6. [Google Scholar]
- [73].Wilhelm P, Stephan D. Journal of Colloid and Interface Science. 2005;293(1):88–92. doi: 10.1016/j.jcis.2005.06.047. [DOI] [PubMed] [Google Scholar]
- [74].Fonseca AC, Frias MA, Bouchet AM, Jarmelo S, Simoes PN, Fausto R, Gil MH, Lairion F, Disalvo EA. Journal of Physical Chemistry, B. 2010;114(17):5946–5952. doi: 10.1021/jp101007b. [DOI] [PubMed] [Google Scholar]
- [75].Uskoković V, Odsinada R, Djordjevic S, Habelitz S. Archives of Oral Biology. 2011;56:521–532. doi: 10.1016/j.archoralbio.2010.11.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [76].Uskoković V. Journal of Biomimetics, Biomaterials and Tissue Engineering. 2010;8:45–78. doi: 10.4028/www.scientific.net/JBBTE.8.45. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [77].Guy Y, Muha RJ, Sandberg M, Weber SG. Analytical Chemistry. 2009;81(8):3001–3007. doi: 10.1021/ac802631e. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [78].Uskoković V, Uskoković DP. Journal of Biomedical Materials Research B: Applied Biomaterials. 2011;96B(1):152–191. doi: 10.1002/jbm.b.31746. [DOI] [PubMed] [Google Scholar]
- [79].Ducheyne P, Kim CS, Pollack SR. Journal of Biomedical Materials Research. 1992;26(2):147–168. doi: 10.1002/jbm.820260203. [DOI] [PubMed] [Google Scholar]
- [80].Orme CA, Giocondi JL. In: Perspectives on Inorganic, Organic, and Biological Crystal Growth: From Fundamentals to Applications. Skowronski M, DeYoreo JJ, Wang CA, editors. Springer; Berlin: 2007. [Google Scholar]
- [81].Zhang Y, Yokogawa Y. Journal of Materials Science. 2008;19:623–628. doi: 10.1007/s10856-006-0047-4. [DOI] [PubMed] [Google Scholar]
- [82].Yao X, Tan S, Jiang D. Journal of Materials Science. 2005;16:161–165. doi: 10.1007/s10856-005-5901-2. [DOI] [PubMed] [Google Scholar]
- [83].Ma J, Liang CH, Kong LB, Wang C. Journal of Materials Science. 2003;14:797–801. doi: 10.1023/a:1025092506583. [DOI] [PubMed] [Google Scholar]
- [84].Sadeghian Z, Heinrich JG, Moztarzadeh F. Journal of Materials Science. 2005;40(17):4619–4623. [Google Scholar]
- [85].Kershner RJ, Bullard JW, Cima MJ. Langmuir. 2004;20(10):4101–4108. doi: 10.1021/la036268w. [DOI] [PubMed] [Google Scholar]
- [86].Cole KS. Biophysical Journal. 1969;6:465–469. doi: 10.1016/S0006-3495(69)86397-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [87].Somasundaran P. Journal of Colloid and Interface Science. 1968;27(4):659–666. [Google Scholar]
- [88].Ong HT, Loo JSC, Boey FYC, Russell SJ, Ma J, Peng K-W. Journal of Nanoparticle Research. 2008;10(1):141–150. [Google Scholar]
- [89].Moulin P, Roques H. Journal of Colloid and Interface Science. 2003;261(1):115–126. doi: 10.1016/s0021-9797(03)00057-2. [DOI] [PubMed] [Google Scholar]
- [90].Dorozhkin SV. Materials. 2009;2(2):399–498. [Google Scholar]
- [91].Rodriguez K, Araujo M. Journal of Colloid and Interface Science. 2006;300(2):788–794. doi: 10.1016/j.jcis.2006.04.030. [DOI] [PubMed] [Google Scholar]
- [92].Valdivieso AL, Bahena JLR, Song SU, rbina RH. Journal of Colloid and Interface Science. 2006;298(1):1–5. doi: 10.1016/j.jcis.2005.11.060. [DOI] [PubMed] [Google Scholar]
- [93].Drzymala J, Sadowski Z, Holysz L, Chibowski E. Journal of Colloid and Interface Science. 1999;220(2):229–234. doi: 10.1006/jcis.1999.6528. [DOI] [PubMed] [Google Scholar]
- [94].Kunz W, Lo Nostro P, Ninham BW. Current Opinion in Colloid and Interface Science. 2004;9:1–18. [Google Scholar]
- [95].Edwards SA, Williams DRM. Current Opinion in Colloid and Interface Science. 2004;9:139–144. [Google Scholar]
- [96].Leontidis E. Current Opinion in Colloid and Interface Science. 2002;7:81–91. [Google Scholar]
- [97].Das MR, Borah JM, Kunz W, Ninham BW, Mahiuddin S. Journal of Colloid and Interface Science. 2010;344(2):482–491. doi: 10.1016/j.jcis.2009.12.048. [DOI] [PubMed] [Google Scholar]
- [98].Nelson DL, Cox MM. Lehninger Principles of Biochemistry. 4th ed W. H. Freeman; New York: 2004. [Google Scholar]
- [99]. Retrieved from http://www.embl-heidelberg.de/cgi/pi-wrapper.pl; http://www.embl.de/cgi/pi-wrapper.pl; http://www.nihilnovus.com/Palabra.html; http://www.scripp-s.edu/~cdputnam/protcalc.html; http://isoelectric.ovh.org.
- [100].Friedli G-L. Interaction of Deamidated Soluble Wheat Protein (SWP) with Other Food Proteins and Metals, PhD Thesis. 1996 Retrieved from http://www.friedli.com/research/research.html.
- [101].Liu Y, Reineke TM. Bioconjugate Chemistry. 2007;18:19–30. doi: 10.1021/bc060029d. [DOI] [PubMed] [Google Scholar]
- [102].Voet D, Voet JG, Pratt CW. Fundamentals of Biochemistry. John Wiley & Sons; New York: 1999. [Google Scholar]
- [103].Adamczyk Z, Nattich M, Wasilewska M. Journal of Colloid and Interface Science. 2011;356(2):454–464. doi: 10.1016/j.jcis.2011.01.009. [DOI] [PubMed] [Google Scholar]
- [104].Wittgenstein L. Tractatus Logico-Philosophicus. Routledge; London: 1918. [Google Scholar]
- [105].Hunter RJ. Zeta Potential in Colloid Science: Principles and Applications. Academic Press; London: 1981. [Google Scholar]
- [106].Wang L, Guan X, Du C, Moradian-Oldak J, Nancollas GH. Journal of Physical Chemistry C. 2007;111(17):6398–6404. doi: 10.1021/jp0675429. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [107].Kosmulski M, Matijević E. Colloid and Polymer Science. 1992;270(10):1046–1048. [Google Scholar]
- [108].Uskoković V, Drofenik M. Surface Review and Letters. 2005;12(2):239–277. [Google Scholar]
- [109].Metrohm, Inc. Application Bulletin No. 188/2 e. Herisau; Switzerland: 2009. [Google Scholar]
- [110].Galster H. pH Measurement–Fundamentals, Methods, Applications, Instrumentation. VCH Verlagsgesellschaft mbH; Weinheim: 1991. [Google Scholar]
- [111].Queeney KM. Why are There So Many Types of pH Electrodes? Mettler Toledo Ingold; Woburn, MA: 2003. [Google Scholar]
- [112].Thermo Fisher Scientific . User Guide: Ross Ultra, Ross, Ross Sure-Flow, and PerpHecT Ross Electrodes. Beverly, MA: 2009. [Google Scholar]
- [113].Uskoković V. Current Nanoscience. 2009;5(3):372–389. doi: 10.2174/157341309788921381. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [114].Uskoković V, Kim M,-K, Li W, Habelitz S. Journal of Materials Research. 2008;32:3184–3195. doi: 10.1557/JMR.2008.0387. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [115].Uskoković V, Li W, Habelitz S. Journal of Crystal Growth. 2011;316:106–117. doi: 10.1016/j.jcrysgro.2010.12.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [116].Nagy IP, Bazsa Gy. Reaction Kinetics and Catalysis Letters. 1991;45(1):15–25. [Google Scholar]
- [117].Ninham B. In: Self-Assembly. Robinson BH, editor. IOS Press; Amsterdam: 2003. [Google Scholar]
- [118].Uskoković V, Drofenik MA. Colloids and Surfaces A. 2005;266:168–174. [Google Scholar]
- [119].Walsh D, Lebeau B, Mann S. Advanced Materials. 1999;11(4):324–328. [Google Scholar]
- [120].Atkins P, de Paula J. Physical Chemistry. 7th ed Oxford University Press; Oxford, UK: 2002. [Google Scholar]
- [121].Phianmongkhol A, Varley J. Journal of Colloid and Interface Science. 2003;260(2):332–338. doi: 10.1016/s0021-9797(03)00086-9. [DOI] [PubMed] [Google Scholar]
- [122].Metrohm, Inc. Application Bulletin No. 188/2 e. Herisau; Switzerland: 2009. [Google Scholar]
- [123].Birdi KS, editor. Handbook of Surface and Colloid Chemistry. CRC Press; Boca Raton, FL: 1997. [Google Scholar]
- [124].Zhu JH, Zhang B, Fang WW, Lao XJ, Yu H. Colloids and Surfaces, B. 2005;43(1):1–6. doi: 10.1016/j.colsurfb.2005.03.010. [DOI] [PubMed] [Google Scholar]
- [125].Ching YI, Kim JC, Kim YH, Tae G, Lee SY, Kim K, Kwon IC. Journal of Controlled Release. 2010;143(3):374–382. doi: 10.1016/j.jconrel.2010.01.017. [DOI] [PubMed] [Google Scholar]
- [126].Cauda V, Schlossbauer A, Kecht J, Zurner A, Bein T. Journal of the American Chemical Society. 2009;131(32):11361–11370. doi: 10.1021/ja809346n. [DOI] [PubMed] [Google Scholar]
- [127].Dorris A, Rucareanu S, Reven L, Barrett CJ, Lennox RB. Langmuir. 2008;24(6):2532–2538. doi: 10.1021/la703003m. [DOI] [PubMed] [Google Scholar]
- [128].Malvern, Ltd. 2010 Retrieved from http://www.malvern.com/LabEng/technology/gel_permeation_chromatography_theory/gpc_sec_theory.htm.
- [129].Andreozzi P, Funari SS, La Mesa C, Mariani P, Ortore MG, Sinibaldi R, Spinozzi F. Journal of Physical Chemistry B. 2010;114(24):8056–8060. doi: 10.1021/jp100437v. [DOI] [PubMed] [Google Scholar]
- [130].Wettig SD, Deubry R, Akbar J, Kaur T, Wang H, Sheinin T, Joseph JW, Slavcev RA. Physical Chemistry Chemical Physics. 2010;12(18):4821–4826. doi: 10.1039/b923817d. [DOI] [PubMed] [Google Scholar]
- [131].Ikonen M, Murtomaki L, Kontturi K. Colloids and Surfaces B. 2010;78(2):275–262. doi: 10.1016/j.colsurfb.2010.03.017. [DOI] [PubMed] [Google Scholar]
- [132].Jachimska B, Wasilewska M, Adamczyk Z. Langmuir. 2008;24(13):6866–6872. doi: 10.1021/la800548p. [DOI] [PubMed] [Google Scholar]
- [133].Nita LE, Chiriac AP, Neamtu I, Bercea M. Colloids and Surfaces B. 2009;76(1):70–75. doi: 10.1016/j.colsurfb.2009.10.013. [DOI] [PubMed] [Google Scholar]
- [134].Park HM, Kim TW. Analytical Chimica Acta. 2007;593(2):171–177. doi: 10.1016/j.aca.2007.04.054. [DOI] [PubMed] [Google Scholar]
- [135].Kaufman ED, Belyea J, Johnsom MC, Nicholson ZM, Ricks JL, Shah PK, Bayless M, Pettersson T, Feldoto Z, Blomberg E, Claesson P, Franzen S. Langmuir. 2007;23(11):6053–6062. doi: 10.1021/la063725a. [DOI] [PubMed] [Google Scholar]
- [136].Lu F, How TY, Kwok DY. Journal of Colloid and Interface Science. 2006;299(2):972–976. doi: 10.1016/j.jcis.2006.03.014. [DOI] [PubMed] [Google Scholar]
- [137].Gleeson JP. Journal of Colloid and Interface Science. 2002;249(1):217–226. doi: 10.1006/jcis.2002.8256. (2002) [DOI] [PubMed] [Google Scholar]
- [138].Chang MH, Dosev D, Kennedy IM. Sensors and Actuators B. 2007;124(1):172–178. doi: 10.1016/j.snb.2006.12.019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [139].Del Nero M, Galindo C, Barillon R, Halter E, Made B. Journal of Colloid and Interface Science. 2010;342(2):437–444. doi: 10.1016/j.jcis.2009.10.057. [DOI] [PubMed] [Google Scholar]
- [140].Xu T, Fu R, Yan L. Journal of Colloid and Interface Science. 2003;262(2):342–350. doi: 10.1016/S0021-9797(03)00208-X. [DOI] [PubMed] [Google Scholar]
- [141].Botelho CM, Lopes MA, Gibson IR, Best SM, Santos JD. Journal of Materials Science. 2002;13(12):1123–1127. doi: 10.1023/a:1021177601899. [DOI] [PubMed] [Google Scholar]
- [142].Ciani L, Ristori S, Bonechi C, Rossi C, Martini G. Biophycial Chemistry. 2007;131(1–3):80–87. doi: 10.1016/j.bpc.2007.09.011. [DOI] [PubMed] [Google Scholar]
- [143].Rezwan K, Meier LP, Rezwan M, Voros J, Textor M, Gauckler LJ. Langmuir. 2004;20(23):10055–10061. doi: 10.1021/la048459k. [DOI] [PubMed] [Google Scholar]
- [144].Ciani L, Ristori S, Salvati A, Calamai L, vMartini G. Biochimica Biophysica Acta. 2004;1664(1):70–79. doi: 10.1016/j.bbamem.2004.04.003. [DOI] [PubMed] [Google Scholar]
- [145].Cherepy NJ, Shen TH, Esposito AP, Tillotson TM. Journal of Colloid and Interface Science. 2005;282(1):80–86. doi: 10.1016/j.jcis.2004.08.064. [DOI] [PubMed] [Google Scholar]
- [146].Ferrari L, Kaufmann J, Winnefeld F, Plank J. Journal of Colloid and Interface Science. 2010;347(1):15–24. doi: 10.1016/j.jcis.2010.03.005. [DOI] [PubMed] [Google Scholar]
- [147].Irigoyen J, Moya SE, Iturri JJ, Llarena I, Azzaroni O, Donath E. Langmuir. 2009;25(6):3374–3380. doi: 10.1021/la803360n. [DOI] [PubMed] [Google Scholar]
- [148].Rosenhahn A, Finlay JA, Petit ME, Ward A, Wirges W, Gerhard R, Callow ME, Grunze M, Callow JA. Biointerphases. 2009;4(1):7–11. doi: 10.1116/1.3110182. [DOI] [PubMed] [Google Scholar]
- [149].Aichmayer B, Margolis HC, Sigel R, Yamakoshi T, Simmer JP, Fratzl P. Journal of Structural Biology. 2005;151:239–249. doi: 10.1016/j.jsb.2005.06.007. [DOI] [PubMed] [Google Scholar]
- [150].Santiago PS, Moura F, Moreira LM, Domingues MM, Santos NC, Tabak M. Biophysical Journal. 2008;94(6):2228–2240. doi: 10.1529/biophysj.107.116780. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [151].Uskoković V. Technology in Society. 2007;29(1):43–61. [Google Scholar]
- [152].Uskoković V, Bertassoni LE. Materials. 2010;3(3):1674–1691. doi: 10.3390/ma3031674. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [153].Whitesides GM. Nature. 2006;442(7101):368–373. doi: 10.1038/nature05058. [DOI] [PubMed] [Google Scholar]
- [154].Kirby BJ, Hasselbrink EF., Jr. Electrophoresis. 2004;25(2):187–213. doi: 10.1002/elps.200305754. [DOI] [PubMed] [Google Scholar]
- [155].Tandon V, Bhagavatula SK, Kirby BJ. Electrophoresis. 2009;30(15):2656–2667. doi: 10.1002/elps.200900028. [DOI] [PubMed] [Google Scholar]
- [156].Renaud L, Kleimann P, Morin P. Electrophoresis. 2004;25(1):123–127. doi: 10.1002/elps.200305696. [DOI] [PubMed] [Google Scholar]
- [157].Uskoković V, Castiglione Z, Cubas P, Zhu L, Li W, Habelitz S. Journal of Dental Research. 2010;89(2):149–153. doi: 10.1177/0022034509354455. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [158].Billinge SJ, Levin I. Science. 2007;316:561–565. doi: 10.1126/science.1135080. [DOI] [PubMed] [Google Scholar]
- [159].Uskoković V. Current Nanoscience. 2008;4:119–129. doi: 10.2174/157341309788921381. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [160].Uskoković V. Advances in Colloid and Interface Science. 2008;141(1–2):37–47. doi: 10.1016/j.cis.2008.02.004. [DOI] [PubMed] [Google Scholar]
- [161].Uskoković V. Trends in Practical Colloid Science. Nova Science Publishers; Hauppauge, NY: 2009. [Google Scholar]
- [162].Khoo KS, The EJ, Leong YK, Ong BC. Langmuir. 2009;25(6):3418–3426. doi: 10.1021/la8036204. [DOI] [PubMed] [Google Scholar]
- [163].Patil S, Sandberg A, Heckert E, Self W, Seal S. Biomaterials. 2007;28(31):4600–4607. doi: 10.1016/j.biomaterials.2007.07.029. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [164].Crocker JC. MRS Bulletin. 1998;23:24–31. [Google Scholar]
- [165].Grier DG. Journal of Physics: Condensed Matter. 2000;12:A85–A94. [Google Scholar]
- [166].Grier DG, Behrens SH. In: Electrostatic Effects in Biophysics and Soft Matter. Holm C, Kekicheff P, Podgornik R, editors. Kluwer; Dordrecht: 2001. [Google Scholar]
- [167].Zahn K, Maret G. Current Opinion in Colloid & Interface Science. 1999;4:60–65. [Google Scholar]
- [168].Attard P. Current Opinion in Colloid and Interface Science. 2001;6:366–371. [Google Scholar]