Relationship between tendon stiffness and failure: a metaanalysis

Abstract

Tendon is a highly specialized, hierarchical tissue designed to transfer forces from muscle to bone; complex viscoelastic and anisotropic behaviors have been extensively characterized for specific subsets of tendons. Reported mechanical data consistently show a pseudoelastic, stress-vs.-strain behavior with a linear slope after an initial toe region. Many studies report a linear, elastic modulus, or Young's modulus (hereafter called elastic modulus) and ultimate stress for their tendon specimens. Individually, these studies are unable to provide a broader, interstudy understanding of tendon mechanical behavior. Herein we present a metaanalysis of pooled mechanical data from a representative sample of tendons from different species. These data include healthy tendons and those altered by injury and healing, genetic modification, allograft preparation, mechanical environment, and age. Fifty studies were selected and analyzed. Despite a wide range of mechanical properties between and within species, elastic modulus and ultimate stress are highly correlated (R² = 0.785), suggesting that tendon failure is highly strain-dependent. Furthermore, this relationship was observed to be predictable over controlled ranges of elastic moduli, as would be typical of any individual species. With the knowledge gained through this metaanalysis, noninvasive tools could measure elastic modulus in vivo and reasonably predict ultimate stress (or structural compromise) for diseased or injured tendon.

tendon is a highly specialized, hierarchical tissue with a predominantly mechanical function in the body (i.e., translating muscle contraction into joint movement). A key functional metric for pathologic or damaged tendon is therefore ultimate strength. This parameter bounds the mechanical capabilities of normal tissue and defines risk of failure in damaged or diseased tissue. Along with ultimate strength, tendon elastic modulus is also commonly reported in many in vitro studies while examining various tendons from different species and in different states of damage or repair.

Applying data from multiple sources under different testing conditions to an in vivo subject is problematic. Whereas some studies have suggested a possible relationship between ultimate stress and elastic modulus in tendon (71), this issue has not been rigorously explored on an interstudy basis. One group reported tendon having relatively constant elastic modulus over three orders of magnitude of body mass (58). However, the range of elastic moduli and ultimate stresses reported in the literature warrant further investigation into whether tendons have constant elastic properties or whether they exhibit a more complex behavior. Additionally, the dependence of tendon failure on strain, suggested by Sharma and Maffulli (65), requires further investigation; if tendon failure is a function of strain and if mechanical behavior is sufficiently linear, elastic modulus will be directly related to ultimate stress.

Animal musculoskeletal systems have evolved to accommodate a wide range of forces. Tendon dimensions have adapted under the influence of daily loading that scales with animal size (57, 58) and factors such as mechanical advantage (6, 7), safety (44), and energy storage (8). However, tendon dimensions alone do not explain the wide variety of mechanical properties reported in the previously published literature. It follows that different tendons have not only adapted in dimensions to allow them to sustain required loads, but also in areas such as composition, microstructure, and cross-linking to exhibit different mechanical properties.

The unique mechanical behavior of healthy tendon can change dramatically due to either natural processes such as aging or traumatic events such as injury or disease. Recently, investigators have been able to quantify the resulting morphological attributes of tendon and correlate them with mechanical changes. Some of these factors include collagen fibril volume fraction (36, 45), collagen fibril diameter (21, 24), tissue hydration (17, 39, 69), and collagen cross-linking (1, 4, 18, 40). Although interstudy inconsistencies mean that none of these factors necessarily predict tendon mechanical properties, they do provide an extensive database of tendon mechanical properties from reliable sources. No investigations have pooled these data broadly to characterize interstudy relationships. This study provides this detailed characterization of tendon failure mechanics, the ultimate goal of which is to relate clinically measurable mechanical properties of tendon to failure properties. Elastic modulus and ultimate stress are compared on the basis of published results for tendon from different species and conditions of health and injury.

METHODS

Identification and selection of studies.

Prior to conducting a literature search, general study inclusion/exclusion criteria were established. Studies were selected only if there was sufficient information to calculate all relevant structural and mechanical properties (gauge length, cross-sectional area, stiffness, ultimate stress, elastic modulus, and ultimate load). For example, if ultimate stress was not given explicitly, the study could be used if cross-sectional area and ultimate load were reported. The strain rate used for the pull-to-failure test in the study was also required for inclusion. It was the goal of this metaanalysis to collect a highly heterogeneous study pool that included many different animals and tendon groups, to determine whether any observed interrelationships between elastic modulus and ultimate stress could be broadly applied.

A search of published literature using the Google Scholar database (studies from 1980 to the present) was performed. The key words tendon, mechanical properties, ultimate stress, and elastic modulus were used in separate searches and in conjunction with injury or healing to identify all relevant articles. An additional search of articles published since 2000 was performed to avoid overlooking any recent relevant research. Articles were examined and selected on the basis of inclusion/exclusion criteria. A final group of studies was selected on the basis of inclusion/exclusion criteria from the articles cited by this initial group of studies.

Data extraction.

The extracted data consisted of objective data only, so all extraction was performed by a single reviewer. Extracted data included animal, tendon, sample size, gauge length (mm), cross-sectional area (mm²), strain rate (%/sec), elastic modulus (MPa), stiffness (N/mm), ultimate stress (MPa), and failure load (N). In some cases, structural data (load, stiffness) were collected to calculate the mechanical properties of the tendon (stress, modulus) by the following relationships:

$$\sigma =F/A$$ 1

$$E=(L_{gage}\ast k)/A$$ 2

where σ represents stress, F represents force, A represents original area, E represents elastic modulus, L_gage represents gage length, and k represents stiffness.

In some studies, the cross-sectional area or gage length of a specific tendon was not explicitly given. In these cases, studies that used the same tendon and mechanical testing setup were consulted. Cross-sectional areas and gage lengths were taken from these related studies and used in the above calculations. Available data were typically given in engineering units (i.e., small deformation metrics for stress and strain), so those metrics are also used in this analysis.

Modulus used to predict failure of tendons.

The failure properties of tendons in individual studies were predicted using one of two methods, both of which assume a constant ratio of ultimate stress to elastic modulus. Although this ratio does not necessarily equal ultimate strain because of the pseudoelastic behavior of tendon and mechanical nonlinearity, it is a conservative estimate of ultimate strain and will be treated as such for the duration of the analysis.

In the first method, the failure stress of a tendon that had been treated (i.e., healing, cross-linked, etc.) was predicted from its modulus value using a ratio based on a control (untreated) data point with known ultimate stress (σ_C) and elastic modulus (E_C). Hence, the regression prediction follows the equation:

$${\sigma }_p=({\sigma }_C/E_C)\ast E_M$$ 3

where σ_P is the predicted ultimate stress of the tendon and E_M is the measured modulus of elasticity for the specific tendon. This method uses data specific to a study (the control group information from the study along with the modulus of the specific tendon).

The second prediction method predicts the ultimate stress of a tendon using a constant ratio (i.e., ultimate strain) on the basis of the relationship between ultimate stress and elastic modulus in the pooled data (Fig. 1A):

$${\sigma }_p=0.0932\ast E_M$$ 4

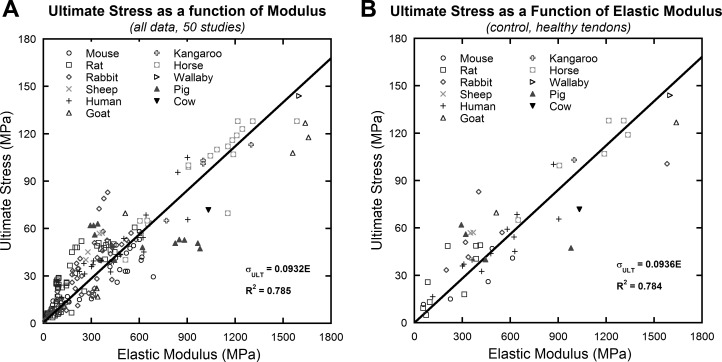
Fig. 1.

Compiled data collected from literature search of 50 studies. Each data point represents the average mechanical behavior of a single group in each study. A linear relationship between elastic modulus and ultimate stress was observed in the compiled data (A) and in the healthy control tendon data (B). Linear curve fits were forced through the origin.

This method uses general information from pooled data along with the modulus of the specific tendon.

To determine the accuracy of each prediction method, both were applied to each data set.

Statistical analysis.

A number of different analyses were used test the accuracy of each prediction method. First, the ratio of predicted to actual stress was calculated. Next, the predicted ultimate stress was plotted against the actual values and fitted with a linear regression, yielding an R² value. Finally, the root-mean-square error (RMSE) calculation was used to test the variance of the predicted compared with the actual values.

Ultimate strain values at different elastic modulus values were compared using ANOVA with Tukey's post hoc analysis using Kaleidagraph (v4.03, Synergy Software, Reading, PA). Significance was set at P = 0.05, trends at P = 0.10.

RESULTS

Literature search results.

The Google Scholar search of published literature yielded 4,660 articles that included the key words used in the search (tendon, mechanical properties, ultimate stress, elastic modulus) along with either the word injury or healing. Fifty of these studies fit the inclusion/exclusion criteria and were included in the metaanalysis (2, 3, 5, 9–13, 15, 16, 19, 20, 22, 23, 25–32, 34, 35, 37–39, 42, 43, 45, 46, 48, 53, 54, 59–64, 66–68, 71–77). Within the numerous animal and tendon groups in these studies, tendons were subjected to a number of modifications including but not limited to the effects of injury and healing, genetic alterations, allograft preparation, in vivo mechanical environment, and age (Table 1).

Table 1.

Studies associated by group

Group	Studies
Injury	Young et al. (1998), Stone et al. (1999), Dahlgren et al. (2002), Awad et al. (2003), Forslund and Aspenberg (2003), Chen et al. (2004), Ferry et al. (2007), Fu et al. (2008), Ansorge et al. (2009), Dyment et al. (2012)
Genetics	Robinson et al. (2004), Lin et al. (2005), Mikic et al. (2008), Rigozzi et al. (2010)
Allografts	Gibbons et al. (1991), Roe et al. (1992), Salehpour et al. (1995), Seto et al. (2009)
Mechanical	Cherdchutham et al. (2001), Lavagnino et al. (2005), Eliasson et al. (2007), Legerlotz et al. (2007), Trudel et al. (2007), Rumian et al. (2009)
Age	Danielsen and Andreassen (1988), Johnson et al. (1994), Cherdchutham et al. (2001)
Other	Galeski et al. (1977), Woo et al. (1980), Butler et al. (1986), Bosch et al. (1992), Yamamoto et al. (1992), Blevins et al. (1994), Itoi et al. (1995), Wang and Ker (1995), Crevier et al. (1996), McGough et al. (1996), Smith et al. (1996), Crevier-Denoix et al. (1997), Haut and Haut (1997), Donahue et al. (2001), Dowling et al. (2002), Batson et al. (2003), Carpenter et al. (2005), Hashemi et al. (2005), Diehl et al. (2006), Birch et al. (2008), Su et al. (2008), Hansen et al. (2010), Thorpe et al. (2010)

Relationship between modulus and ultimate stress.

Ultimate stress and elastic modulus were found to correlate strongly in the data set, including all data, R² = 0.785 (Fig. 1A); and also in healthy control tendons, R² = 0.784 (Fig. 1B). A comparison of animal groups showed that the ratio of ultimate stress to elastic modulus (ultimate strain, ε_ult) varied across animal groups (P < 0.001). When divided into groups on the basis of size, ultimate strain remained significantly different between smaller animals (P < 0.001). Rat tendons (ε_ult = 17.96 ± 7.95%) have a significantly higher ultimate strain compared with mouse (ε_ult = 10.47 ± 4.89%) and rabbit (ε_ult = 12.82 ± 4.86%) tendons (P < 0.001 for both). Results are reported as means ± standard deviation. No significant differences in ultimate strain were found for tendons from the larger animals (P = 0.482).

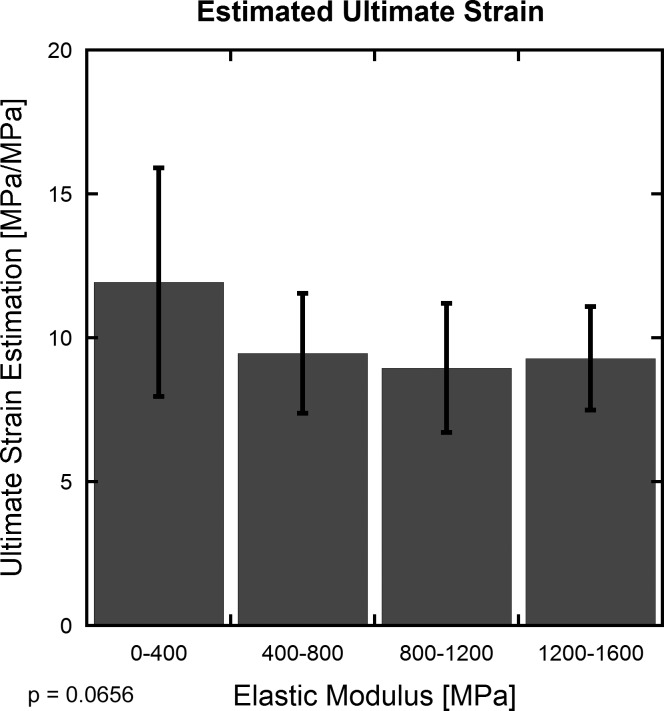
When the pooled data are divided into five groups on the basis of elastic modulus, groups with higher elastic modulus exhibited lower ultimate strain (Fig. 2), and a decreasing trend is observed over the entire data set (P = 0.066). No significance or trend was found between any modulus groups (Fig. 2; P ≥ 0.11).

Fig. 2.

The ratio of ultimate stress to elastic modulus (estimate of ultimate strain) shows a decreasing trend with increasing elastic modulus (standard deviation shown). ANOVA analysis revealed this trend when the whole range of elastic moduli were considered (P = 0.0656), but post hoc analysis found no significance or trends between any pair of groups (P ≥ 0.11). The decrease in estimated ultimate strain is most pronounced in the lowest modulus values, which coincides with the smallest animals and also with groups that underwent more drastic treatments (i.e., genetic knockouts, allografts, etc.). Smaller specimen size may amplify potential edge effects, and more extreme treatments may further result in altered tendon behaviors.

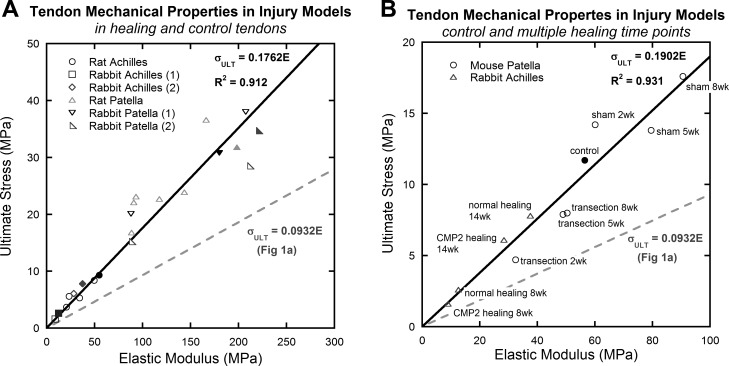
The mechanical behavior of normal and healing (from transection or collagenase-injection injury models) tendons is shown in Fig. 3. Elastic modulus and ultimate stress in these normal and injured populations show a strong linear correlation (R² = 0.912; Fig. 3A), although they have a higher ratio of ultimate stress to elastic modulus than in the original linear curve fit (Fig. 1A). The higher ratio of ultimate stress to elastic modulus (high ultimate strain) in these data follows the trend shown in Fig. 2, because tendons from rabbits, rats, and mice have lower elastic modulus and exhibit higher ultimate strain (noted by the higher ratio of ultimate stress to elastic modulus). Further comparisons showed that for an average elastic modulus of ∼100 MPa, the estimated ultimate strains were similar between injury studies (ε_ult = 18%) and the overall data set (ε_ult = 16%). A detailed examination of the treatment groups of two example studies (28, 31) appears in Fig. 3B.

Fig. 3.

A: mechanical properties of normal and healing (after transection- or collagenase-induced injury) tendon (15, 28, 31, 32, 67). Each data point represents the average mechanical behavior of a single group (i.e., control, “sham” surgery, or healing group) in each study. Tendons induced with an injury and subject to different healing protocols followed the same linear relationship as was observed before. B: details of two studies (28, 31). Control data points are solid, treatment groups are open. Linear curve fits were forced through the origin. Solid lines fit all data in the individual graph, and the trend from Fig. 1A is superimposed on each graph as a dashed line.

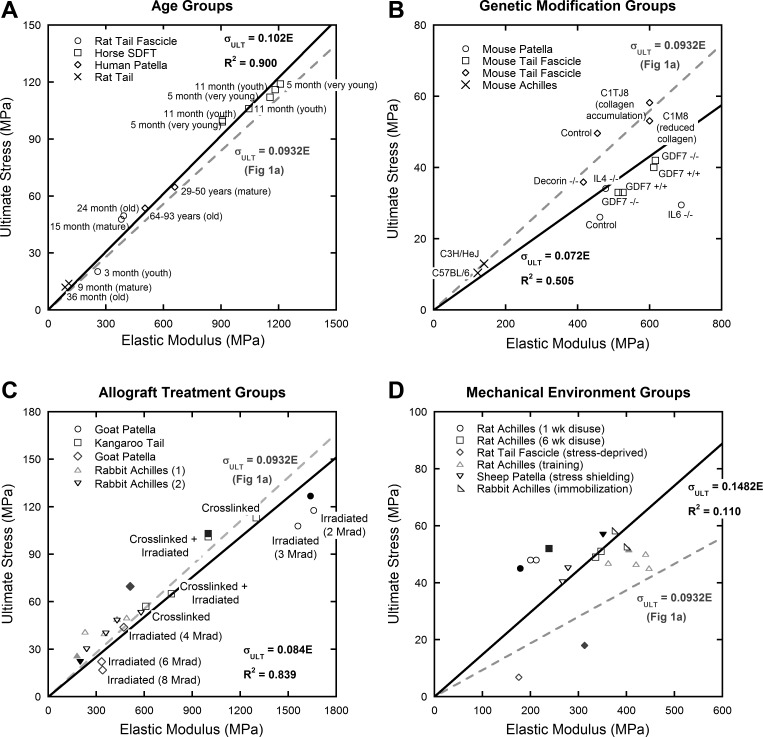
Figure 4 presents data from multiple studies that tested the mechanical properties of tendons that differed in age (sampling from young, mature, and old individuals on the basis of life span of each particular animal), genetic modification (altered expression of interleukins, GDF-7, collagen, and decorin), allograft treatment (cross-linking or irradiation methods prior to implantation), and in vivo mechanical environments (i.e., disuse, vibration, strength training). The ratio of ultimate stress to elastic modulus in studies of animals over multiple age levels had the most linear trend (R² = 0.900; Fig. 4A), followed closely by data from allograft preparation studies (R² = 0.839; Fig. 4C). This is intuitive, because the underlying tendon structure should be similar across groups. The effects of genetic alterations (R² = 0.505; Fig. 4B) and the in vivo mechanical environment (R² = 0.110; Fig. 4D) on tendon mechanics were not highly linear and showed much more variation, which may be due to changes to the tendon structure itself.

Fig. 4.

Mechanical properties of tendons grouped by age (A), genetics (B), allograft treatment (C), and in vivo mechanical environments (D). Each data point represents the average mechanical behavior of a single group in each study. Control data points are solid, treatment groups are open. Linear curve fits were forced through the origin. Solid lines fit all data in the individual graph, and the trend from Fig. 1A was superimposed on each graph as a dashed line. A: age (16, 23, 43): tendon specimens from a range of animal life spans. Rat specimens included youth (3 mo), adult (15 mo), and elderly (24 mo); horse specimens included very young (5 mo) and youth (11 mo); human specimens included adult (29–50 years) and elderly (64–93 years). B: genetics (48, 54, 59, 60): altered expression of interleukins, GDF-7, collagen, and decorin results in altered mechanical behavior, but decreases (or increases) in modulus remain strongly correlated to decreases (or increases) in ultimate stress. C3H/HeJ (C3H) and C57BL/6J (B6) animals are two inbred strains commonly used in skeletal structure function studies; C3H animals demonstrate larger collagen fibrils than B6 animals. “+/+” Indicates an animal that is homozygous positive for a gene, “−/−” indicates a homozygous knockout for that gene. C1TJ8 animals had a mutation at the collagen cleavage site that resulted in accumulation of collagen in the soft tissues, C1M8 animals had a mutation that inhibited collagen formation, which resulted in a 50% reduction in type I collagen. C: allograft treatments (35, 61, 63, 64): common allograft treatments including irradiation (gamma, electron beam) and cross-linking [gluteraldehyde, 1-ethyl-3-[3-dimethyl aminopropyl] carbodiimide (EDC)]. The density of data points prohibits labeling of each point, but combinations of irradiation and cross-linking were used. D: mechanical environment (29, 45, 46, 62, 72): environmental conditions of tendons were varied using stress shielding/immobilization/unloading or physical training methods. Mechanical effects of age and allograft preparation were highly linear. Effects of genetic alterations and differences in mechanical environment were less well defined.

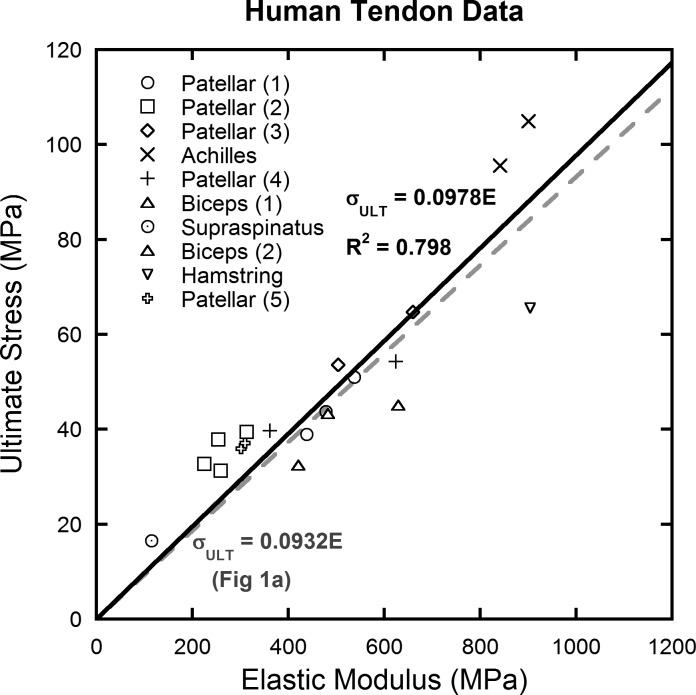
Because clinical translation to human tissue is our highest interest, human data were extracted from the larger data set (Fig. 5) and examined separately (10, 12, 13, 26, 37–39, 42, 43, 53, 75). The data follow the linear trend well (R² = 0.798) and suggest that human tendons fail at about 9.78% strain.

Fig. 5.

Mechanical data extracted from studies on human tendon (10, 12, 13, 26, 37–39, 42, 43, 53, 75). Whereas different tendons have different mechanical properties, they have the same ratio of ultimate stress to elastic modulus (ultimate strain).

Modulus used to predict failure of tendons.

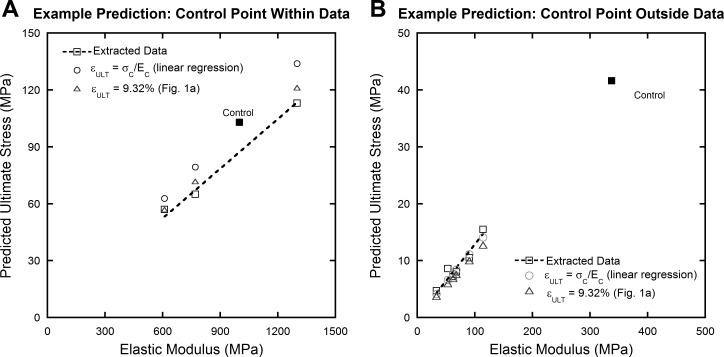
To better understand the prediction of ultimate stress from elastic modulus (and assumed constant ultimate strain), two representative studies were used (Fig. 6). Both of the previously described prediction methods work reasonably well over a range of scales; both high-strength kangaroo tail tendon allografts (61) and smaller, healing rabbit Achilles tendons (77) were accurately predicted. Prediction using a linear regression was also successful whether the control data point, on which the linear regression is based, is within the data set (Fig. 6A) or far outside of it (Fig. 6B).

Fig. 6.

Example predictions using data from studies investigating allograft preparations (A) (61) and Achilles tendon repair (B) (77). Two data sets demonstrate that the prediction methods work well over a range of scales and that the location of the control data point is inconsequential. Control data points are solid, treatment groups are open.

The ratio of predicted to actual values (predicted/actual), R² values, and RMSE for different animal and treatment groups are presented in Tables 2 and 3, respectively. Predictions that assumed a constant ultimate strain (ε_ult = 9.32%; Fig. 1A) performed well in estimating failure properties of altered tendons (R² = 0.832; RMSE = 13.3). Predictions based on a control tendon ultimate strain (linear regression through zero) were even more consistent (R² = 0.959; RMSE = 9.1). The linear regression overpredicted ultimate stress by ∼5% (predicted/actual ratio = 1.048), whereas the prediction assuming ε_ult = 9.32% underestimated ultimate stress by about 7% (predicted/actual ratio = 0.930). If a healthy control point is not known, the ultimate strain of 9.32% acquired from the pooled data appears to accurately approximate ultimate stress from elastic modulus.

Table 2.

Accuracy of prediction methods for different animal groups

	Group	Predicted/Actual Stress	R2	RMSE
ε = σc/Ec (linear regression)	Horse	1.085	0.938	12.6
	Human	0.996	0.989	2.2
	Mouse	1.050	0.928	5.3
	Rabbit	1.126	0.907	9.6
	Rat	1.022	0.844	8.0
	Other	1.125	0.881	13.4
	All	1.048	0.959	9.1
ε = 9.32% (Fig. 1A)	Horse	0.998	0.759	13.2
	Human	0.925	0.802	10.1
	Mouse	1.060	0.789	10.6
	Rabbit	0.653	0.763	14.3
	Rat	0.679	0.707	12.7
	Other	1.071	0.880	15.6
	All	0.930	0.832	13.3

RMSE, root-mean-square error.

Table 3.

Accuracy of prediction methods for different treatment groups

	Group	Predicted/Actual Stress	R2	RMSE
ε = σc/Ec (linear regression)	Age	1.063	0.942	12.9
	Allografts	1.142	0.877	15.1
	Genetics	1.061	0.737	6.7
	Injury	0.994	0.876	5.0
	Mechanics	1.135	0.914	13.3
	Other	0.988	0.991	2.3
	All	1.048	0.959	9.1
ε = 9.32% (Fig. 1A)	Age	0.890	0.983	8.4
	Allografts	0.992	0.905	15.5
	Genetics	1.205	0.041	13.4
	Injury	0.745	0.735	10.2
	Mechanics	0.804	0.797	19.4
	Other	0.871	0.895	10.7
	All	0.930	0.832	13.3

RMSE, root-mean-square error.

When comparing animal groups (Table 2), the linear regression was most reliable for human studies (R² = 0.989; RMSE = 2.2), with prediction values underpredicted by less than 1%. This method also provided good predictions for mouse tendons (R² = 0.928; RMSE = 5.3) with only a 5% overprediction. The linear regression provided more accurate predictions for all animal groups compared with predictions assuming ε_ult = 9.32%, according to RMSE (9.1 vs. 13.3).

When considering treatment groups (Table 3), the failure properties of injured tendons were well predicted by the linear regression (R² = 0.876; RMSE = 5.0). Tendons with genetic modifications were less accurately predicted (R² = 0.737; RMSE = 6.7), with a prediction/actual ultimate stress ratio that overestimated values by ∼6%. Interestingly, the studies grouped into the Other category (Table 3) were most accurately predicted by the linear regression (R² = 0.991; RMSE = 2.3). With the exception of age, the linear regression more accurately predicted failure properties for all treatment groups compared with predictions assuming ε_ult = 9.32%.

DISCUSSION

In the pooled data, a fundamental relationship between ultimate stress and elastic modulus is reported, which correlated strongly (R² = 0.785; Fig. 1A). The same trend held true for the healthy control tendons as a subset (Fig. 1B). This relationship has been suggested to be true in the past (71), but to our knowledge, has never before been shown across multiple studies. Collagen fibrils, the main component contributing to tendon mechanical properties, begin macroscopic failure at 8–10% strain (65); it would therefore appear intuitive that tendons across species and tendon groups would experience failure in a similar strain range and thus demonstrate a correlation between ultimate stress and elastic modulus. This metaanalysis showed that this relationship between ultimate stress and elastic modulus also holds true for a number of different states of pathology, damage, or healing (other than healthy tendon). Within confidence limits, this relationship can be applied to pathomechanics. For example, an injured tendon whose modulus decreases by a certain percentage will also show a proportional decrease in ultimate stress.

This analysis also used the ratio of ultimate stress to elastic modulus as a conservative estimate for ultimate strain. The strain estimate is linearly elastic and based on the linear portion of the stress-strain curve in which the elastic modulus is calculated. This is not inclusive of the strain-stiffening toe region or the strain-softening region before failure at ultimate stress. Tangent modulus values in the nonlinear toe region are much lower than in the linear portion of the stress-strain curve (and therefore undergo more strain for the same stress level), thus contributing to larger actual ultimate stress values being measured than are estimated with this linear model. Whereas ultimate strain tends to decrease with increasing elastic modulus, this trend is not significant when considering specific studies or individual species. Smaller ranges of elastic moduli within these groups make estimations of ultimate strain much more accurate (Fig. 2). Although none of the subsets of data precisely follow the overall trend in Fig. 1A, the variations in ratio of ultimate stress to elastic modulus (ultimate strain) follow the trend found in Fig. 2. For the entire data set, tendons with higher elastic moduli exhibit lower ultimate strain. This can be observed clearly in specific subsets of tendons as well. Injury data, for example (Fig. 3), correlate strongly and show an ultimate strain higher than the pooled data with much smaller values of elastic moduli in those studies. It is also valuable to note that with increasing elastic modulus estimation of ultimate strain becomes much more accurate (Fig. 2), thus making this analysis more applicable to human pathology. The larger variance below ∼400 MPa could be due to inaccuracy in measurements of cross-sectional area, leading to errors in stress calculation, or of initial length, leading to errors in strain calculation.

One goal of this study was to obtain mechanical data from a highly heterogeneous population of tendons. With this heterogeneity comes an inherent lack of continuity in methods between studies. As such, a number of factors could not be controlled or corrected for easily. First, strain rate has been observed to have significant effects on tendon mechanics (39, 60, 70, 75). When the mechanical properties of tendon were normalized assuming a linear relationship with the logarithm of strain rate, the correlation between elastic modulus and ultimate stress just in the strain-rate–focused studies increased only moderately (from R² = 0.562 to R² = 0.666). When the normalization method was applied to the studies with the highest strain rates, ultimate stress did change by an average of 16.9 ± 7.25%, but elastic modulus remained relatively unchanged, differing by an average of less than 3.76 ± 1.60%.

The other factor that was difficult to correct was the differences in measurement techniques. Cross-sectional area measurements varied from study to study, including methods using calibrated digital images (3, 28, 45, 48, 46, 60), cast molds (5, 62, 71), caliper measurements (27, 29, 31, 32, 35, 38, 54, 68, 77), gravimetric measurements (16, 61, 73), ultrasound imaging (19, 20, 22, 75), MRI imaging (72), laser micrometer (2, 43, 64, 67), and specialized area calipers (30, 63, 76). Strain measurements also differed between studies. In general, tendon failure was observed to fall in the range of 10–15% strain, but it did vary from study to study, especially when strain was reported with grip-to-grip vs. on-tissue marker measurements. Specimen length has been observed to have significant effects on measurement of failure strain (47); however, these errors are likely indicative of artifacts due to gripping or other end-effects that are inherent to any mechanical testing system, the correction of which extends beyond the scope of this metaanalysis. If the extracted data were limited by specimen length, the heterogeneity of the pooled data would have been severely limited.

Whereas data on tendon injury and healing are important to consider for their clinical relevance, this metaanalysis included a number of other types of studies that tested differences in age, genetics, allograft preparation, and in vivo mechanical environments (Fig. 4). Of all the groups, those changes in mechanical properties due to age effects seemed to follow a linear trend the best followed closely by allograft preparation effects (R² = 0.900 and 0.839, respectively). Human data (Fig. 5) also show consistent linear behavior for a limited number of available studies (R² = 0.798). In contrast, the groups with genetic alterations (R² = 0.505) and changes in in vivo mechanical environment (R² = 0.110) were not highly linear and showed more variation.

The linear regression through zero prediction method performed more consistently than predictions based on ε_ult = 9.32% from the pooled data (Fig. 1A). However, in predicting the mechanical effects of aging, an assumed constant ultimate strain of 9.32% provided a better prediction than linear regressions from control points (perhaps because the control points are subjective whether they are young, adult, or elderly). It is important to note that the linear regression overpredicted the ultimate stress of tendons by ∼5% (predicted/actual ratio = 1.048), whereas the prediction assuming ε_ult = 9.32% underestimated the ultimate stress by close to the same amount (predicted/actual ratio = 0.930). Although the linear regression is more consistent in predicting failure, it does not provide a safety factor. When applying this linear regression method, this should be taken into account.

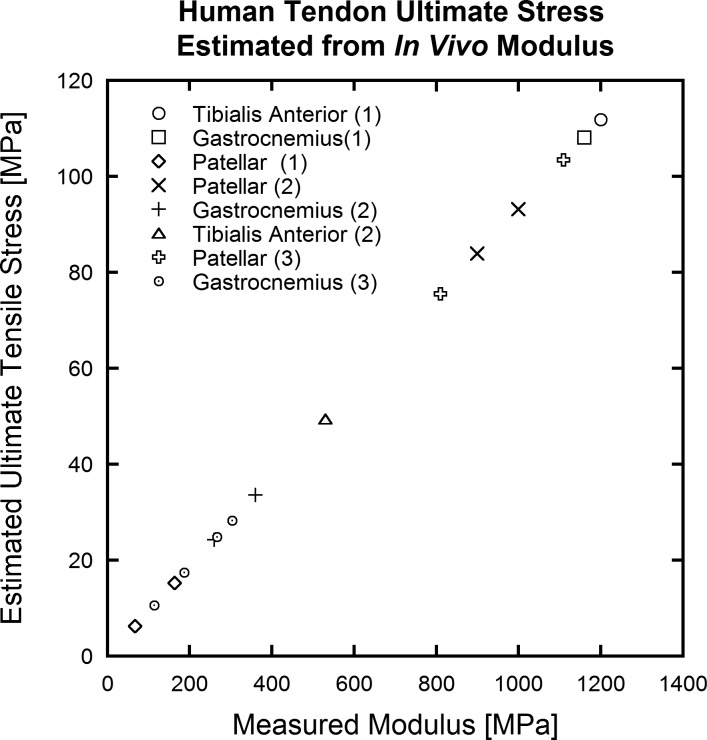
As strain-tracking and force estimation methods continue to improve, the use of ultrasound to mechanically characterize tendon has become a promising technique (14, 33, 41, 49–52, 55, 56) that can be applied in a clinical setting. This metaanalysis suggests that a predictable link exists between elastic modulus and tendon strength. Using these data, ultrasound analysis may then be able to predict failure properties of tendons from subfailure ultrasound measurements of elastic modulus (collected in the linear portion of the stress-strain curve) as in Fig. 7. Such analysis would add functional/mechanical insight to many types of tendon modification, including injury, genetics, altered mechanical environment, and age effects. Similar analysis could also help to evaluate the treatments for tendon injuries.

Fig. 7.

Estimations of ultimate stress on the basis of elastic modulus values collected in vivo. Ultimate stress values fall within the range observed among human data shown in Fig. 5.

Conclusions.

In this metaanalysis we have shown that a linear relationship exists between elastic modulus and ultimate stress that is consistent among tendons of various species, age, and injury status. It is also possible to predict the ultimate mechanical properties of a specific tendon group from a control point and knowledge of the elastic modulus of the tendon, which can be measured noninvasively using ultrasound. Human tendons and those subjected to injury and healing (in animal models) proved to be some of the most predictable types of tendons that closely follow the relationship between elastic modulus and ultimate stress.

GRANTS

Support for this study was provided by National Science Foundation Grant CMS-0553016 and by National Institutes of Health Grants R21-EB008548 and R01-AR059916. The content is solely the responsibility of the authors and does not necessarily represent the official views of the National Institutes of Health.

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the author(s).

AUTHOR CONTRIBUTIONS

Author contributions: A.S.L., S.E.D.-K., R.S.L., and R.V. conception and design of research; A.S.L. performed experiments; A.S.L. analyzed data; A.S.L., S.E.D.-K., R.S.L., and R.V. interpreted results of experiments; A.S.L. and S.E.D.-K. prepared figures; A.S.L. and S.E.D.-K. drafted manuscript; A.S.L., S.E.D.-K., R.S.L., and R.V. edited and revised manuscript; A.S.L., S.E.D.-K., R.S.L., and R.V. approved final version of manuscript.