Selectively bred rat model system for low and high response to exercise training

Abstract

We initiated a large-scale bidirectional selection experiment in a genetically heterogeneous rat population (N/NIH stock, n = 152) to develop lines of low response trainers (LRT) and high response trainers (HRT) as a contrasting animal model system. Maximal treadmill running distance [meters (m)] was tested before (DIST¹) and after (DIST²) standardized aerobic treadmill training over an 8 wk period (3 exercise sessions per week). Response to training was calculated as the change in exercise capacity (ΔDIST = DIST² − DIST¹). A within-family selection and rotational breeding paradigm between 10 families was practiced for both selected lines. For the founder population, exercise training produced a 140 ± 15 m gain in exercise capacity with interindividual variation ranging from −339 to +627 m. After 15 generations of selection (n = 3,114 rats), HRT rats improved 223 ± 20 m as a result of exercise training while exercise capacity declined −65 ± 15 m in LRT rats given the same absolute training environment. The narrow-sense heritability (h²) for ΔDIST was 0.10 ± 0.02. The LRT and HRT lines did not differ significantly for body weight or intrinsic (i.e., DIST¹) exercise capacity. Using pedigree records the inbreeding coefficient increased at a rate of 1.7% per generation for HRT and 1.6% per generation for LRT, ∼30% slower than expected from random mating. Animal models developed from heterogeneous stock and enriched via selection, as presented here, often generate extreme values for traits of interest and may prove more useful than current models for uncovering genetic underpinnings.

low aerobic exercise capacity is linked to a higher probability of harboring elevated complex disease risks and lower survivability (2, 4, 11, 18, 34, 37). In general, an increasing physical fitness level with exercise training is associated with reduced morbidity and mortality rates from all causes (3, 4, 38, 48). Of recent interest are reports demonstrating that there is wide variation for response to exercise training whereby some individuals experience no improvement, or even adverse changes in health indices, while others show large gain (6, 26, 43, 44, 46). The mixture of genetic and environmental backgrounds contributes to the range in training-induced adaptations and creates a considerable challenge for identifying the mechanistic connection between exercise capacity and human health.

Empirically, the genetics that contribute to exercise capacity divide into two parts: 1) an intrinsic component that operates in the sedentary (nontrained state) and 2) an extrinsic component that follows as an adaptive response that accrues from all activity above the sedentary state (8). As an initial strategy in previous work, we first modeled the intrinsic component of exercise capacity by divergent selection on the inborn capacity for endurance treadmill running in rats in the untrained condition (30). The development of this first model provided a direct test of our general hypothesis that a diminished capacity for aerobic energy transfer underlies complex disease risks at all levels of biological organization (aerobic hypothesis) (29). After 11 generations rats bred as high-capacity runners (HCR) went about four-times further on a treadmill running test compared with rats bred as low-capacity runners (LCR) (49). Consistent with our aerobic hypothesis, disease risks including the metabolic syndrome, cardiovascular complications, premature aging, and reduced longevity were associated with selection for low exercise capacity (28, 33, 49).

In 2001, we began the development of a second animal model system for the adaptive response to aerobic exercise training. Early studies by others comparing monozygotic and dizygotic twins suggested that aerobic exercise capacity has a measureable genetic component (7, 41). In 1999, the HEalth, RIsk factors, exercise Training, And GEnetics (HERITAGE) Family Study demonstrated a wide familial inherited heterogenetic pattern for training responsiveness (5). Thus, we reasoned that two-way artificial selection on the magnitude of change in running capacity (ΔDIST) as a result of training across several generations would yield a contrasting animal model system and serve as unique substrate to uncover genetic features responsible for low and high responsiveness to exercise training.

Because genetic selection is directly dependent on narrow-sense heritability (h²), we first drew upon commercially available inbred rat strains to determine if our measure of response to training (ΔDIST) could yield significant h² before taking on the much larger task of artificial selection over many generations. Total phenotypic variance for ΔDIST was partitioned into genetic variance (between-strain) and environmental variance (within-strain) to estimate h² (9). Response to training data from 10 inbred strains yielded an h² of 0.13 (P < 0.001). Based on this result, we initiated a divergent artificial selection program for ΔDIST starting with a founder population of the genetically heterogeneous N/NIH stock of rats. We report here progress across 15 generations of artificial selective breeding that produced contrasting lines of low response trainers (LRT) and high response trainers (HRT).

MATERIALS AND METHODS

Experimental Animals

All procedures were carried out in accordance with the Institute for Laboratory Animal Research Guide for Care and Use of Laboratory Animals and in compliance with guidelines as reviewed by the University Committee of Use and Care of Animals at the University of Michigan. Animals were housed two or three per cage with same-sex littermates in specific pathogen-free facilities. All animals were fed rodent pellet diet (diet #5001; Purina Mills, Richmond, IN), and water was provided ad libitum. The ambient environment was a controlled 12:12 h light-dark cycle with the light cycle occurring in the daytime and a target room temperature of 22°C.

We evaluated three different rat populations for response to training. Population 1 (n = 120) comprised 10 commonly used and phylogenetically diverse inbred strains (6 males and 6 females per strain): PVG, W/F, SR/Jr, ACI, F344, BN, BUF, COP, DA, and LEW purchased from Harlan Sprague-Dawley (Indianapolis, IN). Population 2 (n = 152) was formed of genetically heterogeneous N/NIH rats (89 females and 63 males). In 2000 we obtained 47 N/NIH rats (23 females and 24 males, each from different parental matings) from the original colony maintained by the National Institutes of Health (20) and produced two generations of an in-house colony. The first in-house generation of 70 rats was produced from 29 breeding pairs. The second in-house generation was derived from 19 breeding pairs. Population 2 represents those second-generation rats successfully phenotyped for response to training that served as the founder population for artificial selection. Population 3 (n = 3,114 rats) includes rats produced in a 15-generation selective breeding program for low and high response to training (LRT and HRT).

Experimental Protocol

All rats when about 10 wk of age were started on an 11 wk phenotyping protocol involving: 1) education to treadmill running, 2) a test for maximal running distance in the untrained condition (DIST¹), 3) 8 wk of aerobic exercise training, and 4) a test for maximal running distance in the trained condition (DIST²). The selected trait of response to training was taken as the change in maximal running distance (ΔDIST = DIST² − DIST¹).

Education to treadmill running.

Each rat was introduced to running on a four-lane treadmill (model Exer-4; Columbus Instruments, Columbus, OH) gradually over a 5-day period. The goal of the education was to familiarize each rat to the treadmill such that they could complete 5 min of running at a speed of 10 m/min on a 15° upward slope, an amount below that which is likely to produce a significant change in aerobic capacity (30). The first 2 days of introduction to treadmill running consisted of simply placing the rat on the belt that was moving at a velocity of 10 m/min (15° slope) and picking the rat up and moving it forward if it started to slide off the back of the belt. During introduction days 3–5, the rats learnt that failure to run on the belt resulted in exposure to the electrical stimulus grid located at the back of the treadmill that delivered a stimulus of 1.2 mA of current at 3 Hz. The rats were exposed to the stimulus for ∼1.5 s and then physically placed forward onto the moving belt. This process was repeated as needed during the session to help the rats learn to run to avoid the mild shock. Rats not achieving this minimal running ability were dropped from further testing.

Test for maximal running distance.

Each rat was assessed with a speed-ramped test that we devised to pattern clinical stress tests as a standard screen for exercise capacity (30). Rats exercised on a motorized treadmill (model Exer-4, Columbus Instruments) set at a constant grade of 15° and an initial speed of 10 m/min. Speed was progressively ramped 1 m/min every 2 min until “exhaustion” occurred. The first two times that a rat did not keep pace with the treadmill belt and remained in contact with the shock grid for 2 s, they were placed back on the belt to see if they would continue running. Exhaustion was operationally defined as the third time a rat remained on the grid for 2 s. At that point the stimulus current was shut-off and the rat removed from the treadmill. Total running time and body weight were recorded. Two parameters were used to quantify exercise capacity 1) Total distance run in meters (m) calculated from belt speed (m/min) and duration (min) of the run, and 2) The vertical work during each trial estimated using the equation: work = (running distance) × (body weight) × [sin(15°)] × (9.8 m/s²)/1,000 in which the unit for work was joule (J = kg·m²/s²): distance in m and body weight in g. Tests were carried out on 3 separate days with 48 h rest between each trial. For each rat, the maximal running distance (DIST) of the three tests was considered the best indicator of the exercise capacity and used as the selection criterion (30).

Treadmill training protocol.

Our goal at each generation was to expose every rat to the same amount of training environment. We devised an absolute treadmill exercise protocol that progressed moderately and uniformly in speed and duration each session, independent of each rat's baseline capacity or relative change in capacity across training sessions (32). Animals trained 3 days per week (either Mon.-Wed.-Fri. or Tues.-Thurs.-Sat.) for 8 wk (24 sessions) and the time of day for exercise randomized between 9 AM and 3 PM. The treadmill speed started at 10 m/min on session 1 and increased by 1 m/min every other session up to a maximum speed of 21 m/min. The duration for each training session was set for 20 min at session 1 and incremented by 0.5 min each session to a maximum target of 31.5 min by session 24. The slope of the treadmill was held constant at 15°. This target protocol provided for a total of 618 min of running time, a total distance of 9,865 m, and a cumulative vertical climb of 2,553 m. Not all rats achieved the target training values. Of the 3,114 total rats for which training was attempted, 2,237 rats (72%) completed 100%, 529 rats (17%) completed 90–99%, 103 rats (3%) completed 80–90%, and 10 rats (0.3%) completed 60–80% of the training target. For all other reasons combined (e.g., insufficient compliance with running, culled animals) another 235 (7.5%) rats were removed from the study.

Selective Breeding

From the N/NIH population (population 2), we chose 10 males and 10 females representing the upper 10th percentile and lower 10th percentile for response to training as founder parents for population 3, i.e., lines selected as HRT and LRT, respectively. We used within-family selection where the phenotypically “best” female and male from each LRT and HRT litter are selected as breeders for the next generation. As suggested by Kimura and Crow (27), we followed a schedule of rotational within family breeding that reduced the rate of inbreeding relative to random breeding. At each generation a minimum of 10 families per line were maintained. We chose an additional four to six mating pairs strictly on phenotypic rank to serve as replacement families for those that failed to breed or produce a sufficient number of male and female offspring. Offspring were weaned at 26 days after birth and housed two or three per cage with same-sex littermates. At each generation, ∼100 offspring per line on average were phenotyped for training response across 15 generations.

Genetic Parameters and Heritability

h² for the inbred strain data (population 1) was calculated by the methodology of Hegmann and Possidente (22) with standard errors after Falconer and Mackay (15). The statistical model fitted to the inbred dataset included line, sex, and starting body weight for nine traits (Table 1).

Table 1.

Model summary showing the results of fitting fixed effects and covariates to the change in running capacity for a panel of 10 inbred rat strains (population 1)

Trait	Model P	R2	Strain P	Sex P	BW1 P	Heritability	SE
DIST1	0.0001	0.33	0.0001	0.0019	0.740	0.14	0.064
DIST2	0.0001	0.51	0.0001	0.0001	0.690	0.29	0.091
ΔDIST	0.0001	0.28	0.0001	0.180	0.980	0.13	0.060
BWT1	0.0001	0.93	0.0001	0.0001	—	0.44	0.112
BWT2	0.0001	0.92	0.0001	0.0001	—	0.43	0.111
Δ BWT	0.0001	0.75	0.0001	0.0001	0.890	0.31	0.093
WORK1	0.0001	0.32	0.0001	0.0110	0.076	0.13	0.060
WORK2	0.0001	0.44	0.0001	0.0012	0.610	0.23	0.082
ΔWORK	0.0001	0.26	0.0003	0.140	0.760	0.11	0.057

Distance run or running capacity (DIST), body weight (BWT), and work carried out (WORK) were all measured before training (¹) and after training (²), and the difference between the before and after measurements was calculated (Δ). The columns of the table are: Model P, probability of the overall fit of the model; R², squared correlation coefficient between data and model; Strain P, probability of strain in the model; Sex P, probability of sex in the model. BW¹ P, probability of starting body weight (BWT¹) in the model.

To evaluate the genetic merit of animals in our selection experiment (population 3), we constructed a linear mixed model for ΔDIST using an average information (AI) algorithm with pedigree-based restricted maximum likelihood methods. All models were run in ASReml statistical software (17). The mixed model includes correction factors for each animal treated as fixed effects or covariates (sex, generation, line, litter size, level of inbreeding, total amount of training distance completed, and body weight measured at the end of training), random effects (additive direct genetic effect, additive maternal genetic effect, nongenetic common litter effect, and female founder effect), and the residual. (35) Results from the initial model tested showed sex, generation, line, total training distance (P < 0.001), and body weight after training (P < 0.05) were all significantly associated with ΔDIST. Litter size and inbreeding level were nonsignificant and dropped from the final model. Generation number and line were also dropped because the trends in line by generation were the important effects that we intended to study. Body weight was also excluded from the final model since this may have been a correlated response to selection rather than an effect on it. Random effect terms were tested by including them all in a mixed animal model, which included the final fixed effects chosen above. The model for fitting random effects showed the animal (P < 0.05) and litter effect (P < 0.001) were significantly associated with ΔDIST but maternal genetic and female founder effects were not. The nonsignificant effects were dropped from the final model, and the litter effect was also dropped because in this selection program it was highly confounded with the effect of animal (the additive genetic component).

An animal's breeding value for a trait is defined as the sum of the additive effects of its genes that can be passed on to its progeny. Although the exact breeding value is unknown, an estimated breeding value (EBV) can be made by judging the mean value of its progeny within a known pedigree. The standard method used to achieve this is via Best Linear Unbiased Prediction methodology as originally outlined by C. R. Henderson (23) and widely implemented in many animals and plant breeding schemes. Genetic parameters (heritability, genetic and phenotypic correlations) were calculated for distance run (DIST), body weight (BWT), and work (WORK) carried out before (¹) and after (²) training and their difference (Δ). Heritability was calculated in the narrow sense, as the ratio of the variance due to additive genetic effects to the phenotypic variance; both variances were derived from running the mixed model described above. Correlations were calculated as a series of bivariate analyses between each pair of traits. All genetic parameters were estimated using ASReml statistical software and their standard errors were calculated as described in Gilmour et al., 2009 (17).

Pedigree Checking and Inbreeding Coefficient

Pedigrees for the two selection lines, LRT and HRT, were checked using Pedigree Viewer (version 5.5; Kinghorn, 2012). Since the whole population was developed from a known base population the coefficients of inbreeding (F) for all animals in the population were calculated explicitly using the tabular method (15, 40) and computed from the basic ruling of F_X = f_PQ = ¼(f_AC + f_AD + f_BC + f_BD), where subscripts P and Q indicate the parents of individual X; A and B were the parents of P; and C and D the parents of Q. While specific chromosomal areas may exhibit local levels of autozygosity, an indicator of inbreeding, studies using genome-wide single nucleotide polymorphism genotypes indicate that average levels of inbreeding measured in this way agrees with the results of the pedigree method used in this paper. Such genotyping studies do provide extra information about inbreeding in the form of estimates of variation at the whole animal level (24). For example, Keller et al. (25) quote the genetic relationship between the offspring of first cousins to be 0.0625 ± 0.024.

Intrinsic and Trained Capacity in All Populations

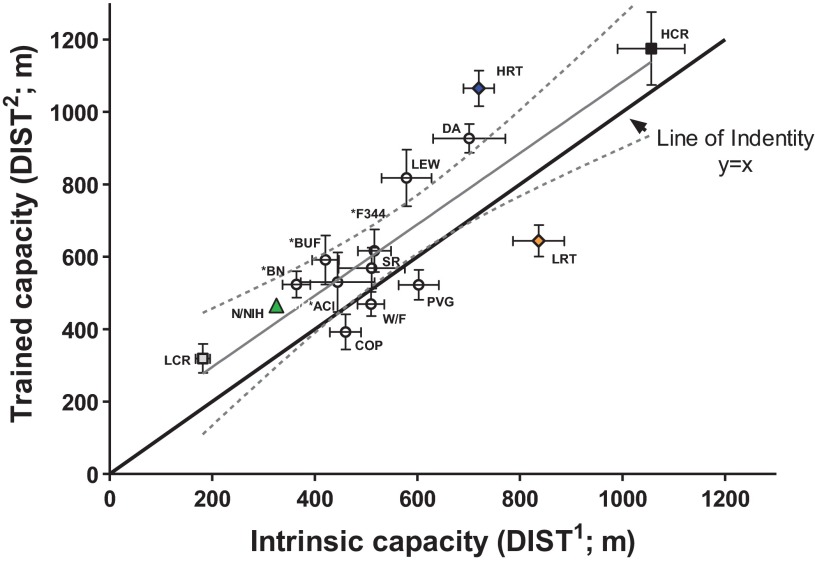
The relationship between mean values for intrinsic (DIST¹, m) vs. trained (DIST², m) capacity were analyzed by linear regression (see Fig. 6). The populations included were: 1) 10 different inbred strains (population 1 rats), 2) genetically heterogeneous N/NIH rats (population 2 rats), 3) rats selectively bred for low and high response to exercise training, LRT and HRT (generation 12, population 3 rats, n = 30 for each selected line), and 4) rats selectively bred for low and high intrinsic running capacity LCR and HCR (generation 12, n = 18 for each selected line). Males and females were equally represented in all groups. As a reference, a line of identity was derived from hypothetical data in which DIST¹ values equal DIST² values (i.e., no response to training).

Fig. 6.

DIST¹ and DIST² for 2 populations of selected lines and 2 populations of nonselected lines. The selection process often carries the phenotypic means beyond the range of a founder population. Plotted are mean (± SE) values for DIST¹ (m) vs. DIST² (m) capacity for: 1) 10 different inbred strains (Fig. 1, population 1 rats), 2) genetically heterogeneous N/NIH rats (Fig. 2A, population 2 rats), 3) rats selectively bred for low and high response to exercise training, LRT and HRT (population 3, generation 12), and 4) rats selectively bred for low and high intrinsic running capacity, LCR and HCR (generation 12). Invariably the selected lines comprised the extreme values for capacity for both intrinsic and trained conditions. Data plotted as linear regression [dotted lines show 95% confidence intervals (CI)] and are compared with a line of identity (DIST¹ = DIST²). y = 0.98x + 98.4, R² = 0.73, CI₉₅ = 0.60 to 1.4. *Inbred strains represented in N/NIH outbred stock. Data shown are for males and females combined.

Data Analysis

Data are presented as means ± SE. The 0.05 level of significance was assigned for declaring differences. The phenotypic distribution for all populations was tested by D'Agostino and Pearson omnibus normality test. Differences between inbred strains for ΔDIST were determined by a Tukey multiple comparison test. Analysis of variance was used to evaluate possible differences between exercise capacity before training and after training. Statistical analysis were performed using GraphPad Prism version 6.01 for Windows (GraphPad Software, La Jolla, CA).

RESULTS

Training Response in a Panel of 10 Inbred Strains (Population 1)

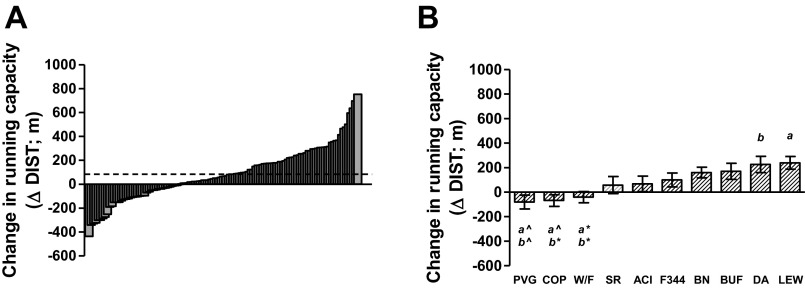
Figure 1A shows the phenotypic variation for the gain in running capacity (m) for a population of 117 individual rats representing 10 different inbred strains for 6 females and 6 males per strain (population 1; 2 male ACI and 1 male W/F did not complete the entire training protocol and were omitted). On average, 8 wk (24 sessions) of moderate endurance treadmill training resulted in an 84 ± 20 m gain in running capacity. The interindividual response to training varied widely from +754 m gain to a −438 m decline (2.7-fold) in running capacity. When separated by strain (Fig. 1B), the response to training phenotype also distributed as a continuum. There was a 3.9-fold difference between the strain that ranked the lowest (PVG) and highest (LEW) for exercise response (−80 ± 57 to +239 ± 52 m, respectively). The strain rank order for response was similar between females and males.

Fig. 1.

Response to exercise training in a rat population made up of 10 different inbred strains (population 1). A: distribution for the change in running capacity (ΔDIST) plotted for 117 individual rats arranged in ascending order. D'Agostino and Pearson omnibus normality test; P > 0.05. B: ΔDIST separated by strain arranged in ascending order. Strains significantly different from each other are denoted by same letter (1-way ANOVA, Tukey; *P < 0.05, ^P < 0.01). Data include both females and males combined.

Table 1 shows the results of a mixed model approach fitting fixed effects (strain, sex, and initial body weight) to estimate the variance components for the trait of response to training calculated as the difference in meters run (ΔDIST = DIST² − DIST¹) (35). Sex (P = 0.18) and initial body weight (P = 0.98) had no significant influence in the model compared with the effect of the strain (P = 0.0001). The h² of response to training (ΔDIST), calculated by the method of Hegmann and Possidente (22) for inbred strains was 0.13 ± 0.06. This estimate for heritability from a panel of inbred strains was based upon two assumptions: First, 20+ generations of strict brother-sister mating produced strains that were genetically identical, thus within-strain trait variation is attributed to environmental variance. Second, each inbred strain represented almost an exclusively homozygous genotype such that variation between inbred strains estimated additive genetic variance (9). A statistical demonstration of an additive genetic effect for ΔDIST among inbred strains, independent of sex, body weight, and level of initial exercise capacity, encouraged us to consider starting a large-scale selection program.

Training Response in a Genetically Diverse Rat Population (Population 2)

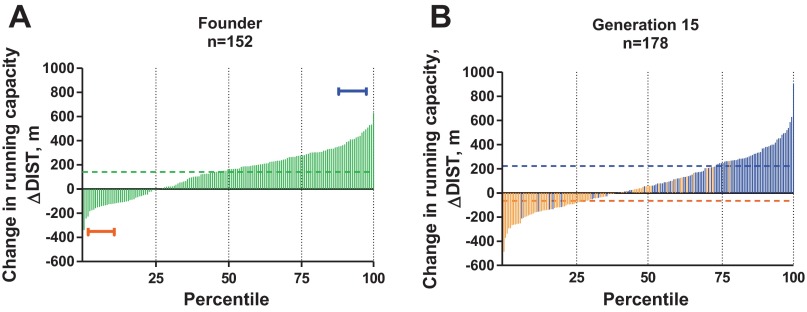
We tested the training response in a genetically heterogeneous population of N/NIH rats. The purpose was to determine whether this population displayed wide enough phenotypic variance for training response such that the rats at the extremes could serve as founding breeders for a selection experiment (20). Figure 2A shows that treadmill exercise training resulted, on average, in a 140 ± 15 m gain in running capacity that ranged between from −339 m to +627 m. Females in the population demonstrated a greater training response than males by the estimates for both gain in running distance (P < 0.0001) and work performed (P < 0.01). Because the variance of response between the sexes (P = 0.66) was similar, we were able to choose 10 mating pairs representing the upper and lower 10th percentile for training response. These 20 mating pairs served as breeders for 10 base families for a high-selected line [HRT; mean superiority (S) = 426 ± 30 m for females vs. 370 ± 32 m for males], and 10 families for a low-selected line (LRT; S = −50 ± 42 m for females vs. −133 ± 48 m for males).

Fig. 2.

Response to exercise training in genetically heterogeneous rat populations as part of a large-scale selective breeding program for low and high response to training (population 2). A: frequency distribution for the ΔDIST for 152 nonselected N/NIH rats shown in ascending order. The brackets indicate the lowest and highest 10th percentile animals that were used as founders to start the low response trainer (LRT) and high response trainer (HRT) selected lines. Dotted line indicates the mean change in running capacity for population 2. B: percentile rank score for the ΔDIST for 178 rats from generation 15 of selection arranged from lowest to highest. Light bars indicate LRT animals, and dark bars indicate HRT animals. Dotted lines indicate the mean change in running capacity for the LRT (light) and HRT (dark) selected lines. D'Agostino and Pearson omnibus normality test; P > 0.05.

Development of LRT and HRT Rats (Population 3)

Using artificial selective breeding, we created a divergent heterogeneous population under the hypothesis that strong selection pressure enriched and probably fixed differentially key response elements between the low and high selected progeny. Figure 2B shows the interindividual variation for gain in running capacity in response to training for generation 15 (G15) of selection. The G15 population distributed as a continuum that ranged from −486 m to 906 m for gain in running capacity. Of those rats bred as HRT, endurance running capacity improved on average by 223 ± 20 m, whereas those bred as LRT declined on average by −65 ± 15 m in response to treadmill training. About 5% of the G15 HRT rats (5 rats out of 91) demonstrated an adverse response to training below the mean response of G15 LRT rats, whereby 1% of the rats bred as G15 LRT (1 rat out of 87) were capable of increasing their treadmill running capacity above the mean training response of the HRT population.

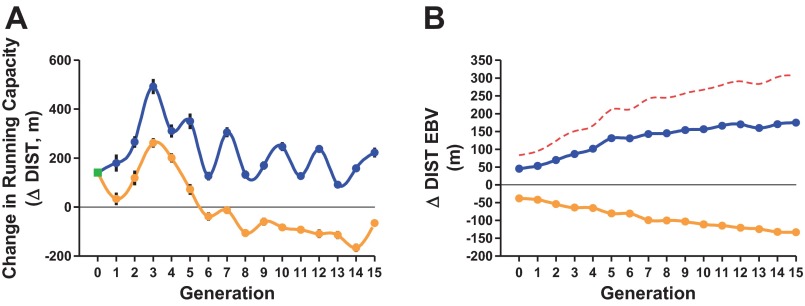
Figure 3 shows the response to selection across 15 generations as a phenotypic trend (Fig. 3A) and as a genetic trend (Fig. 3B) from estimated breeding values. At generation 1, the ΔDIST for the HRT line was 180 ± 35 and 34 ± 26 m for LRT line (a 146 m difference). At G15 the divergence between selected lines about doubled to 288 m. The mean response for G15 HRT was 223 ± 20 vs. −65 ± 15 m for G15 LRT. Figure 3B shows the response to selection for ΔDIST based on EBV. The initial (G1) genetic lift from the selection process was equal to +45 m for the HRT line and −38 m for the LRT line with subsequent mean rates of additive genetic change being +8.6 m and −6.5 m per generation, respectively (HRT: y = 8.6x + 64.0, R² = 0.89; LRT: y = −6.5x − 42.2, R² = 0.98). At G15 the difference between the selected lines based on the ΔDIST EBV was 308 m (175 m HRT vs. −133 m LRT).

Fig. 3.

Response to selection across 15 generations for low and high exercise training capacity (population 3). A: phenotypic trend for ΔDIST across 15 generations of selection for low and high response to training. Mean of the founder population is plotted at generation 0 (box symbol). B: genotypic trend. Each point represents the mean genetic value for ΔDIST represented as estimated breeding values (EBV) for each generation. For both A and B, LRT line shown with light line and HRT line shown with dark line. Dashed line is the difference between the low and high selected lines.

Statistical Model Analysis

Results based on the final statistical model for ΔDIST showed that female animals responded to training better than males (184 ± 18.0 m vs. 147 ± 18.9 m). Animals that were heavier after training had less of a training response with the relationship being −0.13 m/g, while animals that spent more time training ran further by 0.038 m/min. Table 2 shows the key variance component estimates and the heritability values, calculated as the ratio of the additive variance to the phenotypic variance, derived from running the model for the nine measured traits for the first 15 generations of selection. The statistical results indicated that ΔDIST had significant h² of 0.10 ± 0.019. In this population, body weight had the highest heritability, with before (BWT¹) and after training (BWT²) values being similar at ∼0.62 ± 0.032. The difference between body weight before and after training (ΔBWT) was also heritable at ∼0.43 ± 0.041. Trained capacity (DIST²) was more heritable (0.36 ± 0.038 vs. 0.25 ± 0.036) than the intrinsic capacity (DIST¹).

Table 2.

Variance components and heritability estimates for 9 traits derived from the first 15 generations of a heterogeneous rat population selected for response to training

Trait	Additive Variance	Residual Variance	Phenotypic Variance	Heritability ± SE
DIST1	7,795	23,062	30,857	0.25 ± 0.036
DIST2	13,228	23,322	36,550	0.36 ± 0.038
ΔDIST	3,697	31,620	33,318	0.10 ± 0.019
BWT1	336	207	543	0.62 ± 0.032
BWT2	534	310	844	0.63 ± 0.034
ΔBWT	114	148	262	0.43 ± 0.041
WORK1	2,322	7,430	9,752	0.24 ± 0.035
WORK2	6,618	11,428	18,426	0.27 ± 0.039
ΔWORK	1,975	13,503	15,478	0.13 ± 0.023

DIST, BWT (g), and work carried out (J; WORK) were all measured before training (¹) and after training (²), and the difference between the before and after measurements calculated (Δ). Heritability was calculated as the ratio of the additive variance to the phenotypic variance.

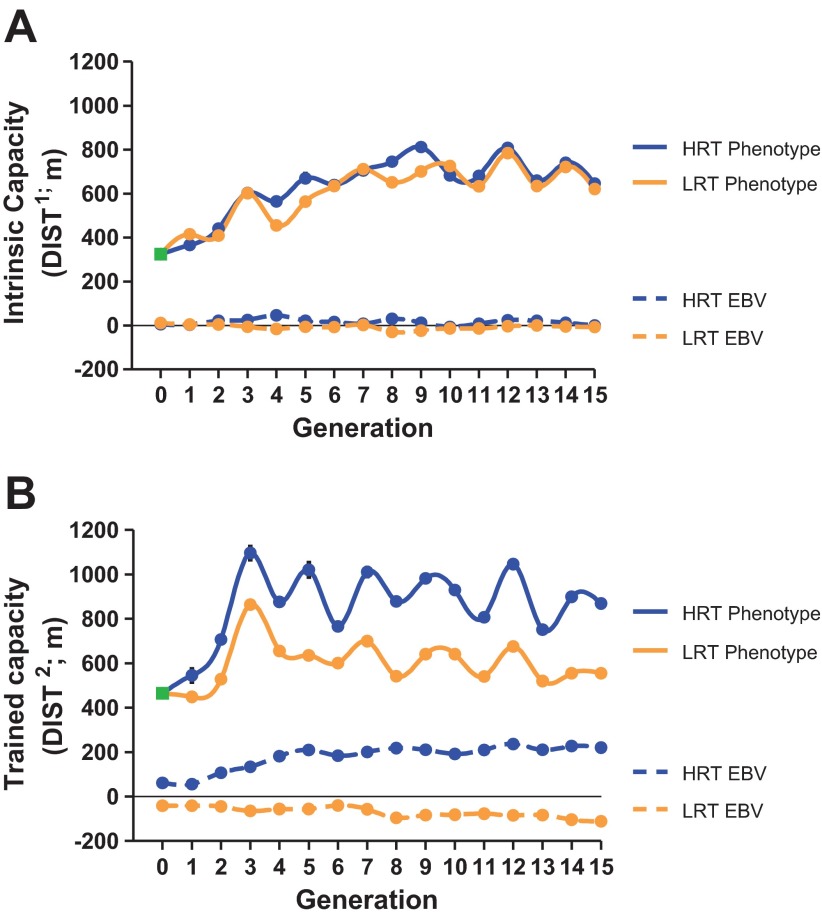
A change in an unselected trait due to the process of selection is termed a correlated response. In previous work, we found body weight to be significantly correlated with intrinsic exercise capacity, with the LCR being heavier than HCR (30, 49). Thus, we calculated the correlated responses to training as both phenotypic and genetic (EBV) trends by lines for both exercise capacity (DIST) and body weight (BWT), before and after training. The correlated response to selection in DIST¹ increased in both lines at approximately the same levels phenotypically but no major genetic change occurred between the lines over the 15 generations (Fig. 4A). The DIST² showed completely the opposite in that the two lines diverged at both the phenotypic and genetic levels (Fig. 4B). Also of importance, we found both the phenotypic and EBV changes for body weight before (BWT¹) and after training (BWT²) over the generations to be small; the HRT line tended to be slightly lighter than the LRT line (i.e., ∼20 g difference in EBV between LRT and HRT selected lines; data not shown).

Fig. 4.

Phenotypic and genotypic trends for intrinsic and trained running capacity across 15 generations of selection (population 3). A: intrinsic capacity (DIST¹, m) phenotypically increased for both LRT and HRT lines across generations as a correlated response to selection but were not different from each other. No genotypic trends (EBV) for DIST¹ were revealed across selection in either line. B: trained capacity (DIST², m) diverged phenotypically between LRT and HRT as a function of selection on ΔDIST. Genotypic trend (EBV) for DIST² also diverged between LRT and HRT across selection. LRT (light lines) and HRT (dark lines). Mean of the founder population is plotted at generation 0 (box symbol).

Table 3 shows phenotypic and genetic correlations between pairs of traits. Care should be taken when interpreting ΔDIST, ΔBWT, and ΔWORK correlations with DIST, BWT, and WORK traits, respectively, due to the part-whole nature of these relationships. Overall, phenotypic correlations were mostly similar to genetic correlations for both exercise and body weight traits. Some exceptions were DIST¹ with ΔDIST and ΔWORK, which differed in both the size and sign. This implies that there was likely some environmental influence on the two traits, which in the phenotype masked the genetic relationship between the traits. The results at the genetic level (correlation of breeding values) suggest that a rat's intrinsic capacity for exercise (DIST¹) and its exercise capacity after training, measured as either distance (DIST²) or (WORK²), are highly correlated (0.88 ± 0.028 and 0.82 ± 0.040, respectively). However, the selected trait, gain in distance (ΔDIST) from training, weakly correlated with DIST¹ (0.14 ± 0.128) or body weight (0.04 ± 0.107) traits, substantiating the lack of correlated responses in these traits mentioned above. In addition, the strong genetic and phenotypic correlations between ΔDIST and DIST² (0.60 ± 0.083 and 0.56 ± 0.015, respectively) further supports the response observed in the selected population. Together, we provide strong statistical evidence that selection on ΔDIST was independent of the intrinsic component and body weight but highly related to the trained component.

Table 3.

Phenotypic (below the diagonal) and genetic (above the diagonal) correlations between various traits and their heritability (on the diagonal in boldface) for the first 15 generations of selection for response to training

	ΔDIST	DIST1	DIST2	BWT1	BWT2	ΔBWT	WORK1	WORK2	ΔWORK
ΔDIST	0.10 ± 0.020	0.14 ± 0.128	0.60 ± 0.083	0.04 ± 0.107	−0.07 ± 0.109	−0.20 ± 0.118	0.18 ± 0.124	0.54 ± 0.090	0.77 ± 0.051
DIST1	−0.44 ± 0.018	0.34 ± 0.038	0.88 ± 0.028	−0.19 ± 0.081	−0.17 ± 0.084	0.01 ± 0.010	0.77 ± 0.041	0.82 ± 0.040	0.40 ± 0.107
DIST2	0.56 ± 0.015	0.49 ± 0.018	0.43 ± 0.038	−0.14 ± 0.073	−0.14 ± 0.074	−0.05 ± 0.089	0.96 ± 0.004	0.81 ± 0.028	0.67 ± 0.067
BWT1	0.05 ± 0.022	−0.18 ± 0.023	−0.12 ± 0.024	0.62 ± 0.032	0.88 ± 0.016	0.15 ± 0.070	0.34 ± 0.079	0.25 ± 0.071	0.10 ± 0.010
BWT2	−0.04 ± 0.022	−0.11 ± 0.024	−0.14 ± 0.025	0.83 ± 0.008	0.63 ± 0.034	0.59 ± 0.046	0.32 ± 0.081	0.25 ± 0.071	0.21 ± 0.099
ΔBWT	−0.16 ± 0.021	0.07 ± 0.024	−0.08 ± 0.025	0.03 ± 0.026	0.59 ± 0.017	0.44 ± 0.041	0.07 ± 0.101	0.23 ± 0.086	0.26 ± 0.110
WORK1	−0.41 ± 0.019	0.89 ± 0.005	0.44 ± 0.018	0.15 ± 0.023	0.17 ± 0.024	0.08 ± 0.024	0.37 ± 0.039	0.28 ± 0.124	0.42 ± 0.103
WORK2	0.54 ± 0.016	0.41 ± 0.020	0.88 ± 0.006	0.16 ± 0.024	0.16 ± 0.024	0.11 ± 0.025	0.38 ± 0.018	0.45 ± 0.039	0.81 ± 0.043
ΔWORK	0.91 ± 0.004	−0.27 ± 0.021	0.63 ± 0.014	0.06 ± 0.022	0.07 ± 0.023	0.05 ± 0.022	−0.28 ± 0.021	0.71 ± 0.011	0.15 ± 0.020

Values are shown ± SE. DIST, BWT, and WORK were all measured before training (¹) and after training (²), and the difference between the before and after measurements calculated (Δ). Heritability derived from bivariate analyses.

Level of Inbreeding

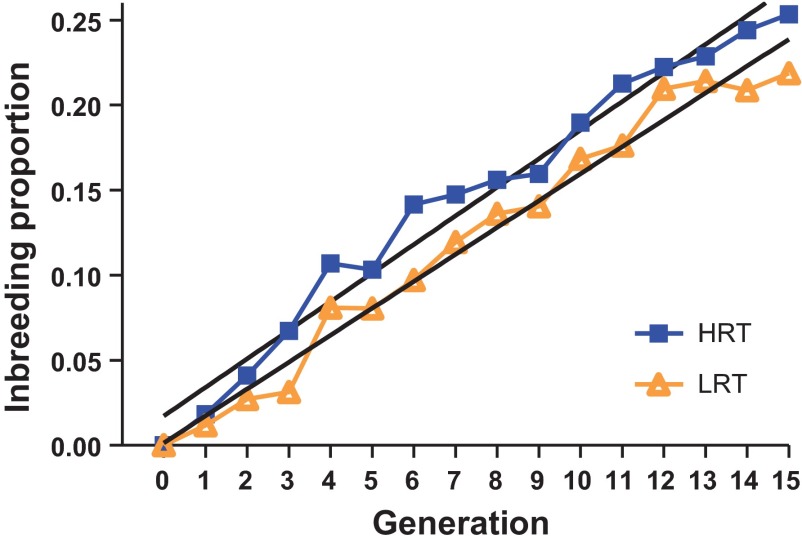
Minimizing loss of heterogeneity (inbreeding) during selection is important because that is the substrate for progress for future generations. If we had randomly selected and mated males and females from 10 families, the expected inbreeding (F) for each line would have been ∼2.5% at each generation. That is, for random mating F = 1/2N_e = 1/2(20) = 2.5% where N_e is the effective population size (i.e., number of parental breeders). To maintain heterogeneity across the 15 generations we used within-family selection and rotational breeding as suggested by Kimura and Crow (27). With equal representation of one male and one female offspring from each family, F reduces to F = 1/4N_e (1.25%/generation with 20 breeders). The actual coefficient of inbreeding calculated from the pedigree by the tabular method (34) was 1.7%/generation for HRT and 1.6%/generation for LRT (Fig. 5). Thus, the practice of a rotational breeding scheme limited loss of heterogeneity at a rate ∼30% less than random breeding.

Fig. 5.

Level of inbreeding across 15 generations of selection (population 3). Mean inbreeding proportions are shown for LRT (light, diamond symbols) and HRT (dark, box symbols) lines. Fitting a linear regression model showed inbreeding increasing at an average rate of 0.017 and 0.016 per generation for the HRT and LRT lines, respectively.

DISCUSSION

The strong statistical association between exercise capacity and survival suggests a link between impaired aerobic energy transfer and disease risk (aerobic hypothesis) (49). Over the past 15 years, the major goal of our lab has been to create heterogeneous rat model systems, via divergent artificial selection, that contrast for the intrinsic and adaptational components of exercise capacity. The assumption is that these segregating models can be used to resolve the intrinsic and response phenotypes at all levels of biological organization to ultimately understand the exercise-disease linkage. Segregation of disease risks with selection for low aerobic capacity in the untrained condition, as demonstrated in numerous studies (31), is consistent with the aerobic hypothesis. Development of the low and high training response models is driven by the general conclusion, as summarized by Pedersen and Saltin (39), that aerobic exercise is an effective prescription for ameliorating a wide range of clinical conditions including insulin resistance, coronary artery disease, cancer, and depression. The diversity of conditions for which a higher level of exercise capacity via intrinsic and/or acquired components associates with health protection suggests a common underlying mechanism (29). The first physiological study interrogating the LRT/HRT (36) shows that rats born in the low exercise response line exhibit a pronounced metabolic dysfunction characterized by insulin resistance, increased adiposity, and impaired exercise-induced angiogenesis. Interestingly, these risk factors were not accompanied by differences in mitochondrial capacity in skeletal muscle but rather by increased stress/inflammatory signaling and altered TGF-β signaling characterized by hyperphosphorylation of a novel exercise-regulated phosphorylation site on SMAD2.

Divergent artificial selection for a complex trait such as exercise capacity, starting with a heterogeneous founder population, produces somewhat ideal genetic models because a collection of contrasting allelic variation is concentrated at the extremes from one generation to the next. In addition, the selection process often carries the phenotypic means for the trait of interest beyond the range of the founder population (14). For perspective, we placed on one plot (Figure 6) both the intrinsic running capacity and the trained capacity for two populations of selected lines and two populations of nonselected lines. The line of regression for the mean of all groups shows an upward parallel shift from the line of identity corresponding to an average gain of 98 m after 8 wk of standardized training. Invariably the selected lines comprised the outermost values for capacity. First, the LCR-HCR rats selected to contrast for low and high intrinsic running capacity plotted at the extremes for intrinsic running capacity but demonstrated only modest gains in trained capacity. Second, a population of LRT and HRT were the furthest from the line of identity for trained capacity but, rather, equal for intrinsic. Third, the genetically heterogeneous N/NIH rats (population 2) recorded nonextreme for intrinsic capacity and a nominal change in trained capacity. Fourth, intrinsic capacity and gain with training for the 10 inbred strains (population 1) were all within the boundaries of the selected population values.

Heritability is often the single most important metric in deciding whether a given phenotype is worth probing for contributing genes and pathways, although as Walsh and Blows point out (47), there are very few traits which have a heritability of zero. It is of some interest that the h² for the selected lines was lowest for response to training, ΔDIST (0.10) relative to h² for distances (DIST) and body weights both before and after training (Tables 2 and 3). One interpretation is that response to exercise (i.e., an adaptation to environment) is more tightly linked with evolutionary fitness. That is, based on Fisher's 1930 Theorem of Natural Selection (16), traits peripherally associated with evolutionary fitness, such as morphology and complex physiology, retain more additive genetic variance because of less pressure from natural selection.

An alternative way of looking at the low heritability of ΔDIST is to put it into the context of the genetics of its components. Using a selection index approach (21) as interpreted by Dickerson (12), one can calculate the heritability of ΔDIST (the selection objective) as b′Gb/b′Pb. The G and P terms are the genetic and phenotypic variance/covariance matrices, respectively, and b is a vector of weights for the component traits, DIST¹ and DIST². These are −1 and +1 in the current selection program. Using data from Table 3, we can then show the heritability of this index to be the same as the heritability of ΔDIST. The other traits, BWT and WORK, can be interpreted in the same way. A low heritability does not mean the additive genetic variance is small, but rather it means a small proportion of the phenotypic variance in the population is caused by variation in genotype. Thus, a low heritability also does not imply there is a low number of genes that mediates the training response (45). Clearly, the results from the selection experiment demonstrate there was sufficient additive genetic variance available to allow a response to selection in both positive and negative directions.

One of the most important findings from the selection experiment was that rats with very different responses to exercise training do not differ for intrinsic exercise capacities or body weights. That is, the two selected lines were similar for DIST¹ at both the genetic and phenotypic levels (Fig. 4A), but a significant difference between the two lines occurred after training, DIST² (Fig. 4B). Additionally, Table 2 shows the residual variance for both DIST¹ and DIST² were similar, but the additive genetic variance for DIST² was almost 50% more than that for DIST¹; hence, distance after training has a higher heritability. Unlike the correlated response to selection we found between body weight and intrinsic exercise capacity in the previously developed rat models for low and high intrinsic capacity (30, 49), both phenotypic and genetic correlations between ΔDIST and BW were minimal (∼5–7%) for the LRT/HRT rats.

Our demonstration of heritability for training response gives justification for future intercross-based quantitative trait locus mapping. While the use of inbred strains simplifies mapping analysis, it also brings features that limit interpretive power mostly related to the abbreviated genotype representation. In a cross between two inbred lines, the F₂ segregating population is limited to representation by only two allelic and three genotypic variants at any given loci. This simplicity diminishes the discovery of linked networks of modifier gene interactions that underlie complex phenotypes (42). The LRT and HRT selected lines, however, were derived from N/NIH stock that originated from the outcross breeding of eight inbred strains (ACI, BN, BUF, F344, M520, MR, WKY, and WN) (20) and thus can theoretically have up to 36 different genotypes represented at any given locus [genotypes = a (a + 1)/2, where a = number of alleles available (15)].

Inbred line-based gene mapping has low resolution because mapping intervals tend to be very large due to a limited number of meioses. Divergent artificial selection generates lines with high value because the mapping resolution will increase due to accumulation of more recombination events with each generation of selection. Haley et al. (19) devised an efficient least squares method for the analysis of crosses between outbred lines that simultaneously uses information from multiple linked markers. Extensions of this approach have been used to successfully explore the genetic architecture of divergently selected outbred animal model systems including chickens lines that differ by ninefold in body weight (10, 13) and tameness vs. aggression behavior in rats (1).

In summary, we used artificial selection to develop a rat model system that contrasted for low and high response to endurance exercise training. These models of LRT and HRT represent the first heterogeneous substrate that can serve as reagents toward understanding the mechanisms that underlie the health benefits of acquired exercise capacity. Although most rats on average have a positive response to the mode of exercise training applied, we demonstrate in both inbred strains and the low artificially selected lines that some genotypes are “exercise resistant” and respond adversely with a reduction in posttraining treadmill running performance.

GRANTS

This work was funded by National Institutes of Health (NIH) Grant R24 RR-017718 and is currently supported by the NIH Office of Research Infrastructure Programs/OD Grant ROD-012098A (to L. G. Koch and S. L. Britton). Additional support was derived from the National Institute of Diabetes and Digestive and Kidney Diseases/Diabetes Research Training Center at the University of Michigan (NIH3P60DK020572-32S2 and NIH5P60 DK20572-P/FS Grants to L. G. Koch).

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the author(s).

AUTHOR CONTRIBUTIONS

Author contributions: L.G.K. and S.L.B. conception and design of research; L.G.K. and S.L.B. performed experiments; L.G.K., G.E.P., and S.L.B. analyzed data; L.G.K., G.E.P., and S.L.B. interpreted results of experiments; L.G.K. and G.E.P. prepared Figs.; L.G.K. and S.L.B. drafted manuscript; L.G.K., G.E.P., and S.L.B. edited and revised manuscript; L.G.K., G.E.P., and S.L.B. approved final version of manuscript.