Response properties from turtle auditory hair cell afferent fibers suggest spike generation is driven by synchronized release both between and within synapses

Abstract

Inner ear hair cell afferent fiber synapses are capable of transferring information at high rates for long periods of time with extraordinary fidelity. As at other sensory synapses, hair cells rely on graded receptor potentials and unique vesicle trafficking and release properties of ribbon synapses to relay intensity information. Postsynaptic recordings from afferent fibers of the turtle auditory papilla identified excitatory postsynaptic currents (EPSCs) that were fast AMPA receptor-based responses with rapid onset and decay times. EPSCs varied in amplitude by ∼15× per fiber, with kinetics that showed a tendency to slow at larger amplitudes. Complex EPSCs were produced by temporal summation of single events, likely across synapses. Complex EPSCs were more efficient at generating action potentials than single EPSCs. Potassium-evoked release increased the frequency of EPSCs, in particular complex events, but did not increase EPSC amplitudes. Temporal summation of EPSCs across synapses may underlie action potential generation at these synapses. Broad amplitude histograms were probed for mechanisms of multivesicular release with reduced external Ca²⁺ or the introduction of Cd²⁺ or Sr²⁺ to uncouple release. The results are consistent with broad amplitude histograms being generated by a combination of the variability in synaptic vesicle size and coordinated release of these vesicles. It is posited that multivesicular release plays less of a role in multisynaptic ribbon synapses than in single synaptic afferent fibers.

primary auditory afferent fibers transfer information regarding frequency, intensity, and timing to the central nervous system (CNS). The high temporal precision and indefatigable nature of the response is a result of pre- and postsynaptic specializations. Fibers typically fire spontaneously at rates up to 100 Hz and translate stimulus intensity in terms of firing rate (Keen and Hudspeth 2006). Presynaptically, the sensory hair cell has specialized ribbon-type synapses that are found at a variety of sensory receptors responsible for translating graded inputs into tonic outputs (Matthews and Fuchs 2010). The specific function of these presynaptic specializations remains unknown.

Innervation patterns vary between auditory end organs. In lower vertebrates, like frog, turtle, and bird, one or at most two afferent fibers innervate a single hair cell, with each fiber making 20–50 synaptic contacts (Martinez-Dunst et al. 1997; Schnee et al. 2011; Sneary 1988). In mammalian inner hair cells, 15–20 afferent fibers innervate each hair cell, but each afferent fiber has a single synapse (Meyer et al. 2009). The functional significance of the different innervation patterns is a focus of the present work.

Postsynaptic recordings of auditory fibers present a remarkably broad range of excitatory postsynaptic current (EPSC) amplitudes, varying by as much as 20-fold (Glowatzki and Fuchs 2002). Rise and decay times are generally very similar between the smallest and largest EPSCs measured in a given fiber. Together these data support the hypothesis of multivesicular release (Glowatzki and Fuchs 2002). Multivesicular release may be due to synchronized fusion of multiple single vesicles, to release of large prefused vesicles, or perhaps to a combination of the two (Fuchs et al. 2003; Matthews and Fuchs 2010). The data presented here support both possibilities.

In turtle auditory papilla, afferent fibers are tuned between 30 and 700 Hz, with Q₁₀ ranging from 0.5 to 7.5, and show phase-locking throughout the frequency range (Crawford and Fettiplace 1980). Hair cells contain calcium channels clustered at synapses responsible for both tuning and synaptic release (Crawford and Fettiplace 1981; Ricci et al. 2000; Tucker and Fettiplace 1995). Release, as measured via capacitance changes, varies with calcium entry and is comprised of multiple components that correlate with morphologically identified vesicle pools (Schnee et al. 2011). No tonotopic differences have been observed at turtle hair cell synapses, other than in the prevalence of synapses in high-frequency hair cells, and thus far no evidence exists to suggest that synapses within a given hair cell vary morphologically or in calcium channel density (Schnee et al. 2005, 2011). This is in contrast to mammalian hair cells, in which variability in ribbon sizes, Ca²⁺ channel number, and postsynaptic glutamate receptor density shows heterogeneity in both pre- and postsynaptic specializations (Frank et al. 2009; Liberman et al. 2011).

The data presented here describe afferent response properties of turtle auditory papilla fibers. The results support the hypothesis that synchronized release of vesicles between synapses is critical for action potential (AP) generation. The data also support a role for multivesicular release.

MATERIALS AND METHODS

Tissue preparation.

Turtles (Trachemys scripta elegans, carapace length 3–6 in.) were euthanized as previously described, and inner ear tissue was removed (Farris et al. 2006; Schnee et al. 2011). All animal procedures were approved by the Administrative Panel on Laboratory Animal Care of Stanford University and are in accordance with the American Physiological Society's “Guiding Principles for the Care and Use of Vertebrate Animals in Research and Training” and all federal regulations. The auditory papilla was separated from other tissue and pinned in a Sylgard-bottomed dish, and the tectorial membrane was removed. No enzyme treatments were used. The auditory papilla was placed in a coverslipped bottom recording chamber and held in place with single strands of dental floss. The external solution contained (in mM) 125 NaCl, 2.8 KCl, 2.8 CaCl₂, 2.2 MgCl₂, 10 HEPES, 6 glucose, 2 ascorbate, 2 creatine, and 2 pyruvate. pH was buffered to 7.6 with NaOH, and the osmolality was maintained at 275 mosmol/kgH₂O. To ensure that the hair cells were not overly hyperpolarized, 100 nM apamin was added to the bath solution to block hair cell small-conductance potassium channels (Tucker and Fettiplace 1996). An apical perfusion pipette (∼50 μm in diameter) was placed near the recording site. In addition, a larger bath pipette was used to maintain circulation at 1–2 ml/min. Recording chambers were placed onto a specialized stage coupled to a BX51 upright Olympus microscope and viewed with a Q-imaging camera (Q-imaging).

Afferent fiber recordings.

Thick-walled borosilicate patch electrodes fire polished to resistances between 5 and 10 MΩ were used for all recordings. Internal solutions contained (in mM) 115 KCl, 10 HEPES, 3 Na₂ATP, 5 creatine phosphate, and 4 MgCl₂; EGTA or in some cases CsCl replaced the KCl. pH was buffered to 7.2 with either KOH or CsOH, and osmolality was maintained at 255 mosmol/kgH₂O. A larger electrode, filled with external solution, was used to make a hole from the apical surface of the papilla to clear a path for the patch electrode. This electrode was used to clean the afferent fiber as well. Patch electrodes were brought up to the nerve ending either near the base of the hair cell or along one of the fingerlike projections. Alexa 488 (50 μM) was often included in the patch electrode to label the ending being recorded. No fiber was found to innervate more than one hair cell. Data were collected with the Multiclamp amplifier (Molecular Probes) connected to a Daq3000 (IOtech) A/D, D/A interface with a Dell personal computer. Data were collected at 10 kHz. Voltage protocols and all recordings were obtained with the jClamp software package.

Multiunit recording.

Turtle half-head preparations were used for multiunit activity measurements from the eighth cranial nerve. The turtle head was split in half and pinned in a Sylgard dissection chamber with either an external solution similar to that used in patch-clamp recordings or bicarbonate-buffered perilymph containing (in mM) 126 NaCl, 2.5 KCl, 13 NaHCO₃, 1.7 NaH₂PO₄, 1.8 CaCl₂, 1 MgCl₂, and 5 glucose (continuously bubbled with 95% O₂-5% CO₂). The brain was removed and the auditory nerve exposed, cutting the connections to posterior ampulla and saccule. The ventral otic membrane was trimmed to allow access to perfusion prior to mounting the preparation in the recording chamber. A perfusion pipette was located ∼5 mm above the otic capsule and connected to a gravity perfusion system with a flow rate of roughly 1 ml/min. The auditory nerve was inserted in an hourglass-shaped suction electrode with a micromanipulator, and compound APs were recorded with a differential AC preamplifier (Grass P55, Astro-Med, West Warwick, RI). One electrode was inserted into the borosilicate suction pipette, and the neutral electrode was in contact with the bath. The signal was band-pass filtered (1 Hz–1 kHz) and amplified 1,000 times. Compound APs were collected through a data acquisition interface (CED Micro 1401 mkII, Cambridge Electronic Design) and analyzed with Spike 2 software (Cambridge Electronic Design). Noise levels were confirmed by blocking afferent activity with 1 μM tetrodoxin (TTX) or the glutamate antagonists 6,7-dinitroquinoxaline-2,3-dione (DNQX; 1 μM) or kynurenic acid (2 mM), and spike threshold was set to 3 × SD of baseline noise. Drugs were applied via the local perfusion system after a baseline firing rate was established. Control perfusion with the external solution (sans drug) was used to confirm that there were no mechanical artifacts.

Data analysis.

Data were analyzed with Mini Analysis (Synaptosoft) or Clampfit software packages. Origin (Microcal) was also used for statistical analysis, curve fitting, and figure generation. Final figures were assembled with Adobe Illustrator. Box plots are presented with individual data points; boxes represent SD and the open star symbol represents the mean of the data. Histograms were fit with the sum of Gaussian distributions of either one, two, or three peaks. Best fit was selected both by the correlation coefficient (r²) and by eye when discriminating multiple peaks (see results for more details). Paired Student's t-tests were used for comparisons of data sets; P values are given with data. All data are presented as means ± SD.

RESULTS

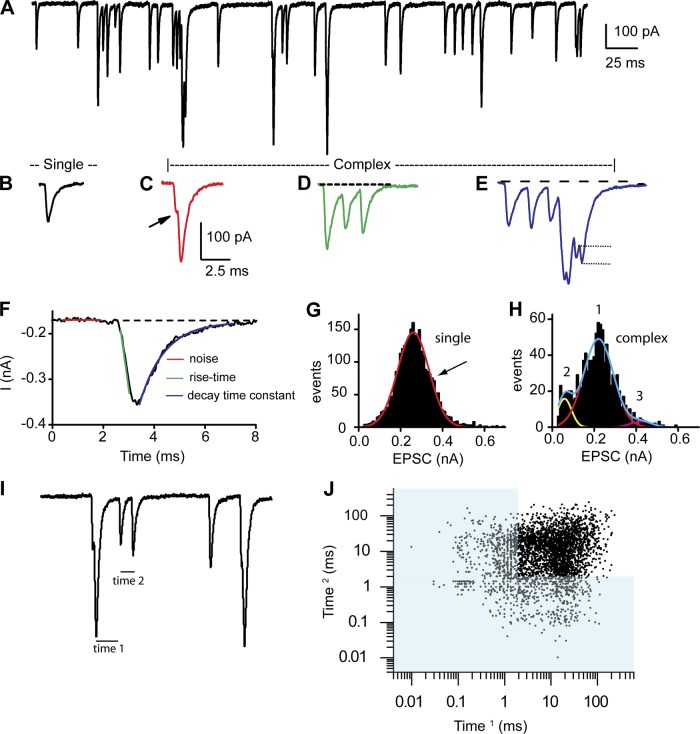
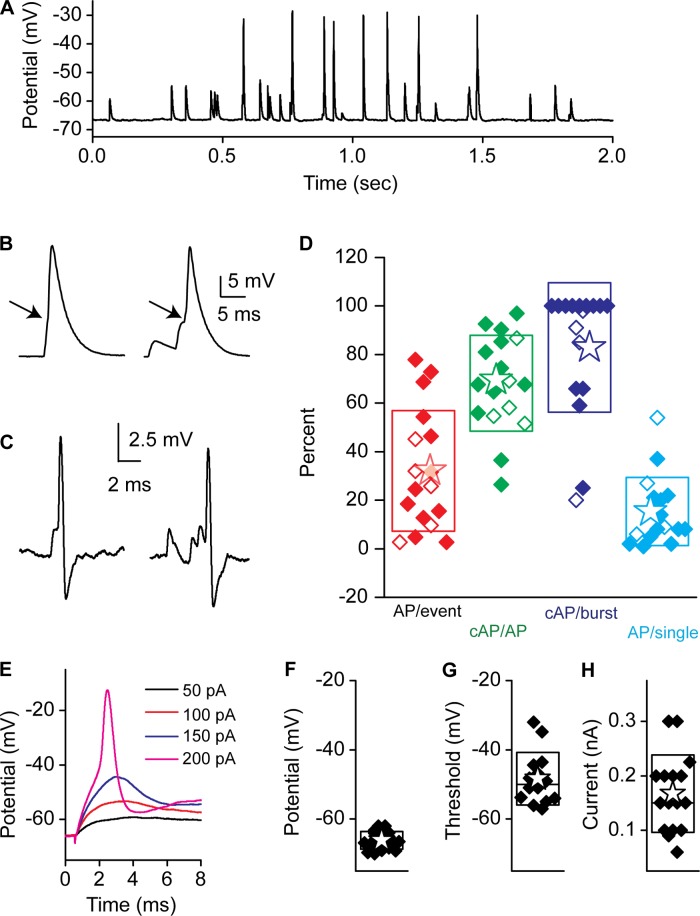
A total of 58 recordings were made from afferent fibers of the turtle auditory papilla. Membrane capacitance, as estimated from a single-decay model fit to a −5-mV step in voltage clamp, averaged 4.2 ± 1.4 pF (n = 58). Fiber membrane potentials were held to −89 mV, with a mean holding current of −107 ± 71 pA (n = 58). Series resistances were corrected up to 70%, resulting in values of 13 ± 7 MΩ (n = 58). Series resistance compensation was critical for obtaining accurate information regarding peak current distributions as well as rise and decay kinetics. Figure 1A presents a representative example of spontaneous fiber activity, where a range of simple and complex EPSCs were consistently observed. Spontaneous activity is used to define postsynaptic recordings under standard external conditions in which the hair cell is not being stimulated. Previous experiments have demonstrated that in vitro hair cells are typically more hyperpolarized than under physiological conditions with resting potentials closer to −60 mV (Farris et al. 2006). At these potentials there is a small calcium current that can drive release (Schnee and Ricci 2003), but, as can be seen, release is at very low rates. Thus spontaneous activity is driven by calcium entry via calcium channels. We define evoked activity as release observed under elevated potassium conditions in which the hair cell will be depolarized to potentials activating a larger proportion of the calcium current. Single EPSCs were defined as those that started and ended at the baseline current and had single rise times as well as exponential decays (Fig. 1B). All other events were considered complex (or bursts) and could present in different forms (Fig. 1, C–E). Steplike increments in the rising phase were observed (Fig. 1C) and assumed to indicate summation of unique events. Often burstlike behavior was observed, where the responses did not return to baseline before the next event occurred; these events could be separated in time, revealing more clearly the individual events (Fig. 1D) or more overlapping (Fig. 1E), where rise and decays could not be assessed. In both cases peaks could be counted to determine the minimum number of EPSCs (complex events) forming the burst. Amplitudes for the single events were measured as the difference between the peak current reached and the baseline prior to the event occurring. Similarly for complex events, the peak amplitudes were measured as the difference in current between each peak value and the start of each event in the burst (typically not a constant baseline value; see Fig. 1E, dotted lines). For spontaneous activity, complex events represented <20% of the total events measured. One representation of this distribution is the use of a recurrence plot, often used to identify complex phase relationships, where sequential interpulse intervals (IPIs) are plotted against each other. Fig. 1, I and J, illustrate this approach, where Fig. 1I is an expanded view of spontaneous EPSCs where IPIs are indicated. Time 1 is first plotted against time 2, and then time 2 is plotted (as time 1) against the next interval. The recurrence plot in Fig. 1J shows that the vast majority of events have IPIs > 3 ms, corresponding to single events (a single EPSC takes ∼3 ms from start to finish). The relatively broad scatter in this plot suggests stochastic behavior of the synapses contributing to the responses.

Fig. 1.

A: spontaneous postsynaptic measurements from an afferent fiber innervating an auditory hair cell from a low-frequency position of the turtle auditory papilla. The fiber was voltage-clamped at −84 mV. B–E: a variety of response types were measured: singles, defined as excitatory postsynaptic currents (EPSCs) with a single rise and decay time starting and ending at the same baseline current (B), and complex responses, defined as having multiple inflections on the rise or decay component (C; see arrow for inflection), as being shifted from baseline for the rise or decay time (D; see dashed line as indicating baseline), and/or as having multiple peaks prior to decaying back to the original baseline (E). The dotted lines in E depict how amplitude was measured for overlapping EPSCs in complex events. A burst is equivalent to D or E. F: measurements made including threshold as 3× the baseline rms noise (red), rise time measurements (green) (10–90% measurements), and decay time constants (blue line), measured as single exponential decays from the peak. G and H: amplitude histograms for the single (G) and complex (H) events measured. Plots were fit with single, double, or triple Gaussian functions as shown. Often single or double Gaussians could be fit; as indicated by arrow in G, in each case the best fit with the fewest peaks was selected (here a single). Fits to individual Gaussians are shown in red and yellow in H and the summed Gaussian in blue. Numbers above each peak represent how peaks are defined in subsequent figures. I: an expanded view of spontaneous EPSCs with the interpulse intervals times 1 and 2 noted. J: time 1 vs. time 2 in a recurrence plot to identify patterns that might suggest differences between individual synapses onto this fiber. Blue shading demarks the time range that would require the interval to be reflecting complex events, as a single EPSC would take longer to complete.

For single events, rise times were measured as the 10–90% time to peak; as will be seen, these can often be quite fast and likely limited by voltage clamp speed. Decay times were fit with an exponential, and it is the time constant of this fit that is reported (Fig. 1F). Histograms for EPSC amplitudes were generated for each fiber with 10-pA bins and sampled for periods of 1–30 s, depending on response frequency. Most often, histograms had a single major peak based on the relative area contributed, with minor peaks of smaller area contribution of either greater or lesser mean amplitude. In cases as depicted in Fig. 1G, single Gaussians were used, as they represented the data as well as a double function would. For other fibers, however, the best fit was a double or triple Gaussian with minor peaks of both greater and lesser value than the main peak as in Fig. 1H.

Pharmacology.

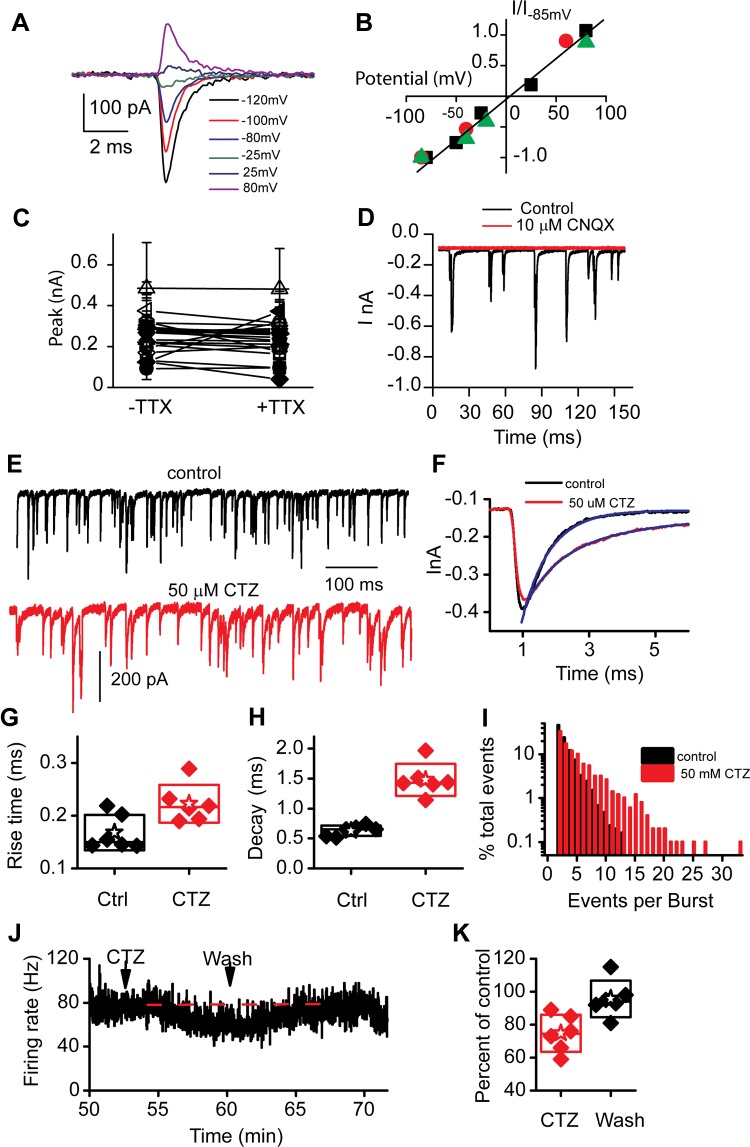
The reversal potential of the EPSCs was determined in three cells by clamping the membrane potential at different values long enough to obtain an amplitude distribution for the events. The major peak current amplitude of each histogram was then plotted against holding potential (Fig. 2, A and B). A reversal potential of −3 ± 3 mV was obtained, showing the mixed cation-conducting behavior typical of glutamatergic receptors. A comparison of amplitude histograms was made in the absence and presence of TTX in order to ensure that unclamped sodium currents were not altering the shapes of the EPSCs measured. The peak amplitudes are plotted in Fig. 2C, where a tendency toward smaller peaks was observed with TTX. For this reason all measurements reported are in the presence of 1 μM TTX. In addition, to ensure that all measured values were of AMPA receptor origin and to assess baseline levels for setting detection thresholds, 10 μM 6-cyano-7-nitroquinoxaline-2,3-dione (CNQX) was used to completely abolish EPSCs (Fig. 2D). Curare was also tested under both normal and high potassium levels to test potential efferent effects altering the responses. No effects of either 10 or 100 μM curare were observed (data not shown).

Fig. 2.

Synaptic potentials are carried by AMPA receptors. Current-voltage plots for spontaneous EPSCs were generated by creating amplitude histograms at different potentials. Current examples are presented in A, and then the peak Gaussian fit to the amplitude histogram is plotted against potential in B. The reversal potential was −3 ± 3 mV for 3 cells with a slope of 13 ± 6 mV⁻¹. C: contamination by non-voltage-clamped sodium currents was investigated by comparing frequency histograms in the absence and presence of tetrodotoxin (TTX; 1 μM); peaks of these histograms are plotted for individual cells, showing no significant change. D: block by 6-cyano-7-nitroquinoxaline-2,3-dione (CNQX) demonstrates that the postsynaptic potential measurements were carried by glutamate AMPA receptor channels. Complete block was observed with 10 μM CNQX. E: cyclothiazide (CTZ) application (red trace, below the control example) suggests that desensitization plays a role in shaping EPSCs. F: single EPSCs of similar magnitude in the absence and presence of CTZ to illustrate the slower rise and decay times. Exponential fits to the decay times are also shown. G and H: summaries of mean rise time (G) and decay time constant (τ; H) are presented in box plots where the box outlines the SD, the star the mean for the group, and the diamonds the individual fiber responses. I: bar graph breaking down the number of individual peaks in each complex event. CTZ increases the number of EPSCs per complex event. J: multiunit recordings from the 8th cranial nerve were measured from the half-head preparation, and the frequency response was plotted. K: application of CTZ consistently reduced firing rates as shown in the box plot, intimating a presynaptic effect on release.

Cyclothiazide.

To investigate the importance of EPSC kinetics, particularly in determining the proportion of single compared with complex events, the effects of cyclothiazide (CTZ) were investigated. CTZ is most commonly used to alter desensitization, but it has also been shown to alter glutamate affinity for receptors (Dzubay and Jahr 1999; Partin et al. 1993, 1994, 1996). Regardless of the specific mechanism of action, CTZ is useful because it can alter EPSC kinetics. Both rise and decay times were slowed by 100 μM CTZ (P < 0.05 for rise times and P < 0.001 for decay time constants; Fig. 2, E–H). Decay times were slowed by a factor of almost 3 (Fig. 2H), a more dramatic effect compared with the rise times. As a result of the slowing of EPSCs, the fraction of complex events increased to 86 ± 5% (n = 3) after CTZ treatment. The number of unitary EPSCs per complex event also increased in the presence of CTZ. Fig. 2I presents a frequency histogram of events per burst showing that in the presence of CTZ there are many more bursts with multiple peaks. This result is not surprising and supports the argument that bursts (complex events) are simply the temporal summation of single events. In addition to the change in release kinetics and the increase in complex events, the frequency of spontaneous release was reduced in four of six cells after CTZ treatment. Changes in frequency of release are typically indicative of a presynaptic action, and thus a decrease in frequency might suggest a presynaptic effect of CTZ. Further support of this decrease in release frequency comes from multiunit recordings from the turtle half-head preparation (Fig. 2J). Application of CTZ (50 μM) reduced afferent firing rates to 74 ± 10% of initial rate (n = 7, P = 0.02), an effect that disappeared after washout of the drug (Fig. 2K). This reduction occurs despite the increase in complex events that are expected to increase firing rates (see below).

Spontaneous activity.

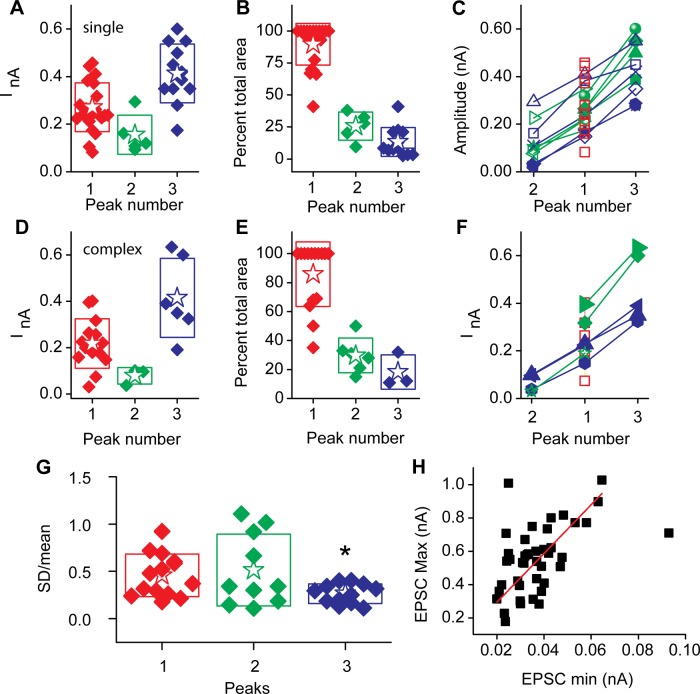
Spontaneous activity was observed in 26 of 33 cells, with EPSC frequencies up to 50 Hz; the mean value was 22 ± 18 Hz (n = 27), with 6 fibers having rates < 5 Hz. A total of 83 ± 17% of the spontaneous EPSCs measured in each fiber were single events. EPSC amplitude histograms were fit to each of the responding fibers, where 13 were best fit by single Gaussian functions, 7 by double Gaussian functions, and 6 by triples. The peak currents, as measured from the Gaussian fits, are presented in box plots (Fig. 3A), with the major peak (based on area of the histogram) plotted as peak 1, the smaller mean amplitude peak as peak 2, and the larger mean amplitude peak as peak 3 (see Fig. 1H). In 20 of 26 cells, the major peak represented at least 80% of the total distribution (Fig. 3B). Individual fiber peak amplitudes are presented in Fig. 3C, showing the broad range of amplitudes. The relative change between peak amplitudes was similar between units (as seen by the similar slopes), indicative of a simple scaling process.

Fig. 3.

Gaussian fits to frequency histograms for spontaneous EPSC amplitudes were generated. A: the peaks to these fits. B: each Gaussian had a major peak based on the relative area, typically ∼80% of total area of histogram. Peak 1 is defined as the peak with the largest area (see Fig. 1H), peak 2 represents amplitudes smaller than the major peak, and peak 3 represents those with peak currents greater than the major peak. C: peak amplitudes for individual cells, where red boxes are those cells with single Gaussian peaks, green are those with 2 peaks, and blue are those with 3 peaks; open symbols indicate a minor peak of smaller peak current than the primary peak, and filled symbols represent those with a minor peak of greater mean amplitude than the primary peak. D–F: complex EPSCs presented in a manner similar to the singles presented in A–C. G: SD of each peak divided by the mean value for each peak to illustrate the relative variance between peaks. Surprisingly, the largest amplitude peaks showed the smallest relative variance and were statistically different from either of the other peaks (t-test, 2-tailed, P < 0.05) H: a relationship was observed between minimum and maximum amplitude EPSC where the red line represents a linear fit with a slope of 15 ± 1 and intercept of 0 (R² = 0.94).

The complex EPSCs represent on average 17% of the total spontaneous activity. The distribution of peak amplitudes as well as the relative area of each peak are presented in Fig. 3, D and E. These values are comparable to those of the single EPSCs, as is the relationship between peaks within given units (Fig. 3F). The similarity in properties between the complex and single events is consistent with the hypothesis that the complex events simply represent increased activity resulting in temporal overlap, likely due to release from multiple synapses or perhaps multiple release sites at a given synapse. In evaluating the afferent fibers with multiple peaked amplitude histograms, a question arises as to whether the underlying mechanisms responsible for achieving each peak were similar. Comparing the relative variance (measured from the width of the individual histogram) to the mean of the histogram provides a measure where a constant ratio among peaks is predicted for similar processes, whereas greater or lower ratio values would suggest more or less complexity. We unexpectedly found less variance for the histograms with the largest mean value (Fig. 3G), perhaps suggesting a more simple release process for these large-amplitude events.

In general, EPSC amplitudes varied by more than an order of magnitude for individual fibers. The mean maximum amplitude was 555 ± 202 pA, while the minimum was 37 ± 14 pA (n = 42). The range of minimum and maximum EPSC amplitudes covaried with a slope of 15 ± 1 (Fig. 3H) (r² = 0.94). This relationship is interesting in that it suggests a constant range of amplitudes within a given fiber that scales between fibers. Hair cells from the turtle papilla have >20 synapses per fiber, and so likely the EPSCs measured are in part the sum across these synapses (Schnee et al. 2005; Sneary 1988). However, the broad range in amplitude histograms is quite typical among ribbon synapses, even those with only single synapses per fiber (Glowatzki and Fuchs 2002; Grant et al. 2010). Therefore, the breadth of amplitude histograms is not simply due to summation across synapses but likely a common feature of individual ribbon synapses.

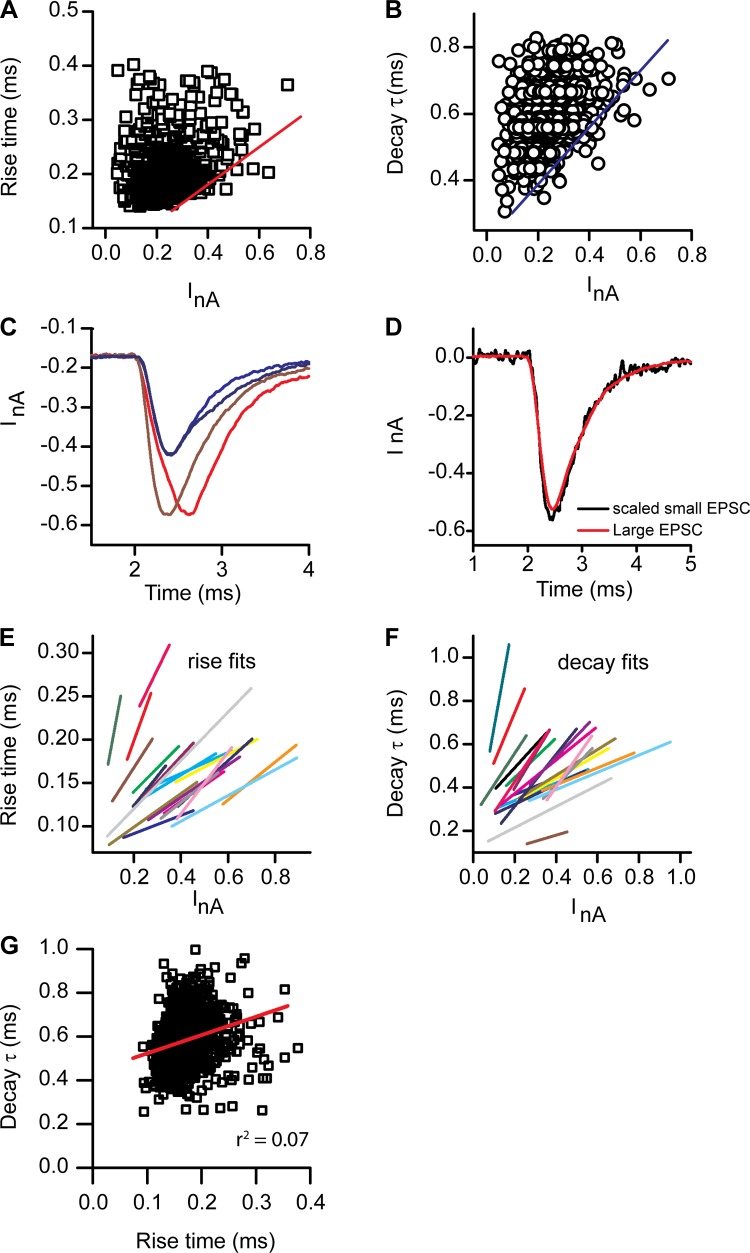
Given the pseudocalcyceal nature of the turtle postsynaptic fiber, it is possible that the space clamp is a potential error source for both kinetic and amplitude values. Plotting the rise time or decay time constant against the peak amplitude of EPSC histograms provides some insight into this issue (Fig. 4, A and B). Rise times varied two- to threefold within individual fibers, as did the decay time constant. The envelope of the plots showed a relationship in which the rise time slowed as current amplitude grew. This is opposite that expected for a space clamp or clamp speed error, where current amplitudes should decrease and kinetics slow as the clamp speed as well as the space clamp is compromised. Additionally, it is clear from the scattergrams that EPSCs may be selected across amplitudes to find very similar kinetic properties, simply by moving horizontally across the scatter (Fig. 4D). Conversely, quite different kinetics can be observed simply by moving vertically along the scatter (Fig. 4C). Figure 4C provides examples for small- and large-amplitude responses where the kinetics are quite different between the EPSCs, while Fig. 4D provides an example of a large-amplitude EPSC with a small (but scaled) EPSC of comparable kinetics.

Fig. 4.

Kinetic analysis of the rise and decay time course for spontaneous EPSCs (singles). A and B: rise time (A) and decay τ (B) plotted against peak current for individual EPSCs showing a great deal of scatter, with both currents and rise times varying 4-fold. A line could be fit to the envelope of the response indicating a trend for larger EPSCs to be slower than smaller (see red and blue lines, respectively). C: examples of EPSCs of similar sizes but different kinetic behavior for both large and small EPSCs. Blue traces show differences in the decay times, while red shows differences in rise time. D: a similar plot where small and large EPSCs were scaled to show that the kinetics were similar. E and F: envelope fits for individual cells for both rise (E) and decay (F) times. Each cell similarly showed the trends for slowing with larger current amplitudes. G: the rise time for a given cell plotted against its decay time to demonstrate that no clear relationship exists (fast rise times are observed with slow decay and vice versa). Red line indicates a fit with r² = 0.02.

Summaries of the envelope fits for the plots of both the rise and decay times against peak amplitude (Fig. 4, E and F) illustrate that every fiber consistently showed a slowing of kinetics with larger EPSC amplitudes. Scattergrams were also created for rise times against decay times to determine whether this kinetics covaried. For all fibers tested no consistent relationship was observed. The scattergram shown in Fig. 4G represents the closest relationship observed, and it is clear from this plot that no pattern is present; a linear fit produced an r² value of 0.02. A lack of relationship argues against space clamp dictating these results and rather supports the idea that there is considerable physiological variability in EPSC kinetics, perhaps in part due to the timing of vesicle release or to the size of vesicles fusing.

Current clamp.

To explore the efficacy of EPSCs in generating postsynaptic APs, current-clamp recordings were obtained using K⁺ as the major intracellular cation. An example of these measurements is presented in Fig. 5, where it is apparent that not all excitatory postsynaptic potentials (EPSPs) were capable of generating APs. This differs from the recent report in mammalian afferent fibers (Rutherford et al. 2012) but is similar to that observed in young rats (Yi et al. 2010) and to previous work in turtle (Crawford and Fettiplace 1980). Just as in voltage clamp, both single and complex events were observed. A higher percentage of complex events was observed in current clamp (39 ± 19%) compared with voltage clamp (17 ± 16, n = 5), most likely as a consequence of EPSPs being significantly slower than EPSCs, thus allowing for more temporal overlap (much like the CTZ experiments). Spikes were defined by identifying the inflection point in voltage change indicative of Na⁺ channel activation (see arrows in Fig. 5B). The mean voltage change for a spike was 56 ± 22 mV (n = 15), with a range of 22–97 mV. The spike amplitude variance suggests that spike generation is at a variable distance from the recording site. Similarly, the occurrence of Na⁺ currents that were not well voltage-clamped, likely due to space clamp issues, supports this contention (data not shown). To ensure that afferent properties were not affected by obtaining the whole cell recording configuration, cell-attached patch data were also investigated. Both current- and voltage-clamp modes were used, and examples of APs evoked from single and complex modes are presented in Fig. 5C (there was no difference between recording modes). EPSPs were relatively inefficient at generating APs, with 35% of EPSPs resulting in spikes (Fig. 5D, AP/event). Of the total APs generated, more than half were generated from complex events [Fig. 5D, cAP/AP (complex AP/all AP)], despite complex events representing only 39% of all events. More than 80% of complex events generated APs (Fig. 5D, cAP/burst) compared with only 17% for single events (Fig. 5D, AP/single), supporting the argument that temporal summation was important for spike generation. The ability of synaptic events to generate APs varied considerably between fibers, from as low as 3% to as high as 90% (Fig. 5D). The reason for this variation is unclear but did seem to correlate with the fraction of complex events for a given unit. These data suggest that spike timing and initiation may be controlled by the ability of synapses to release synchronously, thus creating suprathreshold complex events.

Fig. 5.

A: current-clamp responses from afferent fibers showing excitatory postsynaptic potentials (EPSPs) and EPSP-evoked spikes. B: spikes elicited from single (left) and complex (right) EPSPs. Arrows indicate the inflection that is indicative of regenerative action potentials (APs). C: cell-attached recordings in current clamp of single event-driven (left) and complex event-driven (right) APs. D: the fraction of APs generated from all EPSPs (red), the proportion of APs generated from complex EPSPs (green), the proportion of complex events (bursts) that result in APs (cAP) (dark blue), and the proportion of single EPSPs that result in APs (light blue). Open symbols are from whole cell recordings and filled symbols from cell-attached recordings. E: a fiber's membrane potential response to current step injections. Box plots in F–H present summary data for resting potential (F), spike threshold (G) as measured from the inflection point (see arrow in B), and the current injection required to reach threshold (H).

To determine whether the lack of AP efficiency was in part due to postsynaptic properties, fibers were injected with current at different levels until APs were elicited (Fig. 5E). AP threshold response was measured as −48 ± 8 mV (n = 14; Fig. 5G) compared with a resting potential of −66 ± 3 mV (n = 19; Fig. 5F), indicating that EPSPs needed to depolarize the fiber 18 mV on average to evoke a spike. The average current injection required to elicit a spike was 167 ± 70 pA (n = 16; Fig. 5H). No distinct populations of fibers were identified to suggest that fibers had different thresholds.

Potassium-evoked activity.

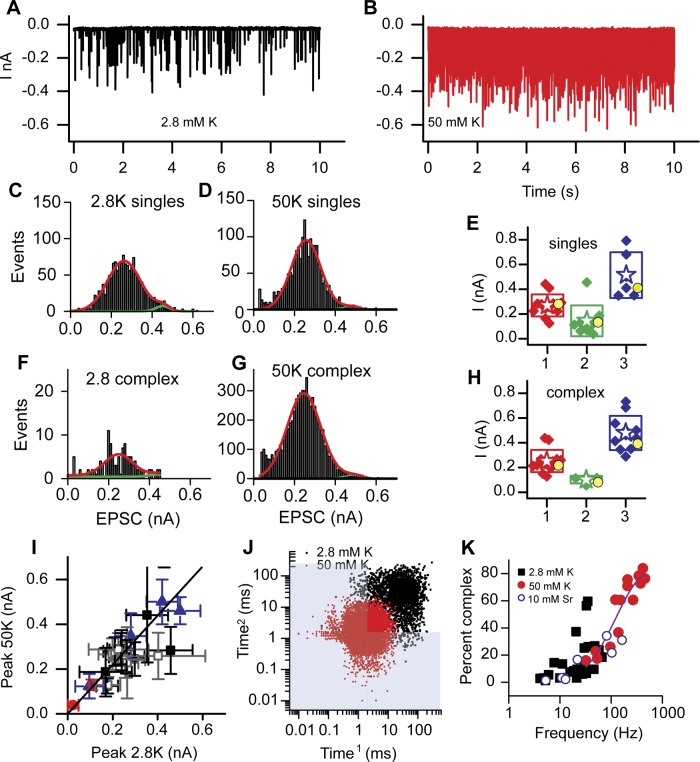
Spontaneous activity from the afferent fibers was low in our recording conditions. This most likely stems from a lack of active mechanotransduction and an improper endolymph-like environment serving to hyperpolarize hair cells away from their normal resting potential (Farris et al. 2006). To mimic more physiological hair cell potentials and to provide more events for analysis, hair cells were exposed to 50 mM K⁺ while the afferent fiber was voltage-clamped to −89 mV. Figure 6, A and B, present an example of a fiber in 2.8 mM and 50 mM K⁺. Release rates increased from 12 ± 14 Hz (n = 13) to 211 ± 144 Hz (n = 13) under these conditions. Fatigue was not observed, and release rates were maintained indefinitely throughout the K⁺ application, which on average lasted 4 ± 1 min (n = 14), attesting to the robustness of these synapses and their ability to maintain vesicle populations for release. Concomitant with the increase in release rate was an increase in the proportion of complex events from 19 ± 6% to 54 ± 25% (n = 13). The number of EPSC peaks within each complex event was 2–16 for evoked release but only up to 6 for spontaneous release, with the vast majority being of the doublet variety.

Fig. 6.

Summary data for K⁺-evoked EPSC activity where A presents spontaneous EPSC activity while B presents activity in the presence of 50 mM K⁺ from a single fiber. C and F plot the amplitude histograms for single and complex events in 2.8 mM K⁺, while D and G present similar plots from the same fiber in 50 mM K⁺. E and H: peak amplitudes from the Gaussian fits are plotted for both single (E) and complex (H) EPSCs. Filled symbols represent the individual cells, stars represent the mean value, and the box presents the SD. Yellow circles represent the mean values from the spontaneously occurring events in Fig. 3. I: peak currents in 2.8 mM K⁺ plotted against the corresponding peak current in 50 mM K⁺. Filled squares indicate peak 1 singles, red circles peak 2 singles, blue triangles peak 3 singles, and open squares complex peak 1 values. The line has an intercept of 0 and a slope of 1, showing no change in peak values between control and stimulated conditions. J: an example of a recurrence plot where black symbols represent data from 2.8 mM K⁺ and red symbols represent data from 50 mM K⁺. The blue shaded area represents the region for complex events. K: frequency of total events (single and bursts) plotted against the proportion of complex events for spontaneous (black) and K⁺-induced (red) release. Line is an exponential fit to the data having an r² of 0.91.

Amplitude histograms were created for both single and complex EPSCs under elevated-K⁺ conditions (Fig. 6, C, D, F, and G). For both single (Fig. 6, C and D) and complex (Fig. 6, F and G) events, there was an increase in the number of fibers with multi-Gaussian distributions in elevated K⁺ compared with spontaneous activity. Peak current amplitudes for the major peaks and both secondary peaks were not different between single and complex events (Fig. 6, E and H; see yellow symbol as mean value from spontaneous recordings). Together these data also support the argument that evoked EPSCs are not larger than spontaneous EPSCs. To further explore this idea, the amplitude peaks measured from the Gaussian fits from spontaneous firing fibers were plotted against the same peaks in elevated K⁺ (Fig. 6I); the error bars are the width of the Gaussian fits. This relationship has a slope of 1 and intercept of 0 and so also supports the argument that the amplitude of EPSCs does not increase with stimulation and that the observed changes are simply a function of the increased probability of release. Interestingly, the shape of the EPSC amplitude distributions varied in some of the fibers during the application of K⁺. The data in Fig. 6 demonstrate that the amplitude histograms do not change when comparing spontaneous and K⁺-evoked measurements; however, they do not directly assess those peaks that were not present in spontaneous activity. In 14 cells investigated under control conditions, prior to K⁺ treatment, 5 showed no activity in control, 6 were single Gaussian distributions, 2 showed three peaks, and 1 showed a single secondary peak of higher amplitude than the major peak. After K⁺ exposure all fibers showed activity. The five originally silent fibers produced double Gaussian distributions, where the secondary peak was larger than the major peak. The complex Gaussian amplitude distributions for spontaneous activity remained the same with the K⁺-evoked responses. Of the six fibers with single Gaussian peaks, two remained singles, two had a smaller minor peak, and two had a minor larger peak. These additional larger peaks were within the range of peaks measured across fibers for spontaneous activity as well. Thus the increased frequency of EPSCs with K⁺ application did not result in larger EPSCs.

To further explore the idea that the increase in complex events was simply a function of the increase in release rate, the average release frequency in each fiber was plotted against the proportion of complex events for both spontaneous and evoked responses (Fig. 6K). An exponential relationship was observed with a correlation coefficient of 0.91, again supporting the idea that the change in proportion of complex events was simply a function of the increase in probability of release, leading to more temporal overlap in EPSCs.

The recurrence plot for a fiber in the absence and presence of 50 mM K⁺ in Fig. 6J supports the conclusion that higher frequencies result in more complex events; the shaded region again demarcates where complex events would be occurring and K⁺ shifts the responses from single events to more complex events. In this example and in many of the generated plots, there are several hot spots suggesting some coordination in the release properties. It is possible that depolarization with K⁺ brings the hair cell closer to its resonant frequency and it is the intrinsic presynaptic resonance that generates coordinated responses (Andor-Ardo et al. 2010).

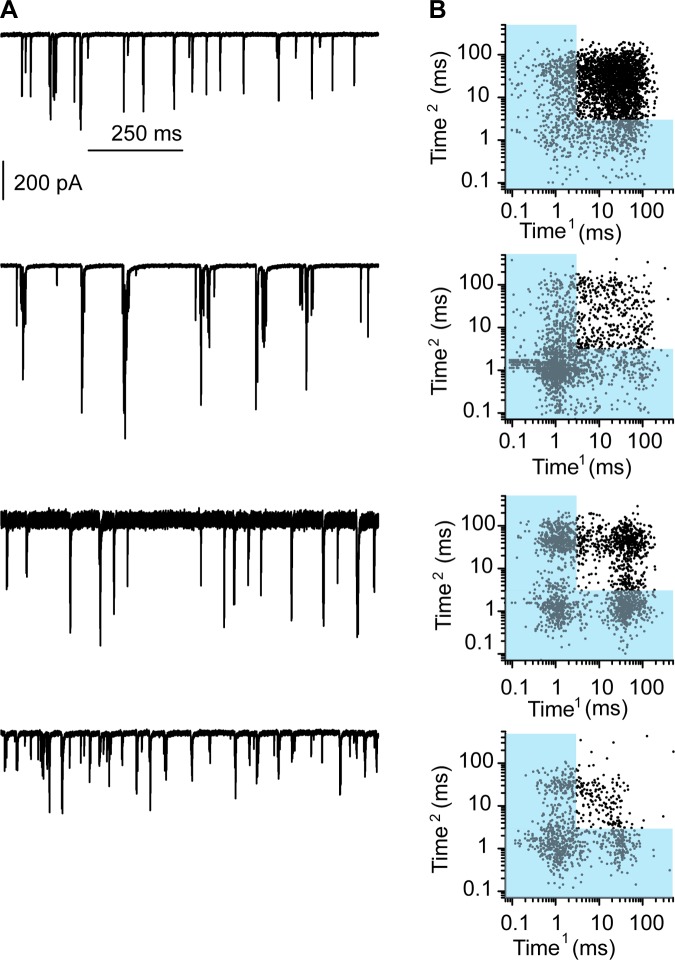
Along these lines there are several outliers in the frequency vs. percent complex plot in Fig. 6K, where the percentage of complex events was much higher than predicted by the release frequency. Figure 7 plots three examples of these outliers, with one example of a more traditional response (Fig. 7, top), showing both 1-s examples of the measurements (Fig. 7A) as well as the recurrence plot (Fig. 7B). Each example shows the prevalence of complex events but also the clustering of responses suggesting presynaptic coordination of release. Likely these outliers represent hair cells whose resting potential is more depolarized (likely having some remaining mechanotransduction current) allowing for electrical resonance to coordinate release properties. This being the case, it would support the argument that temporal summation between synapses to generate complex events that have a high probability of generating APs is an important mechanism used by fibers with multiple synaptic endings.

Fig. 7.

Investigating the relationship between release frequency and complex events revealed several outliers where complex events were at a higher proportion than predicted by frequency. A: examples of spontaneous activity from 4 different cells; the example at top was the most typically observed, and the following 3 examples are outliers from Fig. 6K. B: recurrence plots for each. The outlier plots show a larger percentage of complex events largely due to the patterned responses, suggesting coordinated release between synapses.

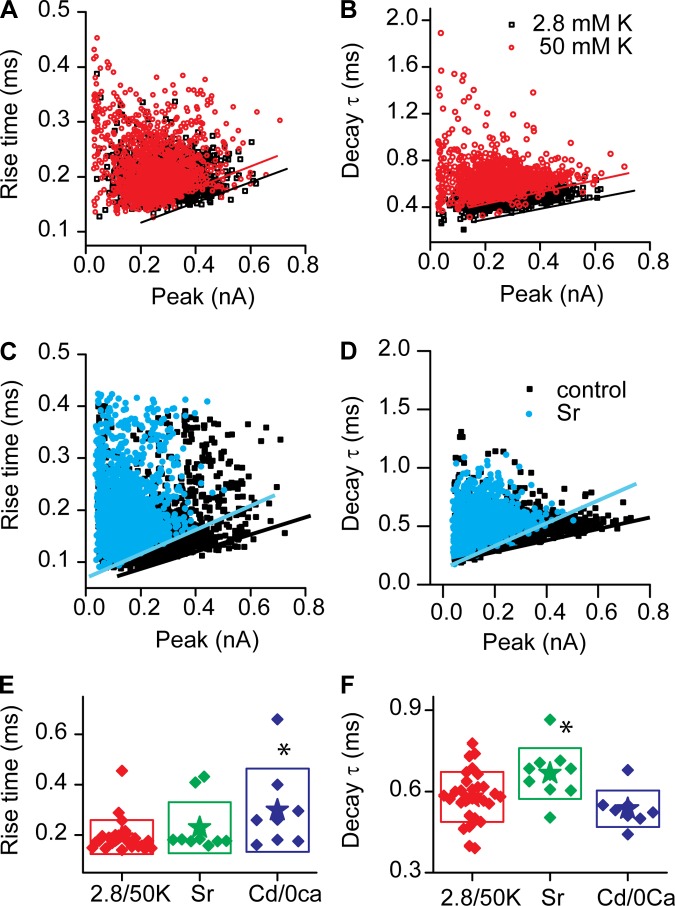
The kinetics of EPSCs was also investigated under stimulated conditions. Plots of rise times and decay time constants against peak current for spontaneous and evoked EPSCs are presented in Fig. 8, A and B. These plots basically overlapped. Fits to the envelope under both conditions were also not different. The rise time slopes were 0.23 ± 0.06 ms/nA and 0.25 ± 0.13 ms/nA (n = 8) for 2.8 and 50 mM K⁺, respectively. Slopes for the decay plots were 0.8 ± 0.4 ms/nA and 0.8 ± 0.5 ms/nA (n = 12) for 2.8 and 50 mM K⁺, respectively.

Fig. 8.

Changing release rates does not alter the kinetics of EPSCs. A and B: plots of rise (A) and decay (B) times against EPSC amplitude in 2.8 mM or 50 mM K⁺ are presented to demonstrate that the envelope of these plots is invariant. Envelopes are indicated by the lines. C and D: similar plots of rise (C) and decay (D) rates in the absence (control) and presence of 10 mM Sr²⁺. Here the envelopes of the plots differ, being steeper in the presence of Sr²⁺. Figure 9 summarizes these data. E: average rise times for all EPSCs in a given fiber for control (red), in the presence of Sr²⁺ (green), or in the low divalent (or 0.1 mM Cd²⁺; blue). *Significantly different from control data at the P < 0.05 level. F: similar plots of decay time constants under these conditions, demonstrating that Sr²⁺ slows the average EPSC decay rate (P < 0.05).

Effects of divalents.

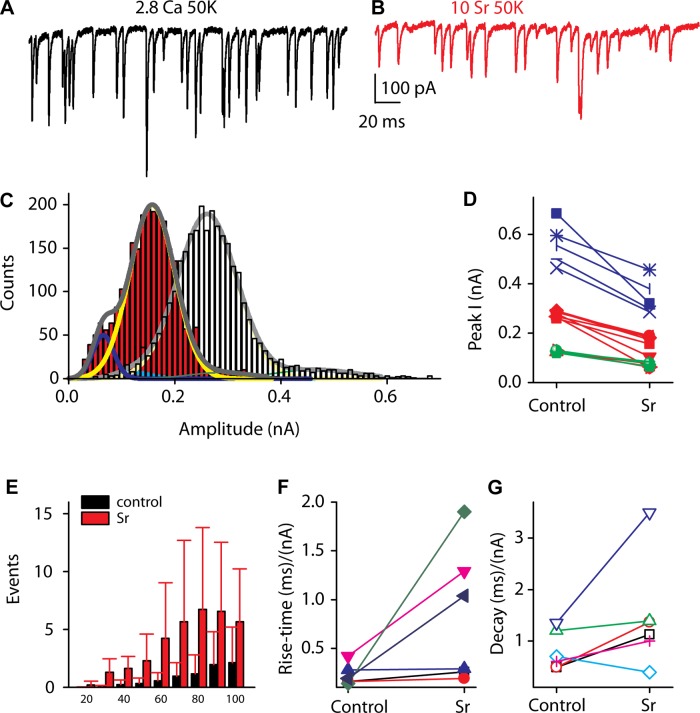
Strontium (Sr²⁺) is often used to replace Ca²⁺ in order to desynchronize release (Xu-Friedman and Regehr 1999, 2000). Typically these experiments are performed in response to presynaptic stimulation where calcium entry is synchronized and becomes desynchronized with Sr²⁺ as Sr²⁺ replaces calcium less efficiently in triggering release. In addition, Sr²⁺ is not well buffered, resulting in continued release after stimulus. Here, there is no directed presynaptic stimulation; however, as activity is driven by Ca²⁺ entry, the hypothesis is that clustered calcium channels summate Ca²⁺ triggering multiple vesicle fusions in a synchronous (coordinated) manner. Sr^2+, therefore might interfere with these release processes and result in reduced frequency and, more importantly, reduced-amplitude EPSCs. We would also predict a reduction in rise and decay times because temporal precision of these coordinated vesicles might be compromised such that mistimed summation will lengthen the activation and deactivation times. Thus the effect of Sr²⁺ on EPSCs was tested to determine whether the broad range in EPSC amplitude might in part be due to synchronous release of vesicles. In the presence of Sr²⁺, release rates, the proportion of complex events, and the peak amplitudes for each major peak in each afferent fiber were reduced. Examples of the EPSCs obtained in the presence of Sr²⁺ are presented in Fig. 9, A and B. Amplitude reductions ranged from 30% to 60% of control peak values (Fig. 9, C and D). Amplitude histograms for one fiber are presented in Fig. 9C to illustrate shift in peak amplitudes. A summary plot of peak amplitudes (Fig. 9D) uses a color scheme similar to previous figures (where green is minor smaller peak, red is major intermediate amplitude peak, and blue is smaller peak of higher amplitude) and shows a consistent decrease in each peak amplitude after Sr²⁺ treatment. However, these amplitudes do not converge onto a unitary event size; rather, it appears as if each peak of the Gaussian represents a unique unitary distribution, perhaps based on vesicle size. Thus these data would suggest that synchronous vesicle fusion may provide an important component of multivesicular release that is superimposed onto a broad range of vesicle sizes. The fraction of complex events was also reduced, likely as a result of the overall decrease in release frequency (Fig. 6K). These data sit exactly on the control data, thus suggesting that the change in complex events is solely due to the frequency change. The rise and decay times still showed a broad spread (Fig. 8, C and D). However, the slopes of the envelopes were steeper, indicating that the rise and decay times were slowed in the presence of Sr²⁺ (Fig. 9, F and G), as predicted if coordinated release were being compromised. Plotting the absolute mean values for rise and decay times (Fig. 8, E and F) results in no difference for Sr²⁺ compared with K⁺ for the rise time; however, the decay time was significantly slower (P < 0.05, 2-tailed paired t-test). In conjunction with the reduced activity and the shift to smaller values for the peaks in the amplitude histograms, there was a major increase in the number of events with peaks below 100 pA (Fig. 9E). The increase in small-amplitude events was broad and did not lend itself to fitting but suggests that desynchronizing release results in smaller-amplitude EPSCs. Together these data support the argument that the broad range of EPSC amplitudes is in part dictated by synchronous release of vesicles but do not suggest that this is the exclusive mechanism.

Fig. 9.

Sr²⁺ reduces frequency and amplitude of EPSC responses. A and B: afferent fiber responses in the presence of 50 mM K⁺ (A) and the same fiber in the presence of 50 mM K⁺ and 10 mM Sr²⁺ (B). C: amplitude histograms in the absence (gray histogram) and presence (red histogram) of Sr²⁺. D: peak amplitudes decreased in the presence of Sr²⁺. Color code is as in previous figures, with red being the primary peak based on histogram area, green the smaller amplitude peak, and blue the larger. E: there is a large increase in the number of small events, those <100 pA. F and G: the envelopes of the rise (F) and decay (G) plots (Fig. 8) are steeper in the presence than in the absence of Sr²⁺.

Sr²⁺ might directly alter AMPA receptor conductance, thereby generating smaller EPSCs simply because the single-channel conductances were reduced. Although many investigations using Sr²⁺ have not identified this as a potential mechanism, it remains plausible (Bender et al. 2006; Clements and Silver 2000). To test this possibility, we recorded EPSCs in the absence and presence of Sr²⁺ at positive and negative potentials. At positive potentials a divalent block of the pore would be removed, thus increasing the mean EPSC amplitude compared with −80 mV. In four cells tested the mean EPSC amplitude changed from 253 ± 72 pA to 223 ± 143 pA in normal Ca²⁺ at −84 and +76 mV, respectively, while in the presence of Sr²⁺ the change was from 150 ± 15 pA to 129 ± 80 pA for −84 and +76 mV, respectively. These data demonstrate that the divalents were not altering the AMPA conductance.

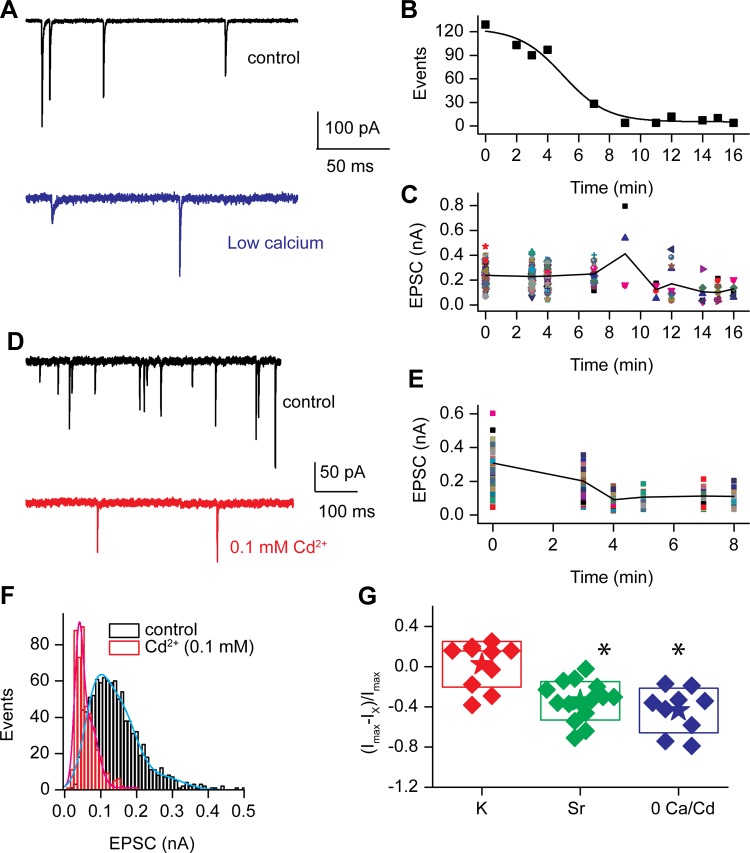
Further attempts at interfering with synchronous release were made by lowering external calcium or using cadmium (Cd²⁺), a known blocker of hair cell calcium channels, to block calcium entry (Fig. 1) (Schnee and Ricci 2003). Both lowering external calcium (Fig. 10, A–C) and introducing Cd²⁺ extracellularly (Fig. 10, D and E) produced a dramatic reduction in the frequency of EPSC release and also reduced the EPSC amplitude. The time course for frequency reduction is plotted for the EGTA solution applied externally in Fig. 10B. Amplitude reduction closely followed the same time course (Fig. 10C). The EGTA solution ultimately resulted in no or extremely few EPSCs that did not allow for generation of frequency histograms; however, the Cd²⁺ experiments maintained release at rates where frequency histograms could be generated (Fig. 10F). The example of a control histogram in Fig. 10F was best fit with the equation for a triple Gaussian curve, having peaks and half-widths of 0.08 ± 0.06, 0.15 ± 0.1, and 0.28 ± 0.1 nA (r² = 0.97). The histogram generated in the presence of Cd²⁺ was best fit with a double Gaussian equation with peaks and half-widths of 0.04 ± 0.008 and 0.07 ± 0.04 nA (r² = 0.88). Thus in this case Cd²⁺ unmasked a smaller population of EPSCs and shifted larger peaks to smaller values very similar to the Sr²⁺ data. Figure 10G plots the relative change in EPSC amplitudes under control and altered divalent conditions to assess amplitude changes under conditions in which the frequency of responses was too low to generate histograms. Under each condition, Sr²⁺ or lowered Ca²⁺ or Cd²⁺, the EPSC amplitude was reduced. The reduction in EPSC amplitude did not reach a quantal value, as is also illustrated by the example in Fig. 10A and from these mean values. If all release were a function of a single vesicle size and the divalent exchange experiments were capable of interfering with coordinated release so as to unveil the individual events, then the EPSC amplitudes would have reduced to a single distribution about a minimal mean amplitude. This was not observed, in that a minimal mean value was not reached; in fact, discrete events were observed down to the noise floor and multiple larger peaks were also observed.

Fig. 10.

Reducing external calcium or blocking calcium channels with cadmium reduced EPSC amplitude and frequency. A: EPSCs at the start (top) and stop (bottom) of a perfusion of an EGTA-buffered external solution. The time course of reduction in frequency is shown in B. The reduction in frequency of release correlated with the reduction of EPSC amplitude. C: individual EPSC amplitudes plotted over perfusion time, demonstrating that although EPSC amplitudes are reduced, large events remain. Similar results were obtained by perfusing 0.1 mM Cd²⁺ onto the preparation. D: examples of EPSCs prior to (top) and at the end of (bottom) perfusion. E: time course of amplitude reduction during Cd²⁺ application where individual EPSC amplitudes are plotted at various time points. F: amplitude histograms for the cell in D for the control and in the presence of Cd²⁺. The control data were fit with the equation for a triple Gaussian, resulting in peaks and half-widths of 0.084 ± 0.06 nA, 0.148 ± 0.1 nA, and 0.28 ± 0.1 nA (r² = 0.97), while the data in the presence of Cd²⁺ were fit with the equation for a double Gaussian, with peaks and half-widths of 0.04 ± 0.008 nA and 0.07 ± 0.04 nA (r² = 0.88). G: relative change in peak amplitude of EPSCs under different conditions including K⁺ (red) Sr²⁺ (green), or low divalent 0 mM Ca²⁺ or Cd²⁺ (blue). *Significant difference at P < 0.05.

DISCUSSION

Recordings from afferent fibers innervating hair cells of the turtle auditory papilla provide insight into the functioning of this synapse. A broad range of EPSC amplitudes and frequencies were observed for both single and complex events. Depolarization increased both the frequency and the proportion of complex events but did not appear to directly increase the amplitude of the EPSCs. Fatigue was not observed, attesting to the ability of these synapses to rapidly replenish their supply of vesicles. Complex events appear to be bursts of single events that overlap in time and are simply a function of the release rate of the individual synapses. Bursts as described in immature mammalian cochlea hair cells were observed in only 1 of 55 recordings from the mature turtle papilla (Glowatzki and Fuchs 2002). Bursts in mammalian immature afferent fibers differ from what was found here in that the complex events underlying the burst were all small-amplitude responses that when summed were the equivalent of a single EPSC. Complex events in turtle auditory papilla had peaks that were comparable to those of the single EPSC events, suggesting that in the turtle bursts are due to temporal overlap of EPSCs arising from different synapses while in mammalian fibers bursts are considered desynchronized EPSCs at a single synapse (Grant et al. 2011).

The wide range of EPSC amplitudes measured at ribbon synapses is the basis for arguments invoking a multivesicular release process whose underlying mechanism could be coordinated release of single vesicles, release of prefused large vesicles, or a combination of both. Direct evidence for either mechanism is limited but compelling (Graydon et al. 2011; Matthews and Sterling 2008), and the basic tenet that multivesicular release is a property of ribbon synapses required to explain amplitude histogram distributions has been validated at several ribbon synapses (Glowatzki and Fuchs 2002; Grant et al. 2011; Graydon et al. 2011; Li et al. 2009). In the turtle, broad histograms were observed, often with multiple peaks. The number of peaks increased with release frequency. At least two scenarios could explain the broad amplitude distribution of EPSCs: vesicle size variability and/or coordinated release of vesicles. Previous measurements of synaptic vesicle diameters followed a Gaussian distribution with a mean of 42 nm and a half-width of 11 nm (Schnee et al. 2005). The range of vesicle size was 25–60 nm, providing an expected volume difference of 14× between the smallest and largest vesicle. This ratio is similar to the range of EPSC amplitudes measured, and so vesicle size could account for the amplitude range of EPSCs measured. Whether the vesicle size distribution reflects prefusion of single vesicles and thus a form of multivesicular release remains to be determined.

Reduction of calcium entry reduced the EPSC range to 7× while desynchronizing release with Sr²⁺ (Xu-Friedman and Regehr 2000) reduced it to 9×, in both cases shifting amplitudes to lower values (Schnee et al. 2005). The changes in peak response with external Sr²⁺ did not reduce the amplitudes to a unitary size, as was reported in frog when hair cells were hyperpolarized (Li et al. 2009). This difference in part may be accounted for by Sr²⁺ being more effective at replacing Ca²⁺ at hair cell synapses than at more conventional synapses. Given that the molecules involved in release are presumed to be different and also that Ca²⁺ channels are clustered so tightly (Beurg et al. 2010; Dulon et al. 2009; Reisinger et al. 2011; Ricci et al. 2000; Roux et al. 2006; Safieddine and Wenthold 1999; Tucker and Fettiplace 1995), this conclusion is plausible. That incomplete desynchronization by Sr²⁺ may be occurring is supported by the slowing of both the rise and decay times of the remaining EPSCs recorded. Recent data from rod bipolar cells similarly found a decrease in EPSC amplitude with calcium channel blocker application (Mehta et al. 2013). These data may support a general property of ribbon synapses and clustered calcium channels, i.e., to coordinate release such that larger EPSCs are generated for a higher probability of reaching threshold.

Together the morphological data and the pharmacological results are consistent with both synchronous vesicle fusion and perhaps prerelease vesicle fusion (to account for vesicle size variability) largely dictating the range of EPSC amplitudes. Data from frog hair cells have similarly argued for synchronous release (Graydon et al. 2011), where amplitude histograms have widths comparable to those in turtle. However, frog data show a much narrower distribution of vesicle sizes, with vesicles ranging in diameter from 24 to 50 nm, which means a volume difference of only 9×, thus requiring synchronous release to account for at least some of the variation in amplitude histogram (Graydon et al. 2011). One problem in each of these studies is the clear identification of synaptic vesicles compared with bulk-endocytosed membrane, sorting and recycling endosomes, or endoplasmic reticulum. Location near the dense body was typically the selected criterion, but this may not be rigorous enough.

The vesicle size variability might reflect a form of multivesicular release where prerelease fusion of vesicles creates a broader distribution of potential EPSC measurements. Supporting this potential mechanism are the data from divalent ions as well as Sr²⁺ treatment. In each case, lowering external calcium, blocking calcium channels with Cd⁺, or desynchronizing release with Sr²⁺ resulted in reduced EPSC amplitudes, although this reduction did not reach a single quantal value. The reduction supports an argument for synchronization; however, the lack of a quantal distribution in EPSCs supports a broad distribution of vesicle sizes prior to release.

On average, the width of the amplitude histograms was ∼15×. Interestingly, although the width of the EPSC frequency histograms was relatively constant, the amplitudes over which this variance occurred also were quite broad, with minimum values between 20 and 70 pA. The mechanism underlying this almost fourfold range is not clear. It is possible that this is a postsynaptic effect with glutamate receptor numbers and/or densities varying between fibers. It is also possible that the concentration of glutamate per vesicle varies (Wu et al. 2007). Alternatively, the mean vesicle size in each ribbon synapse could be variable, as has been reported in CNS synapses (Hu et al. 2008; Qu et al. 2009), and different EPSC amplitudes could simply correspond to the release of vesicle pools of different sizes. Further work is needed to delineate between possibilities.

Complex events were defined as those either with a nonmonotonic rise time or with decays that did not reach baseline prior to the next event initiation (the latter being the most prevalent type of complex event). The sum of complex events creates a burst. The proportion of complex events varied with the frequency of release for a given fiber, as did the number of individual events comprising a single burst. No differences were found between peak amplitudes of single and complex events for a given fiber, in contrast to those of mammalian afferent fibers (Grant et al. 2011). The simplest conclusion from these results is that complex events result from overlapping release events that might arise from individual synapses. Most importantly, it does not appear that any separate mechanism is needed to account for these events. These results are in good agreement with work in frog amphibian papilla (Andor-Ardo et al. 2012), in which a deconvolution algorithm was used to investigate complex events under spontaneous and stimulated conditions and came to very similar conclusions.

Complex events were more efficient at generating APs than single events, implicating summation between synapses as a mechanism by which these pseudocalyceal endings coordinate output to ensure reaching threshold. This would be a particularly useful mechanism for hair cells that are intrinsically tuned, as it would directly translate both frequency and timing information synaptically. The recurrence plots also support this conclusion, showing clusters of responses corresponding to complex events. The limitation, however, is the upper frequency level because the requirement of temporal summation to achieve threshold would ostensibly limit the repetition rate of these complex events to the width of the complex event. The reduction in synapses per afferent fiber in higher-frequency end organs (as in birds and mammals) might be a manifestation of this limitation (Martinez-Dunst et al. 1997). Reducing the number of synapses per fiber and increasing the role of multivesicular release could also represent the underlying evolutionary driving force that culminated at mammalian auditory synapses. For example, the largest EPSCs reported in mammals are 800–1,000 pA, values rarely if ever observed in turtle hair cells (Glowatzki and Fuchs 2002). Multivesicular release may guarantee APs in higher-frequency end organs because the EPSCs remain temporally brief.

The ability of ribbon synapses to sustain release indefinitely has been the focus of work from many laboratories. The turtle auditory papilla is no exception in this ability, with rates over 400 Hz measured with an event simply defined as an EPSC regardless of amplitude (so clearly underestimating vesicle numbers). Recordings were obtained largely from low-frequency hair cells with ∼20 synapses, thus requiring at the very least 20 vesicles per synapse per second. At these rates low-frequency dense bodies (with ∼70 vesicles each) would be depleted in <4 s and the rapidly releasable pool in <1 s. However, including recruitment vesicles within 700 nm of the dense body would allow release to continue for >70 s (Schnee et al. 2005). Therefore, postsynaptic measurements are in accord with presynaptic capacitance measurements, attesting to the ability of these ribbon synapses to recruit vesicles rapidly to the synapse and supporting previous arguments that release and not vesicle recruitment to the ribbon is rate limiting (Schnee et al. 2005, 2011).

In summary, the data presented show a broad range of EPSCs that can in part be accounted for by the range of vesicle sizes but also are in part due to synchronized fusion of vesicles. Complex events that underlie bursts are argued to be due to temporal summation between synapses. Temporal summation results in much more efficient generation of APs and is postulated to be the means of ensuring spike timing in these calyceal types of endings.

GRANTS

This work was supported by National Institute on Deafness and Other Communication Disorders Grant RO1 DC-009913 to A. J. Ricci and Core Grant P30 44992, as well as a Dean's fellowship and a Cajamadrid foundation fellowship to M. Castellano-Muñoz.

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the author(s).

AUTHOR CONTRIBUTIONS

Author contributions: M.E.S. and A.J.R. conception and design of research; M.E.S. and M.C.-M. performed experiments; M.E.S. and A.J.R. analyzed data; M.E.S., M.C.-M., and A.J.R. interpreted results of experiments; M.E.S., M.C.-M., and A.J.R. prepared figures; M.E.S., M.C.-M., and A.J.R. edited and revised manuscript; M.E.S., M.C.-M., and A.J.R. approved final version of manuscript; A.J.R. drafted manuscript.