Integration of texture and disparity cues to surface slant in dorsal visual cortex

Abstract

Reliable estimation of three-dimensional (3D) surface orientation is critical for recognizing and interacting with complex 3D objects in our environment. Human observers maximize the reliability of their estimates of surface slant by integrating multiple depth cues. Texture and binocular disparity are two such cues, but they are qualitatively very different. Existing evidence suggests that representations of surface tilt from each of these cues coincide at the single-neuron level in higher cortical areas. However, the cortical circuits responsible for 1) integration of such qualitatively distinct cues and 2) encoding the slant component of surface orientation have not been assessed. We tested for cortical responses related to slanted plane stimuli that were defined independently by texture, disparity, and combinations of these two cues. We analyzed the discriminability of functional MRI responses to two slant angles using multivariate pattern classification. Responses in visual area V3B/KO to stimuli containing congruent cues were more discriminable than those elicited by single cues, in line with predictions based on the fusion of slant estimates from component cues. This improvement was specific to congruent combinations of cues: incongruent cues yielded lower decoding accuracies, which suggests the robust use of individual cues in cases of large cue conflicts. These data suggest that area V3B/KO is intricately involved in the integration of qualitatively dissimilar depth cues.

humans experience the solid objects that populate their surroundings from multiple viewpoints. To recognize and physically interact with such objects, the visual system requires an estimate of the orientation of the object's surfaces with respect to the line of sight. This orientation is composed of tilt (rotation in the image plane, such as the changing orientation of the hands of a clock over time) and slant (rotation away from frontoparallel, such as changes in the steepness of a hillside road while driving). In estimating slant, the visual system is faced with the difficult challenge of inferring the three-dimensional (3D) surface structure using the information contained within a pair of two-dimensional (2D) retinal images. Perception of surface slant represents a critical step in recognizing and interacting with 3D objects and has been studied extensively with psychophysical methods (Backus et al. 1999; Gillam and Ryan 1992; Hillis et al. 2004; Knill and Saunders 2003; Norman et al. 2006; van Ee and Erkelens 1998), yet its neural basis remains poorly understood.

To achieve slant estimation, the human visual system exploits various sources of information that may be present within the retinal inputs, such as binocular disparity, motion parallax, texture, perspective, and shadow (Braunstein 1968; Gibson 1950; Howard and Rogers 1995; Marr 1982). Given this range of depth cues, the visual system is believed to integrate signals to reduce noise and enhance perceptual judgments (Landy et al. 1995). For instance, adults have greater sensitivity to slant when two cues are available compared with the individual component cues (Hillis et al. 2004; Knill and Saunders 2003). However, relatively little is known about the neural implementation of such cue integration computations.

Here we aimed to test the neural basis of the integration of disparity and texture slant cues using human fMRI. To this end, we exploited multivoxel pattern analysis (MVPA) to discriminate patterns of fMRI activity that were evoked by viewing surfaces with different slants. Thereby, we sought to quantify the information about differences between the viewed stimuli in different portions of the visual cortex. Logically, we might expect a number of different outcomes based on the sensitivity of a given area to different depth cues. First, consider an area that is exclusively sensitive to a given cue, for example, binocular disparity. The presence or absence of other cues should have little effect on the information about disparity contained in this area. Moreover, if different stimuli were presented that contained the same disparity, the area would be insensitive to stimulus differences. Such an area would constitute a pure disparity-processing module, and while potentially elegant from an engineering perspective, it would be biologically unwieldy and is empirically unlikely (Cumming and DeAngelis 2001; Orban 2011; Parker 2007; Welchman 2011). Second, an area might be sensitive to different aspects of the cues that compose a slanted surface but represent this information using different subpopulations. In this case, information about depth from different cues would be colocated but not integrated. The responses of this area would be expected to change in line with manipulations of different cues, and stimulus discrimination (based on the area's activity) would improve when two (or more) cues specified differences in slant between the stimuli. Finally, an area might integrate information from the different depth signals, thereby enhancing discrimination performance when two or more cues specified the same information about slant. Given that improved discrimination performance is expected under the second and third scenarios, how can we differentiate them?

We can conceptualize the information about different depth configurations in terms of bivariate probability density distributions for different slanted stimuli (Fig. 1, A and B). One way for an ideal observer to discriminate between two such distributions would be to use the optimal decision boundary. Under this solution, slant estimates from the two cues remain independent. The improved discrimination performance that this computation would yield can be calculated from the quadratic sum of the discriminabilities of the component cues (Fig. 1B). Alternatively, the visual system might fuse component cue dimensions into a single depth estimate. Under this solution, improved discrimination occurs through a reduction in variance of the depth estimate.

Fig. 1.

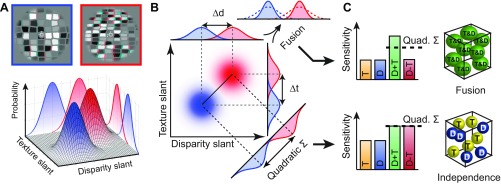
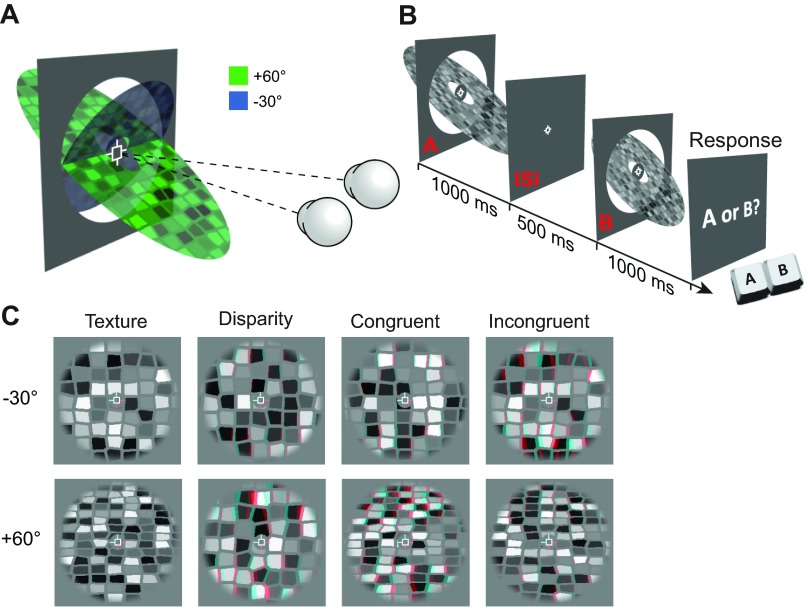
Illustration of the stimulus space and predictions for the discrimination performance of mechanisms based on the independent or fused use of depth cues. A: an observer is presented with 2 different slanted stimuli (anaglyph stereograms at the top), which we denote with red and blue. We can conceptualize detectors for these stimuli based on independent depth estimates from disparity and texture. These detectors yield an estimate for each stimulus with a certain probability density function. The outputs of these detectors are conceptualized as bivariate Gaussian probability distributions (3D plot below)—with 1 distribution for the blue stimulus and 1 for the red stimulus. The marginal projections (i.e., performance of the single-cue detectors) are illustrated on the walls of the 3D plot. B: a planar projection of the bivariate Gaussians (color saturation indicates probability density) to illustrate 2 possible computations when using the information from 2 depth cues. The red and blue stimuli could potentially be discriminated using either cue alone, but with some uncertainty (overlapping probability distributions). Two computations for reducing this uncertainty are illustrated: Independence—separation orthogonal to the optimal discriminating boundary (negative diagonal) and Fusion—multiplication of the probability densities associated with each cue. C: the idealized performance of a mechanism based on Fusion (top) or Independence (bottom). Illustrations on right depict neural implementations within single voxels for the extreme cases of these 2 alternative computations. Each sphere represents a neuronal population that encodes depth from either component cue (yellow and blue) or from a combination of cues (green). An intermediate implementation (not depicted here) would contain all of these population types within a voxel. T, texture; D, disparity.

To test which of these computations (independence or fusion) the visual system uses to achieve improved discrimination performance for combined cues, we assessed changes in fMRI responses related to independent manipulations of each cue. Our logic was that fMRI responses to different depth configurations should be more discriminable when texture and disparity cues were congruent. Furthermore, the extent of this improved discriminability provides a means of distinguishing between the two alternative computations that might underlie cue integration (Ban et al. 2012). In particular, we expect that sensitivity to “single-cue” stimuli (Fig. 2; Texture, Disparity stimuli) should be attenuated by the presence of the conflicting cue only if depth estimates from the two cues are fused into a common representation. In that case, performance for congruent-cue stimuli will exceed that predicted by quadratic summation of performance for single-cue stimuli (Fig. 1C). In contrast, if depth representations are colocated but remain independent, then performance for combined-cue stimuli should be predicted by quadratic summation. Using this logic, we used MVPA to decode information about surface slants defined by disparity, texture, and their congruent and incongruent combinations.

Fig. 2.

A: cartoon illustrating the opposing slanted surfaces tested in the study. The 2 eyes are illustrated fixating the marker at the center of the display. B: sequence of events for a single trial in the behavioral experiment. C: examples of the 2 slant levels for the 4 conditions tested in the experiment. Stimuli are rendered as red-cyan anaglyphs for stereoscopic viewing (red filter over left eye). Note that for the Incongruent condition, the stimuli are labeled according to the slant specified by texture, i.e., in the top (−30°) stimulus, texture signals −30° and disparity signals +60° slant. In the bottom stimulus, texture signals +60° and disparity −30°.

While the experimental logic and methods employed here have previously been used to test for cue fusion (Ban et al. 2012), there are two fundamental differences. First, we test two qualitatively different types of cue: disparity and texture. Whereas motion and disparity are computationally similar cues that can both be used to compute absolute depth (given knowledge of ego-motion, interpupillary distance, and gaze angle), texture provides only relative depth information (Landy et al. 1995). Outputs from independent texture and disparity processing circuits cannot therefore simply be averaged in order to estimate depth. It remains an open question as to whether the integration of qualitatively similar (motion and disparity) and dissimilar (texture and disparity) cue pairings share a common neural substrate. Second, the previous study assessed cue combination for simple depth order relationships between frontoparallel surfaces. Here we test neural responses to slanted surfaces—a far more behaviorally relevant depth structure that is important for the estimation of extended surfaces and a critical step in the processing of complex/curved surfaces and solid 3D objects.

MATERIALS AND METHODS

Observers.

Fifteen healthy observers from the University of Birmingham with normal or corrected-to-normal vision participated in the fMRI experiment. The mean age was 25.8 yr (range = 21–37 yr; 6 women, 9 men). Three participants' data were excluded from analysis because of excessive head movements during scanning, which prevented voxel correspondence necessary for MVPA. Excessive head movement was defined as >10 sharp head movements (≥1-mm displacement between consecutive volumes) or ≥4-mm total displacement over the course of a 7-min run. After runs that exceeded these thresholds were excluded, three participants had fewer than five remaining runs and so were excluded entirely as there were insufficient data for MVPA. In general, participants were able to remain still throughout scanning (the mean maximum head displacement per run for included participants was 1.2 mm vs. 2.8 mm for excluded participants). Participants were screened for stereoacuity and contraindications to MRI prior to the experiment. All experiments were conducted in accordance with the ethical guidelines of the Declaration of Helsinki and were approved by the University of Birmingham STEM ethics committee.

Stimuli.

Stimuli were grayscale stereograms of textured planar surfaces, with slant (rotation about a central horizontal axis) defined independently by texture and disparity (Fig. 2, A and C). Surface textures were generated by Voronoi tessellation of a regular grid of points (1 ± 0.1° point spacing) randomly jittered in two dimensions by up to 0.3° (Knill and Saunders 2003; Nardini et al. 2010). Each texture element (texel) was randomly assigned a gray level and shrunk about its centroid by 20%. This created the appearance of “cracks” between the texels, the width of which also varied with surface slant and thus provided additional texture information. Textures were mapped onto a vertical virtual surface and rotated about the horizontal axis by the specified texture-defined slant angle, before a perspective projection consistent with the physical viewing geometry was applied. From this cyclopean view, binocular disparity was then calculated and applied to each vertex based on the specified disparity-defined slant angle.

Surfaces were presented inside a circular aperture with a radius of 3.5° and a cosine edge profile in order to blur the appearance of depth edges. Stimuli were presented on a mid-gray background, surrounded by a grid of black and white squares (75% density) designed to provide an unambiguous background reference. Texture-defined position in depth—which corresponds to mean texel size—was randomized for each stimulus presentation by increasing point spacing in the initial grid of points by ±10%. This reduced the reliability of mean texel size in a given portion of the stimulus as a cue to surface slant. Disparity-defined position in depth was kept constant across all stimulus presentations.

Stimuli in the single-cue conditions (Texture and Disparity) were intentionally designed to contain a cue conflict for two reasons. First, the premise of our test for cue fusion was that the presence of cue conflict would reduce sensitivity to single-cue conditions only if cues are fused, but not if they remain independent. Second, the presence of both component cues in all stimulus conditions minimized low-level differences that would otherwise complicate comparison of responses to different conditions. For example, monocular presentation (which is frequently used to isolate texture cues in behavioral studies) is known to significantly affect both univariate and multivariate fMRI responses (Büchert et al. 2002; Schwarzkopf et al. 2010). We presented all stimuli binocularly, and stimuli in the Texture condition were given a disparity-defined slant of 0°. To attenuate the reliability of the disparity cue for this condition, the disparity-defined position in depth of each texel was randomly jittered between ±2 arcmin. Similarly, stimuli in the Disparity condition had a texture-defined slant of 0°. Stimuli in the Incongruent condition consisted of each cue signaling one of the two base slant angles (i.e., texture signaled −30° and disparity signaled +60° or vice versa). For the behavioral experiment, the increments applied to create test stimuli shifted texture- and disparity-defined slants in opposite directions to each other (i.e., the absolute slant of both cues either increased or decreased relative to the base slants).

Stimuli were programmed and presented in MATLAB (The MathWorks, Natick, MA) with Psychophysics Toolbox extensions (Brainard 1997; Pelli 1997). Stereoscopic presentation in the scanner was achieved by using two projectors (JVC, D-ILA SX21) containing separate spectral interference filters (INFITEC). The two projections were optically combined with a beam splitter and entered the scanner room through a waveguide. This method produced negligible cross talk between the two images, since the filtered emission spectra for the two projectors contained little overlap. Stimuli were back-projected (1,280 × 1,024, 52 × 41.6 cm) onto a translucent screen inside the bore of the magnet and viewed via a front-surfaced mirror attached to the head coil and angled at 45° above the observers' heads. This resulted in a viewing distance of 65 cm, from which the entire slanted plane stimulus was visible within the binocular field of view. In a separate session, a subset of participants (n = 3) repeated the experiment in the scanner while eye movement data were recorded monocularly with a CRS limbus eye tracker (Cambridge Research Systems, Rochester, UK).

For the initial psychophysical experiment, binocular presentation was achieved with a stereoscope setup consisting of a pair of ViewSonic FB2100x CRT monitors (1,600 × 1,200, 100 Hz) viewed through front-surfaced mirrors at a viewing distance of 50 cm. A subset of participants (n = 5) repeated the experiment on a second stereoscope, which consisted of a pair of Samsung 2233RZ LCD monitors (1,280 × 1,024, 120 Hz). These monitors were viewed through front-surfaced mirrors at a viewing distance of 50 cm, and participants' head position was stabilized by an eye mask, a head rest, and a chin rest. For all display devices in all experiments, linearized gamma tables were calculated based on photometric measurements (Admesy, Ittervoort, The Netherlands) and paired display devices were calibrated to produce matched luminance outputs.

Vernier task.

During experimental scans, participants performed an attentionally demanding Vernier task at fixation and were not required to discriminate slant. This served two purposes. First, it ensured consistent attentional allocation between conditions, making it unlikely that systematic differences in attention could modulate decoding performance. Second, it provided a subjective measure of eye position, allowing us to assess whether there were any systematic differences in eye vergence between conditions. Participants were instructed to fixate a central cross hair fixation marker that was present throughout experimental scans. The fixation marker consisted of a white square outline (side length 0.5°) and horizontal and vertical nonius lines (length 22 arcmin) presented inside a mid-gray disk (diameter 1.25°). One horizontal and one vertical line were presented to each eye in order to promote stable vergence and to provide a reference for a Vernier task (Popple et al. 1998). The Vernier target line subtended 6.4 arcmin in height by 2.1 arcmin in width and was presented at seven evenly spaced horizontal offsets of between ±6.4 arcmin for 500 ms (with randomized onset relative to stimulus) on 50% of TRs. Participants were instructed to indicate, by button press, which side of the central upper vertical nonius line the target appeared, and the target was presented monocularly to the contralateral eye. We obtained a subjective measure of observers' vergence by fitting a cumulative Gaussian psychometric function to the proportion of “target on the right” responses against horizontal target offset. Bias (deviation from the desired vergence position) in participants' judgments was close to zero.

Psychophysics.

In the initial psychophysics experiment conducted prior to the fMRI scans, participants performed a two-interval forced-choice discrimination task in which they were sequentially presented a reference stimulus (1 of the 8 conditions: 2 slants × 4 cue configurations; Fig. 2C) and a test stimulus in a randomized order (Fig. 2B). Each stimulus was presented for 1,000 ms (as in the scanner) with an interstimulus interval of 500 ms between the two. Participants were instructed to indicate which interval contained the more slanted surface (i.e., which was further from frontoparallel). The difference in slant angle (Δd and/or Δt) between reference and test stimuli was controlled via an adaptive staircase method (Watson and Pelli 1983), with a maximum limit of ±20°. This limit was chosen in order to avoid presentation of test slants of greater than 80° [at which point the surface required to fill the stimulus aperture becomes prohibitively large and disparities cannot be fused (Burt and Julesz 1980)] or smaller than 10° (at which point textures cannot be reliably discriminated from frontoparallel). Furthermore, previous studies reported discrimination thresholds of <20° for this type of stimulus (Knill and Saunders 2003).

In the main behavioral experiment, a staircase consisting of 20 trials was run for each base slant in each condition and all conditions were interleaved in a pseudorandomized order. Data were then combined to calculate the just noticeable difference (j.n.d.) for the four different cue configuration conditions (Disparity, Texture, Congruent, Incongruent). Threshold estimates >125% of the maximum slant difference (20°) were substituted with a value of 25°, since these estimates were based on insufficient sampling of the psychometric function (Wichmann and Hill 2001a). This typically occurred for the Incongruent cue condition, as observers required >20° difference between stimulus pairs to reliably judge slant differences. Thus the mean sensitivity for Incongruent stimuli is likely an overestimate of the true sensitivity, and the relatively low SE in this condition is due to capping upper values of the threshold.

To obtain more detailed threshold estimates, a subset of participants (n = 5) were retested over seven separate sessions, in which interleaved staircases were programmed to converge at six different points distributed broadly along the psychometric function. For each condition tested (Texture, Disparity, and Congruent), data from 820 trials were fitted with a cumulative Gaussian psychometric function using a bootstrapping method (Psignifit toolbox; Wichmann and Hill 2001a, 2001b). Parameters for lapse rate (λ) and guess rate (γ) were constrained to the range 0–0.1, while the point of subjective equality (β) was constrained to equal the base slant. Threshold estimates from these data were consistent within participants across sessions and were used in place of the original threshold estimates for the observers and conditions that were retested. This method generally produced slightly lower threshold estimates compared with the single staircase method, since incorrect responses early in a session had less influence on the subsequent sampling range. This was most noticeable for the Texture condition, where all threshold estimates measured with multiple staircases were less than the maximum slant difference tested (20°).

To test for behavioral performance compatible with a fusion computation, we calculated predictions for the minimum bound based on quadratic summation (Fig. 1B). Quadratic summation was calculated with the formula

$$\text{Quadratic}{\displaystyle \sum }=\sqrt{{\text{S}}_{\text{D}}^2+{\text{S}}_{\text{T}}^2}$$ 1

where S_T and S_D are the observer's sensitivities (1/j.n.d.) in each of the single-cue conditions. To further contrast observers' performance on combined-cue conditions against the performance predicted by quadratic summation, we calculated a psychophysical integration index (ψ):

$$\psi =\frac{{\text{S}}_{\text{D}+\text{T}}}{\sqrt{{\text{S}}_{\text{D}}^2+{\text{S}}_{\text{T}}^2}}-1$$ 2

A value of zero for this index would indicate that sensitivity to combined cues was equal to that predicted by quadratic summation of individual cues (the minimum bound for fusion). Integration indices were calculated for each observer and then bootstrapped with 10,000 iterations.

Imaging.

Data were collected at the Birmingham University Imaging Centre with a 3-T Philips Acheiva MRI scanner with an eight-channel head coil. Blood oxygen level-dependent (BOLD) fMRI data were acquired with a gradient echo echo-planar imaging (EPI) sequence [echo time (TE) 34 ms; repetition time (TR) 2,000 ms; voxel size 1.5 × 1.5 × 2 mm, 28 slices covering occipital cortex] for experimental and localizer scans. Slice orientation was close to coronal section but rotated about the mediolateral axis with the ventral edge of the volume more anterior in order to ensure coverage of lateral occipital cortex (Fig. 3B). A high-resolution T1-weighted anatomical scan (voxel size 1 mm isotropic) was additionally acquired for each participant.

Fig. 3.

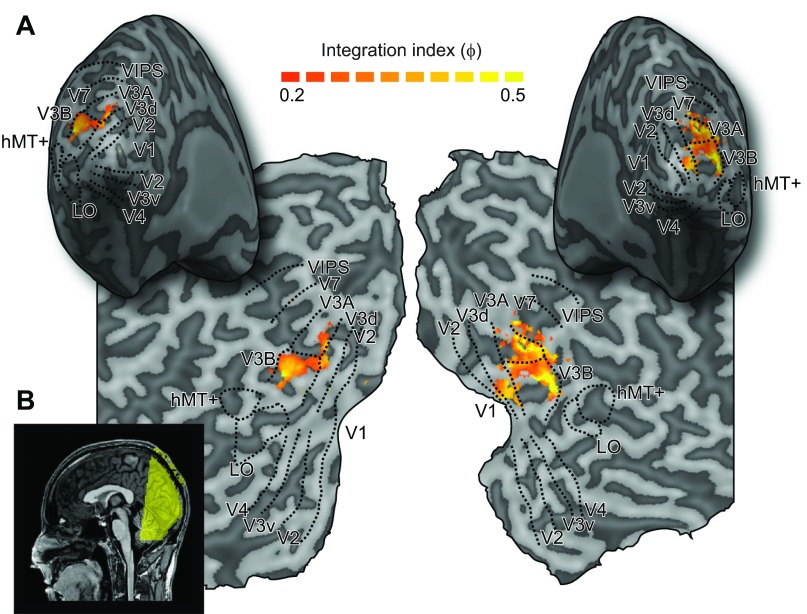
A: representative inflated cortical surface reconstructions and flat maps showing the visual regions of interest from 1 participant. These include retinotopic areas, V3B/KO, human middle temporal complex (hMT+), and the lateral occipital (LO) area. Sulci are rendered a darker gray than gyri. Superimposed on the maps are thresholded fMRI integration indices (see materials and methods, Eq. 3). These were calculated from the results of group searchlight classifier analyses that moved iteratively throughout the measured volume of cortex, discriminating between stimulus slant angles (−30° or +60°) for the Congruent condition and each of the component cue conditions. This procedure confirmed that we had not missed any important areas outside those localized independently. B: sagittal view of a structural MRI scan of 1 participant, with colored overlay illustrating slice orientation for functional scans.

Defining regions of interest.

We localized regions of interest (ROIs) for each participant, using standard retinotopic mapping procedures (Fig. 3A). Retinotopically organized visual areas V1, V2, V3v, V4, V3d, V3A, V3B, and V7 were defined with polar and eccentricity maps, which were generated by fMRI responses to rotating wedge and expanding concentric ring stimulus presentations, respectively (DeYoe et al. 1996; Sereno et al. 1995). V3 was divided into dorsal and ventral quadrants in each hemisphere (V3d and V3v) in line with previous delineation based on both functional and cytoarchitectonic distinctions (Wilms et al. 2010). Area V4 was defined as the region of ventral visual cortex adjacent to V3v containing a representation of the upper quadrant of the contralateral visual field (Tootell and Hadjikhani 2001; Tyler et al. 2005). Area V7 was defined as the region of retinotopic activity anterior and dorsal to V3A (Tootell et al. 1998; Tsao et al. 2003; Tyler et al. 2005).

Area V3B/KO (Tyler et al. 2006; Zeki et al. 2003) was defined as the area comprising the union of retinotopically mapped V3B and an area “KO” that was functionally localized by its preference for motion-defined boundaries compared with transparent motion of black and white dots (P < 10⁴) (Dupont et al. 1997; Tootell and Hadjikhani 2001; Tyler et al. 2006; Zeki et al. 2003). This area contained a full hemifield representation, inferior to V7 and lateral to, and sharing a foveal confluence with, V3A (Tyler et al. 2005). A previous study revealed no clustering of voxels selective for cue integration within V3B/KO that might provide grounds for separating the two areas (Ban et al. 2012; see their Supplementary Fig. S7).

Human middle temporal complex (hMT+/V5) was defined as the set of voxels in lateral temporal cortex that responded significantly more strongly (P < 10⁴) to transparent dot motion compared with a static array of dots (Zeki et al. 1991). Lateral occipital complex (LOC) was defined as the set of voxels in lateral occipito-temporal cortex that responded significantly more strongly (P < 10⁴) to intact compared with scrambled images of objects (Kourtzi et al. 2005). LOC subregion LO, which extended into the posterior inferotemporal sulcus, was defined based on the overlap of functional activations and anatomical structures, consistent with previous studies (Grill-Spector et al. 2000). For a subset of participants (n = 8), regions of the intraparietal sulcus (IPS) [ventral intraparietal sulcus (VIPS), parietooccipital IPS (POIPS), dorsal IPS medial (DIPSM)] were functionally localized based on significantly stronger responses to 3D structure-from-motion than for 2D transparent motion (Orban et al. 1999, 2006) and defined with anatomical landmarks.

fMRI design.

In the fMRI experiment, each run consisted of 24 blocks and began and ended with a 16-s fixation period during which only the background and fixation marker were presented. Each block was 16 s in duration and consisted of a stimulus from one of the eight conditions (a new stimulus was created for each trial) being presented for 1 s followed by a 1-s fixation period. Block order was randomized, and each of the eight conditions was presented for three blocks per run. Eleven observers completed nine runs, and one completed eight.

fMRI data analysis.

Anatomical scans of each participant were transformed into Talairach space (Talairach and Tournaux 1988), and inflated and flattened surfaces were rendered with BrainVoyager QX (BrainInnovation, Maastricht, The Netherlands). Functional data were preprocessed with slice timing correction, head motion correction, and high-pass filtering before being aligned to the participant's anatomical scan and transformed into Talairach space. We ran univariate analyses using random effects (RFX) group GLM analysis to contrast BOLD responses to the two slant angles, for each of the four conditions. Additionally, we contrasted the combination of responses to the two component cue conditions (Texture + Disparity) vs. the Congruent condition and Incongruent vs. Congruent.

For multivariate analyses, we tested the discriminability of BOLD responses to the two different slant angles (60° vs. −30°). Since visual areas differ considerably in size, and ROIs that contain more voxels could yield higher classification accuracies, we selected the same number of voxels across ROIs and observers (Haynes and Rees 2005; Preston et al. 2008; Serences and Boynton 2007). For each ROI we selected gray matter voxels from both hemispheres and ranked them on the basis of their response (as indicated by t values calculated with the standard general linear model) to all stimulus conditions compared with fixation baseline across experimental runs. Pattern size was restricted to voxels showing a t value >0 for the contrast of all stimuli versus fixation. Assessment of the point at which classification accuracies tended to saturate as a function of pattern size resulted in the selection of 300 voxels per ROI. In 11 ROIs (of 120 across all participants) where <300 voxels reached threshold, all voxels above threshold were included in the ROI (mean = 199 ± 16 SE). This voxel selection process has been validated by previous studies (Kamitani and Tong 2005; Preston et al. 2008).

We normalized each voxel time course separately for each experimental run (by calculating z scores) to minimize baseline differences across runs. The multivariate analysis data vectors were produced by applying a 4-s temporal shift to the fMRI time series to compensate for the lag time of the hemodynamic response function and then averaging all time series data points of an experimental condition. Univariate signals were removed before conducting support vector machine (SVM) analysis by subtracting the mean response of all voxels in a given volume from each voxel in that volume. All volumes therefore had the same mean value across voxels but different patterns of activity. We used a support vector machine (SVM^light toolbox, http://svmlight.joachims.org) for classification and performed a ninefold leave-one-out cross-validation, in which data from eight runs were used as training patterns (24 patterns, 3 per run for each slant angle) and data from the remaining run were used as test patterns (3 patterns per slant angle). For each participant, the mean accuracy across cross-validations was taken.

To quantify differences in SVM prediction accuracies between combined-cue conditions and the minimum bound prediction, we calculated an fMRI integration index:

$$\varphi =\frac{d\mathrm{\prime }{{\displaystyle }}_{\text{D+T}}}{\sqrt{d\mathrm{\prime }{{\displaystyle }}_{\text{D}}^2+d\mathrm{\prime }{{\displaystyle }}_{\text{T}}^2}}-1$$ 3

where d′_D+T, d′_D, and d′_T are SVM discriminability in d-prime units, calculated with the formula

$$d\mathrm{\prime }=2\times erfinv\left(2p-1\right)$$ 4

where erfinv is the inverse error function and p is the proportion of correct classifications.

To test for transfer of classifier learning between individual cue conditions, we used recursive feature elimination (RFE) to select the voxels in each ROI that made the greatest contribution to classifier performance (De Martino et al. 2008). Voxels were iteratively discarded independently for each cross-validation for each condition, and the final voxels used for SVM analysis were selected from the intersection of corresponding validations.

In addition to performing our standard ROI analysis, we used a “searchlight” MVPA approach (Kriegeskorte et al. 2006), which sequentially sampled small volumes of cortical voxels within a 9-mm radius, throughout the entire cortical volume. Prior to analysis, a mask was applied to exclude voxels located outside of cortex, and voxels with a t value < 0 for the contrast of all stimuli versus fixation were excluded. For each sample, we ran three SVM classification analyses discriminating the activity evoked by different slants in the Texture, Disparity, and Congruent cue conditions. From these sensitivity values we then calculated the fMRI integration index (ϕ) for each sample (Fig. 3A). Using this approach, we sought to determine whether we had missed any important areas outside of the independently localized ROIs.

Analysis of variance was performed in SPSS (IBM), and Greenhouse-Geisser correction was applied where the assumption of sphericity was not met. We report the results of two different statistical tests that both assess cue fusion: repeated-measures ANOVA and bootstrapped fMRI integration indices. The former test estimates variances based on the sample of SVM sensitivities (12 participants), assuming a normal distribution. The latter estimates variances in a manner that is model free, since the population (10,000 data points) is calculated from permutations of the sample. While ANOVA is a standard parametric test, we include the bootstrap analysis for a more sensitive and direct assessment of our key statistic of interest: sensitivity to Congruent cues relative to quadratic summation of component cue sensitivities.

RESULTS

Psychophysics.

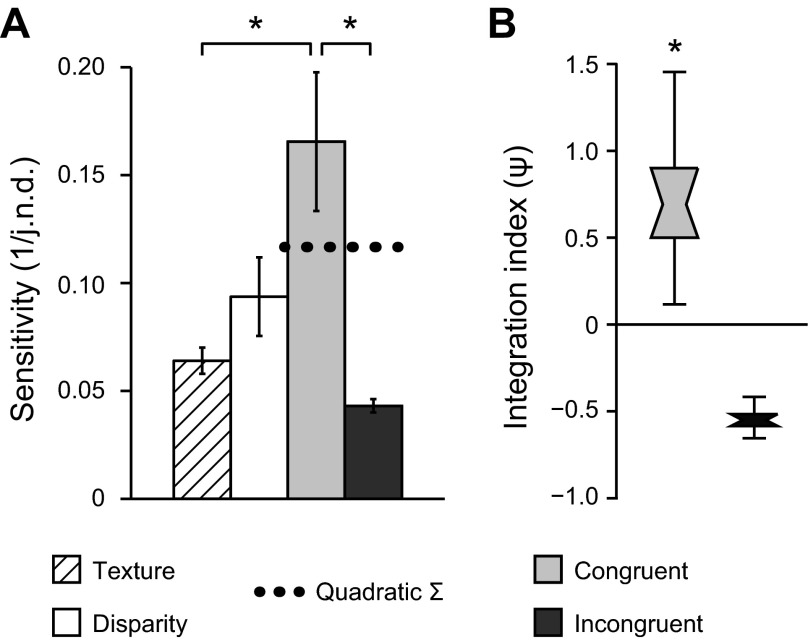
We measured participants' sensitivity to small differences in surface slant defined in the Disparity, Texture, Congruent, and Incongruent conditions. Specifically, we presented two stimuli and asked observers to decide which had the greater slant, using an adaptive staircase procedure to control the slant difference between the two stimuli. We found significant differences in the ability of observers to judge slant under the different conditions [F(1.5,16.9) = 7.191, P < 0.01], with best discrimination performance observed when slant differences were congruently indicated by both texture and disparity (Fig. 4A). This performance was significantly better than that in the two single-cue conditions [Texture condition: F(1,11) = 8.96, P < 0.01; Disparity condition: F(1,11) = 3.60, P = 0.042, 1-tailed], confirming the expectation that slant sensitivity improves for congruent combinations of cues. As discussed in the introduction, an improvement in performance per se would be expected on the basis of both a fusion mechanism and a discrimination based on the outputs of independent detectors. We were therefore interested in the extent of the improved performance in the Congruent cue condition, relative to performance for the single-cue component conditions.

Fig. 4.

Behavioral tests of cue integration. A: bars represent the mean sensitivity across observers (n = 12) and base slants for the 4 experimental conditions. Sensitivity is calculated as the reciprocal of the just noticeable difference (j.n.d.). Error bars show between-observer SE. Dashed horizontal line indicates predicted sensitivity for combined cue conditions based on quadratic summation of the observed sensitivities to individual cue conditions. *P < 0.05. B: distribution plots of bootstrapped psychophysical integration indices for combined-cue conditions. A value of zero indicates that combined-cue performance was equal to that predicted by quadratic summation. Notches represent median, boxes represent 68% confidence intervals, and error bars represent 95% confidence intervals. *P < 0.001.

To assess whether participants integrated information from disparity and texture in line with cue fusion, we used a psychophysical integration index (ψ) that compared performance in the Congruent cue case to the minimum bound expected for fusion using the quadratic summation of component cue accuracies (Fig. 4B). With this index, a value of zero would suggest performance improvements in line with independent access to texture and disparity signals, while a value in excess of zero suggests that signals from the two cues are fused to support perceptual judgments. We found that performance in the Congruent cue condition exceeded the minimum bound for fusion (P < 0.001). However, when the cues were incongruent, ψ did not exceed zero (P > 0.999). Indeed, performance in the Incongruent condition was, on average, lower than the single-cue component conditions, although the low variance observed for this condition was a result of capping maximum threshold estimates (see materials and methods). Together, these results suggest that participants fused the information from Disparity and Texture cues to estimate surface slant.

fMRI.

We measured fMRI responses in ROIs within the visual cortex (Fig. 3) while participants were presented with slanted stimuli (−30° and +60°) defined by Disparity, Texture, Congruent, or Incongruent cues (Fig. 2). Univariate analyses revealed no significant differences in BOLD response to different slants in any condition, except for the Texture condition. For this condition, small clusters of voxels in foveal regions of early visual areas (V1 and V2) showed significant changes in mean response to different texture-defined slants. This result likely reflects differences in spatial frequency between these stimuli. However, we did not find this for any other conditions, suggesting that differences in BOLD responses related to spatial frequency were only detectable in the absence of concomitant differences in disparity gradient. Importantly, none of the cortical areas for which subsequent multivariate analysis suggested cue fusion (see below) showed any reliable differences in univariate response between slants or conditions.

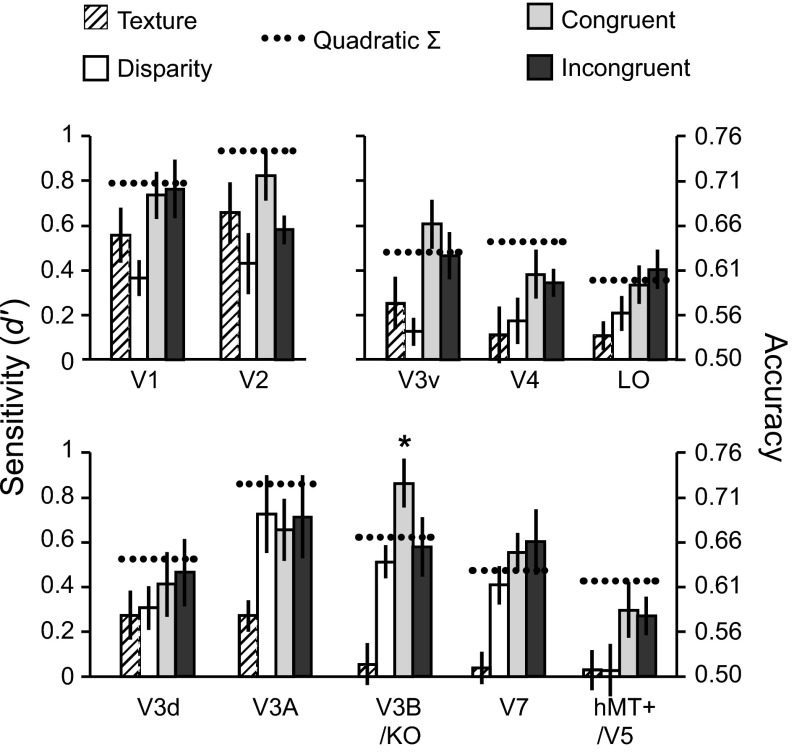
We next quantified the information about the presented stimuli in each ROI by training a machine learning classifier to discriminate the patterns of fMRI activity evoked by the different slants. We were able to reliably decode the presented stimuli in all ROIs, and decoding accuracy varied by condition (Fig. 5). Notably, classifier sensitivity to Texture was close to zero in higher dorsal and ventral areas, yet these same regions showed improved sensitivity for Congruent compared with Disparity conditions. This suggests that these areas do process texture in the absence of cue conflict, and the low classification accuracies observed for the Texture condition may have been related to the dominance of disparity signals in that condition. In contrast, decoding accuracies for Disparity were relatively high in dorsal areas, in line with previous findings for decoding of fMRI responses to disparity (Ban et al. 2012; Preston et al. 2008). Our primary interest, however, was not to compare classification accuracies between ROIs (since these are influenced by various factors besides neural activity) but to assess the relative performance between conditions within each area.

Fig. 5.

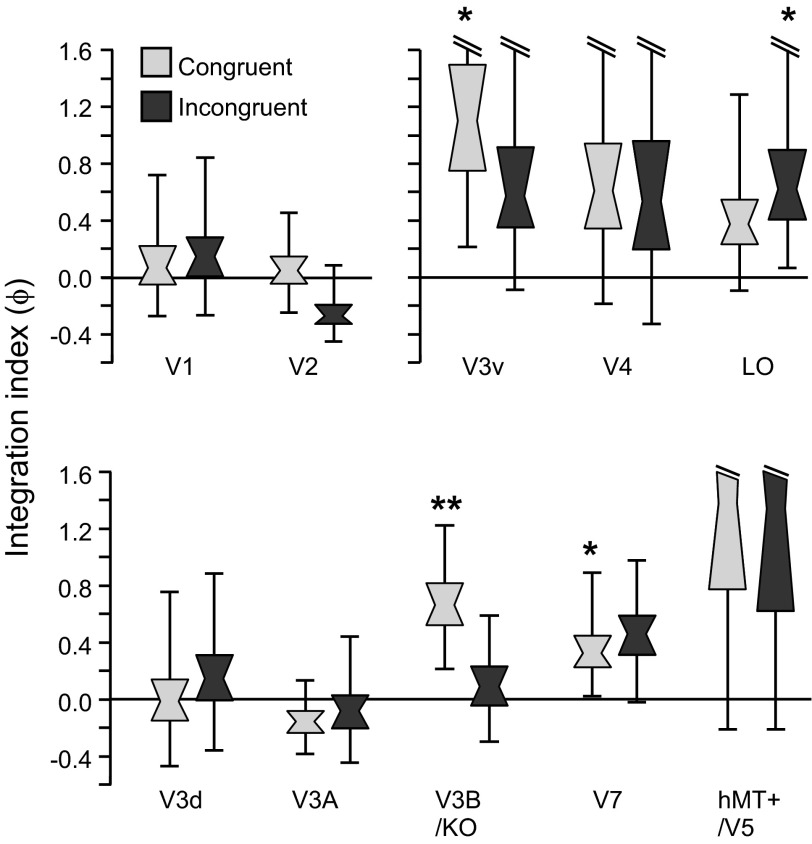
Classifier prediction performance for discriminating +60° vs. −30° slants for all regions of interest. Dashed lines indicate the performance predicted for combined-cue conditions based on quadratic summation of performance observed in the Texture and Disparity (single cue) conditions. Error bars indicate SE. Asterisks indicate areas where sensitivity for congruent cues significantly exceeded performance predicted by quadratic summation (dashed horizontal lines) (P < 0.05).

In early visual cortex (V1 and V2), classifier accuracy was above chance for all conditions. However, it is unlikely that these areas explicitly encode representations of surface slant from texture and/or disparity. Instead, the representations of local disparities and image features represented in these areas are likely to provide important inputs to higher areas that encode depth gradients. This low-level image feature information differs between the different stimulus classes, and as such supports decoding of one slant from the other. Reassuringly, classifier performance for the Congruent condition did not exceed quadratic summation in early visual areas, suggesting that signals related to texture and disparity signals remain independent at this stage of processing.

In contrast, prediction accuracies for the Congruent condition were significantly higher than for either component cue in V3v [F(3,33) = 5.41, P < 0.01] and V3B/KO [F(3,33) = 13.16, P < 0.001]. To assess integration, we calculated the minimum bound prediction based on quadratic summation of classifier sensitivities to individual cues (Fig. 5). Classifier performance for Congruent stimuli was higher than predicted by quadratic summation in areas V3v, V3B/KO, and V7. This difference was only statistically significant in area V3B/KO and—importantly—only when cues were congruent [F(1,11) = 4.16, P = 0.033] but not when they were incongruent [F(1,11) < 1, P = 0.39; Fig. 5]. The pattern of classifier prediction accuracies across conditions in V3B/KO is therefore reminiscent of the pattern of observers' behavioral accuracy for discriminating between slants (Fig. 4).

To quantify the differences between classifier accuracies for combined-cue conditions and the minimum bound prediction, we calculated fMRI integration indices (materials and methods, Eq. 3). In light of previous findings, we anticipated that the cue integration index would exceed zero in V3B/KO for the Congruent condition (Ban et al. 2012). This expectation was confirmed as statistically reliable (after Bonferroni correction for multiple comparisons) in V3B/KO (P = 0.005). In addition, we found integration indices for the Congruent condition above zero (uncorrected significance threshold) in areas V3v and V7 (Fig. 6; Table 1). These results suggest cortical representations that are compatible with the fusion of slant information from the disparity and texture signals.

Fig. 6.

Notched distribution plots of bootstrapped fMRI integration indices for all regions of interest. Plots are shown for the results obtained with Congruent and Incongruent stimuli. A value of zero indicates that combined-cue performance was equal to that predicted by quadratic summation. Notches represent median, boxes represent 68% confidence intervals, and error bars represent 95% confidence intervals. *P < 0.05, **P < 0.001.

Table 1.

Significance tests for integration index ϕ

	P Value
Cortical Region	Congruent ϕ > 0	Incongruent ϕ > 0
V1	0.373	0.314
V2	0.436	0.929
V3v	0.010	0.081
V4	0.125	0.212
LO	0.099	0.023
V3d	0.533	0.360
V3A	0.818	0.637
V3B/KO	0.005	0.358
V7	0.037	0.051
hMT+/V5	0.077	0.102

Bold P value indicates significance after Bonferroni correction for multiple comparisons; italicized P values indicate significance at the uncorrected threshold (P < 0.05). LO, lateral occipital cortex; hMT+, human middle temporal complex.

In addition to the ROI-based analysis, we ran searchlight classification analyses that moved iteratively through the entire cortical volume, in order to identify areas with positive fMRI integration indices (Fig. 3). This analysis revealed that a localized region focused in retinotopically defined area V3B supported the highest integration indices and confirmed that we had not missed any important areas involved in cue integration from our ROIs.

The inclusion of the Incongruent condition afforded an additional test of the idea that representations were fused, rather than colocated but independent. Specifically, if the representations of the two stimulus dimensions (disparity and texture) remain independent, then the performance predicted for the Incongruent condition will be equal to the quadratic sum of the component cues. This can be understood by considering that the separation between two stimulus distributions (as conceptualized in Fig. 1) remains the same, irrespective of the sign of the differences between component cues (Fig. 1B). In contrast, fusion predicts one of two possible outcomes, based on previous theoretical work (Clark and Yuille 1990; Landy et al. 1995). Under “strict” fusion, the variance of the combined cue estimate for an Incongruent stimulus would increase and performance would deteriorate below that of either component cue. Alternatively, under “robust” fusion, performance would revert to the level of one of the two component cues. We found that cue integration indices exceeding the minimum bound were not observed when cues were highly inconsistent in areas V3B/KO and V3v (Fig. 5), while results in area V7 were similar for Congruent and Incongruent cue configurations. In particular, accuracy for Incongruent stimuli in V3B/KO was slightly below that predicted by quadratic summation and not separable from performance in the single-cue disparity cue condition. This result is compatible with the robust fusion of cues in V3B/KO and consistent with the results of Ban et al. (2012).

To assess the extent to which fMRI responses were related to depth structure in general, we tested whether training the classifier on data from one single-cue condition (e.g., Texture) would allow predictions to be made for data obtained in the other single-cue condition (e.g., Disparity). Such transfer between depth signals would suggest generalized depth representations. However, we failed to find any evidence of transfer between cues—specifically, accuracies for transfer between cues were not significantly different from baseline accuracies obtained by performing within-cue tests when the labels given to the classifier were randomly permuted. This result suggests that identical slants in the two single-cue conditions elicited very different patterns of activity. This might reflect insufficient generalized representation of depth structure within individual voxels in the cortical regions tested. However, it might equally reflect the cue conflicts present in the single-cue stimuli. For example, training the classifier to use disparity-related activity to discriminate between slants would not be useful for decoding slant in the Texture condition, where disparity always signaled zero slant.

We also considered the involvement of regions of the IPS. However, searchlight analyses (Fig. 3) revealed that sensitivity to Congruent stimuli did not significantly exceed quadratic summation of sensitivities to component cue stimuli in regions beyond extrastriate cortex. Correspondingly, we did not find reliable decoding accuracies in any of the IPS regions tested (VIPS, POIPS, DIPSM) for the subset of participants for whom we had independently localized parietal regions (n = 8). This might indicate that slant representation is sparsely encoded in these regions (as appears to be the case in inferior temporal cortex; Liu et al. 2004) and therefore unable to significantly bias the activity of individual voxels. Furthermore, these parietal regions might be more sensitive to tilt than slant (Shikata et al. 2001, 2008), or to 3D boundaries than to large surfaces (Theys et al. 2012), since in-plane orientation and object segmentation are more critical for guiding eye movements and grasping responses.

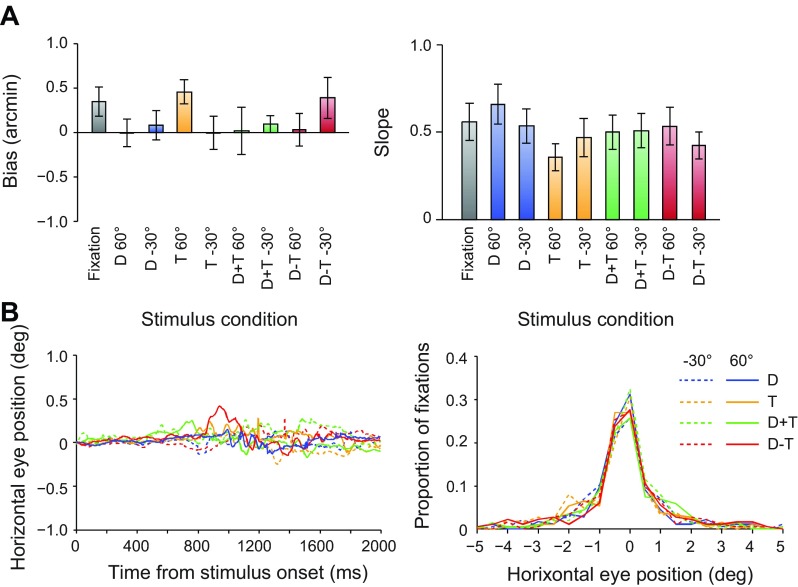
A possible concern is that the decoding accuracies reported here might reflect fMRI activity not related to sensory processes. Our inclusion of control measures was therefore important. In particular, participants performed an attentionally demanding Vernier task at fixation during scans, which ensured consistent attentional allocation between conditions and provided a subjective measure of eye position. Using this method, we found no significant differences in estimated vergence position between conditions (Fig. 7). Although it was not possible to measure eye vergence directly during the scan, we measured eye position (monocularly) while participants performed the task in the scanner during separate test sessions. These measures suggested that observers were able to reliably maintain fixation and revealed no systematic differences in eye position between conditions (Fig. 7). Taken together, these control measures suggest that differential attentional allocation or differences in eye movements are unlikely to account for our findings.

Fig. 7.

Subjective and objective eye movement analysis. A: participants performed a Vernier task during scanning, in which they reported the perceived direction of horizontal offset of a small target relative to the central nonius line of the fixation marker. For each participant we fitted a cumulative Gaussian to the proportion of “right” responses as a function of the horizontal offsets of the targets, to obtain bias and slope measurements. Bias (deviation from the desired vergence position) in participants' judgments was close to zero. Repeated-measures ANOVA revealed no significant effect of condition [F(3,33) = 1.15, P = 0.34], slant angle [F(1,11) < 1, P = 0.95], or interaction [F(3,33) = 2.32, P = 0.09]. Similarly, we found no differences in the slope of the psychometric functions by condition [F(3,33) < 1, P = 0.41], slant [F(1,11) < 1, P = 0.87], or interaction [F(3,33) = 2.81, P = 0.07]. Performance on the Vernier task therefore suggests that participants were able to maintain stable eye vergence (Popple et al. 1998). Error bars show SE between subjects (n = 12). B: we recorded horizontal eye movements for a subset of participants (n = 3) while they lay in the scanner bore, using a monocular eye tracker (Cambridge Research Systems) with a stated accuracy of <0.25° visual angle. No significant differences were observed across conditions for eye position [F(3,6) = 1.39, P = 0.34], number of saccades [F(3,6) = 2.26, P = 0.18], or saccade amplitude [F(3,6) = 1.38, P = 0.34]. Traces of mean eye position aligned to the start of each trial showed only small deviations from fixation, with no systematic differences between conditions.

DISCUSSION

Reliable estimation of 3D surface orientation is a critical step in recognizing and interacting with complex 3D objects and can be enhanced by integrating information from multiple depth cues. Binocular disparity and texture are two important—but qualitatively very different—cues to surface orientation, yet little is known about the neural processes involved in integrating these sources of information. Here we assessed fMRI responses in visual cortex to slanted surfaces defined by texture and disparity cues using two criteria. First, we used a quadratic summation prediction to test for regions where performance for congruent cue stimuli exceeded the performance expected if depth representations from texture and disparity are colocated but independent. Second, we tested whether this result was specific to conditions in which the two cues congruently signaled the same depth configuration. We found that the first criterion was met in visual area V3B/KO and to a lesser extent in V3v and V7, while the second criterion was again met most reliably in V3B/KO but to some extent in V3v. These results suggest that area V3B/KO in particular integrates texture and disparity cues by fusing depth estimates, while other extrastriate visual areas (V3v) might also support fusion computations in addition to independent representations of these cues. Furthermore, the pattern of slant discriminability across stimulus conditions in V3B/KO was consistent with the pattern of behavioral sensitivity to surface slant when observers were tested on a discrimination task. These findings suggest that area V3B/KO plays an important role in the integration of qualitatively and computationally different cues to surface slant.

Surface orientation components: slant and tilt.

Previous neurophysiological studies have reported neuronal responses to surface tilt defined by either texture or disparity in both parietal and temporal cortices (Liu et al. 2004; Tsutsui et al. 2001). In contrast to our manipulation of surface slant, these studies manipulated surface tilt by rotating surfaces with a fixed slant within the plane of the screen. The neural selectivity measured in these studies was therefore for the orientation of the depth gradient, rather than the magnitude of that gradient. Behavioral evidence suggests that sensitivities to tilt and slant components of surface orientation are independent of one another (Norman et al. 2006; Stevens 1983), and neurophysiological evidence also suggests that neural selectivity for these two components may be mostly independent (Liu et al. 2004; Sanada et al. 2012). It is not clear whether the presence of multiple depth cues produces comparable enhancements in perceptual judgment of tilt as for slant. Specifically, tilt selectivity might be less critically dependent on cue integration. Further work is required to examine how cue integration benefits perception of surface orientation involving both tilt and slant components.

Surface orientation processing in dorsal visual pathway.

The present findings complement recent evidence that disparity and relative motion depth cues are integrated in area V3B/KO (Ban et al. 2012). However, the computations involved in extracting depth from motion parallax and disparity cues are qualitatively similar, requiring integration of retinal information across time and space, respectively (Anzai et al. 2001; Rogers and Graham 1982). Taken together, these findings suggest that V3B/KO plays a central role in the integration of depth cues in general, even for qualitatively or computationally quite different sources of information. More importantly, the present findings demonstrate that the same cortical circuits involved in processing simple depth order relations (Ban et al. 2012) also support estimation of more complex and behaviorally relevant depth structures, such as surface slant.

Our finding that V3B/KO (and to a lesser extent V7) plays an important role in the integration of depth cues to surface slant is consistent with existing evidence that emphasizes dorsal pathway involvement in depth processing. Other dorsal areas in extrastriate cortex that have been implicated in the processing of surface orientation include motion-selective areas MT/V5 and MSTd (Nguyenkim and DeAngelis 2003; Sanada et al. 2012; Sugihara et al. 2002; Xiao et al. 1997), which encode information about surface orientation from both motion and disparity cues. Recent evidence suggests that single MT neurons integrate motion and disparity gradient information but display comparatively less selectivity for texture (Sanada et al. 2012). Encoding of depth gradients in these areas could support higher-level representations of 3D surface orientation that are found further along the dorsal stream in posterior parietal cortex (Shikata et al. 2001; Tsutsui et al. 2002).

Parietal cortex has previously been implicated in processing depth from disparity as well as various monocular cues (Durand et al. 2009; Georgieva et al. 2008; Orban 2011; Sereno et al. 2002; Shikata et al. 2001; Srivastava et al. 2009; Tsutsui et al. 2002). In the present study, we observed higher classification accuracy for congruent cues compared with quadratic summation in area V7, which may correspond to the caudal intraparietal area (CIP) in the macaque (although, for more detailed discussions of human-macaque parietal homology, see Orban et al. 2006; Shikata et al. 2008; Tsutsui et al. 2002). It should be noted that VIPS and V7 have been considered to overlap by other groups (Georgieva et al. 2009; Swisher et al. 2007), and they were differentiated here based on different localizer tasks (Chandrasekaran et al. 2007; Orban et al. 1999; Press et al. 2001; Preston et al. 2008). In our study, however, we did not find reliable decoding of activity in intraparietal areas. One reason for this may have been because participants were not required to attend explicitly to the surface slant but instead performed an unrelated attentionally demanding task at fixation. Parietal involvement in the processing of 3D surfaces has previously been shown to be strongly modulated by task (Chandrasekaran et al. 2007; Shikata et al. 2001). A further possibility is that surface slant may be sparsely encoded in parietal cortex, thus precluding the possibility of sufficient biases within voxels to support accurate fMRI decoding (Kriegeskorte et al. 2010). Such a finding would be comparable to the low proportion of single cells that were reported to show selectivity for slant from texture and disparity in inferior temporal cortex (Liu et al. 2004).

Ultimately, 3D surface information in the dorsal stream is likely to facilitate visually guided actions (Cohen and Andersen 2002; Jeannerod et al. 1995; Sakata et al. 1998). Accordingly, various regions of posterior parietal cortex involved in motor planning respond to depth signals, including anterior intraparietal area (AIP) (Durand et al. 2007; Shikata et al. 2001; Srivastava et al. 2009; Taira et al. 2000; Theys et al. 2012) for grasping; the parietal reach region (PRR) (Bhattacharyya et al. 2009); and the lateral intraparietal area (LIP) (Durand et al. 2007; Genovesio and Ferraina 2004), which is involved in saccadic eye movements. However, responses to visual depth signals in these areas appear to be more concerned with 2D retinal shape than 3D shape. For example, AIP neurons predominantly show selectivity for 3D boundaries rather than 3D surface shape (Theys et al. 2012), suggesting a somewhat more rudimentary representation of 3D surfaces compared with that found in CIP (Sakata et al. 1999; Tsutsui et al. 2001). Such specialization might enhance efficiency for computing grasping movements.

Similar distinctions have been reported for areas in inferior temporal cortex in the ventral pathway. Specifically, the lower bank of the superior temporal sulcus (TEs) contains neurons selective for both planar and curved 3D surfaces, whereas neurons in lateral TE are selective only for 2D shape (Janssen et al. 1999, 2000; Liu et al. 2004). Recent evidence suggests communication between cortical areas in higher portions of the dorsal and ventral streams, in the form of synchronized activity between anterior parietal and inferior temporal cortical areas (Verhoef et al. 2011), and anatomical connectivity between CIP and TEs has also previously been shown (Baizer et al. 1991). Indeed, given the utility of depth information common to the goals of action and recognition, it is likely that communication between these two processing pathways occurs at earlier stages.

Previous fMRI studies have identified the involvement of visual areas from both the dorsal and ventral pathways in the processing of 3D surfaces from disparity (Chandrasekaran et al. 2007; Durand et al. 2007, 2009), monocular cues (Georgieva et al. 2008; Orban et al. 1999; Sereno et al. 2002; Shikata et al. 2001; Taira et al. 2001), and combinations of the two (Welchman et al. 2005). We noted that sensitivity to congruent cues was statistically higher than for the component cues in area V3v as well as V3B/KO (Fig. 4A). Although subsequent analysis indicated that V3v does not meet other criteria for cue integration, it is possible that the increased decoding performance (around the level predicted by quadratic summation) is the result of colocated representations of disparity and texture information, as has previously been reported (Georgieva et al. 2008; Janssen et al. 1999; Sereno et al. 2002; Welchman et al. 2005). In contrast to our result, a previous study that measured fMRI adaptation to perspective and disparity cues suggested that both dorsal and ventral extrastriate cortex (specifically, areas hMT+ and LO) represent depth configurations from a combination of these cues (Welchman et al. 2005). This difference might be explained by differences in stimulus configuration: we used randomized Voronoi textures on a single slanted planar surface presented within an aperture, whereas the previous study used regular grids forming a dihedral angle without the use of an aperture. The stimuli in the previous study therefore had a more objectlike structure and appearance (resembling an upright open book), which might increase ventral pathway involvement (Kourtzi and Kanwisher 2001). Another difference is that the size and shape of individual texture elements were randomized in our stimuli, which reduced the reliability of perspective foreshortening and scaling (Knill 1998) compared with those in the previous study. It has previously been reported that both behavioral sensitivity (Rosas et al. 2004) and neural selectivity (Liu et al. 2004) can be dependent on the type of texture pattern presented (e.g., uniform vs. randomized) and might therefore account for differences in results. Finally, although Welchman et al. (2005) did not sample from V3B/KO, it is possible that this area provides important inputs to LO that might convey depth information from multiple cues, given the proximity of the two areas.

Previous studies have suggested an important role for higher ventral areas (LO and posterior inferior temporal gyrus) in the processing of 3D shape from disparity (Chandrasekaran et al. 2007; Georgieva et al. 2009). However, there are several critical differences that might explain the relatively low classification accuracy we obtained for the Disparity condition in area LO. First, our stimuli were slanted planar surfaces, while the other studies used more complex 3D shapes that appeared more objectlike. Second, our disparity stimuli contained texture cue conflicts, while previous studies used random dot stereograms to minimize the reliability of the texture cue. Finally, previous studies reported that univariate BOLD response in ventral areas corresponded to either shape coherence or depth structure, whereas surface coherence was consistent between different slants in our study.

Relation between psychophysical and fMRI results.

Recently, Ban and colleagues (2012) found that training a classifier on fMRI data acquired during the presentation of frontoparallel planes defined by one depth cue (e.g., disparity) produced comparable accuracies whether tested on data from the same cue (disparity) or another cue (motion) in V3B/KO. However, using a similar test, we did not find such cross-cue transfer for texture and disparity cues to surface slant. One possible explanation for the lack of transfer between texture and disparity cue depth representations is that the cue conflicts in our single-cue Texture and Disparity stimuli were more perceptually salient than those in the stimuli of previous studies. Although the results of our behavioral experiment suggested that observers were sensitive to changes in slant for these stimuli, the Texture condition in particular (which contained a conflicting disparity cue that signaled a frontoparallel surface orientation) may represent a special case for human observers. We frequently witness 2D representations of 3D depth in daily life, such as those projected on a television screen. In such instances, we perceive the flat surface of the screen but recognize that the normally informative disparity signal provides no useful information about the intended depth representation in the image. We are then able to “suspend our disbelief” regarding the depiction of depth for the purpose of interpreting the image (Gibson 1978; Goldstein 1987; Koenderink et al. 1992; Vishwanath et al. 2005). Thus while observers showed sensitivity to changes in Texture stimuli when required to make perceptual decisions regarding slant during the behavioral task, changes in slant may have been less perceptually salient for Texture stimuli during the fMRI experiment, in which participants passively viewed stimuli while performing an unrelated attention task. Indeed, a previous fMRI study of texture-defined surface orientation reported significantly stronger activation of parietal regions when subjects performed an orientation discrimination task compared with when they performed a comparably attention-demanding color discrimination task while viewing the same stimuli (Shikata et al. 2001). Top-down processes have been shown to influence choice-related neural activity in sensory cortex (Nienborg and Cumming 2009), and the absence of such top-down processes in our fMRI experiment might account for the relative lack of slant-related variation in fMRI activity for texture in the present study.

The pattern of results across conditions observed in V3B/KO (Fig. 5) is mainly consistent with performance measured at the behavioral level (Fig. 4). One notable difference is that observers exhibited lower perceptual sensitivity to Incongruent stimuli than for either component cue in the behavioral experiment, whereas classifier performance for the Incongruent condition was either comparable to, or exceeded, performance for the component cues in all cortical regions. This behavioral result is consistent with previous reports of mandatory cue fusion in adult observers (Hillis et al. 2002; Nardini et al. 2010) and provides evidence against an independence mechanism at the behavioral level, which would predict performance in the Incongruent condition that matches quadratic summation.

A further distinction can be made between two possible forms of fusion based on performance in the Incongruent condition (Clark and Yuille 1990; Landy et al. 1995). Under strict fusion, depth estimates are combined via weighted averaging using fixed weights, resulting in relative insensitivity to highly incongruent cues. In contrast, robust fusion predicts that one cue (e.g., the less reliable) should be reweighted and can effectively be “vetoed” (Bülthoff and Mallot 1988). In this case, performance would therefore revert to the same level as the more reliable component cue (Ban et al. 2012). While behavioral performance suggests the former, classifier sensitivity in V3B/KO suggests the latter. One possible explanation for this divergence between psychophysical sensitivity and fMRI discriminability in the Incongruent condition is that observers' behavioral performance was adversely affected by the use of an excessively large cue conflict (90°). This has the potential to produce perceptual bistability (Girshick and Banks 2009; van Ee et al. 2002), whereby perception alternates between the depth configurations specified by either one of the two cues. For example, when the disparity signal is perceptually dominant, the texture on the surface will appear anisotropic and heterogeneous (Knill 2003; Rosenholtz and Malik 1997). Failure to consistently select a single cue (e.g., the more reliable) and veto the other could lead to the observed decrement in behavioral performance (Girshick and Banks 2009). As Landy et al. (1995) point out, there is no reason to expect visual performance to be optimized outside of the visual system's normal operating region, such as in the case of our Incongruent stimuli.

Classifier performance for Incongruent stimuli in V3B/KO was slightly above performance for the more reliable of the two single cues (disparity) and slightly below the prediction of quadratic summation (Fig. 5). This might suggest robust fusion, as was previously reported in area V3B/KO for incongruent motion and disparity stimuli (Ban et al. 2012). However, simulations performed by Ban et al. (2012) suggest that it is likely that V3B/KO contains a mixed population of units tuned to both independent and fused cues, whose outputs may be selected based on their relative reliabilities. This idea is consistent with evidence that, even in areas further along the visual processing pathways, approximately half of the recorded neurons displayed selectivity for only one cue (Liu et al. 2004; Tsutsui et al. 2001). By averaging over trials, the block design of our fMRI experiment may have aggregated responses to perceptual interpretations of Incongruent stimuli based alternately on independent and fused estimates. Consistent with this idea, previous work suggests that activity in area V3B/KO changes in line with alternating interpretations of ambiguous 3D stimuli (Brouwer et al. 2005; Preston et al. 2009).

Conclusions.

Estimation of surface slant is essential for interaction with 3D objects, and may be a critical intermediate stage for processing more complex 3D shapes. By combining information from multiple depth cues, observers can increase the reliability of their slant estimate. Previous studies have suggested a variety of locations within visual cortex where representations of surface orientation from different cues overlap. Here we provide evidence that area V3B/KO not only contains colocated depth representations from texture and disparity cues but integrates these cues by fusing depth estimates. Importantly, this finding suggests that V3B/KO is capable of integrating qualitatively different depth cues, which may be important for the enhancement of depth perception observed for combined cues.

GRANTS

This work was supported by a Wellcome Trust and National Institutes of Health studentship (WT091467MA to A. P. Murphy), the Japan Society for the Promotion of Science (H22,290 to H. Ban), and a Wellcome Trust fellowship (095183/Z/10/Z to A. E. Welchman).

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the author(s).

AUTHOR CONTRIBUTIONS

Author contributions: A.P.M., H.B., and A.E.W. conception and design of research; A.P.M., H.B., and A.E.W. performed experiments; A.P.M., H.B., and A.E.W. analyzed data; A.P.M., H.B., and A.E.W. interpreted results of experiments; A.P.M., H.B., and A.E.W. prepared figures; A.P.M. and A.E.W. drafted manuscript; A.P.M., H.B., and A.E.W. edited and revised manuscript; A.P.M., H.B., and A.E.W. approved final version of manuscript.