Patterns of muscle activity for digital coarticulation

Abstract

Although piano playing is a highly skilled task, basic features of motor pattern generation may be shared across tasks involving fine movements, such as handling coins, fingering food, or using a touch screen. The scripted and sequential nature of piano playing offered the opportunity to quantify the neuromuscular basis of coarticulation, i.e., the manner in which the muscle activation for one sequential element is altered to facilitate production of the preceding and subsequent elements. Ten pianists were asked to play selected pieces with the right hand at a uniform tempo. Key-press times were recorded along with the electromyographic (EMG) activity from seven channels: thumb flexor and abductor muscles, a flexor for each finger, and the four-finger extensor muscle. For the thumb and index finger, principal components of EMG waveforms revealed highly consistent variations in the shape of the flexor bursts, depending on the type of sequence in which a particular central key press was embedded. For all digits, the duration of the central EMG burst scaled, along with slight variations across subjects in the duration of the interkeystroke intervals. Even within a narrow time frame (about 100 ms) centered on the central EMG burst, the exact balance of EMG amplitudes across multiple muscles depended on the nature of the preceding and subsequent key presses. This fails to support the idea of fixed burst patterns executed in sequential phases and instead provides evidence for neuromuscular coarticulation throughout the time course of a hand movement sequence.

coarticulation is the tendency for one element of a movement sequence to be generated in a manner that facilitates the movements needed for the preceding or subsequent elements. Neuromuscular control of human speech is the classic example of this phenomenon, and a recent study showed that it also occurs in a series of finger-spelling gestures in American Sign Language. Jerde et al. (2003) showed that joint angles for a target letter hand shape may vary by as much as 60°, depending on the next letter hand shape in a sequence. However, these authors did not characterize the extent of coarticulation in the neural activity that produced these hand shapes, and it is possible that cortically specified targets were not fully achieved due to musculoskeletal damping and blending of successive elements. Furthermore, American Sign Language finger spelling consists of a series of intrinsic hand shapes, but earlier studies of sequences of finger movements to extrinsic targets (keys) failed to find substantial evidence of kinematic coarticulation: in typing (Soechting and Flanders 1992) and in piano playing (Engel et al. 1997). Thus it remains possible that the neural activity that specifies a series of key presses is organized as linked action phases (Johansson and Flanagan 2009).

Previous neurophysiological studies provide a background for understanding the neural control of hand movement sequences. Especially for the distal forelimb of primates, sensorimotor control is generally thought to be organized in a hierarchical manner. At the level of primary motor cortex, both intrinsic and extrinsic parameters may be represented (Kakei et al. 1999), and extrinsic representations may take the form of preferred fragments of movement trajectories (Hatsopoulos and Amit 2012). Griffin et al. (2011) showed that a 500-ms train of microstimulation to motor cortex can replace the high-level command for a certain target balance of muscle activity with a different one. These authors also suggested that low-level feedback loops in the complex spinal circuitry (reviewed by Arber 2012) may help to shape the time course of the electomyographic (EMG) activity as it progresses to the new target balance. Thus motor cortical target commands may be shaped by tactile and proprioceptive feedback in the spinal cord.

As a prelude to the present study, Furuya et al. (2011) provided a detailed kinematic description of the joint rotations for numerous piano key-press sequences. Using data from five professional pianists, these investigators showed that trajectories of joint velocity for a particular digit differed, depending on which sequence was being played. In the present study, we used a subset of these sequences but a larger group of pianists, including amateurs. Our study was designed to determine the extent to which the specification of muscle activation for a given digit is altered, depending on the sequence. We tested for two possible forms of neuromuscular coarticulation. First, we used an analysis of EMG waveforms to describe the temporal alterations in burst shape. Next, as a more restricted test (closer to the high-level target command), we considered the balance of EMG amplitudes across three muscles at burst center, i.e., at the time of the central target key press. Evidence for sequence-specific modulation of EMG waveforms, and especially of burst-center EMG amplitudes, would argue against the hypothesis that this hand movement sequence is executed as a series of distinct action phases. Whereas spinal stretch and unloading reflexes alone may alter burst shapes (Angel 1987), this phenomenon may or may not be accompanied by coarticulation at the level of motor cortex.

METHODS

Subjects.

Ten healthy pianists (9 right handed, 3 male, 37 ± 12 yr) with no known neurological disorders or significant hand injuries participated in the study. Four of the subjects were professional pianists who had won prizes at international and/or national piano competitions, while the other subjects were amateur pianists with a range of training experiences (Table 1). The experimental protocol was approved by the University of Minnesota's Institutional Review Board, and all subjects gave informed consent prior to the experiment.

Table 1.

Subjects' piano experience and performance precision

					IKI
Subject No.	Professional/Amateur	Age, yr	Age Started Playing, yr	Total Playing, yr	Mean ± SD	CV, %	MIDI Velocity ± SD
1	Professional	26	6	20	124 ± 12	10	90 ± 11
2	Professional	28	8	20	124 ± 11	9	94 ± 12
3	Professional	36	4	32	124 ± 17	14	96 ± 12
4	Professional	44	3	40	124 ± 9	7	99 ± 9
5	Amateur	33	5	25	132 ± 15	11	92 ± 10
6	Amateur	19	5	13	160 ± 18	11	87 ± 12
7	Amateur	54	45	10	172 ± 35	20	80 ± 12
8	Amateur	54	6	48	140 ± 18	13	71 ± 13
9	Amateur	40	4	30	126 ± 13	10	80 ± 10
10	Amateur	34	7	7	150 ± 29	19	92 ± 11

IKI, interkeystroke interval; CV, coefficient of variation; MIDI, musical instrument digital interface.

Experimental design.

Subjects were asked to play 14 different excerpts, ranging from 9 to 24 notes, with the right hand from 11 musical pieces which were as follows: “Das wohltemperierte Klavier, vol. 1 no. 15 and vol. 2 no. 1, 2, 10, 15” by Johann Sebastian Bach, “Étude Op. 10 no. 1, 4, 8 and Op. 25 no. 11, 12” by Frédéric Chopin, and “15 Études Op. 72 no. 6” by Moritz Moszkowski. These excerpts were selected for their use of the right hand and collectively for their large number of fingering sequences at multiple key positions where the preceding and subsequent key presses around the key press of one digit were performed by one of the other four digits. The sequences did not include any instances of consecutive use of the same digit or of chords. All notes were 16th notes, and digit number was specified so that all subjects played with the same fingering. Subjects played on a digital piano (Roland ep-5, 61 keys), connected to a Windows computer (SONY VAIO VGN-Z90PS) via a musical instrument digital interface (MIDI) interface (Roland EDIROL UA-4FX). The score and fingering was presented on a computer monitor in front of the piano.

Subjects were instructed to play at a loudness of 100 MIDI velocity in synchrony with a metronome which provided the tempo [interkeystroke interval (IKI) = 125 ms]. Pieces were played with legato touch where a key was not released until the subsequent key was depressed. The loudness was demonstrated, and subjects were allowed to practice to familiarize themselves with the piano and the musical excerpts. Each subject practiced until he or she felt that he or she could play the excerpt consistently without mistakes. Ten successful trials were recorded for each excerpt; mistake trials were discarded (about 5–10% for professionals and 20–25% for amateurs).

Three-key-press sequences.

For the subsequent analysis, the original data set was limited to 10 excerpts by excluding 4 excerpts that contained 16th-note triplets (to further ensure the instruction of uniform IKIs). The data were grouped as three-key-press sequences centered on each of the five target digits. The 10 excerpts yielded varying numbers of unique patterns of fingering and note sequences (i.e., at various piano key locations) for each digit (see Table 2). For the central key press by the thumb, index, middle, ring, and little finger, respectively, we analyzed n = 22, 27, 23, 19, and 15 three-key-press sequences (Table 2).

Table 2.

Key-press sequences centered on each digit and change in postural index

Thumb (1)				Index (2)				Middle (3)				Ring (4)				Little (5)
Fi−1	Fi	Fi+1	ΔPI	Fi−1	Fi	Fi+1	ΔPI	Fi−1	Fi	Fi+1	ΔPI	Fi−1	Fi	Fi+1	ΔPI	Fi−1	Fi	Fi+1	ΔPI
2	1	2	0	1	2	3	1	1	3	1	1	1	4	1	1	1	5	1	−1
2	1	2	0	1	2	3	−2	1	3	2	−3	1	4	3	1	1	5	2	0
2	1	2	0	1	2	3	−2	1	3	4	6	1	4	3	−5	1	5	2	1
2	1	2	0	1	2	4	−2	1	3	5	0	1	4	3	1	1	5	3	6
2	1	3	−1	1	2	4	0	2	3	1	0	1	4	3	−5	1	5	3	5
2	1	3	−6	1	2	5	0	2	3	2	0	1	4	3	1	2	5	1	0
2	1	4	−3	3	2	1	2	2	3	4	−1	1	4	3	6	2	5	2	0
2	1	4	3	3	2	1	2	2	3	4	0	2	4	1	1	2	5	3	0
2	1	4	−3	3	2	1	2	2	3	4	0	2	4	1	−5	3	5	2	0
2	1	4	3	3	2	1	2	2	3	4	0	2	4	2	0	3	5	3	0
2	1	4	−3	3	2	1	2	4	3	2	0	2	4	5	1	3	5	4	−1
2	1	4	−8	3	2	1	1	4	3	2	0	2	4	5	0	4	5	2	1
2	1	5	−4	3	2	1	2	4	3	2	0	3	4	1	−6	4	5	3	0
3	1	2	0	3	2	1	2	4	3	2	0	3	4	2	1	4	5	3	1
3	1	5	−6	3	2	1	1	4	3	2	0	3	4	2	0	4	5	3	1
4	1	2	8	3	2	3	0	4	3	2	0	3	4	3	0
4	1	3	8	3	2	3	0	4	3	2	0	3	4	3	0
4	1	5	−1	3	2	4	0	4	3	4	0	3	4	5	0
4	1	5	−4	3	2	4	0	5	3	1	0	5	4	5	0
5	1	3	6	4	2	1	−1	5	3	2	−2
5	1	4	0	4	2	1	2	5	3	4	0
5	1	5	0	5	2	1	0	5	3	5	0
				5	2	1	−2	5	3	5	0
				5	2	4	0
				5	2	4	0
				5	2	5	0
				5	2	5	0

F_i, digit number performing the ith key press in the sequence; ΔPI, change in postural index. Significant burst-fit subset is in bold.

A postural index (PI) was calculated for pairs of key presses within each three-key-press sequence to determine how the hand posture was changing during the sequence. This PI was adapted from Furuya et al. (2011) and modified to ignore whether the sequence was ascending or descending (which resulted in opposite signed values in the original equation). In the adapted equation:

$$\text{PI}=sgn(F_i-F_{i-1})*\left[(L_i-L_{i-1})-(F_i-F_{i-1})\right]$$

where L_i is the location of the ith keystroke (right is positive), F_i is the digit number performing the ith key press in the sequence (thumb = 1, little = 5), and sgn is an operator that is −1 for negative numbers and +1 for positive. For a pair of key presses, PI is 0 when the hand stays in a neutral position (one finger per key), positive when the hand opens, and negative when the hand closes. For example, when the thumb (F_i−1 = 1) presses the C key (1) and then the index finger (F_i = 2) presses the F key (4), the change in finger is +1, while the change in location is +3, so PI = +2. For a PI less than −2, a special case occurs where the hand is closed to the point of doing a thumb-under maneuver or a similarly extreme posture.

Whereas PI was calculated for each pair of notes, for analysis, we used the change in PI (ΔPI) over the three-key-press sequence. This allowed us to determine if the hand was opening (ΔPI > 0), closing (ΔPI < 0), or maintaining its posture (ΔPI = 0) over the sequence. ΔPI values for each sequence are shown in Table 2 and were used to assess the effect of posture change on multimuscle EMG patterns.

Data acquisition.

A custom LabView script (National Instruments) was used to record MIDI data from the keyboard (1-ms resolution), and a second custom LabView script recorded the signal from a pressure sensor (FlexiForce, Tekscan, South Boston, MA) and EMG activity. The pressure sensor was fixed onto a piano key far outside the range of keys used by the subjects and was used to synchronize the MIDI signal with the EMG offline. At the start of each trial, the experimenter pressed the key containing the pressure sensor, and then the subject was free to begin playing. Muscle activity was recorded as surface EMGs using 2-mm-diameter bipolar Ag/AgCl surface electrodes (Discount Disposables, St. Albans, VT) placed 10 mm apart (see Fig. 2 of Klein Breteler et al. 2007). Custom-made, electrically shielded wire leads were permanently soldered to these electrodes and connected to standard laboratory amplifiers. The ground electrode was placed on the left wrist. EMG was amplified (×1,000), band-pass filtered (60–500 Hz), and then sampled at 1,000 Hz. Seven channels of muscle activity were recorded (Fig. 1D). We collected EMGs from two intrinsic thumb muscles: abductor pollicis brevis (APB) and flexor pollicis brevis (FPB). We also recorded an agonist (flexor) channel for each finger: first dorsal interosseus (FDI), two portions of the flexor digitorum superficialis (FD, FD2), and adductor digiti minimi (ADM). Finally, to allow for a description of patterns of flexor/extensor coactivation, we also recorded one channel of EMG from the extensor of the four fingers, extensor digitorum (ED).

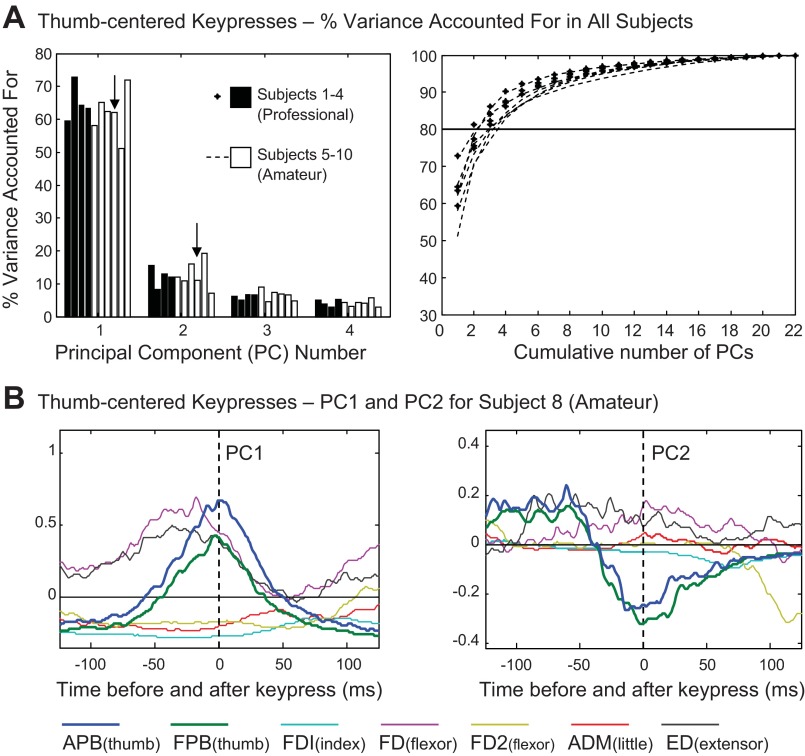
Fig. 2.

Principal component (PC) analysis results for thumb-centered key presses. A: percentage of variance accounted for by PCs 1–4 (left) and cumulative percent variance accounted for by all PCs (right) for each subject. B: waveforms of PC1 (left) and PC2 (right) from subject 8.

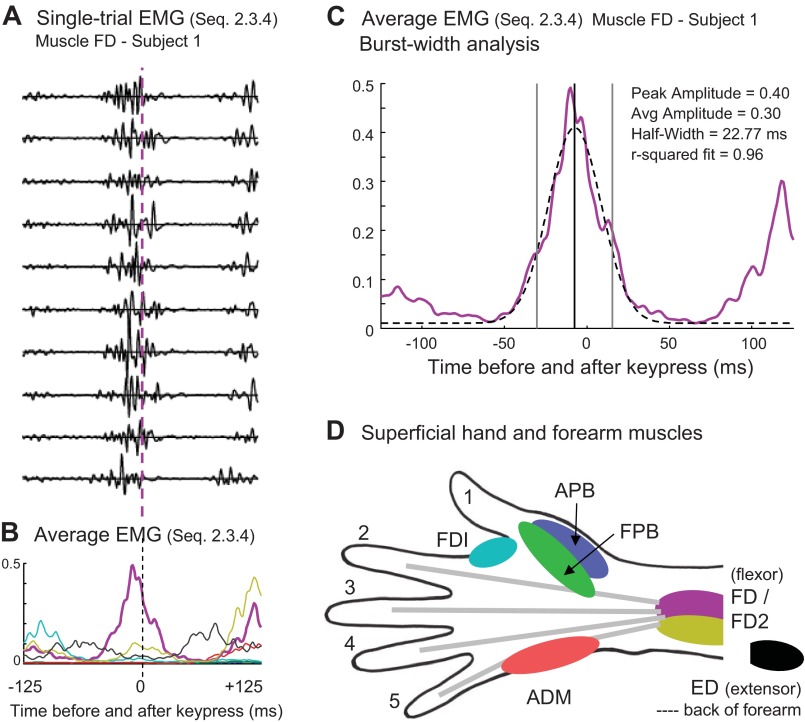
Fig. 1.

Sample EMG data from sequence 2.3.4 for subject 1. A: single trials from flexor digitorum superficialis (FD). B: rectified and averaged EMG for all muscles across repeated trials. C: Gaussian fit for the FD burst in this sequence. D: schematic illustration of approximate locations of hand muscles. FDI, first dorsal interosseus; APB, abductor pollicis brevis; FPB, flexor pollicis brevis; ED, extensor digitorum; ADM, adductor digiti minimi.

EMG data analysis.

The MIDI data contained the onset time of each key press and the velocity of the keystroke. The onset of the pressure associated with the experimenter's key press was defined as the point where pressure was maintained at a level greater than 0.5 SD above the maximum of the baseline. The EMG data were truncated at this start point (which was far in advance of any key press performed by the subject). The EMG signal for each muscle was rectified and then low-pass filtered at 20 Hz prior to subsequent analysis.

The EMG data were aligned on the time of the central key press and truncated at ±125 ms around this time (i.e., the expected times of the preceding and subsequent key presses) and averaged across repeated trials. The data from each channel were then normalized according to the range of activity across the entire truncated set. The amplitude was normalized by subtracting the minimum value for that channel and then dividing by the maximum, yielding a value between 0 and 1. Using data from subject 1, Fig. 1, A and B, shows an example of single-trial, FD EMG data from sequence 2.3.4 (index to middle to ring fingers) and the resulting average EMG for that sequence. The corresponding EMG waveforms for the other six channels are also shown in Fig. 1B, color-coded as indicated in Fig. 1D.

Principal components (PCs) analysis was used to quantify sequence-specific variations in EMG burst characteristics (amplitude, duration, shape, and relative timing across muscles). We used a time-varying PC analysis which was developed in previous studies (Klein Breteler et al. 2007; Santello et al. 2002) and is similar to the time-varying muscle synergy analysis used by d'Avella and Bizzi (2005). As explained by Soechting and Flanders (2008), the advantage of this approach is that it combines data across trials (i.e., the various sequences), but not across muscles, allowing the analysis to reveal tendencies for asynchronous bursting across different muscles as part of the first few PCs.

For each target digit, we applied the analysis to data combined across all sequences centered on that digit (listed in Table 2). Thus the input matrix for this PC analysis was n sequence vectors containing 1,757 points of averaged muscle activity (±125 ms around the central key press = 251 points × 7 muscles). The result of the PC analysis was n PC waveforms computed from the n × n covariance matrix of n sequences and an n × n matrix of weighting coefficients (n ranging from 15 to 27, depending on the target digit, see Table 2). The covariance calculation removes the mean from each column in the input matrix; thus the EMG data for a given sequence could be perfectly reconstructed as the mean plus the weighted sum of each of the n PC waveforms. The PC waveforms are ranked from highest to lowest according to the amount of variance they account for in the data. An arbitrary cutoff of 80% variance accounted for was used to determine the number of PC waveforms to include in further examination of multimuscle activity for different sequences.

We also did a more focused analysis on the burst in a primary agonist muscle around the time of the central key press. One primary muscle was qualitatively chosen for each digit (as the one with the largest amplitude for most subjects) and was used to measure burst center time and burst width. Using a curve fitting tool in Matlab (R2010b, The MathWorks), the average normalized EMG trace for each sequence was fit with a vertically shifted Gaussian curve:

$$y=A{e}^{-{\left(\frac{(x-b)}{c}\right)}^2}+d$$

where A is the amplitude of the burst, b is the horizontal shift from the 0 point in the interval, c is the width of the curve (2 SD), and d was set to be the minimum value of the EMG data across the ±125-ms interval. Using the initial values of A = 0.3, b = 0, and c = 18, the curve-fitting algorithm adjusted the values of A, b, and c to find a local maximum of best fit to the curve. Fits with low r² values due to the presence of adjacent bursts in the data were fit again, excluding the extremities of the interval, so that only the burst associated with the central key press would be included. An example burst-fit is exhibited in Fig. 1C (dashed line). Only fits with r² > 0.6 were deemed acceptable and included in subsequent analyses. Only sequences with acceptable fits for all subjects were included in the regression and discriminant analysis (Table 2, bolded sequences). We used a linear regression of burst width onto IKI to determine whether there was a significant relation within and across subjects.

To assess phasic coactivation (or transient cocontraction) across muscles, for each sequence we used the average EMG amplitudes within the interval defined by the burst width of the primary muscle (the outer vertical lines in Fig. 1C). We calculated a phasic coactivation index by dividing the average extensor (ED) value by the average value of the two muscles that contributed most directly to the key press of a given digit. For the fingers, this amounted to phasic extensor/flexor coactivation, which might transiently increase joint stiffness. For the thumb, however, since ED acts only on the four fingers, an increase in the value of this index signified a tendency to extend or stiffen the fingers, not the thumb.

Finally, we used discriminant analysis to test for a relation between the type of change in hand posture (ΔPI) and the balance of amplitudes across the primary flexor, a secondary flexor, and the extensor EMG bursts. The “classify” function in Matlab (linear method, R2010b) quantified the extent to which a three-key-press sequence could be correctly classified into one of three postural change index categories, where positive, negative, and zero ΔPI reflected hand opening, closing, or maintaining (no change), respectively.

RESULTS

General performance.

As shown in Table 1, the 10 pianists were chosen to exhibit a wide range of levels of expertise and training. Our designation of professional (P) vs. amateur (A) was based on the fact that, for subjects 1–4, piano playing was their main career, whereas subjects 5–10 played recreationally. All subjects learned to play during childhood except for subject 7, who started at age 45 yr. Years of practice ranged from 7 to 48 yr. The 10 subjects were all neurologically normal, but they covered a wide range of ages (19–54 yr). Our goal was to quantify subtle differences in the EMG patterns used by these various pianists and to provide a comprehensive description of the patterns used by normal, healthy adults.

Table 1 also shows the uninstructed differences in speed and loudness across subjects. All subjects played along with a metronome that signaled a mandatory 125-ms IKI, but only professional subjects 1–4 and amateur subject 9 precisely achieved this ideal timing (with average IKIs of 124–126 ms). Subjects 6 and 7 were particularly slow, with average IKIs greater than 150 ms, whereas subjects 5, 8, and 10 had intermediate values. The longer IKIs were also associated with more variability. The IKI coefficient of variation (CV) ranged from just 7% in professional subject 4 to 20% in amateur subject 7, and CV was significantly correlated with IKI across subjects (r² = 0.548).

The keystroke velocity (loudness) also varied across subjects (last column in Table 1). The target level of 100 MIDI velocity was demonstrated at the beginning of the experiment, but no feedback was given during the experiment. Actual velocities tended to be inversely related to IKI, suggesting that the slightly faster subjects also tended to be slightly louder, but the correlation was not strong (r² = 0.185). The loudest pianists (94–99 MIDI units) were three of the four professionals, who also used the fastest IKI (124 ms).

In the next few sections, we will describe the overall patterns of EMG activation for sequences centered on each digit, beginning with the thumb (digit 1), the index finger (digit 2), and then digits 3–5. Our initial EMG analysis was based on the time period ranging from 125 ms prior to the key press of a certain digit to 125 ms after that key press. Then, recognizing that some subjects played slightly faster than others, our subsequent analysis was focused on the somewhat variable time frame of the central EMG bursts (burst center ± burst half-width, see Fig. 1C), thus excluding EMG activity that was more directly related to the previous and the subsequent key presses.

Thumb key-press waveform analysis.

As listed in the left column of Table 2, for the thumb key presses, various other digits (fingering) were used to strike various keys (notes) before and after the central key press. Thus the same fingering may have multiple listings, and, depending on the key locations, these may or may not correspond to different values for the PI (ΔPI). As shown in the column labeled ΔPI, our sample of 22 thumb-centered key-press sequences contained 5 sequences where the hand was opening (+), 10 sequences were the hand was closing (−), and 7 sequences where hand posture was not changing much (0).

Our analysis of the EMG patterns for the thumb key press revealed remarkably consistent patterns across subjects. In professionals and amateurs alike, the first four PCs together accounted for well over 80% of the variance in the EMG patterns across the 22 sequences, with higher order components contributing progressively (Fig. 2A). As expected, in all subjects, PC1 was dominated by bursts of activity in the thumb abductor (APB) and the thumb flexor (FPB), which were nearly simultaneous and of nearly equal amplitude. Representative examples from two subjects are shown in Fig. 2B (amateur subject 8) and Fig. 3 (professional subject 3), where thumb muscle activity is coded in dark blue and green. All subjects also exhibited PC1 activity in the four-finger extensor muscle (ED, black traces), which was more or less burstlike (phasic), ramplike, or sustained (tonic) across the 250-ms interval, depending on the subject. In about one-half of the subjects, the extensor burst was accompanied by a burst in the middle-finger portion of FD (FD, purple trace in Fig. 2B) and would, therefore, provide phasic stiffening of the fingers. However, in some subjects the timing of the ED burst was not coincident with a flexor burst (e.g., subject 3 in Fig. 3). Amateur subjects 6 and 7 had more tonic extensor muscle activity throughout this time period (data not shown). Thus it appears that the thumb key press was generally accompanied by finger extension (ED activity) or stiffening (ED/FD coactivation).

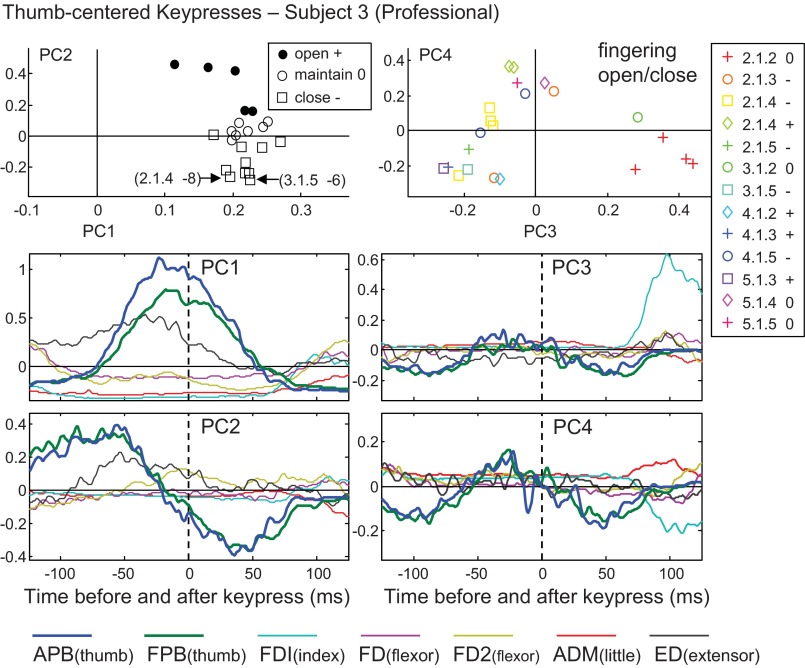
Fig. 3.

PC analysis results for thumb-centered key presses for subject 3. Waveforms for PC1 and PC2 (left) and PC3 and PC4 (right) are shown in the bottom four panels. In the top row, weightings of two PCs are plotted against each other, with symbols grouped by change in hand posture (left) or fingering and change in hand posture (right) for each key-press sequence.

Whereas the examination of PC1 revealed the main bursting pattern that was used for most of the thumb-centered sequences, the higher order components generally contributed to the sequence-specific EMG patterns. As explained under methods, the EMG pattern for each sequence could be reconstructed as a weighted sum of 22 PCs, with various positive or negative weightings. PC1 always had relatively large positive weightings, but the smaller weightings of the higher order components could be positive or negative, depending on the sequence. For the thumb-centered sequences, they tended to contribute to the reconstruction either by changing the amplitude or timing of the central APB/FPB burst (PC2), or by furnishing the activity needed for the preceding or following key presses, around time −125 ms or +125 ms, respectively (PC3, PC4, see Fig. 3).

In 9 of the 10 subjects, the PC2 pattern for the thumb-centered sequences was dominated by ramplike APB/FPB waveforms, that quickly transitioned from positive to negative values just prior to time zero (Figs. 2B and 3). Since PC1 always had positive weighting, adding this PC2 pattern with positive or negative weighting coefficients would serve to alter the timing of the APB/FPB burst with an advance or delay, respectively. Since the PC2 waveform was consistent across subjects, we sought to determine whether its weighting coefficients exhibited a consistent sequence-specific pattern.

In the nine subjects with the similar PC2 waveforms, the sign of its weighting coefficient was related to the sign of the PI (ΔPI). In Fig. 3, using data from a representative subject, the top left plot shows that positive PC2 weightings were used to reconstruct the data for sequences involving a positive change in hand posture (hand opening, black circle symbols), thus serving to advance the timing of the APB/FPB burst. The resulting advance in thumb abduction may have helped to propel the thumb away from the fingers to open the hand. In contrast, negative PC2 weightings corresponded to the sequences with hand closing (square symbols). In hand-closing sequences, the digits were drawn together, including instances involving the thumb-under maneuver (i.e., the thumb and hand crossing one another to reach the next key). In Fig. 3 the two most negative PC2 weightings (open square symbols) corresponded to the most negative changes in posture (2.1.4 was −8, and 3.1.5 was −6). The prolongation of the APB/FPB burst achieved with an inverted (negative) PC2 contribution might tend to prolong the thumb internal rotation beyond the time of the thumb key press. This trend was clearly present in the nine subjects with this PC2 APB/FPB waveform: of the 90 total cases of hand closing (9 subjects × 10 sequences, Table 2), 68 were associated with negative PC2 weighting coefficients (76%).

In many cases, the higher order PCs exhibited waveforms that were nearly flat around zero, but contributed various EMG bursts to the prior or subsequent key presses, at times −125 and +125 ms, respectively. An example is shown in the right panels of Fig. 3. In this case, PC3 had a large positive weighting (red plus symbols) for 2.1.2 fingerings (i.e., ending in the index finger), and hand posture remaining neutral (0). This combination of fingering and ΔPI would be expected to require a large burst in the FDI muscle (light blue trace). PC4 was negative for the 2.1.2 sequences, which also tended to increase the amplitude of this FDI burst. In contrast to PC1 and PC2, the multimuscle composition of PC3 and PC4 was more variable across subjects.

Index key-press waveform analysis.

Similar to the results for the thumb-centered key presses (Fig. 2A), for the index finger-centered key presses, for each of the 10 subjects, the first four PCs together accounted for more than 80% of the variance. In this case there were 27 sequences centered on digit 2 (Table 2, second column) and therefore 27 PCs. Ten of these sequences ended with thumb (digit 1) and hand opening (positive values of the ΔPI), and so this situation was well represented in the data set.

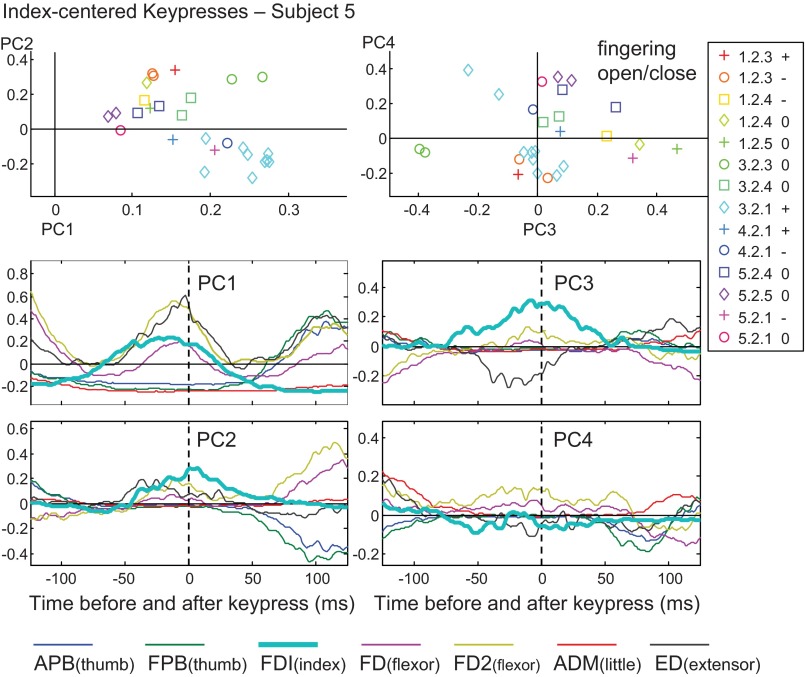
In Fig. 4, we show the results of the analysis of PC1–PC4 using data from subject 5. In this subject, as in all subjects, the central burst of PC1 included activity in two to three flexors of the index finger: FDI (light blue) and one or both portions of the four-finger flexor (FD purple, FD2 gold). In most subjects, PC1 also included a robust burst in the four-finger extensor (ED black); only in amateur subject 7 was the ED activity relatively tonic (data not shown). Compared with the thumb, the PC1 weighting coefficients for the index finger tended to show a wider range of positive values (top left panel in Fig. 4). For example, in 7 of 10 subjects, the PC1 weighting coefficients were close to zero in cases where the little finger was used for key presses before and after the index key press (5.2.5, purple diamond symbols). This implies relatively small flexor bursts, and this sequence may have instead involved forearm pronation.

Fig. 4.

PC analysis for index-centered key presses for subject 5. Top row: weightings for two PCs are plotted against one another, with symbols grouped by key-press sequence and change in posture. Bottom rows: waveforms for PC1, PC2, PC3, and PC4.

For the PC2 of subject 5 (Fig. 4, lower left panel), a negative weighting (inverted waveforms) contributed to a late burst in the thumb muscles, centered around +125 ms (dark blue and green traces). In the upper left plot, fingering 3.2.1 (light blue diamond symbols) exhibits weighting coefficients that were strongly positive for PC1 and negative for PC2, with both providing a robust APB/FPB burst for this subsequent thumb key press. Negative PC2 also served to diminish the FDI burst (light blue trace) by subtracting from the central peak. Remarkably, this somewhat subtle PC2 pattern was seen in all 10 subjects, with the burst of FDI activity being followed by the opposite change in thumb muscle activity. Since FDI does exert some adduction force on the thumb, it may have been mechanically advantageous to quickly decrease FDI thumb adduction just prior to APB thumb abduction, thus tending to couple these EMG waveforms.

The PC3 and PC4 waveforms mainly seemed to contribute to previous and subsequent key presses, but these patterns were variable across subjects. In the case shown in Fig. 4 (right panels), a negative weighting of PC3 diminished the amplitude of the central FDI burst and provided flanking bursts in FD and FD2 (purple and gold), especially for fingering 3.2.3 (green circle symbols). However, for the index-centered key presses, as well as for the sequences centered on the other fingers, PC3 and PC4 often showed very little activity at time zero.

Digits 3–5 waveform analysis.

As for the thumb and index-centered key presses, for digits 3–5, the first four PCs always accounted for more than 80% of the variance. In all cases (digits 1–5) the cumulative variance accounted for plot showed a smooth curve (see Fig. 2A), indicating the higher order PCs contributed to progressively finer details of the EMG pattern. Table 2 lists the sequences that entered each analysis: 23 for the middle finger, 19 for the ring finger, and 15 for the little finger.

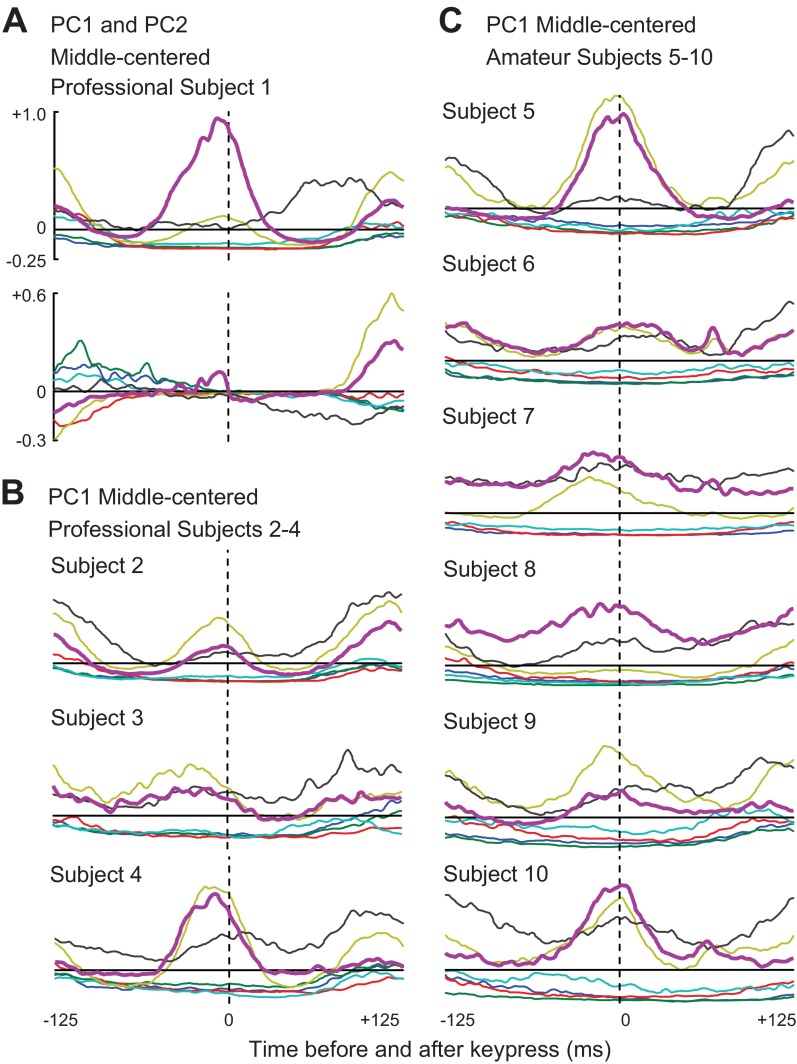
In Fig. 1 we presented single-trial and averaged EMG data from one key-press sequence centered on the middle finger (2.3.4), using data from subject 1. In Fig. 5A, we show the PC1 and PC2 EMG waveforms of subject 1. As in the corresponding single-sequence example (Fig. 1B), this subject's PC1 was dominated by a large burst in FD and a smaller burst in FD2 around time zero. The PC1 of all other subjects also featured a central FD burst (purple traces in Figs. 5, B and C), and more or less activity in FD2 (gold traces), depending on the subject. Thus, in further analyses, the primary agonist muscle for middle-centered sequences was designated to be FD.

Fig. 5.

Waveforms from PC analysis for middle-centered key presses. A: waveforms for PC1 and PC2 from subject 1. PC1 waveforms for professional subjects 2–4 (B) and for amateur subjects 5–10 (C) are shown. Color code is illustrated in Fig. 1D.

In the middle-centered PC1, the amplitude and timing of ED activity was variable across subjects (black traces in Fig. 5). Phasic coactivation of the four-finger extensor (ED) at the same time as the four-finger flexor (FD, FD2) would tend to transiently stiffen the joints of the fingers, and therefore this tendency varied across subjects. We will quantify this feature in the next section using data from the EMG data from each sequence (e.g., Fig. 1B) rather than the patterns summarized by PC1.

Subject 1's middle-centered PC2 (Fig. 5A) had only a very small FD burst near time zero and instead contributed more robustly to the reconstructions of the previous and subsequent EMG bursts. Each of the other nine subjects (data not shown) had a small PC2 FD burst near time zero, with timing that often differed from the PC1 burst, and thus could serve to alter FD burst timing in a sequence-specific manner. However, the activity around times ±125 varied widely across subjects.

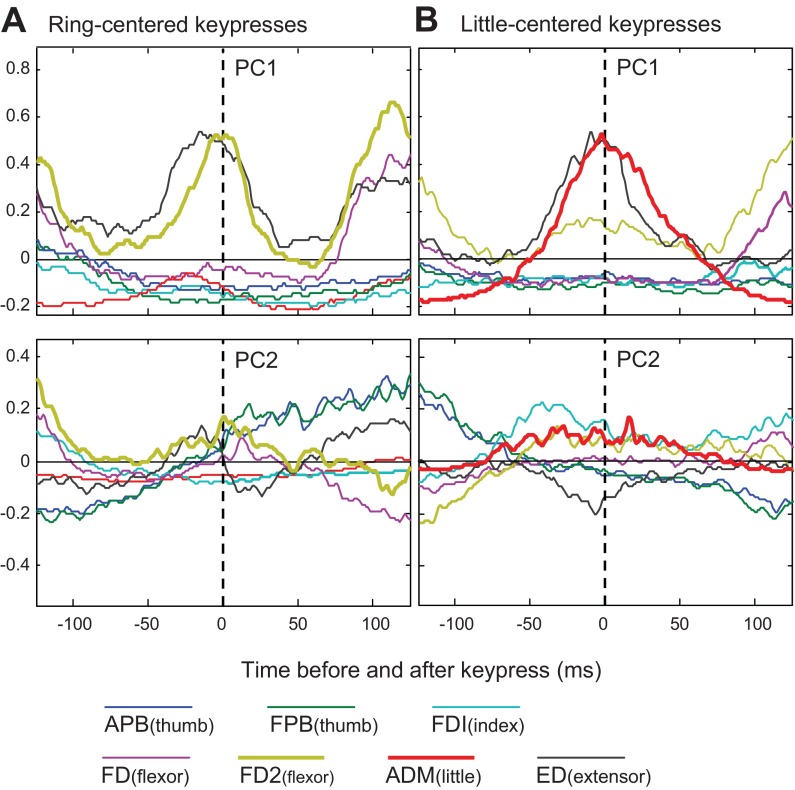
The primary agonist for ring-centered key presses was FD2. As shown for subject 5 in Fig. 6A, in all subjects, PC1 featured a larger peak amplitude in FD2 (gold traces), compared with FD (purple traces). In this subject, PC1 had a robust burst in ED (black trace); the ED burst was smaller in the other subjects. PC2 was remarkably consistent across subjects, featuring a central FD2 burst and a slow transition from negative to positive activity in the thumb muscles APB (dark blue) and FPB (dark green). This latter feature may be related to the fact that about one-half of the ring-centered sequences involved the thumb (see Table 2).

Fig. 6.

Waveforms from PC analysis for subject 5. Waveforms for PC1 and PC2 from ring-centered key-press sequences (A) and from little-centered key-press sequences (B) are shown.

For key presses centered on the little finger (Fig. 6B, subject 5), ADM was clearly the primary agonist; it dominated PC1 for all subjects. The other clear contribution to PC1 was an ED burst. In most cases, the ED burst was nearly simultaneous with ADM, creating phasic coactivation that would serve to transiently stiffen the little finger. PC2 most consistently appeared to contribute by modulating the amplitude, but not the timing of the central ADM and ED bursts. Thus, compared with digits 1–3, our PC analysis suggested that for digits 4 and 5 burst timing (i.e., width and phase in reference to time zero) was relatively consistent across the different sequences.

Analysis of central EMG bursts.

In the previous sections, we used PC waveforms and weighting coefficients to describe the main multimuscle EMG pattern, especially the aspects of the pattern that changed in a sequence-specific manner. We now present the results of a complementary and more highly focused analysis. As shown in Fig. 1C and described under methods, we began by fitting a Gaussian curve to one EMG burst from each of the 106 sequences listed in Table 2. For these fits, we selected one primary agonist muscle for each digit: APB, FDI, FD, FD2, ADM for digits 1, 2, 3, 4, 5, respectively. The fitting was deemed successful (r² > 0.60) for all 10 subjects in 69 cases (bold entries in Table 2), about one-half of the original data set. Further analysis was restricted to this subset (21, 17, 6, 12, 13 sequences digits 1, 2, 3, 4, 5, respectively). The fitting procedure allowed us to define a time frame relative to burst center and, within this time frame, to determine average EMG amplitudes of the primary agonist as well as the antagonist (ED) and a secondary agonist (FPB, FD2, FD2, FD, FD2 for digits 1, 2, 3, 4, 5, respectively).

Pooling data from all 10 subjects, variations in burst width were correlated with the variations in the speed of piano playing. In Fig. 7, burst width is plotted against IKI, using 210, 170, 60, 120, or 130 data points for sequences centered on the thumb (upper left plot) or the fingers (other plots). All slopes were positive and ranged from 1.1 for the index finger, and 1.0 for the little finger (perfect time-base scaling), down to 0.44 for the ring-centered sequences. Data from the professional subjects are indicated by plus symbols, which cluster closer to the origin due to the professional's tendency for shorter and less variable IKIs (see Table 1). Regressions on the smaller subsets of data for individual subjects produced statistically significant correlations (P < 0.05) in only 6 of 50 cases (restricted to the middle and little fingers of amateurs), but significant slopes were always positive (ranging from +1.0 to +3.7).

Fig. 7.

Burst width of the primary agonist muscle and interkeystroke interval (IKI). For each digit, the sequence-average IKI is plotted against burst widths fit to the EMG average for that sequence, for all subjects and for a subset of key-press sequences (bolded in Table 2). The slope of the line, r², and P value for the relation between these variables are shown in each plot.

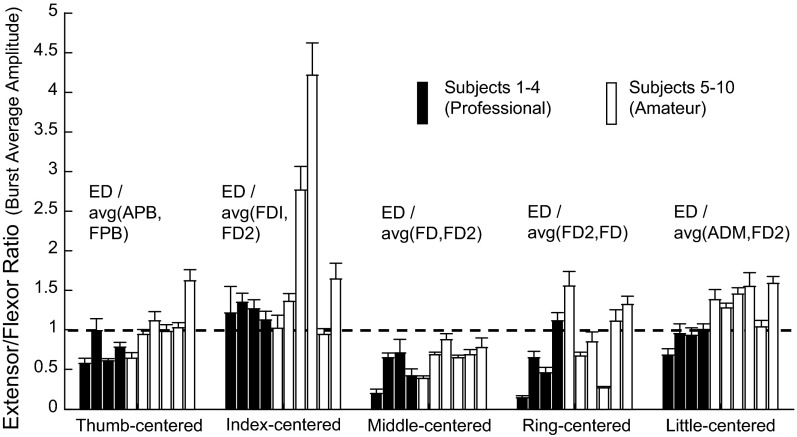
Thus burst width scaled with increasing IKI across subjects, consistent with the idea of time-base scaling of the motor pattern (see Furuya and Soechting 2012). Slowing of the time course of finger flexion might also be enhanced by a tendency for increased extensor activity, if extensor forces decreased the efficacy of flexor forces. Thus we explored the idea that phasic extensor/flexor coactivation was also related to the variation in IKI across subjects. For each subject, using the subset of 69 sequences, we computed a coactivation index as the amplitude of ED activity divided by the mean amplitude of the primary and secondary agonist muscles. Figure 8 shows that in most cases this ratio was close to 1.0, suggesting substantial stiffening of the striking finger at the time of the key press. Phasic coactivation was lower for the middle finger compared with the index finger in most subjects, and it was generally lower for professionals (black bars) compared with amateurs (white bars).

Fig. 8.

Extensor-flexor coactivation. For each digit, the average extensor-to-flexor ratio is plotted for each subject. A value of 1 (horizontal dashed line) indicates EMG amplitudes across the extensor (ED), and the average amplitude of the primary and secondary flexor for that digit were equal.

The coactivation index was restricted to the narrow (about 100 ms) time frame centered on the peak of the primary agonist burst and did not take into account the variable tendencies for ED burst modulation. Whereas our initial EMG burst analysis began by fitting only a primary agonist, we also used the same Gaussian fitting procedure to quantify the extent to which ED bursts were phasic in different subjects. Clearly modulated EMG bursts would be more likely to be well fit (r² > 0.60) by a Gaussian. Considering the full set of 106 sequences listed in Table 2, the percentage of successful burst fits was similar across subjects. In professional subjects 1–4, success rates were 51% on average, ranging from 36% to 67%. In the amateur subjects, the mean rate was 68%, with subject 7 showing the smallest success rate (43%) and thus the least phasic extensor activity among amateurs. Thus, although extensor/flexor coactivation is often thought of as sustained background activity, in piano playing a substantial percentage of this activity was burstlike.

Central balance of EMG levels.

Finally, as a more restricted assessment of neuromuscular coarticulation (compared with the analysis EMG waveforms across 250 ms), we tested the hypothesis that the balance of the EMG amplitudes within the time frame of the central burst varied in a sequence-specific manner. We used discriminant analysis to determine whether the relative amplitudes of three EMGs (those listed in Fig. 8) could be used to correctly identify the type of sequence in which these bursts were embedded. The classification was into the three groups specified by the sign of the ΔPI: hand opening, hand maintaining its posture, or hand closing. Thus correct classification by chance was 33%.

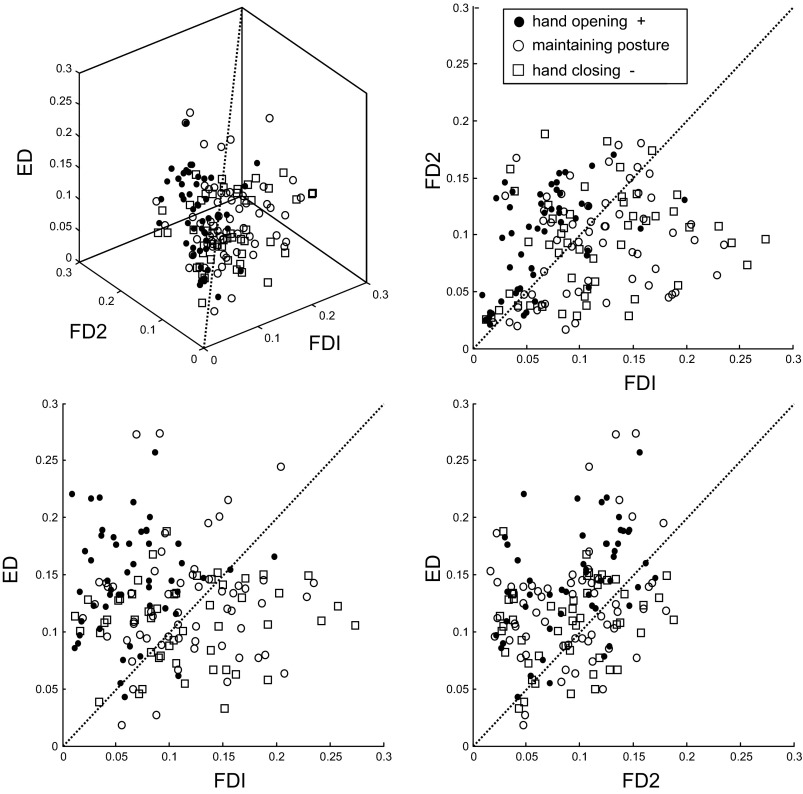
Figure 9 shows an example of this analysis using pooled data across all subjects for the index finger. Extensor (ED) amplitude is plotted on the vertical axis, and the two flexor (FDI and FD2) amplitudes are plotted on horizontal axes. As in Fig. 3, the symbol types indicate the sign of the PI, i.e., whether the hand was opening (black circles), maintaining its posture (white circles), or closing (white squares). The hand-opening sequence (black circles) generally had greater ED and FD2 activity, and it could be reliably discriminated from the other two groups (76% correct classification). As is apparent in Fig. 9, correct classification into the other two groups was closer to chance levels (33% for maintaining and 42% for closing). Note that since each sequence corresponded to only one EMG average per subject, the success of this analysis required consistent EMG patterns across the 10 subjects.

Fig. 9.

EMG amplitudes for index-centered key-press sequences for all subjects. The EMG magnitude for the extensor (ED) and two index finger muscles (FDI, primary; FD2, secondary) are plotted against one another for the subset of key-press sequences used for discriminant analysis (bolded in Table 2). Different symbols indicate the sign of the change in hand posture during the sequence.

Using the muscle triads indicated in Fig. 8, we performed the analogous analysis for sequences centered on the other digits, except for the middle finger where our data subset (bold font in Table 2) included no sequences with hand opening. We achieved correct classification at above 50% (i.e., well above chance) for thumb-centered hand opening (58%), ring-centered hand closing (70%), and little-centered hand opening (53%). Thus in each case tested, the balance of activity across three muscles specified a certain sequence type, even when the analysis was restricted to a time frame of about 100 ms.

DISCUSSION

Despite the diversity in our subject pool, all pianists had similar EMG patterns. We tested for two types of neuromuscular coarticulation and found evidence for both. First, as a conceptual framework, we speculated that the complex spinal circuitry might shape the timing of EMG bursts throughout the sequence, as afferent feedback caused by the movement for one key press may have reflexively influenced the bursting for the next (Angel 1975, 1987; see also Seki at al. 2003; Weiss and Flanders 2011). Second, we assumed that the precise balance of activity across muscles at burst center would be a more sensitive indicator of the motor cortical target command, and a more stringent test of whether the movement sequence was planned as a series of fixed segments.

The first type of coarticulation (waveform timing) was quantified by considering how the addition or subtraction of the PC2 waveform changed the shape of the PC1 bursts. For the thumb and index finger, we found very consistent sequence-specific effects, especially with regard to the type of postural transition (hand opening vs. closing) that the sequences entailed (Fig. 3) and the mechanical interactions between sequential FDI and thumb muscle forces (Fig. 4). For all digits, our PC analysis also indicated changes in the amplitude (Figs. 4–6) of the central agonist burst across the various sequences. We then used a discriminant analysis on data restricted to burst center and combined across the 10 subjects to reveal a second type of coarticulation. In several cases, the balance of EMG levels across three muscles could be used to correctly classify whether the sequence involved a hand opening, closing, or neutral postural change. This analysis depended on being able to pool data across all 10 subjects, and so its success suggests that these trends were consistent across subjects.

Other aspects of the EMG patterns were more variable across subjects, for example the magnitude of phasic extensor/flexor coactivation and the duration of the primary agonist burst, which scaled with slight differences in tempo across subjects. In the following sections, we will discuss basic features of our results in the context of motoneuronal bursting patterns, phasic coactivation, and practice.

EMG burst patterns.

Several groups have proposed that the construction of multimuscle EMG patterns involves a weighted summation of contributions from distinct pre-motoneuronal drives, each of which specifies fixed relative levels of activity across a group of muscles (e.g., Chvatal and Ting 2012). In this conceptualization, our sequence-specific, burst-center reweightings (Fig. 9) would be achieved by reweighting the motor cortical inputs to a modular collection of pre-motoneuronal elements. Giszter and colleagues (2004, 2008) took this modularity theory one step further by also proposing that the pre-motoneuronal drives are composed of phasic bursts of fixed duration, due to the presence in the frog spinal cord of “unit burst generators” (Hart and Giszter 2004, see p. 5269). This idea of temporally fixed modules of multimuscle EMG waveforms is also the basis of the synergy hypothesis of d'Avella and colleagues (2005), a view that differs rather dramatically from synergy control in the uncontrolled manifold hypothesis (Latash et al. 2007).

The idea of fixed burst modules is also in sharp contrast with earlier descriptions of EMG patterns for human arm movement. Gottlieb and colleagues (1989) summarized a large body data from single-joint movements by proposing a speed-sensitive strategy for scaling the duration of EMG busts, and Flanders and colleagues (1992, 1994, 2002) showed how the time-base of EMG waveforms scales with variations in the speed of multijoint reaching movements (see also d'Avella et al. 2008). The present study featured relatively small differences in the speed (or tempo) of piano play, but nevertheless documented scaling of EMG burst durations. Piano playing at different tempos could hypothetically be achieved by scaling IKIs but not burst durations, if the system used unit burst generators. But this idea was not supported by our data. Furthermore, Furuya and Soechting (2012) compared hand kinematics across two explicitly instructed tempos (IKI = 95 or 125 ms) and found that the entire waveform of the velocity of joint rotation scaled along with speed. Interestingly, however, the keystroke MIDI velocities, which correspond to loudness, remained constant across the two tempos, suggesting that durations of joint rotations scaled without concomitant changes in amplitude.

Coactivation and dystonia.

Phasic coactivation was evident between extensor and flexor muscles during piano playing. In PC1, for instance, the ED was more or less phasic and also synchronous with the FD activity (e.g., Fig. 2B). This was not tonic muscular coactivation that plays a role in ensuring stable smooth control of movements in uncertain environments (Franklin and Wolpert 2011). The phasic feature of muscular coactivation suggests fine-tuned modulation of joint stiffness in response to time-varying perturbing forces originating from complex biomechanical linkages within the hand and mechanical interactions between the fingertip and the key.

Although our experiment was not designed to test a range of playing speeds, we found that phasic coactivation tended to be smaller for the experts than for the amateurs (Fig. 8). These findings suggest that skilled fast piano performance may be associated with reduction of coactivation, being in agreement with the idea of minimization of stiffness through practice to fulfill task demands (Burdet et al. 2001; Huang et al. 2012; Thoroughman and Shadmehr 1999).

Focal hand dystonia typically elicits abnormal patterns of muscular activation (Adler et al. 2005; Cohen and Hallett 1988; Young et al. 2011). This involves less obvious alternating agonist-antagonist muscular bursts and longer muscular coactivation compared with healthy controls (Cohen and Hallett 1988). Possible underlying mechanisms include loss of inhibitory control of cortical activity eliciting motoneuronal recruitment (Ruiz et al. 2009; Yazawa et al. 1999) and weaker reciprocal inhibition (Berardelli et al. 1996; Nakashima et al. 1989). The prolonged motoneuronal activity in focal hand dystonia could yield movement slowness in affected pianists. The prolonged coactivation of the patients may also prevent precise modulation of muscular bursts in response to preceding and subsequent key presses, which can elicit rhythmic inaccuracy of successive piano keystrokes (Jabusch et al. 2004).

Practice effects.

In our study, the amateur pianists tended to play slower than the instructed tempo (IKI > 125 ms) and with more variable IKIs (CV = 10–20%) compared with the professional pianists (IKI = 124 ms, CV = 7–14%). Aoki et al. (2005) also demonstrated that, compared with nonmusicians, experienced pianists were more capable of producing rapid individuated tapping finger movements. Analysis of muscle activity in our study revealed that burst width and phasic extensor/flexor coactivation changed with IKI. Therefore, modification of these features is a likely element of the neuromuscular control that is modified through practice.

Despite the wide range of experience, our 10 subjects showed remarkably similar EMG PCs. Parlitz et al. (1998) observed that expert pianists were capable of precisely restricting movement and force production at nonstriking digits, while amateur pianists were unable to restrict the spillover of force to other digits. These differences could be achieved by focusing activation on the flexor motoneurons that act on a single finger or by balancing activation across flexors of the striking digit and extensors of nonstriking digits. Our results demonstrate that highly trained professional pianists use a balance of muscle activity during piano playing to control the action of striking and nonstriking digits. Interestingly, we found very similar multimuscle EMG patterns across all subjects, suggesting that the amateur pianists use the same balance.

GRANTS

This study was supported by National Institute of Neurological Disorders and Stroke Grant R01 NS027484-20.

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the author(s).

AUTHOR CONTRIBUTIONS

Author contributions: S.A.W., S.F., and M.F. conception and design of research; S.A.W. and S.F. performed experiments; S.A.W., N.J.F., and M.F. analyzed data; S.A.W., S.F., N.J.F., and M.F. interpreted results of experiments; S.A.W., N.J.F., and M.F. prepared figures; S.A.W., S.F., and M.F. drafted manuscript; S.A.W., S.F., N.J.F., and M.F. edited and revised manuscript; S.A.W., S.F., N.J.F., and M.F. approved final version of manuscript.