Scaling Pharmacodynamics from In Vitro and Preclinical Animal Studies to Humans

Summary

An important feature of mechanism-based pharmacokinetic/pharmacodynamic (PK/PD) models is the identification of drug- and system-specific factors that determine the intensity and time-course of pharmacological effects. This provides an opportunity to integrate information obtained from in vitro bioassays and preclinical pharmacological studies in animals to anticipate the clinical and adverse responses to drugs in humans. The fact that contemporary PK/PD modeling continues to evolve and seeks to emulate systems level properties should provide enhanced capabilities to scale-up pharmacodynamic data. Critical steps in drug discovery and development, such as lead compound and first in human dose selection, may become more efficient with the implementation and further refinement of translational PK/PD modeling. In this review, we highlight fundamental principles in pharmacodynamics and the basic expectations for in vitro bioassays and traditional allometric scaling in PK/PD modeling. Discussion of PK/PD modeling efforts for recombinant human erythropoietin is also included as a case study showing the potential for advanced systems analysis to facilitate extrapolations and improve understanding of inter-species differences in drug responses.

Introduction

The extrapolation of in silico, in vitro, and preclinical animal studies to predict the likely pharmacokinetic properties of drugs in humans now appears within reach, largely due to advancements in physiologically-based pharmacokinetic (PBPK) modeling.^1,2) Whereas traditional allometry continues to prove useful under certain conditions for inter-species scaling of PK properties, significant progress has been achieved by transitioning from models of data (e.g., classic compartmental models) to those of biological systems. The PBPK modeling approach provides a framework for integrating drug-specific calculated parameters (e.g., octanol:water and blood:tissue partition coefficients) and in vitro measurements (e.g., plasma protein binding and hepatocyte intrinsic clearance) with physiological system-specific parameters (e.g., tissue volumes and blood flows). Given the relative success of anticipating human exposures to drugs and toxicants, ^3,4) there is considerable interest in the development of techniques for the scaling of pharmacodynamic systems. Although drug responses are considerably more complex than processes controlling pharmacokinetics, the shift from empirical to mechanism-based PK/PD modeling^5,6) should provide the best means for translating in vitro and animal data to human clinical pharmacology. ⁷⁾

In this review, we discuss the basic tenets of pharmacodynamics, namely 1) pharmacokinetics or drug exposure as the driving function, 2) capacity-limitation of drug-receptor interactions, and 3) physiological turnover processes and functional adaptation or homeostatic feedback mechanisms. As with PBPK models, these basic components identify drug and system specific properties that might be anticipated using in vitro assays, allometry, and/or preclinical animal experiments. A case study showing how human responses to recombinant human erythropoietin (rHuEpo) can be predicted from scaling a mathematical model developed in rats is provided as an example of utilizing mechanism-based PK/PD models to scale complex pharmacological systems.

Basic Principles of Pharmacodynamics

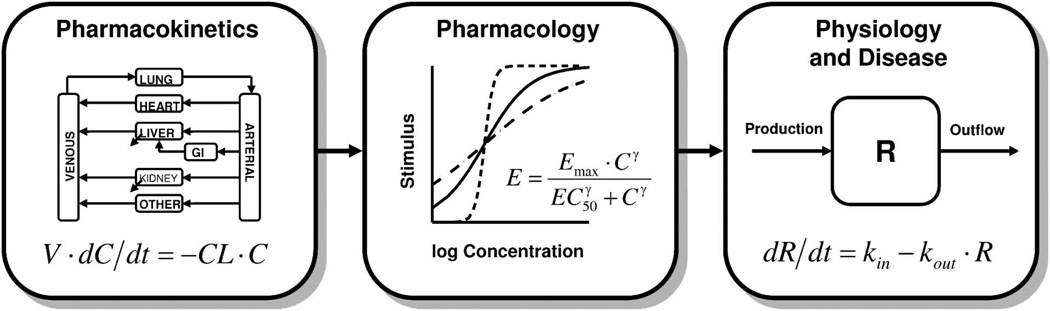
The basic tenets of pharmacokinetics (PK), pharmacology, and physiology continue to form the basis for contemporary pharmacodynamic systems analysis (Fig. 1). Pharmacokinetics, or the processes controlling the time-course of drug concentrations in relevant biological fluids, tissues, and sites of action (biophase), is the driving force for subsequent pharmacological and most toxicological effects. Although mammillary plasma clearance models (simple linear compartmental models) and area/moment analysis are the most commonly applied techniques for characterizing the absorption and disposition (distribution and elimination) properties of drugs, PBPK models provide a comprehensive platform for describing the major processes influencing the concentration time-course and net exposure of drugs in various fluids and tissues (Fig. 1, left panel). Each tissue of interest is anatomically arranged and described by a series of mass balance differential equations. Fick’s law of perfusion/diffusion and drug partitioning are featured along with a capacity-limited function for various drug binding, transport, and elimination processes. This approach provides insights into expected drug concentrations in important tissues, and potentially sites of action, and the intrinsic scalability of predictions across species and molecular drug properties is unparalleled. Whereas traditional PBPK model development has relied on destructive sampling in preclinical studies, advances in noninvasive imaging (such as positron emission tomography and magnetic resonance imaging) and microdialysis may eventually provide even finer details of in vivo drug disposition.^8,9)

Fig. 1.

Major components of mechanism-based PK/PD models.

At the biophase, the law of mass action and the limited concentration of pharmacological targets often manifest as nonlinear, capacity-limited systems.¹⁰⁾ The rate of change of a drug-receptor complex (RC) can be defined as:

$$\frac{dRC}{dt}=k_{on}·(R_{tot}-RC)·C-k_{\mathit{\text{off}}}·RC$$ (1)

where R_tot is the maximum receptor concentration, C is the drug concentration at the site of action, and k_on and k_off are the second-order association and first-order dissociation rate constants. Assuming equilibrium conditions, this equation can be rearranged to yield the general binding equation:

$$RC=\frac{R_{tot}·C}{K_D+C}$$ (2)

where K_D is the equilibrium dissociation constant (k_off/k_on). Based on Clark’s theory of receptor occupancy, the stimulus or drug effect (E) can be directly proportional to the fraction of occupied receptors, such that E=α · RC, thus deriving a classic form of the Hill equation or sigmoid E_max model:

$$E=\frac{E_{\text{max}}·C^{\gamma }}{{\text{EC}}_{50}^{\gamma }+C^{\gamma }}$$ (3)

where E_max is the maximum effect, γ (or Hill coefficient) is a slope term that reflects the steepness of the effect-concentration curve, and the EC₅₀ is a sensitivity parameter representing the drug concentration producing 50% of E_max. The typical stimulus/effect-log concentration relationship is thus curvilinear, and typical profiles for varying values of γ are shown in the center panel of Figure 1.

In contrast to the linear transduction of receptor occupancy (Eq. 3), Black and Leff introduced the operational model of agonism to provide a mechanistic interpretation of concentration-effect curves.¹¹⁾ The stimulus or effect is assumed to be nonlinearly related to the drug-receptor complex:

$$E=\frac{E_{\text{max}}·RC}{K_E+RC}$$ (4)

where K_E is the RC value producing half-maximal effect. Combining Equations 2 and 4 yields:

$$E=\frac{E_{\text{max}}·\tau ·C}{K_D+(\tau +1)·C}$$ (5)

where E_max is a system maximum and ( represents a transducer or efficacy function (R_tot/K_E). This model can accommodate complex relationships, such as partial agonism, where observed capacity and sensitivity properties are actually hybrid terms composed of drug specific (K_D and τ) and system specific (E_max) parameters. Regardless of whether linear or nonlinear transduction is operational, capacity-limitation is a hallmark property of pharmacology, and consequentially, a suitable range of dose-levels (or concentrations) are required to define the parameters of such systems. In addition, the implementation of Equation 5 requires pharmacodynamic data, or at least prior information, on the properties of a full agonist to identify the maximal system response.

Physiological turnover processes and homeostatic feedback mechanisms represent the third major component of pharmacodynamics (Fig. 1, right panel). An open system for a biological substance, R, with zero-order production (k_in) and first-order removal (k_out) can be defined by the following differential equation:

$$dR/dt=k_{in}-k_{out}·R$$ (6)

Assuming a time-invariant baseline or steady-state, the initial or baseline value (R⁰) can be defined as the ratio of the production and loss terms: R⁰=k_in/k_out. A family of basic indirect response models apply to many drugs where interaction with the pharmacological target (Eq. 3) serves to inhibit or stimulate either k_in or k_out.¹²⁾ A series of transit compartments can also be factored into such models to emulate time-dependent transduction processes that often exhibit significant onset delays and exposure-response hysteresis.¹³⁾ Knowledge of the turnover rates for physiological system components is important for the identification of the rate-limiting steps for specific pharmacological responses and might impact study design. Such information might also facilitate the characterization of feedback mechanisms that might result in tolerance and/or rebound phenomena.⁶⁾ As both drugs and diseases often interfere with normal physiological processes, the turnover aspect of both indirect response models¹⁴⁾ and transduction models¹⁵⁾ renders them well suited for the simultaneous consideration of these factors in the time-course of disease progression.

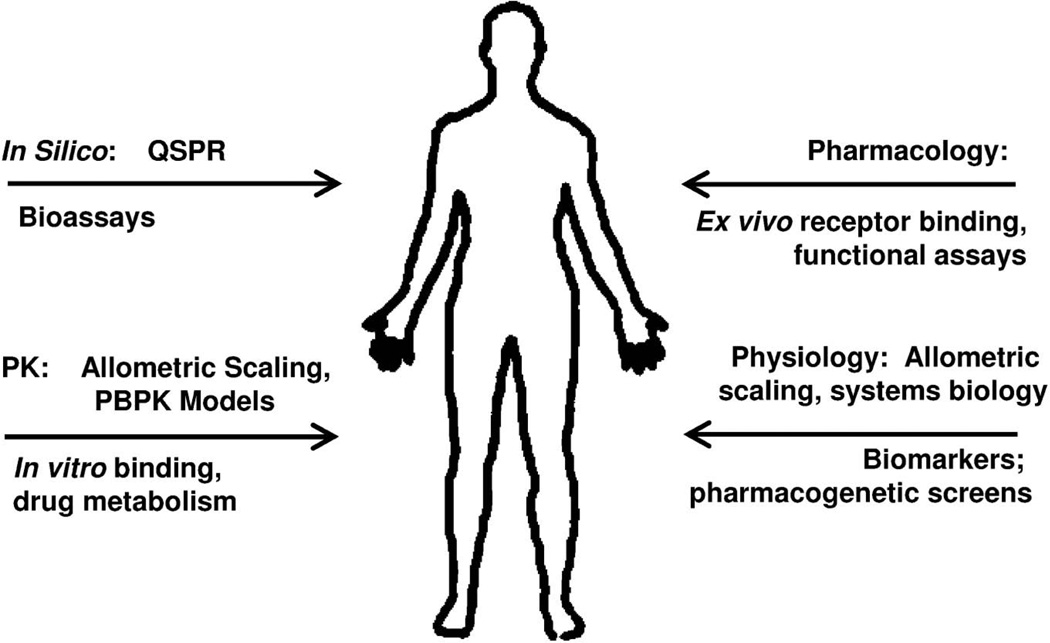
Mechanism-based models seek to integrate these basic components to identify critical pharmacological and (patho)-physiological system properties as well as the rate-limiting steps in responses to drugs.^6,16) Useful models with a potential for translational medicine also provide a structural framework for incorporating in silico, in vitro, and preclinical PK/PD measurements to predict the effects of new drugs in humans and across levels of biological organization (Fig. 2). A discussion of all these methods is beyond the scope of this review, which will focus on in vitro assays and allometric principles in the context of mechanistic PK/PD models. The derivation of quantitative structure-PK/PD relationships (in silico modeling) to predict the exposure-response profiles of new chemical entities has been recently reviewed.²⁾

Fig. 2.

Sources of information that may be integrated into mechanism-based PK/PD models for scaling to human pharmacodynamics.

Predictive techniques (top of arrows) can be augmented by selective measurements (bottom of arrows).

Extrapolation of In Vitro Bioassays

Pharmacodynamic modeling of several systems has revealed that properties of drug interactions with pharmacological targets measured in vitro may be correlated with specific model parameters often reflective of drug potency. Shimada and colleagues developed an ion-channel binding model based on in vitro binding data of calcium channel antagonists, which demonstrate relatively slow rates of association and dissociation.¹⁷⁾ The pharmacologic effect was assumed to be proportional to the concentration of the drug-receptor complex and, as an extension of Equation 1, the rate of change of the effect was defined as:

$$\frac{dE}{dt}=k_{on}·(E_{\text{max}}-E)·C-k_{\mathit{\text{off}}}·E$$ (7)

The inclusion of the binding parameters was sufficient to explain the hysteresis observed between the PK and antihypertensive effect of eight calcium channel antagonists in Japanese patients. The calculated K_D values based on estimates of k_on and k_off were shown to be significantly correlated with those obtained from in vitro experiments. These results suggest that PK and in vitro binding data alone could be used to predict the pharmacodynamic profile of future drugs in this class. Kalvass and colleagues¹⁸⁾ performed extremely insightful PK/PD studies with seven opioids in mice showing the importance of time-course of brain distribution and binding in determining their antinociceptive effects. The EC₅₀ of unbound drugs in brain showed excellent correlation with in vitro receptor binding affinities (K_D). From a drug development perspective, these examples demonstrate how in vitro assays may be coupled with useful PK/PD models to anticipate the outcomes of similar compounds and may guide lead compound selection.

Relative receptor affinity has been shown to be correlated with in vivo estimates of drug potency for several drugs, and in vitro measurements could be used in scaling of EC₅₀ values across species. In a 5-way randomized placebo-controlled crossover study aimed at evaluating the dosing equivalency of four systemically administered corticosteroids, mechanism-based PK/PD models were used to estimate EC₅₀ values for several immunomodulatory effects, including cortisol suppression, lymphocyte and neutrophil trafficking, and ex vivo inhibition of lymphocyte proliferation.^19,20) The estimated potencies for all of these responses were highly correlated with relative receptor affinity (in vitro K_D values normalized to dexamethasone). Differences in protein homology and other genetic sources of variability may result in altered drug binding affinity among species. Chien and colleagues corrected an EC₅₀ value for a competitor drug measured in humans, using several factors including receptor binding, to predict the in vivo human EC₅₀ for a new chemical entity (NCE):²¹⁾

$$E{C}_{50,\mathit{\text{NCE}},\mathit{\text{human}}}={\mathit{\text{EC}}}_{50,\mathit{\text{Competitor}},\mathit{\text{human}}}·{\left(\frac{{\mathit{\text{EC}}}_{50,\mathit{\text{NCE}}}}{{\mathit{\text{EC}}}_{50,\mathit{\text{competitor}}}}\right)}_{\text{rat}}·\delta f_u·\delta K_D$$ (8)

where δf_u and δK_D are correction factors for differences in the free fraction in plasma (f_u) and binding affinity (K_D). For example,

$$\delta K_D={\left(\frac{K_{D,\mathit{\text{human}}}}{K_{D,\mathit{\text{rat}}}}\right)}_{\mathit{\text{NCE}}}·{\left(\frac{K_{D,\mathit{\text{rat}}}}{K_{D,\mathit{\text{human}}}}\right)}_{\text{competitor}}$$ (9)

The scaled EC₅₀ from animal and in vitro data (Eq. 8) was coupled with other projected parameters to simulate a dose-response curve (Eq. 3 with an added baseline) for a new antihypertensive agent, relative to a competitor, in the preclinical phase of development. Monte Carlo simulations included a relatively large confidence interval about expected outcomes; however, data from clinical studies would eventually be used to confirm and update the model.

Traditional Allometric Scaling in PK/PD

Although the structural nature of physiologically-based models makes them uniquely suited for scaling and predicting human drug exposures, the extrapolation of PK-PD models from animals to humans is primarily based on classic allometric principles.²²⁾ There is a general expectation that many physiological processes and organ sizes (θ) tend to obey a power law:²³⁾

$$\theta =a·W^b$$ (10)

with W representing body weight and a and b as drug/process coefficients. The exponent, b, tends to be around 0.75 for clearance processes, 1.0 for organ sizes or physiological volumes, and 0.25 for physiological times or the duration of physiological events (e.g., heart-beat and breath duration, cell lifespans, and turnover times of endogenous substances or processes).²⁴⁾ A theoretical basis for allometric scaling has been proposed by West and colleagues based on the fractal nature of biological systems and energy conservation principles.²⁵⁾ Empirical models have also been coupled with allometric relationships and in vitro metabolism experiments using nonlinear mixed effects modeling to improve the scalability of such models.^26,27)

The basic expectations in pharmacodynamics are that physiological turnover rate constants of most general structures and functions should be predictable among species based on allometric principles, whereas capacity (E_max) and sensitivity (EC₅₀) parameters tend to be similar across species. Brodie and colleagues were the first to examine some PK-PD properties across species, revealing inter-species differences in duration of action and biological half-life, but similarity in plasma concentrations on awakening (i.e., concentration producing a standard response analogous to an EC₅₀), following hexobarbital administration.²⁸⁾ There has long been a general belief that the plasma drug concentration required to elicit a certain (intensity of) action is often similar in experimental animals and humans.²⁹⁾ While interspecies differences in relative receptor affinity and plasma protein binding occur (Eqs. 8 and 9),²¹⁾ there are several examples that show reasonable agreement of such properties between rats and humans for chemically-related series of drugs. Ito and colleagues demonstrated a linear correlation between the logarithm of K_D values of benzodiazepines in rat and human cerebral cortex tissue over several orders of magnitude.³⁰⁾ Cox and coworkers also showed good agreement for the EC₅₀ values of four synthetic opioids between these same species.³¹⁾ Mechanistic modeling was applied to PK/PD data for S(+)-ketoprofen obtained from several species, and estimated parameters further support these basic expectations. Pharmacokinetic parameters were shown to scale proportionally to body weight (albeit with unusual power coefficients), and anti-inflammatory PD parameters exhibited limited ranges that were essentially independent of body weight.³²⁾

Mechanism-Based PK/PD Modeling of rHuEpo

To demonstrate the use of scaling principles within mechanism-based PK/PD models, we present here scaled pharmacodynamic responses using a rat model of rHuEpo PK/PD to anticipate the time-course of several biomarkers in humans. This drug is clinically indicated for the treatment of specific types of anemia, and binding of this endogenous protein to its biological receptor (EPOR) expressed by progenitor cells in bone marrow elicits proliferation and differentiation of erythroid cells, thereby increasing reticulocytes, red blood cells, and hemoglobin concentrations in blood. Erythropoietin exhibits a high degree of homology among mammals, which explains the conserved biological activity of rHuEpo in various species.

The disposition of rHuEpo in several species is polyexponential and nonlinear, and typical PK profiles have been described using a two-compartment model with a concentration-dependent Michaelis-Menten elimination function operating in parallel with a linear nonsaturable clearance pathway.^33–35) Target-mediated drug disposition (TMDD) represents a likely explanation for the capacity-limited elimination of erythropoietin; a condition where a significant proportion of the drug (relative to dose) is bound to its pharmacological target, such that this interaction influences the PK properties of the drug.^36,37) Receptor-mediated endocytosis is a major clearance mechanism for many protein drugs,³⁸⁾ and this saturable process can result in nonlinear drug disposition.³⁹⁾ The binding of erythropoietin to EPOR is specific and results in saturable internalization of the drug-receptor complex. ⁴⁰⁾ Chapel and colleagues demonstrated that bone marrow ablation in sheep produced a significant decrease in erythropoietin clearance, providing experimental evidence that target binding and transport plays a major role in the in vivo disposition of erythropoietin.⁴¹⁾ Interestingly, the simultaneous modeling of PK profiles of rHuEpo from a wide-range of intravenous dose levels in rats, monkeys, and humans revealed that full and reduced TMDD models^42,43) well characterized rHuEpo disposition and provided a basis for linking an established pharmacodynamic model.⁴⁴⁾

Woo and Jusko have provided a comparison of interspecies PK/PD properties of rHuEpo.⁴⁵⁾ Although the prospective use of allometric scaling can be limited,⁴⁶⁾ it is generally considered that peptide and protein drugs are more likely to exhibit allometric PK relationships than small molecules owing to the relative species conservation of mechanisms that control the biodistribution and elimination of such compounds.^47–49) Despite the non-linear disposition of rHuEpo, total systemic clearance and the steady-state volume of distribution show good correlation with body weight. The exponent for clearance (0.708) was close to the expected value of 0.75; however, the exponent for the volume of distribution (0.853) was slightly lower than the expected value (1.0). Pharmacokinetic model specific parameters, such as Michaelis-Menten capacity or V_max, the central volume of distribution, and a first-order rate constant of absorption, also scaled to body weight with exponents of 0.504, 0.983, and −0.349, respectively (based on rat, monkey, and human data). As anticipated, the pharmacological capacity and sensitivity parameters were essentially species-independent.

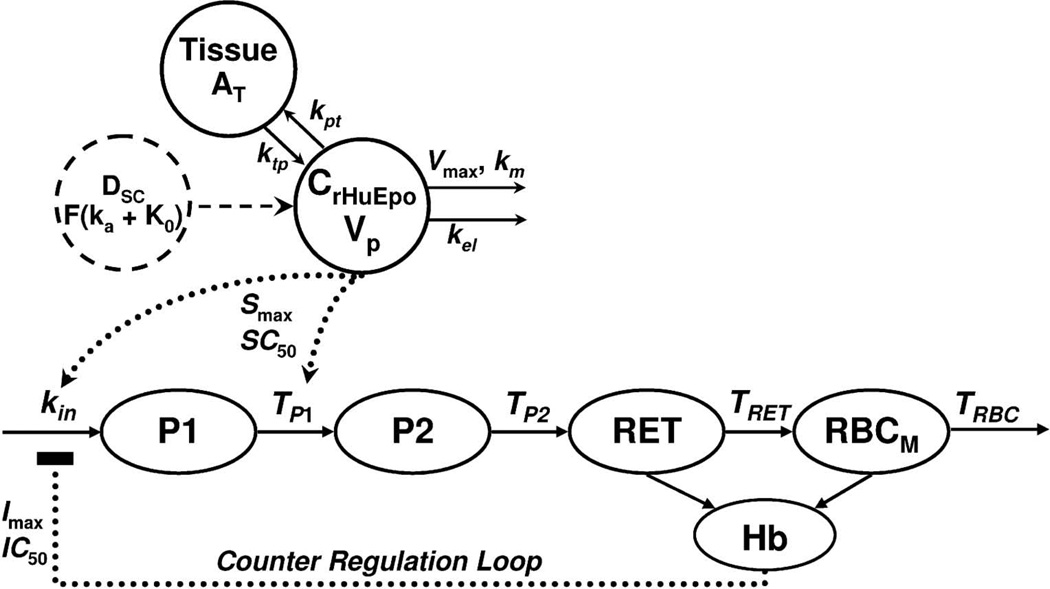
We sought to predict the time-course of reticulocytes, red blood cells, and hemoglobin concentrations in humans after rHuEpo administration from an established PK/PD model developed in rodents. Pharmacodynamic data were extracted from a clinical study in which healthy male volunteers were given 150 IU/kg subcutaneously (SC) three times weekly for 4 weeks.³⁴⁾ The general structure of the PK/PD model for rHuEpo developed from rat preclinical data is shown in Figure 3.³⁵⁾ The PK component of the model can be described by:

$$\frac{d{A}_p}{dt}=\mathit{\text{input}}(t)=(\frac{V_{\text{max}}}{K_m·V_p+A_p}+k_{el}+k_{pt})·A_p+k_{tp}·A_t$$ (11)

$$\frac{d{A}_t}{dt}=k_{pt}·A_p-k_{tp}·A_t$$ (12)

where A_p and A_t represent the amounts of rHuEpo in the central and tissue compartments, V_max and K_m are Michaelis-Menten parameters, V_p is the volume of the central rHuEpo compartment, k_el is first-order elimination rate constant, and k_pt and k_tp are first-order distribution rate constants. The initial conditions of Equations 11 and 12 are zero, and the input function after SC drug administration is defined as:

$$\mathit{\text{Input}}(t)=\{\begin{array}{cc}\frac{F·(1-fr)·\text{Dose}}{\tau }\hfill & ;0<t\le \tau \hfill \\ k_a·F·fr·\text{Dose}·e^{-ka·(t-\tau )}\hfill & ;t>\tau \hfill \end{array}$$ (13)

where F is bioavailability, fr is the fraction of the dose undergoing first-order absorption (k_a), and τ is the time period of zero-order input. This input function is based on the complex absorption profile due in part to the significant role of the lymphatics in the uptake of proteins administered subcutaneously.^50,51)

Fig. 3.

PK/PD model diagram for the absorption and disposition of rHuEpo and drug effects on reticulocytes (RET), red blood cells (RBC), and hemoglobin concentrations (Hb)

Model is described by Equations 11–17 and symbols are defined in the text.

The catenary PD model (Fig. 3) contains two precursor compartments (P₁ and P₂) linked to reticulocyte (RET), red blood cell (RBC), and hemoglobin (Hb) compartments. This model mimics the process of erythropoiesis from bone marrow to blood, and is based on cell life span concepts integrated into indirect response models for drugs that alter the generation of natural cells.⁵²⁾ Cells are assumed to be produced at a constant rate, circulate for a specific duration of time (T_i), and are then eliminated from the system not by a first-order process, but at the same rate as the input, delayed by the cell life span (senescence or conversion to another cell type). The precursor compartments represent early progenitor cells and erythroblasts, and T_P1 and T_P2 are the average times taken for cells to differentiate. The rates of change of the reticulocyte (RET) and mature RBC (RBC_M) counts are described by:

$$\frac{dRET}{dt}=k_{in}·S(t-T_{p1}-T_{p2})·S(t-T_{p2})·I(t-T_{p1}-T_{p2})-k_{in}·S(t-T_{p1}-T_{p2}-T_{\mathit{\text{RET}}})·S(t-T_{p2}-T_{\mathit{\text{RET}}})·I(t-T_{p1}-T_{p2}-T_{\mathit{\text{RET}}})$$ (14)

$$\frac{{dRBC}_M}{dt}=k_{in}·S(t-T_{p1}-T_{p2}-T_{\mathit{\text{RET}}})·S(t-T_{p2}-T_{\mathit{\text{RET}}})·I(t-T_{p1}-T_{p2}-T_{\mathit{\text{RET}}})-k_{in}·S(t-T_{p1}-T_{p2}-T_{\mathit{\text{RET}}}-T_{\mathit{\text{RBC}}})·S(t-T_{p2}-T_{\mathit{\text{RET}}}-T_{\mathit{\text{RBC}}})·I(t-T_{p1}-T_{p2}-T_{\mathit{\text{RET}}}-T_{\mathit{\text{RBC}}})$$ (15)

with T_RET and T_RBC as the average life span of these cells, and k_in is the zero-order production rate constant. The initial conditions for Equations 14 and 15 are RET₀ and RBC₀–RET₀, where RET₀ and RBC₀ are baseline measurements. The stimulation function S(t) was defined as:

$$S(t)=1+\frac{S_{\text{max}}·A_p(t)/V_p}{{SC}_{50}+A_p(t)/V_p}$$ (16)

where S_max is the maximal stimulation factor and SC₅₀ is the rHuEpo concentration resulting in 50% of S_max. Hemoglobin concentrations were calculated as the product of the mean corpuscular hemoglobin (MCH; measured) and sum of RET and RBC_M (Eqs. 14, 15). A counter regulation feedback loop is also included, I(t), driven by the difference in Hb from baseline values, and was defined as:

$$I(t)=1-\frac{I_{\text{max}}·\Delta Hb(t)}{{IC}_{50}+\Delta Hb(t)}$$ (17)

where the maximal inhibition factor (I_max) was fixed to 1, and IC₅₀ is the Hb difference from baseline producing 50% feedback inhibition.

The parameter values, their sources, and scaled-up values in humans used for the PK/PD model simulations are listed in Table 1. Inter-individual variability (IIV) for each parameter used in the Monte Carlo simulations is also reported. Volume, clearance, and first-order rate constants were scaled with allometric exponents of 1, 0.75, and −0.25. The baseline values for RET, RBC, and MCH (and their respective IIV) were considered drug and species independent and were set to literature values for humans.⁵³⁾ Life span parameters were scaled using an allometric exponent of 0.124 which was previously estimated using RBC data obtained from over 20 species.⁴⁵⁾ Only nominal variability was assigned to PK terms (10% CV%), whereas CV% values were set to 20% for S_max and 30% for sensitivity parameters (SC₅₀ and IC₅₀).

Table 1.

Pharmacokinetic and pharmacodynamic parameters of rHuEpo scaled from rats to humans

Parameter	Value	Origin	b (exponent)	Predicted Human Parameter	IIV (%CV)
Pharmacokinetics
Vmax (IU/hr)	0.69	Rat	0.75	37	10
Km (mIU/mL)	67.3	Rat	n.s.	67.3	10
Vp (L)	0.0212	Rat	1	4.28	10
kel (1/hr)	0.224	Rat	−0.25	0.0594	10
ka (1/hr)	0.146	Rat	−0.25	0.0387	10
F	0.586	Rat	n.s.	0.586	10
fr	0.322	Rat	n.s.	0.322	0
kpt (1/hr)	0.171	Rat	−0.25	0.0453	10
ktp (1/hr)	0.148	Rat	−0.25	0.0392	10
τ (hr)	13.5	Rat	n.s.	13.50	0
Pharmacodynamics
Smax	1.87	Rat	n.s.	1.87	20
SC50 (mIU/mL)	65.4	Rat	n.s.	65.4	30
IC50 (g/dL)	1.79	Rat	n.s.	1.79	30
RET0 (×109/L)	48	Human	n/a	48	20
TP1 (hr)	43	Rat	0.124	83	0
TP2 (hr)	3.02	Rat	0.124	5.83	10
TRET (hr)	72.3	Rat	0.124	140	10
TRBC (hr)	1440	Rat	0.124	2780	10
RBC0 (×109/L)	4500	Human	n/a	4500	4
MCH (pg/cell)	30	Human	n/a	30	1.4

n/a, not applicable; n.s., not scaled; RET₀ and RBC₀ are baseline measurements

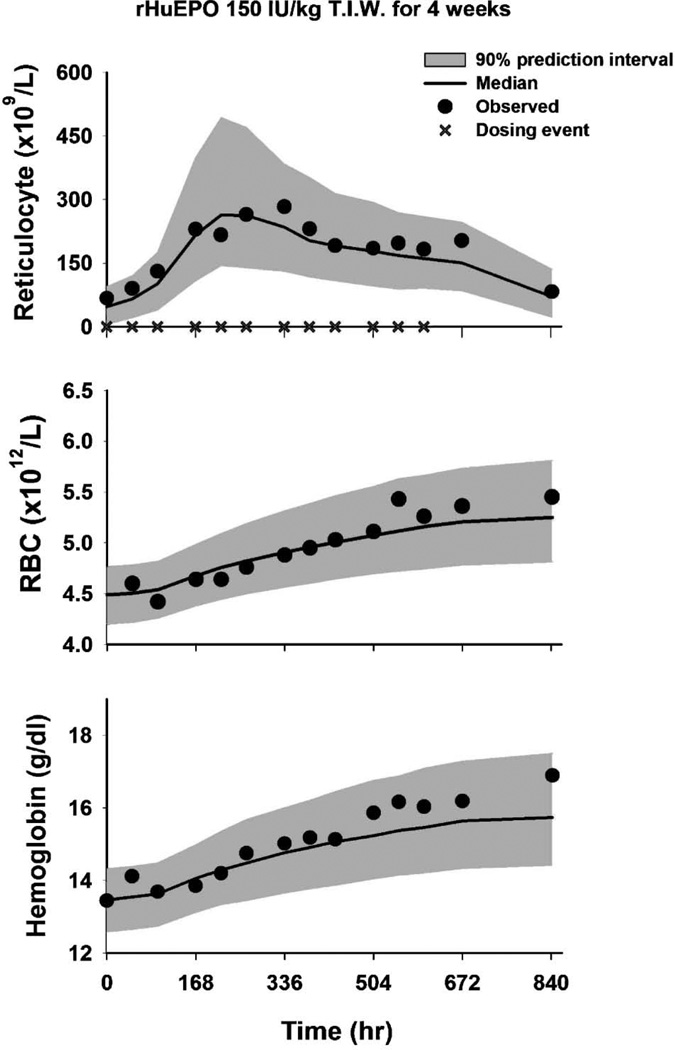
Monte Carlo simulations were conducted using ADAPT II (Biomedical Simulation Resource, USC, Los Angeles), and mean observed data and model predicted profiles are shown in Figure 4. The predicted values of the three biomarkers are in good agreement with observed data, which fall well within the 90% prediction interval (gray areas). The successful scaling of the rat PK/PD model of rHuEpo to human responses demonstrates how basic allometric principles and preclinical data may be integrated using mechanism-based models to make useful predictions. It is important to recognize that the biomarkers of drug activity and preclinical PK/PD models must be meaningful across species. The likelihood of these appears to be greater for macromolecules as compared to small molecules;⁵⁴⁾ however, a similar interspecies scaling approach was shown to apply to two 5-HT_1A receptor agonists.⁵⁵⁾

Fig. 4.

Simulated profiles for reticulocyte, red blood cell (RBC), and hemoglobin concentrations (Hb) in response to rHuEpo given as 150 IU/kg SC three times weekly to healthy male volunteers

The symbols represent original data from Ramakrishnan et al. ³⁴⁾ Solid lines are median predicted profiles using a PK/PD model developed in rats (Fig. 3) and allometrically scaled parameters (Table 1). Shaded regions represent the 90% prediction intervals.

In summary, the scaling of pharmacodynamic data relies heavily on the ability to predict and integrate the fundamental processes controlling drug exposure (pharmacokinetics), drug action (pharmacology), and interactions with physiological systems. Preclinical data and in vitro bioassays can provide important insights into these properties, especially as pharmacodynamic parameters tend to be species independent; however, it is important to verify whether measurements of drug effects are meaningful across species. Notwithstanding the limitations of prospective allometry, such power law relation-ships have proven useful in scaling-up physiological turnover processes and PK properties for many drugs. New techniques are needed to identify conditions under which allometric scaling may or may not be appropriate in PK/PD models. Physiologically-based PK models will likely become commonplace given their intrinsic potential for projecting human PK properties from in vitro and in silico measurements and data obtained in other species. Animal studies can provide preliminary data for the development of mechanism-based PK/PD models, which will continue to evolve toward efficient descriptions of pharmacological systems. Such models offer the best approach toward effectively combining and interpreting the major determinants of drug action across species.