Subpopulation-specific Confidence Designation for More Informative Biomedical Classification

Abstract

Objective

Although classification algorithms are promising tools to support clinical diagnosis and treatment of disease, the usual implicit assumption underlying these algorithms, that all patients are homogeneous with respect to characteristics of interest, is unsatisfactory. The objective here is to exploit the population heterogeneity reflected by characteristics that may not be apparent and thus not controlled, in order to differentiate levels of classification accuracy between subpopulations and further the goal of tailoring therapies on an individual basis.

Methods and materials

A new subpopulation-based confidence approach is developed in the context of a selective voting algorithm defined by an ensemble of convex-hull classifiers. Populations of training samples are divided into three subpopulations that are internally homogeneous, with different levels of predictivity. Two different distance measures are used to cluster training samples into subpopulations and assign test samples to these subpopulations.

Results

Validation of the new approach’s levels of confidence of classification is carried out using six publicly available datasets. Our approach demonstrates a positive correspondence between the predictivity designations derived from training samples and the classification accuracy of test samples. The average difference between highest- and lowest-confidence accuracies for the six datasets is 17.8%, with a minimum of 11.3% and a maximum of 24.1%.

Conclusion

The classification accuracy increases as the designated confidence increases.

1. Introduction

Ensemble learning is the process by which multiple classifiers are combined to solve a problem in computational intelligence [1]. The idea of ensemble learning is to increase prediction accuracy by combining the strengths of a collection of simpler base models [2]. In binary classification problems, majority voting among ensemble members is a common approach for combining class labels to predict the class of an unknown sample [3]. A comprehensive review of ensemble-based methods is provided by Rokach [4].

In addition to simply obtaining a decision (i.e., prediction or classification) from a classifier, it is useful to have a measure of confidence in that decision [5]. With simple majority voting, the very structure of the vote naturally allows assigning a degree of confidence to a particular decision, in that high agreement among ensemble members tends to be associated with high confidence and vice versa [1]. This is related to using ranges of predictions expressed on a probability scale as indicators of prediction confidence, e.g., 0.7 – 1.0 or >0.8 implies high confidence [6, 7]. Of course, a statistical lower confidence limit can be calculated for each decision assuming a binomial distribution; however, its utility will depend on both the size of the ensemble and the degree of independence among the ensemble members. It is also possible to estimate the posterior probability of the class chosen by the ensemble for any given test instance, and use that estimate as the confidence measure for that instance [8]. Alternatively, empirical measures of performance calculated over a set of representative samples are good indicators of the confidence that can be placed in an ensemble’s decisions. In binary classification problems, for example, the positive predictive value and negative predictive value, which arise from a frequentist interpretation of Bayes’ theorem, give overall measures of confidence in predictions made by the ensemble. These two measures, along with overall accuracy, sensitivity and specificity, are common performance measures for assessing the degree of confidence that can be placed in a classifier’s decisions.

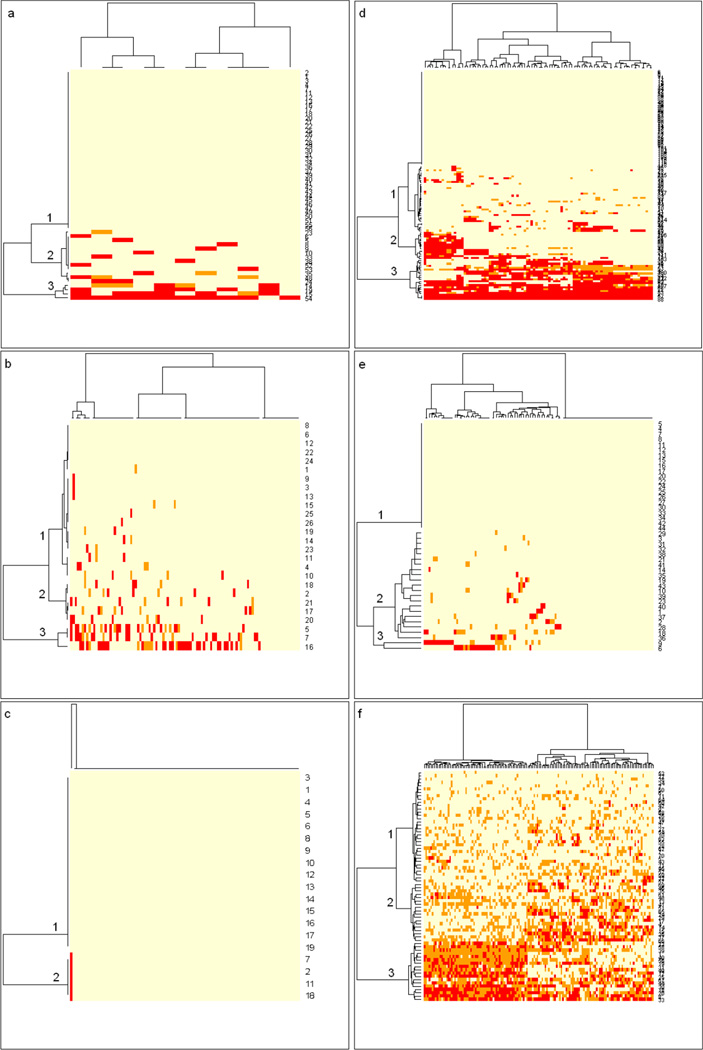
In this paper, we develop a subpopulation basis for calculating the performance measures commonly used to assess majority-voting-based classifications of test instances by ensembles. In particular, we derive a method for assigning subpopulation-specific levels of confidence (highest, intermediate, or lowest) to classifications of unknown samples. We assume that the population of samples being classified is heterogeneous, but can be divided into subpopulations that are internally homogeneous. The heat maps in Fig. 1, to be described fully in section 3, illustrate the approach. Each heat map resulted from a single run of the convex-hull, selective-voting algorithm of Kodell et al. [9] on an approximate 90% sample from one of six datasets in a 10-fold cross-validation. The colored rectangular spots on the heat maps represent voting accuracies of an ensemble of classifiers used to classify a training set of samples. The classifiers in an ensemble are represented by the columns, and the samples in the training set are represented by the rows, the latter having been clustered into either two or three subpopulations according to voting accuracies. A correct vote by an ensemble member is indicated by light yellow, an incorrect vote by red, and an abstention by orange. Dendrograms produced by hierarchical clustering row-wise and column-wise are shown. The tree that represents the subpopulations of samples is shown on the left side of the heat map and the tree that represents the ensemble of classifiers is shown on the top of the heat map. As the heat maps indicate, subpopulation 1 has the highest accuracy, subpopulation 2 has intermediate accuracy, and subpopulation 3 (if available) has the lowest accuracy.

Fig. 1.

Each heat map represents training samples from one representative block of one 10-fold CV, where panels a (colon cancer), b (non-classic glioma), and c (classic glioma) were produced using Method 1 and panels d (gene imprinting), e (soft tissue tumors), and f (breast cancer) were produced using Method 2. The colored rectangular spots on each heat map represent voting accuracies of an ensemble of classifiers used to classify the training set data. The classifiers in the ensemble are represented by the columns, and the samples in the training set are represented by the rows. A correct vote by an ensemble member is indicated by light yellow, an incorrect vote by red, and an abstention by orange. Dendrograms resulting from hierarchical clustering column-wise and row-wise are shown. The tree that represents the subpopulations of samples, clustered into either two or three subpopulations according to voting accuracies, is shown on the left side of the heat map and the tree that represents the ensemble of classifiers is shown on the top of the heat map.

With regard to practical application in a clinical setting, knowing the level of predictivity associated with a patient’s algorithm-derived diagnosis, prognosis, or predicted response to treatment can help attending physicians to choose among treatment options. For example, even if a diagnostic test based on gene expression may not have sufficiently high overall predictive accuracy for general use on all patients, it could still be used selectively for subpopulations of patients for which it does have high accuracy. Already, the selective voting algorithm of Kodell et al. [9] produces individualized classifications of test samples by virtue of not requiring every ensemble member to vote on every sample. The addition of subpopulation-specific characterizations of predictivity to the selective-voting classifications represents another step toward the goal of personalized medicine.

2. Methods

2.1 Classification algorithm

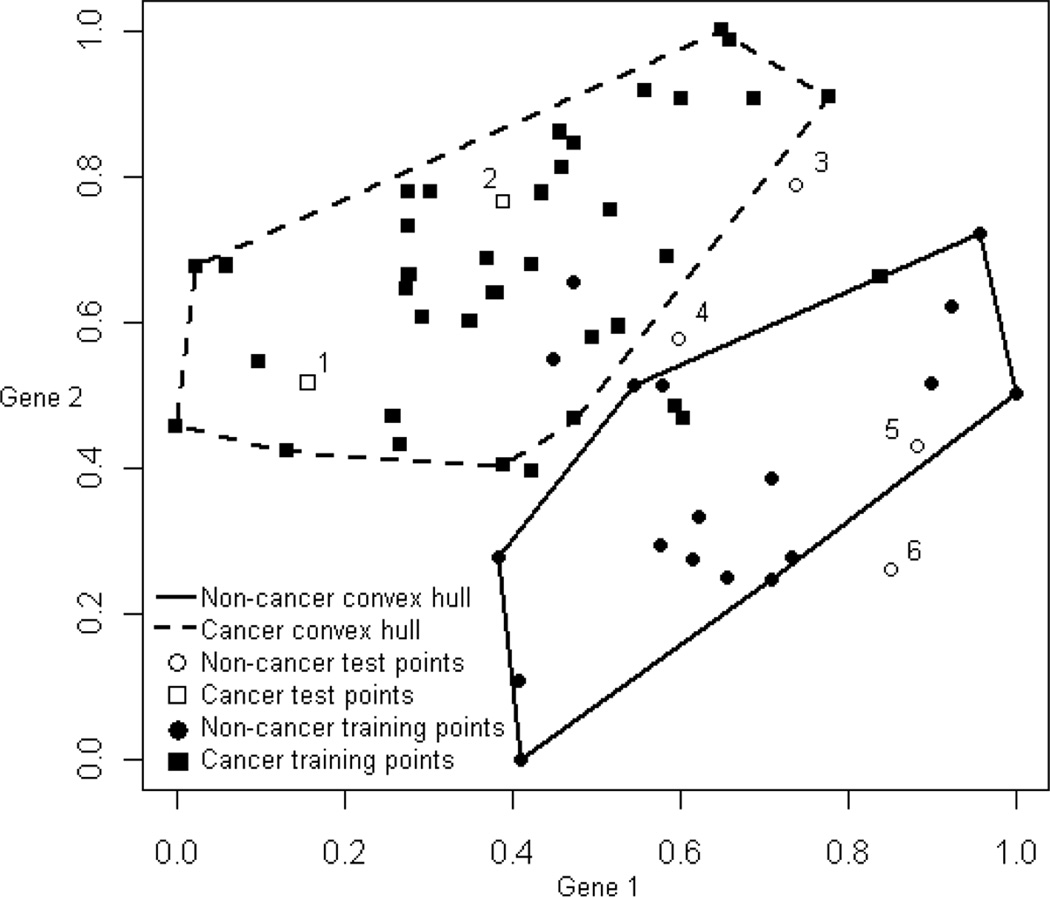
We use the convex-hull, selective-voting algorithm developed by Kodell et al. [9] as our ensemble classifier. Briefly, for each selected pair of predictor variables, the algorithm forms two two-dimensional convex hulls of training points, one for each of the two classes (e.g., positive and negative). These convex hulls are pruned to achieve separation of classes, and each such pair of pruned positive and negative convex hulls serves as a base classifier in the ensemble. A base classifier casts a vote on a test point only if the test point falls inside or behind one of the two pruned convex hulls. This “selective voting” by members of the ensemble gives different vote totals among the test samples. A simple majority of voters decides the classification of a test sample, and some test samples may remain unclassified due to receiving zero votes or tied votes. The algorithm allows several options, including how many bi-variate regression models to consider when choosing pairs of predictor variables as classifiers based on regression R² values, whether to use more- or less-aggressive pruning of convex hulls, and whether to keep all qualified classifiers or only the unique ones. There are also two thresholds that must be met in order for a classifier to be qualified. Default values of these thresholds are used in this paper [9]. Fig. 2 shows two resulting reduced convex hulls after pruning, one for each class, formed by a selected pair of genes from [10] (dataset to be described fully in section 2.5.1). Training points in this figure are represented by filled symbols while test points are represented by unfilled symbols. The test points are labeled 1–6 and are superimposed for illustration purposes only; they are not used to train the algorithm.

Fig. 2.

Two-dimensional pruned convex hulls determined by normalized expression values of two representative genes for 56 colon training samples classified as cancerous or noncancerous. Training points are represented by filled symbols while test points are represented by unfilled symbols. The test points are labeled 1–6 and are superimposed for illustration purposes only; they are not used to train the algorithm. This ensemble member votes correctly on test points 1, 2, 5 and 6, but does not vote on test points 3 and 4. See Kodell et al. [9] for the original figure and a full explanation.

2.2 Identifying subpopulations of training samples

Although conceptually one could divide the heterogeneous population into any number of homogeneous subpopulations, here we restrict attention to exactly three subpopulations, corresponding to highest, intermediate, and lowest predictivity. Unless the population of samples is quite large, it seems impractical to subdivide it into more than three subpopulations. This approach is like that of Tomlins et al. [11], who stratified men with elevated PSA levels into three score groups using tertiles of the distribution of the sum of urine TMPRSS2:ERG fusion transcript and urine PCA3, and showed that prostate cancer diagnosis percentages corresponded to the designations of lowest, intermediate and highest scores. It is also related to the method of Tong et al. [6], but here, instead of using the prediction value as a measure of confidence, we use it for subpopulation assignment (see next section) and measure the confidence on a subpopulation basis. If the samples can be clustered into only two subpopulations, we drop the highest-confidence designation and we designate the two as having intermediate and lowest confidence. If there should be only a single cluster, then we designate it as having lowest confidence only.

We consider two different strategies of clustering training samples into subpopulations, clustering according to distances between accuracy margins and clustering according to Euclidean distances between accuracy vectors. An accuracy margin (AM) for a training sample is the net number of classifiers in the ensemble that voted correctly on that sample. An accuracy vector (AV) for a training sample is the vector having one element for each classifier in the ensemble, where each element indicates whether the classifier voted correctly (1), voted incorrectly (−1) or abstained from voting (0) on that sample. For both clustering strategies, the hierarchical clustering method of Ward [12] is used to form homogeneous subpopulations. We also cluster the base classifiers in order to have better organized heat maps, but it is not a requirement; for this we also use the Ward method in R [13].

An implicit assumption underlying the identification of subpopulations using similarity of voting accuracies for clustering is that samples for which ensemble members have similar voting accuracies (whether high or low) may reasonably be expected to have similar biological characteristics in terms of diagnosis, prognosis, and response to treatment. Put another way, if the predictor variables that define the base classifiers in an ensemble are truly predictive of a biological outcome, then they ought to have similar accuracies for classifying samples with respect to that outcome within a subpopulation. Note that high voting agreement need not imply high accuracy or high confidence. Thus, if subpopulations were defined based on similarity of voting margins or vote vectors (instead of accuracies), they might be comprised of subjects with heterogeneous classification accuracies, which would not lead to meaningful confidence assignments. In addition, even if homogeneous with respect to accuracy, the subpopulations might have a tendency not to include members of both classes, which would defeat the purpose of our method for clinical use.

2.3 Assigning test samples to subpopulations

Clearly, we do not know the accuracy of the selective voting algorithm for test samples. So, although subpopulations are defined in terms of voting accuracies of training samples, we cannot assign test samples to subpopulations on the basis of voting accuracies. However, we do know that for training samples, absolute values of accuracy margins are identical to absolute values of vote margins (hereafter, absolute vote margins). So, for subpopulations that are defined by clustering according to distances between accuracy margins, we use a test sample’s absolute vote margin (VM) to assign it to a subpopulation. We call this Method 1. If the absolute vote margin is within the range of the accuracy margins of a certain subpopulation, we assign the test sample to that subpopulation. If a test sample’s absolute vote margin lies outside the ranges of all the subpopulations, we assign it to the closest subpopulation in terms of the minimum average distance between the test sample’s absolute vote margin and the training samples’ accuracy margins. In case of tied minimum average distances, we assign the sample to the subpopulation with lower accuracy margins.

For subpopulations that are identified by clustering according to Euclidean distances between accuracy vectors, we use a test sample’s vote vector (VV) to assign it to a subpopulation. We call this Method 2. Although, by design, accuracy vectors are similar among training samples within a given subpopulation, vote vectors will not be similar within subpopulations because there are two different classes of training samples in each subpopulation. So, we assign the test sample to the closest subclass within any of the subpopulations, where we use the minimum average Euclidean distance between vote vectors to define closest. If minimum average distances are tied between subclasses of different subpopulations, we assign the test sample to the tied subpopulation with lower accuracy margins. If minimum average distances are tied between subclasses of the same subpopulation, we assign the test sample to the subpopulation with lowest accuracy margins.

To be noted, test samples that receive zero votes or tied votes, hence remain unclassified by the selective voting algorithm, are not assigned to any subpopulation.

2.4 Assessing subpopulation-specific confidence

To assess the degree to which predictions differ among the three subpopulations, we use twenty runs of 10-fold cross-validation (CV) for each of several publicly available datasets. As a matter of convenience we designate class 1 as negative and class 2 as positive in each dataset, although the two classes in the datasets we analyze are not necessarily positive and negative. For each dataset, we calculate the accuracy (ACC), sensitivity (SEN), specificity (SPC), positive predictive value (PPV) and negative predictive value (NPV). ACC is the overall proportion of correct predictions, SEN is the proportion of correct predictions among true positives (class 2), SPC is the proportion of correct predictions among true negatives (class 1), PPV is the proportion of correct predictions among predictions of class 2 and NPV is the proportion of correct predictions among predictions of class 1. We calculate these performance measures for the total population of samples in a dataset, and for each of the three subpopulations (highest confidence, intermediate confidence, and lowest confidence) in order to demonstrate the relationship between the performance measures and the confidence designations (i.e., the performance measures increase as the confidence increases). We also use heat maps to reinforce the performance-confidence relationship.

In addition to the usual performance measures just described, we also calculate the average percentage of known positive (class 2) samples (denoted POS) among the test samples assigned to each subpopulation. Hence, POS/100 represents the subpopulationspecific empirical class 2 probability, and gives insight into how the subpopulations differ with respect to the proportions of class 1 and class 2 samples. Unlike many ensemble classifiers (e.g., tree-based methods), the method of Kodell et al. [9] is not able to provide estimates of class probabilities for individual subjects, other than via the voting proportions themselves which are said to fail in this regard [2]. Estimates of individual class probabilities can be important in their own right, and when averaged in an ensemble can lead to improved classification performance compared to simple majority voting in ensembles like bagged classification trees [2]. Importantly, the method proposed here can provide estimates of subpopulation-specific class probabilities via the ratios of the number assigned to each class in a subpopulation to the total number classified in that subpopulation.

2.5 Analysis of publicly available datasets

We use six publicly available datasets to demonstrate the performance of the subpopulation-confidence method, and to compare the two approaches to defining confidence-specific subpopulations. These are the colon cancer data of Alon et al. [10], the two sets of glioma data (classic and non-classic) of Nutt et al. [14], the gene imprinting data of Greally [15], the soft tissue tumor data of West et al. [16], and the breast cancer data of van’t Veer et al. [17]. To implement the convex-hull selective-voting algorithm, each predictor in each dataset is first mapped to the unit interval by subtracting the minimum value of that predictor among the samples in the dataset and dividing by the difference between the maximum and minimum values.

2.5.1 Colon cancer diagnosis

Alon et al. [10] presented gene expression data on 62 colon tissue samples, 40 samples being from cancerous colon tissue (class 2) and 22 samples being from normal colon tissue (class 1). An initial set of 6500 genes whose expression levels were measured on an Affymetrix oligonucleotide array was reduced by Alon et al. to 2000 genes having the highest intensity levels across the 62 tissue samples. The idea is to use the high-dimensional genomic data to screen samples for colon cancer. We used a pre-processed version of Alon’s data involving log₂-transformation, mean subtraction and standard-deviation division. We did not remove three control genes that were replicated four times each. We downloaded the dataset of raw expression values from http://microarray.princeton.edu/oncology/affydata/index.html (accessed: 10 June 2002).

2.5.2 Distinguishing between glioblastomas and anaplastic oligodendrogliomas

Nutt et al. [14] presented data on both classic and non-classic malignant gliomas. As the authors explained, histological diagnosis is reliable for distinguishing classic glioblastomas from anaplastic oligodendrogliomas, which is important because they follow markedly different clinical courses. However, non-classic lesions are difficult to classify by histological features. Nutt et al. presented microarray data on expression of approximately 3900 genes for 21 classic gliomas (14 glioblastomas: class 1; 7 anaplastic oligodendrogliomas: class 2) and on approximately 2500 genes for 29 non-classic gliomas diagnosed histologically (14 glioblastomas: class 1; 15 anaplastic oligodendrogliomas: class 2). While Nutt et al. used a model built on the classic gliomas to classify the non-classic gliomas in order to compare survival distributions between the model and the histological classifications, here we take the histological diagnoses of both types of gliomas as accurate and simply try to duplicate them with our algorithm. The data are available at http://www.broadinstitute.org/cgi-bin/cancer/publications/pubpaper.cgi?mode=view&paperid=82 (Accessed: 10 February 2012). Following Nutt et al. [14], we removed genes whose expression levels varied < 100 units between samples and genes whose expression varied < 3-fold between any two samples, leaving 3917 genes for classic gliomas. For non-classic gliomas, 2567 genes were kept after we followed Nutt’s preprocessing procedure, and removed genes across which more than one sample had the same minimum value.

2.5.3 Prediction of imprinted genes for predisposition to disease

Greally [15] described the first characteristic sequence parameter that discriminates imprinted regions, and provided data on 131 samples along with 1446 predictors at http://greallylab.aecom.yu.edu/~greally/imprinting_data.txt (Accessed: 1 September 2006), which were downloaded from the UCSC Genome Browser (http://genome.ucsc.edu; Accessed: 1 September 2006). Imprinted genes give rise to numerous human diseases because of the silencing of expression of one of the two homologs at an imprinted locus. Hence, prediction of gene imprinting predicts predisposition to disease. The dataset consists of 43 imprinted genes (class 2) and 88 non-imprinted genes (class 1). Here we used the reduced dataset used by Ahn et al. [18] in which the set of predictors was reduced to 1248 by eliminating those with identical values for more than 98% of the samples.

2.5.4 Distinguishing between DTF-type and SFT-type soft tissue tumors

West et al. [16] presented data on 57 soft tissue tumors, of which 10 were desmoid-type fibromatoses (DTF), 13 were solitary fibrous tumors (SFT), and 34 were other soft tissue tumors of various types. West et al. used gene-expression data to group the other tumors into expression profiles that matched either the DTF profile or the SFT profile. We used a preprocessed version of the dataset of West et al. [16], previously analyzed by Lee et al. [19], which consisted of 4148 genes, obtained from http://smd.stanford.edu/cgi-bin/publication/viewPublication.pl?pub_no=436 (Accessed 22 February 2012). We restricted our attention to 24 DTF-type soft tissue tumors (class 1) and 24 SFT-type soft tissue tumors (class 2), which we derived from Fig. 1 of West et al. [16], after deleting tumors of a certain type that appeared in both classes (leiomyosarcomas: LMS).

2.5.5 Breast cancer prognosis and treatment

van’t Veer et al. [17] presented a gene-expression-based classification analysis of 78 primary breast cancer patients who had undergone surgery. There were 34 patients classified as having a poor prognosis (developed distant metastasis within 5 years: class 2) and 44 patients classified as having a good prognosis (did not develop distant metastasis within 5 years: class 1). The idea is to classify patients according to prognostic status so that patients predicted to have a good prognosis might be spared post-surgery chemotherapy. We used fold changes and p-values provided by van’t Veer et al. on 24,481 genes to select 4741 genes that had no missing values and had at least a two-fold difference and a p-value less than 0.01 in more than 3 tumor samples out of 78. We downloaded the log₁₀-transformed expression values and p-values from http://www.rii.com/publications/2002/vantveer.html (accessed: 17 February 2006).

3. Results

The results for the six datasets are presented separately in Tables 1–6. The first row of each table shows the overall performance of the selective-voting algorithm based on 20 repetitions of 10-fold CV. Column 1 of each table designates the subpopulation confidence, where Method ‘corresponds to ‘clustering training samples according to AM and assigning test samples according to VM’, and Method 2 corresponds to ‘clustering training samples according to AV and assigning test samples according to VV’ (see section 2.2). N (column 2) is the average number of samples in each subpopulation among the total samples that were classified by the selective-voting algorithm across the 20 repetitions, and POS (column 3) indicates the average percentage of positive (class 2) samples among the N samples (i.e., POS/100 is the empirical subpopulation-specific class 2 probability and 1-POS/100 the class 1 probability). The performance measures in columns 4–8 are defined in section 2.4. The same random seed was used in the 20 repetitions of 10-fold CV for the Overall results and for Methods 1 and 2 in each table, but different seeds were used for different tables.

Table 1.

Performance of confidence methods for colon cancer (62 samples: 22 class 1, 40 class 2)^a.

LEVEL	N	POS	ACC	SEN	SPC	PPV	NPV
Overall	61.0(0.9)	65.1(1.3)	90.2(1.4)	91.9(1.0)	86.9(3.3)	92.9(1.8)	85.2(2.0)
Method 1
Highest	20.0(2.4)	82.7(4.3)	94.7(2.7)	96.3(3.2)	86.8(16.2)	97.4(3.0)	84.5(13.8)
Intermediate	36.3(3.0)	60.0(3.6)	89.5(2.2)	90.8(4.0)	87.5(4.8)	91.7(2.7)	86.7(4.9)
Lowest	4.8(1.7)	30.3(17.1)	76.9(18.3)	52.3(42.6)	85.1(18.4)	59.4(42.1)	83.3(16.5)
Method 2
Highest	51.5(2.6)	70.9(1.5)	92.0(1.5)	94.1(1.9)	86.4(4.9)	94.5(1.7)	86.0(4.1)
Intermediate	4.9(1.0)	26.2(21.2)	88.5(12.7)	78.9(31.2)	90.7(15.6)	78.9(31.2)	92.8(12.0)
Lowest	4.7(1.8)	38.6(19.3)	74.6(20.8)	57.8(36.9)	81.3(23.4)	70.2(25.5)	79.1(21.3)

^aThe first row shows the overall performance of the selective-voting algorithm based on 20 repetitions of 10-fold CV. Column 1 designates the subpopulation confidence, where Method 1 corresponds to ‘clustering training samples according to AM and assigning test samples according to VM’, and Method 2 corresponds to ‘clustering training samples according to AV and assigning test samples according to VV’ (see section 2.2). N (column 2) is the average number of samples in each subpopulation among the total samples that were classified by the selective-voting algorithm across the 20 repetitions, and POS (column 3) indicates the average percentage of positive (class 2) samples among the N samples. The performance measures in columns 4–8 are defined in section 2.4. The numbers in parentheses are standard deviations.

Table 6.

Performance of confidence methods for breast cancer (78 samples: 44 class 1, 34 class 2) ^a.

LEVEL	N	POS	ACC	SEN	SPC	PPV	NPV
Overall	77.7(0.7)	43.5(0.2)	67.8(2.9)	60.5(4.4)	73.5(3.1)	63.7(3.6)	70.8(2.6)
Method 1
Highest	16.2(3.7)	25.8(8.9)	76.6(8.7)	72.2(25.0)	78.5(5.5)	51.9(14.9)	89.1(11.5)
Intermediate	48.4(6.0)	49.4(4.4)	67.9(4.2)	61.5(6.1)	74.1(4.3)	69.7(5.5)	66.4(5.9)
Lowest	13.1(4.3)	43.8(10.5)	58.7(11.4)	54.2(19.8)	60.8(19.7)	52.1(15.6)	63.7(14.6)
Method 2
Highest	44.9(3.1)	42.4(3.9)	71.3(4.1)	62.1(7.9)	78.1(4.9)	67.58.4)	73.8(4.0)
Intermediate	16.9(3.9)	46.0(8.3)	66.8(9.7)	63.9(15.6)	69.8(14.0)	64.3(14.3)	69.4(14.0)
Lowest	16.0(2.8)	43.8(12.6)	60.0(12.5)	52.2(19.2)	65.5(15.3)	53.1(22.5)	64.1(13.0)

^aPlease refer to footnote for Table 1.

3.1 Colon cancer diagnosis – results

For the colon cancer data, less-aggressive pruning was used to obtain separation of convex hulls, and only unique qualified pairs of predictors from the 100 models with highest regression R² values were retained as base classifiers. The choice of this configuration gave the highest accuracy for this dataset according to [9], although achieving the highest level of accuracy by the selective-voting algorithm itself is not the main focus of this paper.

Fig. 1a shows the heat map of training samples for one block of 10-fold CV using Method 1. A total of eleven unique classifiers (columns) were retained for this block. Three subpopulations with highest, intermediate and lowest predictivity (labeled as branches 1, 2 and 3 respectively) are identified on the left side of the heat map. The subpopulation with highest predictivity (branch 1) consists of training samples having the highest accuracy margins (all cells are in yellow indicating 100% accuracy). Branch 3 (subpopulation with lowest predictivity) consists of four training samples at the very bottom of the heat map. For this subpopulation, samples received between 1 and 6 correct votes, with many incorrect votes and a few abstentions. The last training sample (id 54 shown on the right side of the heat map), received one correct vote (cell in yellow) from the second classifier from the right and ten incorrect votes (cells in red) from the rest of the classifiers, so the accuracy margin of this sample is −9 according to Method 1. These four samples were clustered together due to their low vote margins, that is, relatively large proportions of incorrect votes. By design, the performance of the classifiers in branch 2 (subpopulation with intermediate predictivity) was in between that of branch 1 and branch 3. Samples in branch 2 did receive abstentions and incorrect votes, but the number of mistakes was less than the number that occurred in branch 3.

For Method 1, subpopulation accuracy, denoted by ACC, increases as the subpopulation confidence increases (Table 1). The highest-confidence subpopulation has the highest ACC (94.7%) and the lowest-confidence subpopulation’s ACC (76.9%) is much below the overall selective-voting ACC (90.2%). The majority of test samples were assigned to the intermediateconfidence subpopulation (average N=36.3) and its ACC (89.5%) is comparable to the selective-voting algorithm’s overall ACC (90.2%). For Method 2, the monotonically increasing pattern between ACC and its subpopulation confidence is preserved. In contrast to Method 1, a large majority of test samples were assigned to the highest-confidence subpopulation (average N=51.5).

3.2 Distinguishing between glioblastomas and anaplastic oligodendrogliomas – results

For the non-classic glioma data set, less-aggressive pruning was used to obtain separation of convex hulls. Fig. 1b shows the heat map of training data for one block of 10-fold CV using Method 1. All qualified sets of classifiers from the 100 models with highest R² values were retained as base classifiers. Branches 1, 2 and 3 show various degrees of predictivity among the subpopulations of highest, intermediate and lowest confidence.

For both methods, the monotonically increasing pattern between ACC and its subpopulation confidence is preserved (Table 2). The overall selective-voting ACC is 78.7%, which is in between the ACC of the intermediate-confidence subpopulation and the ACC of the lowest-confidence subpopulation for Method 1 and in between the ACC of the highestconfidence subpopulation and the ACC of the intermediate-confidence subpopulation for Method 2. For Method 1, a large majority of the test samples were assigned to the lowest-confidence subpopulation (average N=22.8) with 76.4% ACC. For Method 2, in contrast to Method 1, most test samples were assigned to the highest-confidence subpopulation (average N=21.5) and its ACC is 83.5%.

Table 2.

Performance of confidence methods for non-classic glioma (29 samples: 14 class 1, 15 class 2)^a.

LEVEL	N	POS	ACC	SEN	SPC	PPV	NPV
Overall	28.8(0.4)	52.1(0.8)	78.7(5.3)	82.3(7.9)	74.7(6.1)	78.0(4.9)	80.1(7.4)
Method 1
Highest	0.4(0.5)	85.7(37.8)	100.(0.0)	100.(0.0)	100.(0.0)	100.(0.0)	100.(0.0)
Intermediate	5.7(1.8)	57.4(19.7)	86.3(12.7)	79.6(27.2)	93.5(14.2)	93.4(13.2)	81.8(21.2)
Lowest	22.8(1.6)	50.9(5.5)	76.4(6.4)	81.7(10.3)	70.9(9.1)	74.5(7.3)	79.3(10.5)
Method 2
Highest	21.5(1.8)	53.4(5.5)	83.5(3.9)	87.6(5.2)	79.2(7.0)	82.8(5.8)	84.5(7.3)
Intermediate	4.3(1.7)	36.5(24.8)	67.1(27.6)	69.8(39.0)	65.1(28.2)	49.7(40.1)	81.7(23.5)
Lowest	3.1(1.4)	60.1(31.3)	64.3(30.8)	56.3(40.8)	65.6(43.9)	72.2(36.0)	48.3(39.3)

^aPlease refer to footnote for Table 1.

For the classic glioma data set, the same algorithmic configuration used for the non-classic dataset was used to generate the results in Table 3. For Method 1, all the test samples were assigned to the lowest-confidence subpopulation and therefore by design, its performance is identical to the overall performance of the selective-voting algorithm (ACC=85.2%). For the other two subpopulations, since there were no test samples assigned to them, their performance is not available (NA).

Table 3.

Performance of confidence methods for classic glioma (21 samples: 14 class 1, 7 class 2)^a.

LEVEL	N	POS	ACC	SEN	SPC	PPV	NPV
Overall	21.0(0.2)	33.4(0.4)	85.2(5.6)	72.9(9.2)	91.4(6.8)	82.4(12.2)	87.1(3.9)
Method 1
Highest	NA	NA	NA	NA	NA	NA	NA
Intermediate	NA	NA	NA	NA	NA	NA	NA
Lowest	21.0(0.2)	33.4(0.4)	85.2(5.6)	72.9(9.2)	91.4(6.8)	82.4(12.2)	87.1(3.9)
Method 2
Highest	19.8(1.2)	34.2(3.0)	86.3(6.5)	76.0(10.6)	92.0(7.0)	84.6(12.2)	87.8(5.9)
Intermediate	0.1(0.3)	0.0(0.0)	100.(0.0)	NA	100.(0.0)	NA	100.(0.0)
Lowest	1.1(1.1)	15.5(25.7)	75.0(42.7)	0.0(0.0)	78.6(42.6)	0.0(0.0)	75.0(42.7)

^aPlease refer to footnote for Table 1.

For Method 2, in contrast to Method 1 in which all the test points were assigned to the lowest-confidence subpopulation, a large majority of test samples were assigned to the highest-confidence subpopulation (average N=19.8) and very few samples were assigned to the intermediate-confidence (average N=0.1) and lowest-confidence (average N=1.1) subpopulations. The highest-confidence subpopulation’s ACC is 86.3% which is slightly better than the overall ACC (85.2%). For the intermediate-confidence subpopulation, its ACC is 100%. However only 2.1 samples (average N=0.1) across the 20 repetitions of 10-fold CV were assigned to this subpopulation, all of which were negative (average POS=0.0). The ACC of the lowest-confidence subpopulation is 75.0% which is lower than the overall ACC (85.2%) and its standard deviation is fairly large (42.7).

Fig. 1c shows the heat map for training data from one block of 10-fold CV using Method 1. Due to a large number of tied accuracy margins, only two subpopulations were identified in this block. Therefore by design, highest-confidence is not considered in this case. Branch 1, which is free of incorrect votes, is designated as having intermediate-confidence and branch 2 as having lowest-confidence. Only one base classifier did not perform with 100% accuracy on the training set.

3.3 Prediction of imprinted genes for predisposition to disease - results

For the imprinted genes data, less-aggressive pruning was used to obtain separation of convex hulls, and all qualified sets of classifiers from the 100 models with highest R² values were retained as base classifiers. Fig. 1d shows the heat map for training data from one block of 10-fold CV using Method 2. The difference between classifiers’ performance among the subpopulations is clear -- the highest-confidence subpopulation (branch 1) has only correct votes (cells in yellow) while for the lowest-confidence subpopulation (branch 3), incorrect votes (cells in red) occupy a large area, and the intermediate-confidence subpopulation (branch 2) has a mixture of correct votes, abstentions and incorrect votes. To be noted, due to the different distance measure for clustering in Method 2, the tree structures in Fig. 1d, e and f are very different from the ones in Fig. 1a, b and c obtained using Method 1.

For both methods, the monotonically increasing pattern between ACC and its subpopulation confidence is preserved as shown in Table 4 (subpopulations’ ACC in Method 1: Highest 89.0%, Intermediate 73.1%, Lowest 66.1%; in Method 2: Highest 86.2%, Intermediate 75.4%, Lowest 63.8%). The overall selective-voting ACC is 83.4%, which is in between the ACC of the highest-confidence subpopulation and the ACC of the intermediate-confidence subpopulation for both methods. A large majority of the test samples were assigned to the highest-confidence subpopulation for both methods (Method 1: average N=85.3, Method 2: average N=109.2).

Table 4.

Performance of confidence methods for gene imprinting (131 samples: 88 class 1, 43 class 2) ^a.

LEVEL	N	POS	ACC	SEN	SPC	PPV	NPV
Overall	130.8(0.4)	32.7(0.2)	83.5(1.0)	65.9(2.9)	92.1(0.9)	80.3(1.9)	84.8(1.1)
Method 1
Highest	86.2(3.8)	25.3(1.9)	89.2(1.2)	61.1(3.9)	98.6(1.4)	94.1(5.5)	88.2(0.7)
Intermediate	42.9(4.0)	46.6(4.2)	73.0(3.3)	70.5(6.4)	74.9(4.2)	71.0(4.9)	74.6(4.6)
Lowest	1.8(1.3)	65.1(39.2)	65.1(39.2)	67.9(46.4)	57.4(46.5)	70.8(40.3)	55.6(46.4)
Method 2
Highest	109.4(2.5)	29.5(1.4)	86.2(1.3)	66.8(4.0)	94.3(1.4)	83.1(3.7)	87.2(1.2)
Intermediate	10.3(2.5)	44.3(14.1)	74.8(8.9)	64.1(19.0)	84.3(16.2)	77.5(23.0)	74.9(15.0)
Lowest	11.2(2.4)	53.5(14.7)	65.1(11.9)	59.0(23.4)	72.5(20.3)	69.8(25.6)	62.7(17.0)

^aPlease refer to footnote for Table 1.

3.4 Distinguishing between DTF-type and SFT-type soft tissue tumors - results

For the soft tissue tumor data, less-aggressive pruning was used to obtain separation of convex hulls, and all qualified sets of classifiers from the 100 models with highest R² values were retained as base classifiers. Fig. 1e shows the heat map for training data from one block of 10-fold CV using Method 2. Different from the heat map of imprinted gene data in section 3.3, the overall performance of the retained classifiers for this block is better, especially the lowest-confidence subpopulation (branch 3). Also there are quite a few classifiers that do not make any mistakes across the whole set of training samples.

For Method 1, the pattern of monotonic increase between ACC and its subpopulation confidence is preserved (Table 5). For the highest-confidence and intermediate-confidence subpopulations, ACC is 100%. The majority of test samples were assigned to the lowest-confidence subpopulation (average N=32.1) and its ACC is 87.4% which is lower than the overall ACC (91.6%), as it should be. However, the pattern of monotonic increase between ACC and its subpopulation confidence is broken for Method 2; the highest-confidence subpopulation’s ACC (98.3%) is higher than overall ACC (91.6%), but the intermediate-confidence subpopulation’s ACC (57.2%) is much lower than the lowest-confidence subpopulation’s ACC (79.1%). The low subpopulation size (average N=5.1 for both) and correspondingly high standard deviations (20.8 and 18.1) may explain the apparent aberration.

Table 5.

Performance of confidence methods for soft tissue tumor (48 samples: 24 class 1, 24 class 2) ^a.

LEVEL	N	POS	ACC	SEN	SPC	PPV	NPV
Overall	47.9(0.3)	50.0(0.3)	91.6(2.6)	93.3(3.2)	90.0(3.7)	90.4(3.2)	93.2(3.0)
Method 1
Highest	2.4(1.3)	19.3(18.9)	100.(0.0)	100.(0.0)	100.(0.0)	100.(0.0)	100.(0.0)
Intermediate	13.6(2.6)	47.7(8.6)	100.(0.0)	100.(0.0)	100.(0.0)	100.(0.0)	100.(0.0)
Lowest	32.1(2.4)	52.9(3.0)	87.4(4.3)	90.4(4.9)	84.0(5.8)	86.4(5.1)	88.9(4.8)
Method 2
Highest	37.7(2.3)	50.4(2.4)	98.3(1.5)	99.3(1.8)	97.4(2.7)	97.5(2.6)	99.3(1.8)
Intermediate	5.1(1.7)	43.4(19.8)	57.2(20.8)	66.7(27.3)	50.4(28.4)	51.8(25.1)	63.6(31.8)
Lowest	5.1(1.9)	48.0(19.2)	79.1(18.1)	76.7(30.0)	77.1(34.4)	84.3(20.0)	79.4(27.3)

^aPlease refer to footnote for Table 1.

3.5 Breast cancer prognosis and treatment - results

For the breast cancer data, following [9], more-aggressive pruning was used to obtain separation of convex hulls, and all qualified sets of classifiers from the 200 models with highest R² values were retained as base classifiers.

Fig. 1f shows the heat map for training samples from one block of 10-fold CV using Method 2. In this block, the number of abstentions (cells in orange) and the number of incorrect votes (cells in red) are somewhat high across all subpopulations. For branch 3 (lowest-confidence subpopulation), the left side appears to be a mixture of abstentions and incorrect votes. For branches 1 and 2 (highest-confidence subpopulation and intermediate-confidence subpopulation), abstentions are prevalent. The high number of abstentions and incorrect votes in this dataset contribute to the low ACC of the selective-voting algorithm.

As shown in Table 6, the ACC values of the intermediate-confidence subpopulations of Method 1 (67.9%) and Method 2 (66.8%) are comparable to the ACC of selective-voting algorithm (67.8%). As expected, these values are lower than the ACC of the highest-confidence subpopulation for both methods (Method 1: 76.6%, Method 2: 71.3%), while higher than the ACC of the lowest-confidence subpopulation for both methods (Method 1: 58.7%, Method 2: 60.0%). The pattern of monotonic increase between ACC and its subpopulation confidence is preserved for both methods.

4. Discussion

The six datasets offered very different types of data for evaluating the potential of our proposed subpopulation-based method for refining the performance measures of the selectivevoting algorithm. Base-classifier voting is more consistent for classic and non-classic glioma, colon cancer, and soft tissue tumors than for gene imprinting and breast cancer. The heat maps (Fig. 1) show various degrees of predictivity for the subpopulations of training samples, e.g. an almost perfect heat map for the classic glioma dataset (Fig. 1c) vs. a messy looking heat map for the breast cancer dataset (Fig. 1f). The tree structures for Method 1 (Fig. 1a, b and c) and Method 2 (Fig. 1d, e and f) show apparent dissimilarity due to different distance measures for clustering.

The results of both subpopulation methods demonstrate the expected relationship between the performance measures and the confidence designations - the performance measures increase as the confidence increases (except for the soft tissue data using Method 2). Overall, subpopulations with the highest confidence designation performed better than the selective-voting algorithm. This is a very desirable feature for clinical practice and is especially noteworthy when large proportions of test samples are assigned to the highest confidence subpopulation (e.g. using Method 2).

Compared to subpopulations of larger size, the standard deviations for subpopulations of smaller size (a small N in Tables 1–6) tended to be higher and the lack of balance between SEN and SPC and between PPV and NPV tended to be more pronounced. In case of assignment to a subpopulation with a low PPV or NPV, a clinician may want to use other criteria to classify a test sample. Like the overall results of the selective-voting algorithm, performance measures of both methods were biased in favor of the majority class in each subpopulation (determined by the larger of POS or 100-POS) with a few exceptions, e.g., gene imprinting Method 2, lowest confidence. The values of POS/100, taken as empirical subpopulation-specific class 2 probabilities, indicate that class probabilities can differ substantially across subpopulations. Whereas, for the colon dataset POS is highest in the highest-confidence subpopulation (Table 1), the reverse is true for the gene-imprinting dataset (Table 4).

For two adjacent subpopulations of small sizes, it may be advisable to collapse them into a single subpopulation. This could be applied to the intermediate and lowest confidence subpopulations for most of the datasets using Method 2, e.g. colon cancer, intermediate (average N=4.9) and lowest (average N=4.7), which would help to reduce the variability in performance measures and would result in in-between values. If applied to the soft tissue tumor data for Method 2, intermediate (average N=5.1) and lowest (average N=5.1), the inversion of accuracy between the two subpopulations would be avoided. Subpopulations of extremely small sizes could be combined with a larger subpopulation of a higher or lower confidence level. For example, the gene imprinting subpopulation with lowest confidence by Method 1 (average N=1.8) could be combined with the subpopulation of intermediate confidence (average N=43.8), and the classic glioma subpopulation of intermediate confidence by Method 2 (average N=0.1) could be collapsed with either the highest (average N=19.8) or the lowest (average N=1.1) subpopulation.

To be noted, a collapse from 3 subpopulations to 2 as mentioned above could give a different result from predefining 2 subpopulations as clusters, depending on the tree structure and population sizes. For instance, for Fig. 4d, if we predefine the number of subpopulations for gene imprinting as 2 instead of 3, branches 1 and 2 would become one subpopulation and branch 3 would be the other. However, branch 2 appears to have more wrong votes and therefore it should probably be merged with branch 3 instead of branch 1. Also, from the results of Method 2 (Table 4), branch 1 (highest) consists of the majority of the test samples (average N=109.2), while the sizes of branch 2 (intermediate) and branch 3 (lowest) are much smaller (intermediate average N=10.6, lowest average N=11.2). Therefore, it is appealing to combine these two subpopulations, instead of combining branch 2 with a larger branch (branch 1) and leaving the small branch (branch 3) to stand alone. But, for Fig. 1e produced using Method 2, if we predefine the number of subpopulations as 2, branches 2 and 3 would be grouped as one which would match the case of merging the small-size subpopulations of intermediate (average N=5.1) and lowest confidence (average N=5.1) into one (see Table 5). As for datasets with small numbers of samples, e.g., the classic and non-classic glioma data, predefining the number of subpopulations as 2 would probably be fair and it could be the users’ choice to decide whether to collapse or not. If size differences among subpopulations are not very dramatic, e.g. breast cancer data, there might not be a need to collapse them.

As explained by Nutt et al. [14], sub-types of non-classic gliomas are more difficult to distinguish than sub-types of classic gliomas. Our analysis confirms this finding (overall nonclassic glioma ACC=78.7%, overall classic glioma ACC=85.2%); however, if we assign test samples of non-classic gliomas to training-set-based subpopulations of differing degrees of predictivity, the subpopulations having the highest predictivity can achieve the same high diagnostic accuracy as can be achieved for classic gliomas (Tables 2 and 3).

For the soft tissue tumor data of West et al. [16], if we used only samples with exact DTF and SFT designations, we achieved almost 100% accuracy using the selective-voting algorithm, which did not leave room for improving the prediction performance. Consequently, we formed two classes by using the DTF-like and SFT-like clusters of West et al. which included other types of soft tissue tumors, after removing samples with LMS which appeared in both clusters. We observed that when using Method 1, the samples classified into subpopulations with highest confidence and intermediate confidence were those with exact DTF and SFT classifications, and those classified into the lowest-confidence subpopulation were the tumors of other types, which reinforces the performance of our method.

One limitation of our approach as mentioned is that when the sizes of subpopulations are small (a small N in Tables 1–6), the results become more variable, i.e., have large standard deviations. Also, in case of a near-perfect heat map for training samples, e.g. the classic glioma data using Method 1 (Fig. 1c), there is little room for improvement on the performance measures. In this case, we speculate that if more models with lower R² values are retained as classifiers in the selective-voting algorithm, it is possible that the heat map may have a lower proportion of correct votes from the classifiers (even though the accuracy of the selective-voting algorithm may not decrease) and hence there may be some room for improvement for classifying test samples.

We should note that diversity in classifier ensembles has been shown to be a desirable property although its role is complex [18]. With ensemble diversity, one wants each individual classifier to be internally consistent across subjects in a population or subpopulation, but the ensemble of classifiers to have disagreement within subjects while classifying accurately. The use of either accuracy margins or accuracy vectors to cluster subjects into subpopulations offers an opportunity for such diversity although it does not seek it explicitly. However, as concluded by Kuncheva [19], individual accuracy is the leading factor for ensemble success compared to ensemble diversity, which supports our focus on accuracy for defining subpopulations.

Knowing the levels of predictivity associated with a patient’s algorithm-derived diagnosis, prognosis, or predicted response to treatment can contribute significantly to the treatment of patients for specific diseases by helping clinicians to assign therapies on an individualized basis, which is a goal of much current research in the development of drugs and other therapies. Although classification algorithms are promising tools to support clinical diagnosis and treatment of disease, the usual implicit assumption underlying these algorithms, that all patients are homogeneous with respect to characteristics of interest, is unsatisfactory. The proposed subpopulation-based confidence-measure approach using selective-voting convex-hull ensembles exploits the population heterogeneity reflected by characteristics that may not be readily apparent and thus not controlled. We have demonstrated a positive correspondence between our confidence designations derived from training samples and the classification accuracy of test samples. In particular, the highest-confidence subpopulation designated by both Methods 1 and 2 gave higher accuracy than the overall selective-voting accuracy for classifying test samples. Although Method 1 tended to give higher accuracy than Method 2 for the highest-confidence subpopulation, that subpopulation’s size tended to be quite small as a proportion of the total samples. On the other hand, Method 2 tended to assign a large proportion of test samples to the highest-confidence subpopulation.