Mean-Field Description of Ionic Size Effects with Non-Uniform Ionic Sizes: A Numerical Approach

Abstract

Ionic size effects are significant in many biological systems. Mean-field descriptions of such effects can be efficient but also challenging. When ionic sizes are different, explicit formulas in such descriptions are not available for the dependence of the ionic concentrations on the electrostatic potential, i.e., there is no explicit, Boltzmann type distributions. This work begins with a variational formulation of the continuum electrostatics of an ionic solution with such non-uniform ionic sizes as well as multiple ionic valences. An augmented Lagrange multiplier method is then developed and implemented to numerically solve the underlying constrained optimization problem. The method is shown to be accurate and efficient, and is applied to ionic systems with non-uniform ionic sizes such as the sodium chloride solution. Extensive numerical tests demonstrate that the mean-field model and numerical method capture qualitatively some significant ionic size effects, particularly those for multivalent ionic solutions, such as the stratification of multivalent counterions near a charged surface. The ionic valence-to-volume ratio is found to be the key physical parameter in the stratification of concentrations. All these are not well described by the classical Poisson–Boltzmann theory, or the generalized Poisson–Boltzmann theory that treats uniform ionic sizes. Finally, various issues such as the close packing, limitation of the continuum model, and generalization of this work to molecular solvation are discussed.

1 Introduction

Electrostatic interactions between macromolecules and mobile ions in the surrounding solvent play a key role in many important biological processes such as protein folding [1, 2], membrane stabilization [3], gating in ion channels [4], hydrophobic interactions [5], and protein association [6, 7]. In such interactions, ionic sizes or excluded volumes, particular non-uniform ionic sizes of multiple ions, can affect many of the detailed chemical and physical properties of an underlying biological system. For instance, the monovalence cation size can influence the stability of RNA tertiary structures [8]. Differences in ionic sizes can also affect how mobile ions bind to nucleic acids [9, 10, 11]. The ionic size effect is more profound in the ion channel selectivity, see, e.g., [4, 12]. Detailed Monte Carlo simulations and integral equations calculations also confirm some of these experimentally observed properties due to the non-uniformity of ionic sizes [13, 14, 15].

The classical Poisson–Boltzmann (PB) equation is perhaps the most widely used mean-field model of the electrostatics of ionic solutions [16, 17, 18, 19, 20, 21]. It has been successful in many applications, particularly in the biomolecular modeling with an implicit solvent [22, 23, 24, 25, 26]. The PB equation is Poisson’s equation for the electrostatic potential with the charge density including that of mobile ions whose equilibrium concentrations are given by the Boltzmann distributions via the potential. In a variational setting, such distributions are the conditions for equilibrium concentrations that minimize a mean-field electrostatic free-energy functional of ionic concentrations where the potential is determined by Poisson’s equation [27, 28, 29, 30, 31]. Despite its success in many applications, the classical PB theory is known to fail in capturing well the ion-ion correlations and ionic size effects [32, 33, 13, 14, 15].

Recently, there has been a growing interest in incorporating the ionic size effect in a PB-like, simple and efficient, mean-field model [34, 35, 36, 37, 38, 39, 40, 30, 31, 41]. The key idea has been to introduce the local concentration c₀ = c₀(x) of solvent molecules, in addition to those c₁(x), …, c_M(x) of ions of multiple species (M of them assumed), and their corresponding linear sizes a₀, a₁, …, a_M in the electrostatic free energy

$$\int [\frac{1}{2}\rho \psi +k_{B}T\sum _{i=0}^M{c}_i\text{log}(a_i^3{c}_i)]dV.$$ (1.1)

Here

$$\rho =f+\sum _{i=1}^M{z}_{i}e{c}_i$$

is the charge density with f a fixed charge density, z_i the valence of an ion of the ith species, and e the elementary charge, ψ is the electrostatic potential determined by Poisson’s equation, k_B is the Boltzmann constant, and T is the temperature. Notice that the concentration of the solvent molecules is not an independent variable in this functional, since it is defined by

$$a_0^3{c}_0(\mathbf{x})=1-\sum _{i=1}^M{a}_i^3{c}_i(\mathbf{x}).$$

If all a₀, a₁, …, a_M are the same, this mean-field approximation of the free energy can then be derived from a lattice gas model, cf. [34, 40]. Moreover, there are explicit formulas, the generalized Boltzmann distributions, relating equilibrium concentrations and the corresponding electrostatic potential. These distributions, together with Poisson’s equation, lead to the generalized PB equation for the case of a uniform ionic size [34, 35, 40]. See [38, 39, 41] for some applications of this equation. When the ionic sizes are not the same, the situation is quite different. For a system of three ionic species with two different ionic sizes, Chu et al. [37] derived a different size-modified PB equation from a similar lattice gas model and applied this equation to study the ionic size effect in the binding of ions to DNA. For a general system, Tresset [40] derived an expression of the free energy similar to (1.1) with an effective volume fraction of free space, under the assumption that the ionic excluded volumes are dispersed from each other to a reasonable extent. For a general system of multiple ions with different sizes modeled by (1.1), Li [31] derived the equilibrium conditions

$${\left(\frac{a_i}{a_0}\right)}^3\text{log}(a_0^3{c}_0)-\text{log}(a_i^3{c}_i)=\frac{1}{k_{B}T}(z_{i}e\psi -{\mu }_i),i=1,\dots ,M,$$ (1.2)

where μ_i is the chemical potential of the ith ionic species, and proved that this system of algebraic equations has a unique solution (c₁, …, c_M). However, an explicit formula of this solution, and hence Boltzmann-like distributions for the equilibrium concentrations, seem unavailable. Therefore, there is no PB-like equation of the electrostatic potential in the general case.

To obtain the equilibrium ionic concentrations and the corresponding electrostatic potential, we propose in this work to minimize numerically the free-energy functional (1.1), using Poisson’s equation as a constraint. Following [42], we reformulate the electrostatic free-energy functional using both the potential ψ and concentrations c = (c₁, …, c_M), the (ψ, c)-formulation, or using both the electric field E and the concentrations, the (E, c)-formulation, coupled with Poisson’s equation or Gauss’s law, respectively. To solve our constrained optimization problems, we construct a Lagrange multiplier method for the case without the size effect and an augmented Lagrange multiplier method for the general case with the size effect. In order to compare the efficiency of our approaches, we also generalize the local constrained optimization method developed in [43, 42] to the general case including the ionic sizes. We perform extensive numerical tests to demonstrate the efficiency and accuracy of our methods, and to study how surface charges, ionic size differences, and ionic valences, affect the ionic concentration profiles near a charged surface. We recover many detailed properties of ionic concentrations, including the stratification of concentrations, that have been predicted by other refined models. We also find that the ionic valence-to-volume ratio is the key parameter in the stratification.

The rest of the paper is organized as follows: In Section 2, we describe in details the general electrostatic free-energy functional with or without the ionic size effect, using the (ψ, c) and (E, c)-formulations. In Section 3, we develop various kinds of global and local constrained optimization methods for solving numerically our underlying variational problems. In Section 4, we report our numerical results to demonstrate the accuracy and efficiency of our method, and to describe various ionic size effects in an ionic solution. Finally, in Section 5, we draw conclusions and discuss various issues such as the close packing, limitation of the continuum model, and generalization of this work to molecular solvation.

2 Electrostatic Free Energy

We consider an ionic solution that occupies a bounded region Ω in ℝ³.We assume there are M ionic species in the solution, and denote by z_i and N_i the valence and the total number, respectively, of ions of the ith species. Let c_i(x) denote the local ionic concentration at a spatial point x ∈ Ω of the ith ionic species. Then

$${\int }_{\mathrm{\Omega }}{c}_{i}dV=N_i,i=1,\dots ,M.$$ (2.1)

Moreover, the local density at x ∈ Ω of charges of ions is ${\sum }_{i=1}^M{z}_{i}e{c}_i(\mathbf{x})$, where e the elementary charge.

We assume that there are fixed volume charges and surface charges distributed in the interior and on the boundary of the solution region Ω, respectively. We denote by f(x) the local density of the fixed volume charges at an interior point x ∈ Ω. Similarly we denote by σ(x) the local density of the fixed surface charges at a boundary point x ∈ Γ, where Γ = ∂Ω denotes the boundary of Ω. The charge neutrality of the entire solution is given by

$$\sum _{i=1}^M{N}_i{z}_{i}e+{\int }_{\mathrm{\Omega }}fdV+{\int }_{\mathrm{\Gamma }}\sigma dS=0.$$ (2.2)

In equilibrium, the electrostatic free energy of the solution can be expressed in terms of the equilibrium ionic concentrations c = (c₁, …, c_M) as

$$F[c]=F_{\mathit{\text{pot}}}[c]+F_{\mathit{\text{ent}}}[c].$$ (2.3)

Here the potential energy F_pot[c] is given by

$$F_{\mathit{\text{pot}}}[c]={\int }_{\mathrm{\Omega }}\frac{1}{2}(f+\sum _{i=1}^M{z}_{i}e{c}_i)\psi dV+{\int }_{\mathrm{\Gamma }}\frac{1}{2}\sigma \psi dS,$$ (2.4)

where ψ = ψ(x) is the electrostatic potential. It is determined by Poisson’s equation and the boundary condition

$$\nabla ·{\epsilon }_r{\epsilon }_0\nabla \psi =-\left(f+\sum _{i=1}^M{z}_{i}e{c}_i\right)\text{in}\mathrm{\Omega },$$ (2.5)

$${\epsilon }_r{\epsilon }_0\frac{\partial \psi }{\partial n}=\sigma \text{on}\mathrm{\Gamma },$$ (2.6)

where ε₀ and ε_r are the vacuum permittivity and relative permittivity (dielectric coefficient), respectively, and ∂/∂n denotes the normal derivative along the unit exterior normal n at Γ. Here and below we use the SI units. Notice that by Eqs. (2.5) and (2.6) and an integration by parts

$$F_{\mathit{\text{pot}}}[c]={\int }_{\mathrm{\Omega }}\frac{{\epsilon }_r{\epsilon }_0}{2}|\nabla \psi {|}^2=dV.$$

Here the dependence on the equilibrium concentrations c = (c₁, …, c_M) is implicit through the potential ψ. Notice also that Eqs. (2.5) and (2.6) determine the potential ψ uniquely up to an additive constant but the potential energy F_pot[c] is unique.

The entropic part F_ent[c] is given in the form

$$F_{\mathit{\text{ent}}}[c]=k_{B}T{\int }_{\mathrm{\Omega }}Q(c)dV.$$ (2.7)

The integrand Q(c) is commonly defined for the case without the ionic size effect and that with the ionic size effect as follows:

$$Q(c)=\{\begin{array}{cc}\sum _{i=1}^M{c}_i[\text{log}({\mathrm{\Lambda }}^3{c}_i)-1]\hfill & \text{without the size effect},\hfill \\ \sum _{i=0}^M{c}_i[\text{log}(a_i^3{c}_i)-1]\hfill & \text{with the size effect}.\hfill \end{array}$$ (2.8)

For the case without the size effect, the parameter Λ is the de Broglie wavelength. For the case with the size effect, the summation starts from i = 0 and c₀(x) is the local concentration of the solvent at the point x ∈ Ω. For each i with 1 ≤ i ≤ M, the parameter a_i > 0 is the linear size, or more precisely, $a_i^3$ is the volume, of an ion of the ith species. The parameter a₀ > 0 is the linear size of a solvent molecule. The local concentration of solvent c₀ = c₀(x) is defined by the relation

$$a_0^3{c}_0(\mathbf{x})+a_1^3{c}_1(\mathbf{x})+\cdots +a_M^3{c}_M(\mathbf{x})=1\text{for all}\mathbf{x}\in \mathrm{\Omega }.$$

Thus c₀(x) is not an independent field. See [34, 35, 44, 40, 31].

All the properties described above are for the equilibrium concentrations and the corresponding potential. To find analytically and numerically such equilibrium concentrations and potential, and the minimum electrostatic free energy, we use a variational approach. We define an electrostatic free-energy functional

$$F[\psi ,c]={\int }_{\mathrm{\Omega }}[\frac{{\epsilon }_r{\epsilon }_0}{2}{|\nabla \psi |}^2+k_{B}TQ(c)]dV$$

for all possible concentrations c = (c₁, …, c_M) and the electrostatic potential ψ that are not necessary in equilibrium. We minimize this functional under the following constraints:

1. Eq. (2.1) of mass conservation;

2. Eq. (2.2) of charge neutrality;

3. Poisson’s equation (2.5); and

4. The boundary condition (2.6).

Notice that we do not need to assume that c_i(x) ≥ 0 since the term Q(c) involves log c_i(x).

Mathematically, one can prove by the direct method in the calculus of variations that there exist a unique set of concentrations c = (c₁, …, c_M) and a potential ψ, unique up to an additive constant, that minimize the function F[ψ, c] under all the constraints. See [30, 31]. The minimum value of the functional is exactly that given by (2.3), supplemented by (2.4) and (2.7).

Often the electric field E = E(x) is a useful quantity. If the potential ψ is known, then E = −∇ϕ. In general, we define the electrostatic free-energy functional of all possible pairs of concentrations c = (c₁, …, c_M) and electric field E

$$F[\mathbf{E},c]={\int }_{\mathrm{\Omega }}[\frac{{\epsilon }_r{\epsilon }_0}{2}{|\mathbf{E}|}^2+k_{B}TQ(c)]dV,$$

where we use the same letter F. Our underlying problem is then equivalent to finding the minimizer of this functional under the following constraints:

• (a’)Eq. (2.1) of mass conservation;
• (b’)Eq. (2.2) of charge neutrality;
• (c’)
  Gauss’s law

  $$\nabla ·{\epsilon }_r{\epsilon }_0\mathbf{E}=f+\sum _{i=1}^M{z}_{i}e{c}_i\text{in}\mathrm{\Omega };$$
• (d’)
  The boundary condition

  $$-{\epsilon }_r{\epsilon }_0\mathbf{E}·\mathbf{n}=\sigma \text{in}\mathrm{\Gamma };$$
• (e’)
  The compatibility condition

  $$\nabla \times \mathbf{E}=\mathbf{0}.$$

Introduce the Bjerrum length l_B = e²/(4πε_rε₀k_BT). Define $c_i^{\prime }=4\pi l_B{c}_i,N_i^{\prime }=4\pi l_B{N}_i$, Λ′ = (4πl_B)^−1/3 Λ, $a_i^{\prime }={(4\pi l_B)}^{-1/3}{a}_i$, f′ = 4πl_Bf/e, and σ′ = 4πl_Bσ/e. Define also ψ′ = eψ/(k_BT) and E′ = eE/(k_BT). Then for the (ψ, c)-formulation

$$F[\psi ,c]=\frac{{\epsilon }_r{\epsilon }_0{k}_B^2{T}^2}{e^2}F\prime [\psi \prime ,c\prime ],$$

where

$$F\prime [\psi \prime ,c\prime ]={\int }_{\mathrm{\Omega }}[\frac{1}{2}{|\nabla \psi \prime |}^{2}Q\prime (c\prime )]dV,$$

with Q′(c′) defined same as that in (2.8) except all quantities c_i, Λ, and a_i are replaced by their primed counterparts. The constraints and side conditions on (ψ, c) are rescaled to

$$\{\begin{array}{c}{\int }_{\mathrm{\Omega }}{c}_i^{\prime }dV=N_i^{\prime },\hfill \\ \sum _{i=1}^N{N}_i^{\prime }{z}_i+{\int }_{\mathrm{\Omega }}f\prime dV+{\int }_{\mathrm{\Gamma }}\sigma \prime dS=0,\hfill \\ \mathrm{\Delta }\psi \prime -(f\prime +\sum _{i=1}^M{z}_i{c}_i^{\prime })\text{in}\mathrm{\Omega },\hfill \\ \frac{\partial \psi \prime }{\partial n}=\sigma \prime \text{on}\mathrm{\Gamma }.\hfill \end{array}$$

Similarly, for the (E, c)-formulation,

$$F[\mathbf{E},c]=\frac{{\epsilon }_r{\epsilon }_0{k}_B^2{T}^2}{e^2}F\prime [\mathbf{E}\prime ,c\prime ],$$

where

$$F\prime [\mathbf{E}\prime ,c\prime ]={\int }_{\mathrm{\Omega }}[\frac{1}{2}{|\mathbf{E}\prime |}^2,Q\prime (c\prime )]dV.$$ (2.9)

The constraints and side conditions on (E, c) are rescaled to

$$\{\begin{array}{c}{\int }_{\mathrm{\Omega }}{c}_i^{\prime }dV=N_i^{\prime },\hfill \\ \sum _{i=1}^N{N}_i^{\prime }{z}_i+{\int }_{\mathrm{\Omega }}f\prime dV+{\int }_{\mathrm{\Gamma }}\sigma \prime dS=0,\hfill \\ \nabla ·\mathbf{E}\prime =f\prime +\sum _{i=1}^M{z}_i{c}_i^{\prime }\text{in}\mathrm{\Omega },\hfill \\ =-\mathbf{E}\prime ·\mathbf{n}=\sigma \prime \text{on}\mathrm{\Gamma },\hfill \\ \nabla \times \mathbf{E}\prime =\mathbf{0}\text{in}\mathrm{\Omega }.\hfill \end{array}$$

Since the integral of each $c_i^{\prime }$ over Ω is a constant by the mass conservation, we can replace Q′(c′) in the functionals F′[ψ′, c′] and F′[E′, c′] by a simpler one:

$$Q\prime (c\prime )=\{\begin{array}{cc}\sum _{i=1}^M{c}_i^{\prime }(\text{log}{c}_i^{\prime }-1)\hfill & \text{without the size effect},\hfill \\ c_0^{\prime }[\text{log}(a_0^{\prime 3}{c}_0^{\prime })-1]+\sum _{i=1}^M{c}_i^{\prime }(\text{log}{c}_i^{\prime }-1)\hfill & \text{with the size effect},\hfill \end{array}$$

where we keep $a_0^{\prime 3}$ for convenience in later calculations. Note that the sizes $a_i^{\prime }(i=1,\dots ,M)$ are hidden in $c_0^{\prime }$. Now the solutions to the free-energy minimization problems are the same but the minimum values of the free-energy functional are changed by a multiplicative and an additive constants that depend only on the input data ε_r, T, Λ, z_i, a_i, and N_i. For simplicity, we will drop all the primes in the rest of this paper.

We remark that one can also use the Dirichlet boundary condition ψ = ψ₀ on the boundary Γ for some given function ψ₀. In this case, we can derive similarly our variational formulation. Sometimes, the periodic boundary condition can be also used as an approximation when the ionic solution is considered in a confined domain. In addition, we can approximate the surface charge density by a function that is defined on the region so that only the volume charge density appears in our formulation. These approximations can simplify our numerical computations.

3 Numerical Methods

3.1 A Lagrange multiplier method for the case without the size effect

We consider the problem of minimizing F(E, c) defined in (2.9), with Q(c) corresponding to the case without the size effect, under all the constraints listed below Eq. (2.9). The Lagrange multiplier method converts this problem into the following unconstrained optimization problem:

$$\underset{(\mathbf{E},c)}{\text{min}}\underset{(\psi ,\lambda )}{\text{max}}L(\mathbf{E},c,\psi ,\lambda ),$$

where λ = (λ₁, …, λ_M) and

$$L(\mathbf{E},c,\psi ,\lambda )=F(\mathbf{E},c)-{\int }_{\mathrm{\Omega }}\psi K(\mathbf{E},c)dV+\sum _{i=1}^M{\lambda }_i{H}_i(c_i),K(\mathbf{E},c)=\nabla ·\mathbf{E}-\sum _{i=1}^M{z}_i{c}_i-f,$$ (3.1)

$$H_i(c_i)={\int }_{\mathrm{\Omega }}{z}_i{c}_{i}dV-z_i{N}_i,i=1,\dots ,M.$$ (3.2)

Here ψ = ψ(x) is a function on Ω and −ψ is the Lagrange multiplier for the (scaled) Gauss’s law. Each λ_i (1 ≤ i ≤ M) is a real number and is the Lagrange multiplier for the mass conservation constraint for the ith ionic species.

The necessary conditions for (E, c, ψ, λ) to be a saddle point of L are

$$\frac{\partial L}{\partial \mathbf{E}}=\mathbf{E}+\nabla \psi =0,$$ (3.3)

$$\frac{\partial L}{\partial \psi }=-K+(\mathbf{E},c)=0,$$ (3.4)

$$\frac{\partial L}{\partial c_i}=\text{log}{c}_i+z_i\psi +{\lambda }_i{z}_i=0,$$ (3.5)

$$\frac{\partial L}{\partial {\lambda }_i}=H_i(c_i)=0,i=1,\dots ,M,$$ (3.6)

where the first three derivatives are the variational derivatives. By Eq. (3.3), E = −∇ψ in Ω, i.e., the Lagrange multiplier ψ is an electrostatic potential. Moreover, the constraint ∇ × E = 0 is satisfied automatically. By Eq. (3.5),

$$c_i=e^{-{\lambda }_i{z}_i}{e}^{-z_i\psi }\text{in}\mathrm{\Omega }.$$

By Eqs. (3.6) and (3.2),

$$N_i={\int }_{\mathrm{\Omega }}{c}_{i}dV=e^{-{\lambda }_i{z}_i}{\int }_{\mathrm{\Omega }}{e}^{-z_i\psi }dV.$$

It then follows that

$$c_i=\frac{N_i{e}^{-z_i\psi }}{{\int }_{\mathrm{\Omega }}{e}^{z_i\psi }dV}\text{in}\mathrm{\Omega },i=1,\dots ,M.$$

The ultimate unknown variable is ψ. By Eqs. (3.3) and (3.4), ψ is determined by the following nonlocal PB equation

$$-\mathrm{\Delta }\psi =\sum _{i=1}^M\frac{z_i{N}_i{e}^{-z_i\psi }}{{\int }_{\mathrm{\Omega }}{e}^{-z_i\psi }dV}+f,$$

together with some boundary conditions. We choose to use the periodic boundary conditions for efficiency. We solve this boundary-value problem by the fixed-point iterations.

Algorithm.

• Step 0. Initialize ψ₀. Set l = 0. Choose ω ∈ (0, 1). Choose an error tolerance tol > 0.

• Step 1. Find the solution ψ_* by solving

  $$-\mathrm{\Delta }{\psi }_{*}=\sum _{i=1}^M\frac{z_i{N}_i{e}^{-z_i{\psi }_l}}{{\int }_{\mathrm{\Omega }}{e}^{-z_i{\psi }_l}dV}+f$$

  with the periodic boundary condition.

• Step 2. If |ψ_* − ψ_l| < tol in Ω, then stop. Otherwise, set ψ_l+1 = ωψ_l+ (1 − ω)ψ_* and l ← l + 1, and go to Step 1.

3.2 An augmented Lagrange multiplier method for the case with the size effect

We again consider the problem of minimizing F(E, c) defined in (2.9), with Q(c) now corresponding to the case with the size effect, under all the constraints listed below Eq. (2.9). Our augmented Lagrange multiplier method is to solve the following unconstrained optimization problem [45, 46]:

$$\underset{(\mathbf{E},c)}{\text{min}}\underset{(\psi ,\lambda )}{\text{max}}\mathrm{L̂}(\mathbf{E},c,\psi ,\lambda ,r),$$

where r = (r₁, …, r_M) and

$$\mathrm{L̂}(\mathbf{E},c,\psi ,\lambda ,r)=F(\mathbf{E},c)-{\int }_{\mathrm{\Omega }}\psi K(\mathbf{E},c)dV+\sum _{i=1}^M{\lambda }_i{H}_i(c_i)+\sum _{i=1}^M\frac{r_i}{2}{[H_i(c_i)]}^2.$$

Here K and H_i are defined in (3.1) and (3.2), respectively, and all r_i ≥ 0 in the last term of summation are the penalty parameters. We add all the penalty terms (1/2)r_i[H_i(c_i)]² to stabilize and accelerate our numerical iterations.

The necessary conditions for (E, c, ψ, λ, r) to be a saddle point of L̂ are

$$\frac{\partial \mathrm{L̂}}{\partial \mathbf{E}}=\mathbf{E}+\nabla \psi =0,$$ (3.7)

$$\frac{\partial \mathrm{L̂}}{\partial \psi }=-K(\mathbf{E},c)=0,$$ (3.8)

$$\frac{\partial \mathrm{L̂}}{\partial c_i}=-\frac{a_i^3}{a_0^3}\text{log}(1-\sum _{j=1}^M{a}_j^3{c}_j)+\text{log}{c}_i+({\lambda }_i+\psi )z_i+r_i{z}_i{H}_i(c_i)=0,i=1,\dots ,M,$$ (3.9)

$$\frac{\partial \mathrm{L̂}}{\partial {\lambda }_i}=H_i(c_i)=0,i=1,\dots ,M.$$ (3.10)

As in the previous case we have by (3.7) that E = −∇ψ and ∇ × E = 0. Also, Eqs. (3.7) and (3.8) imply that

$$-\mathrm{\Delta }\psi =\sum _{i=1}^M{z}_i{c}_i+f.$$ (3.11)

Since the linear sizes a₀, a₁, …, a_M can be all different, it does not seem to be possible to solve (3.9) analytically to get Boltzmann-like distributions for the dependence of all the concentrations c_i on the potential ψ and parameters λ [40, 31]. Therefore we design an iteration algorithm to solve the coupled system (3.9), (3.10), and (3.11), with, e.g., the periodic boundary condition.

Algorithm.

• Step 0. Initialize c⁽⁰⁾, ψ⁽⁰⁾, ${\lambda }^{(0)}=({\lambda }_1^{(0)},\dots ,{\lambda }_M^{(0)})$, and $r^{(0)}=(r_1^{(0)},\dots ,r_M^{(0)})$. Fix a parameter β > 1. Set l = 0.

• Step 1. Solve by the fast Fourier transform Eq. (3.11) with c_i replaced by $c_i^{(l)}$, with the periodic boundary condition, to obtain the solution ψ^(l+1). Set

  $${\mathbf{E}}^{(l+1)}=-\nabla {\psi }^{(l+1)}.$$

• Step 2. Use Newton’s method to solve Eq. (3.9) with ψ, λ, and r replaced by ψ^(l+1), λ^(l), and r^(l), respectively, to obtain the solution c^(l+1).

• Step 3. Update the Lagrange multipliers

  $${\lambda }_i^{(l+1)}={\lambda }_i^{(l)}+r_i^{(l)}{H}_i(c_i^{(l+1)}),i=1,\dots ,M.$$
  Update the penalty parameters

  $$r_i^{(l+1)}=\beta r_i^{(l)},i=1,\dots ,M.$$

• Step 4. Test convergence. If not, set l ← l + 1 and go to Step 1.

We now detail Newton’s method in Step 2 of our algorithm for solving Eq. (3.9) with a fixed i (1 ≤ i ≤ M). Let us discretize our computational box with a uniform grid of N grid points. We denote by ΔV the volume of each grid cell. Let us also denote by $c_i^1,\dots ,c_i^N$ and ψ¹, …, ψ^N the approximate values at these grid points of the concentration c_i and those of the potential ψ, respectively. Denote

$${\theta }_i^m=-\frac{a_i^3}{a_0^3}\text{log}\left(1-\sum _{j=1}^M{a}_j^3{c}_j^m\right)+\text{log}{c}_i^m+({\lambda }_i+{\psi }^m)z_i+r_i{z}_i^2\left(\mathrm{\Delta }V\sum _{k=1}^N{c}_i^k-N_i\right),m=1,\dots ,N.$$

For each m, ${\theta }_i^m$ is an approximation at the mth grid point of the left-hand side of Eq. (3.9). We need to solve the system of N nonlinear equations

$${\theta }_i^m=0,m=1,\dots ,N,$$ (3.12)

to obtain $c_i^1,\dots ,c_i^N$, provided that all a₀, …, a_M, λ_i, r_i, z_i, ψ¹, …, ψ^N, and ΔV are known. Denote the vectors $\mathrm{\Theta }={({\theta }_i^1,{\theta }_i^2,\cdots ,{\theta }_i^N)}^T$ and $\mathbf{c}={(c_i^1,c_i^2,\cdots ,c_i^N)}^T$, where T denotes the matrix transpose. In a vector form, the system of nonlinear equations (3.12) is simply Θ(c) = 0.

The gradient of Θ with respect to c, denoted ∂Θ/∂c, is a matrix with its (m, n)-entry given by $\partial {\theta }_i^m/\partial c_i^n$. Simple calculations lead to

$$\frac{\partial \mathrm{\Theta }}{\partial \mathbf{c}}=\text{diag}\left(\frac{1}{{\xi }^1},\dots ,\frac{1}{{\xi }^N}\right)+r_i{z}_i^2\mathrm{\Delta }V\mathbf{e}\otimes \mathbf{e},$$

where e is the N-component column vector with all its components equal to 1 and

$${\xi }^m={(\frac{1}{c_i^m}+\frac{a_i^6}{a_0^3-a_0^3{\sum }_{j=1}^M{a}_j^3{c}_j^m})}^{-1},m=1,\dots ,N.$$

Therefore

$$\text{det}\frac{\partial \mathrm{\Theta }}{\partial \mathbf{c}}=\frac{1+r_i{z}_i^2\mathrm{\Delta }V{\sum }_{m=1}^N{\xi }^m}{{\prod }_{m=1}^N{\xi }^m}>0.$$

Hence the matrix ∂Θ/∂c is invertible. By the Sherman–Morrison formula [47],

$${\left(\frac{\partial \mathrm{\Theta }}{\partial \mathbf{c}}\right)}^{-1}=\text{diag}({\xi }^1,\dots ,{\xi }^N)-\frac{r_i{z}_i^2\mathrm{\Delta }V}{1+r_i{z}_i^2\mathrm{\Delta }V{\sum }_{m=1}^N{\xi }^m}\xi \otimes \xi ,$$

where ξ = (ξ¹, …, ξ^N)^T.

Our Newton’s iteration scheme is now

$$\mathbf{c}\leftarrow c-\gamma {(\frac{\partial \mathrm{\Theta }}{\partial \mathbf{c}})}^{-1}\mathrm{\Theta }(\mathbf{c}),$$

where γ > 0 is a numerical parameter. Component-wise, this iteration is

$$c_i^m\leftarrow =c_i^m-\gamma {\xi }^m\left({\theta }_i^m-\frac{r_i{z}_i^2\mathrm{\Delta }V{\sum }_{k=1}^N{\theta }_i^k{\xi }^k}{1+r_i{z}_i^2\mathrm{\Delta }V{\sum }_{k=1}^N{\xi }^k}\right),m=1,\dots ,N,i=1,\dots ,M.$$

We choose γ by using a trial-and-error method to avoid the concentrations $c_i^m$ going outside the range (0, $a_i^{-3}$) for i = 1, …, M. It should be noted that matrix-vector multiplications are avoided in this Newton’s iteration scheme and the complexity of each iteration is O(N).

3.3 A local constrained optimization method

In this subsection, we extend a local optimization method developed in [43, 42] to treat the case with the size effect. We assume that our computational domain is a rectangular parallelepiped (0, L₁) × (0, L₂) × (0, L₃) and discretize it using a uniform grid with the grid spacing h₁, h₂, and h₃ in the three coordinate directions. We denote by ΔV = h₁h₂h₃ the volume of each grid cell. A typical grid associated with n = (n₁, n₂, n₃) is

$${\mathbf{r}}_0(\mathbf{n})=(n_1{h}_1,n_2{h}_2,n_3{h}_3).$$

For such a grid we also denote

$${\mathbf{r}}_{1,}\pm (\mathbf{n})=((n_1\pm 1/2)h_1,n_2{h}_2,n_3{h}_3),{\mathbf{r}}_{2,}\pm (\mathbf{n})=(n_1{h}_1,(n_2\pm 1/2)h_2,n_3{h}_3),{\mathbf{r}}_{3,}\pm (\mathbf{n})=(n_1{h}_1,n_2{h}_2,(n_3\pm 1/2)h_3).$$

We discretize each of the concentrations c_i on all the grid points r₀(n) and the three components E₁, E₂, and E₃ of the electric field E at r_j,+(n) (j = 1, 2, 3). The functional F(E, c) defined in (2.9) with the size effect is now approximated by

$$\frac{F}{\mathrm{\Delta }V}=\frac{1}{2}\sum _{\mathbf{n}}\sum _{j=1}^3{[E_j({\mathbf{r}}_{j,+}(\mathbf{n}))]}^2+\sum _{\mathbf{n}}{c}_0({\mathbf{r}}_0(\mathbf{n}))[\text{log}(a_0^3{c}_0({\mathbf{r}}_0(\mathbf{n})))-1]+\sum _{\mathbf{n}}\sum _{i=i}^M{c}_i({\mathbf{r}}_0(\mathbf{n}))[\text{log}(c_i{\mathbf{r}}_0(\mathbf{n})))-1].$$ (3.13)

Gauss’s law is approximated as

$$\sum _{j=1}^3\frac{E_j({\mathbf{r}}_{j,+}(\mathbf{n}))-E_j({\mathbf{r}}_{j,-}(\mathbf{n}))}{h_j}=\sum _{i=1}^M{z}_i{c}_i({\mathbf{r}}_0(\mathbf{n}))+f({\mathbf{r}}_0(\mathbf{n})).$$

The mass conservation is approximated by

$$\sum _{\mathbf{n}}{c}_i({\mathbf{r}}_0(\mathbf{n}))=\frac{N_i}{\mathrm{\Delta }V},i=1,\dots ,M.$$

The local method developed in [42] (cf. also [43]) is based on local moves or updates of the electric field and ionic concentrations. Let us first consider the update of electric field. Fix a grid cell and one of its two faces perpendicular to the x₃-axis. Let $E_1^{\prime }$, E₂, E₁ and $E_2^{\prime }$ be the four electric field components on the face. We update these values by

$$E_1^{\prime }\leftarrow E_1^{\prime }+\delta E_1^{\prime },E_2\leftarrow E_2+\delta E_2,E_1\leftarrow E_1+\delta E_1,E_2^{\prime }\leftarrow E_2^{\prime }+\delta E_2^{\prime }.$$

Corresponding changes in fluxes are

$$\delta {\varphi }_1^{\prime }=h_2{h}_3\delta E_1^{\prime },\delta {\varphi }_2=h_3{h}_1\delta E_2,\delta {\varphi }_1=h_2{h}_3\delta E_1,\delta {\varphi }_2^{\prime }=h_3{h}_1\delta E_2^{\prime }.$$

In order for Gauss’s law to be satisfied, the flux changes should be the same, i.e.

$$\delta {\varphi }_1^{\prime }=\delta {\varphi }_2=\delta {\varphi }_1=\delta {\varphi }_2^{\prime }=\delta \varphi .$$

The resulting change in the functional is

$$\delta F\mathrm{\Delta }V={(\delta \varphi )}^2(h_1^2+h_2^2)+\mathrm{\Delta }V{h}_1(E_1-E_1^{\prime })\delta \varphi +\mathrm{\Delta }V{h}_2(E_2-E_2^{\prime })\delta \varphi .$$

This change is minimized if

$$\delta \varphi =\frac{\mathrm{\Delta }V}{2(h_1^2+h_2^2)}[h_1(E_1^{\prime }-E_1)+h_2(E_2^{\prime }-E_2)].$$

We now consider the update of the concentrations. Let ${\mathbf{r}}_0^A$ and ${\mathbf{r}}_0^B$ be two adjacent grid points linked by an edge of length Δl. We denote by $c_j^A$ and $c_j^B$ the approximations of the concentration c_j at these two grid points, respectively, for all j = 1, …, M. Fix i (1 ≤ i ≤ M). We update the values $c_i^A$ and $c_i^B$ by

$$c_i^A\leftarrow c_i^A-\delta c\text{and}{c}_i^B\leftarrow c_i^B+\delta c.$$

By Gauss’s law, the flux related to the link between two nodes should be correspondingly changed with the amount ΔE = −Δlz_iδc. Hence the associated change in the functional is

$$\frac{\mathrm{\Delta }F}{\mathrm{\Delta }V}=\frac{1}{2}{(\mathrm{\Delta }l{z}_i\delta c)}^2-E\mathrm{\Delta }l{z}_i\delta c+c_i^A\text{log}\left(1-\frac{\delta c}{c_i^A}\right)+c_i^B\text{log}\left(1+\frac{\delta c}{c_i^B}\right)-\delta c\text{log}\frac{c_i^A-\delta c}{c_i^B+\delta c}+\frac{1-{\sum }_{j=0}^M{a}_j^3{c}_j^A}{a_0^3}\text{log}\left(1+\frac{a_i^3\delta c}{1-{\sum }_{j=0}^M{a}_j^3{c}_j^A}\right)+\frac{1-{\sum }_{j=0}^M{a}_j^3{c}_j^B}{a_0^3}\text{log}\left(1-\frac{a_i^3\delta c}{{1-\sum }_{j=0}^M{a}_j^3{c}_j^B}\right)+\frac{a_i^3\delta c}{a_0^3}\text{log}\left(\frac{{1-\sum }_{j=0}^M{a}_j^3{c}_j^A+a_i^3\delta c}{{1-\sum }_{j=0}^M{a}_j^3{c}_j^B-a_i^3\delta c}\right).$$

Notice that this change is different from that for the case without the size effect [42]. The optimal value δc that minimizes this expression is the solution to the following equation:

$$-E\mathrm{\Delta }l{z}_i+{(\mathrm{\Delta }l)}^2{z}_i^2\delta c-\text{log}\left(\frac{c_i^A-\delta c}{c_i^B+\delta c}\right)+\frac{a_i^3}{a_0^3}\text{log}\left(\frac{1-{\sum }_{j=0}^M{a}_j^3{c}_j^A+a_i^3\delta c}{1-{\sum }_{j=0}^M{a}_j^3{c}_j^B-a_i^3\delta c}\right)=0.$$ (3.14)

Notice from the logarithmic terms in (3.13) that the perturbation δc should be in the interval (I_l, I_r), where

$$I_l=\text{max}\left\{-\frac{1-{\sum }_{j=0}^M{a}_j^3{c}_j^A}{a_i^3},-c_i^B\right\}\text{and}{I}_r=\text{min}\left\{\frac{1-{\sum }_{j=0}^M{a}_j^3{c}_j^B}{a_i^3},c_i^A\right\}.$$

We solve Eq. (3.14) by Newton’s iteration with the initial guess (I_l + I_r)/2.

4 Numerical Results

We now report results of our numerical calculations. We set the Bjerrum length to be l_B = 7Å. We choose our computational domain to be a cube Ω = (0, L) × (0, L) × (0, L) for some L > 0. We assume that this cube contains a spherical colloidal particle, denoted by B_c, of radius R with its center the same as that of the cube. We also assume that a total Z e of fixed surface charges are uniformly distributed over the spherical surface. As in [42], we interpolate the surface charges into their nearest grids. Since the mobile ions cannot penetrate the interface between the solution region and the colloidal particle, all the ionic concentrations are assumed to vanish inside the sphere. This means that the region of the ionic solution is Ω \ B_c, the cube Ω minus the sphere B_c.

4.1 Example 1

In this example, we demonstrate that our method captures qualitatively the essential features of ionic solution. Moreover we show that our method is accurate and is more efficient than some previously proposed local methods.

We consider an ionic solution of sodium chloride occupying the region Ω \ B_c. The number of ionic species M, their valences z₁ and z₂, their linear sizes a₁ and a₂, and the linear size of the solvent molecule a₀ are given by

$$M=2,z_1=-1,z_2=+1,a_1=3.34\AA ,a_2=2.32\AA ,a_0=2.75\AA .$$

The total number of sodium ions N₁, the total number of chloride ions N₂, the total amount of surface charges Ze, the radius R of the sphere B_c, and the linear size of the computational box L are

$$N_1=120,N_2=60,Ze=60e,R=8\AA ,L=80\AA .$$

Our numerical grid consists of a total of 256 × 256 × 256 grid points.

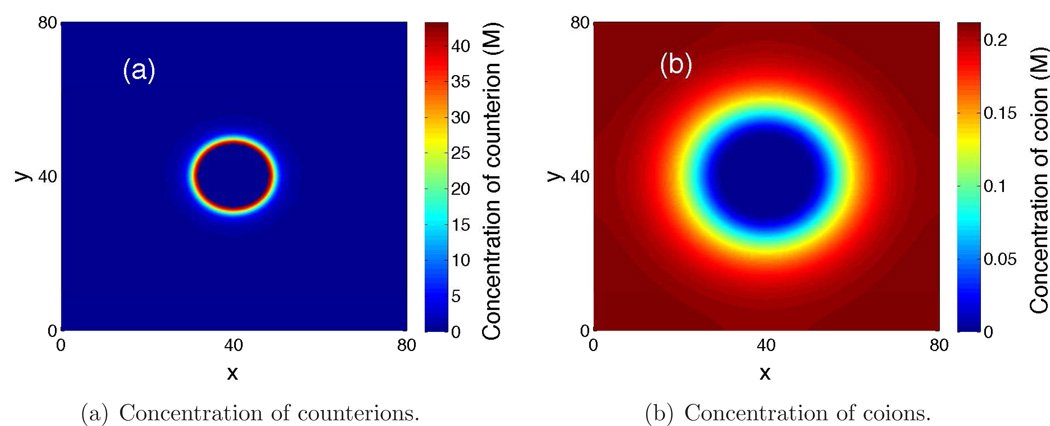
We use our augmented Lagrange multiplier method to numerically minimize the electrostatic free-energy functional (2.9) with the size effect, together with all the corresponding constraints listed below (2.9). Figure 1 shows a two-dimensional cross section of our computed equilibrium concentration of counterions (a) and that of coions (b) in the plane z = 40Å, which is in the middle of the computational box. Due to the presence of surface charges, the counterions—chloride ions—accumulate around the colloidal sphere. In contrast, the coions—sodium ions—are repelled away from the colloidal sphere. Note that the concentration of counterions reaches a saturation value, rather than becoming too high and unphysical as often predicted by the classical PB theory that does not include the ionic size effect.

Figure 1.

(Color online) Ionic concentrations in the mid-plane z = 40Å.

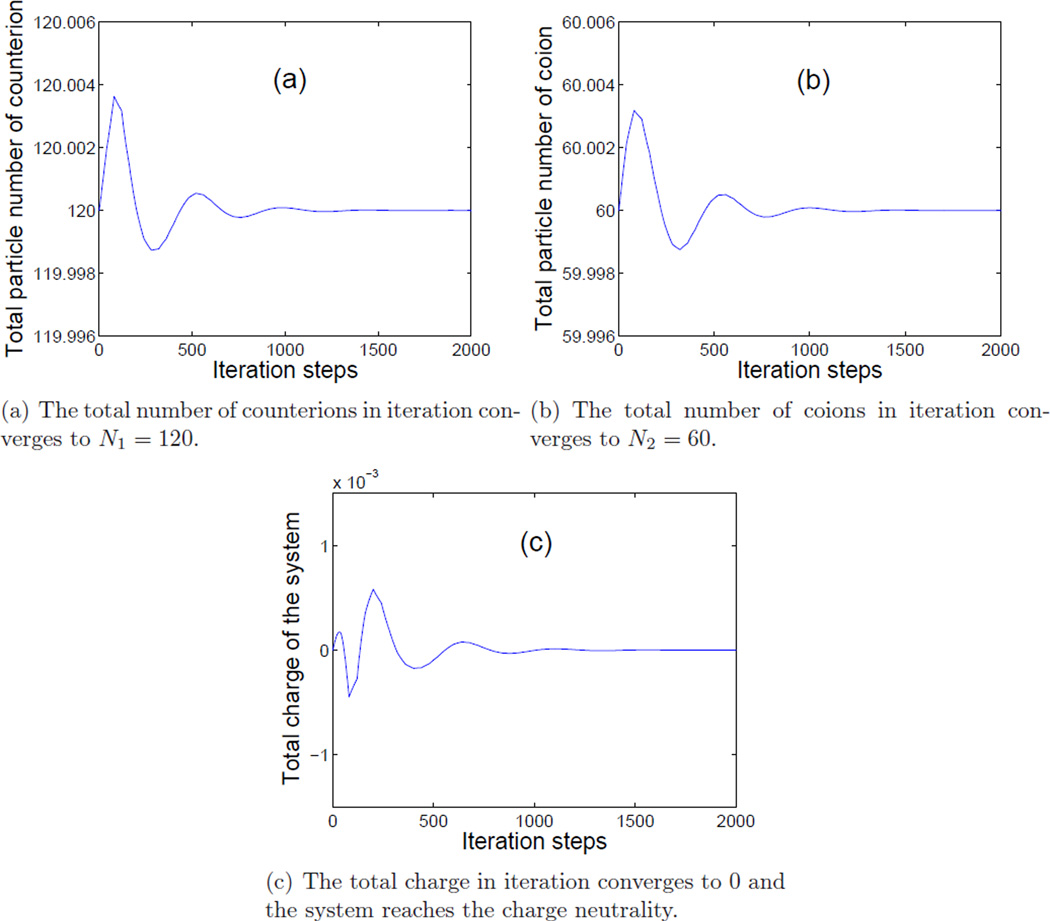
Figure 2 shows the convergence of our numerical iterations of the total number of counterions (a), that of coions (b), and the total charge in the system (c) to their respective values N₁ = 120, N₂ = 60, and 0. This demonstrates that our augmented Lagrange multiplier method preserves very well the constraints of mass conservation (2.1) and charge neutrality (2.2).

Figure 2.

(Color online) Convergence histories.

To compare the efficiency of various methods that we described in Section 3, we also performed the following computations:

1. minimize numerically the free-energy functional (2.9) without the size effect, together with the corresponding constraints, using the local constrained optimization method developed in [42]. This method will be abbreviated as “PBmove”;

2. minimize numerically the free-energy functional (2.9) without the size effect, together with the corresponding constraints, using the Lagrange multiplier method described in Subsection 3.1. This method will be abbreviated as “LagMulti”;

3. minimize numerically the free-energy functional (2.9) with the size effect, together with the corresponding constraints, using the local constrained optimization method described in Subsection 3.3. This method will be abbreviated as “SMPBmove”. (SMPB means Size Modified Poisson–Boltzmann.)

We shall abbreviate our augmented Lagrange multiplier method as “AugLagMulti”.

We run our “PBmove” and “LagMulti” codes and stop at a point at which the two numerical solutions of the concentrations and those of the electric field are close enough. Similarly, we run our “SMPBmove” and “AugLagMulti” codes and stop when the two numerical solutions of the concentrations and those of the electric field are close enough. Table 4.1 shows the maximum and relative maximum differences of these solutions with a grid of size 128 × 128 × 128. With the same solution accuracy, we compare the computational time of these methods in Table 4.2. It is clear that the Lagrange multiplier method and augmented Lagrange multiplier method are much more efficient than the corresponding local constrained optimization methods.

Table 4.1.

Solution differences with the grid size 128×128×128

Algorithms	Max. difference		Relative max. difference
	c	E	c	E
PBmove vs. LagMulti	1.547e-5	7.223e-5	1.405e-5	8.327e-6
SMPBmove vs. AugLagMulti	1.974e-6	4.073e-5	7.364e-5	4.650e-6

Table 4.2.

Computational time (in seconds)

Grid	Without size effect		With size effect
	PBmove	LagMulti	SMPBmove	AugLagMulti
16×16×16	3.13	0.44	15.64	3.12
32×32×32	71.34	3.27	81.11	25.43
64×64×64	1884.11	51.02	2554.79	213.00
128×128×128	54347.59	534.67	72298.27	1738.23

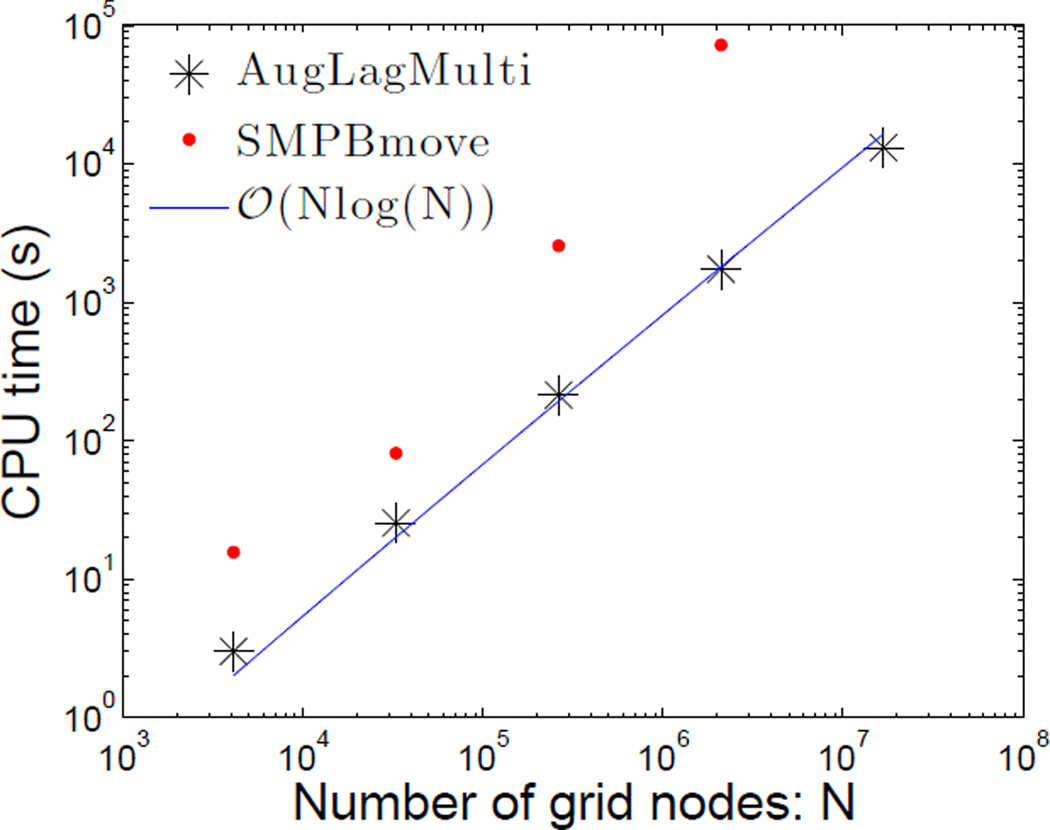
In Figure 3, we plot in the log-log scale the CPU time in seconds vs. the total number of grids N for both “SMPBmove” and “AugLagMulti” applied to the case with the size effect. We see that the latter has the O(N log N) complexity. This is because we use the fast Fourier transform in solving our equations. Clearly, our augmented Lagrange multiplier method is much faster than the local method.

Figure 3.

(Color online) Log-log plot of the CPU time vs. the number of grids for both “SMPBmove” and “AugLagMulti”.

4.2 Example 2

We now investigate the influence of ionic sizes and surface charges on the concentration of counterions in the vicinity of the charged spherical surface which carries uniformly a total of Ze charges with Z > 0. We recall that the spherical colloid of radius R is located in the center of our computational box Ω = (0, L) × (0, L) × (0, L). We use the following parameters:

$$M=2,z_1=-1,z_2=+1,N_1=2Z,N_2=Z,R=14\AA ,L=160\AA .$$

We also use the numerical grid size 256 × 256 × 256. The parameter Z and the linear sizes a₀ of the solvent molecules, a₁ of the counterions, and a₂ of the coions are given for two different cases.

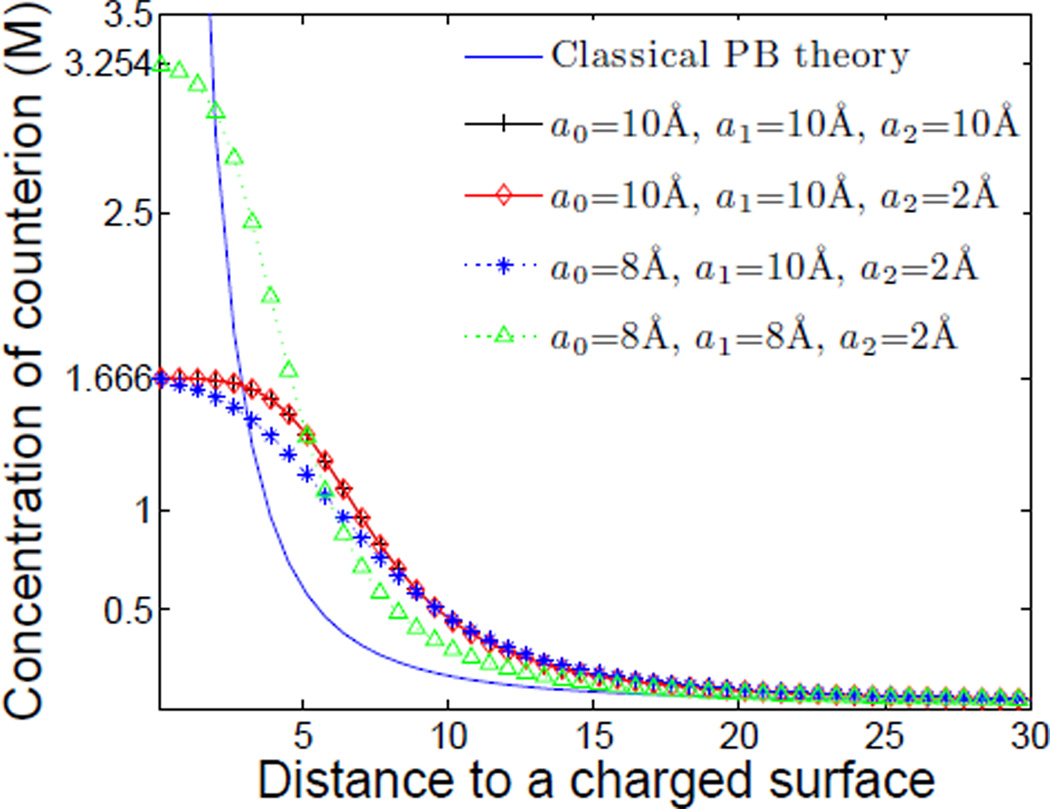
In the first case, we study how ionic sizes affect the equilibrium counterion concentration profile. We fix Z = 60 and choose four sets of the values of linear sizes (a₀, a₁, a₂):

$${(a_0,a_1,a_2)}_I=(10\AA ,10\AA ,10\AA ),{(a_0,a_1,a_2)}_{II}=(10\AA ,10\AA ,2\AA ),{(a_0,a_1,a_2)}_{III}=(8\AA ,10\AA ,2\AA ),{(a_0,a_1,a_2)}_{IV}=(8\AA ,8\AA ,2\AA ).$$

In Figure 4, we plot the concentration profiles for counterions with these choices of the linear sizes. For comparison, we also plot the profile obtained by the classical PB theory. Clearly, the counterion concentration when the size effect is included deviates largely from that of the classical PB solution. The identical profiles of group I and group II indicate that the change of the coion size has very little influence on the distribution of counterions close to the charged surface, since almost all of the coions are distributed away from the surface. A comparison between group II and group III demonstrates clearly that the larger size of the solvent molecule results in a wider saturation region, implying that the solvent molecules present in the saturation region. This verifies the conclusion made in [36] that entropy drives solvent molecules into the saturated region. It should be noted that the saturation concentrations of group II and group III are the same. A comparison between group IV and the other groups implies that the value of the saturation concentration mainly depends on the size of the counterions, rather than the size of solvent molecules or coions. Furthermore, as expected, the counterions accumulate to the close packing concentration $1/a_1^3$, i.e., 1.666 M for a₁ = 10 Å, and 3.254 M for a₁ = 8 Å, in the saturation region.

Figure 4.

(Color online) Counterion concentrations vs. distance in Å to the charged surface with different ionic sizes and with no ionic sizes (the classical PB theory). The linear size of counterions is a₁. The counterion concentration at the charged surface is $1/a_1^3=1.666$ M when a₁ = 10 Å and is $1/a_1^3=3.254$ M when a₁ = 8 Å.

In the second case, we study the relationship between counterion concentrations and the surface charge density. We fix the linear sizes

$$a_0=8\AA ,a_1=10\AA ,a_2=2\AA .$$

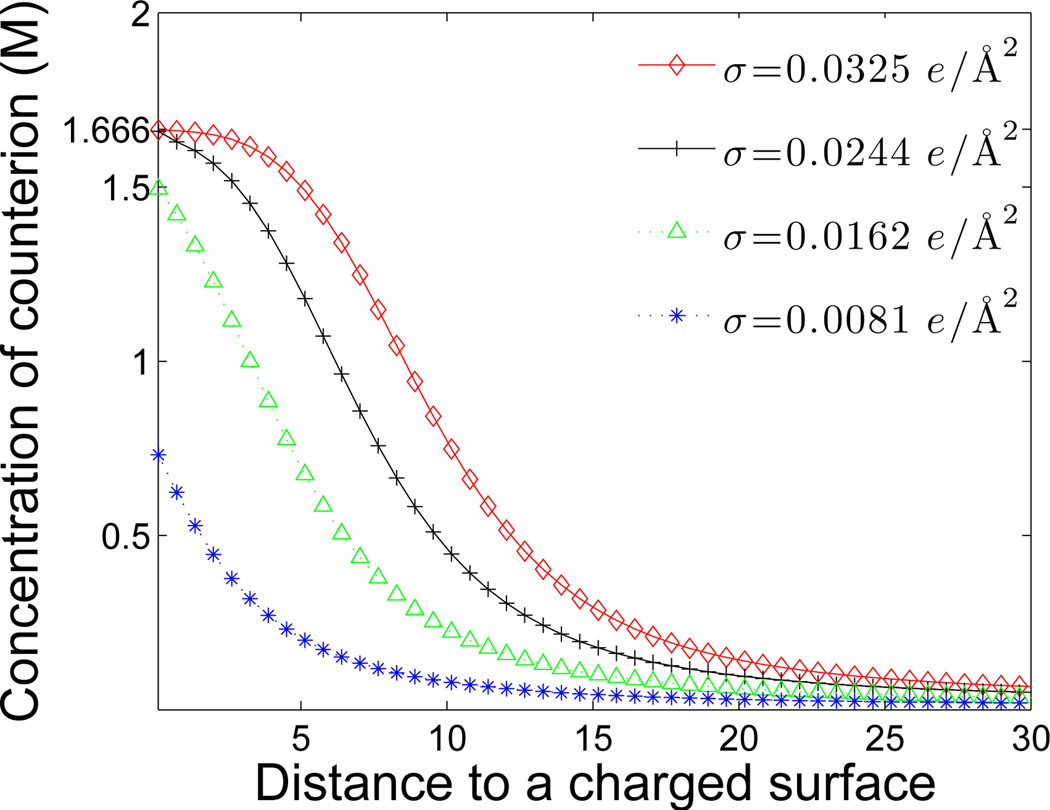
We vary the total fixed surface charge Ze to be

$$Ze=80e,60e,40e,\text{and}20e,$$

which correspond to the surface charge density

$$\sigma =0.0325e/{\AA }^2,0.0244e/{\AA }^2,0.0162e/{\AA }^2,\text{and}0.0081e/{\AA }^2,$$

respectively. As depicted in Figure 5, the surface charge densities σ = 0.0081 e/Ų and σ = 0.0162 e/Ų are not high enough to attract the counterions to form a saturation region. In contrast, higher charged surfaces with charge densities σ = 0.0244 e/Ų and σ = 0.0325 e/Ų make the counterions come to a saturation concentration, 1.666 M, which is determined by the same linear size a₁ = 10Å of counterions. Also, it is easy to see that a higher charged surface density yields a wider saturation region.

Figure 5.

(Color online) Counterion concentration vs. the distance in Å to the charged surface with different values of the surface charge density σ.

4.3 Example 3

We now consider a system with the same geometrical setting but with a highly negatively charged surface of the spherical colloidal particle and with multiple ionic species in the solution occupying the region Ω \ B_c. We assume again that the total surface charge is Z e. Our parameters are

$$M=3,z_1=+3,z_2=+2,z_3=+1,Z=-200,N_1=N_2=N_3=-Z/3,R=10\AA ,L=80\AA .$$

Our numerical grid size is 128 × 128 × 128.

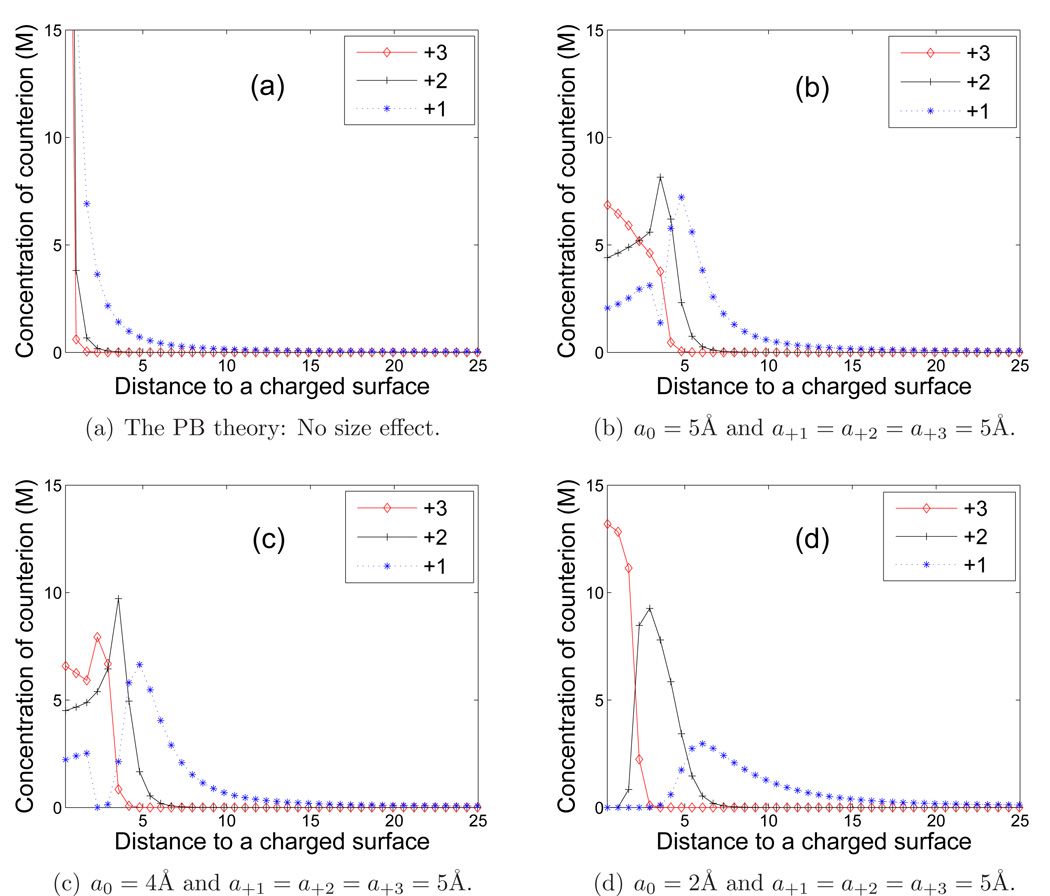
We first use our Lagrange multiplier method described in Subsection 3.1 to minimize the electrostatic free-energy functional that does not include the ionic size effect under the respective constraints to obtain the equilibrium concentrations and the electric field. These are the classical PB solutions of our underlying problems. The resulting concentrations of these multivalent ions are plotted in Figure 6 (a), where +i with i = 1 or 2 or 3 means the concentration of the counterion with the valence +i. We then use our augmented Lagrange multiplier method described in Subsection 3.2 to solve the same constrained optimization problem that includes the ionic size effect. We denote by a_+i the linear size of the counterion with valence +i (i = 1, 2, 3) and consider the following three groups of linear sizes of counterions:

$$\mathrm{\text{Group}}\mathrm{I}:a_0=5\AA ,a_{+1}=5\AA ,a_{+2}=5\AA ,a_{+3}=5\AA ;\mathrm{\text{Group}}\mathrm{I}\mathrm{I}:a_0=4\AA ,a_{+1}=5\AA ,a_{+2}=5\AA ,a_{+3}=5\AA ;\mathrm{\text{Group}}\mathrm{I}\mathrm{I}\mathrm{I}:a_0=2\AA ,a_{+1}=5\AA ,a_{+2}=5\AA ,a_{+3}=5\AA .$$

We plot our computed concentrations of the three counterions in Figure 6 (b) for Group I, (c) for Group II, and (d) for Group III.

Figure 6.

(Color online) Concentrations of multivalent counterions vs. the distance in Å to the charged surface. In the symbols, +i means the concentration of the counterion with the valence +i (i = 1, 2, 3). (a) The classical PB solution: without the size effect. (b) The size effect included with the linear sizes of Group I. (c) The size effect included with the linear sizes of Group II. (d) The size effect included with the linear sizes of Group III.

From Figure 6, we see that the concentration profiles for the counterions predicted by the classical PB theory are monotonically decreasing. They deviate significantly from those predicted by size modified mean-field models. When the ionic size effect is included, concentrations of the counterions are quite moderate, and counterions of different species become stratified, cf. Figure 6 (b)–(d). Notice that the difference between (b), (c), and (d) in Figure 6 is only in the linear size a₀ of the solvent molecule. From Figure 6 (d), we see that, with a smaller size a₀ = 2 Å of the solvent molecule, a stronger stratification occurs in the vicinity of the charged surface. It is also very interesting to observe that, with the same linear size of all the counterions, the counterions with higher valences are easier to be attracted to the charged surface. For instance, the trivalent counterions are attracted first to compensate the surface charge, and then are divalent counterions, and then are monovalent ions. This agrees with some initial predictions in [40] with a Poisson–Fermi formalism.

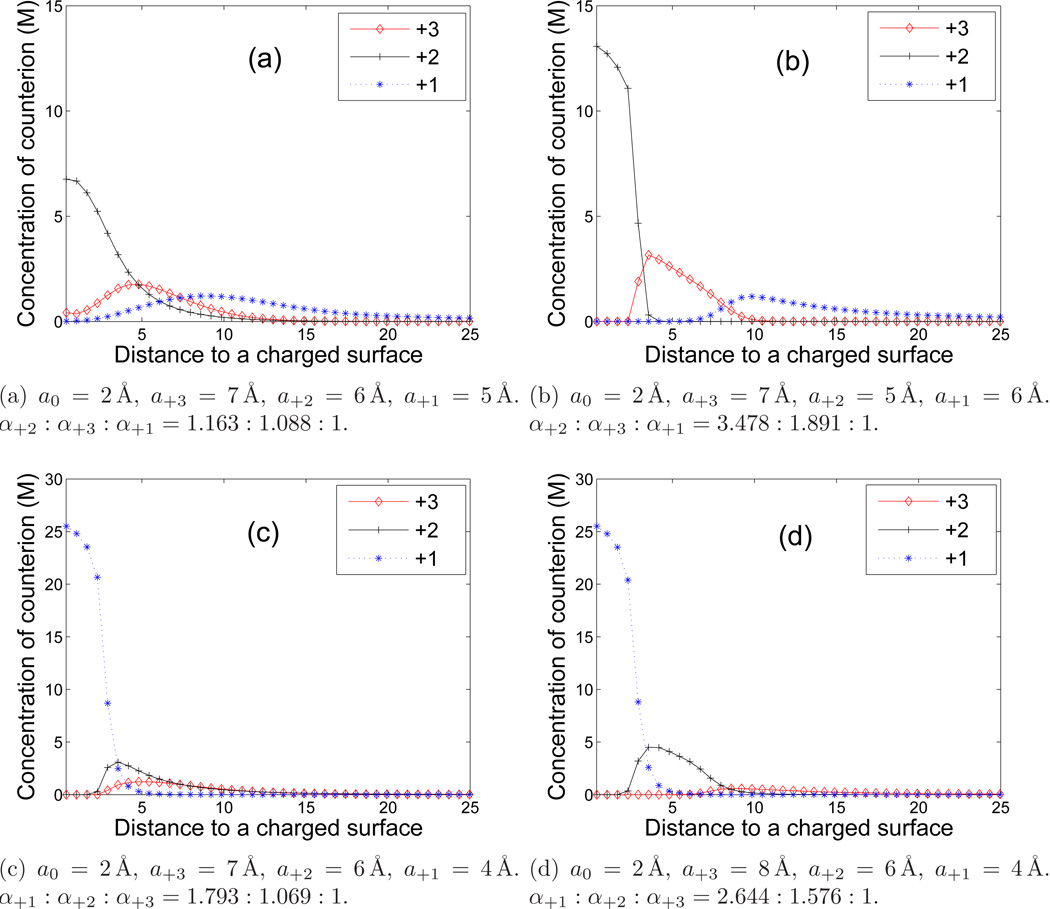
To further investigate the role of the ionic valence and ionic size on the distributions of multiple counterions, we perform a series of more numerical computations with the following different combinations of ionic valences and sizes:

$$(a_0,a_{+3},a_{+2},a_{+1})=(2\AA ,7\AA ,6\AA ,5\AA );(a_0,a_{+3},a_{+2},a_{+1})=(2\AA ,7\AA ,5\AA ,6\AA );(a_0,a_{+3},a_{+2},a_{+1})=(2\AA ,7\AA ,6\AA ,4\AA );(a_0,a_{+3},a_{+2},a_{+1})=(2\AA ,8\AA ,6\AA ,4\AA ).$$

For each set of linear sizes, we plot in Figure 7 the concentration profiles of all the three counterions. After analyzing the differences among the plots, we realize that the stratification behavior of the counterions in the vicinity of the charged surface is determined by the ionic valence-to-volume ratios, i.e., by the parameters

$${\alpha }_i=\frac{z_i}{a_i^3},i=1,\dots ,M.$$

Figure 7.

(Color online) Concentrations of multivalent counterions vs. the distance in Å to the charged surface. In (a) and (b), α₊₂ > α₊₃ > α₊₁. In (c) and (d), α₊₁ > α₊₂ > α₊₃.

Figure 7 (a) and (b) show that the divalent counterions are distributed closest around the surface, and then are the trivalent counterions, and then are the monovalent counterions, since in this case

$${\alpha }_{+2}>{\alpha }_{+3}>{\alpha }_{+1}.$$

Moreover, we observe that the larger differences of α_i the stronger stratification. For instance, the stratification phenomenon in Figure 7 (b) is stronger than that in Figure (7) (a), since the differences of the values of α_i in Figure 7 (b) are larger than those in Figure 7 (a). In Figure 7 (c) and (d), we see that the monovalent counterions are distributed closer to the charged surface than the other two counterions, as α₊₂ is greater than the other two counterparts α₊₃ and α₊₁. With larger differences among α_i, Figure 7 (d) exhibits more pronounced stratification layers than those in Figure 7 (c) in the vicinity of the charged surface.

5 Conclusions

In this work, we study numerically the mean-field electrostatic free-energy functional (1.1) for an ionic solution with multiple ions of possible different valences and ionic sizes. We develop (ψ, c)-formulation and (E, c)-formulation of the free energy and design an augmented Lagrange multiplier method for our underlying constrained optimization problem.

Our numerical tests demonstrate that our method is accurate and efficient. In particular, our method improves largely the efficiency of a local relaxation method that has been previously proposed. It is worth to note that the complexity of our iteration method is in fact similar to that of Newton’s iteration method which is a robust method for treating the nonlinearity in the PB equation. In both methods, a linear boundary-value problem of Poisson type equation is solved in each iteration. Therefore, our method is promising in future applications, e.g., the level-set variational implicit-solvent modeling of charged biomolecules [48, 49].

We apply the continuum model (1.1) and our numerical method to study how the ionic sizes, the ionic valences, the size of a solvent molecule, and the surface charge density affect the counterion concentrations near a charged surface. We find the following:

1. The classical PB theory that does not include the ionic size effect gives a poor prediction of the counterion concentration near the charged surface;

2. The counterion concentrations reach saturation values in a region near the charged surface. As the size of the counterion decreases, the saturation value increases and the width of the saturation region decreases. This value is not affected much by the size of coions and that of the solvent molecule;

3. The concentrations of multiple species of counterions with different valences exhibit stratification layers, resulting from the competition of counterions in binding to the charged surface. The ionic valence-to-volume ratios

   $$\frac{z_i}{a_i^3},i=1,\dots ,M,$$

   are the key parameters in determining the structure of these layers. For instance, the counterions with the highest valence-to-volume ratio form the top layer in the region closest to the charged surface and then becomes the second top layer in the next region, and so on. Those counterions with the lowest valence-to-volume ratio form the bottom layer in the region closest to the charged surface but the top in the region further away.

We note that several physical effects are neglected in the continuum model used here. These include the Stern layer of counterions surrounding a charged surface due to the ionic steric hindrance, the image charge effect, and the nonuniformity of the dielectric permittivity.

The current study is clearly in the direction of pushing a continuum model to its maximum capacity in terms of capturing microscopic details of ionic solutions. But how far can we go in this direction? To answer this question, we address a number of issues related to our studies.

The first issue is about the optimal packing of ions in a fixed space. Our current model and method predict that a full, 100% packing: for the case of only one species of counterions in the solution, the concentration of the counterions near the charged surface is exactly the inverse of the ionic volume. In real systems, however, only a fraction of a spatial region of unit volume can be occupied by the ions. To capture this partial packing, we can introduce some packing parameters λ_i with 0 < λ_i < 1 (i = 0, …, M) in the entropic part of our free-energy functional (1.1) as

$$k_{B}T\sum _{i=0}^M{\int }_{\mathrm{\Omega }}{c}_i\text{log}({\lambda }_i^{-1}{a}_i^3{c}_i)dV.$$

Effectively, we are enlarging the volumes $a_i^3$ and our results will then predict the correct packing of counterions near the charged surface. One of course needs to adjust the parameters λ_i to achieve quantitatively an optimal result.

Second, we have found that the ionic valence-to-volume ratios play a key role in determining some of the important properties of the concentration profiles for counterions near the charged surface, particularly for systems with multiple ionic species of multiple valences and different sizes. It is then necessary to understand how such parameters affect quantitatively the concentration profiles, the stratification structure, and the free energy of an underlying system. It will be also interesting to see how our findings with these important parameters can be applied to the study of some important issues of real biological systems, e.g., the selectivity of ions passing through ion channels.

Third, the differences between a uniform ionic size and non-uniform ionic sizes are only explored numerically in our current work. With the assumption on the charge neutrality of ions in the solution, Li [31] obtained (1.2), the implicit Boltzmann distributions that relate the equilibrium ionic concentrations c₁, …, c_M and the electrostatic potential ψ. If all the sizes are the same, then we have explicit formulas for these concentrations depending on the potential, the generalized Boltzmann distributions, cf. [31]. Consequently, it is possible to study such differences analytically.

Finally, we point out that a mean-field model like (1.1) does not capture ion-ion correlations. In fact, Li [31] proved rigorously that, under the assumption of charge neutrality of ions in the solution and using the function (1.1), the negative induced charge density $-{\sum }_{i=1}^M{z}_{i}e{c}_i$, as an implicitly defined function of the potential ψ, is the derivative of a strictly convex function. This important analytical property implies that the classical PB-like mean-field model like (1.1), with or without the size effect included, fails in predicting the ion mediated like-charge attractions [50, 51, 44, 31]. One way to circumvent this problem is to introduce nonlocal or convolution terms in the free-energy functional [52]. But it is unclear if such an approach will be accurate and efficient for large charged systems. It therefore remains still challenging to develop systematically theories and methods that include the ion-ion correlation, the ionic size effect, and other microscopic properties of ions and that can be applied to efficient studies of large biological systems.