Abstract
With the goal of non-invasively localizing cardiac ischemic disease using body-surface potential recordings, we attempted to reconstruct the transmembrane potential (TMP) throughout the myocardium with the bidomain heart model. The task is an inverse source problem governed by partial differential equations (PDE). Our main contribution is solving the inverse problem within a PDE-constrained optimization framework that enables various physically-based constraints in both equality and inequality forms. We formulated the optimality conditions rigorously in the continuum before deriving finite element discretization, thereby making the optimization independent of discretization choice. Such a formulation was derived for the L2-norm Tikhonov regularization and the total variation minimization. The subsequent numerical optimization was fulfilled by a primal-dual interior-point method tailored to our problem’s specific structure. Our simulations used realistic, fiber-included heart models consisting of up to 18,000 nodes, much finer than any inverse models previously reported. With synthetic ischemia data we localized ischemic regions with roughly a 10% false-negative rate or a 20% false-positive rate under conditions up to 5% input noise. With ischemia data measured from animal experiments, we reconstructed TMPs with roughly 0.9 correlation with the ground truth. While precisely estimating the TMP in general cases remains an open problem, our study shows the feasibility of reconstructing TMP during the ST interval as a means of ischemia localization.
Keywords: Inverse Problem, Electrocardiography, Finite Element Method, PDE Optimization, Myocardial Ischemia, Bidomain Model, Total Variation
1 Introduction
Electrocardiography (ECG) aims to non-invasively capture the electrophysiological activity of the heart by measuring its resulting potential field at the body surface. Because of recent advances in computational modeling, computing power and imaging technology, ECG is evolving from a basic clinical tool into a new era of personalized healthcare, in which computer models integrate not only unprecedented complexity and realism but also biophysical information specific to individual subjects [27]. Subject-specific computer models, typically in anatomical or physical aspects, are poised to promote mechanistic and functional studies at various biological levels ranging from cells up to organs, opening promising opportunities for clinical diagnosis, intervention planning and therapy delivery. Essential to this emerging paradigm, and the overarching goal of this study, is the development of computational methods that efficiently handle enough model complexity and realism to be useful for clinical needs.
The foundation of ECG is an inverse source problem governed by partial differential equations (PDEs) which describe the bioelectric source/conduction model of the heart and body. The most biophysically accurate yet tractable heart model is the bidomain approach [25], in which the cardiac source is represented by the transmembrane potential (TMP), embedded within interleaved intracellular and extracellular domains. Research on recovering this source model from body-surface ECG has been limited compared with the studies on other cardiac source models, such as epicardial potentials [2] or activation time [8]. Inverse ECG problems are generally ill-posed, and recovering TMP is more difficult and computationally demanding than recovering other source models [23].
This study aimed to inversely calculate the TMP throughout the myocardium from the body-surface potentials with the specific goal of localizing myocardial ischemia. A leading cause of cardiac death [18], myocardial ischemia typically results from occlusion of coronary arteries. The disease occurs when the blood flow shortage causes cardiac myocytes to undergo acidosis and anoxia, resulting in a progressive deterioration of electrical and mechanical activity of the affected heart tissue, ultimately leading to life threatening rhythm abnormalities. Traditional ECG diagnosis needs expert interpretation and has limited ability to localize ischemic regions. The ability to acquire a whole-heart TMP map will greatly enhance clinicians’ ability to identify the location and extent of ischemia. While reconstructing the TMP through all time remains an open problem, this is not necessary for ischemia localization, which may be achieved instead by identifying spatial nonuniformity of the TMP at the plateau phase.
Our major contribution lies in presenting a new computational methodology for inverse TMP estimation using measured ischemia data obtained from animal experiments. Inverse ECG problems are conventionally solved in several steps. Based on the physical model, one derives a mathematical transformation that relates the unknown source parameters directly to the measurements, and then minimizes the misfit between the predicted and measured data. The misfit term is typically augmented with regularization terms in order to mitigate the ill-conditioning. This approach, essentially an unconstrained optimization scheme, allows constraints only on the source parameters, and hence is inadequate for complex formulations such as the bidomain model. In contrast, we treated our inverse problem in a PDE-constrained optimization framework that incorporates the whole PDE model as a constraint. Our approach offers ample flexibility not only for adjusting the underlying physical model but also for applying various physically-based constraints simultaneously.
PDE-constrained optimization has been a frontier in scientific computing research over the last decade, and numerous theoretical accomplishments [11] have laid the foundation for its application. Its initial introduction to ECG problems [23] was limited to quadratic objective functions with equality constraints. Here we extended that inaugural work by allowing nonlinear objective functions and constraints in both equality and inequality forms.
Solving PDE-constrained optimization numerically is more challenging than solving an ordinary optimization problem or a PDE alone. The task involves forming the optimality conditions and solving them through iterative methods, with each iteration solving the entire PDE system at least once. As such, most existing PDE solvers cannot be directly used when a PDE becomes a constraint in the optimization context. Also, the large size of the discretized PDE constraints poses a challenge for contemporary optimization algorithms.
To tackle these difficulties, one needs not only to efficiently integrate generic optimization algorithms, advanced PDE solvers such as adaptive finite element methods, and large-scale scalable linear algebraic solvers such as the Newton-Krylov method [3], but also to create a framework that exploits the mathematical structure specific to the physical model being considered, in our case bioelectric models. Such integration has yet to be fulfilled. Rather, most engineering studies formulate the inverse problem in a discrete, algebraic form based on a predefined mesh, and then use numerical optimization methods. However, such a practice does not guarantee mathematical rigor and may lead to inconsistencies when simulations are performed over different meshes.
This study investigated the formulation, discretization and numerical solution of our PDE-constrained optimization framework realized by the finite element method. We explored two minimization schemes: the Tikhonov regularization and the total variation (TV) regularization. Our contribution features the following new ingredients: (1) formulating optimality conditions in the continuum before discretization, thereby achieving consistency over multi-scale simulation; (2) comparing this approach with the discretize-then-optimize approach; (3) deriving robust finite element formulation for both the Tikhonov and the TV regularization; (4) incorporating inequality constraints in optimization, handled by a tailored primal-dual interior-point method that exploits the block-matrix structure so as to optimize numerical efficiency.
This paper is organized as follows. Section 2 describes the mathematical model. Section 3 describes the optimization framework for the inverse problem, its finite element solutions, and the primal-dual interior method. Section 4 presents numerical experiments. Section 5 discusses computational and biophysical issues.
1.1 Background and Related Work
Inverse ECG problems have been formulated in terms of various heart source models, such as dipoles models, epicardial potentials, the activation wavefront, the monodomain model and the bidomain model (see an overview by Gulrajani [10]). Among these models the bidomain model is the most physically realistic, and its source, the TMP (whose time course is known as the “action potential”), is described by numerous membrane kinetic models that account for electrophysiological activities at the cell level [29]. The bidomain model is the predominant choice for simulating cardiac electrical activity at the tissue/organ level [4,25], and has been widely used to investigate the relation between the cellular origins and extracardiac consequences of myocardial ischemia [13,17]. Ischemia manifests its electrophysiological effects by altering cell membrane kinetics and accordingly the TMP, leading to elevation/depression in the ST segment of the ECG signal—the hallmark of myocardial ischemia in clinical ECG diagnosis, see [26] for a review of electrophysiological modeling of ischemia.
While reproducing the entire TMP (with the bidomain model) from the body surface potentials remains a challenge, it appears more tractable to solve a simplified problem of reconstructing ischemia-induced spatial variation of TMP amplitude during the plateau phase. In this phase, there is normally about 200 ms of relatively stable and uniform TMP amplitude, resulting in a nearly equipotential condition throughout the heart and correspondingly on the body surface—the isopotential ST segment of the ECG signal. In ischemic cells, however, the plateau-phase TMP suffers from attenuated amplitudes, forming a voltage difference between healthy and ischemic regions. The voltage difference results in extracardiac currents and ultimately the hallmark ST-segment shift in the body surface ECG potentials. The resulting ECG patterns are temporally stable and spatially fairly simple, suggesting that suitable reconstruction may be feasible.
Partly because of its severe ill-conditioning, the problem of reconstructing the myocardial TMP from body-surface potentials has seen minimal progress [23] in comparison with other inverse ECG problems. One study reconstructed the TMP only at the heart surface [22], and this approach compared favorably with recovering epicardial extracellular potentials [21]. Another approach sought the integral of TMP over the ST segment rather than at one time instant, thereby making the inverse solution more robust to input noise [15]. A level-set framework has been proposed that parameterizes the TMP by the size and location of ischemia [19,24,28]. A recent study attempted to directly compute the TMP within the heart via the PDE-constrained optimization approach [23], but the study was limited to 2D models and synthetic data. Our study extends that approach both by advancing computational methods and by using measured ischemia data from animal experiments.
1.2 Mathematical Notation
We use regular lower-case letters for a variable or a continuous function, and boldface lower-case letters for a vector. Different fonts for the same letter usually mean the continuous or discrete version of the same physical quantity. For example, u denotes a continuous potential field, and its numerical discretization is denoted by a real vector u ∈ ℝn. An upper-case calligraphic letter represents a continuous functional or operator operating on a continuous function, e.g.,
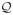 in the expression
in the expression
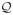 u. A bold capital letter denotes a matrix and is the discrete version of the operator given by the same letter if it exists. For example, Q is the discrete version of
u. A bold capital letter denotes a matrix and is the discrete version of the operator given by the same letter if it exists. For example, Q is the discrete version of
 .
.
2 The Bioelectric Model
The bioelectric model, illustrated in Fig 1, consists of a static bidomain heart model coupled with a quasi-static torso conduction model, described as follows:
| (1) |
| (2) |
Fig. 1.
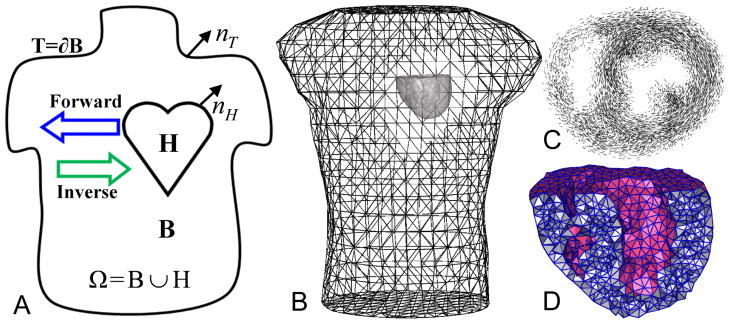
Panel (A): the problem domain. (B): the heart/torso geometry. (C): fiber structure of a 1 cm-thick slice of the heart. (D): a cross-sectional view of the heart mesh.
Here H and B represent the domain of the heart and the torso volume. Eq (1) is the static bidomain heart model, which consists of an extracellular potential field denoted by ue and an intracellular potential field denoted by ui (not explicitly present in this equation). The transmembrane potential, defined as v = ue − ui, forms the source term of the model. The variables σi and σe represent the intra- and extracellular conductivity, modeled by symmetric, positive-definite second-order tensors dependent upon spatial location. Eq (2) states that the torso is a passive volume conductor, with ub denoting the potential and σt denoting the conductivity of the torso volume.
The above model satisfies the following boundary conditions at the torso surface T and the heart-torso interface H:
| (3) |
| (4) |
| (5) |
| (6) |
Here Eq (3) assumes no current flows across the torso surface. Eq (4) assumes the continuity of potentials on ∂H. Eq (5) dictates the conservation of the current flowing across the heart boundary. Eq (6) dictates that the intracellular current, σi∇ui, stops at the heart boundary, and only the extracellular current flows into the torso, yielding Eq (5).
The above model and boundary conditions can be jointly expressed by a Poisson equation:
| (7a) |
| (7b) |
| (7c) |
| (7d) |
| (7e) |
where the boundary conditions (4)–(6) have been implicitly assumed in this formulation. Details of this model can be found in [23,24] and Chapter 5 of [10].
The forward problem and the inverse problem associated with this physical model are stated as follows. Given the transmembrane potential v, the forward problem is to calculate u (the extracellular potential throughout the torso and heart volumes) by solving Eq (7a). Its corresponding inverse problem is to reconstruct v based on a sampling of u measured on the body surface. Both the forward and inverse problems assume that domain geometry and conductivities are known and remain fixed.
An important property of the forward/inverse problem is that it admits non-unique solutions. From Eq (7a) one may see that the mapping between v and u is affine and non-injective: if u0 is the solution of a given v0, so is u0 + c for any constant c. We enforce the uniqueness in the forward problem by requiring u satisfy the following constraint:
| (8) |
where d(x) denotes the measured body-surface potential field. This constraint enables one to consider u as a function of v. It also reasonably describes the situation of the inverse problem where one needs to fit the unknown u to the known d.
The non-uniqueness of the solution to the inverse problem refers to the fact that v0 and v0 +c yield identical u for any constant c. Such non-uniqueness reflects the physical understanding that the electric source is essentially induced by the currents (gradient of potentials) rather than the potential field itself. In practice all the potential fields that differ by a constant are treated as identical because the choice of any particular potential field depends solely on how to pick the ground reference.
2.1 Galerkin Formulation and Finite Element Solution of the Forward Model
This paper solves the elliptic PDE by the Galerkin-based finite element method. Assuming that u ∈ ℍ1(Ω), v ∈ ℍ1(H) (here ℍk(·) denotes the kth-order Hilbert-Sobolev space defined over a domain), the variational form of Eq (7) after applying the Green’s divergence theorem and the natural boundary conditions is given as follows:
| (9) |
Our finite element discretization is described by the following definition.
Definition 1
Let Ωh denote a tessellation of Ω and Hh denote a tessellation of H. Let be the global finite element basis functions associated with Ωh and be the global basis functions associated with Hh. Assume u and v are discretized by . Let u = (u1, u2, …, uNu)T and v = (v1, v2, …, vNv)T denote the two coefficient vectors.
In this study we adopted the linear finite element method, in which case each φi and ψi is a hat function associated with the node i of the mesh Ωh or Hh. Accordingly, u and v contains the voltage values at mesh nodes. These implications are henceforth assumed in this paper unless explicitly mentioned.
Applying Definition 1 to Eq (9) and choosing our test space to be the same as our trial space (the traditional Galerkin formulation), we obtain a matrix system as follows:
| (10) |
where A ∈ ℝNu×Nu is the stiffness matrix, Ai,j = 〈∇φi, σ∇φj〉Ω; R ∈ ℝNu×Nv, Ri,j = 〈∇φi, σi∇ψj〉H. Here 〈·, ·〉Ω denotes the inner product taken over the space L2(Ω), defined as
| (11) |
It is worth noting that ue and v may be discretized by different trial spaces. This practice is desirable in inverse simulations, as we will see later that the inverse calculation prefers both a fine heart mesh for an accurate conduction model and a coarser heart mesh for representing the source term v.
When implementing an ECG simulation, one should ensure that boundary conditions at the heart-torso interface are applied properly. Another set of boundary conditions alternative to Eq (5) and (6) also lead one from the Poisson Equation given by Eq (7a) to the same variational formulation Eq (9). The alternative boundary conditions state that nH · σi∇v = 0 and nH · (σi + σe)∇ue = 0. It differs from Eq (6) in that it assumes zero Neumann condition on the transmembrane potential, whereas Eq (6) assumes zero Neumann condition on the intracellular potential. There has been controversy over the choice between the two boundary condition sets. Later studies have shown that Eq (6) matches experiments more faithfully, but simulation scientists are advised to be aware of this subtle difference. See Chapter 5.9 of [10] for more discussions.
3 Inverse Problem
The inverse problem of estimating the transmembrane potential can be formulated as an optimization problem in which all the physical quantities are governed by a set of PDEs. This PDE-constrained optimization problem can be expressed in an abstract form as follows:
| (12a) |
| (12b) |
In the optimization community, v and u are often known as the control variable and state variable, respectively. The first term of the functional J is the misfit between predicted and observed data, measured by a certain Lp norm at the body surface T. The operator
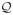 : ℍ1(Ω) → Lp(T) is the volume-to-surface projector. The second term of J is a regularization term for stabilizing the minimization, where v0 denotes a prior estimation of v. The operator
: ℍ1(Ω) → Lp(T) is the volume-to-surface projector. The second term of J is a regularization term for stabilizing the minimization, where v0 denotes a prior estimation of v. The operator
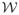 : ℍ1(H) → Lp(H) defines certain regularity conditions to be imposed on v. Common choices for
: ℍ1(H) → Lp(H) defines certain regularity conditions to be imposed on v. Common choices for
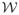 (v) are v, ∇v, or Δv. The parameter β ≥ 0 controls the amount of regularization. e(u, v) = 0 is an abstract notation for the physical model. In our problem it refers to the PDE Eq (7) with proper boundary conditions. The last two constraints represent abstract inequality bounds for u and v, with
(v) are v, ∇v, or Δv. The parameter β ≥ 0 controls the amount of regularization. e(u, v) = 0 is an abstract notation for the physical model. In our problem it refers to the PDE Eq (7) with proper boundary conditions. The last two constraints represent abstract inequality bounds for u and v, with
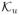 and
and
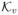 denoting proper cones.
denoting proper cones.
The term “proper cone” is frequently used in optimization literature to define generalized inequality relation. A set
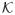 is called a convex cone if for all x1, x2 ∈
is called a convex cone if for all x1, x2 ∈
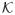 and θ1, θ2 ≥ 0, we have θ1x1 + θ2x2 ∈
and θ1, θ2 ≥ 0, we have θ1x1 + θ2x2 ∈
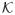 . A cone is proper when it is convex, closed, solid and pointed (if x ∈
. A cone is proper when it is convex, closed, solid and pointed (if x ∈
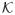 and −x ∈
and −x ∈
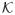 , x must be zero). Given a proper cone
, x must be zero). Given a proper cone
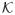 , its dual cone
, its dual cone
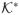 is defined by
is defined by
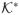 = {y|xTy ≤ 0, ∀x ∈
= {y|xTy ≤ 0, ∀x ∈
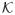 }. Note that
}. Note that
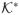 is also convex. More information about cones can be found in [5].
is also convex. More information about cones can be found in [5].
It has been proven that Eq (12a) admits a solution if the objective, the constraints and the feasible sets all satisfy certain conditions on convexity, closure and continuity [12]. In practical scenarios these conditions are normally satisfied. All practical solutions to the problem stated in Eq (12) amounts to solving its optimality conditions, also known as the Karush-Kuhn-Tucker (KKT) conditions given as:
| (13) |
| (14) |
| (15) |
| (16) |
| (17) |
where p, λ are the Lagrange multipliers associated with each constraint;
and
are the dual cones of
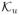 and
and
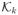 .
.
In the rest of this section, we will elaborate on how to populate the abstract concept presented above in practical simulations in the context of finite element methods. Our goal is to translate the mathematical formulation into a numerical system for efficient numerical optimization. In particular we will address the following four topics in the subsequent subsections: (1) Tikhonov regularization, (2) finite element formulation of the PDE constraint, (3) total variation regularization and its finite element formulation, and (4) inequality constraints and a primal-dual method for numerical optimization.
3.1 Tikhonov Regularization
Perhaps the most popular regularization approaches to ill-conditioned problems, the Tikhonov regularization uses the L2 norm for the objective functional given by Eq (12a), yielding:
| (18) |
Because of its quadratic nature, the Tikhonov regularization can be readily integrated with the variational formulation of the optimality conditions to be described in the next section. When the regularizer is of the Sobolev-norm type such as
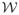 (v) = v, ∇v, or Δv, we can compute it via a finite element formulation as given in [40]:
(v) = v, ∇v, or Δv, we can compute it via a finite element formulation as given in [40]:
| (19) |
where M and S are the mass and stiffness matrices respectively, based on the finite element discretization of v. Their Cholesky factor conceptually serves as the equivalent of
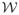 , though such factorization is often not necessary when implementing the optimization.
, though such factorization is often not necessary when implementing the optimization.
Our finite element formulation for
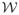 as provided in Eq (19) is superior to the common expedient practice of discretizing
as provided in Eq (19) is superior to the common expedient practice of discretizing
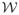 directly over a given mesh. Independent of mesh size, our formulation not only ensures consistency under multiscale discretization but also allows adaptive refinement during optimization iterations. Moreover, mesh-grid-based discrete derivative operators are not strictly compatible with the Galerkin finite element discretization because the field has less regularity at nodes than within elements, whereas our formulation does not have this problem.
directly over a given mesh. Independent of mesh size, our formulation not only ensures consistency under multiscale discretization but also allows adaptive refinement during optimization iterations. Moreover, mesh-grid-based discrete derivative operators are not strictly compatible with the Galerkin finite element discretization because the field has less regularity at nodes than within elements, whereas our formulation does not have this problem.
3.2 Discretize the PDE constraint in the variational form
There are two approaches to numerically tackling the problem given in Eq (13): discretize-then-optimize (DTO) or optimize-then-discretize (OTD). The DTO approach discretizes all the quantities (both the objective and constraints) into vectors or matrices and treats the discretized problem as a pure algebraic optimization problem. The OTD approach derives the optimality conditions in continuous function spaces before discretizing those conditions into numerical systems. Although the DTO approach is more popular among the engineering community, the OTD approach preserves more faithfully the structure inherent in the underlying infinite-dimensional optimization problem. This approach is less subject to mesh size, enables individualized discretization for each quantity, and facilitates adaptive refinement techniques. Therefore we adopted the OTD approach whenever possible. The rest of this section presents the continuous optimality conditions and their discretization by finite element methods.
For illustration purposes we minimize the Tikhonov functional given by Eq (18), and assume that the minimization problem is subject only to the PDE constraint Eq (7). The Lagrangian functional for this constrained optimization problem, denoted by
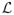 : ℍ1(Ω) × ℍ1(H) × ℍ−1(Ω) → ℝ, is defined as
: ℍ1(Ω) × ℍ1(H) × ℍ−1(Ω) → ℝ, is defined as
| (20) |
where p ∈ ℍ−1(Ω) is the Lagrange multiplier function. The optimality condition states that the optimal solution is situated at the stationary point of the Lagrangian functional. By taking the Gâteaux derivatives of
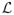 at the optimal solution (u, v, p) in the perturbation direction (ũ, ṽ, p̃), we obtain a set of equations as follows:
at the optimal solution (u, v, p) in the perturbation direction (ũ, ṽ, p̃), we obtain a set of equations as follows:
| (21a) |
| (21b) |
| (21c) |
Eq (21) is the variational form of the KKT condition, and Eqs (21a) – (21c) are called the variational form of the control equation, the adjoint equation and the state equation, respectively. This set of differential equations are linear with respect to u, v and p because the objective is quadratic and the constraint takes the linear equality form. In general they are nonlinear PDEs. We now discuss how to discretize them by the finite element method.
The key to applying the Galerkin finite element discretization to Eq (21) is to take the perturbation in each finite element basis functions. We discretize u and v according to Definition 1, and assume that p is discretized by the same trial space as for u: . Let p = (p1, p2, …, p Nu)T. The perturbation p̃ and ũ are chosen from the finite-dimensional space {φi}, and ṽ chosen from {ψj} as given in Definition 1. Eq (21) then yields a 3 × 3 block matrix system for numerical computation, given as follows:
| (22) |
which is a symmetric system where each block is given below: (here 〈·, ·〉 denotes the inner product defined in Eq (11))
| (23) |
The remaining task is to numerically solve the large linear system Eq (22), which is known to be positive indefinite. Existing methods include the BiStabCG [23], the adjoint method, and computing the Schur complement [5,35] (the one adopted in this paper). The adjoint method is widely used especially for large-scale linear systems. The method affects discretization considerations to be discussed in Section 3.2.1 so we describe it here: it acquires the derivative of J with respect to v (by solving the state and adjoint equations sequentially), then applies one step of gradient descent of J, and repeats the above two steps until J is minimized.
3.2.1 Optimize-then-Discretize versus Discretize-then-Optimize
Here we compare the two approaches and show under what conditions they are equivalent. As will be shown, the connection and distinction between the two approaches are manifested by one fact: they result in identical numerical optimality conditions only when the state variable u and the adjoint variable p are discretized by the same trial space. Based on this understanding we discuss several theoretical and practical concerns of the two approaches.
The DTO approach applies the finite element discretization to the objective functional and the constraint PDE, yielding an algebraic optimization problem of the form
| (24) |
subject to Eq (10), where Q is the matrix version of the volume-to-surface projector
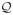 , and MT and MH are identical to those given by Eq (23). The KKT conditions of this problem are exactly Eq (22). The discrete adjoint vector p multiplies to the stiffness matrix A, indicating that its continuous version, p, is discretized by the trial space of the state variable u.
, and MT and MH are identical to those given by Eq (23). The KKT conditions of this problem are exactly Eq (22). The discrete adjoint vector p multiplies to the stiffness matrix A, indicating that its continuous version, p, is discretized by the trial space of the state variable u.
The two approaches differ when the state and adjoint variables are represented by different trial spaces. When the same trial space is chosen for both variables, the KKT system (22) is a symmetric matrix, and its reduced equation with respect to the control variable v, obtained by eliminating the state and adjoint variables, is the full derivative of the objective functional J with respect to v. With state and adjoint variables discretized by different trial spaces, Eq (22) becomes nonsymmetric, and its reduced equation generally does not strictly represent the derivative of J with respect to v. This subtle difference in the representation of derivatives is worth noting, because in practice Eq (22) is often not solved as a whole (e.g., by BiCGStab [23]) but instead by the adjoint method, which depends on evaluating the derivative of J to v (see Section 3.2.1).
There is no conclusion as to whether the state and adjoint variables should use identical trial spaces, and the choice depends on each problem’s structure and computational resources. The OTD approach typically requires more developmental efforts than the other. Most finite element solvers are designed for solving PDEs directly but not for optimization purposes. On the other hand, there exist many numerical optimization solvers designed for problems given in algebraic forms. One may fulfill the discretize-then-optimize approach by applying finite element discretization and numerical optimization sequentially. However, to fulfill the OTD approach one must merge the PDE and optimization solvers. In some complex scenarios, the continuous optimality conditions are not even achievable, for instance when non-linear inequality constraints or the Lp-norm are concerned. In our problem, the potential field u is smooth (from the biophysics of the problem), and p admits two more weak derivatives than u, so we believe it unnecessary to discretize p by different trial functions.
3.3 Total Variation Regularization
The total variation (TV) regularization tends to reconstruct discontinuity in the solution, a feature that is appealing to our inverse problem since the transmembrane potential field is assumed to have sharp variation between healthy and ischemic regions. A number of inverse ECG studies have adopted the TV regularization and reported superior reconstructions than the Tikhonov regularization [9,30]. Our study complements their work by integrating TV implementation with PDE-constrained optimization. Existing ECG studies have implemented the TV regularization in a algebraic form, requiring the transfer matrix and the gradient-operator matrix based on a given mesh. These matrices may either become unavailable in PDE-constrained optimization (such as the transfer matrix) or have poor numerical accuracy when high-resolution irregular meshes are used (such as the gradient-operator matrix). In contrast, we formulated the TV regularization in the continuum followed by a rigorous finite element discretization, thereby ensuring that the TV regularization has dimension-independent performance over different discretizations.
To simplify illustration, we present a TV minimization problem that contains only the PDE constraint, described as follows:
| (25) |
| (26) |
where TV (v) is the total variation functional, and ε is a small positive constant introduced to overcome the singularity where ∇v = 0. In this paper we set ε = 10−6. The Gâteaux derivative of the TV term in the direction ṽ, along with its strong form expression, is given by:
| (27) |
The major difficulty of the total variation minimization is to cope with the highly anisotropic and nonlinear term . This topic has been extensively studied by the image processing community over the past decade [42]. Numerous algorithms have been proposed for the ε-smoothed minimization, such as the parabolic-equation-based time marching scheme, the primal-dual variant of Newton’s method [6], the fixed-point iteration [38], or the second-order cone programming. More recent methods tackle the original, unsmoothed minimization problem by exploiting its dual formulation [41,42].
However, the achievements made by the imaging community do not naturally translate themselves to PDE-constrained optimization problems. The imaging community mostly consider the Euler-Lagrange equation, which is essentially the strong form of the optimality condition for the total variation minimization. The imaging community tackles the strong-form equations by finite difference methods since imaging problems are based on regular grids. In contrast, PDE-constrained optimization problems are typically defined on irregular meshes for which the finite element method is more appropriate, thereby requiring both the optimality conditions and the PDEs to be formulated in the variational form. Even if it is sometimes expedient to circumvent the variational formulation by adopting the DTO approach and devising discrete, mesh-node-based operators, we do not advocate such a practice because those discrete operators may not be rigorously compatible with finite element formulation. For example, a field approximated by linear finite elements is not differentiable at mesh nodes, so a mesh-node-based discrete gradient operator may be improper, losing desirable numerical structures that could have been obtained with regular grids, such as symmetry or positive-definiteness.
However, a major difficulty is that the total variation minimization is not naturally compatible with Galerkin finite element methods. Our aim here is to propose a framework that “almost naturally” adapts the TV minimization to finite element formulation. We do not intend to propose new algorithms for the TV minimization, but instead our goal is to transfer the aforementioned algorithms proposed by the imaging community into the finite element formulation. In this paper, we adopted the fixed-point iteration because of its robustness. However, it is worth noting that our finite element formulation is not limited to the fixed-point iteration, but can be naturally applied to other TV-minimization algorithms such as the primal-dual Newton’s method [6]. Further discussion is presented in Section 5.1.
3.3.1 Fixed Point Iteration
The basic idea of the fixed point iteration (and most other iterative methods) is to solve a sequence of linearized minimization problems, each of which can be solved in the same way as we solve the Tikhonov minimization in Eq (22). (All the matrix blocks in Eq (22) will remain unchanged except MH, which will be replaced by a linearized version of
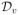 TV.)
TV.)
To linearize
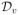 TV, the fixed point iteration fixes the denominator of Eq (27) to its value at the step k, and computes the (k + 1) step, vk+1, by the following formula:
TV, the fixed point iteration fixes the denominator of Eq (27) to its value at the step k, and computes the (k + 1) step, vk+1, by the following formula:
| (28) |
Here the denominator becomes a known scalar field over the domain H. Applying the finite element discretization on vk+1 and letting the perturbation ṽ range over the test space, one obtains a linear system identical to Eq (22) except that MH is replaced by the following formula:
| (29) |
One solves that linear system to obtain vk+1, then updates Eq (29) and continues iteration until convergence is reached. Essentially a quasi-Newton scheme, the fixed point iteration is linearly convergent and has been reported to be rather robust with respect to the parameter ε and β [38]. Its convergence domain becomes smaller with a decreased ε, but the drop-off is gradual.
A major feasibility concern about the finite element formulation of the fixed-point method is its high computational cost: Each iteration of the fixed-point method needs to compute Eq (29), which amounts to forming a stiffness matrix for the finite element heart mesh. Because ∇vk is a nonconstant field in each element, quadrature points are needed to evaluate the integrand and integral in Eq (29), and such evaluation is required in each fixed-point iteration. In order to reduce repeated calculation of Eq (29), one needs to store the coefficients of local basis functions in all elements, but this consumes a large amount of memory. Therefore we believe that the finite element formulation of the TV minimization is generally impractical due to its high computational cost.
However, the computational cost becomes feasible in a special case when linear tetrahedral elements are used. In this case, ∇vk is a constant in each clement, and hence the integration of the numerator of Eq (29) can be precomputed for each element. The calculation of Eq (29) in each fixed-point iteration is simplified to two steps: (1) updating ||∇v|| and M(v) at each element and (2) assembling all local M(v) matrices into the global matrix. The first step is a scalar-matrix multiplication only in the case of linear tetrahedral elements; with non-simplex elements or high-order basis functions, this step would involve differentiation and integration at all quadrature points, thereby increasing the computation by times where nq is the number of quadrature points in each Euclidean dimension. Given the above consideration, we advocated and adopted the linear tetrahedral elements for the TV regularization in this study.
3.4 Inequality Constraints and Primal-Dual Interior Point Method
So far we have described how to handle equality-formed constraints, such as the PDE constraint. It is often desirable to impose lower or upper bounds on physical quantities concerned in a physical model. Such inequality constraints reflect prior physical knowledge about the electric potential fields or the current fields. These bounds may concern particular parts of the domain, such as vepicardium ≤ 0, or contain spatially dependence such as vepicardium ≤ vendocardium.
Inequality constraints are usually handled by interior-point methods, which roughly fall into two categories: the barrier method and the primal-dual method. The primal-dual method is often more efficient and stable than the barrier method. In this study we used as our optimization solver the software SDPT3, which employs an infeasible primal-dual method for solving conic programming problems [34]. In view of the large size of our PDE-constrained optimization problem, a generic solver like SDPT3 may become inefficient. We present here a primal-dual formulation tailored to our optimization problem, explicitly exposing the block-matrix structures. Our purpose is to let the generic solvers fully exploit these structures so as to improve the computation efficiency.
Since inequality constraints are often pointwise bounds, we incorporate them in a discrete form after we perform the finite element formulation (see Section 3.2 and 3.3). Our optimization problem can be stated as follows:
| (30a) |
| (30b) |
Here Eq (30a) denotes the optimization problem with only the PDE constraint. It can be either Eq (24) or Eq (25). Each inequality constraint on v is represented by ci(v), with
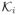 ⊆ ℝki denoting a proper cone of ki dimensions, and so does each ĉj(u) and
⊆ ℝki denoting a proper cone of ki dimensions, and so does each ĉj(u) and
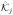
We now present how to solve the above optimization problem by a primal-dual interior-point method. The primal-dual method optimizes both the primal and dual formulation of the given problem. It approaches the optimal solution via a sequence of interior points (points that are strictly within the subspace dictated by the inequality constraints). The interior points are generated by relaxing the complementary slackness in the KKT conditions. At each iteration, the method seeks the Newton step for solving the KKT equations, determines the proper step length, and moves to the next interior point until the gap between the primal objective and dual becomes sufficiently small.
We followed the primal-dual method outlined in Chapter 11 of [5], which considers only scalar-valued inequalities, and we extend it to general inequalities associated with various cones. First, define the Lagrangian for Eq (30) as follows:
where each qi ∈ ℝki×1 is the Lagrange multipler vector for each inequality constraint; p ∈ ℝn×1 is the adjoint vector for the discretized PDE constraint.
The primal-dual method considers a relaxed version of the KKT optimality conditions given below:
| (31) |
where
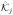 ci(v) is the Jacobian matrix of ci(v), and θi is the degree of the generalized logarithm associated with the cone
ci(v) is the Jacobian matrix of ci(v), and θi is the degree of the generalized logarithm associated with the cone
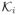 (see [5] for more information about the generalized logarithm).
(see [5] for more information about the generalized logarithm).
 ĉj(u) and θ̂j are defined in the same way. t > 0 is a scalar parameter. rcentral = 0 is named the complementary slackness condition. In the primal-dual method, this condition is relaxed by the addition of θi/t term.
ĉj(u) and θ̂j are defined in the same way. t > 0 is a scalar parameter. rcentral = 0 is named the complementary slackness condition. In the primal-dual method, this condition is relaxed by the addition of θi/t term.
The primal-dual search direction is the Newton step for the non-linear Equation (31). Let the current point be denoted by (u, v, p, q, q̂), the Newton system is expressed in a block-matrix structure:
| (32a) |
| (32b) |
Here a little explanation of the notation is needed. c denotes the aggregate of {ci(v)} and accordingly Eq (32b) represents its Hessian with respect to v. Since each ci(v) is vector-valued, its Hessian
 ci(v) is a third-order tensor. The Hessian matrix of the jth component of ci is denoted by
denotes the jth component of the vector qi. Similarly, ĉ denotes the aggregate of {ĉj(u)}, and
and
are defined in the same way. The rest matrix blocks involved in Eq (32) are given below in the Matlab format:
ci(v) is a third-order tensor. The Hessian matrix of the jth component of ci is denoted by
denotes the jth component of the vector qi. Similarly, ĉ denotes the aggregate of {ĉj(u)}, and
and
are defined in the same way. The rest matrix blocks involved in Eq (32) are given below in the Matlab format:
| (33) |
and the rest quantities, , Dĉ(u), and diag(ĉ(u)), are defined similarly to Eq (33).
After obtaining the Newton step, we did not investigate other optimization algorithms. We relied on SDPT3 to determine the step size and convergence criteria. SDPT3 employs an infeasible primal-dual predictor-corrector path-following method [35].
Based on physical considerations, one may customize a variety of inequality constraints either by designing the function ci(v) (or ĉi(u)) or by setting the inequality type (via proper cones). Here we present two types of inequality constraints commonly used in ECG simulation, both of which use an affine function in the form of ci(v) = Gv + g. The first type imposes a point-wise bound on the potential field at a user-specified domain of interest, taking the form Gv + g ≤ 0. In this case, the cone corresponding to the point-wise inequality is the non-negative orthant, whose associated generalized logarithm has a degree of θi = ki (to be used in Eq (31)). The second type of constraint bounds the current density field (the gradient of the potential field) by applying a second-order cone in the following way:
| (34) |
| (35) |
where Dx,y,z are the discrete partial-derivative operators, and s gives the current density at each node. The generalized logarithm associated with the second-order cone has a degree of θi = 2.
4 Numerical Experiments and Results
Here we present numerical experiments with the goal of verifying the aforementioned optimization framework and inverse algorithms. We conducted three simulation experiments: 1) an isotropic heart conduction model with synthetic ischemia data, 2) an anisotropic heart model with empirical ischemia data, and 3) an isotropic heart model with empirical ischemia data. The first experiment verifies our inverse algorithm under a strictly controlled setting. The second one simulates the most physically realistic situation. The third one explores whether our inverse calculation is feasible for a typical clinical situation in which patient-specific myocardial conductivity and fiber structure information are not available.
4.1 Simulation Setup
Our simulation of the PDE model Eq (7) is based on an in situ experiment that consisted of a live canine heart perfused with blood from a second animal and suspended in a human-torso-shaped tank filled with an electolytic medium that simulates human-body electrical conductivity [20], as shown in Fig 1. The heart and torso geometries were discretized by tetrahedral meshes, derived from anatomical MRI scans by the segmentation software, Seg3D [7], and an automated mesh generation software system, BioMesh3D [1]. Table 1 describes the mesh configuration. Each element of the heart mesh contained a 3 × 1 vector giving the local fiber orientation, derived from diffusion-tensor MRI imaging of the heart carried out postmortem over 16–24 hours. The conductivities of the heart tissue are listed in Table 2.
Table 1.
Mesh configuration.
| Mesh | Heart node number | Heart element number | Heart average edge length | Torso node number | Torso element number | Torso average edge length |
|---|---|---|---|---|---|---|
| Mesh 1 | 3,301 | 16,546 | 4.5 mm | 11,649 | 76,550 | 12.1 mm |
| Mesh 2 | 6,545 | 36,694 | 3.3 mm | 17,299 | 11,1183 | 10.2 mm |
| Mesh 3 | 17,805 | 103,520 | 2.1 mm | 25,914 | 170,355 | 8.0 mm |
Note: All meshes maintain an identical torso surface discretization (771 nodes and 1538 triangles.)
Table 2.
Conductivities of healthy heart tissues. Unit: Siemens/meter.
| Type | Extracellular logitudinal | Extracellular transverse | Intracellular longitudinal | Intracellular transverse | Body |
|---|---|---|---|---|---|
| Isotropic Data | 0.5 | 0.5 | 0.5 | 0.5 | 1.0 |
| Anisotropic Data | 0.16 | 0.05 | 0.16 | 0.008 | 0.22 |
Note: only the relative ratios among these conductivities matter in numerical simulation. The anisotropic data are according to [31].
Our forward and inverse simulations were performed by the following procedure. Given a configuration of transmembrane potentials (which we will describe later with each experiment), we conducted the forward simulation to obtain the body-surface potentials. The forward simulation used a finer torso mesh than did the inverse simulation, so as to avoid the so-called “inverse crimes” of biasing the solution by using the same mesh for forward and inverse simulations [16]. After adding Gaussian noise to the body-surface potentials, we inversely calculated the heart potentials and compared them with ground truth values. Two regularization methods were used for the inverse calculations: the Tikhonov regularization with the gradient constraint (henceforth abbreviated as the Tikhonov) and the total variation regularization as given by Eq (30). The regularizer weight parameter, β, was determined by the discrepancy principle: starting from 10−4, it iteratively decreased by a factor of five until the misfit between the reconstructed body-surface potentials and their true values dropped below the noise ratio, which was known a priori. β was normally determined within five iterations. All the computation in this study was carried out using 12 CPUs (AMD Opteron 8360 SE, 2.5GHz) and 96 GB memory on a shared-memory workstation.
We evaluated the inverse solutions using four metrics: (1) the correlation coefficient (CC) between the true and computed TMPs, (2) the Haussdorff distance between the true and estimated ischemic regions, (3)the sensitivity error ratio, and (4) the specificity error ratio. The last three metrics were used only in Section 4.2 where the “true” ischemic region was known. The correlation coefficient between the reconstructed potentials (denoted as a vector ûH) and the ground truth (denoted as uH) is defined as follows:
| (36) |
The Haussdorff distance, defined below, measures the proximity of the boundaries of two shapes:
| (37) |
The sensitivity error ratio is defined as the percentage of the true ischemic region that is not detected out of the entire true ischemic region (in terms of their volumes). This metric describes the false negative (related to Type II error), characterizing the sensitivity of an ischemia estimation. The specificity error ratio is defined as the percentage of the misjudged ischemic region out of the entire estimated ischemic region (in terms of their volumes). This metric describes the false positive (related to Type I error), characterizing the specificity of an ischemia estimation.
4.2 Synthetic Ischemia Data
To produce synthetic data that mimic acute ischemia myocardium, we set the transmembrane potential (TMP) during the ST interval to 0 mV in the healthy tissue and −30 mV in the ischemic tissue, as suggested by [17]. This setting is equivalent to assigning the TMP to any other absolute values that maintain a 30-mV difference in amplitude between healthy and ischemia regions. The magnitude of voltage difference was not critical to our inverse calculation, because ischemic regions would later be identified by thresholding the potential field. We specified realistically shaped and located ischemic regions in heart meshes derived from animal experiments, and regarded the mesh nodes belonging to the ischemic regions as “ischemic” and set the rest of the nodes as “healthy”. The TMP was then set as stated above, with a linear transition at the boundary between the two regions. We describe a case of anterior transmural ischemia depicted in Fig 2. Both the heart and the torso volume have isotropic conductivities according to Table 2.
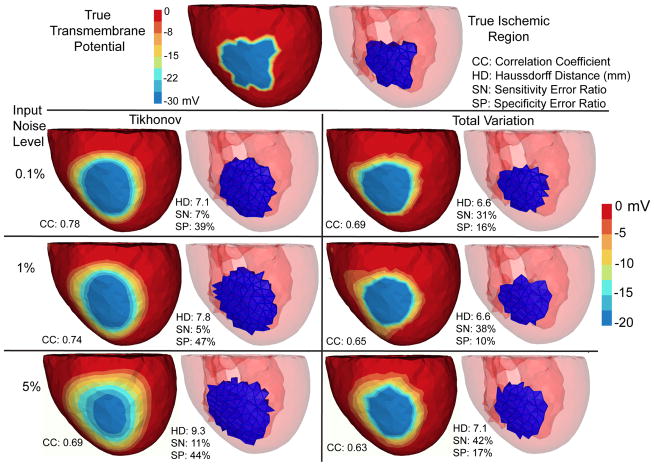
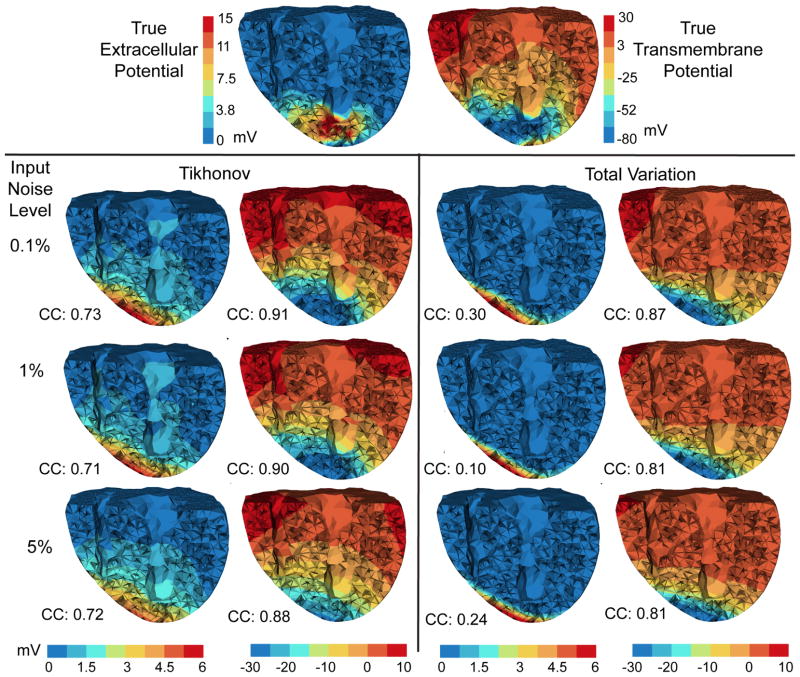
Fig. 2.
Inverse solutions based on Mesh 1 with synthetic ischemia data, obtained by the Tikhonov and the total variation methods. Ischemic regions are indicated by the blue color. All the calculated TMPs are in the same color scale. This figure is to be considered with Fig 4. The input noise is i.i.d. Gaussian imposed on each node on the body surface. The noise level indicates the noise-to-signal ratio in the root-mean-square sense. Such noise setting holds for all experiments in this paper.
Once we inversely reconstructed the TMP field v, we estimated the ischemic regions by a thresholding scheme: if the average of v in an element (over its four vertices) was below the threshold, the element was regarded as “ischemic”. The threshold value was determined by
| (38) |
| (39) |
where v̄ is the mean of v, vmin is the minimum of v, and v5% denotes the low 5% quantile of v. The threshold generally takes the value of t1, and the term t2 acts on rare occasions when vmin is abnormally low because v contains several outlier values. (This occurred only when we performed the TV method with the maximum noise.) Such a threshold reflects the hypothesis that the ischemic TMP should be notably below the average value over the whole heart domain because the ischemic regions account for a minor portion of the whole myocardium.
We conducted inverse simulations with three meshes. Fig 2 shows the reconstruction based on Mesh 1. Fig 3 shows the reconstruction over finer meshes. Fig 4 evaluates the estimated ischemic regions by the sensitivity error and the specificity error. These figures intend to explore three major issues: (1) the comparison between the Tikhonov and the TV methods, (2) the performance of each methods under multiple discretization scales, and (3) the impact of input noise levels on each method. These three issues also form our analysis framework for the experiments in Section 4.3 and 4.4.
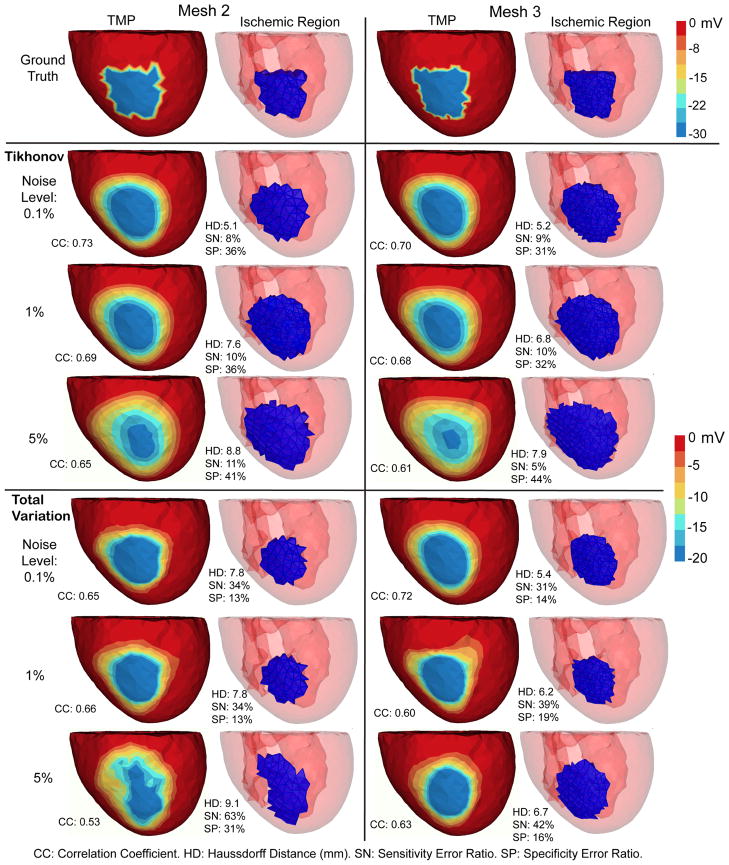
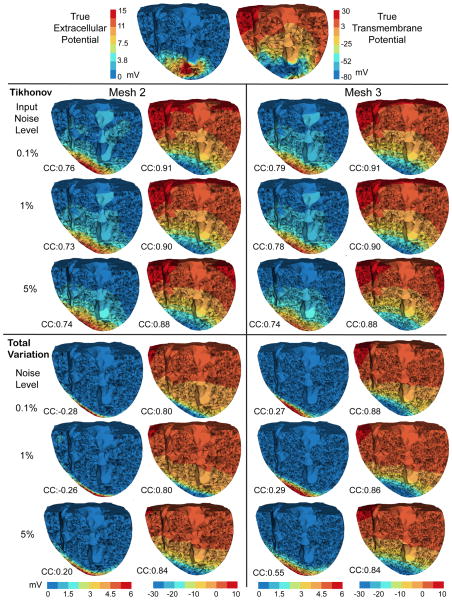
Fig. 3.
Inverse solutions based on Mesh 2 and Mesh 3, with synthetic ischemia data. Tikhonov and total variation solutions are presented. TMP stands for the transmembrane potential. Ischemic regions are denoted by the blue region. All the calculated TMPs are in the same color scale. This figure is to be compared with Fig 2 and Fig 4. The mesh profiles are given in Table 1.
Fig. 4.
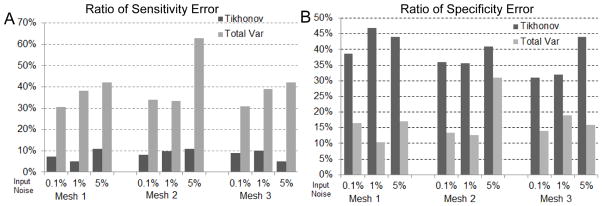
Accuracy of ischemia localization with synthetic ischemia data, in terms of the ratios of sensitivity error (Panel A) and of specificity error (Panel B). This figure is to be compared with Fig 2 and Fig 3.
Overall, both the Tikhonov and TV methods achieved satisfying reconstruction of the TMP and the ischemic region, consistently over multiple noise levels and mesh sizes (as demonstrated by Fig 3). The amplitude of reconstructed TMP was roughly two thirds of that of the ground truth, but the reconstruction achieved a high correlation ranging from 0.7 to 0.8, which in turn resulted in a good ischemic region localization, with the Haussdorff distance ranging from 5 to 10 mm. Fig 2 shows that the Tikhonov solutions have a smooth transition at the ischemia border zone, whereas the total variation solutions preserve a sharp transition. In Fig 3, the TMP fields from the total variation method still exhibit an ellipsoid shape at the ischemic region (the blue region), similar to the Tikhonov solution except having a sharper border that the latter. This difference illustrates the essence of the fixed-point iteration: it works via solving a sequence of Tikhonov minimization problems.
Fig 4 shows that the Tikhonov solutions tended to overestimate the ischemic region whereas the total variation solutions tended to underestimate. The Tikhonov solutions typically missed about 10% of the true ischemic region while this ratio is above 30% in the TV solutions. On the other hand, the TV solutions estimate the ischemic region with a high specificity (the misjudge ratio ≈ 15%), whereas this ratio for the Tikhonov solutions ranges from 30% to 50%.
4.3 Measured Ischemia Data with an Anisotropic Heart Model
This test was the most realistic simulation in our study. Ischemia was introduced into a perfused, live, beating canine heart by adjusting the blood flow to the left anterior coronary artery, which we controlled by means of a thin glass cannula, external blood lines and a rotating pump. The extracellular potentials were recorded at 1 KHz sampling rate at 247 nodes on the epicardial surface, and at 400 nodes within the ventricular myocardium (by inserting 40 fiberglass needles, each carrying 10 electrodes along its length). Data postprocessing included gain adjustment, baseline adjustment, registration to the same heart geometry derived from MRI scans, and extrapolating the potentials throughout the heart volume using volumetric Laplacian interpolation. Our simulation used the potentials at the time instant placed after the QRS complex by 40% of the duration of the ST interval, which was measured from the end of QRS complex to the peak of the T wave. At this time, the TMPs throughout the heart are believed to stay stably in the plateau phase and to be nearly constant in a healthy heart. We used an anisotropic heart model coupled with an isotropic torso model. Their conductivity values were taken from Table 2 in the “Anisotropic Data” category.
It is not possible to measure TMP throughout the heart, so the verifiable ground truth is not the TMP but the extracellular potential, which we measured by means of epicardial and intramyocardial electrodes. We first calculated the heart TMP from the measured extracellular potential, and treated that as the true TMP. This task was fulfilled by solving a well-posed optimization problem defined as follows:
| (40) |
where u0 denotes the measured extracellular potential and Eq (7) is the bioelectric model. In practice the misfit ||u − u0|| is typically below 10−9.
Since we did not know the exact ischemic region, we examined the reconstructed transmembrane and extracellular potential fields. Our examination revolved around the roles of three simulation parameters: 1) the Tikhonov method versus the total variation (TV) method, 2) inverse solutions under multiple scales, and 3) the impact of input noise. Fig 5 compares the inverse solutions by both methods. Fig 6 shows the inverse solutions over multiple discretization scales.
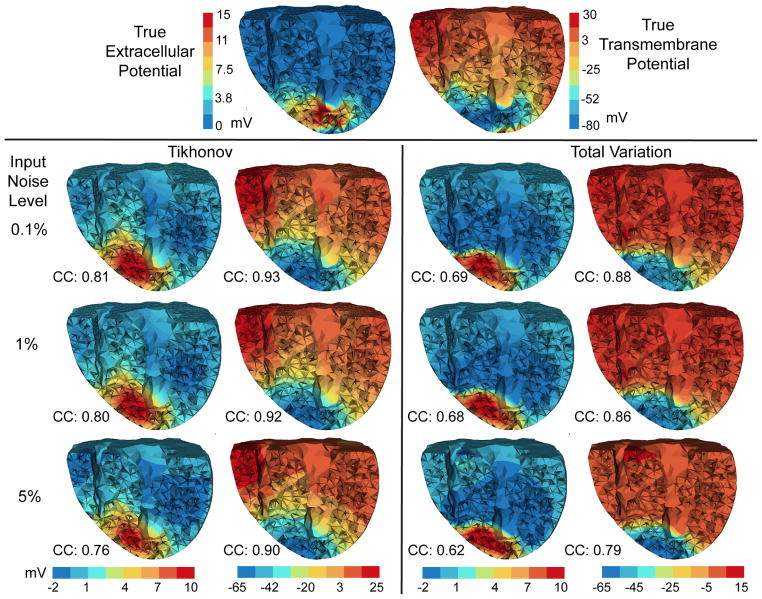
Fig. 5.
Inverse solutions based on Mesh 1 using the anisotropic inverse model and measured ischemia data. Reconstructed heart potentials (by Tikhonov and total variation methods) are visualized at the same cross section. Figures in each column are in the same color scale. CC denotes the correlation coefficient between each reconstructed potential and the ground truth (the top row).
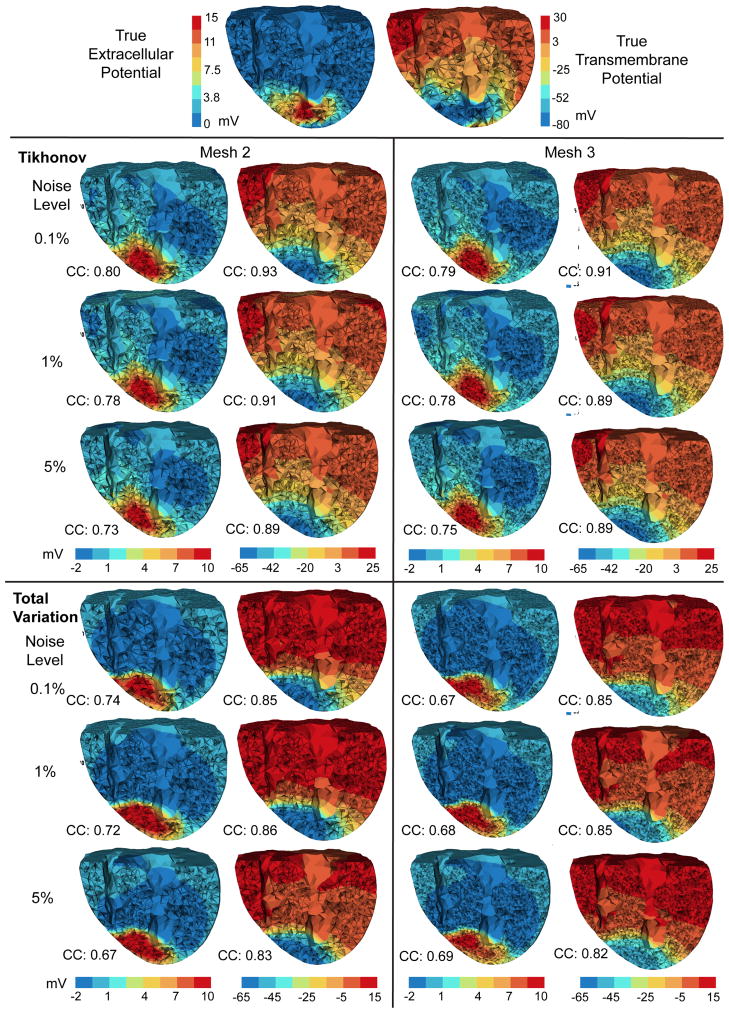
Fig. 6.
Inverse solutions based on Mesh 2 and Mesh 3, using the anisotropic model and the measured ischemia data. Each column of reconstructed heart potentials are in the same color scale. CC: the correlation coefficient between the computed potential and the ground truth (the top row).
Overall both the Tikhonov method and the TV method yielded good reconstructions consistently under different discretization scales: the reconstructed transmembrane potential had a correlation of 0.9 with the truth, and the correlation was 0.8 for the extracellular potential. As anticipated, the Tikhonov method yielded a smoothed solution whereas the TV method yielded a sharper reconstruction (see Fig 5). The true transmembrane potential exhibited a smooth transition at the ischemia border rather than behaving like a stepwise function. This feature partly explains why the Tikhonov method slightly outperformed the TV method in terms of the correlation coefficient. On the other hand, the total variation method seemed to better delineate the ischemic border zone than did the Tikhonov.
Fig 7 presents the computation time of the inverse calculation. The TV method took 5–6 times longer than the Tikhonov method, because each fixed point iteration of the TV method is equivalent to solving one Tikhonov minimization problem. In both methods, the number of iterations was independent of the problem size. However, the time each iteration takes scales with the problem size, because the implementation of the interior-point method typically involves an LTDL Cholesky factorization of a symmetric positive definite matrix, whose size is dictated by the number of control variables. Our results indicate that Mesh 2 (approximately 6500 nodes on heart) may be an appropriate resolution for conducting the TV method on moderate computational platforms.
Fig. 7.
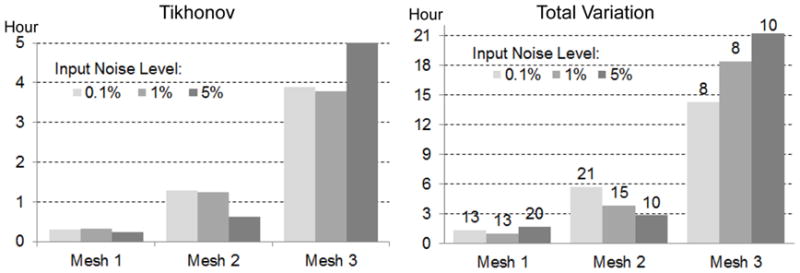
Inverse computation time of the Tikhonov (left) and the total variation regularization (right) based on the anisotropic heart model and measured ischemia data (shown by Fig 5 and Fig 6). Each column bar represents the time based on the given mesh and the torso-surface input noise level. In the right panel, the number on each bar gives the number of fixed-point iterations.
4.4 Measured Ischemia Data with an Isotropic Heart Model
This test explored whether it is possible to estimate real heart potentials with reasonable accuracy without using anisotropic conductivities because such information is not generally available in any remotely realistic clinical scenarios except by means of rule-based estimation [37]. We first conducted forward simulation using the anisotropic heart model and voltage data described in Section 4.3, and then conducted inverse simulation using the isotropic heart model described in Section 4.2.
The results are presented in a similar way as in Section 4.3. The computational times in this experiment were close to those shown in Fig 7, so they are not presented here due to space limitations. Fig 8 and Fig 9 compare the reconstructions by the Tikhonov and and total variation methods under multiple discretization scales. In both methods, reconstructed TMPs were still good though they were slightly worse than their counterparts in Section 4.3 with the anisotropic inverse heart model (either by visual inspection or by the correlation coefficient.) The Tikhonov method behaved robustly over different mesh sizes and noise levels but less so of the TV method. The Tikhonov method estimated the extracellular potential reasonably whereas the TV method yielded a poor estimation. Note that the true TMP and the true extracellular potential were related by the anisotropic model, but the calculated TMP and extracellular potential in this test were related by the isotropic heart model, so one should not expect to accurately estimate both of them simultaneously. Our inverse calculation treated the TMP as the “source” and the primary reconstruction goal.
Fig. 8.
Inverse solutions of an isotropic inverse model following an anisotropic forward simulation, using measured ischemia data. Mesh 1 is being used. Each column of reconstructed heart potentials are in the same color scale.
Fig. 9.
Inverse solutions of the isotropic heart model following an anisotropic forward simulation, based on Mesh 2 and Mesh 3. Each column of reconstructed heart potentials are in the same color scale.
5 Discussion
The goal of this study is to develop the PDE-constrained optimization methodology to solve the inverse problem of ischemia localization. We assume that the given physical model adequately characterizes the underlying electrophysiology, so our simulation experiments serve to verify our inverse method rather than to validate the physical model. The simulation results demonstrate that our inverse method was able to reconstruct the transmembrane potential with a 0.8–0.9 correlation with the experimentally measured ischemia data. A noteworthy merit of PDE-constrained optimization is that it enables one to impose constraints on almost any quantity in the physical model so as to overcome the numerical ill-conditioning of the inversion. Adopting an “optimization-then-discretization” approach, we obtained consistent inversion results when simulating the physical model under multiple discretization resolutions. The discussion is organized in two categories: (1) biophysical aspects of ischemia modeling and localization and (2) computational features of our approach that are of general interest to PDE-governed inverse problems.
5.1 Biophysical Considerations
Tikhonov versus total variation in ischemia localization
With the PDE-constrained optimization approach, we were able to recover ischemic zones with higher accuracy than any previously published approach (to our knowledge). The two methods, Tikhonov and total variation (TV), performed adequately but with different strengths and weaknesses. The Tikhonov method yielded higher sensitivity whereas the TV method showed better specificity. As Fig 4 shows, the Tikhonov method tended to overestimate ischemic regions but missed less than 10% of the true ischemic region. In contrast, the TV method underestimated the ischemic region (typically missing 30%–40% of the true ischemic region), but nearly 90% of its estimated ischemic region was correct. Hence in clinical practice, one might use the TV method for a conservative estimate of ischemia and the Tikhonov method for a worst-case estimate. With measured ischemia data, the Tikhonov method slightly outperformed the TV method in terms of the correlation coefficient of recovered TMPs, but the TV method delineated the ischemic border more precisely than the Tikhonov method (Fig 6). When the heart anisotropy information was unavailable, the Tikhonov method outperformed the TV method (Fig 8). Although it is widely believed that the Tikhonov method tends to yield overly smoothed solutions, our measured data showed that the ischemic potential distribution was smoother than a stepwise function, indicating that the Tikhonov method may be more appealing than one would anticipate.
In terms of robustness and computation cost, the Tikhonov method performed robustly over different discretization resolutions and input noise levels, whereas the TV method became less stable when the noise level rose to 5% with high-resolution heart models (Fig 3). Such observations suggest combining the two methods in inverse calculation: one may use the Tikhonov solution as the initial guess for the subsequent TV iterative algorithm so as to achieve convergence with fewer iterations.
Border zone consideration
The ischemic border zone, marking the transition between the healthy and ischemic regions and characterized by a spatial transition of TMP, is of great clinical interest. The spatial gradient of TMP in the border zone results in “injury currents”, which are believed to be the primary electric source causing the ST segment shift [17]. Therefore, the shape and width of border zones should be considered when choosing the resolution for the heart geometry. A border zone is often estimated to be between 5–10 mm in thickness [33], and the grid size of our mesh ranged between 5 mm (Mesh 1) and 2 mm (Mesh 3) so as to keep adequate spatial resolution for the border zone.
Our simulations indicated that the border-zone transition could be reasonably reconstructed whether it was sharp or smooth. In our synthetic study, the border zone was set to be one-element wide and accordingly the synthetic TMP had a sharper transition than normal. Nevertheless, the TV method tackled such condition well (Fig 3). In our measured data study, the border zone transition was smoother than in the synthetic setting, and the Tikhonov method yielded good recovery (Fig 6). (See [33] for detail of the experimental ischemic data we used.) These tests indicated that recovering the voltage transition in border zones should not create extra technical difficulty to the overall goal of recovering the TMP.
Impact of anisotropy and homogeneity in tissue conductivity
Several simulation studies based on realistic ischemia data have shown that fiber rotation and tissue anisotropy fundamentally impacts the forward calculation of epicardial extracellular potential distributions and of body-surface ST-shift patterns [26]. However, in clinical practice the heart fiber information of an individual patient is generally not available, though there are emerging techniques for estimating this information on a patient-specific basis [36]. Therefore, it is worth inquiring whether it is possible to reasonably reconstruct the myocardial TMP without the information of heart anisotropy, while the input body-surface potentials actually result from an anisotropic heart. We explored this possibility in Section 4.4. In our inverse calculation, the TMP was the control variable whereas the extracellular potential was subject to the TMP via an isotropic bidomain heart model. We found that without including the heart anisotropy, one still may achieve an TMP estimation with as high as 0.85 correlation with the truth, but would estimate the extracellular potential poorly (see Fig 8 and Fig 9).
This finding has two indications. First, it confirms a previous assumption held by the ECG community that the heart anisotropy is critical for predicting extracellular epicardial potentials [14]. Our finding confirms this assumption from the reverse side (i.e., lack of anisotropy prevents accurate estimation of extracelluar potentials). The second indication is that the heart anisotropy is less critical to the inverse calculation. Our conjectured explanation is that given the TMP source, the body-surface potentials are dominated by the attenuation and superposition effects of the torso volume, and the effect of myocardial anisotropy is overwhelmed. Therefore, if the torso’s effects can be properly resolved in the inverse calculation (which is the main purpose of regularization), it is possible to estimate the TMP with moderate accuracy without heart anisotropy information.
One limitation of our inverse study is its assumption of homogeneous conductivity throughout the heart, excluding ischemia-induced conductivity variation. In reality, such regional variation of conductivity may significantly alter the heart potential patterns. Although there are some experimental and simulation data that quantify the tissue conductivity variation associated with ischemia [32], such data cannot be applied to ischemia localization before one knows the location of ischemic regions. One way to overcome this dilemma is to adopt an iterative scheme: one solves a homogeneous heart model in the first round of inversion, estimates ischemic regions, and then uses this information to create an inhomogeneous heart model to be used in a second round of inversion. Such iteration may continue for several rounds until the estimated ischemic region converges. This topic deserves future research.
Resolution of the geometric model
Our inverse simulation features the use of a much finer heart model (17,000 nodes) than those reported in previous inverse ECG studies (typically about 1,000 nodes). Moreover, we found inversion with a higher model resolution would still be feasible with more computation resources available. A main reason for using a coarse heart model (essentially a low-dimensional parameterization of the control variable) is to constrain the ill-conditioning of the inverse system. However, our experiments indicate that this resolution concern can be mitigated by the optimize-then-discretize approach, thus offering clinical scientists more flexibility to choose the resolution based on their practical need. Such flexibility may not only enable cardiac diagnosis to reach higher levels of detail than previously possible, such as identifying the ischemic border zone (typically about 5 mm) or the conduction velocity (about 2 mm/millisecond), but also allow scientists to balance the sensitivity and specificity of the diagnosis via adjusting the numerical system.
Future work
The ischemia scenario considered in this paper is simplified in that we assumed a single region of nearly transmural ischemia. A natural extension will be to evaluate this approach under more realistic ischemic scenarios such as multiple ischemic regions, subendocardial ischemia and intramural ischemia. It is also worthwhile to connect mechanistic studies of these ischemia with localization [13]. Another novel direction will be to recover the TMP over the entire cardiac cycle for diagnosis of activation-related cardiac diseases.
5.2 Computational Considerations
Individualized discretization
In this study we used the same mesh to discretize the control variable v, the state variable u, and the adjoint variable p, but this is not necessary. Individual and adaptive discretization of each variable deserves further investigation. In inverse problems, one often wishes to discretize the control variable v coarsely so as to exert certain projective regularization effect, meanwhile taking a finer discretization of the state variable u [39]. The discretization concern for the adjoint variable has been discussed in Section 3.2.1. In our problem, p does not need to stress stronger regularity than u, so the same discretization for both is fine unless computation resource becomes a serious bottleneck. It is straightforward to incorporate individual discretization into our framework, see Eq (10) for the PDE constraint and Eq (21) for the optimality conditions.
Adaptive hp finite element refinement
PDE-constrained optimization is computationally intensive: each iteration of the optimization involves solving the entire PDE system once. Computational efficiency can be improved in two ways: achieving convergence with fewer iterations, or reducing the numerical cost in each iteration. Adaptive finite element methods (FE) take effects in the latter way by discretizing PDEs differently in each optimization iteration. While adaptive FE refinements for PDEs have been well established both in theory and in practice, they have not yet been widely adopted in PDE-constrained optimization, partly because most practical optimization solvers are algebraic, preventing change of discretization between iterations (otherwise the finite-dimensional convergence criteria become meaningless). Adaptive PDE-constrained optimization requires two conditions: the optimize-then-discretize approach and a refinement strategy based on certain FE error estimates. This paper addressed the first one, and a meaningful topic for future work is to investigate finite element refinement schemes in terms of both mesh shapes and basis functions.
Advanced algorithms for total variation
We fulfilled the TV minimization using the fixed-point iteration, a choice that is a relatively robust but certainly not optimal in performance. Our intention is to derive a rigorous finite element formulation for the TV minimization rather than to thoroughly explore TV algorithms. Our finite element formulation can be naturally adapted to more advanced TV algorithms as those reviewed in [42]. The traditional TV algorithms, such as the fixed-point method, form the optimization problem in the primal space alone. In such cases, the standard Newton’s method is not recommended because its quadratic convergence domain is small when ε → 0 (see Eq (25)) [6,38]. In contrast, advanced TV algorithms formulate the minimization in both the primal and dual spaces, such as the primal-dual Newton method [6] or the dual-space formulation [42]. The primal-dual formulation not only achieves quadratic convergence, but also removes the expediency of smoothing variable ε, thus allowing one to directly pursue the original TV solution (without ε). In the aforementioned primal-dual algorithm literature, the strong form of the KKT systems and their linearization were derived and then solved by finite difference schemes. Integrating our finite element formulation with the primal-dual algorithms will require (1) deriving the KKT system in the variational form and (2) discretizing the functional variables by finite element expansion. Exploring the nuances of such integration is worth further investigation.
Formulation in general Sobolev spaces
We formed the variational optimality conditions of the PDE-constrained optimization in the L2 space, with the inner product taking equal weights between the trial and test spaces (see Eq (11)). The optimality conditions can also be formed in the general Sobolev spaces as described in the classical literatures of finite element methods. A proper choice of the variational formulation should take into account two issues: 1) the inherent structure of the given optimization functional and PDE constraints and 2) the regularity of the finite element solution. Reexamining the finite element theories for PDEs in the context of constrained optimization deserves further investigation.
6 Conclusion
We proposed a general PDE-constrained optimization framework for solving the inverse ECG problem with application in myocardial ischemia localization. Our main contribution lies in developing dimension-independent inverse algorithms that perform consistently over multiple discretization scales. With synthetic ischemia data, we localized ischemic regions with approximately a 10% false-negative rate or a 20% false-positive rate up to 5% input noise. With measured ischemia data, we reconstructed heart TMPs with approximately 0.9 correlation with the ground truth. The Tikhonov method tended to overestimate ischemic regions but with good sensitivity, whereas the total variation method tended to underestimate ischemic regions but with high specificity. To our knowledge this study was the first inverse-ECG-based myocardial ischemia localization using measured heart data while still achieving adequate precision for clinical use, despite the limitation that the body-surface potentials were simulated rather than measured. We believe the approach of PDE-constrained optimization will benefit a broad range of bioelectromagnetic problems in heart and brain research.
Acknowledgments
We express our thanks to Kedar Aras and Dr. Darrell Swenson for providing data from animal experiments and to Dr. Sarang Joshi for his inspiration. We acknowledge the Treadwell Foundation and the Cardiovascular Research and Training Institute at the University of Utah for their support of acquiring the experimental data. This work is supported by the NIH/NIGMS Center for Integrative Biomedical Computing, Grant 2P41 GM103545-14. We thank the reviewers for their constructive comments.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- 1.SCIRun: A Scientific Computing Problem Solving Environment, Scientific Computing and Imaging Institute (SCI) 2011 Download from: http://www.scirun.org.
- 2.Barr RC, Ramsey M, Spach MS. Relating epicardial to body surface potential distributions by means of transfer coefficients based on geometry measurements. IEEE Transactions on Biomedical Engineering. 1977;24(1):1–11. doi: 10.1109/TBME.1977.326201. [DOI] [PubMed] [Google Scholar]
- 3.Biros G, Ghattas O. Parallel Lagrange-Newton-Krylov-Schur methods for PDE-constrained optimization. Part I: The Krylov-Schur solver. SIAM Journal of Scientific Computing. 2005;27(2):687–713. [Google Scholar]
- 4.Bishop MJ, Plank G. Bidomain ECG simulations using an augmented monodomain model for the cardiac source. IEEE Tran Biomed Eng. 2011;58(8):2297–2307. doi: 10.1109/TBME.2011.2148718. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Boyd S, Vandenberghe L. Convex Optimization. Cambridge University Press; 2004. [Google Scholar]
- 6.Chan TF, Golub GH, Mulet P. A nonlinear primal-dual method for total variation-based image restoration. SIAM Journal of Scientific Compting. 1999;20(6):1964–1977. [Google Scholar]
- 7.CIBC, seg3D: Volumetric Image Segmentation and Visualization. Scientific Computing and Imaging Institute (SCI) 2011 Download from: http://www.seg3d.org.
- 8.Cuppen JJM, van Oosterom A. Model studies with the inversely calculated lsochrones of ventricular depolarization. IEEE Trans on Biomed Eng. 1984;31(10):652–659. doi: 10.1109/TBME.1984.325315. [DOI] [PubMed] [Google Scholar]
- 9.Ghosh S, Rudy Y. Application of L1-norm regularization to epicardial potential solution of the inverse electrocardiography problem. Annals of Biomedical Engineering. 2009;37(5):902–912. doi: 10.1007/s10439-009-9665-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Gulrajani RM. Bioelectricity and biomagnetism. John Wiley & Sons Inc; 1998. [Google Scholar]
- 11.Hinze M, Pinnau R, Ulbrich M, Ulbrich S. Analytical Background and Optimality Theory, vol. 23 of Mathematical Modelling: Theory and Applications. Springer; Netherlands: 2009. pp. 1–95. [Google Scholar]
- 12.Hinze M, Pinnau R, Ulbrich M, Ulbrich S. Discrete Concepts in PDE Constrained Optimization, vol. 23 of Mathematical Modelling: Theory and Applications. Springer; Netherlands: 2009. pp. 157–232. [Google Scholar]
- 13.Hopenfeld B, Stinstra JG, MacLeod RS. Mechanism for ST depression associated with contiguous subendocardial ischemia. Journal of Cardiovascular Electrophysiology. 2004;15:1200–1206. doi: 10.1046/j.1540-8167.2004.04072.x. [DOI] [PubMed] [Google Scholar]
- 14.Hopenfeld B, Stinstra JG, MacLeod RS. The effect of conductivity on ST-segment epicardial potentials arising from subendocardial ischemia. Annals of Biomedical Engineering. 2005;33(6):751–763. doi: 10.1007/s10439-005-3236-2. [DOI] [PubMed] [Google Scholar]
- 15.Jiang Y, Qian C, Hanna R, Farina D, Dössel O. Optimization of the electrode positions of multichannel ECG for the reconstruction of ischemic areas by solving the inverse electrocardiographic problem. International Journal of Bioelectromagnetism. 2009;11(1):27–37. [Google Scholar]
- 16.Kaipio J, Somersalo E. Statistical inverse problems: discretization, model reduction and inverse crimes. Journal of Computational Applied Math. 2007;198(2):493–504. [Google Scholar]
- 17.Li D, Li CY, Yong AC, Kilpatrick D. Source of electrocardiographic st changes in subendocardial ischemia. Circ Res. 1998;82:957–970. doi: 10.1161/01.res.82.9.957. [DOI] [PubMed] [Google Scholar]
- 18.Lloyd-Jones D, et al. Heart disease and stroke statistics–2010 update: A report from the american heart association. on behalf of the American Heart Association Statistics Committee. Circulation. 2010;121(7):e46–215. doi: 10.1161/CIRCULATIONAHA.109.192667. [DOI] [PubMed] [Google Scholar]
- 19.MacLachlan MC, Sundnes J, Skavhaug O, Lysaker M, Nielsen BF, Tveito A. A linear system of partial differential equations modeling the resting potential of a heart with regional ischemia. Math Biosci. 2007;210(1):238–252. doi: 10.1016/j.mbs.2007.04.005. [DOI] [PubMed] [Google Scholar]
- 20.MacLeod RS, Taccardi B, Lux RL. Electrocardiographic mapping in a realistic torso tank preparation. 1995 [Google Scholar]
- 21.Messnarz B, Seger M, Modre R, Fischer G, Hanser F, Tilg B. A comparison of noninvasive reconstruction of epicardial versus transmembrane potentials in consideration of the null space. IEEE Trans Biomed Eng. 2004;51(9):1609–1618. doi: 10.1109/TBME.2004.828038. [DOI] [PubMed] [Google Scholar]
- 22.Messnarz B, Tilg B, Modre R, Fischer G, Hanser F. A new spatiotemporal regularization approach for reconstruction of cardiac transmembrane potential patterns. IEEE Trans Biomed Eng. 2004;51(2):273–281. doi: 10.1109/TBME.2003.820394. [DOI] [PubMed] [Google Scholar]
- 23.Nielsen BF, Cai X, Lysaker M. On the possibility for computing the transmembrane potential in the heart with a one shot method: An inverse problem. Math Bioscience. 2007;210(2):523–553. doi: 10.1016/j.mbs.2007.06.003. [DOI] [PubMed] [Google Scholar]
- 24.Nielsen BF, Lysaker M, Tveito A. On the use of the resting potential and level set methods for identifying ischemic heart disease: An inverse problem. Journal of computational physics. 2007;220(2):772–790. [Google Scholar]
- 25.Potse M, Dube B, Richer J, Vinet A, Gulrajani RM. A comparison of monodomain and bidomain reaction-diffusion models for action potential propagation in the human heart. IEEE Transactions on Biomedical Engineering. 2006;53(12):2425–2435. doi: 10.1109/TBME.2006.880875. [DOI] [PubMed] [Google Scholar]
- 26.Rodriguez B, Trayanova N, Noble D. Modeling cardiac ischemia. Annals of the New York Academy of Sciences. 2006;1080(1):395–414. doi: 10.1196/annals.1380.029. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Rudy Y. From Genes and Molecules to Organs and Organisms: Heart. Vol. 9. Academic Press; Oxford: 2012. pp. 268–327. [Google Scholar]
- 28.Ruud TS, Nielsen BF, Lysaker M, Sundnes J. A computationally efficient method for determining the size and location of myocardial ischemia. IEEE Transactions on Biomedical Engineering. 2009;56(2):263–272. doi: 10.1109/TBME.2008.2009068. [DOI] [PubMed] [Google Scholar]
- 29.Sachse F. Computational Cardiology: Modeling of anatomy, electrophysiology, and mechanics. Springer; 2004. [Google Scholar]
- 30.Shou G, Xia L, Liu F, Jiang M, Crozier S. On epicardial potential reconstruction using regularization schemes with the l1-norm data term. Physics in medicine and biology. 2011;56(1):57. doi: 10.1088/0031-9155/56/1/004. [DOI] [PubMed] [Google Scholar]
- 31.Stinstra JG, Hopenfeld B, MacLeod RS. On the passive cardiac conductivity. Annals of Biomedical Engineering. 2005;33(12):1743–1751. doi: 10.1007/s10439-005-7257-7. [DOI] [PubMed] [Google Scholar]
- 32.Stinstra JG, Shome S, Hopenfeld B, MacLeod RS. Modelling passive cardiac conductivity during ischaemia. Med Biol Eng Comput. 2005;43(6):776–782. doi: 10.1007/BF02430957. [DOI] [PubMed] [Google Scholar]
- 33.Swenson DJ, Aras KK, Burton BM, MacLeod RS. Evaluation the electrical border zone approximation with subject specific ischemia models. Journal of Cardiovascular Electrophysiology. under review. [Google Scholar]
- 34.Toh K, Todd M, Tutuncu R. SDPT3—a Matlab software package for semidefinite programming. Optimization Methods and Software. 1999;11:545–581. [Google Scholar]
- 35.Toh K, Todd M, Tutuncu R. On the implementation and usage of SDPT3—a Matlab software package for semidefinite-quadratic-linear programming, Version 4.0. 2010 [Google Scholar]
- 36.Vadakkumpadan F, Arevalo H, Ceritoglu C, Miller M, Trayanova N. Image-based estimation of ventricular fiber orientations for personalized modeling of cardiac electrophysiology. IEEE Transactions on Medical Imaging. 2012;31(5):1051–1060. doi: 10.1109/TMI.2012.2184799. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Vadakkumpadan F, Arevalo H, Prassl A, Chen J, Kickinger F, Kohl P, Plank G, Trayanova N. Image-based models of cardiac structure in health and disease. WIREs Syst Biol Med. 2010;2(4):489–506. doi: 10.1002/wsbm.76. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Vogel CR, Oman ME. Iterative methods for total variation denoising. SIAM Journal of Scientific Compting. 1996;17(1):227–238. [Google Scholar]
- 39.Wang D, Kirby RM, Johnson CR. Resolution strategies for the finite-element-based solution of the ECG inverse problem. IEEE Trans Biomed Eng. 2010;57(2):220–237. doi: 10.1109/TBME.2009.2024928. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Wang D, Kirby RM, Johnson CR. Finite-element-based discretization and regularization strategies for 3D inverse electrocardiography. IEEE Transactions on Biomedical Engineering. 2011;58(6):1827–1838. doi: 10.1109/TBME.2011.2122305. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Zhu M, Chan T. Tech rep. Dept of Math, University of California; Los Angeles: 2008. An efficient primal-dual hybrid gradient algorithm for total variation image restoration. [Google Scholar]
- 42.Zhu M, Wright S, Chan T. Duality-based algorithms for total-variation-regularized image restoration. Computational Optimization and Applications. 2010;47(3):377–400. [Google Scholar]