Nonparametric estimation of benchmark doses in environmental risk assessment

Summary

An important statistical objective in environmental risk analysis is estimation of minimum exposure levels, called benchmark doses (BMDs), that induce a pre-specified benchmark response in a dose-response experiment. In such settings, representations of the risk are traditionally based on a parametric dose-response model. It is a well-known concern, however, that if the chosen parametric form is misspecified, inaccurate and possibly unsafe low-dose inferences can result. We apply a nonparametric approach for calculating benchmark doses, based on an isotonic regression method for dose-response estimation with quantal-response data (Bhattacharya and Kong, 2007). We determine the large-sample properties of the estimator, develop bootstrap-based confidence limits on the BMDs, and explore the confidence limits’ small-sample properties via a short simulation study. An example from cancer risk assessment illustrates the calculations.

1. Introduction

1.1. Benchmark risk analysis

An important objective in environmental risk assessment is estimation of the severity and likelihood of damage from hazardous stimuli to humans or to the environment (Stern, 2008). To identify the damaging effects of a hazardous agent, investigators often consider bioassays on small mammals or other biological systems, or epidemiological analyses of human populations at risk. This risk is quantified via a function R(x), which is typically the probability of exhibiting the adverse effect in a subject exposed to a particular dose or otherwise-quantifiable exposure level, x, of the hazardous agent. A major effort in risk analysis involves dose-response modeling, i.e., modeling of the risk function R(x). Commonly, observations are taken as proportions of responding subjects at each x. This is the ‘quantal response’ setting, and it is common in carcinogenicity testing, environmental toxicity analysis, and many other biomedical risk investigations (Piegorsch, 2002).

When conducting environmental risk/safety studies that generate dose-response data, an increasingly popular statistical technique is benchmark analysis (Crump, 1984, 2002). The strategy manipulates components of the dose-response curve to yield the benchmark dose (BMD) of the agent necessary to induce a predetermined change in the adverse effect, relative to background levels. The pre-specified target change is called the benchmark response (BMR). If the exposure is measured as a concentration, one refers to the exposure point as a benchmark concentration, or BMC. Risk analysts use BMDs or BMCs for setting exposure limits or other so-called ‘points of departure’ when assessing the effects of hazardous environmental stimuli (Kodell, 2005).

Statistical inferences in benchmark analysis focus on 100(1 − α)% confidence limits for the benchmark dose. Driven by public health or other safety considerations, only one-sided, lower limits are employed, denoted as BMDLs (Crump, 1995). Where needed for clarity, we add a subscript for the BMR level at which each quantity is calculated: BMD_100BMR and BMDL_100BMR; 0 < BMR < 1. In this fashion, BMDs and BMDLs – or BMCs and BMCLs, etc. – are employed for risk characterization and management by a variety of agencies, including the U.S. Environmental Protection Agency (EPA), the U.S. Food and Drug Administration (FDA), the Organisation for Economic Co-operation and Development (OECD), and many others (Faustman and Bartell, 1997).

With quantal data we assume a binomial model: Y_i ~ indep. Bin. (N_i, R(x_i)), where N_i is the number of subjects tested and R(x_i) is the function representing the probability of response at dose x_i (i = 1, …, n). For risk-analytic considerations the exposed subjects’ differential risk adjusted for any spontaneous or background effects is often of interest. This leads to consideration of excess risk functions such as the extra risk R_E(x) = {R(x) − R(0)}/{1 − R(0)} (Piegorsch and Bailer, 2005, §4.2). With proportion and incidence data the BMD is determined by setting R_E(x) = BMR over x > 0 and finding the smallest solution. The method is a form of inverse non-linear regression and except for the use of an excess risk function upon which to base the inversion, is essentially equivalent to estimation of an ‘effective dose’ such as the well-known median effective dose, ED₅₀ (Piegorsch and Bailer, 2005, §4.1).

1.2. Model dependence

A fundamental concern with benchmark analysis is its potential sensitivity to specification of the dose-response function, R(x). A wide variety of parametric forms has been proffered for R(x) when estimating BMDs. Most operate well at (higher) doses near the range of the observed quantal outcomes; however, these different models can produce wildly different BMDs at very small levels of risk when applied to the same set of data (Faustman and Bartell, 1997; Kang et al., 2000). Past strategies to avoid parametric model dependencies in low-dose risk analysis generally relied on the so-called No-Observed-Adverse-Effect Level (NOAEL), which did not require specification of R(·). Substantial statistical instabilities have been identified with use of the NOAEL for risk estimation, however, and contemporary analysts recommend against use of this dated technology (Kodell, 2009; Izadi et al., 2012). Needed is a modern statistical methodology that can avoid instabilities and inadequacies resulting from uncertain model specification.

Recent work in this direction has led to some intriguing advances, including model averaging techniques motivated from both frequentist (Moon et al., 2005; Faes et al., 2007; Wheeler and Bailer, 2009) and Bayesian (Bailer et al., 2005; Morales et al., 2006) perspectives. Other work has adopted the Bayesian paradigm to study non- and semi-parametric approaches for BMD estimation (Wheeler and Bailer, 2012; Roy et al., 2012).

Alternatively, we consider a (frequentist) nonparametric estimator for the observed dose-response pattern without call to a specific parametric form, and then invert this to construct a model-independent estimator for the BMD. Model-free curve estimation has seen only limited implementation in risk assessment. Krewski et al. (1991) provided perhaps the earliest such effort of any substance, in their discussion of ways to avoid model specification in low-dose risk extrapolation, but they did not connect this to the modern machinery of benchmark analysis. More recently, Dette et al. (2005) and Dette and Scheder (2010) (along with the references found therein) discussed kernel-based nonparametric estimation for effective doses, such as the ED₅₀, from a quantal-response experiment. As noted above, ED₅₀ estimation shares many similarities with BMD estimation, although Dette and his co-authors did not connect their work to problems in risk analysis. Bhattacharya and Lin (2010) produced an adaptive, isotonic regression-based method for estimating nonparametric effective doses in the larger area of bioassay analysis, but also considered explicitly the benchmark dose problem. Their approach was based on earlier work of Bhattacharya and Kong (2007), henceforth ‘BK’, and they constructed dose estimates inverted from the original risk function R(x), not from excess risk functions such as R_E(x). Nonetheless, adaptations and extensions of the BK technique can be effectively manipulated to calculate BMDs and BMDLs with quantal data, and we focus herein on such operations. Section 2 reviews the BK methodology and expands upon it to construct BMDs from a nonparametrically estimated extra risk function. Section 3 explores ways to calculate corresponding BMDLs, using nonparametric bootstrap methods. Section 4 evaluates the small-sample performance of these bootstrap-based BMDLs via a short simulation study, and Section 5 illustrates the methods with a modern example from cancer risk assessment. Section 6 ends with a brief discussion.

2. Model-independent benchmark analysis

2.1. Isotonic dose-response estimators

We continue to assume a binomial structure for our quantal-response data: Y_i ~ indep. Bin. (N_i, R(x_i)), i = 1, …, n. We write the sample proportions as p_i = Y_i/N_i, and assume the dose values are ordered such that 0 = x₁ < x₂ < ··· < x_n. Rather than rely on any parametric specifications on the dose-response function, however, we mimic the strategy taken by BK and only oblige R(·) to satisfy simple continuity and monotonicity assumptions. Imposition of monotonicity constraints is not new in quantal-response analysis; e.g., Müller and Schmitt (1988) described a monotonized kernel smoothing approach for estimating an effective dose such as ED₅₀, which was then expanded upon by Dette et al. (2005) – mentioned above – and Yuan and Yin (2011), among others. Our focus here with the BK strategy is driven by a number of factors: as shown below, the method has a naturally intuitive nature and is fairly straightforward to implement. (In §6 we will also briefly explore some smoothing extensions of the approach.)

Formally, we require R(x) to be an absolutely continuous function R: ℝ → [0, 1] such that R(a) ≤ R(b) for any ordered reals a ≤ b. Notice that such an R(·) possesses the characteristics of a continuous cumulative distribution function (c.d.f.).

Initially, the BK strategy views the monotonized sequence {R(x₁), R(x₂), …, R(x_n)} as the estimation target, for which the unique maximum likelihood estimator (MLE) is the isotonic sequence

$${\stackrel{\sim }{p}}_i=\underset{1\le u\le i}{max}\underset{i\le v\le n}{min}\frac{{\sum }_{j=u}^v{Y}_j}{{\sum }_{j=u}^v{N}_j}$$ (2.1)

(Ayer et al., 1955). This ensures p̃₁ ≤ ··· ≤ p̃_n, and may be obtained via the well-known pool-adjacent-violators (PAV) algorithm (Silvapulle and Sen, 2004, §2.4). For a model-independent, isotonic estimator of the function R(x), BK construct a linear interpolating spline from the PAV estimates p̃_i:

$$\stackrel{\sim }{R}(x)=\{\begin{array}{ll}{\stackrel{\sim }{p}}_i\hfill & \text{if}x=x_i;\hfill \\ {\stackrel{\sim }{p}}_i+\frac{{\stackrel{\sim }{p}}_{i+1}-{\stackrel{\sim }{p}}_i}{x_{i+1}-x_i}(x-x_i)\hfill & \text{if}{x}_i\le x<x_{i+1}\hfill \end{array}$$ (2.2)

for i = 1, …, n − 1, and R̃(x_n) = p̃_n. If focus is on estimation of an ED₅₀, or more generally any ED_100π for a fixed π ∈(0, 1), one simply inverts the isotonic estimator in Equation (2.2) at that π. This achieves a model-independent estimate of the effective dose: ${\widehat{\text{ED}}}_{100\pi }=inf\{x:\stackrel{\sim }{R}(x)=\pi \}$. By viewing R(x) as a c.d.f. and ${\widehat{\text{ED}}}_{100\pi }$ as its πth sample quantile, BK show that this ED estimator is unique, consistent, and asymptotically normal under a set of typical regularity conditions.

Applied to benchmark analysis, this approach can be manipulated to produce model-independent estimates of the BMD. For notational simplicity, we denote BMD_100BMR as ξ_100π, where π = BMR. Differing from an effective dose, the BMD is defined by inverting the extra risk R_E(x) = {R(x) − R(0)}/{1 − R(0)} at the desired level of π = BMR ∈ (0, 1): ξ_100π = inf{x > 0 : R_E(x) = π}. Thus we mimic the BK construction and build an isotonic estimator for R_E(x) from the PAV-constrained values in Equation (2.1). The result is a linear interpolating spline connecting the suitably adjusted, monotonized, pointwise estimates of the extra risks at each x_i: R̃_E(x) = {R̃(x) − R̃(0)}/{1 − R̃(0)}, or

$${\stackrel{\sim }{R}}_E(x)=\{\begin{array}{ll}\frac{{\stackrel{\sim }{p}}_i-{\stackrel{\sim }{p}}_1}{1-{\stackrel{\sim }{p}}_1}\hfill & \text{if}x=x_i;\hfill \\ \frac{1}{1-{\stackrel{\sim }{p}}_1}\{{\stackrel{\sim }{p}}_i-{\stackrel{\sim }{p}}_1+\frac{{\stackrel{\sim }{p}}_{i+1}-{\stackrel{\sim }{p}}_i}{x_{i+1}-x_i}(x-x_i)\}\hfill & \text{if}{x}_i\le x<x_{i+1}.\hfill \end{array}$$ (2.3)

for i = 1, …, n − 1, and R̃_E(x_n) = (p̃_n − p̃₁)/(1 − p̃₁).

2.2. Model-independent BMDs

We employ the model-independent, isotonic estimator in (2.3) to calculate a similarly model-independent estimator for the BMD: as one would do with any estimated extra risk function, simply invert R̃_E(x) at the specified BMR = π and find the smallest positive solution. That is, take ξ̃_100π = inf{x > 0: R̃_E(x) ≥ π}. Using arguments similar to those employed by BK and Bhattacharya and Lin (2010), we can show that this point estimator possesses asymptotic qualities similar to its simpler cousin based on (2.2). Formally, for convergence we have:

Lemma 2.1

For a given π = BMR ∈ (0, 1) assume the BMD, ξ_100π, is the unique positive solution to R_E(ξ) = π, and also assume there exists some γ > 0 such that

$${\theta }_{\gamma }=\underset{\mid x-{\xi }_{100\pi }\mid \le \gamma }{min}\{R_E^{\prime }(x)\}>0.$$

Let the estimator ξ̃_100π be defined via ξ̃_100π= inf{x > 0: R̃_E(x) ≥ π}. Then ξ̃_100π → ξ_100π a.s. as N* → ∞ and n → ∞, for

$$n\le M\sqrt{N^{\ast }/log(N^{\ast })},$$ (2.4)

where N*= min_i=1,…,n{N_i} and $M=(b-a){\theta }_{\gamma }/\sqrt{\frac{8}{3}(7+{\epsilon }_o)}$ for some ε_o > 0 and some bounded interval [a, b] ⊂ [ξ_100π − γ, ξ_100π + γ] that contains the true ξ_100π.

Asymptotic normality also follows:

Lemma 2.2

For a given π = BMR ∈ (0, 1) assume the risk function R(x) is twice differentiable, its first derivative R′(x) has a lower bound, and its second derivative R″(x) has an upper bound, all in some neighborhood of the true BMD, ξ_100π. As above, let N* = min_i=1,…,n{N_i} and assume the ratio of N* to max_i=1,…,n{N_i} and the ratio of min_{i=1,…,n−1}{x_i+1 − x_i} to max_{i=1,…,n−1}{x_i+1 − x_i} are both bounded away from zero. Then for ξ̃_100π = inf{x > 0: R̃_E(x) ≥ π} and p₁ = Y₁/N₁,

$$\frac{\sqrt{N^{\ast }}({\stackrel{\sim }{\xi }}_{100\pi }-{\xi }_{100\pi })}{\delta ({\widehat{\lambda }}_{\pi })}\stackrel{L}{\to }N\left(0,\frac{{\lambda }_{\pi }(1-{\lambda }_{\pi })}{{[R^{\prime }({\lambda }_{\pi })]}^2}\right)$$

as N*/n^1/4 → ∞, where λ_π = R(0) + π{1 − R(0)}, λ̂_π = p₁ + π(1 − p₁), and

$$\delta (\lambda )=\sum _{i=1}^{n-1}\left\{1+{\left[\frac{R^{-1}(\lambda )-x_i}{x_{i+1}-x_i}\right]}^2\right\}{ℐ}_{{𝔸}_i}(\lambda ),$$

with 𝔸_i = [R(x_i), R(x_i+1)] (i = 1, …, n − 2), 𝔸_n−1 = [R(x_n−1), R(x_n)] and ℐ_𝔸(λ) as the indicator function such that ℐ_𝔸(λ) = 1 if λ ∈ 𝔸 and ℐ_𝔸(λ) = 0 otherwise.

We give brief sketches of the proofs for these lemmas in the Appendix.

Notice that since R̃_E(x) is a form of isotonic, continuous, linear interpolating spline, we can solve for our model-independent estimator ξ̃_100π = inf{x > 0: R̃_E(x) ≥ π} explicitly:

$${\stackrel{\sim }{\xi }}_{100\pi }=\{\begin{array}{ll}{x}_i+\frac{(1-{\stackrel{\sim }{p}}_1)\pi -({\stackrel{\sim }{p}}_i-{\stackrel{\sim }{p}}_1)}{{\stackrel{\sim }{p}}_{i+1}-{\stackrel{\sim }{p}}_i}(x_{i+1}-x_i)\hfill & \text{if}\frac{{\stackrel{\sim }{p}}_i-{\stackrel{\sim }{p}}_1}{1-{\stackrel{\sim }{p}}_1}<\pi <\frac{{\stackrel{\sim }{p}}_{i+1}-{\stackrel{\sim }{p}}_1}{1-{\stackrel{\sim }{p}}_1}\text{for}i=1,\dots ,n-1\hfill \\ x_i\hfill & \text{if}\pi =\frac{{\stackrel{\sim }{p}}_i-{\stackrel{\sim }{p}}_1}{1-{\stackrel{\sim }{p}}_1}\text{for}i=2,\dots ,n.\hfill \end{array}$$ (2.5)

(We discuss below strategies to accommodate the unusual case when ξ = BMR > {p̃_n − p̃₁}/{1 − p̃₁}.)

These results help motivate use of ξ̃_100π in practice. In particular, for risk/regulatory purposes the BMDL can be built from ξ̃_100π as a large-sample, lower, 100(1 − α)% confidence limit on BMD; denote this by ξ_100π. One possible construct is the simple Wald limit ξ_100π = ξ̃_100π − z_ασ̃_π, where z_α is the upper-α critical point from a standard normal distribution and σ̃_π is the estimated large-sample standard error of ξ̃_100π. Notice from Lemma 2.2, however, that computation of σ̃_π depends upon the underlying risk function, creating difficulties if we are unwilling to fully specify the form of R(x) (as is our basic premise). BK encountered a similar predicament for their model-independent $\widehat{\text{ED}}$ estimator based on (2.2), and appealed instead to the bootstrap (DiCiccio and Efron, 1996) for making confidence statements. They found that their nonparametric bootstrap-based inferences could achieve respectable stability for inverse-dose estimation, and so we also consider the bootstrap to build model-independent BMDLs. We explore this in the next section.

3. Model-independent bootstrap BMDLs

Appeal to bootstrapping for construction of confidence limits in risk assessment has seen a number of recent applications, and is becoming an accepted approach for calculating critical risk-analytic quantities such as the BMDL. Most authors employ it under some form of parametric specification, however; cf., e.g., Zhu et al. (2007), Wheeler and Bailer (2008), West et al. (2009), Buckley et al. (2009) and the references therein. Here, we develop a bootstrap-based approach for building BMDLs with our model-independent estimator from (2.5).

In keeping with our general estimation strategy, we assume no parametric form for R(x), although we do continue to impose our continuity and monotonicity assumptions. We also continue to assume a binomial parent distribution for the data. To perform the bootstrapping, we begin with the original proportions Y_i/N_i (i = 1, …, n) and resample each n-dose quantal response B > 0 times. That is, in the bth resample at each x_i we generate the pseudo-random variate $Y_{ib}^{\ast }$ from Bin.(N_i, Y_i/N_i), i = 1, …, n. We then apply the PAV algorithm to the $Y_{ib}^{\ast }$s to yield the monotonized bootstrap sequence

$${\stackrel{\sim }{p}}_{ib}^{\ast }=\underset{1\le u\le i}{max}\underset{i\le v\le n}{min}\frac{{\sum }_{j=u}^v{Y}_{jb}^{\ast }}{{\sum }_{j=u}^v{N}_j}.$$

From these we produce an isotonic bootstrap estimate of the extra risk via (2.3). Denote this as ${\stackrel{\sim }{R}}_{E,b}^{\ast }(x)$. We then apply (2.5) to find a bootstrapped ${\stackrel{\sim }{\xi }}_b^{\ast }$. (For simplicity here we suppress the BMR subscript π on ξ̃, but it is understood that all these operations are conducted for a fixed, pre-specified π = BMR.) Following suggestions by Moerbeek et al. (2004) and West et al. (2009) for the number, B, of bootstrap resamples, we work with B = 2000.

Two special cases occur when Y_i = 0 or when Y_i = N_i at any i. If so, the resampling will always produce $Y_{ib}^{\ast }=0$ or $Y_{ib}^{\ast }=N_i$, respectively, generating no new bootstrap information (Bailer and Smith, 1994). Various remedies for this are possible (Buckley et al., 2009); in keeping with our nonparametric strategy, we refrain from applying any parametric-model constructs. Instead, we add a small constant ε > 0 to the numerator and twice it to the denominator of the observed proportions Y_i/N_i. That is, whenever Y_i = 0 or Y_i = N_i, we replace Y_i/N_i with {Y_i + ε}/{N_i + 2ε}. This shrinks the proportion away from 0 or from 1 and towards $\frac{1}{2}$. (Shrinkage towards any fixed value is admittedly arbitrary, and we chose $\frac{1}{2}$ here simply as an objective, default, shrinkage target. If in practice a different target were available based on experiment- or stimulus-specific considerations, it could be easily employed instead.) We experimented with a variety of possible values for ε, and found that only a slight amount of shrinkage was needed to stabilize the bootstrap calculations. We settled on $\epsilon =\frac{1}{4}$, i.e., whenever Y_i = 0 or Y_i = N_i, replace Y_i/N_i with $\{Y_i+\frac{1}{4}\}/\{N_i+\frac{1}{2}\}$.

To find a lower 100(1 − α)% confidence limit on the BMD, we collect the ${\stackrel{\sim }{\xi }}_b^{\ast }$s together to produce a bootstrap distribution for ξ̃. From this, we apply the well-known percentile method (DiCiccio and Romano, 1988): order the B bootstrapped ${\stackrel{\sim }{\xi }}_b^{\ast }$ values into ${\stackrel{\sim }{\xi }}_{(1)}^{\ast }\le {\stackrel{\sim }{\xi }}_{(2)}^{\ast }\le \cdots \le {\stackrel{\sim }{\xi }}_{(B)}^{\ast }$ and report the lower αth percentile: ${\underset{\_}{\xi }}_{100\pi }-{\stackrel{\sim }{\xi }}_{(\alpha B)}^{\ast }$. This represents a model-independent, nonparametric BMDL for use in risk assessment practice.

4. BMDL performance evaluation

4.1. Simulation design

To investigate the performance of our model-independent BMD, ξ̃_100π, and BMDL, ξ_100π, in finite-sample settings we conducted a short series of Monte Carlo simulations. We set the BMR to the standard default level π = 0.10 (U.S. EPA, 2012), and for ξ_100π = ξ₁₀ operated at 95% nominal coverage. The design was chosen to involve either four dose levels, x = 0, 0.25, 0.5, 1.0, corresponding to a standard design in cancer risk experimentation (Portier, 1994), or six dose levels, x = 0, 0.0625, 0.125, 0.25, 0.50, 1.0, expanding on the four-dose geometric spacing. We also included a modified six-dose design x = 0, 0.1, 0.2, 0.4, 0.6, 1.0 that gives less focus to doses near x = 0. Equal numbers of subjects, N_i = N, were taken per dose group. We fixed the total sample size at (or as near as possible to) ΣN_i = 100, 200, 400, or 4000, so that the per-dose sample sizes were N = 25, 50, 100, or 1000 for the four-dose design and N = 16, 33, 66, or 666 for the six-dose designs.

For the underlying dose-response patterns we chose three popular quantal-response models from cancer risk assessment (Schlosser et al., 2003):

• constrained multi-stage, $R(x)=1-exp\{-{\sum }_{j=0}^k{\beta }_j{x}^j\}$, where β_j ≥ 0 (j = 0, 1, …, k);

• log-probit, R(x) = γ₀ + (1 − γ₀)Φ(β₀ + β₁ ln[x]), where γ₀ ∈ (0, 1); or

• Weibull, R(x) =γ₀ + (1 − γ₀)(1 − exp{−e^β₀x^β₁}), where γ₀∈ (0, 1) and β₁ ≥ 1.

(Here Φ(·) is the standard normal c.d.f.) For the constrained multi-stage specification we set k = 2 to produce a comparable three-parameter model. Note that with the log-probit we define R(0) = γ₀.

To set the parameters for each model, we fixed R(x) at the three doses x = 0, $\frac{1}{2}$, 1 and solved for the three unknowns. Based on typical patterns seen in cancer risk assessment (Bailer and Smith, 1994; Buckley and Piegorsch, 2008), we set risks at x = 0 between 1% and 30%, and increased the other risk levels to produce a variety of (strictly) increasing forms ending with high-dose risks at x = 1 between 10% and 90%. The actual specifications and resulting parameter configurations for the various models are given in Table 1; we also include the corresponding values of ξ₁₀. For each configuration (labeled A–F), 2000 individual, pseudo-binomial, data sets were simulated to produce point estimates ξ̃₁₀.

Table 1.

Models and configurations (including true BMD, ξ₁₀, at BMR = 0.10) for the Monte Carlo evaluations.

	Configuration:	A	B	C	D	E	F
Constraint:	R(0) =	0.01	0.01	0.10	0.05	0.30	0.10
	$\text{R}(\frac{1}{2})=$	0.04	0.07	0.17	0.30	0.52	0.50
	R(1) =	0.10	0.20	0.30	0.50	0.75	0.90
Model	Parameters
Constrained multi-stage	β0	0.0101	0.0101	0.1054	0.0513	0.3567	0.1054
	β1	0.0278	0.0370	0.0726	0.5797	0.4796	0.1539
	β2	0.0675	0.1761	0.1788	0.0622	0.5501	2.0433
	ξ10	1.0602	0.6756	0.5911	0.1783	0.1818	0.1925
Log-probit	γ0	0.0100	0.0100	0.1000	0.0500	0.3000	0.1000
	β0	−1.3352	−0.8708	−0.7647	−0.0660	0.3661	1.2206
	β1	0.7808	0.9794	0.9456	0.8189	1.2261	1.9626
	ξ10	1.0711	0.6575	0.5789	0.2267	0.2608	0.2794
Weibull	γ0	0.0100	0.0100	0.1000	0.0500	0.3000	0.1000
	β0	−2.3506	−1.5460	−1.3811	−0.4434	0.0292	0.7872
	β1	1.6310	1.7691	1.6341	1.0716	1.4483	1.9023
	ξ10	1.0634	0.6716	0.5874	0.1852	0.2072	0.2025

From Lemma 2.1 we expect ξ̃_100π → ξ_100π in sufficiently large samples. To study the pattern of this convergence we calculated the median value of ξ̃₁₀ from the 2000 simulated data sets at each model parameterization in Table 1, and subtracted from this the corresponding, true value of ξ₁₀ to produce an estimate of median bias.

To construct the 95% BMDL, B = 2000 bootstrap samples were generated from each simulated data set as described in §3, and ξ₁₀ was taken as the lower 5th percentile of this bootstrap collection. Coverage was then evaluated as the event ξ₁₀ ≤ ξ₁₀. (Notice that the approximate standard error of the empirical coverage proportion over the original 2000 simulated data sets is $\sqrt{(0.05)(0.95)/2000}=0.005$.) All of our calculations were performed with the R statistical programming environment (R Development Core Team, 2011).

4.2. Infinite BMDs

An unusual artifact we uncovered while conducting our Monte Carlo computations was that for some dose-response patterns, calculation of a nonparametric BMD can occasionally break down. One obvious case is when the BMR is set too high, so that the isotonic extra risk estimator never reaches the desired benchmark response over the range of the doses, i.e., R̃_E(x) < π = BMR, ∀x ∈ [0, x_n]. If so, there is no solution to the BMD-defining relationship R̃_E(ξ) = π. Of course, if the extra risk were estimated using a fully parametric (non-decreasing) function one could simply extrapolate the function outside of the dose range to acquire the solution. To imitate this strategy with our nonparametric estimator, suppose that R̃_E(x) from (2.3) is strictly increasing along its final segment between x_n−1 and x_n. Then if R̃_E(x) < π ∀x ≤ x_n, we simply extend this final line segment past x_n until it intersects with the horizontal line at π, and solve for the ξ̃_100π at that intersection point. While admittedly one should apply any such extrapolations past the range of the data with great caution, this strategy nonetheless allows us to report an objective estimate for the BMD in this unusual case.

The extrapolative estimate for the BMD will still fail if the final line segment from (2.3) is flat, i.e., if p̃_n−1 = p̃_n (or when p̃_n−2 = p̃_n−1 = p̃_n, etc.). When this occurs, the data are in effect telling us that the nonparametrically estimated dose response cannot attain the BMR, no matter how large x grows. Correspondingly, in such an instance we simply drive the estimator ξ̃_100π to ∞, or, equivalently, report it as undefined.

Operationally, when any ‘infinite’ ξ̃_100π was observed in our bootstrap procedure, we set the estimate equal to machine infinity. If this occurred for more than 100(1 − α)% of the bootstrapped ξ̃*s, we defined ξ_100π itself as ‘infinite’, and viewed this as failure to cover the true ξ_100π.

4.3. Simulation results

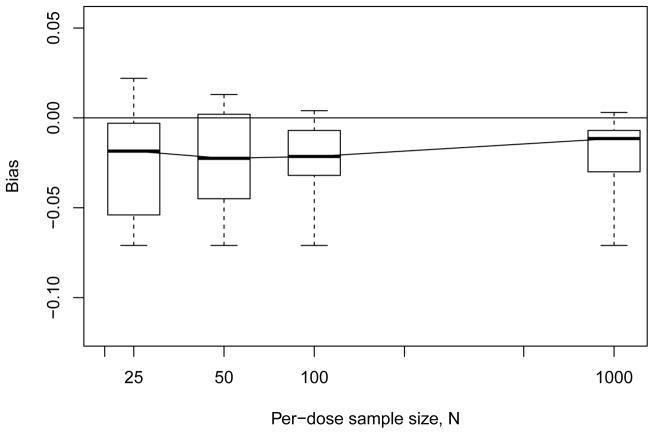
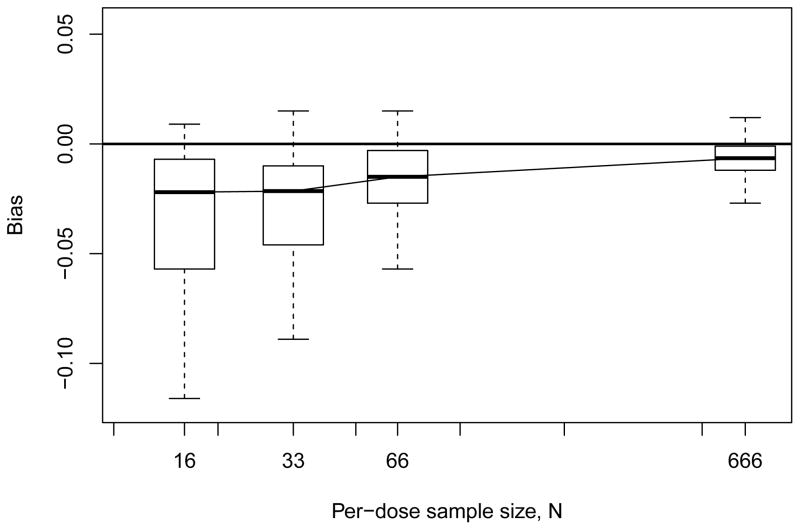
We summarize the results from our Monte Carlo study in a series of figures. Complete details are available from the authors, or in Xiong (2011). Recall that we fix BMR = 0.10 and for the BMDL we operate at nominal 95% coverage. We begin with small-sample bias in the estimator: Figure 1 displays summary boxplots of the median biases observed with the four-dose design across all model configurations, plotted as a function of per-dose sample size N. We see that a small-but-consistent negative bias is evidenced, even as N grows large, although variation in the bias decreases at larger sample sizes. Figure 2 displays the corresponding results for the geometric six-dose design, where the negative bias is still evidenced; however, for large N the bias is smaller and has tighter variation. (Results for the modified six-dose design – not shown – were roughly similar.) On a relative scale the bias is not exceptional and in fact is not wholly unexpected: bias can be a recurring issue with isotonic regression estimators (Wright, 1978; Zhao and Woodroofe, 2012). Here, all our simulation models are convex over the dose range and thus more often than not will produce convex dose-response patterns in the p̃_is. Linearly interpolating between these may lead to slight overestimation of the extra risk, which would translate as underestimation of ξ_100π. While easy to calculate, the linear interpolator in (2.3) can restrict the method’s ability to capture nonlinearity in the dose response, especially when n is small. We discuss some adjustments for this in §6.

Figure 1.

Median empirical bias from Monte Carlo evaluations for model-independent BMD estimator ξ̃₁₀ with geometric four-dose design. Horizontal line indicates zero bias.

Figure 2.

Median empirical bias from Monte Carlo evaluations for model-independent BMD estimator ξ̃₁₀ with geometric six-dose design. Horizontal line indicates zero bias.

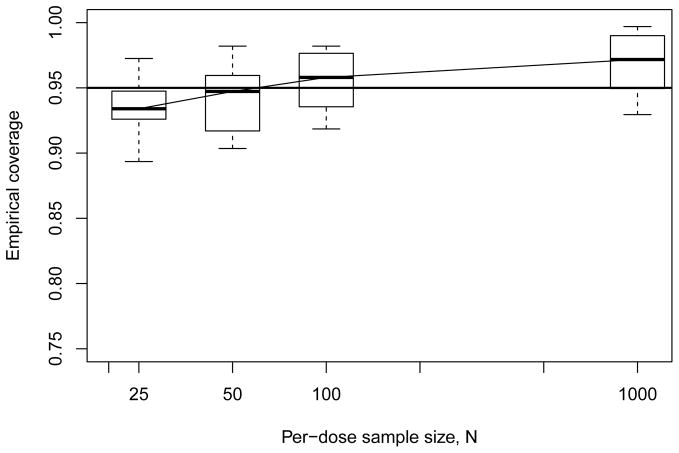
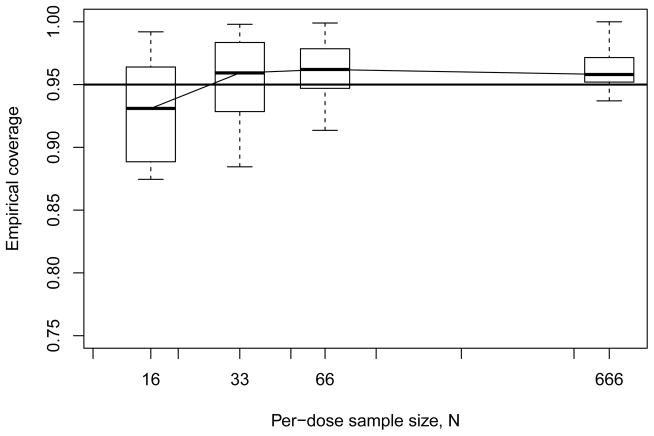
Moving to our results for empirical coverage, we next display summary boxplots of the coverages recorded across all model configurations as a function of per-dose sample size N. Figure 3 presents the results for the geometric four-dose design: we see median coverages center near the nominal level, and generally lie within Monte Carlo sampling variability of nominal, although a pattern of slight undercoverage is observed at the lower sample sizes.

Figure 3.

Empirical coverage rates from Monte Carlo evaluations for model-independent bootstrap BMDL ξ₁₀ with geometric four-dose design. Horizontal line indicates 95% nominal coverage level.

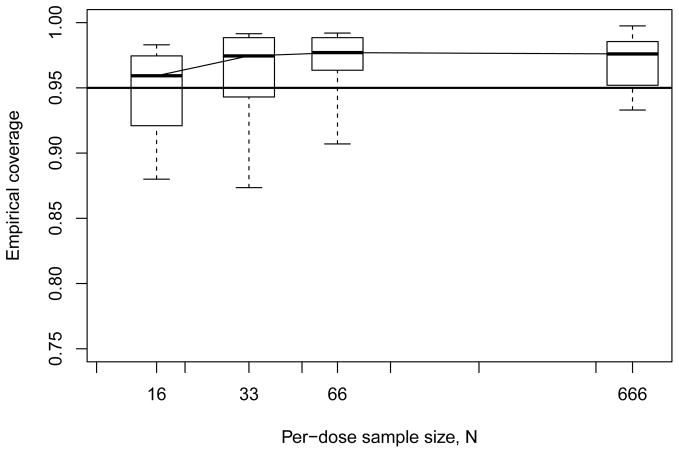
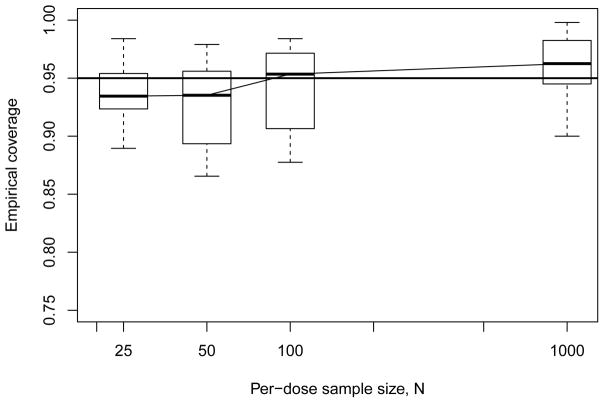
Figure 4 displays results for the geometric six-dose design. The coverage patterns appear somewhat more stable than those in Figure 3, although there is also a slight skew towards undercoverage. Variability in the coverage rates is again greater at smaller sample sizes; we found that this was most common with the constrained (k = 2) multi-stage model. Decreasing the per-dose sample sizes while increasing the number of doses appears to yield greater stability at larger sample sizes, but the effect appears to reverse when sample sizes drop.

Figure 4.

Empirical coverage rates from Monte Carlo evaluations for model-independent bootstrap BMDL ξ₁₀ with geometric six-dose design. Horizontal line indicates 95% nominal coverage level.

Results for the modified 6-dose design appear in Figure 5. Here, rise in variation is seen again at small sample sizes, similar to that in Figure 4, but the pattern of median coverage is more similar to Figure 3. As perhaps expected when the design deemphasizes doses near to zero, more variation in the coverage rates and more cases of below-nominal coverage occurred, particularly at small sample sizes. The effect was, however, not dramatic.

Figure 5.

Empirical coverage rates from Monte Carlo evaluations for model-independent bootstrap BMDL ξ₁₀ with modified six-dose design. Horizontal line indicates 95% nominal coverage level.

On balance, our simulation results indicate stable large-sample coverage characteristics for the model-independent, bootstrap limit ξ_100π at the standard level of π = BMR = 0.10. Slight undercoverage is evidenced with smaller sample sizes in selected instances, suggesting that the method should be applied when sufficient data are available to help validate its asymptotic motivation.

Given the consistent, if slight, negative bias exhibited by the isotonic estimator ξ̃_100π, we also considered use of a more complex bootstrapping procedure that can adjust for such bias: the bias-corrected, accelerated (BCa) bootstrap. The BCa approach augments the standard percentile method: it includes a bias correction along with an ‘acceleration’ parameter which are used in tandem to adjust the percentile level for determining ξ_100π (DiCiccio and Efron, 1996). As above, we set the nominal confidence level to 95% and took π = BMR = 0.10. We evaluated coverage provided by the BCa approach using ξ̃_100π as the point estimator, focusing on the standard four-dose design. Not surprisingly, the resulting BMDLs exhibited slightly tighter empirical coverages at smaller sample sizes and with the more spread-out, shallow response configurations ‘A’ and ‘B’. (Generally speaking, a more-shallow response will yield a higher BMD.) Improvements were not seen across all configurations studied, however, and the percentile method operated about as well as the BCa for larger sample sizes. [Details are available in Xiong (2011).] From this, we can recommend use of BCa-based BMDLs when samples sizes are very small and/or for shallow response patterns; however, both methods appear to operate adequately in the majority of cases we studied.

We also conducted Monte Carlo coverage evaluations for the case of BMR = 0.01. While less common, this smaller BMR may be employed when sufficient data are available to support inferences at extreme low doses (Kodell, 2009). Our results [not shown; details are available in Xiong (2011)] were generally similar to those seen above; in particular, the coverage rates again converged to the nominal 95% level as the sample size increased. At the lowest sample sizes, however, they appeared much more variable, and often in the direction of undercoverage. We encountered a few empirical coverage rates that dropped below 60% with some of the low-response-rate models, especially configurations ‘A’ and ‘B’. This is, in fact, consistent with established benchmark experience: when response rates are very small at low doses, and if the N_is do not counter by being adequately large, insufficient information will be available to perform effective inferences if the BMR is set very low. We therefore urge caution in practice when employing these methods with very small sample sizes, particularly under very shallow or low-response patterns.

5. Numerical example: Formaldehyde carcinogenesis in laboratory animals

To illustrate how the isotonic BMD equations come together when analyzing quantal data, consider the following example on the carcinogenic potential of formaldehyde, CH₂O. Formaldehyde is a well-known industrial compound, occupational and environmental exposures to which are extensive. Schlosser et al. (2003) reported on nasal squamous cell carcinomas observed in laboratory rats after chronic, two-year, CH₂O inhalation exposure. Because it is a gas, the CH₂O exposure measure, x, is actually a concentration (in ppm) here. Thus technically we will compute benchmark concentrations (BMCs) based on the quantal carcinogenicity data. Six CH₂O concentrations were studied: x = 0.0, 0.7, 2.0, 6.0, 10.0, and 15.0 ppm. Since intercurrent mortality often occurs in such chronic-exposure studies, the final tumor incidences were adjusted for potential differences in animal survival. Table 2 lists the survival-adjusted quantal responses provided in Schlosser et al. (2003).

Table 2.

Formaldehyde carcinogenicity data from Schlosser et al. (2003).

Exposure conc. (ppm), xi	0.0	0.7	2.0	6.0	10.0	15.0
Adjusted tumor incidence, Yi	0	0	0	3	21	150
Animals at risk, Ni	122	27	126	113	34	182

Of interest is calculation of the BMC (and more importantly, a 95% lower confidence limit, BMCL) to help inform risk characterization of this potential carcinogen. We operate at BMR = 0.10. To illustrate application of our model-independent methodology, we assume only that the true dose response is continuous and monotone non-decreasing over x ≥ 0. From Table 2 the observed response is already non-decreasing, so the per-concentration PAV estimates p̃_i are simply the observed proportions: p̃₁ = p̃₂ = p̃₃ = 0, ${\stackrel{\sim }{p}}_4=\frac{3}{113},{\stackrel{\sim }{p}}_5=\frac{21}{34}$, and ${\stackrel{\sim }{p}}_6=\frac{150}{182}$. Constructing the isotonic extra risk estimator from Equation (2.3) and setting it equal to BMR = 0.10 produces the model-independent estimate ξ̃₁₀ = 6.50 ppm.

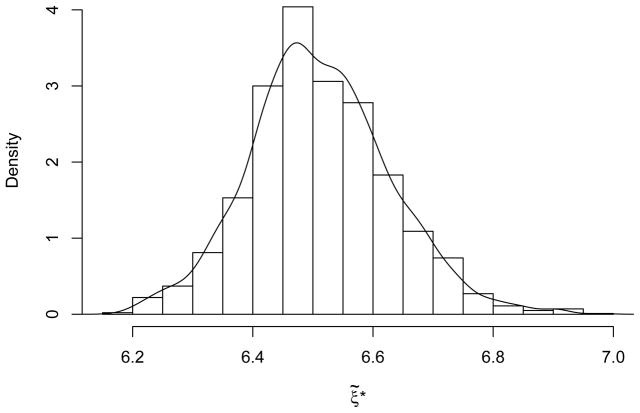
For the BMCL we apply the percentile bootstrap as described in §3. Generating B = 2000 resamples from the original data, we produced the bootstrap distribution displayed in Figure 6. (No occurrences of infinite ξ̃*s were observed among the bootstrap resamples.) Our 95% BMCL is the lower 5th percentile from this distribution: ξ₁₀ = 6.33 ppm. By comparison, Schlosser et al. (2003) reported a BMC₁₀ of 6.90 ppm with corresponding 95% BMCL₁₀ = 6.25 ppm under the log-probit model (considered best able to describe the tumor data via a “statistical goodness-of-fit criterion”). Both sets of values rest in similar ranges, and provide comparable points of departure for conducting further risk-analytic calculations on formaldehyde carcinogenicity. We find that our model-independent approach operates similarly to established parametric analyses for these data, while also freeing the risk assessor from uncertainties about the quality of any parametric assumptions made to support the benchmark computations.

Figure 6.

Probability histogram (and overlaid density estimator) of bootstrap distribution for ${\stackrel{\sim }{\xi }}_{10}^{\ast }$with formaldehyde carcinogenicity data from Table 2.

6. Discussion and extensions

Herein, we consider a model-independent, nonparametric method for estimating benchmark doses (BMDs) in quantitative risk analysis. Placing emphasis on cancer risk assessment, our approach estimates the BMD without the need to specify a particular parametric dose-response model. Environmental risk analysts can apply our results to construct inferences for the BMD, avoiding concerns over parametric model adequacy and expanding past the many, varied parametric models seen in practice.

Of course, some caveats and qualifications are in order. Focus herein has been on introducing the model-independent estimator ξ̃_100π and exploring its asymptotic properties. We recognize that more complete evaluations are needed to study the operating characteristics of ξ̃_100π and of the corresponding BMDL ξ_100π. The three model forms employed in our simulation study from §4 were motivated primarily from our own experience with them in cancer risk assessment and from their favored use by Schlosser et al. (2003). As we presented them, however, these three models do not differ greatly, even when studied across the various parameterizations in Table 1. Thus we do not wish to leave readers with a sense that model choice is unimportant. Indeed, many possible models have been proffered for use with quantal carcinogenicity data, and our isotonic method’s capabilities under a fuller range of possible dose-response patterns/shapes are open for further study.

Extensions to more-general nonparametric estimation of shape-constrained regression functions may also be possible, where information on the shape of the dose response can be used to improve quality of the estimation process. Indeed, as noted earlier, the linear interpolator in (2.3) restricts the method’s ability to capture nonlinearity in the observed response. This is particulary true when the dose spacings are sparse and wide, as is common in many cancer risk assessment studies. (Often, as few as n = 3 doses/concentrations are employed, which spreads the placement even farther apart. We do not recommend application of our techniques to such sparse designs.) For a relatively simple adjustment, consider the following, smoothed extension: start by creating an expanded set of dose values {x̌_j} over which to apply the isotonic estimator in (2.2). Between each original, adjacent dose pair x_i < x_i+1 (i = 1, …, n − 1) add two additional ‘pseudo-doses’ and space each pair of pseudo-doses equidistant between their bounding, original doses. Thus between x_i = x̌_3i−2 and x_i+1 = x̌_3i+1 take ${\stackrel{⌣}{x}}_{3i-1}=x_i+\frac{1}{3}(x_{i+1}-x_i)$ and ${\stackrel{⌣}{x}}_{3i}=x_{i+1}-\frac{1}{3}(x_{i+1}-x_i)$, i = 1, …, n − 1. Notice that this set of J = 3n − 2 expanded doses is again ordered: x̌₁ < ··· < x̌_J. Next, compute the estimated isotonic risks from (2.2) at every x̌_j; call these p̌_j = R̃(x̌_j), j = 1, …, J. This gives an expanded isotonic set of n responses and 2(n − 1) ‘pseudo-responses’ from which to construct a smoothed risk:

$$\stackrel{⌣}{R}(x)=\frac{{\sum }_{j=1}^J{\stackrel{⌣}{p}}_{j}K\left(\frac{x-{\stackrel{⌣}{x}}_j}{h}\right)}{{\sum }_{j=1}^{J}K\left(\frac{x-{\stackrel{⌣}{x}}_j}{h}\right)},$$ (6.1)

where K(·) is a univariate kernel function and h is a global bandwidth for the smoother. We choose K(·) as the standard Gaussian kernel and select h via generalized cross-validation (Green and Silverman, 1994, §3.3). Notice that (6.1) is just the standard Nadaraya-Watson kernel smoother (Opsomer, 2002), with monotonicity imposed on the p̌_js. Also, since the Gaussian kernel K(·) is log-concave Ř(x) will be monotone (Mukerjee, 1988), as desired. From this, the smoothed extra risk is simply Ř_E(x) = {Ř(x) − Ř(0)}/{1 − Ř(0)}, and at a fixed π = BMR we can invert this to achieve the smoothed isotonic estimator ξ̌_100π = inf{x > 0: Ř_E(x) ≥ π}. To find the BMDL, ξ̌_100π, we again apply the percentile bootstrap method from §3.

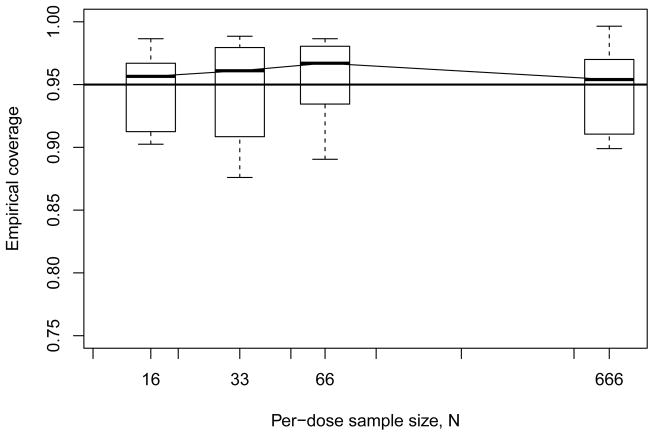
To briefly explore how this smoothed construction compares with our simpler, linearly-interpolated BMDL ξ_100π, we returned to our simulation study in §4, and applied the bootstrap/smoothed strategy to our simulated data. For simplicity, we operated at only BMR = 0.10 and considered just the four- and six-dose geometric designs. Nominal coverage was again set to 95%. Figures 7 and 8 display summary boxplots of the resulting coverage results, for comparison with Figures 3 and 4, respectively. We see roughly similar patterns at n = 4 doses, although coverage with the smoothed BMDLs appears to be more variable. By contrast, with the geometric six-dose design the smoothed BMDL exhibits empirical coverages closer to nominal. Upon closer inspection, we found that the smoothing in Ř_E(x) tended to bow in the extra risks slightly closer to x = 0. This was independent of the true underlying model, and consequently led to slightly lower BMDLs than those produced from the linear interpolator, particulary with the four-dose design (cf. the slightly larger undercoverage seen in Figure 7). For example, applying this smoothing strategy to the formaldehyde carcinogenicity data in Table 2 produces a slightly smaller point estimate and bootstrap BMDL: ξ̌₁₀ = 6.27 ppm and ξ̌₁₀ = 6.08 ppm, respectively. (The smoothing operation may have particular influence with these data, since we have three consecutive zero responses.) In any case, for achieving our goal to recover greater curvature in the estimated dose response, this limited investigation suggests that further development of kernel smoothers may prove advantageous in expanding the nonparametric benchmark approach.

Figure 7.

Empirical coverage rates from Monte Carlo evaluations for model-independent bootstrap BMDL₁₀ based on smoothed isotonic interpolator under geometric four-dose design. Horizontal line indicates 95% nominal coverage level.

Figure 8.

Empirical coverage rates from Monte Carlo evaluations for model-independent bootstrap BMDL₁₀ based on smoothed isotonic interpolator under geometric six-dose design. Horizontal line indicates 95% nominal coverage level.

It is also of interest to study in greater depth how our estimators’ large-sample features manifest themselves in small samples. Our asymptotic results require both the number of doses n and the per-dose sample sizes N_i to grow large. In practice, however, one often encounters resource constraints that restrict one or both of these factors. As suggested above, we can gain greater information about the pattern of dose response, and therefore about ξ_100π, if we increase the number of doses. Can increasing n to, say, 10 doses improve the small-sample operating characteristics of the BMDL if resource constraints or animal-welfare concerns force the N_is down to perhaps only 10 subjects/dose? [Or, even lower? The OECD runs its avian toxicity test with n = 10 doses and as little as a single bird per dose, i.e., N = 1! We should note that their recommended design includes a sequential sampling scheme that can help increase power and estimation accuracy (OECD, 2010).] For example, Bhattacharya and Lin (2011) were able to show that an adaptive nonparametric estimator based on inverting (2.2) proved competitive with more doses but few observations/dose; how this extends to estimation with extra risk functions is yet another open question. We are studying all of these inter-related issues for model-independent benchmark analysis, and hope to report on them in a future manuscript.

Appendix

In this Appendix we give proofs for the asymptotic results from Lemmas 2.1 and 2.2. They follow similar outlines as their counterparts based on R̃(x) in BK and Bhattacharya and Lin (2010), hence we provide only brief sketches here.

Proof of Lemma 2.1 (Sketch)

The core approach of our result is to establish that ξ̃_100π and ξ_100π both lie in an interval such that |ξ̃_100π − ξ_100π| shrinks to zero as n → ∞ and N* → ∞, and where (2.4) is satisfied. To do so, one shows that under these conditions p̃_i converges to R(x_i) uniformly for all i, and from this that {p̃_i − p̃₁}/{1 − p̃₁} converges to R_E(x_i). Since the p̃_is are monotone non-decreasing, it follows that linearly interpolating the quantities {p̃_i − p̃₁}/{1 − p̃₁} as in (2.3) produces an estimator that converges a.s. to the extra risk at dose x for all $x\in \left[x_{\text{o}},x_{\text{o}}^{\prime }\right]$, where $0<{\varphi }_{\text{o}}=R_E(x_{\text{o}})<{\varphi }_{\text{o}}^{\prime }=R_E(x_{\text{o}}^{\prime })<1$, provided R(0) ≥ ϕ_o. [If R(0) = 0, then the problem reduces to the setting in BK.] Viewing ξ_100π as the inverse of the strictly increasing extra risk function with a derivative bounded away from zero, this is a continuous function of π = BMR, as is ξ̃_100π. One then shows that if ξ̃_100π is found by inverting R̃_E(x), |ξ̃_100π − ξ_100π| will be bounded above by a value that itself approaches zero, and hence ξ̃_100π will converge to ξ_100π, uniformly, with probability one, on the interval $\left[{\varphi }_{\text{o}},{\varphi }_{\text{o}}^{\prime }\right]$. This attains an outcome complementary to that achieved by BK, extending their results to estimation of R_E(x) and ξ_100π via (2.3) and (2.5), respectively.

Proof of Lemma 2.2 (Sketch)

The proof of asymptotic normality for ξ̃_100π extends arguments given by Bhattacharya and Lin (2010). Fix π = BMR ∈ (0, 1) and denote the associated, true BMD at that π as ξ_100π, satisfying {R(ξ_100π) − R(0)}/{1 − R(0)} = π. Recognize that for a given value of R(0), R_E(x) is a monotone function of R(x). In terms of R(·), we can define ξ_100π via R(ξ_100π) = R(0) + π{1 − R(0)}; the corresponding PAV-based estimator ξ̃_100π satisfies R̃(ξ̃_100π) = p₁ + π(1 − p₁), where R̃ is given in (2.2). We have then essentially reframed the problem in terms of the original risk function, as in BK and Bhattacharya and Lin (2010). As BK showed, as both N* and n approach ∞, and with R(x) strictly increasing in a neighborhood of ξ_100π, the monotonized MLE will collapse to the usual MLE, i.e., one may view p̃_i → p_i (i = 1, …, n). Now take advantage of the independence among the p_is and, under the conditions listed in Lemma 2.2, apply Theorem 2.3(a) from Bhattacharya and Lin (2010), which specifies the asymptotic normality of estimators based on inverting the PAV-estimated risk function. Here, conditional on p₁ we apply their Theorem to ξ̃_100π and achieve the result given in the statement of the Lemma.